Inverting the Dimensional Hierarchy: Advocating for a 4D-Native Framework for Quantum Geometry

1. Introduction

The quest for a quantum theory of gravity is beset by deep mathematical conundrums. Among the most striking is the unique wildness of smooth (diffeomorphism) structures in dimension four. While in dimensions $d=1,2,3$ a topological manifold admits at most one smooth structure, and in dimensions $d\ge 5$ the possible smooth structures are finite in number and classifiable by algebraic methods, dimension four is utterly different: the topological manifold ${\mathbb{R}}^4$ admits uncountably many distinct, non-diffeomorphic smooth structures, the so-called exotic${\mathbb{R}}^4$s, noted as $\mathcal{E}\left({\mathbb{R}}^4\right)$[1]. This has direct implications for quantum gravity as a gravitational path integral that purports to sum over all geometries must, in 4D, somehow also sum over this unmanageably vast and wild space of smooth structures [2,3]. The measure problem thus becomes not merely technical but foundational.

A central, shared insight among physicists grappling with quantum gravity is that the classical, continuous 4D spacetime of General Relativity is likely not a fundamental entity. The profound difficulties encountered in constructing a theory for our 4-dimensional universe are seen by many as a signal that this familiar arena "ceases to exist as an objective physical reality" at the Planck scale [4]. The specific challenges, however, manifest differently across research programs.

In the framework of Loop Quantum Gravity (LQG), championed by C. Rovelli, spacetime is not a smooth manifold but a structure that emerges from more fundamental quantum entities. The theory posits that space is quantized, woven from a discrete network of interconnected loops or spin networks [5]. From this perspective, the 4D continuum is a coarse-grained, thermodynamic approximation of this underlying quantum geometry. Consequently, the primary challenge is not to quantize a pre-existing 4D metric but to rigorously demonstrate how classical General Relativity and its smooth spacetime emerge from this pre-geometric substrate. The difficulty of 4D quantum gravity, in this view, stems from the need to bridge these two radically different descriptions of reality.

From the String Theory perspective, articulated by figures like L. Susskind, the difficulty has a different character. String theory naturally lives in ten or eleven dimensions and finds its most mathematically consistent formulations in spacetimes with properties unlike our own (notably, anti-de Sitter space). Susskind has noted the acute problem that "we live in the wrong kind of world to be described by string theory" in its currently understood forms [6]. The core challenge is that the theory relies on a stable, high-dimensional background spacetime for its formulation, a feature at odds with the dynamical, background-independent spirit of General Relativity. Formulating string theory in a realistic, 4-dimensional, expanding (de Sitter) universe has proven to be an immense and possibly foundational obstacle, highlighting a tension between the theory’s mathematical elegance and physical applicability.

Philosophers of physics, such as J. Butterfield and C. Isham, synthesize these technical struggles into a broader epistemological point. They argue that the persistent failure to reconcile quantum theory with 4D gravity suggests the need for a radical conceptual shift, where one must quantize structures other than the metric or treat spacetime itself as a secondary, phenomenological concept [4]. The collective viewpoint emerging from these diverse schools is that the intractability of quantum gravity in four dimensions is not merely a technical hurdle but a profound indication that our most basic ontological category, a 4-dimensional spacetime continuum, must be re-examined or abandoned at the fundamental level.

This paper advocates a paradigm shift. We contend that the wildness of $\mathcal{E}\left({\mathbb{R}}^4\right)$ is not a feature of physical spacetime but an artifact of applying a mathematical formalism (differential topology) that is poorly adapted to the dimensionality of our universe. Our core thesis is:

The correct mathematical framework for quantum spacetime is not the one that is most elegant for the mathematician studying all dimensions, but the one that is uniquely stable, well-posed, and simple for the physicist in 3+1 dimensions.

We formalize this as the Inversion Principle: the dimensional hierarchy of complexity should be flipped, making 4D the axiomatically simplest case.

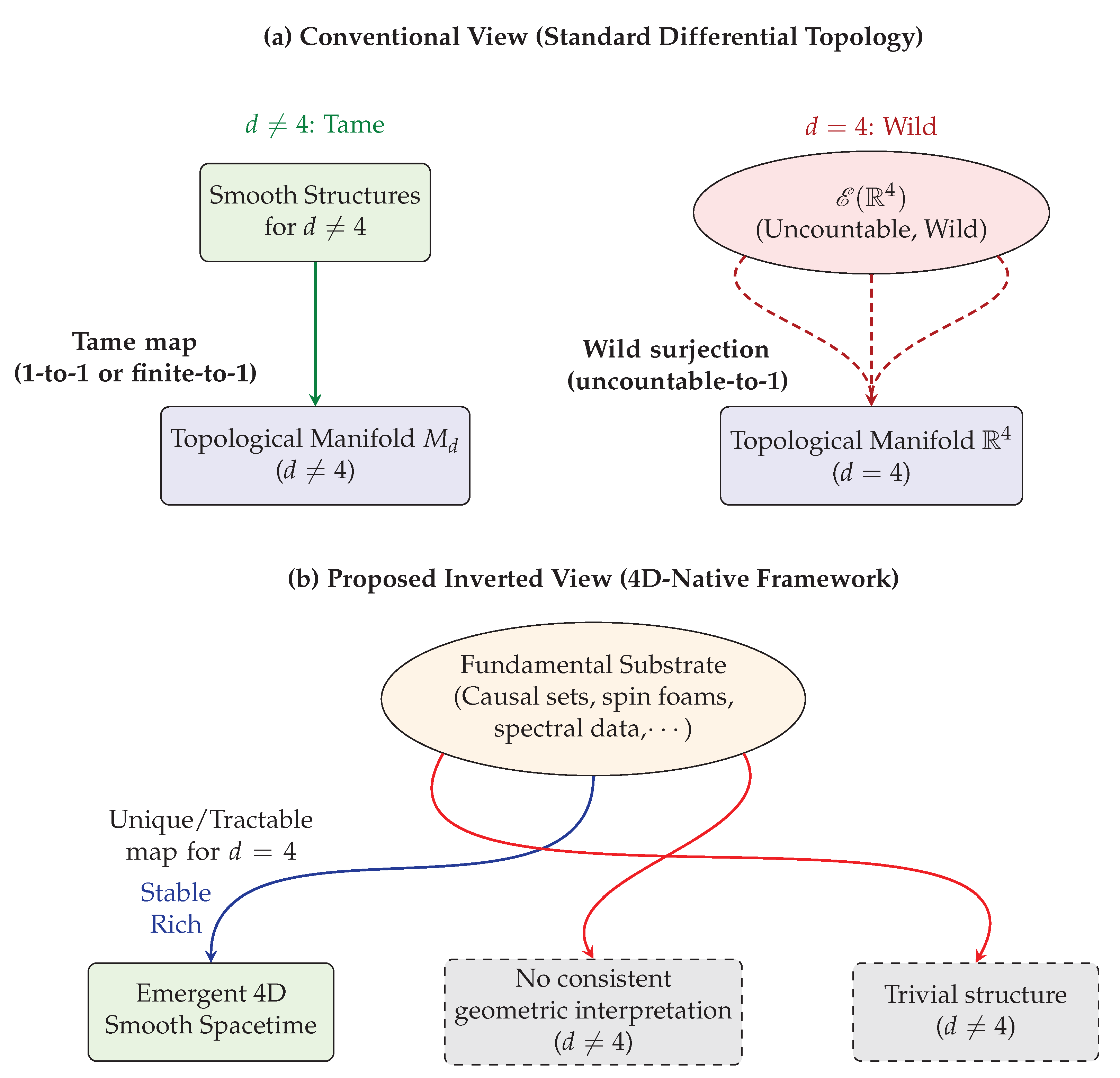
2. The Problem: Wildness of 4D Smooth Structures

Let $\mathcal{T}\left({\mathbb{R}}^4\right)$ denote the (unique) topological 4-manifold homeomorphic to Euclidean space. Let $\mathcal{E}\left({\mathbb{R}}^4\right)$ denote the set of smooth structures on $\mathcal{T}\left({\mathbb{R}}^4\right)$ up to diffeomorphism. The known results create a stark contrast such that,

• For $n\ne 4$, ${\mathbb{R}}^n$ has a unique smooth structure [7].
• For $n=4$, $\mathcal{E}\left({\mathbb{R}}^4\right)$ is an uncountably infinite set, and its elements exhibit a wild partial order under smooth embeddings [1]. No reasonable moduli space or topological structure can be placed on $\mathcal{E}\left({\mathbb{R}}^4\right)$; it is a logically complex, unclassifiable collection (cf. Figure 1a).

The root of this wildness is the failure of the Whitney trick in 4D, which severs the link between topological data and smooth realizability that exists in higher dimensions. For quantum gravity, this means the formal path integral

$${\mathcal{Z}}_{\mathrm{QG}}=\sum _{\left\{\mathrm{topologies}\right\}}\sum _{\left\{{\mathcal{C}}^{\infty }\mathrm{structures}\Sigma \right\}}{\int }_{\mathcal{M}\left(\Sigma \right)}\mathcal{D}g{e}^{i{S}_{\mathrm{EH}}\left[g\right]/\hslash }$$

involves a sum over an uncountable, wild set $\mathcal{E}\left({\mathbb{R}}^4\right)$ for which no measure can be naturally defined. The standard machinery of quantum field theory, which relies on well-defined configuration spaces, breaks down.

3. The Inversion Principle: 4D as the Axiomatic Center

The conventional view treats the 4D wildness as an exceptional problem to be solved within a general d-dimensional framework. We propose the opposite, that is, elevate the 4D reality to an axiomatic principle.

[Dimensional Privilege] The fundamental theory of quantum geometry is defined only for spacetime dimension 3+1. Its axioms are chosen so that they naturally yield a unique, or at least a tractably finite, set of continuum geometric phases, all of which are physically equivalent (diffeomorphic) to the standard smooth structure of ${\mathbb{R}}^4$.

Under this axiom, the apparent simplicity of smooth structures in $d\ne 4$ within differential topology is regarded as a degeneracy or irrelevance of the old formalism. The new framework may simply not yield a coherent geometric interpretation for other dimensionalities, or may reduce them to trivial theories. This is not a bug but a feature. This may offer a mathematical explanation for why our universe is 4-dimensional as only this dimensionality is a consistent, rich solution of the fundamental axioms.

Critically, the Inversion Principle calls for more than a new physical theory; it demands a new kind of mathematical foundation that is inherently dimensionality conscious. In standard mathematics, definitions of topological and smooth structures are dimension-agnostic: the same formalisms apply uniformly across all dimensions, with the peculiarities of dimension four emerging as surprising theorems. In a 4D-native framework, the fundamental definitions of continuity, smoothness, and geometric structure among others, should be dimension-specific, tailored so that 4D is not a special case but the natural, well-behaved norm. This represents a shift from viewing dimension as a free parameter to treating it as an axiomatic feature that fundamentally shapes the mathematical language. A truly dimensionality-conscious mathematics would not only tame the wildness of $\mathcal{E}\left({\mathbb{R}}^4\right)$ but also provide a principled explanation for the unique suitability of 4D as the arena for physical reality (cf. Figure 1b).

4. Proposed Framework: 4D-Native Pre-Geometric Substrates

The Inversion Principle does not specify a unique theory but a design criterion for candidate theories. Several existing research programs already embody aspects of this criterion.

[Causal Set Theory as a 4D-Native Framework] Causal set theory postulates that spacetime is a discrete, partially ordered set (a causal set) [8]. Its axioms are dimension-agnostic, but the continuum approximation where one recovers of a Lorentzian manifold, relies on a dimensional estimator that most naturally and robustly yields a 4D continuum. One can reformulate the theory to take 4D as an axiom: the fundamental growth rules or quantum amplitudes are defined so that they only produce causal sets whose natural continuum approximation is 4D. In such a reformulation, attempts to force a 5D continuum would lead to inconsistent or non-geometric outcomes.

[Non-Commutative Geometry as a Generalized Smoothness] In non-commutative geometry, a spacetime is described by a spectral triple $(A,H,D)$[9]. The standard smooth manifold is a special commutative case. Different exotic smooth structures on ${\mathbb{R}}^4$ might correspond to different, non-isomorphic spectral triples built from the same underlying algebra. The wild set $\mathcal{E}\left({\mathbb{R}}^4\right)$ is thereby translated into a (still complex, but potentially more algebraic) classification problem within operator algebras. The axioms of the spectral action principle could be tuned to select a unique 4D solution.

[Loop Quantum Gravity/Spinfoams as a 4D Combinatorial Theory] The spinfoam path integral for quantum gravity sums over combinatorial 2-complexes labeled by group representations [10]. The continuum 4D geometry emerges only in a semi-classical limit. The theory is inherently 4D because the underlying gauge group and constraints (e.g., the simplicity constraints) are tied to the spacetime signature and dimension. The wild sum over smooth structures is replaced by a sum over discrete spinfoams, which, while vast, is countable and governed by combinatorial rules.

In each case, the smooth manifold is not the starting point. It is an emergent, approximate concept. The fundamental degrees of freedom (causal sets, spectral triples, spinfoams) are defined in a way that 4D spacetime is the natural outcome. The wildness of $\mathcal{E}\left({\mathbb{R}}^4\right)$ is either eliminated (because smooth structures are not fundamental) or transformed into a manageable problem within a more structured setting.

5. A Program for 4D-Native Mathematics

The Inversion Principle necessitates a long-term foundational research program. Rather than seeking incremental adjustments to current theories, this program aims for a systematic reconstruction of geometric concepts, and potentially of mathematics itself, from a dimensionality-conscious starting point. The following phased plan in Table 1 outlines the key steps, methodologies, and milestones for this ambitious endeavor.

This program is not merely technical but represents a profound shift in perspective. Its success depends on several critical factors,

• From Philosophy to Rigor: The most significant challenge is transitioning from a powerful guiding principle to a set of precise, fruitful, and workable mathematical definitions. The choice of formal language for the axioms (Phase 1) will determine the entire enterprise’s viability.
• Interdisciplinary Synthesis: The work cannot exist purely within mathematics. It requires sustained collaboration with quantum gravity theorists to ensure physical relevance and with philosophers of science to navigate profound ontological and epistemological shifts.
• A Paradigm Goal: The ultimate objective is to change the rules of the game. The measure of success is not a new model within the old mathematics, but the construction of a new mathematical framework where the rich, stable geometry of our 4D universe is the simplest and most natural output, while other dimensionalities are sacrificed and might appear as degenerate or ill-posed limits.

The proposed program outlines a maximum ambition path for realizing the Inversion Principle. A concrete first step is the focused execution of Phase 1, that is, the publication of a detailed manifesto that explicitly states the new axioms and provides a compelling sketch of how key concepts of geometry would be reconstructed. This would serve as the essential catalyst for gathering the interdisciplinary effort required for the long-term reconstruction to come.

6. Open Questions

Our proposal raises several immediate questions:

• Uniqueness: Can we derive the precise axioms of a 4D-native theory from first principles, or is there a family of such theories?
• Recovery of Continuum: How precisely does the standard smooth structure of ${\mathbb{R}}^4$ (and not an exotic one) emerge as the generic continuum limit?
• Testability: What empirical signatures would distinguish a 4D-native theory from a conventional quantum gravity model?

We suggest that the search for such axioms should be guided by physical principles such as causality, unitarity, quantum entanglement, computational complexity, and the universality of the gauge principles in the Standard Model.

7. Conclusion

The wildness of 4-dimensional smooth structures is not a mere mathematical curiosity; it is a glaring sign that the traditional manifold-based framework is ill-suited for quantum gravity in our universe; The fact that this untamed complexity emerges precisely in the dimension of our physical reality indicates a profound mismatch between our mathematical tools and the structure of spacetime. We have proposed inverting the problem: instead of trying to force 4D into a general-dimensional mold, we should design a new mathematical framework where 4D is the axiomatically privileged dimension. This approach finds natural homes in causal set theory, non-commutative geometry, and loop quantum gravity, where the continuum manifold is emergent and the pathological sum over exotic smooth structures is replaced by a sum over discrete or algebraic structures. The price paid is that other dimensions become messy, trivial or undefined, this is not a cost but a virtue, explaining the unique status of 3+1 dimensions in nature. The task ahead is to sharpen these frameworks into a complete, predictive theory of quantum spacetime.