Introduction
Golden section method is an important single variable optimization method for finding the minimum or maximum of an objective function [
1]. Briefly, the method relies on an initial guess for the left and right bracket of the minimum value, and progressively compares the function evaluation at two internal points to decide on which bracket to be omitted in the next iteration. Usually, the Golden ratio is used to partition the interval between the left and right bracket into the two internal points. Doing it this way allows the Golden section method to move towards the minimum point with successive iterations.
However, the minus point for using a fixed ratio Golden section method is that it may not handle rapidly changing part of the objective function well, with the attendant negative effect of missing a global minimum point. Hence, this work proposes the use of a dynamic ratio Golden section method where the partition ratio is determined by the relative ratio of the function evaluations at the left and right internal point, x1 and x2. Ideally, for large relative ratio indicative of a rapidly changing function, the partition ratio, r, will shift the x2 internal point closer to the right bracket in order to better capture the rapidly changing nature of the objective function. Noting here that the relative ratio will be recalculated at each iteration, and is likely to change with each iteration, thereby, earning the method the name of a dynamic ratio Golden section.
Algorithmic Logic of the New Method
In contrast to the standard implementation for Golden section, my fixed ratio Golden section implementation first defines as first guess for the left and right bracket (point A and B). Using the golden ratio, these two points help calculate two internal points (x1 and x2). Function evaluations are performed for these two internal points, and the results are compared. In the case where f(x1) value is lower than f(x2) value, the right bracket is moved to x2. Conversely, if f(x1) value is higher than f(x2) value, then the left bracket is moved to x1. And the single variable optimization proceeds until the difference between x1 and x2 is smaller than the set tolerance of the optimization exercise.
Enhanced dynamic ratio Golden Section method uses the relative difference between the function evaluations of x1 and x2 to determine the next ratio to be used in partitioning the interval. For example, if the function evaluations of x1 and x2 is significantly different, then the ratio to be used should help move x2 towards the right bracket in order to track the large dynamic changes in function evaluation better. Conversely, if the function evaluation of x1 and x2 is not too far apart, then the standard Golden ratio should be used to partition the interval.
Source Code Implementation
Results and Discussion of Demonstrative Use of the Numerical Method
Demonstrative use of the dynamic ratio Golden section method is performed on a budget Lenovo laptop with AMD Ryzen 7000 series CPU (Model: 7520U at 2.80 GHz) and AMD Radeon integrated graphics (with 2 GB video RAM), 16 GB of RAM, and 512 GB solid state drive.
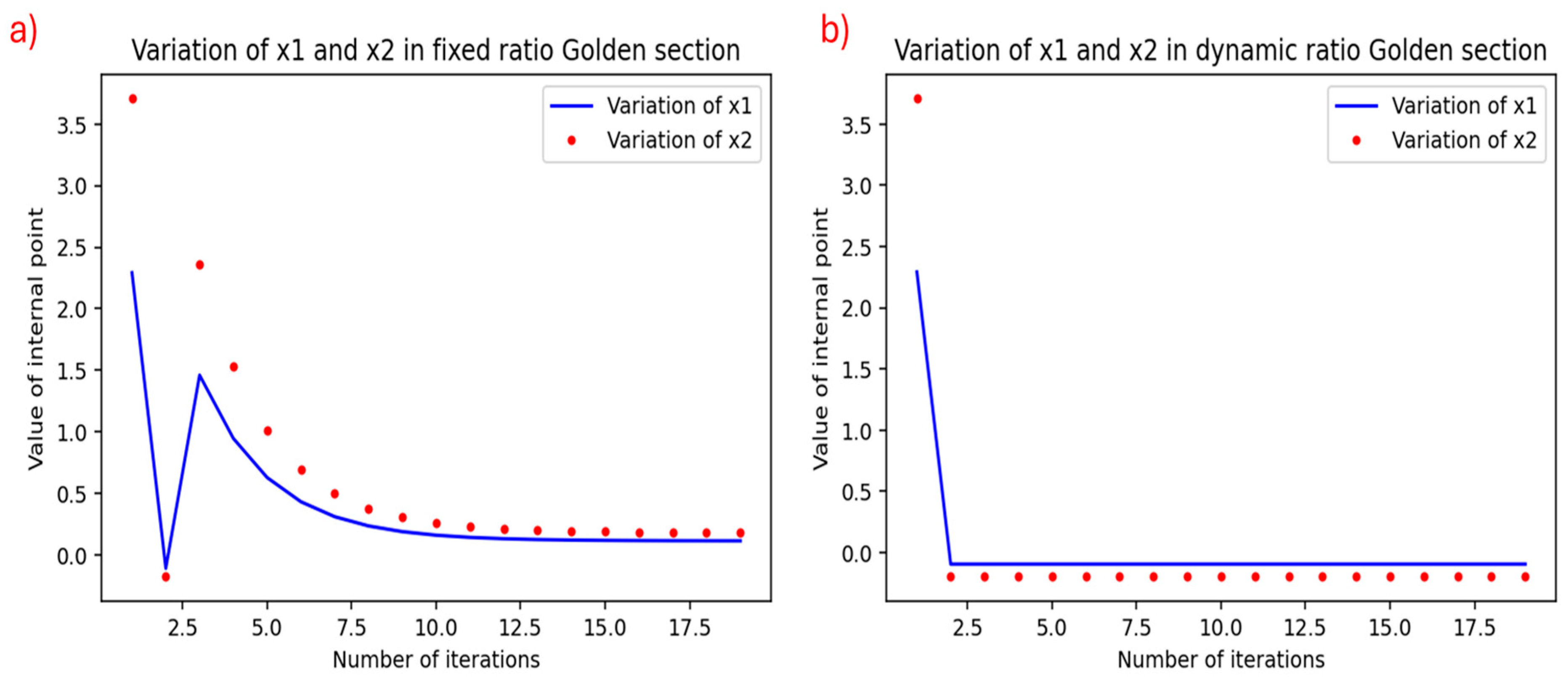
Shown here is the data from demonstrative use of the fixed ratio and dynamic ratio Golden section method in finding the minimum x for solving a quadrative objective function with minimum y-axis value of 10 at x = 0. Hence, the minimum x1 and x2 should be close to zero. The issue here is how fast both algorithms get to the minimum value of zero.
In
Figure 1a, it is clear that the fixed ratio Golden section method does progressively move x2 internal value point to zero over a course of 12 iterations. But, on
Figure 1b, it is shocking to see that the dynamic ratio Golden section method could move the x2 internal point to zero in just 3 iterations. Hence, the dynamic ratio Golden section method does show initial (preliminary) promise of faster convergence to the minimum point compared to the fixed ratio Golden section method.
Conclusions
Numerical methods in all engineering disciplines seek to determine an approximate but fairly good estimate of the true optimum in different optimization scenarios. One good single variable optimization method is the Golden section method. In its typical implementation as a fixed ratio (i.e., Golden ratio) Golden section method, path to convergence to the minimum of maximal point is progressive. Here, a different method to implement Golden section method is described. Principally, the innovation here is the use of a dynamic ratio Golden section method in order to allow the capture or more precise following of the objective function curve, especially in regions of rapidly changing value. To this end, the dynamic ratio will partition the bracketing region and place the x2 internal point closer to the right bracket in order to follow the rapidly changing function. Demonstrative use of this dynamic ratio Golden section method on a quadratic function with minimum y-value of 10 shows fast convergence to minimum point of zero in 3 iterations compared to 12 iterations for the conventional fixed ratio Golden section method.
Funding
No funding was used in this work.
Conflicts of interest
The author declares no conflicts of interest.
References
- Hernandez, S.; Flores, I.; Vázquez, J. Improved Golden-Section Algorithm for the Multi-Item Replenishment Problem. J. Appl. Res. Technol. 2012, vol. 10. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).