Critical Depth and the Scaling Law Paradox: A Refactored Resource Model

1. Introduction

1.1. Background

Our societies composed by individuals, families, groups, communities and … can be seen as a super-organism. Interestingly, individuals are subject to a phenomenon knows as homeostasis. Though biological in its root, it has various embodiments and also drives other aspects in some of our civilizations.

From biology to virtually all of modern science discipline, we teach and practice science in a siloed way. Indeed, from natural philosophy to natural sciences, we now, mostly have a faculty for each artificially delimited area or field. Naturally, we end-up producing super-specialized individuals for which, the reading of a “global landscape” much becomes much harder. The power of “zooming out” can be exemplified for instance: theoretically, with the Langland programs [1] and technically, with the reconstruction of the first picture of a black hole [2].

In the information age and beyond, the extreme inter-connectivity coupled to a containerization of knowledge and skills generates a shortage in individuals capable of reading the whole “partition”. We have thus developed techniques/metrics to mitigate this issue such as SLAs for services, MTBF for industrial equipments…

All of this to say what?

Our reliance on expectation and predictability have almost become an acquired/required state.

From the initial feats of deep learning in computer vision [3,4], passing by the introduction of the Transformer-neural architecture [5], we can see for one part, the Neural Scaling Laws as a form of answer to this societal “need” for insurance and assurance. In a second part, there is the pure scientific endeavor of trying to understand and study a phenomenon.

In closing, we also need to take into account the current developments in science and how it is performed. The lens taken in this work somehow echoes and is, a byproduct of the aforementioned elements. The growing body of knowledge, the digitalization of virtually every layers of our societies (which is possible because of the storage, compute/computing devices) naturally guide us to consider a form of “mechanization” of mathematics – the language of science. In other words, from the pencil and symbolic resolutions, we transition to the compute and constructive mathematics.

1.2. Motivation

One of the recurring questions is:

1s mathematics {discovered or invented} ⟺ {revealed or engineered}?

This seemingly innocuous question is gaining momentum and becoming the center of attention of current artificial intelligence research.

The analysis and developments as to why this is the case are beyond the scope and goal of this work. However, we will give an overview of its grounding and trajectory.

In order to do so, we will borrow the nomenclature of software engineering: static and dynamic – which can characterize the state of binary or library.

In a static sense, we can list the following elements as catalysts of the process:

-

The advent of the modern computing device or, commonly known as the computer,

-

The increasing size of our knowledge corpus – development of storage capabilities.

With an apparent incidental aspect, what could be qualified as the dynamic part of the process:

-

The digital $(0,1)$-spectrum nature of our computing devices,

-

The accelerating pace at which our body of knowledge grows; it almost naturally arises that, we need to be building on solid/sound ground.

The conjunction of the aforementioned elements leads/favors/pushes to the mechanization of mathematics and by extension: Science.

Science practitioners allies in this evolution is: the theorem provers (TP) or interactive theorem provers (ITP) – which interestingly, also underwent a “natural” co-evolution. In light of the previous development, this co-evolution of PL can also be segmented dyadically:

-

A form of “awareness” of the technological advancements and evolving environment i.e.: we move from, the local thinking/logic to innate network aware data types/structures.

-

On a syntactic level: we move away from manually allocating memory buffers to, powerful one-line design patterns of high-level programming languages – increased abstraction.

Similarly, TPs and ITPs have gained in: automation and “expressiveness” – closer to natural language. To name a few, from Mizar [6], Coq [7], Isabelle [8], passing by Metamath [9] to Lean [10]. An interesting read with respect to the evolution of impact of formalization and theorem provers can be found in: Mathematical Proof Between Generations [11].

Historically, the tribe1 of symbolists did not live up to the great expectations of the time. However, closer to us, we observe a resurgence of this paradigm either in a hybrid approach such as: neurosymbolic AI or, as a tool that is queried by Large Language Models.

In light of these elements, we naturally thought to inscribe ourselves into this evolution by making use of formal logic. Applied to a rather foundational piece of work [13] whose objective is to unravel/understand the behavior of these Large Language Models.

Figure 1. Source: The master algorithm: how the quest for the ultimate learning machine will remake our world Domingos [12].

Figure 1. Source: The master algorithm: how the quest for the ultimate learning machine will remake our world Domingos [12].

1.3. Recall and Preliminary Information

Neural Scalings Laws (NSLs) are power laws derived from the observation and study of a class Transformer-neural architecture i.e.: Generative Pretrained Transformer [14].

Succeeding to the exposed points (Section 1.1) and motivating the study of NSL, we can add the following technically rooted ones [15]:

-

For the understanding of Deep Neural Networks – the articulation/interaction between data and model architecture,

-

From an efficiency perspective – considering both: fuel (data) and energy factors.

The landscape of Neural Scaling Laws (NSLs)

Neural Scaling Laws have been studied and derived from both an empirical and theoretical perspectives.

For the empirically-derived studies, we can cite the following works:

-

Scaling Laws for Neural Language Models [16]

-

Training Compute-Optimal Large Language Models [17]

-

Chinchilla Scaling: A replication attempt [18]

For the theoretically-derived investigation works, we can point to the following (not exhaustive):

-

Learning Curve Theory [19]

-

A Resource Model For Neural Scaling Law [13]

-

A Neural Scaling Law from the Dimension of the Data Manifold [20]

-

Explaining neural scaling laws [21]

-

Scaling Laws for Deep Learning [22]

-

A Solvable Model of Neural Scaling Laws [23]

-

Information-Theoretic Foundations for Neural Scaling Laws [24]

Given the fast pace of developments in the fields of eXplainable AI (XAI), the aforementioned research constitutes only an excerpt/snapshot of the active research landscape.

1.4. NSLs – The Power Laws Recap

From the aforementioned works, the key theoretical predictions for neural scaling law exponents from recent foundational works:

-

L: the test loss (e.g., cross-entropy or MSE),

-

N: the number of model parameters,

-

D: the number of training tokens (dataset size),

-

d: the intrinsic dimension of the data manifold Sharma and Kaplan [20].

The following summarizes the key empirical power-law scaling exponents for neural language models as derived from large-scale experiments:

-

L: the test loss (typically cross-entropy in nats),

-

N: the number of non-embedding model parameters,

-

D: the number of training tokens,

-

C: the training compute budget (FLOPs), with $C\propto ND$.

1.4.1. Summary of Key Scaling Exponents

Key Insights:

• Data Manifold Dimension (d): Both Sharma and Kaplan [20] and Bahri et al. [21] link the scaling exponent to the intrinsic dimension d of the data. The difference in the predicted factor (4 vs. 1) arises from different assumptions about the nature of the approximation (e.g., piecewise constant vs. piecewise linear).
• Information-Theoretic View: Jeon and Roy [24] decomposes the loss into an estimation error ($\propto 1/D$) and a misspecification error ($\propto 1/N$). This leads to a compute-optimal scaling where $N\propto D\propto \sqrt{C}$, implying equal scaling exponents of 1 for both N and D in the variance-limited regime.
• Random Feature Models: Maloney et al. [23] shows that the scaling exponent is directly inherited from the power-law decay of the data’s feature spectrum. This provides a direct, solvable link between data distribution statistics and model performance.
• Power Laws and Zipf’s Law: Hutter [19] demonstrates that if the underlying data features follow a Zipf distribution, the resulting learning curve will also be a power law, with the exponent $\beta$ being a function of the Zipf parameter.
• Resource-Based Model: Song et al. [13] proposes that the total loss scales as $L\propto N^{-1}$ where N is the total allocated neurons. By assuming $N_p\propto N^3$, they derive $L\propto N_p^{-1/3}$, matching the Chinchilla result [17]. This model hinges on the “homogeneous growth” conjecture and the assumption that resource scales with width.

Table 1. Theoretical predictions for the scaling exponent $\alpha$ in the relation $L\propto N^{-\alpha }$ or $L\propto D^{-\alpha }$.

Paper	Scaling Law	Exponent $\mathit{\alpha }$
Sharma and Kaplan [20]	$L\left(N\right)\propto N^{-\alpha }$	$\alpha \approx {\displaystyle \frac{4}{d}}$
Bahri et al. [21] (2024)	$L\left(N\right)\propto N^{-\alpha }$, $L\left(D\right)\propto D^{-\alpha }$	$\alpha \approx {\displaystyle \frac{1}{d}}$
Jeon and Roy [24]	Optimal allocation: $N_{\mathrm{opt}}\propto \sqrt{C}$, $D_{\mathrm{opt}}\propto \sqrt{C}$	${\alpha }_N={\alpha }_D=1$
Maloney et al. [23]	For a kernel spectrum ${\lambda }_i\propto i^{-(1+\alpha )}$	$L\left(N\right)\propto N^{-\alpha }$, $L\left(D\right)\propto D^{-\alpha }$
Hutter [19]	For Zipf-distributed features with exponent $\alpha +1$	$L\left(D\right)\propto D^{-\beta }$, where $\beta ={\displaystyle \frac{\alpha }{1+\alpha }}$
Song et al. [13]	$L\left(N\right)\propto N^{-1}$ (resource scaling), and $N_p\propto N^3$	$\alpha ={\displaystyle \frac{1}{3}}$ for $L\propto N_p^{-\alpha }$

Table 1. Theoretical predictions for the scaling exponent $\alpha$ in the relation $L\propto N^{-\alpha }$ or $L\propto D^{-\alpha }$.

Paper	Scaling Law	Exponent $\mathit{\alpha }$
Sharma and Kaplan [20]	$L\left(N\right)\propto N^{-\alpha }$	$\alpha \approx {\displaystyle \frac{4}{d}}$
Bahri et al. [21] (2024)	$L\left(N\right)\propto N^{-\alpha }$, $L\left(D\right)\propto D^{-\alpha }$	$\alpha \approx {\displaystyle \frac{1}{d}}$
Jeon and Roy [24]	Optimal allocation: $N_{\mathrm{opt}}\propto \sqrt{C}$, $D_{\mathrm{opt}}\propto \sqrt{C}$	${\alpha }_N={\alpha }_D=1$
Maloney et al. [23]	For a kernel spectrum ${\lambda }_i\propto i^{-(1+\alpha )}$	$L\left(N\right)\propto N^{-\alpha }$, $L\left(D\right)\propto D^{-\alpha }$
Hutter [19]	For Zipf-distributed features with exponent $\alpha +1$	$L\left(D\right)\propto D^{-\beta }$, where $\beta ={\displaystyle \frac{\alpha }{1+\alpha }}$
Song et al. [13]	$L\left(N\right)\propto N^{-1}$ (resource scaling), and $N_p\propto N^3$	$\alpha ={\displaystyle \frac{1}{3}}$ for $L\propto N_p^{-\alpha }$

Table 2. Empirical scaling exponents from major experimental works.

Paper	Scaling Law	Exponent	Optimal Scaling Policy
Kaplan et al. [16]	$L\left(N\right)\propto N^{-{\alpha }_N}$	${\alpha }_N\approx 0.076$	$N_{\mathrm{opt}}\propto C^{0.73}$
	$L\left(D\right)\propto D^{-{\alpha }_D}$	${\alpha }_D\approx 0.095$	$D_{\mathrm{opt}}\propto C^{0.27}$
	$L\left(C\right)\propto C^{-{\alpha }_C}$	${\alpha }_C\approx 0.050$
Hoffmann et al. [17]	$L\left(N\right)\propto N^{-\alpha }$	$\alpha \approx 0.339$	$N_{\mathrm{opt}}\propto C^{0.50}$
(Chinchilla)	$L\left(D\right)\propto D^{-\beta }$	$\beta \approx 0.285$	$D_{\mathrm{opt}}\propto C^{0.50}$
	$L\left(C\right)\propto C^{-\gamma }$	$\gamma \approx 0.50$
Besiroglu et al. [18]	$L\left(N\right)\propto N^{-\alpha }$	$\alpha \approx 0.348$	$N_{\mathrm{opt}}\propto C^{0.51}$
(Replication attempt)	$L\left(D\right)\propto D^{-\beta }$	$\beta \approx 0.366$	$D_{\mathrm{opt}}\propto C^{0.49}$

Table 2. Empirical scaling exponents from major experimental works.

Paper	Scaling Law	Exponent	Optimal Scaling Policy
Kaplan et al. [16]	$L\left(N\right)\propto N^{-{\alpha }_N}$	${\alpha }_N\approx 0.076$	$N_{\mathrm{opt}}\propto C^{0.73}$
	$L\left(D\right)\propto D^{-{\alpha }_D}$	${\alpha }_D\approx 0.095$	$D_{\mathrm{opt}}\propto C^{0.27}$
	$L\left(C\right)\propto C^{-{\alpha }_C}$	${\alpha }_C\approx 0.050$
Hoffmann et al. [17]	$L\left(N\right)\propto N^{-\alpha }$	$\alpha \approx 0.339$	$N_{\mathrm{opt}}\propto C^{0.50}$
(Chinchilla)	$L\left(D\right)\propto D^{-\beta }$	$\beta \approx 0.285$	$D_{\mathrm{opt}}\propto C^{0.50}$
	$L\left(C\right)\propto C^{-\gamma }$	$\gamma \approx 0.50$
Besiroglu et al. [18]	$L\left(N\right)\propto N^{-\alpha }$	$\alpha \approx 0.348$	$N_{\mathrm{opt}}\propto C^{0.51}$
(Replication attempt)	$L\left(D\right)\propto D^{-\beta }$	$\beta \approx 0.366$	$D_{\mathrm{opt}}\propto C^{0.49}$

Key Insights:

• Kaplan et al. [16] established what’s most likely the foundational empirical scaling laws, finding that loss scales with a very shallow power law in N and D. Their analysis suggested a highly model-heavy optimal scaling policy ($N\propto C^{0.73}$).
• Hoffmann et al. [17] revisited this with an extensive experimental sweep and found significantly steeper scaling exponents. Their key conclusion was that model and data should be scaled equally, leading to the “Chinchilla scaling” law where $N_{\mathrm{opt}}\propto D_{\mathrm{opt}}\propto C^{0.5}$.
• Besiroglu et al. [18] attempted to replicate the parametric fit from Hoffmann et al. [17]. They found that the originally reported parameters were inaccurate due to an optimizer issue, and their corrected fit yields exponents that are consistent with the equal-scaling policy but with a slightly higher data exponent ($\beta >\alpha$).

1.5. Epicenter of Our Attention

Similar to the approach taken by Besiroglu et al. [18], we however are, interested in strengthening the posited assumptions Song et al. [13] through formalization using propositional logic.

We start our analysis by recalling the developments of [13] in Section 2. Then, we follow-up with our formalization in Section 2.4 where we propose a Refactored-resource based Model.

Afterwards, equipped with those results, we dive into the critical depth conjecture Section 2.6 and motivate around it.

Finally, we incrementally propose a phase transition interpretation of the Neural Scaling Laws in Section 2.7, Section 2.8, Section 2.9.

Acknowledged Logical Inconsistency

As explained in section (Section 1.1), we noticed the logical inconsistency that is brought up by the authors themselves after their developments [13][Last § before 5. Related Works].

2. Methods

Based on the previous assessment, we decide to take a formalization approach to: A Resource Model For Neural Scaling Law Song et al. [13].

Notation: throughout this work, for shortness sake, we refer to [13] as the: Resource-based Model.

2.1. Resource-Based Model – Specific Nomenclature

We start by recalling the symbols and conventions used in Song et al. [13]:

Table 3. Key symbols and terms used in the paper [13].

Symbol / Term	Definition
ℓ, ${\ell }_{\mathrm{total}}$	Total test loss of the composite task.
N, $N_{\mathrm{total}}$	Total number of allocated neurons across all subtasks i.e. the “resource”.
$N_{\mathrm{subtask}}$	Number of allocated neurons for a specific subtask.
$N_{\mathrm{width}}$	Number of neurons in a single layer (network width).
$N_{\mathrm{depth}}$	Number of layers in the network (network depth).
$N_p$	Total number of model parameters.
$\alpha$	Importance weight (penalty) assigned to a subtask during training.
Module	A functional subnetwork responsible for a specific subtask.

Table 3. Key symbols and terms used in the paper [13].

Symbol / Term	Definition
ℓ, ${\ell }_{\mathrm{total}}$	Total test loss of the composite task.
N, $N_{\mathrm{total}}$	Total number of allocated neurons across all subtasks i.e. the “resource”.
$N_{\mathrm{subtask}}$	Number of allocated neurons for a specific subtask.
$N_{\mathrm{width}}$	Number of neurons in a single layer (network width).
$N_{\mathrm{depth}}$	Number of layers in the network (network depth).
$N_p$	Total number of model parameters.
$\alpha$	Importance weight (penalty) assigned to a subtask during training.
Module	A functional subnetwork responsible for a specific subtask.

2.2. Resource-Based Model – Axioms & Conjectures

In this section, we recall and review Song et al. [13] internal logic:

2.2.1. Hypotheses

In the following, we list their empirically-derived (toy model) hypotheses of [13]:

• ${\ell }_{\mathrm{subtask}}\propto N_{\mathrm{subtask}}^{-1}$ (Single task scaling),
• Homogeneous growth of resource allocation – the ratios of $N_i$ are constant as the network grows.
• Linear additivity of subtask losses – the total loss is the sum of subtask losses.

2.2.2. Axioms

• Assumption 1: $N\propto N_{\mathrm{width}}$
• Assumption 2: $N_{\mathrm{depth}}\propto N_{\mathrm{width}}$
• Assumption 3: $N_p\propto N_{\mathrm{width}}^2·N_{\mathrm{depth}}$

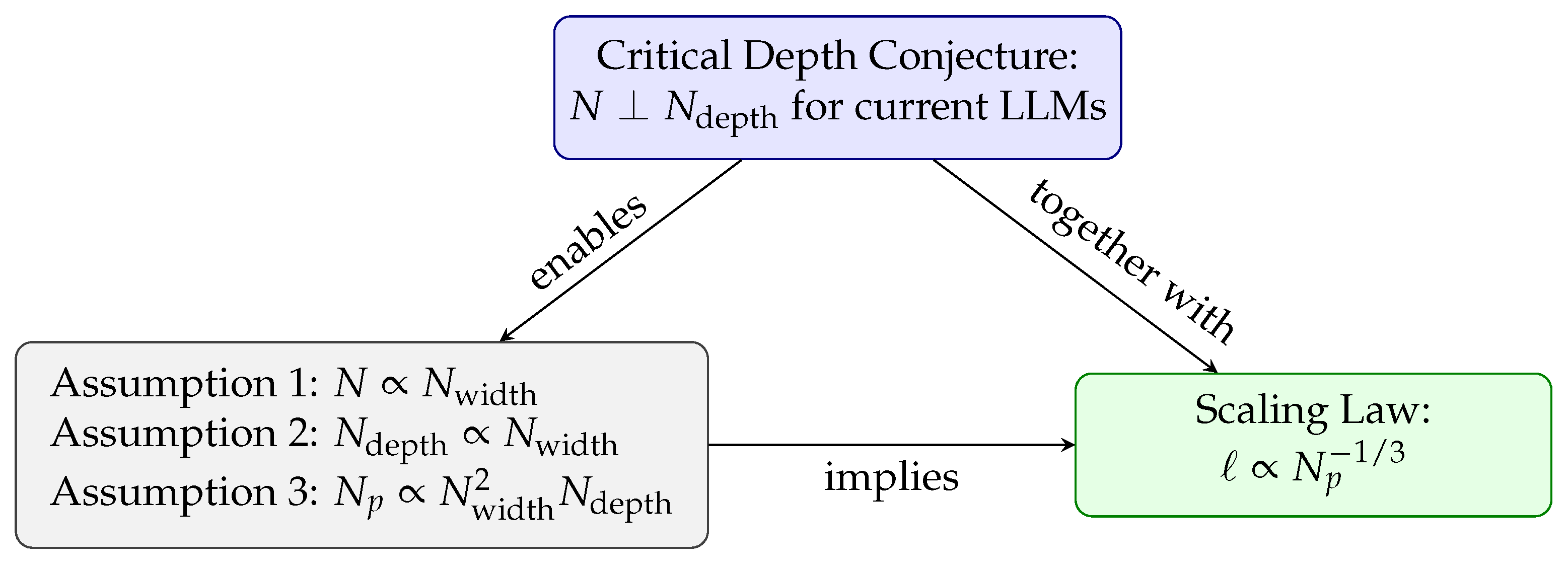
2.2.3. Conjecture – Critical Depth Conjecture

Critical Depth Conjecture

In the Resource-based Model [13], they formulate the hypothesis that above a certain depth, increasing the depth does not increase the effective resource pool N.

Additionally, it considers that current LLMs are beyond this depth threshold.

Through our formalization, we observe that, this conjecture is actually the key piece justifying the otherwise inconsistent internal logic.

2.3. Resource-Based Model Logic Relies on “Critical Depth” Conjecture

As illustrated in the Figure 2, the internal logic of the Resource-based Model for NSLs holds because of the introduction of the testable hypothesis around the Critical Depth Conjecture.

Formally, without the critical depth conjecture, the composition of Assumption 1 (Section 2.2) and the homogeneous growth leads to a contradiction.

That is, the homogeneous growth hypothesis states that the total allocated resource N grows proportionally with the network size. If the network size grows as $N_{width}^2$, then so should N also grow as $N_{width}^2$. Thus, the paper’s: Assumption 1 ($N\propto N_{\mathrm{width}}$) contradicts this – which is without taking into account the critical depth conjecture.

In other words, if the critical depth conjecture holds then, it allows for the derivation of the Chinchilla-like scaling law: $\ell N_p^{-1/3}$ [17].

In the next section (Section 2.4), we observe that, through our Z3 formalization, this is indeed the crux of their reasoning upon which the consistency of the paper [13] relies.

Ultimately, we construct a model that resolves the logical inconsistency in the absence of the critical depth conjecture i.e. by a refactoring Assumption 1 as: $N\propto N_{width}{N}_{depth}$ for the resource model.

2.4. Key Tricks for Formalizing Resource-Based Model in Z3

Mentioned several times earlier and intrigued by the critical depth conjecture, we decided to bring a new perspective on the Resource-based Model [13] through propositional logic (also known as zeroth-order logic) and the Z3 solver/prover [25].

Using this approach, our expectations were twofold:

-

Through mechanized mathematics, we would like to confirm the Resource-based Model’s internal logic,

-

As a “byproduct”, working with machine-assistance, we could expect “angles” to be revealed that might not be readily visible.

Practically, we use Z3’s Python wrapper: z3-solver==4.15.1.0

The process of translating the Resource-based Model [13] into a model checking instance requires a particular attention to the following point2:

-

In order to verify the properties we are interested in, it often necessary to reduce the the “space” search of the verifier/solver,

-

Linked to the previous point, the problem so expressed lives in a pure “mathematical realm”. That is, the solver/prover has no awareness or intelligence about the nature of solution found.

In other words, a solution can be perfectly fine from a mathematical point of view but might not describe a physical plausibility or sensical configuration of our problem.

Hereafter, we list the key tricks used to construct our model in Z3. Full source code is available at: https://github.com/emergentcog/research/tree/da2ec7921650bc82309b2793be6fd2dfb7ff6984/nsl-z3/src

2.4.1. Modeling Scaling Exponents Instead of Absolute Values (The Core Trick)

In order to avoid trivial solutions that appears when using equalities, we make use of the scaling exponents as variables.

This is motivated because of:

-

Scaling laws are about how quantities change relative to each other as size increases,

-

By focusing on exponents (where $N\propto s^{{\exp }_N}$), we capture the essence of power-law relationships,

-

This eliminates trivial solutions such as: zero while preserving the scaling behavior.

2.4.2. Enforcing Physical Plausibility with Positivity Constraints

In the following, we enforce that all exponents to be positive.

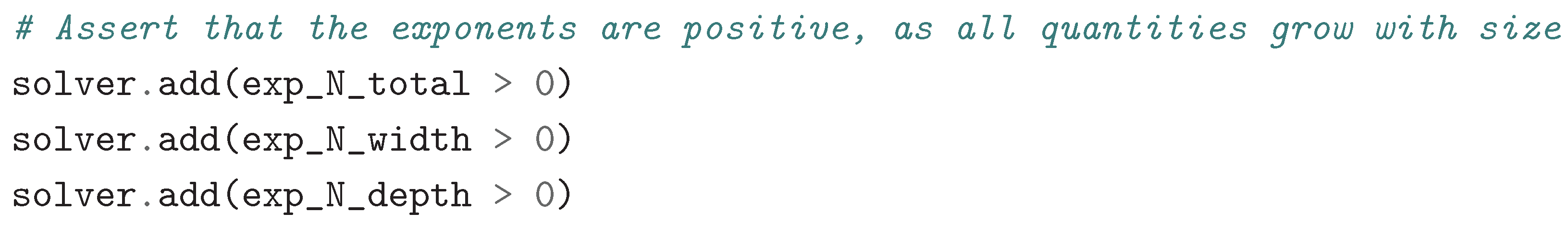This is motivated because of:

-

In the context of neural network scaling, the width, depth, resources quantities should increase as model size increases,

-

Without this constraint, mathematically valid but physically meaningless solutions would satisfy the equations,

-

This is the key to discarding “trivial cases” that don’t embody a physical reality.

2.4.3. Correctly Translating Functional Relationships to Exponent Relationships

In the following, we seek to ensure the proper conversion of multiplicative relationships to additive exponent relationships.

This is motivated by the multiplicative law of exponents: $b^m*b^n=b^{m+n}$ i.e. to multiply exponents with the same basis is to addition their exponents.

2.4.4. Identifying the Precise Nature of the Contradiction

This part deals for the case when the system is unsatisfiable i.e. when a contradiction occurs:

Assumption 1: expNtotal = expNwidth

Assumption 2: expNdepth = expNwidth

Homogeneous Growth: expNtotal = expNwidth + expNdepth

Combining the previous gives:

expNwidth = expNwidth + expNwidth -> expNwidth = 0

But the positivity constraint requires:

expNwidth > 0

The lines of code that shows the unsatisfiable cases are (skipped some lines $[...]$ because of layout issues):

2.4.5. Separating Internal Consistency from Physical Plausibility

In the following, we follow the paper’s derivation based on its assumptions.

This shows the paper’s derivation is correct with respect to its internal logic. The issue isn’t with the derivation but with the physical validity of Assumption 1. In this case, it reveals that, the critical depth conjecture is a necessary condition for Assumption 1.

2.5. NSLs Derivation Based on Refactored Logic

As we have seen, the Resource-based Model relies on the critical depth conjecture.

What does happen, when we logically proceed with the assumptions (Section 2.2) but without:

$$\begin{array}{cc}\hfill N& \propto N_{width}·N_{depth}\propto N_{width}^2(\mathrm{since}{N}_{depth}\propto N_{width})\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \ell & \propto N_p^{-2/3}\hfill \end{array}$$

(2)

The complete development of our logical derivation can be found in Appendix B.

At this point, we have two explanatory neural scaling models:

• The Resource-based Model relying on the critical depth conjecture which predicts: $\ell \propto N_p^{-1/3}$
• Our Refactored-resource Model uses the original paper assumptions without being indexed on the critical depth conjecture. Thus, we considers that the total number of allocated resources N should scale not only with the width but also with the depth of the network.
  It follows that, we derive a prediction relation loss of: $\ell \propto N_p^{-2/3}$.

Like two crossing lines defining at least one angle, these two models allow for a refined perspective on the Neural Scaling Laws.

It raises the following questions, either:

-

The $\ell \propto N^{-1}$ equation (A1) doesn’t hold when depth is scaled up, or,

-

The critical depth conjecture is topical and most of current Large Language Models (LLMs) are operating in a special regime – which we explore in the next sections to propose a proto-Unified Scaling Law (Section 3.3).

2.6. Pivoting Around the Critical Depth Conjecture

One of the key components we have been involved with; and, which is at the crux of Deep Neural Networks revolves around the notions of depth and width.

To further explore this point, we focus on the following two works:

• Width is Less Important than Depth in ReLU Neural Networks Vardi et al. [26]
• Do Wide and Deep Networks Learn the Same Things? Uncovering How Neural Network Representations Vary with Width and Depth Nguyen et al. [27]

Relating Resource-based Model with Vardi et al. [26]

The Resource-based Model paper’s derivation of $\ell \propto N_p^{-1/3}$ relies on:

-

Assumption 1: $N\propto N_{\mathrm{width}}$ (resource scales only with width)

-

Assumption 2: $N_{\mathrm{depth}}\propto N_{\mathrm{width}}$ (depth scales with width)

-

Assumption 3: $N_p\propto N_{\mathrm{width}}^2·N_{\mathrm{depth}}$

These assumptions combined with the homogeneous growth hypothesis ($\ell \propto N^{-1}$) leads to $\ell \propto N_p^{-1/3}$.

However, Theorem 3.1 Vardi et al. [26][p.4] contradicts Assumption 1 (Section 2.2).

If depth can compensate for width, then:

-

The total effective resource N should scale with $N_{\mathrm{width}}·N_{\mathrm{depth}}$

-

With $N_{\mathrm{depth}}\propto N_{\mathrm{width}}$, this gives $N\propto N_{\mathrm{width}}^2$

-

Combined with $N_p\propto N_{\mathrm{width}}^3$, this yields $\ell \propto N_p^{-2/3}$

This latest point is in line i.e. matches our Refactored-resource Model predictor (2). Interestingly, using two approaches, we observe the same scaling law of: $\ell \propto N_p^{-2/3}$.

The exponent has a steeper value: $-2/3\approx -0.67$ than Chinchilla’s: $-0.34$ .

What do we make of this discrepancy?

In the next sections, we bring forth a possible explanation and unification so to speak.

Before that, we consider the works of: Vardi et al. [26] and Nguyen et al. [27] with respect to the Resource-based Model.

For one thing, the mix of theoretical and empirical work allows a finer discriminative process – this is with respect to the selection of results.

Secondly, by now, we should be accustomed that, Deep Neural Networks have a tendency to call out theory.

Relating the Resource-based Model with Nguyen et al. [27]

From this work, we find and report a number of interesting elements backing up the Resource-based Model.

From the following extract:

Together these results demonstrate that the block structure arises from preserving and propagating the first principal component across its constituent layers.

[...]

This result suggests that block structure could be an indication of redundant modules in model design, and that the similarity of its constituent layer representations could be leveraged for model compression.

This might explain why beyond a threshold depth doesn’t bring additional value. In sense, they have “no other choice” than to replicate what has been already be seen/extracted i.e. no new circuits or modules.

From the following extract:

We show that depth/width variations result in distinctive characteristics in the model internal representations, with resulting consequences for representations and outputs across different model initializations and architectures.

This aspect might explain why, the Resource-based Model’s homogeneous growth hypothesis ($\ell \propto N^{-1}$) works even across disparate neural networks designs.

Different neural architectures allocate resources differently across subtasks, but the total resource N (i.e. effective number of non-redundant modules) scales primarily with width.

From the following extract:

Through further analysis, we show that the block structure arises from the preservation and propagation of the first principal component of its constituent layer representations. Additional experiments with linear probes (Alain & Bengio, 2016) further support this conclusion and show that some layers that make up the block structure can be removed with minimal performance loss.

We can link this to at least the following two points:

• Based on excerpt, we can interpret this as empirical evidence that Resource-based Model mainly scales with width than depth,
• Additionally, we can link this, to the notion of super weights developed in Yu et al. [28] or, more precisely, to its negative counter-part($\neg \mathrm{super}\mathrm{weights}$ i.e. those not representing the super weights); their ablation leading to a negligible effect on the network’s performances.

Penultimately, from these two works, we extract and relate to the Resource-based Model the following points:

Table 4. Connecting Theoretical Results, Empirical Observations, and the Resource-based Model.

Theorem 3.1 – Theoretical Result [26]	Block Structure – Empirical Finding [27]	Resource-based Model Implication [13]
Any wide network can be approximated by a narrow-deep network	DNNs develop redundant “blocks” of similar layers	Beyond a critical depth, additional depth creates redundancy rather than new capabilities
Depth can theoretically compensate for width	The block structure emerges as networks get deeper	The effective resource N scales primarily with width, not depth
Requires polynomial increase in depth	The block structure grows with depth	Current LLMs are potentially beyond the critical depth where depth scaling becomes ineffective

Table 4. Connecting Theoretical Results, Empirical Observations, and the Resource-based Model.

Theorem 3.1 – Theoretical Result [26]	Block Structure – Empirical Finding [27]	Resource-based Model Implication [13]
Any wide network can be approximated by a narrow-deep network	DNNs develop redundant “blocks” of similar layers	Beyond a critical depth, additional depth creates redundancy rather than new capabilities
Depth can theoretically compensate for width	The block structure emerges as networks get deeper	The effective resource N scales primarily with width, not depth
Requires polynomial increase in depth	The block structure grows with depth	Current LLMs are potentially beyond the critical depth where depth scaling becomes ineffective

In closing, we can outline the following points:

-

The dichotomy between width and depth. Theorem 3.1 Vardi et al. [26] shows that depth can compensate for width. However, from [27], block structures show that after a certain threshold they accumulate redundancy.

-

Can this threshold be related to the critical depth conjecture?

In the positive, it could accredit the fact that most Large Language Models operate under this regime i.e. beyond this threshold.

-

The Resource-based Model posits that resources N are allocated following: $N\propto N_{width}$ which subsequently also rely on the previous point.

However, the slight performance drop due to the ablation of some layers from the block structures cannot readily be linked to the scale based on width. Indeed, we saw that the notion of super weights [28] might very well be connected to this aspect.

2.7. Dyadic Nature of Neural Scaling Laws: Making Sense of $N_p^{-1/3}$ ∧ $N_p^{-2/3}$

Using two distinct approaches, we observed the following neural scaling law: $N_p^{-2/3}$. As described earlier, it has a steeper slope than Chinchilla’s empirically-derived law: $-0.34$ which is matched by the Resource-based Model with a factor of: $N_p^{-1/3}$.

To obtain these results, the two approaches we use/consider are:

• Our Refactored-resource Model (Section 2.5) derived through logic and the use of Z3 solver,
• The other approach is derived from the theoretical reasoning developed in (Section 2.6) based on the work of Vardi et al. [26]. Which relies around:

  This means that any wide network can be approximated up to an arbitrarily small accuracy, by a narrow network where the number of parameters increases (up to log factors) only by a factor of L.

  and where L is the network’s depth factor. They establish an asymmetry between a neural network of width n and depthL. They show that depth has more weight, an increased expressive power than width – this latter requiring an exponential increase to compensate for depth reduction.

In the following sections, we propose a direction to answer the question raised in Section (Section 2.6). That is, how, and can we “reconcile” these two predictors?

The answer is inspired by the field of statistical mechanics and the concept of phase transitions.

Thus, our “unification”3 attempt is inspired by that dynamic i.e. translating it into a dual regime. By attempt, we mean the combination of: $N_p^{-1/3}$, $N_p^{-2/3}$ and $N_p^{-1/2}$.

2.8. Ternary Nature of Neural Scaling Laws: The $N_p^{-1/2}$ Scaling Law

At this point, there remains a predictor to be fitted into the landscape i.e.: $N_p^{-1/2}$, this brings the number of identified predictors to three.

Indeed, from their toy experiment, the Resource-based Model [13][p.9] argues the following:

We conjecture: (1) there exists a critical depth such that above the critical depth, further increasing depth does not help; (2) current LLMs are beyond the critical depth. If these conjectures are indeed true, they would then give a testable hypothesis that the better way to scale up current LLMs is by scaling up the width but keeping the depth constant, which will give a faster scaling $\ell \propto N_p^{-1/2}$.

This introduces the $N_p^{-1/2}$ predictor beyond the critical depth conjecture and as further developed in Section (Section 2.9) in the redundancy phase.

Hereafter, we bring forth additional elements strengthening the $N_p^{-1/2}$ neural scaling law and the regime within which it takes operates.

2.8.1. Theoretical Foundations

In this section, we advance two theoretical contributions for the case of the $N_p^{-1/2}$ scaling law.

The first supporting argument comes from the Resource-based Model itself and its derivation is as follows:

• Assumption 1: $N\propto N_{\mathrm{width}}$,
• Assumption 3: $N_p\propto N_{\mathrm{width}}^2·N_{\mathrm{depth}}$,
• Fixing depth gives: $N_p\propto N_{\mathrm{width}}^2$ and $N\propto N_{\mathrm{width}}$ leads to: $N_p\propto N^2$.
• Because $N^{-1}$, we have: $\ell \propto N_p^{-1/2}$

We make two interlinked remarks:

• This development holds because of their critical depth conjecture and constitutes a pillar of their research,
• This conjecture is also the root cause of our work.

The second theoretical argument is sourced from: [29][Lemma 4.1] which we reproduce hereafter for convenience sake (1).

Lemma 1.

For any distribution $\mathcal{D}$, any interpolating learning rule A, and any sample size m:

$$-log\left(1-\underset{S\sim {\mathcal{D}}^m}{\mathbb{E}}\left[L\left(A\left(S\right)\right)\right]\right)\le {\displaystyle \frac{I(S;A(S\left)\right)}{m}}\le {\displaystyle \frac{\mathbb{E}[\parallel A(S)\parallel ]}{m}}.$$

This mathematical argument is developed in the context of Minimum Description Length(MDL).

We use Lemma 1(1) to back up $N_p^{-1/2}$ neural scaling law in the beyond critical depth conjecture. As above, with a fixed depth, in this regime, we argue that increasing width leads to a better optimization trajectory:

-

${\displaystyle \frac{\mathbb{E}[\parallel A(S)\parallel ]}{m}}$ remains constant i.e. same description length,

-

It creates redundant representation of the same minimal descriptions,

-

By the central limit theorem (CLT), we argue that, error to decrease by: ${\displaystyle \frac{1}{\sqrt{N}}}$,

-

Hence, $N_p^{-1/2}$ because when $N_p\propto N^2$ when depth is fixed.

In other words, within this mathematical framework, the network creates multiple instances of the same minimal description. The final prediction is an average of these implementations [29]. This statistical averaging explains why width-only scaling yields $\ell \propto N_p^{-1/2}$ rather than the $\ell \propto N_p^{-1/3}$ of standard scaling.

Using the Resource-based Model’s homogeneous growth hypothesis – where the ratios of allocated resources(neurons) are kept constant as the model gets larger is what enables this averaging to occur.

In closing, we saw that the $N_p^{-1/2}$ neural scaling law is rooted in the original Resource-based Model [13] and is linked to the critical depth conjecture.

Furthermore, to fortify this scaling law, we provided an additional mathematical argument entrenched in the Minimum Description Length(MDL) principle [29].

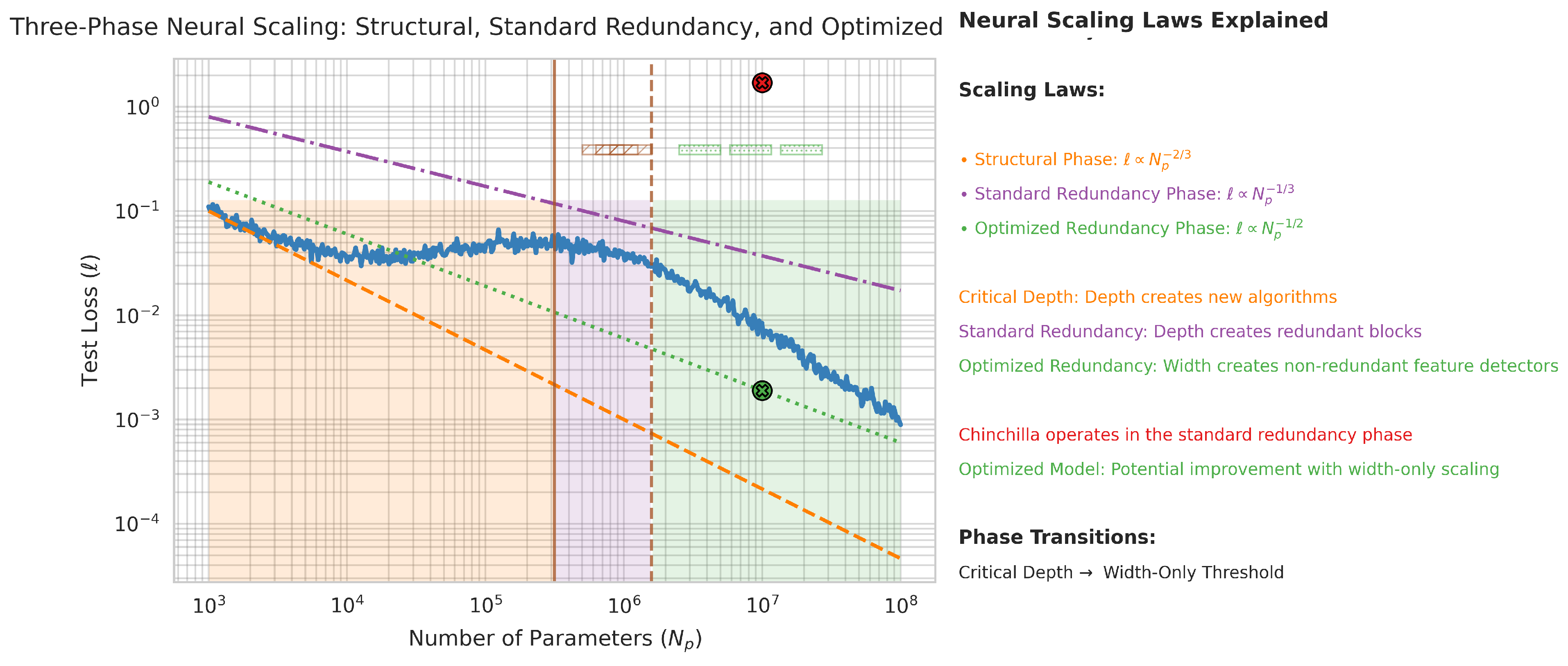
2.9. Critical Depth Conjecture as a Phase Transition

In this section, using a number of arguments rooted in different sources, we argue and make a case for a phase transition interpretation for the three neural scaling laws:

• $N_p^{-1/3}$ – from the Resource-based Model [13] which matches Chinchilla’s [17],
• $N_p^{-2/3}$ – from our Refactored-resource Model (Section 2.5),
• $N_p^{-1/2}$ – from the arguments we develop in Section (Section 2.8).

Indeed, as mentioned throughout this work, the internal logic of the Resource-based Model holds precisely because of the introduction of the critical depth conjecture – without it the paper’s logic collapses.

We articulate the critical depth conjecture as a phase transition composed of the following three-regime profile:

1. Structural Phase – below critical depth:

• The network builds new capabilities, it tries to learn “new algorithms”, the main resource is depth,
• The loss scales as: $\ell \propto N_p^{-2/3}$,
• This phase is not affected by the $N_p^{-1/2}$ scaling law.

2. Redundancy Phase – above critical depth:

In this phase, we have two possible scaling trajectories:

• Standard trajectory with $\ell \propto N_p^{-1/3}$ – where depth and width are jointly scaled up,
• Width-only trajectory with $\ell \propto N_p^{-1/2}$ – where depth is fixed and only width is increased.
  Thus, making the $\ell \propto N_p^{-1/2}$ neural scaling law is an alternative scaling trajectory in the redundancy phase.

Figure 3. Schematic Illustration of 3 Regimes Phase Transition.

Figure 3. Schematic Illustration of 3 Regimes Phase Transition.

3. Results

3.1. Duality: Width ∧ Depth

Based on our developments, we can formulate the following propositions with respect to the relation between the width and depth of neural-based architectures:

-

Width enables parallel processing of features,

-

Whereas, depth enables sequential composition of operations. In other words, it seems that depth is linked to the expressivity capabilities of a network.

In the context of Large Language Models, the observation about width is interesting because large language reasoning models are based on declinations of the Transformer-neural architecture(TNA) [5]; within which, most of the parameters are to be found in the feedforward neural network(FFNN) component used to extract features.

Combined with the self-attention mechanism, this allowed TNA to address the performance/scaling bottleneck issue that we were facing in natural language processing(NLP) tasks using recurrent neural networks(RNNs).

Additionally, the theoretical insight on depth Vardi et al. [26] finds an empirical illustration with Nguyen et al. [27] discovery of block structures – where they observe that the increase of depth beyond a certain threshold builds redundancy.

3.2. Paving the Path Through: {Theoretical ∧ Logic ∧ Empirical} Explorations

Our formalized re-interpretation of the hypotheses developed in [13] uses the approach of SAT/SMT solvers. Though constrained by the known “limitations” of classical symbolic AI, this can be seen as a proto/primitive-automated “reasoning” engine. The gap needs to be closed – is being closed?

Additionally, this is not without recalling the pioneering work [30] with systems such as: CAIA and MALICE.

In our case, the use of propositional logic and the (Z3) solver [25] allows to derive the following two interesting points:

• Lead to the formulation of the Refactored-resource Model (Section 2.5) with: $\ell \propto N_p^{-2/3}$
• Strengthened the critical depth conjecture even though it may seem paradoxical at first sight.
• Lead to the expression of a 3 regimes phase transition proposal (Section 2.9).

3.3. Prescriptive Scaling Guidance

-

The Resource-based Model holds around the homogeneous growth and critical depth conjecture.

-

On the other hand, our Refactored-resource Model which doesn’t rely on other conjectures than the original Resource-based Model assumptions (Section 2.2).

This is not to be interpreted “sequentially”. Instead, it outlines the refinement that we derived using a combination of approaches summarized in Section (Section 3.2). The story goes like the following:

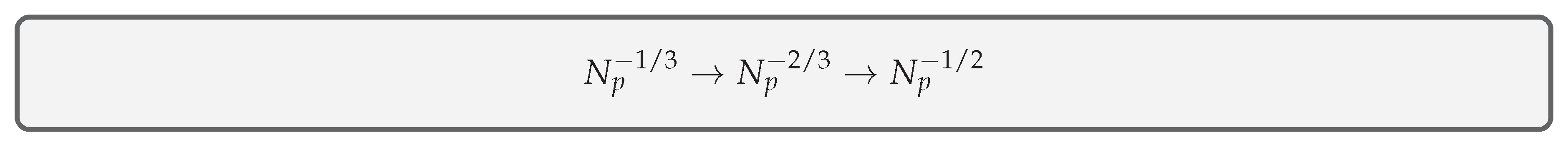
• At first, we have the standard Neural Scaling Laws: $N_p^{-1/3}$,
• Second, we derived $N_p^{-2/3}$ that we conjecture taking place below the critical depth,
• And third, jointly with the original Resource-based Model and our developments in Section (Section 2.8), we endorsed and backed up: $N_p^{-1/2}$.

Compared to the current practice our proposal gives the following benefit:

• Current practice (scaling width and depth): $\ell \propto N_p^{-1/3}\approx N_p^{-0.33}$
• Our proposal beyond the critical depth (scaling width only): $\ell \propto N_p^{-1/2}=N_p^{-0.50}$

This means that for the same increase in parameters:

• Current scaling reduces loss by approximately 33%,
• The proposed scaling would reduce loss by 50%.

4. Discussion & Conclusions

In this work, we studied Neural Scaling Laws (NSLs). Namely, through the lens of the paper: A Resource Model For Neural Scaling Law Song et al. [13].

We expressed through propositional logic and the Z3 SMT solver [25] the paper’s internal logic. Through this process, we were able to acknowledged a logical inconsistency between the conducted derivation in the absence of the critical depth conjecture. This formalization allowed us to formulate refinements on the classical Neural Scaling Laws (NSLs).

Moreover, using a framework inspired in statistical mechanics, we expressed a three-regime phase transition scaling laws.

Furthermore, in very close agreement with Chinchilla’s [17] experimentally-derived scaling law, the Resource-based Model [13] predicts: $\ell \propto N_p^{-1/3}$.

Through the combined use of logic, empirical and theoretical approaches, we were able to express a new {profile, dynamic} of the Neural Scaling Laws.

Ultimately, we propose a transition from predictive to prescriptive expression of Neural Scaling Laws (NSLs).

To be specific, below the critical depth, we have a structural phase, where we argue that, the loss scales following: $\ell \propto N_p^{-2/3}$. Above the critical depth, a redundancy phase, with a loss following the classical: $\ell \propto N_p^{-1/3}$ (where most of current LLMs operate).

Finally, an optimized trajectory where depth is fixed and a scaling is based on width following: $\ell \propto N_p^{-1/2}$.

4.1. Further Research Paths

In light of our developments, we propose the following lines of research to be of interest for understanding Neural Scaling Laws (NSLs):

-

For LLMs, investigate the optimal depth-to-width ratio(s),

-

NSLs are derived from: power laws ←learning curves← data [19].

-

Further investigate the critical depth conjecture/phenomenon, from a physics-basis perspective?

-

Using this work as a basis, can we shed some light on one of the challenges in LLMs e.g.: Why Can’t Transformers Learn Multiplication? Reverse-Engineering Reveals Long-Range Dependency Pitfalls Bai et al. [31]

5. Broader Impact Statement

Conditioned on the applicability of our results, we consider the following aspects.

Potential Reduction in Resource Requirements

A reduction in the computational resources required for training and operating frontier AI models has complex and multifaceted consequences that are, by definition, challenging to weigh and are beyond the scope of this work.

However, from a global perspective, lowering the computational barrier to entry has a cascade of effects. It democratizes access to frontier AI research, making powerful tools available to a wider range of actors. Like many transformative technologies, this carries a superposition of benefits and risks: it can accelerate positive innovation and scientific discovery while simultaneously lowering the barrier for potential misuse.

In conclusion, while some industry labs are developing frameworks to address the unique challenges of frontier AI–such as preparedness [32] and responsible scaling policies [33]–the field itself remains in a dynamic and uncertain state. Navigating its development is akin to constructing a bridge while simultaneously walking across it.

Appendix B.1. Step 1: The Foundational Hypotheses (From the: A Resource Model for Neural Scaling Laws) Paper’s Experiments

The paper establishes two key empirical findings from its toy experiments; that we also concur with.

• Hypothesis 1 (Single Task Scaling): For a single subtask, the loss ${\ell }_{\mathrm{subtask}}$ is inversely proportional to the number of allocated neurons $N_{\mathrm{subtask}}$ for that task.

  $${\ell }_{\mathrm{subtask}}\propto N_{\mathrm{subtask}}^{-1}$$
• Hypothesis 2 (Homogeneous Growth): For a composite task with multiple subtasks, when the network grows, the ratios of allocated neurons between any two subtasks remain constant. This means the total number of allocated neurons $N_{\mathrm{total}}$ increases, and each subtask’s allocation increases by the same factor.
  From these two hypotheses, the paper derives:
• Theorem (Composite Task Scaling): For a composite task, the total loss ${\ell }_{\mathrm{total}}$ is inversely proportional to the total number of allocated neurons $N_{\mathrm{total}}$.

  $${\ell }_{\mathrm{total}}\propto N_{\mathrm{total}}^{-1}$$

This is our first key equation:

$$\ell \propto N^{-1}$$

(A1)

(For simplicity sake, we drop the “total” subscript; N now represents the total resource.)

Appendix B.2. Step 2: Defining the Total Resource N

This is where our derivation diverges from the paper.

• The Resource-based ModelAssumption (A1): $N\propto N_{\mathrm{width}}$
  This assumes the total resource N scales only with the network’s width. This is the source of the inconsistency and trigger of our work.
• Our Refactored Assumption: $N\propto N_{\mathrm{width}}·N_{\mathrm{depth}}$

This is based on the paper’s own evidence (Section 3.2) that a “module” can span on multiple layers. Therefore, the total number of allocated neurons N should scale with the total number of neurons in the network’s hidden layers.

-

The number of neurons per layer is $N_{\mathrm{width}}$,

-

The number of layers is $N_{\mathrm{depth}}$,

-

Therefore, the total number of neurons is $\propto N_{\mathrm{width}}·N_{\mathrm{depth}}$.

This is our second key equation:

$$N\propto N_{\mathrm{width}}·N_{\mathrm{depth}}$$

(A2)

Appendix B.3. Step 3: Incorporating the Scaling of Depth

The paper’s Assumption 2 is widely observed in practice (e.g., Chinchilla Hoffmann et al. [17]):

• Assumption 2: $N_{\mathrm{depth}}\propto N_{\mathrm{width}}$

This means that as models are scaled up, their depth and width are increased at the same rate.

We substitute this into our corrected equation (A2):

$$\begin{array}{cc}\hfill N& \propto N_{\mathrm{width}}·N_{\mathrm{depth}}\hfill \\ \hfill N& \propto N_{\mathrm{width}}·\left(N_{\mathrm{width}}\right)(\sin \mathrm{ce}{N}_{\mathrm{depth}}\propto N_{\mathrm{width}})\hfill \\ \hfill N& \propto N_{\mathrm{width}}^2\hfill \end{array}$$

This is our third key equation:

$$N\propto N_{\mathrm{width}}^2$$

(A3)

Appendix B.4. Step 4: Relating Parameters N_p to Architecture

The Resource-based Model’s Assumption 3 is standard for transformer models, where the vast majority of parameters are in the MLP (feed-forward) layers:

• Assumption 3: $N_p\propto N_{\mathrm{width}}^2·N_{\mathrm{depth}}$

We again substitute $N_{\mathrm{depth}}\propto N_{\mathrm{width}}$:

$$\begin{array}{cc}\hfill N_p& \propto N_{\mathrm{width}}^2·N_{\mathrm{depth}}\hfill \\ \hfill N_p& \propto N_{\mathrm{width}}^2·\left(N_{\mathrm{width}}\right)(\sin \mathrm{ce}{N}_{\mathrm{depth}}\propto N_{\mathrm{width}})\hfill \\ \hfill N_p& \propto N_{\mathrm{width}}^3\hfill \end{array}$$

This is our fourth key equation:

$$N_p\propto N_{\mathrm{width}}^3$$

(A4)

Appendix B.5. Step 5: Relating N_p to N

We now have two equations in terms of $N_{\mathrm{width}}$:

-

From A3: $N\propto N_{\mathrm{width}}^2$

-

From A4: $N_p\propto N_{\mathrm{width}}^3$

We can express a direct relationship between $N_p$ (number of parameters) and N (total resources) by eliminating $N_{\mathrm{width}}$.

• From equation A3 ($N\propto N_{\mathrm{width}}^2$), we can solve for $N_{\mathrm{width}}$:

  $$N_{\mathrm{width}}\propto N^{1/2}$$
• Substitute this into equation A4:

  $$\begin{array}{cc}\hfill N_p& \propto {\left(N^{1/2}\right)}^3\hfill \\ \hfill N_p& \propto N^{3/2}\hfill \end{array}$$

This is our fifth key equation:

$$N_p\propto N^{3/2}$$

(A5)

We can rearrange this to express N in terms of $N_p$:

$$N\propto N_p^{2/3}$$

Appendix B.6. Step 6: Deriving the Final Scaling Law

We now have everything to derive the final scaling law:

-

From Step 1, we have the loss scaling with the resource: $\ell \propto N^{-1}$

-

From Step 5, we have the resource scaling with the parameters: $N\propto N_p^{2/3}$

We substitute the second into the first:

$$\begin{array}{cc}\hfill \ell & \propto N^{-1}\hfill \\ \hfill \ell & \propto {\left(N_p^{2/3}\right)}^{-1}\hfill \\ \hfill \ell & \propto N_p^{-2/3}\hfill \end{array}$$

Note: the value is steeper $-2/3\approx -0.67$ than Chinchilla’s: $-0.34$

Appendix D.1. Hypotheses

Homogeneous Growth Hypothesis (Hypothesis 2):

If a neural network with N neurons allocates resources $N_i$ to subtask i, then if the network size is scaled up (along width) such that $N\to aN$, all the resources are scaled up by the same factor a, i.e., $N_i\to a{N}_i$.

This implies that the ratios $N_i/N_j$ remain constant as the network scales.

Single-Task Scaling (Hypothesis 1):

For a single subtask, the loss scales inversely with its allocated neurons: ${\ell }_i\propto N_i^{-1}$.

Composite Loss (Hypothesis 3 – Linear Additivity):

The loss of a composite task can be decomposed as a linear summation of the losses of its subtasks: $\ell ={\sum }_i{\alpha }_i{\ell }_i$.

Appendix D.2. Derivation of the Total Loss Under Homogeneous Growth

Given:

• ${\ell }_i={\displaystyle \frac{c_i}{N_i}}$ for some constants $c_i$,
• $N_i=r_{i}N$, where $r_i$ is a fixed ratio (${\sum }_i{r}_i=1$) due to homogeneous growth,

then:

$$\begin{array}{cc}\hfill \ell & =\sum _i{\alpha }_i{\ell }_i=\sum _i{\alpha }_i{\displaystyle \frac{c_i}{N_i}}=\sum _i{\alpha }_i{\displaystyle \frac{c_i}{r_{i}N}}={\displaystyle \frac{1}{N}}\sum _i{\displaystyle \frac{{\alpha }_i{c}_i}{r_i}}.\hfill \end{array}$$

Since the sum ${\sum }_i{\displaystyle \frac{{\alpha }_i{c}_i}{r_i}}$ is a constant (independent of total network size N), we obtain:

$$\ell \propto N^{-1},$$

Appendix D.3. Summary

The homogeneous growth hypothesis implies that the total composite loss scales as:

$$\begin{array}{c}\hfill \ell \propto N^{-1}\end{array}$$

(A6)

where $N={\sum }_i{N}_i$ is the total number of allocated neurons across all subtasks.