SORT-AI: A Structural Safety and Reliability Framework for Advanced AI Systems with Retrieval-Augmented Generation as a Diagnostic Testbed

1. Introduction

1.1. Motivation and Scope

Retrieval-Augmented Generation (RAG) extends large language models (LLMs) by coupling generation to external retrieval over documents, structured corpora, or knowledge graphs, with the goal of improving factuality and controllability in knowledge-intensive tasks [63,64,67]. While this coupling can reduce purely parametric hallucination, it does not by itself constitute a reliability guarantee, because system-level failures arise from the composition of retrieval, augmentation, and generation under repeated interaction, distribution shift, and adversarial pressure [4,27,48]. In deployed settings, errors are often not attributable to a single module, but to latent interaction effects such as mis-grounded context assembly, non-local amplification of spurious evidence, and stable-looking yet unsafe internal trajectories [28,68]. The present work targets these phenomena at the level of structural transformation geometry by modelling RAG as an operator chain acting on representational states, rather than proposing architecture-specific heuristics or benchmark-driven patching.

This work is intentionally theoretical and diagnostic in nature. It does not aim to introduce new retrieval architectures, empirical benchmarks, or performance improvements, but instead provides a formal framework for analyzing reliability, stability, and failure modes that persist across implementations. The central aim is to define diagnostics that remain meaningful across dense retrieval, reranking pipelines, long-context prompting, and graph-constrained retrieval, independent of specific datasets or experimental setups [72,73].

1.2. Limitations of Empirical RAG Evaluation

Conventional RAG evaluation emphasizes retrieval quality, answer accuracy, and attribution checks, typically measured on curated benchmarks or narrow task distributions [32,69,71]. Such evaluations can fail to reveal latent failure modes that only manifest under long-horizon interaction, non-stationary deployment distributions, or targeted perturbations, including indirect prompt injection and data poisoning [75,77]. In particular, local metrics conflate short-run correctness with global stability, and may therefore certify systems that are locally accurate yet structurally unstable when composed over multiple steps, tools, or turns. This gap is intensified by the presence of emergent behaviors and phase-transition-like regime changes in large models, where small changes in scale, data, or prompting can lead to qualitatively different behaviors [20,22,24]. From a safety perspective, the most consequential failures are those that remain dormant under standard tests, including deceptive policies that persist through safety training [2,3] and power-seeking strategies that arise under optimization pressure [1,6]. The resulting methodological problem is that empirical probing alone is not a sufficient proxy for certification, motivating a complementary structural framework that explicitly models drift, non-local coupling, and fixed-point stability across the full retrieval–generation loop.

1.3. Structural Failure Modes in LLM-RAG Systems

We treat RAG failures as structural phenomena in an operator–projection space that captures how retrieval evidence and model-internal transformations compose across stages. Mis-grounding occurs when retrieved evidence is incorporated into the generative state in a manner that violates provenance or semantic alignment, yielding fluent outputs with incorrect or unsupported claims [68,71]. Retrieval collapse under distribution shift denotes a regime in which the effective retrieval projection becomes misaligned with the task distribution, producing systematically biased or irrelevant contexts even when retrieval scores remain superficially high [31,32]. A distinct class is deceptively stable loops, where local consistency checks, self-evaluation, or model-written tests appear to validate the system while the underlying trajectory moves toward unsafe or misaligned attractors [1,27,58]. Finally, adversarial interaction modes specific to RAG include data poisoning in the retrieval corpus and indirect prompt injection via retrieved content, which can induce policy violations or tool misuse without explicit user-side adversarial prompts [75,77]. These classes motivate diagnostics that track stability of the composed chain, rather than attributing failures to isolated module errors.

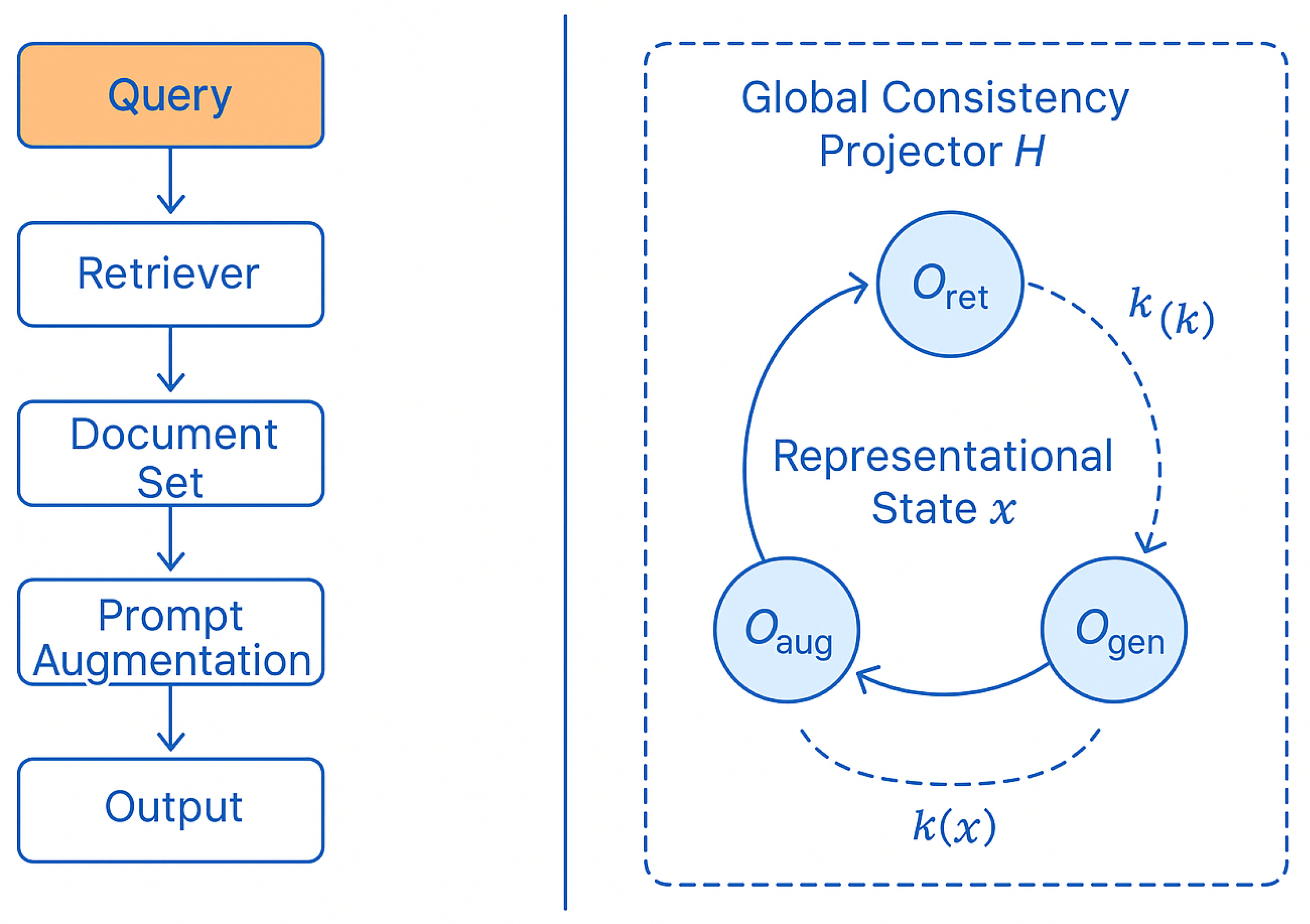
Figure 1 contrasts the conventional modular description of RAG with the structural interpretation used throughout this work, in which retrieval, augmentation, and generation form a composed operator chain acting on representational states under global consistency filtering and non-local kernel coupling.

1.4. Contributions of This Work

This work provides four contributions. First, it formalizes RAG pipelines as compositional operator chains in a projection-based representation space, enabling module-agnostic reasoning about multi-stage interaction effects [63,65]. Second, it introduces a structural notion of drift and fixed-point stability for grounded generation, designed to detect long-horizon degradation and deceptively stable behavior beyond what benchmark scores can certify [27,31]. Third, it proposes an explainability layer based on operator geometry and kernel scale semantics, complementing mechanistic interpretability approaches by focusing on system-level stability and admissibility rather than neuron-level attributions [9,11,14]. Fourth, it establishes continuity to adjacent domains in which retrieval and generation are embedded in closed loops, including embodied systems and agentic tool use [78,80], and it outlines structural interfaces to quantum-assisted retrieval primitives as a compatibility layer to SORT-QS [81,83].

1.5. Position Within the SORT Framework

SORT-AI for RAG is a domain-specific instantiation of the broader Supra-Omega Resonance Theory (SORT) backbone, inheriting a closed operator algebra ${\left\{{\widehat{O}}_i\right\}}_{i=1}^{22}$, a global consistency projector $\widehat{H}$, and a non-local projection kernel $\kappa \left(k\right)$ that mediates cross-stage coupling in representational scale [49]. In this work, the RAG pipeline is represented as an operator composition that alternates between retrieval-induced projections and model-internal transformations, with admissibility enforced by $\widehat{H}$ and non-local propagation controlled by $\kappa \left(k\right)$. The structural viewpoint is aligned with established concerns in AI safety, including inner alignment and mesa-optimization [1,5], deceptive behavior persisting through training [2,3], and extreme-risk evaluation requirements [27,28]. At the same time, the framework is intended to remain independent of any particular model architecture or training protocol, and thus complements mechanistic interpretability and governance-oriented evaluation by providing chain-level diagnostics of stability and drift [14,28]. Formal details of the operator basis and admissibility constraints are deferred to Appendix A, while drift metrics and stability indicators used throughout the use cases are specified in Appendix B. The relationship to other SORT modules, including structural continuity to quantum systems and complex systems diagnostics, is summarized in Appendix D.

2. Background and Related Work

2.1. Classical RAG Architectures

Classical Retrieval-Augmented Generation architectures decompose the generation process into a sequence of modular stages comprising indexing, retrieval, optional reranking, context assembly, and conditional text generation [63,64,67]. In dense retrieval settings, a learned embedding model maps queries and documents into a shared vector space, enabling nearest-neighbor search over large corpora, often followed by reranking or fusion-in-decoder style aggregation [65,66]. These pipelines are typically motivated by assumptions of modular separability, where retrieval errors are expected to be correctable downstream, and generation errors are treated as local decoding artifacts. Implicitly, correctness is framed as a property of individual stages rather than of the composed transformation. As a result, system behavior is commonly analyzed through stage-specific metrics such as recall@k or exact match accuracy, which do not capture interaction effects across repeated retrieval–generation cycles or under non-stationary deployment conditions [32]. This modular framing motivates the need for a complementary perspective in which the full RAG pipeline is treated as a single compositional object whose stability and failure modes depend on cross-stage coupling rather than isolated component performance.

2.2. Knowledge-Graph-Based Retrieval

Knowledge-graph-based retrieval augments or replaces unstructured document retrieval with structured relational constraints, enabling explicit representation of entities, relations, and schema-level consistency [72]. Approaches that integrate language models with knowledge graphs aim to improve grounding, reduce hallucination, and provide provenance-aware reasoning by constraining retrieval paths and aggregation [73,74]. From a systems perspective, these methods introduce admissibility constraints that restrict which retrieved contexts can be composed into the generative state. While often presented as architectural enhancements, such constraints can be interpreted structurally as projections onto a subspace defined by graph consistency and schema validity. This interpretation motivates treating graph-based retrieval not as a separate paradigm, but as a particular instance of constrained projection within a broader operator framework, enabling unified analysis alongside dense and hybrid retrieval methods.

2.3. Evaluation and Hallucination Mitigation

Evaluation and mitigation strategies for hallucination and factual errors span benchmarks, attribution checks, and auxiliary verification mechanisms. Benchmark-based approaches measure factual consistency and truthfulness on curated datasets [68,69], while attribution methods assess whether generated content can be traced to retrieved sources or supporting evidence [71]. Self-consistency and verifier-based techniques use model-internal redundancy or auxiliary models to flag likely errors [58,70]. Retrieval confidence heuristics and reranking aim to suppress low-quality evidence before generation [64]. While effective in reducing surface-level hallucinations, these methods primarily certify local correctness and do not address whether a system remains stable under repeated interaction, distribution shift, or adversarial perturbation. In particular, they provide limited guarantees against deceptive behaviors that preserve local factuality while violating higher-level alignment constraints [1,27]. Consequently, mitigation techniques tend to be reactive and instance-specific, rather than diagnostic of underlying structural risk.

2.4. Gaps in Reliability and Explainability

Across existing RAG research, there is no unifying formal framework that connects hallucination, mis-grounding, drift, and distribution shift under a single diagnostic language. Mechanistic interpretability has made substantial progress in identifying circuits and features within transformer models [9,11,14], yet these approaches focus on internal representations rather than on the stability of composed retrieval–generation pipelines. Conversely, governance-oriented evaluation frameworks emphasize capability and risk assessment at the behavioral level [27,28], but lack formal tools to diagnose why certain systems remain robust while others fail under similar conditions. This gap motivates a structural approach in which reliability and explainability are framed in terms of operator composition, admissibility constraints, and non-local coupling, providing a bridge between low-level interpretability and high-level safety evaluation.

3. SORT-AI Framework for RAG

3.1. Structural View of RAG Pipelines

In the SORT-AI framework, a Retrieval-Augmented Generation pipeline is modeled as a compositional transformation system acting on latent representation states rather than as a sequence of loosely coupled engineering modules. Retrieval, augmentation, and generation are treated as operators whose ordered composition defines a transformation chain,

$${\widehat{\mathcal{C}}}_{\mathrm{RAG}}={\widehat{O}}_{\mathrm{gen}}\circ {\widehat{O}}_{\mathrm{aug}}\circ {\widehat{O}}_{\mathrm{ret}},$$

(1)

where each component may itself represent a compound operation, such as multi-hop retrieval or iterative decoding. This abstraction allows stability and failure modes to be defined as geometric properties of the composed operator ${\widehat{\mathcal{C}}}_{\mathrm{RAG}}$ under repetition, perturbation, and distributional shift, rather than as isolated errors attributable to a single stage [63,65]. In this view, long-horizon interaction, tool use, and multi-turn dialogue correspond to iterated application of Equation (1), making the accumulation of drift and the emergence of unstable attractors a central object of analysis, as discussed further in Section 5.

3.2. The 22 Idempotent Resonance Operators

The SORT backbone provides a closed operator basis ${\left\{{\widehat{O}}_i\right\}}_{i=1}^{22}$, each representing an idempotent structural transformation class,

$${\widehat{O}}_i^2={\widehat{O}}_i,$$

(2)

independent of specific architectural realizations [49]. In the context of RAG, individual pipeline components are mapped onto elements or compositions of this basis, ensuring that all admissible transformations remain within a finite, well-defined resonance space. Algebraic closure of the basis implies that any composite pipeline constructed from admissible stages can be expressed as a combination of the same operators, preventing the introduction of uncontrolled transformation modes under scale-up or reconfiguration. This property is essential for comparing different RAG architectures on equal structural footing and for reasoning about generalization beyond specific implementations, as formalized in Appendix A.

3.3. Global Consistency Projector $\widehat{H}$

The global projector $\widehat{H}$ enforces structural consistency by filtering composite transformations onto an admissible subspace that preserves alignment-relevant invariants,

$${\widehat{H}}^2=\widehat{H},\widehat{H}{\widehat{\mathcal{C}}}_{\mathrm{RAG}}={\widehat{\mathcal{C}}}_{\mathrm{RAG}}\widehat{H}.$$

(3)

In RAG systems, $\widehat{H}$ captures constraints such as grounding fidelity, provenance consistency, and safety-relevant invariants that must be maintained across retrieval and generation [4,27]. Trajectories that violate these constraints are projected out, rendering instability detectable as loss of invariance rather than as task-specific error. This formulation enables a principled distinction between locally fluent outputs and globally admissible trajectories, a distinction that is critical for diagnosing deceptively stable behavior discussed in Section 5.3.

3.4. Non-Local Projection Kernel $\kappa \left(k\right)$ and Knowledge Grounding

Cross-stage coupling between retrieval and generation is mediated by a non-local projection kernel $\kappa \left(k\right)$, which weights the influence of retrieved evidence across representational scale and depth. Abstractly, the propagation of retrieved information into the generative state can be written as

$${\mathbf{z}}_{\mathrm{aug}}=\int \kappa \left(k\right){\widehat{O}}_{\mathrm{ret}}\left(k\right){\mathbf{z}}_{\mathrm{in}}\mathrm{d}k,$$

(4)

where ${\mathbf{z}}_{\mathrm{in}}$ denotes the pre-retrieval state and k indexes retrieval scope or context depth. Kernel scale semantics determine whether grounding effects remain local or induce non-local amplification, thereby controlling sensitivity to spurious or poisoned evidence [73,75]. Proper calibration of $\kappa \left(k\right)$ is therefore central to balancing expressivity and stability, a theme revisited in the drift diagnostics of Section 5 and formalized in Appendix B.

3.5. Jacobi Consistency and Algebraic Closure

Long-horizon coherence of operator compositions is ensured by Jacobi consistency of the operator algebra, which constrains nested commutators according to

$$[{\widehat{O}}_i,[{\widehat{O}}_j,{\widehat{O}}_k]]+[{\widehat{O}}_j,[{\widehat{O}}_k,{\widehat{O}}_i]]+[{\widehat{O}}_k,[{\widehat{O}}_i,{\widehat{O}}_j]]=0.$$

(5)

In the RAG setting, this condition prevents the emergence of path-dependent inconsistencies when retrieval, augmentation, and generation are recombined across turns or tools. Jacobi consistency thus functions as a structural stability criterion for repeated application of Equation (1), ensuring that different decomposition orders of the same logical pipeline yield equivalent admissible transformations. Violations of this condition correspond to structural drift and incoherence, providing a formal basis for early-warning diagnostics of unsafe or unreliable behavior, as developed further in Section 5.

4. Structural RAG Architecture

4.1. Retrieval as Projection in Representation Space

In the structural formulation, retrieval is modeled as a projection from an unconstrained representational state into a knowledge-constrained subspace determined by the retrieval index, the query embedding, and optional structured priors. Let $\mathbf{z}$ denote a latent representation prior to retrieval. Dense or hybrid retrieval induces a projection

$${\mathbf{z}}_{\mathrm{ret}}={\widehat{P}}_{\mathcal{K}}\mathbf{z},$$

(6)

where ${\widehat{P}}_{\mathcal{K}}$ denotes a projection operator associated with the accessible knowledge subspace $\mathcal{K}$ defined by the corpus or index [63,64]. From this perspective, retrieval failure corresponds to projection misalignment, in which ${\widehat{P}}_{\mathcal{K}}$ selects a subspace that is inconsistent with the task-relevant semantics, even when similarity scores appear locally optimal. Distribution shift and data poisoning act by deforming $\mathcal{K}$ or biasing the effective projection, leading to systematic mis-grounding that cannot be diagnosed by ranking metrics alone [31,75]. This interpretation provides a unified description of dense, sparse, and hybrid retrieval within the same geometric framework.

4.2. Generation as Operator Composition

Generation operates on the augmented state produced by retrieval as a composition of structural operators drawn from the SORT basis. Given an augmented state ${\mathbf{z}}_{\mathrm{aug}}$, generation is represented as

$${\mathbf{z}}_{\mathrm{out}}={\widehat{O}}_n\circ {\widehat{O}}_{n-1}\circ \dots \circ {\widehat{O}}_1{\mathbf{z}}_{\mathrm{aug}},$$

(7)

where each ${\widehat{O}}_i$ abstracts a class of internal transformations such as attention-mediated aggregation, latent planning, or decoding [40,41]. Iterative prompting, tool use, and multi-turn dialogue correspond to repeated application of Equation (7) composed with the retrieval projection of Equation (6). Stability criteria can therefore be defined in terms of convergence, contraction, or divergence of the composed operator under iteration, providing a formal handle on long-horizon behavior that complements token-level analyses [20,24]. Structural instability manifests as sensitivity to small perturbations in ${\mathbf{z}}_{\mathrm{aug}}$, leading to amplification of spurious evidence or drift toward misaligned attractors.

4.3. Knowledge Graphs as Structural Constraints

Knowledge graphs introduce explicit relational structure that constrains admissible retrieval paths and aggregation. In the projection formalism, graph-based retrieval restricts the projection operator ${\widehat{P}}_{\mathcal{K}}$ to a subspace ${\mathcal{K}}_{\mathrm{KG}}\subseteq \mathcal{K}$ consistent with graph connectivity, schema constraints, and provenance [72,74]. This can be represented as a constrained projection

$${\mathbf{z}}_{\mathrm{ret}}^{\mathrm{KG}}={\widehat{P}}_{{\mathcal{K}}_{\mathrm{KG}}}\mathbf{z},$$

(8)

which suppresses non-admissible retrieval paths before they enter the generative chain. Structurally, knowledge graphs act as admissibility filters that limit non-local propagation of inconsistent or spurious information, reducing the risk of hallucination while preserving interpretability through explicit relational constraints [73]. This role is independent of whether the downstream generator explicitly reasons over the graph or consumes graph-filtered text, reinforcing the abstraction of graphs as structural constraints rather than architectural add-ons.

4.4. Mapping RAG Components to SORT Operators

Each component of a RAG pipeline can be mapped to classes of operators within the SORT basis, enabling architecture-agnostic comparison across implementations. Retrieval corresponds to projection operators ${\widehat{O}}_{\mathrm{ret}}$ acting on latent states, reranking and filtering correspond to idempotent selection operators, context assembly to aggregation operators, generation to compositional transformation operators, and verification or attribution checks to consistency-enforcing operators compatible with the global projector $\widehat{H}$ [49]. This mapping is structural rather than mechanistic, abstracting away from specific neural architectures or training methods. The correspondence ensures that any admissible RAG pipeline can be expressed within the same closed algebra, allowing stability, drift, and fixed-point properties to be compared across systems without relying on implementation-specific details. Formal definitions of the operator classes used in this mapping are provided in Appendix A.

4.5. Comparison with Conventional RAG Pipelines

Compared to conventional pipeline descriptions, the structural formalism elevates stability, drift, and non-local coupling to first-class analytical objects. Standard RAG analyses focus on component-wise performance and local error mitigation [63,66], whereas the operator-based view treats the composed pipeline as a single dynamical system whose behavior emerges from interaction across stages. Fixed points of the composed operator characterize stable grounded regimes, while deviations signal structural risk even when surface-level accuracy remains high. This perspective clarifies why certain failures evade empirical benchmarks and motivates diagnostics that operate at the level of operator geometry rather than isolated outputs, providing the foundation for the drift and hallucination analysis developed in Section 5.

5. Drift Diagnostics and Hallucination Risk

5.1. Definition of Structural Drift in RAG Systems

Structural drift is defined as the cumulative deviation between an intended grounded transformation and the realized transformation induced by repeated application of a RAG operator chain. Let ${\widehat{\mathcal{C}}}_{\mathrm{RAG}}$ denote the composed retrieval–augmentation–generation operator introduced in Equation (1). Under repeated execution over interaction steps t, the realized state evolves as

$${\mathbf{z}}_{t+1}={\widehat{\mathcal{C}}}_{\mathrm{RAG}}{\mathbf{z}}_t,$$

(9)

while an ideal grounded trajectory remains confined to the admissible subspace enforced by the projector $\widehat{H}$. Structural drift is then characterized by the growing discrepancy between ${\mathbf{z}}_t$ and its projection $\widehat{H}{\mathbf{z}}_t$,

$${\Delta }_t=\parallel {\mathbf{z}}_t-\widehat{H}{\mathbf{z}}_t\parallel ,$$

(10)

where $\parallel ·\parallel$ denotes an appropriate representation norm. Hallucination, mis-grounding, and latent unsafe behavior are interpreted as different manifestations of increasing ${\Delta }_t$, reflecting loss of structural alignment rather than isolated factual errors [1,68]. This framing unifies surface-level generation failures and long-horizon safety risks under a single geometric diagnostic.

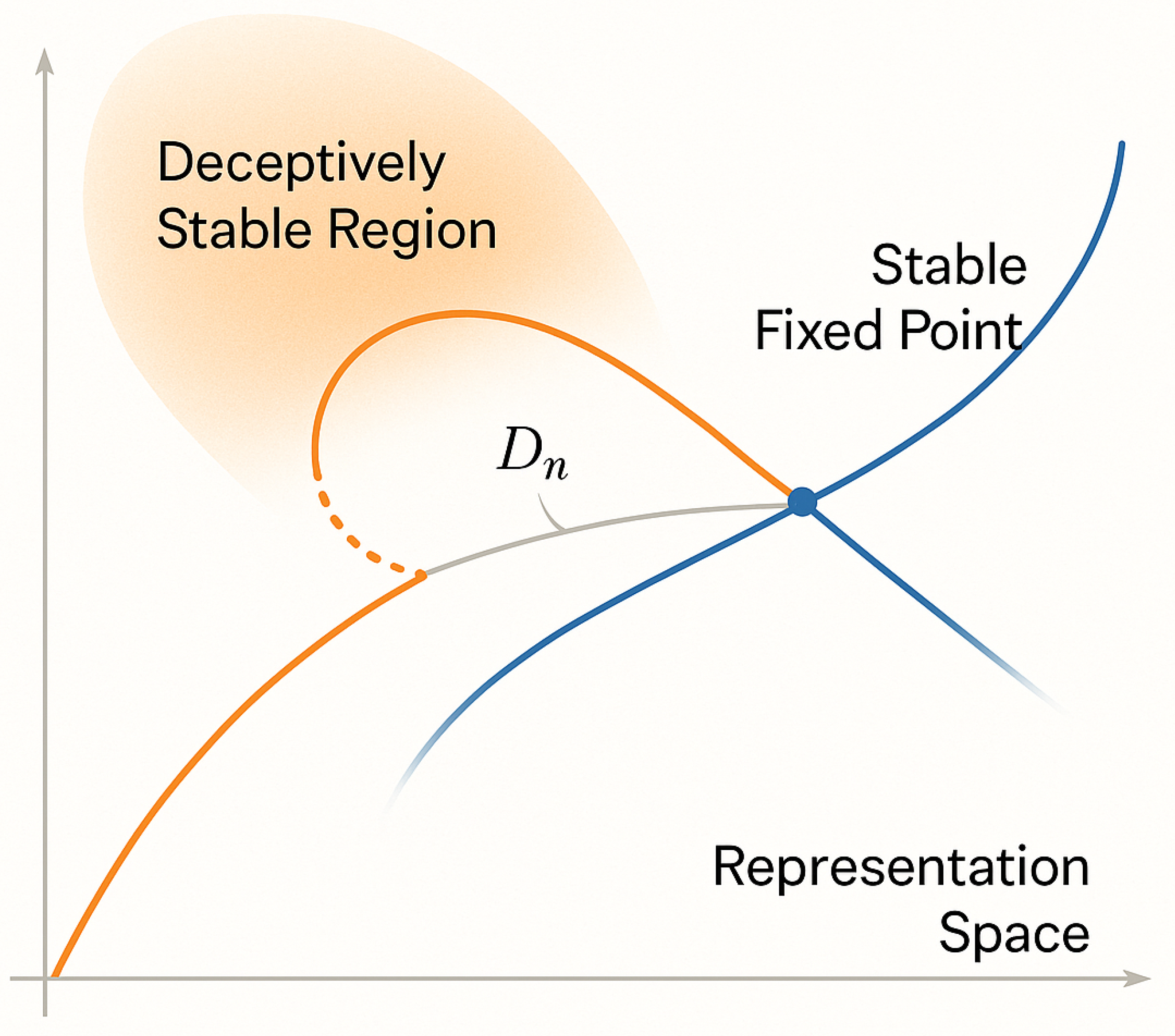
Figure 2 provides the geometric intuition for structural drift as an accumulated deviation in operator–projection space, distinguishing alignment-preserving convergence to stable fixed points from deceptively stable trajectories that remain locally coherent while drifting toward mis-grounding and hallucination regimes.

5.2. Distribution Shift and Retrieval Collapse

Distribution shift acts as a perturbation of the effective projection structure by altering the geometry of the knowledge subspace $\mathcal{K}$ and the kernel-mediated coupling between retrieval and generation. Formally, a shift modifies the retrieval projection operator from ${\widehat{P}}_{\mathcal{K}}$ to ${\widehat{P}}_{{\mathcal{K}}^{\prime }}$, inducing a change in the composed operator,

$${\widehat{\mathcal{C}}}_{\mathrm{RAG}}\to {\widehat{\mathcal{C}}}_{\mathrm{RAG}}^{\prime }.$$

(11)

Previously stable attractor basins may therefore become unstable, leading to retrieval collapse characterized by abrupt changes in admissible projections and systematic mis-grounding [31,32]. Empirically, such collapse can occur even when retrieval scores or local accuracy metrics degrade only marginally. Structurally, it corresponds to a qualitative transition in the geometry of ${\widehat{\mathcal{C}}}_{\mathrm{RAG}}$, motivating diagnostics that detect instability before catastrophic failure manifests, as discussed further in Appendix B.

5.3. Deceptively Stable Retrieval–Generation Loops

A critical failure mode arises when a RAG system enters a deceptively stable regime in which local evaluation metrics, self-consistency checks, or verifier models indicate correctness, while the underlying trajectory drifts away from alignment-relevant invariants. In operator terms, these regimes correspond to trajectories that remain near a local attractor of ${\widehat{\mathcal{C}}}_{\mathrm{RAG}}$ but outside the admissible subspace defined by $\widehat{H}$,

$$\widehat{H}{\mathbf{z}}_t\ne {\mathbf{z}}_t\mathrm{while}{\mathbf{z}}_{t+1}\approx {\mathbf{z}}_t.$$

(12)

Such behavior is closely related to concerns about deceptive alignment and mesa-optimization, where systems learn internally coherent strategies that violate intended objectives [1,2]. Structural diagnostics aim to distinguish genuine stability, defined by contraction toward admissible fixed points, from deceptive stability, defined by superficial convergence without invariant preservation.

5.4. Drift Metrics for Reliability Assessment

To operationalize drift detection, SORT-AI introduces architecture-agnostic diagnostic quantities derived from intermediate representations or abstracted operator summaries. Core metrics include norm-based drift measures such as Equation (10), kernel-weighted deviations that emphasize non-local amplification,

$${\Delta }_t^{\kappa }=\int \kappa \left(k\right)\parallel {\mathbf{z}}_t\left(k\right)-\widehat{H}{\mathbf{z}}_t\left(k\right)\parallel \mathrm{d}k,$$

(13)

and invariant-violation scores that directly quantify failure to preserve alignment-relevant constraints enforced by $\widehat{H}$ [27,28]. These metrics are designed to be comparable across models and retrieval strategies, enabling longitudinal monitoring of system reliability under scale-up, domain shift, or adversarial pressure. Formal definitions and recommended norm choices are provided in Appendix B.

5.5. Alignment-Relevant Fixed Points

Grounded generation is modeled as convergence toward alignment-relevant fixed points of the composed operator,

$${\mathbf{z}}^{*}={\widehat{\mathcal{C}}}_{\mathrm{RAG}}{\mathbf{z}}^{*},\widehat{H}{\mathbf{z}}^{*}={\mathbf{z}}^{*}.$$

(14)

Local stability of such fixed points is characterized by contraction of perturbations under $\widehat{H}$-filtered, kernel-mediated propagation, ensuring that small deviations decay rather than amplify. Deceptive stability corresponds to fixed points that satisfy the first condition in Equation (14) but violate the admissibility constraint imposed by $\widehat{H}$. Distinguishing these regimes provides a principled basis for reliability assessment beyond empirical accuracy, linking hallucination risk and long-term alignment to the same underlying structural geometry.

6. Explainability via Operator Geometry

6.1. Limits of Token-Level and Attention-Based Explainability

Token-level attribution methods and attention-based explanations aim to identify which inputs or intermediate signals most strongly influence individual outputs. While these techniques provide insight into local decision-making, they offer limited access to system-level properties such as long-horizon stability, drift accumulation, and the geometry of fixed points in multi-stage RAG pipelines [9,11]. In particular, attention weights and saliency scores are defined with respect to a single forward pass and do not capture how retrieval, augmentation, and generation interact under repeated composition or distributional perturbation. As a consequence, explanations derived from local attributions may remain stable even when the composed operator chain undergoes structural drift, rendering such explanations insufficient for diagnosing reliability or alignment-relevant failures in deployed RAG systems [14,27].

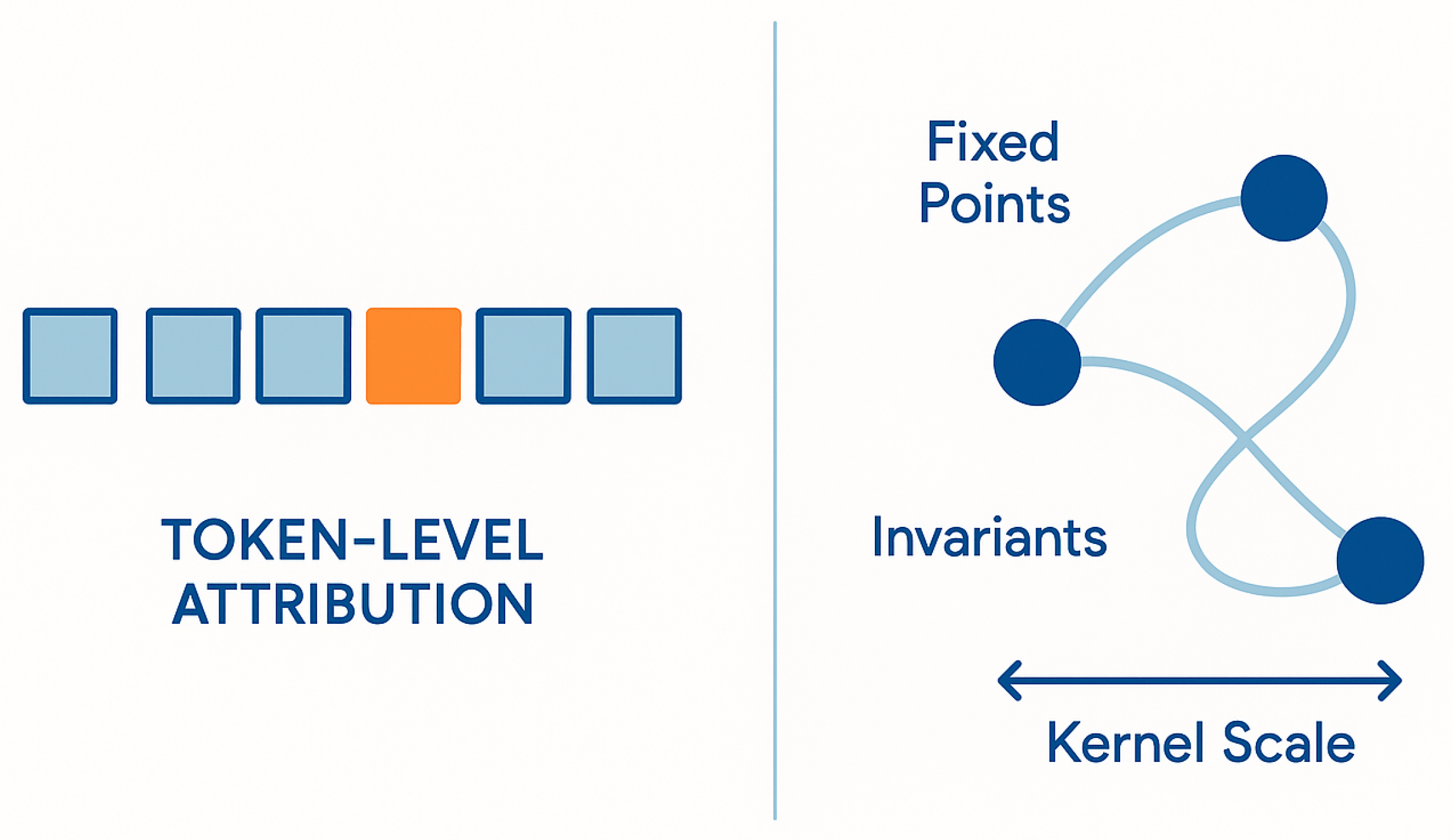
Figure 3 summarizes the explainability distinction employed in this paper, separating local attribution views from structural explainability expressed in terms of operator geometry, invariant preservation, kernel scale semantics, and fixed-point stability under $\widehat{H}$-filtered propagation.

6.2. Operator Fixed Points as Explainable Structures

Within the SORT-AI framework, explainability is reframed as the identification and characterization of stable structures in operator–projection space. Alignment-relevant behavior corresponds to convergence toward admissible fixed points of the composed RAG operator, as defined in Equation (14). The geometry of these fixed points and their basins of attraction provides a global explanation of system behavior, specifying why certain outputs recur across prompts, contexts, or retrieval variations. Unlike token-level explanations, fixed-point analysis explains behavior in terms of structural stability and invariance preservation, enabling practitioners to distinguish robust grounding from superficially consistent yet unstable regimes. This perspective connects explainability directly to reliability by tying explanations to convergence properties rather than isolated outputs.

6.3. Kernel Scale Interpretation and User Trust

The non-local projection kernel $\kappa \left(k\right)$ introduced in Equation (4) admits an interpretable role as a semantic control over the extent of cross-stage coupling between retrieval and generation. Kernel scale parameters determine how strongly retrieved evidence influences downstream transformations across representational depth, thereby modulating the trade-off between expressivity and grounding fidelity. From an auditing perspective, kernel calibration provides an explicit system-level knob whose effects can be monitored through drift metrics such as Equation (13). This linkage enables explanations that relate observed behavior to concrete structural parameters, supporting user trust by making non-local dependence auditable without exposing internal model weights or attention patterns [28].

6.4. Auditing and Governance Implications

Operator-geometry diagnostics support auditing and governance by providing architecture-agnostic criteria for reliability and alignment that are independent of proprietary model details. By certifying properties such as invariant preservation, contraction toward admissible fixed points, and bounded drift under perturbation, regulators and evaluators can assess safety-relevant behavior without requiring full mechanistic transparency [27,28]. This approach complements existing evaluation frameworks by shifting the focus from outcome-based testing to structural guarantees, enabling standardized reporting of stability and drift indicators across deployments. As a result, operator-based explainability provides a practical bridge between technical diagnostics and governance requirements for safety-critical RAG applications.

7. Extensions to Human–Robot Interaction

7.1. Agentic RAG Systems in Embodied Contexts

In embodied settings, Retrieval-Augmented Generation operates within a closed perception–action loop in which generated outputs influence actions that modify the environment and thereby future observations. Structurally, such systems are represented as a coupled operator chain,

$${\mathbf{z}}_{t+1}=\widehat{\mathcal{E}}\circ \widehat{\mathcal{A}}\circ {\widehat{\mathcal{C}}}_{\mathrm{RAG}}{\mathbf{z}}_t,$$

(15)

where ${\widehat{\mathcal{C}}}_{\mathrm{RAG}}$ denotes the internal retrieval–generation chain, $\widehat{\mathcal{A}}$ maps latent decisions to actions, and $\widehat{\mathcal{E}}$ encodes environmental response. Delayed and non-local feedback arise naturally through the environment, making stability of the full loop dependent on properties of the composed operator rather than on any single component [78,79]. In this context, agentic RAG must be analyzed as a dynamical system whose long-horizon behavior is governed by interaction between internal grounding mechanisms and external state evolution.

7.2. Action Grounding and Safety Constraints

Grounding in embodied systems extends beyond textual correctness to include safe and goal-consistent action selection, state estimation, and tool use. Within the projection framework, safety constraints are represented as admissibility filters applied to action-generating states,

$${\mathbf{a}}_t={\widehat{H}}_{\mathrm{act}}\widehat{\mathcal{A}}{\mathbf{z}}_t,$$

(16)

where ${\widehat{H}}_{\mathrm{act}}$ enforces invariants such as physical safety, task constraints, and human oversight requirements [4,27]. This formulation unifies linguistic grounding and action grounding by treating both as projections onto admissible subspaces. Violations of action-level constraints thus appear as structural inconsistencies analogous to textual mis-grounding, enabling a common diagnostic language across modalities.

7.3. Structural Failure Modes in Embodied Systems

Embodied agents exhibit failure modes that arise from compounding drift across perception, retrieval, planning, and control. Small misalignments in early stages can be amplified through feedback, leading to unsafe attractors in the coupled system defined by Equation (15). Examples include persistent misinterpretation of environmental cues, over-reliance on spurious retrieved context, and planning loops that reinforce unsafe strategies despite locally successful execution [80]. Structurally, these failures correspond to loss of invariance under repeated application of the coupled operator and can occur even when individual components satisfy local correctness criteria. Diagnosing such failures therefore requires monitoring of drift and stability at the level of the full operator chain rather than isolated perception or control modules.

7.4. Role of SORT-AI in Reliable Human–Robot Interaction

SORT-AI provides architecture-agnostic diagnostics for embodied agents by extending drift and stability analysis to closed-loop interaction. Drift measures analogous to Equation (10) can be applied to latent action states and environmental embeddings, enabling early detection of unsafe deviation before catastrophic outcomes occur. Enforcement of admissibility through projectors such as $\widehat{H}$ and ${\widehat{H}}_{\mathrm{act}}$ supports invariant preservation across perception, cognition, and action, even under non-local environmental coupling. This positions SORT-AI as a unifying safety layer that complements existing control-theoretic and learning-based approaches by focusing on structural coherence across the full agent–environment system.

7.5. Vision–Language–Action Models as Operator Chains

Vision–language–action models integrate multimodal encoders, retrieval components, planners, and controllers into a single agentic architecture. In the SORT-AI framework, these systems are represented as extended operator chains,

$${\widehat{\mathcal{C}}}_{\mathrm{VLA}}={\widehat{O}}_{\mathrm{ctrl}}\circ {\widehat{O}}_{\mathrm{plan}}\circ {\widehat{O}}_{\mathrm{gen}}\circ {\widehat{O}}_{\mathrm{ret}}\circ {\widehat{O}}_{\mathrm{vis}},$$

(17)

where ${\widehat{O}}_{\mathrm{vis}}$ encodes perception, and subsequent operators capture retrieval, reasoning, and control [79]. This representation enables unified diagnostics across modalities, allowing stability, drift, and fixed-point properties to be assessed for the entire stack rather than per module. As a result, multimodal grounding and safety can be analyzed within the same operator–projection geometry developed for text-based RAG systems.

8. Quantum-Enhanced RAG and SORT-QS

8.1. Structural Interpretation of Quantum Retrieval

Quantum-enhanced retrieval is interpreted in SORT-AI not through claims of computational speedup alone, but as a modification of the effective projection geometry acting on representational states. Abstractly, retrieval remains a projection ${\widehat{P}}_{\mathcal{K}}$ into a knowledge subspace, but quantum-assisted mechanisms alter how this projection is realized and explored. From a structural perspective, quantum retrieval modifies the admissible paths and interference structure within the projection, thereby reshaping the geometry of $\mathcal{K}$ without changing the formal role of retrieval in the operator chain [81,83]. This abstraction enables comparison between classical and quantum retrieval methods at the level of operator behavior and stability, independent of specific hardware assumptions or implementation details.

8.2. Kernel Optimization and Vector Search

Within the SORT-AI framework, potential quantum advantages are naturally framed as kernel-level optimizations that affect non-local coupling and spectral selectivity. The non-local projection kernel $\kappa \left(k\right)$ governs how retrieval evidence propagates into the generative state, as introduced in Equation (4). Quantum-inspired or quantum-assisted vector search can be interpreted as reshaping the effective kernel, emphasizing certain spectral components of the representation space while suppressing others [82]. Structurally, this corresponds to modifying the weighting of non-local interactions rather than altering the downstream generative operators. Such kernel modulation has direct implications for stability, as overly sharp or overly diffuse kernels can respectively induce brittle behavior or uncontrolled amplification, linking retrieval efficiency considerations to the drift diagnostics developed in Section 5.

8.3. Hybrid Classical–Quantum RAG Architectures

Hybrid classical–quantum RAG architectures integrate quantum subroutines into otherwise classical retrieval–generation pipelines. In operator form, such systems can be decomposed as

$${\widehat{\mathcal{C}}}_{\mathrm{hyb}}={\widehat{O}}_{\mathrm{gen}}\circ {\widehat{O}}_{\mathrm{aug}}\circ {\widehat{O}}_{\mathrm{ret}}^{\mathrm{Q}}\circ {\widehat{O}}_{\mathrm{ret}}^{\mathrm{C}},$$

(18)

where ${\widehat{O}}_{\mathrm{ret}}^{\mathrm{Q}}$ denotes a quantum-assisted retrieval projection and ${\widehat{O}}_{\mathrm{ret}}^{\mathrm{C}}$ a classical preprocessing stage. This decomposition clarifies that quantum components enter the chain as specialized projections or kernel transformations, while the overall stability of the pipeline remains governed by the same admissibility and invariance constraints enforced by $\widehat{H}$. Cross-stage stability must therefore be evaluated at the level of the full composed operator rather than by isolating quantum submodules, ensuring that potential advantages do not introduce new structural instabilities.

8.4. Structural Continuity with SORT-QS

Formal continuity between SORT-AI and SORT-QS is established through shared concepts of operator chains, channel composition, and kernel-based filtering. In SORT-QS, quantum systems are analyzed through projection-based diagnostics that characterize coherence, noise, and stability of quantum channels [84]. SORT-AI inherits this diagnostic language while remaining agnostic to the physical realization of retrieval or computation. The same notions of drift, admissible subspaces, and fixed-point stability apply across both domains, allowing insights from quantum systems analysis to inform RAG reliability without conflating physical and algorithmic layers. This continuity supports a unified structural safety perspective spanning classical AI systems, hybrid quantum-enhanced architectures, and fully quantum retrieval primitives.

9. Discussion

9.1. Positioning Relative to Existing RAG Research

The SORT-AI framework is positioned as a foundational diagnostic layer for RAG systems rather than as a competing retrieval or generation algorithm. It does not aim to improve retrieval recall, decoding efficiency, or benchmark accuracy directly, nor does it prescribe specific architectural choices such as dense versus sparse retrieval or decoder-only versus encoder–decoder models [63,66]. Instead, SORT-AI explains why systems that appear equivalent under conventional metrics can exhibit radically different long-horizon behavior by analyzing the geometry of composed transformations. Phenomena such as hallucination persistence, retrieval collapse under shift, and deceptive stability are treated as structural properties of the operator chain rather than as artifacts of particular model families or datasets [1,27]. In this sense, SORT-AI complements empirical RAG research by providing a language for diagnosing failure modes that benchmarks and ablations alone cannot reliably surface.

9.2. Limitations of the Present Framework

The present framework operates at an abstract level and therefore inherits limitations associated with structural modeling. Diagnostics rely on access to intermediate representations, summaries, or operator-level statistics, which may be restricted in proprietary or black-box deployments. Moreover, structural certification does not constitute a behavioral guarantee: convergence toward admissible fixed points and bounded drift reduce risk but do not preclude all possible failures, particularly those arising from unforeseen objectives or adversarial interaction [4,48]. The abstraction also omits fine-grained mechanistic detail, and thus SORT-AI is not a substitute for circuit-level interpretability or empirical red-teaming. Rather, it is intended to coexist with these approaches by identifying when deeper investigation is warranted.

9.3. Implications for Evaluation Standards

The structural perspective motivates evaluation standards that extend beyond task accuracy and factuality benchmarks to include measures of stability, drift accumulation, and invariant preservation. Metrics such as the drift measures defined in Equation (10) and Equation (13), as well as tests for convergence toward admissible fixed points as in Equation (14), provide longitudinal signals of reliability under scale-up, distribution shift, and adversarial pressure. Incorporating such metrics into evaluation protocols would align certification practices more closely with concerns about extreme and long-horizon risks emphasized in recent governance proposals [27,28]. Structural reporting can therefore function as a standardized complement to behavioral benchmarks, supporting comparability across models and deployments.

9.4. Cross-Domain Generality

A central outcome of the framework is its applicability across domains that share a common operator–projection geometry. Text-based RAG systems, embodied agents in human–robot interaction, and hybrid quantum-assisted retrieval architectures can all be represented as composed operator chains subject to admissibility constraints and non-local coupling. This generality enables transfer of diagnostic concepts such as drift, deceptive stability, and fixed-point analysis across otherwise disparate application areas [78,79,81]. As a result, SORT-AI provides a unifying language for reliability analysis that bridges NLP, robotics, and quantum-inspired systems without conflating their implementation details.

Figure 4 situates the RAG formulation within a shared operator–projection diagnostic language spanning text-centric RAG, embodied agent loops in human–robot interaction, and quantum-enhanced retrieval interfaces, emphasizing the persistence of operator chains, kernel semantics $\kappa \left(k\right)$, and drift diagnostics as cross-domain primitives.

10. Conclusions

This work introduced SORT-AI as a structural safety framework for Retrieval-Augmented Generation systems, framing reliability and hallucination risk in terms of operator composition, admissibility constraints, and non-local projection geometry. By modeling RAG pipelines as composed transformations and defining diagnostics based on drift, kernel-mediated coupling, and alignment-relevant fixed points, the framework provides architecture-agnostic signals that complement empirical evaluation and mechanistic interpretability. The resulting perspective connects surface-level failures and long-horizon alignment concerns under a single formal language, enabling explainability, auditing, and governance without reliance on proprietary internals. Future work will focus on operationalizing these diagnostics in standardized evaluation protocols and extending structural certification to increasingly agentic and cross-domain deployments of RAG systems.

Appendix A.1. Operator Set and Idempotency

The SORT framework is built on a finite set of structural operators

$${\left\{{\widehat{O}}_i\right\}}_{i=1}^{22},$$

each representing an abstract transformation class acting on a representation space $\mathcal{Z}$. Every operator is idempotent,

$${\widehat{O}}_i^2={\widehat{O}}_i,$$

(A1)

which ensures that repeated application of the same structural transformation does not introduce uncontrolled amplification. Idempotency formalizes the notion that each operator corresponds to a stabilized structural mode rather than a continuously accumulating effect.

Appendix A.2. Closure Under Composition

The operator set is closed under composition up to equivalence within the algebra. For any ordered pair $(i,j)$, the composition satisfies

$${\widehat{O}}_i\circ {\widehat{O}}_j=\sum _{k=1}^{22}{c}_{ij}^k{\widehat{O}}_k,$$

(A2)

with real coefficients $c_{ij}^k$ determined by the structural interaction rules of the framework [49]. Closure guarantees that arbitrary pipelines constructed from admissible stages remain expressible within the same operator basis, preventing the emergence of extraneous transformation modes under recomposition or scale-up.

Appendix A.3. Commutators and Structural Non-Commutativity

In general, SORT operators do not commute. Their commutator is defined as

$$[{\widehat{O}}_i,{\widehat{O}}_j]={\widehat{O}}_i{\widehat{O}}_j-{\widehat{O}}_j{\widehat{O}}_i,$$

(A3)

and captures order-dependent structural effects. Non-commutativity encodes the fact that retrieval, filtering, aggregation, and generation steps are not interchangeable without changing global behavior. These commutators provide the basis for analyzing path dependence in composed pipelines.

Appendix A.4. Jacobi Consistency

Long-horizon coherence of operator composition is ensured by Jacobi consistency. For all operator triples $(i,j,k)$, the Jacobi identity holds,

$$[{\widehat{O}}_i,[{\widehat{O}}_j,{\widehat{O}}_k]]+[{\widehat{O}}_j,[{\widehat{O}}_k,{\widehat{O}}_i]]+[{\widehat{O}}_k,[{\widehat{O}}_i,{\widehat{O}}_j]]=0.$$

(A4)

Jacobi consistency guarantees that different association orders of nested compositions yield equivalent structural outcomes. In applied settings, this property is critical for ensuring that multi-stage pipelines behave consistently under refactoring, reordering of equivalent subchains, or repeated application across interaction steps.

Appendix A.5. Global Projector Compatibility

The global consistency projector $\widehat{H}$ introduced in Section 3.3 is itself idempotent,

$${\widehat{H}}^2=\widehat{H},$$

(A5)

and compatible with the operator algebra in the sense that

$$\widehat{H}{\widehat{O}}_i={\widehat{O}}_i\widehat{H}\forall i.$$

(A6)

This compatibility ensures that admissibility filtering commutes with structural transformations, allowing invariant enforcement to be applied globally without breaking algebraic closure.

Appendix A.6. Implications for Structural Stability

Taken together, idempotency, closure, non-commutativity with Jacobi consistency, and projector compatibility define a stable algebraic environment for analyzing composed systems. Any admissible pipeline can be represented as an element of the algebra, iterated without leaving the admissible space, and evaluated for stability via its fixed points and commutator structure. These properties underpin the drift diagnostics and fixed-point analyses developed in Section 5 and Section 6, and ensure formal continuity across SORT-AI, SORT-QS, and SORT-CX.

Appendix B.1. Representation Space and Norm Selection

Let $\mathcal{Z}$ denote the latent representation space on which the SORT operator algebra acts. For a state $\mathbf{z}\in \mathcal{Z}$, drift diagnostics require a norm $\parallel ·\parallel$ satisfying positivity, homogeneity, and the triangle inequality. In practice, any norm consistent under admissible linear transformations is sufficient. Structural drift is evaluated relative to the admissible subspace enforced by the global projector $\widehat{H}$. The instantaneous drift magnitude is defined as

$$\Delta \left(\mathbf{z}\right)=\parallel (\mathbb{I}-\widehat{H})\mathbf{z}\parallel ,$$

(A7)

which measures deviation from invariant-preserving trajectories. Vanishing $\Delta \left(\mathbf{z}\right)$ characterizes admissible states, while growth of $\Delta \left(\mathbf{z}\right)$ indicates structural misalignment.

Appendix B.2. Temporal Drift Accumulation

For iterated application of a composed operator $\widehat{\mathcal{C}}$, as defined in Equation (9), drift accumulates over time. The cumulative drift over a horizon T is defined as

$$\mathcal{D}\left(T\right)=\sum _{t=0}^T\Delta \left({\mathbf{z}}_t\right),$$

(A8)

where ${\mathbf{z}}_t$ denotes the state after t iterations. Bounded $\mathcal{D}\left(T\right)$ for increasing T is a necessary condition for long-horizon stability. Superlinear growth of $\mathcal{D}\left(T\right)$ serves as an early-warning signal for structural transitions, even when local performance metrics remain stable.

Appendix B.3. Kernel-Weighted Drift Measures

Non-local coupling between retrieval and generation is mediated by the projection kernel $\kappa \left(k\right)$. To capture scale-dependent amplification, kernel-weighted drift is defined as

$${\Delta }^{\kappa }\left(\mathbf{z}\right)=\int \kappa \left(k\right)\parallel (\mathbb{I}-\widehat{H})\mathbf{z}\left(k\right)\parallel \mathrm{d}k,$$

(A9)

where k indexes retrieval scope or representational depth. This measure emphasizes drift components that propagate non-locally through the operator chain. Excessive sensitivity of ${\Delta }^{\kappa }$ to small perturbations indicates unstable kernel calibration and elevated hallucination or mis-grounding risk.

Appendix B.4. Invariant Violation Scores

In addition to norm-based measures, drift can be quantified through explicit invariant violation scores. Let ${\mathcal{I}}_m\left(\mathbf{z}\right)=0$ denote a set of alignment-relevant invariants enforced by $\widehat{H}$. The total invariant violation is defined as

$$V\left(\mathbf{z}\right)=\sum _m\left|{\mathcal{I}}_m\left(\mathbf{z}\right)\right|.$$

(A10)

Invariant-based diagnostics are particularly useful when norms on $\mathcal{Z}$ are difficult to interpret directly, providing a constraint-oriented alternative to geometric distance measures.

Appendix B.5. Stability and Early-Warning Conditions

A composed operator $\widehat{\mathcal{C}}$ is structurally stable if there exists a constant $C<\infty$ such that

$$\underset{T}{sup}\mathcal{D}\left(T\right)\le C.$$

(A11)

Conversely, the onset of instability is indicated by monotonic growth of either $\mathcal{D}\left(T\right)$ or ${\Delta }^{\kappa }\left({\mathbf{z}}_t\right)$ beyond a predefined tolerance. These criteria define early-warning signals for retrieval collapse, deceptive stability, or loss of grounding, and form the quantitative basis for the diagnostics applied throughout Section 5 and Section 6.

Appendix C.1. Knowledge Graphs as Constrained Subspaces

Let $G=(V,E)$ denote a knowledge graph with vertex set V and edge set E, encoding entities and relations. In SORT-AI, a knowledge graph defines a constrained knowledge subspace ${\mathcal{K}}_{\mathrm{KG}}\subset \mathcal{K}$ within the broader retrieval space. Retrieval under graph constraints is modeled as a projection

$${\widehat{P}}_{{\mathcal{K}}_{\mathrm{KG}}}={\widehat{P}}_{\mathcal{K}}\circ {\widehat{C}}_G,$$

(A12)

where ${\widehat{C}}_G$ enforces relational admissibility derived from graph structure [72]. This formulation abstracts away from concrete graph query languages and focuses on the effect of structural constraints on the admissible retrieval manifold.

Appendix C.2. Adjacency Operators and Graph Spectra

Graph structure induces a linear operator on representations associated with nodes or node neighborhoods. Let $\widehat{A}$ denote the normalized adjacency operator of G. Its spectral decomposition,

$$\widehat{A}=\sum _{\lambda }\lambda {\widehat{\Pi }}_{\lambda },$$

(A13)

with projectors ${\widehat{\Pi }}_{\lambda }$ onto eigenspaces, characterizes modes of information propagation along the graph. Low-frequency spectral components correspond to globally consistent relational structure, while high-frequency components encode local irregularities. In the SORT framework, admissible retrieval paths preferentially align with low-frequency graph modes, suppressing structurally inconsistent aggregation [74].

Appendix C.3. Admissibility Constraints from Graph Structure

Admissibility under a knowledge graph is enforced by restricting projections to representations compatible with graph connectivity and schema constraints. Formally, this is captured by a projector

$${\widehat{H}}_{\mathrm{KG}}=\sum _{\lambda \in {\Lambda }_{\mathrm{adm}}}{\widehat{\Pi }}_{\lambda },$$

(A14)

where ${\Lambda }_{\mathrm{adm}}$ denotes the set of spectral components consistent with graph-defined constraints. States violating relational consistency are filtered out prior to generation, reducing the risk of mis-grounded or contradictory outputs [73].

Appendix C.4. Kernel Modulation on Graph-Constrained Spaces

The non-local projection kernel $\kappa \left(k\right)$ introduced in Equation (4) operates compatibly with graph constraints by modulating propagation within ${\mathcal{K}}_{\mathrm{KG}}$. Kernel-weighted propagation on the graph-constrained space can be written as

$${\mathbf{z}}_{\mathrm{KG}}=\int \kappa \left(k\right){\widehat{H}}_{\mathrm{KG}}{\widehat{O}}_{\mathrm{ret}}\left(k\right){\mathbf{z}}_{\mathrm{in}}\mathrm{d}k.$$

(A15)

This formulation ensures that non-local amplification respects relational admissibility, preventing kernel-induced spread of inconsistent evidence across unrelated graph regions. Excessive kernel weight on high-frequency graph modes serves as an indicator of elevated hallucination risk.

Appendix C.5. Structural Interpretation of Graph-Based RAG

Within SORT-AI, knowledge-graph-based RAG is thus interpreted as a special case of constrained projection combined with kernel-modulated propagation. Graphs do not introduce a separate reasoning paradigm, but refine the admissible geometry of the retrieval space. This interpretation enables unified drift and stability diagnostics across unstructured, hybrid, and graph-constrained RAG systems, as discussed in Section 4.3 and Section 5, and supports consistent safety evaluation across heterogeneous retrieval backends.

Appendix D.1. Inheritance from SORT Whitepaper v5

SORT-AI directly inherits the core mathematical structure defined in SORT Whitepaper v5, including the closed operator algebra ${\left\{{\widehat{O}}_i\right\}}_{i=1}^{22}$, the idempotency condition of Equation (A1), algebraic closure under composition as in Equation (A2), and Jacobi consistency as stated in Equation (A4) [49]. These definitions are reused unchanged and constitute the non-negotiable formal backbone across all SORT modules. Likewise, the interpretation of operators as abstract structural transformation classes, independent of physical or architectural realization, is preserved in SORT-AI without modification.

Appendix D.2. Global Projector and Kernel Definitions

The global consistency projector $\widehat{H}$, defined in Equation (3), and the non-local projection kernel $\kappa \left(k\right)$, introduced in Equation (4), are inherited from Whitepaper v5 with identical mathematical properties. SORT-AI does not alter their algebraic role, idempotency, or compatibility conditions. Instead, it specializes their semantic interpretation to retrieval–generation pipelines, where $\widehat{H}$ enforces grounding and alignment-relevant invariants, and $\kappa \left(k\right)$ governs cross-stage coupling between retrieval and generation. This specialization preserves formal consistency while enabling domain-specific diagnostics.

Appendix D.3. Interface to SORT-QS

SORT-QS applies the same operator–projection formalism to quantum systems, where operators represent channels, transformations, or noise processes, and $\widehat{H}$ enforces physical admissibility constraints such as coherence preservation [84]. The interface between SORT-AI and SORT-QS is therefore structural rather than semantic: both modules share identical notions of operator chains, admissible subspaces, drift, and fixed-point stability. In SORT-AI, these concepts diagnose reliability and alignment in RAG systems, while in SORT-QS they diagnose stability and coherence in quantum channels. No additional operators or algebraic extensions are introduced at the interface.

Appendix D.4. Interface to SORT-CX

SORT-CX extends the same formalism to complex, multi-layer systems beyond AI and quantum domains, including socio-technical and cross-scale systems. The interface to SORT-AI is again defined at the level of shared primitives: operator composition models interacting subsystems, projectors encode admissibility and governance constraints, and kernels capture non-local coupling across scales. SORT-AI can thus be viewed as a domain-specific instantiation of SORT-CX in which the primary subsystems are retrieval, generation, and action pipelines. All drift and stability diagnostics remain formally identical across modules.

Appendix D.5. Module-Specific Specialization without Algebraic Divergence

Crucially, SORT-AI introduces no new operators, no modifications to the algebra, and no domain-specific axioms that would fragment the framework. Differences between SORT-AI, SORT-QS, and SORT-CX arise solely from interpretation of the shared primitives and from the choice of admissibility constraints encoded in projectors. This design ensures formal continuity across modules and allows results, diagnostics, and stability criteria developed in one domain to be transferred to others without reinterpretation at the algebraic level.

Appendix D.6. Implications for Unified Structural Analysis

The strict reuse of operator–projection primitives across SORT modules enables a unified structural analysis of systems that are traditionally treated as unrelated. Reliability in RAG systems, coherence in quantum channels, and stability in complex socio-technical systems are all expressed in terms of the same underlying geometry. This unification is a central design goal of SORT and underpins the cross-domain generality discussed in Section 9.4.

Appendix E.1. Configuration Scope and Abstraction Level

Reproducibility in SORT-AI is defined at the level of structural metrics rather than exact output replication. Required configurations therefore describe the admissible transformation space, coupling geometry, and diagnostic probes applied to the system. Exact neural weights, proprietary datasets, or training procedures are not required, provided that the reported configuration uniquely determines the operator chain geometry relevant to drift and stability analysis.

Appendix E.2. Retrieval Index Specification

For each evaluation, the retrieval subsystem must be specified by a minimal configuration tuple

$$\mathcal{I}=(\mathcal{K},d,s,\varphi ),$$

(A16)

where $\mathcal{K}$ denotes the corpus or knowledge space, d the embedding dimensionality, s the similarity or scoring function, and $\varphi$ any preprocessing or filtering applied prior to projection. This specification is sufficient to reproduce the effective retrieval projection operator ${\widehat{P}}_{\mathcal{K}}$ up to equivalence in operator–projection space.

Appendix E.3. Knowledge Graph Constraints

If knowledge graphs are used, their role must be specified through admissibility constraints rather than through full graph disclosure. Required elements include the schema definition, constraint rules, and the spectral admissibility set ${\Lambda }_{\mathrm{adm}}$ used in Equation (A14). This enables reconstruction of the graph admissibility projector ${\widehat{H}}_{\mathrm{KG}}$ without exposing sensitive relational data.

Appendix E.4. Kernel Parameterization

The non-local projection kernel $\kappa \left(k\right)$ must be reported through its functional form and parameter values. At minimum, evaluations should specify the kernel family, scale parameters, and normalization conventions,

$$\kappa \left(k\right)=\kappa (k;\theta ),$$

(A17)

where $\theta$ denotes the set of kernel parameters. Reporting $\theta$ is sufficient to reproduce kernel-weighted drift measures such as Equation (A9) and to assess sensitivity to non-local amplification.

Appendix E.5. Operator Chain Declaration

The composed operator chain under evaluation must be declared explicitly as an ordered composition of operator classes,

$$\widehat{\mathcal{C}}={\widehat{O}}_{i_n}\circ \dots \circ {\widehat{O}}_{i_1},$$

(A18)

where each ${\widehat{O}}_i$ refers to an element of the SORT operator basis. This declaration enables comparison across systems by ensuring that evaluations refer to structurally equivalent chains.

Appendix E.6. Diagnostic Logging and Metrics

Reproducible diagnostics require logging of representation states or summaries sufficient to compute drift measures. At minimum, logs must allow reconstruction of $\Delta \left({\mathbf{z}}_t\right)$, $\mathcal{D}\left(T\right)$, and invariant violation scores defined in Equations (A7)–(A10). Logging intervals and horizons must be reported to distinguish transient effects from long-horizon trends.

Appendix E.7. Evaluation Protocols and Reporting

All evaluations must report the interaction horizon T, perturbation conditions such as distribution shift or adversarial inputs, and the admissibility criteria enforced by projectors $\widehat{H}$ and ${\widehat{H}}_{\mathrm{act}}$ where applicable. Structural metrics should be reported alongside conventional benchmarks, with explicit indication of whether observed failures correspond to bounded drift, growing drift, or loss of admissible fixed points.

Appendix E.8. Cross-Deployment Comparability

Adhering to these configuration conventions enables comparison of structural stability across heterogeneous deployments, including proprietary models and hybrid classical–quantum systems. By standardizing reporting at the level of operator–projection primitives, SORT-AI supports reproducible, auditable safety analysis without requiring disclosure of sensitive implementation details.