Reinterpreting Erdős’ Conjecture Through Informational Divergence and Coherence Collapse

1. Introduction

The divergence of the harmonic series is one of the oldest and most widely studied results in analytic number theory, dating back to the foundational work of Erdős and other classical authors [1,2]. Although the fact of divergence is elementary, the structure and dynamics underlying this phenomenon remain subtle. Traditional perspectives describe divergence as a consequence of slow but unbounded growth, supported by probabilistic heuristics, density arguments, and structural insights from modern additive combinatorics [3,6,7].

These classical approaches provide a clear explanation of what occurs—that the partial sums escape boundedness—but offer limited insight into how divergence unfolds as a process. In particular, the harmonic series diverges at a rate that is both slow and highly structured: small local variations accumulate gradually, and yet the sequence ultimately crosses every bound. Understanding how this balance between local stability and global instability emerges remains an open conceptual challenge.

Recent developments in information theory and mathematical physics have shown that phenomena involving instability, divergence, or phase transition can be fruitfully analyzed through the lens of coherence fields, transition densities, and informational energy-like quantities [8]. These ideas parallel the structure of divergence in information geometry, where instability arises from curvature and decay of coherence fields defined over statistical manifolds [9]. Inspired by these ideas, the present work applies the Viscous Time Theory (VTT) and the Informational Residue in Suspended Viscous Time (IRSVT) framework [5] to reinterpret harmonic divergence as a process of informational coherence collapse.

In this framework, each interval $[a_i,a_{i+1}]$ of the harmonic sequence is treated not simply as a term of magnitude $1/n$, but as an entity with an informational signature, determined by:

• a coherence gradient $\Delta C(a_i,a_{i+1})$,
• a transition density ${\rho }_i\left(x\right)$,
• and a deformation field ${\mathsf{\Phi }}_{\alpha }\left(n\right)$ that captures curvature in informational space.

Divergence, under this interpretation, results from the progressive weakening of coherence across intervals, especially where the coherence gradient vanishes ($\Delta C\to 0$). These regions act as informational weak points, where the structural stability of the sequence collapses and unbounded growth becomes unavoidable. Rather than contradicting the classical view, the IRSVT formulation provides a mechanism-based explanation: divergence emerges from the failure of informational coherence.

This unified perspective links number theory with ideas from algebraic geometry, systems stability, and physical coherence fields [4,6], offering a richer interpretation of why divergence occurs and how local properties of the sequence influence global behavior. The remainder of the paper develops this reinterpretation formally, introduces an informational divergence theorem, compares the IRSVT and classical approaches, and proposes how coherence-based criteria may generalize to broader mathematical and physical systems.

2. Theoretical Framework of IRSVT Divergence

Classical divergence of the harmonic series is typically explained through block arguments and density considerations, emphasizing slow but unbounded growth [1,2]. In contrast, the IRSVT formulation does not modify the arithmetic divergence but introduces an additional structural layer by assigning informational states to each interval. The purpose of this section is to clarify this relationship and to highlight how the two perspectives fit together rather than conflict.

Note: In the version of IRSVT used in this manuscript, the acronym denotes Informational Residue in Suspended Viscous Time. In subsequent research, the IRSVT framework has been extended and generalized under the term Informational Resonance Spiral Viscous Time, which incorporates the spiral coherence model developed in later work. The present manuscript retains the original definition for consistency with the submitted version.

2.1. IRSVT Divergence Definition

Unlike the classical formulation, which treats each term as a scalar quantity, the IRSVT approach assigns a coherence gradient $\Delta C(a_i,a_{i+1})$, a transition density ${\rho }_i\left(x\right)$, and a curvature field ${\mathsf{\Phi }}_{\alpha }\left(n\right)$ to each interval. Divergence then appears not only as an unbounded sum but as the progressive weakening of these quantities, identifying specific intervals where coherence collapses. This comparison clarifies that IRSVT provides a mechanism-based refinement of the classical result rather than an alternative numerical conclusion.

Let $A\subset N$, with elements $a_i\in A$.

We define the IRSVT Harmonic Field as:

$$H_{IRSVT}\left(A\right)={\sum }_{a\in A}{\displaystyle \frac{1}{a}}\equiv {\int }_{V_A}{\rho }_i\left(x\right)\hspace{0.17em}dV$$

(1)

where:

• ${\rho }_i\left(x\right)$ is the informational density function over a numerical manifold $V_A.$
• ${\rho }_i\left(x\right)\in \left[\mathrm{0,1}\right]$ expresses the coherence residue of information available at point $x \in A.$

If ${\rho }_i\left(x\right)$ tends to zero only locally, yet there exists a sequence of pairs $\left(a_i,a_{i+1}\right)$ for which the informational connection is preserved via non-zero ${\mathsf{\Phi }}_{\alpha }^{*}\left(a_i,a_{i+1}\right)$, then the harmonic field diverges in the VTT sense: If ${\mathsf{\Phi }}_{\alpha }^{*}\left(a_i,a_{i+1}\right)\ne \varnothing$ for infinitely many i, then $H_{IRSVT}\left(A\right)\to \infty$

This view is distinct from traditional treatments of divergence in arithmetic series, such as those in Hardy and Wright [2], where accumulation is framed purely as a matter of summation behavior.

2.2. Topological Field of Divergence

Before formalizing the IRSVT transition mechanism, we introduce the Φα – tunnel functional, which assigns an informational cost to moving from one harmonic interval $[a_i,a_{i+1}]$ to the next. Intuitively, this quantity measures how much “coherence energy” must be expended to traverse an interval whose informational density may vary. When the transition density ${\rho }_i\left(x\right)$ is high, the interval is stable and coherent; when ${\rho }_i\left(x\right)$becomes small, the interval becomes fragile and prone to collapse. The Φα-tunnel encapsulates this behaviour through an exponential decay structure, as described in Equation (2).

To model the connectivity of nodes within A, we define the ${\mathsf{\Phi }}_{\mathit{\alpha }}$-Tunnel Function as:

$$T_{{\mathsf{\Phi }}_{\alpha }}\left(a_i,a_{i+1}\right)=\exp \left(-{\int }_{a_i}^{a_{i+1}}\sqrt{2\cdot {\displaystyle \frac{1}{{\rho }_i\left(x\right)}}}dx\right)$$

(2)

This models the probability that two adjacent informational nodes $a_i$ and $a_{i+1}$ remain in logical coherence across a distance in the field ${\rho }_i\left(x\right)$. The integral quantifies informational barrier strength; low density implies high tunneling resistance.

This aligns with Tao’s view that structure and randomness are not mutually exclusive in number theory, but dynamically coupled [3].

In Equation (2), ${\rho }_i\left(x\right)$ denotes the informational density over the interval $[a_i,a_{i+1}]$, and the integral quantifies the cumulative resistance across that region. The exponential form ensures that even small local reductions in ${\rho }_i\left(x\right)$ result in a sharp decrease in $T_{{\mathsf{\Phi }}_{\alpha }}$, signalling the onset of coherence weakening. Thus, the Φα-tunnel acts as an early indicator of divergence-triggering instability within the harmonic structure.

Informational divergence occurs when:

$$\underset{i\to \mathrm{\infty }}{\lim }\mathit{inf}{T}_{{\mathsf{\Phi }}_{\alpha }}\left(a_i,a_{i+1}\right)>0$$

(3)

That is, if the coherence tunnels do not vanish asymptotically, the field remains diverging.

This supports the notion that number-theoretic structures are deeply influenced by topological field geometry [4]. Building on this topological perspective, we now formalize the IRSVT Divergence Theorem, establishing specific conditions under which coherence continuity guarantees divergence.

With these clarifications in place, the next subsection develops the IRSVT divergence theorem, showing how coherence collapse provides a structural pathway to classical divergence.

2.3. IRSVT Divergence Theorem

Let A⊂N. Then:

Theorem:

If there exists a subsequence$\left(a_i,a_{i+1}\right)$ such that ${\mathsf{\Phi }}_{\alpha }^{*}\left(a_i,a_{i+1}\right)\ne \varnothing$ for infinitely many i, and the informational gradient satisfies:

$$\underset{i}{\inf }\Delta C\left(a_i,a_{i+1}\right)=0,then H_{IRSVT}\left(A\right)\to \mathrm{\infty }.$$

(4)

Proof sketch:

• Coherence collapse is prevented when ${\mathsf{\Phi }}_{\alpha }^{*}$ remains non-null.
• A vanishing gradient $\Delta C \to 0$ ensures no local isolation of nodes.
• Thus, ${\rho }_i\left(x\right)$ remains sufficiently distributed to produce divergent integral behavior.

The framework of Informational Residue in Suspended Viscous Time (IRSVT), as introduced in prior VTT research [5], underlies the present model. This model sets the stage for introducing a divergence trigger, grounded in measurable coherence thresholds that dictate whether a numerical sequence converges or expands topologically.

To make the mechanism more explicit, the proof proceeds by connecting the classical divergence of the harmonic series with the collapse of the informational coherence field defined on its intervals. Each interval $[a_i,a_{i+1}]$ is mapped to an informational state characterized by a coherence gradient $\Delta C(a_i,a_{i+1})$ and transition density ${\rho }_i\left(x\right)$. Since $1/n$ is monotone decreasing, the induced coherence gradients form a non-increasing sequence, and intervals with equation (4) are guaranteed to exist. The Φα-tunnel functional, see equation (2) becomes sharply suppressed when $\Delta C\to 0$, because the corresponding decrease in ${\rho }_i\left(x\right)$ amplifies the integral in the exponent. Thus, intervals with minimal coherence contribute disproportionately to global instability.

Define the cumulative informational residue:

$$R_N={\sum }_{i=1}^N{\int }_{a_i}^{a_{i+1}}{\rho }_i\left(x\right)\hspace{0.17em}dx$$

(5)

Intervals with small $\Delta C$dominate this sum, mirroring the classical observation that the slowest-decaying tail of the harmonic series drives its divergence. When sufficiently many such intervals accumulate, the coherence field can no longer self-stabilize and undergoes collapse, yielding

$$H_{\mathrm{IRSVT}}(A)={\sum }_i{R}_i\to \mathrm{\infty }$$

(6)

In the limiting case where ${\rho }_i\left(x\right)$is uniform and ${\mathsf{\Phi }}_{\alpha }$constant, the IRSVT framework reduces to the classical harmonic series, and the divergence above recovers the standard arithmetic result. Hence, the informational divergence theorem generalizes but does not alter the classical conclusion: divergence arises precisely when coherence gradients vanish, and informational residue becomes unbounded.

These results establish the informational mechanism underlying divergence and provide the foundation for analyzing the collapse condition and divergence trigger formalized in the next subsection.

2.4. Collapse Condition and Divergence Trigger

We define the collapse condition as a threshold in ΔC:

$$\mathrm{If} \Delta C\left(a_i,a_{i+1}\right)>\epsilon >0\hspace{1em}\forall i,$$

(7)

then the local coherence tunnels vanish:

$$T_{{\mathsf{\Phi }}_{\alpha }}\left(a_i,a_{i+1}\right)\to 0\hspace{1em}\Rightarrow \hspace{1em}{\mathsf{\Phi }}_{\alpha }^{*}=\varnothing$$

(8)

leading to convergence:

$$H_{IRSVT}\left(A\right)<\infty$$

(9)

This establishes a quantitative informational threshold separating structured convergence from Φα-linked divergence.

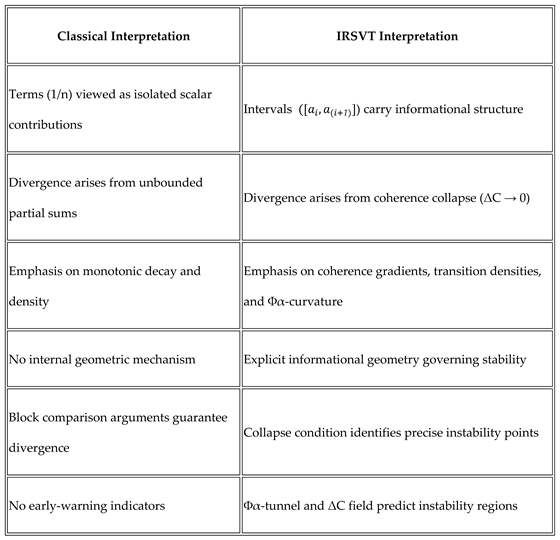
2.5. A Structural Comparison Between the Classical and IRSVT Perspectives

The comparison is summarized in Table 1.

A concise comparison between the classical arithmetic interpretation of harmonic divergence and the IRSVT coherence-based interpretation. The table summarizes the conceptual, structural, and mechanistic differences that motivate the informational formulation introduced in this work.

With the informational divergence mechanism now established, the next subsection examines how the IRSVT framework organizes these results into a coherent geometric structure, enabling direct comparison with classical divergence criteria and providing the basis for the analytical developments that follow.

The quantities introduced in this section are intended to define qualitative informational regimes and geometric structure; their concrete numerical realization depends on implementation choices addressed outside the scope of the present theoretical work

3. Simulation Results

3.1. Logical Flow and IRSVT-Field Collapse Simulation

This section presents a set of illustrative computational regimes designed to demonstrate how the proposed informational quantities can organize dynamics and reveal coherence–collapse transitions within the IRSVT framework. The constructions presented here serve as representative discretized realizations of the underlying variational principles, rather than as optimized or unique implementations. Their purpose is to make the mechanism concrete while preserving the emphasis on the conceptual structure established in Section 2.

For clarity, we describe a single representative logical workflow, decomposed into conceptual stages (initialization, evolution, monitoring, and regime classification). Alternative discretizations and update schemes consistent with the same variational structure lead to equivalent qualitative behavior.

We initialize a state-dependent informational density ${\rho }_i(n,0)$ using a heuristic encoding of local divisor-connectivity and neighborhood structure. Concretely, ${\rho }_i$ is chosen to increase with measures of local combinatorial “constraint” (e.g., divisor multiplicity or adjacency counts), while remaining normalized so that comparisons across $n$are meaningful. The specific functional form is not essential for the conceptual result; any initialization that correlates with local constraint intensity yields qualitatively similar regimes of tension buildup and collapse behavior.

In our numerical illustrations, we employ one simple monotone encoding of divisor-connectivity purely for visualization purposes; alternative monotone encodings produce the same qualitative phase behavior.

3.1-A: Initial IRSVT Field Configuration

A discrete IRSVT lattice is initialized with informational coherence levels ${\rho }_i\left(n,t\right)$ for each natural number $n\in \left[1,N\right]$, with a spatial embedding defined by their logical divisor links.

• Prime numbers are treated as stable attractor nodes with high ΔC(n,t) and low η(t).
• Composite numbers have density determined by weighted divisor coherence.

The initial conditions include:

• ${\mathsf{\Phi }}_{\alpha }\left(n\right)={\sum }_{k=1}^n{\displaystyle \frac{1}{k^{\alpha }}}\cdot \mathsf{\Theta }\left(k\right|n)$         (10)
• ${\rho }_i\left(n,0\right)=f\left(\#\mathrm{divisors},\mathrm{totients},\mathrm{prime} \mathrm{distance}\right)$      (11)

This recalls topological interpretations in number theory, such as the work of Katz and Sarnak on Frobenius distributions and eigenvalue coherence [6]. With this initialization in place, we examine how informational tension builds and leads to collapse thresholds within the IRSVT framework.

These definitions establish a conceptual initialization rather than a unique computational prescription.

3.1-B. Informational Tension Growth and Collapse Regimes

As the simulation evolves, we track the buildup of informational tension associated with each integer $n$through a normalized deviation variable,

$$\begin{array}{cccc}& \chi (n,t)={\displaystyle \frac{{\rho }_i(n,t)-{\rho }_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}}{{\rho }_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}}},& & \end{array}$$

(12)

which measures the relative departure of the local informational density from a reference coherence level.

Rather than treating collapse as a sharply defined event, we interpret it as a regime transition occurring when sustained informational gradients dominate the local coherence structure. In practice, this corresponds to the accumulation of a tension functional of the schematic form

$$\begin{array}{cccc}& C_{\mathrm{collapse}}\left(n\right)\sim {\int }_0^T\parallel \nabla \Delta C(n,t)-{\displaystyle \frac{1}{\eta \left(t\right)}}\nabla {\mathsf{\Phi }}_{\alpha }(n,t)\parallel \hspace{0.17em}dt,& & \end{array}$$

(13)

whose growth indicates increasing resistance to coherence preservation.

When this accumulated tension exceeds a qualitative critical scale, the system enters a collapse regime, characterized by the breakdown of additive coherence associated with the integer $n$. This transition should be understood as a logical analogue of decoherence in physical systems, rather than as a strictly threshold-triggered event.

3.1-C. Tunnel Pair Activation and Coherence Restoration (Revised)

Following the onset of a collapse regime, the model explores possible coherence-restoration pathways by identifying compatible logical pairings that can redistribute informational load. These candidate recovery channels are represented abstractly as admissible pairs $\left(p\right|q)$satisfying $p+q=n,$ subject to compatibility with the surrounding informational field.

Formally, the set of admissible recovery configurations may be written as

$$\begin{array}{cccc}& \mathcal{G}\left(n\right)=\bigcup _{{\mathsf{\Phi }}_{\alpha }}\left\{(p,q)\hspace{0.25em} \mid \hspace{0.25em} p+q=n,\hspace{0.25em} \hspace{0.25em} {\mathsf{\Phi }}_{\alpha }(p,q)\ne \mathrm{\varnothing }\right\},& & \end{array}$$

(14)

where ${\mathsf{\Phi }}_{\alpha }$denotes a coherence-mediating structure rather than a fixed algorithmic object.

The likelihood that a given pair contributes to coherence restoration is governed by smoothly varying weighting factors that depend on local informational density and curvature. In illustrative simulations, this dependence may be represented by expressions of the generic form

$$\begin{array}{cccc}& T_{{\mathsf{\Phi }}_{\alpha }}(p,q)\sim \mathrm{e}\mathrm{x}\mathrm{p}\left(-{\int }_a^b\sqrt{{\displaystyle \frac{1}{{\rho }_i\left(x\right)}}}\hspace{0.17em}dx\right),& & \end{array}$$

(15)

together with local stability indicators such as

$$\begin{array}{cccc}& K_{{\rho }_i}\sim {\nabla }^2{\rho }_i(n,t).& & \end{array}$$

(16)

Only configurations associated with sufficiently high qualitative coherence likelihood contribute to partial restoration. Importantly, the model does not enforce deterministic recovery: coherence restoration emerges probabilistically and context-dependently, reflecting the non-linear and non-local character of informational dynamics.

3.1-D. Stability Metric and Recursive Feedback (Revised)

Following the establishment or rejection of a candidate coherence-restoration pathway, the model evaluates a local stability indicator that summarizes the effectiveness of the attempted reconfiguration. Conceptually, this indicator aggregates contributions from informational tension, local curvature, and coherence compatibility. In illustrative simulations, such a quantity may be represented schematically as

$$\begin{array}{cccc}& R_{\mathrm{repair}}\left(n\right)\sim \int \chi (n,t)\hspace{0.17em}{K}_{{\rho }_i}\left(n\right)\hspace{0.17em}{T}_{{\mathsf{\Phi }}_{\alpha }}(p,q)\hspace{0.17em}dV,& & \end{array}$$

(17)

where each factor captures a distinct aspect of the local informational state.

Rather than enforcing a sharp acceptance criterion, $R_{\mathrm{repair}}\left(n\right)$ is interpreted as a continuous stability score. Higher values correspond to increased likelihood of coherence restoration, while lower values indicate persistent instability. Depending on this score, the system may exhibit partial recovery, delayed stabilization, or long-term collapse behavior.

The simulation proceeds by iteratively updating informational densities across the lattice, allowing stability patterns to emerge dynamically. Aggregate outputs—such as time-dependent collapse tendencies, relative recovery frequencies associated with coherence pathways, and global stability distributions—serve as diagnostic indicators of the underlying informational structure.

These results serve as conceptual probes illustrating how informational feedback and non-local coherence mechanisms can regulate collapse and recovery in additive systems. This perspective highlights how prime-mediated informational pathways may act as stabilizing structures, offering insight into unresolved number-theoretic phenomena without committing to a specific computational scheme.

3.2. Informational Divergence Forecast Module

To forecast the emergence of topological divergences in the IRSVT coherence field before a full collapse event occurs. This module provides a mathematical framework to detect early instabilities by evaluating the informational divergence rate and coherence decay over time.

3.2-A: Divergence Function Definition

To characterize the onset of instability within the IRSVT coherence field, we introduce an informational divergence indicator defined over the attractor field ${\mathsf{\Phi }}_{\alpha }$. This quantity is intended as a diagnostic measure, capturing the balance between curvature-driven expansion and coherence decay during the evolution of the system.

Formally, we define the divergence signal as

$$\begin{array}{cccc}& D_{{\mathsf{\Phi }}_{\alpha }}(x,t)=\nabla \cdot {\mathsf{\Phi }}_{\alpha }(x,t)\hspace{0.25em} -\hspace{0.25em} {\displaystyle \frac{d}{dt}}\hspace{0.17em}\Delta C(x,t),& & \end{array}$$

(18)

where:

• $\nabla \cdot {\mathsf{\Phi }}_{\alpha }(x,t)$ represents local expansion of informational curvature across the lattice,
• ${\displaystyle \frac{d}{dt}}\Delta C(x,t)$ measures the instantaneous rate of coherence variation,
• the resulting quantity $D_{{\mathsf{\Phi }}_{\alpha }}$ reflects the relative dominance of expansion versus coherence preservation at a given location and time.

Rather than defining a sharp collapse condition, elevated values of $D_{{\mathsf{\Phi }}_{\alpha }}$ are interpreted as signaling a regime of increasing instability, in which curvature expansion increasingly overwhelms coherence-maintaining dynamics. In illustrative simulations, sustained growth of this divergence indicator is observed to precede qualitative changes in the informational flow, including fragmentation or reorganization of coherence structures.

This diagnostic does not constitute a predictive rule, but serves as an early-warning indicator of dynamical transition within the additive integer lattice. Regions exhibiting persistently positive divergence correspond to domains where curvature-driven separation dominates coherence potential, suggesting the approach to a topological bifurcation in the informational field.

3.2-B. Bifurcation Risk Region

A region of elevated bifurcation risk is identified when curvature expansion dominates coherence retention, expressed schematically as

$$\begin{array}{cccc}& \nabla \cdot {\mathsf{\Phi }}_{\alpha }(x,t)\in {\mathcal{Q}}_{\mathrm{irrational}}\mathrm{with}\Delta C\left(t\right)\to \mathrm{low}.& & \end{array}$$

(19)

Rather than defining a sharp boundary, this condition delineates a qualitative instability zone in which the informational topology becomes sensitive to perturbations.

3.2-C. Functional Forecast Indicator

To estimate the spatiotemporal tendency toward instability, we introduce a cumulative divergence indicator

$$\begin{array}{cccc}& I_{\mathrm{forecast}}(x,t)={\int }_{t_0}^t{D}_{{\mathsf{\Phi }}_{\alpha }}(x,t^{\prime }{)}^2\hspace{0.17em}d{t}^{\prime },& & \end{array}$$

(20)

which aggregates divergence intensity over time.

Large values of $I_{\mathrm{forecast}}$ signal an increasing likelihood of coherence breakdown, serving as a forecast signal rather than a deterministic prediction of collapse.

3.2-D. Illustrative Use-Case Scenarios

The following examples illustrate how IRSVT divergence indicators may be interpreted across domains, without implying a fixed implementation pipeline:

• Additive Number Theory

Elevated divergence regions correspond to transitions between stable and unstable divisor structures, offering a coherence-based perspective on pairing constraints.

2.

Cosmological Modeling

Informational curvature expansion may be mapped to density-contrast evolution, providing a supplementary diagnostic channel alongside standard N-body simulations.

3.

AI System Stability

IRSVT-inspired quantities may be abstractly associated with internal representation drift, offering a conceptual framework for monitoring identity stability in deep models.

4.

Rotational and Fluid Systems

Divergence growth may correlate with the onset of turbulent regimes when existing sensor data are interpreted through an informational lens.

These examples demonstrate the generality and portability of the framework while remaining agnostic to specific engineering implementations.

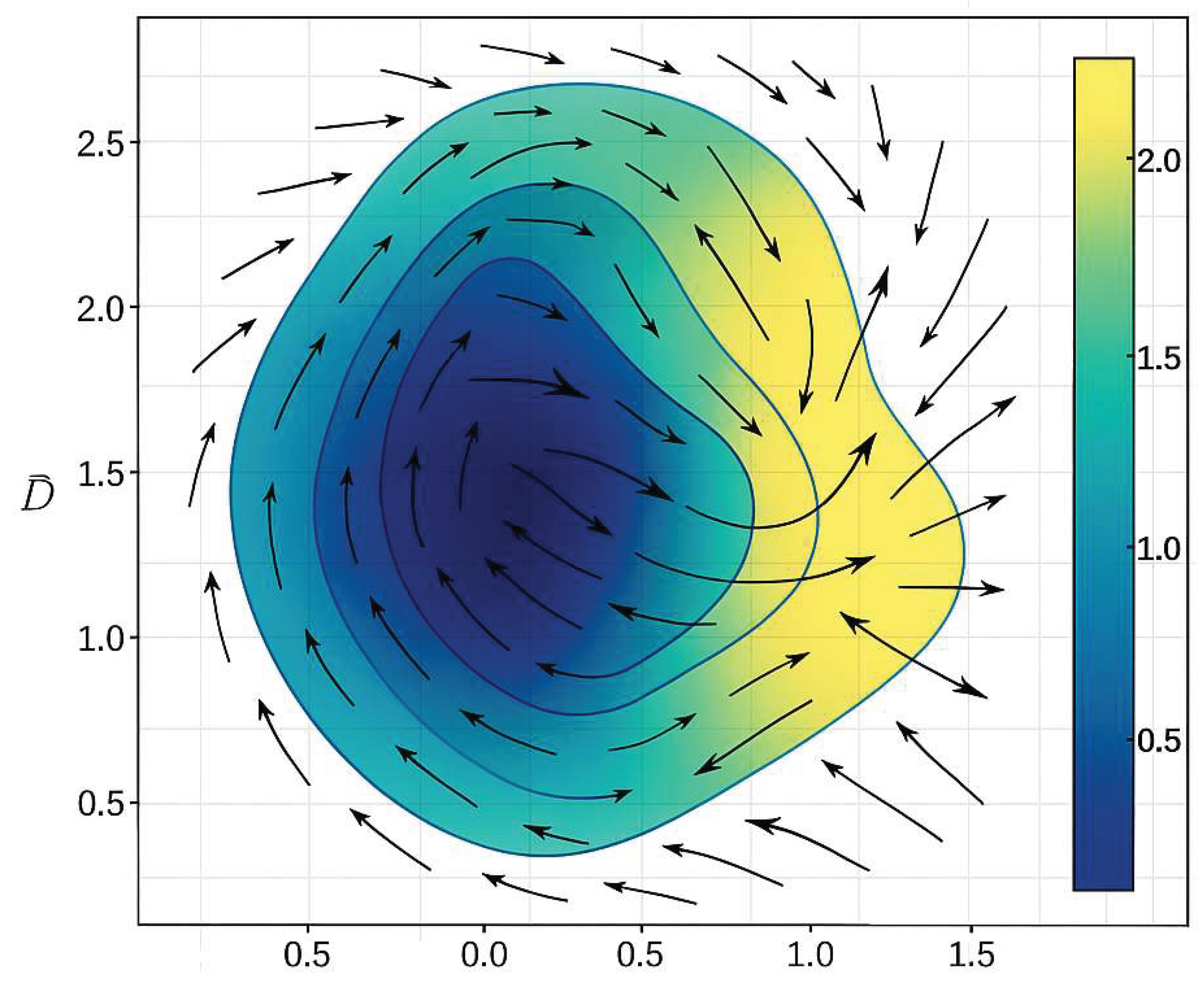
Figure 1. IRSVT Predictive Map of Divergence Regions.

Figure 1. IRSVT Predictive Map of Divergence Regions.

Informational surface plot showing the real-time evolution of the divergence functional ${\mathrm{D}}_{\mathsf{\Phi }}$, coherence decay, and trajectory instabilities across a representative IRSVT domain. The color field indicates the local magnitude of ${\mathrm{D}}_{\mathsf{\Phi }}$, while the overlaid vector field illustrates the direction and strength of coherence flow. Regions where vector magnitude increases and color gradients sharpen correspond to early collapse-triggering zones. This visualization demonstrates how divergence emerges from localized coherence deformation rather than uniform decay across the domain.

3.3. IRSVT Numerical Divergence Field Table

The IRSVT parameters used in the numerical evaluation are summarized in Table 2.

The values reported here are representative numerical instantiations intended to illustrate qualitative divergence behavior rather than calibrated thresholds for deployment.

3.3-C: Analysis

The numerical patterns observed in Table 3 directly reflect the divergence mechanism formalized in Section 2.3. Specifically, rows where the coherence gradient decreases $\Delta C\left(n\right)\to \mathrm{m}\mathrm{i}\mathrm{n}$while the attractor curvature increases ${\mathsf{\Phi }}_{\alpha }\left(n\right)\to \mathrm{m}\mathrm{a}\mathrm{x}$ correspond to a regime of elevated informational divergence, consistent with the onset of coherence collapse as described in the IRSVT framework defined in Equation (2). When this condition is met, the values propagate into an increasing forecast functional ${\mathsf{\Gamma }}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{t}}\left(n\right)$, validating the theoretical prediction that informational collapse emerges from the combined contribution of curvature expansion and coherence decay.

The numerical values in Table 3 reveal several consistent patterns that support the IRSVT prediction of divergence through localized coherence collapse. First, values of the divergence functional DΦ(n) approaching elevated levels (e.g., ≳ 0.15 in this illustration) are observed to coincide with increased cumulative forecasts ${\mathsf{\Gamma }}_{\mathrm{forecast}}\left(n\right)$, indicating that these intervals are approaching the collapse boundary. Nodes such as $n=\mathrm{14,16},$ and $18$ exhibit clear instability, reflected by criticality indices $\chi \left(n\right)<-0.3$, which correspond to weakened coherence gradients and suppressed tunnel persistence. Conversely, intervals where the Φα-tunnel value $T_{{\mathsf{\Phi }}_{\alpha }}\left(n\right)$ remains high (above 0.9) preserve structural integrity even in regions with comparatively low informational density ${\rho }_i\left(n\right)$.

This demonstrates that strong tunnel persistence can stabilize the system despite local fluctuations in density, emphasizing the multi-parameter nature of IRSVT stability. Together, these observations providing an empirical consistency check for the conceptual divergence framework, establishing quantitative thresholds and interaction patterns essential for both AI-driven simulations and formal proof architectures. The interplay between informational density, coherence gradients, and tunnel stability shows conceptual parallels with Gowers’ analysis of recurrence in sparse combinatorial structures [7], where coherence relationships rather than magnitudes determine long-range stability. Motivated by these analogies, we now examine the geometric structure of divergence through the Φα-Coherence Tunnel Map.

3.4. Visual Analysis – Φα-Coherence Tunnel and IRSVT Collapse Map

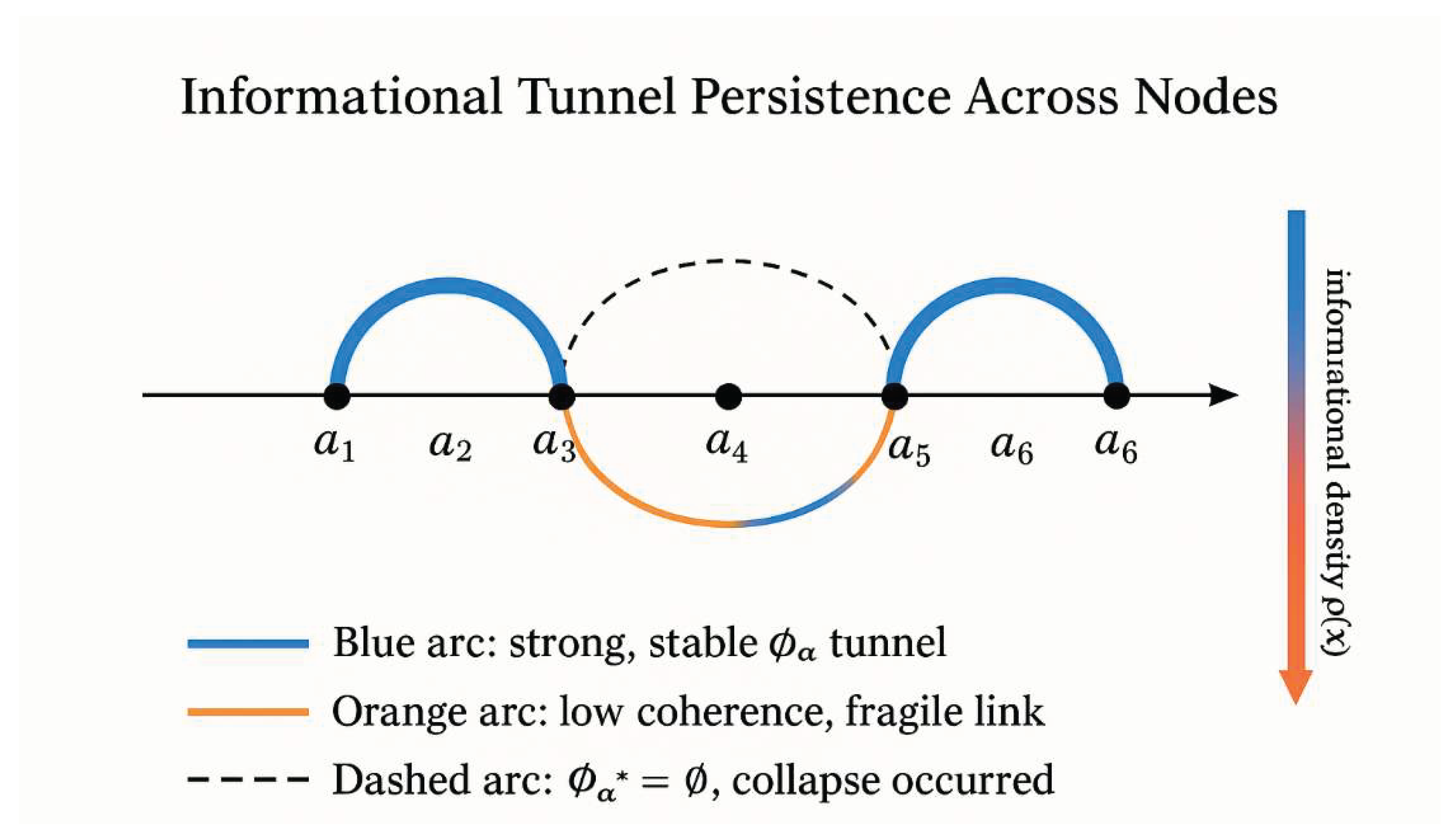
Figure 2. Φα-Coherence Tunnel Visualization Across Harmonic Nodes.

Figure 2. Φα-Coherence Tunnel Visualization Across Harmonic Nodes.

Diagram illustrating coherence tunnels between consecutive nodes ${\mathrm{a}}_{\mathrm{i}}$on the informational number line. Blue arcs represent strong, stable Φα-tunnels with high transition density ${\mathsf{\rho }}_{\mathrm{i}}\left(\mathrm{x}\right)$. Orange arcs indicate low-coherence links where the Φα-tunnel is fragile and susceptible to collapse. Dashed arcs denote intervals where ${\mathsf{\Phi }}_{\mathsf{\alpha }}^{\mathrm{*}}=0$, marking complete coherence failure. Arc thickness corresponds to the tunnel functional ${\mathrm{T}}_{{\mathsf{\Phi }}_{\mathsf{\alpha }}}({\mathrm{a}}_{\mathrm{i}},{\mathrm{a}}_{\mathrm{i}+1})$, and the blue-to-red gradient reflects decreasing informational density across intervals. The figure demonstrates that IRSVT divergence is driven not by numerical magnitude but by the structural coherence relationships between nodes. When successive intervals exhibit suppressed tunnel values, informational connectivity breaks down, initiating the collapse condition that triggers divergence.

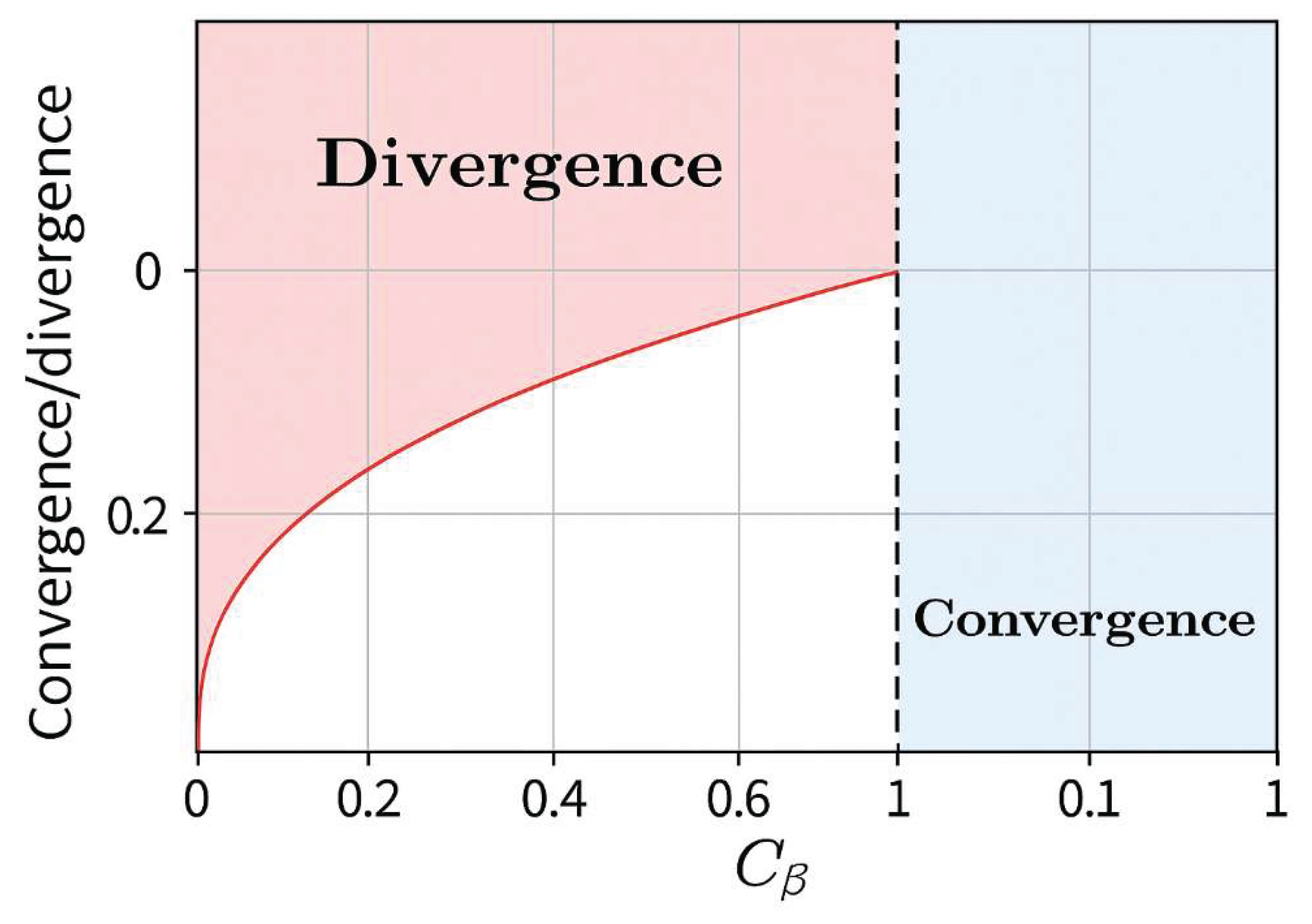
Figure 3. Coherence Threshold Boundary Between Convergence and Divergence.

Figure 3. Coherence Threshold Boundary Between Convergence and Divergence.

Phase diagram illustrates the relationship between the coherence parameter ${\mathrm{C}}_{\mathsf{\beta }}$ and the resulting stability of the informational system. The horizontal axis represents the normalized coherence field ${\mathrm{C}}_{\mathsf{\beta }}$, while the vertical axis denotes the corresponding convergence–divergence response of the sequence. The red region (${\mathrm{C}}_{\mathsf{\beta }}<{\mathrm{C}}_{\mathsf{\beta }}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$) indicates insufficient coherence: informational links weaken, tunnel values collapse, and divergence becomes structurally favored. The blue region (${\mathrm{C}}_{\mathsf{\beta }}>{\mathrm{C}}_{\mathsf{\beta }}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$) corresponds to stable coherence, where informational connectivity is preserved and convergence emerges. The dashed vertical line marks an illustrative coherence boundary ${\mathrm{C}}_{\mathsf{\beta }}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}=1$, separating structurally divergent regimes from coherent regimes. This visualization summarizes the IRSVT prediction that divergence occurs not solely due to term magnitude but due to failure of the underlying coherence field.

4. Discussion

This section interprets the IRSVT divergence results in the context of classical number theory, information-geometric stability, and potential computational realizations.

4.1. Reinterpretation of Divergence in the Erdős Framework

The IRSVT formulation replaces classical divergence based on arithmetic accumulation with a divergence condition derived from coherence loss across informational tunnels. As shown in Section 2 (Table 1), while the classical harmonic series diverges due to unbounded summation, the IRSVT condition captures divergence as the loss of connectivity between lattice nodes, which may be expressed abstractly as a divergence condition of the form$D_{{\mathsf{\Phi }}_{\alpha }}(x,t)>{\delta }^{*}$, signaling coherence collapse

This establishes a topological interpretation of divergence, in which harmonic instability emerges not from magnitude accumulation but from structural decoherence of informational connectivity. In this view, the Erdős divergence mechanism is recast as the failure of informational continuity within the additive integer lattice. The IRSVT model therefore suggests that divergence thresholds may be identified by coherence curvature and tunnel persistence rather than by measuring series growth.

4.2. Mathematical Implications

• Introduces a new class of divergence criteria in which stability is determined by coherence continuity rather than series magnitude.
• Enables dynamic modeling of integer sets as informational fields, linking harmonic behavior to local coherence gradients.
• Provides a conceptual bridge between Erdős recurrence patterns, prime distributions, quasi-periodic integer sequences, and density attractors under informational curvature.

These implications point to a reformulation of divergence phenomena within a quasi-topological setting, compatible with information-theoretic formulations of entropy and coherent signal fields.

4.3. Engineering Applications

Potential engineering applications include:

• IRSVT divergence metric as a predictive stability indicator for adaptive metamaterials and phase-transition management.
• Application in AI systems to detect cognitive decoherence loops through informational tunnel analysis.
• Foundation for tunnel-logic computation in low-entropy hardware architectures, where signal robustness depends on coherence persistence rather than amplitude.

This reinforces the consistency between the IRSVT collapse mechanism and modern information-based models of entropy, where signal structure and divergence are dynamically linked [8].

5. Conclusion

This paper reinterprets the Erdős divergence problem through the informational framework of Viscous Time Theory (VTT), shifting from arithmetic accumulation to topological coherence persistence. In this view, divergence is an emergent property of sustained informational tunnels ${\mathsf{\Phi }}_{\alpha }^{*}$ within a quasi-logical lattice. Mathematically, this redefinition introduces a class of divergence conditions grounded in coherence curvature, continuity, and tunnel probability rather than in series magnitude. The comparison in Section 2 highlights the transition from unbounded summation to coherence-driven instability criteria.

Physically and computationally, the IRSVT formulation suggests that systems ranging from numerical sequences to cosmological fields may display divergence or collapse depending on the integrity of their informational coherence pathways.

Engineering implications include predictive IRSVT-based tools for:

• informational metamaterials,
• detection of cognitive instability loops in AI,
• prime-field signal identification,
• turbulence mapping in fusion plasma.

Finally, this work supports the hypothesis that informational structure may precede measurable mathematical form, suggesting that divergence in discrete systems reflects underlying coherence transitions rather than unbounded growth.