Review of the Problems Solved Using the Constrained Bayesian Methods

1. Introduction

As is known, there are four main approaches (philosophies) to statistical hypothesis testing, which differ from each other in the formalization of the problem, the metrics introduced, and the characteristics of the information used. These approaches are: Fisher’s [1], Neyman-Pearson’s [2], Jeffrey’s (so-called Bayesian) [3] (so-called parallel methods) and Wald’s (so-called sequential method) [4]. Based on these ideas, many methods have been developed and successfully used to solve various problems.

Since the late 1970s, we have been developing a new approach (philosophy) for testing hypotheses, which we have called the Constrained Bayesian Method (CBM).

As is known, two types of errors can be made when testing hypotheses: rejecting the true hypothesis (decision) and accepting the false hypothesis (decision). The measures of the possibility of making these decisions, i.e. probabilities, are called the levels of the first type (Type I) and second type (Type II) errors, respectively.

Unlike the classical Bayesian method, where an unconstrained optimization problem is solved, namely, the general loss function containing type I and type II errors is minimized, in CBM the minimization is performed of one type of error under the condition of imposing restrictions on another type of errors.

Depending on the constraints, it is possible to formulate seven different tasks, which allows us to very flexibly choose the appropriate task based on the characteristics of the problem to be solved [5]. In three of them, the levels of type I errors are limited and the levels of type II errors are minimized. In the following four, Type II error rates are limited and Type I error rates are minimized.

For clarity, let us give one formulation for each of these two groups.

2. Constrained Bayesian Method

Let us introduce the following notations: $x\in R^n$ is $n$ dimensional random variable with distribution density $p(x;\theta )$; $H_i:{\theta }_i\in {\Theta }_i$, $i=1,2,...,S$, are $S$ quantity testable hypotheses, where ${\Theta }_i\subset {\Omega }^m$, $i=1,2,...,S$; ${\Theta }_i$ are non-intersecting subsets $\cup {\Theta }_i={\Omega }^m$; ${\Omega }^m$ is $m$ dimensional parameter space; $p(H_i)$ is a priori probability of $H_i$ hypothesis; $p(x|H_i)$ is the density of the distribution of $x$ under the fairness of $H_i$ hypothesis; ${\Gamma }_j$ is the area of acceptance of $H_j$ hypothesis; $L_1(H_i,{\delta }_j(x)=1)$ and $L_2(H_i,{\delta }_j(x)=0)$ are losses caused by wrongly accepting and wrongly rejecting hypotheses.

2.1. Restrictions on the Conditional Probabilities of Accepting True Hypotheses (CBM 2)

The average loss caused by incorrectly accepting hypotheses is minimizing

$$r_{\delta }=\underset{\left\{{\Gamma }_j\right\}}{\min }\left\{{\displaystyle {\sum }_{i=1}^{S}p(H_i){\displaystyle {\sum }_{j=1}^S{\displaystyle {\int }_{{\Gamma }_j}{L}_1(H_i,{\delta }_j(x)=1)p(x|H_i)dx}}}\right\},$$

(1)

subject to

$${\displaystyle {\sum }_{j=1}^S{\displaystyle {\int }_{R^n-{\Gamma }_j}{L}_2(H_i,{\delta }_j(x)=0)p(x|H_i)dx}}\le r_2,i=1,...,S.$$

(2)

The solution of this problem gives

$${\Gamma }_j=\left\{x:{\displaystyle {\sum }_{i=1}^{S}p(H_i)L_1(H_i,{\delta }_j(x)=1)p(x|H_i)}<{\displaystyle {\sum }_{i=1}^S{\lambda }_i{L}_2(H_i,{\delta }_j(x)=0)p(x|H_i)}\right\},$$

(3)

where the Lagrange multipliers ${\lambda }_i$, $i=1,...,S$, are determined so that the equalities in (2) hold.

2.2. Restrictions on Posterior Probabilities of Rejecting True Hypotheses (CBM 7)

In this case, we are looking for the maximum of the average probability of accepting true hypotheses (let us call it the average power of the criterion)

$$G_{\delta }=\underset{\left\{{\Gamma }_j\right\}}{\max }\left\{{\displaystyle {\sum }_{i=1}^{S}p(H_i){\displaystyle {\sum }_{j=1}^S{\displaystyle {\int }_{{\Gamma }_j}{L}_2(H_i,{\delta }_j(x)=0)p(x|H_i)dx}}}\right\},$$

(4)

at the following restrictions

$${\displaystyle {\sum }_{i=1}^{S}p(H_i){\displaystyle {\int }_{{\Gamma }_j}{L}_1(H_i,{\delta }_j(x)=1)p(x|H_i)dx}}\le r_7,j=1,...,S.$$

(5)

Lagrange’s method gives us

$$\begin{array}{l}{\Gamma }_j=\left\{x:{\displaystyle {\sum }_{i=1}^{S}p(H_i)L_2(H_i,{\delta }_j(x)=0)p(x|H_i)}>{\lambda }_j{\displaystyle {\sum }_{i=1}^{S}p(H_i)L_1(H_i,{\delta }_j(x)=1)p(x|H_i)}\right\},\\ j=1,...,S\end{array}$$

(6)

where, ${\lambda }_j$ are determined so that the equalities in (5) hold.

3. General Characterization of the CBM

CBM turned out to be a generalization of existing methodologies, which gives unique results in terms of the optimality of the obtained decisions under the conditions of the minimum number of observations. Constrained Bayesian methodology surpasses in existing methodologies in that: 1) it uses all the information that existing methodologies use; 2) at formalization, all features of formalization of existing methodologies are taken into account.

In particular, the constrained Bayesian methodology uses not only the loss function and a priori probabilities to make decisions, as the classical Bayesian methodology does, but also the significance level of the criterion, as the frequentist (Neiman-Pearson) methodology does, and it is data-dependent like the Fisher methodology. The combination of these capabilities has increased the quality of the decisions made in the Constrained Bayesian methodology compared to other methodologies.

Constrained Bayes methodology has been used to test various types of hypotheses, such as simple, composite, asymmetric, multiple hypotheses, for which the superiority of CBMs compared to existing methods has been theoretically proven in the form of theorems and practically demonstrated by the results of many example calculations [5,6]. When testing the mentioned hypotheses, the constrained Bayesian methodology allows to obtain such decision rules, which, without any coercion, naturally allow to minimize practically all existing criteria of optimality of the decision, such as: type I, II and III error rates; false acceptance rate ($FAR$); pure directional false discovery rate ($pdFDR$); mixed directional false discovery rate ($mdFDR$); Family-wise error rates of type I and type II ($FWERI$, $FWERII$) and others.

To illustrate what has been said, let us quote some results obtained using the mentioned methodology.

Let us define the summary risk (SR) of making an incorrect decision when testing hypotheses as a weighted sum of the probabilities of making incorrect decisions, i.e.

$$r_S(\Gamma )={\displaystyle {\sum }_{i=1}^S{\displaystyle {\sum }_{j=1,j\ne i}^{S}L(H_i,H_j)p(H_i){\displaystyle {\int }_{{\Gamma }_j}p(x|H_i)dx}}}.$$

(7)

Here $L(H_i,H_j)$ is the sum function of losses caused by both types of errors.

It is clear that for given losses and probabilities, SR depends on decision areas. Let us note: ${\Gamma }^{CBM}$ and ${\Gamma }^B$ are the regions of acceptance of hypotheses, respectively, in constrained Bayesian (CBM) and Bayesian (B) methods; $r_S({\Gamma }^{CBM})$ and $r_S({\Gamma }^B)$ are, respectively, the summary risks (SR) in constrained Bayesian and Bayesian methods.

The following theorem is equitable [5,7].

Theorem 1.

For given losses and probabilities, SR of making incorrect decision in CBM is a convex function of  $\lambda$ with a maximum at  $\lambda =1$. By increasing or decreasing  $\lambda$ , SR decreases, and in the limit, i.e., at  $\lambda \to \infty$ or  $\lambda \to 0$, SR tends to zero.

From the theorem directly follows the following.

Corollary 1.

At the same conditions SR of making the incorrect decision in CBM is less or equal to SR of the Bayesian decision rule, i.e., $r_S({\Gamma }^{CBM})\le r_S({\Gamma }^B)$.

Similar to Corollary 1, it is not difficult to be convinced that SR of making an incorrect decision in the CBM does not exceed the SR of the frequentist method, that is,  $r_S({\Gamma }^{CBM})\le r_S({\Gamma }^f)$, where  $r_S({\Gamma }^f)$ is the SR of the frequentist method.

The following theorem is equitable [8].

Theorem 2.

Let us assume that probability distributions  $p\left(x|H_i\right)$, $i=1,...,S$, are such that, at increasing number of repeated observations  $n$, the entropy concerning distribution parameter  $\theta$, in relation to which the hypotheses are formulated, decrease. In such a case, for all given values  $0<{\alpha }_1<1$ and  $0<{\beta }_1<1$ there can always be found such a finite, positive integer number  $n^{*}$ that inequalities  $\alpha \left({\overline{x}}_n\right)<{\alpha }_1$ and  $\beta \left({\overline{x}}_n\right)<{\beta }_1$, where the number of repeated observations is  $n>n^{*}$, take place.

Here $\alpha \left({\overline{x}}_n\right)$ and $\beta \left({\overline{x}}_n\right)$ are the probabilities of errors of the first and the second types, respectively, in constrained Bayesian task when the decision is made on the basis of arithmetic mean of the observation results ${\overline{x}}_n$ calculated by $n$ repeated observations. That is, the CBM allows us to make a decision by increasing information so that the levels of possible first and second type errors are restricted to any desired level.

Let us bring examples of the use of the CBM in cases of different types of hypotheses (simple, composite, asymmetric, multiple) and show its advantage over existing methods.

4. Simple Hypotheses

4.1. Parallel Methods

Example 1 [9]. Suppose that $X_1,X_2,...,X_n$ are independent identically distributed (i.i.d.) random variables with distribution law $N(x;\theta ,1)$. Let us test the basic hypothesis $H_0:\theta =-1$ against the alternative $H_A:\theta =1$.

Below, when discussing examples, we assume that the hypotheses are a priori equally probable.

Table 1 presents the results of testing hypotheses using various criteria for various $\overline{x}$ calculated from $n=4$ observations.

The results of the computation show that the Berger ($T^C$ and $T^{*}$ criteria), Bayesian, and Neyman-Pearson methods accept the alternative hypothesis on the basis of $\overline{x}=0$, i.e. $B(x)=1$, when there is no basis for such a decision [9]. Both hypotheses are equally likely to be true or false.

In this respect, Fisher’s $p$-value test is better because it rejects the hypothesis $H_0$ but says nothing about $H_A$. However, the probability value $p$ does not provide any information about the existence of another possible hypothesis instead of $H_0$. In this situation, CBM gives the most logical answer, because it confirms that both hypotheses are equally true or equally false, that is, an unambiguous decision cannot be made in this case. For other values of the statistic $\overline{x}$, all the considered methods make correct decisions with different error probabilities. But even in these cases, the advantage of CBM is obvious, because it gives us the error levels of Type I and Type II for which one of the testable hypotheses can be accepted according to the given statistic $\overline{x}$.

4.2. Sequential Methods

Example 2 [9]. Let us consider the scenario of Example 1, but assume that the data is obtained sequentially.

The results of the computation of 17 random samples generated by $N(x;1,1)$ sequentially processed are given in Table 2, where the arithmetic mean of the observations $x_k,...,x_m$ is indicated by ${\overline{x}}_{k,m}$.

4.3. Sequential Methods

Example 3 [9]. Let us consider the scenario of Example 1, but assume that the data is obtained sequentially.

The results of the computation of 17 random samples generated by $N(x;1,1)$ sequentially processed are given in Table 3, where the arithmetic mean of the observations $x_k,...,x_m$ is indicated by ${\overline{x}}_{k,m}$.

The table shows that the Wald and Berger $T^{*}$ tests give the same results, although the error probabilities in the Berger test are slightly lower than in the Wald test due to the fact that Berger calculated the error probabilities with a given value of the statistic. In the Wald criterion, they are determined by the decision thresholds. Out of 17 observations, correct decisions were made 7 times based on 3, 3, 5, 1, 1, 3, and 1 observations in both tests, and all decisions were correct. The average number of observations in making a decision is equal to 2.43. With the Bayesian-type sequential method, correct decisions for the same sample were made 10 times based on 1, 2, 2, 1, 3, 2, 1, 1, 3, and 1 observations, and all decisions were also correct. The average number of observations in making a decision is equal to 1.7.

5. Composite Hypotheses

Similar to the cases above, where CBM is optimal for testing simple hypotheses in parallel and sequential experiments, it retains optimal properties when testing composite hypotheses. Also, it easily, without much effort, overcomes Lindley’s paradox, which arises when testing a simple hypothesis against a composite hypothesis. These facts are shown theoretically and based on the computation of specific examples in the work [10].

6. Testing Multiple Hypotheses

For several last decades, multiple hypotheses testing problems have attracted significant attention because of their huge applications in many fields (see, for example, [11–17 and so on]).

CBM maintains optimal properties when testing multiple hypotheses. For example, in [18] were considered $d$ individual hypotheses about parameters ${\theta }_1,...,{\theta }_d$ of sequentially observed vectors $X_1,X_2,...$

$$H_0^{(1)}:{\theta }_1\in {\Theta }_{01} vs H_A^{(1)}:{\theta }_1\in {\Theta }_{11},$$

$$H_0^{(2)}:{\theta }_2\in {\Theta }_{02} vs H_A^{(2)}:{\theta }_2\in {\Theta }_{12},$$

$$H_0^{(d)}:{\theta }_k\in {\Theta }_{0d} vs H_A^{(d)}:{\theta }_k\in {\Theta }_{1d}.$$

(8)

The following stopping rule in the sequential test was developed

$$T=\inf \left\{m:{\displaystyle {\cap }_{j=1}^d\left\{{\Lambda }_m^{(j)}\notin \left({\lambda }_{*j},{\lambda }_j^{*}\right)\right\}}\right\},$$

(9)

where ${\lambda }_{*j}$ and ${\lambda }_j^{*}$ are Lagrange multipliers obtained in CBM; ${\Lambda }_m^{(j)}$ is the likelihood ratio (10) for the $j$th parameter ($j=1,...,d$) calculated on the basis of $m$ sequentially obtained observation results

$${\Lambda }_m={\displaystyle \frac{p(x^1|H_1)\cdot \cdot \cdot p(x^m|H_1)}{p(x^1|H_0)\cdot \cdot \cdot p(x^m|H_0)}},m=1,2,...$$

(10)

The following theorem was proved [18]

Theorem 3. A sequential Bonferroni procedure for testing multiple hypotheses (8) with stopping rule (9), rejection regions  ${\Lambda }_T^{(j)}>{\lambda }_j^{*}$, and acceptance regions  ${\Lambda }_T^{(j)}<{\lambda }_{*j}$, where  ${\lambda }_j^{*}$ and  ${\lambda }_{*j}$ are defined in CBM for  ${\beta }_j=\beta /d$ and  ${\alpha }_j=\alpha /d$, controls both error rates at levels  $FWE{R}_I\le \alpha$ and  $FWE{R}_{II}\le \beta$.

The computed results (given in [18]) clearly demonstrate the validity and optimality of the developed scheme in comparison with the existing methods.

7. Testing Multiple Hypotheses with Directional Alternatives in Sequential Experiments

Testing a simple basic hypothesis versus composite alternative is a common, well-studied problem in many scientific works [19,20,21,22,23,24,25,26]. In many problems, whether to make a decision in favor of the alternative hypothesis as well as making sense of the direction of difference between parameter values, defined by basic and alternative hypotheses, is important; that is, making a decision whether the parameter outstrips or falls behind the value defined by the basic hypothesis is meaningful [27,28,29,30,31,32,33]. Such problems occur, for example, in microarray data analysis, imaging analysis, biological applications and genetic research [32,34] and many others.

For parametrical models, this problem can be stated as

$$H_0:\theta ={\theta }_0 \mathrm{vs.} H_{-}:\theta <{\theta }_0 \mathrm{or} H_{+}:\theta >{\theta }_0,$$

(11)

where $\theta$ is the parameter of the model, ${\theta }_0$ is known. These alternatives are called skewed or directional alternatives.

In many applications, the case of multiple directional hypotheses is considered, i.e. the testing hypotheses are the following [29,31,33,34,35]

$$H_i^{(0)}:{\theta }_i=0 vs H_i^{(-)}:{\theta }_i<0 or H_i^{(+)}:{\theta }_i>0,i=1,...,m.$$

(12)

where $m$ is the number of individual hypotheses about parameters ${\theta }_1,...,{\theta }_m$ that must be tested by test statistics $X=\left(X_1,X_2,...,X_m\right)$, where $X_i\approx f\left(x_i|{\theta }_i\right)$.

The following theorem for hypotheses (11) is proved in [36].

Theorem 4.

Let us assume that the probability distributions  $p(x|H_i)$, $i\in \Psi$, where  $\Psi \equiv \left\{-,0,+\right\}$, are such that, at increasing number of observations  $n$ in the sample, the entropy concerning distribution parameter  $\theta$, in relation to which the hypotheses are formulated, decreases. In such case, for given set of hypotheses  $H_0$,  $H_{-}$ and  $H_{+}$, there always exists such sample of size  $n$ on the basis of which decision concerning tested hypotheses can be made with given reliability when Lagrange multipliers are determined for  $n=1$ in decision making regions and the condition  $mdFDR\le q$ is satisfied.

For multiple directional hypotheses (12) the stopping rule is as follows:

$$T=\inf \left\{n:{\displaystyle \underset{i=1}{\overset{m}{\cap }}\left[t_i\left(X^{(1)},X^{(2)},...,X^{(n)}\right)\in \hspace{1em}only\hspace{1em}one\hspace{1em}\right]of{\Gamma }_j^i,j\in \Psi }\right\},$$

where $X^{(i)}$, $i=1,...,n$, are independent $m$-dimensional observation vectors with correlated parameters; ${\Gamma }_j^i$ is $j$-th hypothesis acceptance region for $i$-th sub-set of hypothesis.

The following theorem is proved in [36].

Theorem 5.

Let’s for each sub-set of directional hypotheses of multiple hypotheses (12) one of the possible stated task of CBM is used with the restriction levels providing the condition $mdFD{R}_i\le q_i$

,  $i=1,...,m$. Then, if  $q_i$,  $i=1,...,m$, are taken so that  ${\displaystyle {\sum }_{i=1}^m{q}_i}=q$, the following condition  $tmdFDR\le q$ is fulfilled.

Here $tmdFDR$ is the total mixed directional false discovery rate that was introduced in [36].

8. Testing Composite Hypotheses Concerning Normal Distribution with Equal Parameters

In a large variety of practical situations, a normal distribution with equal parameters, that is $N\left(\theta ,\theta \right)$, may be postulated as a useful model for data [37,38,39].

Let us consider a random variable $X$ distributed as $N\left(\theta ,\theta \right)$. The problem is to test the hypotheses

$$H_0:\theta ={\theta }_0,{\theta }_0>0\hspace{1em}\mathrm{vs.}\hspace{1em}{H}_{-}:0<\theta <{\theta }_0\hspace{1em}\mathrm{or}\hspace{1em}{H}_{+}:\theta >{\theta }_0,$$

(13)

on the basis of independent identically distributed (i.i.d.) random variables $X_1,X_2,...,X_n$.

The following theorems for directional alternatives were proved in [36].

Theorem 6.

CBM 7, at satisfying a condition  ${\displaystyle \frac{r_7^{-}+r_7^{+}}{K_1\cdot P_{\min }}}=q$ (i.e. $r_7^{-}+r_7^{+}=q\cdot K_1\cdot P_{\min }$), where  $0<q<1$,  $P_{\min }=\min \left\{p(H_{-}),p(H_0),p(H_{+})\right\}$, ensures a decision rule with  $mdFDR$ (i.e. with  $SER{R}_{III}$) less or equal to  $q$, i.e. with the condition  $mdFDR=SER{R}_{III}\le q$.

Theorem 7.

CBM 7, at satisfying a condition  ${\displaystyle \frac{r_7^{-}+r_7^0+r_7^{+}}{K_1\cdot P_{\min }}}=q$ (i.e. $r_7^{-}+r_7^0+r_7^{+}=q\cdot K_1\cdot P_{\min }$), where  $0<q<1$,  $P_{\min }=\min \left\{p(H_{-}),p(H_0),p(H_{+})\right\}$, ensures a decision rule with  $mdFDR+FAR$ less or equal to  $q$, i.e. with the condition  $mdFDR+FAR\le q$.

Here, we have: $FAR=P(x\in {\Gamma }_0|H_{-})+P(x\in {\Gamma }_0|H_{+})$ as the false acceptance rate; $r_7^{-}$, $r_7^0$, $r_7^{+}$ are restriction levels in CBM 7; $K_1$ is the loss for incorrect acceptance of hypothesis.

Moreover, the following theorems are proven in [39].

Theorem 8.

CBM 2, for hypotheses (12), ensures a decision rule with the error rates of the Type-I and Type-II restricted by the following inequalities

$$\alpha \le {\displaystyle \frac{r_2^0}{K_0\cdot p(H_0)}},$$

$$\beta \le {\displaystyle \frac{r_2^{-}}{K_0\cdot p(H_{-})}}+{\displaystyle \frac{r_2^{+}}{K_0\cdot p(H_{+})}}.$$

(14)

Theorem 9.

CBM 2, for hypotheses (12), ensures a decision rule with  $r_{\delta }$ the averaged loss of incorrectly accepted hypotheses and  ${\alpha }_s$  the averaged loss of incorrectly rejected hypotheses restricted by the following inequalities

$$r_{\delta }\le {\displaystyle \frac{K_1}{K_0}}\left[r_2^{-}+r_2^0+r_2^{+}\right],$$

$${\alpha }_s\le r_2^{-}+r_2^0+r_2^{+}.$$

(15)

Correctness of these theorems and superiority of CBM over Bayes method are clearly demonstrated by computation results.

9. Testing Equi-Correlation Coefficient

Symmetric Multivariate Normal Distribution (SMND) is widely used in many applications of different spheres of human activities such as psychology, education, genetics and so on [40]. It is also used extensively in statistical inference procedures, e.g., in analysis of variance (ANOVA) for modeling of the error part [41].

Let the $k$-dimensional random vector $X$ follow the $k$-variate normal distribution with zero mean vector and correlation matrix $W$ of the following structure:

$$W=(1-\rho )\cdot I_{k\times k}+\rho \cdot J_{k\times k},$$

(16)

where $I_{k\times k}$ is an identity matrix and $J_{k\times k}$ is matrix of ones.

The support of $\rho$, $\left(-1/(k-1),1\right)$ assures the non-singularity of the correlation matrix $W$ [41].

The problem, we want to solve, can be formulated as follows: to test

$$H_0:\rho ={\rho }_0 \mathrm{vs.} H_{-}:-1/(k-1)<\rho <{\rho }_0 \mathrm{or} H_{+}:{\rho }_0<\rho <1,$$

(17)

$$\rho ,{\rho }_0\in \left(-1/(k-1),1\right).$$

on the basis of the sample $Y_1,...,Y_n$. Here $Y_i$ is the Helmert orthogonal transformation $Y_1,Y_2,...$ on uncorrelated multivariate normal vectors sequence $X_1,X_2,...$, i.e. $Y_i=H\cdot X_i,$ $i=1,2,...,$ where $H$ is the Helmert matrix given as [41]

$$H=\left[\begin{array}{lllll}{\displaystyle \frac{1}{\sqrt{k}}}& {\displaystyle \frac{1}{\sqrt{k}}}& {\displaystyle \frac{1}{\sqrt{k}}}& ...& {\displaystyle \frac{1}{\sqrt{k}}}\\ {\displaystyle \frac{1}{\sqrt{2}}}& -{\displaystyle \frac{1}{\sqrt{2}}}& 0& ...& 0\\ {\displaystyle \frac{1}{\sqrt{6}}}& {\displaystyle \frac{1}{\sqrt{6}}}& -{\displaystyle \frac{2}{\sqrt{6}}}& 0& ...& 0\\ ...& ...& ...& ...& ...& ...\\ {\displaystyle \frac{1}{\sqrt{k(k-1)}}}& ...& {\displaystyle \frac{1}{\sqrt{k(k-1)}}}& -{\displaystyle \frac{(k-1)}{\sqrt{k(k-1)}}}\end{array}\right].$$

(18)

i.e. $Y_i$ is $k$-dimensional random vector with independent components each of which has zero mean and variances determined by

$$v_1=1+(k-1)\rho \mathrm{and} v_2=...=v_k=1-\rho .$$

(19)

The probability density function (pdf) of $Y_i$ is

$$p(Y_i|\rho )={(2\pi )}^{-{\displaystyle \frac{k}{2}}}{\left|V\right|}^{-{\displaystyle \frac{1}{2}}}\cdot \exp \left\{-{\displaystyle \frac{1}{2}}{Y}_i\cdot V^{-1}\cdot Y_i^T\right\},i=1,...,n.$$

(20)

The joint pdf of the sample $Y_1,...,Y_n$ has the following form [42]

$$p(Y_1,...,Y_n|\rho )={(2\pi )}^{-kn/2}\cdot {\left|V\right|}^{-{\displaystyle \frac{n}{2}}}\cdot \exp \left\{-{\displaystyle \frac{1}{2}}{\displaystyle \sum _{i=1}^n{Y}_i\cdot V^{-1}\cdot Y_i^T}\right\}=$$

$$={(2\pi )}^{-kn/2}{(1+(k-1)\rho )}^{-{\displaystyle \frac{n}{2}}}{(1-\rho )}^{-{\displaystyle \frac{n(k-1)}{2}}}\cdot \exp \left\{-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{V_{1n}}{1+(k-1)\rho }}+{\displaystyle \frac{V_{2n}}{1-\rho }}\right)\right\},$$

(21)

where $V_{1n}$ and $V_{2n}$ are defined by ratio

$$V_{1n}={\displaystyle {\sum }_{i=1}^n{y}_{i1}^2}and{V}_{2n}={\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=2}^k{y}_{ij}^2}},$$

(22)

where $Y_i=\left(y_{i1},y_{i2},...,y_{ik}\right)$, $i=1,...,n$.

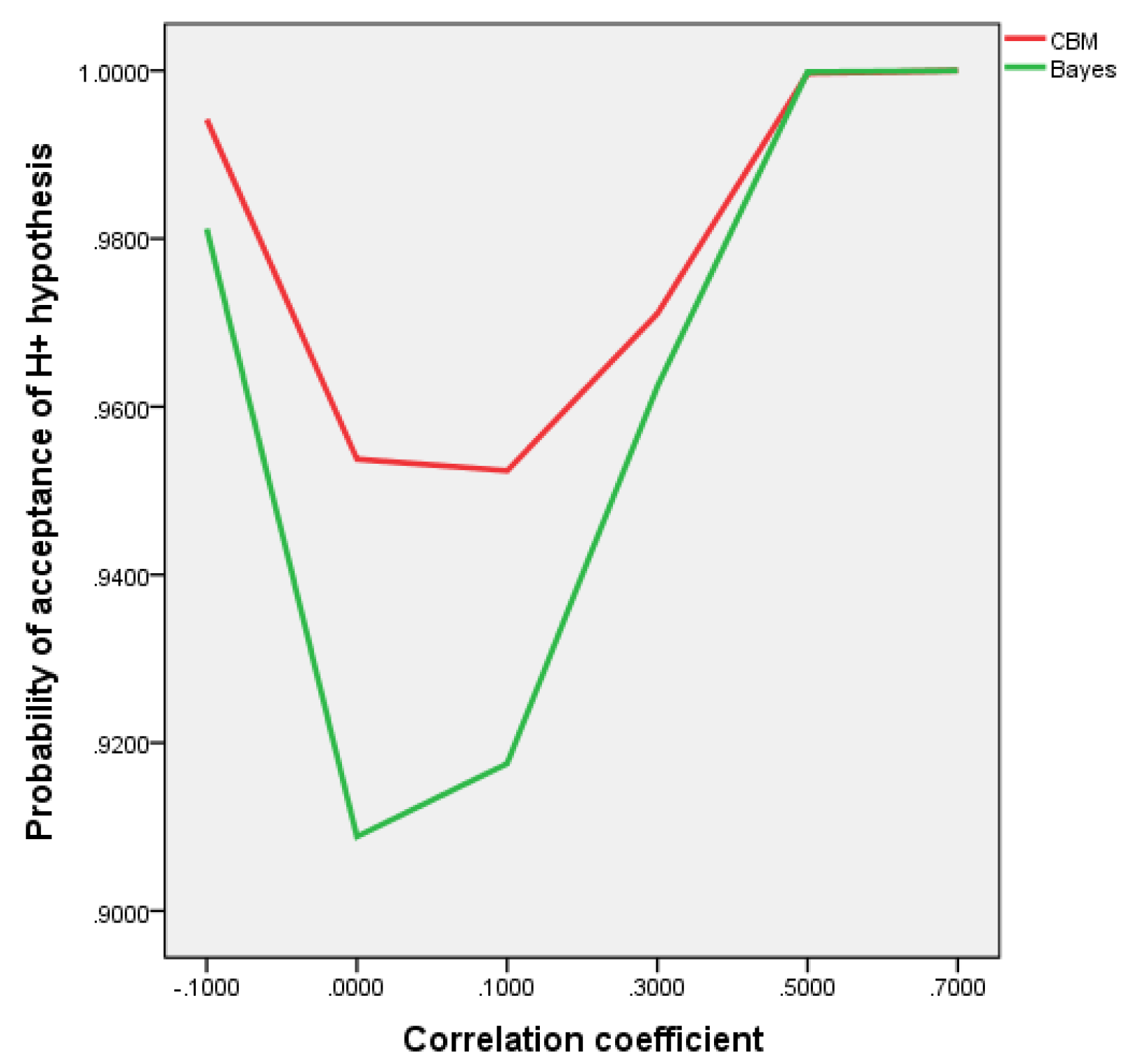
To test hypotheses (17) were applied CBM using the maximum likelihood estimation and Stein’s approach [43]. Simulation results showed that CBM using Stein’s approach gives opportunities to make decisions with higher reliability for testing (17) hypotheses then Bayes method (see Figure 1).

The samples for making decisions are generated by (21) with $\rho \in ({\rho }_0,1)$ for the size $m=5000$.

11. Conclusion

A brief review of the application of CBM to test different types of statistical hypotheses arising in many practical problems are considered above. It confirms the advantage of the CBM over existing classical methods at testing simple, composite, asymmetric, multiple hypotheses of different kinds. Obtained results, published in many important scientific publication, confirm the flexibility of the method and its great ability to deal with difficult problems.