Submitted:
06 December 2025
Posted:
08 December 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. The Theoretical Basis
2.1. Information Transformation
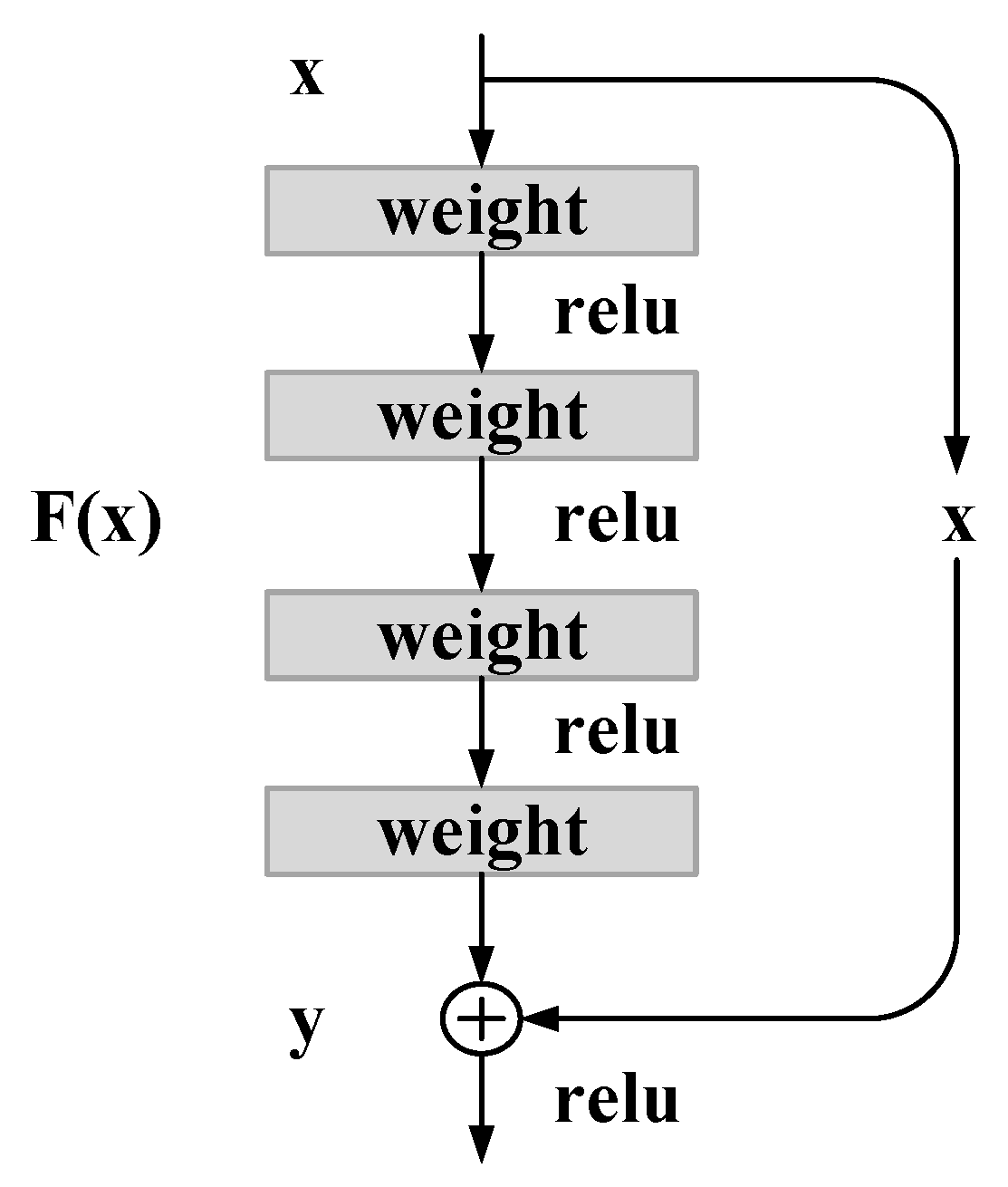
2.2. Training and Reasoning of Residual Neural Networks
2.3. Diagnostic Condition Assessment
2.4. Diagnostic Category Assessment
3. Performance Verification and Result Analysis
3.1. Case Description and Model Construction
| Motor Load (HP) | Motor Speed (rpm) | Normal | Inner Raceway | Ball | Outer Raceway Center |
|---|---|---|---|---|---|
| 0 | 1797 | - | 7 mils | 7 mils | 7 mils |
| 1 | 1772 | - | 7 mils | 7 mils | 7 mils |
| 2 | 1750 | - | 7 mils | 7 mils | 7 mils |
| 3 | 1730 | - | 7 mils | 7 mils | 7 mils |
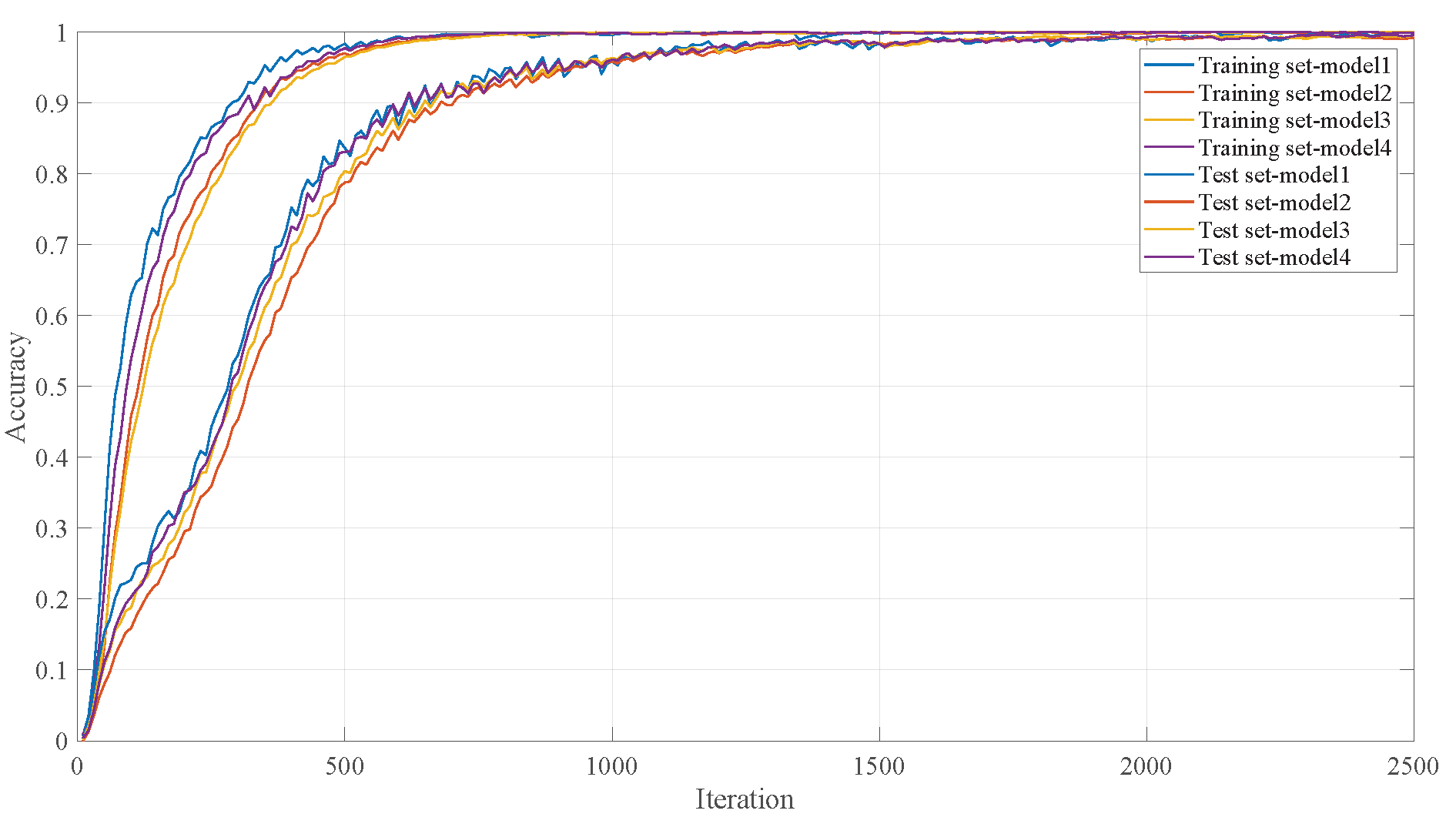
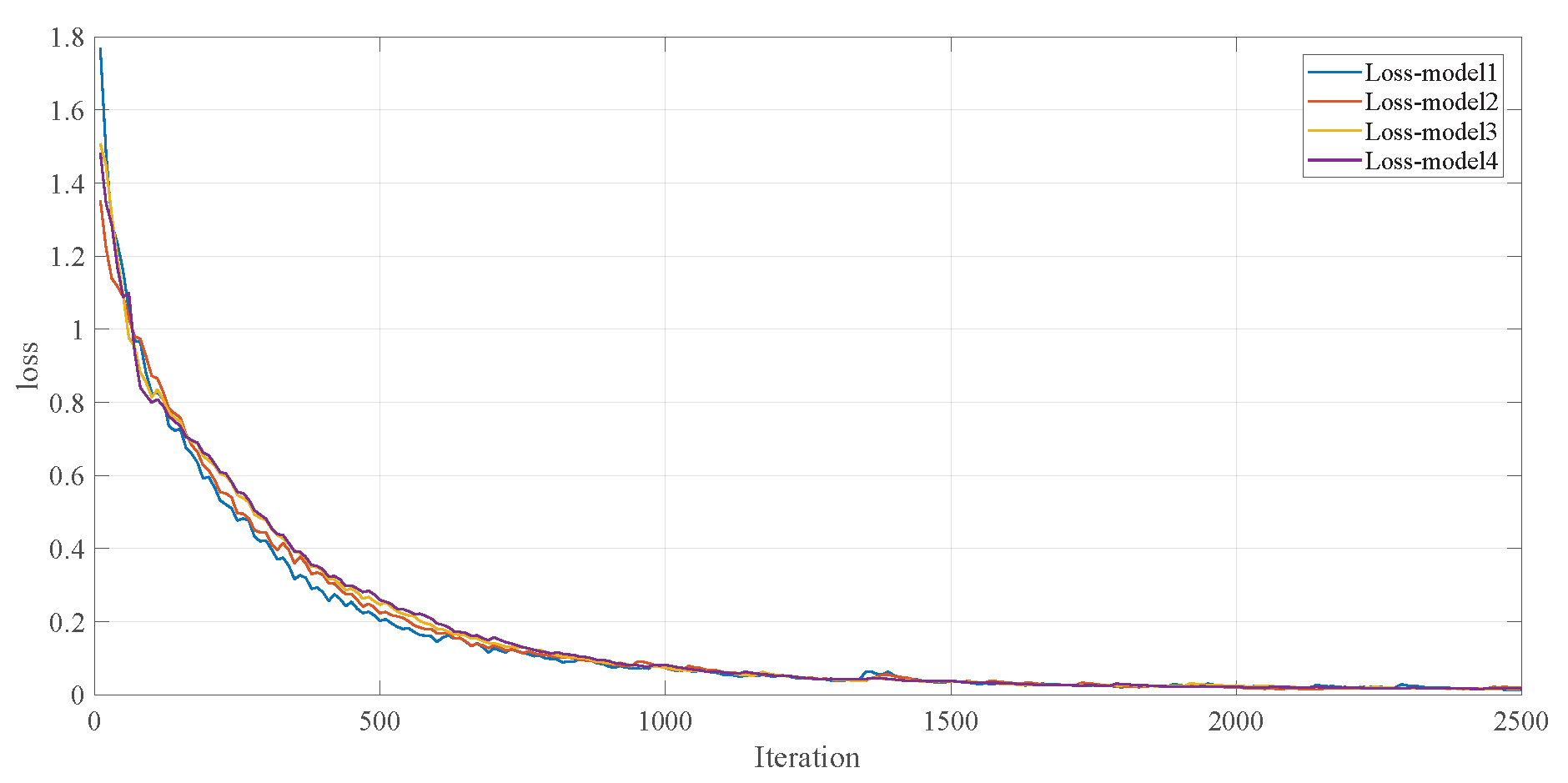
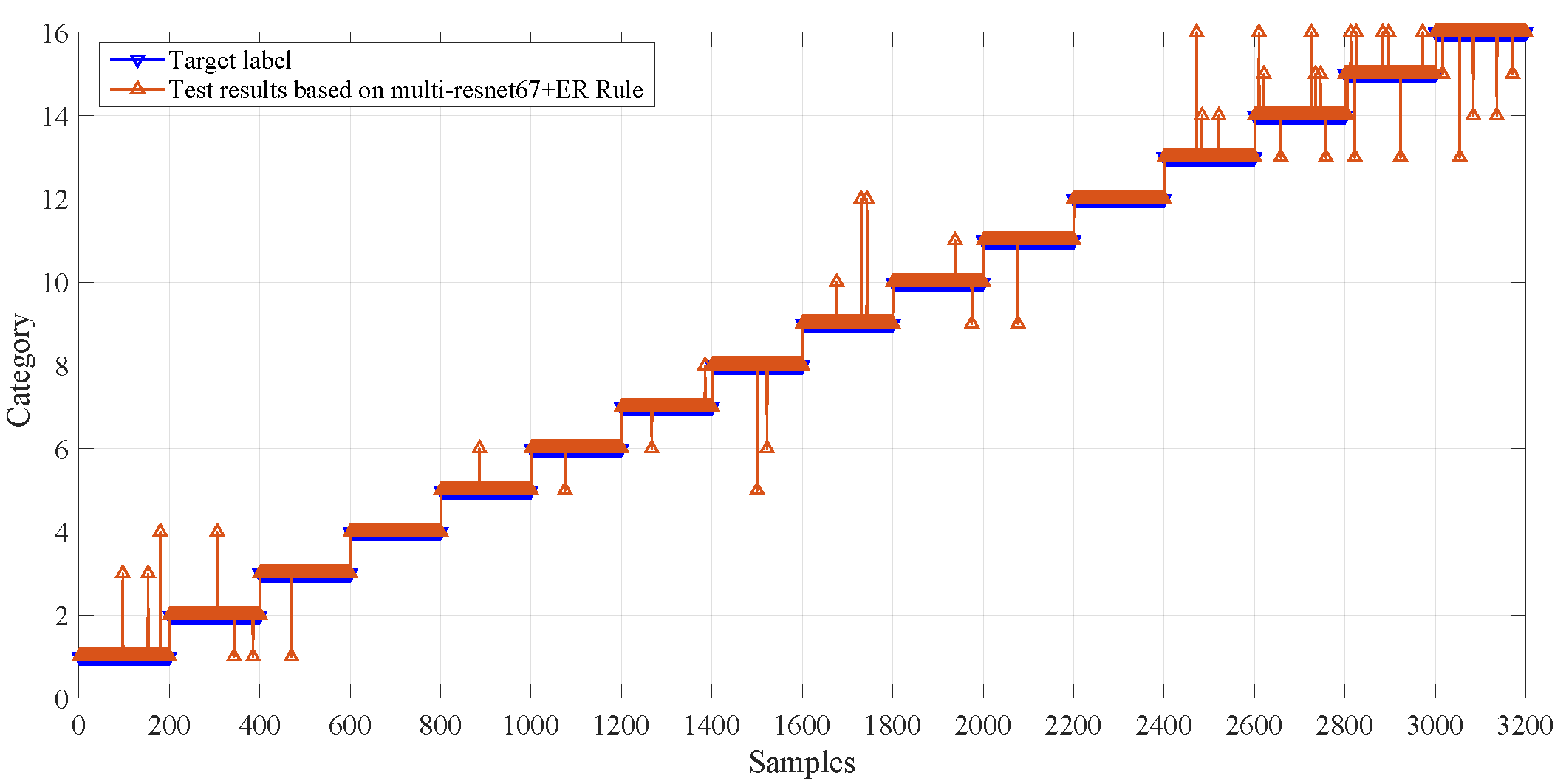
3.2. Model Training and Result Analysis
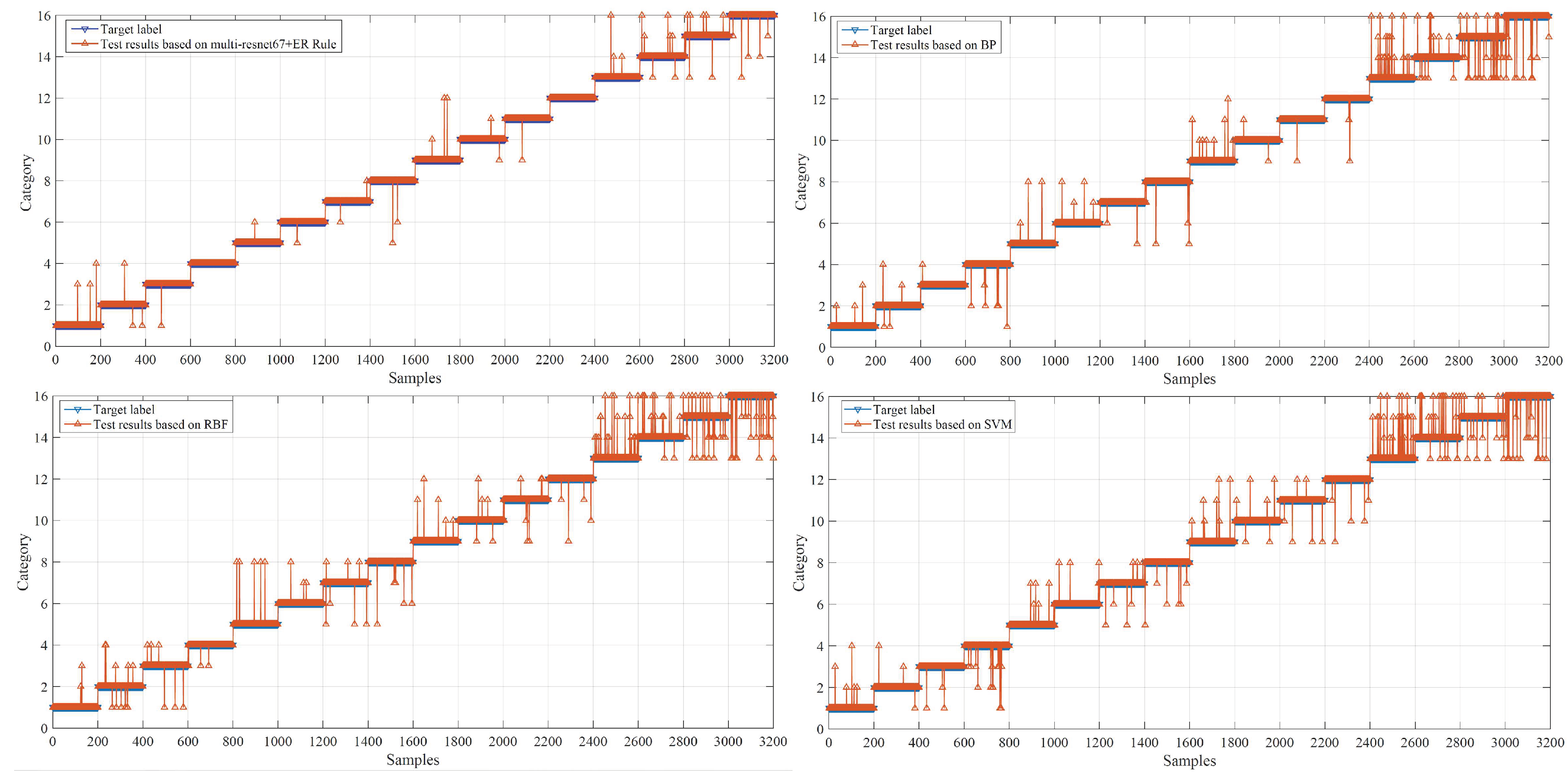
3.3. Experimental Comparison
4. Conclusions
- 1.
- Multi-residual neural network structure was proposed to deep extract and classify the micro faults based on the spectrum diagram;
- 2.
- Diagnostic condition assessment and diagnostic category assessment mechanism were conducted by using ER Rule based on the models’ relative credibility.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ER Rule | Evidence Reasoning Rule |
| ResNet | Residual Network |
| STFT | Short-Time Fourier Transform |
| BP | Back Propagation network |
| RBF | Radial Basis Function network |
| SVM | Support Vector Machine |
| ES | Expert System |
| UKF | Unscented Kalman Filter |
| CFMDAS | Car Failure and Malfunction Diagnosis Assistance System |
| OLA | Online Approximator |
| ANN | Artificial Neural Network |
| EMD | Empirical Mode Decomposition |
| CWRU | Case Western Reserve University |
| HP | horsepower |
| RPM | Revolutions Per Minute |
References
- Afgan, N. H.; Carvalho, M. G.; Pilavachi, P. A. An expert system concept for diagnosis and monitoring of gas turbine combustion chambers. Appl. Therm. Eng. 2006, 26, 766–771.
- Andrea, T.; Andrea, L. Energy system diagnosis by a fuzzy expert system with genetically evolved rules. Int. J. Thermodyn. 2008, 11.
- Nan, C.; Khan, F.; Iqbal, M. T. Real-time fault diagnosis using knowledge-based expert system. Process Saf. Environ. Protection 2008, 86, 55–71.
- Mostafa, S. A.; Ahmad, M. S.; Mohammed, M. A. Implementing an expert diagnostic assistance system for car failure and malfunction. Int. J. Comput. Sci. Issues 2012, 9.
- Bo, M.; Zhi-Nong, J.; Zhong-Qing, W. Development of the task-based expert system for machine fault diagnosis. In Proceedings of the J. Phys.: Conf. Ser., 2012; pp. 012043.
- Kodavade, D. V.; Apte, S. D. A universal object oriented expert system frame work for fault diagnosis. Int. J. Intell. Sci. 2012, 2, 8.
- Hsiao, T.; Weng, M. C. A hierarchical multiple-model approach for detection and isolation of robotic actuator faults. Robotics and Autonomous Systems 2012, 60, 154–166.
- Yang, Q. M.; Sun, Y. X. Automated fault accommodation for discrete-time systems using online approximators. In Proceedings of the 30th Chinese Control Conference, Shanghai, 2011; pp. 4264–4269.
- Avram, R. C.; Zhang, X.; Muse, J. Quadrotor actuator fault diagnosis and accommodation using nonlinear adaptive estimators. IEEE Trans. Control Syst. Technol. 2017, 1–8.
- Zhao, B.; Skjetne, R.; Blanke, M. Particle filter for fault diagnosis and robust navigation of underwater robot. IEEE Trans. Control Syst. Technol. 2014, 22, 2399–2407.
- Barman, D.; Sarkar, S.; Das, G.; Das, S.; Purkait, P. DFA and DWT based severity detection and discrimination of induction motor stator winding short circuit fault from incipient insulation failure. In Proceedings of the 2015 International Conference on Electrical, Electronics, Signals, Communication, and Optimization, Visakhapatnam, 2015; pp. 1–6.
- Sugumaran, V.; Rao, A. V.; Ramachandran, K. I. A comprehensive study of fault diagnostics of roller bearings using continuous wavelet transform. Int. J. Manuf. Syst. Des. 2015, 1, 27–46.
- Liang, J.; Yang, Z. X. A novel wavelet transform-empirical mode decomposition based sample entropy and SVD approach for acoustic signal fault diagnosis. In Proceedings of the 6th International Conference on Advances in Swarm and Computational Intelligence, Beijing, China, 2015; pp. 232–241.
- Zhang, Z. Y.; Wang, Y.; Wang, K. S. Fault diagnosis and prognosis using wavelet packet decomposition, Fourier transform and artificial neural network. J. Intell. Manuf. 2013, 24, 1213–1227.
- Namdari, M.; Jazayeri-Rad, H. Incipient fault diagnosis using support vector machines based on monitoring continuous decision functions. Eng. Applicat. Artif. Intell. 2014, 28, 22–35.
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444.
- Krizhevsky, A.; Sutskever, I.; Hinton, G. E. ImageNet classification with deep convolutional neural networks. In Proceedings of the NIPS, 2012.
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the CVPR, 2015.
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the CVPR, 2014.
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the NIPS, 2015.
- Xu, K.; Ba, J.; Kiros, R.; Cho, K.; Courville, A.; Salakhutdinov, R.; Zemel, R. S.; Bengio, Y. Show, attend and tell: Neural image caption generation with visual attention. In Proceedings of the ICML, 2015.
- Yao, L.; Torabi, A.; Cho, K.; Ballas, N.; Pal, C.; Larochelle, H.; Courville, A. Describing videos by exploiting temporal structure. In Proceedings of the ICCV, 2015.
- Huval, B.; Wang, T.; Tandon, S.; Kiske, J.; Song, W.; Pazhayampallil, J.; Andriluka, M.; Rajpurkar, P.; Migimatsu, T.; Cheng-Yue, R.; others. An empirical evaluation of deep learning on highway driving. arXiv 2015, preprint at https://arxiv.org/abs/1504.01716 .
- Bojarski, M.; Del Testa, D.; Dworakowski, D.; Firner, B.; Flepp, B.; Goyal, P.; Jackel, L. D.; Monfort, M.; Muller, U.; Zhang, J.; others. End to end learning for self-driving cars. arXiv 2016, preprint at https://arxiv.org/abs/1604.07316 .
- Greenspan, H.; van Ginneken, B.; Summers, R. M. Guest editorial deep learning in medical imaging: Overview and future promise of an exciting new technique. IEEE Trans. Med. Imaging 2016, 35, 1153–1159.
- Ali, S. D. The impact of deep learning on investments: Exploring the implications one at a time. Predictive Anal. Futur. 2016, 13, 49–50.
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016; pp. 770–778.
- Griffin, D. Signal estimation from modified short-time Fourier transform. IEEE Trans. Acoust. Speech, Signal Process. 1984, 32, 236–243.
- Kwok, H. K.; Jones, D. L. Improved instantaneous frequency estimation using an adaptive short-time Fourier transform. IEEE Trans. Signal Process. 2000, 48, 2964–2972.
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016; pp. 2818–2826.
- Sun, Y. J.; Zhang, S.; Miao, C. X. Improved BP neural network for transformer fault diagnosis. J. China Univ. of Mining and Technol. 2007, 17, 138–142.
- Yi, Q.; Zhan-Ming, L.; Er-Chao, L. Fault detection and diagnosis for non-Gaussian stochastic distribution systems with time delays via RBF neural networks. ISA Trans. 2012, 51, 786–791.
- Lv, G.; Cheng, H.; Zhai, H. Fault diagnosis of power transformer based on multi-layer SVM classifier. Proceedings of the Chinese Society of Universities 2005, 75, 9–15.

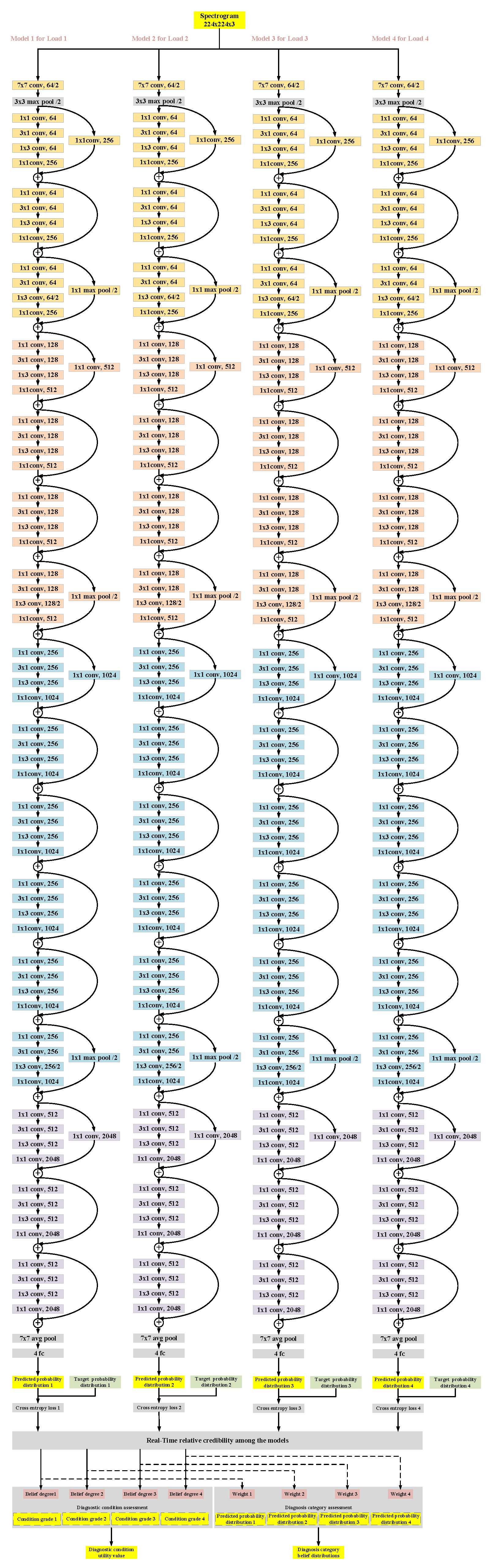
| Residual Unit | Output Size | Network Layer Parameters | Unit Number | Sub-Model NUMBER |
|---|---|---|---|---|
| - | 112×112 | 7×7 conv, 64/2 | 1 | 4 |
| - | 56×56 | 3×3 max pool, 64/2 | 1 | |
| unit_1 | 56×56 | 1×1, 64; 3×1, 64; 1×3, 64; 1×1, 256 | 2 | |
| unit_1 | 56×56 | 1×1, 64; 3×1, 64; 1×3, 64/2; 1×1, 256 | 1 | |
| unit_2 | 28×28 | 1×1, 128; 3×1, 128; 1×3, 128; 1×1, 512 | 3 | |
| unit_2 | 28×28 | 1×1, 128; 3×1, 128; 1×3, 128/2; 1×1, 512 | 1 | |
| unit_3 | 14×14 | 1×1, 256; 3×1, 256; 1×3, 256; 1×1, 1024 | 5 | |
| unit_3 | 14×14 | 1×1, 256; 3×1, 256; 1×3, 256/2; 1×1, 1024 | 1 | |
| unit_4 | 7×7 | 1×1, 512; 3×1, 512; 1×3, 512; 1×1, 2048 | 2 | |
| unit_4 | 7×7 | 1×1, 512; 3×1, 512; 1×3, 512/2; 1×1, 2048 | 1 | |
| 1×7×2 | 1×1 | 7×7 mean pool, 2048 | 1 | |
| 1×7×2 | - | 4 fc, Softmax | 1 | |
| ER Rule | 1 | |||
| Model | Training Set | Test Set |
|---|---|---|
| Multi-resnet-67+ER Rule | 0.9916 | 0.9734 |
| Wavelet packet+ BP | 0.9772 | 0.9646 |
| Wavelet packet+ RBF | 0.9706 | 0.9553 |
| Wavelet packet +SVM | 0.9634 | 0.9521 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





