1. Introduction
Alternative investments have been a topic of discussion and curiosity for investors looking for new alternatives for diversification. Private equity (PE) is an alternative investment made in a privately owned company to acquire partial or full financial ownership of that company to obtain a profitable return (Moon, 2006). In capital markets, private equity has been gaining relevance as it has presented a continuous and rapid growth in the last decade, but it has also served as a powerful tool used to improve the performance of the economy as it pushes forward struggling companies with strong potential adding financial and strategic value. In only 5 years, from January 2020 to July 2025, 5.242 trillion dollars were raised in private equity markets (LSEG, 2025)
As PE’s relevance continues to make a deep impact in the economy, it is considered a strong alternative for investment that is also easier to access; for instance, in 2025 in the United States, 401(k) or employer-sponsored retirement plans are now open to invest in private markets, such as venture capital and private equity (Wolter, 2025). Its appeal is also based on higher returns than those earned in public markets. For instance, between 1986 and 2023 the Global PE index, which tracks the performance of equity funds worldwide, outperformed the MSCI World Index (global equity benchmark) for about 500 basis points (Cambridge Associates LLC., 2023).
This appealing instrument also carries risk. Even though it’s a long-term instrument, it is illiquid and the secondary market for private equity positions is not transparent, making it difficult for funds to rebalance their PE investments, requiring an additional premium for holding such risk (Sorensen et al., 2014).
Several instruments for valuation in private equity are commonly used; even though the International Private Equity and Venture Capital Valuation Guides (IPEV) provide recommendations for alternative funds, they are not mandatory for financial reporting standards. In terms of valuation methods, the Modigliani and Miller theorem (Modigliani & Miller, 1958), financial ratios such as IRR, PME (Kaplan & Schoar, 2005), comparable public companies, comparable acquisitions and the most common one, discounted cash flow (DCF) (Hooke, 2024). Baldi (2005) documented that because of the high level of leverage that is present in LBOs, the APV method of valuation is noteworthy as well. Finnerty, J. D., & Park, R. W. (2018) proposed a valuation model where PE funds receive a call option on the fund’s leverage equity investment portfolio, giving them a share of the fund’s profit.
An option is a derivate contract which provides hedging against losses, which makes it an attractive insurance model for private equity. Merton (1974) provided a model to incorporate equity as a call option regarding the firm’s asset with debt being the strike price. Finnerty & Park, (2018) proposed a valuation model where PE funds receive a call option on the fund’s leverage equity investment portfolio, giving them a share of the fund’s profit. Therefore, the use of real options in private equity valuation brings a precise and dynamic model which can make a solid assessment of all available alternatives for the company to invest, bringing long-term benefits and a solid appraisement versus the competitive environment private equity lives in.
Binomial models have been used in the past as a suitable model to portrait the uncertainty of possible outcomes, visualizing payoffs and adopting flexibility with its path dependent options given by a clear sequential decision-making process. By using binomial models, the impact of interest rates may vary across deals, as in some cases there is strong sensitivity, while in others the results remained unaffected.
Previous research has explored how methodologies such as Black and Scholes can be applied directly to study the impact interest rates have over real option valuation of private equity (Vilches, 2025). The contribution of this paper is to apply a discrete time binomial model which captures uncertainty by modeling decision points over time incorporating flexibility needed in private equity valuation.
Real option valuation provides the possibility for a certain period to either choose for or against making investment decision, without committing too early or not making an irreversible decision right away (Carlsson & Fullér, 2003). Option pricing theory-based investment valuation provides a model were flexibility and risk are taken into consideration (Lucius, 2001). When sectors such as energy, climate, real estate, or firms that present increased volatility, traditional project evaluation techniques become insufficient as they do not provide valuation models featuring uncertainty. Real options approach can deal which such issues (Fernandes et al., 2011).
Academic financial literature on real options has grown over the past decades, but its adoption in valuation models has not (Lambrecht, 2017). Even in the late 1800, financial markets were complex and in need for a more sophisticated valuation model (Kairys & Valerio III, 1997) but until 1977, the real option concept appeared referring to investment opportunities as options to delay, expand, switch, suspend, contract and abandon (Myers, 1977). Black & Scholes (1973) and Merton, (1974) introduced the financial approach of option pricing technique valuation in corporate liabilities. However, Cox, Ross and Rubinstein (1979), provided a discrete time model, allowing early exercise of the option. This offers a stronger approach as in private equity decisions are made before maturity, becoming a more realistic model.
Cox-Ross-Rubinstein (CRR) building binomial trees, gives to the researcher or the practitioner a model where changes in volatility, rates and time can affect the valuation, becoming more suitable for the private equity environment.
This paper will consider the binomial lattice option-pricing model approach developed by Cox et al. (1979), which advances the Black and Scholes option valuation, introducing a discrete time binomial model, where options are valued constructing hedging portfolios. In this model, the discrete process consists in either moving up or down as a risk neutral probability.
The variables applied to this study correspond to the parameters of the Cox-Ross-Rubinstein (1979) binomial lattice model, adapted to track private equity valuation under uncertainty, using an American style real option, as early exercise is allowed. The option value at time t , represents the value of the investment opportunity at each decision node within the lattice. The option value in the up state and down state capture the potential outcomes of the value in the next period, depending on market movements. Risk neutral probability determines the likelihood of an upward movement, and represents the probability of the downward movement. The risk-free rate is the continuously compounded rate used to discount expected payoffs one step backward in the lattice, as it compares the expected future value with the early exercise value at each node, with 100 steps. For the risk neutral probability, it represents the likelihood of an upward movement of the underlying asset, adjusting expected returns so that all assets grow at the risk-free rate. This way, the model captures decision making flexibility in private equity investments.
Backward induction value (American style):
: Option value at time t
Option value in the up state at time t+1
Option value in the down state at time t+1
Risk neutral probability of an up move
Risk neutral probability of the down move
Risk-free rate
Risk neutral probability:
To apply the binomial lattice model, each variable represents an essential element of the investment, helping explain how the option value changes over time. These parameters describe the value of the firm, the cost of the investment, the level of risk, time horizon, and the probability of changes in value.
Data selection
Table 1.
Companies deal information.
Table 1.
Companies deal information.
| Company |
Buyers |
Deal Size ($B) |
Deal Announcement |
Deal Completion |
| Qualtrics international Inc |
Silver Lake |
$10.00 |
03/12/23 |
29/06/23 |
| Toshiba Tec Corp |
Japan Industrial Partners |
$16.00 |
23/03/23 |
20/12/23 |
| Univar Solutions LLC |
Apollo Funds |
$8.10 |
14/03/23 |
08/01/23 |
| Coupa Software Inc |
Thoma Bravo |
$6.10 |
12/12/22 |
03/01/23 |
| Dell Technologies Inc |
Silver Lake |
$24.40 |
02/05/23 |
09/12/23 |
| Refinitiv (London Stock Exchange Group PLC) |
Blackstone |
$27.00 |
08/01/19 |
29/01/21 |
| McAfee Corp |
Permira |
$14.00 |
11/08/21 |
03/01/22 |
| Squarespace Inc |
Permira |
$7.20 |
05/01/24 |
17/10/24 |
The selection of these eight private equity deals was guided by representativeness, transparency and data availability, as they capture a broad spectrum of industries, including technology, software, industrials, chemicals and financial services, portraying heterogeneity in volatility, leverage and sensitivity to macroeconomic factors, as interest rates. These deals were completed between 2019 and 2024, period where high fluctuations happened in the U.S interest rates, capturing a broad spectrum of monetary policy changes, from historically low levels to sharp increases beginning in 2022. These deals were included only if there was complete data on the deal value, and each company was selected if there was sufficient data available to estimate volatility to perform the Cox-Ross-Rubinstein model.
T= Maturity, average time holding period of the PE firm. According with a study of S&P Global, the average holding period in 2023 is 7.1 years. (2023)
r= Risk free rate. Used as a proxy with the U.S Board of Governors of the Federal Reserve System (US). (2024) from 2019-2023.
Table 2.
FEDFUNDS interest rates.
Table 2.
FEDFUNDS interest rates.
| Observation Date |
FEDFUNDS |
| Jan-19 |
2.16 |
| Jan-20 |
0.38 |
| Jan-21 |
0.08 |
| Jan-22 |
1.68 |
| Jan-23 |
5.02 |
() Volatility= standard deviation for the price of the stock of daily returns over the last two years prior the private equity deal:
Table 3.
Volatility of companies.
Table 3.
Volatility of companies.
| Company |
σ |
| Qualtrics International Inc |
0.43 |
| Toshiba Tec Corp |
13.407 |
| Univar Solutions LLC |
0.159 |
| Coupa Software Inc |
2.316 |
| Dell Technologies Inc |
0.226 |
| Refinitiv (London Stock Exchange Group PLC) |
19.299 |
| McAfee Corp |
0.154 |
| Squarespace Inc |
0.372 |
5. Conclusions
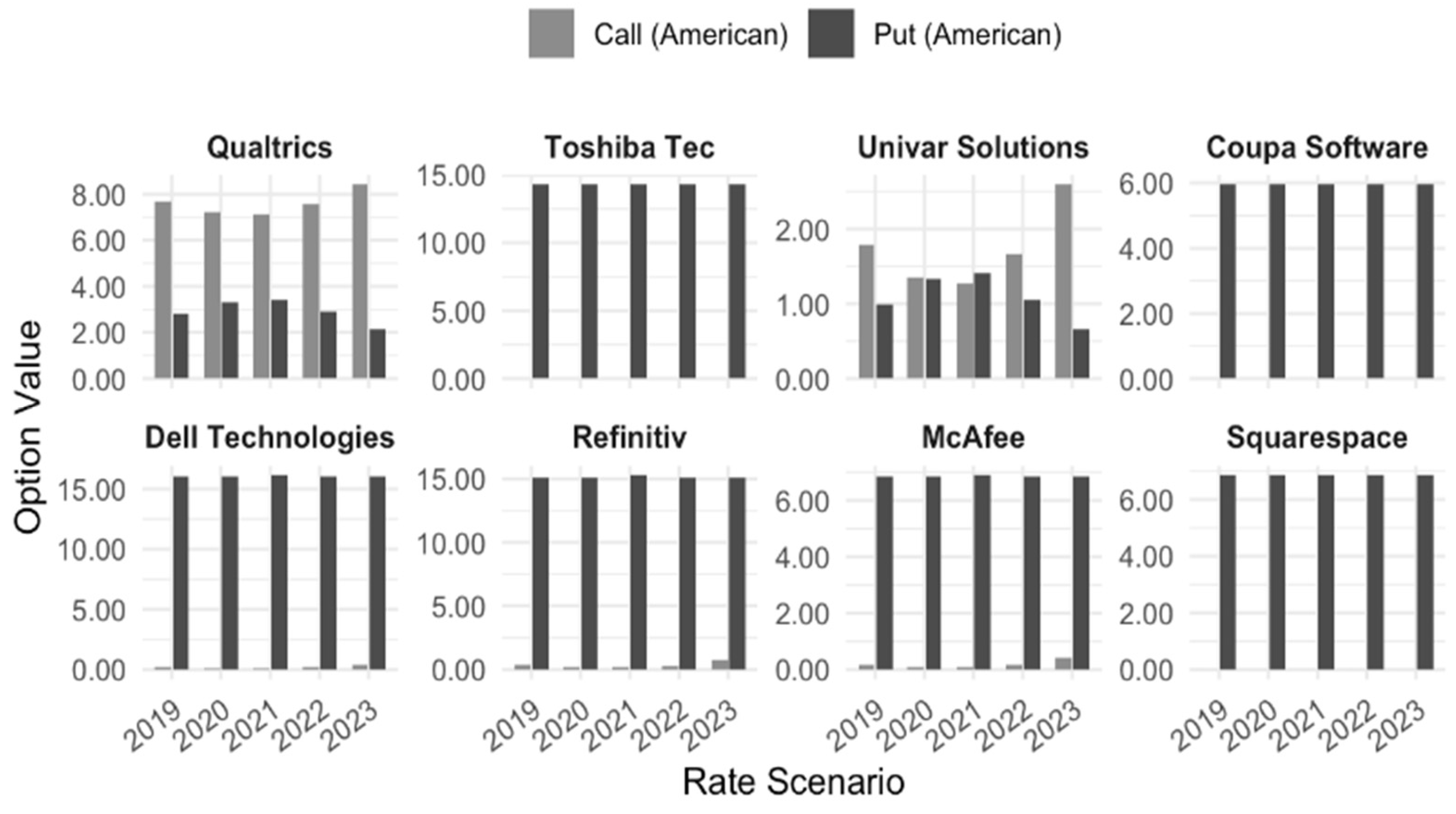
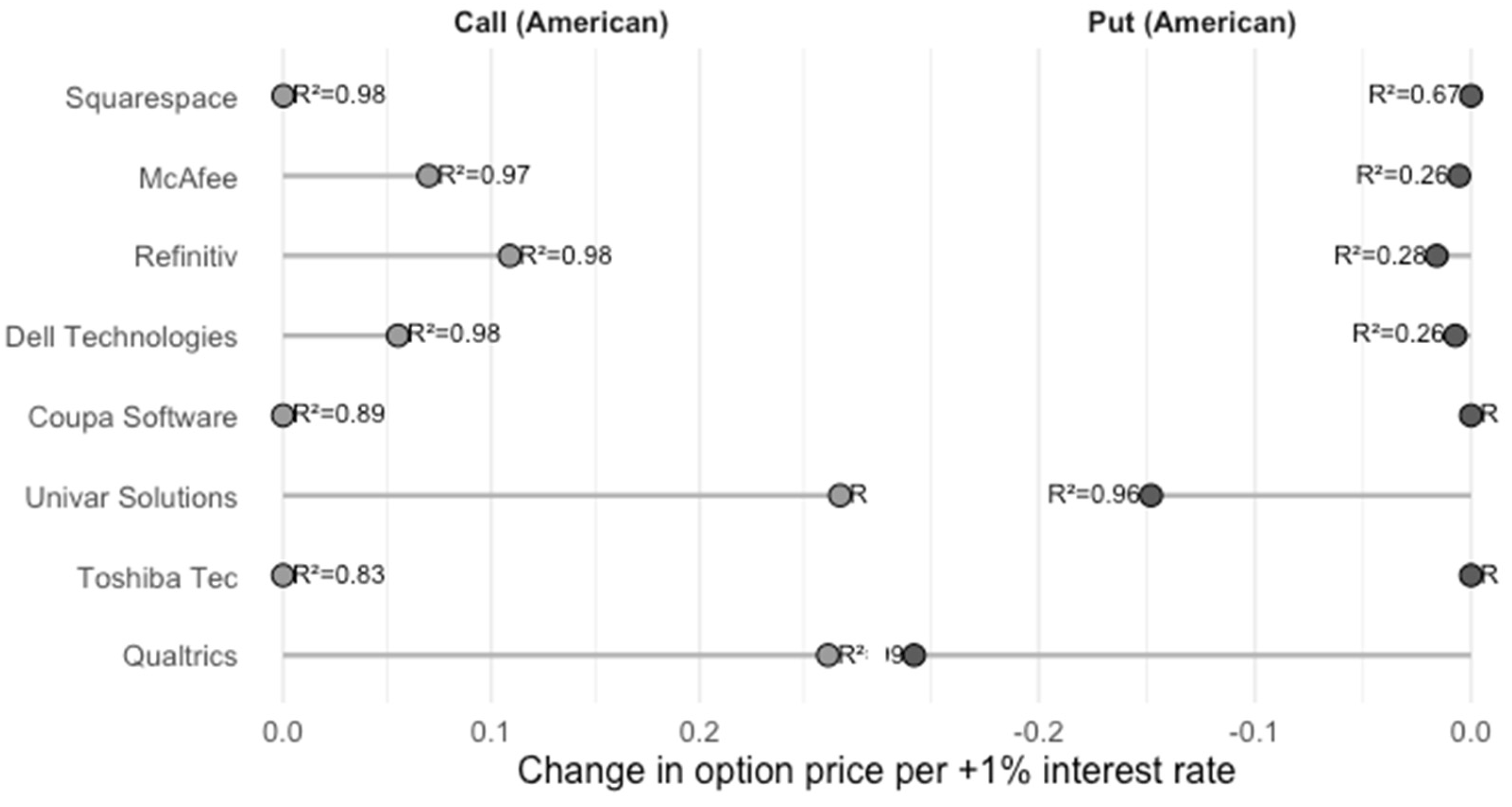
These results provide evidence that American put options are the main source of value in PE deals, while call options play a secondary role. As put options have additional impact, they act as a stable agent against losses in interest rate variation scenarios, which is desirable when making private equity valuations, as investors in PE face illiquidity and significant exposure to macroeconomic conditions. Call options are only meaningful in few companies, and their values move predictably in changes in interest rates as they influence the upside potential of deals. Downside protection is more valuable than upside side due to illiquidity, long holding periods and elevated debt exposure. Put options act as a stabilizing mechanism, reducing potential losses when interest rate volatility reduces firm’s valuations. In this sense, they serve as a hedging tool, preserving the capital and ensuring the exposure to macroeconomic movements remain stable.
Call options exhibit significant value only in some cases, such as firms with high growth expectations like tech companies. Call option values move predictably with movements of the interest rate, as rate reductions increase the present value of cash flows and its given upside potential.
To ensure that results have robustness, the binomial tree was divided into 100 steps, ensuring convergence in results. Volatility estimates were adjusted by +- 10 percent to evaluate how sensitive option values were to small changes in such parameter, and the average private equity holding period of 7.1 provided a wide variation to see how time to maturity affected the results.
Previous studies, as Ballestra et al. (2017) Trigeorgis (1993) or Sorensen et al (2014) demonstrated the need to incorporate uncertainty into investment analysis. However, these and plenty of research has been made in continuous or European-style frameworks, where early exercise is not model and it’s a vital characteristic in private equity deals. By presenting a binomial lattice model, a more realistic model provides more accuracy to PE valuation, incorporating changing macroeconomic conditions.
In conclusion, interest rates act as a strong influence in the upside potential in real option valuation, emphasizing that monetary policy directly affect returns in valuations. Private equity investors should monitor and measure the impact of interest rates on their upside opportunities, rather than focusing on the risk of capital loss, making their PE deal’s valuation solid with rate-sensitive models, and being a strong variable to measure potential growth. Previous and traditional valuation models (Hooke, 2024) miss to capture the uncertainty and complexity private equity has, as the Cox-Ross-Rubinstein binomial framework allows investors to generate an accurate calculation given the proper characteristics of volatility and illiquidity PE presents.