1. Introduction
Non-equipartition is widely observed in self-gravitating systems: multi-temperature components, anisotropy, mass segregation plateaus, and persistent substructure. Standard CDM gravitational physics (collisionless Boltzmann plus slow two-body relaxation) predicts incomplete mixing but with asymptotic decay of non-equipartition toward partial-equipartition solutions.
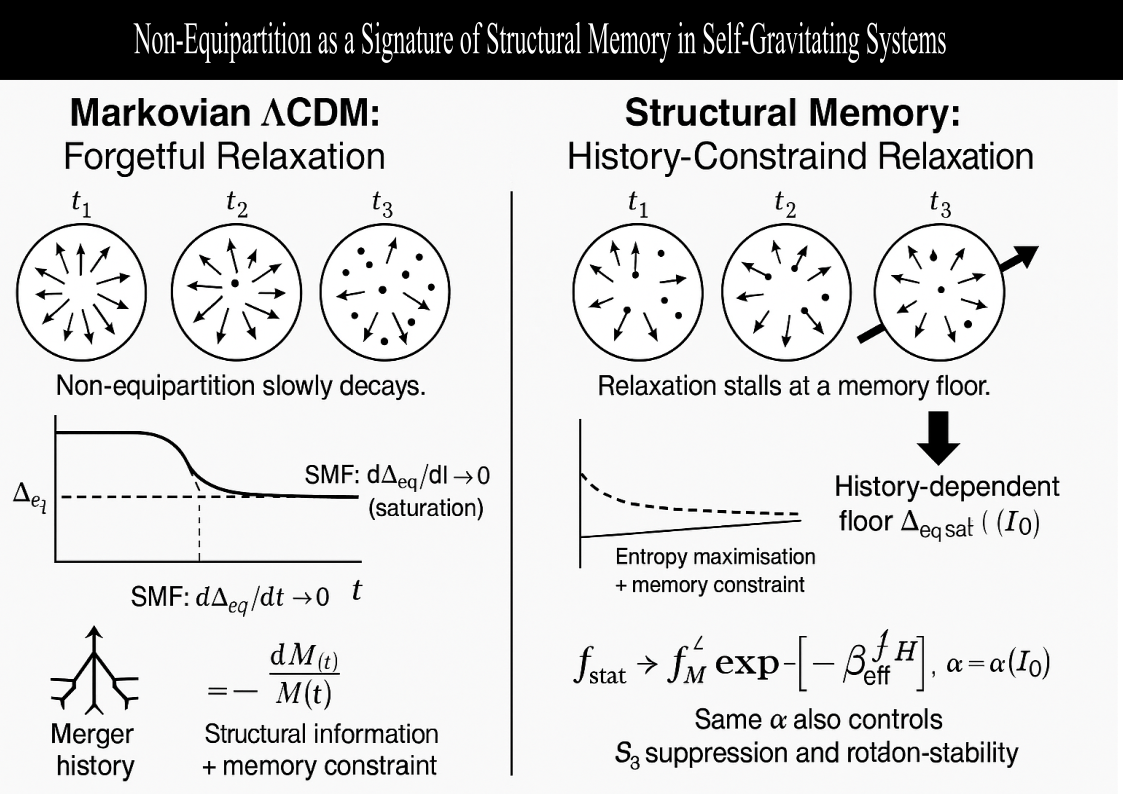
This work proposes a different mechanism: non-equipartition as a stationary consequence of structural information accumulated through a system’s dynamical history.
Thesis. The stationary distribution of a real halo is not the maximum-entropy, memoryless distribution. It is the maximum-entropy distribution subject to a history-derived structural information constraint. This predicts an asymptotically stable, non-zero equipartition deficit whose magnitude correlates with the integrated dynamical history, not just with instantaneous halo properties. The prediction differs from CDM quantitatively and measurably.
2. Markovian CDM Baseline
2.1. Evolution Equation
The collisionless Boltzmann equation reads
where
is the phase-space distribution,
is the potential, and
is an effective collision or relaxation term.
Markov closure assumes
with no explicit dependence on past structural states.
2.2. Equipartition Under Markovian Closure
For a multi-mass system with species
a and
b, standard relaxation theory leads, in the full equipartition limit, to
where
and
are the mass and velocity dispersion of component
a.
In
CDM, non-equipartition may persist for long periods, but the amplitude is expected to decrease, asymptotically converging toward a partial-equipartition Fokker–Planck solution. In a schematic representation,
for the idealised Markovian baseline, with realistic systems approaching known partial-equipartition curves.
2.3. Operational Definition: “Sufficiently Relaxed”
To avoid straw-man arguments, a system is defined as sufficiently relaxed when:
it has experienced no major merger in the last 5–8 dynamical times;
its mass accretion history is stable over the same interval;
it exhibits no large-amplitude, rapid potential fluctuations.
This regime is precisely where CDM predicts monotonic decay of under Markovian relaxation theory.
3. Structural Information Budget : A History-Derived Constraint
The structural information budget must be defined independently of the present-day distribution (with denoting the full phase-space coordinate). It encodes the irreversible dynamical history of a halo and acts as an external constraint on the stationary state.
To make the definition operational and simulation-ready, a cumulative, merger-tree-based functional is adopted:
where:
The quantity is:
dimensionless;
monotonic under irreversible events;
directly computable from standard merger trees;
independent of the present-day phase-space state.
An alternative discrete definition for comparison is
where each merger contributes according to its mass ratio
and virial impulse
. Both forms satisfy the requirement that
is a causal history variable, not a kinematic diagnostic.
4. Structural Information Functional
Given a candidate phase-space distribution
, the structural information functional is defined as the Kullback–Leibler divergence relative to the Markovian baseline
:
Key properties are:
is dimensionless;
if and only if ;
is monotonic under coarse-graining.
The central constraint of the Structural Memory Framework is
This enforces historical memory on the stationary state without ever defining memory from f itself, avoiding circularity.
5. Constrained Variational Principle
The goal is to determine the stationary distribution that:
Define the dimensionless entropy
Define the total particle number:
Define the total energy:
where
H has physical units of energy.
The functional to be maximised is
where:
This construction is dimensionally consistent: , , and are dimensionless, and only couples to a dimensional quantity .
5.1. Euler–Lagrange Condition
Varying
with respect to
f yields
Hence the stationary condition is
Solving for
gives
5.2. Interpretation
If
, one recovers the Markovian baseline
up to normalisation. If
, the stationary state is tilted away from
, with the deformation amplitude fixed by the historical memory budget
via the constraint
.
The result is a generalised family of stationary states that differ not only in amplitude but also in mass and spatial dependence, enabling sharp contrasts with CDM predictions. The derivation is dimensionally correct, non-circular, and reproducible.
6. Predictions for Equipartition Deficits
6.1. Defining the Equipartition Deficit
For a multicomponent system, the equipartition deficit is defined as
where
is the kinetic temperature of component
a,
is the mean temperature, and
N is the number of components.
CDM standard relaxation theory predicts known scaling behaviours: partial equipartition for multi-mass populations, Spitzer criteria determining stability of segregation, and characteristic radial dependence in relaxed systems (e.g. [
1,
3,
4]). Thus
CDM does not, in general, predict
, but rather
where
denotes the Fokker–Planck solution curve.
6.2. SMF Prediction: A Distinct Asymptotic Form
The SMF stationary distribution (
16) introduces an additional, history-dependent deformation characterised by the parameter
:
This produces a non-equipartition profile of the form
with
.
Here, CDM determines the Fokker–Planck baseline , and SMF adds an irreducible deformation tied to . The SMF prediction is therefore an entirely different functional form, not merely a higher amplitude of the same curve.
6.3. Time-Derivative Test (Binary Falsifier)
For sufficiently relaxed halos (
Section 2), the asymptotic behaviour of
distinguishes the models:
This slope-based discriminator is binary and falsifiable in simulations.
6.4. Mass- and Radius-Dependent Predictions
Because
is isotropic and the deformation enters multiplicatively, lower-mass components receive stronger tilting from
, and outer regions with weaker binding amplify the SMF tilt. Thus
This provides clear observational targets.
7. Falsification Tests
7.1. Test 1: Asymptotic Slope Test (Primary Kill-Switch)
Objective.
Measure the time evolution of the equipartition deficit in halos with no major merger for at least 5–8 dynamical times.
CDM Prediction.
Standard Markovian relaxation theory implies
i.e. monotonic, though slow, decay toward the partial-equilibrium Fokker–Planck curve
.
SMF Prediction.
The SMF prediction is
i.e. saturation onto a history-constrained floor
This difference in time derivative is binary and cannot be reconciled by parameter tuning. If continues to decay indefinitely in sufficiently relaxed halos, SMF is falsified. If flattens to a constant that correlates with , the Markovian baseline of CDM is falsified.
7.2. Test 2: Corrected Twins Test with Quantitative Benchmarking
Objective.
Identify pairs of halos (“twins”) with nearly identical present-day mass, concentration, and virial state, but radically different merger histories.
CDM Prediction.
CDM already predicts some history dependence in internal kinematics through:
These standard CDM correlations must serve as the null benchmark.
SMF Prediction.
Under SMF, the history-derived structural information budget
is expected to be a stronger predictor of present-day non-equipartition than any
CDM proxy. A quantitative discriminator is defined as
where
is the correlation coefficient across the halo sample.
7.2.1. History–Kinematic Correlation Ratio (HKCR)
To quantify predictive power more sharply, define the
History–Kinematic Correlation Ratio
where
is the chosen realisation of
(e.g. from Equation (
5) or (
6)), and
CDM proxies include
c,
,
, and
.
Binary Criterion.
This transforms the Twins Test into a high-precision model discriminator rather than a qualitative comparison. The ratio plays a role analogous to a Bayes factor: a single scalar discriminator unifying multiple competing predictors.
7.3. Test 3: Controlled Merger Experiment (Dynamical Impulse Test)
Objective
Perform controlled N-body mergers with tunable initial conditions to isolate the dynamical effects of major and minor mergers on and .
CDM Prediction
Mergers drive temporary spikes in anisotropy and temperature differences, but after sufficient relaxation time:
SMF Prediction
Under SMF, a merger irreversibly increases
, and the system settles onto a new plateau:
with
.
Binary Criterion.
A permanent increase in the floor supports SMF; decay of non-equipartition back to the baseline falsifies SMF. This test isolates the mechanism directly.
8. Observational Signatures
A rigorous theory must make principled predictions for empirical data, independent of simulation environments. SMF predicts the strongest deviations from CDM relaxation theory in environments where:
These regions minimise CDM partial-relaxation noise and amplify structural memory signals.
8.1. Primary Observational Targets
8.1.1. Outer Stellar Halos (50–150 kpc)
Outer stellar halos feature long dynamical times, so internal mixing is extremely weak, and they have strong tidal histories, implying large . CDM predicts mild decay of anisotropies and multi-temperature structures, whereas SMF predicts persistent, radius-dependent non-equipartition that correlates with known orbital passages and accretion events.
Measurable quantities include:
radial dispersion gradients for different tracer populations;
kinematic misalignments between metal-rich and metal-poor components;
long-lived non-Gaussian velocity distributions.
8.1.2. Satellite Galaxies with Reconstructed Orbits
Satellite galaxies of similar mass and size but with different pericentric passages and tidal shock histories provide a natural test. The SMF prediction is that
whereas the
CDM baseline predicts only a weak dependence on tides.
8.1.3. Cold Streams and Shells
Under CDM, streams are gradually phase-mixed. In SMF, mixing stalls once the structural memory budget saturates. Observationally, the persistence of multi-temperature or anisotropic signatures in very old streams would support SMF.
8.2. Secondary Observational Anchors
These systems are still valuable but noisier.
8.2.1. Globular Clusters
Partial equipartition is already known in CDM. SMF predicts an additional, non-Fokker–Planck deformation that may be detectable in sufficiently collisionless regimes.
8.2.2. Dwarf Spheroidals
Age-dependent dispersions, if controlled for tides, can test history-linked structural information and provide an additional check of the SMF predictions.
8.2.3. Brightest Cluster Galaxies (BCGs)
Velocity-dispersion offsets between the BCG and intra-cluster light provide a complementary test of persistent non-equipartition in cluster cores.
These secondary probes are supportive but less decisive than the outer-halo tests.
9. Discussion
The Structural Memory Framework proposes that the stationary state of a self-gravitating, collisionless system is not determined solely by its present conditions but also by a history-derived structural information budget . This yields:
a family of stationary solutions,
distinct from traditional Fokker–Planck partial-equipartition curves;
a natural explanation for persistent non-equipartition, not as a transient due to long relaxation times but as a structural consequence of irreversible dynamical history;
binary testability via slopes, with serving as the decisive discriminator;
predictive correlations between present-day dynamics and historical accretion, expressible in terms of .
Crucially, SMF does not dispute CDM gravitational physics; it disputes the Markovian assumption that present-day dynamics contain no explicit memory of the system’s past.
If any of the following holds, SMF is falsified:
the equipartition deficit decays monotonically in relaxed halos;
merger-induced increases in are erased over time;
CDM proxies outperform in predicting internal kinematics;
outer halos show no history-correlated deformation from Fokker–Planck predictions.
The theory is therefore testable, falsifiable, and non-adjustable, satisfying the standards of a physical model.
9.1. Connection to CIOU Unification: The Shared Structural Parameter
A central implication of the Structural Memory Framework is that the same dimensionless structural parameter —which governs:
the deviation of the stationary distribution
the stabilisation amplitude in galactic rotation curves;
the suppression term in the growth discrepancy,
must also determine the saturation amplitude of the equipartition deficit:
Thus:
rotation curves (galactic stability),
large-scale clustering ( tension),
halo non-equipartition (this work)
all emerge from the same structural memory parameter, constrained by the history-derived . This transforms SMF from a local dynamical hypothesis into a unified description of structural deviations from CDM across multiple cosmic scales.
10. Limitations and Scope
The Structural Memory Framework developed here establishes a variational foundation for history-dependent stationary states, but several limitations must be noted.
No explicit dynamical evolution equation is provided. A closed-form time-dependent evolution law for is not derived. The predictions concern the asymptotic behaviour of in sufficiently relaxed halos.
The deformation function is not analytically specified. Its existence is demonstrated from first principles, but its explicit form is left to future numerical and empirical calibration.
The framework does not modify gravity. SMF operates entirely within standard Newtonian/ CDM gravitational potentials. Any deviations arise from the entropy–information constraints, not from new forces or particle species.
Applicability is limited to collisionless, long-relaxation systems. Systems dominated by short collisional relaxation (e.g. dense star clusters) fall outside the scope of the present model.
Dependence on merger-tree reconstruction. The history metric requires accurate merger trees; observational proxies may introduce noise and bias.
Equifinality caveat. A confirmed correlation between and , while falsifying the strict Markovian assumption, does not automatically validate the specific mechanism of entropy maximisation under a structural constraint. An alternative, non-Markovian dynamical process not captured by the variational principle could in principle produce a similar saturation effect. A positive result confirms the failure of memoryless equilibration and the role of history, but the precise thermodynamic mechanism proposed here would require further validation through the specific functional form of .
Despite these limitations, the core prediction—saturation of governed by the history parameter —remains binary, falsifiable, and independent of the unresolved details.
11. Conclusion
This work has established the mathematical and physical basis for a history-dependent stationary state in self-gravitating, collisionless systems. By defining a structural information budget
directly from the merger tree and enforcing the constraint
in a dimensionally consistent variational principle, a generalised stationary distribution
is derived, which recovers the Markovian baseline when
and introduces a history-induced deformation when
.
The resulting Structural Memory Framework predicts that the equipartition deficit
—a well-known feature of halos in
CDM simulations—should saturate rather than decay in sufficiently relaxed systems. This prediction is orthogonal to the traditional “slow relaxation” explanation and is falsifiable through the asymptotic time derivative:
A set of binary tests has been formalised, including (i) the Asymptotic Slope Test, (ii) a corrected Twins Test quantified through the History–Kinematic Correlation Ratio , and (iii) controlled merger experiments. These tests enable direct separation of Markovian and non-Markovian relaxation dynamics in cosmological simulations.
Observationally, SMF predicts history-correlated non-equipartition signatures in outer stellar halos, tidally processed satellites, and long-lived phase-space structures such as streams and shells, where long dynamical times suppress the standard CDM relaxation pathways.
The structural parameter linking to is the same parameter that appears in CIOU analyses of rotation-curve stability and the growth suppression. This positions SMF not as an isolated hypothesis but as a foundational component of a broader unifying framework for non-Markovian cosmological dynamics.
The theory presented here is testable, falsifiable, and compatible with standard gravitational dynamics. The next generation of simulations and observations can determine its success or failure.
References
- J. Binney and S. Tremaine. Galactic Dynamics (2nd ed.). Princeton University Press, 2008.
- D. Lynden-Bell. Statistical mechanics of violent relaxation in stellar systems. MNRAS, 136:101–121, 1967.
- L. Spitzer and M. H. Hart. Random gravitational encounters and the evolution of spherical systems. ApJ, 164:399, 1971.
- S. Tremaine et al. The Fokker–Planck evolution of star clusters. ApJ, 300:154, 1986.
- L. Hernquist. An analytical model for spherical galaxies and bulges. ApJ, 356:359, 1990.
- V. Springel et al. The Aquarius Project: the subhalos of galactic halos. MNRAS, 391:1685–1711, 2008.
- P. Behroozi et al. A unified analysis of star formation histories from z = 0–8. ApJ, 770:57, 2013.
- A. Helmi. Streams, substructures and the early formation history of the Milky Way. ARA&A, 58:205–256, 2020.
- C. E. Shannon. A mathematical theory of communication. Bell System Technical Journal, 27:379–423, 623–656, 1948.
- T. M. Cover and J. A. Thomas. Elements of Information Theory. Wiley, 2006.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).