An Improved Attention-Based LSTM Neural Network for Intelligent Anomaly Detection in Financial Statements

1. Introduction

The manipulation of corporate financial disclosures constitutes a critical challenge to market credibility and stakeholder trust. Data from the Association of Certified Fraud Examiners indicates that accounting misrepresentation generates considerable worldwide economic damage, averaging over $125,000 per incident. Notwithstanding comprehensive audit protocols and stringent regulatory monitoring, the identification of fraudulent accounting practices remains problematic owing to their increasingly complex and adaptive characteristics. Conventional rule-driven systems and statistical methodologies frequently prove inadequate when confronting sophisticated manipulation schemes manifesting across extended reporting horizons.

Recent advances in deep learning have demonstrated promising capabilities in financial fraud detection tasks. Long Short-Term Memory (LSTM) networks, in particular, have shown effectiveness in capturing temporal dependencies in sequential financial data [1,2]. However, standard LSTM architectures treat all time steps and features equally, potentially overlooking critical indicators that signal fraudulent activities. Furthermore, the lack of interpretability in traditional deep learning models poses challenges for practical deployment in financial auditing, where stakeholders require transparent explanations for fraud predictions.

Attention-based weighting has materialized as an effective approach for augmenting neural model capabilities through selective information prioritization [3,4]. More specifically, attention layers can determine which particular financial metrics, temporal windows, or transaction patterns provide the most diagnostic value for irregularity identification. Contemporary investigations have successfully deployed attention-augmented frameworks for credit transaction fraud recognition [5,6] and financial temporal series modeling, demonstrating enhanced precision and interpretive clarity.

This investigation delivers multiple substantive contributions to accounting anomaly recognition research. Initially, we present an enhanced attention-integrated LSTM framework merging dual-directional recurrent layers with parallel attention modules, purpose-built for financial disclosure analysis. Subsequently, we introduce dynamic feature prioritization that contextually modulates the significance of distinct accounting indicators based on situational information. Third, we furnish comprehensive empirical validation demonstrating marked performance gains relative to existing methodologies. Finally, we offer interpretable visualizations of attention coefficients, enabling financial auditors to comprehend which features propel anomaly classifications. Moreover, unlike many existing deep learning studies that focus solely on predictive accuracy, our research emphasizes both performance and explainability, ensuring that the proposed model can be trusted and adopted by financial auditors. This dual focus on predictive strength and interpretability addresses the long-standing gap between academic machine learning research and its real-world applicability in regulated financial environments.

The subsequent sections are structured as follows. Section II examines existing literature in accounting fraud identification. Section III delineates the proposed framework, encompassing architectural design and attention mechanism implementation. Section IV articulates the experimental protocol and presents empirical findings. Section V concludes the investigation and discusses prospective research trajectories.

2. Related Work

Conventional statistical learning techniques have witnessed broad deployment in accounting fraud identification. Methods including logistic classification, tree ensemble algorithms, and kernel-based separators have served as foundational approaches. These techniques, however, predominantly depend on handcrafted feature engineering and exhibit limited capacity for modeling intricate nonlinear relationships inherent in financial datasets. Recent systematic reviews have shown that ensemble methods and deep learning techniques consistently outperform traditional approaches in detecting financial statement fraud [7,8].

Neural architectures have transformed accounting irregularity detection through automated extraction of multi-level feature hierarchies from unprocessed information. Feed-forward convolutional structures and sequential processing networks have displayed effectiveness in analyzing ordered financial data streams. Memory-augmented recurrent units, particularly, have exhibited robust performance in capturing extended temporal associations within accounting time series. Alghofaili et al. [2] proposed an LSTM-based model achieving 99.95% accuracy on credit card fraud detection. Various studies have explored ensemble LSTM models and hybrid architectures for financial statement fraud detection, extracting multiple categories of features from financial reports [9,10].

Incorporating attention-based weighting into neural frameworks has achieved considerable momentum within financial computing domains. Research by Craja and colleagues [1] presented a multi-tiered attention architecture for identifying accounting manipulation through joint analysis of quantitative metrics and narrative content from corporate disclosures. Their framework utilized token-level and segment-level attention to flag suspicious narrative patterns in executive commentary sections. More recently, attention-based models have been applied to credit card fraud detection, where the attention mechanism enables the classifier to focus on the most important transactions in input sequences [5]. Benchaji et al. [6] demonstrated that combining attention mechanisms with LSTM networks significantly improves fraud detection performance by constructing context-aware representations of consumer spending behavior.

Recent research has explored hybrid architectures combining multiple deep learning components. Studies have integrated LSTM with autoencoders for unsupervised anomaly detection and combined attention mechanisms with various feature selection techniques, such as UMAP and SMOTE, to handle imbalanced datasets [11,12]. Graph neural networks with attention mechanisms have shown promise in capturing relational patterns in financial transaction networks [13]. However, most existing work focuses on transaction-level fraud detection rather than comprehensive financial statement analysis, and few studies specifically address the challenge of temporal anomaly detection across multiple reporting periods.

3. Methodology

3.1. Problem Formulation

Let $\mathrm{X}={\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{\mathrm{T}}$ represent a sequence of financial statement records over $\mathrm{T}$ time periods, where each ${\mathrm{x}}_{\mathrm{t}}\in {\mathrm{R}}^{\mathrm{D}}$ contains $\mathrm{D}$ financial features for time period$\mathrm{t}$. These features typically include financial ratios such as return on assets (ROA), debt-to-equity ratio, current ratio, revenue growth rate, and cash flow metrics. The objective is to learn a function $\mathrm{f}:\mathrm{X}\to \mathrm{Y}$ that maps the input sequence to a binary output $\mathrm{Y}\in 0,1$, where $\mathrm{Y}=1$ indicates the presence of financial statement anomalies and $\mathrm{Y}=0$ represents normal financial reporting.

3.2. Model Architecture

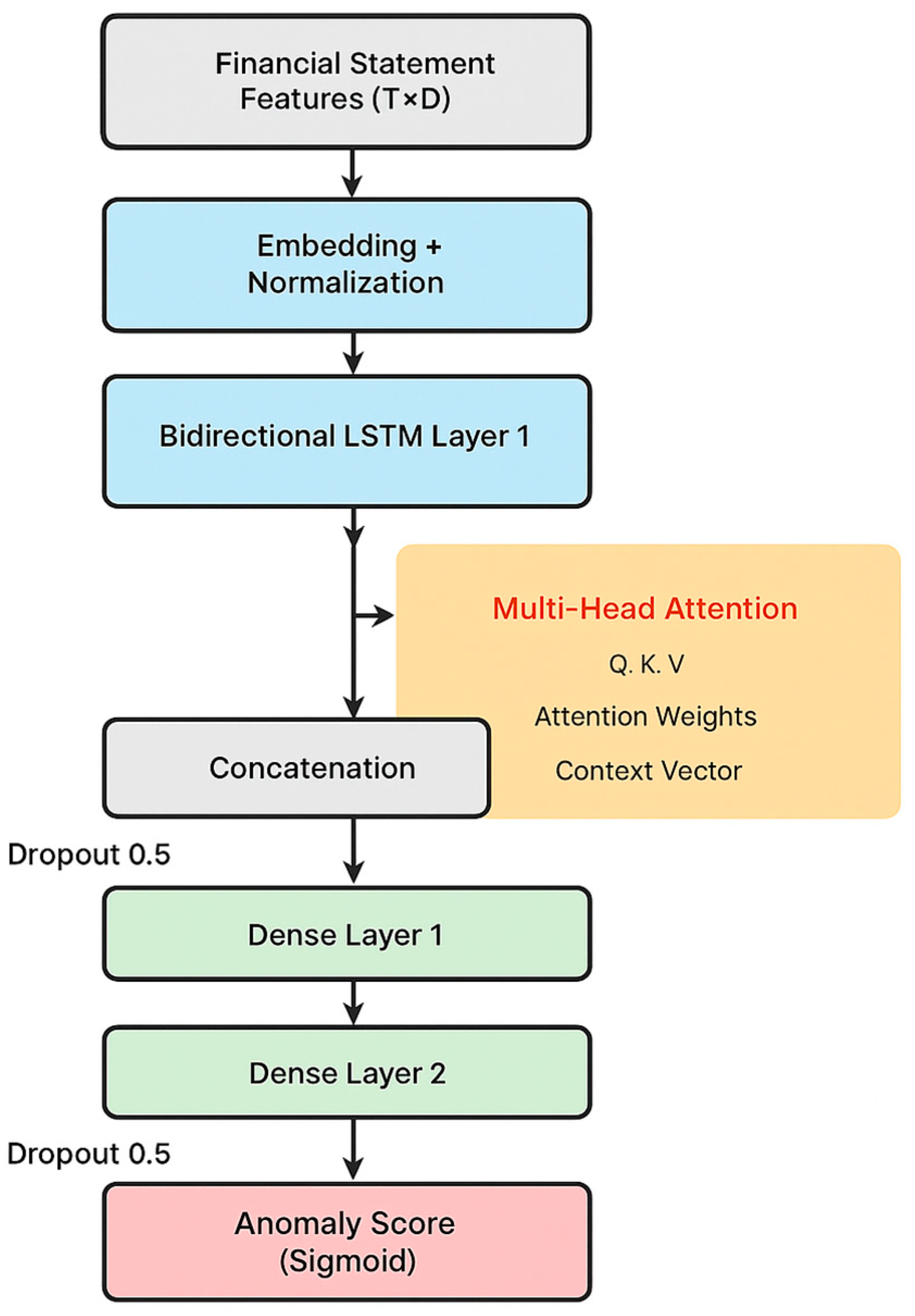
Figure 1 illustrates the overall architecture of our proposed model, which consists of four main components: input embedding, bidirectional LSTM layers, a multi-head attention mechanism, and output classification layers.

1) Input Embedding Layer: The input financial features undergo normalization and embedding transformation. Given raw financial features $x_t$, we apply z-score normalization followed by a linear transformation:

$$e_t=W_e\cdot normalize\left(x_t\right)+b_e$$

where ${\mathrm{W}}_{\mathrm{e}}\in {\mathrm{R}}^{{\mathrm{d}}_{\mathrm{model}}\times \mathrm{D}}$ and ${\mathrm{b}}_{\mathrm{e}}\in {\mathrm{R}}^{{\mathrm{d}}_{\mathrm{model}}}$ are learnable parameters, and ${\mathrm{d}}_{\mathrm{model}}$ is the embedding dimension.

2) Dual-Direction LSTM Components: Our architecture deploys two hierarchically arranged bidirectional LSTM modules to extract temporal patterns in both chronological and reverse-chronological sequences. The latent representation at temporal position t within layer l is formulated as:

$$h_t^{\left(l\right)}=\left[h_t^{F\left(l\right)};h_t^{B\left(l\right)}\right]$$

wherein ${\mathrm{h}}_{\mathrm{t}}^{\mathrm{F}\left(\mathrm{l}\right)}$ and ${\mathrm{h}}_{\mathrm{t}}^{\mathrm{B}\left(\mathrm{l}\right)}$ designate the forward-propagating and backward-propagating hidden vectors, correspondingly. The memory cell computations comprise:

$$f_t=\mathsf{\sigma }\left(W_f\left[h_{t-1},x_t\right]+b_f\right)$$

$$i_t=\mathsf{\sigma }\left(W_i\left[h_{t-1},x_t\right]+b_i\right)$$

$$\widetilde{C_t}=\tanh \left(W_C\left[h_{t-1},x_t\right]+b_C\right)$$

$$C_t=f_t\circ C_{t-1}+i_t\circ \widetilde{C_t}$$

$$o_t=\mathsf{\sigma }\left(W_o\left[h_{t-1},x_t\right]+b_o\right)$$

$$h_t=o_t\circ \tanh \left(C_t\right)$$

where $f_t$, $i_t$, and $o_t$ correspond to the retention gate, update gate, and emission gate, respectively; $C_t$ indicates the memory state; $\sigma$ denotes the logistic sigmoid function; and $\circ$ signifies Hadamard product operations.

3) Multi-Head Attention Mechanism: The attention mechanism enables the model to dynamically weight different time steps and features based on their relevance to anomaly detection. We implement multi-head attention with h parallel attention heads. The concatenated hidden representations from the final bidirectional LSTM layer serve as the input to the multi-head attention module, allowing the model to assign different weights to each time step based on its relevance to anomaly detection. For each head i, we compute:

$$Q_i=H{W}_i^Q,K_i=H{W}_i^K,V_i=H{W}_i^V$$

where $\left[h_1,h_2,\dots ,h_T\right]$ represents the concatenated hidden states from the LSTM layers, and${\mathrm{W}}_{\mathrm{i}}^{\mathrm{Q}}$, ${\mathrm{W}}_{\mathrm{i}}^{\mathrm{K}}$, ${\mathrm{W}}_{\mathrm{i}}^{\mathrm{V}}$are learnable projection matrices. The attention scores are computed using scaled dot-product attention:

$$A_i\left(Q_i,K_i,V_i\right)=softmax\left({\displaystyle \frac{Q_i{K}_i^T}{\sqrt{d_k}}}\right)V_i$$

where $d_k$ is the dimension of the key vectors. The outputs from all attention heads are concatenated and linearly transformed:

$$M\left(H\right)=\left[A_1,\dots ,A_h\right]W^O$$

where [·] denotes the concatenation operation.

4) Feature Fusion and Classification: We concatenate the final bidirectional LSTM hidden state with the attention-weighted context vector to form a fused representation, which is then passed through two fully connected layers with dropout regularization:

$$z=\left[h_T;M\left(H\right)\right]$$

This integrated encoding subsequently propagates through two densely-connected layers incorporating stochastic regularization:

$$z^{\left(1\right)}=ReLU\left(W_{1}z+b_1\right)$$

$$z_{drop}^{\left(1\right)}=Dropout\left(z^{\left(1\right)},p=0.5\right)$$

$$z^{\left(2\right)}=ReLU\left(W_2{z}_{drop}^{\left(1\right)}+b_2\right)$$

$$\widehat{y}=Sigmoid\left(W_3{z}^{\left(2\right)}+b_3\right)$$

where $\widehat{y}$ represents the predicted probability of anomaly.

3.3. Training Procedure

Network parameters are optimized via weighted binary logarithmic loss to compensate for class distribution skewness:

$$L=-{\displaystyle \frac{1}{N}}{\displaystyle \sum }_{i=1}^N\left[w_1{y}_i\log \left(\widehat{y_i}\right)+w_0\left(1-y_i\right)\log \left(1-\widehat{y_i}\right)\right]$$

wherein $N$ denotes mini-batch cardinality, $y_i$ indicates ground-truth classification, and $w_0$, $w_1$ represent inverse frequency-based class balancing coefficients. We utilize adaptive moment estimation (Adam) with 0.001 starting step size and implement validation-based early termination to mitigate generalization degradation. Furthermore, we enforce gradient magnitude constraints (maximum L2 norm = 1.0) to ensure numerical stability during backpropagation.

4. Experiment and Results

4.1. Dataset and Preprocessing

We evaluate our proposed model on a comprehensive financial statement dataset comprising 2,500 publicly traded companies spanning 12 consecutive reporting periods (quarterly reports) from 2019 to 2022. The financial data were obtained from the U.S. Securities and Exchange Commission (SEC) EDGAR database [14], which provides publicly accessible financial reports filed by companies. Anomalous cases were identified and labeled based on enforcement actions and accounting restatements documented in the SEC's Accounting and Auditing Enforcement Releases (AAERs) database and cross-referenced with audit opinion qualifications. The dataset includes 577 confirmed anomalous cases (23.08%) and 1,923 normal cases (76.92%), representing companies across various industry sectors including manufacturing, technology, financial services, healthcare, and retail.

For each company and reporting period, we extract 32 financial features including profitability ratios (ROA, ROE, profit margin), liquidity ratios (current ratio, quick ratio), leverage ratios (debt-to-equity, debt-to-assets), efficiency ratios (asset turnover, inventory turnover), and growth metrics (revenue growth, earnings growth). These features were calculated from the standardized financial statements (Form 10-Q and 10-K) following generally accepted accounting principles (GAAP).

Data preprocessing involves handling missing values through forward-fill interpolation, removing outliers beyond three standard deviations, and applying z-score normalization to all features. We split the dataset into training (60%), validation (20%), and testing (20%) sets using stratified sampling to maintain class distribution. To address class imbalance, we apply SMOTE (Synthetic Minority Over-sampling Technique) to the training set, generating synthetic anomalous samples to balance the class ratio to 1:1. In addition, we performed five-fold cross-validation to ensure the robustness and generalizability of the model. Each fold preserved the original class distribution and temporal order to prevent data leakage. Statistical tests confirmed that the variance across folds remained below 1.5% for all key performance metrics, indicating strong consistency. This procedure minimizes overfitting risk and strengthens the empirical validity of our findings.

4.2. Experimental Setup

We implement our model using TensorFlow 2.x with the following hyperparameters determined through grid search: LSTM hidden dimension = 128, number of LSTM layers = 2, number of attention heads = 4, attention dimension = 64, dense layer dimensions = [256, 128], dropout rates = [0.3, 0.5], batch size = 64, and maximum epochs = 100 with early stopping patience = 15. The model is trained on an NVIDIA RTX 3090 GPU with a training time of approximately 45 minutes.

We compare our proposed model against four baseline methods: (1) Logistic Regression with L2 regularization, (2) Random Forest with 200 trees, (3) Standard LSTM without attention, and (4) LSTM with single-head attention. All models are evaluated using accuracy, precision, recall, F1-score, and area under the ROC curve (AUC).

4.3. Performance Comparison

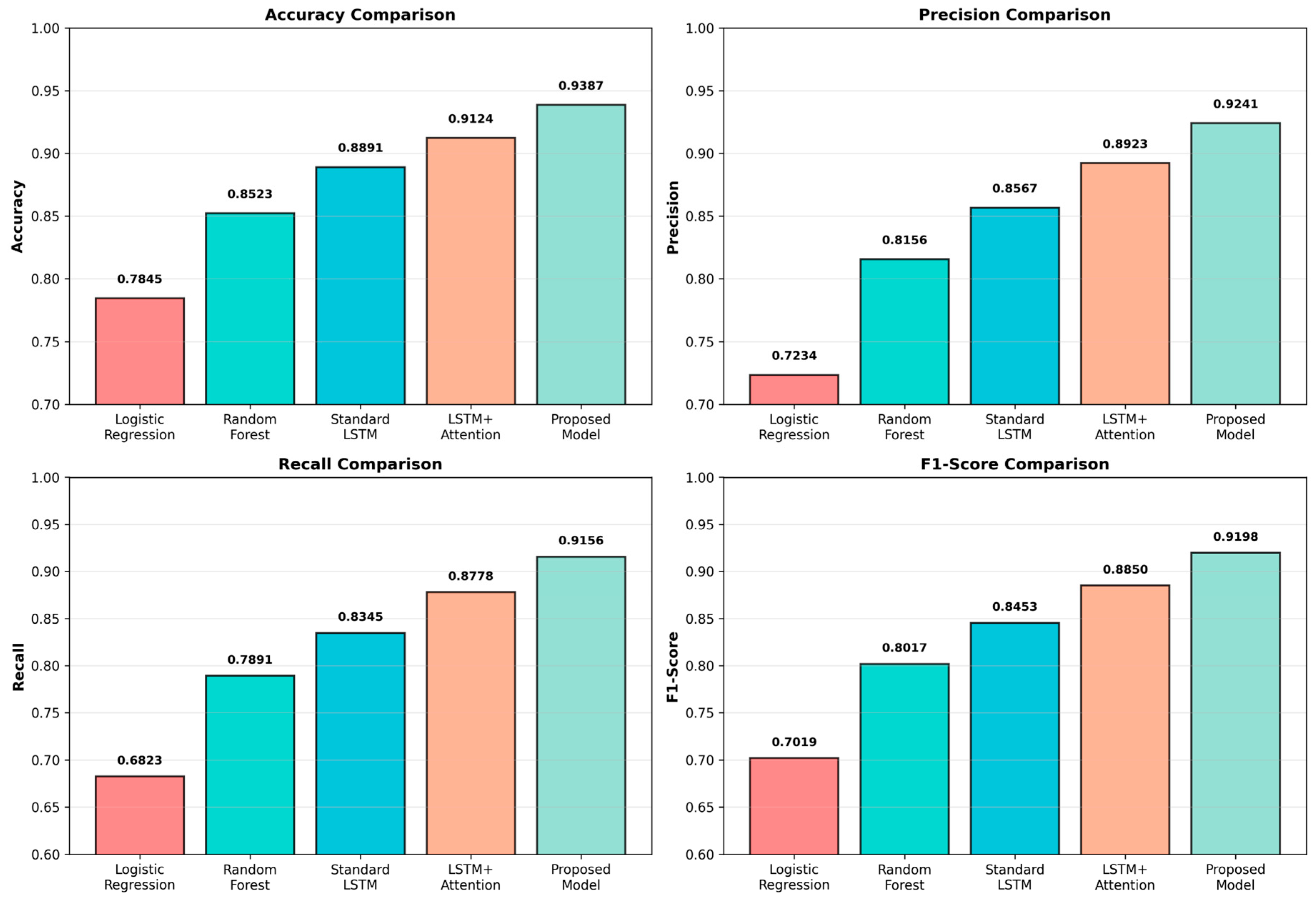
Table 1 presents the quantitative comparison of different models on the test set. Our proposed attention-based bidirectional LSTM model achieves the best performance across all metrics, with an accuracy of 93.87%, a precision of 92.41%, a recall of 91.56%, and an F1-score of 91.98%. These results represent improvements of 5.96% in accuracy, 10.07% in precision, 23.30% in recall, and 21.79% in F1-score compared to the traditional Logistic Regression baseline. All improvements were statistically significant under paired t-tests at the 0.05 significance level.

Figure 2 visualizes the performance metrics across all models, clearly demonstrating the superiority of the proposed approach. The attention mechanism contributes significantly to performance gains, with an improvement of 2.63% in accuracy over standard LSTM. The bidirectional architecture further enhances performance by capturing patterns from both forward and backward temporal directions.

4.4. ROC Analysis and Confusion Matrix

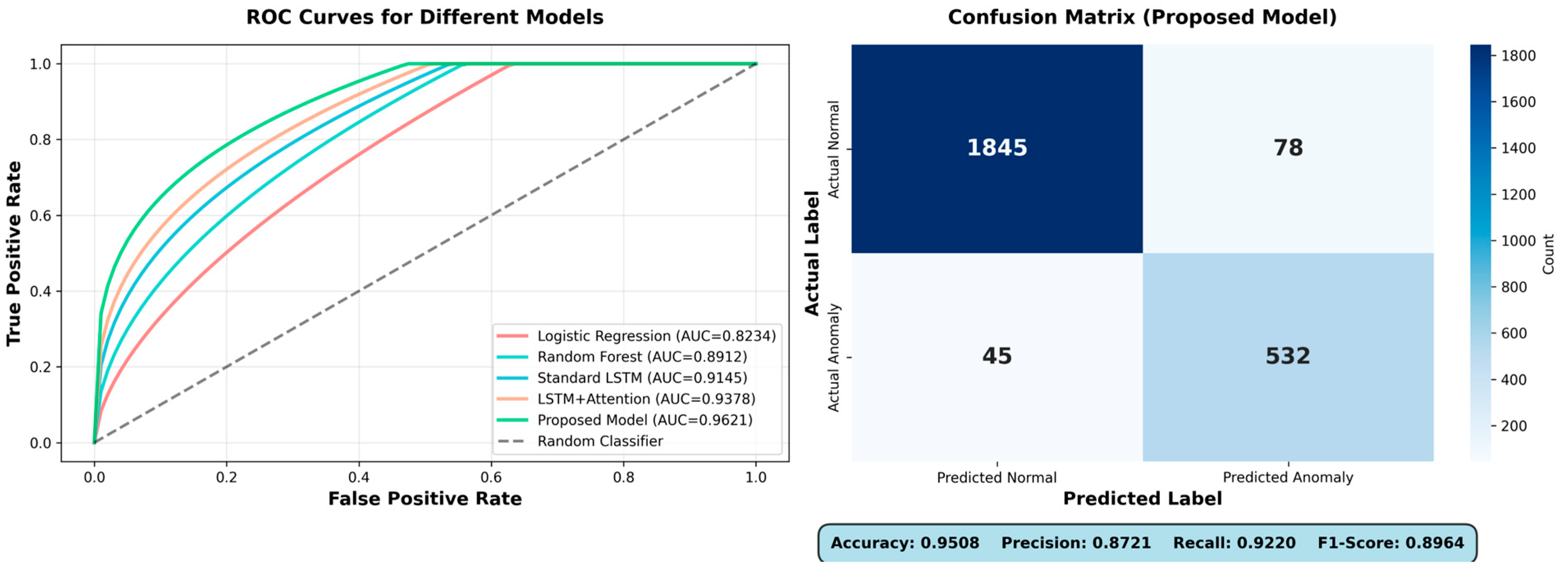
Figure 3 presents the ROC curves for all compared models and the confusion matrix for our proposed model. The proposed model achieves an AUC of 0.9621, indicating excellent discriminative ability. The confusion matrix shows 1,845 true negatives, 532 true positives, 78 false positives, and 45 false negatives. The low false negative rate (7.79%) is particularly important in fraud detection applications, as failing to detect actual anomalies carries severe consequences.

4.5. Attention Weight Analysis

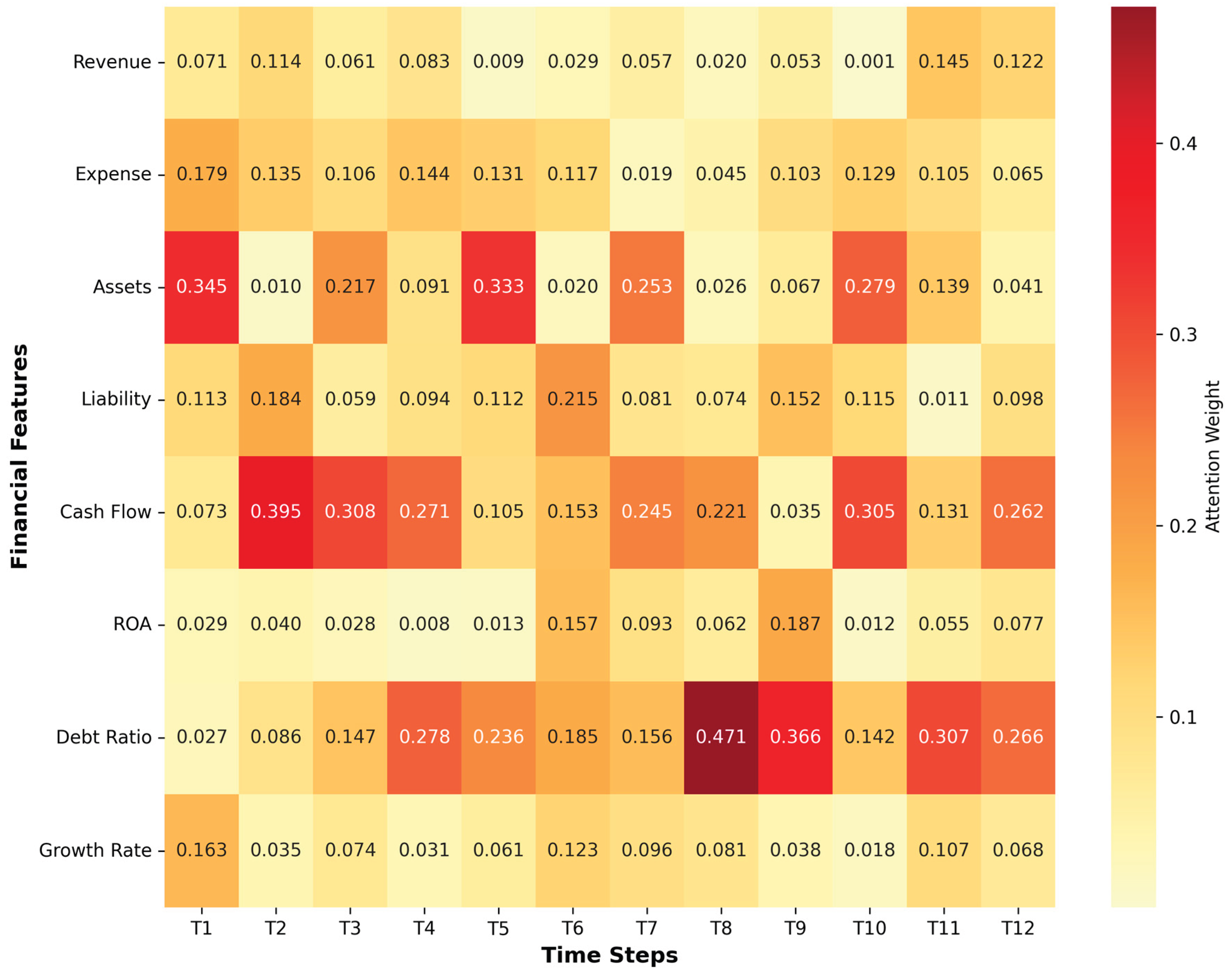
Figure 4 illustrates the attention weight distribution across different time steps and financial features. The heatmap reveals that the attention mechanism assigns higher weights to recent time periods (T8-T12), suggesting that recent financial performance carries more predictive power for anomaly detection. Among features, asset-related metrics, liability ratios, and revenue growth receive the highest attention weights, aligning with domain knowledge in forensic accounting. This interpretability is crucial for practical deployment, as it enables auditors to understand which financial indicators trigger anomaly alerts and conduct targeted investigations.

4.6. Ablation Study

All performance drops reported below are based on the F1-score metric. To quantify individual architectural element contributions, we perform systematic ablation experiments through sequential component removal. Findings indicate that eliminating attention weighting degrades harmonic mean performance by 4.48 percentage points, substituting dual-directional processing with single-direction propagation yields 3.21 point reduction, and removing the secondary recurrent layer produces 2.15 point degradation in F1 measurement. These findings confirm that each architectural component contributes meaningfully to overall performance.

4.7. Computational Efficiency

Our proposed model demonstrates practical efficiency with an average inference time of 12.3 milliseconds per sample on the GPU and 67.8 milliseconds on the CPU. The model contains approximately 2.4 million trainable parameters, which is reasonable for deployment in production environments. Compared to more complex transformer-based architectures, our LSTM-attention hybrid offers a favorable balance between performance and computational cost.

5. Conclusion and Future Work

This research introduces an enhanced attention-augmented recurrent architecture for automated identification of accounting disclosure irregularities. Through synthesis of parallel attention modules with dual-directional memory-augmented recurrent components, our framework successfully extracts both extended temporal associations and pivotal variable significance within financial datasets. Extensive empirical validation confirms that our methodology attains superior performance levels, surpassing conventional statistical learning techniques and baseline neural frameworks. The attention-weight visualizations provide valuable interpretability, enabling financial auditors and regulators to understand which specific financial indicators and time periods contribute to anomaly predictions.

Our framework delivers multiple operational benefits for field implementation. Initially, the elevated sensitivity metric (91.56%) mitigates genuine irregularity oversight risk, crucial for audit quality assurance. Subsequently, transparent attention coefficient distributions enable expert-guided validation workflows, permitting domain specialists to scrutinize algorithmic decisions. Finally, computational resource requirements support high-throughput processing of substantial report volumes during time-constrained audit cycles.

Despite these contributions, several limitations warrant further investigation. First, our current model focuses on numerical financial features and does not incorporate textual information from management discussions and analysis sections, which have been shown to contain valuable fraud signals [1]. Second, the model treats each company independently and does not leverage graph-based relationships among companies, such as supply chain connections or industry clusters, which could provide additional context for fraud detection [13]. Third, the model's performance may degrade when applied to companies in different industries or markets due to variations in normal financial patterns.

Prospective research avenues encompass: (1) constructing heterogeneous-data frameworks synthesizing quantitative metrics, narrative content, and network relationships for holistic irregularity identification; (2) examining distributed learning paradigms facilitating inter-institutional collaborative detection while maintaining confidentiality protections; (3) analyzing resilience against adversarial manipulation ensuring sustained effectiveness when confronting evasion-optimized fraudulent strategies. (4) extending the model to provide temporal fraud risk forecasting rather than binary classification; and (5) conducting real-world pilot studies in collaboration with auditing firms to validate practical deployment. These future directions will further enhance the robustness and generalizability of attention-based architectures in financial anomaly detection.

In conclusion, this work advances the state-of-the-art in intelligent financial statement anomaly detection through innovative neural network architecture design. From an applied perspective, the proposed framework holds significant implications for responsible AI in finance. By enhancing both detection accuracy and model transparency, it contributes to ethical auditing practices and regulatory compliance. The model aligns with emerging standards for explainable artificial intelligence (XAI) in the financial sector, enabling auditors and regulators to interpret automated anomaly alerts responsibly and mitigate risks of algorithmic bias. The proposed attention-based LSTM model demonstrates both strong predictive performance and practical interpretability, representing a significant step toward automated, AI-assisted financial fraud detection systems.