Effective Medium Theory for Silica Nanoparticles

1. Introduction

Silica nanoparticles (SNPs), with radii typically ranging from 30 to 150 nanometers, are utilized in many fields, including drug delivery, battery anodes, and functional coatings [1,2,3]. Their tunable optical properties make them particularly suitable for fabricating anti-glare (anti-reflection) films [4]. In designing a multilayer anti-glare film, the effective dielectric constant is a critical material property [5]. Ideally, for a perfect anti-reflection coating, the dielectric constant $\epsilon \left(d\right)$should vary continuously from that of the substrate to that of air, where d is the film thickness [6].

Various dielectric models for heterogeneous mixtures have been explored over the years, and summaries of these mixing formulas are available in the literature [7,8,9,10]. However, predicting the dielectric constant of SNP mixtures presents two main challenges. The first is the presence of strong surface plasmon resonances, particularly when a metallic shell is involved [11,12]. The second is the unavoidable size distribution of SNPs, which drastically alters the optical properties of the composite medium, especially when the particle radius approaches the wavelength of light. To address these issues, we incorporate Mie solutions into an effective medium theory (EMT) framework, such as the Clausius-Mossotti (CM) relation, and average the effective dielectric constant over the SNP radius distribution.

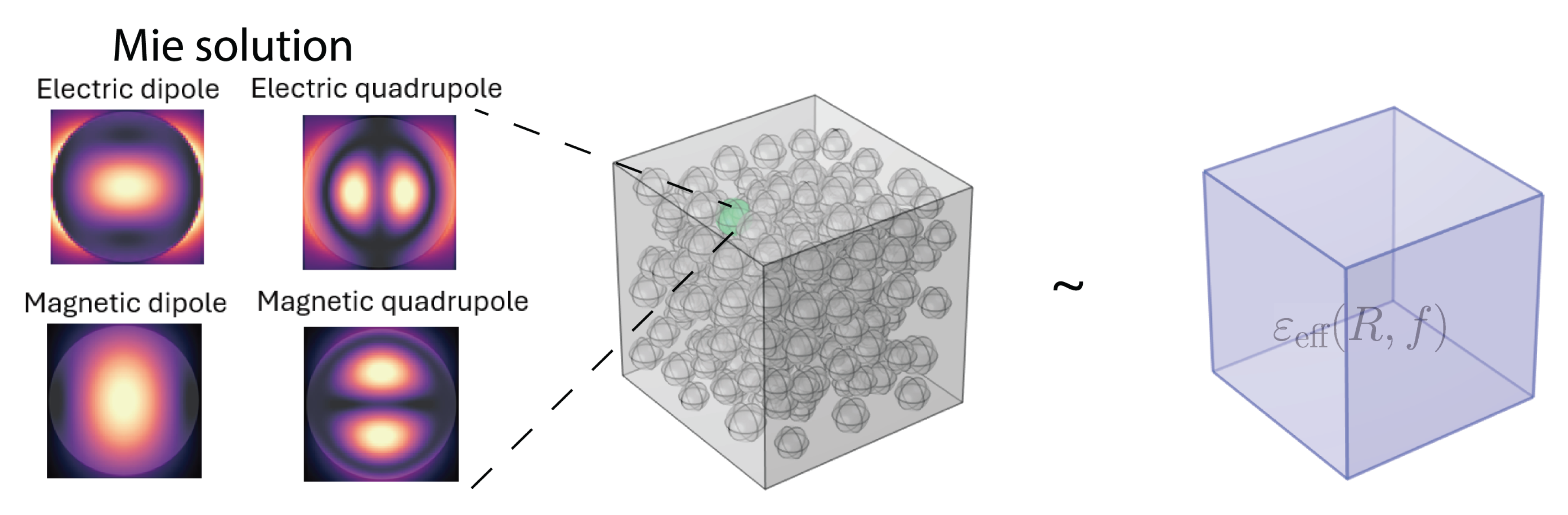
In this work, we develop an EMT for randomly distributed silica nanoparticles by combining the CM relation with Mie solutions for unshelled, shelled, mixed and hollow structures. We validate our EMT against numerical calculations performed with the finite-element method using the commercial software COMSOL Multiphysics. This EMT provides a tool for designing functional films by controlling the filling ratio and radius of SNPs with significantly reduced computational effort. The general concept of this work is illustrated in Figure 1.

The paper is organized as follows. In Section II, we begin with the classical CM relation, replace the polarizability with the Mie solution, and develop the EMT for unshelled, shelled, mixed and hollow SNP media. In Section III, we compare the reflection and transmission coefficients obtained from our EMT for all four structures with those from the finite-element simulations. A discussion and summary are provided in Section IV.

2. CM Relation and Mie Solutions

We begin with the well-known CM relation, which connects the effective dielectric constant ${\epsilon }_{\mathrm{eff}}$ of two-component mixture to its local polarizability $\alpha$ as

$${\displaystyle \frac{{\epsilon }_{\mathrm{eff}}-{\epsilon }_d}{{\epsilon }_{\mathrm{eff}}+2{\epsilon }_d}}={\displaystyle \frac{f}{4\pi R^3{\epsilon }_0}}\alpha ,$$

(1)

where f and R are the filling ratio and mean radium of the SNPs. Substituting the static polarizability $\alpha =4\pi {\epsilon }_0{R}^3{\displaystyle \frac{\epsilon -1}{\epsilon +2}}$ into the Eq. (1) yields the widely used Maxwell-Garnett (MG) equation:

$${\epsilon }_{\mathrm{eff}}={\displaystyle \frac{(2f+1)\epsilon -2f+2}{(1-f)\epsilon +2+f}}.$$

(2)

Notably, the value of ${\epsilon }_{\mathrm{eff}}$ in MG equation is irrelevant of the radius of SNPs. However, as the size of the SNPs increases, contributions from quadrupole and higher-order multipoles become significant. Furthermore, surface plasmon resonances cannot be ignored when a metallic shell is considered, as these effects depend critically on the ratio of the incident wavelength to the SNP radius.

2.1. Effective Polarizability

To address these limitations, we combine the Mie solution with the CM relation by replacing the local polarizability with an effective polarizability ${\alpha }_{\mathrm{eff}}$, defined such that:

$${\sigma }_{\mathrm{ext}}={\displaystyle \frac{k}{{\epsilon }_0}}\mathrm{Im}\left({\alpha }_{\mathrm{eff}}\right),$$

(3)

where ${\sigma }_{\mathrm{ext}}$ is extinction cross-section, and $k={\displaystyle \frac{2\pi n_d}{\lambda }}$ with $n_d$ the refractive index of the medium and $\lambda$ the wavelength of light. Within the Mie theory framework, the extinction cross-section is given by

$${\sigma }_{\mathrm{ext}}={\displaystyle \frac{2\pi R^2}{q^2}}\mathrm{Re}\left[\sum _n(2n+1)(a_n+b_n)\right],$$

(4)

where $a_n$ and $b_n$ are the coefficients of Mie solution for electric and magnetic fields, respectively, n denotes the multipole expansion order such that $n=1,2$ for dipole and quadrupole terms, and $q={\displaystyle \frac{2\pi R{n}_d}{\lambda }}$ is the size parameter.

Combining Eqs. (2) and (3) we obtain the effective polarizability in terms of Mie coefficients as

$${\alpha }_{\mathrm{eff}}={\displaystyle \frac{2\pi R^3{\epsilon }_0}{q^3}}\sum _{n}i(2n+1)(a_n+b_n).$$

(5)

For an unshelled (homogeneous) sphere, the Mie coefficients $a_n$ and $b_n$ are given by

$$\begin{array}{cc}\hfill a_n& ={\displaystyle \frac{n_1{\psi }_n\left(q_1\right){\psi }_n^{\prime }\left(q\right)-{\psi }_n\left(q\right){\psi }_n^{\prime }\left(q_1\right)}{n_1{\psi }_n\left(q_1\right){\zeta }_n^{\prime }\left(q\right)-{\zeta }_n\left(q\right){\psi }_n^{\prime }\left(q_1\right)}},\hfill \\ \hfill b_n& ={\displaystyle \frac{{\psi }_n\left(q_1\right){\psi }_n^{\prime }\left(q\right)-n_1{\psi }_n\left(q\right){\psi }_n^{\prime }\left(q_1\right)}{{\psi }_n\left(q_1\right){\zeta }^{\prime }\left(q\right)-n_1{\zeta }_n\left(q\right){\psi }_n^{\prime }\left(q_1\right)}},\hfill \end{array}$$

(6)

where $q_1={\displaystyle \frac{2\pi n_{1}R}{\lambda }}$ with $n_1$ the refractive index of the SNPs, and ${\psi }_n$, ${\zeta }_n$ are the spherical functions of Bessel and Hankel of the first kind, respectively. The Mie coefficients for a shelled structure (a core-shell particle) can be derived similarly and are expressed as [13]

$$\begin{array}{cc}\hfill a_n^{\left(2\right)}& ={\displaystyle \frac{{\psi }_n\left(q\right)[{\psi }_n^{\prime }\left(q_2\right)-A{\kappa }^{\prime }\left(q_2\right)]-n_2{\psi }_n^{\prime }\left(q\right)[{\psi }_n\left(q_2\right)-A_n{\kappa }_n\left(q_2\right)]}{{\zeta }_n\left(q_2\right)[{\psi }_n^{\prime }\left(q_w\right)-A{\kappa }^{\prime }\left(q_2\right)]-n_2{\zeta }_n^{\prime }\left(q_2\right)[{\psi }_n\left(q_2\right)-A_n{\kappa }_n\left(q_2\right)]}},\hfill \\ \hfill b_n^{\left(2\right)}& ={\displaystyle \frac{n_2\psi \left(q\right)[{\psi }_n^{\prime }\left(q_2\right)-B_n\kappa \left(q_2\right)]-{\psi }_n^{\prime }\left(q\right)[{\psi }_n\left(q_2\right)-B_n{\kappa }_n\left(q_2\right)]}{n_2{\zeta }_n\left(q\right)[{\psi }_n^{\prime }\left(q_2\right)-B_n{\zeta }_n^{\prime }\left(q_2\right)]-{\zeta }_n^{\prime }\left(q\right)[{\psi }_n\left(q_2\right)-B_n{\kappa }_n\left(q_2\right)]}},\hfill \end{array}$$

(7)

where $q_2={\displaystyle \frac{2\pi R_2{n}_2}{\lambda }}$ with $n_2$ and $R_2$ the refractive index and the radius of the shell, $\kappa$ is the Bessel function of the second kind, and $A_n$, $B_n$ are defined as

$$\begin{array}{cc}\hfill A_n& ={\displaystyle \frac{n_2{\psi }_n(n_2{q}_1/n_1){\psi }_n^{\prime }\left(q_1\right)-n_1{\psi }^{\prime }(n_2{q}_1/n_1){\psi }_n\left(q_1\right)}{n_2{\kappa }_n(n_2{q}_1/n_1){\psi }_n^{\prime }\left(q_1\right)-n_1{\kappa }_n^{\prime }(n_2{q}_1/n_1)\psi \left(q_1\right)}},\hfill \\ \hfill B_n& ={\displaystyle \frac{n_2{\psi }_n\left(q_1\right){\psi }_n^{\prime }(n_2{q}_1/n_1)-n_1\psi (n_2{q}_1/n_1){\psi }_n^{\prime }\left(q_1\right)}{n_2{\kappa }_n^{\prime }(n_2{q}_1/n_1){\psi }_n\left(q_1\right)-n_1{\kappa }_n(n_2{q}_1/n_1){\psi }_n^{\prime }\left(q_1\right)}}.\hfill \end{array}$$

(8)

These Mie coefficients are computed numerically [14]. The maximum order n for the multipole expansion is determined by the Wiscombe criterion, that is $n_{\mathrm{cut}}=x+4x^{1/3}+2$ with $x=q$.

We now compare the local (static) polarizability with the effective polarizability derived from Mie theory for shelled and hollow structures. For a core-shell particle, the local polarizability in the electrostatic approximation is [11]

$$\alpha =4\pi {\epsilon }_0{R}_2^3\left[{\displaystyle \frac{({\epsilon }_2-{\epsilon }_d)({\epsilon }_1+2{\epsilon }_2)+f_R({\epsilon }_1-{\epsilon }_2)({\epsilon }_d+2{\epsilon }_2)}{({\epsilon }_2+2{\epsilon }_d)({\epsilon }_1+2{\epsilon }_2)+f_R(2{\epsilon }_2-{\epsilon }_d)({\epsilon }_1-{\epsilon }_2)}}\right]$$

(9)

where $R_1$ (${\epsilon }_1$) and $R_2$ (${\epsilon }_2$) are the radius (dielectric constant) of the core and shell, respectively, and $f_R=R_1^3/R_2^3$ is the volume ratio of core. The effective polarizability of shelled and hollow structures can be calculated by combining Eqs.(4) and (6).

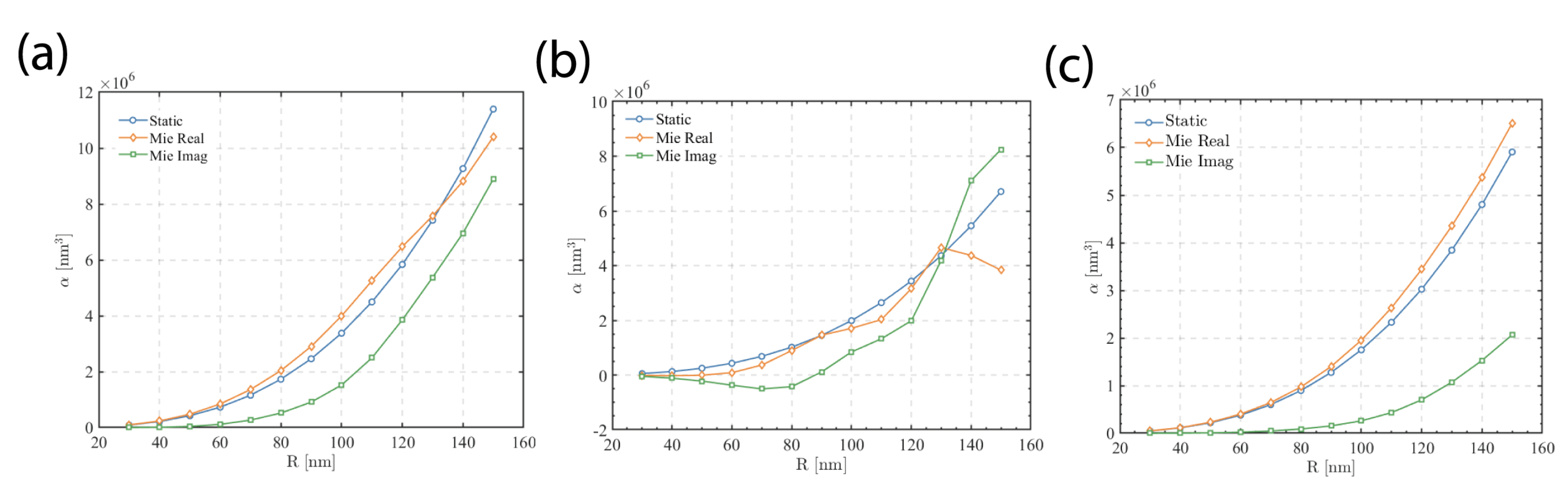
Figure 2 shows a comparison between the polarizabilities obtained from the static approximation and the Mie solution for three different structures: unshelled spheres, silver-shelled spheres, and hollow spheres. The refractive indices of the host medium and the silica are set to 1.0 and 1.45, respectively. For the core-shell particles, the core radius is 80% of the shell radius. The dielectric function of silver is taken from experimental data [15]. As seen in Fig. 2, for a small size parameter $R/\lambda$ (with $\lambda =380$ nm), the local and effective polarizabilities agree well. A key distinction is that the effective polarizability possesses a non-zero imaginary part, which is absent in the local approximation.

Figure 2. Comparison of effective polarizability of SNPs obtained by static approximation and Mie solution for (a) unshelled, (b) Ag-shelled and (c) hollow structures for different radii.

Figure 2. Comparison of effective polarizability of SNPs obtained by static approximation and Mie solution for (a) unshelled, (b) Ag-shelled and (c) hollow structures for different radii.

2.2. Effective Dielectric Constant

Using the effective polarizability ${\alpha }_{\mathrm{eff}}$, the effective dielectric constant can be calculated from the CM relation in Eq. (1), with $\alpha$ replaced by ${\alpha }_{\mathrm{eff}}$. In practice, SNPs synthesized via conventional routes exhibit a size distribution. To account for this, we model the distribution of radii R using a Gaussian function

$$P\left(R\right)={\displaystyle \frac{1}{2\pi {\sigma }^2}}{e}^{-{\displaystyle \frac{{(x-\mu )}^2}{2{\sigma }^2}}},$$

(10)

where $\mu$ is the mean value of R, and $\sigma$ is the standard derivation. The effective dielectric constant is then averaged over this distribution as

$${\displaystyle \frac{{\epsilon }_{\mathrm{eff}}-{\epsilon }_m}{{\epsilon }_{\mathrm{eff}}+2{\epsilon }_m}}={\displaystyle \frac{f}{\langle R^3\rangle }}{\int }_{R_{\min }}^{R_{\max }}P\left(R^{\prime }\right){\alpha }_{\mathrm{eff}}\left(R^{\prime }\right)d{R}^{\prime },$$

(11)

where $R_{\min }$ and $R_{\max }$ are the the lower and upper cutoff radii for the integration, and $\langle R^3\rangle$ is the mean cubed radius. By substituting the Mie solution for ${\alpha }_{\mathrm{eff}}$ and truncating the multipole expansion to include dipole and quadrupole terms, we obtain a working formula for the effective dielectric constant

$${\epsilon }_{\mathrm{eff}}=1-3f{\int }_{R_{\min }}^{R_{\max }}P\left(R\right){\displaystyle \frac{3(a_1+b_1)+5(a_2+b_2)}{2i{q}^3+f(3(a_1+b_1)+5(a_2+b_2))}}dR,$$

(12)

where q takes $q_2$ for the shelled structure, and we set ${\epsilon }_d=1$.

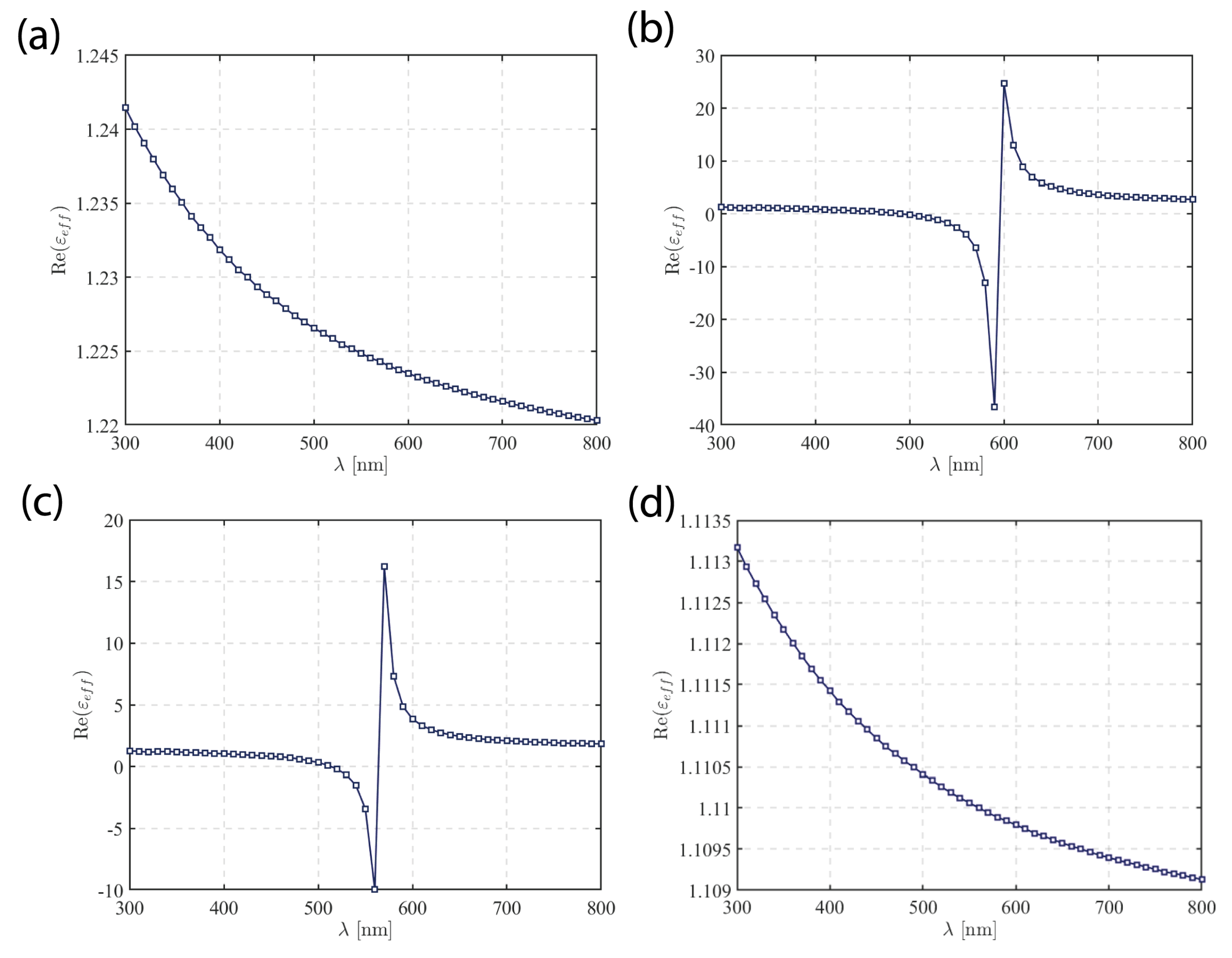
The calculated real part of the effective dielectric constant for unshelled, Ag-shelled, mixed, and hollow SNPs is plotted in Fig. 3 for different wavelengths. The filling ratio is 0.25, and the mean radius of the SNPs is 35 nm, and $\sigma =3\mathrm{nm}$. $R_{\min }$ and $R_{\max }$ are set as 10 nm and 50 nm, respectively. The dielectric constant of host medium is set as 1.0. The integration was performed with 5000 sampling points. For the mixed structure, we set the ratio between unshelled and silver-shelled spheres is 1:1. Figure 3 shows that the dielectric function decreases monotonically with increasing wavelength for unshelled and hollow structures. In contrast, for the silver-shelled and mixed structures, distinct singularities appear near 600 nm and 550 nm, respectively, due to plasmon resonances.

3. Validation of EMT

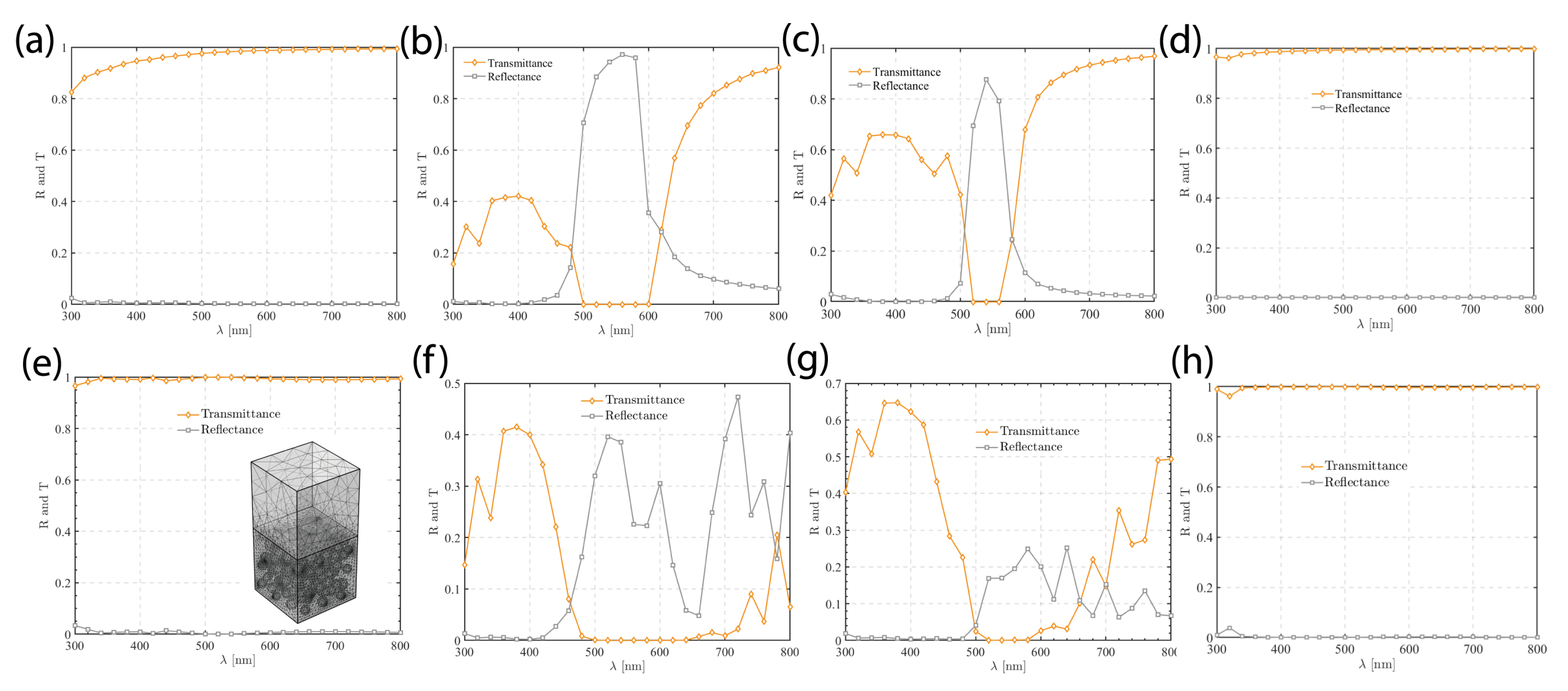
We now validate our EMT by comparing its predictions for reflectance and transmittance with results from full-wave finite-element method simulations as displayed in Figure 4. The simulation geometry with meshed structure is shown in the inset of Fig. 4(e): incident light propagates along the z-direction with the electric field polarized along the x-axis.m, and periodic boundary conditions are adopted along x- and y-directions.

Figure 4(a)-(d) shows that the EMT, based on Mie solutions, generally reproduces the trends in the finite-element method results, particularly for the unshelled and hollow structures. For the Ag-shelled structure, the finite-element method results [Figure 4(e) to (h)] exhibit several resonance peaks at wavelengths longer than 500 nm, which are not fully captured by the EMT. This discrepancy may be attributed to finite-size effects and spatial correlations between particles in the FEM simulation, which are not accounted for in the quasi-static, mean-field EMT.

4. Summary

We have developed an effective medium theory for silica nanoparticles by integrating Mie solutions with the Clausius-Mossotti relation. This theory calculates the effective polarizability using the full set of Mie coefficients, incorporating both electric and magnetic multipole contributions. We applied this framework to three types of structures: unshelled spheres, Ag-shelled spheres, and hollow spheres. The transmittance and reflectance predicted by our effective medium theory were compared with those from finite-element simulations, showing good agreement for non-plasmonic structures and capturing the overall behavior for plasmonic ones. Our results provide a practical and computationally efficient tool for analyzing the optical properties of silica nanoparticles with various structures, aiding in the rational design of functional films for applications such as anti-glare coatings.