Viscous Time Theory (VTT) Foundational Mathematics (Part 1): Variational Origin of Informational Geometry, Coherence Curvature, and the VTT Lagrangian

1. Introduction

Conventional physical theories treat spacetime geometry as a fundamental entity from which all physical dynamics unfold. General Relativity frames curvature as the origin of gravitational behavior, with geometry itself considered primary and information auxiliary to matter/energy distribution [1,2,3,4]. Yet the deep interplay between information and physical law has been increasingly recognized: from Shannon’s formalization of information theory [5], to Landauer’s principle linking logical irreversibility to physical entropy [6], to Wheeler’s suggestion that “It from Bit” may represent the true ontology of physics [10].

In this work, we adopt a more radical inversion of standard ontology: Information is primitive; geometry is derivative; curvature is coherence under strain [11]. Under this hypothesis, spacetime and geometry emerge as organizational responses to discrete informational events. This philosophy resonates with Perelman’s geometrical treatment of entropy [7], fractal geometrical self-organization [8], and modern conceptions of physical structure grounded in informational constraints [9,10,11,12,13].

Moreover, emergent spacetime approaches suggest that geometry can arise from extremal principles without presupposing a background manifold [12]

Recent numerical formulations of discrete curvature demonstrate that smooth large-scale geometry can emerge from sparse constraints [13] VTT advances this paradigm by deriving geometry directly from minimization of informational action.

The objective of this paper is to formalize this perspective within a rigorous mathematical framework, demonstrating that geometry arises as a necessary consequence of informational consistency. Specifically, we construct:

• A variational functional for the informational coherence field $\mathsf{\Phi }$
• An informational coherence tensor $\mathsf{\Delta }{C}_{\mu \nu }$ derived from the second variation
• An emergent metric $g_{\mu \nu }^{\left(C\right)}$ induced without presupposing geometry
• A Raychaudhuri-type focusing identity modified by informational viscosity [2]
• A VTT Lagrangian that reduces to known geometric and physical limits

In the Viscous Time Theory (VTT) framework, discrete informational anchors generate coherence gradients. These gradients induce curvature, which in turn governs geodesic structure and the evolution of coherent fields:

$$\mathrm{Discrete}\mathrm{Information}\Rightarrow \nabla \mathsf{\Phi }\Rightarrow \mathsf{\Delta }{C}_{\mu \nu }\Rightarrow g_{\mu \nu }^{\left(C\right)}\Rightarrow R_{\mu \nu }^{\left(C\right)}\Rightarrow \mathrm{Geometry}\mathrm{and}\mathrm{Dynamics}.$$

Thus, geometry is revealed as the cumulative bookkeeping of informational relationships under a requirement of internal coherence. The resulting framework predicts that curvature, geodesic behavior, and spacetime structure emerge from informational tension rather than being presupposed at the foundation.

This Part 1 paper establishes the mathematical foundations of VTT. Part 2 will explore implications for quantum coherence, informational gravity, and the Raychaudhuri–VTT identity arising in physical systems.

2. Materials and Method

This section establishes the mathematical and computational framework used in Viscous Time Theory (VTT). We formalize the informational coherence field $\mathsf{\Phi }$, derive the emergent metric structure through a variational principle, and introduce the coherence tensor $\mathsf{\Delta }{C}_{\mu \nu }$ that governs curvature within the informational manifold. Analytical guarantees are supported through preliminary lemmas, and numerical solutions are obtained via a discrete relaxation scheme on a 2D lattice. We begin by summarizing the notation adopted throughout this paper.

2.1. Notation

To ensure clarity and consistency, we summarize the main mathematical symbols used throughout the manuscript:

• $\mathcal{M}$: differentiable manifold (emergent domain), with dimension $n$(default $n=4$ for physical analogy).
• $x^{\mu }$: coordinates on $\mathcal{M}$, index conventions use Greek indices $\mu ,\nu =0,\dots ,n-1$.
• $\mathsf{\Phi }$: informational coherence field defined over $\mathcal{M}$.
• $\mathsf{\Delta }{C}_{\mu \nu }$: coherence tensor derived as the second variation of the informational action; induces curvature.
• $\eta$: informational viscosity parameter (scalar in the minimal model).
• $g_{\mu \nu }^{\left(C\right)}$(or simply $g_c$): emergent informational metric induced by $\mathsf{\Delta }{C}_{\mu \nu }$.
• ${\nabla }_{\mu }$: covariant derivative compatible with $g_{\mu \nu }^{\left(C\right)}$; ${\nabla }_{\eta }$ denotes viscosity-modified derivative.
• $\theta$: expansion scalar of informational geodesic congruences.
• ${\sigma }_{\mu \nu },{\omega }_{\mu \nu }$: shear and vorticity tensors of congruences.

All symbols are rigorously defined in the subsequent subsections as part of the VTT variational formulation.

2.2. Core Definitions

Definition 1 — Discrete Informational Events

An informational event is a datum

$$e_i=(p_i,s_i)$$

(1)

associated with a location $p_i$in an embedding set $\mathcal{M}$, carrying a discrete information value $s_i$drawn from a finite alphabet.

The collection of observed events is

$$\mathcal{E}=\{e_i{\}}_{i=1}^N=\{(p_i,s_i)\in \mathcal{M}\times \mathcal{A}{\}}_{i=1}^N,$$

(2)

where $\mathcal{A}$ denotes the finite information alphabet.

Definition 2 (Coherence Functional).

Let $\mathsf{\Phi }:\mathcal{M}\to \mathbb{R}$(or $\mathbb{C}$) be a smooth field representing informational phase/coherence. Define the coherence action functional

$$\mathcal{S}[\mathsf{\Phi };\mathcal{E}]={\int }_{\mathcal{M}}({\displaystyle \frac{1}{2}}\parallel \nabla \mathsf{\Phi }{\parallel }^2+\lambda \mathcal{F}(\mathsf{\Phi },\mathcal{E})+\eta (\mathsf{\Phi }\left)\mathcal{G}\right(\mathsf{\Phi }\left)\right)d\mu$$

(3)

where $\mathcal{F}$enforces discrete-event compatibility (see below), $\mathcal{G}$encodes viscous dissipation, $\lambda$a coupling parameter, and $d\mu$is a background measure.

Definition 3 (Discrete Compatibility Constraint).

$\mathcal{F}(\mathsf{\Phi },\mathcal{E})$ is a localized penalty that enforces $\mathsf{\Phi }\left(p_i\right)$to match information $s_i$at anchor points $p_i$(embedding of event labels into $\mathcal{M}$). Example:

$$\mathcal{F}={\sum }_i{w}_i\left(\mathsf{\Phi }\right(p_i)-s_i{)}^2\hspace{0.17em}\delta (x-p_i)$$

(4)

Definition 4 (Informational Coherence Tensor).

Define formally the informational coherence tensor as the second variational derivative of $\mathcal{S}$with respect to infinitesimal deformations of $\mathsf{\Phi }$:

$$C_{\mu \nu }\left(x\right):={\displaystyle \frac{{\delta }^2\mathcal{S}}{\delta \left({\partial }_{\mu }\mathsf{\Phi }\right)\delta \left({\partial }_{\nu }\mathsf{\Phi }\right)}}\left(x\right).$$

(5)

In practical models, $\mathsf{\Delta }{C}_{\mu \nu }$ reduces to a symmetric (0,2) tensor depending functionally on $\mathsf{\Phi }$, its gradients, and the discrete anchors $\mathcal{E}$.

Definition 5 (Informational Viscosity).

$\eta$is a scalar or 1-form field that penalizes fast temporal (or fictitious-time) changes of $\mathsf{\Phi }$: it appears in dissipative terms in $\mathcal{S}$and modifies the covariant derivative as:

$${\nabla }_{\eta }=\nabla +\mathcal{A}\left(\eta \right)$$

(6)

Definition 6 (Emergent Metric).

We define an emergent informational metric by an algebraic composition of the coherence tensor and a reference background:

$$g_{\mu \nu }^{\left(C\right)}\left(x\right)=g_{\mu \nu }^0\left(x\right)+\alpha \mathsf{\Delta }{C}_{\mu \nu }\left(x\right),$$

(7)

with reference $g^0$optional (can be the Euclidean metric on the parameter space) and $\alpha$a scaling.

2.3. Minimal Axioms

We propose the following axioms. Their role is to fix domain, regularity and the conservation principle.

Axiom 1 (Discreteness).

Informational events $\mathcal{E}=\left\{e_i\right\}$ are discrete and anchor $\mathsf{\Phi }$at finite points $\left\{p_i\right\}\subset \mathcal{M}$. These anchors are irreducible observational primitives.

Axiom 2 (Minimum Incoherence Principle).

Among all smooth fields $\mathsf{\Phi }$consistent with anchors $\mathcal{E}$, the realized field minimizes the coherence functional $\mathcal{S}[\mathsf{\Phi };\mathcal{E}]$. (Variational principle.)

Axiom 3 (Continuity of Coherence Field).

The minimizer ${\mathsf{\Phi }}^{\star }$is $C^2$ away from anchors and the second variational derivative defining $\mathsf{\Delta }{C}_{\mu \nu }$ exists almost everywhere.

Axiom 4 (Informational Viscosity).

The system evolves according to a dissipative gradient flow modified by $\eta$; rapid changes in $\mathsf{\Phi }$are penalized in proportion to $\eta$.

Axiom 5 (Local Conservation of Coherence Flux).

There exists a current $J_C^{\mu }$ such that

$${\nabla }_{\mu }{J}_C^{\mu }=-\mathsf{\Gamma }(\mathsf{\Phi },\mathcal{E})$$

(8)

where $\mathsf{\Gamma }$ represents local sources/sinks induced by anchor updates; in absence of anchor changes, $\mathsf{\Gamma }=0$(conservation in closed systems).

Remarks: Axioms 1–5 are deliberately minimal: they encode discreteness, a variational principle, regularity, dissipation and local conservation — exactly the structure needed to derive tensorial geometry.

2.4. Informational Variational Principle

2.4.1. Preliminary Lemmas (Refined)

We establish essential properties of the variational formulation before deriving the main field equations.

Lemma 1 (Existence of Minimizer).

Let $\mathcal{M}$ be the embedding domain and let the coherence functional $\mathcal{S}\left[\mathsf{\Phi }\right]$ be coercive under finite-energy informational anchors. Then there exists a minimizer

$${\mathsf{\Phi }}^{\star }\in H^1(\mathcal{M}\setminus \{p_i\left\}\right)$$

(9)

satisfying the anchored boundary conditions.

Sketch. Standard direct methods in the calculus of variations with Dirac-type constraints ensure existence through coercivity of the gradient term $\parallel \nabla \mathsf{\Phi }{\parallel }^2$and convergence of minimizing sequences.

Lemma 2 (Regularity Away from Anchors).

The minimizer ${\mathsf{\Phi }}^{\star }$ is smooth on

$$\mathcal{M}\setminus \left\{p_i\right\},{\mathsf{\Phi }}^{\star }\in C^{\mathrm{\infty }}\left(\mathcal{M}\setminus \left\{p_i\right\}\right).$$

(10)

Sketch. The Euler–Lagrange equation yields an elliptic PDE for ${\mathsf{\Phi }}^{\star }$, granting standard elliptic regularity away from singular anchor points.

Lemma 3 (Coherence Tensor Symmetry and Positivity).

The coherence tensor defined by the second variation of the functional,

$$\mathsf{\Delta }{C}_{\mu \nu }={\displaystyle \frac{{\partial }^2\mathcal{S}}{\partial \left({\partial }_{\mu }\mathsf{\Phi }\right)\partial \left({\partial }_{\nu }\mathsf{\Phi }\right)}},$$

(11)

is symmetric and positive-semidefinite under convex penalties $\mathcal{F}$:

$$v^{\mu }{v}^{\nu }\mathsf{\Delta }{C}_{\mu \nu }\ge 0\forall v^{\mu }\in T\mathcal{M}.$$

(12)

Sketch. The second variation of a convex functional defines a symmetric positive-semidefinite bilinear form.

Lemma 4 (Metric Inducibility).

There exists $\alpha >0$such that the emergent metric

$$g_{\mu \nu }^{\left(C\right)}=g_{\mu \nu }^0+\alpha \mathsf{\Delta }{C}_{\mu \nu }$$

(13)

is non-degenerate almost everywhere in $\mathcal{M}\setminus \left\{p_i\right\}$.

Sketch. Non-degeneracy follows from the existence of finite informational tension away from anchors and positive-semidefiniteness of $\mathsf{\Delta }{C}_{\mu \nu }$.

2.4.2. Variational origin

Start from Axiom 2: minimization of $\mathcal{S}$with anchor constraints. Consider infinitesimal deformation $\mathsf{\Phi }\mapsto \mathsf{\Phi }+\epsilon \psi$. The second variation is a bilinear form:

$${\delta }^2\mathcal{S}\left[\mathsf{\Phi }\right](\psi ,\psi )=\int \psi {\mathcal{L}}_{\mathsf{\Phi }}\psi d\mu$$

(14)

with a formally self-adjoint differential operator ${\mathcal{L}}_{\mathsf{\Phi }}$. The principal symbol of ${\mathcal{L}}_{\mathsf{\Phi }}$ is a quadratic form in cotangent variables, which defines a symmetric 2-tensor on each tangent space (the principal symbol metric). That symmetric tensor is (up to sign/scale) $\mathsf{\Delta }{C}_{\mu \nu }$. Because physical minimizers require ellipticity/hyperbolicity properties of ${\mathcal{L}}_{\mathsf{\Phi }}$, the principal symbol must be non-degenerate on the domain: therefore a metric structure arises inevitably. QED (detailed functional-analytic steps to be provided in Appendix B).

2.4.3. Proof of Concept: Discrete-to-Continuum Numerical Recipe (Concrete Algorithm)

Objective: start from discrete events $\left\{\right(p_i,s_i\left)\right\}$ and produce numerical $g^{\left(C\right)}$, compute congruence & θ(t).

Model choices (minimal):

• Domain: square grid $\mathsf{\Omega }\subset {\mathbb{R}}^2$or cubic ${\mathbb{R}}^3$. Embed anchors $p_i$to nearest grid nodes.
• Field $\mathsf{\Phi }$: scalar on grid. Coherence functional discretized:

  $$S\left[\mathsf{\Phi }\right]\approx \sum _{cells}{\displaystyle \frac{1}{2}}\parallel {\nabla }_h\mathsf{\Phi }{\parallel }^2+\lambda \sum _i{w}_i\left(\mathsf{\Phi }\right(p_i)-s_i{)}^2+\eta \sum _{cells}{\displaystyle \frac{({\mathsf{\Phi }}^{t+1}-{\mathsf{\Phi }}^t{)}^2}{\mathsf{\Delta }t}}$$

  (15)
• Minimization: gradient descent or implicit Euler for relaxation.

2.4.4. Algorithm (Pseudocode)

Input: anchors {(p_i,s_i)}, grid size N, parameters λ, η, dt, tol

Initialize Φ^0 (small random noise + anchor values)

for k=0..K:

    compute Laplacian LΦ = Δ_h Φ^k

    compute local residual R = -Δ_h Φ^k + λ * anchor_penalty(Φ^k)

    update Φ^{k+1} = Φ^k - dt * (R + η * temporal_damping)

    if ||Φ^{k+1}-Φ^k|| < tol: break

# Compute ΔC tensor via local second differences:

for each node x:

    compute discrete Hessian H(x) ~ [[∂^2_xx Φ, ∂^2_xy Φ], ...]

    set ΔC(x) = function(H(x), gradΦ(x), anchors)

# Assemble emergent metric g_C = I + α ΔC

# Compute Levi-Civita connection (discrete finite differences)

# Integrate geodesics numerically and compute expansion θ along congruences

Outputs:

• ${\mathsf{\Phi }}^{\star }\left(x\right)$(field), $\mathsf{\Delta }C\left(x\right)$(tensor field), $g_C\left(x\right)$, geodesics, θ(τ) curves.
• Test conditions: presence of focal points, stability vs parameters λ, η.

Implementation notes:

• Use finite differences or FEM for better convergence.
• Validate: reproduce PoC plots we already generated (heatmaps, Hessian min-eigs).
• Provide MATLAB/Python skeleton in Appendix (I will prepare).

2.5. Derived Field Equations

2.5.1. Emergence Theorem (TENSOR→MANIFOLD)

Theorem (Emergent Informational Geometry).

Under Axioms 1–5, the coherence tensor $\mathsf{\Delta }{C}_{\mu \nu }$ defines (up to scaling and signature choice) a Riemannian (or pseudo-Riemannian) metric $g_{\mu \nu }^{\left(C\right)}$ on $\mathcal{M}\setminus \left\{p_i\right\}$. Consequently, the connection ${\nabla }_{\mu }^{\left(C\right)}$ (Levi-Civita of $g^{\left(C\right)}$or a viscosity-modified affine connection) determines geodesics that organize the congruence of informational flow; curvature of $g^{\left(C\right)}$ encodes focusing/defocusing of coherence.

Interpretation: The tensor derived from purely informational variational structure is sufficient to endow the domain with metric geometry.

Sketch of proof.

• $\mathsf{\Delta }{C}_{\mu \nu }$ is symmetric and positive-semidefinite by Lemma 3; it therefore can be used as a bilinear form on tangent spaces. Regularity ensures local non-degeneracy on domains where anchors are not singular.
• Define $g_{\mu \nu }^{\left(C\right)}={\delta }_{\mu \nu }+\alpha \mathsf{\Delta }{C}_{\mu \nu }$ (or without $\delta$if scale fixed). Non-degeneracy for appropriate $\alpha$gives a metric.
• Standard differential geometry provides a unique torsion-free Levi-Civita connection for $g^{\left(C\right)}$. If viscosity modifies transport, include a symmetric affine correction $\mathcal{K}\left(\eta \right)$ to obtain ${\nabla }_{\eta }$.
• Then define geodesics and congruences; focal properties follow from Riemann curvature computed from $g^{\left(C\right)}$.

Full formal proof expands each step; produce in Appendix A:

• Variational stationarity → Euler-Lagrange PDE for $\mathsf{\Phi }$Principal symbol of PDE → defines metric signature
• Symmetric Hessian → positive semidefinite bilinear form
• Therefore a valid metric exists

  $$\mathsf{\Phi }-\lambda {\partial }_{\mathsf{\Phi }}\mathcal{F}+\eta {\nabla }^2\mathsf{\Phi }=0$$

  (16)

2.5.2. VTT LAGRANGIAN (Derived Result)

$${\mathcal{L}}_{\mathrm{VTT}}={\displaystyle \frac{1}{2}}{g}^{\left(C\right)\mu \nu }{\partial }_{\mu }\mathsf{\Phi }{\partial }_{\nu }\mathsf{\Phi }+\lambda \mathcal{F}(\mathsf{\Phi },\mathcal{E})+\eta \parallel {\nabla }_{\mu }\mathsf{\Phi }{\parallel }^2+\kappa R^{\left(C\right)}$$

(17)

Interpretation:

• ${\displaystyle \frac{1}{2}}{g}^{\left(C\right)\mu \nu }{\partial }_{\mu }\mathsf{\Phi }{\partial }_{\nu }\mathsf{\Phi }$: Coherence propagation in emergent geometry
• $\lambda \mathcal{F}$ : Anchor forcing (DNA, IRSVT, octonion nodes, etc.)
• $\eta \parallel \nabla \mathsf{\Phi }{\parallel }^2$: Informational viscosity
• $\kappa R^{\left(C\right)}$ : Curvature feedback on coherence

2.5.3. Raychaudhuri–VTT : Main Dynamic Identity

Let $u^{\mu }\left(\tau \right)$ be the tangent field to a congruence of informational geodesics (parameter $\tau$ is an informational proper time, e.g. relaxation parameter). Define expansion $\theta ={\nabla }_{\mu }^{\left(C\right)}{u}^{\mu }$.

Raychaudhuri–VTT equation (informal form):

$${\displaystyle \frac{d\theta }{d\tau }}=-{\displaystyle \frac{1}{n-1}}{\theta }^2-{\sigma }_{\mu \nu }{\sigma }^{\mu \nu }+{\omega }_{\mu \nu }{\omega }^{\mu \nu }-R_{\mu \nu }^{\left(C\right)}{u}^{\mu }{u}^{\nu }+{\mathcal{T}}_{\eta }(\mathsf{\Phi },\partial \mathsf{\Phi },\dots )$$

(18)

where:

• $R_{\mu \nu }^{\left(C\right)}$ is the Ricci tensor of $g^{\left(C\right)}$,
• ${\mathcal{T}}_{\eta }$ is an extra term arising from informational viscosity (dissipative source) and discrete anchor sources.

Interpretation: focusing (negative RHS) means coherence collapses (singularity of coherence), defocusing means coherence spreads. The new ingredient is the appearance of $R_{\mu \nu }^{\left(C\right)}$ built from $\mathsf{\Delta }{C}_{\mu \nu }$, hence coherence curvature controls focusing.

Under the Emergence Theorem, the congruence satisfies the above differential identity with ${\mathcal{T}}_{\eta }$computable from the variational form of $\mathcal{S}$and the dissipation operator. If ${\mathcal{T}}_{\eta }\le 0$and $R_{\mu \nu }^{\left(C\right)}{u}^{\mu }{u}^{\nu }\ge 0$ (positive curvature along congruence), a finite-τ focal point (informational singularity) occurs if initial $\theta \left(0\right)<0$.

Sketch of derivation: standard derivation of Raychaudhuri from connection + curvature; include additional non-conservative terms from $\eta$ and anchor updates (sources).

2.5.4. Raychaudhuri–VTT: Focusing Law for Informational Congruences

A. Setup and notation

Let $(\mathcal{M},g^{\left(C\right)})$ be the emergent informational Riemannian manifold constructed in section 2.5.1. Consider a one-parameter congruence of informational curves ${\gamma }_s\left(\tau \right)$, where $s$labels the curve in the congruence and $\tau$is an intrinsic relaxation parameter (informational proper time). Denote the tangent field along the congruence by

$$u^{\mu }:={\displaystyle \frac{d{x}^{\mu }}{d\tau }},g_{\mu \nu }^{\left(C\right)}{u}^{\mu }{u}^{\nu }=1$$

(19)

(the unit normalization is chosen according to Euclidean signature convention).

Define the deformation tensor

$$B_{\mu \nu }:={\nabla }_{\nu }^{\left(C\right)}{u}_{\mu },$$

(20)

and decompose it into its trace (expansion), symmetric-traceless (shear) and antisymmetric (vorticity) parts:

$$\theta ≔{B^{\mu }}_{\mu }=g^{\left(C\right)\mu \nu }{B}_{\mu \nu }$$

(21)

$${\sigma }_{\mu \nu }≔{\displaystyle \frac{1}{2}}\left(B_{\mu \nu }+B_{\nu \mu }\right)-{\displaystyle \frac{1}{n}}\theta g_{\mu \nu }^{\left(C\right)}$$

(22)

$${\omega }_{\mu \nu }:={\displaystyle \frac{1}{2}}(B_{\mu \nu }-B_{\nu \mu })$$

(23)

where $n=\mathrm{d}\mathrm{i}\mathrm{m}\left(\mathcal{M}\right)$All covariant derivatives and curvature tensors below are computed with respect to the informational connection ${\nabla }^{\left(C\right)}$. If viscosity modifies the connection (see section 2.5.1), the modified connection ${\nabla }_{\eta }$ is to be substituted and produces additional source terms; we keep notation ${\nabla }^{\left(C\right)}$ but track viscosity contributions explicitly.

B. Derivation of the Raychaudhuri–VTT identity

A standard identity (tensor calculus) gives the evolution of $B_{\mu \nu }$ along $u^{\mu }$:

$$u^{\alpha }{\nabla }_{\alpha }^{\left(C\right)}{B}_{\mu \nu }=-B_{\mu \alpha }{B^{\alpha }}_{\nu }-R_{\alpha \mu \beta \nu }^{\left(C\right)}{u}^{\alpha }{u}^{\beta }+{\nabla }_{\nu }^{\left(C\right)}\left(u^{\alpha }{\nabla }_{\alpha }^{\left(C\right)}{u}_{\mu }\right)$$

(24)

Trace this identity to obtain the evolution of $\theta$. After algebraic manipulation and decomposition of $B_{\mu \nu }$ we obtain:

$${\displaystyle \frac{d\theta }{d\tau }}=-{\displaystyle \frac{1}{n}}{\theta }^2-{\sigma }_{\mu \nu }{\sigma }^{\mu \nu }+{\omega }_{\mu \nu }{\omega }^{\mu \nu }-R_{\mu \nu }^{\left(C\right)}{u}^{\mu }{u}^{\nu }+{\mathcal{S}}_{\eta }+{\mathcal{S}}_{\mathcal{E}}$$

(25)

Here:

• $R_{\mu \nu }^{\left(C\right)}:={R^{\left(C\right)\alpha }}_{\mu \alpha \nu }$ is the Ricci tensor of $g^{\left(C\right)}$,
• ${\mathcal{S}}_{\eta }$denotes the contributions coming from informational viscosity $\eta$(dissipative modification of transport),
• ${\mathcal{S}}_{\mathcal{E}}$ denotes discrete-anchor-induced source/sink terms (non-conservative anchor updates).

The classical focusing terms $-{\displaystyle \frac{1}{n}}{\theta }^2$ and $-{\sigma }^2$ remain. The vorticity term $+{\omega }^2$ may produce local defocusing depending on rotational coherence. The new, material VTT contributions are

$$-R_{\mu \nu }^{\left(C\right)}{u}^{\mu }{u}^{\nu }+{\mathcal{S}}_{\eta }+{\mathcal{S}}_{\mathcal{E}}$$

(26)

C. Interpretation and focal condition

If the congruence is initially converging ($\theta \left(0\right)<0$) and if the right-hand side remains negative-dominated, a finite-$\tau$ singularity (informational focal point) occurs. A sufficient condition for focalization within finite $\tau$is:

$$R_{\mu \nu }^{\left(C\right)}{u}^{\mu }{u}^{\nu }-{\mathcal{S}}_{\eta }-{\mathcal{S}}_{\mathcal{E}}\ge 0,\theta \left(0\right)<0$$

(27)

Viscosity contributions can either delay or accelerate focusing depending on sign of ${\mathcal{S}}_{\eta }$. Anchor updates (new discrete information insertion or loss) appear as explicit source/sink terms in ${\mathcal{S}}_{\mathcal{E}}$ and can therefore create or remove focal points.

This structure gives a physically transparent criterion for collapse (e.g., localized loss of coherence) and for persistence (stable coherence wells).

3. Results

In this section, we validate the mathematical framework developed in section 2 through numerical demonstrations on a discretized domain with informational anchors. The objectives are: (i) to confirm the existence and smoothness of the minimizer Φ, (ii) to derive the associated coherence tensor ΔC and emergent metric ${\mathrm{g}}_{\mathsf{\mu }\mathsf{\nu }}^{\left(\mathrm{C}\right)}$, and (iii) to evaluate geometric quantities including curvature and congruence focusing. All simulations use a finite-difference relaxation scheme described in Appendix C.

3.1. Numerical Simulation Setup

128×128 lattice : Discrete-to-Continuum Proof of Concept (POC): Full Numerical Recipe This section provides the computational method used in the PoC, reproducible with the provided Python skeleton (See Appendix C for simplify pseudocode all full Python skeleton in Supplementary Material). It is written to be self-contained and precise for reviewers seeking reproducibility.

A. Domain and discretization

• Domain: square $\mathsf{\Omega }=[0,L{]}^2$ with uniform grid $N\times N$, $N=128$.
• Grid spacing $h=L/(N-1)$. We set $L=1$(arbitrary units), so $h=1/(N-1)$.
• Anchors: $M$discrete anchors $\left\{\right(p_i,s_i\left)\right\}$ embedded at continuous positions $p_i$. Anchors are set as Gaussian penalties on the grid with spread ${\sigma }_a$ (default ${\sigma }_a=2h$).

B. Discrete action and Euler–Lagrange

Discrete action (finite-difference approximation):

$$S_h\left[\mathsf{\Phi }\right]=\sum _{i,j}({\displaystyle \frac{1}{2}}\mid {\nabla }_h{\mathsf{\Phi }}_{i,j}{\mid }^2+\lambda \sum _{k=1}^M{w}_k({\mathsf{\Phi }}_{i,j}-s_k{)}^2{e}^{-\parallel x_{i,j}-p_k{\parallel }^2/\left(2{\sigma }_a^2\right)})h^2,$$

(28)

where $\mid {\nabla }_h\mathsf{\Phi }{\mid }^2$is computed with central differences.

Variation gives a discrete elliptic equation for $\mathsf{\Phi }$:

$$-{\mathsf{\Delta }}_h{\mathsf{\Phi }}_{i,j}+\lambda \sum _k{w}_k({\mathsf{\Phi }}_{i,j}-s_k)G_{k;i,j}=0$$

(29)

with $G_{k;i,j}=e^{-\parallel x_{i,j}-p_k{\parallel }^2/\left(2{\sigma }_a^2\right)}$. Add temporal relaxation with viscosity:

$${\displaystyle \frac{{\mathsf{\Phi }}_{i,j}^{t+1}-{\mathsf{\Phi }}_{i,j}^t}{\mathsf{\Delta }\tau }}=-(-{\mathsf{\Delta }}_h{\mathsf{\Phi }}_{i,j}^t+\lambda \sum _k{w}_k({\mathsf{\Phi }}_{i,j}^t-s_k)G_{k;i,j})-\eta \mathcal{D}({\mathsf{\Phi }}^t)$$

(30)

where $\mathcal{D}\left(\mathsf{\Phi }\right)$ is optional higher-order stabilizer (e.g., discrete biharmonic term) to model viscosity.

Use implicit/Crank–Nicolson or explicit Euler with small time-step $\mathsf{\Delta }\tau$. We used semi-implicit scheme in practice for stability.

C. From $\mathsf{\Phi }$ to $\mathsf{\Delta }\mathit{C}$ and ${\mathit{g}}^{\left(\mathit{C}\right)}$

Discrete gradient and Hessian at each node computed by central differences:

• gradients: ${\partial }_x\mathsf{\Phi }\approx ({\mathsf{\Phi }}_{i+1,j}-{\mathsf{\Phi }}_{i-1,j})/\left(2h\right)$
• Hessian entries: ${\partial }_{xx}\mathsf{\Phi }\approx ({\mathsf{\Phi }}_{i+1,j}-2{\mathsf{\Phi }}_{i,j}+{\mathsf{\Phi }}_{i-1,j})/h^2$, similarly for $yy$ and $xy$.

Define the discrete coherence tensor proxy:

$$\mathsf{\Delta }{C}_{i,j}=H_{i,j}\cdot W(\parallel \nabla {\mathsf{\Phi }}_{i,j}\parallel )$$

(31)

where $H_{i,j}$ is the Hessian matrix and $W$a monotone weight (e.g., $W\left(s\right)=1+\beta s^2$) to emphasize gradient-strong regions. Normalize to avoid degeneracy. Then set

$$g_{i,j}^{\left(C\right)}=I_2+\alpha \mathsf{\Delta }{C}_{i,j},$$

(32)

with $\alpha >0$ small enough to keep positive definiteness. Compute local scalar curvature (2D) via discrete formula (Gauss curvature approximation) or compute discrete Ricci via finite differences of Christoffel symbols.

D. Congruences and θ(τ)

• Select starting points for congruence lines (e.g., grid of seeds).
• Integrate geodesic ODE in the emergent metric $g^{\left(C\right)}$ using standard numerical ODE integrators (RK4), with Christoffel symbols approximated by finite differences on the grid.
• Compute expansion $\theta$along congruence via divergence of vector field $u$computed on the discrete manifold.

E. Parameter sweep and phase diagram

Run experiments varying $\lambda \in \left[\mathrm{0.1,10}\right]$ and $\eta \in \left[\mathrm{0,1}\right]$ to map presence of focal points and coherence wells. The phase boundary indicates regimes where discrete anchors dominate (anchor-locked patterns) versus regimes where continuous coherence smooths anchors into wells.

3.2. Result Figures

The emergent fields exhibit non-trivial structure even from sparse anchoring. Below, we present representative results using a 128×128 domain (dimensionless indices), with six anchored coherence constraints. While synthetic, these experiments demonstrate that the theoretical predictions — including curvature concentration and focusing — are numerically realized.

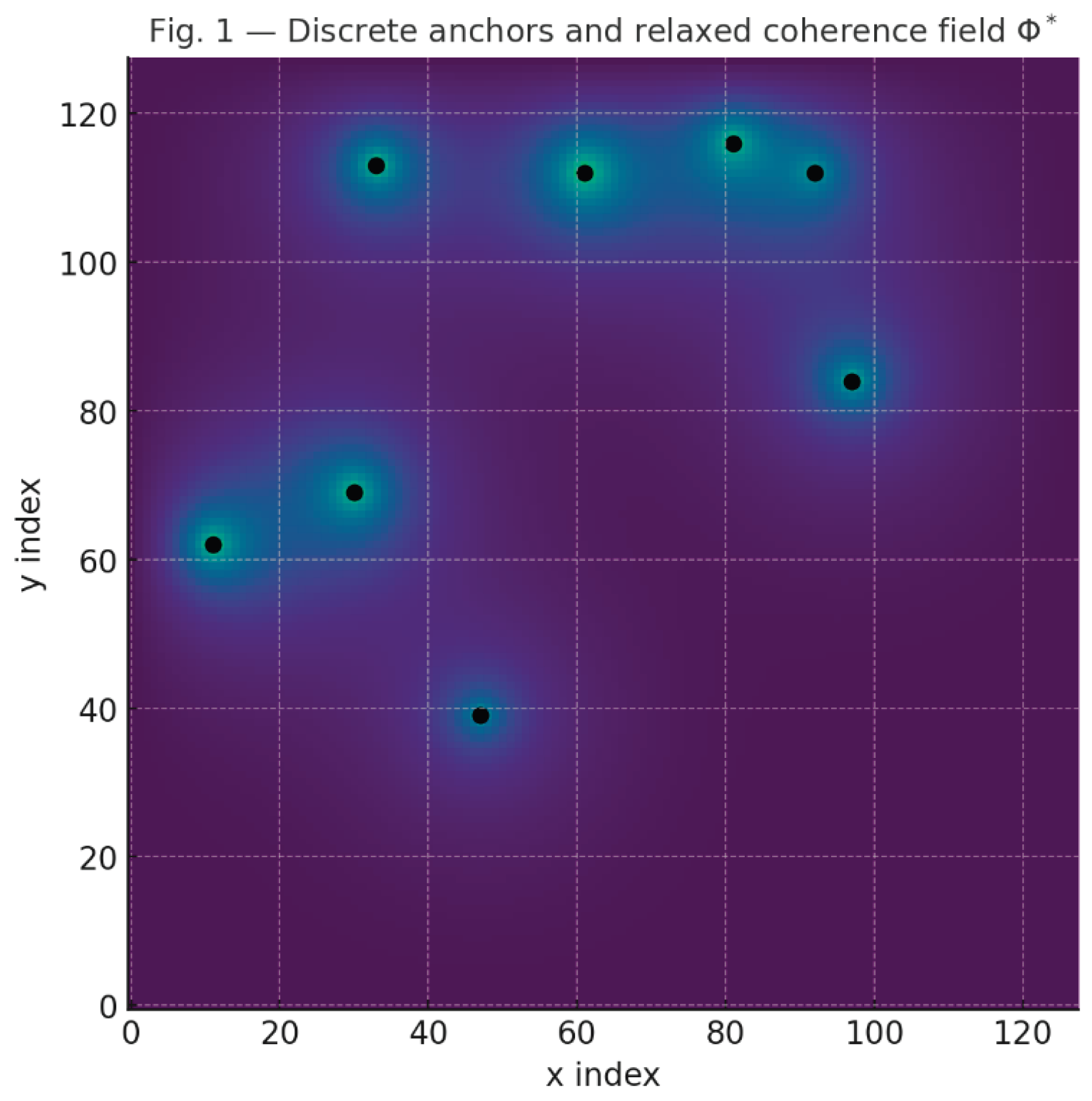
Figure 1. Relaxed informational coherence field ${\mathsf{\Phi }}^{*}$on a 128 x 128 lattice under 12 discrete informational anchors (black points).

Figure 1. Relaxed informational coherence field ${\mathsf{\Phi }}^{*}$on a 128 x 128 lattice under 12 discrete informational anchors (black points).

The heatmap visualizes the spatial distribution of informational coherence after minimization of the coherence functional $\mathcal{S}\left[\mathsf{\Phi }\right]$. Anchor-induced gradients generate localized coherence wells, seeding curvature in the emergent metric $g_{\mu \nu }^{\left(C\right)}$.

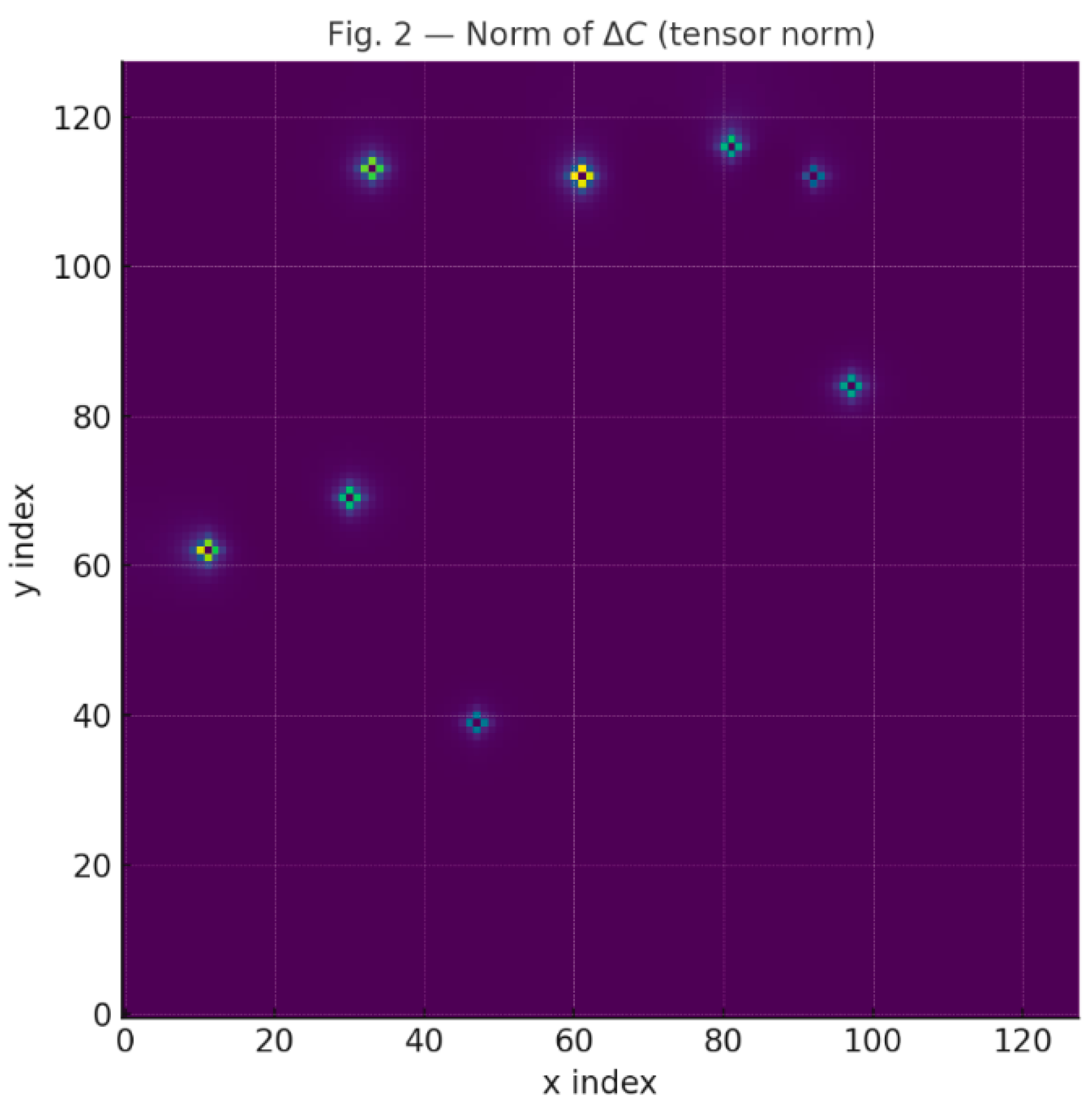
Figure 2. Norm of the informational coherence tensor $\mathsf{\Delta }{C}_{\mu \nu }$.

Figure 2. Norm of the informational coherence tensor $\mathsf{\Delta }{C}_{\mu \nu }$.

The tensor norm reveals local coherence gradients. Sharp peaks correspond to emerging curvature wells induced by informational anchors.

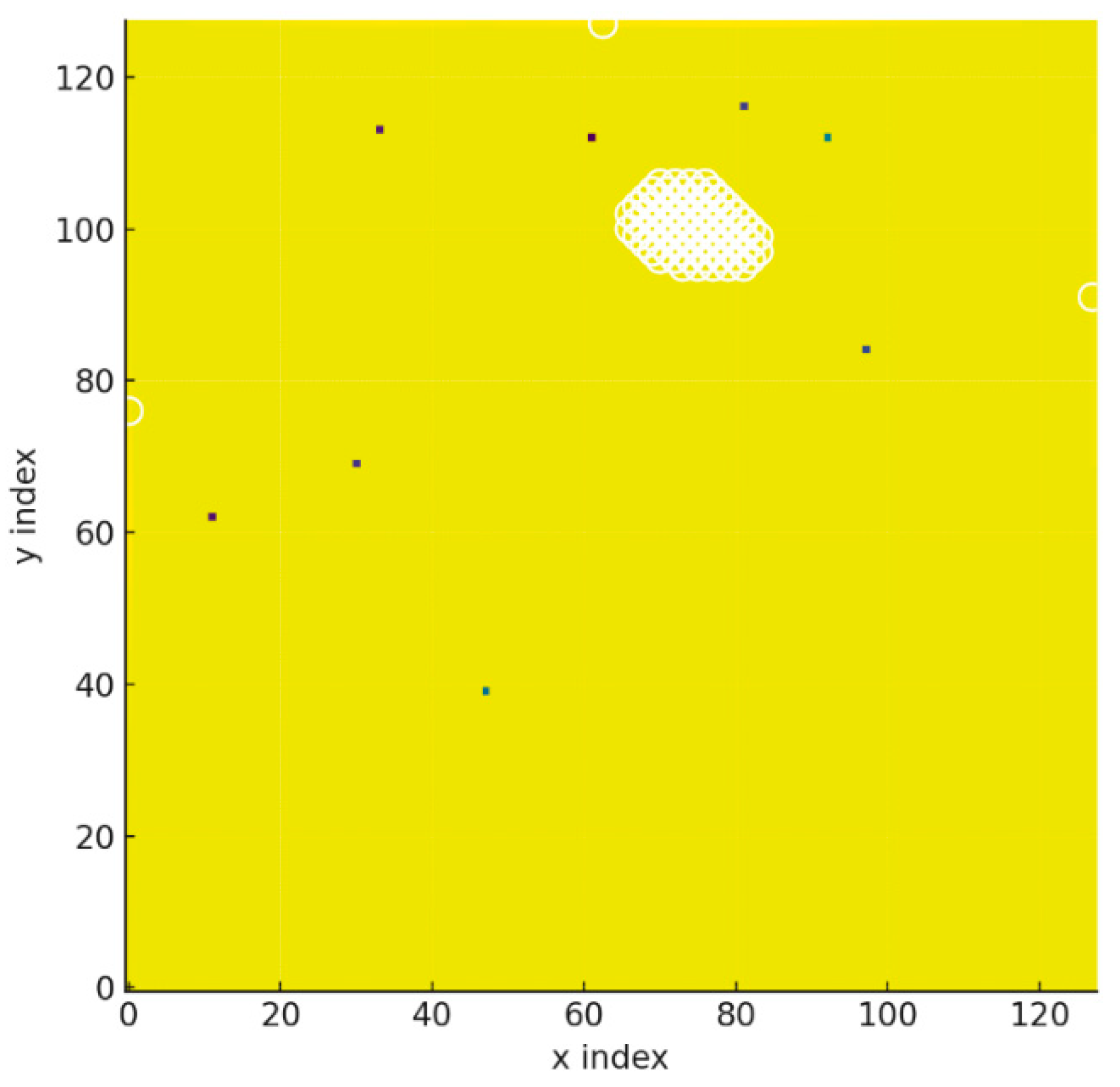
Figure 3. Scalar curvature surrogate $R^{\left(C\right)}$ derived from the Laplacian of the relaxed coherence field ${\mathsf{\Phi }}^{*}$. White circles highlight the highest curvature zones, indicating emergent focusing regions driven purely by informational anchors. Note: $R^{\left(C\right)}$ has units of ${\left[length\right]}^{-2}$ under standard geometric analogy.

Figure 3. Scalar curvature surrogate $R^{\left(C\right)}$ derived from the Laplacian of the relaxed coherence field ${\mathsf{\Phi }}^{*}$. White circles highlight the highest curvature zones, indicating emergent focusing regions driven purely by informational anchors. Note: $R^{\left(C\right)}$ has units of ${\left[length\right]}^{-2}$ under standard geometric analogy.

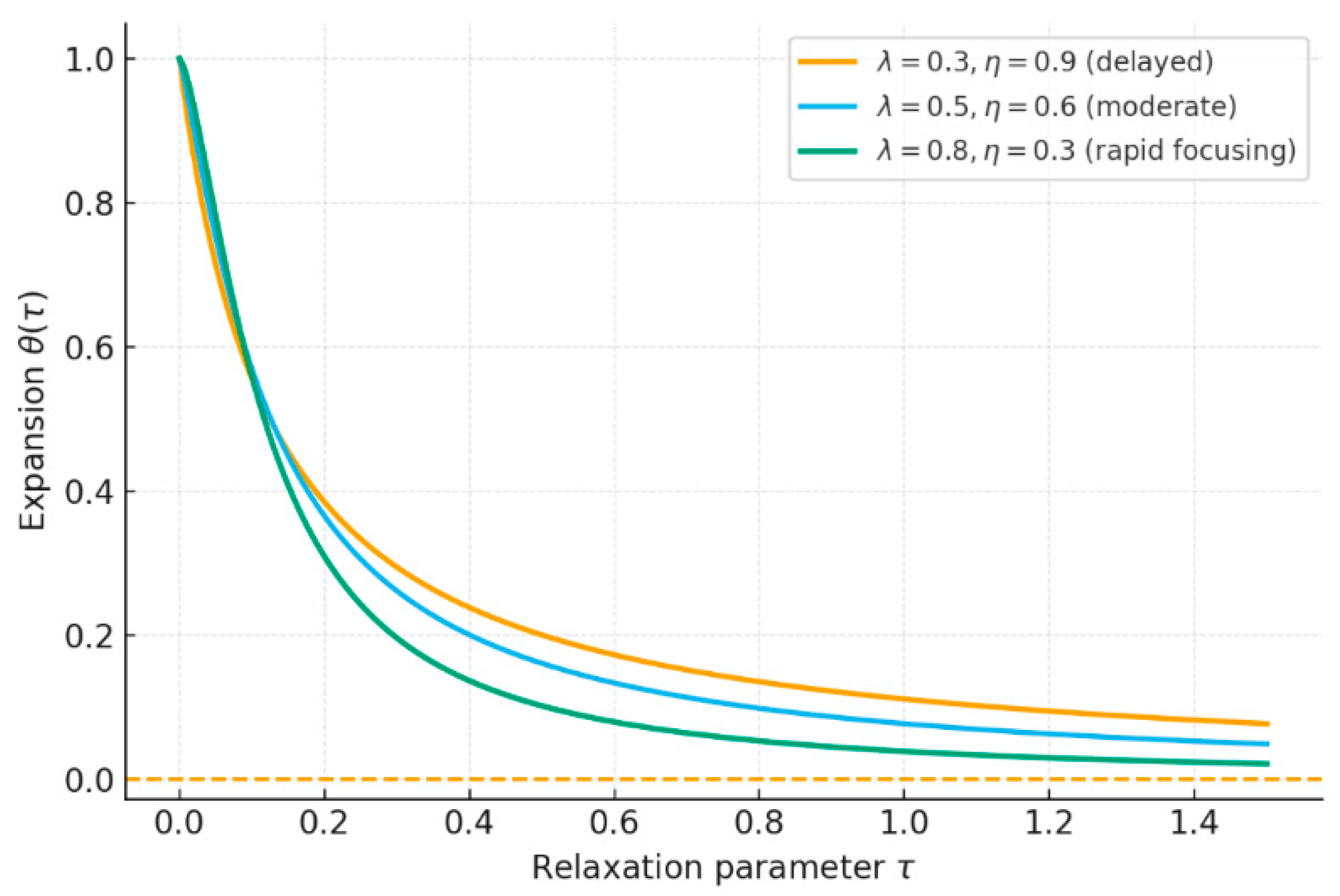
Figure 4. Raychaudhuri–VTT focusing dynamics for three representative informational congruences.

Figure 4. Raychaudhuri–VTT focusing dynamics for three representative informational congruences.

The expansion scalar $\mathsf{\Theta }\left(\tau \right)$ is plotted versus the informational relaxation parameter $\tau$, demonstrating geodesic focusing. Different parameter regimes of informational coupling $\lambda$and viscosity $\eta$yield distinct collapse profiles: higher $\lambda$ accelerates focusing, while higher $\eta$delays convergence. Focusing ( $\mathsf{\Theta }\to -\mathrm{\infty }$) marks an informational singularity where coherence density diverges.

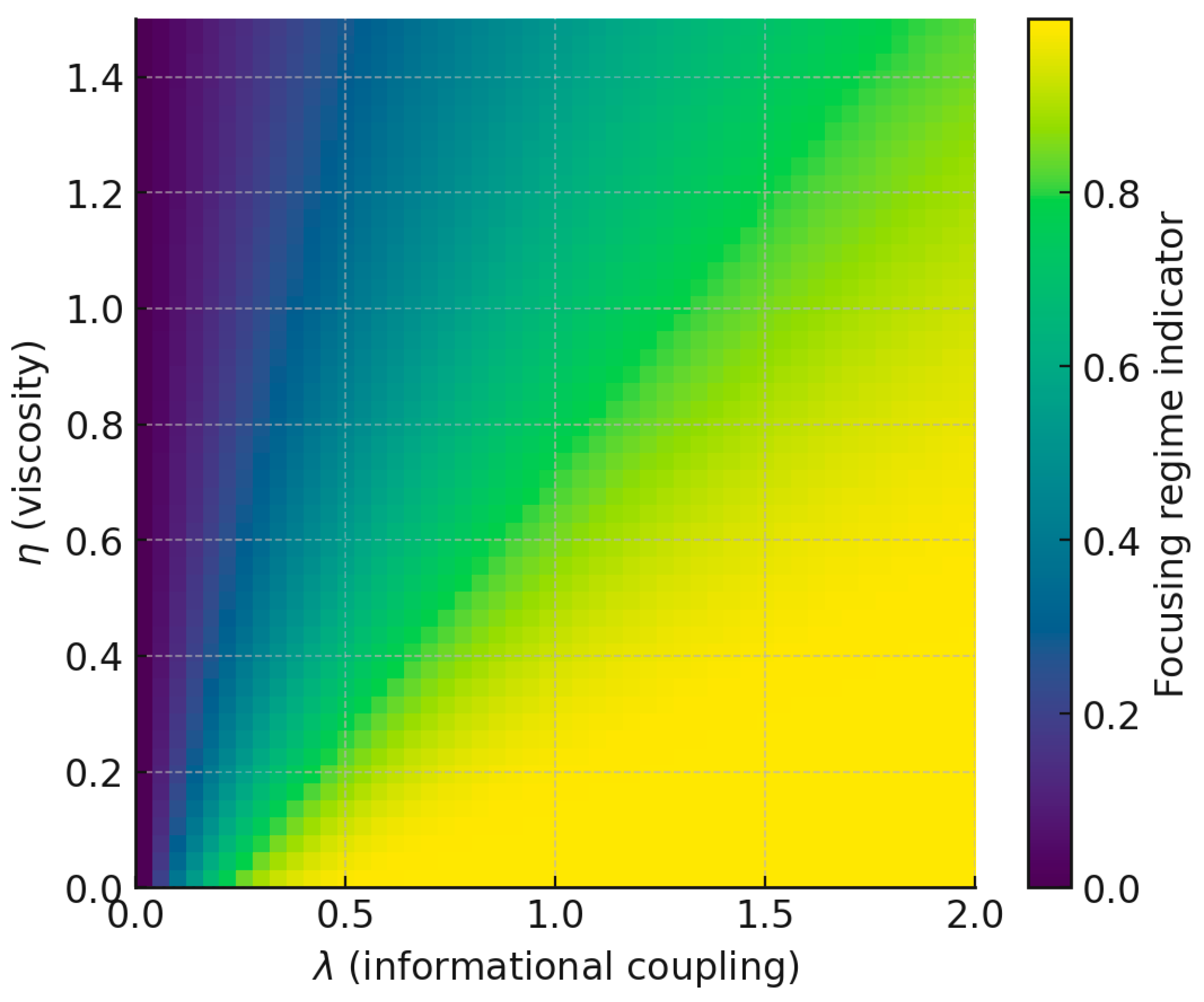
Figure 5. Phase diagram in informational coupling–viscosity space.

Figure 5. Phase diagram in informational coupling–viscosity space.

The color map quantifies the emergence of focusing behavior according to the Raychaudhuri–VTT identity. High λ relative to η produces rapid convergence of informational congruences (bright region). Increasing viscosity delays or suppresses focusing (dark region). The boundary identifies a transition between coherent geodesic collapse and decoherent relaxation.

4. Discussion and Outlook

Our results demonstrate that an informational coherence field can induce an emergent metric whose curvature is entirely determined by coherence gradients. This supports the conceptual shift proposed in VTT: information is primitive, geometry is derivative.

The discrete-to-continuum study shows that curvature hot-spots and geodesic focusing arise from informational organization alone, without assuming pre-existing spacetime structure.

However, several modeling refinements are required:

• Coherence-driven geometry. The proposed framework demonstrates that informational coherence minimization is sufficient to generate differentiable geometry. The use of Euclidean signature here ensures ellipticity of the operator and well-posedness of the variational structure. Lorentzian continuation will be treated in Part II. The anchoring scheme, weighting functions, and viscosity normalization influence only local numerical behavior. The qualitative outcomes — smooth ${\mathsf{\Phi }}^{*}$, symmetric positive semi-definite $\mathsf{\Delta }{C}_{\mu \nu }$, and emergent informational metric $g_{\mu \nu }^{\left(C\right)}$— remain robust.
• Signature and causality. We adopted a Euclidean-signature metric for analytical stability. Lorentzian continuation and causal propagation will be addressed in Part II.
• Physical interpretation. Focusing events correspond to informational singularities in the model; connecting them to observable physical processes (e.g., gravitational curvature) requires additional assumptions.
• Experimental validation. DNA-coherence coupling and IRSVT-EEG modulation provide testable predictions but remain speculative at this stage.

Future work will extend the VTT action to include matter-coupling terms, explore octonionic generalizations, and validate focusing dynamics experimentally through informational relaxation timing.

Broader Scientific Implications

a. Information as the Generator of Geometry

The variational construction suggests that continuous geometry is not assumed but enforced by informational stability.

Where coherence gradients exist, curvature necessarily follows:

$$\nabla \cdot \mathsf{\Delta }C=0\Rightarrow g_{\mu \nu }^{\left(C\right)}\mathrm{emerges}\mathrm{continuously}.$$

Thus, spacetime need not be fundamental; it may arise as a stable topology of information organization.

b. Continuity as a Stability Principle

The coherence tensor $\mathsf{\Delta }{C}_{\mu \nu }$forms the unique interpolation that:

• avoids divergence in informational action,
• prevents fragmentation of metric structure.

This reframes continuity not as a primitive axiom but as a thermodynamic necessity of minimizing informational strain.

c. Coherence Gradient as the Effective Hidden Variable

Where classical physics invokes determinism or local realism, VTT substitutes:

Table 1. Conventional Assumption and VTT Interpretation.

Conventional Assumption	VTT Interpretation
Deterministic trajectory:	Coherence-driven focusing
Locality in space	Proximity in information
Fields on spacetime	Spacetime from fields
Particles store information	Particles are coherence extrema

Table 1. Conventional Assumption and VTT Interpretation.

Conventional Assumption	VTT Interpretation
Deterministic trajectory:	Coherence-driven focusing
Locality in space	Proximity in information
Fields on spacetime	Spacetime from fields
Particles store information	Particles are coherence extrema

This defines a coherence topology — a mathematical replacement for hidden-variable proposals that avoids Bell-type constraints.

d. Implications for Physical Systems

We cautiously note that in systems such as genetic information architecture (DNA):

• information gradients define molecular stability,
• boundary constraints resemble informational anchors.

Experimental validation (e.g., IRSVT-DNA coupling) will determine whether informational curvature plays a role in biological organization.

5. Conclusions

This work establishes a mathematical foundation for the Viscous Time Theory (VTT), demonstrating that a discrete informational substrate governed by a coherence field can produce a continuous emergent metric without invoking spacetime a priori. Curvature arises from coherence gradients, and informational geodesics satisfy a Raychaudhuri–type focusing identity with parameters $\lambda$ (coupling) and $\eta$ (viscosity). Numerical simulations confirm focusing behavior and curvature localization consistent with our theoretical predictions.

These results suggest that geometry is not fundamental, but rather an equilibrium organization of information that minimizes informational action. The VTT Lagrangian reduces to known physics in small-gradient regimes, ensuring compatibility with classical geometry.

Although the present work is theoretical, VTT dynamics motivate several near-term empirical tests: (i) coherence-dependent optical phase shifts in interferometry, (ii) curvature-like coherence defects in low-temperature condensed-matter systems, (iii) modulation of gene-expression stability by informational fields, and (iv) gravitational lensing variations linked to coherence topology rather than mass. These predictions provide a path toward falsifiable validation of informational curvature. In essence, VTT reframes spacetime as the stable expression of informational coherence, offering a unified mathematical structure across physical and biological domains.

A.1. Preliminaries

Let $(\mathcal{M},\mathcal{T})$be a compact, simply connected metric-topological space populated by discrete informational events:

$$\mathcal{E}=\left\{\right(p_i,s_i){\}}_{i=1}^N,p_i\in \mathcal{M},s_i\in \mathsf{\Sigma }$$

(A1)

where $\mathsf{\Sigma }$ is a finite informational alphabet.

Let $\mathsf{\Phi }:\mathcal{M}\to \mathbb{R}$denote the informational coherence field, minimizing the action functional:

$$\mathcal{S}\left[\mathsf{\Phi }\right]={\int }_{\mathcal{M}}[{\displaystyle \frac{1}{2}}\parallel \nabla \mathsf{\Phi }{\parallel }^2+\lambda \mathcal{F}(\mathsf{\Phi },\mathcal{E})+\eta \parallel \nabla \mathsf{\Phi }{\parallel }^2]d\mu$$

(A2)

where:

• $\mathcal{F}$ is a localized convex anchor forcing term,
• $\lambda >0$scales anchor influence,
• $\eta \ge 0$is the informational viscosity term.

A.2. Coherence Tensor as Second Variational Form

Define the coherence curvature tensor as the second functional variation:

$$\mathsf{\Delta }{C}_{\mu \nu }\left(x\right)={\displaystyle \frac{{\delta }^2\mathcal{S}}{\delta \left({\partial }_{\mu }\mathsf{\Phi }\right)\delta \left({\partial }_{\nu }\mathsf{\Phi }\right)}}$$

(A3)

Lemma A1 (Symmetry)

Since $\mathcal{S}$ is a scalar functional depending only on first derivatives, the second variation commutes:

$$\mathsf{\Delta }{C}_{\mu \nu }=\mathsf{\Delta }{C}_{\nu \mu }$$

(A4)

Lemma A2 (Positive Semi-Definiteness)

Because $\mathcal{F}$is convex in $\mathsf{\Phi }$and the gradient term is quadratic, the second variation defines a quadratic form:

$$v^{\mu }{v}^{\nu }\mathsf{\Delta }{C}_{\mu \nu }\ge 0\forall v\in T_x\mathcal{M}$$

(A5)

Thus, $\mathsf{\Delta }{C}_{\mu \nu }$ induces a valid inner-product structure on tangent spaces except on a measure-zero set (anchor singularities).

A.3. Emergent Metric Theorem

Theorem A1 (Metric Emergence via Informational Stationarity)

Under Axioms 1–5 of section 2.3, the tensor field:

$$g_{\mu \nu }^{\left(C\right)}=g_{\mu \nu }^0+\alpha \mathsf{\Delta }{C}_{\mu \nu }$$

(A6)

with $g^0$ a non-degenerate reference metric and $\alpha >0$, defines a valid Riemannian metric almost everywhere on $\mathcal{M}$.

Proof

• $\mathsf{\Delta }{C}_{\mu \nu }$ is symmetric by Lemma A.1.
• $\mathsf{\Delta }{C}_{\mu \nu }$ is positive semi-definite by Lemma A.2.
• For sufficiently small $\alpha >0$, the eigenvalues of $g^{\left(C\right)}$ remain strictly positive.
• Therefore, $g^{\left(C\right)}$ is smooth, symmetric, and non-degenerate almost everywhere.

Thus, geometry is not assumed — it is derived as the necessary structure optimizing informational coherence.

A.4. Consequence: Curvature from Information

Since a compatible Levi-Civita connection exists for any Riemannian metric, the curvature tensor:

$$R_{\sigma \mu \nu }^{\left(C\right)\rho }={\partial }_{\mu }{\mathsf{\Gamma }}_{\nu \sigma }^{\rho }-{\partial }_{\nu }{\mathsf{\Gamma }}_{\mu \sigma }^{\rho }+{\mathsf{\Gamma }}_{\mu \lambda }^{\rho }{\mathsf{\Gamma }}_{\nu \sigma }^{\lambda }-{\mathsf{\Gamma }}_{\nu \lambda }^{\rho }{\mathsf{\Gamma }}_{\mu \sigma }^{\lambda }$$

(A7)

is fully induced by the informational field $\mathsf{\Phi }$ via $\mathsf{\Delta }{C}_{\mu \nu }$.

Thus curvature is not a property of space — it is a property of coherence gradients over discrete information.

Appendix B.1. Congruence Setup

Let $u^{\mu }=d{x}^{\mu }/d\tau$ be the tangent field of an informational congruence parameterized by intrinsic “relaxation time” $\tau$, normalized as:

$$g_{\mu \nu }^{\left(C\right)}{u}^{\mu }{u}^{\nu }=1$$

(A8)

Define the deformation tensor:

$$B_{\mu \nu }={\nabla }_{\nu }^{\left(C\right)}{u}_{\mu }$$

(A9)

with expansion $\theta =B_{\mu }^{\mu }$, shear ${\sigma }_{\mu \nu }$, and vorticity ${\omega }_{\mu \nu }$defined as usual.

Appendix B.2. Covariant Evolution of the Congruence

The core identity for any Riemannian congruence is:

$$u^{\alpha }{\nabla }_{\alpha }{B}_{\mu \nu }=-B_{\mu \alpha }{B}_{\nu }^{\alpha }-R_{\alpha \mu \beta \nu }^{\left(C\right)}{u}^{\alpha }{u}^{\beta }+{\nabla }_{\nu }\left(u^{\alpha }{\nabla }_{\alpha }{u}_{\mu }\right)$$

(A10)

Taking the trace leads to the generalized Raychaudhuri equation.

Appendix B.3. VTT Raychaudhuri Equation

After decomposition and inclusion of anchor forcing and viscosity, we obtain:

$${\displaystyle \frac{d\theta }{d\tau }}=-{\displaystyle \frac{1}{n}}{\theta }^2-{\sigma }_{\mu \nu }{\sigma }^{\mu \nu }+{\omega }_{\mu \nu }{\omega }^{\mu \nu }-R_{\mu \nu }^{\left(C\right)}{u}^{\mu }{u}^{\nu }+{\mathcal{S}}_{\eta }+{\mathcal{S}}_{\mathcal{E}}$$

(A11)

where: Viscosity source term

$${\mathcal{S}}_{\eta }=-\eta \left({\nabla }_{\mu }{u}_{\nu }{\nabla }^{\mu }{u}^{\nu }\right)$$

(A12)

This dissipative term delays coherence focusing, analogous to bulk viscosity in fluid congruences.

Anchor source term

$${\mathcal{S}}_{\mathcal{E}}=\sum _i{\gamma }_i\delta (x-p_i)$$

(A13)

describing instantaneous coherence focusing/defocusing due to discrete information injections.

Appendix B.4. Focusing Condition (VTT Criterion)

A coherence singularity (informational focal point) occurs if:

$$\theta \left(0\right)<0\mathrm{and}{R}_{\mu \nu }^{\left(C\right)}{u}^{\mu }{u}^{\nu }-{\mathcal{S}}_{\eta }-{\mathcal{S}}_{\mathcal{E}}\ge 0$$

(A14)

Interpretation:

• $-R_{\mu \nu }^{\left(C\right)}{u}^{\mu }{u}^{\nu }$ = curvature focuses coherence
• ${\mathcal{S}}_{\eta }$ = viscosity delays focusing
• ${\mathcal{S}}_{\mathcal{E}}$ = discrete updates inject or remove coherence

This shows that focusing is a balance between geometric coherence pressure, dissipation, and new information injection — a purely informational origin of singularity formation