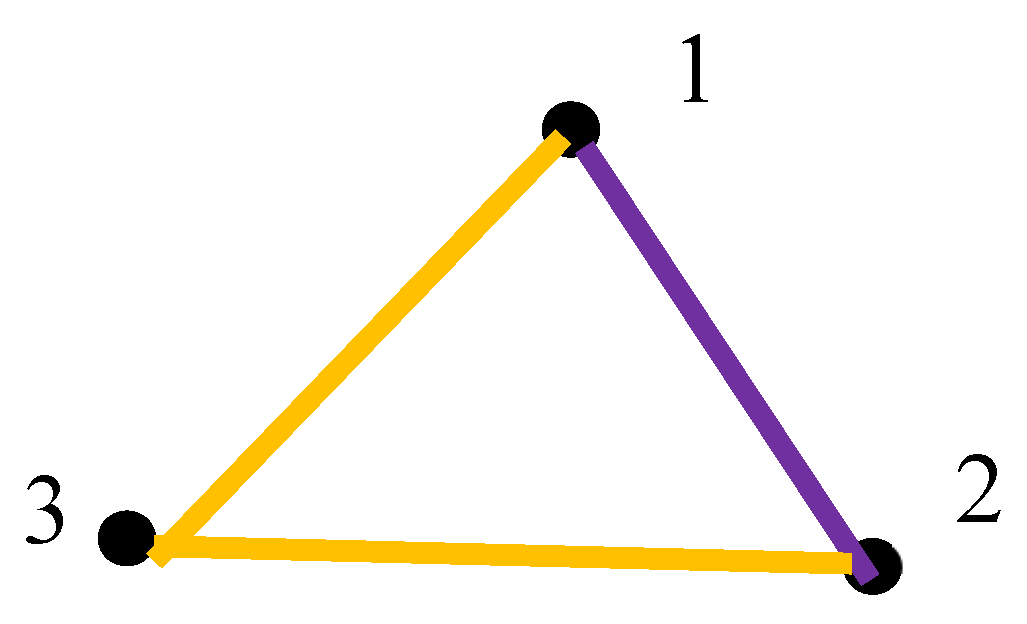Jordan Curves: Ramsey Approach and Topology

1. Introduction

The study of combinatorial constraints in geometric and topological settings is a classical theme connecting discrete mathematics, graph theory, and topology. In particular, Ramsey theory provides a fundamental framework for understanding the inevitability of certain substructures in sufficiently large or richly connected systems [1,2,3,4,5,6,7,8,9,10,11,12]. In parallel, the Jordan curve theorem offers a foundational topological insight: any simple closed curve in the plane partitions the plane into two complementary regions, an interior and an exterior, each of which is connected and uniquely determined by the curve [13,14,15,16,17,18]. Hales emphasized that although the statement is intuitively obvious, the rigorous proof is non-trivial, and the theorem has become a milestone in the pursuit of mathematical rigor [14]. Today the Jordan curve theorem is considered fully proved, both mathematically and formally [14].

This work explores the intersection of these two domains. Specifically, we investigate how the Jordan curve theorem naturally induces a canonical two- or three-coloring of arcs connecting points located on a Jordan curve, or more generally on Jordan surfaces in higher dimensions. By classifying each connecting arc according to whether it lies entirely within the interior, the exterior, or on the boundary of the curve or surface, we obtain a well-defined colored complete graph on the vertex set of points [3,4]. The combinatorial constraints imposed by classical Ramsey numbers then guarantee the existence of monochromatic subgraphs—most notably, triangles in the two-color case and more generally in three-color extensions [34].

We establish that these monochromatic configurations are topologically invariant: they persist under arbitrary homeomorphisms of the ambient space, reflecting intrinsic properties of the embedding rather than geometric specifics [19]. This invariance extends naturally to higher-dimensional analogues via the Jordan–Brouwer separation theorem, where surfaces and hypersurfaces replace planar curves, and connecting arcs may traverse interior, exterior, or boundary regions.

By formalizing this framework, we reveal a general principle: codimension-one separation, combined with Ramsey-type combinatorial reasoning, imposes unavoidable structural constraints on systems of connecting arcs. This provides a foundation for understanding topologically constrained networks, geodesic configurations, and other spatial systems where connectivity and separation interact under robust combinatorial rules.

2. Results

2.1. Ramsey Theorem for Arcs Connecting Points Located on the Jordan Curves

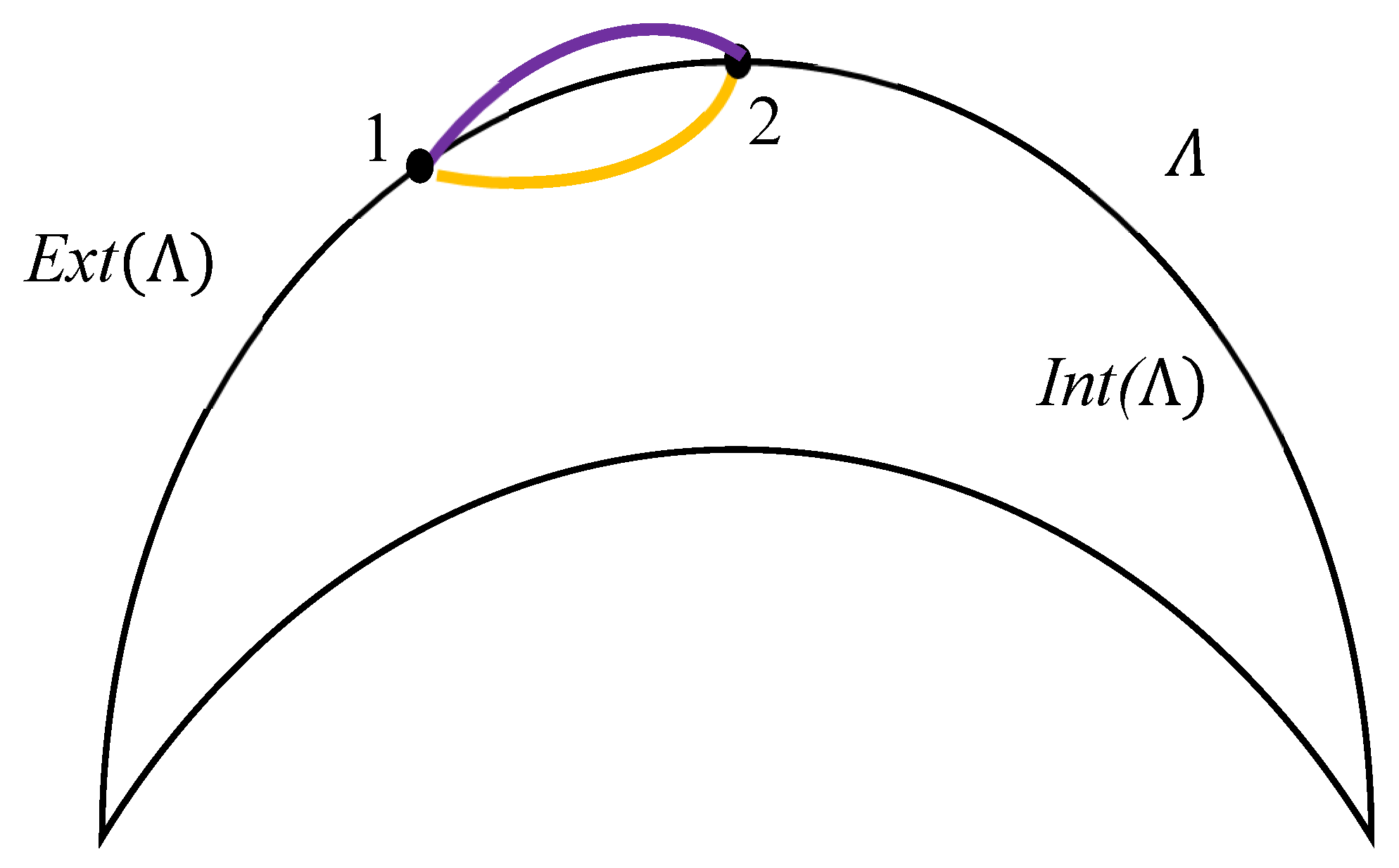
Consider the Jordan curve $\Lambda$ depicted in Figure 1, $\Lambda \subset {\mathbb{R}}^2$, denotes the Euclidean plane — the set of all ordered pairs of real numbers:${\mathbb{R}}^2=\left\{x,y∣x,y\in \mathbb{R}\right\}$, which is the standard 2-dimensional real coordinate space, equipped with the usual Euclidean topology and geometry. Curve $\Lambda$ divides the plane into two regions: the interior (denoted $Int\left(\Lambda \right)$ in Figure 1), bounded by the curve, and an unbounded exterior (denoted $Ext\left(\Lambda \right)$ in Figure 1), containing all of the nearby and far away exterior points. Consequently ${\mathbb{R}}^2=Int\left(\Lambda \right)\cup \Lambda \cup Ext\left(\Lambda \right)$.

We consider two points belonging to Jordan curve $\Lambda$ denoted respectively “1” and “2” (see Figure 1). We propose to connect these points with two kinds of pathways/arcs. The interior arc, denoted${\gamma }_{12}^{\left(int\right)}$, is a continuous path whose endpoints lie on the curve, ${\gamma }_{12}^{\left(int\right)}\left(0\right)=1 \mathrm{a}\mathrm{n}\mathrm{d} {\gamma }_{12}^{\left(int\right)}\left(1\right)=2,$and whose interior lies entirely in the bounded region Int Λ, hence, ${\gamma }_{12}^{\left(int\right)}\subset Int\Lambda \cup \Lambda ,$ is correct (see Figure 1). These pathways are colored with gold (see Figure 1). The exterior arc, denoted${\gamma }_{12}^{\left(ext\right)}$, is a continuous path whose endpoints lie on the curve, ${\gamma }_{12}^{\left(ext\right)}\left(0\right)=1 \mathrm{a}\mathrm{n}\mathrm{d} {\gamma }_{12}^{\left(ext\right)}\left(1\right)=2,$and whose interior lies entirely in the unbounded region Ext Λ, thus, ${\gamma }_{12}^{\left(ext\right)}\subset Ext\Lambda \cup \Lambda ,$ is correct (see Figure 1). These pathways are colored with purple (see Figure 1).

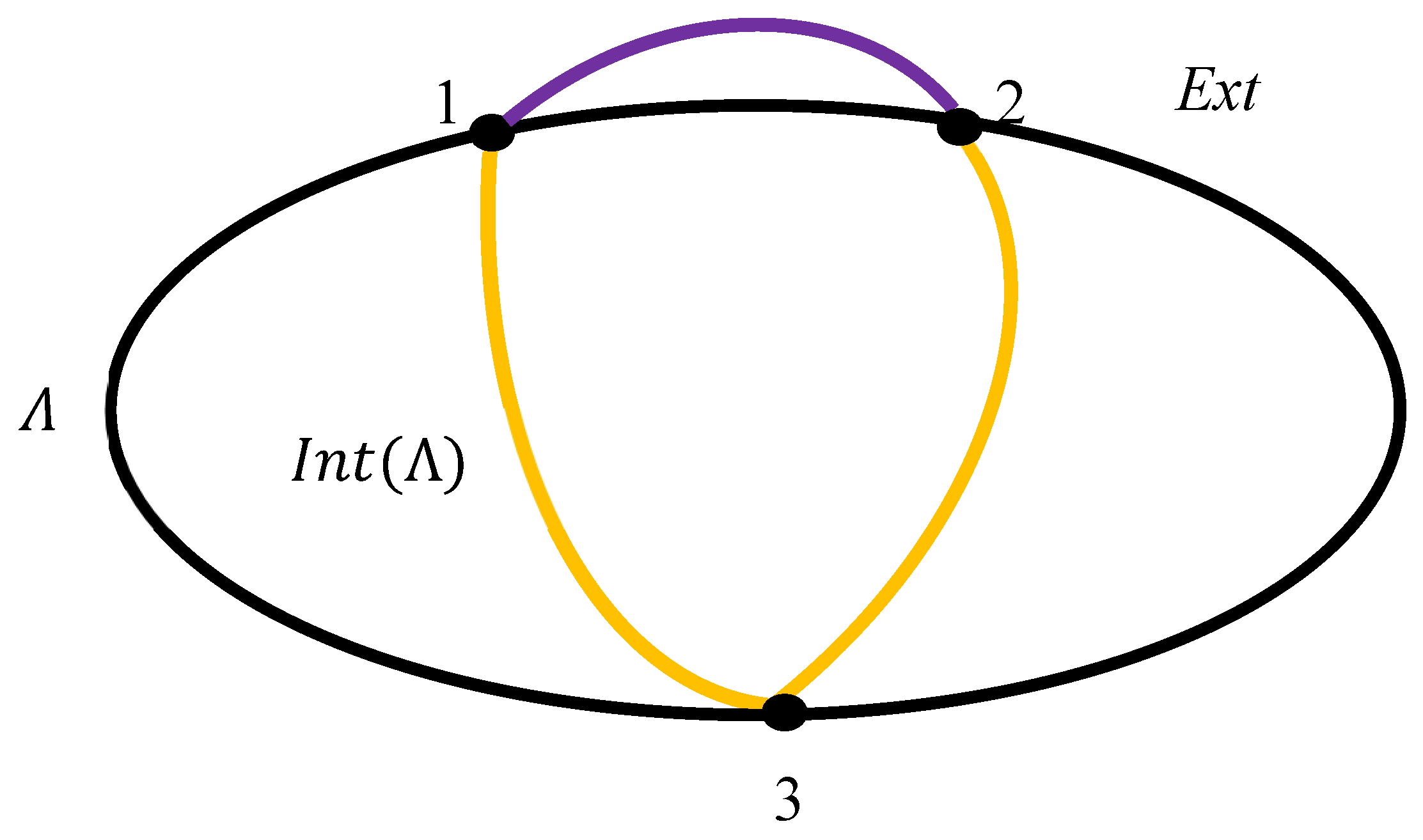
Now consider three points located on the Jordan curve, depicted in Figure 2. Pairs of points are connected with a single arc/edge denoted ${\gamma }_{ik}, i,k=1,\dots ,3.$ The arc is defined as follows: ${\gamma }_{ik}:\left[\mathrm{0,1}\right]\to {\mathbb{R}}^2, {\gamma }_{ik}\left(0\right)=i, {\gamma }_{ik}\left(1\right)=k$. The edges/arcs are bi-colored. The interior arc, denoted${\gamma }_{ik}^{\left(int\right)}$, is a continuous path whose endpoints lie on the curve, ${\gamma }_{ik}^{\left(int\right)}\left(0\right)=i \mathrm{a}\mathrm{n}\mathrm{d} {\gamma }_{ik}^{\left(int\right)}\left(1\right)=k,$and whose interior lies entirely in the bounded region Int Λ, hence ${\gamma }_{ik}^{\left(int\right)}\subset Int\Lambda \cup \Lambda ,$ is correct (see Figure 2). These pathways are colored with gold (see Figure 2). The exterior arc, denoted${\gamma }_{ik}^{\left(ext\right)}$, is a continuous path whose endpoints lie on the curve, ${\gamma }_{ik}^{\left(ext\right)}\left(0\right)=i \mathrm{a}\mathrm{n}\mathrm{d} {\gamma }_{ik}^{\left(ext\right)}\left(1\right)=k,$and whose interior lies entirely in the unbounded region Ext Λ, thus, ${\gamma }_{ik}^{\left(ext\right)}\subset Ext\Lambda \cup \Lambda ,$ is correct (see Figure 2). These pathways/arcs are colored with purple (see Figure 2).

The introduced coloring gives rise to the complete, bi-colored graph, shown in Figure 3.

Now consider six points located on the Jordan curve $\Lambda$. We connect the points with two kind of links/arcs. Pairs of points are connected with a single arc/edge denoted ${\gamma }_{ik}, i,k=1,\dots ,6.$ The arc connecting the points is colored with gold when its interior belongs to the interior of the curve $Int\left(\mathsf{\Lambda }\right)$; the arc connecting the points is colored with purple when its interior belongs to the exterior of the curve $Ext\left(\mathsf{\Lambda }\right)$. It should be emphasized that the relations “to be connected with the gold link” and “to be connected with the purple link are not transitive [11].

By the classical Ramsey theorem, since $R\left(\mathrm{3,3}\right)=6$, every 2-coloring of the edges of the complete graph on six vertices contains a monochromatic triangle. Therefore, in our configuration there exists at least one “triangle” whose three constituent arcs have the same color. In the sequel we provide a formal mathematical proof of this theorem in the topological setting of arcs on the Jordan curve.

Axiom 1: Euclidian plane: ${\mathbb{R}}^2=\left\{x,y∣x,y\in \mathbb{R}\right\}$ is the Euclidean plane equipped with the standard Euclidean topology.

Axiom 2: Jordan curve.

A Jordan curve $\mathsf{\Lambda }\subset {\mathbb{R}}^2$ is a subset homeomorphic to the unit circle $S^1$. By the Jordan curve theorem $\exists !Int\left(\mathsf{\Lambda }\right),Ext\left(\mathsf{\Lambda }\right)\subset {\mathbb{R}}^2,$such that ${\mathbb{R}}^2=Int\left(\mathsf{\Lambda }\right)\bigcup \mathsf{\Lambda }\bigcup Ext\left(\mathsf{\Lambda }\right)$, where $Int\left(\mathsf{\Lambda }\right)$ and Ext$\left(\mathsf{\Lambda }\right)$ are disjoint connected open sets.

Axiom 3: Let $V=\left\{\mathrm{1,2},\mathrm{3,4},\mathrm{5,6}\right\}$ denote six distinct points on $\Lambda .$

Axiom 4: Connecting arcs. For every unordered pair of distinct points $\left\{i,k\right\}\subset V$ there exists at least one simple continuous arc ${\gamma }_{ik}:\left[\mathrm{0,1}\right]\to {\mathbb{R}}^2, {\gamma }_{ik}\left(0\right)=i, {\gamma }_{ik}\left(1\right)=k,\mathrm{s}\mathrm{u}\mathrm{c}\mathrm{h}$that either: $\left(\forall t\in \left(\mathrm{0,1}\right)\right)\left({\gamma }_{ik}\left(t\right)\in Int\left(\mathsf{\Lambda }\right)\cup \mathsf{\Lambda }\right)$ or $\left(\forall t\in \left(\mathrm{0,1}\right)\right)\left({\gamma }_{ik}\left(t\right)\in Ext\left(\mathsf{\Lambda }\right)\cup \mathsf{\Lambda }\right)$. The endpoints of all the arcs lie on $\mathsf{\Lambda }.$We define: ${\gamma }_{ik}\in {\mathsf{\Gamma }}^{\left(int\right)}⟺{\gamma }_{ik}\left(\left(\mathrm{0,1}\right)\right)\subset Int\left(\mathsf{\Lambda }\right)\cup \mathsf{\Lambda }$ and ${\gamma }_{ik}\in {\mathsf{\Gamma }}^{\left(ext\right)}⟺{\gamma }_{ik}\left(\left(\mathrm{0,1}\right)\right)\subset Ext\left(\mathsf{\Lambda }\right)\cup \mathsf{\Lambda }$, where ${\mathsf{\Gamma }}^{\left(int\right)}$ is the set of all arcs whose interiors (excluding endpoints) lie entirely inside the interior region $Int\left(\mathsf{\Lambda }\right)$, and ${\mathsf{\Gamma }}^{\left(ext\right)}$ is the set of all arcs (excluding endpoints) that go outside the Jordan curve, lying entirely in the unbounded exterior region Ext$\left(\mathsf{\Lambda }\right).$

Definition 1:

Coloring function. Define a coloring function $C:{\left|V\right|}^2\to \left\{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d},\mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e}\right\}$ by:

$$C\left(i,k\right)=\left\{\begin{array}{c}\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d}, if {\gamma }_{ik}\in {\mathsf{\Gamma }}^{\left(int\right)}\\ \mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e}, if {\gamma }_{ik}\in {\mathsf{\Gamma }}^{\left(ext\right)}\end{array}\right\}, \mathrm{or} C:\left(\begin{array}{c}V\\ 2\end{array}\right)\to \left\{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d},\mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e}\right\}.$$

Theorem 1.

Ramsey property on the Jordan curve. Let $\Lambda \in {\mathbb{R}}^2$ be a Jordan curve. And let $V=\left\{1,\dots ,6\right\}$ be six distinct points on $\Lambda$ . For every coloring $C:\left(\begin{array}{c}V\\ 2\end{array}\right)\to \left\{gold, purple\right\}$ it is true:

$$\forall C:{\left|V\right|}^2\to \left\{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d},\mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e}\right\}, \exists A\subset V\left(\left|A\right|=3\right)\forall \left\{i,k\right\}\subset A, C\left(i,k\right)=c, \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{s}\mathrm{o}\mathrm{m}\mathrm{e} c\in \left\{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d},\mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e}\right\}$$

(1)

That is: every two-coloring of the six connecting arcs among six points on Λ yields a monochromatic triangle.

2.2. Topological Invariance of the Introduced Coloring Scheme

Now consider topological properties of the introduced coloring scheme. Under any homeomorphism h: ${\mathbb{R}}^2\to {\mathbb{R}}^2$, $h\left(\mathsf{\Lambda }\right)$ is a Jordan curve, and $C^{\prime }\left(\left\{i,k\right\}\right)=C\left(\left\{h\left(i\right),h\left(k\right)\right\}\right)$ defines the same coloring structure because:

$$h\left(Int\left(\mathsf{\Lambda }\right)\right)=Int\left(h\left(\mathsf{\Lambda }\right)\right);h\left(Ext\left(\mathsf{\Lambda }\right)\right)=Ext\left(h\left(\mathsf{\Lambda }\right)\right).$$

(2)

Hence, the existence of a monochromatic triangle is a topological invariant under plane homeomorphisms. Let us supply a formal proof to this.

Formal proof.

Consider $\mathsf{\Lambda }\subset {\mathbb{R}}^2$, which is a Jordan curve, with the interior Int(Λ) and exterior $Ext\left(\mathsf{\Lambda }\right)$. $V=\left\{\mathrm{1,2},\mathrm{3,4},\mathrm{5,6}\right\}\subset \mathsf{\Lambda }$ are six distinct points. For each unordered pair $\left\{i,k\right\}\subset V$ there is a simple arc ${\gamma }_{ik}$ joining i and k and either ${\gamma }_{ik}\left(\left(\mathrm{0,1}\right)\right)\subset Int\left(\mathsf{\Lambda }\right)\cup \mathsf{\Lambda }$or ${\gamma }_{ik}\left(\left(\mathrm{0,1}\right)\right)\subset Ext\left(\mathsf{\Lambda }\right)\cup \mathsf{\Lambda }.$ Arcs ${\gamma }_{ik}$are colored. The coloring function is defined by Definition 1.

Let $h:{\mathbb{R}}^2\to {\mathbb{R}}^2$ be a homeomorphism and define ${\Lambda }^{\prime }≔h\left(\Lambda \right)$ and $V^{\prime }≔h\left(V\right)=\left\{h\left(1\right),\dots ,h\left(6\right)\right\}\subset {\mathsf{\Lambda }}^{\prime }$. Define the induced coloring $V^{\prime }$ on $C^{\prime }$ by the same rule (see Definition 1) applied to arcs between points of$V^{\prime }$ (or equivalently by $C^{\prime }\left(h\left(i\right),h\left(k\right)\right)≔C\left(i,k\right).$ We prove:

$$\left(\exists \mathrm{m}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{c}\mathrm{h}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c} \mathrm{t}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e} \mathrm{i}\mathrm{n}\left(V,C\right)\right)⟺\left(\exists \mathrm{m}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{c}\mathrm{h}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c} \mathrm{t}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e} \mathrm{i}\mathrm{n}\left(V^{\prime },C^{\prime }\right)\right)$$

(3)

Because h is a homeomorphism, it is a bijection with continuous inverse; thus it maps open sets to open sets and connected sets to connected sets. By the Jordan curve theorem Int(Λ) and $Ext\left(\mathsf{\Lambda }\right)$ are the two complementary connected open components of ${\mathbb{R}}^2\setminus \mathsf{\Lambda }$. Hence, $h\left(Int\left(\mathsf{\Lambda }\right)\right)$ and$h\left(Ext\left(\mathsf{\Lambda }\right)\right)$ are complementary connected open components of ${\mathbb{R}}^2\setminus h\left(\mathsf{\Lambda }\right)={\mathbb{R}}^2\setminus {\mathsf{\Lambda }}^{\prime }$. Uniqueness of the two complementary components implies:

$$h\left(Int\left(\mathsf{\Lambda }\right)\right)=Int\left({\mathsf{\Lambda }}^{\prime }\right),h\left(Ext\left(\mathsf{\Lambda }\right)\right)=Ext\left({\mathsf{\Lambda }}^{\prime }\right).$$

(4)

We prove that arcs and colors are preserved by h. Let ${\gamma }_{ik}:\left[\mathrm{0,1}\right]\to {\mathbb{R}}^2$ be a simple arc with${\gamma }_{ik}\left(0\right)=i,{\gamma }_{ik}\left(1\right)=k$. Consider the image arc ${\gamma }_{h\left(i\right)h\left(k\right)}^{\prime }=h\circ {\gamma }_{ik}:\left[\mathrm{0,1}\right]\to {\mathbb{R}}^2$. This is a simple continuous arc joining h(i) and h(k). If ${\gamma }_{ik}\left(\mathrm{0,1}\right)\subset Int\left(\mathsf{\Lambda }\right),$ then by Equation (2):

$${\gamma }_{h\left(i\right)h\left(k\right)}^{\prime }\left(\left(\mathrm{0,1}\right)\right)=h\left({\gamma }_{ik}\left(\mathrm{0,1}\right)\right)\subset h\left(Int\left(\mathsf{\Lambda }\right)\right)=Int\left({\mathsf{\Lambda }}^{\prime }\right),$$

(5)

so, ${\gamma }_{h\left(i\right)h\left(k\right)}^{\prime }\in {\mathsf{\Gamma }}^{\left(int\right)}$ for ${\mathsf{\Lambda }}^{\prime }$. Likewise if ${\gamma }_{ik}\left(\mathrm{0,1}\right)\subset Ext\left(\mathsf{\Lambda }\right)$ then by Equation (2) ${\gamma }_{h\left(i\right)h\left(k\right)}^{\prime }\in {\mathsf{\Gamma }}^{\left(ext\right)}.$ Therefore the color of the edge $\left\{i,k\right\}$ equals the color of the edge $\left\{h\left(i\right),h\left(k\right)\right\}$; formally we obtain:

$$C\left(i,k\right)=C^{\prime }\left(h\left(i\right),h\left(k\right)\right)\mathrm{for} \mathrm{every} \left\{i,k\right\}\subset V.$$

(6)

Now consider the image of a monochromatic triangle. Suppose $A\subset V$ with $\left|A\right|=3$ is a monochromatic triangle in (V,C), i.e., there exists coloring $c\in \left\{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d},\mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e}\right\}$, such as that $\forall \left\{i,k\right\}\subset A,$ $C\left(i,k\right)=c.$ Let $A^{\prime }:=h\left(A\right)\subset V^{\prime }.$ From Equation (6) we have for every $\left\{i,k\right\}\subset A$:

$$C^{\prime }\left(h\left(i\right),h\left(k\right)\right)=C\left(i,k\right)=c.$$

(7)

Thus, A′ is a 3-element subset of V′, whose three edges are all colored c, i.e., a monochromatic triangle in $\left(V^{\prime },C^{\prime }\right)$. Conversely, since $h^{-1}$ is also a homeomorphism, the same argument with $h^{-1}$ shows that any monochromatic triangle in (V′,C′) pulls back to a monochromatic triangle in (V,C). Hence the existence of a monochromatic triangle is equivalent for (V,C) and (V′,C′).

We conclude that because a homeomorphism h: ${\mathbb{R}}^2\to {\mathbb{R}}^2$ maps interiors to interiors and exteriors to exteriors, it preserves the classification of each connecting arc as interior-type or exterior-type. Therefore, the coloring induced by interior/exterior is preserved under h, and consequently the statement “there exists a monochromatic triangle among the six points on Λ” is invariant under any such h. Thus, Theorem 2, is proven:

Theorem 2:

The existence of a monochromatic triangle in the bi-colored complete graph induced by the interior/exterior coloring of arcs on a Jordan curve Λ is invariant under every plane homeomorphism $h:{\mathbb{R}}^2\to {\mathbb{R}}^2$.

2.3. Jordan Curves, Ramsey Coloring and Geodesic Lines

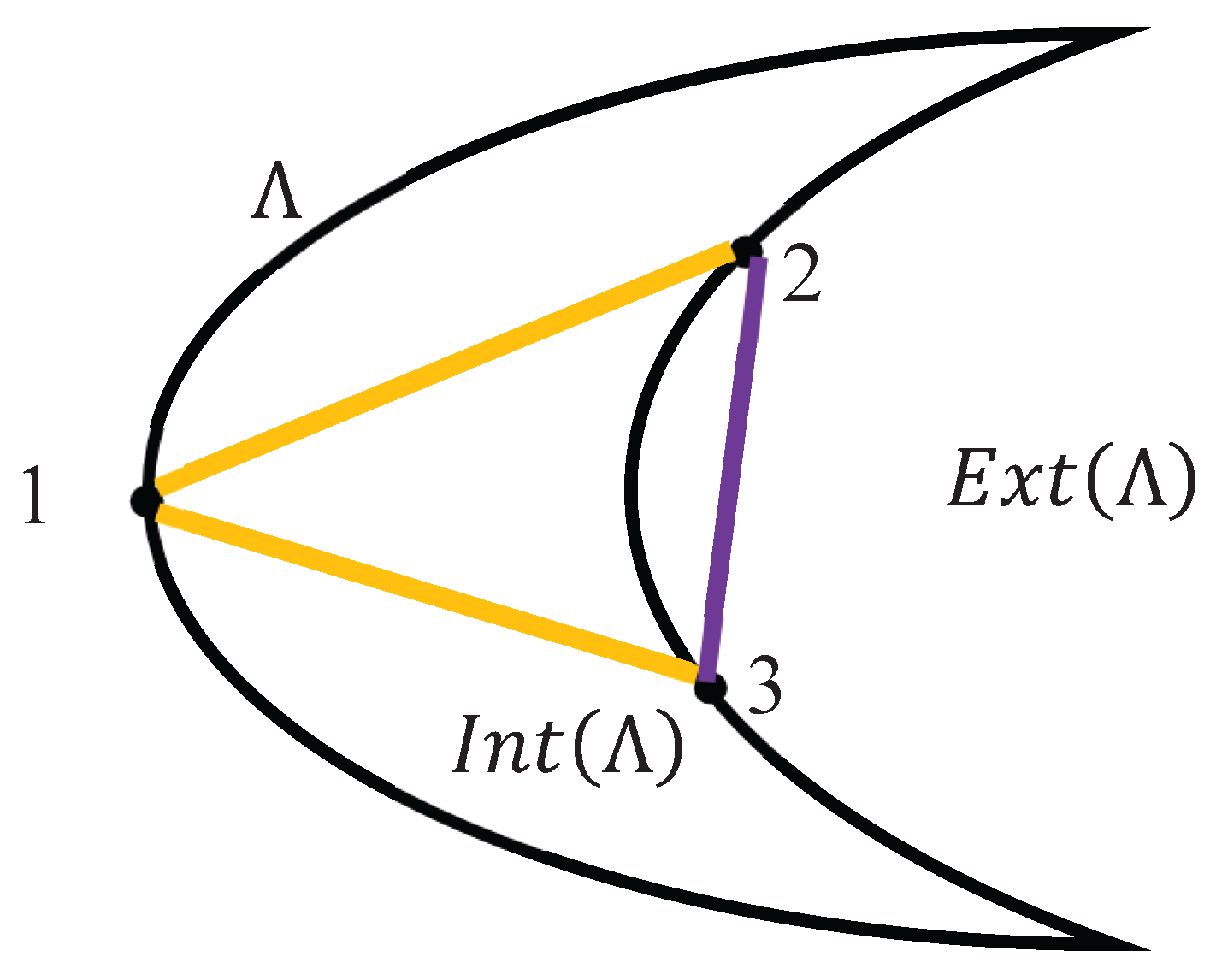
We now demonstrate a corollary that follows directly from the introduced approach. Consider three points $\left\{\mathrm{1,2},3\right\}$ located on the Jordan curve $\Lambda$, as illustrated in Figure 3. The points are connected with the geodesic arcs denoted ${\gamma }_{ik}^{\left(g\right)},i,k=1,\dots ,3\left[20\right].$If our Jordan curve $\Lambda$ is embedded into the Euclidian plane, the geodesic arcs${\gamma }_{ik}^{\left(g\right)}$ are simply straight line segments, as shown in Figure 3.

We impose the following restriction: geodesic arcs (with endpoints excluded) completely belong to the interior of the curve $Int(\mathsf{\Lambda }$), or alternatively to the exterior of the curve$Ext\left(\mathsf{\Lambda }\right)$. Obviously, this restriction may be frustrated. However, if this restriction is kept true, following corollary immediately stems from Theorem 1 and Theorem 2.

Corollary 1.

Let Λ be a Jordan curve, and let six distinct points $\left\{1,\dots ,6\right\}$ be located on $\Lambda$. Connect each pair of points i, k with a geodesic arc ${\gamma }_{ik}, i,k=1,\dots ,6.$ Assume that the interior of each geodesic arc ${\gamma }_{ik}$ lies entirely either in the interior region Int(Λ) or in the exterior region Ext(Λ). Color ${\gamma }_{ik}$ gold if it belongs to $Int\left(\mathsf{\Lambda }\right)$ and purple if it belongs to Ext(Λ). Then every such two-coloring of the complete set of geodesic arcs among the six points on Λ contains a monochromatic triangle.

The corollary implies a universal combinatorial restriction on any geodesic network formed by six points on a Jordan curve, provided each geodesic lies entirely in either the interior or exterior of the curve (the imposed restriction is kept, namely each geodesic arc ${\gamma }_{ik}$ lies entirely either in the interior region Int(Λ) or in the exterior region Ext(Λ)). Regardless of the specific geometry of the embedding (Euclidean, spherical, or Riemannian), the geodesic connection pattern cannot be arbitrary: a monochromatic triangle must necessarily appear. This establishes a Ramsey-type inevitability in geodesic configurations - a purely topological constraint independent of curvature or metric form. It means: any sufficiently connected system of geodesics on or around a closed boundary possesses a minimal region of local geometric coherence (the monochromatic triangle).

Now address the topological aspect of the corollary. Because the coloring (interior/exterior) is invariant under plane homeomorphisms, the corollary suggests that triples of mutually interior (or mutually exterior) geodesics represent topologically stable structures. Such monochromatic geodesic triangles can be viewed as minimal invariant configurations under continuous deformations of the curve. In geodesic theory, this corresponds to stable clusters of shortest paths or mutually non-intersecting minimal connections that persist under deformation.

From a metric geometry perspective, the corollary constrains how geodesic triangulations of regions bounded by Jordan curves can be formed. It guarantees the existence of a coherent triangular cell entirely contained either in the interior or exterior region, for arbitrary six points located on the Jordan curve.

2.4. Three-Colored Approach to the Points Located on the Jordan Curve

Consider the Jordan curve $\Lambda$ depicted in Figure 1 and the pair of points located on $\Lambda$. Now we propose to connect the points with three kinds of pathways/arcs. The interior of the first kind of pathway colored gold and denoted ${\gamma }_{12}^{\left(int\right)}$belongs to the interior of the Jordan curve $Int\mathsf{\Lambda }$, as shown in Figure 1; ${\gamma }_{12}^{\left(int\right)}\subset Int\left(\mathsf{\Lambda }\right)\cup \mathsf{\Lambda }$. The interior second kind of pathway/arc, which is colored purple belongs to the exterior of the Jordan curve E; ${\gamma }_{12}^{\left(ext\right)}\subset Ext\left(\mathsf{\Lambda }\right)\cup \mathsf{\Lambda }$. And the third kind of the pathway colored black belongs to the Jordan curve itself,${\gamma }_{12}^{\left(\mathsf{\Lambda }\right)}\subset \mathsf{\Lambda }$. The endpoints of the arcs lie on the Jordan curve $\Lambda .$ This coloring gives rise to the triple-colored scheme, equivalent to the complete, triple-colored Ramsey graph, in which the points belonging to $\Lambda$ are the vertices of the graph, and the edges are colored alternatively with black, gold and purple according to the aforementioned coloring procedure. The Ramsey number $R\left(\mathrm{3,3},3\right)=17.$ This result gives rise to the following theorem:

Theorem 3

Let Λ be a Jordan curve in the plane and let $S=\left\{1,\dots ,n\right\}\subset \mathsf{\Lambda }$ be a set of distinct points on $\mathsf{\Lambda }.$ For every unordered pair $\left\{i,j\right\}\subset S$ assume one selects exactly one connecting arc of one of the three types:

i)

an interior arc ${\gamma }_{ij}^{\left(int\right)} \mathrm{s}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{f}\mathrm{y}\mathrm{i}\mathrm{n}\mathrm{g}$ ${\gamma }_{ij}^{\left(int\right)}\subset Int\left(\mathsf{\Lambda }\right)\cup \mathsf{\Lambda }$ (color the edge gold),

ii)

an exterior arc ${\gamma }_{ij}^{\left(ext\right)} \mathrm{s}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{f}\mathrm{y}\mathrm{i}\mathrm{n}\mathrm{g}$ ${\gamma }_{ij}^{\left(ext\right)}\subset Ext\left(\mathsf{\Lambda }\right)\cup \mathsf{\Lambda }$ (color the edge purple),

iii)

a boundary arc ${\gamma }_{ij}^{\left(\mathsf{\Lambda }\right)}$ $\mathrm{s}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{f}\mathrm{y}\mathrm{i}\mathrm{n}\mathrm{g}{\gamma }_{ij}^{\left(\mathsf{\Lambda }\right)}\subset \mathsf{\Lambda }$ (color the edge black).

Thus, every unordered pair $\left\{i,j\right\}$ is assigned exactly one of three colors (gold, purple, black). If $n\ge 17$, then the resulting 3-colored complete graph on the vertex set S contains a monochromatic triangle. In other words: for any choice of 17 points on Λ and any admissible assignment of the three arc-types to each pair, there exist three indices $a,b,c\in S$, for which the three connecting arcs ${\gamma }_{ab},{\gamma }_{bc},{\gamma }_{ca}$ all have the same type (all interior, all exterior, or all on Λ).

The statement is a direct translation of the classical Ramsey theorem for three colors: the Ramsey number $R\left(\mathrm{3,3},3\right)=17,$ so every 3-coloring of the edges of the complete graph $K_{17}$ contains a monochromatic triangle. Our coloring produces a 3-coloring of the complete graph on S (the color of edge $\left\{i,j\right\}$ is determined by which of the three arc-types was chosen). Therefore. for $n\ge 17$ a monochromatic triangle exists. It is noteworthy, that in contrast to gold and purple arcs, black arcs are unique for a given pair of the points on the given Jordan curve $\Lambda .$ The extension to geodesic lines is obvious. Indeed, when geodesic lines${\gamma }_{ik}^{\left(g\right)}$, connecting 17 given points, which lie on the Jordan curve $\Lambda$, and ${\gamma }_{ik}^{\left(g\right)}$ lie in the interior or exterior of $\Lambda$ or on the curve $\Lambda$ itself, the three-colored scheme may be introduced and appearance of monochromatic triangle is inevitable.

2.5. 3D and nD Extension of the Suggested Approach

The introduced three-colored approach enables the 3D extension. Now we work in the Euclidean 3-space:

Axiom 1 - Euclidean space: ${\mathbb{R}}^3\left\{\left(x,y,z\right)∣x,y,z\in \mathbb{R}\right\}$,

Axiom 2 - Jordan surface. A Jordan surface is a topological embedding of the 2-sphere: $\mathsf{\Sigma }\subset {\mathbb{R}}^2,\mathsf{\Sigma }\simeq S^2$. By the Jordan–Brouwer separation theorem: there exist two connected open sets: $Int\left(\mathsf{\Sigma }\right)$ and $Ext\left(\mathsf{\Sigma }\right)\subset {\mathbb{R}}^3$, such that ${\mathbb{R}}^3=Int\left(\mathsf{\Sigma }\right)\bigcup \mathsf{\Sigma }\bigcup Ext\left(\mathsf{\Sigma }\right)$, with $Int\left(\mathsf{\Sigma }\right)$ bounded and $Ext\left(\mathsf{\Sigma }\right)$ unbounded. The two regions disjoint and each having boundary exactly $\mathsf{\Sigma }$. This is the 3D analogue of the Jordan curve theorem.

Axiom 3. Vertex set $V=\left\{1,\dots ,N\right\}$ be N distinct points lying on the Jordan surface $\mathsf{\Sigma }.$

Axiom 4. Connecting arcs. For every unordered pair of distinct points $\left\{i,k\right\}\subset V$ there exists at least one simple continuous arc ${\gamma }_{ik}:\left[\mathrm{0,1}\right]\to {\mathbb{R}}^3,{\gamma }_{ik}\left(0\right)=i,{\gamma }_{ik}\left(1\right)=k$, such that exactly one of the following holds:

${\gamma }_{ik}\left(0.1\right)\subset Int\left(\mathsf{\Sigma }\right)\bigcup \mathsf{\Sigma }$ (the interior path); ${\gamma }_{ik}\left(0.1\right)\subset Ext\left(\mathsf{\Sigma }\right)\cup \mathsf{\Sigma }$ (the exterior path);${\gamma }_{ik}\left(0.1\right)\subset \mathsf{\Sigma }$ (the surface path). We define the three classes of paths ${\mathsf{\Gamma }}^{\left(int\right)}$, ${\mathsf{\Gamma }}^{\left(ext\right)}$, ${\mathsf{\Gamma }}^{\left(surf\right)}$ as the sets of simple arcs whose interiors lie entirely in $Int\left(\mathsf{\Sigma }\right),$ $Ext\left(\mathsf{\Sigma }\right)$, and $\mathsf{\Sigma }$ respectively. Now we define three-coloring:

$$C_{ik}=\left\{\begin{array}{c}gold \mathrm{i}\mathrm{f}{\gamma }_{ik}\in {\mathsf{\Gamma }}^{\left(int\right)}\\ purple \mathrm{i}\mathrm{f}{\gamma }_{ik}\in {\mathsf{\Gamma }}^{\left(ext\right)}\\ black \mathrm{i}\mathrm{f}{\gamma }_{ik}\in {\mathsf{\Gamma }}^{\left(surf\right)}\end{array}\right\}.$$

(8)

Equivalently, C is a map $C:\left(\begin{array}{c}V\\ 2\end{array}\right)\to \left\{gold,purple,black\right\}$.

Thus, following extension of Theorem 3 emerges.

Theorem 4.

Let $\mathsf{\Sigma }\subset {\mathbb{R}}^3$ be a Jordan surface and let $V\subset \mathsf{\Sigma }$ be a set of 17 distinct points. For every choice of simple connecting arcs as in Axiom 4 and the induced 3-coloring defined by Equation (8), $C:\left(\begin{array}{c}V\\ 2\end{array}\right)\to \left\{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d},\mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e},\mathrm{b}\mathrm{l}\mathrm{a}\mathrm{c}\mathrm{k}\right\}$, there exists a monochromatic triangle:

$$\forall C:\left(\begin{array}{c}V\\ 2\end{array}\right)\to \left\{gold,purple,black\right\},\exists A\subset V,A=3,\mathrm{a}\mathrm{l}\mathrm{l} \mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}\mathrm{s} \mathrm{o}\mathrm{f}A\mathrm{h}\mathrm{a}\mathrm{v}\mathrm{e} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{a}\mathrm{m}\mathrm{e} \mathrm{c}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{r}.$$

Because the coloring is purely combinatorial, the result reduces to the classical Ramsey theory for three colors. Theorem generalizes to every dimension $n\ge 3$ with the same simple reduction to classical Ramsey theory, provided we keep the same hypotheses (points lie on a hypersurface homeomorphic to a sphere and every pair of points is assigned one allowed connecting arc whose interior lies entirely in exactly one of the regions provided by Jordan–Brouwer Theorem). The topology only determines the allowed types of edge; the combinatorial Ramsey conclusion then follows immediately. In contrast to the case of $\mathsf{\Lambda }\subset {\mathbb{R}}^2$, now for $\mathsf{\Sigma }\subset {\mathbb{R}}^3$ black arcs are not unique for a given pair of the points.

The extension for bi-colored scheme applied to the n-dimension space is trivial and it is formulated as follows:

Let $\mathsf{\Sigma }\subset {\mathbb{R}}^n$ be a Jordan surface and let $V\subset \mathsf{\Sigma }$ be a set of six distinct points. The points are connected with the arcs, which interiors belong to the exterior, or, alternatively, interior of the surface. Coloring function is defined in Section 2.1. For every coloring$C:\left(\begin{array}{c}V\\ 2\end{array}\right)\to \left\{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d},\mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e}\right\}$ it is true: $\forall C:{\left|V\right|}^2\to \left\{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d},\mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e}\right\},\exists A\subset V\left(\left|A\right|=3\right)\forall \left\{i,k\right\}\subset A,C\left(i,k\right)=c, \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{s}\mathrm{o}\mathrm{m}\mathrm{e} c \in \left\{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d},\mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e}\right\}$.

2.6. Ramsey Approach to the Infinite Set of Points on the Jordan Curve

Let $\mathsf{\Lambda }\subset {\mathbb{R}}^2$ be a Jordan curve, and let $X\subset \mathsf{\Lambda }$ be an infinite set of points. For any unordered pair $\left\{A,B\right\}\subset X$ assign a color according to the following rule: the edge AB is colored gold if the interior of the arc connecting A and B lies entirely in the interior region $Int\left(\mathsf{\Lambda }\right)$; the edge AB is colored purple if the interior of the arc connecting A and B lies entirely in the exterior region $Ext\left(\mathsf{\Lambda }\right)$. The assignment of each pair to exactly one of the two colors is given by Axioms 1–4 of Section 2.1, which guarantee the well-definedness of the interior/exterior arc classification. Then, according to the infinite Ramsey theorem the complete graph $K_X$ on the vertex set X, with edges colored gold and purple, contains an infinite monochromatic clique. That is, there exists an infinite subset $Y\subset X$ such that all edges between points of Y have the same color (either all gold or all purple).

Formal Proof.

By Axioms 1–4 of Section 2.1, the construction described above yields a 2-coloring: $\chi :\left(\begin{array}{c}X\\ 2\end{array}\right)\to \left\{\mathrm{g}\mathrm{o}\mathrm{l}\mathrm{d},\mathrm{p}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{e}\right\}$ of the complete graph on the infinite vertex set X. The Infinite Ramsey Theorem states that for every infinite set X and every 2-coloring of its 2-element subsets, there exists an infinite subset Y⊂X such that all pairs $\left\{A,B\right\}\subset Y$ have the same color. Applying the Infinite Ramsey Theorem to the coloring $\chi$, we obtain an infinite subset $Y\subset X$ such that every pair of points in Y is colored identically—either all gold or all purple. Thus $K_Y$ is an infinite monochromatic clique embedded in the edge-colored graph determined by Λ.

Again, homeomorphisms preserve interior and exterior regions and they also preserve interior/exterior classification of arcs. Thus, the infinite monochromatic clique is carried to another infinite monochromatic clique. We conclude that $K_Y$ is a topological invariant.

4. Discussion

The results presented in this work demonstrate that the classical Ramsey theorem, when combined with the topological structure imposed by the Jordan curve theorem, yields a family of universal combinatorial constraints on any system of arcs connecting points located on a Jordan curve or its higher-dimensional analogues. The crucial mechanism behind these constraints is that a Jordan curve Λ partitions the plane into two topologically distinguished regions, namely its interior and exterior - which in turn define a natural and robust two-coloring of all connecting arcs.

These results reveal a general principle: the separation properties of codimension-one topological boundaries, i.e., subsets whose dimension is exactly one less than that of the ambient space and which partition the surrounding space into distinct regions. For example, a Jordan curve in the plane (${\mathbb{R}}^2)$, is a 1-dimensional boundary separating the plane into interior and exterior regions, and a Jordan surface in 3-dimensional space (${\mathbb{R}}^3)$ is a 2-dimensional boundary separating space into interior and exterior. Such boundaries provide the topological mechanism by which connecting arcs can be classified as interior, exterior, or boundary-type, enabling the application of Ramsey-theoretic combinatorial constraints in a manner that is invariant under continuous deformations of the ambient space.

Theorem 1 shows that even in the simplest case of six points on Λ, the induced coloring must contain at least one monochromatic triangle. This statement is purely combinatorial, yet its applicability is purely topological: the conclusion depends neither on the geometric shape of Λ nor on the specific form of the connecting arcs, but only on the separation properties provided by the Jordan curve. Theorem 2 strengthens this conclusion by proving that the existence of such monochromatic triangles is invariant under arbitrary plane homeomorphisms, and therefore reflects an intrinsic topological feature of any arc-configuration on Λ.

The framework extends naturally in two directions. First, by allowing a third class of arcs—those lying on Λ itself—one obtains a three-coloring corresponding to three types of connectability (interior, exterior, boundary). Ramsey theory then forces the appearance of monochromatic triangles once the number of points reaches the classical threshold $R\left(\mathrm{3,3.3}\right)=17$. Second, by replacing Jordan curves with Jordan surfaces (or more generally, Jordan–Brouwer hypersurfaces), the interior/exterior/surface classification persists in higher dimensions, enabling analogous results for arc systems in ${\mathbb{R}}^3$ and ${\mathbb{R}}^n$. In all cases, the combinatorial Ramsey constraints survive because the topological separation properties are preserved under continuous deformations.

Finally, the infinite version of Ramsey’s theorem shows that for any infinite point set on Λ the interior/exterior coloring necessarily produces an infinite monochromatic clique. Since homeomorphisms also preserve this structure, such cliques constitute stable, deformation-invariant combinatorial patterns within the arc-graph induced by Λ.

Overall, these results reveal that the interaction between codimension-one topological boundaries and combinatorial colorings gives rise to structurally unavoidable configurations—monochromatic triangles and infinite monochromatic subsets—that persist independently of geometric details. This suggests potential applications to geometric graph theory, topological network analysis, and the study of geodesic or minimal-path configurations constrained by closed boundaries.

5. Conclusions

In this work we established a unified topological-combinatorial framework in which the Jordan curve theorem and classical Ramsey theory interact to produce universal structural constraints on arc-configurations supported on Jordan curves and their higher-dimensional analogues. By assigning colors to arcs according to whether they lie in the interior or exterior of a Jordan curve, we obtain a canonical bi-colored complete graph whose structure is independent of geometric details and determined solely by the topology of the embedding.

These results highlight a general principle: the separation properties of codimension-one topological boundaries, i.e., subsets whose dimension is exactly one less than that of the ambient space and which partition the surrounding space into distinct regions, govern the combinatorial constraints. For example, a Jordan curve in ${\mathbb{R}}^2$ is a 1-dimensional boundary separating the plane into interior and exterior regions, while a Jordan surface in ${\mathbb{R}}^3$ is a 2-dimensional boundary separating space into interior and exterior. The codimension-one property ensures that arcs connecting points can be consistently classified as interior, exterior, or boundary-type, enabling the application of Ramsey-theoretic reasoning in a topologically invariant manner. Arcs may be geodesic lines connecting the points located on the boundaries. Ramsey theorem imposes constraints on the networks built of colored geodesic lines.

The finite Ramsey results show that any configuration of sufficiently many points on a Jordan curve necessarily contains monochromatic cycles - most notably, monochromatic triangles in the two-color setting of Theorem 1, and monochromatic triangles in the three-color extension governed by the classical number $R\left(\mathrm{3,3.3}\right)=17$. The infinite version of Ramsey’s theorem guarantees the presence of infinite monochromatic cliques in any infinite point set on Λ. Crucially, we proved that these monochromatic configurations are invariant under all homeomorphisms of the plane: the interior/exterior arc-classification itself is a topological invariant, and thus the resulting Ramsey-forced structures inherit this invariance.

The framework extends naturally beyond the plane. By invoking the Jordan–Brouwer separation theorem, we showed that analogous colorings and Ramsey phenomena arise for arcs lying inside, outside, or on Jordan surfaces and hypersurfaces in higher dimensions. This demonstrates that the interplay between codimension-one separation topology and Ramsey theory is not restricted to curves but reflects a deeper combinatorial rigidity inherent to such embeddings.

Taken together, these results reveal a robust principle: whenever a codimension-one boundary partitions space into distinct regions, the induced colorings of connecting arcs inevitably contain universal Ramsey-type substructures that remain stable under continuous deformations. This principle opens promising avenues for applications in geometric graph theory, boundary-constrained networks, topological data analysis, and physical systems where minimal or constrained paths interact with separating surfaces.