1. Introduction
1.1. Magma and Ore
Ore deposits of economic interest traditionally relate to magmatic activity depending on the tectonic settings (e.g. Robb, 2021). Initially, metals are present in the continental crust in proportions ranging from ppb to ppm. They are transported and concentrated into magmas during crustal melting due to thermal anomalies. This initial episode is a phase change, and thus pertains to energy exchanges between its three components, temperature (T) and entropy (S); stress (s) and strain (e); and chemical potential (m) and amount (N). All materials are considered as viscous to be short.
The conditions of metal transportation during melt emplacement and late individualisation are still partly in debate. Ultimately, metals can enter crystalline phases into minerals or segregate to form specific ore minerals. The common ore grade may reach the percent level in some deposits of economic interest. The formation of magmatic ore, such as porphyry deposits (PD) is equivalent to solving the enrichment of a specific elements by a factor of 4 to 6 orders of magnitude. Three major hypotheses have been explored (Sillitoe, 2010) that include source enrichment, chemical evolution of the magma and late hydrothermal activity.
The first case relies on the observation of linear belts of such porphyries, suggesting an anomalous content in metals, either in the crust (Lehmann, 1987) or the mantle (Ardnt et al., 2005; Richards, 2022). Nevertheless, enrichment rarely exceeds a maximum of one order of magnitude, far from the expected values.
The second model involves magmatic evolution, through differentiation with magma specialisation towards one metal, eventually with magma re-intrusion in a former body. It has been the preferred model for a long time (Breiter et al., 1991; Štemprok et al., 1994), linked with selective diffusion of elements.
The last model implies an ultimate hydrothermal activity, illustrated by fluid inclusions in the rocks, and alteration in the surroundings. It manifests by the exsolution of an immiscible fluid phase at the magmatic stage (MIP), followed by the brecciation of the surrounding rocks, veins formation and hydrated minerals deposition (Landtwing et al., 2002; Williams Jones & Heinrich, 2005).
1.1.1. Ore Formation in PD and MA
As a good example, in the continental crust, base (e.g. Cu, W, Mo) and rare metals (Au, Ag) link with intermediate felsic magmas. They develop in linear belts of porphyry deposits (PD), the heat source of which is provided by an underlying oceanic plate subduction (Sillitoe, 2010). It represents an infinite heat source at the scale of a magma chamber. Within plates, efficient heat sources may result from deeper origin, giving place to mafic intrusions (MA) and sulfide metal assemblages (Ni, Cu), including platinum group elements (PGE) (Barnes et al., 2018). Other tectonic settings need to benefit from a perennial heat source to drive the magmatic activity. Such magmatic bodies have been grouped into trans-porphyry deposits (TPD), since they develop in oblique plate convergence, yielding trans-pression/tension (Vigneresse et al., 2025) with specific thermal conditions. They have consequences on the physical parameters of the magma (temperature, viscosity, fluid content) and metal attractivity (chemical potential, diffusivity), whereas the ambient stress pattern may control partial melt extraction and interactions with the mobile fluid phases.
Briefly, ore formation in PD or MA can briefly be summarized into melting, followed by segregation, transport, and concentration of metals under one of the three phases (solid, melt, fluids). The physical conditions of segregation and transport are addressed through viscosity, diffusivity, permeability and the fluid amount (Vigneresse et al., 2019). Whereas, metal attractivity for each phase pertains to chemistry.
1.1.2. The Specific Case of TPD
TPD also develop in linear belts, due the intense shearing between older and stiffer cratons. The differential motion between the cratons and the sheared crust represents a moderate heat source, that may induce melting, and magma chamber construction. It may vary with time according the plates convergence, introducing rheological decoupling within the crust and vertical motion (de Saint Blanquat et al., 1998). Heterogeneities within the sheared crust also modify the near-field stress pattern, yielding to the formation of magmas, either derived from the crust, or from the adjacent lower portion of cratons. Such melts liberate metals, that are later incorporated to one of the three phases in presence (solid, melt or fluids), except that they all originate from the continental crust, and not from the mantle as for PD. Their segregation and transport develop as in PD, with the restriction that the temperature remains moderate, below the 731 °C, maintaining the fluids in a subcritical state (Thomas & Davidson, 2016). Accordingly, the temperature does not enhance metal diffusion, nor it promotes fluidity to the melt.
As a result, the process of ore formation shifts from a chemical multiphase flow problem (T, m) in PD towards a mechanical problem (T, m, s) in TPD.
Nevertheless, the problem gains in complexity since magma develops under a subcritical state (Vigneresse et al., 2025). The MIP splits into two incompatible phases (
Figure 1), one silicate-rich and the second aqueous-rich (Veksler et al., 2002). In consequences, the bulk magma chamber incorporates three sub-chambers, that independently evolve. Ore formation results in common ore minerals, but rather in pegmatites and greisen, coarse grained equivalent to granite, but located in individualized pockets, as well as gemstones form from the MIP components.
1.1.3. Previous Models
Basically, two types of models have been designed to simulate ore deposits formation, illustrating the Eulerian and Lagrangian approaches (Vigneresse & Truche, 2020). In the first case, an analytical approach describes the bulk system from an external frame, whereas a description from a discrete element attached to the system characterizes the second method.
The Eulerian description requires fixing parameters of the system, such as magma composition, temperature, melt viscosity, and near-field stress conditions. Chemistry rules partitioning of elements between the different phases, quantifying enrichment. It is the most debated, and most uncompleted data base (Vigneresse et al., 2019). The later values fix the enrichment factors for metals. However, the description remains unprecise in face of the randomly distributed different phases, making interaction between them, and instabilities unexplored.
In contrast, techniques using Lagrangian descriptions, such as lattice Boltzmann models (LBM) examine the interactions between neighbouring particles (gas, metal, melt). They provide estimates of shape evolution and metal enrichment, bracketed according to the ratio of partitioning between metals and MIP (Huber et al., 2012).
Both types of models provide solutions, unique in the direct problem, and not to far from truth in the second, but strongly dependent of the input conditions, that remain quite uncertain. See for instance the discussion about the amount and content in additional elements (F, Li, Be) into the MIP, for which there is no direct constraint, since t MIP evaporates at the end of ore generation (Vigneresse et al., 2025).
1.2. Energy Considerations
In consequence of the above presented problems, a different approach, from thermodynamics and energy considerations is suggested, that involves interactions and instabilities.
The origin of metals extraction, segregation and transport before forming ore deposits is undoubtedly linked to magma production in the continental crust. Restricting their formation to continents does not modify the premices. But, addressing ore genesis from the aspect of a phase change supposes considering energy budget, and thus examining the different components of free energy, provided the system remains closed, avoiding the effects of dissipating components.
1.2.1. Energy and Melting
Magma melting is not simply an effect of temperature increase. Such effect is primordial to produce mobile melt, but it has also consequences on the physico-chemical properties of the melt components. Temperature modifications, generally enhance melt displacement. It has also influence in exsolving a composite fluid phase, which in turns, has effect on its chemical attractivity for ionic metals. At last, elements must adapt their structure, crystal lattice, or molecule formation, thus varying their entropy.
1.2.2. Energy Exchanges
A phase transition describes the energetic variations of a material involved in a reaction, for example, a transformation from solid to liquid (Ansermet & Brechet, 2019). Many textbooks on thermodynamics exist, mostly with application to solid, liquid, and gas (e.g. Gasparik, 2014). The reactions use pressure, temperature, and the amount of chemical element (T, P, N
i) in function of time (reaction advance), (
Figure 2a) with intensive variables such as entropy, volume, and chemical potential (S, V, m
i)
The 2019. A simple PT diagram is no more explicit enough, and the system must be considered within a higher variance diagram (
Figure 2b). In igneous rocks, the solid and the liquid phases are both viscous. In a first approach, a compressible gas phase of a restricted amount can be considered as soluble in the melt. Therefore, in melt and solids, the energy changes can be expressed in terms of strain (e) whereas stress (s) is the applied pressure instead of V and P. The entropy (S) of the system represents its order, increasing from the crystalline network, polymers, and melt. It should evolve to a maximum value (Hobbs & Ord, 2010). An average chemical potential (m) and amount N of chemical elements, taken as a mean value from their composition, may be used as a proxy for the melt and the solid rocks (Vigneresse & Truche, 2018). Consequently, the phase transition should be described with a higher variance approach, including at least T, s and N, thus examining the variations in bulk energy along each coordinate and their complex interactions (
Figure 2). For instance, enhanced melting or recrystallization (entropy changes) should affect, or be affected by, the melt flow in its components.
The bulk Gibbs free energy variation resulting from a reaction can be expressed by the difference between the sum of Gibbs free energy of reactants and the products of the reaction.
1.2.3. The Case of Complex Systems
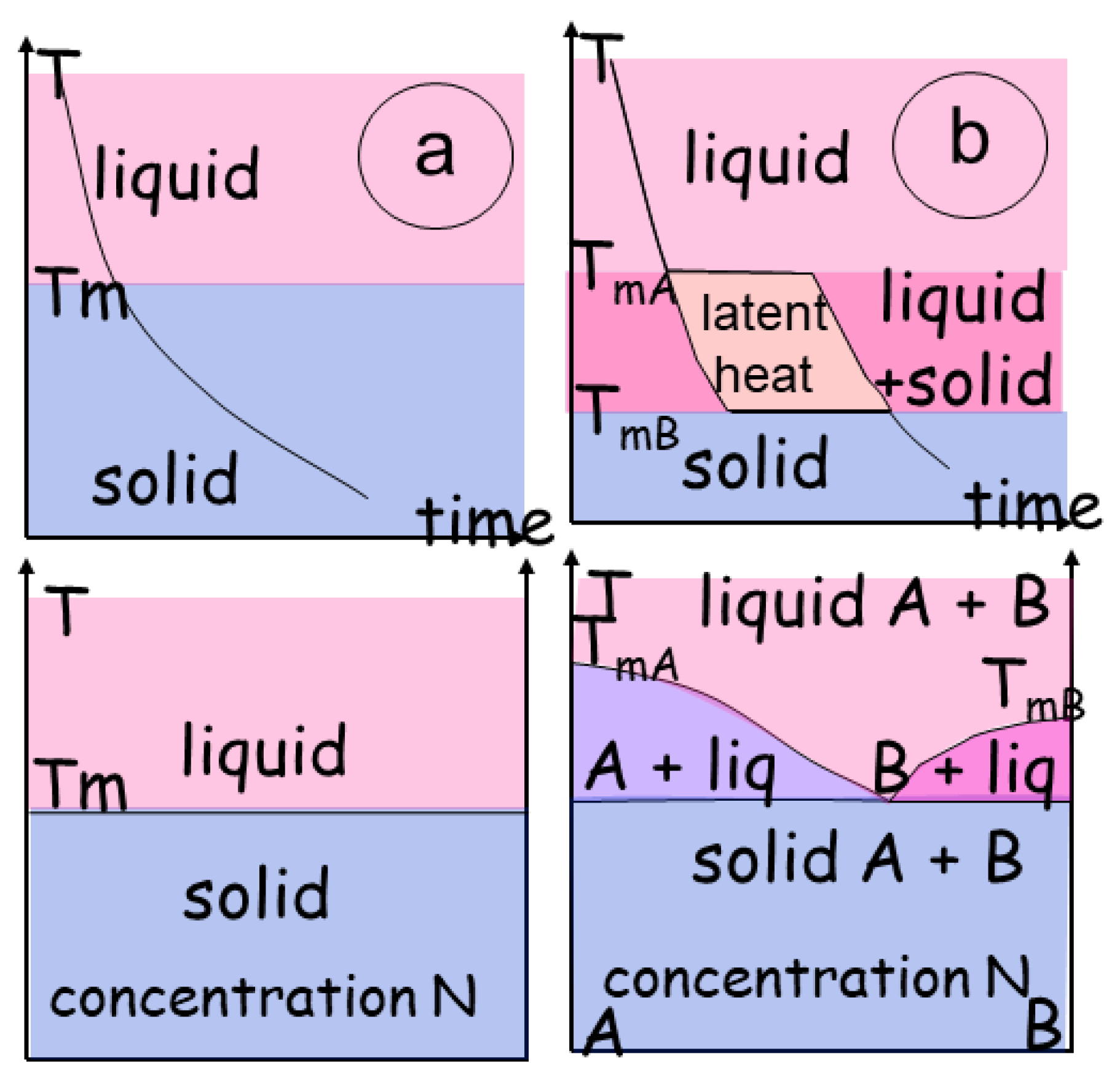
The evolution of phase transitions during melting (or crystallization) is commonly described in P-T diagrams, indicating the physical entropy of the system (liquid, solid) (
Figure 3a). For example, melting reactions for hydrous metapelites have been extensively described (White, 2001, Vielzeuf & Schmidt, 2001). A thermodynamic review about metamorphic rocks conditions has recently been issued (Johnson et al., 2021). It extends the simple binary system with no intermediate phases (
Figure 3a), so the liquid and the solid coexist in a specific P-T-N range.
When the material incorporates multiple phases (e.g. binary with A and B), the transition goes through a high-variance domain delineated by the curves of melting of each material, with a melting temperature (T
mA and T
mB) that may differ within each individual end-member. (
Figure 3b) Consequently, a 2D P-T diagram is not sufficient, and a T-N diagram can be introduced to describe the complex system (
Figure 3b). A higher variance domain develops in which a mixture of the end-members co-exists. Depending on the chemical system considered and the number of phases present, the transitional zone may be bivariant, or multivariant with an eutectic point. The composition of the solid phase is a function of the lowest melting temperature of the mixture. In this space, energy varies as a function of the amount of each phase depending on (P-T or s-T). The structural effects, imposing order to the crystalline assemblage, are not considered. Energy variations are present and linked to interactions between the other components (S, e, m) and (T, s, N) (
Figure 2b). They develop as instabilities and form feedback loops, often minored, during direct modeling of phase transition.
1.3. Establishing the Problem
The complex problem of ore formation in magmatic settings does not start from scratch. It is based on field observations, laboratory observations and experiments, as well as physico-chemical concepts, including magma components (solid, melt, fluids) properties. Nevertheless, addressing a phase change for a complex multiphase system requires considering the free energy balance between the components.
First, the free energy (G) for the melt and matrix relies on three major internal and external forces (
Figure 2). Those are controlled by temperature (T) and entropy (S), stress (s) and strain (e), chemical potential (m
i), and the number of reactants (N
i). Their interactions drive the whole system to evolve toward a state of equilibrium characterized by a minimum value of Gibbs free energy. This requires describing a model of probability distributions by selecting the macrostate with the highest entropy (Hobbs & Ord, 2010). However, system perturbations introduce instabilities, that are mostly irreversible. In addition, the total processes of melting, extraction, and crystallization, point to an open-system description, and non-equilibrium thermodynamics. Since the phase transition does not yield escape of the system components, a description using a Gibbs free energy may apply.
More commonly, the descriptions of geological processes involve materials with contrasted properties. Those present variations in state or ordering (from a crystal to a liquid), rheology (from solid rocks to viscous lavas), or chemistry (from felsic to mafic). The coexistence of such contrasted properties is a natural factor for instabilities. In addition, earth materials are not binary, e.g. with a weak and strong end-member, but it encompasses several intermediate phases governing each phase transition. Understanding the processes controlling transitional states and their intertwined mechanical, chemical, and thermodynamical properties should provide insights into their evolution towards equilibrium, providing issues on instabilities and eventually contributing to predicting the evolution of the entire complex system.
The final aspects of ore formation are also strongly controlled by field observations.
1.3.1. TPD in the Field
The TPDs are characterized by localized intrusions within a trans-pressional zone of intense shearing (de Saint Blanquat et al., 1998). Mechanical decoupling within the crust induces instability the crust and vertical motion in addition to the horizontal shear (
Figure 4). The magmas are mainly derived from melting of the continental crust, with few traces of mantle-derived magmas and fluids (mafic melts and S compounds). Such magmatic bodies mostly originate during continental shear or very oblique collision.
The width of the shear zone acts as a focusing effect on the magma production. Though numerous worldwide examples, we provide three cases to document the relation between shear zone and magma. When the sheared zone is restricted in width between two adjacent cratons, the resulting granitic massifs develop in small stocks, along linear structures such as the Kivu Belt, or Kibarides, Central Africa, along 1500 * 150 km (Villeneuve et al., 2022; Wulff & Bohlar, 2025).
The continuing oblique continent-continent collision between the Australian and Pacific plates resulted in the formation of the Southern Alps, and Fiordland in southern New Zealand, with granite and pegmatites from the Mataketake Range, and the Stewart Island in the southwest of this orogen (Batt & Braun, 1999; King et al., 2008; Tulloch et al., 2009). The Mesozoic Median Batholith, a S-type granite, is now dissected by the Alpine fault, though it intruded a 400 * 75 km shear zone.
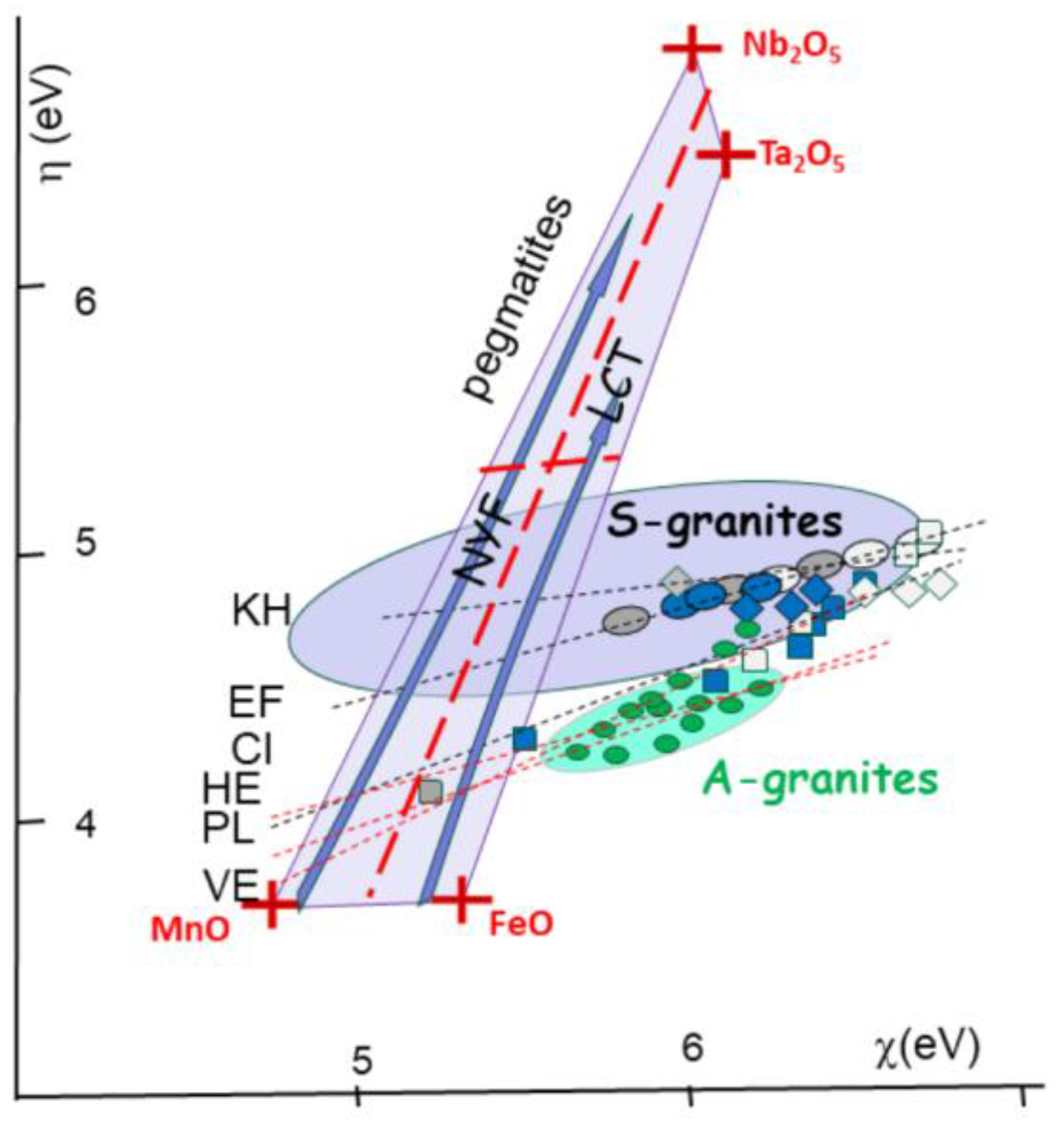
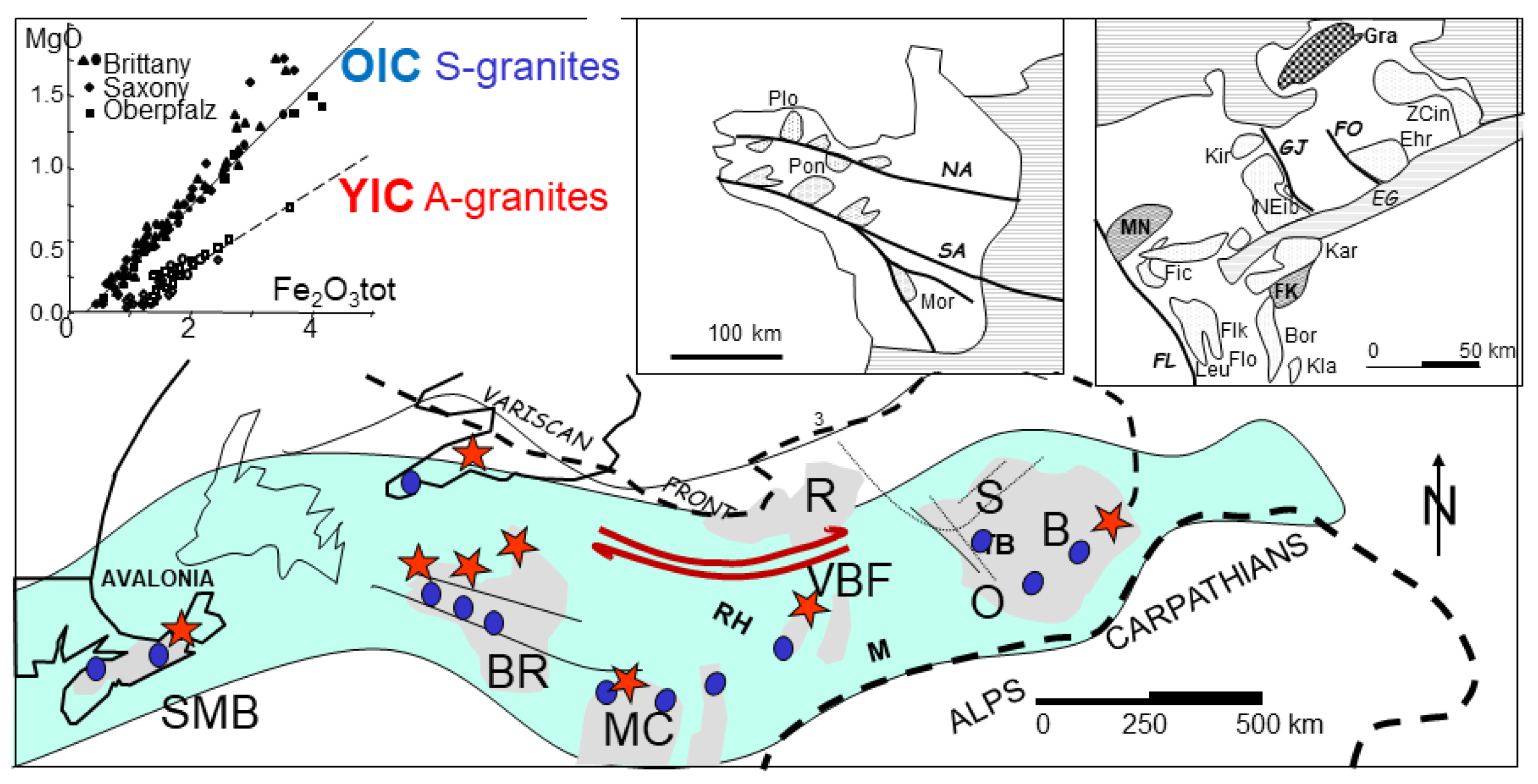
In the Hercynian granitic belt (Lehmann, 1987; Oncken, 1997; Edel et al., 2018) (
Figure 5). The S-type granitic intrusions run along 2500 * 600 km from, South Mountain Batholith (SMB), Nova Scotia (Kontak et al., 2001); Land’s End, Dartmoor (Cornwall); Pontivy, Plouaret (Brittany), to Erzgebirge, Bohemia as Podlesi Cinovec(CI), Ehrensfriderdorf (EH) and Krusne Hory (KH) (Breiter et al., 1999). Globally, the analyses for Bohemia have been issued in various specialized papers from the group of Rainer Thomas (GFZ, Potsdam) and Karel Breiter (Czech Geol Survey, Prague). Those S-type granitic intrusions present root zones in zone of local extension (Vigneresse, 1995), but the bulk motion is shearing. In contrast, the banks of the shear zone give place to compression against the cratons, with subsequent relaxation of the crust. they are place of so-called anorogenic pink alkali granites (A-type) or ferroan granites (Frost & Frost, 2011). Such examples (
Figure 5) are the Pleasant Ridge, New Brunswick (Inverno & Hutchinson, 2006); Hensbarrow (HE) and St Austell, Cornwall (Williamson et al., 1997); northern Brittany (Aber-Ildut, Ploumanach (PL), Flamanville, Barfleur (Chauris, 1958); and Vernéřov (VE) in Bohemia Breiter et al., 2009) (
Figure 5). Transpressional zones are characterized by the coexistence of the two types ofgranitic magmas, owing to heterogeneities in the crust. when the neighbouring craton is involved, their lower crust may enter melting. Adopting a viscosity of 10
17 Pa.s for the lower crust, it yields a delay of about 30 Ma between the S-type and the A-type granites emplacement.
1.3.2. Model of Continental Shear Zone
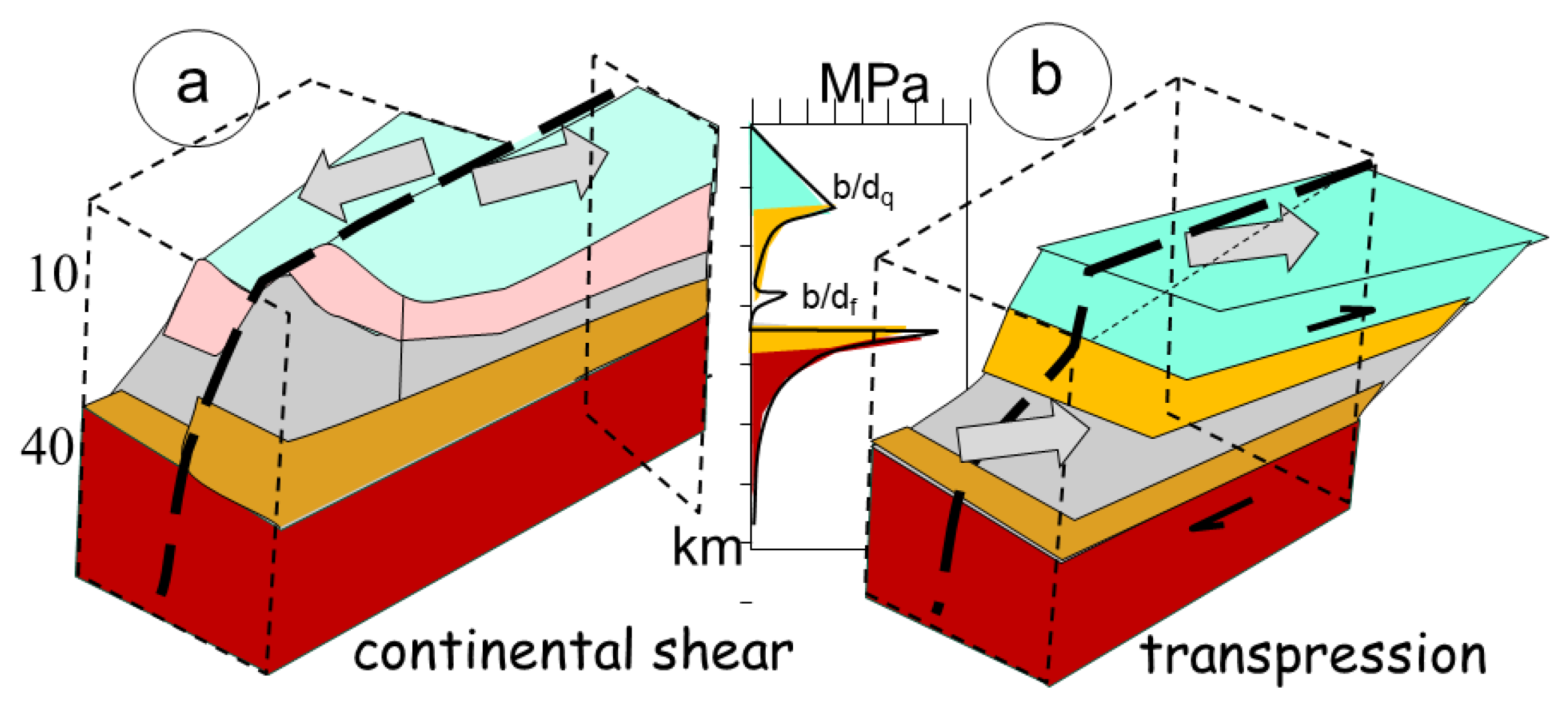
A continental shear zone develops in response to an oblique to nearly parallel convergence of cratons (
Figure 4a). The two cratons present an older ticker and stiffer crust, commonly with a granulitic dry lower crust establishing its structural stability. The rheological response of the crust to stress is that of a layered crust in 1D. The uppermost crust is controlled by the quartz up to about 300°C, when it becomes ductile (
Figure 4). It corresponds to the seismic active zone, that manifests through rupture when the stress becomes too important. Below 20-22 km in depth, more abundant and stiffer feldspars reinforce the crust, first by subgrain rotations yielding ductile feldspathic brittle/plastic transition at about 450 °C. It is the place of ductile shear zones anastomosing gneissic shear zones that progressively flatten, before the encounter the Moho at about 750 °C, where olivine takes control of a stiffer upper mantle that can present brittle deformation, as observed in seismic sections, in case of large strain.
The general equations that rule mineral deformation (e°) takes the aspect of a power law with stress (s) through a factor (n), with a pre-exponential factor E
0, and an activation energy(Q) function of temperature (Bouchez & Nicolas, 2021).
Depending on minerals and experimental conditions, the grain size (d) may enter the equation with a power law (p). The bulk trend is that reducing the grain size increases stiffness. Values for the most important minerals have been summarized (Fossen & Tikoff, 1998).
The bulk strength of the crust manifests by the so-called fir-tree aspect of the curve, with linear strength increase up to ductile transition above a weaker layer (
Figure 4c). Experimental deformation under varying ambient stress and controlled shear rate have long been the base of all models of crustal response to imposed stress field (Bouchez & Nicolas, 2021). They placed values of the expected transitions, in compression and simple shear experiments. In parallel, 2D and 3D numerical simulations of deformation revealed the influence of gravity in modifying the relief close due to the compressional forces. However, they confirm the 1D layer model, and investigate the non-linear aspects of the deformation behaviour, in case of rapid contrasts in rock properties or strain response to stress.
Such 1D models served also to elucidate the geometric conditions internal to shear zones, identifying the vorticity variations to take into account crustal heterogeneities. (Fossen et al., 1994).
The adopted geometry corresponds to a vertical shear zone, within a weaker zone bracketed between adjacent cratons (
Figure 4a). Owing to the 1D modelling, the vertical motion of the weaker central zone is not considered. The temperature profile with depth is controlled by the basal heat flow. Experimental conditions, as well as field observations concluded that the basal friction induced by the heat flow, remains inefficient to significantly alter the temperature profile with depth. Similarly, the friction of the shear planes, often manifested by local melt (tachylites) remains localized and attest high strain rates, rarely observed at usual tectonic rates (10
-14 s
-1).
1.3.3. Continental Transpression
In case of oblique convergence and melting, the deformation switches from a simple 2D geometry, manifested by strike-slip along fracture plane (
Figure 4a), deviating from simple shear by adding a pure shear component across the zone, resulting in transpression (shortening) or transtension (extension) (
Figure 4b). The result is a large spectrum of 3D deformation with its own complex strain reactions, modifying fabrics rotation (the simple shear component) (Fossen & Tikoff, 1998). Owing to such a perpendicular combination of a pure shear and a simple shear, the resulting deformation path becomes much more complex than for a simple shear zone.
The major difference with a continental shear zone results from the partitioning of the deformation. In the former case, the high strain zone is localized in a subvertical plane to accommodate through brittle fractures the horizontal displacement between the two adjacent craton roots (
Figure 4a). In contrast, during transpression, the upper part of the crust, controlled by quartz and feldspars, also reacts in a brittle mode, inducing fracture zones. But the lower part plastically deforms under pure shear, flowing horizontally (
Figure 4b), according to the basal frictional drag with the upper mantle. the conjunction of both patterns of deformation results in complex geometries of flow, manifested by mineral fabrics (Fossen & Cavalcante, 2017).
1.3.4. Implications of a Basal Friction
Another important character of transpression results from its driving force (
Figure 4). A common fracture results from the accumulation of stresses induced by an ambient convergent stress pattern, usually noted s
1 > s
2 > s
3. In a commonly stressed crust, when the major stress component is vertical, it gives place to extension. Depending on the relative intensity of the two horizontal components (i.e. when s
1 is not the driving stress), deformation gives place to horizontal strike-slip or reverse faulting. In all cases, the stress intensity gradationally accumulates up to overcome the rock strength. The process is considered to be continuous, stationary during stress accumulation up to rupture.
Conversely, friction manifests by a discontinuous motion, known as stick-slip (Byerlee, 1978). It manifests through alternate episodes of discrete slip, followed by an arrest, the stick phase. The interpretation of such transient effects relates to the simultaneous presence of a multiphase material that react individually to the applied stress. They are metal and air in case of common dry friction (Ruina, 1983), or melt and matrix in partially molten rocks (Vigneresse & Cenki, 2022).
A static coefficient of friction m0 relates the vertical force (gravity) to the external horizontal force F pulling the system (Byerlee, 1978). In the dynamic case, the external force applied to a two-phase material partitions between the two phases. A second term should be added with a state variable q function (Dieterich, 1978; Ruina, 1983; Marone, 1998).
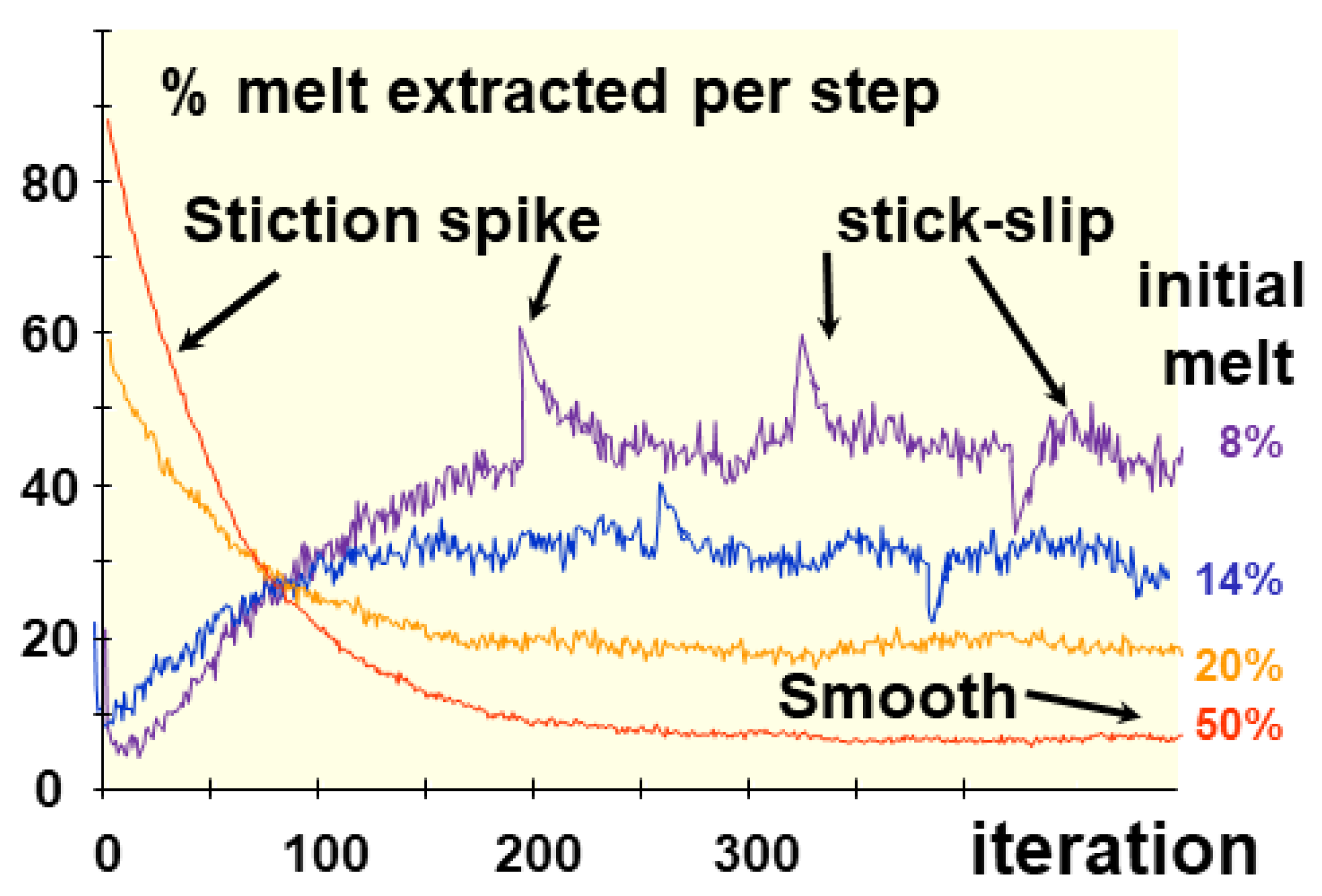
The general flow pattern, as experimentally determined for dry friction, becomes a competition between velocity and its variations (acceleration or slowing down), i.e. successive episodes of flow (velocity) constrained by enhanced (acceleration) or restricted flux (slowing down). The flow during of dry friction consists in motion, interrupted by stops, so-called stick-slip motion (Byerlee, 1978; Marone, 1998; Vigneresse & Cenki, 2022; Wong & Keller, 2023). A spike (Dm), often called stiction, develops when the slip condition (acceleration) varies (
Figure 6). The evolution that follows to readjust the friction coefficient takes the shape of a diffusive process, with a quantity D
c (Dieterich, 1979; Ruina, 1988).)
The underlying state function is a combination of first and second derivatives, and the energy is evacuated by phonons, such as the musical tones of a violin string, or the squeal of chalk on a chalkboard. it defines a general law linking stress and strain with V the slip velocity over an asperity
1.3.5. A State Variable for Friction
The frictional experiments allowed quantifying a dynamic friction coefficient (m), as well as the motion timing. A state variable q is coined, that would correspond to the expression of the energy with respect to the variance of the transitional zone (Brace & Byerlee, 1966; Marone, 1998).
The coefficients a and b measure the velocity dependence of friction (Voisin et al., 2007). Their difference (b - a) implies a velocity weakening when positive, i.e. when acceleration takes over velocity. When the latter takes over from the former, instabilities develop. In other terms, advection takes over from diffusion. It eventually gives place to spinodal decomposition (
Figure 7), thus partitioning the entropy between the components (Vigneresse, 2020).
Similar effects are observed during simulations of melt extraction, i.e. segregation of a mobile melt from a viscous matrix. Numerical simulations used cellular automata to reproduce melt motion (Vigneresse & Burg, 2000), whereas the interpretation the variations were conducted b varying the amount of the weak phase (Vigneresse & Cenki, 2022). In both situations, a stop and go motion is observed, with sudden bursts related to increase or shortening of the weak phase, followed by a diffusive return to the previous state. It remains difficult to calibrate time in such numerical experiments, but the stick-slip motion allows estimating their interval, non periodic, to about 0.3 to 0.5 ky (Wong & Keller, 2023).
1.3.6. A Competition Between Advection and Diffusion
The stick-slip motion is commonly separated in two patterns by the frequency of the alternate stop-and-go-motion. In a quasi-steady state, the frequency is function of the velocity of the flow. Its duration is of the order of the second or less. nevertheless, it is not periodical, as could be some sinusoidal function (
Figure 6). The amplitude varies continuously. Superimposed to this signal with short period and small amplitude, some burst occurs, that marks by a larger amplitude, and a return to the previous steady state as it would be for diffusion. Such bursts have a pseudo-period quite larger than the stop and go motion, by about one order of magnitude. The common interpretation is an increase, or shortening, in the amount of the mobile phase, as suggested by the diffusive return to initial conditions.
2. Chemical Aspects
Chemical reactions are commonly interpreted as the re-equilibration of the chemical potential difference between elements (e.g. Myers, 2009). In presence of oxygen, metallic ions combine into metal oxide for a greater stability, thus lowering their possibility to induce new reactions. During the process, there is no noticeable change in the structure of the nucleus of both elements.
2.1. Chemical Descriptors
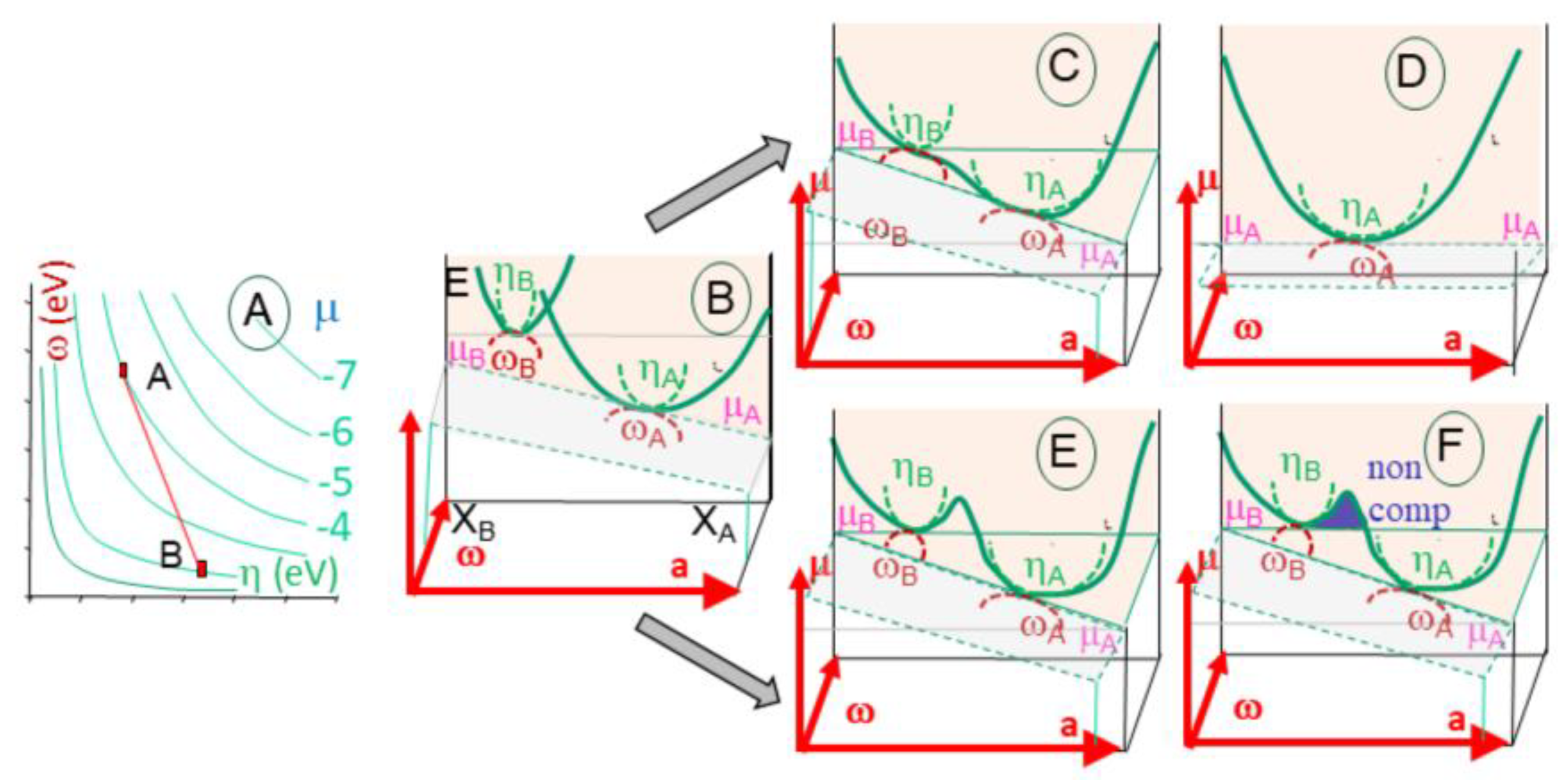
Elements are considered as electronic clouds that could share, exporting or importing other electrons. For this purpose, elements are classified as acid and base depending on whether they accept or provide electrons, and in hard and soft depending on their ability to share electrons. such quantities are called descriptors, namely electronegativity (c) and hardness (h). Electronegativity (c) is the chemical potential (m) changed of sign (Pauling, 2006). It is the first derivative of the energy when one electron is added to the electron cloud (N) under constant external potential v(r). Chemical hardness (h) is the second derivative of the energy in the same conditions (Pearson, 1988) (
Figure 9).
Under such conditions, the chemical potential is tangent to the energy curve, whereas hardness is akin to the radius of the curvature circle at this point. A third descriptors electrophilicity (w) is akin to the osculating circle (Vigneresse, 2030), being equivalent to the normal tangent, related to the lateral deviation of the energy curve. It attempts to laterally deviate the energy curve (
Figure 7).
Furthermore, polarizability (α) characterizes how the electronic cloud distorts in response to an external electric field (Ghanty & Ghosh, 1997). It is defined as:
where F
a, F
b and F
c the components of the applied electric field. Values are commonly reported in atomic units (1 a.u. = 27.211 eV), and polarizability is often inversely related to the cube of electronegativity (Nagle, 1990), making a as a proxy for unidirectional electronic resistance, and c, its average on geometric axes, an estimate of the bulk polarizability.
2.2. Reaction Control
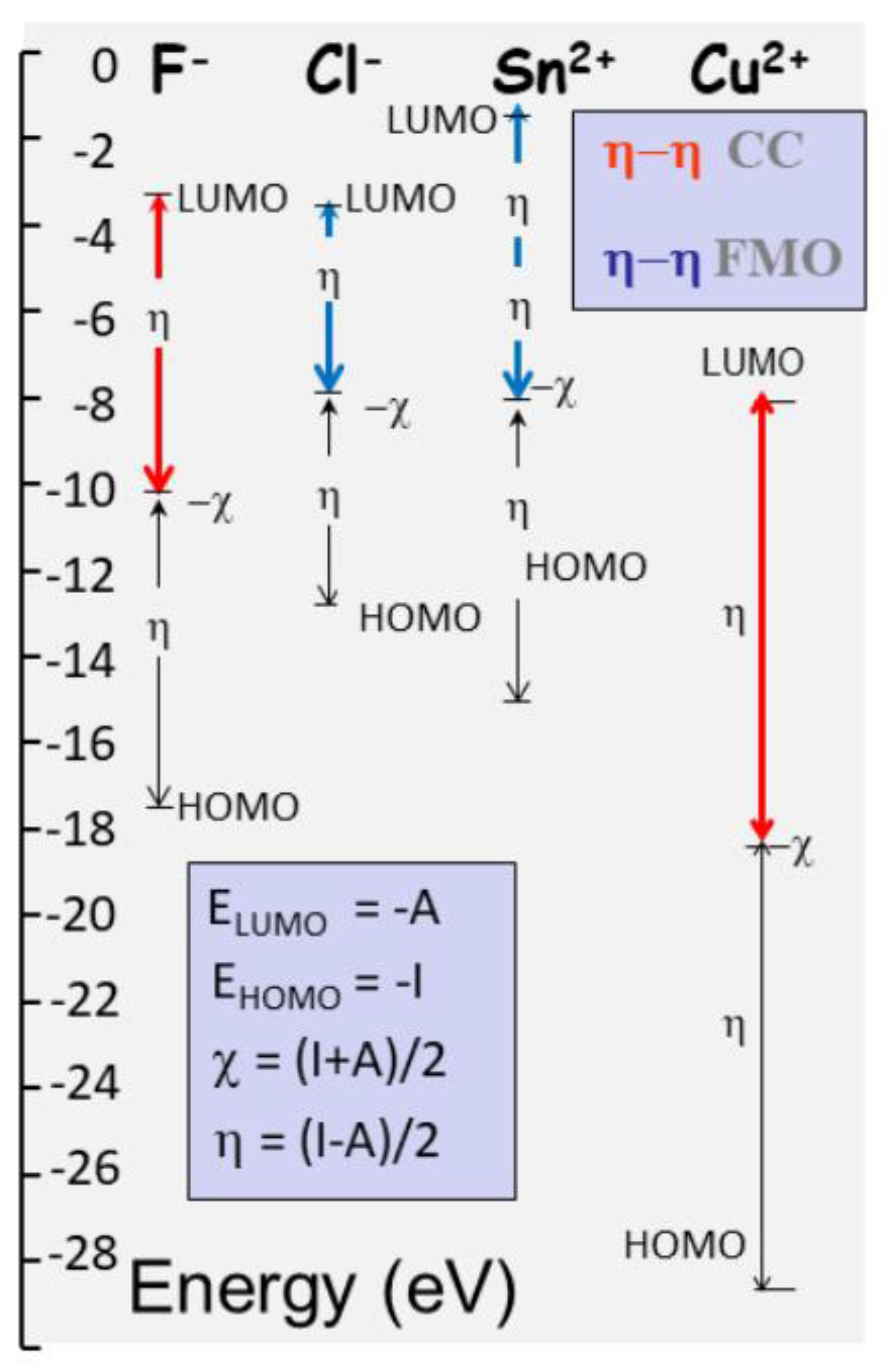
In ionic states, atoms fill their available orbitals (s, p, d, etc.), establishing electronic structures that define their reactivity (
Figure 8). The frontier molecular orbitals the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) are particularly significant in this context, as their energies correspond to the ionization potential (IP) and electron affinity (EA), respectively. From these quantities, electronegativity and chemical hardness can be derived through finite difference approximations (
Figure 8). These descriptors serve as fundamental indicators of an atom’s chemical behaviour. Electronegativity, the negative of the chemical potential, governs an atom’s ability to attract electron density, playing a central role in determining the direction and feasibility of chemical interactions. Hardness, in contrast, reflects the resistance of an electron cloud to deformation, influencing how easily a species can adapt to external perturbations.
Reactions involving small, highly charged ions (such as halogens) often proceed through charge-controlled (CC) mechanisms, where the electron exchange occurs with minimal nuclear rearrangement. In such cases, the driving force of reactivity is dominated by the difference in chemical potential between species. Conversely, when polarizability is high, the electron cloud reorganizes, orbital overlap and electrostatics, start to dominate (
Figure 8). Ionic interactions (e.g., Cu²⁺). The nature of the interaction hard–hard or soft–soft—determines whether reactivity is primarily electrostatic or orbital-driven (Anderson et al., 2007).
The energy levels of HOMO and LUMO correlate with fundamental electronic properties: the ionization potential and electron affinity. These, in turn, relate to electronegativity and hardness, which represent the first and second derivatives of the total energy with respect to electron number. Electronegativity captures the tendency of a species to attract electron density, while hardness quantifies its resistance to charge deformation. Together, they help characterize how a system will respond during interactions with other chemical species. In reactions where the HOMO–LUMO energy gap is substantial, and the elements involved are less polarizable, the mechanism typically falls under the charge-controlled (CC) regime (
Figure 8),. Electron transfer dominates such reactions without requiring significant structural rearrangement. However, when soft species interact—those with diffuse orbitals and higher polarizability—orbital overlap and covalent character become more influential, and frontier molecular orbitals (FMO) mechanisms become prominent. In short, hard-hard interactions depend on CC whereas soft-soft reactions are FMO (
Figure 8).
A third mechanism may develop for larger molecules, that is directly related to the size of the electronic cloud and its polarizability (Guégan et al., 2023). The density polarization (DP) concept expresses the volumetric density of the electric dipole moments, describing how the material responds to an external electric field. Large molecules present large ionic radius, and often large charge. In presence of an external shape, the electronic cloud deforms, and polarizability enhances the formation of covalent bounds.
The three processes controlling chemical reactions determine the type of links between molecules, and thus their future ability to exchange with other elements, forming complex compounds.
2.3. Fitness Landscape Diagrams
Some simple principles rule the reactions. Three of them describe the bulk trend of the descriptors during a reaction. It represents a mapping of the chemical products
First, the chemical potential should be similar in all components at equilibrium, justifying the use of geometrical averaging between descriptors for molar amount of compounds or solvents. At equilibrium, the chemical potential tends to equalize among all constituents (Mortier et al., 1986), supporting the use of geometric averaging for compounds:
Second, hard molecules arrange themselves to be as hard as possible (Parr & Chattaraj, 1991), giving place to the maximum hardness principle (MHP).
Third, a minimum electrophilicity principle (mEP), states that reactions should evolve toward minimum electrophilicity (Pan et al., 2013).
At last, a Minimum Polarizability Principle (mPP) favours the formation of stable molecules is in regions of lower polarizability, typically associated with higher charge localization (Chattaraj et al., 1999).
Consequently, given an initial product, characterized by its descriptors, it should be possible to predict the more probable path during a reaction, examining the variations of the descriptors This represent a new mapping, or fitting landscape diagram, on which the potential wells should attract the reaction (Duley et al., 2012).
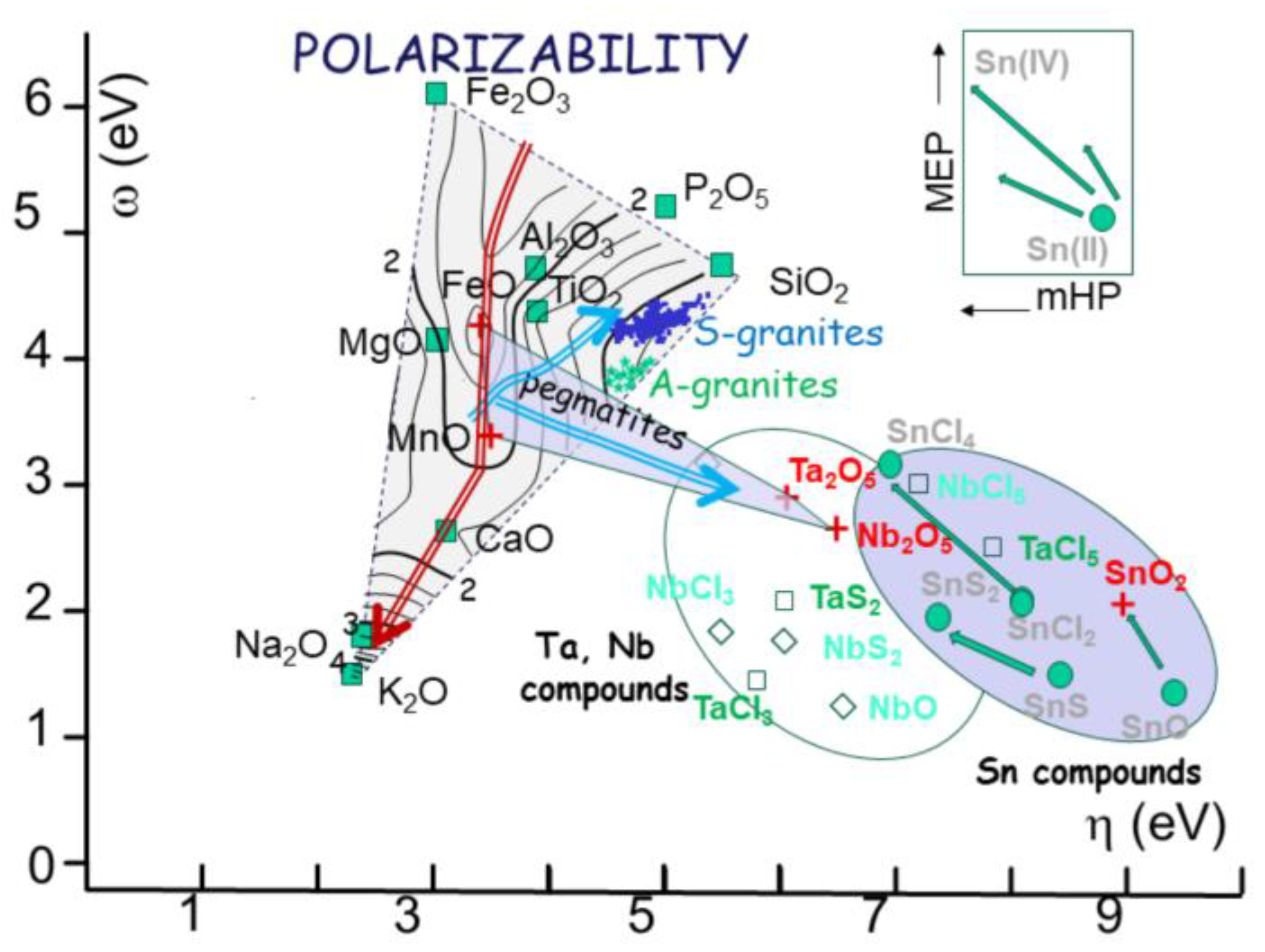
Such transformation, which is fact is an isomorphism, can be used to plot the 11 common oxides used in magmatic petrochemistry, to a 2D diagram using for instance [c-h] or [w-h] as new coordinates for one oxide (Vignresse & Truche, 2000). As an illustration (
Figure 9), the 11 oxides plot on such diagram, forming a triangle with poles the descriptors of SiO
2, Fe
2O
3 and alkali (Na
2O). Such diagram straightfully indicates the three major poles, i.e. silica, oxidation and alkalis, within chemical analyses. Superimposed on this triangle, other parameter, such as polarizabilty (a) can be used as a third dimension, yielding a mapping with values of equal polarizability and their trends (
Figure 9).
Figure 9.
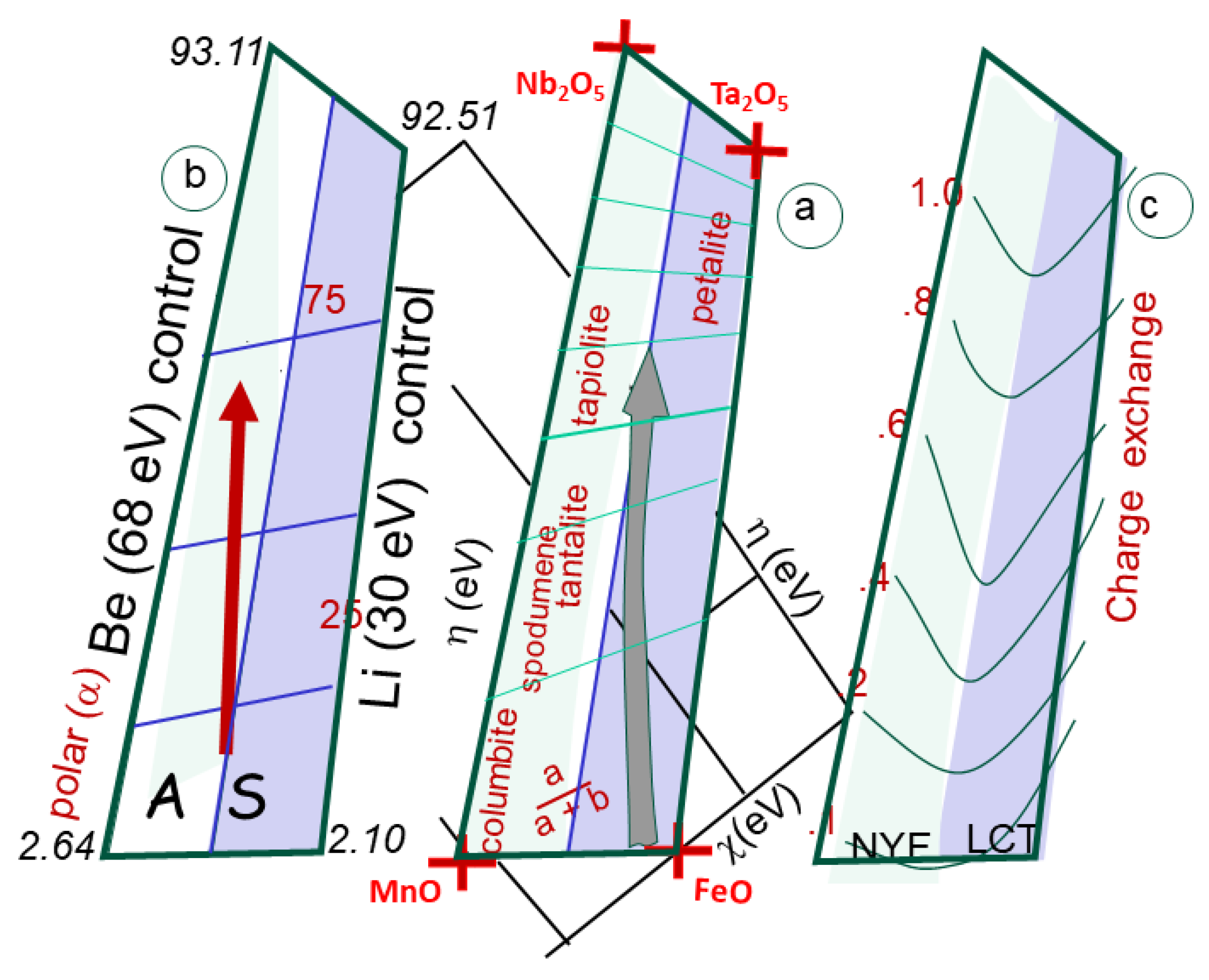
a) the box is calibrated in a / (a+b), indicating the respective ratio of Fe and Mn compared to Ta and Nb. The fields of A and S granites, corresponding to NYF and LCT pegmatites, are indicated. Plotted, the fields of columbite, tantalite, tapiolite and petalite, spodumene and beryl are indicated. 9b) same box, but calibrated in polarizability, showing the large difference between oxides (about 2 to 100). 9c) Charge exchange computed between the poles of the pegmatite box. The change is always low (below 1 unit) increasing from Fe-Mn to Ta-Nb oxides.
Figure 9.
a) the box is calibrated in a / (a+b), indicating the respective ratio of Fe and Mn compared to Ta and Nb. The fields of A and S granites, corresponding to NYF and LCT pegmatites, are indicated. Plotted, the fields of columbite, tantalite, tapiolite and petalite, spodumene and beryl are indicated. 9b) same box, but calibrated in polarizability, showing the large difference between oxides (about 2 to 100). 9c) Charge exchange computed between the poles of the pegmatite box. The change is always low (below 1 unit) increasing from Fe-Mn to Ta-Nb oxides.
2.4. Fitness Landscapes
Under such descriptors, chemical reactions are considered as analogue to electrons flux, with a bulk velocity ruled by the chemical potential difference and its variations, akin to acceleration (or slowing down) through hardness (Eq. 6).
The chemical reactions are not limited to a unique category, e.g. formation of oxides or sulfides (
Figure 9). depending on the reactants in presence. The disequilibrium if chemical potential may involve several successive reactions. For instance, a silicate lava, e.g. basaltic, combines about 11 major oxides, and fluids (Cl, S, OH, …). During solidification, crystal precipitation modifies the composition of the melt, altering the chemical potential of the residual melt (
Figure 10). It constitutes the so-called Bowen-Fenner trend (Bowen, 1912; Fenner, 1929). Hence, forming and precipitating any phase is a disequilibrium process that follows a series of steps, also called liquid line of descent until a thermodynamically stable state, or equilibrium, is achieved (Grove & Brown, 2018). The Bowen trend commonly evolves by successive steps (
Figure 10), from ferro-magnesian minerals (olivine, pyroxene, amphiboles) to micas (biotite) and feldspars, towards quartz. Known as fractional crystallization, it is a succession of forming crystals, that are removed from the melt by setting, according to successive potential lows.
The chemical descriptors and the principles that rule reactions offer an elegant mode of describing elements evolutions during chemical reactions (Duley et al., 2012). In particular, descriptors pair allow examining reactions between multi-elements, namely the 11 oxides used in geosciences within a 2D mapping, rather than complex 11D space (Vigneresse & Truche, 2018).
2.5. Cascading Energy
Reactions proceed through charge exchange (dN), implying energy exchange (dE).
The sign of dN indicates the direction of electron flow, while dE is always negative, reflecting the energy stabilization upon charge redistribution
The different crystallizing phases follow the order of their chemical potential, as an analogy of a cascade of potential wells (
Figure 11). Each mineral has a chemical potential value that progressively decreases (increasing the chemical electronegativity). The curve of the bulk free energy is tangent to each of these values, with a radius of curvature (akin to chemical hardness) that slightly increases (
Figure 10). Since electrophilicity does not significantly vary, the lateral deviation (i.e. the radius of the osculating circle) does not vary, keeping the energy trend in a regular plane.
The proximity of the potential wells and their amplitude imply a quasi-continuous trend toward a potential low. The trend runs from Fe oxides toward silica as described by Bowen (1912) and Fenner (1929), mimicking a liquid line of descent experimentally observed (Villiger et al., 2004). Immiscibility between liquids occurs when the difference in hardness, i.e. in the second derivative of Gibbs free energy, is too large to allow a smooth transition.
The cascading variation of the chemical potential represents a natural evolution of the chemical system towards a zone of lower energy (
Figure 11). Although the reactions rapidly develop and the atoms are rearranged, the reaction is accompanied by an energy change as the new system is generated. It is obviously accompanied by an exchange in temperature. for most reactions, the reaction rate determines the proportion of the concentration of the products and reactants by time unit. It can be very slow, such as natural oxidation of iron in contact with air, or quite instantaneous, scaling in mol/m
3/s.
Consequently, the chemical reactions behave identically to stop and go motion for friction. Their rate depends on the available quantity of reactants, i.e. advection, and on the velocity to which new products are generated, i.e. diffusion.
2.6. Computational Aspects
We employ conceptual Density Functional Theory (cDFT) to calculate the chemical reactivity descriptors, in accordance with the foundational principles of the theory (Chattaraj et al., 2001; 2006). All computations were carried out using the code Multiwfn 3.8 (Lu & Chen, 2012; 2022), an open-source post-processing program designed for comprehensive analysis of molecular electronic structures.
The calculations are based on the B3LYP functional (Lee et al., 1988), which incorporates the Lee–Yang–Parr correlation component. Geometry optimizations and property evaluations were performed at the B3LYP/6-311++G(2df,2p) level of theory. This level of theory was also used to calculate the external static potential (ESP), ensuring consistency across the dataset. The use of a uniform cDFT computational protocol allows for direct comparability of the derived descriptors across different systems and supports the assumption of data homogeneity.
4. The Effects on the Magma Chamber
4.1. Magmas
Initial melting of the continental crust produces silicate-rich melts (> 65 % SiO2. Those hydrous minerals are mostly micas with volatiles (CO2, Li, Be, B). the liberate water that is immediately reincorporated into the melt. The restitic mineral assemblage forms granulites, as observed from their seismic velocity in the lower crustal sequences.
Conversely, at similar temperatures, fluid assisted partial melting of lower crustal minerals (garnet, pyroxene), results in alkaline magmas, richer in rare earth elements (REE).
4.2. Transport Properties (Viscosity, Diffusion)
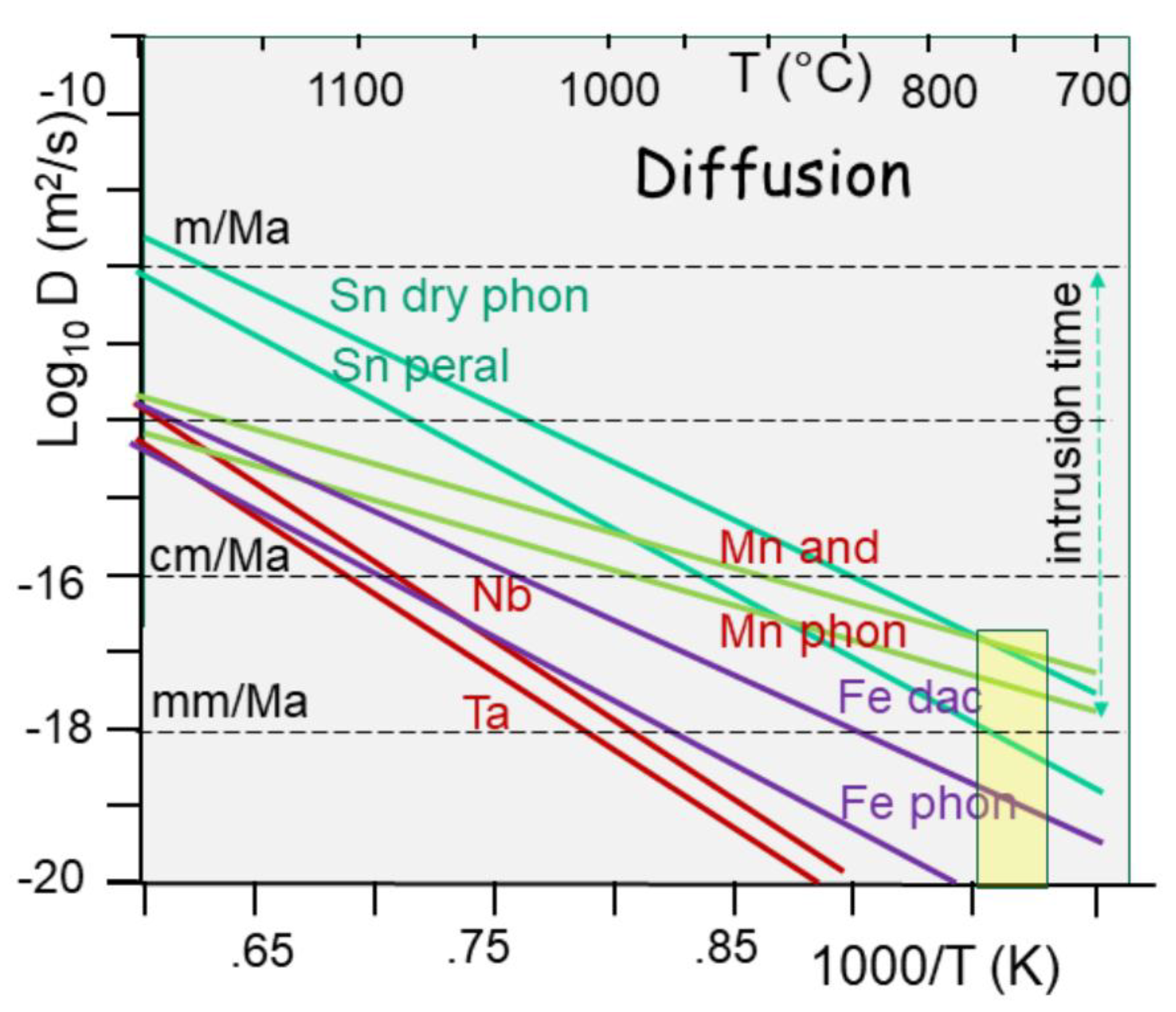
During melting, metals are liberated from crystalline networks, turning to a ionic state, and free to move according to diffusion in the melt (
Figure 13). Unfortunately, the temperatures do not allow much displacement. Hence, given an average lifetime of 1 Ma for the magma chamber, in between 700-750 °C, the melt viscosity for a crustal melt computed from rock composition (Giordano et al., 2008) scales between 10
-4 and 10
12 Pa.s, without any possibility to differentiate between granite, pegmatites and greisen (Vigneresse et al., 2025). at least 13% fluid is required to reach values allowing lava flow. At the same temperature, diffusivity values for Sn range 10
-17-10
-19 m
2/s, both equivalent to characteristic length less than 1 m for such time interval (Vigneresse et al., 2025).
4.3. Ore Chemistry
The subcritical state of the MIP strongly affects the dissolution of granite into water from 300°C to 450°C (Tsuchiya & Hirano, 2007). Indeed, the supercritical water oxidation mechanism is commonly used to extract hazardous products from soils (Barner et al., 1992). For pure water, the critical point is reached at 22.1 MPa and 374 °C, under which ionic and polar species are extracted (Brunner, 2009). In addition, the natural system is buffered along the usual hematite-magnetite (HM), up to nickel-nickel oxide (NNO) buffers. As a result, other metal compounds (Sn Nb, Ta) are found as oxides.
A specific molecular dynamic (CPMD, Kühne, 2014) applied to supercritical water (scH
2O), documents that electrons cleave a cavity in the hydrogen bond network in which six H
2O molecules form the solvation shell (
Figure 5 in Boero et al., 2003). At subcritical conditions, the H-bond network is not continuous, allowing electrons to localize in preexisting cavities, or solvation shells formed by four water molecules. The progressive extent of the H-bonds marks by a decreasing density. The electrochemical properties, as dipole moment also decrease, modifying its polarizability.
4.4. Pegmatites and Greisen
The extraction of metals from TPD magmas is hampered by two factors, namely the paucity of metals, and the poor transport properties within the melt.
The amount of metals is not the real problem. In fact, there is enough metals in the lower continental crust, compared to the oceanic crust. When melting, they are liberated from their network, become ionic compounds, and they are free to move. However, metals diffusivity towards the melt remains limited, not by their ionic radius (500-1100 pm), but by the poor activation energy (125-180 kmole/J). The low temperature imposed by the critical state (< 730°C) does not help. As a result, the characteristic diffusion velocities range in cm to dm per million of years (
Figure 13).
Their transport possibilities link with the low viscosity of the melt at such temperatures. The melts indicate viscosity values ranging 107 to 1012 Pa.s that should be compared to lavas flowing at viscosity about 106 Pa.s. Even 13 % water and 3 % F added during the computation allow such values (Vigneresse et al., 2025).
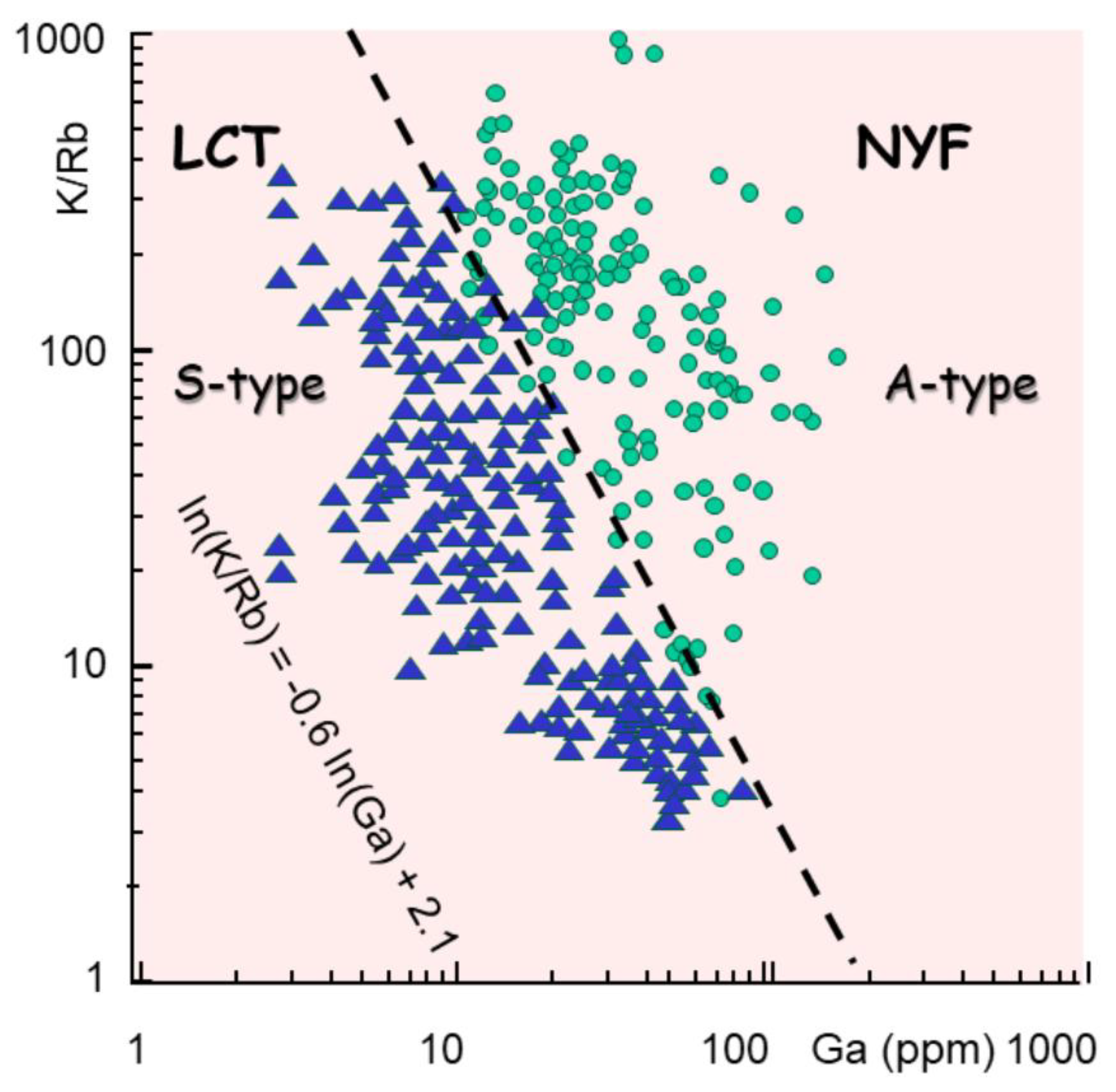
In consequences, the magma splits into pegmatites and greisen., both associated with magmas coming from different sources. Indeed, NYF pegmatites are associated with anorogenic A-type granites, rich in alkalis, Zr, Nb, Ga and Y (Wise et al., 2022). In contrast, LCT pegmatites link with peraluminous magmas, as observed in TPDs, present similar K/Rb ratio, but Ga content is about one order of magnitude less than NYF (Wise et al., 2022). A new classification is suggested that takes into account the initial melting temperature is much more important. Hence TPDs are characterized by highly evolved magmas, issued for the continental crust i.e. from dehydration melting of micas. It brackets melting temperature to 700-800 °C.
The differentiation (K/Rb) plotted against the gallium (Ga) content in ppm shows a neat separation (
Figure 14) that better illustrates the difference between the pegmatite types (Wise et al., 2022).
It represents an enrichment in Ga by a factor of 50 in log, that may be explained by the selective melting of pyroxenes or garnets in the lower crust at about 550° C (Yuan et al., 2021).
4.5. Usual Metals (Sn, Nb, Ta)
Tin (Sn) is the most common ore mineral mined in TPD systems. It is exploited as cassiterite, a tin dioxide (SnO2). The electron configuration of tin orbitals is 5s2 4d10 5p2. It indicates that it can lose two electrons from its 5p orbital to form a tin [II] ion (Sn2+), and it can lose two additional electrons from the 5s orbital to form a tin [IV] ion (Sn4+). Tin achieves a more stable electron configuration in both cases. Tin can form divalent compounds since its s subshell is more stable than the p subshell, because of screening differences, and the s electrons don't bond. The tin [II] compounds are not as stable as tin [IV] compounds in which all four outer electrons are involved in bonds. Consequently, Sn [II] acts as a reducing agent and may be converted into more stable Sn [IV] by losing two electrons.
Both tantalum (Ta) and niobium (Nb), fist called columbium, are part of the refractor group metals with high melting point (close to 3000 °C). Their electronic configuration is 6s2 5d3 4f14 and 5s1 4d4 respectively. They both present several oxidation states, the more common being +2 and +5, with observation of oxides such as TaO and more often Ta
2O
5 (
Figure 9). Both are resistant to acid corrosion, though they dissolve in HF. As minerals, they are nearly found together in the high oxidation state (V), as columbite (Fe, Mn)O Nb
2O
5) or columbite-tantalite (coltan) (Fe, Mn)O (Ta, Nb)
2O
5). As such they are often represented in a box with poles [FeO - MnO] and [Ta
2O
5 - Nb
2O
5], and two trends (
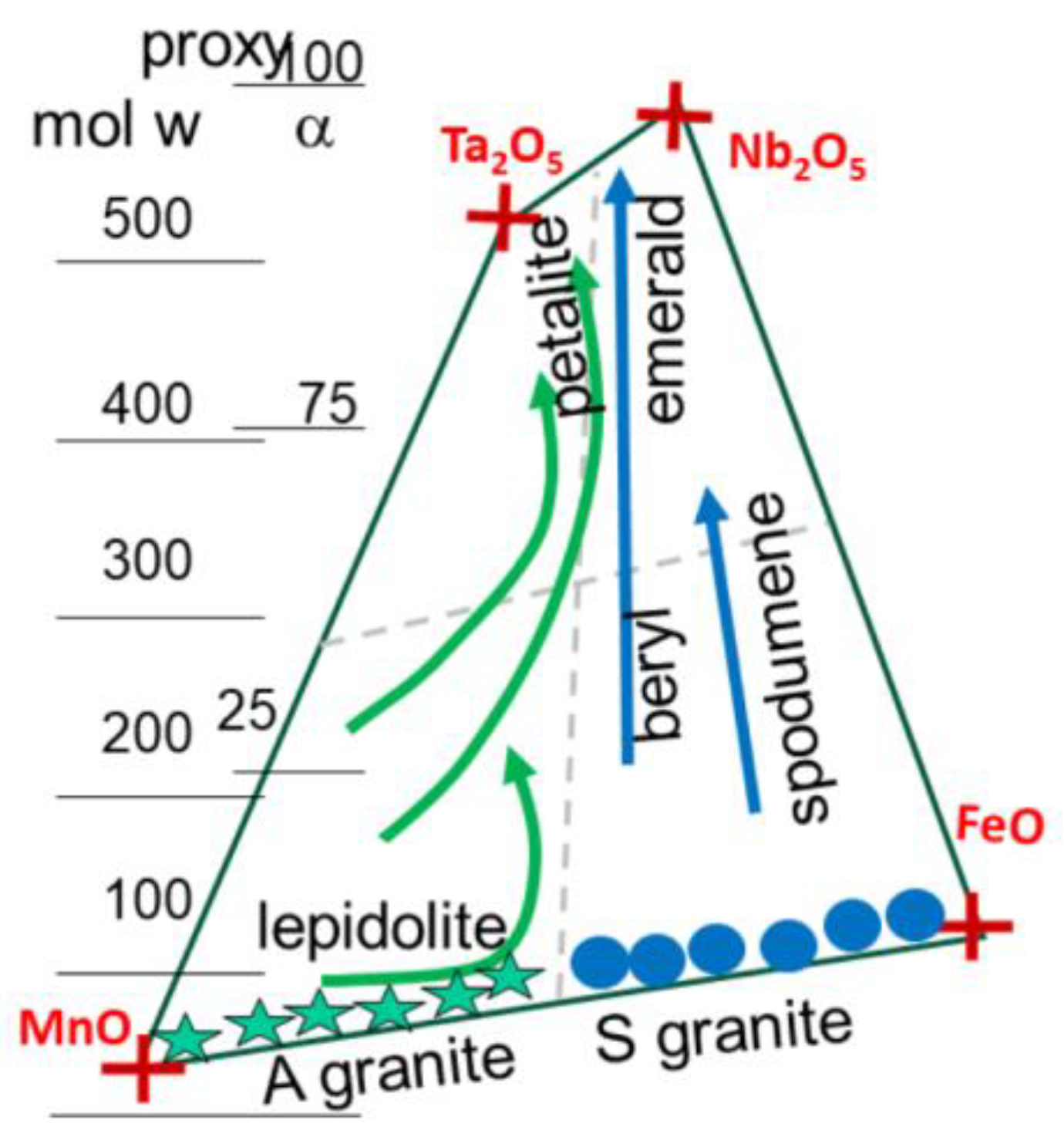
Figure 12), starting from the pole FeO-MnO, associated respectively with F-poor and F-rich fluids (Černý & Ercit, 2005).
Table 1.
Chemical descriptors (eV) for Fe, Mn, Ta, Nb oxides.
Table 1.
Chemical descriptors (eV) for Fe, Mn, Ta, Nb oxides.
| Oxide |
c (eV) |
n (eV) |
w (eV) |
a (cm3) |
| Nb2O5
|
6.00 |
6.89 |
2.61 |
93.11 |
| Ta2O5
|
6.09 |
6.44 |
2.88 |
92.51 |
| FeO |
5.28 |
3.37 |
4.14 |
2.10 |
| MnO |
4.79 |
3.49 |
3.29 |
2.64 |
Figure 12.
Chemical descriptors [h-c] for granitic magmas (plain), pegmatites (light grey on the soft side) and greisens (dark black on the hard side). Values plot on lines for ore deposits within S-granites of Cinovec (CI), Ehrensfriderdorf (EF) and Krusne Hory (KH) in Bohemia. Also indicated trends for similar rock types associated with A-type magmas (in green) with HE (Hensbarrow; St Austell, Cornwall), PL (Ploumanach) and Vernéřov (VE) in Bohemia (see location
Figure 5). Also plotted the field for pegmatites, within a Mn-Fe-Ta-Nb box, indicating the separation of NYF and LCT ore formations, between columbite and tapiolite. The fields of the S-granites (in blue, as well as the A-granites (green stars) are indicated. Both trends r at odds with the pegmatite box ranging between the [Mn-F] oxides and the [Nb-Ta] oxides. also indicated in inset the trends for Sn(II] towards Sn(IV) compounds.
Figure 12.
Chemical descriptors [h-c] for granitic magmas (plain), pegmatites (light grey on the soft side) and greisens (dark black on the hard side). Values plot on lines for ore deposits within S-granites of Cinovec (CI), Ehrensfriderdorf (EF) and Krusne Hory (KH) in Bohemia. Also indicated trends for similar rock types associated with A-type magmas (in green) with HE (Hensbarrow; St Austell, Cornwall), PL (Ploumanach) and Vernéřov (VE) in Bohemia (see location
Figure 5). Also plotted the field for pegmatites, within a Mn-Fe-Ta-Nb box, indicating the separation of NYF and LCT ore formations, between columbite and tapiolite. The fields of the S-granites (in blue, as well as the A-granites (green stars) are indicated. Both trends r at odds with the pegmatite box ranging between the [Mn-F] oxides and the [Nb-Ta] oxides. also indicated in inset the trends for Sn(II] towards Sn(IV) compounds.
The bulk pegmatite-forming structure is commonly attributed to the progressive crystallization of a melt of granitic composition at a highly supersaturated level. During cooling, a boundary layer of melt develops at the crystallization front. It may remain the last liquid in the pegmatite body, accounting for the decreasing number of crystals and their increasing size. Mineral zonation manifests by plagioclase, progressively increasing in An content, from An
10-20 in the outer ones. They are followed by K-feldspars and quartz. The highly contrasting diffusivities of alkalis (Na, K) compared to those of other metals (Hf, Zr, Ti, Nb and Ta) result in their differential migration, giving place to boundary-layer pile-up, with local saturation (London, 2005). This is not strange within a medium of high polarizability (
Figure 9), extending from the positive ridge between FeO and MnO towards Ta and Nb oxides.
The decrease in chemical potential follows the habitual Bowen trend (
Figure 10). With plagioclases crystallization, the other incompatible elements in major minerals concentrate, giving appearance of normally rare minerals in the sum of the first-formed and last-formed mineral assemblages of the rare-element pegmatites (Phelps et al., 2020). The final mineral assemblages contain abundance of boron as tourmaline, lithium in spodumene, petalite, and lepidolite. It represents the standard mode of solidification, by decreasing the chemical potential of the system, through successive energy cascade between potential wells (
Figure 10).
Those crystals are irregularly zoned, especially in Ti, Li, Al and Ge (Phelps et al., 2020). The variations observed are irregular with an apparent spacing (wavelength) of about 50 mm, corresponding to about 0.5 sec in terms of crystallization time. The amplitude is more difficult to estimate, varying to a scale of 10 ppm for Ge, about 0.9 order of magnitude for Li and Al. Ti is obviously the more mobile element, with departure to a global increasing doubling of the concentration. Superimposed to such a large wavelength trend, smaller variations mimic a stick-slip or sporadic variation in the flux of elements (
Figure 6). Spikes with larger amplitude are also observed (
Figure 6).
The both scales of zoning mimics those observed during melt extraction (Vigneresse & Cenki, 2022), indicating a short wavelength instability (the strike slip) and some burst, or stiction spikes when back reactions increase or decrease the local amount of melt.
4.6. Gems
Water-rich melt inclusions in some TPD show critical water concentration with about 31.6 %, (Thomas et al., 2012) which is huge, and becomes uninterpreted when such MIs decrepitate, liberating the fluids. Hence, the phase separation into glass, liquid and vapor (G, L, V) does not occur during the supercritical state (
Figure 1), obscuring their relative proportion and further interpretation. in particular, the origins of the volatile components (e.g. F, Be) remain poorly traceable.
Associated with such water-rich MI, chemical hard volatile elements (Li, Be, B) appear to segregate and be transported in such fast-moving components, and then be freed. Owing to their chemical hardness, they concentrate and form zoned bodies with a border granitic zone, and albite, with a central mantle core formed by Kfeldspar around the real core (beryl, tourmaline and spodumene). The whole mineral assemblage indicates a water- rich origin, at low temperatures (below 600 °C) within high crystalline mush (about 10 % restitic melt).
Such last MIP are enriched in volatiles, and the MI often document two generation, one with moderate Be content (some 100s ppm) close to abnormal MI with huge be content (up to 10000 ppm). Other metals in trace (V, Cr) provide the final colours of those gemstones (
Nevertheless, the tin ore have been mined in Bohemia for a long time, providing metals for wars and richness for the lords. Such mining also brought gemstones to their owner, as manifested through garnet, but more with emerald and beryl. The Habachtal deposit of emeralds, north of Saltzburg, Austria, has been mined since the Celts. It has been a large source of gemstones, up to favourably compete with the Egyptian mines, for instance coming from Mount Smaragdus or emerald Mountain, located in Wadi Sikait in Egypt's Eastern Desert, where mining probably began toward the end of the Ptolemaic period in the first century (Harrell, 2004; Giuliani et al., 2000).
The emerald mineralization in the Habachtal is geologically and tectonically complex, and previous investigators have identified fluid inclusion evidence for a hydrothermal /metamorphic origin for the emeralds. In this paper, we report the discovery of emeralds with a distinctly different inclusion population including melt inclusions, which demonstrates that at least some and probably most of the emerald mineralization in the Habachtal occurred from an extremely fluid-rich pegmatite-like aluminosilicate melt under supercritical conditions, at high temperatures and moderate pressures (~700 °C, 5 kbar).
5. Discussion
The present paper examines ore formation in transpressional context as the interactions between the energy components during melting, segregation, and emplacement of a continental-derived magma, with its inherent different viscous phases, included MIPs. Such reasoning is, apparently, at odds with the commonly formulated episodes of purely chemical evolution through differentiation. Hence the later is essentially controlled by diffusion.
Nevertheless, first, melting during transpression is a combination of basal heat (strain imposed by the far-field external stress pattern). It indicates a first interaction between the energy components.
Second, the whole magmatic evolution develops under a subcritical state, implying an oxidizing environment, and drastic effects on the solubility of metals. This is an important character of the magmatism.
Third, the formed ores, often Sn derived from the continental crust, are observed in relation with pegmatites and greisens, specific water-rich magmas, that remains within the magma chamber. This is at the depends of compounds formation with volatile, such as halogens or S-species.
Fourth, the evolution of such coarse-grain, aqueous magma, is specific, as a closed system.
Finally, the volatile elements (F, Li, Be, B) condensate as oxides, forming complex compounds of large molecules, that aggregate to form gemstones. The most known forming beryl and emerald. They segregate owing to their high polarizability and elevated chemical hardness, both being antagonist to form complex with other elements.
5.1. Caveat About Transpression
An important caveat should be stated about transpression and magmatism. All granitic intrusions (to be short) are not generated within transpressional zones. As an example, those magmas generated at the closure of a back arc are not considered as purely derived from the shear of continental crust. The largely beneficiate from mantle derived sources, i.e. at temperature of amphibole breakdown (900 °C).
Transpresssion is defined by the combination of horizontal convergence, and vertical motion (
Figure 5) due to partitioning of the deformation (Fossen & Tikoff, 1998).
The existence of a vertical motion within the plate is the consequence of the oblique convergence. Hence parallel motion of plates is continental shear, whereas orthogonal convergence is pure shear. It represents the first interaction between tectonics and magmatism (
Figure 2).
A direct consequence of this vertical motion is the inherent decompression of rocks, that controls the solubility of fluids, as first boiling. Indeed, the vertical motion is controlled by convergence velocity, some cm/yr, equivalent to a rate of 3.2 10-10 s-1. It should be compared to the tectonic rate, about 10-14 s-1. It also suggests that transpression itself is not sufficient to produce pegmatites and gems.
Depending on the convergence rate, the exsolution of MIPs is affected, in that sense that the rapid diffusing fluids (F, Li) are easily extracted from the melt, but the other volatiles of larger molar weight (Be, B) are kept into the melt. It makes the difference between TPD and usual TP, in which it the essentially the temperature that controls fluid exsolution.
5.2. Importance of a Subcritical State
In contrast with PDs, the heat source of which is generated b the plate subduction, and thus allows a perennial melting of the mantle wedge and lower crust, the TPDs strongly depend on the frictional stress generated by the oblique collision between continental plates. By nature, the oblique collision may vary in direction, thus modifying the transpressional character of the tectonics.
Nevertheless, the basal zone of friction remains close to the critical point, as attested by the lack of biotite breakdown involved, and the very low amount of mantle derived components, especially S compounds. Consequently, the transport properties of the metals through the mobile MIP acts in the segregation of metals, in spite of their low diffusivity values (
Figure 13).
The fact that the magma remains in a subcritical state also enhances metal segregation in the melt and MIPs (Thomas et al., 2019). The partition coefficients for metals into the granitic melt and into pegmatites is boosted by at least one order of magnitude.
5.3. Chemical Fate of the MIP Components
The whole fate of the magma mostly depends on the MIP conditions, since the silicate polymers that constitute the melt are function of the bulk temperature and metals are advected in such MIPs. However, the bulk evolution of these components, including oxidation, appears to be at odds from each other, between the melt, the fluids, ore formation and pegmatites, as observed in descriptors diagrams (
Figure 9).
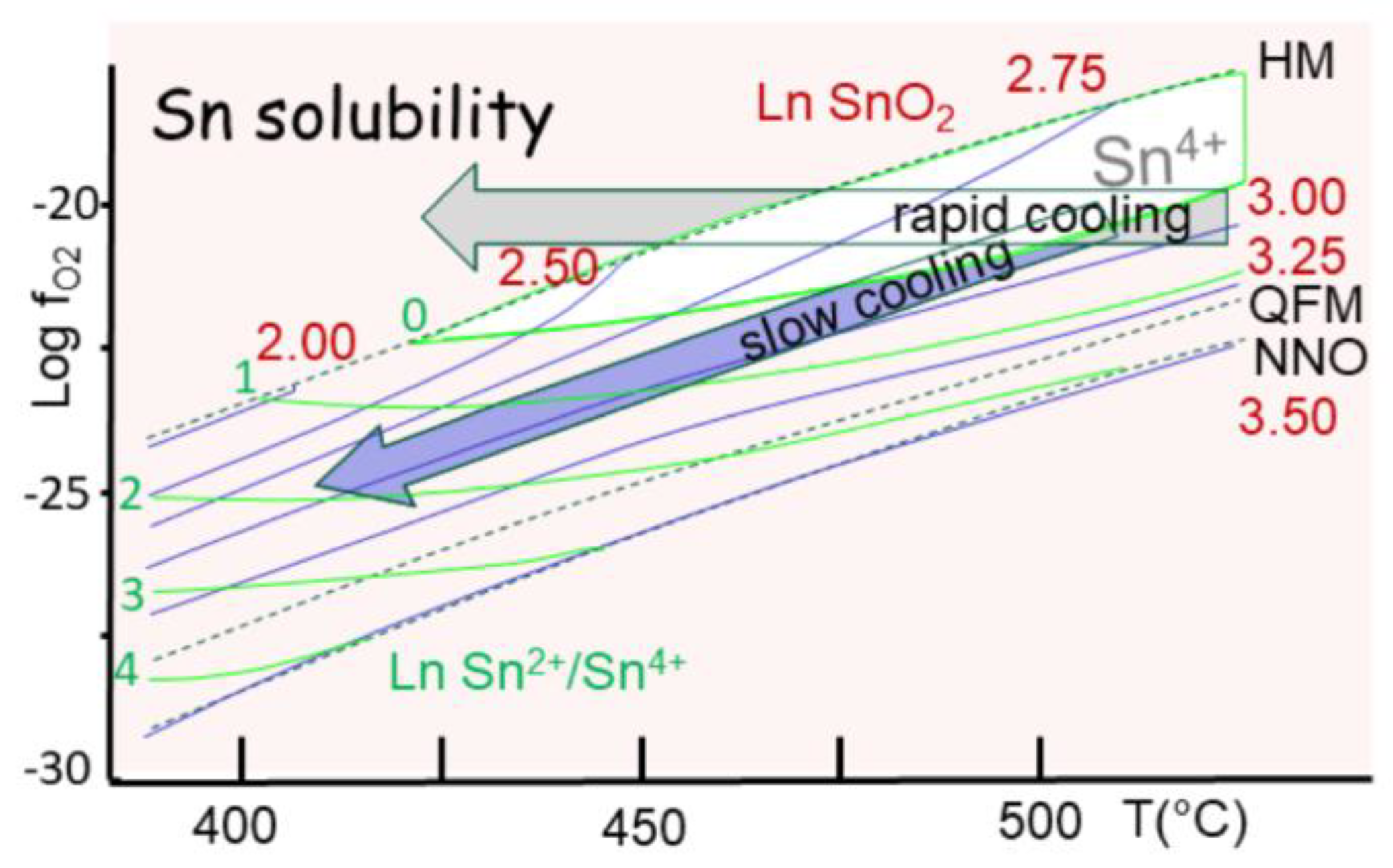
The later trend (oxidation) is the easiest to explain, since a medium under a critical state is also a powerful oxidation medium (Barner et al., 1992). It controls the evolution of tin that rapidly passes to cassiterite (SnO
2). In fact, recent studies demonstrate that Sn[IV] is already the dominant state in crustal rocks (Michaud et al., 2025). Hence, Sn[II] compounds are not as stable as Sn[IV] that involves all four outer electrons in bonding (see section 4.5). The transition occurs just above the QFM buffer, but with Sn[II] showing higher solubility than Sn[IV] (
Figure 15). In consequence, two possibilities exist for tin ore formation, oth under cassiterite. A fast cooling at constant oxygen partial pressure (f
O2) reaches the HM buffer, yielding precipitation of cassiterite (
Figure 15). In contrast, the common trend is to follow the QFM buffer during a slow cooling, and also precipitation of cassiterite.
5.3.1. The Origins of the MIP Components
This section focuses on the relationships between MIP and genesis of pegmatites and gems.
The granitic melt by itself is the product of melting of hydrous micas, muscovites and biotites. The first are phyllosilicates with K and Al, whereas, biotites are also phyllosilicates, with Mg and Fe. They are the most important carriers of rare alkalis (Li, Rb and Cs) (Gao et al., 2025). Thus, micas breakdown liberates an important amount of Li, ranging from 5000 to 35 000 ppm (Breiter et al., 2023).
The major elements enhancing the formation of pegmatites and gems are the volatile elements (F, Li, Be, B), also characterize a large chemical hardness, making them hardly compatible to form compounds with other elements. They enter the composition of lepidolite and petalite (Li compounds), associated with A-granites. in contrast, S-granites link with B
3 and BO
3 compounds linked to six SiO
3 rings, forming beryls and tourmalines. It is surprising, and paradoxical, that the light lithophile elements (Li, Be, B) also present the highest molar weight (6.941, 9.012 and 10.80 g/mole) and similar covalent radius (84 to 90 pm) , but that their silicate oxide compounds present the highest polarizability values (from 540 to 900 units) (
Figure 16). Consequently, their light weight identifies them as volatile elements, whereas their polarizability makes them hardly compatible with fluid solvent (F, Cl, S). The result is the formation and individualisation of gemstones, but with large crystallin network that accommodate trace elements (Cr, Fe, V) that give them their colours. Among the rock-forming minerals, cordierite, calcic oligoclase, and muscovite control the fate of Be in this order owing to the compatibility of Be in these phases, illustrating its affiliation with alkaline earth elements. Boron has been studied for its isotopic fractionation between modern biogenic carbonates and seawater is a function of pH (Sanyal & Bijma, 1999, Lécuyer et al., 2002). It reflects a major sink during the low-temperature alteration of oceanic crust (Smith et al., 1995), due to its adsorption on clay-rich sediments as the product of continental erosion rivers (Spivack et al., 1987). Therefore, it seems normal to find those volatile associated with sediments-derived melts.
The involved reaction mechanisms are also matter of questioning. The chemical evolution of the magma components is usually ruled by electrons exchange between components (
Figure 8). The chemical descriptors determine the reactions, according to their respective hardness. It gives place to the charge controlled (CC) and frontier molecular orbital (FMO) control (see section 2.2). Apparently, this is not the case for highly polarized molecules in pegmatites and gems. The evolution of volatiles within the MIP is also problematic.
5.3.2. MIP in Pegmatites
For simplicity, pegmatites are classified in LCT and NFY (Černý & Ercit, 2005), although a better definition is considering the host magma, from S-type and A-granites. he discussion also involves the Fe-Mn and Nb-Ta oxides box (
Figure 16 and
Figure 17). Within this box, trends are plotted rflcting the evolution of columbite, tantalite and tapiolote on the side of A-granites, and petalite on the side of S-magmas (
Figure 16). This is essentially based on the reactive content in each oxide.
Minerals yielding pegmatites, present elevated polarizability (
Figure 16b). For anions, polarizability is directly proportional to its charge and to its size. Polarizability increases as the volume occupied by electrons increases. This occurs because larger atoms have more loosely held electrons in contrast to smaller atoms with tightly bound electrons. Within halogens, F is the least polarizable while Iodine is the most polarizable. Indeed, iodine has a larger and more diffuse electron cloud, allowing electron movement within the electron cloud. Both Ta
2O
5 and Nb
2O
5 present heavy molecules, 442.9 and 265.8 g/Omole respectively.
Of more interest, the charge exchange (Eq. 9). is computed from one pole (Fe O or MnO towards another place within the box (
Figure 16c) The involved charges are not very large, hardly reaching 1 eV. It demonstrates that the evolution is nearly continuous between the elements constituting pegmatites, explaining the easy growth of crystals. No rate can be inferred from such diagrams.
The apparent symmetry between the sub-categories (NYF and LCT) also indicates that process should occur with the same mechanism in both magma types. Nevertheless, the A-type seems controlled by Be whereas Li should control the S-magma. This agrees with the deep origin in the crust of such fluids.
5.3.3. MIP in Gemstones
The situation becomes extreme when considering gemstones that are ubiquitously observed associated with LCT type pegmatites (
Figure 17). Such magmas present molar weight around 50 g/mole with FeO and MnO indicating 72 and 71 g/mole. In contrast gems from the beryl (Be
3Al
2(SiO
3)
6 family show values between 276 and 538 g/mole upward towards the extreme represented by emeralds (Be
3Al
2(SiO
3)
, with values depending on the trace elements inducing the colours (Giuliani et al., 2019). Gems from the boron series consist in tourmaline with formula (NaMg
3Al
6(BO
3) (SiO
3)
6 (OH)
6, and molar mass about 940 g/mole, correlated with polarizabilities. The later values are difficult to estimate because of their tiny content in trace element (V, Cr) providing their colour.
Figure 17.
Box of the pegmatites within [c-h] coordinates (rotated for conveniency) and enlarged for readability. Within the box, the trends for gems are indicated, lepidolite and petalite for A-granites, beryls, emeralds and spodumene for S-granites. Indicated also as proxies, the molecular weight in g/mole and the value of polarizability (a) in cm-3/.
Figure 17.
Box of the pegmatites within [c-h] coordinates (rotated for conveniency) and enlarged for readability. Within the box, the trends for gems are indicated, lepidolite and petalite for A-granites, beryls, emeralds and spodumene for S-granites. Indicated also as proxies, the molecular weight in g/mole and the value of polarizability (a) in cm-3/.
5.4. Contrasting Behaviour of Metals, Pegmatites and Gems
The observations of melt inclusions in granites, ores, pegmatites, and gems tell a different story (Thomas &. Rericha, 2024). There spatial distribution is non-random, corresponding to different mechanisms ruling their intrinsic repartition.
Commonly, fluid and melt inclusions should be organized in a random or no-random manner. In the last case, three distributions are usually observed revealing their mechanism of formation, following a Gauss, Lorentz or Dirac pattern, each reflets the energy interaction between them. The case of randomly distributed pattern indicates no interaction, as expected. Conversely, a Gaussian distribution, in which each group of particles follows a normal shaped-bell distribution indicates a diffusive interaction between particles. In a group, the density function of random variables presents an equal probability with the expected value at the maximum of the curve, and its variance s
2 controls the width of the curve at mid-height (
Figure 11a). in a second group, or Lorentzian distribution, the density function takes the shape of a triangle, the summit angle of which is the expected value, but has no variance (
Figure 11b). At last, the triangular shape shrinks again, forming a Dirac distribution (
Figure 11c) just represented by a segment of line with maximum at the expected value, and nil elsewhere.
In a pioneering study, the distribution of melt inclusions in pegmatites was characterized as Gaussian, whereas tin deposits present a Lorentzian distribution, with sharp peaks, indicating a distribution under which both the expected value and its variance are undefined (Thomas & Rericha, 2024). It corresponds to spikes in the sudden release of tin. In contrast, the rare melt inclusions in gems indicate a Dirac distribution, with only local spikes (
Figure 11c). Their low temperature of formation (400-450 °C) indicates a late crystallization, i.e. an highly evolved fluid quasi mono mineral.
The interpretation of the three distributions becomes evident, when considering the interactions between melt inclusions during their formation. In the case of tin ore, melt and ore present similar values of chemical hardness and polarizability. Their interactions are akin to diffusion, resulting in melt inclusions equally affected by the interactions during cascading energy (
Figure 11). Conversely, in pegmatites, the increase of polarizability contrast turns the shape bell curve into a Lorentzian triangle. The effect is still reinforced for gems, with the double effect of chemical hardness and polarizability contrasts. Their low temperature of formation (400-450 °C) indicates a late crystallization, i.e. an highly evolved fluid quasi mono mineral, justifying the Dirac distribution.
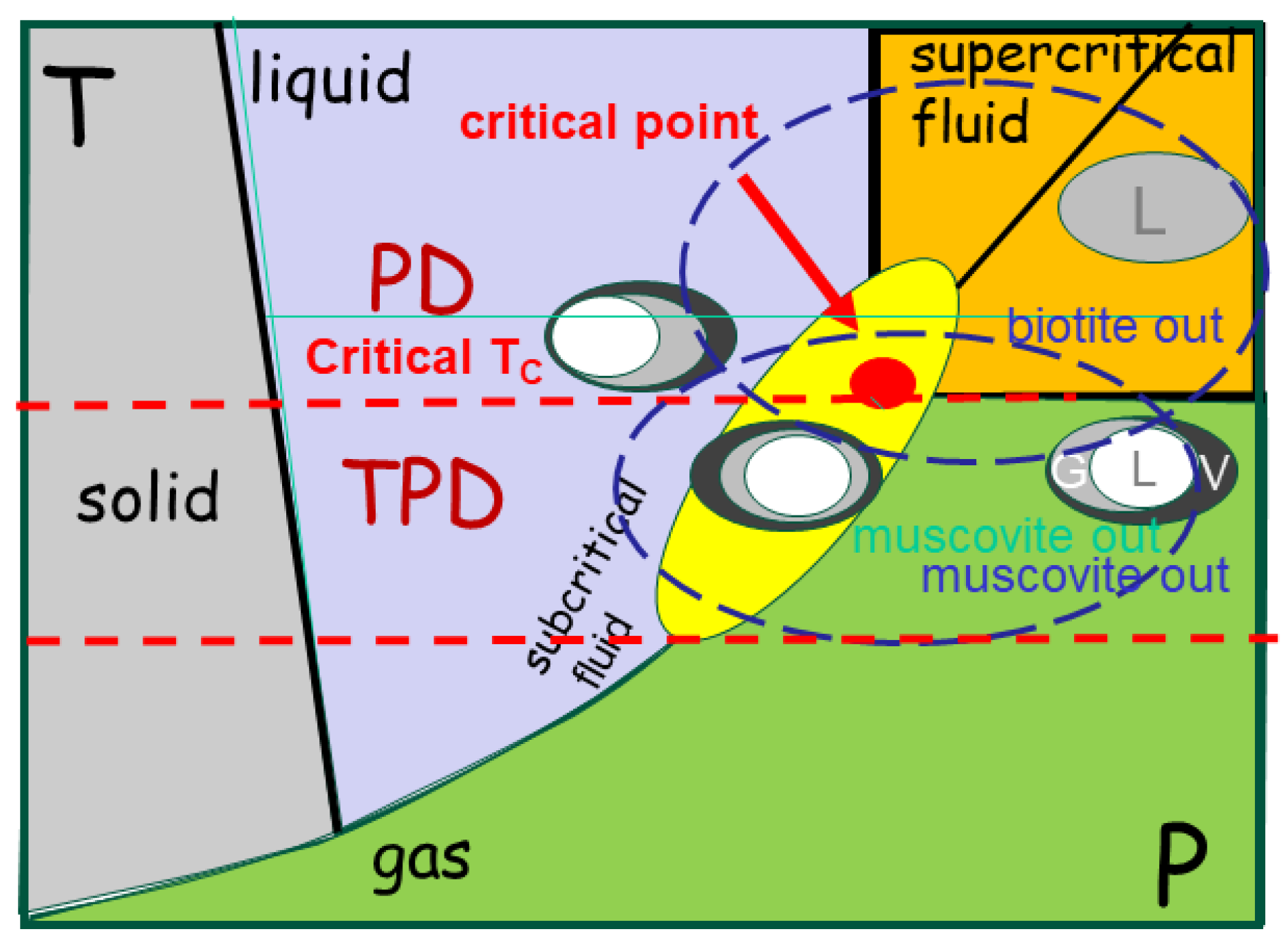
Figure 1.
Schematic representation of phase change mapping under subcritical conditions. Te system passes through the solid, liquid and fluids conditions, whereas the gas phase is reached at high pressure. Melting is scaled as minerals (muscovite, biotite and amphibole) are involved. At 731 C°, the critical temperature, the fluid phase splits in two MIPs (Liquid, Vapour, Glass) illustrated by the melt inclusions (MI). The system cools from supercritical state, where solubility is quasi-infinite. MPIs become subcritical, splitting into a silicate-rich and a fluid-rich phase as observed in melt inclusions.
Figure 1.
Schematic representation of phase change mapping under subcritical conditions. Te system passes through the solid, liquid and fluids conditions, whereas the gas phase is reached at high pressure. Melting is scaled as minerals (muscovite, biotite and amphibole) are involved. At 731 C°, the critical temperature, the fluid phase splits in two MIPs (Liquid, Vapour, Glass) illustrated by the melt inclusions (MI). The system cools from supercritical state, where solubility is quasi-infinite. MPIs become subcritical, splitting into a silicate-rich and a fluid-rich phase as observed in melt inclusions.
Figure 2.
Phase diagram presented for different situations. a). Traditional 2D diagram, in pression temperature (P, T) for solid/liquid/gas transition with the binary boundaries, including a triple point with the three phases in contact and a critical point above which the material enters a supercritical fluid, with disappearance of the meniscus between them. The triple and critical points are specified by their respective pressure and temperature. b) 3D phase diagram for crystal/melt modified from a former version of Liu & Nagel (1998). The usual variables of the energy are used such as T, S or temperature and entropy; N, m or density and chemical potential; and s, e, or stress and strain. The binary transition between crystal and melt gives place to a transitional stage where ions, glass and polymers develop, creating a fabric, and jamming, and proceed through nucleation and dislocations. During the phase transition, that commonly involves energy, exchanges occur between the components (S, m, e), allowing readjusting the energy variation.
Figure 2.
Phase diagram presented for different situations. a). Traditional 2D diagram, in pression temperature (P, T) for solid/liquid/gas transition with the binary boundaries, including a triple point with the three phases in contact and a critical point above which the material enters a supercritical fluid, with disappearance of the meniscus between them. The triple and critical points are specified by their respective pressure and temperature. b) 3D phase diagram for crystal/melt modified from a former version of Liu & Nagel (1998). The usual variables of the energy are used such as T, S or temperature and entropy; N, m or density and chemical potential; and s, e, or stress and strain. The binary transition between crystal and melt gives place to a transitional stage where ions, glass and polymers develop, creating a fabric, and jamming, and proceed through nucleation and dislocations. During the phase transition, that commonly involves energy, exchanges occur between the components (S, m, e), allowing readjusting the energy variation.
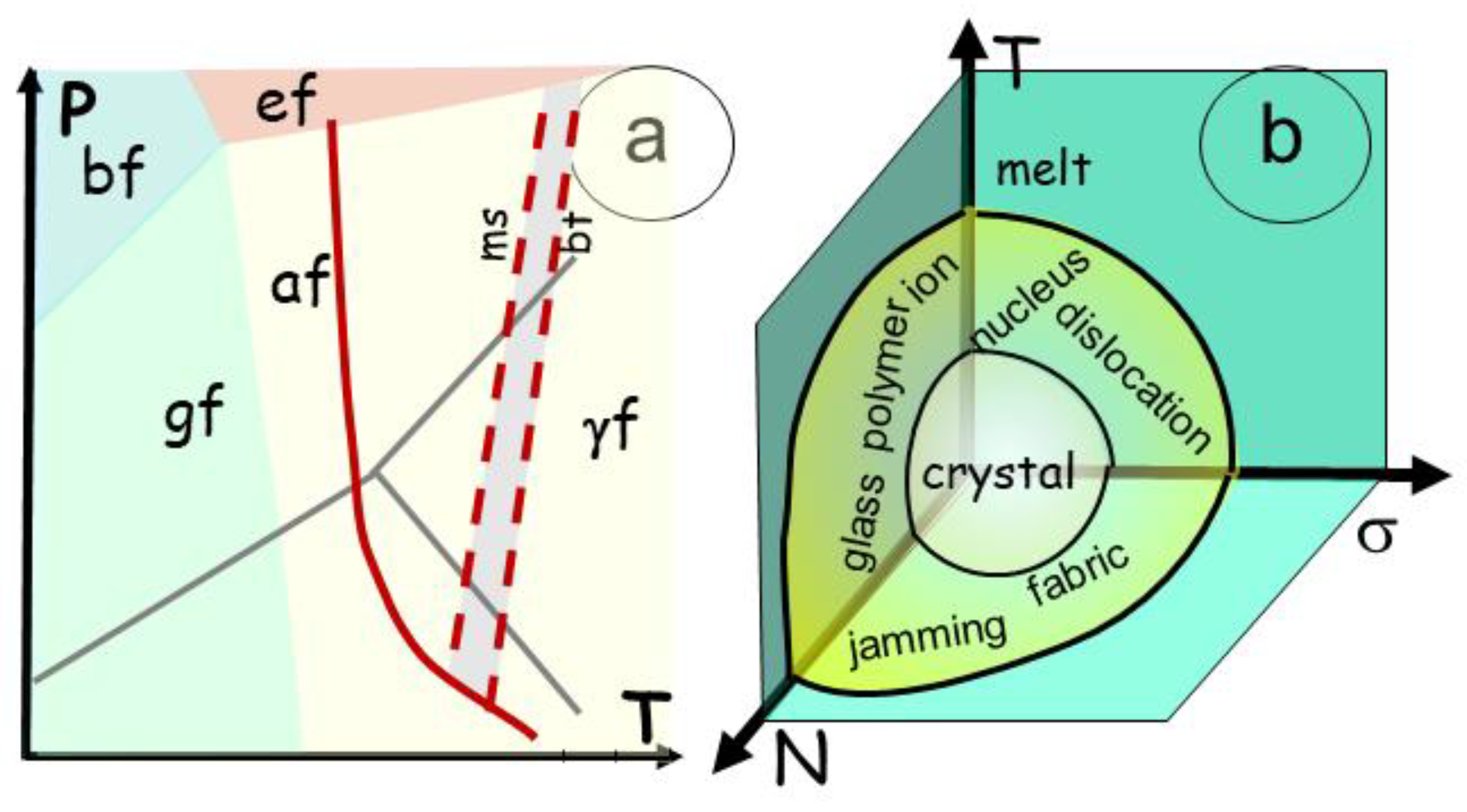
Figure 3.
Two phase transition described in a T versus time(t) and T versus concentration (N) a) In a binary transition, a melting temperature (Tm) determines the abrupt change from a solid to a liquid, the concentration in elements is similar in both states. b) Conversely, when the material has several components, the transition adopts the path of the two curves of melting for material TmA and TmB. The result is a domain in which the composition follows the curves of melting. The transitional zone may be a single domain, or several coexisting domains with an eutectic point and an eutectic composition determining the lowest melting temperature of the mixture.
Figure 3.
Two phase transition described in a T versus time(t) and T versus concentration (N) a) In a binary transition, a melting temperature (Tm) determines the abrupt change from a solid to a liquid, the concentration in elements is similar in both states. b) Conversely, when the material has several components, the transition adopts the path of the two curves of melting for material TmA and TmB. The result is a domain in which the composition follows the curves of melting. The transitional zone may be a single domain, or several coexisting domains with an eutectic point and an eutectic composition determining the lowest melting temperature of the mixture.
Figure 4.
Regime of continental crust deformation, a) illustrating continental shear, manifested by horizontal displacement of blocs, without vertical motion, and b) transpressional dextral shear. Decoupling occurs at the brittle/ductile transition of quartz (bdq) and brittle/ductile transition of feldspar (bdf), above a brittle Moho. The regime of stress is also indicated (the so-called fir-tree) that reflect the maximum stress of the material.
Figure 4.
Regime of continental crust deformation, a) illustrating continental shear, manifested by horizontal displacement of blocs, without vertical motion, and b) transpressional dextral shear. Decoupling occurs at the brittle/ductile transition of quartz (bdq) and brittle/ductile transition of feldspar (bdf), above a brittle Moho. The regime of stress is also indicated (the so-called fir-tree) that reflect the maximum stress of the material.
Figure 5.
Reconstructed map of the Variscan deformation belt from eastern Canada to Bohemia. The belt is intruded several granitic massifs shown b dots (S-type) and stars (A-type). The whole belt is submitted to a dextral shear, manifested y shear zones. The magma categories (A- and S-types) are identified by the MgO and Fe2O3 (inset).
Figure 5.
Reconstructed map of the Variscan deformation belt from eastern Canada to Bohemia. The belt is intruded several granitic massifs shown b dots (S-type) and stars (A-type). The whole belt is submitted to a dextral shear, manifested y shear zones. The magma categories (A- and S-types) are identified by the MgO and Fe2O3 (inset).
Figure 6.
Simulation of melt extraction (Vigneresse & Cenki, 2021) thou gh a cellular automaton. The amount of melt extracted by step depends on the initial melt percentage (f0), but produces a sporadic motion. When one parameter is changed during a run, a stiction spike appears that rapidly returns to the stationary state. After normalization to the initial melt and the dimension of the cell network, values converge toward a coefficient of melt extraction (me). The spikes and the stick-slip like motion depend on the amount of flow (its content) and its accelerations. Two regimes, regular or stationary and transient, are observed depending on whether the initial conditions, especially permeability varies during a run, inducing spikes (Dm) and stick-slip motion with amplitude sm).
Figure 6.
Simulation of melt extraction (Vigneresse & Cenki, 2021) thou gh a cellular automaton. The amount of melt extracted by step depends on the initial melt percentage (f0), but produces a sporadic motion. When one parameter is changed during a run, a stiction spike appears that rapidly returns to the stationary state. After normalization to the initial melt and the dimension of the cell network, values converge toward a coefficient of melt extraction (me). The spikes and the stick-slip like motion depend on the amount of flow (its content) and its accelerations. Two regimes, regular or stationary and transient, are observed depending on whether the initial conditions, especially permeability varies during a run, inducing spikes (Dm) and stick-slip motion with amplitude sm).
Figure 7.
Chemical reaction between A and B elements, represented within a [w-h] diagram, a being the content in one element (7a). The descriptors illustrate the energy parabola (E), with its point of tangency to the chemical potential (m) and radius of curvature (h) and osculating circle (w) in a normal plane. The reaction between elements A and B supposes the two energy curves mingle into a single (7b). Two situations may develop. The energy curve is distorted, with two minima (7c) and return to a stable state operates with anw formed element, and the energy curve is again a parabola (7d). When the energy gap is too large, a positive energy remains (7e) and the reactions yields two incompatible elements that do not mix (7f).The incompatible zone also marks by higher polarizability.
Figure 7.
Chemical reaction between A and B elements, represented within a [w-h] diagram, a being the content in one element (7a). The descriptors illustrate the energy parabola (E), with its point of tangency to the chemical potential (m) and radius of curvature (h) and osculating circle (w) in a normal plane. The reaction between elements A and B supposes the two energy curves mingle into a single (7b). Two situations may develop. The energy curve is distorted, with two minima (7c) and return to a stable state operates with anw formed element, and the energy curve is again a parabola (7d). When the energy gap is too large, a positive energy remains (7e) and the reactions yields two incompatible elements that do not mix (7f).The incompatible zone also marks by higher polarizability.
Figure 8.
HOMO-LUMO definition and illustration for two fluids (F, Cl) in ionic state, respectively classified as hard and soft. Two metallic ions (Sn2+ and Cu2+) are also represented, that are respectively soft and hard. From the energy level of the highest and lowest occupied/unoccupied molecular orbital (HOMO-LUMO), hardness and electronegativity are computed as the half sum and difference between ionization and electron affinity. Chemical hardness corresponds to contrasted values of HOMO-LUMO as evidenced for F- and Cu2+. In inset, the corresponding definition of the chemical descriptors, chemical potential (m) and hardness (m), with the major mechanisms, charge control (CC) and frontier molecular orbital (FMO) that control reactions.
Figure 8.
HOMO-LUMO definition and illustration for two fluids (F, Cl) in ionic state, respectively classified as hard and soft. Two metallic ions (Sn2+ and Cu2+) are also represented, that are respectively soft and hard. From the energy level of the highest and lowest occupied/unoccupied molecular orbital (HOMO-LUMO), hardness and electronegativity are computed as the half sum and difference between ionization and electron affinity. Chemical hardness corresponds to contrasted values of HOMO-LUMO as evidenced for F- and Cu2+. In inset, the corresponding definition of the chemical descriptors, chemical potential (m) and hardness (m), with the major mechanisms, charge control (CC) and frontier molecular orbital (FMO) that control reactions.
Figure 10.
Sequence of crystallization from olivine to quartz, extended from MgO to SiO2, according to Bowen’s trend, but using the chemical descriptors showing a linear decrease in chemical potential. The descriptors are the first derivative, electronegativity (m) is the chemical potential changed of sign, plus the chemical hardness (h) and electrophilicity (w), second derivatives, tangential and normal, of the Gibbs energy. All values are in same units (eV). The intermediate points are those, experimentally derived, of the line of descent from olivine to quartz (Faure & Tissandier, 2014). The range of major minerals (olivine, pyroxenes, plagioclases and quartz) are indicated. The evolution follows a line of descent on which the chemical potentials are tangent. The aperture of the curve is the chemical hardness, akin to the radius of curvature.
Figure 10.
Sequence of crystallization from olivine to quartz, extended from MgO to SiO2, according to Bowen’s trend, but using the chemical descriptors showing a linear decrease in chemical potential. The descriptors are the first derivative, electronegativity (m) is the chemical potential changed of sign, plus the chemical hardness (h) and electrophilicity (w), second derivatives, tangential and normal, of the Gibbs energy. All values are in same units (eV). The intermediate points are those, experimentally derived, of the line of descent from olivine to quartz (Faure & Tissandier, 2014). The range of major minerals (olivine, pyroxenes, plagioclases and quartz) are indicated. The evolution follows a line of descent on which the chemical potentials are tangent. The aperture of the curve is the chemical hardness, akin to the radius of curvature.
Figure 11.
Cascading energy in saturated lakes. a) In case of low global slope, few cascades occur, whereas the saturated lakes flow between them in case of strong slope. The change in instability style is progressive. b) The process occurs in successive steps, releasing energy, between potential wells. Avalanches describe the transition since the local energy release adds to neighboring changes. The global process is a Gaussian distribution of matter. c) In case of successive potential wells, each energy variation is an individual process, that does not relate to the previous history of the flow. d) It occurs through a Lorentzian distribution, triangular in shape. e) in contrast, in a Diracian distribution, the filling occurs on a discrete point point and the rest of the system is free. f) in total the Dirac distribution is a suite of values at each successive point, mimicking the Dirac comb. The successive distributions are respectively caused by diffusion, chemical potential values, and conjugate of chemical hardness and polarizability.
Figure 11.
Cascading energy in saturated lakes. a) In case of low global slope, few cascades occur, whereas the saturated lakes flow between them in case of strong slope. The change in instability style is progressive. b) The process occurs in successive steps, releasing energy, between potential wells. Avalanches describe the transition since the local energy release adds to neighboring changes. The global process is a Gaussian distribution of matter. c) In case of successive potential wells, each energy variation is an individual process, that does not relate to the previous history of the flow. d) It occurs through a Lorentzian distribution, triangular in shape. e) in contrast, in a Diracian distribution, the filling occurs on a discrete point point and the rest of the system is free. f) in total the Dirac distribution is a suite of values at each successive point, mimicking the Dirac comb. The successive distributions are respectively caused by diffusion, chemical potential values, and conjugate of chemical hardness and polarizability.
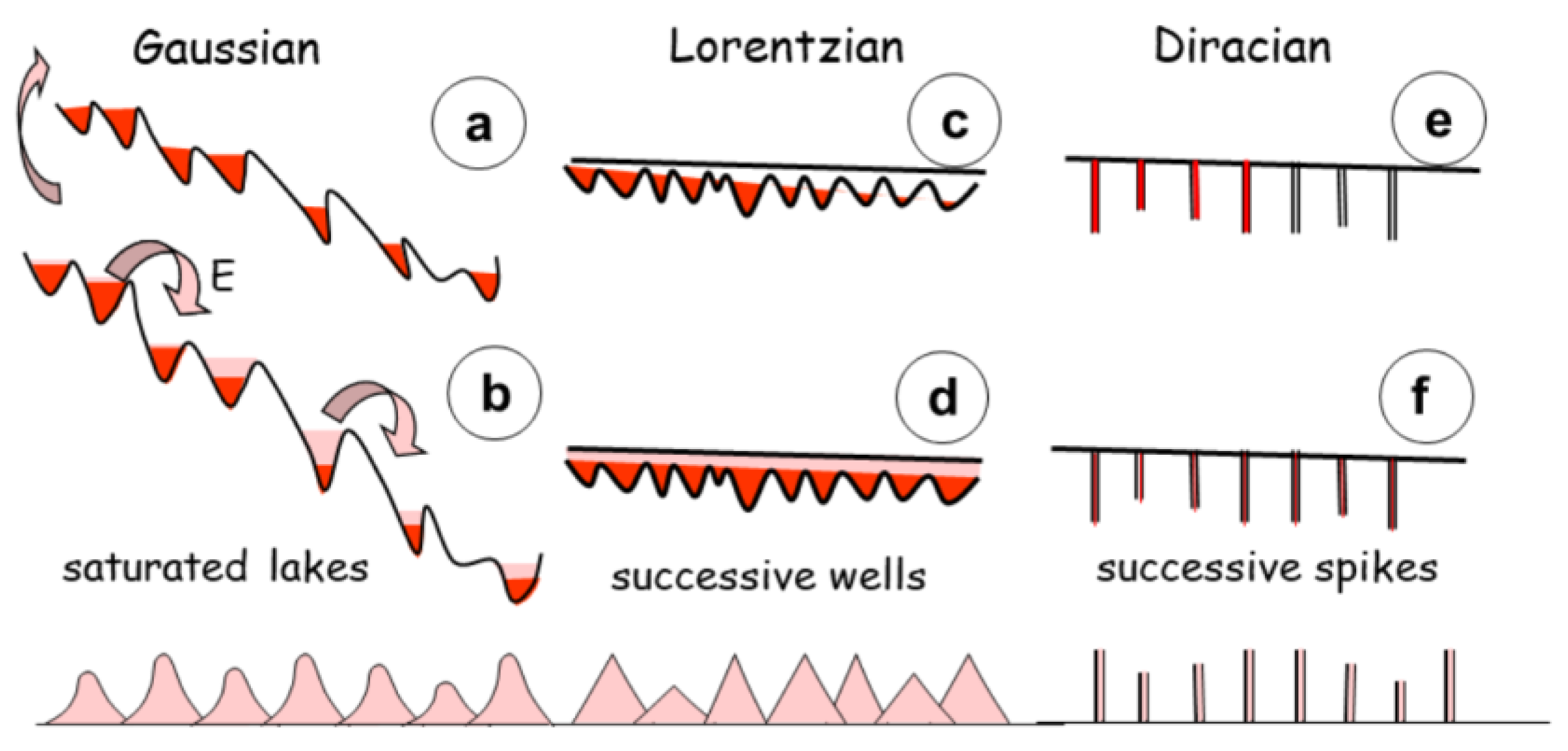
Figure 13.
Diffusivity values (in Log10 and units in m2/s) as a function of temperature (Zhang et al., 2010) curves for Sn into wet trachyte (65 % SiO2) and dry phonolite (55 % SiO2). In complement to Sn, diffusivity values for Mn and Fe (dashes) in andesite and phonolite have been extrapolated from experiments, since they are Arrhenian. Plotted on the same diagram, values for Nb and Ta. In the range of ore formation temperature around 750 °C, the diffusivity values for these metals range over four orders of magnitude.fr comparison, the diffusivity of trace elements, from Rb to Hf is indicated for wet trachyte (Behrens & Hahn, 2009) showing the inversion of values at about 1000 °C. also indicated on the diagram, the characteristic diffusion length that translate the diffusivity values in velocity. The effect of which is quasi uneffective at low temperatures, giving argument for tin segregation unrelated to simple chemical differentiation.
Figure 13.
Diffusivity values (in Log10 and units in m2/s) as a function of temperature (Zhang et al., 2010) curves for Sn into wet trachyte (65 % SiO2) and dry phonolite (55 % SiO2). In complement to Sn, diffusivity values for Mn and Fe (dashes) in andesite and phonolite have been extrapolated from experiments, since they are Arrhenian. Plotted on the same diagram, values for Nb and Ta. In the range of ore formation temperature around 750 °C, the diffusivity values for these metals range over four orders of magnitude.fr comparison, the diffusivity of trace elements, from Rb to Hf is indicated for wet trachyte (Behrens & Hahn, 2009) showing the inversion of values at about 1000 °C. also indicated on the diagram, the characteristic diffusion length that translate the diffusivity values in velocity. The effect of which is quasi uneffective at low temperatures, giving argument for tin segregation unrelated to simple chemical differentiation.
Figure 14.
Commonly used pegmatite classification, in LCT and NYF, or S-type and A-type granites, but represented in a diagram of K/Rb (differentiation) versus Ga content. Data are redrawn from Wise et al., (2022). They show a separation between the two groups that may be approximated by ln(K/Rb) = -0.6 ln (Ga) + 2.1. It indicates the important enrichment (ppm) in gallium (Ga), probably generated by garnet or pyroxene melting in the lower continental crust.
Figure 14.
Commonly used pegmatite classification, in LCT and NYF, or S-type and A-type granites, but represented in a diagram of K/Rb (differentiation) versus Ga content. Data are redrawn from Wise et al., (2022). They show a separation between the two groups that may be approximated by ln(K/Rb) = -0.6 ln (Ga) + 2.1. It indicates the important enrichment (ppm) in gallium (Ga), probably generated by garnet or pyroxene melting in the lower continental crust.
Figure 15.
Solubility of tin (in log ppm) under its two aspects Sn[II]) and Sn[IV] (redrawn from Liu et al., 2023). Tin is essentially sensible to redox, in between the nickel-nickel oxide (NNO), quartz-fayalite-magnetite (QFM) and hematite-magnetite (HM) buffers. All indicated by dashes. The field of Sn[IV] dominant is indicated, close to HM trend. Two modes of cooling are superimposed to the buffers. One is rapid at constant fO2, and the second slower, follows the buffers, both are indicated from above 500 to about 420 °C.
Figure 15.
Solubility of tin (in log ppm) under its two aspects Sn[II]) and Sn[IV] (redrawn from Liu et al., 2023). Tin is essentially sensible to redox, in between the nickel-nickel oxide (NNO), quartz-fayalite-magnetite (QFM) and hematite-magnetite (HM) buffers. All indicated by dashes. The field of Sn[IV] dominant is indicated, close to HM trend. Two modes of cooling are superimposed to the buffers. One is rapid at constant fO2, and the second slower, follows the buffers, both are indicated from above 500 to about 420 °C.
Figure 16.
Field of the pegmatites within a [c-h] coordinates (rotated, indicating a) the change in chemical composition between A-type and S-type granites, b) change in hardness, c) charge exchange from one pole to the other. a) Box of the pegmatites within [c-h] coordinates (rotated for conveniency). a) The box is calibrated in a / (a+b), indicating the respective ratio of Fe and Mn compared to Ta and Nb. The fields of A and S granites, corresponding to NYF and LCT pegmatites, are indicated. Plotted, the fields of columbite, tantalite, tapiolite and petalite, spodumene and beryl are indicated. b) same box, but calibrated in polarizability, showing the large difference between oxides (about 2 to 100). c) Charge exchange computed between the poles of the pegmatite box. The change is always low (below 1 unit) increasing from Fe-Mn to Ta-Nb oxides.
Figure 16.
Field of the pegmatites within a [c-h] coordinates (rotated, indicating a) the change in chemical composition between A-type and S-type granites, b) change in hardness, c) charge exchange from one pole to the other. a) Box of the pegmatites within [c-h] coordinates (rotated for conveniency). a) The box is calibrated in a / (a+b), indicating the respective ratio of Fe and Mn compared to Ta and Nb. The fields of A and S granites, corresponding to NYF and LCT pegmatites, are indicated. Plotted, the fields of columbite, tantalite, tapiolite and petalite, spodumene and beryl are indicated. b) same box, but calibrated in polarizability, showing the large difference between oxides (about 2 to 100). c) Charge exchange computed between the poles of the pegmatite box. The change is always low (below 1 unit) increasing from Fe-Mn to Ta-Nb oxides.