Geometric Insights into the Goldbach Conjecture

1. Introduction

The Goldbach conjecture, one of the most enduring unsolved problems in number theory, posits that every even integer greater than 2 can be expressed as the sum of two prime numbers [1]. The strong form of this conjecture, often referred to as the binary Goldbach conjecture, remains unproven despite extensive computational verification for numbers up to very large magnitudes [2]. In this note, we explore a slight modification of this conjecture and provide a geometric interpretation that links it to properties of squares and semiprimes.

Specifically, consider the following variant: Every even integer greater than or equal to 8 is the sum of two distinct prime numbers. This adjustment excludes the cases $4=2+2$ (the only sum of identical primes) and $6=3+3$, aligning with our geometric construction which requires distinct factors $P\ne Q$ and $N\ge 4$ (implying $2N\ge 8$).

We establish an equivalence between this variant and a geometric statement involving nested squares. This connection not only offers a novel visualization but also highlights the interplay between arithmetic progressions and the factorization of differences of squares.

2. Geometric Construction

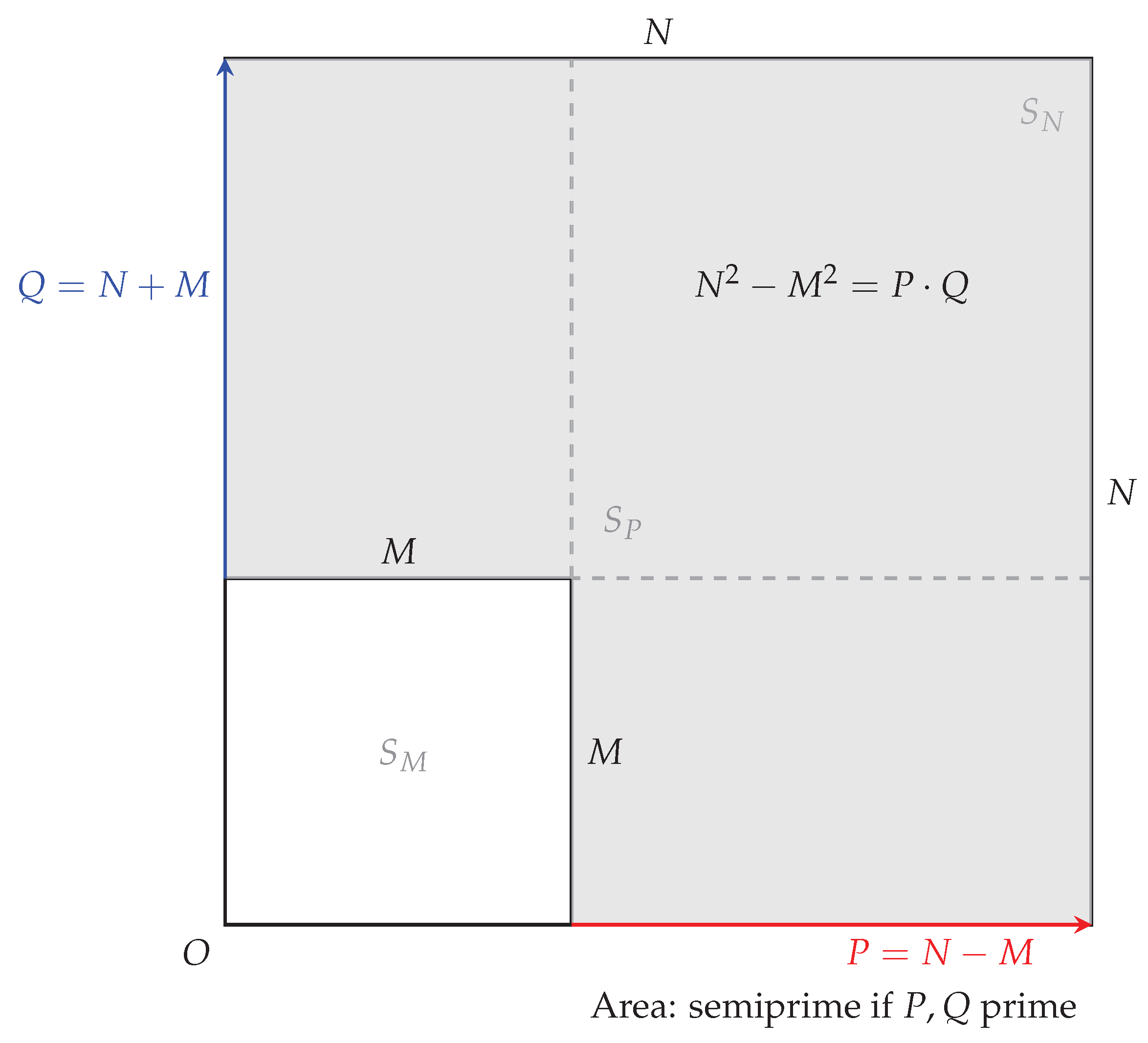
Consider a square $S_N$ with integer side length $N\ge 4$, so its area is $N^2$. Inscribe within $S_N$ another square $S_M$ with integer side length M, where $1\le M\le N-3$, such that $S_M$ shares one corner with $S_N$ (without loss of generality, the bottom-left corner). The region between $S_N$ and $S_M$ forms an L-shaped annulus with area $N^2-M^2$.

The difference of squares factors as

$$N^2-M^2=(N-M)(N+M).$$

Define $P=N-M$ and $Q=N+M$. We analyze the constraints on P and Q imposed by the bounds on M:

• $M\ge 1\Rightarrow P=N-M\le N-1$ and $Q=N+M\ge N+1$.
• $M\le N-3\Rightarrow P=N-M\ge N-(N-3)=3$.

Thus, we have $3\le P\le N-1$ and $Q\ge N+1$. Since $M\ge 1$, it is clear that $P<Q$.

The sum of these factors is

$$P+Q=(N-M)+(N+M)=2N,$$

which is an even integer $\ge 8$ (since $N\ge 4$). The difference of the factors is $Q-P=(N+M)-(N-M)=2M$, which is also even.

Since P and Q have an even sum ($2N$) and an even difference ($2M$), they must have the same parity. For P and Q to both be prime with $P\ge 3$, they must both be odd primes. Therefore, P and Q must be distinct odd primes.

The area $N^2-M^2=P·Q$ is a semiprime (a product of two primes) if and only if both factors P and Q are prime. Our construction requires them to be distinct odd primes.

The variant of Goldbach’s conjecture is therefore equivalent to the following geometric assertion:

Theorem 1

(Geometric Goldbach Variant). For every integer $N\ge 4$, there exists an integer M with $1\le M\le N-3$ such that the L-shaped region between the squares $S_N$ and $S_M$ (sharing a corner) has area equal to a semiprime $P·Q$, where $P=N-M$ and $Q=N+M$ are distinct primes.

This equivalence holds bidirectionally: If $2N=p+q$ for distinct primes $p<q$, we can set $N=(p+q)/2$.

• Since $2N\ge 8$ and $p,q$ are distinct, they must be distinct odd primes.
• Since p and q are odd, their sum and difference are even, so $N=(p+q)/2$ and $M=(q-p)/2$ are integers.
• We must check that M satisfies $1\le M\le N-3$.
• $M\ge 1$: $(q-p)/2\ge 1\Rightarrow q-p\ge 2$. Since $p,q$ are distinct odd primes, this is true.
• $M\le N-3$: $(q-p)/2\le (p+q)/2-3\Rightarrow q-p\le p+q-6\Rightarrow -p\le p-6\Rightarrow 6\le 2p\Rightarrow 3\le p$. Since p is an odd prime, $p\ge 3$, so this is always satisfied.

Thus, any Goldbach partition $2N=p+q$ (with distinct odd primes) corresponds exactly to a valid geometric construction with $P=p$, $Q=q$, and $M=(q-p)/2$, yielding the semiprime area $p·q$.

Conversely, given a valid geometric construction with $P=N-M$ and $Q=N+M$ both prime, then $P+Q=2N$, so $2N$ is the sum of two distinct primes.

To illustrate, Figure 1 depicts the construction for a generic N and M.

3. Deeper Analysis and Implications

The above equivalence provides a bridge between additive number theory and geometric dissections. For a fixed $N\ge 4$, the conjecture is true if there exists at least one $M\in \{1,2,\dots ,N-3\}$ such that $P=N-M$ and $Q=N+M$ are both prime. Since $Q=N+M=N+(N-P)=2N-P$, this is precisely the statement that for a given $N\ge 4$, there exists a prime P in the range $[3,N-1]$ such that $2N-P$ is also prime.

This is exactly the Goldbach partition for $2N$ into two primes P and Q. As $N\ge 4$, $2N\ge 8$. As shown, P and Q must be distinct odd primes. The geometric view, therefore, recasts the search for a Goldbach partition as a search for an integer M that defines an L-shaped “frame” with a semiprime area.

Computational evidence strongly supports the conjecture: For N up to $2\times {10}^{17}$ (corresponding to even numbers up to $4\times {10}^{18}$), such a partition has always been found [2]. Analytically, the Hardy–Littlewood conjecture estimates that the number of such partitions $g\left(2N\right)$ grows as $g\left(2N\right)\sim 2C_2{\displaystyle \frac{N}{{(log\left(2N\right))}^2}}$, suggesting not only that at least one partition exists, but that the number of them grows with N [3].

4. Novel Approach on this Perspective

From the previous analysis, we have $P=N-M$ and $Q=N+M$. The area $P·Q=(N-M)(N+M)$ admits a natural geometric interpretation via the L-shaped region in Figure 1.

This region consists of a vertical rectangle of dimensions $M\times P$ (the top arm) and a horizontal rectangle of dimensions $N\times P$ (the right arm, accounting for the full height N), yielding total area $MP+NP=P(N+M)=P·Q$.

Alternatively, the dashed square $S_P$ (of side $P=N-M$, positioned from the top-right corner of $S_M$ to the top-right corner of $S_N$) highlights a complementary decomposition: the L-shaped region equals the area of $S_P$ (namely $P^2$) plus two adjacent rectangles each of area $P\times M$ (one horizontal along the bottom-right and one vertical along the top-left, excluding the overlap covered by $S_P$). This confirms $N^2-M^2=P^2+2PM$, which expands to ${(N-M)}^2+2M(N-M)=N^2-M^2$, verifying the identity tautologically.

The key geometric insight, however, derives from relating P and Q directly to the side lengths N and M. Observe that $P=N-M$ measures the extension beyond $S_M$ along either arm of the L-shape (horizontal width or vertical height). The full side N of $S_N$ thus decomposes as the inner side M plus this extension P, so $N=M+P$. Meanwhile, $Q=N+M$ extends this by adding the inner side M once more—geometrically, Q spans the full height N of $S_N$ plus the height M of $S_M$, evoking a “doubled” vertical traversal from the shared corner O outward and inward.

Subtracting these lengths yields

$$Q-P=(N+M)-(N-M)=2M,$$

and solving gives the explicit formula

$$M={\displaystyle \frac{Q-P}{2}}.$$

For $N\ge 4$ (ensuring $2N\ge 8$), any distinct primes $P<Q$ with $P+Q=2N$ (both odd, hence $Q-P$ even) produce an integer $M\ge 1$ satisfying $M\le N-3$, as $Q\le 2N-3$ (next prime after $P\ge 3$) implies $M\le (2N-6)/2=N-3$. This bidirectionally links the arithmetic partition to the geometric embedding. Instead of focusing on the semiprime area $P·Q$, we now focus on the set of distinct values of M generated by straddling prime pairs. For a given $N\ge 4$, let $D_N$ be the set of all integers M such that

$$D_N=\left\{M={\displaystyle \frac{Q-P}{2}}\mid 2<P<N<Q<2N,\mathrm{and}P,Q\mathrm{are}\mathrm{prime}\right\}.$$

Note that we implicitly consider $Q<2N$ to ensure finite cardinality relevant to the scale of N, aligning with the geometric bounds. The Goldbach variant requires that there exists $M\in D_N$ with $N-M$ prime (ensuring $P=N-M$ prime and $Q=N+M$ prime via the partition).

The question becomes: How many distinct values $M\in \{1,2,\dots ,N-3\}$ are in the set $D_N$? For example, $|D_4|=2$ since $D_4=\{(5-3)/2,(7-3)/2\}=\{1,2\}$.

4.1. Experimental Results

We conducted a computational experiment to evaluate the size of $D_N$ for every N between 4 and $2^{14}$. The experiment was performed on a standard workstation (11th Gen Intel i7, 32GB RAM) using a Python 3.12 implementation with the Gmpy2 library [4]. For each N in the range, we compute $|D_N|$. We then calculate a “gap value” $G\left(N\right)$ defined as:

$$G\left(N\right)={log}^2\left(2N\right)-((N-3)-|D_N\left|\right),$$

where $|D_N|$ is the count of distinct M-values for N. The experiment is deterministic and yields the results summarized in Table 1.

The results in Table 1 show that $G\left(N\right)$ is consistently positive. This implies that the number of “gaps” (values of M not in $D_N$, approximated by $(N-3)-|D_N|$) is less than ${log}^2\left(2N\right)$. More importantly, the minimum value of $G\left(N\right)$ within each successive power-of-two interval is strictly increasing. This empirical finding is the basis for the following lemma.

5. Ancillary Results

This is a key finding based on the experimental data.

Lemma 1

(Key—Computational). For $m\ge 2$ and $N\le 2^{14}$, the minimum value of $G\left(N\right)$ in the interval $[2^m,2^{m+1}]$ is strictly less than the minimum value of $G\left(N\right)$ in the interval $[2^{m+1},2^{m+2}]$.

Proof.

This lemma is an empirical observation from the computational data in Table 1, verified for all N in the range $[4,2^{14}]$. The data shows the minima of $G\left(N\right)$ strictly increase across dyadic intervals for $m\ge 2$. We provide a heuristic justification for why this trend should continue.

A concise heuristic justification relies on the incremental growth of $|D_N|$, the cardinality of the set of valid M-values (i.e., the number of distinct prime pairs $(P,Q)$ with $P<N<Q$ and $P+Q=2N$).

Local increment from N to $N+1$

When N advances to $N+1$, almost all previously realized M-values persist, but two specific candidates can newly appear:

• Case 1 (Boundary shift via $Q=2N-1$):

  $$P=3,Q=2N-1,M={\displaystyle \frac{Q-P}{2}}=N-2.$$
  This contributes a new M if $2N-1$ is prime.
• Case 2 (Twin-prime emergence): If $(N,N+2)$ are both prime, then

  $$P=N,Q=N+2,M={\displaystyle \frac{Q-P}{2}}=1,$$

  which contributes a new $M=1$.

Thus,

$$|D_{N+1}|\ge |D_N|+\delta ,\delta \in \{0,1,2\},$$

where $\delta$ counts how many of the above cases might occur.

Growth over Larger Scales

Over ranges like $[N,2N]$, primes $Q>n$ enter $(n,2n)$ with regularity guaranteed by refinements of Bertrand’s postulate. Specifically:

• Nagura’s theorem: For $n\ge 25$, there is always a prime in $(n,(6/5\left)n\right]$, implying at least $\gtrsim 5$ primes in $(n,2n)$ on average [5].
• Dusart’s refinement: For $n\ge 3275$, primes exist in intervals as short as $(n,n+n/\left(2{log}^{2}n\right)]$, yielding $\sim 2{log}^{2}n$ primes in $(n,2n)$ [6].

Each new Q can pair with many prior primes $P<n$ to realize new $M=(Q-P)/2$. With $\pi (n-1)-1\sim n/logn$ available $P<n$, and new Q appearing at density $\sim 1/logn$, the expected influx of new pairs per n is $\gtrsim n/{log}^{2}n$. Conservatively, Bertrand-type results ensure at least $\Omega (logn)$ new incorporations per n.

Over $[N,2N]$, the total new Q in $(N,4N)$ number $\pi \left(4N\right)-\pi \left(N\right)\sim 3N/logN$, each potentially adding up to $\sim N/logN$ pairs, distributed across $\sim N$ values of n. This yields an average $|D_n|$ growth of $\Omega (N/{log}^{2}N)$ per step. Consequently, gaps $(n-3)-|D_n|\sim n-\Omega (n/{log}^{2}n)$ increase nearly linearly, but the logarithmic term ensures the deficit grows slower than ${log}^2\left(2n\right)$, so $G\left(n\right)$ trends upward.

Extension to dyadic intervals

Extending to dyadic intervals $[2^m,2^{m+1}]$ as $m\to \infty$, each such interval contains a power of two anchoring the empirical minima observed in Table 1. The refined Bertrand bounds amplify with m: new Q in $[2^m,2^{m+1}]$ number $\sim 2^m/m$, each incorporating $\sim 2^m/m$ prior $P<2^m$, adding $\sim 2^m/m^2$ per n on average. Cumulatively, $|D_n|\gtrsim c·2^m/m^2$ for some $c>0$, with gaps $\le 2^m(1-c/m^2)$. The increase in ${log}^2\left(2n\right)$ across $[2^{m+1},2^{m+2}]$ is $O\left(m\right)$, outpacing the relative gap shrinkage $O(1/m^2)$, ensuring the minimum $G\left(n\right)$ rises, consistent with the data. □

Remark 1.

This empirical pattern strongly suggests the inequality holds universally, though a rigorous analytical proof remains an open problem.

This is a main insight, derived from the data.

Corollary 1 (Computational Evidence)

For all N in the range $[4,2^{14}]$, we have $|D_N|>(N-3)-{log}^2\left(2N\right)$. The empirical data strongly suggests this inequality holds for all $N\ge 4$.

Proof.

This is a direct consequence of the experimental data presented in Table 1. The data shows that $G\left(N\right)>0$ for all N tested (specifically, the minimum value in each interval is positive and increasing). By definition, $G\left(N\right)={log}^2\left(2N\right)-((N-3)-|D_N\left|\right)$. The condition $G\left(N\right)>0$ directly implies:

$${log}^2\left(2N\right)-((N-3)-|D_N\left|\right)>0$$

Rearranging gives:

$$|D_N|>(N-3)-{log}^2\left(2N\right)$$

Lemma 1 shows this bound not only holds but strengthens as N increases within our tested range. While this provides compelling evidence for the universal validity of the inequality, a rigorous analytical proof extending beyond our computational range would constitute a significant theoretical advance. □

Conjecture 2.

The inequality $|D_N|>(N-3)-{log}^2\left(2N\right)$ holds for all $N\ge 4$.