Dynamic Portfolio Optimization with Data-Aware Multi-Agent Reinforcement Learning and Adaptive Risk Control

1. Introduction

The integration of multi-agent reinforcement learning into dynamic portfolio optimization represents an important direction in the convergence of artificial intelligence and financial technology. The research background stems from the increasingly complex and dynamic nature of global financial markets. With the diversification of asset classes, the rise in trading frequency, and the increase in market volatility, traditional static investment strategies can no longer effectively respond to rapidly changing risk environments. Conventional portfolio optimization models, often built on the mean-variance framework or under the assumption of market stationarity, tend to ignore market uncertainty and dynamic interactions, resulting in poor performance in complex financial scenarios. In recent years, reinforcement learning has shown clear advantages in dynamic decision-making problems. By interacting with the environment, it can achieve self-adaptive policy optimization, offering new theoretical and technical pathways for dynamic portfolio adjustment. However, single-agent reinforcement learning faces challenges such as state explosion and low exploration efficiency in high-dimensional asset spaces, which lay the foundation for introducing multi-agent mechanisms to enable distributed learning and collaborative decision-making [1].

In financial systems, there exist complex coupling and competitive relationships among different assets, market participants, and trading behaviors, which cannot be effectively captured by a single decision-maker. Multi-agent reinforcement learning can model each asset or strategy module as an independent agent, which achieves globally optimal dynamic allocation through game-playing, cooperation, and information sharing. Each agent continuously adjusts its investment weights based on local market feedback and global reward signals, forming a dynamic balance and adaptive mechanism at the system level. This distributed intelligent decision-making paradigm not only alleviates the computational bottlenecks of traditional centralized optimization but also enhances system stability and robustness under conditions of high volatility and uncertainty. Moreover, the multi-agent framework provides new insights into risk diversification. Through the heterogeneity and independence of agents' strategies, the system can maintain overall resilience under local shocks, achieving a dynamic equilibrium between risk minimization and return maximization [2].

Over the long-term evolution of macroeconomics and financial markets, the core challenge of investment decision-making lies in achieving adaptive optimality under uncertainty. With the rise of high-frequency trading, quantitative investment, and algorithmic decision-making, market structures exhibit stronger dynamic feedback characteristics, and the mutual influence among investors has become increasingly significant. Multi-agent reinforcement learning offers a new paradigm for modeling such complex interactions [3]. In non-stationary, nonlinear, and non-convex environments, it can capture implicit patterns through continuous learning and game-based mechanisms. Reinforcement learning has emerged as a broadly applicable paradigm across a wide spectrum of research and engineering domains, encompassing large language models (LLMs) [4], computer vision [5], and system architecture [6]. Its core principle, learning through interaction and feedback, enables intelligent agents to make sequential decisions, optimize long-term objectives, and adapt dynamically to complex environments. In LLMs, reinforcement learning facilitates preference alignment and controllable text generation through human or automated feedback [7]. In computer vision, it drives adaptive visual reasoning, scene exploration, and active perception tasks [8]. Within system architecture, reinforcement learning supports intelligent resource management, scheduling, and self-optimization in distributed and cloud-based infrastructures [9-10]. The diversity of these applications highlights the generality and flexibility of reinforcement learning as a universal framework for adaptive learning and decision-making across data-driven, embodied, and cyber-physical systems. In particular, when facing macroeconomic policy changes, geopolitical risks, and black-swan events, this method can dynamically adjust investment weights and risk preferences, achieving rapid policy adaptation and robust optimization. This research direction aligns with the development trend of intelligent finance and reflects the essential shift of financial markets from "static allocation" to "adaptive optimization."

From the perspective of financial technology development, dynamic portfolio optimization based on multi-agent reinforcement learning holds significant theoretical and practical value. On one hand, it breaks through the limitations of traditional portfolio optimization constrained by deterministic assumptions and linear modeling, providing an intelligent decision-making framework suited for complex environments. Through the reward mechanism and policy iteration process of reinforcement learning, optimal investment strategies can be autonomously explored without explicit supervision signals. Through the collaborative and competitive dynamics among agents, resources can be dynamically allocated, and information can be efficiently utilized. On the other hand, this research has direct implications for intelligent advisory systems, asset management, and financial risk control. With the explosive growth of market data and continuous improvements in computational power, developing distributed intelligent systems capable of optimal multi-asset and multi-timescale allocation has become a key issue in the advancement of financial intelligence [11].

In summary, the study of dynamic portfolio optimization based on multi-agent reinforcement learning not only reflects the deep integration of artificial intelligence into financial decision-making but also reveals the underlying mechanisms of cooperation among intelligent agents in complex systems. It breaks the static boundaries of traditional financial optimization models and achieves fine-grained modeling and adaptive responses to dynamic market structures through competition, cooperation, and self-adaptation among agents. This research direction is of great importance for enhancing the intelligence level of portfolio management, strengthening the stability and resilience of financial systems, and promoting the construction of an intelligent financial ecosystem. In the future, with the continuous progress of algorithmic theory, computing infrastructure, and financial data systems, multi-agent reinforcement learning is expected to become a core framework for dynamic asset allocation and risk management, providing more flexible, efficient, and interpretable solutions for intelligent investment decision-making [12].

2. Related Work

Existing research on portfolio optimization mainly focuses on traditional financial theories and machine learning methods. The core objective is to maximize returns under risk constraints. Early approaches were primarily based on the mean-variance model and the capital asset pricing theory, emphasizing the construction of static optimal weights using historical returns and covariance matrices. However, these methods assume that markets are stationary and that returns follow a normal distribution, which makes them inadequate for handling the dynamic and nonlinear nature of financial markets. To address these limitations, some studies have introduced robust optimization and extended risk measures, such as conditional value at risk and downside risk, to enhance the model's resistance to disturbances. Yet, because these methods depend on predefined risk models and statistical assumptions, they still face challenges such as amplified prediction errors and unstable parameter estimation in real markets. As a result, they fail to capture complex market feedback and non-stationary dynamics [13].

With the rise of data-driven quantitative investment, machine learning methods have been increasingly applied to portfolio optimization. Algorithms such as regression, clustering, and deep neural networks are used for return prediction, risk estimation, and feature extraction, enabling automation in strategy optimization. The emergence of reinforcement learning further allows investment strategies to update continuously through interaction with the environment, achieving adaptive learning of market states. Single-agent reinforcement learning models define states, actions, and rewards, transforming investment decisions into dynamic optimization processes. This helps reduce dependence on static assumptions in traditional models. However, since a single agent must handle high-dimensional portfolios, long-term dependencies, and strategy balance simultaneously, it often suffers from training instability, slow convergence, and overfitting in complex financial scenarios. These issues limit its applicability in large-scale asset allocation tasks.

In recent years, multi-agent reinforcement learning has become an important direction for addressing high-dimensional decision-making problems. This approach divides a complex system into multiple agents, each with local decision-making capabilities, which interact and cooperate in a shared environment to achieve distributed optimization and complementary strategies. In the context of portfolio management, different agents can represent various asset classes, strategy modules, or risk preferences. Through competition and cooperation, they achieve dynamic equilibrium in overall returns. Some studies propose mechanisms of centralized training with decentralized execution, improving learning efficiency while maintaining global coordination. Others explore multi-agent collaboration based on communication mechanisms to cope with incomplete market information and delayed feedback. These studies indicate that the multi-agent framework can better model the interactive behaviors and non-stationary characteristics of multiple market participants, providing new technical pathways for dynamic financial optimization [14]. The development of robust modeling techniques for financial risk assessment and systemic forecasting has benefited from advances in deep temporal modeling and attention mechanisms. For example, recent work integrates feature attention with temporal modeling to enable collaborative risk assessment, capturing both local and global dependencies in financial sequences [15]. Similarly, deep attention models have been shown to enhance systemic risk forecasting by extracting intricate relationships from high-dimensional time series, laying the foundation for adaptive learning in volatile markets [16].

To capture the structural complexity of financial systems, graph-based approaches have gained significant traction. Graph neural networks (GNNs) have been successfully applied to default risk identification by modeling enterprise credit relationship networks, effectively representing relational and topological information within corporate finance [17]. Knowledge-enhanced neural modeling has also been used to identify financial risks by leveraging functional and structural priors, further improving detection and interpretability [18].

With the increasing demands of dynamic environments, reinforcement learning (RL) has become a popular paradigm for resource management and decision optimization. Recent advancements demonstrate that RL-driven scheduling algorithms can efficiently adapt to the complexities of multi-tenant distributed systems, achieving robust task allocation under uncertainty [19]. Extending this idea, multi-agent reinforcement learning (MARL) frameworks have been introduced for large-scale environments, where collaboration and competition among agents improve global performance in resource scaling and allocation tasks [20]. These collaborative mechanisms are also supported by the synergistic integration of deep learning and neural architecture search, which provides scalable solutions for evolving system complexity [21]. Reinforcement learning has also shown promising applications in autonomous resource management, particularly in microservice architectures. By modeling system dynamics and employing adaptive policy iteration, RL agents can autonomously manage resource allocation, balancing throughput and latency under fluctuating loads [22]. Attention-augmented recurrent networks further enhance forecasting accuracy in financial markets, illustrating the benefit of temporal context-awareness in sequential decision-making [23]. Moreover, the collaborative evolution of intelligent agents across microservice systems highlights the flexibility and resilience achieved by distributed RL paradigms [24].

In addition to RL and GNNs, deep Q-learning has been applied to model audit workflow dynamics, enabling intelligent decision-making in complex and regulated environments [25]. Heterogeneous graph neural networks with graph attention have advanced the state-of-the-art in fraud detection, demonstrating the value of relational reasoning in identifying subtle patterns of anomalous behavior [26]. Spatiotemporal graph neural networks have also been employed to forecast multi-level service performance, showing that integrating spatial and temporal information provides a more comprehensive foundation for risk-sensitive decision making [27].

From a methodological standpoint, integrating causal inference with graph attention has facilitated structure-aware data mining, enabling models to capture non-trivial relationships and enhance interpretability in heterogeneous financial data [28]. Finally, self-supervised graph neural networks offer a promising direction for extracting robust features from heterogeneous information networks, providing the necessary representation power to support advanced asset allocation strategies and risk identification in dynamic, real-world scenarios [29].

3. Method

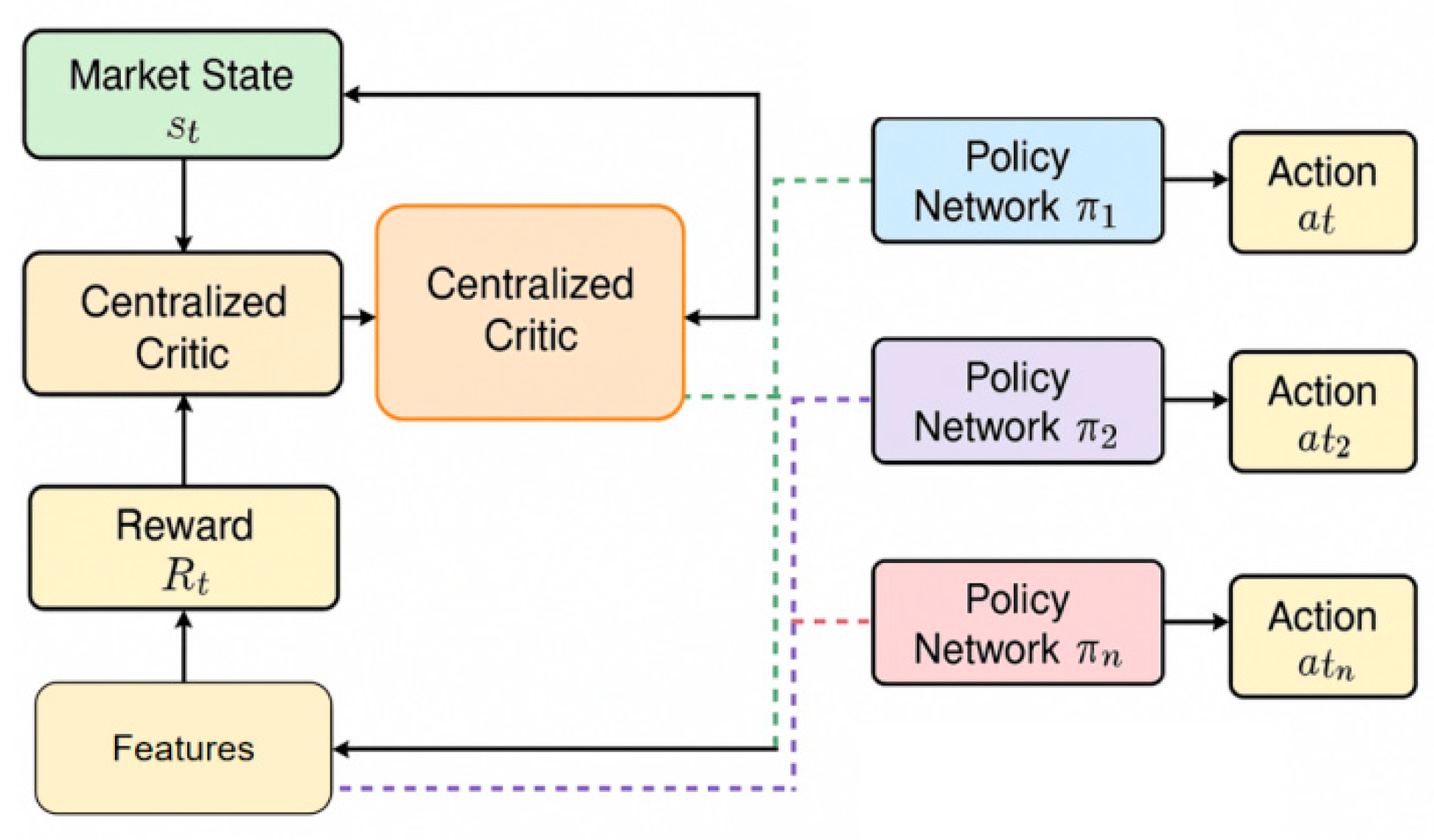
The dynamic portfolio optimization method proposed in this study is built upon a multi-agent reinforcement learning framework, designed to enable adaptive adjustment of asset weights through collaboration and strategic interaction among agents. Within this system, multiple agents are instantiated, each representing a distinct asset class or strategic unit. These agents continuously refine their investment behaviors by interacting with the market environment. At each time step, the state of the environment is represented as a set of market feature vectors, denoted as follows:

$$s_t=[r_t,v_t,p_t,{\sigma }_t]$$

(1)

Where $r_t$ represents the yield characteristic, $v_t$ represents the trading volume characteristic, $p_t$ represents the price trend signal, and ${\sigma }_t$ represents the volatility indicator. Each agent outputs an action $s_t$ based on its current state $a_t^i$, which is the allocation ratio for the i-th asset. Using the strategy function ${\pi }_i(a_t^i|s_t)$, the agent continuously optimizes its decision-making in a dynamic environment to maximize the expected return of the overall portfolio within risk constraints. The model architecture is shown in Figure 1.

The goal of reinforcement learning is to maximize the expected future reward, and the reward function is defined as:

$$\mathrm{J}(\pi )=\mathrm{E}[{\displaystyle \sum _{\mathrm{t}=0}^{\mathrm{T}}{\gamma }^{\mathrm{t}}{\mathrm{R}}_{\mathrm{t}}}]$$

(2)

Where ${\mathrm{R}}_{\mathrm{t}}$ is the immediate reward obtained at time step t, and $\gamma \in (0,1)$ is the discount factor used to balance short-term and long-term benefits. The reward function takes into account both the rate of return and the risk constraint, and is usually defined as ${\mathrm{R}}_{\mathrm{t}}=f(r_t,ris{k}_t)$ to ensure robustness in a highly volatile market. The policy update is completed by gradient ascent. According to the policy gradient theorem, the update direction is:

$${\nabla }_{\theta }\mathrm{J}({\pi }_{\theta })=\mathrm{E}[{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)Q^{\pi }(s_t,a_t)]$$

(3)

Where $Q^{\pi }(s_t,a_t)$ represents the state-action value function, which is used to measure the expected benefits of taking an action in a specific state.

To enable collaboration and information sharing among multiple agents, the model employs a centralized training and decentralized execution architecture. During the training phase, a global critic network receives the combined state and action information of all agents, guiding each agent to update its policy network. During the execution phase, each agent makes decisions based solely on local observations, improving the system's adaptability and scalability in real-world markets. Specifically, the global value function is defined as:

$$Q_{global}(S_t,A_t)=E[{\displaystyle \sum _{k=t}^T{\gamma }^{k-t}{R}_k|S_t,A_t}]$$

(4)

Where $S_t$ is the joint set of all agent states, and $A_t$ is the joint action vector. This structure enables the agent to capture overall market dynamics while maintaining flexibility in local decision-making during the learning process, thereby achieving multi-level portfolio optimization.

Furthermore, to ensure the controllability of the strategy under risk constraints, this paper introduces a dynamic risk penalty mechanism. The model embeds a risk balance term in the reward calculation to curb overly concentrated investment behavior. Assuming the risk measure of the portfolio at time t is $Var(r_t)$, the adjusted reward function can be expressed as:

$$R{\text{'}}_t=r_t-\lambda Var(r_t)$$

(5)

Where λ is the risk adjustment coefficient, which controls the trade-off between risk and return. By incorporating this term into the reinforcement learning optimization objective, the model can dynamically constrain risk exposure, ensuring stable and controllable investment decisions in a highly volatile environment. Overall, this method, through the organic combination of multi-agent collaboration, adaptive learning, and risk regulation mechanisms, achieves continuous responsiveness and optimized decision-making in a dynamic market.

4. Experimental Results

A. 

Dataset

This study uses the NASDAQ-100 Stock Dataset as the primary data source. The dataset contains historical trading data of the constituent stocks of the NASDAQ-100 Index in the United States. It covers a long time span and includes multi-dimensional market features. The dataset provides daily information such as opening price, closing price, highest price, lowest price, trading volume, and technical indicators, reflecting the dynamic changes of market behavior across different industry sectors. Its diversified asset structure and significant volatility provide a realistic and challenging financial environment for reinforcement learning models. This helps to evaluate the capability of dynamic portfolio optimization under complex market conditions.

During the data preprocessing stage, missing values were filled, outliers were smoothed, and features were standardized to ensure stability and comparability of the data distribution. A multi-dimensional feature matrix was then constructed, incorporating return rates, volatility, volume changes, and technical momentum indicators into the state space. This formed the environmental state representation used as input for the multi-agent reinforcement learning model. To enhance the temporal dynamics and continuity of the data, a sliding window mechanism was also introduced during feature extraction. This allowed the model to capture the interaction between short-term market trends and long-term risk characteristics.

Furthermore, to ensure model generalization and evaluation consistency, the dataset was divided into training, validation, and testing sets according to chronological order, with a ratio of 7:2:1. The training set was used for iterative policy learning by the agents, the validation set was used for tuning hyperparameters and risk constraint coefficients, and the testing set was used to evaluate model performance on unseen market data. The dataset's high dimensionality and time-varying characteristics make it an ideal platform for testing the performance and stability of the multi-agent reinforcement learning framework in portfolio optimization tasks.

B. 

Experimental Results

This paper first gives the results of the comparative experiment, as shown in Table 1.

As shown in Table 1, the proposed multi-agent reinforcement learning model demonstrates significant advantages in the task of dynamic portfolio optimization. Compared with other baseline models, the method achieves the highest annualized return (AR) of 16.92%. This indicates that the designed cooperative decision-making mechanism can more effectively capture market state changes and dynamically adjust investment weights. Traditional reinforcement learning models such as DQN and SARSA tend to fall into local optima when dealing with non-stationary markets, leading to slower return growth. In contrast, the proposed method introduces an interactive multi-agent structure that enables information sharing and risk diversification among strategies, resulting in stronger adaptability to multi-asset environments. In terms of risk management, the proposed model demonstrates a maximum drawdown (MDD) of just 14.37%, markedly lower than that achieved by other benchmark algorithms. This indicates that under highly volatile and uncertain market conditions, the model effectively mitigates loss propagation through its integrated risk-penalty mechanism and adaptive adjustment strategy. In contrast, traditional single-agent architectures depend primarily on individual experience updates, leading to delayed responses during extreme market fluctuations. The global critic network introduced in this study jointly assesses the action feedback from multiple agents, enabling a dynamic equilibrium between return and risk, and consequently minimizing the portfolio’s exposure to systemic risks in turbulent market environments.

The Sharpe ratio, which comprehensively measures both return and risk, also confirms the effectiveness of the proposed method in risk-adjusted performance. Experimental results show that the Sharpe ratio of the proposed model reaches 1.28, which is considerably higher than that of other reinforcement learning algorithms. This suggests that the model can achieve higher returns per unit of risk. The improvement comes from the centralized training and decentralized execution mechanism, which allows each agent to make flexible local decisions while maintaining global consistency and stability of the overall strategy. This structure enhances the convergence speed and robustness of the global policy, ensuring strong performance across different market states.

Furthermore, the improvement in the Hit Ratio provides additional evidence of the model's stability and consistency in trading decisions. The proposed model achieves a Hit Ratio of 0.68, which is noticeably higher than the range of 0.55-0.62 observed in other methods. This result indicates that the multi-agent structure can form a robust decision pattern through long-term interaction. By performing distributed learning of market features and complementary strategy updates, the agents effectively reduce the frequency of incorrect trades and improve the consistency of returns across consecutive trading periods. Overall, the proposed approach achieves systematic improvements in return enhancement, risk control, and decision robustness, fully validating the advantages and potential application value of the multi-agent reinforcement learning framework in dynamic portfolio optimization.

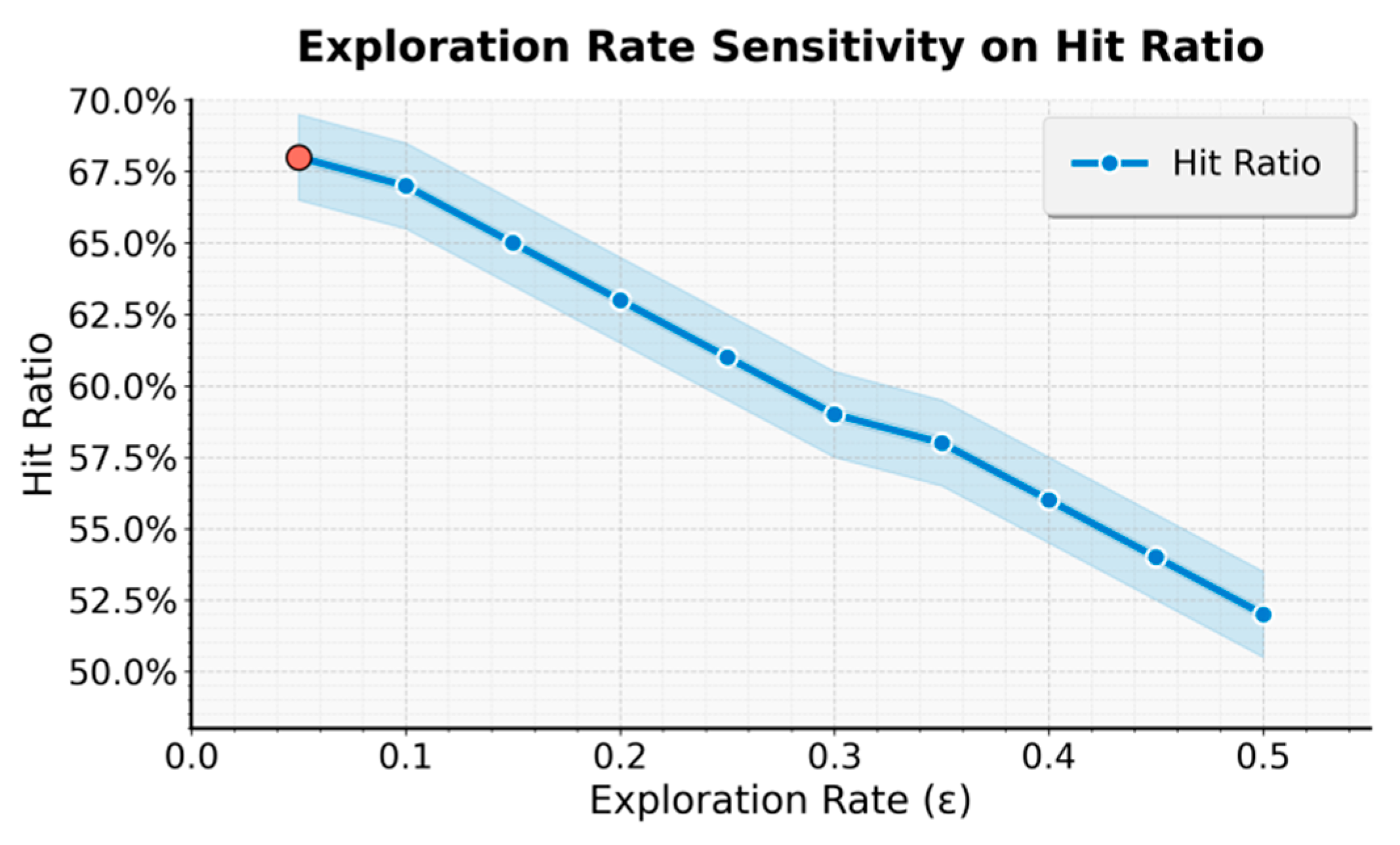
This paper also presents an experiment on the sensitivity of exploration rate to hit ratio, and the experimental results are shown in Figure 2.

As shown in Figure 2, with the gradual increase in the exploration rate, the model's Hit Ratio shows a steady downward trend. This indicates that excessive random exploration weakens the precision of investment decisions. When the exploration rate is low, the model can effectively balance exploration and exploitation, and the Hit Ratio remains at a high level. This suggests that agents can execute optimal strategies efficiently under familiar market conditions, leading to stable return growth. However, as the exploration rate continues to rise, the frequency of non-optimal actions increases, causing higher policy volatility and reducing the consistency and stability of trading decisions.

This result indicates that the proposed multi-agent reinforcement learning framework is highly sensitive to the exploration rate in dynamic portfolio optimization tasks. Excessive exploration disrupts the coordination structure among agents and causes instability in local learning, which weakens the overall risk control capability of the portfolio. When the exploration rate becomes too high, the communication and feedback mechanisms among agents are easily affected by noise, leading to biased value estimation by the global critic. As a result, the system struggles to maintain stable decision-making in non-stationary markets.

From a reinforcement learning perspective, the configuration of the exploration rate plays a crucial role in determining both the convergence speed of the policy and the stability of returns. The proposed model achieves optimal performance under a relatively low exploration rate, demonstrating strong adaptability and efficient experience transfer in dynamic market environments. Owing to its centralized training and decentralized execution framework, each agent can accumulate historical experience while maintaining a controlled degree of exploration. This design ensures continuous perception of evolving market trends and underlying risk structures. Consequently, the balanced mechanism significantly enhances the directional consistency of policy updates, enabling the model to identify and exploit profit opportunities effectively even with limited exploratory behavior.Overall, this experiment verifies the robustness and controllability of the proposed model in policy parameter adjustment. Changes in the exploration rate not only affect the Hit Ratio but also reflect the model's stability and adaptability under different levels of market uncertainty. Moderate exploration helps the model maintain flexibility and innovation, while excessive exploration leads to increased return volatility and risk diffusion. Through the systematic analysis of exploration rate sensitivity, this study further confirms that the proposed multi-agent reinforcement learning framework can achieve stable policy evolution under controllable risk, providing theoretical support and parameter guidance for dynamic portfolio optimization.

5. Conclusions

This study proposes an adaptive decision-making framework based on multi-agent reinforcement learning for dynamic portfolio optimization. The research focuses on market non-stationarity, inter-asset coupling, and risk-constrained optimization, constructing a policy architecture that combines centralized training with decentralized execution. This design achieves a dynamic balance between return enhancement and risk control. Through continuous interaction in reinforcement learning, the model can automatically adjust investment weights in complex financial environments to handle multi-source uncertainty and dynamic market changes. Experimental results show that the proposed method outperforms traditional single-agent models in return stability, drawdown control, and decision consistency, verifying the effectiveness and scalability of multi-agent coordination mechanisms in financial decision optimization.

The main contribution of this study is the introduction of multi-agent reinforcement learning into portfolio optimization, enabling joint modeling of return and risk at the policy level. Unlike traditional static optimization methods, this framework allows dynamic strategy migration and self-correction under multi-dimensional market signals. The cooperative game structure among agents enables the model to exploit inter-asset correlations while mitigating slow convergence and overfitting through information sharing and value integration mechanisms. Moreover, the introduction of a risk penalty and dynamic weighting mechanism in the model provides a feasible path for achieving long-term stable returns in the financial domain and establishes a theoretical foundation for sustainable optimization in intelligent investment systems.

From an application perspective, the proposed multi-agent reinforcement learning approach demonstrates strong generality and practical relevance. It can be applied not only to traditional stock investment but also extended to diverse financial scenarios such as futures, cryptocurrencies, fund allocation, and quantitative arbitrage. In the field of risk management, this framework offers automated risk monitoring and strategy adjustment mechanisms for asset management institutions and trading systems. At the macro level, its adaptive features enable the system to respond more effectively to market policy adjustments and sudden shocks, providing data-driven support for financial stability assessment and dynamic asset allocation. With the advancement of computing resources, the model also has potential for broader applications in high-frequency trading and multi-market interaction modeling.

Future research will further explore the integration of causal reasoning and uncertainty estimation mechanisms into the multi-agent reinforcement learning framework to enhance robustness and interpretability under extreme market conditions. In addition, incorporating graph neural networks or generative models may allow for more precise modeling of time-varying structural dependencies among assets, capturing cross-asset and cross-temporal risk transmission paths. Furthermore, reducing computational complexity and energy consumption while maintaining stable returns will become a key direction for achieving sustainable development in intelligent financial systems. Overall, this study provides new theoretical insights and technical pathways for the integration of artificial intelligence and quantitative finance and offers valuable references for building intelligent investment decision systems with self-learning, self-regulation, and adaptive capabilities.