Multi-Domain Intelligent State Estimation Network for Highly Maneuvering Target Tracking With Non-Gaussian Noise

1. Introduction

In the context of Earth observation (EO), target tracking aims to estimate target states from noisy EO measurements acquired by satellite, radar, and UAV sensors. It supports UAV object tracking [1,2,3,4], remote sensing surveillance [5,6,7], and traffic control [8,9,10]. Within the domain of target tracking, the problem of tracking highly maneuvering targets is widely recognized as a fundamental challenge [11,12,13]. Specially, highly maneuvering targets are characterized by motion involving high speeds, frequent maneuvers, and long-duration maneuvers. Tracking such targets presents two main challenges. The first challenge is high-speed and high-frequency maneuvers [14]. Such maneuvers cause rapid motion changes and result in error accumulation. The second challenge arises from non-Gaussian noise with different intensities and distributions [12], causing instability in state estimation results and divergence in tracking performance. Currently, multiple paradigms have been proposed to solve these challenges. They can be classified into two types, which are model-based methods and data-driven methods.

For model-based methods [15,16,17,18,19,20,21], the interacting multiple model (IMM) filter [19] is a fundamental algorithm to solve rapidly changing patterns problem [22]. It combines several predefined motion models and works with the improved Kalman filter [15,17,23,24,25,26,27,28,29] to achieve reliable tracking in nonlinear systems. To enhance adaptability under non-Gaussian noise, Xu et al. [30] proposed an EM-based extended Kalman filter (EKF) tracker that decomposed non-Gaussian noise into Gaussian components and incorporated bias compensation, significantly improving angle-of-arrival target tracking under non-Gaussian noise conditions. Building on the idea of Gaussian decomposition, Chen et al. [31] proposed a joint probability data association based on noise-interaction Kalman filter (JPDA-IKF), which decomposed non-Gaussian noise into multiple Gaussian components and fused their results to enhance multitarget tracking performance in complex maritime environments. To further capture multimodal noise and motion characteristics, Wang et al. [32] introduced Gaussian mixture models (GMMs) into the IMM-KF, allowing accurate switching and fusion across multiple motion. Liu et al. [33] proposed an IMM-MCQKF algorithm that integrated the maximum correntropy criterion into the quadrature Kalman filter within an IMM framework, improving state estimation under non-Gaussian noise and maneuvering target scenarios. Xie et al. [34] proposed an adaptive TPM-based parallel IMM algorithm that integrated online transition probability adaptation with a threshold-controlled model-jumping mechanism within the IMM framework.

The above model-driven methods require accurate motion patterns and covariance noise parameters based on manual experiences. Indeed, constructing an accurate and well-matched model is challenging, and such prior information cannot be obtained promptly and reliably before tracking [22]. Additionally, these methods process trajectories only in the temporal domain and do not fully exploit multi-domain information. As a result, by neglecting the latent representational information in noisy observations, their sensitivity to maneuverability is reduced under non-Gaussian noise.

For data-driven methods, precise kinematic modeling of target motion is unnecessary. They leverage the strength of data mining to capture complex dynamics. They can be broadly categorized into two types, which are end-to-end architectures and hybrid architectures that integrate traditional algorithm. The former constructs an end-to-end model to directly map the input observations to the output states, eliminating the need for manually designed intermediate feature extraction. Cai et al. [35] proposed an adaptive LSTM-based tracking method that incorporated measurement–prediction errors to improve accuracy and adaptability for maneuvering targets. Liu et al. [11] learned the residual between the ground truth and estimation trajectories. This framework mainly consisted of BiLSTM layers [36,37,38] and enabled target state estimation without the need for a pre-defined model set. Building upon these, Zhang et al. [13,39] employed an enhanced transformer architecture to achieve further reductions in state estimation RMSE. Shen et al. [40] also proposed Transformer-based nonlinear target trackers, including a classical Transformer for smoothing and prediction and a recursive Transformer for filtering and prediction, achieving superior accuracy and efficiency in nonlinear radar target tracking. PCRLB [41] propose a physics-informed data-driven autoregressive nonlinear filter (DAF) based on the Transformer. Its end-to-end architecture embedded known dynamics and measurement models into the training process, ensuring physically consistent and efficient state estimation.

The above end-to-end data-driven methods primarily use a single end-to-end model to capture complex nonlinear functions often leads to convergence difficulties in practice. Moreover, a wide variation range of target motion may degrade method performance and generalization.

The latter hybrid methods [12,42,43,44,45,46,47,48,49,50,51,52,53,54,55,55] integrate deep learning with model-driven approaches, thereby combining the strengths of both paradigms. These methods retain the framework of model-driven algorithms while incorporating deep learning modules to estimate variable parameters. By involving less functional learning and relying on simpler architectures, they achieve lower computational cost and enhanced interpretability. KalmanNet [42] integrated a structural state space model with dedicated recurrent neural networks (RNN) to estimate the Kalman gain. It operated within the KF framework and effectively addressed non-linearity. Building on this idea, KalmanFormer [53] employed a Transformer to learn the Kalman Gain. To handle mismatches between state and observation models, Split-KalmanNet [43] calculated the Kalman gain through the Jacobian of the measurement function and leveraged two RNNs with a split architecture. Cholesky-KalmanNet [45] further enhances state estimation by providing and enforcing transiently precise error covariance estimation. Recursive KalmanNet [48] extended this line of research by employing the recursive Joseph’s formulation, thereby enabling accurate state estimation with consistent uncertainty quantification under non-Gaussian noise. Latent-KalmanNet [44] advanced the framework by jointly learning a latent representation and Kalman-based tracking from high-dimensional signals. More recently, MAML-KalmanNet [54] integrated model-agnostic meta-learning with artificially generated labeled data to achieve fast adaptation and accurate state estimation under partially unknown models. In addition, Liu $et$$al.$ [12] introduced a digital twin system that combined the Unscented Kalman filter with intelligent estimation models. Zhu $et$$al.$ [56] developed an adaptive IMM algorithm that employed a neural network to estimate TPMs in real time, thereby reformulating IMM as a generalized recurrent neural network. Fu $et$$al.$ [46] proposed deep learning–aided Bayesian filtering methods for guarded semi-Markov switching systems with soft constraints, addressing the challenge of state estimation under complex sojourn times and state-dependent transitions. Furthermore, Jia $et$$al.$ [50] proposed a Multiple Variational Kalman-GRU model to capture multimodal ship dynamics and provide reliable trajectory prediction.

This paradigm endows the network with stronger generalization ability and interpretability. Considering these advantages, we adopt this paradigm in our work. However, existing hybrid approaches that integrate deep learning into traditional model-driven frameworks still have notable limitations. They typically rely solely on temporal-domain processing and fail to exploit complementary information from spatial and frequency domains, thereby restricting their effectiveness. In addition, when dealing with maneuvering targets, these methods often emphasize local temporal features while overlooking broader global motion patterns, which are critical for capturing abrupt changes in dynamics.

To overcome these issues, we propose a versatile and adaptive tracking framework called the Multi-Domain Intelligent State Estimation Network (MIENet) for highly maneuvering target tracking that can effectively handle non-Gaussian noise. MIENet first applies a nonlinear transformation for coordinate system conversion and comprises two main models. Due to the nonlinear, heavy-tailed, and spatially correlated characteristics of non-Gaussian noise, standard Gaussian-based methods fail to remove it effectively. The independent module in MIENet enables adaptive learning of these complex noise features, thereby improving convergence stability and denoising efficiency. Furthermore, leveraging multi-domain information helps capture the statistical characteristics of non-Gaussian noise. Therefore, the first model, termed the Fusion Denoising Model (FDM), mitigates non-Gaussian observation noise by integrating temporal, spatial, and frequency-domain features.

As discussed in [12], bias in ${\mathit{F}}_{\mathit{k}}$ causes rapidly growing deviations, while bias in the initial state $x_0$ results in linear growth. Hence, errors from an inaccurate transition matrix become much greater than those from an incorrect initial state as the trajectory extends. The main challenge in estimating the maneuvering target motion model lies in the uncertainty of ${\mathit{F}}_{\mathit{k}}$, whose exact form is typically unknown; thus, accurately estimating its key parameters is critical to avoid computational bias. Motivated by this, the second model, termed the Parameter Estimation Model (PEM), estimates the turn rate of target motion from temporal–spatial information. The estimated parameters are then incorporated into the UKF to achieve accurate tracking of highly maneuvering targets. The entire tracking process is iteratively updated using a fixed sliding-window mechanism. The main contributions of this work are summarized as follows:

• We propose a MIENet to estimate target state and motion patterns from non-Gaussian observation noise. The multi-domain information of target trajectories can be well incorporated, thus helping to infer the latent state of targets.
• We design a FDM to handle noise with varying intensities and distributions. It employs a novel Inverted-UNet and FFT-based weighting to integrate temporal, spatial, and frequency-domain features within an encoder–decoder framework.
• We develop a PEM to estimate target motion patterns by fusing local and global spatial–temporal features. Considering that the state transition matrix ($\mathit{F}$) characterizes motion dynamics and enables trajectory inference, we further introduce a physically constrained loss function (PCLoss) to help PEM estimate the key turn rate parameter ($\omega$) in $\mathit{F}$.
• Experiments on the LAST [11] and SV248S [57] datasets demonstrate the superior performance of our method in various highly maneuvering scenes. Compared with existing methods, our method is more robust to observation noise with varying intensities and distributions.

The rest of this paper is outlined as follows: Section 2 analyses the state-space formulation of tracking systems. Section 3 gives the detailed introduction of MIENet. This is followed by Section 4 about the experiments and Section 5 concludes this paper.

2. Problem Formulation

Our method is dedicated to maneuvering target tracking and shows limited dependence on the observation modality. Using the LAST dataset as an example, we analyze a radar tracking system. As shown in Figure 1, the system structure is based on range and azimuth observations [12]. Initially, due to the long distance of the target and the limited measurement resolution, we ignore the shape of targets and treat them as points in space [14]. The relationship of target states and observations is represented by the state space model (SSM) as follows,

$$\mathbf{State}\mathbf{Equation}:{\mathit{x}}_{\mathit{k}}={\mathit{F}}_{\mathit{k}}{\mathit{x}}_{\mathit{k}-\mathbf{1}}+{\mathit{n}}_{\mathit{k}},$$

(1)

$$\mathbf{Observation}\mathbf{Equation}:{\mathit{z}}_{\mathit{k}}=\mathit{h}\left({\mathit{x}}_{\mathit{k}}\right)+{\mathit{m}}_{\mathit{k}},$$

(2)

where ${\mathit{x}}_{\mathit{k}}$ and ${\mathit{z}}_{\mathit{k}}$ are target states and observations at time step k, respectively. ${\mathit{x}}_{\mathit{k}}$ is defined as $[p_{x,k},p_{y,k},v_{x,k},v_{y,k}]$, where $[p_{x,k},p_{y,k}]$ is the two-dimensional position, and $[v_{x,k},v_{y,k}]$ is the corresponding velocity. ${\mathit{z}}_{\mathit{k}}$ is defined as $[d_k,{\theta }_k]$, where $d_k$ and ${\theta }_k$ are the range and azimuth of the target detected by the sensor. ${\mathit{n}}_{\mathit{k}}$ and ${\mathit{m}}_{\mathit{k}}$ are additive noise at time step k; ${\mathit{F}}_{\mathit{k}}$ and $\mathit{h}(·)$ are the state transition matrix and observation function.

2.1. State Equation

For most 2D maneuvering tracking scenes, Constant Turn (CT) models [14] are representative maneuvering patterns that can approximate most motion behaviors. The ${\mathit{F}}_{\mathit{k}}$ is defined as:

$$\begin{array}{c}{\mathit{F}}_{\mathit{k}}=\left[\begin{array}{cccc}1& 0& {\displaystyle \frac{sin\left({\omega }_k{s}_{\tau }\right)}{{\omega }_k}}& {\displaystyle \frac{cos\left({\omega }_k{s}_{\tau }\right)-1}{{\omega }_k}}\\ 0& 1& {\displaystyle \frac{1-cos\left({\omega }_k{s}_{\tau }\right)}{{\omega }_k}}& {\displaystyle \frac{sin\left({\omega }_k{s}_{\tau }\right)}{{\omega }_k}}\\ 0& 0& cos\left({\omega }_k{s}_{\tau }\right)& -sin\left({\omega }_k{s}_{\tau }\right)\\ 0& 0& sin\left({\omega }_k{s}_{\tau }\right)& cos\left({\omega }_k{s}_{\tau }\right)\end{array}\right],\end{array}$$

(3)

where ${\omega }_k$ denotes the turn rate at time step k. It is a critical parameter whose accuracy significantly affects performance. The symbol $s_{\tau }$ represents the sampling interval of trajectories. If ${\omega }_k$ equals to zero, the motion model is simplified to Constant Velocity (CV) model, which could be defined as:

$$\begin{array}{c}{\mathit{F}}_{\mathit{k}}=\left[\begin{array}{cccc}1& 0& s_{\tau }& 0\\ 0& 1& 0& s_{\tau }\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right].\end{array}$$

(4)

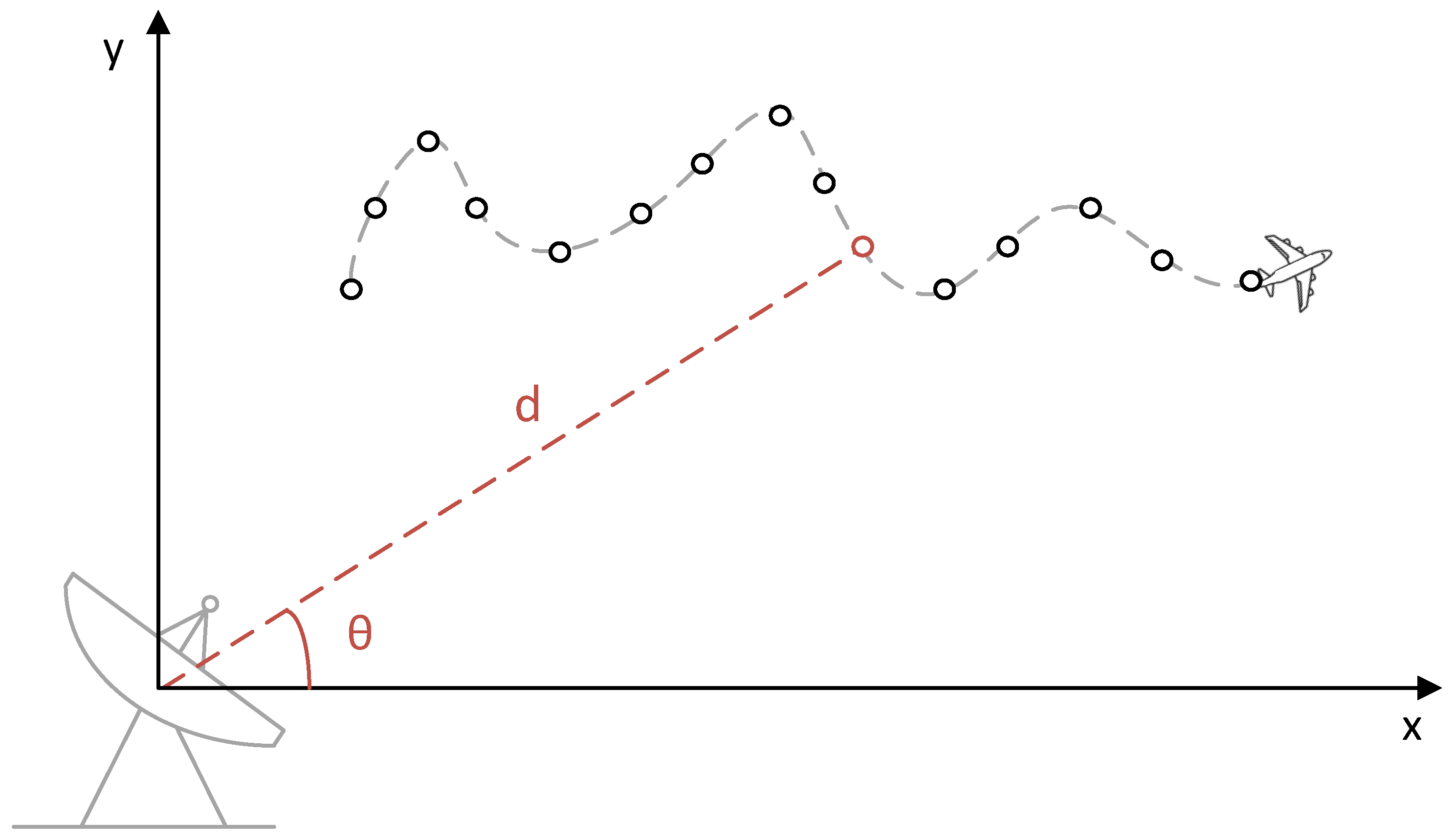
2.2. Observation Equation

For common radar tracking system, the detector at $(r_x,r_y)$ provides range and azimuth measurements contaminated by additive noise. The polar coordinate system of observations is given as:

$$\begin{array}{c}\left[\begin{array}{c}{d}_k\\ {\theta }_k\end{array}\right]=\left[\begin{array}{c}\sqrt{{(p_{x,k}-r_x)}^2+{(p_{y,k}-r_y)}^2}\\ \sqrt{arctan((p_{y,k}-r_y)/(p_{x,k}-r_x))}\end{array}\right]+\left[\begin{array}{c}{q}_{d,k}\\ q_{\theta ,k}\end{array}\right],\end{array}$$

(5)

where $q_{d,k}$ and $q_{\theta ,k}$ are additive noise in range and azimuth angle observations at time step k.

Subsequently, The polar coordinate system is transformed into the Cartesian system as the input of our method. In this step, additive noise is converted into non-Gaussian noise by nonlinear transformation. The process is formulated as follows:

$$\begin{array}{c}\left[\begin{array}{c}{p}_{x,k}\\ p_{y,k}\end{array}\right]=\left[\begin{array}{c}{d}_{k}cos\left({\theta }_k\right)\\ d_{k}sin\left({\theta }_k\right)\end{array}\right]+\left[\begin{array}{c}{r}_x\\ r_y\end{array}\right].\end{array}$$

(6)

2.3. Problem Addressed in This Work

The main task is to estimate the target states (${\mathit{x}}_{\mathit{k}}$) based on the nonlinear observation (${\mathit{z}}_{\mathit{k}}$). This work addresses two primary challenges. First, the observations are often corrupted by diverse types of noise. In practice, for nonlinear observations, the noise distributions we processed are rarely Gaussian; instead, they may vary in intensity, exhibit non-Gaussian characteristics, or change dynamically across different environments. Second, maneuvering targets introduce additional difficulties due to their highly dynamic and uncertain motion patterns. A key challenge lies in accurately estimating critical motion parameters in the state transition matrix (${\mathit{F}}_{\mathit{k}}$). Errors in estimating such parameters can severely degrade trajectory inference, as the deviation induced by model mismatch often grows increasingly with trajectory length. This work aims to design a robust framework for stable and reliable tracking of highly maneuvering targets. The framework can effectively handle non-Gaussian noise and accurately estimate key motion parameters.

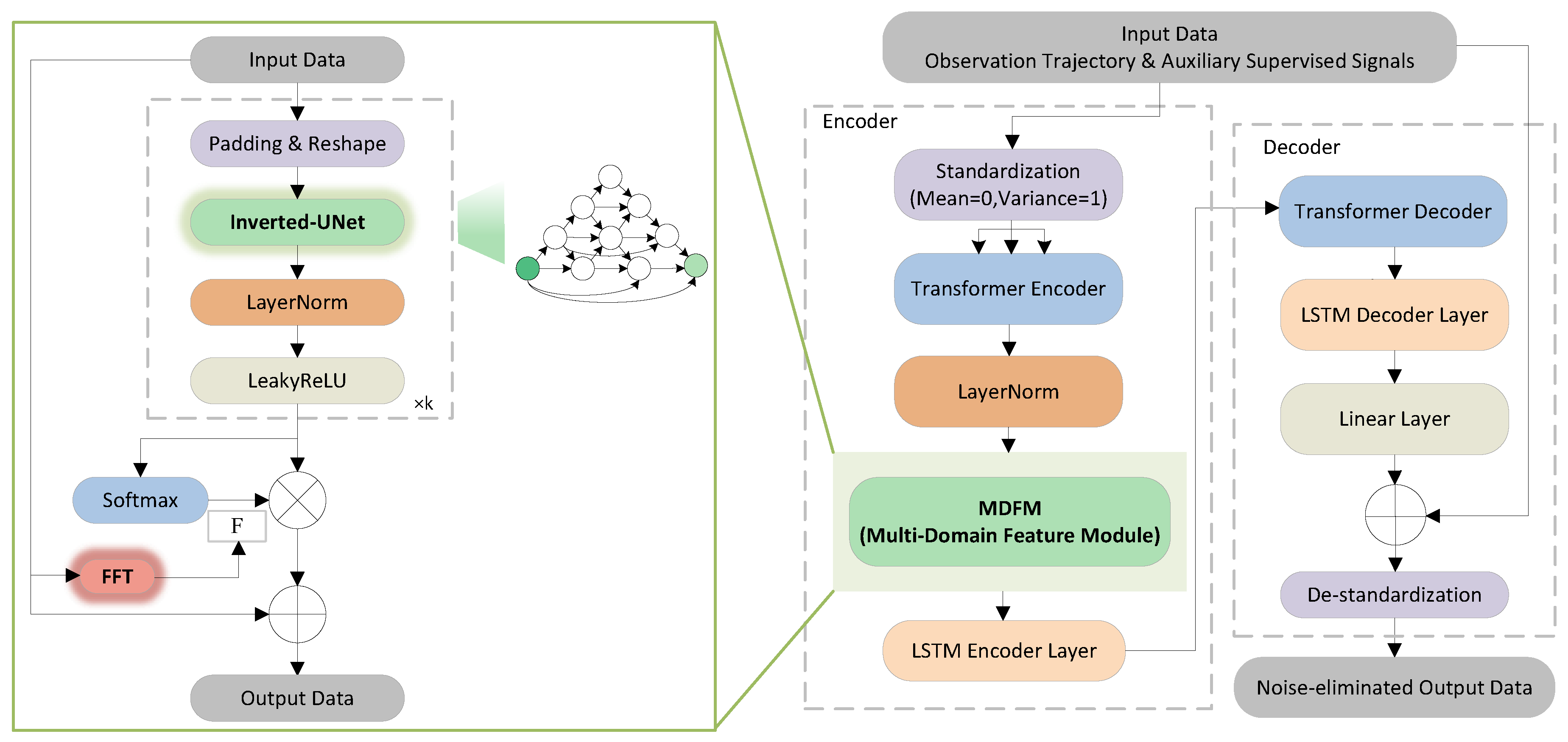
3. Multi-Domain Intelligent State Estimation Network

In this work, we introduce our MIENet in details. The overall architecture of the proposed method is shown in Figure 2.

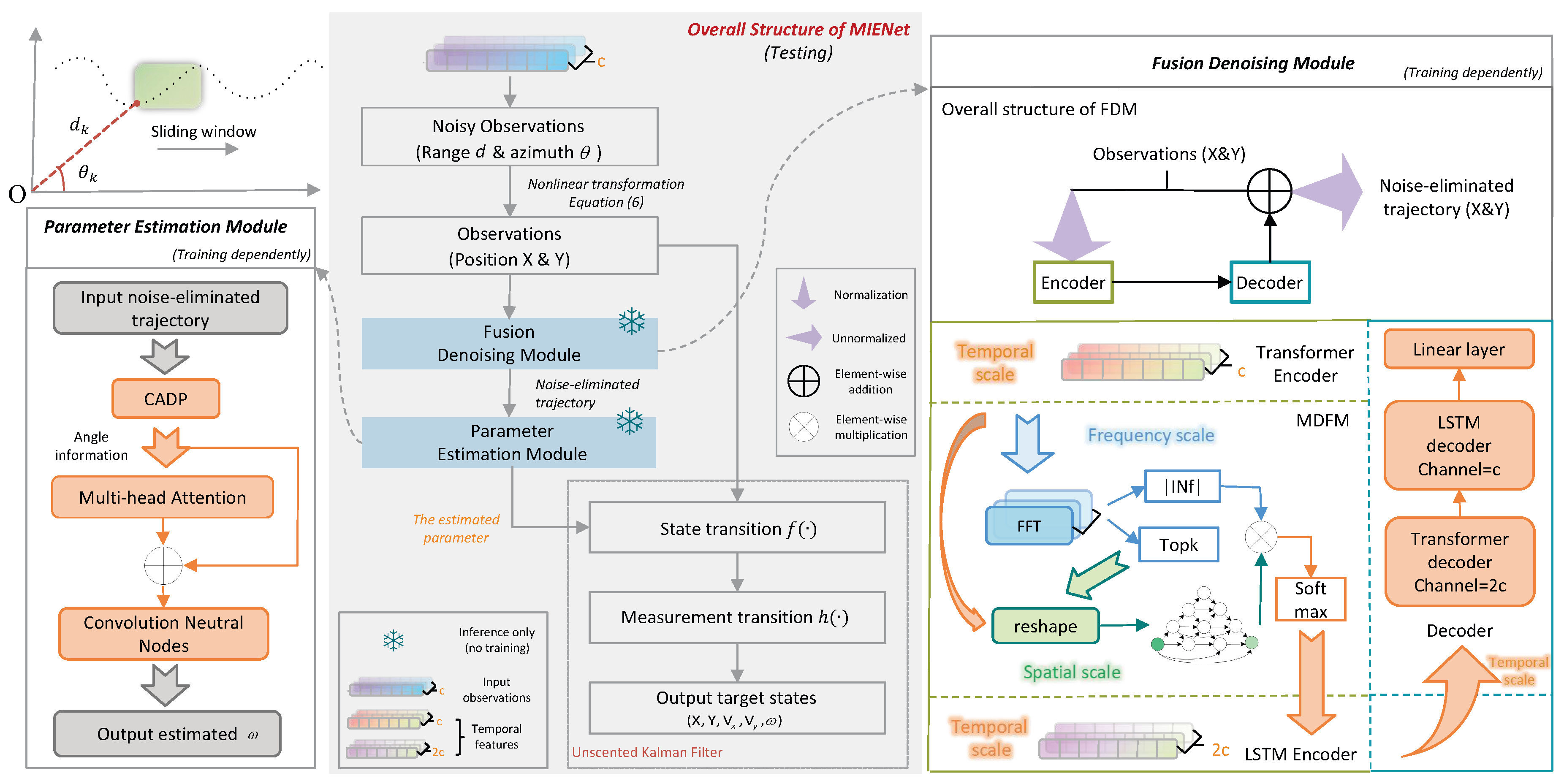
3.1. Overall Architecture

As illustrated in Figure 2, we segment the acquired trajectories using a sliding window, and our MIENet processes fixed-length noisy polar-coordinate trajectories as input. It first applies a nonlinear transformation (Equation (6)) to convert polar coordinates ($d_k,{\theta }_k$) into Cartesian coordinates ($p_{x,k},p_{y,k}$). In this process, additive noise is transformed into non-Gaussian noise. A fusion denoising model (FDM, Section 3.2) is then employed to suppress non-Gaussian observation noise by integrating temporal, spatial, and frequency-domain features. Subsequently, a parameter estimation model (PEM, Section 3.3) estimates the turn rate from the denoised trajectories output by the FDM. It leverages both local and global temporal–spatial information. The estimated parameter is then incorporated into a UKF for maneuvering target tracking. Notably, the FDM and PEM are trained independently and evaluated jointly with the UKF in testing. A summary of the overall tracking process is provided in Algorithm 1. Subsequently, the FDM and PEM are described in detail.

Algorithm 1 MIENet tracking process

Input:   Noisy observations $\mathit{z}$ with N time steps. Output:   Target states $\mathit{x}$ with N time steps.    1: Initialization: Independently trained FDM and PEM; Fixed model input length is n.    2: for $k=1$ in N do    3:    while $k\le N-n$ do    4:      Segment extraction: ${\mathit{z}}_{\mathit{seg}\left(\mathit{n}\right)}$    5:      Position recovery with equation (5), to get noisy position sequences: ${\mathit{d}}_{\mathit{seg}\left(\mathit{n}\right)}$    6:      Noise elimination: ${\mathit{D}}_{\mathit{seg}\left(\mathit{n}\right)}=\mathrm{FDM}\left({\mathit{d}}_{\mathit{seg}\left(\mathit{n}\right)}\right)$    7:      Turn rate estimation: $\widetilde{w_k}=\mathrm{PEM}\left({\mathit{D}}_{\mathit{seg}\left(\mathit{n}\right)}\right)$    8:      Calculate state transition matrix with equation (3): $\tilde{\mathit{F}}=\mathit{F}\left(\widetilde{w_k}\right)$    9:    end while  10:    Prediction and update of UKF filter: ${\tilde{\mathit{x}}}_{\mathit{k}}\to {\mathit{x}}_{\mathit{k}}$  11: end for

3.2. Fusion Denoising Model

3.2.1. Motivation

In practice, the statistical characteristics of observation noise exist not only in the temporal domain but also in the spatial and frequency domains. Temporal features alone are insufficient to capture oscillatory energy distributions in the frequency domain or spatial structural correlations, both of which are essential for robust denoising and stable tracking under non-Gaussian noise.

As noted in [58], the encoder-decoder structure enables effective separation of noise and signal in the latent space, ensuring noise suppression during reconstruction. However, traditional encoder-decoder structure consists of an encoder, a decoder, and plain connections. The encoder is used to increase feature dimension while reducing the spatial resolution. Decoder helps to recover the spatial resolution to match the size of input trajectories. Such architectures mainly emphasize hierarchical semantic features derived from temporal information. Although deepening the network or modifying the encoder submodules can capture higher-level representations, they do not explicitly address the multi-domain characteristics of observation noise. This motivates the design of a dedicated module within the encoder–decoder framework to explicitly extract and fuse temporal, spatial, and frequency-domain features.

3.2.2. The Overall Structure of FDM

As illustrated in Figure 3, the framework adopts a symmetric encoder–decoder structure with an additional multi-domain feature module (MDFM). The input trajectories are converted from polar to Cartesian coordinates and segmented into fixed-length sequences. These processed sequences are subsequently fed into the transformer encoder to extract temporal-domain features. The MDFM further captures frequency-domain and spatial-domain information, and fuses them with temporal dynamics. Finally, the fused multi-domain features are passed into the decoder subnetworks for trajectory reconstruction and prediction.

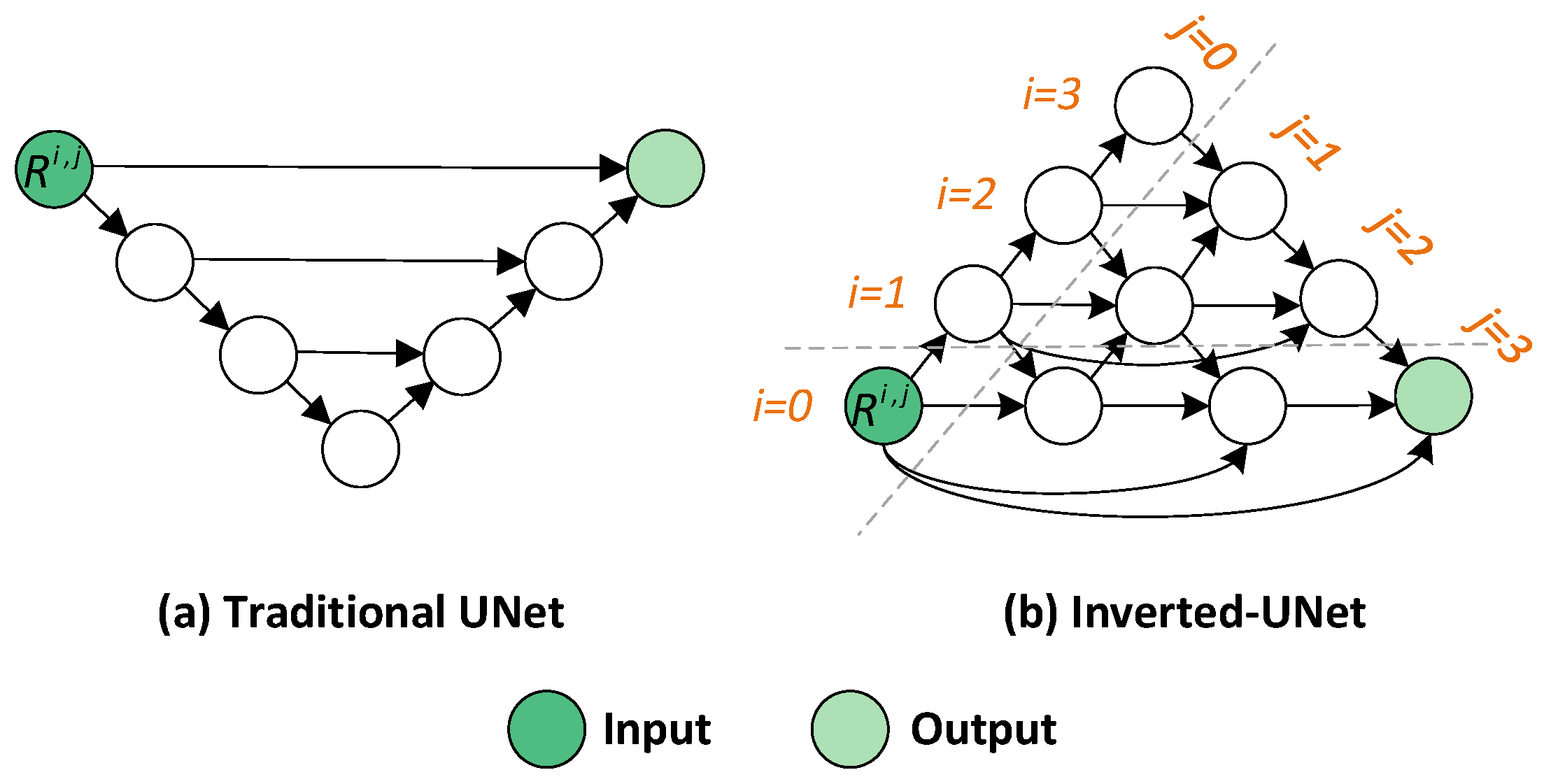
3.2.3. The Multi-Domain Feature Module

As shown in Figure 3, the multi-domain feature module (MDFM) is embedded within the encoder to enhance feature representation beyond the temporal domain. It first performs padding and reshaping on the input data, and then passes it through the Inverted-UNet. The Inverted-UNet is specifically designed to capture both multi-channel spatial structures while maintaining computational efficiency, which is critical for robust trajectory representation. The extracted features are then normalized with Layer Normalization and activated by a LeakyReLU, with this block repeated p times according to experimental results.

In parallel, the Fast Fourier Transform (FFT) is applied to the temporal features to reveal frequency-domain amplitude distributions. These amplitudes are used as weights, allowing the model to emphasize oscillatory patterns that are often hidden in noisy observations. The denoised spatial features from the Inverted-UNet and the weighted frequency-domain information are fused through a softmax layer.

By combining the Inverted-UNet and FFT, MDFM explicitly leverages spatial structures and frequency-domain energy patterns, providing a more comprehensive feature representation that significantly improves noise suppression. The following sections present a detailed description of these two key components.

(1)

The Inverted-UNet

For low-dimensional trajectory sequences, the traditional dense U-Net (Figure 4(a)) is unsuitable, as its initial downsampling step leads to an immediate loss of information. Based on this idea, we design a novel Inverted-UNet (Figure 4(b)). It first upsamples the multi-channel trajectory features to preserve spatial structure, then downsamples them to restore the original trajectory shape. Skip connections promote gradient flow.

Assume $R^{i,j}$ denotes the output of each node, where i is the $i^{th}$ upsampling layer in the encoder and j is the $j^{th}$ neighboring layer. To balance network performance and computational efficiency, the Inverted-UNet is designed with a depth of four layers, where the indices i and j take values from 0 to 3. The computation of each node feature is illustrated as follows,

$$\begin{array}{c}{R}^{i,0}=UP\left(R^{i-1,0}\right),\end{array}$$

(7)

$$\begin{array}{c}{R}^{i,1}=[UP\left(R^{i-1,1}\right),R^{i,0},DN\left(R^{i+1,0}\right)],\end{array}$$

(8)

$$\begin{array}{c}{R}^{i,2}=[SK\left(R^{i,0}\right),R^{i,1},DN\left(R^{i+1,1}\right)],\end{array}$$

(9)

$$\begin{array}{c}{R}^{i,3}=Conv[SK\left(R^{i,0}\right),R^{i,2},DN\left(R^{i+1,2}\right)],\end{array}$$

(10)

where $UP$ and $DN$ denote upsampling and max-pooling with a stride of 2, respectively; $Conv$ denotes the convolution layer. $SK$ denotes skip connection. $[·,·]$ denotes the concatenation layer.

(2)

FFT-Based Weighting

We apply Fast Fourier Transform (FFT) to extract their spectrum amplitude distribution. These serve as weights in the softmax layer to fuse different features. This approach utilizes temporal and frequency domains information to assess the importance of different signals. The process is illustrated as follows,

$$\begin{array}{c}IN=\sum _{n=0}^{N-1}I{N}_{\mathrm{input}}·e^{-j2\pi fn/N},\end{array}$$

(11)

$$\begin{array}{c}{A}_u=\left|IN\right|,\end{array}$$

(12)

$$\begin{array}{c}{W}_{\mathrm{normal}}=Softmax(A_u,{\tilde{R}}^{0,3})(u=1,2,..,6),\end{array}$$

(13)

where $I{N}_{\mathrm{input}}$ represents the fixed-length input trajectory segment of the MDFM, generated through a sliding window mechanism. f denotes the frequency index, N is the length of each fixed trajectory segment, and n refers to the time-domain sampling index. The operator $|·|$ computes the magnitude in the frequency domain. ${\tilde{R}}^{0,3}$ denotes the output feature, which is subsequently processed by the Inverted-UNet, LayerNorm, and LeakyReLU modules in sequence.

3.3. Parameter Estimation Model

3.3.1. Motivation

In most 2D maneuvering tracking scenes, constant Turn (CT) models are important maneuvering patterns [11,12,14], where the motion pattern ${\mathit{F}}_{\mathit{k}}$ and its turn rate ($w_k$) are defined in Equation (3). The changing turn rate of a target affects the direction of its trajectory. Short-term trajectory features reflect instantaneous velocity variations and local motion trends, whereas long-term features characterize the overall motion pattern and the magnitude of velocity. Therefore, parameter estimation based on historical trajectory information requires a special module to extract both global and local spatial features.

As noted in [59], despite achieving accurate predictions with large-scale training data, networks still struggle to acquire inductive biases aligned with the underlying world model when adapting to new tasks. To address this limitation, the loss function becomes a crucial mechanism for embedding physical constraints into the learning process. Therefore, in our work, the PEM loss function should be designed to ensure that ${\mathit{F}}_{\mathit{k}}$ complies with physical laws and avoids calculation bias in the network output.

3.3.2. The Overall Structure of PEM

As illustrated in Figure 5, PEM takes a denoised trajectory as input. It first uses a cross-and-dot-product (CADP) [12] to extract trajectory shape information by calculating the sine and cosine of the intersection angle. The equations are shown below:

$$\begin{array}{c}{s}_k^{\sin }={\displaystyle \frac{\mathrm{\Delta }{p}_{x,k}\mathrm{\Delta }{p}_{y,k+1}-\mathrm{\Delta }{p}_{y,k}\mathrm{\Delta }{p}_{x,k+1}}{|\mathrm{\Delta }{\mathbf{p}}_{\mathbf{k}}\left|\right|\mathrm{\Delta }{\mathbf{p}}_{\mathbf{k}+\mathbf{1}}|}},\end{array}$$

(11a)

$$\begin{array}{c}{s}_k^{\cos }={\displaystyle \frac{\mathrm{\Delta }{p}_{x,k}\mathrm{\Delta }{p}_{x,k+1}+\mathrm{\Delta }{p}_{y,k}\mathrm{\Delta }{p}_{y,k+1}}{|\mathrm{\Delta }{\mathbf{p}}_{\mathbf{k}}\left|\right|\mathrm{\Delta }{\mathbf{p}}_{\mathbf{k}+\mathbf{1}}|}},\end{array}$$

(11b)

where $\mathrm{\Delta }{p}_{x,k}=p_{x,k}-p_{x,0}$, $\mathrm{\Delta }{p}_{y,k}=p_{y,k}-p_{y,0}$, $\mathrm{\Delta }{\mathbf{p}}_{\mathbf{k}}={[\mathrm{\Delta }{p}_{x,k},\mathrm{\Delta }{p}_{y,k}]}^{\mathrm{T}}$.

Subsequently, the trajectory shape information is fed into multi-head attention with convolution neutral nodes (MHCN) to capture both global and local features from temporal and spatial domains. The attention output is fused with the original CADP features via a residual connection, and the result is further refined by convolutional neural nodes. Specially, a novel physically constrained loss function is applied during training to avoid bias in computing ${\mathit{F}}_{\mathit{k}}$.

3.3.3. Physics-Constrained Loss Function

Considering the loss function design, we impose constraints on ${\mathit{F}}_{\mathit{k}}$ to enforce consistency with physical motion dynamics, thereby preventing the network from producing biased or physically implausible estimates. The estimation focuses on the key unknown parameter (the turn rate ${\omega }_k$) to minimize loss values. This approach enables PEM to directly obtain the time-to-time variation of the turn rate. Moreover, it could avoid calculation bias and achieve maneuvering target tracking at a higher turn rate (typically ${\omega }_k$>10°/s, e.g. Transport Aircraft [60]). However, estimating only a single parameter as the loss is insufficient, as it may lead to a large search space and cause network divergence. Therefore, we further introduce computational constraints on ${\mathit{F}}_{\mathit{k}}$. RMSE [11] measures the error between estimated parameters and their true values, serving to construct the loss function as follows:

$$\begin{array}{c}Loss={\lambda }_{1}RMSE\left(\widetilde{{\mathit{F}}_{\mathit{k}}}\right)+{\lambda }_{2}RMSE\left(\widetilde{{\omega }_k}\right),\end{array}$$

(14)

where $\widetilde{{\mathit{F}}_{\mathit{k}}}$ and $\widetilde{{\omega }_k}$ are estimated parameters, and ${\mathit{F}}_{\mathit{k}}$ and ${\omega }_k$ are real parameters. ${\lambda }_1$ and ${\lambda }_2$ represent distinct loss weights set to 0.8 and 0.2, respectively.

4. Experiments

In this section, we first introduce our training protocol. Then, we compare our MIENet to several state-of-the-art state estimation methods. Finally, we present ablation studies to investigate our work.

4.1. Implementation Details

Our MIENet is trained using the publicly available LAST dataset [11], and the implementation details are provided in Table 1. For testing, we primarily evaluate our method on the LAST dataset [11], while experiments on the SV248S dataset [57] are provided as supplementary validation to demonstrate its applicability to visual tracking.

For training on the LAST datasets [11], all trajectories involve both CV and CT kinetic patterns. The observed range in training data contains additive Gaussian noise with a mean of 0 and a standard deviation of 10, while the observed azimuth contains additive Gaussian noise with a mean of 0 and a standard deviation of 0.006. After nonlinear transformation (Equation (6)), the observation noise becomes non-Gaussian. We use RMSE as the evaluation metric for the network performance. Our MIENet was trained with a batch size of 10, using the Adam optimizer with an initial learning rate of 0.01. To prevent the network from converging to a local minimum, the learning rate was adjusted using the Cosine Annealing method. All experiments were conducted on an NVIDIA 4090 GPU.

For testing on the LAST dataset [11], detailed parameter settings of testing scenes are provided in the caption of Table 2. We perform highly maneuvering scenes where ${\omega }_k$ is more than 10°/s (e.g. Transport Aircraft [60]) and each part has a maneuvering time exceeding 20 seconds. Specially, they also include abrupt turn rates (e.g., from -30°/s to 70°/s). Specifically, in the first test scene, the target is more than 20km away from the radar sensor. The angular velocities gradually decrease, and the second segment lasts up to 52.6 seconds. This tracking scenario presents a greater challenge than those discussed in previous papers [11,12]. In the second scene, the initial state matches the first scene, but we change the direction of the turn rate and increase its value, with turns lasting up to 40 seconds in the first and third segments. In the third scene, the radar senor is closer to the target, within a range of less than 4.5km. In the forth scene, the turn rate changes are more significant in both magnitude and direction (from -30°/s to 70°/s, and then from 70°/s to -10°/s) compared to the previous three trajectories. The four scenes vary in terms of target distance and maneuvering capability, which highlights the diversity and comprehensive coverage of the evaluation environments.

For testing on the SV248S dataset [57], the observations are generated using the results of the STAR [62] method, since our approach does not rely on a detector or an acceleration module tailored for image processing. Under this formulation, the observed and estimated coordinates $(p_{x,k},p_{y,k})$ are directly comparable without any nonlinear transformation. We evaluate our method on all scenes included in the SV248S dataset, following the same evaluation protocol as STAR. The algorithm ranking is determined according to two criteria: the 5-pixel precision metric and the area under the curve (AUC) of the success plot, corresponding to the precision rate (PR) and success rate (SR), respectively [62].

4.2. Comparison to the State-of-the-Art (SOTA)

To demonstrate the superiority of our method, we compare our MIENet to several state-of-the-art (SOTA) methods, including traditional methods (UKF-A [61], IMM [19] combining multiple CT motion patterns) and deep learning-based methods (ISPM [12]).

4.2.1. Quantitative Results

(1)

The LAST Dataset

To objectively evaluate the tracker performance, we record the momentary RMSEs over 100 Monte Carlo simulations.

Quantitative results are shown in Table 3. The improvements achieved by our MIENet over traditional methods are significant. That is because, our MIENet can learn multi-domain features that are robust to scene variations and leverages both local and global information to capture latent motion patterns. In contrast, the traditional methods are usually designed for specific scenes (e.g., specific motion pattern and measurement environment). Moreover, as shown in Figure 6, we set each scene with three different noise levels. With the increase of noise, traditional methods suffer a dramatic performance decrease while our MIENet maintains accuracy. That is because, the performance of traditional methods rely heavily on manually chosen parameters (e.g., the process noise covariance $\mathit{Q}$ and the measurement noise covariance $\mathit{R}$) and cannot adapt to various noise. It is worth noting that our method preserves error stability more effectively than traditional approaches when abrupt changes occur in turn rate direction or magnitude. Moreover, it remains robust as it does not require re-adjustment of the noise parameters ($\mathit{Q}$ and $\mathit{R}$) under changing environmental noise.

As shown in Table 3, the improvements achieved by MIENet over deep learning-based methods (i.e., ISPM) are obvious. That is because, we redesign FDM and PEM is optimized for highly maneuvering target tracking. The Inverted-UNet combined with FFT-based softmax weighting enables fusion of spatial and frequency domain information. The physics-constrained loss function can avoid calculation bias. Consequently, multi-domain information of trajectories can be maintained and fully learned in the network. In the tracking process, our MIENet takes 47.2ms per iteration and ISPM takes 11.3ms. Both algorithms are suitable for real-time applications.

(2)

The SV248S Dataset

Quantitative results are presented in Table 4 and Table 5. The proposed MIENet demonstrates applicability to remote visual tracking, effectively reducing localization errors across various target classes, difficulty levels, and attribute categories without requiring retraining. These results further indicate that our method can be readily extended to two-dimensional visual object tracking tasks.

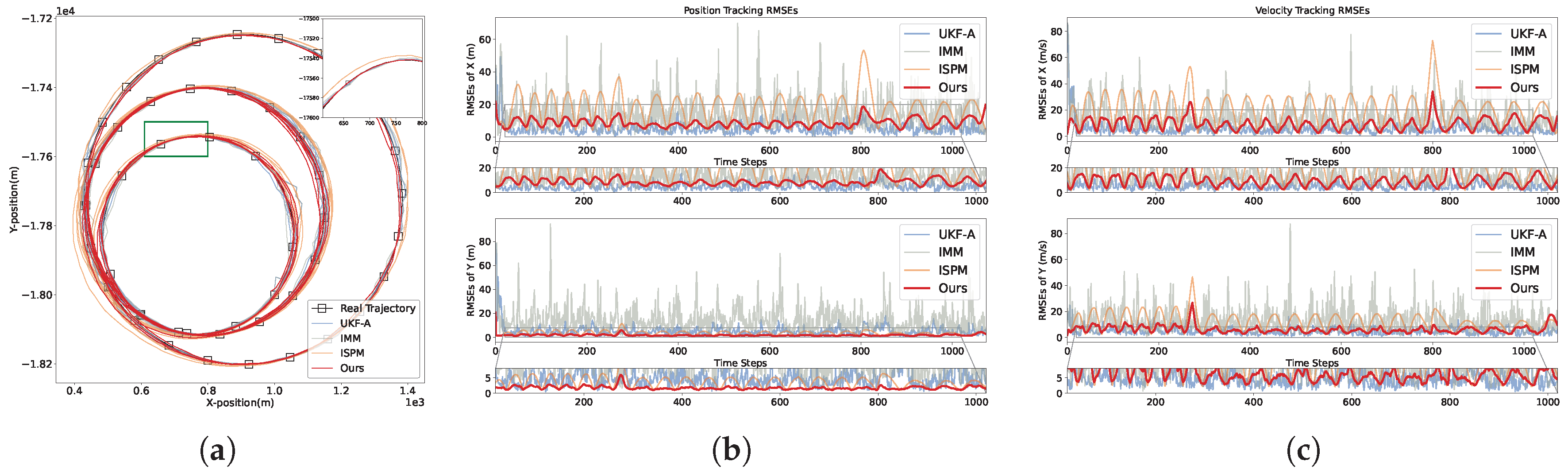
4.2.2. Qualitative Results

(1)

The LAST Dataset

Qualitative results are shown in Figure 8. Compared with traditional methods, our method can produce output with precise target states and true velocity direction. Nonetheless, the traditional methods only perform well on low-noise scenes with slowly varying turn rates. Moreover, as shown in Figure 7b and Figure 7c, our MIENet can reduce peak tracking error. That is because, traditional methods detect pattern switching only after accumulating errors. This causes delay and peak error accumulation. The deep learning-based methods (i.e., ISPM) perform much better than traditional methods. However, due to highly maneuvering scenes, ISPM lacks multi-domain information and physical constraints, which leads to large parameter estimation errors. Our MIENet is more robust to various highly maneuvering target tracking.

Figure 7. Trajectory estimation results for the first scene, along with the corresponding time-varying position and velocity errors. Our MIENet can achieve output with the lowest state estimation error and the smallest fluctuations.

Figure 7. Trajectory estimation results for the first scene, along with the corresponding time-varying position and velocity errors. Our MIENet can achieve output with the lowest state estimation error and the smallest fluctuations.

Figure 8. Trajectory estimation results for the second, third, and fourth maneuvering target tracking scenarios. Our MIENet shows superior tracking accuracy, especially during periods of maneuvering transitions.

Figure 8. Trajectory estimation results for the second, third, and fourth maneuvering target tracking scenarios. Our MIENet shows superior tracking accuracy, especially during periods of maneuvering transitions.

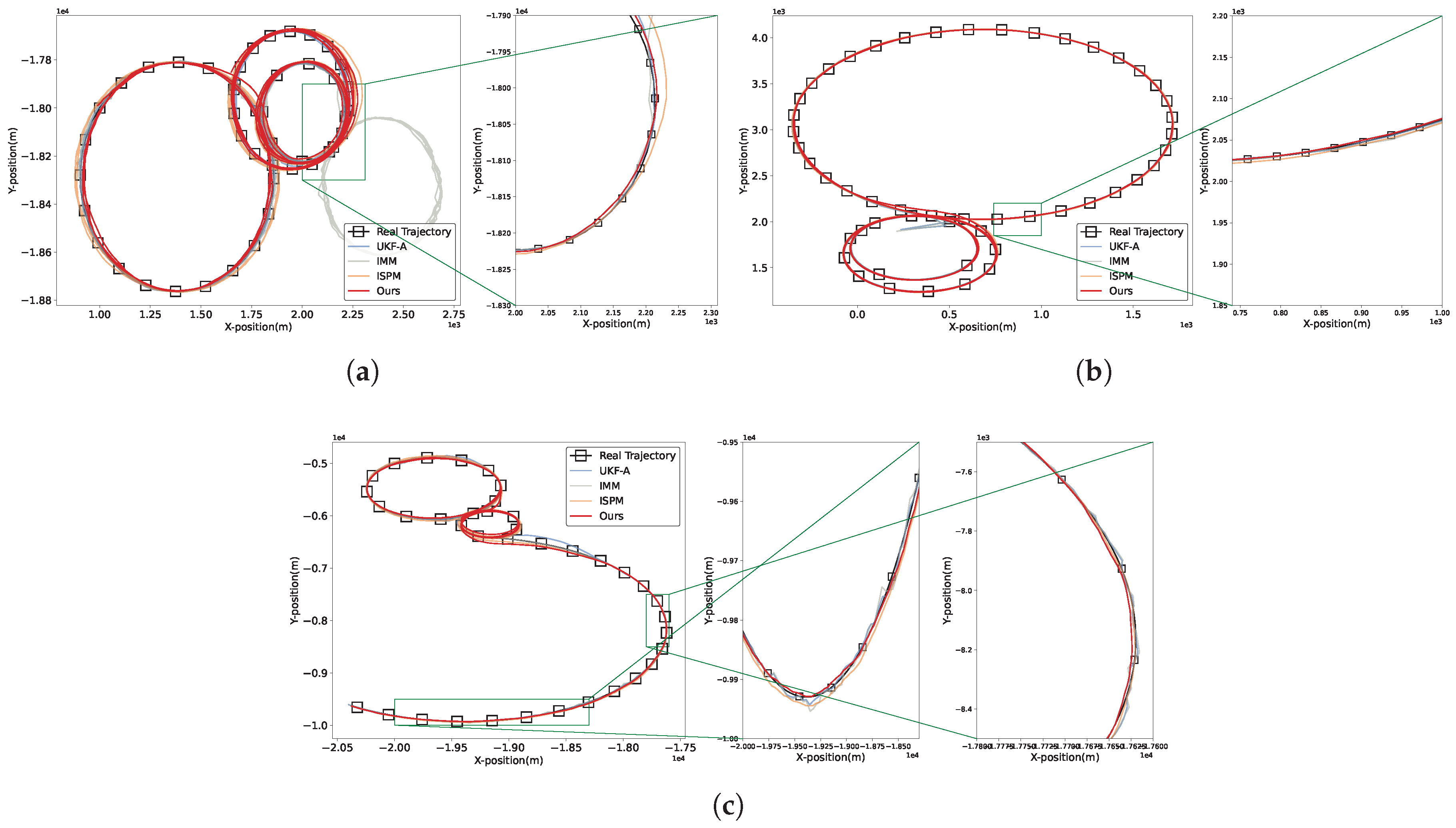
(2)

The SV248S Dataset

Qualitative results are shown in Figure 9. Our MIENet is capable of performing satellite localization in remote sensing images.

4.3. Ablation Study

In this section, we compare our MIENet with several variants. The objective is to investigate the potential benefits arising from our chosen modules and network design.

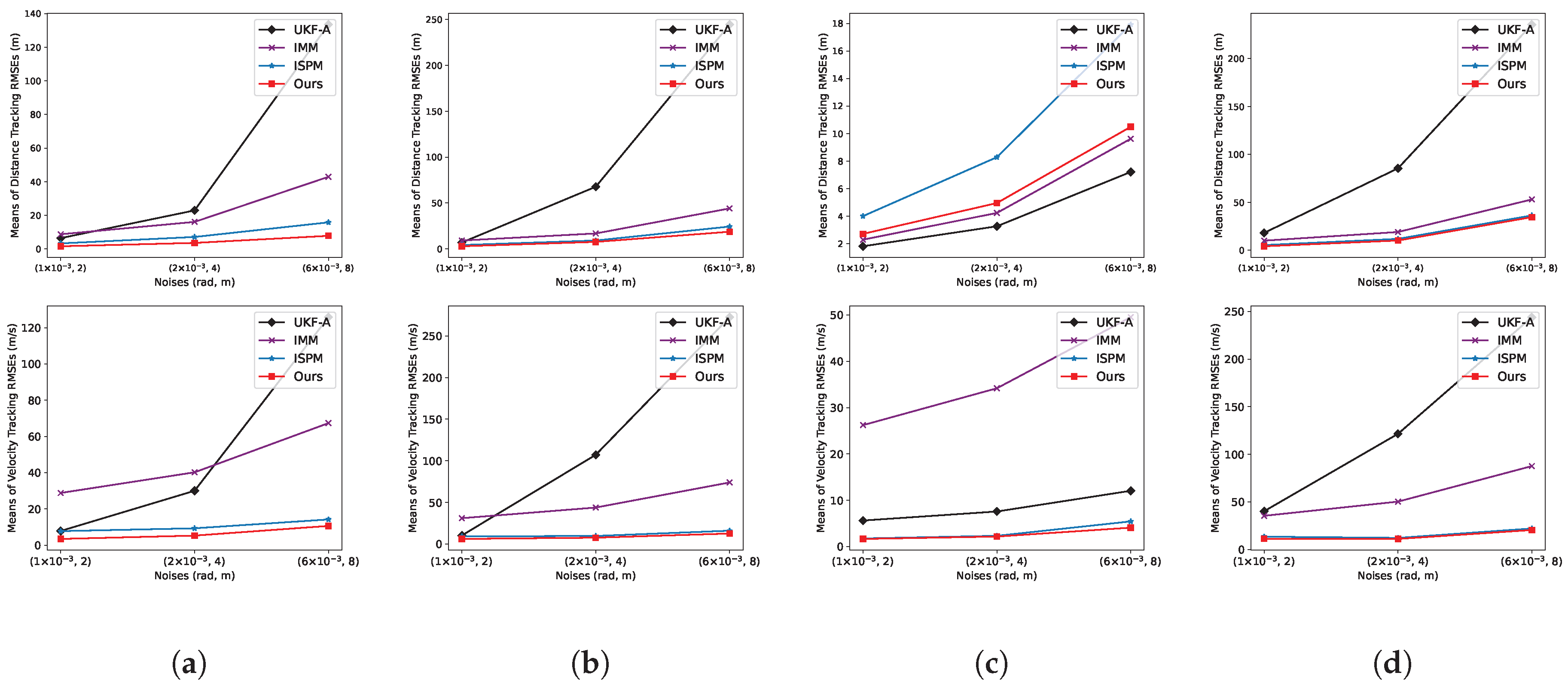
4.3.1. Ablation Study on the Magnitude and Distribution of Noise

As shown in Table 6 and Table 7, we evaluate the denoising performance under injected Gaussian-distributed and Uniform-distributed additive noise at three intensity levels to assess adaptability and generalization. Importantly, although the injected noise follows Gaussian or Uniform distributions in the input space, the nonlinear observation transformation distorts these distributions, producing non-Gaussian noise in the observation space.

Our method reduces RMSEs by at least 60% (with an average reduction of 66.4%) for cases with Gaussian-injected noise and at least 55% (with an average reduction of 63.28%) for cases with Uniform-injected noise. This consistent improvement demonstrates that FDM effectively exploits multi-domain information in observations, making it applicable to denoising tasks under varying noise levels and across different non-Gaussian noise distributions induced by nonlinear transformations.

4.3.2. Ablation Study on MDFM

MDFM is used for temporal, spatial and frequency-domain features enhancement to achieve better feature fusion. To investigate the benefits introduced by this module, we compare its effects on FDM and MIENet.

• FDM w/o MDFM: As shown in Table 8, the original FDM achieves a 61.2% reduction in RMSE, while removing the MDFM module decreases the reduction to 48.3%. The results are averaged over three noise intensity levels. This performance gap demonstrates that the Inverted-UNet is essential for denoising, as it extracts and fuses spatial-domain features more effectively from noisy observations.
• MIENet w/o MDFM: As shown in Table 9, our MIENet achieves position and velocity RMSEs of 7.78m and 10.64m/s, respectively. In ablation 1, removing the MDFM module increases RMSEs to 15.83m and 29.61m/s. That is because, FDM, as a component of MIENet, effectively suppresses noise and thereby contributes to its tracking performance.

4.3.3. Ablation Study on Multi-head Attention

We evaluate the contribution of multi-head attention (MHN) to MIENet and present the results in Table 9. In ablation 2, removing the MHN module increases RMSEs to 16.9m and 14.07m/s. That is because, our proposed MHN can capture historical global information about trajectories to enhance temporal domain features.

4.3.4. Ablation Study on Loss Function Design

The PCLoss function for PEM replaces the single parameter with eight unknown parameters. Results are shown in Table 9. Both Ablation 3 and our method demonstrate that the PCLoss function reduces the distance RMSE by 21.41% and the velocity RMSE by 21.47%. That is because, the PCLoss function can incorporate physical constrains and prevent bias in the calculations.

5. Conclusions

In this paper, we propose a versatile and adaptive multi-domain intelligent state estimation network to enhance highly maneuvering target tracking that can handle non-Gaussian noise. To address the challenges of converting noisy observation trajectories into clean inputs, we design FDM with an encoder-decoder architecture. This model enables reduction in RMSEs by at least 60% through exploiting multi-domain features. To achieve a more accurate motion model for state estimation, we propose PEM to capture temporal domain information across both global and local spatial scales. We also redesign the loss function to avoid calculation bias. Finally, experimental results demonstrate that our method achieves the state-of-the-art performance and maintains robustness across various noise levels and distributions.

There are two promising directions for future work. First, this paper considers only range and azimuth observations, incorporating Doppler measurements may further enhance maneuvering target tracking. Second, this work is restricted to tracking in the two-dimensional X–Y plane, extending the framework to three-dimensional scenarios is a valuable direction.