Submitted:
27 October 2025
Posted:
28 October 2025
You are already at the latest version
Abstract
Keywords:
Introduction
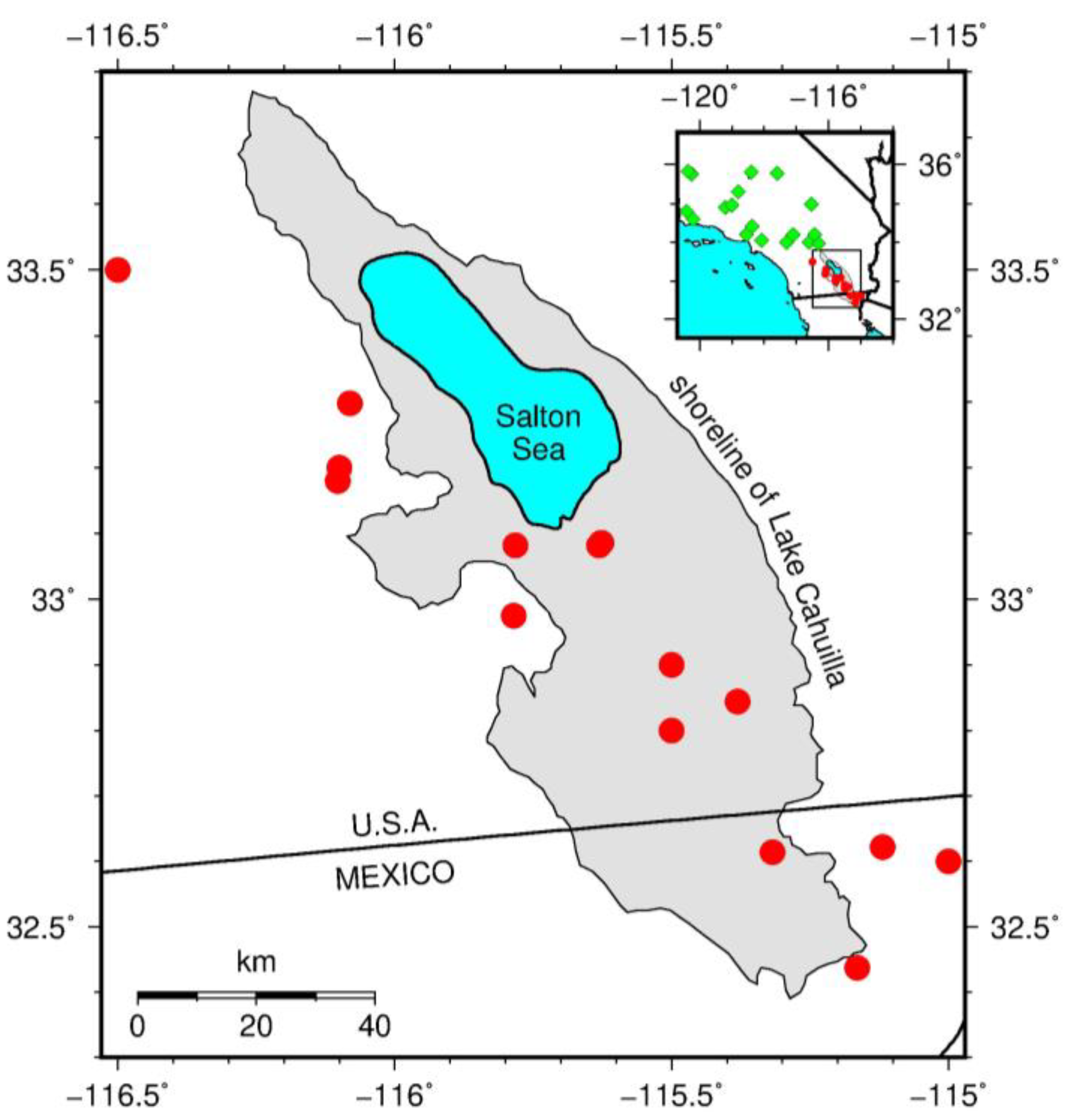
Data
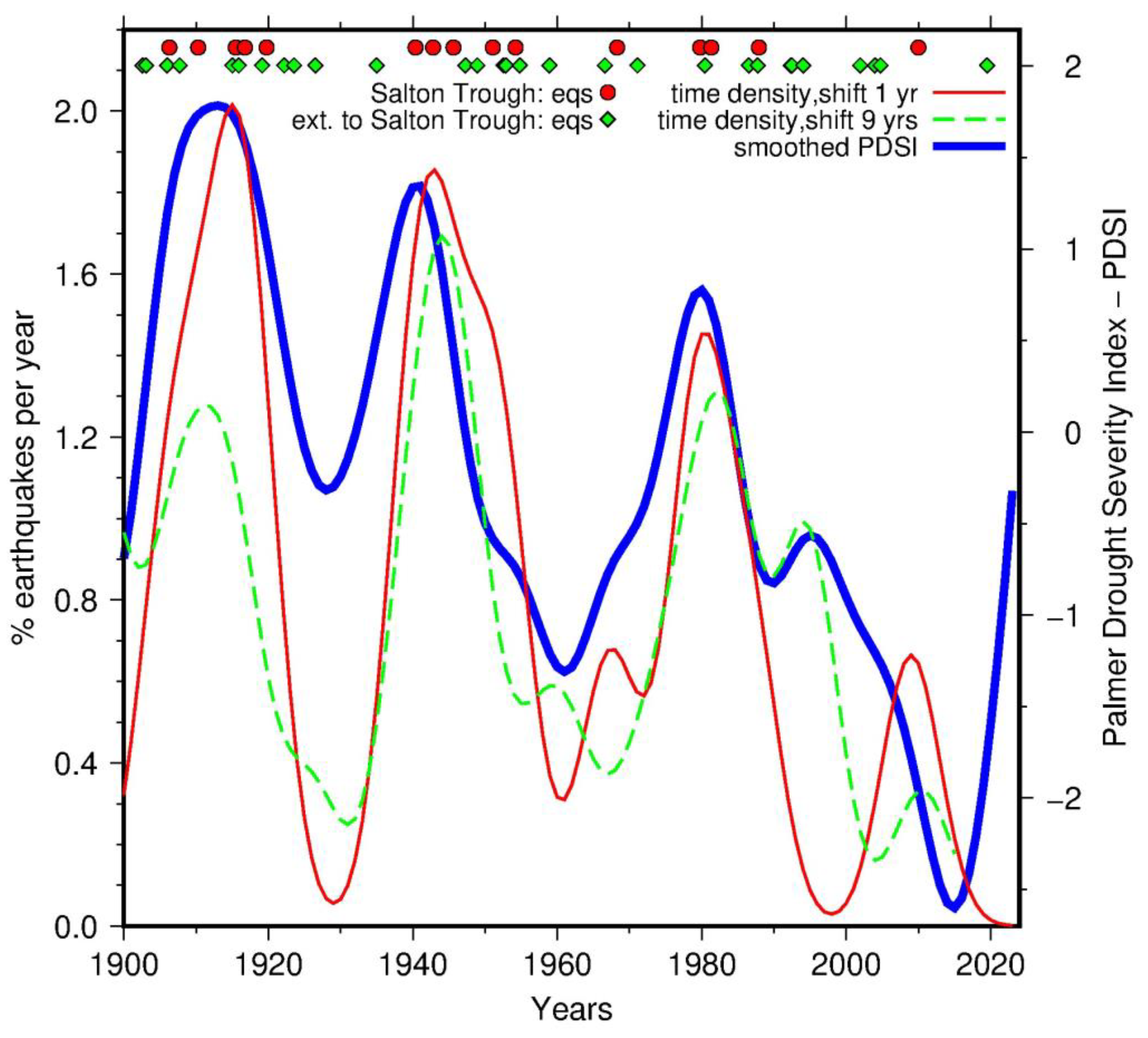
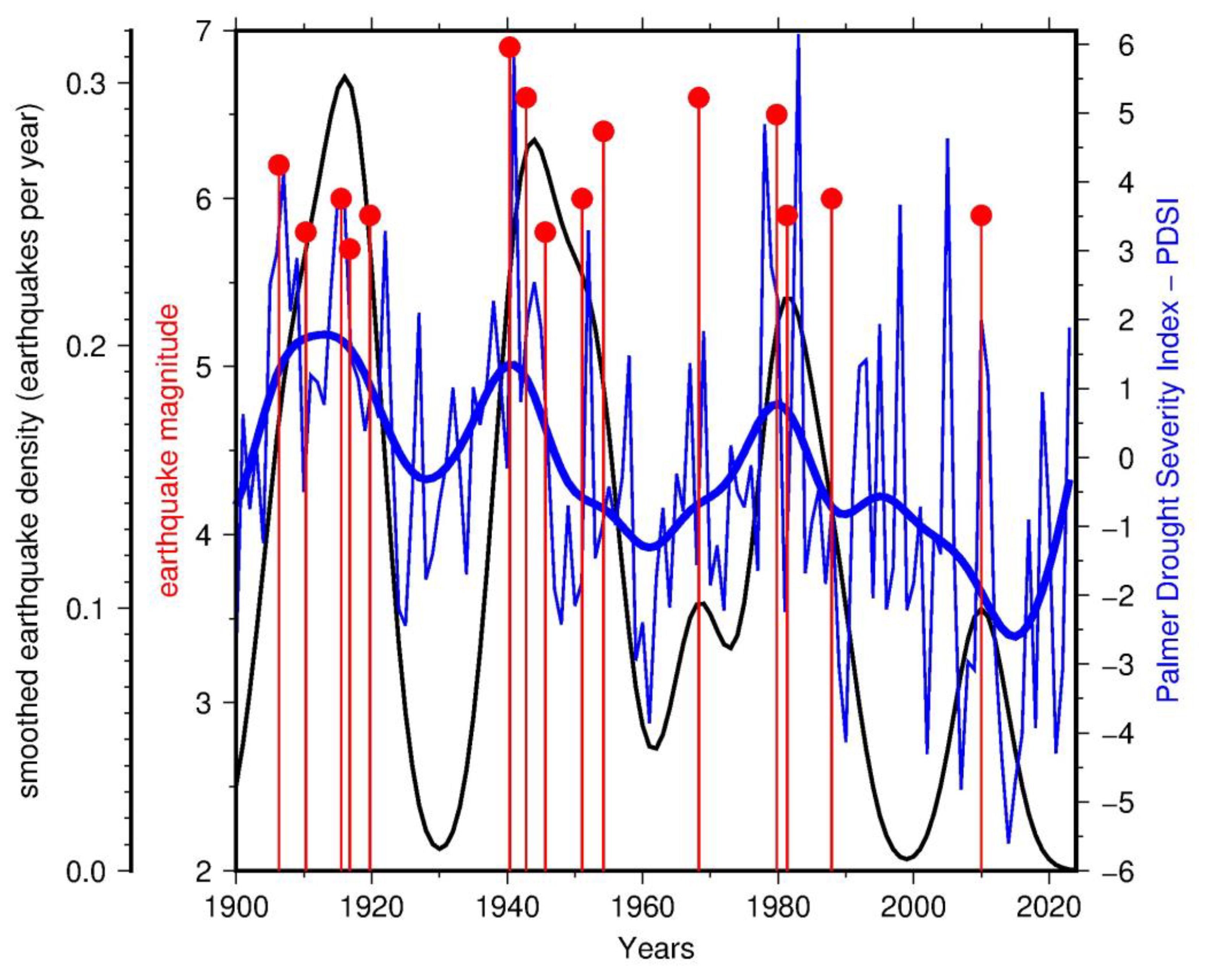
Methods
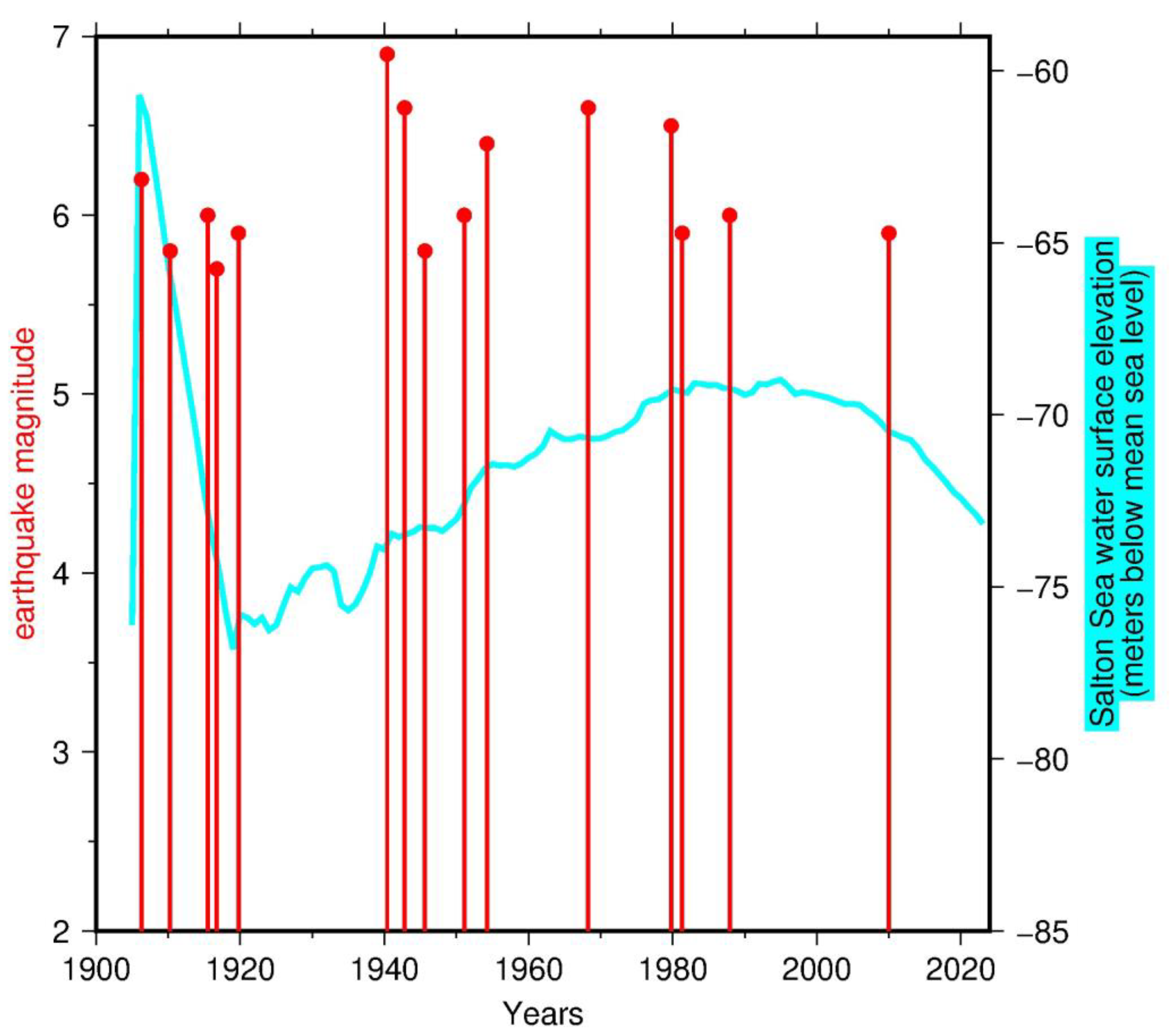
Results
Discussion
Conclusions
Data and Resources
Acknowledgments
References
- Althouse, A.D. (2016). Adjust for multiple comparisons? It’s not that simple. Ann. Thorac. Surg, 101, 1644-1645. [CrossRef]
- Bettinelli, P., J. -P. Avouac, M. Flouzat, L. Bollinger, G. Ramillien, S. Rajaure, et al. (2008). Seasonal variations of seismicity and geodetic strain in the Himalaya induced by surface hydrology. Earth Planet. Sci. Lett. 266, 332–344. [CrossRef]
- Bollinger, L., F. Perrier, J.-P. Avouac, S. Sapkota, U. Gautam, and D. R. Tiwari (2007). Seasonal modulation of seismicity in the Himalaya of Nepal, Geophys. Res. Lett. 34, L08304. [CrossRef]
- Bowman, A. W. , and A. Azzalini (1997). Applied Smoothing Techniques for Data Analysis, Oxford Univ. Press, Oxford, United Kingdom.
- Bragato, P.L. (2021). Statistical Relationship Between the Decrease of Major Seismicity and Drought in Southern California Since 1900, Front. Earth Sci. 9, 790412. [Google Scholar] [CrossRef]
- Bragato, P.L. , and M. Sugan (2014). Decreasing Rate of M≥7 Earthquakes in the Northern Hemisphere since 1900, Seismological Res. Lett. 85, 1234–1242. [CrossRef]
- D’Agostino, N., F. Silverii, O. Amoroso, V. Convertito, F. Fiorillo, G. Ventafridda, et al. (2018). Crustal deformation and seismicity modulated by groundwater recharge of karst aquifers. Geophys. Res. Lett. 45, 12253–12262. [CrossRef]
- Dai, A. (2011). Characteristics and Trends in Various Forms of the Palmer Drought Severity Index during 1900-2008. J. Geophys. Res. 116, D12115. [CrossRef]
- De Luca, G., G. Di Carlo, and M. Tallini (2018). A record of changes in the Gran Sasso groundwater before, during and after the 2016 Amatrice earthquake, central Italy, Sci. Rep. 8, 15982. [CrossRef]
- Ellsworth, W.L. (2013). Injection-induced Earthquakes, Science 341, 1225942. [CrossRef]
- Firth, D. (1993). Bias Reduction of Maximum Likelihood Estimates. Biometrika, 80, 27–38.
- Gardner, J. K. , and L. Knopoff (1974). Is the sequence of earthquakes in southern California, with aftershocks removed, Poissonian? Bull. Seismol. Soc. Am, 64, 1363–1367. [CrossRef]
- Hainzl, S., T. Kraft, J. Wassermann, H. Igel, and E. Schmedes (2006). Evidence for rainfall-triggered earthquake activity. Geophys. Res. Lett, 33, L19303. [CrossRef]
- Heinze G, Ploner M, Jiricka L, Steiner G (2025). logistf: Firth’s Bias-Reduced Logistic Regression (1.26.1) [R package]. https://CRAN.R-project.org/package=logistf. [CrossRef]
- Hooper, R. (2025). To adjust, or not to adjust, for multiple comparisons, Journal of Clinical Epidemiology 180, 111688. [CrossRef]
- Hill R.G., M. , Weingarten, T.K. Rockwell, and Y Fialko (2023). Major southern San Andreas earthquakes modulated by lake-filling events, Nature 618, 761-766. [CrossRef]
- Huang, L.-S., J. McRaney, T.-L. Teng, and M. Prebish (1979). A preliminary study on the relationship between precipitation and large earthquakes in Southern California. Pageoph 117, 1286–1300. [CrossRef]
- Kraft, T., J. Wassermann, E. Schmedes, and H. Igel (2006). Meteorological triggering of earthquake swarms at Mt. Hochstaufen, SE-Germany. Tectonophysics, 424, 245–258. [CrossRef]
- King, G., and L. Zeng (2001). Logistic regression in rare events data. Political Analysis 9, 137-163. [CrossRef]
- Lindsey, E.O., and Y. Fialko (2016). Geodetic constraints on frictional properties and earthquake hazard in the Imperial Valley, Southern California, J. Geophys. Res. 121, 1097-1113. [CrossRef]
- Liritzis, I. , and B. Petropoulos (1994). The relationship between precipitation and shallow earthquakes (M≥5 1/2) revisited, Europ. Seism. Comm. XXIV. Gen. Assembly 1, 1973–1979.
- Liritzis, Y., and B. Petropoulos (1992). A preliminary study of the relationship between large earthquakes and precipitation for the region of Athens, Greece, Earth Moon Planet 57, 13–21. [CrossRef]
- Luttrell, K., D. Sandwell, B. Smith-Konter, B. Bills, and Y. Bock (2007). Modulation of the earthquake cycle at the southern San Andreas Fault by lake loading, J. Geophys. Res. 112, B08411. [CrossRef]
- Mao, S., W. L. Ellsworth, Y. Zheng, and G. C. Beroza1 (2025). Depth-dependent seismic sensing of groundwater recovery from the atmospheric-river storms of 2023. Science. [CrossRef]
- Mueller, C. S. (2019). Earthquake Catalogs for the USGS National Seismic Hazard Maps, Seismol. Res. Lett. 90, 251–261. [CrossRef]
- Mulargia, F., and A. Bizzarri (2014). Anthropogenic triggering of large earthquakes. Sci. Rep. 4, 6100. [CrossRef]
- Oglesby, L. C. (2005). The Salton Sea: geology, history, potential problems, politics, and possible futures of an unnatural desert salt lake, Memoirs of the Southern California Academy of Sciences 10, Los Angeles, CA.
- Palmer, W. C. (1965). Meteorological Drought, Res. Paper No.45, Dept. of Commerce, Washington, D.C.
- Panda, D., B. Kundu, V.K. Gahalaut, R. Bürgmann, B. Jha, R. Asaithambi, et al. (2018). Seasonal modulation of deep slow-slip and earthquakes on the main Himalayan thrust, Nat. Commun. 9, 4140. [CrossRef]
- Peduzzi, P., J. Concato, E. Kemper, T.R. Holford, and A.R. Feinstein (1996). A simulation study of the number of events per variable in logistic regression analysis, J. Clin. Epidemiol 49, 1373–1379. [CrossRef]
- 35. van Smeden M, Moons KG, de Groot JA, et al. Sample size.
- Perneger, T.V. (1998). What’s wrong with Bonferroni adjustments. BMJ, 316, 1236-1238. [CrossRef]
- R Core Team (2012), R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.
- Rockwell, T.K. , Meltzner A.J., Haaker E.C., Madugo, D. (2022). The late Holocene history of Lake Cahuilla: two thousand years of repeated fillings within the Salton Trough, Imperial Valley, California. Quaternary Science Reviews, 282, 107456. [CrossRef]
- Rockwell, T.K. , and Y. Klinger (2023). 2000 yrs of earthquakes inferred from subsidence events on the Imperial fault, California: effect of lake-level changes and implication for variable slip rates, Earth and Planetary Science Letters 618, 118271. [CrossRef]
- Rothman, K.J. (1990). No adjustments are needed for multiple comparisons. Epidemiol, 1, 43-46. [CrossRef]
- Scharer, K.M. , and D. Yule (2020). A maximum rupture model for the Southern San Andreas and San Jacinto Faults, California, derived from paleoseismic earthquake ages: observations and limitations, Geophys. Res. Lett. 47, e2020GL088532. doi.org:10.1029/2020GL088532.
- Stolte, M., S. Herbrandt, and U. Ligges (2024). A comprehensive review of bias reduction methods for logistic regression. Statistics Surveys 18, 139–162. [CrossRef]
- Talwani, P., L. Chen, and K. Gahalaut (2007). Seismogenic Permeability,ks. J. Geophys. Res. 112, B07309. [CrossRef]
- Tostrud, M.B. (1997). The Salton Sea, 1906-1996, computed and measured salinities and water levels (draft), Colorado River Board of California, Glendale. California.
- Venables, W. N. , and B.D. Ripley (2002). Modern Applied Statistics with S. 4th Ed, Springer, New York.
- Vose, R. S., S. Applequist, M. Squires, I. Durre, M.J. Menne, C.N. Williams, et al. (2014). Improved Historical Temperature and Precipitation Time Series for U.S. Climate Divisions, J. Appl. Meteorol. Climatol. 53, 1232–1251. [CrossRef]
- Wang, Q., D. D. Jackson, and Y.Y. Kagan (2009). California Earthquakes, 1800-2007: a unified catalog with moment magnitudes, uncertainties, and focal mechanisms, Seism. Res. Lett. 80, 446–457. [CrossRef]
- Wang, C-Y., and Manga, M. (2010). Earthquakes and Water. Springer-Verlag, Berlin and Heidelberg, Germany. [CrossRef]
- Wessel, P., J. F. Luis, L. Uieda, R. Scharroo, F. Wobbe, W.H.F. Smith, and D. Tian (2019). The Generic Mapping Tools version 6, Geochemistry, Geophys., Geosystems 20, 5556–5564. [CrossRef]
- Williams, A. P., I. C. Benjamin, and J.E. Smerdon (2022). Rapid intensification of the emerging southwestern North American megadrought in 2020–2021. Nat. Clim. Change. [CrossRef]
- Zaliapin, I. , and Y. Ben-Zion (2020). Earthquake declustering using the nearest-neighbor approach in space-time-magnitude domain. J. Geophys. Res, 125, e2018JB017120. [CrossRef]
- Zhuang, J., Y. Ogata, Y., and D. Vere-Jones (2002). Stochastic declustering of space-time earthquake occurrences, J. Am. Stat. Assoc. 97, 369–380. [CrossRef]
| case | earthquake catalog | covar. | n. eqs | period (yrs) |
m (n.tests) |
lag (yrs) |
a | b | pb | Bonferroni correction 0.05/m |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Salton Trough, M≥5.7 | PDSI | 15 | 1900-2023 | 11 | 1 | -2.19±0.33 | 0.40±0.13 | 0.0024 | 0.0046 |
| 2 | Salton Trough, M≥5.7 | SSL | 15 | 1900-2023 | 11 | 0 | -4.36±5.67 | 0.09±0.08 | 0.2647 | - |
| 3 | out of Salton Trough,M≥5.7 | PDSI | 30 | 1900-2023 | 11 | 9 | -1.42±0.25 | 0.31±0.11 | 0.0038 | 0.0046 |
| 4 | Salton Trough, M≥5.7 Firth’s bias reduction |
PDSI | 15 | 1900-2023 | 1 | 1 | -2.12±0.32 | 0.38±0.12 | 0.0023 | - |
| 5 | Salton Trough, M≥5.7 cat. (Mueller 2019) |
PDSI | 15 | 1900-2023 | 1 | 1 | -2.06±0.30 | 0.27±0.12 | 0.0270 | - |
| 6 | Salton Trough, M≥5.7 pind>0.9 |
PDSI | 13 | 1900-2023 | 1 | 1 | -2.34±0.34 | 0.38±0.14 | 0.0055 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





