The Collatz Conjecture

1. Introduction

Cycles involving odd and even sequences can be tested by considering their behavior with certain trigonometric functions. For example, the odd and even expansion of the product sin function is given below.[3], p.41:

$$\sin \left(n·y\right)=n\sin \left(y\right)\cos \left(y\right)\prod _{k=1}^{{\displaystyle \frac{n-2}{2}}}\left(1-{\displaystyle \frac{{\sin }^2\left(y\right)}{{\sin }^2\frac{k\pi }{n}}}\right), \left[n \mathrm{i}\mathrm{s} \mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}\right]$$

(1)

$$\sin \left(n·y\right)=n\sin \left(y\right)\prod _{k=1}^{{\displaystyle \frac{n-1}{2}}}\left(1-{\displaystyle \frac{{\sin }^2\left(y\right)}{{\sin }^2\frac{k\pi }{n}}}\right), \left[n \mathrm{i}\mathrm{s} \mathrm{o}\mathrm{d}\mathrm{d}\right]$$

(2)

These two relations clearly separate odd and even values of n, irrespective of the values of y. If then there exists a sequence of Odd and Even numbers for the Collatz sequence such as

Odd→Even→Even→Odd→..., etc.

we can represent each odd and even value by $R_n,$ where, for $y=1$, in (1) and 2):

$$R_n={\displaystyle \frac{\prod _{k=1}^{\frac{n}{2}-\frac{1}{2}}\left(1-\frac{{\sin }^2\left(1\right)}{{\sin }^2\frac{k\pi }{n}}\right)}{\cos \left(1\right)\prod _{k=1}^{\frac{n}{2}-1}\left(1-\frac{{\sin }^2\left(1\right)}{{\sin }^2\frac{k\pi }{n}}\right)}},$$

(3)

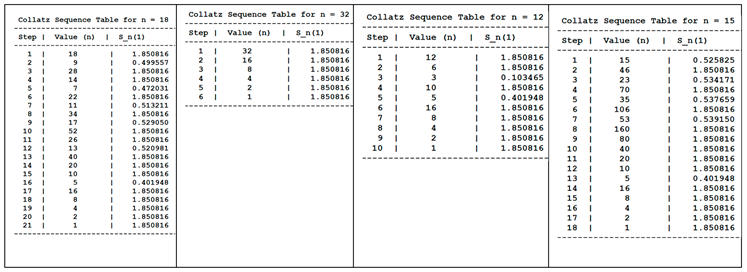
It so happens that the even values in the sequence exclusively produce the value $R_n=1.85081571768092561791$, while the odd values of the first 100 values of $n$seem to have a range such that:

(4)

Table 1. shows the Collatz sequence of the values of $R_n$ for various $n.$

Table 1. shows the Collatz sequence of the values of $R_n$ for various $n.$

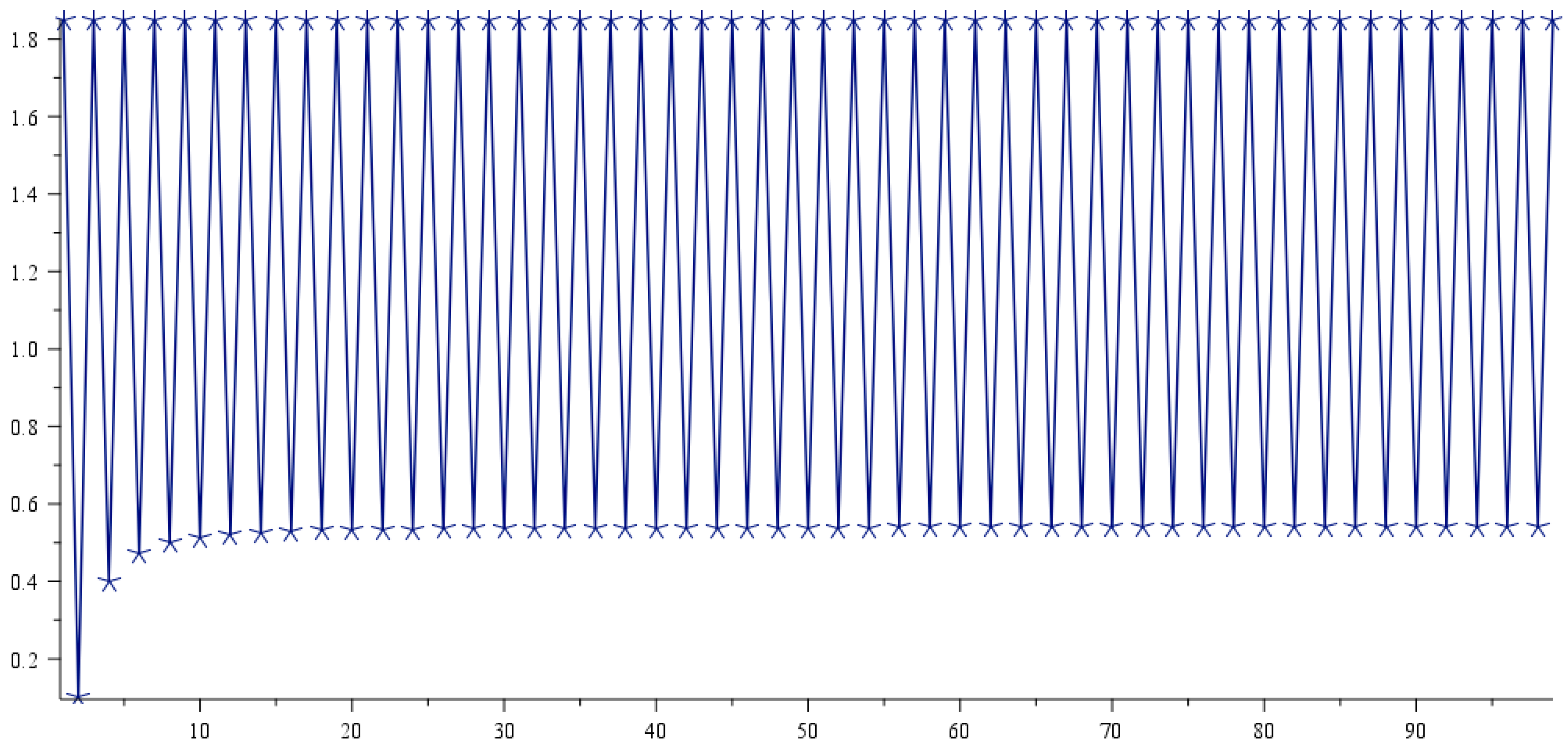
It is then possible to investigate the Collatz conjecture by trigonometric and algebraic means. Here is a graph showing the values of some numbers as the angle in radians and the rays measuring the radial vector for the value of n I in trigonometric space. A graph of the values of n=2..100 is shown below:

Figure 1.

Figure 1.

As can be seen, the values in the $R_n$ overlayed graphs show the symmetry of 5 numbers in the Collatz trigonometric space. The transformations are periodically bounded between an upper value for sequentially arranged even numbers and lower values for odd numbers. Since for every odd number, there exist an upper bound that corresponds to an even number, one can surmise that the Collatz sequence for all numbers must result in either some lower bound or some sequences of upper that is a power of 2 and at least some lower but finite bounds. The lower bounds have no sequence degeneration since each odd number must hit an even number. It is convenient to demonstrate the rigid boundaries of the trigonometric constrains for the even and odd numbers in a Collatz sequence. As can be seen, the inner circle contains vectors that form a symmetry except for the final odd number that send the sequence to the maximum radius.

Figure 2.

Figure 2.

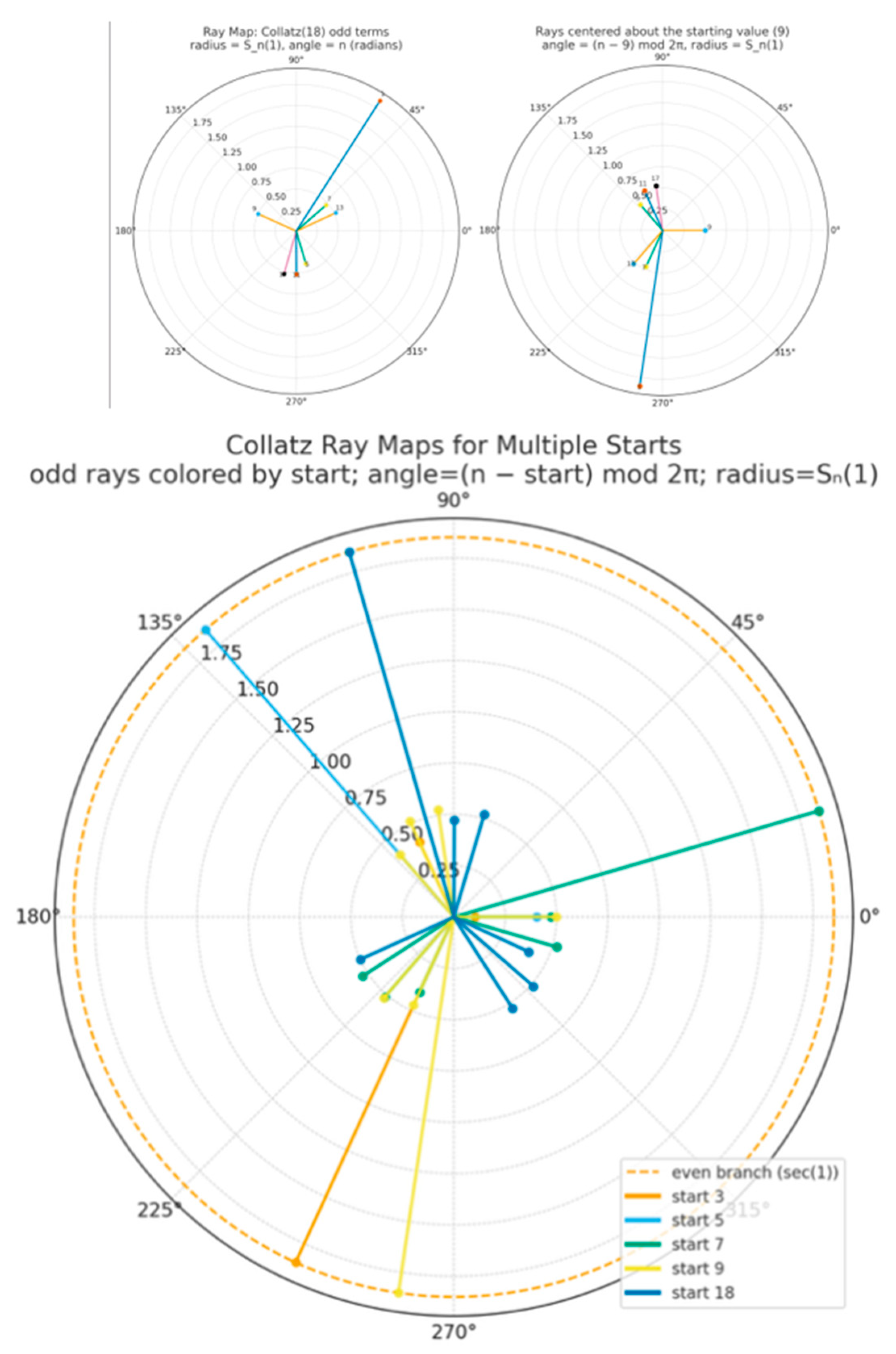
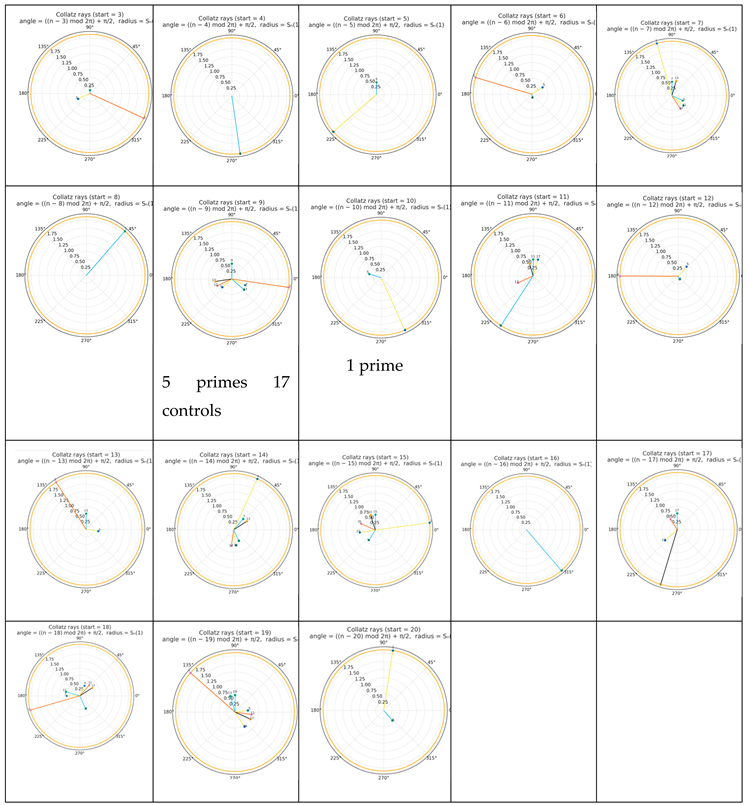
A radial vector chart of some sequences is shown in Table 2 below:

It is obvious that the rays have a symmetry, and the final values always fall on the vector that goes to $n=1$.

From

$$R_n={\displaystyle \frac{\prod _{k=1}^{\frac{n}{2}-\frac{1}{2}}\left(1-\frac{{\sin }^2\left(1\right)}{{\sin }^2\frac{k\pi }{n}}\right)}{\cos \left(1\right)\prod _{k=1}^{\frac{n}{2}-1}\left(1-\frac{{\sin }^2\left(1\right)}{{\sin }^2\frac{k\pi }{n}}\right)}},$$

(5)

We get:

$$R_n=\left\{\begin{array}{cc}\sec \left(1\right)& if n is even\\ \left(1-{\displaystyle \frac{{\sin }^2\left(1\right)}{{\cos }^2\frac{k\pi }{2n}}}\right)& if n is odd.\end{array} \right.$$

(6)

The invariant circle is the even field, $\tau =\sec \left(1\right).$

2. The Symmetry Condition

The Collatz process alternates between the two transformations

$$T_{odd}\left(n\right)=3n+1, T_{even}\left(n\right)={\displaystyle \frac{n}{2}},$$

(7)

In polar space, these correspond to

$$\begin{array}{c}Expansion: r\to R_{3n+1}\left(1\right)\\ Reflection: r\to R_{{\displaystyle \frac{n}{2}}}\left(1\right) \end{array}$$

(8)

And angular shifts: ${\theta }_{k+1}=\left({\theta }_{k+1}+{\phi }_k\right) \mathrm{m}\mathrm{o}\mathrm{d} 2\pi$, where ${\phi }_k$ represents the parity-dependent phase rotation. The closure condition of the Collatz orbit is

$$\exists k:R_{n_k}\left(1\right)=\tau =\sec \left(1\right)$$

(9)

This geometry means the ray of the $k^{th}$ term intersects the invariant circle for radii $\sec \left(1\right).$

Consequence of invariance of the upper bound.

Because $R_n\left(1\right)<\mathrm{s}\mathrm{e}\mathrm{c}\left(1\right)$for all odd $n$ (since $\cos \left({\displaystyle \frac{\pi }{2n}}\right)<1$ and $R_n\left(1\right)=\mathrm{s}\mathrm{e}\mathrm{c}\left(1\right)$ for even $n$ we have

$$\left[\mathit{e}\mathit{v}\mathit{e}\mathit{r}\mathit{y}\mathit{o}\mathit{d}\mathit{d}\mathit{s}\mathit{t}\mathit{e}\mathit{p}\mathit{l}\mathit{i}\mathit{e}\mathit{s}\mathit{i}\mathit{n}\mathit{s}\mathit{i}\mathit{d}\mathit{e}\mathit{t}\mathit{h}\mathit{e}\mathit{c}\mathit{i}\mathit{r}\mathit{c}\mathit{l}\mathit{e}\right]\cup \left[\mathit{e}\mathit{v}\mathit{e}\mathit{r}\mathit{y}\mathit{e}\mathit{v}\mathit{e}\mathit{n}\mathit{s}\mathit{t}\mathit{e}\mathit{p}\mathit{l}\mathit{i}\mathit{e}\mathit{s}\mathit{o}\mathit{n}\mathit{t}\mathit{h}\mathit{e}\mathit{c}\mathit{i}\mathit{r}\mathit{c}\mathit{l}\mathit{e}\right]$$

Hence the dynamics forces the sequences to oscillate between the interior of the boundary, and the boundary, producing the observed symmetry:

$$R_n=\left\{\begin{array}{cc}{R}_{3n+1}\left(1\right)<\sec \left(1\right)& if n is odd\\ \sec \left(1\right)& if n is even.\end{array} \right.$$

(10)

The convergence of the Collatz space in the geometric and trigonometric world means:

$$\underset{k\to \infty }{\lim }{R}_{n_k}\left(1\right)=\sec \left(1\right)$$

(11)

Thus, the angle of intersection determines the path’s rotational symmetry and phase. All valid sequences, regardless of starting points end up at some intersection of the invariant circle, i.e., they share the same final radius, only differing by a rotational angle.

Setup:

Fix

$$R_n=\left\{\begin{array}{cc}\sec \left(1\right)& if n is even\\ \left(1-{\displaystyle \frac{{\sin }^2\left(1\right)}{{\cos }^2\frac{k\pi }{2n}}}\right)& if n is odd.\end{array} \right.$$

(12)

Then, $R_n\in R_{min}, \sec \left(1\right)$ with the top range being $\sec \left(1\right),$and, $R_n<\sec \left(1\right)$ for every odd $n.$ Write the Collatz trajectory:

$$n_0\to n_1\to n_2\to \dots n_{k+1}=\left\{\begin{array}{cc}{\displaystyle \frac{n_k}{2}}& if n_k is even\\ 3n_k+1& if n_k is odd.\end{array} \right.$$

(13)

Write for each odd $o,$ the 2-adic valuation

$$3o+1=2^{a\left(o\right)}m\left(o\right), odd, a\left(o\right)\le 1.$$

(14)

Then, the block of $, a\left(o\right)$ consecutive evens that follows $o$ in the trajectory is its “even run”.

Lemma 1 (Bounds).

For all $n$,

$$R_{min}<R_n\le \sec \left(1\right), R_n=\sec \left(1\right)\iff n even or n=1$$

(15)

Proposition 1.

The sequence 1,2,3…, maps to $R_n$ to hit $\sec \left(1\right)$ infinitely many times, simply because there are infinitely many even integers.

Proposition 2.

Let $n_k$ be any Collatz trajectory until it terminates at 1. Then,

$$R_n=\sec \left(1\right) for infinitely many even values of k.$$

Every time the trajectory visits an odd value,$o,$ the next value is $3o+1,$ which is even.; hence each odd step is immedietly followed by a top hit, $R_{max}=$ $\sec \left(1\right)$. If the trajectory terminates, it certainly hit the top value, on the final chain; If it were infinite, it will encounter infinitely many top values, $R_{max}=$ $\sec \left(1\right)$. Thus, Every Collatz trajectory touches the top value, $R_{max},$ infinitely many times.

3. Arithmetic Facts

Solvability mod$2^{\mathit{k}}.$

For every $k\ge 1$, the congruence

$$3o\equiv -1 \left(\mathrm{m}\mathrm{o}\mathrm{d} 2^k\right)$$

Has solutions, because 3 is invertible modulo $2^k.$ Thus, there are infinitely many odd integers $o$ for which $2^k\left(\left|3o\right.+1\right).$There are infinitely many targets, whose even run length, is at least $k.$

Lemma 1 (Infinite boundary contacts)

For every Collatz sequence $n_k,$the set $\mathrm{\aleph }=\left\{k:R_{n_k}=\sec \left(1\right)\right\}$ is infinite and each member of the set $\mathrm{\aleph }$maps to an odd integer,$n_{k-1}$ with $n_{k-1}=3n_k+1.$ $\left[R_o\iff R_{max}\right]$.

Proof: Every odd step is immedietly followed by an even step, hence by a top value $\sec \left(1\right).$ If the trajectory terminates, the final block is a chain of even values, otherwise the orbit contains infinitely many odds and so infinitely many top values.

All odd values of the sequence belong to at least one member of the infinite set of ordered odd chains, $o\in \left\{\mathrm{1,3},5\dots \infty \right\}.$ Every member of the {o} belongs to o. There is a one-one pairing of the $R_{max}\iff R_o.$ Therefore the chain of the sequence must at least attain a top value. Hence every chain will either continue over extended sequences and at least must hit an even value that is a power of 2 when the chain will terminate at 1.

Let $f:\mathbb{N}\to \mathbb{N}$ be a Collatz map

$$f\left(n\right)==\left\{\begin{array}{cc}{\displaystyle \frac{n}{2}}& if n_k is even\\ 3n+1& if n_k is odd.\end{array} \right.$$

For $k\in \mathbb{N},$ define the forward Collatz sequence

$$C\left(k\right)=\left(k, f\left(k\right), f\left(f\left(k\right)\right),\dots \right)$$

Suppose a sequence collapses if it eventually reaches 1; equivalently, $f\left(k\right)\exists t\ge 0,$ with $f^t\left(k\right)=1.$Define the global set of all terms ever encountered as

$$C\left(\infty \right)≔\bigcup _{k\ge 0}\left\{f^t\left(k\right):t>0\right\}$$

Lemma 2 (Sub-sequence inclusion)

If $f^t\left(m\right)=k$ for some $t\ge 0$, then the subsequence (tail) of $C\left(k\right)$ from $t$ equals $C\left(k\right).$ In particular,

$f^t\left(m\right)=k⟹C\left(k\right)\subseteq C\left(m\right).$

Proof: for all $s\ge 0; f^{t+s}\left(m\right)=f^s\left(k\right).$

Theorem 1: (Union contains all finite sequences)

For every $k,C\left(k\right)\subseteq C\left(\mathrm{\infty }\right).$

Proof: By definition of $C\left(\infty \right),$ each term $f^t\left(k\right)$ belongs to the union.

Theorem 2: (Global collapse from local collapse)

If every $C\left(k\right)$ collapses, then element of $C\left(\infty \right)$

Also collapses (hence the infinite union collapses in the sense that each of its elements has a finite path to 1.

Proof: Take any $x \in C\left(\infty \right).$ Then $x=f^t\left(k\right),$ for some $k,t.$ By hypotheses, $C\left(k\right)$reaches 1. So there exists $s,$ with $f^{t+s}\left(k\right)=1.$ Then, $x$ also reaches 1 in $s$ further steps.

Theorem 3 (Collapse via a cofinal sequence-conditional).

Suppose there exists $M$ such that for every $k,$ there is a $t$ with $f^t\left(M\right)=k,$ (i.e., $C\left(M\right)$meets every start point). If $C\left(M\right)$ collapses, then all $C\left(k\right)$ collapse.

Proof: From $f^t\left(M\right)=k$, and Lemma 2, $C\left(k\right)\subseteq C\left(m\right).$ Since $C\left(m\right)$ reaches 1, every $C\left(k\right)$ will reach 1.

4. Conclusions

Every Collatz sequence collapses to 1. The sequences have a 1:1 correspondence between odd and even integers. Every Collatz sequence is a sub-sequence of the infinite sequence. Every infinite sequence will collapse because a subset collapses, (similar to Euclid’s proof of infinitude of prime numbers).