Graph-Attention-Regularized Deep Support Vector Data Description for Semi-Supervised Anomaly Detection: A Case Study in Automotive Quality Control

1. Introduction

Anomaly detection is a critical issue in machine learning, with applications in manufacturing, industrial process control, medical diagnosis, cybersecurity, and disaster management [1,2,3,4,5]. The primary objective is to learn a representation of normal operating conditions and identify deviations as anomalies. Unlike standard supervised classification, anomaly detection is characterized by severe class imbalance, where anomalies are rare, diverse, and often scarcely labeled, while normal samples are abundant. However, despite this abundance, labeling a sample as truly normal is often costly and challenging. In many operational settings, normal labeling requires expert review against process specifications, additional quality-control checks (sometimes destructive or time-consuming), or prolonged observation to rule out hidden faults. These steps consume engineer time and test resources and can cause production downtime, making exhaustive normal labeling economically impractical at scale. For instance, in automotive quality management, current practice for windshield-wiper noise relies on expert assessment: after controlled recordings, mel frequency cepstral coefficients/spectrogram features are computed, and an expert labels the noise types [6].

Early efforts in one-class classification introduced support vector data description (SVDD) and the one-class support vector machine (OC-SVM) as core frameworks. SVDD learns a minimum-radius hypersphere that encloses the normal training data, predicting observations outside the decision boundary as anomalies [7]. The OC-SVM learns a maximum-margin separator from the origin in feature space to capture the support of the normal distribution [8]. While these models produce compact, interpretable decision boundaries, they generally require a clean set of normal samples and do not utilize unlabeled data, thereby limiting their effectiveness when normal labeling is costly and unlabeled observations are abundant.

Graph-based semi-supervised learning offers a systematic approach to utilize unlabeled data by representing adjacency and manifold structure. The basic concepts of spectral graphs and Laplacian regularization define the cluster assumption through the concept of smoothness across neighborhoods [9,10]. Recent studies and applications in graph anomaly detection indicate extensive utilization across nodes, edges, subgraphs, and whole graphs [11,12,13]. SVDD has been extended using semi-supervised methods that utilize the structure of unlabeled data while employing a small number of labeled normal observations to guide the boundary. In order to leverage large unlabeled data without hard pseudo-labels, a common practice is to enhance the SVDD objective with manifold/graph regularization so that points connected on a similarity graph remain close in the learned representation [9,10]. One SVDD variant, graph-based semi-supervised SVDD (S3SVDD), leverages global/local geometric structure with limited labels by utilizing a $k$-nearest neighbor ($k$-NN) spectral graph and a Laplacian smoothness term in the SVDD objective to exploit unlabeled data [14]. Similarly, semi-supervised subclass SVDD proposes a new formulation that utilizes global/local geometric structure with limited labels [15]. Separately, a manifold-regularized SVDD for noisy label detection was introduced, showing that incorporating a graph Laplacian into the SVDD objective improves robustness to label noise while still leveraging abundant unlabeled data [16]. In addition, a semi-supervised convolutional neural network (CNN) with SVDD has demonstrated practical viability in industrial monitoring [17]. While traditional graph-based SVDD variants have shown potential, these methods typically rely on fixed, pseudo-labeled neighbor graphs (e.g., $k$-NN with a chosen metric and $k$) and uniform edge weights, which can over-connect across data density breaks, propagate contamination from suspect (anomalous) neighbors, and require careful tuning [9,14,18,19,20].

The introduction of deep learning has led to significant advances in deep anomaly detection. Deep SVDD (DeepSVDD) extended the SVDD framework by combining it with a deep encoder that maps data into a latent representation enclosed by a hypersphere [21]. Autoencoders and their variants have been widely adopted to learn low-dimensional embeddings and reconstruction-based anomaly scores in industrial and time-series contexts [22,23]. Additionally, self-supervised anomaly detection has emerged as a promising direction by utilizing contrastive learning and related pretext objectives that enhance representation quality under limited labels [24,25]. However, common deep anomaly detection methods often use objectives that are indirectly aligned with the decision boundary (e.g., reconstruction error), leverage unlabeled data using proxy tasks rather than task-aware constraints in the decision boundary learner, and offer limited interpretability of decisions [26,27,28,29,30,31].

Motivated by the aforementioned challenges, this paper presents Graph-Attention-Regularized Deep SVDD (GAR-DSVDD). Specifically, we develop a semi-supervised Deep SVDD that trains a deep encoder and a one-class hypersphere end-to-end, while exploiting unlabeled structures with a center-pull regularizer on a learned graph. To build this graph, we introduce an attention-weighted latent $k$-NN mechanism that assigns label and score-aware importance to neighbors, emphasizing prototypical normal observations and down-weighting suspect or anomalous samples, thereby mitigating label scarcity and limiting error propagation from contaminated edges. Unlike iterative pseudo-labeling methods, our training uses unlabeled data directly through the center-pull and graph smoothness regularizers, which stabilize optimization and reduce computation. For safety-critical deployment, per-instance attention weights provide transparent explanations over the top-$k$ neighbors. Comprehensive experiments on a simulated dataset and an industrial windshield-wiper acoustics case study show that GAR-DSVDD achieves superior detection of subtle anomalies compared with classical and deep learning benchmarks, while reducing labeling effort and operator subjectivity.

The remainder of the paper is structured as follows. Section 2 reviews preliminaries and notation for semi-supervised anomaly detection. Section 3 presents the proposed GAR-DSVDD method. Section 4 describes the experimental setup and reports results on simulated datasets and the windshield-wiper acoustics case study, along with sensitivity analyses. Section 5 discusses findings, conclusions, and potential future work directions.

2. Preliminaries

2.1. Data and Basic Notation

Given a training dataset $\mathcal{X}=\left\{x_i\mid x_i\in {\mathbb{R}}^p,i=1,\dots ,n\right\}$ that decomposes into two disjoint subsets: a small set of labeled normal samples ${\mathcal{X}}_{\mathcal{l}}^{+}$ and a large unlabeled set ${\mathcal{X}}_{\mathcal{u}}$, with

$$\mathcal{X}={\mathcal{X}}_{\mathcal{l}}^{+}\cup {\mathcal{X}}_{\mathcal{u}},{\mathcal{X}}_{\mathcal{l}}^{+}\cap {\mathcal{X}}_{\mathcal{u}}=\mathrm{\varnothing }.$$

Let $L\subset \left\{1,\dots ,n\right\}$ be the index set of labeled normal observations and $U=\{1,\dots ,n\}\setminus L$ the unlabeled indices, with $\left|L\right|=\mathcal{l}$, $\left|U\right|=u$, and label rate $\rho =\mathcal{l}/n$. The unlabeled pool is assumed predominantly normal and may contain a small contamination of anomalies, upper-bounded by $\epsilon \in \left[\mathrm{0,1}\right)$. Features are standardized by coordinate (z-scoring). A learnable encoder ${\varphi }_{\theta }:{\mathbb{R}}^p\to {\mathbb{R}}^s$ maps each input to a latent representation, where $\theta$ denotes the encoder’s trainable parameters; we write ${\mathcal{z}}_i={\varphi }_{\theta }\left(x_i\right)$ and collect latents as $\mathcal{Z}={\left\{{\mathcal{z}}_i\right\}}_{i=1}^n$. We stack them row-wise in $Z={\left[{\mathcal{z}}_1,\dots ,{\mathcal{z}}_n\right]}^{\mathrm{\top }}\in {\mathbb{R}}^{n\times s}$. We use ${‖·‖}_2$ for the Euclidean norm and $⟨\cdot ,\cdot ⟩$ for the standard inner product in ${\mathbb{R}}^s$. This setting follows the deep one-class paradigm: the normal class is to be enclosed within a compact latent region while avoiding pseudo-labels for the unlabeled pool. Instead, ${\mathcal{X}}_{\mathcal{u}}$ informs the latent geometry via a graph defined over ${\mathcal{z}}_i$ (details in §3).

Prior work motivating this formulation includes Deep SVDD–style one-class modeling and graph-based semi-supervised learning that leverages unlabeled geometry [9,10,21].

2.2. Latent One-Class Score

We summarize the normal set by a latent center $\mathit{c}\in {\mathbb{R}}^s$ and a soft margin (squared radius) used for score calibration

$$m=\mathrm{softplus}\left(\eta \right),\eta \in \mathbb{R}.$$

Given latents $\mathcal{Z}={\left\{{\mathcal{z}}_i\right\}}_{i=1}^n$ with ${\mathcal{z}}_{\mathcal{i}}={\varphi }_{\theta }\left(x_i\right)$, the per-sample anomaly score is

$$f_i={‖{\mathcal{z}}_i-\mathit{c}‖}_2^2-m.$$

(1)

A sample is more anomalous as $f_i$ increases; the decision boundary is $f=0$. Eq. (1) gives the deep “hypersphere” view of SVDD in latent space, where $\mathit{c}$ summarizes the normal set and ${\varphi }_{\theta }$ maps inputs to latents. The offset $m>0$ specifies the boundary tolerance (squared radius) via a softplus parameterization, ensuring positivity and smooth gradients near the boundary. The center $\mathit{c}$ is typically initialized as the mean of $\left\{{\mathcal{z}}_i:x_i\in {\mathcal{X}}_{\mathcal{l}}^{+}\right\}$ to stabilize early training. The score is scale-aware: increasing $m$ relaxes the boundary, whereas decreasing $m$ tightens the enclosure, preserving the boundary-level interpretation (distance to $\mathit{c}$ versus tolerance $m$). During training, $m$ is treated as a calibration constant, so choosing a train-quantile threshold on f is equivalent to thresholding the same quantile of $d^2={‖\mathcal{ }\mathcal{z}\mathcal{ }-\mathcal{ }\mathit{c}‖}_2^2$.

3. Graph-Attention-Regularized Deep SVDD

We now detail GAR-DSVDD. The objective has three parts: (i) a one-class enclosure on labeled normal observations, (ii) an unlabeled neighbor-smoothness on squared distances over an attention-weighted directed, row-normalized $k$-NN graph, and (iii) standard parameter regularization.

3.1. Latent Attention-Weighted $k$-NN Graph

We construct a directed row-normalized graph $G=\left(\mathcal{V},\mathcal{E}\right)$ over the latent set ${\left\{{\mathcal{z}}_i\right\}}_{i=1}^n$, where each latent is produced by the encoder ${\mathcal{z}}_{\mathcal{i}}={\varphi }_{\theta }\left(x_i\right)$, and we stack them row-wise as $Z={\left[{\mathcal{z}}_1,\dots ,{\mathcal{z}}_n\right]}^{\mathrm{\top }}\in {\mathbb{R}}^{n\times s}$. For each node $i$, define the directed neighborhood ${\mathcal{N}}_k\left(i\right)$ as the indices of the $k$-NN of ${\mathcal{z}}_{\mathcal{i}}$ under a base metric (Euclidean by default). Each candidate edge $(i,j)$ carries a base affinity ${\kappa }_{\mathrm{base}}\left({\mathcal{z}}_i,{\mathcal{z}}_j\right)\in \left[\mathrm{0,1}\right]$, chosen as either a Gaussian kernel or a constant:

$${\kappa }_{\mathrm{base}}\left({\mathcal{z}}_i,{\mathcal{z}}_j\right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-{‖{\mathcal{z}}_i-{\mathcal{z}}_j‖}_2^2/{\sigma }^2\right)\mathrm{or}{\kappa }_{\mathrm{base}}\left({\mathcal{z}}_i,{\mathcal{z}}_j\right)\equiv 1.$$

To emphasize true normal observations and suppress suspect connections (possible anomalies), we compute score-aware attention on each edge. With $H$ heads, the per-head logits are

$$e_{ij}^{\left(h\right)}={\displaystyle \frac{q_h{\left({\mathcal{z}}_i\right)}^{\mathrm{\top }}{v}_h\left({\mathcal{z}}_j\right)}{\sqrt{s_{att}}}}-\gamma \left(\max \left(0,f_i\right)+\max \left(0,f_j\right)\right),h=1,\dots ,H,$$

where ${\mathit{q}}_h\left(\cdot \right),{\mathit{v}}_h\left(\cdot \right):{\mathbb{R}}^s\to {\mathbb{R}}^{s_{\mathrm{a}\mathrm{t}\mathrm{t}}}$are linear projections (shared across pairs for head $h$), $s_{\mathrm{a}\mathrm{t}\mathrm{t}}$ is the attention width, $\gamma \ge 0$ is a contamination reducing coefficient, and $f_i={‖{\mathcal{z}}_i-\mathit{c}‖}_2^2-m$ is the current one-class score (Eq. (1)). We normalize within ${\mathcal{N}}_k\left(i\right)$ using a temperature ${\tau }_a$-scaled softmax:

$${\alpha }_{ij}^{\left(h\right)}={\displaystyle \frac{\exp \left(e_{ij}^{\left(h\right)}/{\tau }_a\right)}{{\sum }_{u\in {\mathcal{N}}_k\left(\mathcal{i}\right)}\exp \left(e_{iu}^{\left(h\right)}/{\tau }_a\right)}},j\in {\mathcal{N}}_k\left(i\right), {\tau }_a>0$$

and aggregate heads by averaging

$${\tilde{a}}_{ij}={\displaystyle \frac{1}{H}}{\sum }_{h=1}^H{\mathsf{\alpha }}_{ij}^{\left(h\right)}.$$

We integrate attention with the base affinity using $\mu \in \left[\mathrm{0,1}\right]$ and then row-normalize the outgoing weights:

$${\tilde{w}}_{ij}=(1-\mu ){\kappa }_{\mathrm{base}}\left({\mathcal{z}}_i,{\mathcal{z}}_j\right)+\mu {\tilde{a}}_{ij}(j\in {\mathcal{N}}_k\left(i\right)),{\widehat{\mathrm{w}}}_{\mathrm{i}\mathrm{j}}={\displaystyle \frac{{\tilde{\mathrm{w}}}_{\mathrm{i}\mathrm{j}}}{{\sum }_{u\in {\mathcal{N}}_k\left(\mathrm{i}\right)}{\tilde{w}}_{iu}}}.$$

Edges outside ${\mathcal{N}}_k\left(i\right)$ have weight $0$ (${\tilde{w}}_{ij}=0$ if $j\notin {\mathcal{N}}_k\left(i\right)$). Row-normalization preserves scale across heterogeneous densities (outgoing weights sum to 1) and reduces error propagation by down-weighting high-score (potentially anomalous) edges during training. We compute attention weights without back-propagation and keep them fixed between graph refreshes. Prior work motivating the attention graphs to interpret unlabeled data geometry includes [9,10,32].

To keep training tractable, we do not materialize a full graph at every step. Instead, we rebuild a latent-space $k$-NN index periodically and, for each mini-batch, form edges as the union of (i) cached neighbors of the batch points and (ii) within-batch $k$-NN edges—preserving local geometry for the smoother while keeping computation practical.

3.2. Unlabeled Geometry via Neighbor-Smoothness on Squared Distances

Let

$$d_i^2={‖{\mathcal{z}}_i-\mathit{c}‖}_2^2,\hspace{1em}\hspace{1em}\mathit{d}={\left[d_1^2,\dots ,d_n^2\right]}^{\top }.$$

Unlabeled samples help create a smooth decision boundary by discouraging sharp variations of $d_i^2$ along high weight edges of the attention-weighted graph (described in §3.1):

$${\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\sum _{j\in {\mathcal{N}}_k\left(i\right)}{\widehat{w}}_{ij}{\left(d_i^2-d_j^2\right)}^2.$$

(3)

Penalizing differences of $d_i^2$ (rather than feature vectors) aligns the boundary with high-density regions without collapsing representations and preserves the simple one-class test rule on $f$.

The derivatives of ${\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}$ are

$${\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}}{\partial d_i^2}}={\displaystyle \frac{2}{n}}\left(\sum _{j\in {\mathcal{N}}_k\left(i\right)}{\widehat{w}}_{ij}\left(d_i^2-d_j^2\right)+\sum _{u:i\in {\mathcal{N}}_k\left(u\right)}{\widehat{w}}_{ui}\left(d_i^2-d_u^2\right)\right),$$

and by the chain rule

$${\displaystyle \frac{\partial d_i^2}{\partial {\mathcal{z}}_i}}=2\left({\mathcal{z}}_i-\mathit{c}\right),{\displaystyle \frac{\partial d_i^2}{\partial \mathit{c}}}=-2\left({\mathcal{z}}_i-\mathit{c}\right),{\displaystyle \frac{\partial {\mathcal{z}}_i}{\partial \theta }}={\nabla }_{\theta }{\varphi }_{\theta }\left(x_i\right),$$

so

$$\begin{gathered} {\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}}{\partial {\mathcal{z}}_i}}={\displaystyle \frac{4}{n}}\left({\mathcal{z}}_i-\mathit{c}\right)\left(\sum _{j\in {\mathcal{N}}_k\left(i\right)}{\widehat{w}}_{ij}\left(d_i^2-d_j^2\right)+\sum _{u:i\in {\mathcal{N}}_k\left(u\right)}{\widehat{w}}_{ui}\left(d_i^2-d_u^2\right)\right), \\ {\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}}{\partial \mathit{c}}}=-{\displaystyle \frac{4}{n}}\sum _{i=1}^n\left({\mathcal{z}}_i-\mathit{c}\right)\left(\sum _{j\in {\mathcal{N}}_k\left(i\right)}{\widehat{w}}_{ij}\left(d_i^2-d_j^2\right)+\sum _{u:i\in {\mathcal{N}}_k\left(u\right)}{\widehat{w}}_{ui}\left(d_i^2-d_u^2\right)\right), \end{gathered}$$

and

$${\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}}{\partial \theta }}=\sum _{i=1}^n{\left({\nabla }_{\theta }{\varphi }_{\theta }\left(x_i\right)\right)}^{\mathrm{T}}{\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}}{\partial {\mathcal{z}}_i}}.$$

During training, we rebuild the graph periodically and hold ${\widehat{w}}_{ij}$ fixed within each interval, so we do not back-propagate through the weights in this term.

3.3. Labeled-Normal Enclosure

Labeled normal observations ${\mathcal{X}}_{\mathcal{l}}^{+}$ anchor the hypersphere in latent space through a distance-based objective:

$${\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}={\displaystyle \frac{1}{\left|{\mathcal{X}}_{\mathcal{l}}^{+}\right|}}\sum _{x_i\in {\mathcal{X}}_{\mathcal{l}}^{+}}{‖{\mathcal{z}}_i-\mathit{c}‖}_2^2+\beta {‖\mathit{c}‖}_2^2,$$

(4)

where ${\mathcal{z}}_i={\varphi }_{\theta }\left(x_i\right)$, $\mathit{c}\in {\mathbb{R}}^s$ is a latent center summarizing the normal set. and $\beta \ge 0$ weakly centers the hypersphere. This formulation directly penalizes the squared distance of labeled normal observations from $\mathit{c}$ yielding stable gradients and a simple coupling to the encoder.

The gradients of ${\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}$ are

$$\begin{gathered} {\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}}{\partial {\mathcal{z}}_i}}={\displaystyle \frac{2}{\left|{\mathcal{X}}_{\mathcal{l}}^{+}\right|}}\left({\mathcal{z}}_i-\mathit{c}\right)\mathrm{f}\mathrm{o}\mathrm{r}{x}_i\in {\mathcal{X}}_{\mathcal{l}}^{+},{\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}}{\partial {\mathcal{z}}_i}}=0otherwise, \\ {\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}}{\partial \mathit{c}}}=-{\displaystyle \frac{2}{\left|{\mathcal{X}}_{\mathcal{l}}^{+}\right|}}\sum _{x_i\in {\mathcal{X}}_{\mathcal{l}}^{+}}\left({\mathcal{z}}_i-\mathit{c}\right)+2\beta \mathit{c}. \end{gathered}$$

Since ${\mathcal{z}}_i={\varphi }_{\theta }\left(x_i\right)$, by the chain rule

$${\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}}{\partial \theta }}={\displaystyle \frac{2}{\left|{\mathcal{X}}_{\mathcal{l}}^{+}\right|}}\sum _{x_i\in {\mathcal{X}}_{\mathcal{l}}^{+}}{\left({\nabla }_{\theta }{\varphi }_{\theta }\left(x_i\right)\right)}^{\mathrm{T}}\left({\mathcal{z}}_i-\mathit{c}\right).$$

3.4. Unlabeled Center-Pull

To stabilize training when the labeled normal set ${\mathcal{X}}_{\mathcal{l}}^{+}$ is small, we add a label-free pull of the unlabeled latents toward the center $\mathit{c}$. This acts on raw squared distances $d_i^2={‖{\mathcal{z}}_i-\mathit{c}‖}_2^2$ and complements the neighbor smoothness. The graph term equalizes differences of $d_i^2$ along edges and is largely insensitive to the global level of $d_i^2$; with few labelled observations this can cause scale drift and a poorly calibrated score $f=d^2-m$. Moreover, early graphs may include contaminated edges (unlabeled anomalies can appear inside or near the hypersphere), so smoothing alone can propagate their influence. The center-pull softly anchors the mean of $d^2$ for the normal unlabeled pool, reducing drift and reducing contamination while the graph term aligns local variations.

We define

$${\mathcal{L}}_{cp}={\displaystyle \frac{1}{\left|{\mathcal{X}}_u\right|}}\sum _{x_i\in {\mathcal{X}}_u}{‖{\mathcal{z}}_i-\mathit{c}‖}_2^2.$$

(5)

This imposes a global constraint by shrinking the mean of $d_i^2$ over $x_i\in {\mathcal{X}}_u$ toward $\mathit{c}$. Unlike ${\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}$—which is local and relative—${\mathcal{L}}_{cp}$ fixes the overall scale and prevents drift when labels are scarce, improving calibration of $f=d^2-m$.

The gradients are

$$\begin{gathered} {\displaystyle \frac{\partial {\mathcal{L}}_{cp}}{\partial {\mathcal{z}}_i}}={\displaystyle \frac{2}{\left|{\mathcal{X}}_u\right|}}\left({\mathcal{z}}_i-\mathit{c}\right)\mathrm{f}\mathrm{o}\mathrm{r}{x}_i\in {\mathcal{X}}_u,{\displaystyle \frac{\partial {\mathcal{L}}_{cp}}{\partial {\mathcal{z}}_i}}=0otherwise, \\ {\displaystyle \frac{\partial {\mathcal{L}}_{cp}}{\partial \mathit{c}}}=-{\displaystyle \frac{2}{\left|{\mathcal{X}}_u\right|}}\sum _{x_i\in {\mathcal{X}}_u}\left({\mathcal{z}}_i-\mathit{c}\right). \end{gathered}$$

Since ${\mathcal{z}}_i={\varphi }_{\theta }\left(x_i\right)$, by the chain rule

$${\displaystyle \frac{\partial {\mathcal{L}}_{cp}}{\partial \theta }}={\displaystyle \frac{2}{\left|{\mathcal{X}}_u\right|}}\sum _{x_i\in {\mathcal{X}}_u}{\left({\nabla }_{\theta }{\varphi }_{\theta }\left(x_i\right)\right)}^{\mathrm{T}}\left({\mathcal{z}}_i-\mathit{c}\right).$$

3.5. GAR-DSVDD Objective Function

The total loss combines unlabeled geometry, labeled-normal enclosure, and unlabeled center pull:

$$\begin{gathered} \underset{\theta ,\mathit{c}}{\min }\mathcal{L}\left(\theta ,\mathit{c}\right)={\lambda }_u\underset{\mathrm{unlabeled}\mathrm{geometry}}{\underbrace{{\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}}}+\underset{\mathrm{labeled}\mathrm{normals}}{\underbrace{{\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}}}+{\mathrm{\lambda }}_{\mathrm{c}\mathrm{p}}\underset{\mathrm{unlabeled}\mathrm{center}-\mathrm{pull}}{\underbrace{{\mathcal{L}}_{\mathrm{c}\mathrm{p}}}}, \\ {\mathrm{\lambda }}_u,{\mathrm{\lambda }}_{\mathrm{c}\mathrm{p}}\ge 0 \end{gathered}$$

(6)

with ${\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}$, ${\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}$, and ${\mathcal{L}}_{\mathrm{c}\mathrm{p}}$ as in Eqs. (3), (4), and (5), respectively, the scalars ${\lambda }_u,{\mathrm{\lambda }}_{\mathrm{c}\mathrm{p}}$ control the strengths of the graph regularizer and unlabeled center pull.

Together, ${\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}$, ${\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}$, and ${\mathcal{L}}_{\mathrm{c}\mathrm{p}}$ play complementary roles: ${\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}$ anchors the center $\mathit{c}$ using trusted labeled normals, preventing center drift; ${\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}$ enforces local consistency of squared distances on the attention-weighted, row-normalized $k$-NN graph, transferring structure from the unlabeled pool without collapsing features; and ${\mathcal{L}}_{\mathrm{c}\mathrm{p}}$ imposes a global moment constraint on unlabeled data, fixing the overall scale of $d^2$ and improving calibration of the score $f=d^2-m$.

We train $\left(\theta ,\mathit{c}\right)$ jointly using the AdamW optimizer. The attention-weighted $k$-NN graph is recomputed every $T$ epochs and held fixed within those intervals. No gradients flow through the attention computation or through $m$. At deployment, a testing observation $x_{test}$ can be labeled as an anomaly if its $f_{test}$ score exceeds a train-quantile threshold ${\mathrm{\tau }}_{thr}$ otherwise it will be considered as normal.

In summary, GAR-DSVDD combines a deep one-class boundary with graph-based semi-supervision in a way that is both robust and label-efficient. By regularizing squared distance (scores)—not features—over an attention-weighted latent $k$-NN graph, it aligns the decision boundary with the data manifold without collapsing representations and preserves the simple test-time rule $f\left(x\right)>{\mathrm{\tau }}_{\mathrm{thr}}$. Score-aware attention selectively down-weights suspicious neighbors, curbing over-smoothing from contaminated edges and density breaks. In addition to this, local, edge-wise smoothing of $d^2$, an unlabeled center-pull imposes a global moment constraint that stabilizes the overall scale of the distance field, improving score calibration when labeled normal observations are scarce. Because unlabeled data enter only through these geometric regularizers (no pseudo-labels), a small labeled set is enough to anchor the hypersphere while the unlabeled pool shapes the boundary. Thus, the proposed method effectively utilizes information from labeled and unlabeled observations for enhanced anomaly detection in semi-supervised settings.

Algorithm: GAR-DSVDD (training)

Inputs: ${\mathcal{X}}_{\mathcal{l}}^{+}$, ${\mathcal{X}}_{\mathcal{u}}$; ${\varphi }_{\theta }$; graph params $\left(k,\sigma ,\mu ,H,{\tau }_a\right)$; weights $\left({\lambda }_u,{\lambda }_{cp},\beta \right)$; refresh period T ; total epochs $T_{\mathrm{epochs}}$.

Outputs: $\theta ,\mathit{c},$ decision threshold ${\tau }_{thr}$. Initiation: Compute ${\mathcal{z}}_i={\varphi }_{\theta }\left(x_i\right)$ for $x_i\in {\mathcal{X}}_{\mathcal{l}}^{+}$; set $\mathit{c}\leftarrow {\displaystyle \frac{1}{\left|{\mathcal{X}}_{\mathcal{l}}^{+}\right|}}{{\sum }_{x_i\in {\mathcal{X}}_{\mathcal{l}}^{+}}\mathcal{z}}_i$. Build graph (t = 0): Compute latents for all data; form k-NN; compute multi-head attentions ${\alpha }_{ij}^{\left(h\right)}$ with temperature ${\tau }_a$; average to ${\tilde{a}}_{ij}$; integrate via μ; row-normalize to obtain ${\widehat{w}}_{ij}$. For t = 1, …, Tepochs: a) Forward on mini-batch $\mathcal{B}$: ${\mathcal{z}}_i={\varphi }_{\theta }\left(x_i\right),d_i^2={‖{\mathcal{z}}_i-\mathit{c}‖}_2^2$, and for attention/monitoring $f_i={‖{\mathcal{z}}_i-\mathit{c}‖}_2^2-m$. b) Loss: $\mathcal{L}={\lambda }_u{\mathcal{L}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}+{\mathcal{L}}_{\mathrm{e}\mathrm{n}\mathrm{c}}+{\lambda }_{\mathrm{c}\mathrm{p}}{\mathcal{L}}_{\mathrm{c}\mathrm{p}}$. c) Backpropagation + AdamW updates for $(\theta ,\mathit{c})$. d) Graph refresh: if $t\mathrm{m}\mathrm{o}\mathrm{d}T=0$: recompute latents; rebuild k-NN, attentions and row normalize ${\widehat{w}}_{ij}$ Threshold selection: ${\tau }_{thr}\leftarrow \mathrm{Quantile}of\left(f_i:x_i\in {\mathcal{X}}_{\mathcal{l}}^{+}\right)$ or via validation.

Inference (testing) Given xnew: Compute latent ${\mathcal{z}}_{new}={\varphi }_{\theta }\left(x_{new}\right)$. Score $f\left(x_{new}\right)={‖{\mathcal{z}}_{new}-\mathit{c}‖}_2^2-m$. Predict anomaly if $f\left(x_{new}\right)>{\tau }_{thr}$ otherwise normal.

(Note: ${\tau }_a$ is the attention softmax temperature; ${\tau }_{thr}$ is the decision threshold).

4. Experiments

In order to evaluate the performance of the proposed method, we apply it to a semi-supervised setting over a simulated dataset to visualize behavior and an industrial case study in the domain of industrial automotive quality management, where windshield wiper reversal noise is detected.

4.1. Experimental Setup

Experiments are conducted on a simulated two-dimensional dataset and a real industrial windshield-wiper acoustics dataset to compare the proposed GAR-DSVDD against established methods, including DeepSVDD, OCSVM, classical SVDD, and S3SVDD. All deep models share the same encoder capacity and optimization schedule for fairness. Threshold calibration follows each method’s policy: for GAR-DSVDD and DeepSVDD, we use a train-quantile rule at a fixed level over labeled-normal scores, whereas OCSVM, SVDD, and S3SVDD use their native decision functions. Across both experiments, training follows a semi-supervised setting: a small subset of labeled normal samples and a large unlabeled pool that may include a small contamination of anomalies (bounded by $\epsilon$). We construct four disjoint partitions: labeled normal observations, unlabeled, validation, and a held-out test set.

Performance is evaluated on the held-out test split using four measures derived from the confusion counts—true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN).

Overall accuracy (fraction of correctly classified instances):

$$\mathrm{Accuracy}={\displaystyle \frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}}.$$

Detection rate (also called recall or true positive rate), measuring how many anomalies are correctly detected:

$$\mathrm{Detection}\mathrm{Rate}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}}.$$

The F1 score summarizes the trade-off between precision and detection rate under class imbalance. Define precision as

$$\mathrm{Precision}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}},$$

then

$$\mathrm{F}1={\displaystyle \frac{2\mathrm{Precision}\times \mathrm{Detection}\mathrm{Rate}}{\mathrm{Precision}+\mathrm{Detection}\mathrm{Rate}}}={\displaystyle \frac{2\mathrm{TP}}{2\mathrm{TP}+\mathrm{FP}+\mathrm{FN}}}.$$

Balanced accuracy, averaging sensitivity (detection rate) and specificity (true negative rate). First define specificity

$$\mathrm{Specificity}={\displaystyle \frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}}},$$

then

$$\mathrm{Balanced}\mathrm{Accuracy}={\displaystyle \frac{1}{2}}\left(\mathrm{Detection}\mathrm{Rate}+\mathrm{Specificity}\right).$$

For each dataset/seed, we test the directional alternative $H_1$​: GAR-DSVDD > benchmark on the F1 score using paired $t$-tests and Wilcoxon signed-rank tests across seeds and report their p-values.

4.2. Simulated Data

In the simulated study, we utilize a two-cluster, two-dimensional dataset that has separable centers and evaluate it under a semi-supervised setting. We draw $n_{\mathrm{norm}}=1000$ normal observations and $n_{\mathrm{anom}}=500$ anomalies, label a small fraction of normal observations $\left(\rho =0.03\right)$, set unlabeled contamination to $\epsilon =0.20$, and reserve $20\%$ for validation and$20\%$for testing. 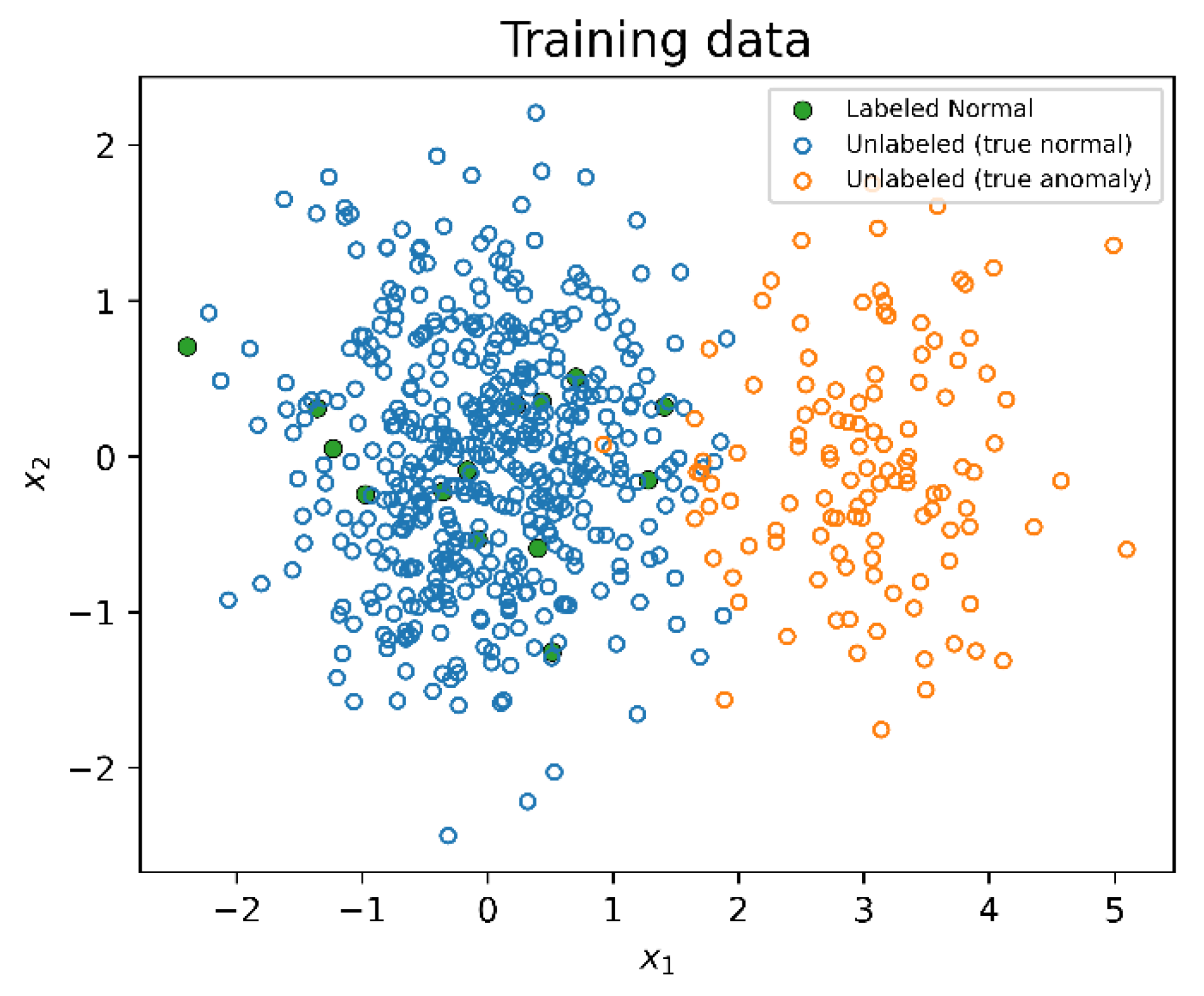Figure 1 shows the training dataset used for the experiment, where labeled and unlabeled observations are used to train GAR-DSVDD and S3SVDD, while the other methods use labeled observations only. We carried out a total of 10 experiments, using different seeds when generating the data. The training set for one of the experiments is illustrated in Figure 1.

All deep methods share the same encoder ${\mathrm{\varphi }}_{\mathrm{\theta }}$ for fairness: a two-layer MLP with hidden widths $64-64$ mapping $x\mapsto \mathcal{z}={\mathrm{\varphi }}_{\mathrm{\theta }}\left(x\right)\in {\mathbb{R}}^{16}$ with ReLU activations. Our method constructs a latent $k$-NN graph $G$ on $\left\{{\mathcal{z}}_i\right\}$ with $k=9$ and attention weights ($8$ heads, key dimension $s_{att}=32$). The attention-weighted graph is recomputed every $T=5$ epochs and held fixed between refreshes; no gradients flow through the attention computation. We optimize the objective in Eq. (6) using AdamW for $120$ epochs with refresh rate $T=5$ and learning rate $5\times {10}^{-4}$, graph regularizer strength ${\lambda }_u=1300$, and unlabeled center pull strength ${\lambda }_{\mathrm{c}\mathrm{p}}=0.9$. Lastly, we calibrate $m$ by setting it to the same train-quantile used for threshold selection over labeled normals.

As for the remaining methods, DeepSVDD is trained on labeled normal using the same applicable parameters of the proposed method, OSCVM uses $\mathrm{\nu }=0.1$, SVDD uses radial basis function (RBF) kernel parameter $\gamma =1$, and S3SVDD uses RBF kernel parameter $\gamma =1$ with $k$ = 9. The deep methods use a train-quantile rule at $q=0.95$, and the native decision function is used for the rest.

The performance results of the proposed methods compared to benchmarking methods over all testing performance metrics for an experiment are shown in Table 1, whereas Table 2 compares their F1 score over 10 different testing sets where the data was generated using different seeds.

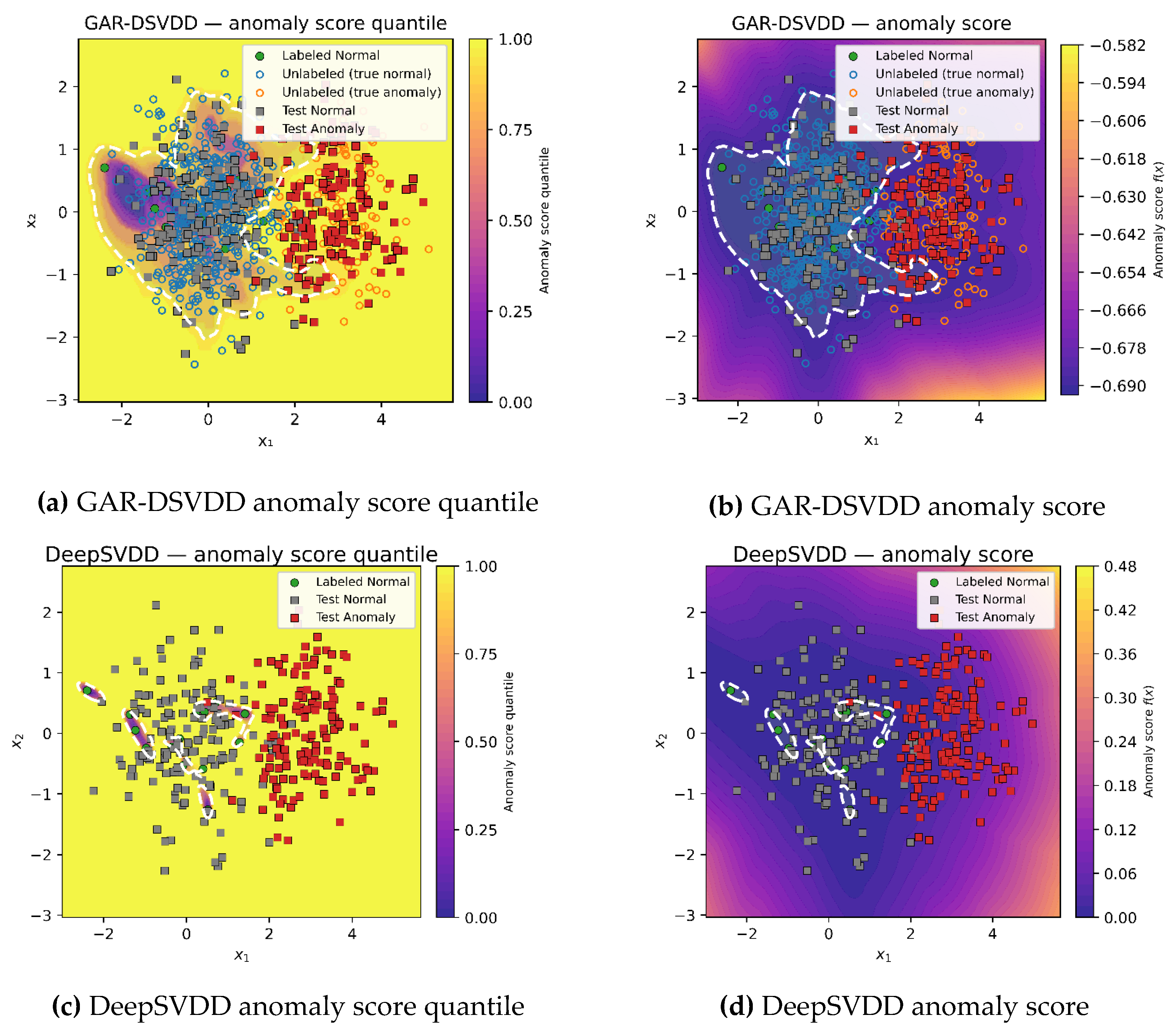
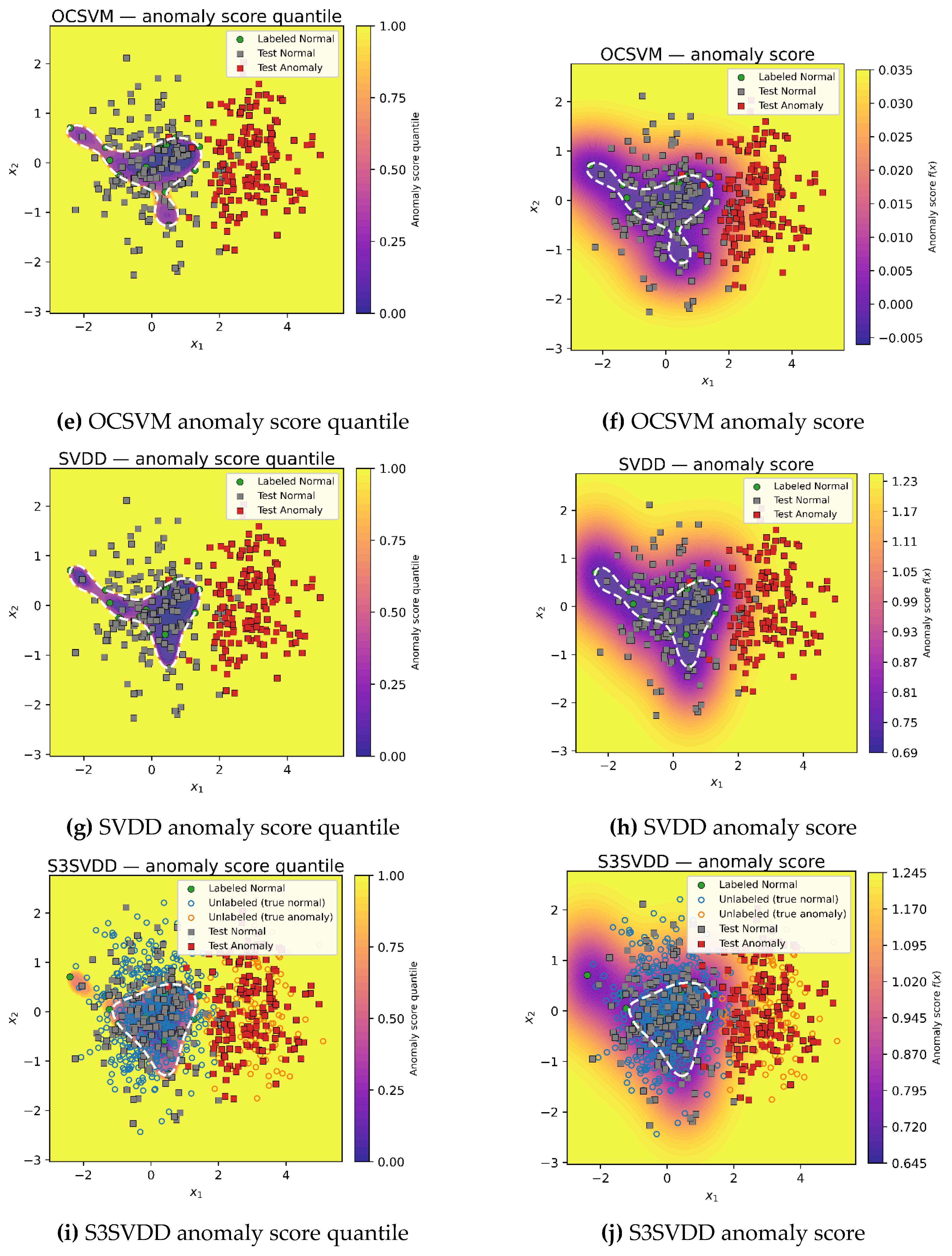
DeepSVDD trains only on labeled normal observations and learns a tight hypersphere where many normal observations on low-density areas fall outside it, thus, increasing false positive rate and reducing overall accuracy, and F1 despite having high detection rate. OCSVM lacks representation learning and geometry-aware regularization, thus constructing a narrow decision boundary where detection rate remains high, but specificity and overall accuracy suffer, leading to a lower F1 score. Since classical SVDD does not utilize unlabeled-geometry guidance, it builds a decision boundary based on labeled observation alone, thus, obtaining a tight hypersphere yielding to a high false positive rate and reduced accuracy and F1 score. Incorporating a fixed-weight graph S3SVDD shows similar performance to SVDD as fixed-weight graph cannot truly suppress influence of suspect (anomalous) neighbors, thus, assumes that most unlabeled observations are anomalous and constructs a narrow hypersphere.

In contrast, the attention-weighted GAR-DSVDD achieves the best F1 and balanced accuracy, among all other methods, by pairing high detection and lower false positives. Attention down weights influence from suspect neighbors in the unlabeled graph, limiting score dispersal from contaminated (anomalous) points and keeping the boundary near density valleys. The center pull regularizer on unlabeled observations prevents over smoothing decision boundary, preserving overall accuracy, while labeled normal observations ensure that the hypersphere is anchored to the normal region. Overall, GAR-DSVDD yields a more robust hypersphere across all experiments.

The obtained anomaly score and its quantiles are shown in Figure 2. In the figure, the ${95}^{th}$ quantile contour for the anomaly score is drawn to indicate the decision boundary for the deep methods, where the native decision boundary is shown for the shallow methods. Note that DeepSVDD and GAR-DSVDD use a single hypersphere in latent space as its decision region based on the learned quantile. In the figure, after the encoder’s nonlinear mapping back to input space, this can look complex or even disconnected, despite being one sphere in the learned latent space.

4.3. Case Study: Windshield-Wiper Acoustics

This section presents our case study on windshield wiper acoustics. We analyzed windshield-wiper sound recordings gathered under tightly controlled laboratory conditions. Each sample was captured from production wiper assemblies inside an anechoic chamber while a sprinkler system supplied water to replicate rainfall. To eliminate confounding noise sources, the vehicle’s engine remained off, and the wiper motor was powered by an external supply. A fixed in-cabin microphone recorded the acoustic pressure signal, which was calibrated and expressed in decibels at a constant sampling rate. Domain specialists reviewed the recordings and assigned ground-truth labels covering reversal noise fault phenomena alongside normal operation. The dataset consists of a total of 120 windshield wiper recordings, where 61 recordings are for normal operations and 59 for faulty (anomalous) operations. These expert annotations are treated as ground truth for evaluation.

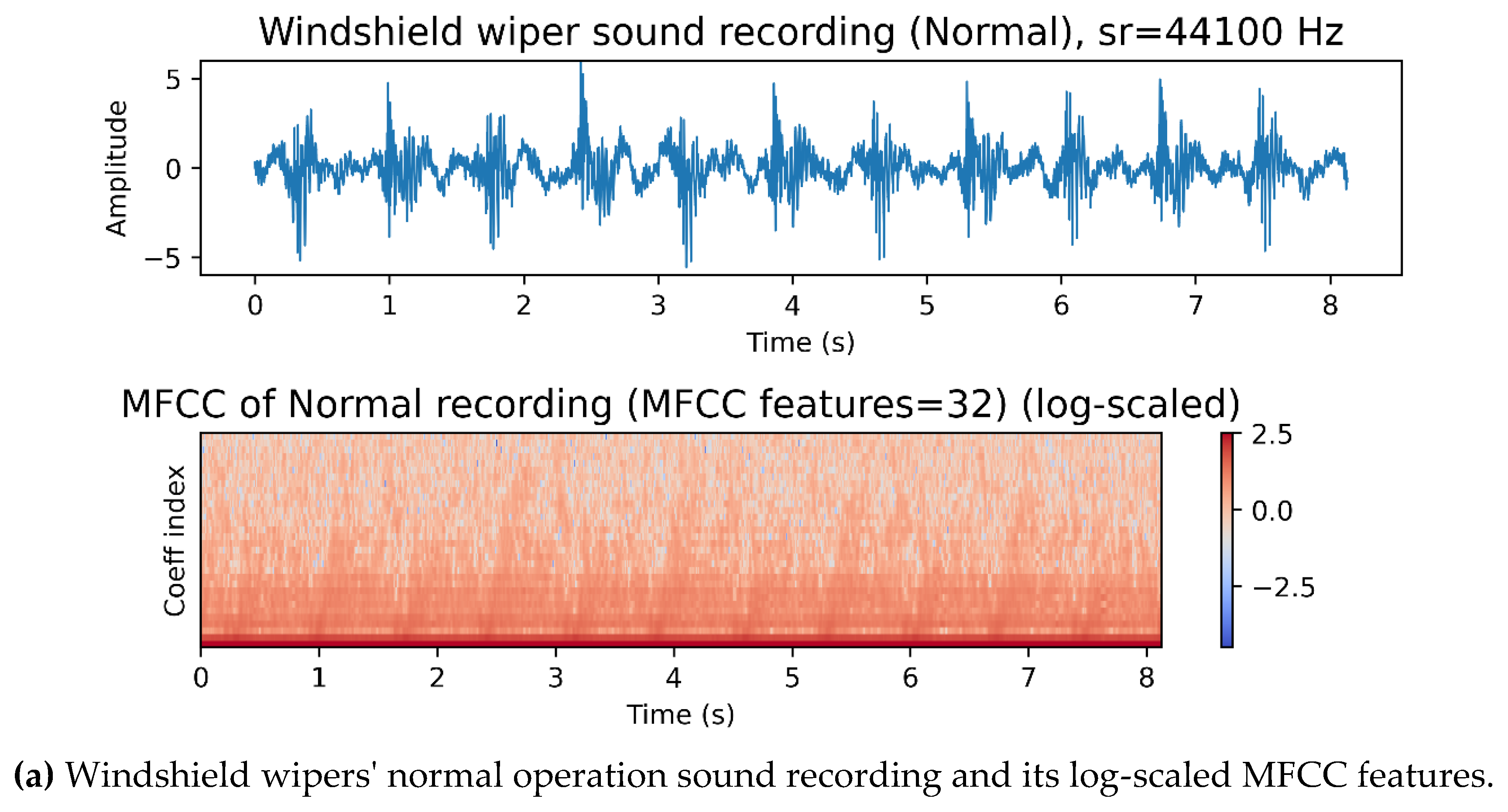
Each observation is a single full recording summarized as a fixed-length vector from recording descriptors, in line with recent acoustic research for sound analysis. We compute 32 MFCCs to capture the spectral envelope on a perceptual scale, together with first- and second-order deltas to encode short-term dynamics; these cepstral families remain standard and effective in contemporary studies. We also include a 12-bin chroma profile to reflect tonal/resonant structure and simple spectral/temporal statistics—spectral centroid, spectral bandwidth, spectral roll-off at 95%, root-mean-square (RMS) energy, and zero-crossing rate (ZCR)—which are routinely used and compared in modern journal work. For every multi-frame descriptor with $r$ coefficients, we pool across time by concatenating the per-coefficient mean and standard deviation, so each such descriptor contributes $2r$ values; scalar descriptors contribute two values (mean and standard deviation). Summing up all parts yields a $226-$dimensional vector per recording of means and standard deviations across time that we use for the reversal-noise dataset. These choices (MFCCs with deltas, chroma, and spectral statistics with mean/std pooling) align with recent papers documenting their efficacy and definitions across environmental-sound, speech-emotion, smart-audio, and urban-acoustic applications [33,34,35]. 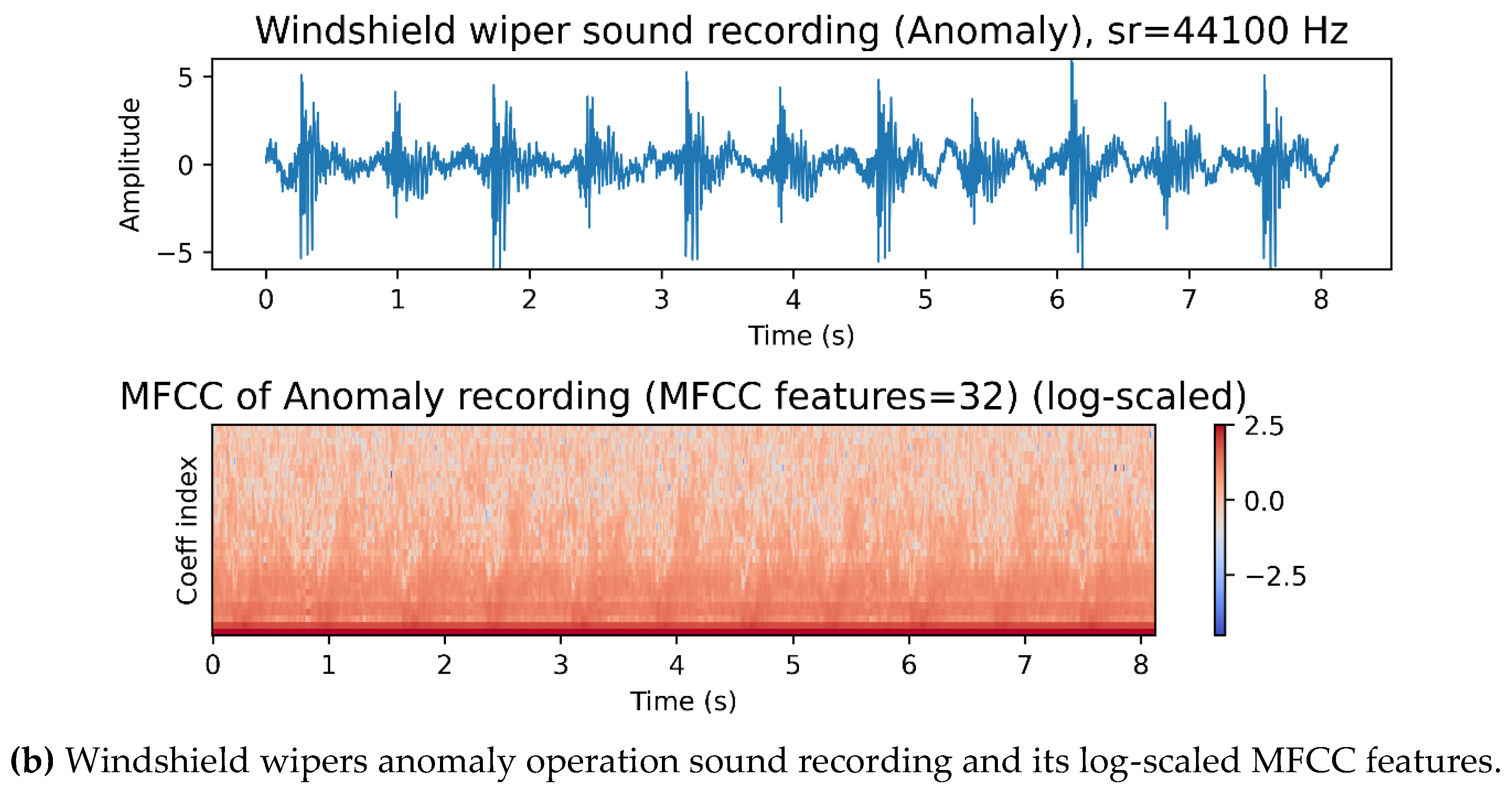Figure 3 shows normal and anomaly operation recordings of windshield wipers with their corresponding MFCC features on the log scale. Table 3 summarizes the feature extraction methods used for acoustic analysis of the windshield wiper sound recordings.

We follow the same semi-supervised protocol as in the simulated study: a small subset of labeled-normal clips is provided, and a large unlabeled pool may include mild anomaly contamination; the remainder is split into validation (for hyperparameter selection) and a held-out test set. Concretely, we use a 60/20/20 split for train/validation/test. Within the training portion, we label 10% of the normal observations ($\rho =0.10$) and place the rest into the unlabeled set with anomaly contamination ratio $\epsilon =0.10$. All deep methods use the shared encoder ${\varphi }_{\theta }$: a two-layer MLP $64-64\to 16$ with ReLU activations. For our method, GAR-DSVDD, we build a latent $k$-NN graph with $k=3$ and multi-head attention (8 heads, key dimension 32) over the encoder representations. The attention-weighted graph is recomputed every $T=5$ epochs and held fixed between refreshes; no gradients flow through the attention computation. The objective in Eq. (6) for 120 epochs using AdamW (learning rate $5\times {10}^{-4}$), graph regularizer strength ${\lambda }_u=8$, and unlabeled center pull strength ${\lambda }_{\mathrm{c}\mathrm{p}}=1000$. $m$ is calibrated by setting it to the same train-quantile used for threshold selection over labeled normals.

Benchmarks are configured to match their best settings from the wiper runs: DeepSVDD is trained on labeled normal observations with the same encoder/optimizer, soft-boundary objective regularizer value $=1000$; OCSVM uses $\mathrm{\nu }=0.1$ with an RBF kernel $\gamma =0.01$; SVDD uses an RBF kernel with $\gamma =1.0$; and S3SVDD employs a $k-$NN graph with $k=3$ and RBF $\gamma =0.01$. The deep methods apply a train-quantile rule with $q=0.95$, while OCSVM, SVDD, and S3SVDD use their native decision function.

The performance of GAR-DSVDD and the existing methods overall performance metrics are presented in Table 4. Table 5 shows the F1 score over 10 different testing sets that were prepared using 10 different seeds for statistical validation.

Due to the extreme challenges represented by this dataset and the semi-supervised experiment settings with very few training labeled normal observation, all benchmarking methods perform poorly for anomaly detecting as they fail to utilize unlabeled observations in constructing their decision boundaries as indicated by the F1 and accuracy metrics. The decision boundary obtained by these methods tend to be very narrow, causing most testing observations to be detected as anomalies while increasing the false positive rates, as seen by the specificity metric for these methods.

In contrast, GAR-DSVDD maintains perfect detection while achieving a higher specificity by leveraging an attention-weighted latent $k$-NN graph that weakens edges in mixed or uncertain neighborhoods, thus, effectively utilizing information from unlabeled observation. This reduces the graph-driven propagation of elevated scores into nearby normal observations, keeps the decision boundary aligned with low-density regions, and prevents the false positive rates that undermine the other methods. Furthermore, the learned neighbor attention weights serve as per-instance attributes, indicating which historical normal observations most influence a observation’s score. In an industrial setting, these attributions can streamline expert review and reduce the volume of fully verified normal labels required over time, aligning the method with label-efficiency needs in automotive quality control.

4.4. Sensitivity Analysis

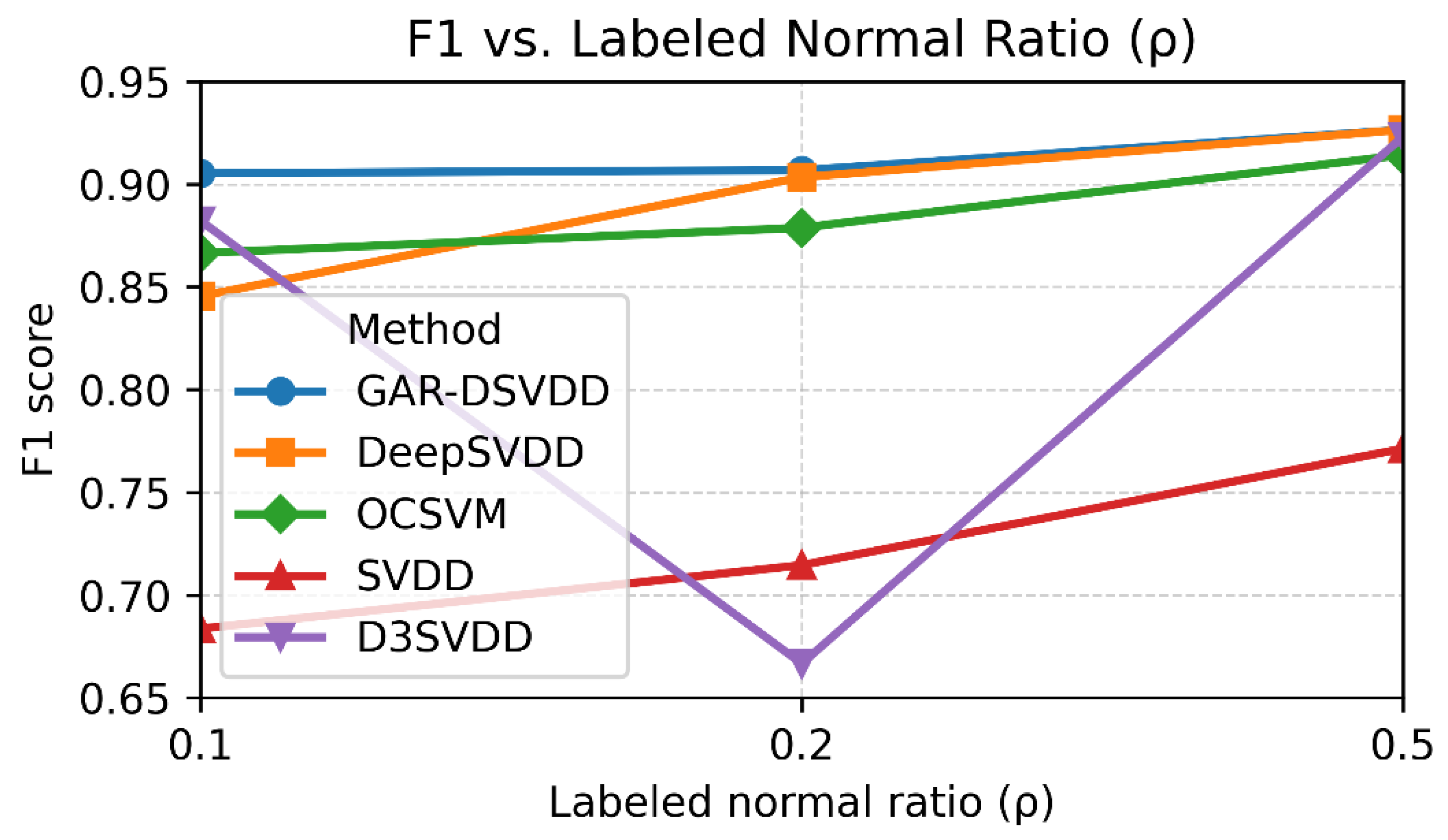
In this section, we perform sensitivity analysis over the simulated data. In Table 6 and Figure 4 we show the effect of increasing the normal labeled observations ratio $\rho$ over the F1 performance of the methods. Across labeled-normal ratios $\rho \in \{0.10,0.20,0.50\}$, the results show a clear label-efficiency advantage for our semi-supervised GAR-DSVDD in the low-label setting, with supervised baselines gradually converging as ρ increases. With scarce labels, GAR-DSVDD leads, consistent with its attention-weighted graph regularization that leverages unlabeled structure while mitigating contamination. As the label budget grows to a moderate level, GAR-DSVDD remains best, but the gap narrows, particularly with DeepSVDD, which benefits directly from richer labeled evidence. OCSVM improves steadily with more labels yet trails the deep methods, while classical SVDD consistently lags despite incremental gains. S3SVDD exhibits non-monotonic behavior, sensitive to label density and split composition, but becomes more competitive with increased labeling ratio. In summary, when only a small portion of data can be labeled, our target operating point, GAR-DSVDD outperforms all alternatives; as labeling increases, purely supervised approaches like DeepSVDD catch up and have similar performance, whereas OCSVM and SVDD continue to benefit but remain behind, and S3SVDD’s competitiveness depends on the labeling setting.

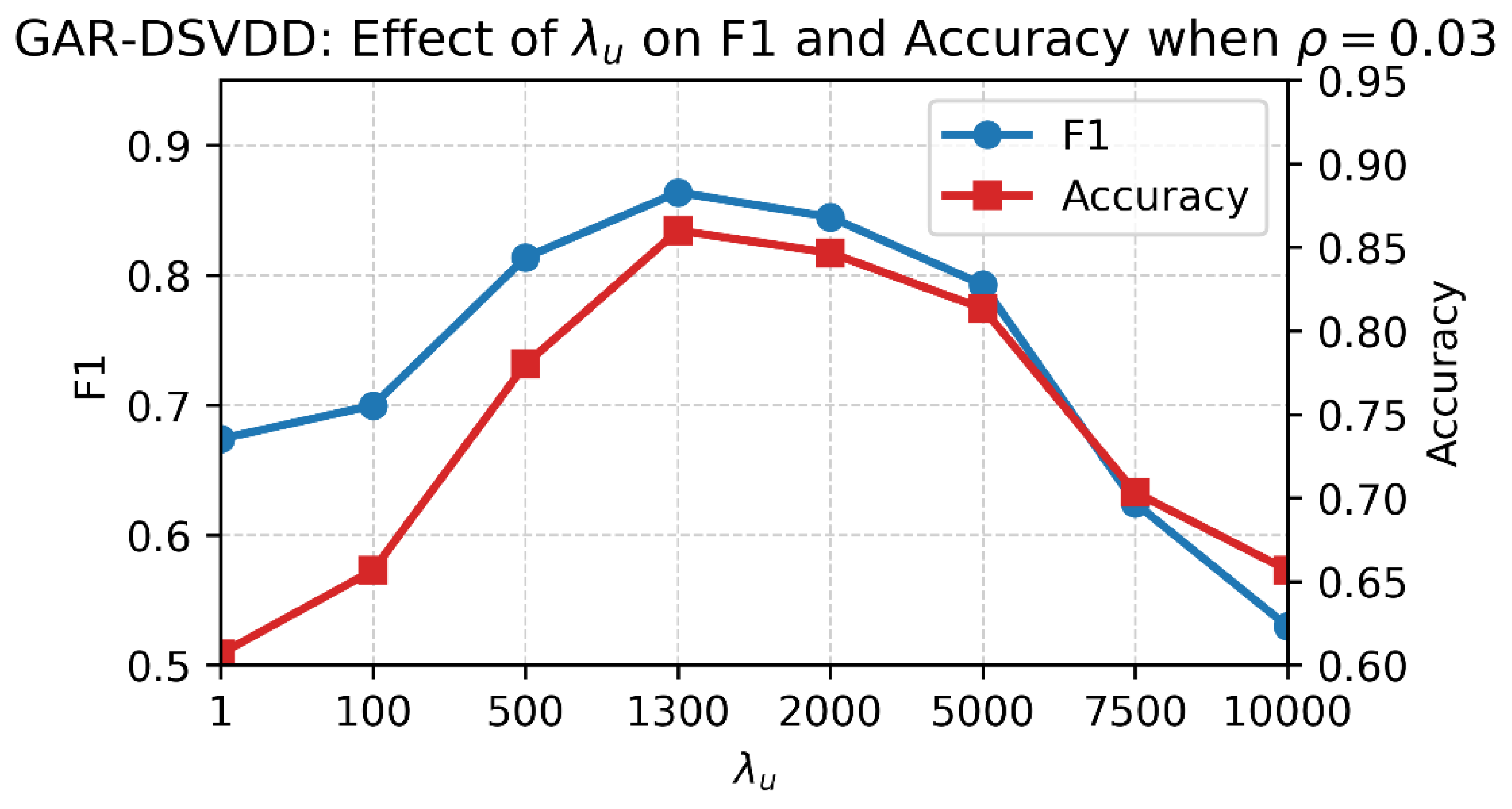
Moreover, by setting $\rho =0.03$, we analyze the effect of ${\lambda }_u$ on F1 and accuracy of GAR-DSVDD, as illustrated in Figure 5. For small ${\lambda }_u(\approx 1-500)$, less importance is given to unlabeled geometry, thus, the unlabeled information is underutilized, leading to narrow decision boundary and underperforming results. Increasing ${\lambda }_u$ gives more importance to the graph-loss term (unlabeled geometry), which expands the decision boundary with consistent gains in performance. The performance is highest near ${\lambda }_u\approx$1300, where the boundary best balances the influence of labeled data information, unlabeled geometry, and central-pull term on unlabeled observations. At higher ${\lambda }_u$ values, excessive emphasis on unlabeled geometry over-smooths the graph structure, widening the decision boundary and allowing anomalous unlabeled observations to be included within the decision boundary, thereby degrading performance. These findings indicate that ${\lambda }_u$ should be carefully selected via validation to allow an optimal construction of the decision boundary that keeps anomalous unlabeled observations outside and expands enough to keep normal behavior observations inside.

5. Conclusions

Identifying anomalies is a critical issue in applications such as manufacturing, industrial process control, cybersecurity, disaster management, and medical diagnosis, as they provide information about deviations from normal behaviour in critical environments [1,2,3,4,5]. Among available approaches, SVDD-based procedures remain attractive for their compact decision boundaries and test-time simplicity.

In this paper, we presented a GAR-DSVDD for semi-supervised anomaly detection. The method encloses labeled normal observations with a deep one-class boundary while propagating score-level smoothness over an attention-weighted latent $k$-NN graph to leverage abundant unlabeled data. The attention mechanism reduces over-smoothing from questionable neighbors and respects local density breaks, improving specificity without sacrificing detection. Experiments on simulated data and a windshield-wiper acoustics case study demonstrate that GAR-DSVDD outperforms classical and deep baselines under scarce labels significantly.

Considering future work, many industrial datasets contain multiple normal classes (e.g., distinct operating conditions or product variants). Our current formulation targets a single normal class; extending it to multi-normal settings is a natural next step. One direction is to learn several hyperspheres using a shared encoder, where each hypersphere retains its corresponding normal class while discouraging overlapping with others; the graph attention can be made class-aware to limit cross-class leakage. Finally, online updates with periodic graph refresh and automatic selection of graph/attention hyperparameters would enhance robustness in evolving production environments.