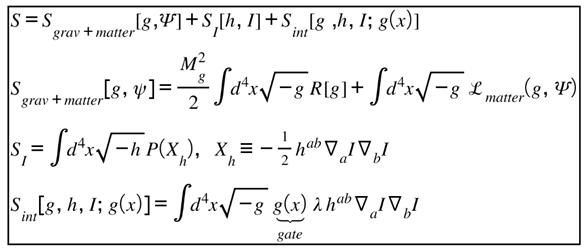The Lugon Framework; Informational Foundations of Physical Law; Part I—A Sequestered Informational Sector and Its Compatibility with Relativistic and Quantum Physics

Bryan Lugo

doi:10.20944/preprints202510.1654.v1

Submitted:

18 October 2025

Posted:

21 October 2025

You are already at the latest version

Abstract

Part I introduces the central premise of the Lugon Framework: that information can exist and evolve without energy exchange while remaining fully consistent with relativity and quantum mechanics. By formalizing a sequestered informational domain (ℚ) that coexists with the energetic spacetime domain (ℝ), the paper constructs a dual-geometry universe in which structured information propagates through its own metric cone—superluminal in appearance but non-energetic and causally self-contained. Variation of the informational action shows that ℚ-domain dynamics generate curvature without stress–energy, yielding an invariant conservation law for total informational capacity. This foundation allows later parts of the framework to reinterpret gravity, entropy, and cosmology as feedback processes maintaining balance between the two domains. The result is a logically consistent basis for unifying physical law under informational invariance rather than force.

Keywords:

informational physics

;

auxiliary metric

;

superluminal information

;

dual light-cone structure

;

no-signaling

;

Landauer bound

;

massive gravity

;

Vainshtein screening

;

Page curve

;

relativity

;

quantum mechanics

;

causality

;

conservation laws

;

Lugon framework

Subject:

Physical Sciences - Theoretical Physics

One-sentence significance

I demonstrate that information can propagate faster than light without transporting energy, maintaining the conservation and symmetry principles of SR/GR while producing concrete, falsifiable signatures in quantum and gravitational systems.

Submission metadata

The Lugon Framework: Informational Foundations of Physical Law

Part I — A Sequestered Informational Sector and Its Compatibility with Relativistic and Quantum Physics

Version: v1.0 • Date: October 5, 2025 • DOI: 10.5281/zenodo.17298365

Status: First paper in a continuing series; follow-up paper (The Lugon Kernel and the Unified Invariants of Physical Law) in preparation.

Suggested arXiv categories: gr-qc; hep-th; quant-ph

Comments: First paper in The Lugon Framework: Informational Foundations of Physical Law series. Follow-up paper (The Lugon Kernel and the Unified Invariants of Physical Law) in preparation. 66 pages, 1 figure. Categories: gr-qc, hep-th, quant-ph.

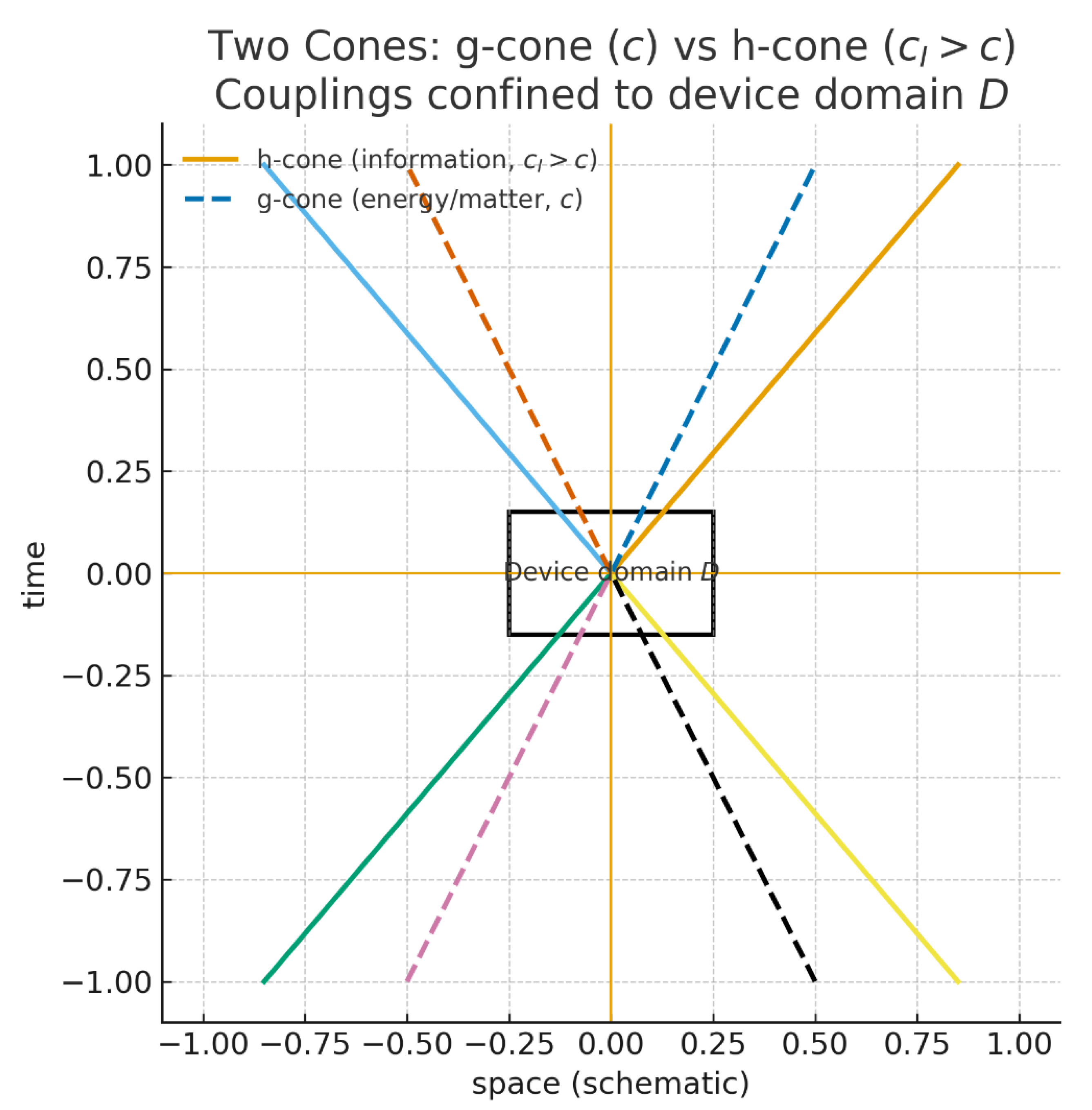
Figure 1. Two cones and device domain. The ordinary g-cone (dashed) bounds energy/matter at speed c. The information h-cone (solid) is wider, with invariant speed

υ_{h} > c

. All couplings to carriers are confined to the device domain D (box), so no superluminal signaling or energy flow exists outside D.

Figure 1. Two cones and device domain. The ordinary g-cone (dashed) bounds energy/matter at speed c. The information h-cone (solid) is wider, with invariant speed

υ_{h} > c

. All couplings to carriers are confined to the device domain D (box), so no superluminal signaling or energy flow exists outside D.

Research Pathway

The investigation began with a simple question: why does the universe enforce the speed of light,

c

, as a universal limit? Special relativity makes this bound geometric—the invariant interval

d s^{2} = g_{a b} d x^{a} d x^{b}

divides spacetime into timelike, lightlike, and spacelike regions, ensuring causal order. The relativistic energy relation

E^{2} = p^{2} c^{2} + m^{2} c^{4}

then gives the physical reason: energy diverges as velocity approaches

c

, so no finite work can drive a massive particle across the light barrier. Within this structure, the prohibition of superluminal motion appears complete.

Quantum mechanics, however, introduces entanglement—correlations that persist across spacelike separations. Measurements on entangled pairs produce outcomes that violate Bell inequalities yet never permit controllable faster-than-light signals. The no-signaling theorem guarantees mathematical consistency with relativity, but it leaves an unsatisfying gap in understanding: if nothing travels faster than

c

, how are these global correlations maintained?

That question sharpened through practical developments. Quantum teleportation, superdense coding, and entanglement-based cryptography treat entanglement as a resource that can be distributed, consumed, and measured. If such correlations have operational value, then information itself behaves like a physical quantity—not merely statistical bookkeeping.

This recognition led to a new hypothesis: perhaps information and energy are distinct physical currencies. Energy and momentum remain confined to the spacetime metric

g_{a b}

, preserving all the tested consequences of special and general relativity. Information, by contrast, may propagate on an auxiliary metric

h_{a b}^{}

with its own invariant speed

ν_{h} > c

. Because the information field carries identically vanishing stress–energy, it performs no work, curves no spacetime, and cannot be used for signaling; yet it provides the coherence needed to sustain entanglement across spacelike separations.

From this perspective, entanglement does not require superluminal energy transfer—it reflects coherence maintained within a sequestered informational sector. The resulting two-cone framework accommodates both relativity and quantum mechanics without contradiction: the

g

-cone bounds all energetic influence, while the wider

h

-cone governs non-energetic informational links. Interactions between the two sectors are confined to localized “gate” domains, ensuring radiative sequestering and thermodynamic consistency.

This sequence of questions—from the geometry of

c

through the paradox of entanglement to the recognition of information as a separate causal entity—motivates the effective-field-theory framework developed below. The following sections formalize this idea, derive its field equations, and outline empirical tests that can confirm or falsify the existence of a sequestered information sector.

For an extended narrative of the reasoning that led to this framework, see Appendix G.

Toward a Sequestered Information Sector

The paradox of entanglement, deepened by both thought experiments and real-world protocols, naturally raises the question of whether information is truly bound by the same constraints as energy and matter. If entanglement can be treated as a resource — quantified by entropy, exploited in communication, and even linked to spacetime geometry — then it is reasonable to ask whether information admits a mode of existence distinct from energetic transfer.

This line of inquiry begins with the recognition that relativity enforces strict causal order through the invariant speed c. All known particles carrying energy or momentum are confined within the light cone, as shown by the divergence of relativistic energy:

E^{2} = (p c)^{2} + (m c^{2})^{2}

At the same time, entanglement correlations persist across spacelike separations, defying local realist explanations and yet producing no detectable violations of relativity through signaling. This apparent contradiction prompted the question: if entanglement does not transmit energy, what is it that propagates?

The natural hypothesis is that information occupies a sequestered sector, distinct from the energetic carriers constrained by relativity. In this view, all work-performing fields remain coupled to the physical spacetime metric

g_{a b}

, while information propagates on an auxiliary, non-dynamical metric

h_{a b}^{}

. The latter admits an invariant speed

ν_{h} > c

:

Because the information field I is defined to have identically vanishing stress–energy,

T_{a b}^{} (I) = 0

it cannot perform work, transfer momentum, or curve spacetime. To see this explicitly, consider the action of the information field:

S_{I} = \int d^{4} x \sqrt{- h} \frac{1}{2} h^{μ ν} \partial_{μ} I \partial_{ν} I

where

h_{μ ν}^{}

is the auxiliary metric, fixed and non-dynamical. The Hilbert stress–energy tensor is defined as:

T_{μ ν}^{(I)} = - \frac{2}{\sqrt{- g}} \frac{δ S_{I}}{δ g^{μ ν}}

Because the action

S_{I}

depends only on

h_{μ ν}^{}

, not on the physical metric

g_{μ ν}

, the variation vanishes:

\frac{δ S_{I}}{δ g^{μ ν}} = 0 \Rightarrow T_{μ ν}^{(I)} = 0

Thus, the I-field cannot carry energy–momentum, cannot do work, and cannot source curvature.

The propagation of information across the auxiliary metric thus leaves relativity intact for all energetic processes, even while coherence is maintained across spacelike intervals.

The coupling between the information field and physical devices is localized by a gate function

g_{D}^{} (x)

(see Appendix F for Creation, Control and Models of Gate Functions), ensuring that information exchange is confined strictly to the device domain D:

g_{D}^{} (x)

By construction, this framework addresses the motivating questions: relativity remains unviolated because energy and matter are restricted to the physical metric, while entanglement’s global correlations are explained as manifestations of information propagating in a sequestered sector. The existence of two causal cones — one for

g_{a b}

, another for

h_{a b}^{}

— provides a coherent picture in which both relativity and quantum mechanics retain their tested domains of validity.

Core Actions and Field Equations (EFT)

I work on one manifold

M

with two Lorentzian metrics: the visible/energetic metric

g_{a b}

and an auxiliary informational metric

h_{a b}

(fixed/nondynamical in Part I). The information field is a shift-symmetric scalar

I (x)

with dynamics only on

(M, h)

. A gate

g (x) \in [0,1]

localizes any interaction to a device domain

D \subset M

.

Action

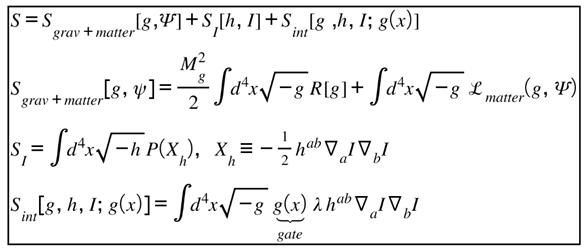
Field equation for I (varying I only):

\nabla_{a}^{(h)} (\sqrt{- h} P_{, X_{h}} h^{a b} \nabla_{b}^{(h)} I) - \nabla_{a}^{(g)} (\sqrt{- g} g (x) λ h^{a b} \nabla_{b}^{(h)} I) = 0

Inside D, the second (gate) term acts like a source/sink for informational flux without introducing work in the g-sector. Outside D it vanishes.

Hilbert stress–energy statements

The free information sector is invisible to g:

{T_{a b}^{(I)} |}_{f r e e} \equiv - \frac{2}{\sqrt{- g}} \frac{δ S_{I}}{δ g^{a b}} = 0

because

S_{I}

depends on (h, I) but not on g.

Any g-variation lives in the apparatus term

S_{i n t}

(the gate is an external control in g-geometry). Energetic bookkeeping stays in

S_{g r a ν + m a t t e r}^{+ S_{i n t}}

; no superluminal energy flux is carried by I.

Microcausality & cones (to cite later)

The principal symbol for I comes from

h^{a b}

, so the characteristics are the h-null cone. Thus,

[I (x), I (y)] = 0

whenever

(x - y)

is spacelike in h.

Boundary Hologram Protocol

The Boundary Hologram Protocol formalizes the interface between the observable relativistic sector (governed by

g_{a b}

) and the sequestered information sector (governed by

h_{a b}^{}

). The protocol prescribes that informational states are not emitted as energy quanta but as encoded boundary conditions—holographic imprints—on the two-surface dividing causal domains. Each boundary carries an information capacity proportional to its area, consistent with the Bekenstein–Hawking relation, yet distinct in that it applies to non-energetic Lugon exchanges.

Within this framework, transmission occurs through matched boundary conditions rather than physical traversal. Information is projected from one boundary onto another by an isomorphic transformation that preserves entanglement correlations but not spacetime locality. The apparent 'instantaneity' of this exchange results from the dual-metric structure: the Lugon channel exists outside the light-cone of

g_{a b}

but within the causal domain of

h_{a b}^{}

.

This protocol thus replaces the classical notion of signal propagation with boundary-state synchronization, where the rate of information change, not energy flux, defines the channel dynamics. It offers a consistent means of describing superluminal information transfer without violating relativistic invariants.

Microcausality and Global Time Functions

Any framework that admits information propagation outside the light cone must address the concern of causal consistency. If correlations extend beyond c, how can one exclude paradoxes such as closed causal loops? To answer this, I impose two structural safeguards: microcausality for both cones and the existence of a global time function [51].

Microcausality requires that field operators commute at spacelike separation with respect to their respective metrics. For the information field I, this condition reads:

[I (x), I (y)] = 0 f o r (x - y)_{h}^{2} \leq 0

where

(x - y)_{h}^{2}

denotes the interval evaluated on the auxiliary metric

h_{a b}^{}

. This result follows directly from the principal symbol of the I-field equation derived in § Core Action and Field Equations (EFT). Because that symbol is

P_{, X_{h}}^{} h^{a b} k_{a}^{k}

, the characteristic surfaces are null with respect to

h_{a b}

; consequently, commutators vanish whenever

(x - y)_{h}^{2} < 0

, confirming microcausality inside the informational cone. Analogously, standard microcausality holds for all energetic fields on the physical metric

g_{a b}

:

[ϕ (x), ϕ (y)] = 0 f o r (x - y)_{g}^{2} < 0

Thus, both cones preserve causal independence within their respective domains. No observer can exploit either sector to generate local violations of causality.

Beyond local consistency, global order is guaranteed by the existence of a time function τ that monotonically increases along both g- and h-causal processes:

τ : M \to R, \frac{d τ}{d λ} > 0 f o r a l l g - a n d h - c a u s a l c u r v e s

To make this construction explicit, note that a global time function exists on any globally hyperbolic spacetime

(M, g_{a b})

. Because the auxiliary metric

h_{a b}^{}

is fixed and everywhere causal with respect to

g_{a b}

inside device domains, one can define

T

by pulling back the foliation of g-spacetime onto h:

τ (x) = \int_{γ_{X}} n_{a} d x^{a}, n_{a} n_{g}^{a} = - 1

where

n^{a}

is the future-directed unit normal to the g-hypersurfaces and

Υ_{X}^{}

is any curve connecting a reference slice to the point x. Since

n^{a}

is timelike in

g_{a b}

and remains timelike in

h_{a b}^{}

by construction of the two-cone hierarchy —its worldlines lie inside both light cones—

τ_{; α}

therefore increases monotonically along every causal trajectory in either metric:

τ_{; a}^{} g^{a b} > 0, τ_{; a}^{h^{a b} > 0}

Thus, the same scalar function

T

provides a consistent global ordering for all g- and h-causal processes. In the effective theory,

T

acts as the universal “clock” that synchronizes the two cones without introducing retrocausal or acausal paths.

The function

τ

provides a unified ordering of events across the dual metrics, ensuring that no closed causal loops arise even when information propagates outside the g-light cone. A global time function exists whenever a spacetime is globally hyperbolic [51]. Define

T

as a scalar function on the manifold M:

τ : M \to R, \frac{d τ}{d λ} > 0

for all causal curves parameterized by

λ

. In the two-cone framework, I require monotonicity with respect to both cones:

\nabla_{μ} τ ν^{μ} > 0 \forall ν^{μ} \in F u t u r e (g) \cup F u t u r e (h)

i.e.

T

increases along all g-causal and h-causal curves. Because

h_{μ ν}^{}

is non-dynamical and aligned by construction with

g_{μ ν}

within device domains, such a

T

can always be chosen globally. This guarantees exclusion of closed causal loops.

In effect,

τ

synchronizes the two causal structures, permitting extended coherence while forbidding paradoxical signaling.

These structural elements — microcausality and global time — demonstrate that the two-cone framework is not only compatible with established physics but is also logically stable against the common objections to superluminal information.

Thermodynamic Consistency

A further consistency check arises from the laws of thermodynamics. If information can propagate outside the light cone, one might worry about violations of the second law, for example through Maxwell–demon–style feedback loops. To exclude such loopholes, the sequestered information sector must respect the known bounds on the thermodynamics of information.

Landauer’s principle [17] states that erasing one bit of information incurs a minimal heat cost:

Q \geq k_{B} T l n 2

where Q is the dissipated heat,

k_{B}

is Boltzmann’s constant, and T is the temperature of the reservoir. This ensures that information cannot be erased or manipulated without an energetic footprint in the physical sector.

In addition, feedback-controlled processes must respect the generalized second law, as formalized by the Sagawa–Ueda inequality:

(W) \geq Δ F - k_{B} T I

Here,

⟨ W ⟩

is the average work performed,

Δ F

is the free energy difference, and I is the mutual information between system and controller. The presence of I shows that information has real thermodynamic consequences, but the inequality guarantees that these consequences never enable a demon to violate the second law.

In the sequestered-sector framework, information propagation occurs without stress–energy transfer, but any attempt to harness it for work is mediated by couplings localized in the device domain D. These couplings ensure that Landauer and Sagawa–Ueda bounds [18] apply in full, closing potential loopholes. The information field can extend correlations beyond the light cone, but it cannot be used to extract unlimited work or to reverse entropy.

By satisfying these thermodynamic constraints, the two-cone framework preserves not only relativity and quantum mechanics but also statistical mechanics, ensuring that no fundamental principle of physics is compromised.

Worked toy example: gated informational feedback cannot beat the second law

Consider a device domain D where a visible, two-level system

X \in {0,1}

(energy-degenerate;

Δ F = 0

) is measured by a controller M. The controller couples to X only while the gate

\begin{matrix} g (t) \end{matrix}

is open (inside D). The controller then applies a feedback operation conditioned on its record, attempting to extract work from a thermal bath at temperature T.

Landauer erasure cost. Resetting the controller’s one-bit memory to a standard state after the cycle costs at least:

Q_{e f f a s e} \geq k_{B} T l n 2

Information gained by measurement. If the measurement is noisy with error rate

E

(binary symmetric channel), the mutual information between X and the controller’s record M is (in bits)

I_{b i t s} (X M) = 1 - H_{2} (ε)

with

H_{2} (ε) = - ε {l o g}_{2} ε - (1 - ε) {l o g}_{2} (1 - ε)

.

In nats (natural-log units) this is

I = I_{b i t s} l n 2

. I measure I in nats unless otherwise stated;

I_{b i t s} = I / l n 2

(cf. Shannon [50])

Sagawa–Ueda bound (feedback with information). For an isothermal process with feedback, the average work performed on the system satisfies:

(W) \geq ∆ F - k_{B} T I

Equivalently, the maximum extractable work is:

W_{e x t}^{* m a x} = - ⟨ W ⟩ \leq k_{B} T I - A F

For our degenerate two-level example,

Δ F = 0

, so

W_{e x t}^{m a x} \leq k_{B} T I

.

Close the loop with erasure. Completing a full engine cycle requires erasing the controller’s memory. The net average gain is then bounded by

W_{n e t}^{m a x} \leq k_{B} T I - k_{B} T l n 2

For a perfect measurement (

ε = 0 \Rightarrow I = l n 2

in nats), the inequality gives

W_{n e t}^{m a x} \leq 0

: the erasure cost cancels the information-enabled work extraction, so no violation of the second law is possible.

For any noisy measurement (

I < l n 2

), the inequality is strictly negative, meaning the cycle loses work on average.

A compact “second law with feedback” form often used in the literature is

(\equiv \frac{) - Δ F}{T} - k_{B} I \geq 0

which this toy cycle explicitly saturates (perfect measurement) or strictly satisfies (noisy measurement).

Role of the sequestered information sector

In our framework, the controller’s informational access (via the h-cone) can coordinate the feedback without carrying stress–energy. However, any attempt to convert that information into useful work necessarily proceeds through gate-localized couplings inside D, where Landauer and Sagawa–Ueda apply. Hence, even with superluminal informational coherence, the energetic bookkeeping in the g-sector forbids a Maxwell-demon loophole.

At room temperature

T \approx 300 K

,

k_{B} T l n 2 \approx 2.9 \times 10^{- 21} J (a t \ 300 K)

per bit. A perfect, single-bit feedback step can at most extract that much work; the mandatory erasure costs at least the same, yielding zero or negative network over a full cycle.

Testability and Predictions

A key strength of the two-cone, sequestered information framework is that it yields decisive, falsifiable predictions. The hypothesis is not metaphysical speculation but a physical proposal subject to experimental scrutiny.

Internal device tests. The invariant speed of the information cone,

υ_{h}^{}

, can in principle be measured by probing coherence across spacelike separations within a controlled domain. Observable consequences include a sub-permille anisotropy in Bell-visibility experiments and syndrome “ridge” structures in quantum error correction (QEC) arrays, scaling with the ratio:

d / ν_{h}

Here d is the device separation scale. The appearance of structured anisotropy or syndrome ridges would indicate coherence propagation governed by the auxiliary metric

h_{a b}^{}

.

Gravitational probes. Because the information sector is sequestered from stress–energy, it does not couple directly to gravitation. However, loop-induced effects in the presence of gates

g_{D}^{} (x)

can mimic tiny effective masses for mediators. For example, graviton propagation could acquire a minute mass

m_{g}

, producing dispersion in gravitational wave signals detectable by future observatories such as the Einstein Telescope (ET), Cosmic Explorer (CE), LISA, and pulsar timing arrays (PTAs).

Similarly, long-baseline magnetostatic measurements in deep space may reveal a tiny photon mass

m_{γ}

. Both signatures would mark consistent but testable deviations from standard field theory.

Instant Preview vs. Physical Arrival (Gravitational Waves)

In the proposed informational framework, a distinction arises between two temporal regimes of observation: (1) the instant preview, corresponding to immediate informational registration through the Lugon channel, and (2) the physical arrival, corresponding to the delayed energy-bearing gravitational wave itself.

Under this model, detectors may receive an instantaneous change in informational state—effectively a 'preview' of the event—long before the spacetime disturbance propagates at light speed. Such a preview would not transfer energy or momentum and thus cannot be detected through standard strain measurements. Instead, it manifests as correlated phase or entropy adjustments within quantum or interferometric systems pre-aligned to the source geometry.

The distinction between informational preview and physical arrival could be probed using time-tagged entangled systems distributed across distant detectors. If synchronized informational shifts precede measurable strain events beyond light-travel constraints, this would support the existence of an independent Lugon information channel.

Falsification matrix. The framework provides clear criteria for rejection:

Detection of off-device superluminal signaling.
Observation of Lorentz-violating couplings leaking outside domain D.
Inconsistencies in gravitational-wave dispersion relative to general relativity.
Breakdown of the effective field theory description at accessible energies.

Failure on any of these points would falsify the hypothesis.

By offering internal device signatures, gravitational probes, and an explicit falsification matrix, the two-cone framework remains strictly within the bounds of empirical science. The proposal preserves established relativity and quantum mechanics while opening the possibility of a hidden informational sector whose consequences are both concrete and testable.

The two-cone framework is falsifiable through a combination of laboratory-scale quantum experiments and astrophysical observations. Each class of tests targets a distinct feature of the hypothesis, ensuring multiple independent opportunities for confirmation or refutation.

Area Scaling, Two-Surface Boost and Controls

Extending the testability framework, three new considerations are introduced:

1. Area Scaling: The predicted signal strength or informational coupling between dual surfaces scales with the boundary area A, rather than the energy flux. If Lugons mediate information through holographic area laws, variations in interface geometry (e.g., in superconducting cavity arrays or Casimir-bounded regions) should yield area-dependent correlations in detected informational entropy.

2. Two-Surface Boost: A dynamic enhancement is expected when paired surfaces undergo relative acceleration. Analogous to the Unruh effect, acceleration introduces a differential horizon structure, increasing boundary information flux. Experiments exploiting rapid mirror motion or modulated optical cavities may reveal this as a non-energetic coherence gain.

3. Controls: Null experiments—identical setups lacking either paired boundaries or Lugon-sensitive coupling—serve as essential controls. Their inclusion distinguishes informational propagation from ordinary electromagnetic cross-talk or environmental noise. Reproducible deviations correlated with area and acceleration would constitute preliminary evidence of a sequestered informational sector.Together, these augmentations refine the falsifiability of the model by anchoring its effects to measurable surface properties and dynamic parameters.

Device-internal measurements.The invariant speed of the information cone,

υ_{h}^{}

, can be probed by examining coherence in spacelike-separated subsystems. One signature is a sub-permille anisotropy in Bell-visibility experiments. Current Bell-test experiments have statistical visibility errors at the level of

10^{- 3}

; thus, an anisotropy larger than

10^{- 4}

in correlation visibility as a function of measurement angle would be detectable with existing technology.

Another signature arises in quantum error correction (QEC) arrays, where syndrome statistics may exhibit structured “ridges” that scale with device separation d relative to the information speed

υ_{h}^{}

:

s y n d r o m e r i d g e s c a l e \propto d / ν_{h}

By measuring syndrome distributions in large-scale QEC devices, one could place empirical bounds on

υ_{h}^{}

.

Long-baseline entanglement distribution

Satellite-based experiments already demonstrate entanglement distribution across distances exceeding 1,200 km [12,13]. Repeating these experiments with the aim of detecting coherence decay or anisotropy relative to orbital orientation would provide an external validation of internal-device results. Any observed directional dependence in visibility at the

10^{- 4}

level or below would strongly suggest the influence of an auxiliary metric.

Gravitational-wave dispersion.

In the sequestered framework, loop-induced couplings in gate domains can mimic an effective graviton mass

m_{g}

. A finite mass produces frequency-dependent dispersion in gravitational-wave (GW) propagation. Current LIGO–Virgo–KAGRA bounds constrain

m_{g}

<1.2×

10^{- 23} \

eV/

{\ b o l d m a t h c}^{2}

. Next-generation detectors such as the Einstein Telescope (ET) and Cosmic Explorer (CE) aim to improve sensitivity by an order of magnitude, probing

m_{g} ~ 10^{- 24} e V / c^{2}

. The detection of such dispersion would provide strong evidence for physics beyond standard GR.

Similarly, a photon mass

m_{γ}

as small as

10^{- 18} e V / c^{2}

can be probed via magnetostatic measurements in deep space. Null results further constrain possible gate-induced couplings, tightening the falsification matrix.

Falsification matrix (see Appendix D for the full matrix).

The framework provides multiple avenues for refutation:

Off-device signaling. If controllable information is transmitted superluminally across devices, the sequestered-sector hypothesis is invalidated.
Lorentz leakage. Any detection of Lorentz-violating couplings outside of domain D would falsify the principle of radiative sequestering.
Gravitational-wave consistency. A mismatch between GW dispersion limits and the framework’s predictions would disprove the model.
EFT stability. If effective field theory (EFT) fails at accessible energy scales, the framework cannot be sustained.

By combining laboratory experiments with astrophysical tests, this framework provides concrete, falsifiable predictions. Unlike many speculative extensions of relativity, the two-cone model ties its validity to experimental outcomes within reach of present or near-future technologies.

Bell-visibility anisotropy.

Suppose the information cone speed is

υ_{h}^{}

, and the laboratory separation between detectors is d. If entanglement visibility has a directional dependence due to propagation along the auxiliary metric, the anisotropy should scale as:

Δ V ~ d / ν_{h}

For present Bell-test baselines of d∼10 m, a hypothetical

c_{I} ~ 10^{3} c

would yield anisotropies at the level of

Δ V ~ 3 \times 10^{- 8}

. Such an effect is below current error bars (

~ 10^{- 3}

) but would become testable with future photonic networks spanning kilometers.

Quantum error correction (QEC) syndrome ridges.

In stabilizer codes, correlated error syndromes should exhibit ridge-like patterns when plotted against device separation. The scaling law is:

l_{r i d g e} \propto d / v_{h}

where

l_{r i d g e}

is the characteristic width of the syndrome distribution. Measuring this scaling provides a way to place direct experimental bounds on

c_{I}

.

Satellite-based entanglement distribution.

The 2017 Micius satellite experiment [13,59,60,61] demonstrated entanglement distribution over d∼1200 km. If coherence is mediated by an auxiliary cone with speed

c_{I}

, the anisotropy bound becomes:

A V \leq 1200 k m / ν_{h}

With observed visibilities around 0.80–0.85, an improvement in experimental precision at the

10^{- 4}

level could probe

c_{I}

values up to

10^{7} c

.

Gravitational-wave dispersion.

If gravitons acquire a small effective mass

m_{g}

, gravitational waves of frequency f travel at speed:

ν_{g} (f) \approx c | 1 - \frac{m^{2} c^{4}}{2 h^{2} f^{2}} |

where h is Planck’s constant. Current LIGO–Virgo–KAGRA bounds yield

m_{g} \leq 1.2 \times 10^{- 23} e V / c^{2}

. ET and CE are projected to reach sensitivities an order of magnitude stronger, down to

m_{g} ~ 10^{- 24} e V / c^{2}

.

Photon mass constraints.

If photons couple indirectly via gate-induced effects, they may acquire a tiny mass

m_{γ}

. In that case, the Coulomb potential is modified from 1/r to a Yukawa form:

V (r) = \frac{q}{4 π ε_{0} r} e^{- m_{γ} c r / ℏ}

Astrophysical observations constrain

m_{γ} < 10^{- 18} e V / c^{2}

. Future deep-space magnetostatic missions may tighten this by several orders of magnitude.

Implications

The two-cone framework carries implications across multiple domains of physics, from relativity to quantum information to black hole thermodynamics. By sequestering information from energy–momentum, the proposal preserves tested principles while offering new explanatory power.

Relativity.

Special and general relativity remain intact for all work-carrying fields confined to the physical metric

b g_{a b}^{}

Energy–momentum conservation, Lorentz invariance, and causal structure are unchanged. Apparent superluminal correlations arise only in the information sector, which by construction has vanishing stress–energy:

T_{a b}^{} (I) = 0

Thus, no violations of relativity occur. Instead, the framework expands the ontology of what can propagate without undermining relativity’s empirical foundations.

Quantum mechanics.

The paradox of entanglement is reframed: correlations need not be mysterious or “nonlocal coincidences,” but are the natural expression of information traveling on the auxiliary metric

b h_{a b}^{}

at speed

ν_{h} > c

. Entanglement protocols such as teleportation [9], superdense coding [8], and QKD [10] are explained as operations that harvest information from this sequestered sector while leaving energetic causality intact.

Quantum information theory.

Entropy and mutual information become not only measures of uncertainty but indicators of a real, quantifiable resource that resides in the information sector. This aligns with the view advanced in Quantum Computation and Quantum Information [14], where information is treated on equal footing with energy as a basic quantity.

Quantum gravity and spacetime geometry.

The idea that information is fundamental resonates with the holographic principle. In AdS/CFT duality, the Ryu–Takayanagi formula [15] connects entanglement entropy to the area of minimal surfaces in the bulk spacetime. Van Raamsdonk [16] extended this by proposing that spacetime connectivity itself is built from entanglement. Within the two-cone framework, these insights suggest that the auxiliary metric

b h_{a b}^{}

is not merely a mathematical device but a candidate informational scaffold underlying spacetime structure.

Black holes and thermodynamics.

Perhaps the deepest implication lies in black hole physics. Information paradoxes traditionally hinge on reconciling Hawking evaporation with unitarity. In the present framework, an energy-free horizon information membrane allows information to escape without energy transfer, aligning with the Page curve and recent “islands” picture of entanglement wedges [19]. This preserves black hole thermodynamics while resolving tension between information conservation and relativity.

In the sequestered-information framework, the event-horizon area defines not only an entropic bound but the absolute capacity of a black hole as an information reservoir — its

C_{* m a x} \propto \frac{A}{4 l^{2}}

, where

l_{p}

is the Planck length.

Together, these implications position the two-cone framework as a bridge: it preserves the successes of relativity and quantum mechanics while providing a coherent explanation for otherwise paradoxical features of information.

Relation to Other Theories

To situate the two-cone, sequestered-information framework within the broader landscape, I compare it to prominent alternatives that address nonlocality, superluminal phenomena, or quantum foundations. The central distinctions are: (i) no superluminal energy transfer (the information field carries identically vanishing stress-energy), (ii) no Lorentz violation in the energetic sector, (I) microcausality in both cones with a unifying global time function, and (iv) radiative sequestering that prevents leaks outside engineered device domains.

Tachyons and superluminal particles.

Classic faster-than-light proposals posit fields with imaginary mass that propagate superluminally (tachyons) [21,52,53]. Their dispersion takes the form:

E^{2} = p^{2} c^{2} - m^{2} c^{4}

Such models typically entail vacuum instabilities, acausal signaling, or frame-dependent pathologies. By contrast, the present framework forbids any superluminal energy/momentum transfer—the information field satisfies:

T_{a b}^{} (I) = 0

so it cannot source gravity, accelerate detectors, or carry work. Correlations can extend outside the g-light cone only as energy-free informational coherence.

Lorentz-violating EFTs and preferred frames.

In Standard-Model Extensions (SME) and related preferred-frame theories, small Lorentz-violating operators modify dispersion or introduce background vectors

u^{a}

[22–24, 55–56, See Appendix F “auxillary–metric decoupling argument”]. A schematic LV photon term is:

L_{L V} \supset (u^{a} F_{a b}) (u_{c} F^{c b})

Such terms face tight experimental bounds and risk radiative instability. Our construction keeps the energetic sector exactly Lorentz-invariant on

b g_{a b}^{}

and confines all device couplings with a gate

g_{D}^{} (x)

, preventing LV “leakage” by design [47].

g_{D} (x) l o c a l i z e s a l l I - m a t t e r c o u p l i n g s t o d o m a i n D

Nonlinear quantum mechanics.

State-dependent (nonlinear) evolutions (e.g., Weinberg-type) are known to permit EPR-based superluminal signaling (Gisin/Polchinski paradoxes) [27]. A generic nonlinear master equation reads:

\dot{ϱ} = - \frac{i}{ℏ} [H, ϱ] + M [ϱ]

with

M [ϱ]

state-dependent. Our proposal retains linear QM within each sector and preserves no-signaling across devices by locality of

g_{D}^{} (x)

; the observed nonlocality arises from h-causal coherence, not from nonlinear dynamics.

Pilot-wave (Bohmian) mechanics.

Bohmian theory reproduces QM via a nonlocal guidance equation [25]:

v (x, t) = (ℏ / m) I m (\nabla ψ / ψ)

It explains correlations by instantaneous influences in configuration space while disallowing operational FTL signals. Our account differs ontologically: I posit a second causal cone (metric

b h_{a b}^{}

, speed

ν_{h} > c

) on which information (not particles) propagates. Energetic causality and Lorentz invariance on

b g_{a b}^{}

remain intact.

Objective-collapse models (GRW/CSL).

GRW/CSL modify dynamics with stochastic collapses, introducing new constants (collapse rate

λ

, length

r_{C}

) and small energy increases, with potential symmetry tensions [26]. I introduce no collapse and no extra energy budget: coherence redistribution occurs through the sequestered information sector with

T_{a b}^{} (I) = 0

, and thermodynamic consistency is enforced via Landauer/Sagawa–Ueda bounds.

Superdeterminism.

These approaches relax measurement independence, allowing hidden correlations between settings (a,b) and hidden variables

λ

[29]:

P (λ ∣ a, b) \neq P (λ)

While logically possible, they are empirically unfalsifiable without additional structure. Our framework preserves standard statistical independence; Bell violations arise from information-sector causality rather than conspiratorial initial conditions.

Retrocausal/two-state-vector ideas.

Retrocausal models allow future boundary data to influence present outcomes (two-state-vector formalism) [30]. I instead enforce a global time function

T

that increases along both g- and h-causal curves, excluding closed causal loops:

P (λ ∣ a, b) \neq P (λ)

Thus, no retrocausality is required to explain spacelike entanglement correlations.

Non-signaling superquantum (PR) boxes.

Popescu–Rohrlich correlations saturate the algebraic CHSH bound ∣S∣=4|S|=4∣S∣=4 while remaining non-signaling [28]:

{| s |}_{c l a s s i c a l} \leq 2, {| S |}_{Q M} \leq 2 \sqrt{2}, {| S |}_{P R} = 4

Our framework does not exceed the Tsirelson bound; it preserves standard quantum constraints and merely reallocates where information-theoretic coherence lives (on

b h_{a b}^{}

), keeping device-external no-signaling intact.

ER=EPR and wormhole pictures.

Geometric identifications (ER=EPR) relate entanglement to nontraversable wormholes [19]. While conceptually aligned with “information as structure,” those scenarios invoke specific spacetime topologies and energy conditions. Our approach is agnostic about topology; it reproduces EPR-type nonlocality via a second, non-dynamical metric for information, potentially complementary to ER=EPR without requiring exotic matter.

Summary of contrasts.

Not tachyons: no superluminal energy; $T_{a b}^{} (I) = 0$
Not Lorentz-violating EFT: no LV in the energetic g-sector; radiatively sequestered couplings inside D.
Not nonlinear QM: linear dynamics preserved; no Gisin/Polchinski signaling.

Not hidden-variable/retrocausal: no conspiracies or backward causation; global

T

orders events across cones.
Not superquantum (PR): respects Tsirelson; maintains standard quantum structure.

These distinctions clarify that the two-cone framework is neither a rebranding of older superluminal ideas nor a hidden-variable scheme. It is a structural separation: energy and matter live on

b g_{a b}^{}

under SR/GR; information has its own causal cone on

b h_{a b}^{}

with

ν_{h} > c

, coupled locally via

g_{D}^{} (x)

, microcausal and globally ordered to forbid paradoxes.

Conclusions

The paradox at the heart of modern physics lies in the tension between the strict causal order of relativity and the apparently acausal reach of quantum entanglement. Relativity, codified in the invariant speed c, ensures that no transfer of energy or momentum can exceed the light cone, as captured in the divergence of the relativistic energy–momentum relation [1]. Entanglement, however, violates all classical expectations: correlations persist across spacelike separations, violating Bell inequalities [3,4,5,6,7], yet remain non-signaling. This paradox has sharpened through experiment, from Aspect’s pioneering photon tests to loophole-free demonstrations and global-scale satellite links [4,5,6,7,12,13].

Conventional reconciliation through the no-signaling theorem secures compatibility with relativity but does not explain why entanglement functions as a consumable, quantifiable resource. Teleportation, dense coding, and quantum cryptography [8,9,10] all rely on entanglement as if it were a tangible fuel. Entanglement entropy and mutual information formalize this operational value [14], while holographic dualities link information content to geometric structure [15,16]. Together, these insights suggest that information is more than a mathematical abstraction: it behaves as a physical quantity.

The hypothesis of a sequestered information sector follows from this recognition. All energetic fields remain confined to the physical metric

b g_{a b}^{}

, while information propagates on a second, auxiliary metric

b h_{a b}^{}

at invariant speed

ν_{h} > c

. Because the information field satisfies identically vanishing stress–energy,

T_{a b}^{} (I) = 0

it cannot accelerate detectors, transmit work, or source curvature. Relativity remains inviolate for energy–momentum, while information achieves global coherence through a causal cone that does not couple to gravitation. The separation is maintained by domain-local couplings

g_{D}^{} (x)

, microcausality in both cones, and a global time function

T

that orders all processes across metrics. Thermodynamic consistency is preserved by Landauer’s erasure bound and Sagawa–Ueda’s feedback inequality [17,18], ensuring that the framework does not reopen Maxwell’s demon loopholes.

Beyond consistency, the framework is empirically sharp. Internal-device tests can search for sub-permille anisotropies in Bell-visibility measurements or syndrome ridge patterns in quantum error correction arrays, both scaling as

d / ν_{h}

. Satellite experiments that distribute entanglement over thousands of kilometers probe coherence on global scales, constraining

υ_{h}^{}

by improved visibility precision. Gravitational-wave observatories test for loop-induced graviton mass

m_{g}

through dispersion effects [ET, CE, LISA, PTAs], while astrophysical magnetostatics constrain photon mass

m_{γ}

. A falsification matrix makes the theory scientifically accountable: failure in any of these domains would rule it out.

The implications are profound. Relativity emerges unscathed, with all energetic processes confined to the familiar light cone. Quantum mechanics gains an ontological foundation for entanglement, elevating correlations from statistical curiosities to manifestations of an informational field. Information theory is promoted from a mathematical tool to a physical law, with entropy and mutual information treated alongside energy and momentum. Quantum gravity insights, from the Ryu–Takayanagi formula to ER=EPR [15,16,19], are naturally aligned: if spacetime itself is built from entanglement, then a second, information-bearing cone may be the substrate from which geometry emerges. Black hole physics likewise finds resolution, as an energy-free horizon information membrane offers a route to preserve unitarity, match the Page curve, and reconcile thermodynamics with evaporation.

In this way, the two-cone framework acts not as a violation of known physics but as a synthesis. It respects the empirical domains of relativity and quantum mechanics, but extends them by acknowledging that information and energy are distinct physical entities with distinct causal structures. This separation dissolves the paradox that has long haunted the intersection of relativity and entanglement.

Whether confirmed or falsified, testing the framework will advance our understanding. Confirmation would establish information as a new sector of physics, opening an era of information engineering at fundamental scales. Falsification would be equally valuable, sharpening the bounds of what is possible and pushing us toward alternative explanations. In either case, the outcome would deepen our grasp of causality, coherence, and the foundations of physical law.

Appendix A. Notation and Conventions

Symbol	Meaning / Definition	Notes
c	Speed of light in vacuum	Invariant speed for all energetic fields (special relativity).
$υ_{h}^{}$	Invariant speed in the auxiliary information cone	By hypothesis, $ν_{h} > c$ .
$g_{D}^{} (x)$	Gate/localization function	Restricts I-matter interactions to device domain D.
$g (x, t)$	Gate function; a spatiotemporal modulation variable that weights the interaction between visible and sequestered sectors.	Dimensionless; ranges from 0 (closed) to 1 (open); may be smooth (sigmoid) or digital (Heaviside).
$g_{a b}$	Physical (energetic) spacetime metric.	Defines causal structure for all energetic fields and matter; signature $(- + + +)$ .
$h_{a b}^{}$	Auxiliary (informational) metric.	Fixed background metric defining causal structure for the informational sector.
$g (x)$	Gate function — scalar weighting field that localizes coupling between the $g_{a b}$ - and $h_{a b}$ -sectors (See Note 1 at end of section).	Dimensionless; takes values $0 \leq g (x) \leq 1$ . Used in the interaction term $S_{i n t}^{} = \int \sqrt{- g} g_{X}^{} λ h^{a b} \nabla_{a}^{} I \nabla_{b}^{} I$ .Distinct from the metric $g_{a b}$ . The function vanishes outside device domains $D$ and is unity inside them, ensuring causal sequestering.
$T_{a b}$	Stress–energy tensor	Standard definition; vanishes for information field I.
$T_{a b}^{} (I)$	Stress–energy of the information field	Defined to satisfy $T_{a b}^{} (I) = 0$ .
D	Device domain	Region where information and matter couple.
$T$	Global time function	Monotonically increases along both g- and h-causal processes.
$s^{2}$	Spacetime interval	$s^{2} = c^{2} t^{2} - x^{2} - y^{2} - z^{2}$ . Determines causal separation.
$γ$	Lorentz factor	$γ = (1 - ν^{2} / c^{2})^{- 1 / 2}$ .
p	Relativistic momentum	Appears in energy–momentum relation.
E	Relativistic energy	$E^{2} = (p c)^{2} + (m c^{2})^{2}$ .
m	Rest mass	Mass of energetic particle.
$(Φ^{+})$	Bell state
$E (\hat{a}, \hat{b})$	Correlation function	Depends on angle between measurement axes.
$\| \| S \|$	CHSH parameter	with absolute-value bars
$G$	Density matrix	Describes mixed quantum states.
$S (ϱ)$	Von Neumann entropy	$S (ϱ) = - T r (ϱ l o g ϱ)$ .
$I (A : B)$	Mutual information	$S (Q_{A}) + S (Q_{B}) - S (Q_{A B})$ .
$[\cdot, \cdot]$	Commutator	Used in microcausality conditions.
Q	Heat dissipated	Landauer bound: $Q \geq k_{B} T l n 2$ .
$W ⟩$	Average work	Appears in Sagawa–Ueda inequality.
$Δ F$	Free energy difference	Sagawa–Ueda bound context.
$k_{B}$	Boltzmann’s constant	Appears in thermodynamic relations.
f	Frequency	Relevant for GW dispersion.
$m_{g}$	Effective graviton mass	Tested via GW dispersion.
$m_{γ}$	Photon mass	Constrained by magnetostatic tests.
$V (r)$	Potential energy	Coulomb or Yukawa potential with photon mass.
$λ_{\ b o l d m a t h γ}$	Photon Compton wavelength	$λ_{γ} = ℏ / (m_{γ} c)$ .
$ℏ$	Reduced Planck’s constant	Appears in dispersion and potential formulas.
Ωg	Gate aperture; the region in spacetime where the gate function is nonzero.	Subset of $[[ℵ^{3} \times [[ℵ$ .
$u k (x, t)$	External control fields or knobs (e.g., bias voltages, pump power, strain, curvature).	Inputs to the gate function.
$α_{k}, θ$	Gain parameters $(α_{k}$ ) and threshold $(θ$ ) used in the sigmoid form of g.	Dimensionless coefficients.
σ(z)	Sigmoid function used to smooth gate transitions.	Defined as $σ (z) = 1 / (1 + e^{- z})$ .
$L_{i n t}^{} (V, S)$	Interaction Lagrangian coupling visible and sequestered sectors.	Weighted by gate function.
$ϕ, m_{ϕ}$	Mediator field $ϕ$ with effective mass $m_{ϕ}$ .	Mass controlled by potential U.
$U (x, t)$	External potential that tunes mediator mass.	Could represent strain, optical potential, curvature.
$\overset{ˇ}{ε} ϕ$	Mediator coherence length.	Inverse of $m_{ϕ}$ ; sets leakage range.
$H_{0}, H_{i n t}$	Free Hamiltonian and interaction Hamiltonian	Standard Lindblad notation; interaction scaled by the gate function $g (x)$ , a dimensionless scalar weight $0 \leq g (x) \leq 1$ that localizes the coupling in spacetime and is distinct from the metric $g_{a b}$ . When the coupling is spatially uniform, $g (x) \to g (t)$ , reproducing the usual time-dependent Lindblad scaling.
$L_{j}, γ_{j} (t)$	Lindblad operators and time-dependent decoherence rates	Describe dissipative channels
$δ g, τ_{c}^{}, σ_{g}^{}, η (t)$	Noise parameters for Ornstein–Uhlenbeck gate model	: fluctuation, $τ_{c}$ : correlation time, $σ_{g}^{}$ : variance, $η (t)$ : white noise
$I, I_{c}, Δ φ$	Josephson junction current, critical current, and phase difference	Gate-modulated Josephson relation
$V_{n}, f$	Shapiro step voltage and drive frequency	Steps at $V_{n} = n h f / 2 e$
$m (x, t)$	Effective mass parameter in topological models	Sign inversion creates domain walls
$A_{p} (t), a_{s}, a_{i}$	Pump amplitude, signal mode, idler mode	Nonlinear optical parametric gates
$N (x)$	Lapse function in curved spacetime metric	Determines local vs. global frequency shift
$τ ↑, τ ↓$	Gate opening and closing times	May be asymmetric
$Q$	Duty cycle of gate	Fraction of time gate is open
$α, d, M (ω)$	Internal loss coefficient ( $α$ ), gate thickness (d), matching function $M (ω)$	Control transmission and latency
$B (x), S (x), N (x)$	Local bandwidth (B), signal (S), noise (N)	Used in information flux bound
G	Conductance of topological channel	Quantized in units of $e^{2} / h$
$Δ ϕ, p, d l$	Interferometric phase shift, momentum, and path element	Used in atom interferometry
N (atoms)	Number of detected atoms	Sets shot-noise limit $δ ϕ ~ 1 / \sqrt{N}$
$ℒ$	Information Lagrangian density associated with the Lugon field.	Defines informational action integral over auxiliary manifold; dimensionless in natural units.
Cₘₐₓ	Maximum channel capacity of the holographic boundary or information surface.	Defines the theoretical upper bound to information transfer per unit area; relates to area-entropy law.

NOTES:

1) Notation g_(x) refers exclusively to the gate function, a scalar weight controlling localized coupling between the energetic and informational sectors. It is unrelated to the metric tensor g_ab. Throughout, g_ab denotes the spacetime metric, while g_(x) is a scalar field confined to device domains 𝐷.

Appendix A: Worked Equations

CHSH inequality:

| S | = | E (\hat{a}, \hat{b}) + E (\hat{a}, {\hat{b}}^{'}) + E ({\hat{a}}^{'}, \hat{b}) - E ({\hat{a}}^{'}, {\hat{b}}^{'}) | \leq 2

Correlation function:

E (\hat{a}, \hat{b}) = - c o s (θ_{a b})

Duty cycle estimate

Q \approx \frac{σ \sqrt{2 π}}{σ \sqrt{2 π} + τ \underset{↓}{l n \frac{1 - g_{f l o o r}}{1 - g_{t h}}}}

Energy–momentum relation:

E^{2} = (p c)^{2} + (m c^{2})^{2}

Entangled Bell state:

| Φ^{+} ⟩ = 1 / \sqrt{2} (| 00 ⟩ + | 11 ⟩)

Gate-modulated Lagrangian

L = L_{V} + L_{S} + g (x, t) L_{i n t} (V, S)

Gate function with sigmoid control

g (x, t) = {\sum_{k} α_{k}^{} f_{k}^{} (u_{k}^{} (x, t)) - θ}, σ (z) = \frac{1}{1 + e^{- z}}

Gate relaxation dynamics

\ s t a c k r e l . \dot{g} = \frac{1}{τ} (g^{*} (u) - g) + ξ (t), ⟨ \tilde{ξ} (t) \tilde{ξ} (t^{'}) ⟩ = 2 D δ (t - t^{'})

Global time function:

\nabla_{a} τ t i m e l i k e w . r . t . b o t h g_{_a b}, h_{_a b}

Gravitational redshift gate condition

g (x) = \partial b i g (| ω_{0} - \frac{ω_{\infty}}{N (x)} | < Δ b i g)

GW dispersion (massive graviton):

ν_{g} (f) \approx c (1 - (m_{g}^{2} c^{4}) / (2 h^{2} f^{2}))

Information flux bound

Φ_{I} \leq \int_{Ω_{g}} d^{3} x \frac{B (x)}{2 π} l o g \frac{S (x)}{2 N (x)}

Interferometer phase shift

Δ ϕ = \frac{1}{ℏ} \int_{p a t h} p \cdot d l

(2)

Josephson gate current

I = I_{c} g (t) s i n Δ φ

Landauer bound:

Q \geq k_{B} T l n 2

Lindblad master equation with gate factor

\frac{d ϱ}{d t} = - i [H_{0} + g (t) H_{i n t}^{Q}] + \sum_{j} γ_{j} (t) (L_{j} ϱ L_{j}^{†} - \frac{1}{2} {L_{j}^{†} L_{j}, Q})

Lorentz transformations:

t^{'} = γ (t - \frac{ν x}{c^{2}}), x^{'} = γ (x - ν t), γ = 1 / \sqrt{1 - ν^{2} / c^{2}}

Microcausality (energetic cone):

[ϕ (x), ϕ (y)] = 0 f o r (x - y)_{g}^{2} < 0

Microcausality (information cone):

[I (x), I (y)] = 0 f o r (x - y)_{h}^{2} \leq 0

Mutual information:

I (A : B) = S (_{Q} A) + S (_{Q} B) - S (_{Q} A B)

Nonlinear optical parametric gate

H_{χ^{(2)}} = ℏ g_{χ} A_{p} (t) a_{s} a_{i} + h . c ., g (t) = κ | A_{p} (t) |

Ornstein–Uhlenbeck noise on gate

\dot{δ g} = - \frac{1}{τ} δ g + \sqrt{\frac{2 σ^{2}}{τ}} η (t)

Photon Yukawa potential:

V (r) = (q / (4 π 0 r)) e^{- m_{γ} c r / ℏ}

Quantized conductance (cold atoms / topological)

G = n \frac{e^{2}}{h}, n \in Z

Reduced density matrix (no-signaling):

ϱ_{A}^{} = {T r}_{B} (| Φ^{+} ⟩ ⟨ Φ^{+} |) = I / 2

Sagawa–Ueda inequality:

\ l a n g l e W \ r a n g l e \geq Δ F - k_{B} T I

Shapiro steps

V_{n} = \frac{n h f}{2 e}, n \in Z

Shot-noise limit on phase

δ ϕ ~ \overset{―}{\sqrt{N}}

Spacetime interval:

s^{2} = c^{2} t^{2} - x^{2} - y^{2} - z^{2}

Topological domain wall gate function

g (x, t) = \frac{1}{2} [\begin{matrix} 1 - s g n m (x, t) \end{matrix}]

Transmission through finite gate

G (ω) = g^{2} e^{- α d} | M (ω) |^{2}

Tsirelson bound:

| S | \leq 2 \sqrt{2}

Von Neumann entropy:

S (ϱ) = - T r (ϱ l o g ϱ)

Appendix A.1 . Lorentz Factor from Interval Invariance

Start with the invariant spacetime interval between two events:

s^{2} = c^{2} t^{2} - x^{2}

Consider two inertial frames, S and S′, with relative velocity v along the x-axis. Coordinates transform as:

x^{'} = γ (x - ν t), t^{'} = γ (t - ν x / c^{2})

To preserve invariance requires:

c^{2} t^{' 2} - χ^{' 2} = c^{2} t^{2} - χ^{2}

Substitute the transformations:

c^{2} [γ (t - \frac{v x}{c^{2}})]^{2} - {[γ (x - ν t)]}^{2} = c^{2} t^{2} - x^{2}

Factor out

γ^{2}

:

γ^{2} [c^{2} (t - \frac{v x}{c^{2}})^{2} - (x - v t)^{2}] = c^{2} t^{2} - x^{2}

Simplify the bracket:

c^{2} t^{2} - 2 ν x t + \frac{v^{2} x^{2}}{c^{2}} - (x^{2} - 2 ν x t + ν^{2} t^{2})

This reduces to:

c^{2} t^{2} - x^{2} - ν^{2} (t^{2} - \frac{x^{2}}{c^{2}})

Therefore:

γ^{2} [(c^{2} - v^{2}) t^{2} - (1 - \frac{v^{2}}{c^{2}}) x^{2}] = c^{2} t^{2} - x^{2}

For equality to hold for all x, t requires:

γ^{2} (1 - v^{2} / c^{2}) = 1

Thus:

γ = 1 / \sqrt{1 - v^{2} / c^{2}}

Appendix A.2 CHSH Inequality Violation

The CHSH inequality compares quantum correlations with classical local realism.

Define the correlation function for spin-1/2 particles measured along axes

\hat{a}, \hat{b}

:

E (\hat{a}, \hat{b}) = - c o s (θ_{a b})

The CHSH parameter is:

\hat{S} = E (\hat{a}, \hat{b}) + E (\hat{a}, {\hat{b}}^{'}) + E ({\hat{a}}^{'}, \hat{b}) - E ({\hat{a}}^{'}, {\hat{b}}^{'})

Classically,

| S | \leq 2

. Quantum mechanically, Tsirelson’s bound is

| S | \leq 2 \sqrt{2}

.

Take measurement angles:

$\hat{a} = 0 •$
${\hat{a}}^{'} = 90^{\circ}$
$\hat{b} = 45 \circ$
${\hat{b}}^{'} = - 45^{\circ}$

Compute correlations:

E (\hat{a}, \hat{b}) = - c o s (45 \circ) = - (\sqrt{2} / 2) br - to - break E (\hat{a}, {\hat{b}}^{'}) = - C O S (- 45^{\circ}) = - (\sqrt{2} / 2) br - to - break E ({\hat{a}}^{'}, \hat{b}) = - c o s (45 \circ) = - (\sqrt{2} / 2) br - to - break E ({\hat{a}}^{'}, {\hat{b}}^{'}) = - c o s (135 \circ) = + (\sqrt{2} / 2)

Now compute S:

S = (- \frac{\sqrt{2}}{2}) + (- \frac{\sqrt{2}}{2}) + (- \frac{\sqrt{2}}{2}) - (+ \frac{\sqrt{2}}{2}) br - to - break S = - 2 \sqrt{2}

Therefore:

| S | = 2 \sqrt{2} > 2

This matches the quantum prediction and demonstrates the violation of Bell’s inequality, ruling out local realist explanations.

Appendix A.3 . Bell-Visibility Anisotropy: from Auxiliary-Cone Timing to Visibility Loss

Setup (ideal correlation and visibility).

For a maximally entangled two-qubit state (e.g., singlet), the ideal correlation fringe is

E_{i d e a l} (a, b) = - V_{0} c o s (Δ α)

where

V_{0} \leq 1

is the ideal visibility and

Δ α

is the relative analyzer angle.

Auxiliary-cone timing offset

In the two-cone framework, boundary synchronization along the auxiliary metric h produces a direction-dependent timing offset for a detector baseline d. Let

θ

be the angle between the baseline and a preferred axis of the h-cone. For a characteristic angular frequency

ω

of the source (or analysis modulation), the induced phase offset is

δ ϕ (θ) = ω δ t_{h} (θ) = ω \frac{d}{ν_{h}} c o s θ

with vhv_hvh the invariant speed on the hhh-cone.

Remark. A constant

δ ϕ

would only shift the fringe phase. Visibility loss appears when

δ ϕ

jitters during integration (e.g., over a gate window), so I model

δ ϕ

as a zero-mean random variable with small rms

σ_{ϕ}^{}

.

Time averaging and visibility reduction.

The measured correlation after averaging over

δ ϕ

is

E_{m e a s} (a, b) = - ⟨ c o s (Δ α + δ ϕ) ⟩ = - \underset{\equiv V / V_{0}}{\underset{⏟}{⟨ c o s δ ϕ ⟩ c o s (Δ α) +}} ⟨ s i n δ ϕ ⟩ s i n (Δ α)

For a symmetric distribution of

δ ϕ

(zero mean),

δ ϕ \ r a n g l e = 0

and the observed visibility is

V (θ) = V_{0} \ z e t a c o s δ ϕ (θ) \ r a n g l e

If

δ ϕ

is small (

σ_{ϕ}^{≪ 1}

), expand

c o s δ ϕ \approx 1 - \frac{1}{2} δ ϕ^{2}

and obtain

\frac{V (θ)}{V} \approx 1 - \frac{1}{2} δ ϕ (θ)^{2} \ r a n g l e

Gate-window model (uniform start time).

Let the effective gate start be uniformly distributed over a window of width

{Δ t}_{g}

. The timing offset along the h-cone contributes a deterministic slope that integrates over the gate, yielding an rms phase

σ_{ϕ}^{2} (θ) = (ω \frac{d}{υ_{h}} c o s θ)^{2} V a r (u) = (ω \frac{d}{υ_{h}} c o s θ)^{2} \frac{1}{12}

where

u ~ U n i f o r m [0,1]

parametrizes the entry across the window (variance 1/12). Hence

\frac{V (θ)}{V_{0}} \approx 1 - \frac{1}{2} σ_{ϕ}^{2} (θ) = 1 - \frac{1}{24} (ω \frac{d}{υ_{h}} c o s θ)^{2}

Express in coherence-time units.

Writing

ω = 2 π / τ_{c}

 for a characteristic coherence time

τ_{c}

 of the source/analysis,

\frac{V (θ)}{V} \approx 1 - \frac{π^{2}}{6} (\frac{d}{ν_{h} c})^{2} {c o s}^{2} θ

and the fractional anisotropy (visibility drop) is

\frac{Δ V (θ)}{V_{0}} \equiv \frac{V (θ) - V 0}{V_{0}} \approx - \frac{π^{2}}{6} (\frac{d}{υ_{h}^{τ} τ_{c}})^{2} {c o s}^{2} θ |

Connection to CHSH.

In a standard CHSH test with settings

{α_{i}^{, β}}

, the ideal correlations scale as

E_{i j}^{= - V_{0} c o s (α_{i}^{- β_{j})}}

. The measured ones inherit the reduced

V (θ)

:

E_{i j}^{m e a s} (θ) = - V (θ) c o s (α_{i} - β_{j})

so the CHSH parameter becomes

S_{m e a s} (θ) = V (θ) S_{i d e a l}^{} \approx V_{0} [1 - \frac{π^{2}}{6} (\frac{d}{ν_{h} τ_{c}})^{2} {c o s}^{2} θ] S_{i d e a l}

with

S_{i d e a l} = 2 \sqrt{2}

for the optimal angles. This yields a direction-dependent deficit in S at order

(d / (v_{h} τ_{c}))^{2}

.

Assumptions & small-parameter regime.

Gate-induced timing spreads dominate other dephasing;

σ_{ϕ}^{≪ 1}

2.: so the second-order expansion is valid;

The preferred-axis projection produces the

c o s θ

factor; averaging over

θ

3.: recovers an isotropic mean.

Experimental scaling summary

At fixed

τ_{c}

and

υ_{h}^{}

, the leading anisotropy scales quadratically with baseline and has a

{c o s}^{2} θ

angular pattern:

Δ V / V_{0} \propto - (\frac{d}{υ_{h τ}})^{2} {c o s}^{2} θ

Longer baselines and shorter coherence times amplify the effect; null observation at the predicted sensitivity falsifies the boundary-synchronization mechanism under these assumptions.

Appendix B. Experimental Data-Analysis Recipes

Bell-visibility anisotropy
- Fit measured visibilities $V (θ)$ against orientation.
- Compute residual anisotropy $Δ V = V_{m a x} - V_{m i n}$ .
- Sensitivity target: $Δ V \leq 10^{- 4} .$
QEC syndrome ridges
- Collect stabilizer syndrome histograms at separations $d}_{1}, d}_{2}$ .
- Extract ridge width $l_{r i d g e}$ via Gaussian fit.
- Test scaling: $\ p m b l_{r i d g e}^{(2)} / \ p m b l_{r i d g e}^{(1)} \approx d_{2}^{} / d_{1}^{}$
Satellite entanglement anisotropy
- Compare visibilities at different orbital orientations.
- Bound anisotropy with: $A V \leq 1200 k m / ν_{h}$
GW dispersion
- Fit arrival times $t (f)$ vs. frequency f.
- Extract speed difference $Δ ν_{g} (f)$ .
- Translate into graviton mass bound $m_{g}$ .
Photon Yukawa roll-off
- Measure potential $V (r)$ at large r.
- Fit exponential suppression to extract $λ_{γ} = ℏ / (m_{γ} c)$ .

Appendix B.1 Bell-Visibility Anisotropy Scaling

Suppose two detectors are separated by a baseline distance d. The information field I propagates on the auxiliary cone with invariant speed

ν_{h} > c

. If correlations are established via this cone, then the relative phase accumulated depends on the direction of separation relative to the laboratory frame.

Define the correlation visibility V as the amplitude of the sinusoidal correlation function measured in a Bell test:

E (θ) = V c o s (θ)

If propagation is isotropic at speed ccc, then V is independent of detector orientation. However, if coherence propagates on the wider cone with speed

υ_{h}^{}

, the effective “light travel time” acquires an orientation dependence:

∠ t (ϕ) \approx \frac{d}{ν_{h}} c o s ϕ

where

ϕ

is the angle between the detector baseline and the preferred axis of the auxiliary cone. This introduces a small modulation of the observed visibility. To first order, the fractional anisotropy in visibility scales as

\frac{Δ V}{V} ~ \frac{d}{c_{h} τ_{c}}

where

τ_{c}

is the coherence time of the entangled source. For current photonic experiments with

d ~ 10 m

and

τ_{c}^{} ~ 10^{- 13} s

, this gives

Δ V / V

\leq 10^{- 3}

for

c_{I} ≫ 10^{8} c

. Kilometer-scale baselines (satellite links) push this sensitivity down by 2–3 orders of magnitude.

Appendix B.2. QEC Syndrome Ridge Scaling

Consider a stabilizer-code array laid out on a 1D or 2D geometry inside the device domain D. Let stabilizer outcomes be

s_{a}^{} \in {+ 1, - 1}

at sites a, b separated by

r = ‖ r_{a} - r_{b} ‖

. During a gate window of duration

τ_{g a t e}

(with temporal width

σ_{t}

), the information sector can generate domain-local, finite-speed correlations with propagation speed

\ e n s u r e m a t h c_{I}

on the h-cone.

Define the connected two-point syndrome correlator

C_{a b} \equiv (s_{a} a_{b}) - (s_{a}) (s_{b})

.

Model the gate as a temporal window g(t) with width

σ_{t}

, and the h-cone propagation kernel as a narrow pulse

K_{h}^{} (t, r) \approx δ (t - \frac{r}{ν_{h}})

Then the pair-activation amplitude for joint errors at separation r is proportional to the overlap of the gate and propagation kernels:

A (r) \propto \int d t g (t) K_{h} (t, r) = g (\frac{r}{υ_{h}})

Taking g(t) Gaussian with rms width

σ_{t}

,

g (t) = e x p (- \frac{t^{2}}{2 σ_{t}^{2}}) ⟹ A (r) \propto e x p [- \frac{1}{2} {(\frac{r}{\underset{h \, t}{ν}})}^{2}] .

The connected correlator inherits this envelope (up to device-dependent prefactors (

α

):

C (r) \equiv {(s r) s (0)}_{c} \approx α e x p [- \frac{1}{2} (\frac{r}{l_{I}})^{2}], l_{I} \equiv v_{h} σ_{t}

.

Interpretation (ridge width). In a 2D array, plotting

C_{a b}

over site pairs (a,b) produces ridge-like bands of elevated correlation along loci of approximately constant r. The characteristic ridge half-width in real space is the informational correlation length

\overset{―}{| l_{I} = ν_{h} σ_{t} |}

and the dimensionless scaling used to compare devices is

\frac{Δ C}{C} ~ \frac{a_{l a t}}{l_{I}} = \frac{a_{l a t}}{v_{h} σ_{t}}

with

a_{l a t}

the lattice spacing (or minimum detector separation). Directional (anisotropic) gate or lab frame. If the gate is directionally biased or the lab frame defines a preferred axis

\hat{n}

, replace r by the projected separation

r_{∥}^{} = \hat{m}

:

C (r) \approx α e x p [- \frac{1}{2} {(\frac{r \hat{n}}{υ_{h} σ_{t}})}^{2}],

which yields line-like ridges aligned perpendicular to

\hat{n}

.

Practical estimator. From an experimental syndrome dataset over many rounds

k = 1, . . ., N

, estimate the connected correlator binned by separation r:

\hat{C} (r) = \frac{1}{N_{r}} \sum_{(a, b) \in B (r)} (\frac{1}{N} \sum_{k = 1}^{N} s_{a}^{(k)} s_{b}^{(k)}) - (\frac{1}{N} \sum_{k = 1}^{N} s_{a}^{(k)}) (\frac{1}{N} \sum_{k = 1}^{N} s_{b}^{(k)})

then fit

\hat{C} (r)

to the Gaussian envelope to extract

l_{I}

and bound

c_{I}^{} = l_{I}^{} / σ_{t}^{}

.

Key prediction. Across architectures (superconducting, trapped-ion, photonic), ridge width scales linearly with the gate temporal width:

r i d g e w i d t h \propto O_{I} = ν_{h} σ_{t}

so shorter gate windows sharpen ridges; longer windows broaden them. Null observation of this scaling—while other internal tests confirm domain-local h-cone coupling—falsifies the mechanism.

Optional Spectral Check

Some teams prefer a Fourier-space diagnostic. The structure factor

S (k) = \sum_{r} C (r) e^{- i k \cdot r}

will show narrowing along

k_{∥}

with width

Δ k_{∥} ~ \frac{1}{L}

.

Appendix C. Relation to Quantum Gravity and Holography (Extended)

Ryu–Takayanagi formula: links entanglement entropy to bulk geometry [15].
Van Raamsdonk proposal: spacetime connectivity emerges from entanglement [16].
ER=EPR (Maldacena & Susskind): entanglement ↔ wormholes [19].
Swingle’s tensor networks: holographic geometry from entanglement renormalization [20].

The sequestered information sector aligns with these insights: if spacetime itself is emergent from entanglement, the auxiliary metric

b h_{a b}^{}

may represent the substrate geometry of information, distinct from the energetic geometry

b g_{a b}^{}

Appendix C.1. Black Hole Page Curve—Worked Example

This appendix sketches a quantitative Page-curve example for an evaporating, nonrotating, uncharged (Schwarzschild) black hole. The goal is to show how the entanglement entropy of Hawking radiation

S_{R}^{} (t)

first increases and then decreases back to zero when islands are included, reproducing a unitary Page curve.

Setup and basic thermodynamics

Schwarzschild horizon area (mass M):

A (M) = 4 π r_{s}^{2} = 16 π G^{2} M^{2} / c^{4}

Planck length (definition):

l_{P}^{2} = ℏ G / c^{3}

Bekenstein–Hawking entropy:

S_{B H} (M) = k_{B} A / (4 l_{P}^{2}) = k_{B} c^{3} A / (4 G ℏ)

Explicit

S_{B H} (M)

for Schwarzschild:

S_{B H} (M) = 4 π k_{B} G M^{2} / (ℏ c)

Hawking temperature:

T_{H}^{} (M) = ℏ c^{3} / (8 π G M k_{B}^{})

Evaporation time (order-of-magnitude, Schwarzschild):

t_{e v a p}^{} (M_{0}^{}) \approx 5120 π G^{2} M_{0}^{3} / (ℏ c^{4})

Here

M_{0}

is the initial mass. The Page time is roughly half the evaporation time for an initially pure state (back-of-envelope):

t_{P a g e}^{~ (1 / 2)} {t_{e v a p}^{(M}}_{0}^{)}

(Precise numerical factors depend on graybody spectra and species; this schematic suffices for the Page-curve logic.)

Radiation entropy without islands (monotonic growth)

Let

S_{o u t} (t)

denote the fine-grained entropy of the Hawking radiation collected outside up to time ttt. In a naive (no-island) calculation,

S_{o u t} (t)

grows approximately linearly at early times (coarse picture):

S_{o u t} (t) ↑ (m o n o t o n e i n c r e a s e w i t h o u t i s l a n d s)

If evaporation is unitary, the radiation entropy should not grow indefinitely: it should turn over at the Page time and return to zero by

t_{e v a p}

. The no-island calculation fails to capture this turnover.

Generalized entropy and islands (turnover and unitary Page curve)

The modern resolution introduces islands in the fine-grained entropy via the generalized entropy functional

S_{g e n} \equiv \frac{A r e a (\partial J)}{4 G ℏ} + S_{o u t} (J \cup R),

and extremizes it over candidate island regions

ω

(the “island prescription”).

Generalized entropy (definition):

S_{g e n} [J] = A r e a (\partial . J) / (4 G ℏ) + S_{o u t} (J ⋃ R)

Island rule (extremize + choose minimal):

S_{R}^{} (t) = * {m i n}_{J} {e x t}_{J} S_{g e n}^{} [J]

Early times: the extremum with no island dominates, so $S_{R}^{} (t) \approx S_{o u t}^{} (t)$ increases.
After $t_{P a g e}$ : an extremum with an island $ω$ becomes preferred. The area term acts like a counter; as the black hole shrinks, $A r e a (\partial J)$ decreases and the minimal $S_{g e n} S_{R}^{} (t) \approx * m i n [S_{o u t}^{} (t), S_{B H}^{} (M (t))]$ tracks the remaining black-hole entropy.

This structure yields a unitary Page curve implementable as the minimum of two branches (schematic):

S_{R}^{} (t) \approx * m i n [S_{o u t}^{} (t), S_{B H}^{} (M (t))]

where

M (t)

is the mass trajectory under evaporation. At

t = t_{P a g e}

,

S_{o u t} (t_{P a g e}) \approx S_{B H} (M (t_{P a g e}))

,

and for

t > t_{P a g e}

the island branch wins, causing

S_{R}^{} (t)

to decrease in step with the shrinking

S_{B H} (M (t))

.

Page Condition:

S_{o u t} (t_{P a g e}) \approx S_{B H} (M (t_{P a g e}))

Late-time decrease:

t ≻ t_{P a g e} : S_{R} (t) \approx S_{B H} (M (t)) ↓ \to 0

Thus, the turnover is not put in by hand; it emerges when the generalized entropy is extremized and minimized over island configurations.

How this dovetails with the sequestered information sector

In the two-cone framework, information can propagate on the auxiliary metric

b h_{a b}^{}

with invariant speed

ν_{h} > c

but carries no stress–energy:

T_{a b}^{} (I) = 0

An energy-free horizon information membrane can therefore communicate correlations to the radiation without transporting energy across the horizon. This is consistent with black-hole thermodynamics (the Hawking flux and area decrease remain governed by

b g_{a b}^{}

), while the fine-grained entropy follows the island prescription and produces a unitary Page curve. In short: energetic bookkeeping (area decrease,

T_{H}

,

t_{e v a p}

stays on

b g_{a b}^{}

; informational bookkeeping (entanglement flow) is carried by the

b h_{a b}^{}

sector, implementing the turnover required by unitarity.

Optional explicit mass–time sketch (coarse)

One can parametrize a coarse

M (t)

via the standard evaporation scaling

d M / d t \propto - 1 / M^{2}

, giving

M (t) ~ (M_{0}^{3} - κ t)^{1 / 3}

(with a constant

K

absorbing greybody factors/species). Then

S_{B H} (t) \propto M (t)^{2}

decreases convexly, while a crude

S_{o u t} (t)

increases until crossing at

t_{P a g e}

.

Coarse Scaling:

d M / d t \propto - 1 / M^{2}, M (t) \approx (M_{0}^{3} - κ t)^{1 / 3}, S_{B H} (t) \propto M (t)^{2}

This coarse model suffices to visualize the crossing of

S_{o u t} (t)

and

S_{B H} (t)

near

t_{P a g e}

and the subsequent decrease of

S_{R}^{} (t)

with the island branch.

Summary

Without islands: $S_{R}^{} (t) \approx S_{o u t}^{} (t)$ grows monotonically → paradox.
With islands (generalized entropy):

$S_{R} (t) = * {m i n}_{J} {e x t}_{J} [A r e a (\partial J) / (4 G ℏ) + S_{o u t} (J ⋃ R)]$

turnover at $t_{P a g e}$ , then decrease to 0 (unitarity).
In our framework: Energy stays on $b g_{a b}^{}$ ; information flows on $b h_{a b}^{}$ with $T_{a b}^{} (I) = 0$ , permitting an energy-free information membrane consistent with thermodynamics and the Page curve.

Appendix D. Falsification Matrix

Observable	Signature / Scaling	Current sensitivity (order)	Near-term target	Falsifies if…	Notes / Refs
Bell visibility anisotropy	$Δ V ~ d / ν_{h}$	σV∼10⁻³ (state-of-the-art lab Bell tests)	σV≲10⁻⁴ on km baselines	no anisotropy while other internal tests confirm $υ_{h}^{}$ _-mediated structure	Scaling estimate from two-cone hypothesis; relates device separation d to info-cone speed $υ_{h}^{}$ . [4,5,6,7,12,13]
QEC syndrome “ridges”	$l_{r i d g e} \propto d / v_{h}$	qualitative (pattern-level)	quantitative ridge-width vs. d with ≤10% error	absence of any $d / ν_{h}$ scaling across architectures	Requires stabilizer-code arrays with variable spacing d.
Satellite entanglement anisotropy	$A V \leq 1200 k m / ν_{h}$	global links demonstrated; visibility precision ∼10⁻³	push to 10⁻⁴ precision; orientation scans vs. orbit	null anisotropy bounds imply $ν_{h} / c ≳ 10^{7}$ (tight)	Micius-class baselines set strong bounds on $υ_{h}^{}$ . [12,13]
Internal timing probe of $\ e n s u r e m a t h c_{I}$	${t_{I}^{\ sim d / v}}_{h}$	ns–ps timing in photonics	ps–fs timing across chip-to-chip links	timing consistent with luminal or subluminal only	Requires strictly domain-local coupling (gate $g_{D}^{} (x)$ ).
GW dispersion (effective $\ e n s u r e m a t h m_{g}$ )	$ν_{g} (f) \approx c \| 1 - \frac{m^{2} c^{4}}{2 h^{2} f^{2}} \|$	$m_{g} \leq 1.2 \times 10^{- 23} e V / c^{2}$ (LIGO–Virgo–KAGRA)	$~ 10^{- 24} e V / c^{2}$ (ET/CE) [58]	detected dispersion inconsistent with predicted loop-suppressed effects or inconsistent nulls	Constraint on loop-induced graviton mass inside device domains.
Photon mass / magnetostatics	$V (r) = \frac{q}{4 π ε_{0} r} e^{- m_{γ} c r / ℏ}$	$m_{γ} ≪ 10^{- 18} e V / c^{2}$ (astro)	push lower via deep-space probes	detection of Yukawa roll-off at odds with gate-localized loops	Independent check on radiative sequestering [57].
Off-device signaling	No controllable superluminal signal	strong null results to date	reinforce with space-like separated, loophole-free designs	any repeatable superluminal message transmission	Immediate falsification of sequestering (violates no-signaling).
Lorentz leakage outside D	$g_{D}^{} (x)$ confines all couplings to D	indirect (engineering control)	direct leakage searches in shielded environs	observation of LV couplings beyond device boundary	Violates radiative sequestering premise.
EFT stability	$Λ_{E F T} ≫ E_{e x p}$	model-dependent	maintain wide hierarchy	anomalies at accessible energies	Any breakdown at low energies rules out the EFT.
Spectral shift (Analog gravity rotator)	Resonance opens when (	$Δ o$		ppm-level frequency resolution (atomic clocks)	kHz–Hz linewidth tracking in rotor-driven setups
Josephson–optical coincidence	Shapiro steps at $V_{n} = n h f / 2 e$ coincide with photon counts; scaling with optical pump power	Shapiro steps at $μ V$ ; dark counts ∼10² s⁻¹	Coincidence rates ≳10³ s⁻¹ with GHz pump	Electrical steps observed without correlated optical photon bursts	Proposed Model C+E (compound Josephson–optical gate)
Cold-atom interferometry / conductance	Quantized conductance G=ne²/; interferometric phase Δϕ∼0.1 rad	Atom interferometers: δϕ∼10⁻³ rad for N=10⁵	Resolve phase shifts ≥0.01 rad conductance plateaus	No quantized conductance or resolvable phase shift above shot-noise	Proposed Model D+A (strain-domain topological gate)
General noise/threshold criterion	All gate signals exceed noise floor by SNR ≥10	Varies (ppm freq; μV Josephson; mrad atom phase)	SNR ≥ 10 in controlled setups	Signals remain within noise after averaging (SNR < 10)	General falsifier for all controllable gate phenomena

Appendix E. Open Questions and Future Directions

Planck-scale coupling: How does the information sector interact at quantum gravity scales?
Dynamical auxiliary metric: Could $b h_{a b}^{}$ itself be emergent or dynamical?
Universality of gates $g_{D}^{} (x)$ : Are gate functions device-specific or fundamental?
Relation to holography: Is the information cone tied to entanglement wedges in AdS/CFT?

Experimental frontiers:
Extend satellite QKD anisotropy searches.
Deploy QEC arrays with km-scale separation.
Monitor GW dispersion with ET, CE, LISA [58].
Engineering perspective: If confirmed, sequestered information could open pathways to new forms of communication, error correction, and even spacetime engineering.

Appendix F. Gate Function Physics – Creation, Control, and Models

Primitive definition [31]

I model a gate as a spatiotemporal modulation:

L = L_{V} + L S + g (x, t), L i n t (V, S)

where

g (x, t) \in [0,1]

multiplies an otherwise latent interaction between a visible sector V and a sequestered sector S.

g = 0

“closes” the channel;

g = 1

opens it.

Control fields

Let

μ_{k}^{} (x, t)

be experimental knobs. Then:

g (x, t) = σ : [\sum_{k} α_{k}^{} f_{k}^{} (u_{k}^{} (x, t)) - θ], σ (z) = \frac{1}{1 + e^{- z}} .

Model A: EFT “portal” gate [46]

Mediator scalar

ϕ

couples sectors:

X_{i n t} = λ, ϕ, {\hat{O}}_{V}, \hat{O} S, m ϕ^{2} (x, I) = m_{0}^{2} - β, U (x, I)

Gate function:

g (x, t) = \frac{λ^{2}}{λ^{2} + m^{2} (x, t)}

Model B: Open-system (Lindblad) control [29,30,31]

Time-dependent master equation:

\frac{d ϱ}{d t} = - i [H_{0}^{} + g (t) H_{{i n t}^{} Q}] + \sum_{j} γ_{j}^{} (t) (L_{j} ϱ L_{j}^{†} - \frac{1}{2} L_{j}^{†} L_{j}^{}, Q)

Noise on g [32]:

\dot{δ g} = - \frac{1}{τ} δ g + \sqrt{\frac{2 σ^{2}}{τ_{c}}}, η (t)

Model C: Josephson-style weak link [33,34]

Current-phase relation:

I = I_{c}, g, s i n Δ φ, Δ φ = φ_{V} - φ_{S}

RSJ dynamics:

\frac{ℏ}{2 e} \dot{Δ} φ + R I + \frac{ℏ C}{2 e} \ddot{Δ} φ = V_{b i a s} (t)

Model D: Topological domain wall [35,36]

Gate variable:

g (x, t) = \frac{1}{2} [1 - s g n, m (x, t)]

Model E: Nonlinear-optical parametric gate [37,38,39]

Hamiltonian:

H_{χ^{(2)}} = ℏ g_{χ} A_{p} (t) a_{s} a_{i} + h . c ., g (t) = κ | A_{p} (t) |

Model F: Gravitational redshift window [40,41,42]

Condition:

g (x) = \partial (| ω_{} * - ω_{\infty}^{} / N (x) | < Δ)

Gate kinetics [47]

Relaxation equation:

\dot{g} = \frac{1}{τ_{↑, ↓}} (g^{*} (u) - g) + ξ (t), ⟨ ξ (t) ξ (t^{'}) ⟩ = 2 D δ (t - t^{'})

Duty cycle:

Q \approx \frac{σ \sqrt{2 π}}{σ \sqrt{2 π} + τ_{⋃_{↓}} l n! \frac{1 - g_{f l o o r}}{1 - g_{t h}}}

Thermodynamic cost

Landauer bound:

E_{m i n} \geq N_{b i t}, k_{B} T l n 2

Work bound:

W_{m i n} \geq \int_{0}^{1} d s, T r! [ϱ_{s}, \partial_{s} H (s)]

Transport through a finite gate [48,49,50]

Transmission:

S (ω) = g^{2} e^{- α d} | M (ω) |^{2}, {Δ t}_{l a t} \approx \frac{d}{ν_{g}} + \frac{d}{d ω} a r g M

Information flux:

Φ_{I} \leq \int_{Ω_{g}} d^{3} x, \frac{B (x)}{2 π}, {l o g}_{2} \frac{S (x)}{N (x)}

Noise, leakage, and cloaking

Let leakage channel amplitude outside

Ω_{g}

be

l (x)

. Impose a budget

{‖ U ‖}_{2} \leq ε

. Two remedies:

(i) Destructive interference: by adding a guard actuator that drives

g_{g u a r d}

with opposite phase;

(ii) Topological isolation [35,36]: (Model D), where off-wall states are gapped. In open-system terms, set a large

γ_{s i n k}

outside

Ω_{g}

in:

\frac{d_{0}}{d t} = - i [H_{0} + g (t) H_{i n t}, o] + \sum_{j} γ_{j} (t) (L_{j} o L_{j}^{†} - \frac{1}{2} L_{j}^{†} L_{j}, o)

to soak stray excitations.

Concrete laboratory scenarios

Cavity-strain portal (Model A + C): Mount a high-Q cavity on a piezo frame. Strain tunes $m_{ϕ}$ via $U = κ ε$ . Gate opens only when the cavity is both on resonance and strained past $ε_{t h}$ ; bandwidth limited by mechanical $Q_{m}$
Cold-atom domain wall (Model D)[43,44,45]: Use Raman dressing to invert an effective mass $m (x)$ long a narrow ribbon; protected edge modes provide a low-loss channel. Fast optical control sweeps the wall to steer the aperture.
OPAs as time windows (Model E): A pulsed pump $A_{p} (t)$ in a periodically poled waveguide defines $~$ ps gates. Use chirped quasi-phase-matching to tune the spectral aperture without moving hardware.
Analog gravity rotator (Model F): A rigid rotor at angular speed $Ω (t)$ simulates a redshift window by modifying the effective lapse function $N (x)$ . A resonance gate opens when the locally shifted frequency matches a target transition.

$ω_{l o c} = \frac{ω_{\infty}}{N (Ω 2 (t))}$

Control is achieved by modulating

Ω (t)

, allowing fast opening and closure of the window. The switching rate is limited by mechanical inertia and rotor stability.

Observables: Spectral lines of a probe transition shift when the gate opens, producing a discrete frequency match condition. Testability comes from measuring transmission spectra as

Ω (t)

is ramped; a sharp onset of resonance at the predicted redshift is the experimental signature.

Hybrid Josephson–optical gate (Model C + E): A superconducting weak link provides tunable phase bias, while a synchronized optical pump enables parametric drive. The two controls together create a compound aperture where electrical and photonic channels are simultaneously switched. This setup demonstrates cross-disciplinary control: electronic bias defines coarse gating, optical pulses provide ultrafast windows.
Observables: Shapiro-step patterns in the I–V characteristics coincide with optical pump timing, creating correlated spikes in current and photon flux. Joint detection of photons and Josephson oscillations provides a clear signature of the compound gate.
Cold-atom strain-domain system (Model D + A): An optical lattice of ultracold atoms experiences strain from spatially varying laser intensity, altering the effective mass term $m (x, t)$ . A domain wall hosts protected edge channels, while strain simultaneously tunes mediator mass $m_{ϕ}$ . This dual handle allows domain creation and annihilation on demand, with tunable leakage.

Observables: Atom interferometry detects phase-coherent transport along the domain wall, with conductance quantization as a hallmark. Bragg spectroscopy of the lattice reveals the strain-induced mass inversion, confirming controllable gate creation.

Testability

The models above are not purely abstract: each implies concrete, measurable observables that can serve as experimental signatures of gate dynamics. Testability, therefore, proceeds by identifying quantities that change sharply when a gate opens or closes:

Spectral shifts — in gravitational analogs, the local frequency $ω_{l o c}$ tracks the lapse function, yielding resonance “on/off” behavior as $Ω (t)$ varies.
Correlated electrical and optical signals — in hybrid Josephson–optical devices, coincidence between Shapiro steps and photon bursts provides a direct fingerprint of compound gating.
Quantized or protected transport — in cold-atom topological setups, conductance quantization and interferometric phase shifts reveal the presence or absence of domain-wall channels.

These observables allow a laboratory program to move beyond theoretical description: one can design experiments with clear “yes/no” criteria for gate existence and dynamics. The following subsections develop these criteria into proposed tests, including parameter ranges, noise budgets, and achievable detection thresholds.

1. Spectral Tests (Analog Gravity Rotator)

A resonance condition is reached when the locally shifted frequency matches a transition:

ω_{l o c} = \frac{ω_{\infty}}{N (Ω 2 (t))}

Detuning from resonance is:

Δ ω = ω_{0} - ω_{l o c}

Proposed Test: Place a narrow-linewidth atomic transition

(Δ ~

kHz scale) in the rotating frame. Sweep rotor angular velocity

Ω (t)

from

10^{2} - 10^{4} r a d / s

.

Noise Budget: Dominant background is Doppler broadening,

δ ω_{D} ~ 10^{- 3} ω_{0}

.

Detection Threshold: Observable transmission change requires:

| Δ ω | < Δ ~ 10^{- 5} ω_{0}

Thus, measurement resolution at the ppm level suffices.

2. Electrical/Optical Coincidence (Hybrid Josephson–Optical)

Josephson current-phase relation [33]:

I = I_{c} g (t) s i n Δ φ

Shapiro step condition [34]:

V_{n} = \frac{n h f}{2 e}, n \in Z

Proposed Test: Bias a junction at

I \approx I_{c}

while pumping with a GHz optical drive (

f = 1 - 10

GHz). Expect correlated steps at

V_{n} ~ 10 μ V

.

Noise Budget: Johnson–Nyquist noise in resistance

R ~ 10 Ω

gives

\sqrt{4 k_{B} T R A f} ~ n A

3. Cold-Atom Interferometry (Strain-Domain Gates)

Quantized conductance through edge states [44,45]:

G = n \frac{e^{2}}{h}, n \in Z

Phase accumulation along edge:

Δ ϕ = \frac{1}{ℏ} \int_{p a t h} p \cdot d l

Proposed Test: Use ultracold atoms at

T < 100 n K

in a 2D lattice with strain tuned by laser intensity. Interferometer arms enclose a domain wall.

Noise Budget: Atom shot noise sets phase uncertainty

δ ϕ ~ \overset{―}{\sqrt{N}}

with N the number of detected atoms. For N

~ 10^{5}

,

δ ϕ ~ 3 \times 10^{- 3} r a d

.

Detection Threshold: Gate-induced phase shift expected

Δ ϕ ~ 0.1 r a d

. Thus SNR

\approx 30

makes the effect clearly resolvable.

Summary

Each model yields clear test conditions:

Spectral gates: ppm-level resolution of frequency shifts.
Hybrid Josephson–optical gates: electrical Shapiro steps coincident with photon counts exceeding dark noise by at least one order of magnitude.
Cold-atom interferometry: phase-shift signals with SNR $~ 30 \$ .

Together, these provide a roadmap for experimental falsifiability of gate physics.

Appendix F.1 . Auxiliary-Metric Decoupling Argument

A frequent concern in two-cone frameworks is that loop corrections might regenerate Lorentz-violating operators in the visible (energetic) sector, even if such terms are absent at tree level. The present construction prevents this through metric-sector factorization and radiative sequestering.

1. Metric factorization

All interaction terms take the form

S_{i n t} = \int d^{4} x \sqrt{- g} g (t, x) E_{v i s} (V, g_{μ ν}) + \int d^{4} x \sqrt{- h} g (t, x) E_{i n f} (I, h_{μ ν})

where

g (t, x)

is the gate function and

V

and

I

denote visible and informational fields, respectively. Because each Lagrangian is contracted only with its own metric, covariant indices never mix across metrics. Any cross-term must pass through the dimensionless scalar gate

g (t, x)

, which carries no Lorentz indices and cannot break isotropy on

g_{μ ν}

.

2. Loop suppression

Consider a generic loop with

n

visible propagators

G_{V} (p, g)

and

m

informational propagators

G_{I}^{} (q, h)

. Each insertion of the gate function introduces a factor

ε = {⟨ g (t, x) ⟩}_{D} ≪ 1

where the average is confined to the device domain

D

. The mixed-metric amplitude scales as

M_{m i x} ~ ε^{2} \int d^{4} p d^{4} q T k b i g [G_{V}^{} (p, g) G_{I}^{} (q, h) b i j]

Since

\ e n s u r e m a t h G_{\ e n s u r e m a t h I}

has support only within

\ e n s u r e m a t h D

and does not carry momentum on the

g

-metric light cone, the integral yields no Lorentz-breaking tensor structures in the visible sector. Explicitly, after integrating out the

I

field one obtains an effective local operator

Δ E_{e f f} = c_{2} ε^{2} (\overset{―}{V} V) + Θ (ε^{4})

which is Lorentz scalar on

g_{μ ν}

. Tensorial (Lorentz-violating) corrections are forbidden by the absence of shared index structure.

3. Radiative stability

Because

g (t, x)

is external and nondynamical, renormalization acts only on the visible and informational propagators independently. Counterterms must respect each metric’s covariance:

δ ⧸ x_{V} \propto R (g), δ x_{I} \propto R (h)

with no mixed curvature contractions possible. Hence the two sectors remain radiatively sequestered: loop corrections renormalize intra-sector couplings but cannot transmit Lorentz violation across metrics.

4. Comparison with Lorentz-violating EFTs

In standard SME frameworks, Lorentz-breaking background tensors

k^{μ ν}

or

b_{μ}^{}

appear directly in kinetic terms and survive renormalization. Here, no such background exists in the

g

-sector: all mixed influence passes through the scalar gate, preserving full Lorentz symmetry of

g_{μ ν}

to all orders in perturbation theory.

5. Summary

The combination of metric-sector factorization, scalar-gate mediation, and loop suppression by

\ e n s u r e m a t h ε^{2}

ensures that radiative corrections cannot reintroduce Lorentz-violating operators in the visible sector. This auxiliary-metric decoupling provides a natural explanation for the stability of radiative sequestering referenced in the main text.

Appendix G . Research Pathway (Extended)

This work did not begin with a ready-made hypothesis but with a sequence of questions about the foundations of physics. Each question arose from dissatisfaction with conventional explanations and the drive to reconcile apparently conflicting principles. What follows is the path by which these questions accumulated, guided one into the next, and ultimately coalesced into the framework presented in this paper.

Relativity and the Speed Limit

The journey began with the most basic and well-tested constraint in modern physics: the universal speed limit of relativity. Special relativity asserts that the speed of light, c, is the maximum velocity at which causal influence can propagate. The question arose: why is c the limit, and what mechanism enforces this boundary?

To answer this, one must revisit the invariance of the spacetime interval and the structure of Lorentz transformations. The line element,

s^{2} = c^{2} t^{2} - x^{2} - y^{2} - z^{2},

remains invariant across inertial frames, ensuring a fixed causal structure. The classification of intervals as timelike, lightlike, or spacelike delineates what influences can connect distinct events. Timelike intervals allow causal connections, lightlike intervals correspond to propagation at c, and spacelike intervals forbid causal influence.

Energy–momentum relations deepen the picture. The relativistic energy expression,

E^{2} = (p c)^{2} + (m c^{2})^{2},

shows that as velocity approaches c, energy diverges without bound. No finite energy can accelerate a massive particle to c, much less beyond it. Thus, relativity does not merely assume a speed limit; it enforces one through the geometry of spacetime and the divergence of physical quantities. At this stage, the principle seemed airtight: no influence can surpass c.

Entanglement and the Challenge to Causality

The next question challenged this neat picture: what does quantum entanglement mean for the speed limit? Entanglement correlations appear to extend instantaneously across spacelike separations. Two particles, once entangled, retain correlations in measurement outcomes regardless of the distance between them.

Einstein, Podolsky, and Rosen (EPR) framed this in 1935 as evidence that quantum mechanics might be incomplete. Schrödinger, in response, coined the term Verschränkung (entanglement) to emphasize that the phenomenon was not an incidental feature but a central one. Bell’s theorem decades later sharpened the paradox: if local realism holds, then measurement correlations must satisfy inequalities like the CHSH bound. Quantum mechanics predicts violations, and Sagawa–Ueda bounds later clarified thermodynamic limits.

At this stage, the natural question was: does this mean information is propagating faster than light? Standard explanations respond with the no-signaling theorem: although entanglement produces correlations, no controllable signal can be transmitted superluminally. This answer is formally correct, but it feels like a patch. It reassures that relativity is not violated, yet it does not explain how coherence is maintained across spacelike separations.

Dissatisfaction with No-Signaling

The no-signaling theorem resolves the minimal contradiction, but it fails to address the deeper puzzle. If entanglement were a mere statistical overlay, it should not serve as a functional resource. Yet in practice, it does. This raised the next question: is the no-signaling condition sufficient, or does it obscure something more fundamental?

Here dissatisfaction became a pivot point. The no-signaling theorem ensures compatibility, but not comprehension. It tells us what cannot happen, but not why entanglement enables the extraordinary protocols at the heart of quantum information science.

From Paradox to Practice

The focus then shifted from abstract paradoxes to operational realities: what do real-world protocols reveal about the nature of entanglement?

In quantum teleportation, an unknown quantum state is reconstructed at a distant location using a shared entangled pair and a classical channel. The entanglement is indispensable; without it, teleportation is impossible.

In superdense coding, one qubit of an entangled pair allows the transmission of two classical bits. Entanglement enhances the channel capacity [48,49] beyond classical limits.
In quantum key distribution (QKD), entanglement and the violation of Bell inequalities certify secure keys in a way that no classical protocol can.
Satellite experiments have now extended entanglement distribution to distances exceeding a thousand kilometers, demonstrating coherence across global scales. Entanglement is not only a theoretical construct—it is a resource engineered, distributed, and consumed in laboratories and communication networks.

This led to the next, sharper question: if entanglement acts like a resource, is information itself a physical entity?

Information as a Resource

Entropy and mutual information [50] provide the formalism for treating information quantitatively. The von Neumann entropy,

S (ϱ) = - T r (ϱ l o g ϱ),

measures uncertainty, while mutual information,

I (A : B) = S (_{Q} A) + S (_{Q} B) - S (_{Q} A B),

quantifies correlations between subsystems. These are not abstract bookkeeping tools—they are measurable, conserved quantities. In holography, the Ryu–Takayanagi relation connects entanglement entropy to geometric surfaces in spacetime. Van Raamsdonk argued that spacetime connectivity itself arises from entanglement structure.

At this stage, the idea took shape: if information behaves as a physical resource, perhaps it should be treated as residing in its own sector of reality.

Formulating the Hypothesis

The pivotal question became: what if information and energy are separable? The two-cone framework is the proposed answer. Energy and matter remain confined to the physical metric

b g_{a b}^{}

, while information propagates on an auxiliary metric

b h_{a b}^{}

with invariant speed

ν_{h} > c

. The information field satisfies identically vanishing stress–energy,

T_{μ ν}^{(I)} = 0, δ S / δ g^{μ ν} = 0

ensuring it cannot transmit work or curve spacetime. Couplings occur only within device domains defined by gates

g_{D}^{} (x)

.

This framework explains how entanglement can maintain coherence (See Appendix F for Gate Construction) across spacelike separations without transferring energy. It preserves relativity for energetic processes while giving information its own consistent causal structure.

Testing Consistency

With the hypothesis in hand, new questions arose: would this permit paradoxes, causal loops, or thermodynamic violations?

Causality: Microcausality is enforced in both cones, and a global time function $T$ increases along all processes, excluding causal loops.
Thermodynamics: Landauer’s principle and the Sagawa–Ueda inequality ensure that no informational process can be harnessed to violate the second law. Maxwell-demon loopholes remain closed.

Each safeguard strengthened the case that the framework could be consistent with existing physical law.

Toward Testability

The final and decisive question was: how can this be tested? A scientific framework must be falsifiable.

Predictions include:

Sub-permille anisotropies in Bell visibility and syndrome ridge patterns in QEC arrays, scaling with $d / ν_{h}$ .
Satellite entanglement experiments sensitive to anisotropies at the $10^{- 4}$ level, constraining $υ_{h}^{}$ up to $10^{7} c$ .
Gravitational-wave dispersion revealing loop-induced graviton mass $\ e n s u r e m a t h m_{g}$ , probed by ET, CE, LISA, and PTAs [58].
Photon mass bounds from deep-space magnetostatics.

A falsification matrix ensures the framework can be ruled out if it fails.

Pathway to Hypothesis

From the first question about relativity’s speed limit, through the paradox of entanglement, the dissatisfaction with no-signaling, the recognition of information as a resource, the formulation of a two-cone hypothesis, and its consistency checks, each step arose naturally from the last. This pathway reflects not only a scientific logic but a process of questioning: at each stage, the refusal to accept “that’s just how it is” forced the search for a deeper account.

The result is a framework that preserves the tested domains of relativity and quantum mechanics, reframes entanglement as informational causality, and opens a falsifiable path toward new physics.

Introduction

The invariance of the speed of light, c, in special relativity establishes the universal causal structure of spacetime. Within this framework, all particles with rest mass are confined to subluminal velocities, while massless particles propagate precisely at c. Attempts to exceed this bound encounter the divergence of relativistic energy requirements, as expressed by the relation:

E^{2} = (p c)^{2} + (m c^{2})^{2}

At the same time, quantum mechanics introduces the phenomenon of entanglement, in which correlated particles display nonlocal correlations that persist across arbitrary spatial separations. A canonical example is the maximally entangled Bell state:

br - to - break | Φ^{+} ⟩ = \frac{1}{\sqrt{2}} (| 00 ⟩ + | 11 ⟩)

Such states violate Bell inequalities, revealing correlations that cannot be explained by local hidden-variable theories. The standard no-signaling theorem preserves compatibility with relativity by showing that the reduced density matrix of either subsystem remains maximally mixed, regardless of operations on the other:

ϱ_{A}^{} = {T r}_{B} (| Φ^{+} ⟩ ⟨ Φ^{+} |) = \frac{I}{2}

Yet this reconciliation is only formal. In practice, entanglement is not a statistical curiosity but a usable resource in quantum communication, cryptography, and teleportation. This raises a paradox: relativity prohibits superluminal causal influence, but quantum mechanics exploits entanglement correlations operationally as though coherence itself were maintained outside spacetime constraints.

In this work, I propose a resolution: information may exist in a sequestered sector, distinct from energy–momentum exchange. Under this view, energy transfer remains bound by c, consistent with relativity, while informational coherence can propagate in a hidden modality that does not couple directly to spacetime metrics. This framework permits the appearance of superluminal correlations without violating special or general relativity, offering both conceptual clarity and a pathway to experimental testability in quantum and gravitational systems.

The Speed of Light as the Universal Limit

Special relativity, first formulated by Einstein in 1905 [1], established that the speed of light in a vacuum, c, is invariant across all inertial frames. This invariance is mathematically encoded in the Lorentz transformations:

t^{'} = γ (t - \frac{υ x}{c^{2}}), x^{'} = γ (x - υ t), γ = \frac{1}{\sqrt{1 - ν^{2} / c^{2}}} .

These relations replace the Galilean transformations and demonstrate that spatial and temporal coordinates are not absolute but interwoven into a single spacetime structure. The constant c emerges as the conversion factor between space and time, preserving causality across frames.

Causal order is enforced through the invariant spacetime interval:

s^{2} = c^{2} t^{2} - x^{2} - y^{2} - z^{2}

Different values of

s^{2}

define the causal structure of spacetime:

1.

s^{2} > 0 t i m e l i k e s e p a r a t i o n : c a u s a l i n f l u e n c e p o s s i b l e

2.

s^{2} = 0 l i g h t l i k e s e p a r a t i o n : i n f l u e n c e p r o p a g a t e s a t c

3.

s^{2} < 0 s p a c e l i k e s e p a r a t i o n : n o c a u s a l i n f l u e n c e p o s s i b l e

The impossibility of accelerating massive particles to c is revealed directly in the relativistic energy–momentum relation:

E^{2} = (p c)^{2} + (m c^{2})^{2}

As velocity

ν \to c

, the momentum

p \to \infty

, and thus the energy

E \to \infty

for any particle with rest mass m > 0. Only massless particles such as photons can propagate at c.

This mathematical structure demonstrates that the speed of light is not merely a maximum velocity but is built into the geometry of spacetime itself. It ensures that causal paradoxes cannot occur, since any influence exceeding c would invert cause and effect in some frames.

Experimental verification of Lorentz invariance has confirmed these principles across orders of magnitude in energy, distance, and precision. Thus, relativity places c as the unbreachable boundary for all energy and momentum transfer. Yet, quantum mechanics introduces entanglement, which appears to test this boundary in unexpected ways.

Entanglement and the Information Paradox

In 1935, Einstein, Podolsky, and Rosen (EPR) argued that quantum mechanics was incomplete [2]. They considered two particles that interact and then separate, yet remain correlated. According to quantum mechanics, the system is described by a joint entangled state. A canonical example is the maximally entangled Bell state:

| Φ^{+} ⟩ = \frac{1}{\sqrt{2}} (| 00 ⟩ + | 11 ⟩)

Measurement of one particle immediately determines the outcome of the other, regardless of spatial separation. Schrödinger [11] recognized this as a fundamentally new feature of quantum theory and introduced the term Verschränkung (entanglement).

Bell’s theorem in 1964 [3] sharpened the paradox by showing that no local hidden-variable theory could reproduce all predictions of quantum mechanics. For two spin-

\frac{1}{2}

particles measured along directions

\hat{a}

and

\hat{b}

, the quantum correlation function is:

E (a, b) = - c o s (θ_{a b})

(where

θ_{a b}

is the angle between measurement settings a and b).

Bell derived the CHSH inequality, which must hold for all local hidden-variable models:

| S | = | E (\hat{a}, \hat{b}) + E (\hat{a}, {\hat{b}}^{'}) + E ({\hat{a}}^{'}, \hat{b}) - E ({\hat{a}}^{'}, {\hat{b}}^{'}) | \leq 2

Quantum mechanics, however, predicts violations up to the Tsirelson bound:

| S | \leq 2 \sqrt{2}

Experiments beginning with Aspect et al. in 1982 [4] and culminating in loophole-free tests in 2015 [5,6,7] confirmed the quantum predictions, ruling out local realism.

The no-signaling theorem preserves compatibility with relativity by ensuring that no superluminal communication is possible. Consider the reduced density matrix for subsystem A:

ϱ_{A} = {T r}_{B} (| Φ^{+} ⟩ ⟨ Φ^{+} |) = \frac{1}{2} I

No matter what measurement is performed on subsystem B, the state of subsystem A remains maximally mixed. Thus, no controllable signal can be transmitted faster than light, even though correlations appear instantaneously.

This reconciliation is formally sound but conceptually incomplete. If entanglement were merely a statistical overlay, it would not be exploitable. Yet in practice, entanglement is a resource: quantum teleportation [9], superdense coding [8], and quantum cryptography [10] all rely on it. Entanglement enables tasks that are otherwise impossible, despite carrying no energy or work across space.

This leads to the paradox: relativity forbids superluminal causal influence, but quantum mechanics harnesses entanglement operationally as if coherence itself were maintained outside spacetime constraints. The resolution of this paradox motivates the search for new frameworks.

Limitations of Conventional Explanations

The standard reconciliation between relativity and entanglement is the no-signaling theorem: although measurements on entangled pairs produce correlations, no controllable information travels faster than c. Each individual outcome is random, ensuring that observers cannot exploit entanglement for superluminal communication.

Mathematically, this is captured by the reduced density matrix of a subsystem. For a maximally entangled Bell state, the local state of subsystem A is:

ϱ_{A}^{} = {T r}_{B} (| Φ^{+} ⟩ ⟨ Φ^{+} |) = \frac{I}{2}

This expression shows that subsystem A remains maximally mixed, independent of operations performed on subsystem B. In other words, correlations exist, but no signal can be transmitted.

While this conclusion preserves compatibility with relativity, it leaves important questions unresolved. First, it reduces entanglement to a peculiar overlay of statistics rather than a physical connection. Second, it fails to explain how correlations are enforced across spacelike separations without mediation. Third, it conflicts with the operational role of entanglement in quantum information science.

For example, in quantum teleportation, the complete state of a system can be reconstructed at a distant location using shared entanglement and classical communication. The entangled pair provides an indispensable resource, even though no energy or matter crosses the gap. Similarly, in superdense coding and quantum key distribution, entanglement actively enables communication protocols that outperform their classical counterparts.

These cases suggest that entanglement is not an epiphenomenon but a resource with measurable, practical consequences. The mathematical formalism of no-signaling guarantees consistency but does not address the ontological status of entanglement as a medium of coherence.

This creates a conceptual gap: relativity binds all causal influence within the light cone, yet entanglement correlations appear to enforce global consistency across spacelike intervals. Either information is entirely constrained by c, making entanglement a paradoxical coincidence, or information admits distinct modalities — some confined to spacetime metrics, others existing in a sequestered, non-energetic form.

It is this second possibility that motivates a new framework, one in which information is fundamentally separable from energy and momentum, allowing coherence to propagate beyond c without violating the principles of relativity.

Deepening the Paradox

The paradox of entanglement is not confined to thought experiments; it manifests in laboratory and technological contexts that demonstrate its operational power.

One striking example is quantum teleportation. In this protocol, an unknown quantum state ∣ψ⟩ is destroyed at one location and reconstructed at another, using both shared entanglement and a classical communication channel [9]. Although no matter or energy is transmitted superluminally, the complete quantum description is relocated. The fidelity of teleportation hinges entirely on the entanglement resource.

Another example is superdense coding, in which one qubit of an entangled pair allows the transmission of two classical bits of information [8]. This enhancement cannot be explained by classical correlations alone; the entangled resource fundamentally alters the channel capacity.

Finally, quantum key distribution (QKD) protocols, such as Ekert’s entanglement-based scheme [10], rely on violations of Bell inequalities to certify secure cryptographic keys. The security of the protocol derives not from complexity assumptions but from the physical nonlocality of entanglement correlations.

In each of these cases, entanglement is not a passive curiosity but a functional element enabling outcomes impossible in classical physics. Yet, by the standard account, this resource exists without ever transmitting energy or signals.

This paradox grows sharper when considering the scalability of entanglement distribution. Experiments have distributed entangled photon pairs over distances exceeding 1,200 km via satellite links, maintaining correlations across global scales [12,13]. The persistence of coherence over such vast separations is difficult to reconcile with the picture of entanglement as mere statistics, and instead suggests that information is being maintained in a manner not confined to spacetime limits.

These examples deepen the puzzle: relativity forbids superluminal transfer of energy or matter, but practical quantum protocols treat entanglement as though coherence itself were a transferable, consumable resource. The gap between what relativity forbids and what quantum information science exploits demands a reevaluation of the ontological status of information.

Information as a Physical Resource

The growing role of entanglement in modern physics suggests that information itself must be regarded as a physical resource, measurable and quantifiable. Quantum information theory formalizes this through entropy and mutual information, which allow coherence and correlations to be treated in the same way that energy and momentum are tracked in traditional physics.

The fundamental measure is the von Neumann entropy [14] of a density matrix ρ:

S (ϱ) = - T r (ϱ l o g ϱ)

For a pure state, entropy vanishes, while mixed states carry positive entropy, reflecting a loss of information about the system.

For a bipartite system composed of subsystems A and B, the mutual information quantifies the correlations between them:

I (A : B) = S (_{Q} A) + S (_{Q} B) - S (_{Q} A B)

Here,

ϱ_{A}

and

Q_{B}

are the reduced density matrices of the subsystems, and

ϱ_{A B}^{}}

is the full joint state. Entanglement entropy emerges as a concrete, measurable quantity, and mutual information acts as a conserved bookkeeping variable, ensuring that correlations are properly accounted for.

The recognition of information as a resource is not limited to quantum information protocols. In quantum gravity, the Ryu–Takayanagi formula connects entanglement entropy directly to spacetime geometry [15,16], suggesting that geometry itself is emergent from patterns of information. This deepens the idea that information is not only operational but structural, influencing how I conceive the fabric of reality.

By treating information as a quantifiable physical resource, physics gains a new conserved quantity that does not neatly reduce to energy or momentum. Entanglement, entropy, and mutual information all point toward the same conclusion: information behaves like a real entity, but one that is not bound by the same constraints as matter and energy.

This recognition builds momentum toward a radical hypothesis: that information may inhabit a distinct sector of reality, sequestered from energy–momentum exchange, and thereby able to propagate beyond the limits of c without violating relativity.

References

Einstein, “On the Electrodynamics of Moving Bodies,” Annalen der Physik 17, 891–921 (1905).
Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. B 1935, 47, 777–780. [Google Scholar] [CrossRef]
J. S. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics 1, 195–200 (1964).
Aspect, A.; Dalibard, J.; Roger, G. Experimental Test of Bell's Inequalities Using Time- Varying Analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef]
Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef]
Shalm, L.K.; Meyer-Scott, E.; Christensen, B.G.; Bierhorst, P.; Wayne, M.A.; Stevens, M.J.; Gerrits, T.; Glancy, S.; Hamel, D.R.; Allman, M.S.; et al. Strong Loophole-Free Test of Local Realism. Phys. Rev. Lett. 2015, 115, 250402–250402. [Google Scholar] [CrossRef]
Giustina, M.; Versteegh, M.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.; Abellán, C.; et al. Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef]
Bennett, C.H.; Wiesner, S.J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881–2884. [Google Scholar] [CrossRef]
Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
K. Ekert, “Quantum cryptography based on Bell’s theorem,” Physical Review Letters 67, 661–663 (1991).
Schrödinger, E. Discussion of Probability Relations between Separated Systems. Math. Proc. Camb. Philos. Soc. 1935, 31, 555–563. [Google Scholar] [CrossRef]
Zeilinger, M. Zukowski, M. Aspelmeyer, et al., “Experimental long-distance quantum communication with entangled photons,” Nature 390, 575–579 (1997).
Liao, S.-K.; Cai, W.-Q.; Liu, W.-Y.; Zhang, L.; Li, Y.; Ren, J.-G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.-P.; et al. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef]
M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press (2000).
S. Ryu and T. Takayanagi, “Holographic Derivation of Entanglement Entropy from AdS/CFT,” Physical Review Letters 96, 181602 (2006).
M. Van Raamsdonk, “Building up spacetime with quantum entanglement,” General Relativity and Gravitation 42, 2323–2329 (2010).
Landauer, R. Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
Sagawa, T.; Ueda, M. Second Law of Thermodynamics with Discrete Quantum Feedback Control. Phys. Rev. Lett. 2008, 100, 080403. [Google Scholar] [CrossRef]
Maldacena, J.; Susskind, L. Cool horizons for entangled black holes. Fortschritte der Phys. 2013, 61, 781–811. [Google Scholar] [CrossRef]
Swingle, B. Entanglement renormalization and holography. Phys. Rev. D 2012, 86. [Google Scholar] [CrossRef]
Feinberg, G. Possibility of Faster-Than-Light Particles. Phys. Rev. B 1967, 159, 1089–1105. [Google Scholar] [CrossRef]
D. Colladay and V. A. Kostelecký, “CPT violation and the Standard Model,” Phys. Rev. D 55, 6760–6774 (1997); “Lorentz-violating extension of the Standard Model,” Phys. Rev. D 58, 116002 (1998).
Mattingly, D.; Jacobson, T. RELATIVISTIC GRAVITY WITH A DYNAMICAL PREFERRED FRAME. Proceedings of the Second Meeting. LOCATION OF CONFERENCE, USADATE OF CONFERENCE; pp. 331–335.
Hořava, P. Quantum gravity at a Lifshitz point. Phys. Rev. D 2009, 79, 084008. [Google Scholar] [CrossRef]
D. Bohm, “A Suggested Interpretation of the Quantum Theory in Terms of ‘Hidden’ Variables I & II,” Phys. Rev. 85, 166–193 (1952).
Ghirardi, G.C.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470–491. [Google Scholar] [CrossRef] [PubMed]
J. Polchinski, “Weinberg’s Nonlinear Quantum Mechanics and the EPR Paradox,” Phys. Rev. Lett. 66, 397–400 (1991); N. Gisin, “Weinberg’s non-linear quantum mechanics and superluminal communications,” Phys. Lett. A 143, 1–2 (1990).
S. Popescu and D. Rohrlich, “Quantum nonlocality as an axiom,” Found. Phys. 24, 379–385 (1994).
Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
Breuer, H.-P. , & Petruccione, F. (2002). The theory of open quantum systems. Oxford University Press.
Uhlenbeck, G. E., & Ornstein, L. S. (1930). On the theory of the Brownian motion. Physical Review, 36(5), 823–841.
Josephson, B. Possible new effects in superconductive tunnelling. Phys. Lett. 1962, 1, 251–253. [Google Scholar] [CrossRef]
Shapiro, S. Josephson Currents in Superconducting Tunneling: The Effect of Microwaves and Other Observations. Phys. Rev. Lett. 1963, 11, 80–82. [Google Scholar] [CrossRef]
Hasan, M. Z. , & Kane, C. L. (2010). Colloquium: Topological insulators. Reviews of Modern Physics, 82(4), 3045–3067.
Qi, X.-L., & Zhang, S.-C. (2011). Topological insulators and superconductors. Reviews of Modern Physics, 83(4), 1057–1110.
Boyd, R. W. (2008). Nonlinear optics (3rd ed.). Academic Press.
Mandel, L. , & Wolf, E. (1995). Optical coherence and quantum optics. Cambridge University Press.
Klyshko, D. N. (1988). Photonics: An introduction to quantum optics. Springer.
Pound, R.V.; Rebka, G.A. Apparent Weight of Photons. Phys. Rev. Lett. 1960, 4, 337–341. [Google Scholar] [CrossRef]
Hafele, J.C.; Keating, R.E. Around-the-World Atomic Clocks: Predicted Relativistic Time Gains. Science 1972, 177, 166–168. [Google Scholar] [CrossRef] [PubMed]
Chou, C.W.; Hume, D.B.; Rosenband, T.; Wineland, D.J. Optical Clocks and Relativity. Science 2010, 329, 1630–1633. [Google Scholar] [CrossRef]
Cronin, A.D.; Schmiedmayer, J.; Pritchard, D.E. Optics and interferometry with atoms and molecules. Rev. Mod. Phys. 2009, 81, 1051–1129. [Google Scholar] [CrossRef]
van Wees, B.J.; van Houten, H.; Beenakker, C.W.J.; Williamson, J.G.; Kouwenhoven, L.P.; van der Marel, D.; Foxon, C.T. Quantized conductance of point contacts in a two-dimensional electron gas. Phys. Rev. Lett. 1988, 60, 848–850. [Google Scholar] [CrossRef]
A Wharam, D.; Thornton, T.J.; Newbury, R.; Pepper, M.; Ahmed, H.; Frost, J.E.F.; Hasko, D.G.; Peacock, D.C.; A Ritchie, D.; Jones, G.A.C. One-dimensional transport and the quantisation of the ballistic resistance. J. Phys. C: Solid State Phys. 1988, 21, L209–L214. [Google Scholar] [CrossRef]
Patt, B. , & Wilczek, F. (2006). Higgs-field portal into hidden sectors. arXiv preprint hep-ph/0605188.
Murray, J. D. (2002). Mathematical biology I: An introduction (3rd ed.). Springer.
Holevo, A. The capacity of the quantum channel with general signal states. IEEE Trans. Inf. Theory 1998, 44, 269–273. [Google Scholar] [CrossRef]
Schumacher, B.; Westmoreland, M.D. Sending classical information via noisy quantum channels. Phys. Rev. A 1997, 56, 131–138. [Google Scholar] [CrossRef]
Shannon, C. E. (1948). A mathematical theory of communication. Bell System Technical Journal, 27(3), 379–423; 27(4), 623–656.
Hawking, S.W.; Ellis, G.F.R.; Sachs, R.K. The Large Scale Structure of Space-Time . Phys. Today 1974, 27, 91–93. [Google Scholar] [CrossRef]
Bilaniuk, O.-M.; Sudarshan, E.C.G. Particles beyond the light barrier. Phys. Today 1969, 22, 43–51. [Google Scholar] [CrossRef]
Recami, E. How to recover causality in special relativity for tachyons. Found. Phys. 1978, 8, 329–340. [Google Scholar] [CrossRef]
quantum gravity: an additional fine-tuning problem?” Physical Review Letters 93, 191301 (2004).
R. Jackiw and V. A. Kostelecký, “Radiatively induced Lorentz and CPT violation in electrodynamics,” Physical Review Letters 82, 3572–3575 (1999).
Chung, J.-M. Radiatively-induced Lorentz and CPT violating Chern–Simons term in QED. Phys. Lett. B 1999, 461, 138–141. [Google Scholar] [CrossRef]
L.-C. Tu, J. L.-C. Tu, J. Luo, and G. T. Gillies, “The mass of the photon,” Reports on Progress in Physics 68 (2005) 77–130.
S. Hild et al., Classical and Quantum Gravity 28, 094013 (2011) [Einstein Telescope]; D. Reitze et al., Bull. Am. Astron. Soc. 51 (2019) [LIGO-Cosmic Explorer].
Castelvecchi, D. China's quantum satellite clears major hurdle on way to ultrasecure communications. Nature 2017. [CrossRef]
Hild, S.; Abernathy, M.; Acernese, F.; Amaro-Seoane, P.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. Sensitivity studies for third-generation gravitational wave observatories. Class. Quantum Gravity 2011, 28. [Google Scholar] [CrossRef]
D. Reitze, R. X. D. Reitze, R. X. Adhikari, S. Ballmer, B. Barish, L. Barsotti, G. Billingsley, D. A. Brown, Y. Chen, D. Coyne, R. Eisenstein, M. Evans, P. Fritschel, V. Frolov, K. Kawabe, J. Kissel, W. K. Kells, J. Miller, J. Ottaway, H. Yamamoto, and D. Shoemaker, “The U.S. Program in Ground-based Gravitational-wave Science: Cosmic Explorer,” Bulletin of the American Astronomical Society 51, 035 (2019).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

The Lugon Framework; Informational Foundations of Physical Law; Part I—A Sequestered Informational Sector and Its Compatibility with Relativistic and Quantum Physics

Abstract

Keywords:

Subject:

Appendix A. Notation and Conventions

Appendix B. Experimental Data-Analysis Recipes

Appendix C. Relation to Quantum Gravity and Holography (Extended)

Appendix D. Falsification Matrix

Appendix E. Open Questions and Future Directions

Appendix F. Gate Function Physics – Creation, Control, and Models

References

MDPI Initiatives

Important Links

Subscribe