1. Introduction
Fish passes are essential structures ensuring the longitudinal connectivity of river systems, enabling fish migration across artificial barriers such as dams and weirs [
1,
2,
3,
4]. The design of these systems is guided by several European standards and recommendations, among which the DVWK [
5] is one of the most influential, providing detailed criteria on admissible flow velocities and geometrical configurations.
Defining target species is a key prerequisite in fishway design, as fish exhibit diverse swimming abilities, behavioral patterns, and hydraulic preferences. For rheophilic species such as
Salmo trutta fario (brown trout), moderate flow velocities (0.3–1.5 m/s) and adequate resting pools are required, whereas for sedentary or benthic species like
Cottus gobio, flow uniformity and low turbulence are critical [
6].
This paper presents a numerical hydraulic analysis of several configurations of technical pool-type fishways using three-dimensional CFD modeling, with a focus on structures designed for mountain rivers with moderate slopes (~4.5%), aiming to optimize hydraulic conditions for trout species.
2. Materials and Methods
The hydraulic analysis was carried out using the finite element method applied to fluids (Computational Fluid Dynamics – CFD). The three-dimensional flow modeling was conducted in ANSYS Fluent, based on the Navier–Stokes equations for turbulent flow, using the Reynolds-Averaged Navier–Stokes (RANS) approach with the standard k–ε turbulence model.
Boundary conditions included a constant inflow discharge representative of mountainous catchments (Q = 0.08 m³/s), a pressure outlet free surface, and no-slip lateral boundaries. Four geometric variants were analyzed, differing in the number and dimensions of internal baffles and slot openings.
Results were evaluated in terms of flow velocity distributions and streamline patterns, with particular attention to high-velocity zones and resting areas relevant for fish passage efficiency.
Theoretical Background
The numerical modeling of the flow was performed based on the fundamental equations of fluid mechanics, namely the continuity and Navier–Stokes equations for turbulent flow, solved in the Reynolds-averaged form (RANS).
Reynolds-averaged momentum equation (Navier–Stokes) [
7]:
where:
, represent the components of the mean velocity;
, represent the mean pressure;
, represent the fluid density;
, represent the dynamic viscosity;
, represent the Reynolds stress terms, modeled using a turbulence model.
To close the system of equations, the
standard k–ε turbulence model was employed, introducing two additional equations for the turbulent kinetic energy
and its dissipation rate
[
7]:
where,
, is the turbulent viscosity.
The constant values used were:
; ; ; ; .
3. Case Study and Results
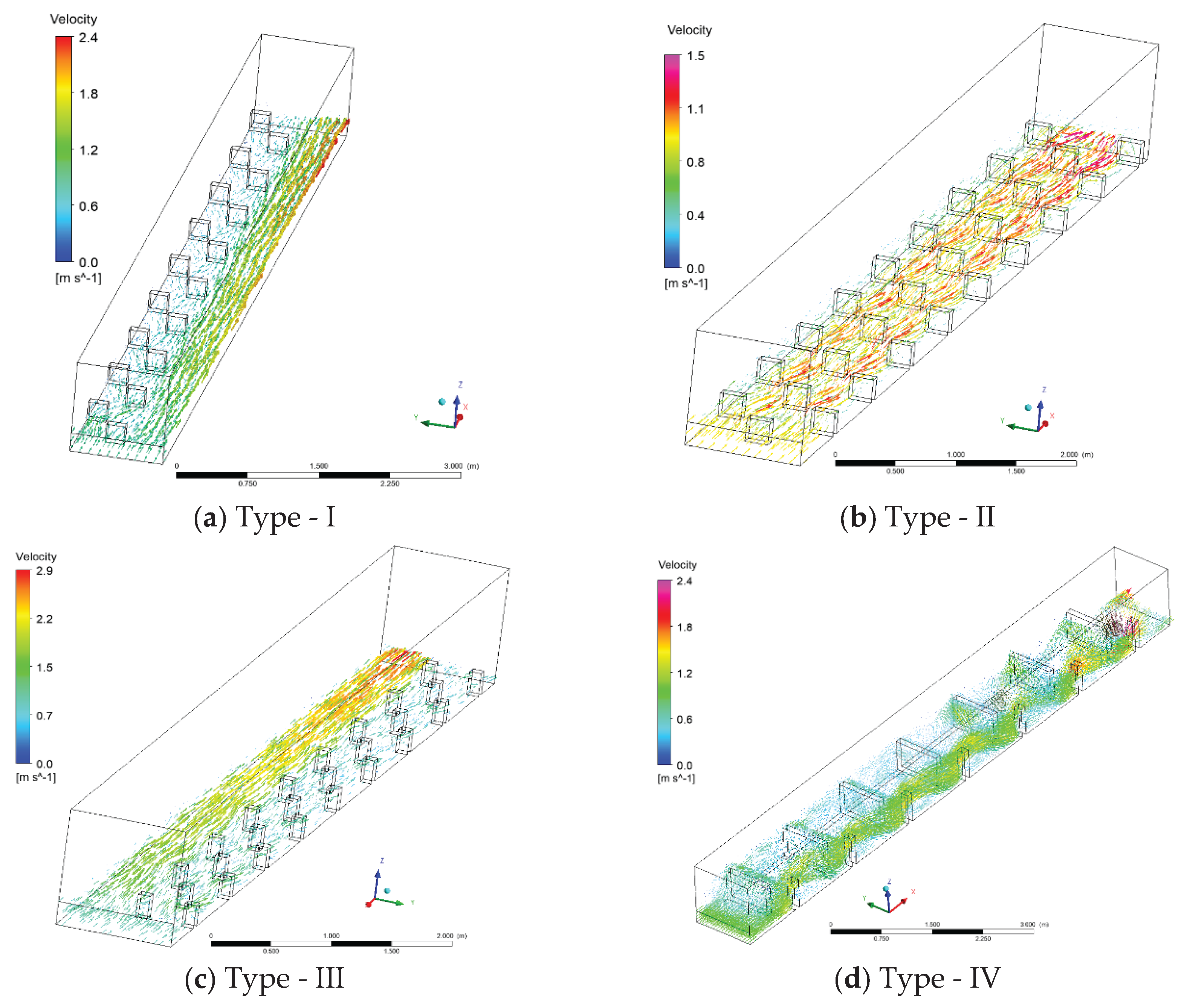
The CFD simulations were conducted for four pool-type fishway configurations, each 10 m long and 1.0 m wide, with a longitudinal slope of 4.5%.
- -
Variant 1: Two rows of internal baffles (20×20 cm); 1.0 m spacing.
- -
Variant 2: Three rows of baffles (20×20 cm); 1.0 m spacing.
- -
Variant 3: Three rows of baffles (20×10 cm); 1.0 m spacing.
- -
Variant 4: Three rows of baffles (50×75 cm; 50×12.5 cm); 1.25 m spacing.
The three-dimensional modeling was performed in ANSYS Fluent, using the finite volume method for the discretization of the control volume. The computational domain was divided into approximately 450,000–600,000 tetrahedral cells, refined in the slot areas and around the weirs, where the velocity gradient is highest.
Boundary conditions were defined as follows:
- -
Inlet: constant inflow Q=0.08 m3/s, uniformly distributed;
- -
Outlet: pressure outlet condition (atmospheric pressure);
- -
Walls: no-slip condition (u=0, at wall contact);
- -
Free surface: treated as a symmetry plane to ensure numerical stability.
For each geometric configuration, the following parameters were analyzed:
- -
velocity field ;
- -
maximum velocity in the slot ();
- -
stagnation zones (velocities < 0.3 m/s);
- -
specific turbulence (via the k parameter);
- -
total pressure distribution ().
Based on these parameters, the configurations satisfying the
DVWK-M 232 (1996) [
8] recommendations for trout were identified, namely:
,
,
.
Significant differences in maximum velocity distribution were observed, ranging from 0.65 m/s to 1.35 m/s, depending on slot geometry and baffle height. Variants 2 and 3 provided the most favorable hydraulic patterns for Salmo trutta fario, ensuring moderate flow velocities and resting zones, while Variant 4 exhibited pronounced turbulence and less favorable flow conditions.
Figure 1 shows the analyzed constructive solutions.
4. Discussions
The comparative CFD analysis revealed that increasing the number of baffles leads to smoother energy dissipation and more uniform velocity fields. For Salmo trutta fario, sustained swimming velocities between 0.4–1.2 m/s and short-term maxima up to 1.8 m/s are acceptable. Variants 2 and 3 met these conditions, providing continuous passage zones and resting areas (v < 0.3 m/s). Variant 4 exhibited strong recirculations and local velocity peaks exceeding 1.4 m/s, potentially harmful to juvenile fish.
The CFD results confirm DVWK and FAO [
9,
10] design recommendations, emphasizing the need for controlled turbulence and energy gradients to maintain biological efficiency. Streamline visualization indicated that longitudinal, low-turbulence flow paths correspond to higher passage efficiency (E > 85%), while chaotic flow structures reduce fish orientation and success rates.
5. Conclusions
The CFD analysis confirmed that multi-baffle fishways with narrow longitudinal slots provide the most suitable hydraulic conditions for trout migration in mountain regions.
Future research should address other sedentary or less mobile species, such as Cottus gobio, by optimizing slot geometry and reducing slope gradients.
CFD modeling has proven to be an effective tool for fishway design optimization, enabling realistic flow representation and biologically informed engineering design.
References
- Čubanová, L.; Rumann, J.; Vidová, A.; Almikaeel, W.; Rebenda, F. Verification of Hydraulic Parameters of Nature-like Fish Pass. Water 2023, 15, 2478. [CrossRef]
- Brandl, A.; Laaha, G.; Käfer, S.; Mader, H. Key Factors for the Findability of Fish Passes in Large Epipotamal Rivers: The Case of the River Drava. Water 2022, 14, 1530. [CrossRef]
- Hämmerling, M.; Kałuża, T.; Tymiński, T.; Plesiński, K. The Use of a Multi-Criteria Decision Analysis Method to Select the Most Favourable Type of Fish Pass in Mountainous Areas. Water 2024, 16, 3118. [CrossRef]
- Turker, M.S.; Kucukali, S. Creating Micro-Habitat in a Pool-Weir Fish Pass with Flexible Hydraulic Elements: Insights from Field Experiments. Water 2025, 17, 2294. [CrossRef]
- Fritsch, P. et al. (2011). Wassergewinnung. In: Mutschmann/Stimmelmayr Taschenbuch der Wasserversorgung. Vieweg+Teubner. [CrossRef]
- UTZINGER, J., ROTH, C. and PETER, A. (1998), Effects of environmental parameters on the distribution of bullhead Cottus gobio with particular consideration of the effects of obstructions. Journal of Applied Ecology, 35: 882-892. [CrossRef]
- Hurnik, M.; Ciuman, P.; Popiolek, Z. Eddy–Viscosity Reynolds-Averaged Navier–Stokes Modeling of Air Distribution in a Sidewall Jet Supplied into a Room. Energies 2024, 17, 1261. [CrossRef]
- DVWK, 1996. Fischaufstiegsanlagen – Bemessung, Gestaltung, Funktionskontrolle, Merkblatt 232.
- FAO/DVWK Fish passes – Design, dimensions and monitoring. Rome, FAO. 2002. 119p.
- Larinier, Michel & G, MARMULLA. (2004). Fish passes: types, principles and geographical distribution - an overview. Proceedings of the Second International Symposium on the Management of Large Rivers for Fisheries. 2.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).