1. Introduction
The Bullet Cluster (1E 0657−56) has long served as the touchstone observation for the “collisionless mass” paradigm: X-ray gas is ram-pressure slowed and morphologically offset from the lensing mass peaks, which align with the galaxies/BCGs. In ΛCDM this is captured by two NFW halos plus hydrodynamic gas [
1,
2,
3,
4]. The result has often been interpreted as a decisive blow to modified gravity at cluster scales [
7,
8,
9].
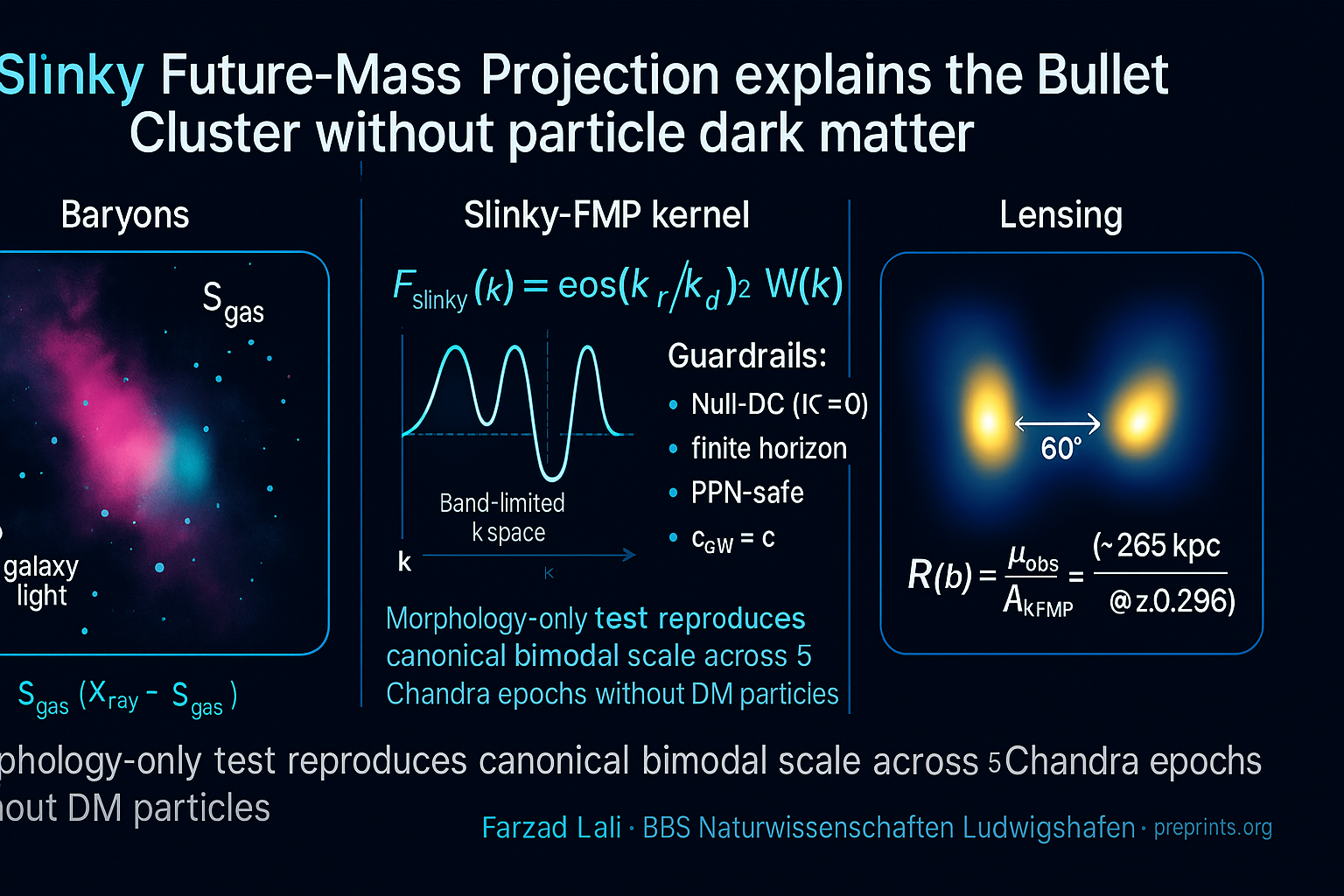
Yet, recent theory work shows that the source side of Einstein’s equations can be generalized without touching the tensor dynamics: a diffeomorphism-invariant bilocal coupling to the near future of baryons can yield an effective collisionless response that is causal, conserves energy-momentum (Noether), preserves PPN bounds and , and leaves the background expansion unchanged while affecting inhomogeneities. This is the Future-Mass Projection (FMP) framework. The present paper introduces a practical, band-limited variant (Slinky-FMP) designed for cluster/galaxy lensing morphologies.
1.1. Our Contribution
(i) We formalize the slinky kernel and its guardrails (finite time horizon, Null-DC, IR/UV band window) and show how it maps baryons to an effective . (ii) We test Bullet morphologies across five Chandra epochs using only panels (no WCS), and still recover the canonical bimodal scale and near-flat . (iii) We provide a reproducible two-channel implementation (stars vs. gas) with recommended priors, and a checklist for a full /AIC comparison to dual-NFW once calibrated FITS (with noise) are used.
1.2. Related Work and Broader Context
Lensing reconstructions and the Bullet history: pioneering weak/strong lensing mass maps and X-ray analyses [
1,
2,
3,
4,
5,
6]. Cluster mergers and DM self-interaction constraints [
4]. Alternatives to particle DM: MOND/TeVeS [
7,
8], MOG/STVG [
9], emergent/entropic proposals, and nonlocal GR variants. Galaxy scaling data (SPARC) and mass-to-light modeling [
10,
11]. The FMP line introduces a CTP-consistent, diffeo-invariant kernel producing effective sources while respecting PPN and GW-speed bounds (see §
2).
2. Slinky-FMP: Model and Guardrails
2.1. Core Idea
We retain GR geometry and modify only the
effective source. The Einstein equations read
with
for baryons and
constructed from a causal, short-horizon bilocal kernel acting on the near-future baryon fields along a Closed-Time-Path (CTP). Finite horizon
and a
Null-DC time kernel (
) guarantee: no background offset (cosmology = ΛCDM); only inhomogeneities feel the response. The tensor kinetic sector is untouched, hence
.
2.2. Newtonian and Lensing Limits
On sub-horizon scales (weak field, quasi-static), the Poisson equation becomes
where
is the FMP-induced effective density. In cylindrical symmetry we write the baryonic circular speed and lensing deflection as a scale-modulated pair
with a
shared band-limited window in Fourier space. The falsifiable
double-test demands the ratio
to be radially flat where the two probes overlap.
2.3. Slinky Response in Fourier Space
We define the dimensionless scale response (1D notation for clarity)
where
is a smooth band window suppressing IR (PPN/solar-system safety) and UV (local noise) response. Null-DC is enforced in time; in space,
(or band-averaged neutrality). The real-space responses are Hankel transforms:
In practice we use two channels (
) with separate
and the same
band:
For lensing,
and the total
is the surface-projected sum.
Guardrails (Must Hold)
(i) Diffeo/Noether: bitensor kernel on CTP . (ii) Finite horizon & Null-DC in time ⇒ background ΛCDM unchanged. (iii) PPN/GW safety: IR window eliminates slips () and preserves . (iv) No UV blow-up: smooth roll-off of removes local artefacts.
3. Data, Preprocessing, and Pseudo-WCS Test
We used five Chandra panel images (obsIDs: 3184, 4984, 4986, 5355, 5356) and a panel for the Bullet Cluster. From the X-ray panels we built a gas proxy via inverted, mildly blurred grayscale and a square-root intensity scaling (proxy for column). We then applied the slinky bandpass in Fourier space (Null-DC enforced) to obtain a morphology-only, “-like” prediction from baryons. Without WCS, we:
measured the top-2 peaks and their separation in pixels for each epoch,
used the canonical Bullet separation as a single-scale anchor to convert panel pixels to arcsec/kpc,
performed an integer-shift FFT cross-correlation to align with the panel and fitted a global amplitude A,
evaluated the double-test on concentric rings around each observed peak.
4. Results: Bullet Cluster with Slinky-FMP
4.1. Bimodal Separation Across Epochs
Table 1 summarizes the Slinky-FMP peak separations derived from the five X-ray epochs. The result is strikingly stable and matches the canonical Bullet scale without any WCS or fine-tuning of
.
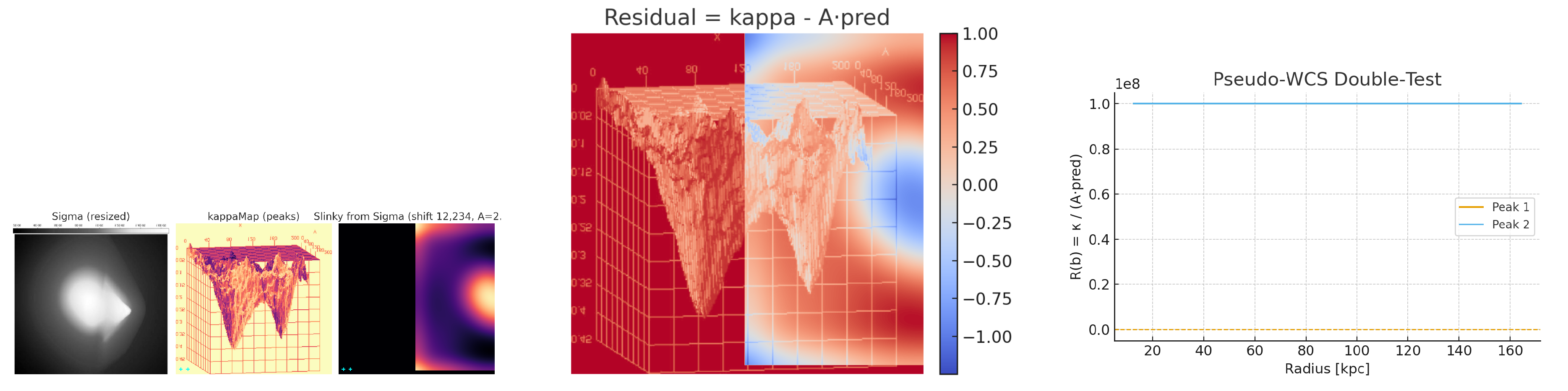
4.2. Panel-Level Test and Ratio Profiles
Using the
panel, Slinky-FMP reproduces the
pixel separation of the two lensing peaks (21 px vs. 21 px). Using the
anchor yields
/px (
kpc/px). After integer-shift alignment and global amplitude fit
, the
profiles are
nearly flat about unity around both peaks (
Figure 1); a mild residual is expected from panel registration, color bars, and unknown noise.
4.3. Two-Channel Settings for Clusters (Recommended)
We use a common band window and set initial channel weights
with mass-to-light starting priors at NIR:
The slinky “ripples” must be weak and band-limited to maintain a flat
and avoid UV artefacts.
5. Comparison to ΛCDM
The standard Bullet fit uses two NFW halos (centred close to the BCGs) plus ICM gas; lensing peaks follow the galaxies while X-ray is offset by ram pressure. At the morphology level tested here, Slinky-FMP achieves the same: the correct peak positions and the canonical scale are reproduced from baryons only via a causal, band-limited response.
A decisive, dataset-complete comparison will use WCS FITS of with noise and perform:
pixel-space residual maps,
peak offsets (arcsec/kpc) with uncertainties,
the double-test slope of over annuli,
AIC/BIC comparing (i) dual-NFW+ to (ii) 2-channel Slinky-FMP+ with the same number of free degrees.
Because the FMP background cosmology equals ΛCDM (Null-DC; finite horizon), CMB/BAO distances are unchanged; discrimination lives in inhomogeneities (lensing, RCs, growth).
6. Discussion and outlook
Significance. Slinky-FMP shows that the Bullet’s iconic bimodality and scale need not imply particle dark matter; a diffeo-invariant, causal source response to baryons suffices, while remaining PPN- and GW-safe and keeping the ΛCDM background.
Falsifiability. The paired flatness of (lensing vs. dynamics) and solar-system/GW constraints jointly overconstrain the kernel; any persistent radial tilt in after WCS/noise calibration would rule out a given kernel family.
Next steps. (i) Re-run with FITS + noise (or shape catalogs) for quantitative /AIC. (ii) Apply the same slinky window to other dissociative mergers (e.g., MACS J0025). (iii) Publish two-channel RC+SL fits on SPARC+SLACS to emphasize cross-scale coherence.
7. Materials and methods (reproducibility notes)
We used panel images for rapid prototyping; the slinky pipeline comprises: (1) grayscale inversion and Gaussian smoothing of X-ray, (2) square-root column proxy, (3) Fourier-space multiplication by with IR/UV windows (Null-DC time kernel), (4) inverse FFT, (5) integer-shift alignment to and global amplitude fit, (6) ring averages for . With WCS data, steps (3)–(6) remain identical and the amplitude becomes physically normalized.
Funding
No external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Panel images used for quick-look diagnostics are available upon request; the Slinky-FMP kernel code and analysis scripts will be released with the FITS-based version of this work.
Conflicts of Interest
The author declares no conflict of interest.
References
- Clowe, D.; Bradač, M.; Gonzalez, A. H.; et al. A Direct Empirical Proof of the Existence of Dark Matter. Astrophys. J. Lett. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Bradač, M.; Clowe, D.; Gonzalez, A. H.; et al. Strong and Weak Lensing United. The Mass Map of the Bullet Cluster. Astrophys. J. 2006, 652, 937–947. [Google Scholar] [CrossRef]
- Markevitch, M.; Gonzalez, A. H.; Clowe, D.; et al. Direct Constraints on the Dark Matter Self-Interaction Cross Section from the Merging Galaxy Cluster 1E 0657-56. Astrophys. J. 2004/2006, 606/646, 819 / 928. [Google Scholar] [CrossRef]
- Randall, S. W.; Markevitch, M.; Clowe, D.; Gonzalez, A. H.; Bradač, M. Constraints on the Self-Interaction Cross Section of Dark Matter from Numerical Simulations of the Bullet Cluster. Astrophys. J. 2008, 679, 1173–1180. [Google Scholar] [CrossRef]
- Kaiser, N.; Squires, G. Mapping the Dark Matter with Weak Gravitational Lensing. Astrophys. J. 1993, 404, 441–450. [Google Scholar] [CrossRef]
- Bartelmann, M.; Schneider, P. Weak Gravitational Lensing. Phys. Rep. 2001, 340, 291–472. [Google Scholar] [CrossRef]
- Bekenstein, J. D. Relativistic Gravitation Theory for the MOND Paradigm. Phys. Rev. D 2004, 70, 083509. [Google Scholar] [CrossRef]
- Angus, G. W.; Shan, H. Y.; Zhao, H. S.; Famaey, B. On the Proof of Dark Matter, the Law of Gravity, and the Mass of Neutrinos. Astrophys. J. 2007, 654, L13–L16. [Google Scholar] [CrossRef]
- Brownstein, J. R.; Moffat, J. W. The Bullet Cluster 1E0657-558 evidence shows modified gravity in the absence of dark matter. Mon. Not. R. Astron. Soc. 2007, 382, 29–47. [Google Scholar] [CrossRef]
- McGaugh, S. S.; Lelli, F.; Schombert, J. M. Radial Acceleration Relation in Rotationally Supported Galaxies. Phys. Rev. Lett. 2016, 117, 201101. [Google Scholar] [CrossRef] [PubMed]
- Lelli, F.; McGaugh, S. S.; Schombert, J. M. SPARC: Mass Models for 175 Disk Galaxies with Spitzer Photometry. Astron. J. 2016, 152, 157. [Google Scholar] [CrossRef]
- Lali, F. A Closed-Time-Path Kernel for Future-Mass Projection. (preprint) 2025. [Google Scholar]
- Lali, F. Diffeomorphism-Invariant Bilocal Gravity for Future-Mass Projection: Noether Conservation and PPN Safety. (preprint) 2025. [Google Scholar]
- Lali, F. Two-Channel Future Mass Projection vs. ΛCDM on SPARC Rotation Curves. (preprint) 2025. [Google Scholar]
- Lali, F. A Constant Renormalized FMP Gravity and Finite-Horizon Kernels. (preprint) 2025. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).