A Characterization of the Logistic q-Distribution

1. Introduction

Quantum calculus, which stands for a contemporary field of study, addresses the principles of calculus without the traditional reliance on limits. Over the recent years, several research works have been oriented towards q-calculus [1,2,3,4,5], a branch of mathematics that bridges the gap between mathematical theory and physical applications. The origins of quantum calculus date back to the pioneering work of F.H. Jackson [5] in the early 20Th century. A comprehensive overview of the fundamental concepts of quantum calculus is displayed in the book written by Kac and Cheung [11]. Chung et al. [13] introduced the q-addition operator and explored its properties, subsequently applying it to the study of the q-logarithmic and q-exponential functions [17]. The applications of quantum calculus extend to a wide range of mathematical domains, including number theory, difference equations (as exemplified in [6]), orthogonal polynomials, and probability theory.

Within the framework mathematical physics and probability, the q-distribution transcends classical distributions in terms of generality. Diaz [15] introduced this concept in the continuous domain, while Charalambos [3] extended it to the discrete domain. The q-distribution entails constructing a q-analogue of the conventional distribution. Mathai [8] examined the q-analogue of the gamma distribution as far as Lebesgue measure is concerned.

The central target of this paper is to establish a quantum representation for the standard logistic distribution within the framework of quantum calculus logistic q–distribution noted by q–L$(0,1)$. This representation is particularly designed for the interval ${\mathbb{R}}_q=[-{\delta }_q,{\delta }_q]$, the q–analogue of $\mathbb{R}$, where 0 denotes the location parameter and 1 designates the scale parameter.

At this level, the value of ${\delta }_q$ is determined by the formula ${\delta }_q={\displaystyle \frac{1}{1-q}}$, with q being a fixed number falling within the range of 0 to 1 and ${\delta }_q$ being the q–analogue of $+\infty$ in quantum calculus.

As q approaches 1, the representation converges back to the ordinary logistic distribution.

To achieve the quantum representation of the logistic distribution, we need to find the q-analogues of key elements: $\mathrm{d}x$, ${\displaystyle \frac{{\mathrm{e}}^x}{{(1+{\mathrm{e}}^x)}^2}}$, and 1.

Jackson in [5,6] set forward the q-analogue of the exponential function $e^x$ determined by

$$e_q^x=\sum _{n=0}^{\infty }{\displaystyle \frac{x^n}{{\left[n\right]}_q!}},$$

and

$$\begin{array}{c}\hfill {\left[n\right]}_q!=\left\{\begin{array}{cc}1\hfill & \mathrm{if}n=0,\hfill \\ {\displaystyle {\left[n\right]}_q{[n-1]}_q\dots {\left[1\right]}_q}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(1)

It is clear that $e_q^0=1$, implying that it is based on the convention $0^0=1,$ and $D_q{e}_q^x=e_q^x.$

Then, the q-analogue of the function ${\displaystyle \frac{{\mathrm{e}}^x}{{(1+{\mathrm{e}}^x)}^2}}$ is determined by function ${\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}$, while the Lebesgue measure $dx$ is replaced with the Jackson measure $d_{q}x$. To represent 1 in the quantum context, we introduce a new function named $c\left(q\right)=1+{\mathrm{e}}_q^{-{\delta }_q}$. By accomplishing these steps, we establish the desired quantum representation of the Logistic distribution, offering deeper insights into the interplay between quantum calculus and traditional ones.

The q–analogue of the Riemann integral in quantum calculus is provided by the Jackson integral, also known as q–integral. Using the q–integral and the q–analog of the classical exponential function, denoted by ${\displaystyle E_q^x=\sum _{j=0}^{+\infty }{q}^{j(j-1)/2}\frac{x^j}{\left[j\right]!}}$, we can introduce a new definition of the Fourier transform in quantum calculus, called the q–Fourier transform. At this stage, q is a real number lying strictly between 0 and $1(0<q<1)$.

The q–Fourier transform plays a crucial role in characterizing the logistic q–distribution, denoted by $q–L(0,1)$. Furthermore, we can invest solutions in q–differential equations to further demonstrate the characterization of this distribution.

In $\left[y\right]$, the density of the exponential q–distribution ${\xi }_q\left(\lambda \right)$ is indicated by

$${\xi }_q\left(x\right)={\left[\lambda \right]}_q{E}_q^{-q{\left[\lambda \right]}_{q}x}{\mathbb{1}}_{[0,{\displaystyle \frac{1}{1-q}}]}\left(x\right),for\lambda >0,$$

and the q–cumulative function of the exponential q–distribution is expressed as

$$F_q\left(x\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{for}x<0,\hfill \\ 1-E_q^{-{\left[\lambda \right]}_{q}x},\hfill & \mathrm{for}0\le x\le {\delta }_q={\displaystyle \frac{1}{1-q}},\hfill \\ 1,\hfill & \mathrm{for}x>{\delta }_q={\displaystyle \frac{1}{1-q}}.\hfill \end{array}\right.$$

We recall certain basic definitions recorded in [5,6,8,12]. We fix a real number 0 < q < 1. We shall start with the q–derivative and the Jackson q–integral. The q–derivative of function $f:\mathbb{R}\to \mathbb{R}$ at $x\in \mathbb{R}0$ is determined in terms of

$$D_{q}f\left(x\right)={\displaystyle \frac{f\left(qx\right)-f\left(x\right)}{(q-1)x}}.$$

It is also known as the Jackson derivative. We notice that it is linear. In this respect,

$$D_q(f\left(x\right)+g\left(x\right))=D_{q}f\left(x\right)+D_{q}g\left(x\right).$$

It has a product rule analogous to the ordinary ones, with two equivalent forms:

$$D_q\left(f\left(x\right)g\left(x\right)\right)=g\left(x\right)D_{q}f\left(x\right)+f\left(qx\right)D_{q}g\left(x\right)=g\left(qx\right)D_{q}f\left(x\right)+f\left(x\right)D_{q}g\left(x\right).$$

Similarly, it satisfies a quotient rule,

$$D_q\left({\displaystyle \frac{f\left(x\right)}{g\left(x\right)}}\right)={\displaystyle \frac{g\left(x\right)D_{q}f\left(x\right)-f\left(x\right)D_{q}g\left(x\right)}{g\left(qx\right)g\left(x\right)}},g\ne 0.$$

For example the q–derive of function $x^n$ for an integer $n\ge 1$ is indicated by:

$$D_q{x}^n={\left[n\right]}_q{x}^{n-1},$$

where ${\left[n\right]}_q={\displaystyle \frac{q^n-1}{q-1}}=1+q+...+q^{n-1}.$

A right inverse of the q–derivative is obtained via the Jackson integral. For $a,b\in \mathbb{R}$ the Jackson integral or q–integral of the function $f:\mathbb{R}\to \mathbb{R}$ on $[a,b]$ is expressed as:

$$\begin{array}{c}\hfill {\int }_a^{b}f\left(x\right)d_{q}x=(1-q)\sum _{n=0}^{\infty }{q}^n\left(bf\left(q^{n}b\right)-af\left(q^{n}a\right)\right).\end{array}$$

It is clear that if q approaches 1, the q–derivative approaches the Newton derivative and the Jackson integral approaches the Riemann integral.

The q-analogue of the rule of integration by parts is provided in terms of:

$$\begin{array}{c}\hfill {\int }_a^{b}g\left(x\right)D_{q}f\left(x\right){\mathrm{d}}_{q}x={\left[f\left(x\right)g\left(x\right)\right]}_a^b-{\int }_a^{b}f\left(qx\right)D_{q}g\left(x\right){\mathrm{d}}_{q}x.\end{array}$$

2. Logistic q-Distribution

The basic purpose of this paragraph is to introduce the modeling of the probability density function of the logistic distribution within the framework of quantum calculus. The function representing this density is denoted as $f_q$ and is defined on the interval $[-{\delta }_q,{\delta }_q]$, where ${\delta }_q={\displaystyle \frac{1}{1-q}}$ is a specific parameter associated with the distribution.

We also know that

$${\mathrm{e}}_q^x=\prod _{k=0}^{+\infty }{\displaystyle \frac{1}{1-(1-q)q^{k}x}},$$

therefore

$$\begin{array}{cc}\hfill {\mathrm{e}}_q^{-{\displaystyle \frac{x}{(q-1)}}}& =\prod _{k=0}^{+\infty }{\displaystyle \frac{1}{1-q^{k}x}}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & \end{array}$$

(3)

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{1}{1-x}}\prod _{k=1}^{+\infty }{\displaystyle \frac{1}{1-q^{k}x}}.\hfill \end{array}$$

(4)

If x goes to 1, then we obtain

$${\mathrm{e}}_q^{-{\displaystyle \frac{x}{(q-1)}}}\to +\infty .$$

Hence,

$${\mathrm{e}}_q^{{\delta }_q}=+\infty ,\mathrm{and}{\delta }_q={\displaystyle \frac{1}{1-q}}.$$

From this perspective, we define the normalizing constant $c\left(q\right)$ by

$$c\left(q\right)=1+{\mathrm{e}}_q^{-{\delta }_q},\mathrm{and}{\delta }_q={\displaystyle \frac{1}{1-q}},\mathrm{for}0<q<1.$$

Proposition 1.

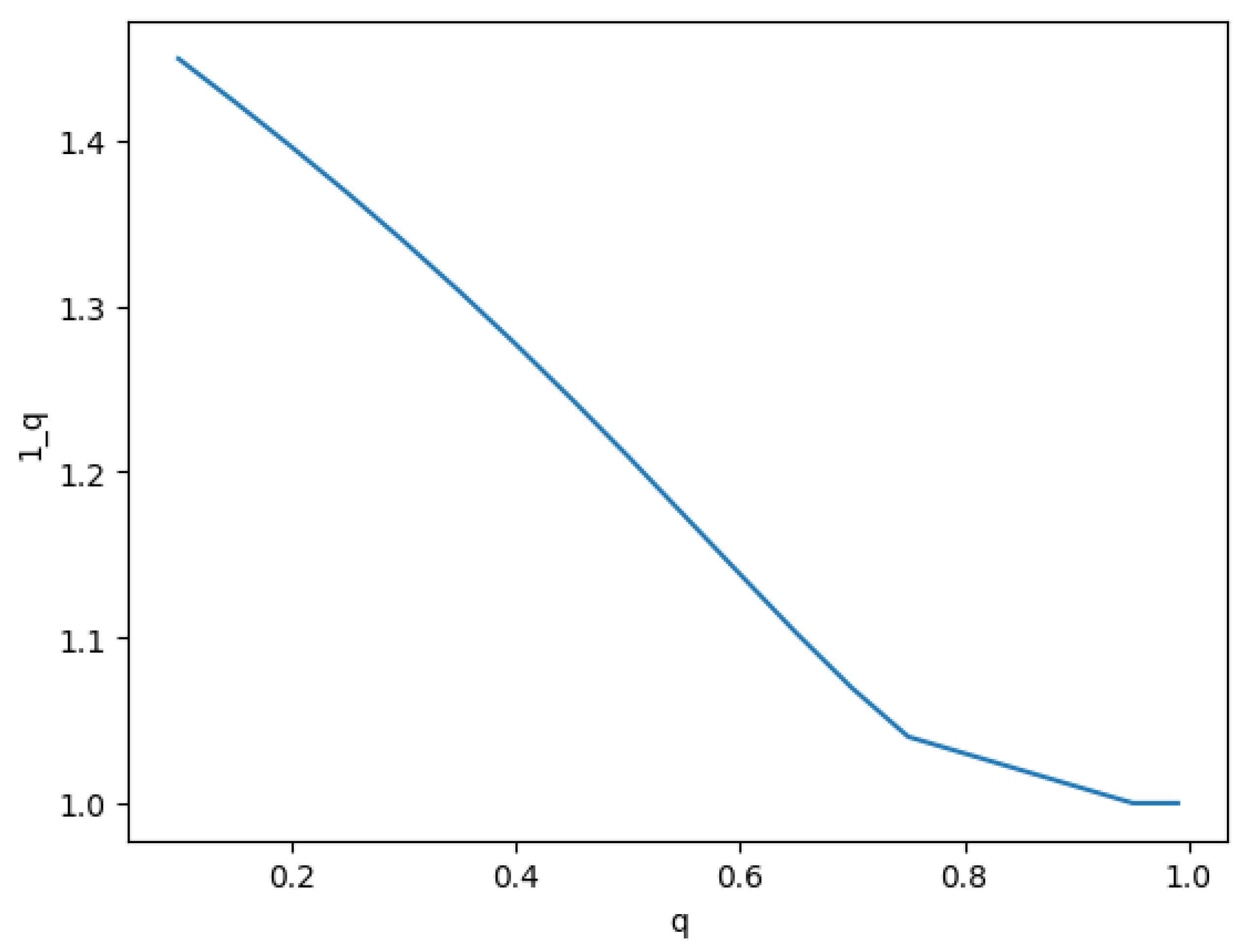
The normalization constant $c\left(q\right)$ tends to 1 as q approaches 1 with ${\delta }_q={\displaystyle \frac{1}{1-q}}$.

$$\underset{q\to 1}{lim}c\left(q\right)=\underset{q\to 1}{lim}1+{\mathrm{e}}_q^{-{\delta }_q}=1.$$

Démonstration. 

Since

$${\displaystyle {\mathrm{e}}_q^x=\prod _{k=0}^{+\infty }\frac{1}{1-(1-q)q^{k}x},}$$

then

$$\begin{array}{cc}\hfill \underset{q\to 1}{lim}{\mathrm{e}}_q^{-{\delta }_q}& =\underset{q\to 1}{lim}\left({\displaystyle \prod _{k=0}^{+\infty }\frac{1}{1+q^k}}\right)\hfill \\ \hfill & \\ \hfill & =\underset{n\to +\infty }{lim}\left(\underset{q\to 1}{lim}\prod _{k=0}^n{\displaystyle \frac{1}{1+q^k}}\right)\hfill \\ \hfill & \\ \hfill & =\underset{n\to +\infty }{lim}\left(\underset{q\to 1}{lim}\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{1}{1+q}}{\displaystyle \frac{1}{1+q^2}}\dots {\displaystyle \frac{1}{1+q^n}}\right)\right)\hfill \\ \hfill & \\ \hfill & =\underset{n\to +\infty }{lim}{\left({\displaystyle \frac{1}{2}}\right)}^n\hfill \\ \hfill & \\ \hfill & =0.\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill \underset{q\to 1}{lim}c\left(q\right)& =\underset{q\to 1}{lim}(1+{\mathrm{e}}_q^{-{\delta }_q})\hfill \\ \hfill & =1.\hfill \end{array}$$

□

Figure 1 depicts a plot of $c\left(q\right)$ as a function of q.

Figure 1. Plot of $c\left(q\right)$ as a function of q.

Figure 1. Plot of $c\left(q\right)$ as a function of q.

Note that c(q) approaches 1 as q goes to 1.

We are now prepared to formally introduce the logistic q–distribution.

Definition 1.

The probability q-density function of the standard logistic q-distribution, denoted by $f_q$, is specified by

$$f_q\left(x\right)=c\left(q\right){\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathbb{1}}_{]-{\delta }_q,{\delta }_q[}\left(x\right),\mathrm{for}{\delta }_q={\displaystyle \frac{1}{1-q}},(\mathit{refer}\mathit{to}\mathit{Figure}2)$$

and $c\left(q\right)=1+{\mathrm{e}}_q^{-{\delta }_q}$ for the normalizing constant.

Remark 1.

$$\begin{array}{cc}\hfill {\int }_{-{\delta }_q}^{{\delta }_q}{f}_q\left(x\right){\mathrm{d}}_{q}x& =c\left(q\right){\int }_{-{\delta }_q}^{{\delta }_q}{\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathrm{d}}_{q}x\hfill \\ \hfill & =c\left(q\right){\left[-{\displaystyle \frac{1}{1+{\mathrm{e}}_q^x}}\right]}_{-{\delta }_q}^{{\delta }_q}\hfill \\ \hfill & =c\left(q\right)\left({\displaystyle \frac{-1}{1+{\mathrm{e}}_q^{{\delta }_q}}}\right)+c\left(q\right)\left({\displaystyle \frac{1}{1+{\mathrm{e}}_q^{-{\delta }_q}}}\right)\hfill \\ \hfill & =0+1=1.\hfill \end{array}$$

3. Logistic q–Cumulative

The q-cumulative q-distribution function(q-cdf), of a real random variable X follows q-density $f_q\left(x\right)=c\left(q\right){\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathbb{1}}_{[-{\delta }_q,{\delta }_q]}\left(x\right)$, which is provided $F_q\left(t\right)={\mathbb{P}}_q(x\le t)={\int }_{-{\delta }_q}^t{f}_q\left(x\right){\mathrm{d}}_{q}x$, for $t\in [-{\delta }_q,{\delta }_q]$, ${\delta }_q={\displaystyle \frac{1}{1-q}}$.

Theorem 1.

The standard logistic q-distribution has a q-cumulative q-distribution function defined as follows

$$F_q\left(t\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{for}t<-{\delta }_q,\hfill \\ \\ 1-{\displaystyle \frac{c\left(q\right)}{1+{\mathrm{e}}_q^t}},\hfill & \mathrm{for}-{\delta }_q\le t\le {\delta }_q,\hfill \\ \\ 1,\hfill & \mathrm{for}t>{\delta }_q.\hfill \end{array}\right.(\mathit{refer}\mathit{to}\mathit{Figure}3)$$

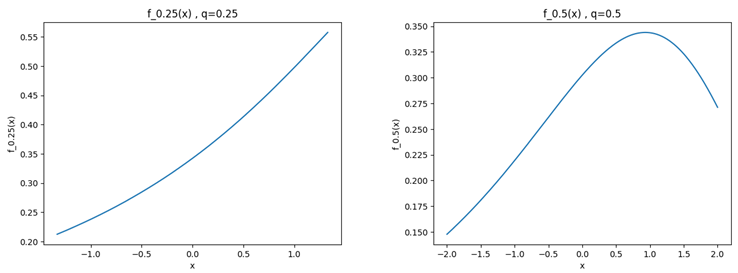
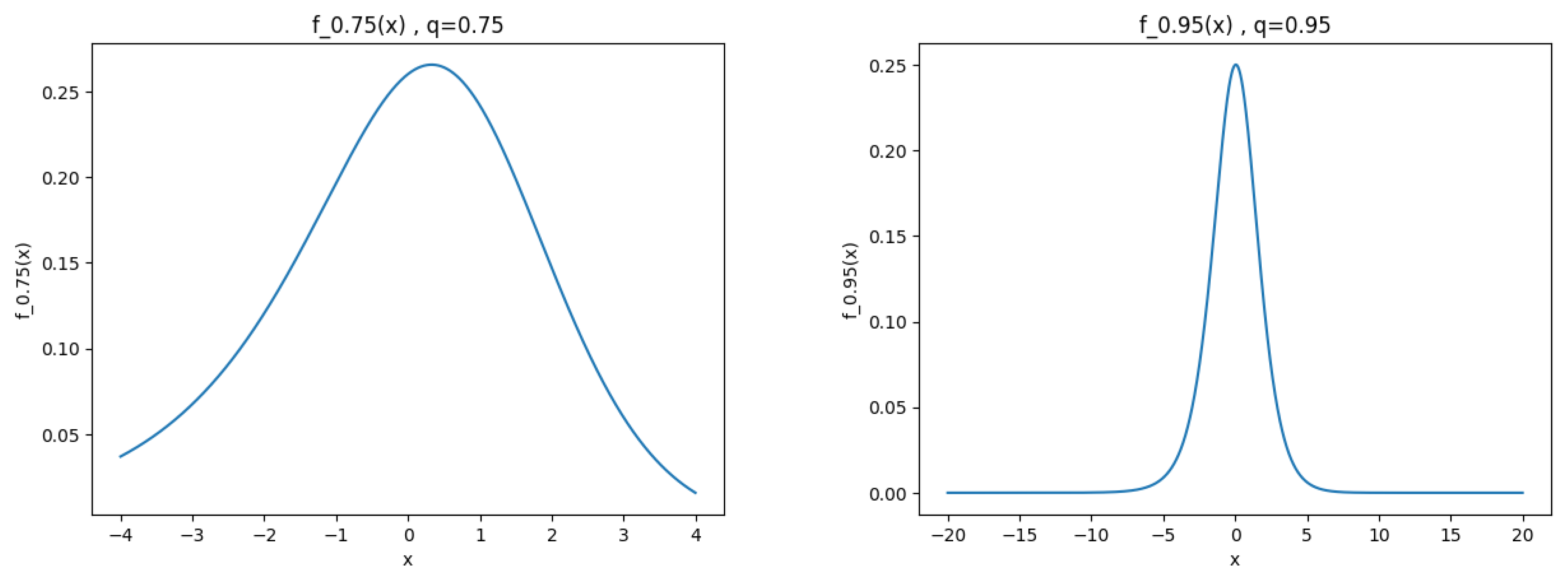
Figure 2 exhibits the logistic q–density curves, for different values of q. It is worth noting that as q tends to 1, the logistic q–density become compatible with the ordinary case.

Démonstration. 

For $x\in [-{\delta }_q,{\delta }_q]$, using the definition 2.1, we get

$$\begin{array}{cc}\hfill F_q\left(t\right)& ={\int }_{-{\delta }_q}^t{f}_q\left(x\right){\mathrm{d}}_{q}x=c\left(q\right){\int }_{-{\delta }_q}^t{\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathrm{d}}_{q}x\hfill \\ \hfill & =c\left(q\right){\left[-{\displaystyle \frac{1}{1+{\mathrm{e}}_q^x}}\right]}_t^{-{\delta }_q}=c\left(q\right){\displaystyle \frac{-1}{1+{\mathrm{e}}_q^t}}+c\left(q\right){\displaystyle \frac{1}{1+{\mathrm{e}}_q^{-{\delta }_q}}}\hfill \\ \hfill & =1-{\displaystyle \frac{c\left(q\right)}{1+{\mathrm{e}}_q^t}}.\hfill \end{array}$$

□

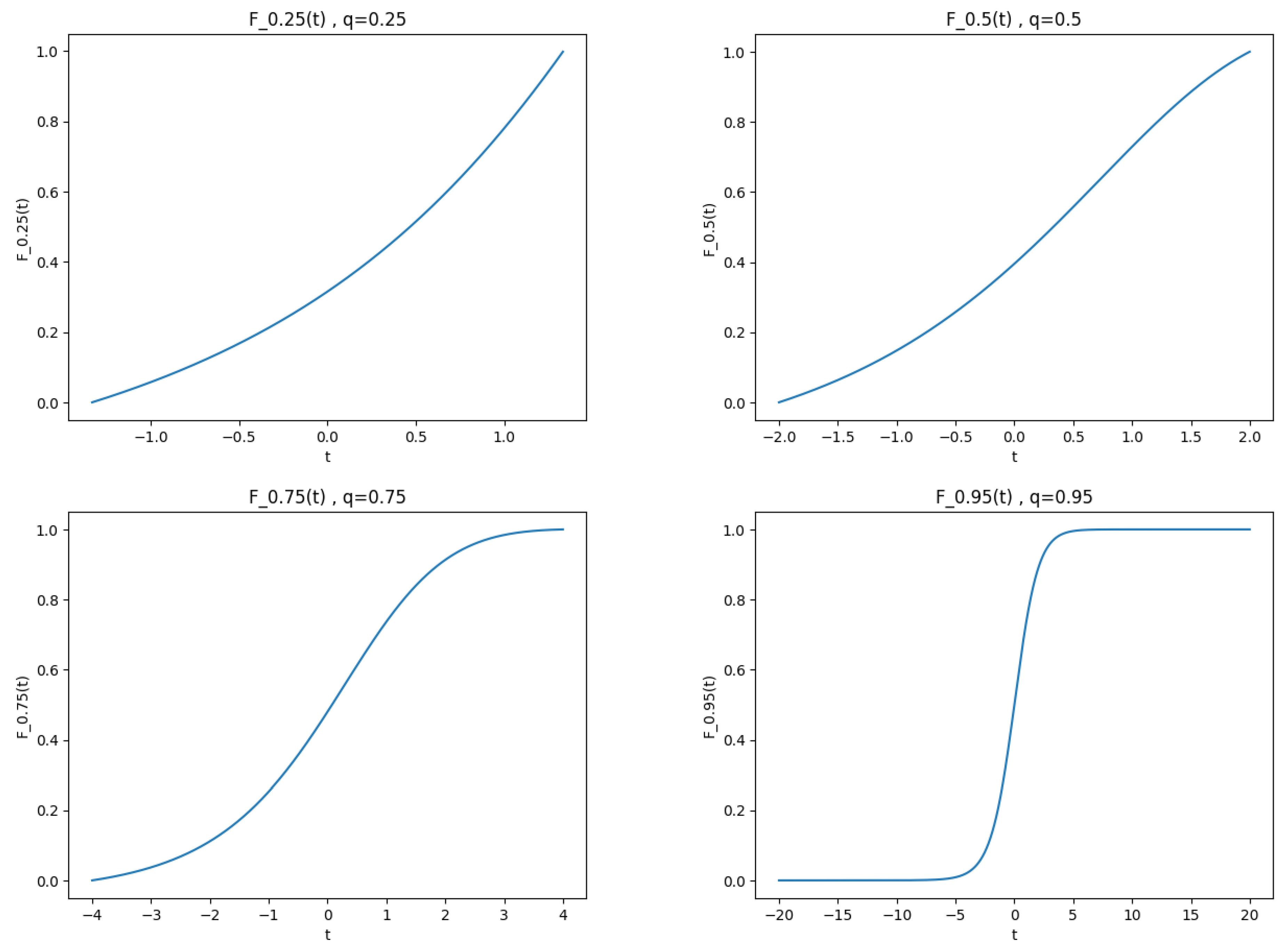
Figure 3 plots the curves of the logistic q-cumulative q-distribution function for different values of q. We notice that this function is always monotone. Besides, the curve converges to the logistic cumulative distribution function curve when q tends to 1.

Remark 2.

We have:

1.

${\displaystyle \underset{q\to 1}{lim}{F}_q\left(t\right)=\frac{1}{1+{\mathrm{e}}^{-t}}}$

2.

${\displaystyle \underset{q\to 1}{lim}\left\{\underset{t\to 0}{lim}{F}_q\left(t\right)\right\}=\frac{1}{2}.}$

4. q-Expected and q-Variance Values

In quantum calculus, the q–expected and q–variance of standard logistic q–distribution are well defined with q–expected and q–variance representing the q–analogue of ordinary expected and variance.

Díaz et al. [15,16] introduced the notion of moment in the theory of the q–calculus. It is expressed as follows:

$$q{M}_n={\int }_{\mathbb{R}}{x}^{n}f\left(x\right)d_{q}x,\forall n\in \mathbb{N}.$$

The q–mean of a random variable X with q–density function $f_q\left(x\right)$ is expressed by

$${\mathbb{E}}_q\left(X\right)={\int }_{\mathbb{R}}xf\left(x\right)d_{q}x=q{M}_1.$$

The q–variance of a random variable X with q–density function $f_q\left(x\right)$ is indicated by:

$${\mathbb{V}}_q\left(X\right)={\mathbb{E}}_q\left(X^2\right)-{\left({\mathbb{E}}_q\left(X\right)\right)}^2=q{M}_2-{\left(q{M}_1\right)}^2.$$

Theorem 2.

Let X be a random variable with a q-density $f_q$ of the standard logistic q–distribution. Then,

1.

The q-expected of X is provided by

$${\mathbb{E}}_q\left(X\right)=-{\delta }_q+c\left(q\right)(1-q){\delta }_q\sum _{j=0}^{+\infty }\left({\displaystyle \frac{q^j}{1+{\mathrm{e}}_q^{q^{j+1}{\delta }_q}}}+{\displaystyle \frac{q^j}{1+{\mathrm{e}}_q^{-q^{j+1}{\delta }_q}}}\right),\mathit{for}\mathit{all}{\delta }_q={\displaystyle \frac{1}{1-q}}.$$

2.

The q-variance of X is denoted by

$${\mathbb{V}}_q\left(X\right)={\delta }_q^2+c\left(q\right){\left[2\right]}_q{\mathbb{E}}_q\left({\displaystyle \frac{X(1+{\mathrm{e}}_q^X)}{{\mathrm{e}}_q^X}}\right)-{\left[{\mathbb{E}}_q\left(X\right)\right]}^2.$$

• Let $f_q\left(x\right)=c\left(q\right){\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathbb{1}}_{[-{\delta }_q,{\delta }_q]}\left(x\right),$ is q-density of standard logistic q–distribution. In this regard, for ${\delta }_q={\displaystyle \frac{1}{1-q}}$

  $$\begin{array}{cc}\hfill {\mathbb{E}}_q\left(X\right)& ={\int }_{\mathbb{R}}x{f}_q\left(x\right){\mathrm{d}}_{q}x\hfill \\ \hfill & =c\left(q\right){\int }_{-{\delta }_q}^{{\delta }_q}{\displaystyle \frac{x{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathrm{d}}_{q}x\hfill \\ \hfill & =c\left(q\right){\int }_{-{\delta }_q}^{{\delta }_q}x{\mathrm{D}}_q\left(-{\displaystyle \frac{1}{1+{\mathrm{e}}_q^x}}\right){\mathrm{d}}_{q}x\hfill \\ \hfill & =c\left(q\right){\left[{\displaystyle \frac{-x}{1+{\mathrm{e}}_q^x}}\right]}_{-{\delta }_q}^{{\delta }_q}+c\left(q\right){\int }_{-{\delta }_q}^{{\delta }_q}{\displaystyle \frac{1}{1+{\mathrm{e}}_q^{qx}}}{\mathrm{D}}_q\left(x\right){\mathrm{d}}_{q}x\hfill \\ \hfill & =c\left(q\right)\left[{\displaystyle \frac{-{\delta }_q}{1+{\mathrm{e}}_q^{{\delta }_q}}}-{\displaystyle \frac{{\delta }_q}{1+{\mathrm{e}}_q^{-{\delta }_q}}}\right]+c\left(q\right){\int }_0^{{\delta }_q}{\displaystyle \frac{1}{1+{\mathrm{e}}_q^{qx}}}+{\displaystyle \frac{1}{1+{\mathrm{e}}_q^{-qx}}}{\mathrm{d}}_{q}x\hfill \\ \hfill & =-{\delta }_q+c\left(q\right)(1-q){\delta }_q\sum _{j=0}^{+\infty }\left({\displaystyle \frac{q^j}{1+{\mathrm{e}}_q^{q^{j+1}{\delta }_q}}}+{\displaystyle \frac{q^j}{1+{\mathrm{e}}_q^{-q^{j+1}{\delta }_q}}}\right).\hfill \end{array}$$
• We have,

  $$\begin{array}{cc}\hfill {\mathbb{E}}_q\left(X^2\right)& =c\left(q\right){\int }_{-{\delta }_q}^{{\delta }_q}{\displaystyle \frac{x^2{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathrm{d}}_{q}x\hfill \\ \hfill & =c\left(q\right){\int }_{-{\delta }_q}^{{\delta }_q}{x}^2{\mathrm{D}}_q\left({\displaystyle \frac{-1}{1+{\mathrm{e}}_q^x}}\right){\mathrm{d}}_{q}x\hfill \\ \hfill & =c\left(q\right){\left[-{\displaystyle \frac{x^2}{1+{\mathrm{e}}_q^x}}\right]}_{-\delta }^{{\delta }_q}+c\left(q\right){\int }_{-{\delta }_q}^{{\delta }_q}{\left[2\right]}_q{\displaystyle \frac{x}{1+{\mathrm{e}}_q^{qx}}}{\mathrm{d}}_{q}x\hfill \\ \hfill & ={\delta }_q^2+c\left(q\right){\left[2\right]}_q{\mathbb{E}}_q\left({\displaystyle \frac{X(1+{\mathrm{e}}_q^X)}{{\mathrm{e}}_q^X}}\right).\hfill \end{array}$$
  As a result,

  $${\mathbb{V}}_q\left(X\right)={\delta }_q^2+1_q{\left[2\right]}_q{\mathbb{E}}_q\left({\displaystyle \frac{X(1+{\mathrm{e}}_q^X)}{{\mathrm{e}}_q^X}}\right)-{\left[{\mathbb{E}}_q\left(X\right)\right]}^2.$$

5. q–Fourier Transform

In this section, we use the q- exponential $E_q^x$ and the definition of the Jackson q-integral as well as its properties to define the q-Fourier transform and determine certain properties that characterize this operator.

The q-exponential $E_q^{ix}$ is bounded for all x in $]-{\delta }_q,{\delta }_q[$, where i denotes the imaginary unit.

The q–Fourier transform can be used in the analysis and the resolution of problems in quantum calculus.

With q always being a fixed number falling within the range of 0 to 1.

Definition 2.

The q–Fourier transform of a function f, denoted by ${\widehat{f}}^q$, is a function defined on ${\mathbb{R}}_q=]-{\delta }_q,{\delta }_q[$ by:

$${\widehat{f}}^q\left(t\right)={\int }_{-{\delta }_q}^{{\delta }_q}{E}_q^{-itqx}f\left(x\right){\mathrm{d}}_{q}x,\forall t\in ]-{\delta }_q,{\delta }_q[.$$

Remark 3.

Let $\alpha \in \mathbb{R}$. Then, the q-derivative of q–exponential $E_q^{\alpha x}$ is written as

$$D_q{E}_q^{\alpha x}=\alpha E_q^{\alpha qx}.$$

Proposition 2.

Let f be a function and $D_{q}f$ its q–derivative. Accordingly, if f and $D_{q}f$ are q–integrable on ${\mathbb{R}}_q=]-{\delta }_q,{\delta }_q[$, then the q–Fourier transform of $D_{q}f$ in ${\mathbb{R}}_q=]-{\delta }_q,{\delta }_q[$ is determined by the following relation:

1.

$it{\widehat{f}}^q\left(t\right)={\widehat{\left(D_{q}f\right)}}^q\left(t\right)+E_q^{it{\delta }_q}f(-{\delta }_q)-E_q^{-it{\delta }_q}f\left({\delta }_q\right).$

2.

$it{\widehat{\left(f{\mathbb{1}}_{]0,{\delta }_q[}\right)}}^q\left(t\right)={\widehat{\left(D_{q}f{\mathbb{1}}_{]0,{\delta }_q[}\right)}}^q\left(t\right)+f\left(0\right)-E_q^{-it{\delta }_q}f\left({\delta }_q\right).$

The q–Fourier transform of f is provided by

$${\widehat{f}}^q\left(t\right)={\int }_{-{\delta }_q}^{{\delta }_q}{E}_q^{-itqx}f\left(x\right){\mathrm{d}}_{q}x,\forall t\in ]-{\delta }_q,{\delta }_q[.$$

Therefore,

1.

$${\widehat{f}}^q\left(t\right)={\int }_{-{\delta }_q}^{{\delta }_q}{E}_q^{-itqx}f\left(x\right){\mathrm{d}}_{q}x={\int }_{-{\delta }_q}^{{\delta }_q}{D}_q\left(-{\displaystyle \frac{1}{it}}{E}_q^{-itx}\right)f\left(x\right){\mathrm{d}}_{q}x.$$

Using the q–integration by parts, we obtain:

$$\begin{array}{cc}\hfill {\int }_{-{\delta }_q}^{{\delta }_q}{D}_q\left(-{\displaystyle \frac{1}{it}}{E}_q^{-itx}\right)f\left(x\right){\mathrm{d}}_{q}x=& {\displaystyle \frac{1}{it}}{\left[-E_q^{-itx}f\left(x\right)\right]}_{-{\delta }_q}^{{\delta }_q}+{\displaystyle \frac{1}{it}}{\int }_{-{\delta }_q}^{{\delta }_q}{E}_q^{-itqx}{D}_{q}f\left(x\right){\mathrm{d}}_{q}x\hfill \\ \hfill =& {\displaystyle \frac{1}{it}}\left[-E_q^{-it{\delta }_q}f\left({\delta }_q\right)+E_q^{it{\delta }_q}f(-{\delta }_q)\right]+{\displaystyle \frac{1}{it}}{\int }_{-{\delta }_q}^{{\delta }_q}{E}_q^{-itqx}{D}_{q}f\left(x\right){\mathrm{d}}_{q}x.\hfill \end{array}$$

According to the definition of the q–Fourier transform, we can infer that:

$${\widehat{\left(D_{q}f\right)}}^q\left(t\right)={\int }_{-{\delta }_q}^{{\delta }_q}{E}_q^{-itqx}{D}_{q}f\left(x\right){\mathrm{d}}_{q}x.$$

Consequently,

$$\begin{array}{cc}\hfill {\widehat{f}}^q\left(t\right)=& {\displaystyle \frac{1}{it}}\left[-E_q^{-it{\delta }_q}f\left({\delta }_q\right)+E_q^{it{\delta }_q}f(-{\delta }_q)\right]+{\displaystyle \frac{1}{it}}{\widehat{\left(D_{q}f\right)}}^q\left(t\right)\hfill \\ \hfill =& {\displaystyle \frac{1}{it}}\left({\widehat{\left(D_{q}f\right)}}^q\left(t\right)+E_q^{it{\delta }_q}f(-{\delta }_q)-E_q^{-it{\delta }_q}f\left({\delta }_q\right)\right).\hfill \end{array}$$

Thus,

$$it{\widehat{f}}^q\left(t\right)={\widehat{\left(D_{q}f\right)}}^q\left(t\right)+E_q^{it{\delta }_q}f(-{\delta }_q)-E_q^{-it{\delta }_q}f\left({\delta }_q\right).$$

2.

Since $e_q^x{E}_q^{-x}=e_q^{-x}{E}_q^x=1$, then $E_q^x={\displaystyle \frac{1}{e_q^{-x}}}$ and since $e_q^0=1$, then $E_q^0=1$.

The q-Fourier transform of the function $\left(f{\mathbb{1}}_{]0,{\delta }_q[}\right)$ is expressed in terms of

$${\widehat{\left(f{\mathbb{1}}_{]0,{\delta }_q[}\right)}}^q\left(t\right)={\int }_{-{\delta }_q}^{{\delta }_q}{E}_q^{-itqx}f\left(x\right){\mathbb{1}}_{]0,{\delta }_q[}{\mathrm{d}}_{q}x={\int }_0^{{\delta }_q}{D}_q\left(-{\displaystyle \frac{1}{it}}{E}_q^{-itx}\right)f\left(x\right){\mathrm{d}}_{q}x.$$

Using the q–integration by parts, we obtain

$$\begin{array}{cc}\hfill {\int }_0^{{\delta }_q}{D}_q\left(-{\displaystyle \frac{1}{it}}{E}_q^{-itx}\right)f\left(x\right){\mathrm{d}}_{q}x=& {\displaystyle \frac{1}{it}}{\left[-E_q^{-itx}f\left(x\right)\right]}_0^{{\delta }_q}+{\displaystyle \frac{1}{it}}{\int }_0^{{\delta }_q}{E}_q^{-itqx}{D}_{q}f\left(x\right){\mathrm{d}}_{q}x\hfill \\ \hfill =& {\displaystyle \frac{1}{it}}\left[-E_q^{-it{\delta }_q}f\left({\delta }_q\right)+E_q^{0}f\left(0\right)\right]+{\displaystyle \frac{1}{it}}{\int }_0^{{\delta }_q}{E}_q^{-itqx}{D}_{q}f\left(x\right){\mathrm{d}}_{q}x\hfill \\ \hfill & ={\displaystyle \frac{1}{it}}\left[-E_q^{-it{\delta }_q}f\left({\delta }_q\right)+f\left(0\right)\right]+{\displaystyle \frac{1}{it}}{\int }_0^{{\delta }_q}{E}_q^{-itqx}{D}_{q}f\left(x\right){\mathrm{d}}_{q}x.\hfill \end{array}$$

According to the definition of the q–Fourier transform, it follows that

$${\widehat{\left(D_{q}f{\mathbb{1}}_{]0,{\delta }_q[}\right)}}^q\left(t\right)={\int }_{-{\delta }_q}^{{\delta }_q}{E}_q^{-itqx}{D}_{q}f\left(x\right){\mathbb{1}}_{]0,{\delta }_q[}{\mathrm{d}}_{q}x={\int }_0^{{\delta }_q}{E}_q^{-itqx}{D}_{q}f\left(x\right){\mathrm{d}}_{q}x.$$

Therefore,

$$\begin{array}{cc}\hfill {\widehat{\left(f{\mathbb{1}}_{]0,{\delta }_q[}\right)}}^q\left(t\right)=& {\displaystyle \frac{1}{it}}\left[-E_q^{-it{\delta }_q}f\left({\delta }_q\right)+f\left(0\right)\right]+{\displaystyle \frac{1}{it}}{\widehat{\left(D_{q}f{\mathbb{1}}_{]0,{\delta }_q[}\right)}}^q\left(t\right)\hfill \\ \hfill =& {\displaystyle \frac{1}{it}}\left({\widehat{\left(D_{q}f{\mathbb{1}}_{]0,{\delta }_q[}\right)}}^q\left(t\right)+f\left(0\right)-E_q^{-it{\delta }_q}f\left({\delta }_q\right)\right).\hfill \end{array}$$

Hence,

$$it{\widehat{\left(f{\mathbb{1}}_{]0,{\delta }_q[}\right)}}^q\left(t\right)={\widehat{\left(D_{q}f{\mathbb{1}}_{]0,{\delta }_q[}\right)}}^q\left(t\right)+f\left(0\right)-E_q^{-it{\delta }_q}f\left({\delta }_q\right).$$

Proposition 3.

The q–Fourier transform has the following properties:

1.

Linearity: Let f and g be two functions such that their q–Fourier transforms are indicated respectively by ${\widehat{f}}^q$ and ${\widehat{g}}^q$. Then,

$${\widehat{(\alpha f+\beta g)}}^q\left(t\right)=\alpha {\widehat{f}}^q\left(t\right)+\beta {\widehat{g}}^q\left(t\right),\forall \alpha ,\beta \in \mathbb{R}.$$

2.

If f is an even function, then the q–Fourier transforms ${\widehat{f}}^q$ is denoted by

$${\widehat{f}}^q\left(t\right)=2{\int }_0^{{\delta }_q}f\left(x\right)Co{s}_q\left(tqx\right){\mathrm{d}}_{q}x.$$

3.

If f is an odd function, then the q–Fourier transforms ${\widehat{f}}^q$ is stated as

$${\widehat{f}}^q\left(t\right)=-2i{\int }_0^{{\delta }_q}f\left(x\right)Si{n}_q\left(tqx\right){\mathrm{d}}_{q}x.$$

4.

Let $x\mapsto xf\left(x\right)$, where $|x^{\alpha }xf\left(x\right)|$ is a bounded function, then the q-derivative of the q–Fourier transform ${\widehat{f}}^q$ is specified by

$$D_q\left({\widehat{f}}^q\right)\left(t\right)=-iq{\widehat{\left(xf\right(x\left)\right)}}^q\left(t\right).$$

1.

Let $f,g$ be two functions. For all $\alpha ,\beta \in \mathbb{R}$, we get

$$\begin{array}{cc}\hfill {\widehat{(\alpha f+\beta g)}}^q\left(t\right)& ={\int }_{-{\delta }_q}^{{\delta }_q}\left(\alpha f+\beta g\right)\left(x\right)E_q^{-itqx}{\mathrm{d}}_{q}x\hfill \\ \hfill & ={\int }_{-{\delta }_q}^{{\delta }_q}\alpha f\left(x\right)E_q^{-itqx}+\beta g\left(x\right)E_q^{-itqx}{\mathrm{d}}_{q}x\hfill \\ \hfill & =\alpha {\int }_{-{\delta }_q}^{{\delta }_q}f\left(x\right)E_q^{-itqx}{\mathrm{d}}_{q}x+\beta {\int }_{-{\delta }_q}^{{\delta }_q}g\left(x\right)E_q^{-itqx}{\mathrm{d}}_{q}x\hfill \\ \hfill & =\alpha {\widehat{f}}^q\left(t\right)+\beta {\widehat{g}}^q\left(t\right).\hfill \end{array}$$

2.

The ${\mathrm{Cos}}_q\left(x\right)={\displaystyle \frac{{\mathrm{E}}_q^{ix}+{\mathrm{E}}_q^{-ix}}{2}}$ function is an even function and the ${\mathrm{Sin}}_q\left(x\right)={\displaystyle \frac{{\mathrm{E}}_q^{ix}-{\mathrm{E}}_q^{-ix}}{2i}}$ is an odd function. From this perspective,

$$E_q^{-itqx}={\mathrm{Cos}}_q\left(tqx\right)-i{\mathrm{Sin}}_q\left(tqx\right).$$

Therefore,

$$\begin{array}{cc}\hfill {\widehat{f}}^q\left(t\right)& ={\int }_{-{\delta }_q}^{{\delta }_q}f\left(x\right)E_q^{-itqx}{\mathrm{d}}_{q}x\hfill \\ \hfill & ={\int }_{-{\delta }_q}^{{\delta }_q}f\left(x\right)\left({\mathrm{Cos}}_q\left(tqx\right)-i{\mathrm{Sin}}_q\left(tqx\right)\right){\mathrm{d}}_{q}x\hfill \\ \hfill & ={\int }_{-{\delta }_q}^{{\delta }_q}f\left(x\right){\mathrm{Cos}}_q\left(tqx\right){\mathrm{d}}_{q}x-i{\int }_{-{\delta }_q}^{{\delta }_q}f\left(x\right){\mathrm{Sin}}_q\left(tqx\right){\mathrm{d}}_{q}x.\hfill \end{array}$$

Since f is an even function, we have

$${\widehat{f}}^q\left(t\right)=2{\int }_0^{{\delta }_q}f\left(x\right){\mathrm{Cos}}_q\left(tqx\right){\mathrm{d}}_{q}x.$$

3.

Since f is an odd function, we have

$${\widehat{f}}^q\left(t\right)=2i{\int }_0^{{\delta }_q}f\left(x\right){\mathrm{Sin}}_q\left(tqx\right){\mathrm{d}}_{q}x.$$

4.

The q-derivative of the q–Fourier transform ${\widehat{f}}^q$ is obtained by:

$$\begin{array}{cc}\hfill D_q{\widehat{f}}^q\left(t\right)& =D_q\left({\int }_{-{\delta }_q}^{{\delta }_q}f\left(x\right)E_q^{-itqx}{\mathrm{d}}_{q}x\right)\hfill \\ \hfill & ={\int }_{-{\delta }_q}^{{\delta }_q}f\left(x\right)D_q\left(E_q^{-itqx}\right){\mathrm{d}}_{q}x\hfill \\ \hfill & =-iq{\int }_{-{\delta }_q}^{{\delta }_q}xf\left(x\right)E_q^{-itqx}{\mathrm{d}}_{q}x\hfill \\ \hfill & =-iq{\widehat{\left(xf\right(x\left)\right)}}^q\left(t\right).\hfill \end{array}$$

6. A Characterization of the q–Logistic q-Distribution

The new characterization of the standard logistic q–distribution q–L$(0,1)$ rests upon a novel procedure, namely the q–Fourier transform and the q-Differential Equation.

A characterization of the relationship between the logistic q–distribution and the q–exponential distributions is determined via the cumulative distribution function (cdf).

6.1. q-Differential Equations

Let g be a q–differentiable function. We define the q–differential equation $\left(E_q\right)$ as follows:

$$\left(E_q\right):D_{q}y\left(x\right)-{\displaystyle \frac{g\left(x\right)-D_{q}g\left(x\right)}{g\left(qx\right)}}y\left(x\right)=0,\mathrm{and}x\in ]-{\delta }_q=-{\displaystyle \frac{1}{1-q}},{\delta }_q={\displaystyle \frac{1}{1-q}}[.$$

The solutions of $\left(E_q\right)$ are represented by the following proposition:

Proposition 4.

The q–differential equation $\left(E_q\right)$ admits the solution:

$$y\left(x\right)={\displaystyle \frac{k{\mathrm{e}}_q^x}{g\left(x\right)}},\forall x\in ]-{\delta }_q=-{\displaystyle \frac{1}{1-q}},{\delta }_q={\displaystyle \frac{1}{1-q}}[,k\in \mathbb{R}.$$

We set $y\left(x\right)={\displaystyle \frac{k{\mathrm{e}}_q^x}{g\left(x\right)}}.$ Then,

$$\begin{array}{cc}\hfill D_{q}y\left(x\right)& =D_q\left({\displaystyle \frac{k{\mathrm{e}}_q^x}{g\left(x\right)}}\right)\hfill \\ \hfill & ={\displaystyle \frac{g\left(x\right)k{D}_q{\mathrm{e}}_q^x-k{\mathrm{e}}_q^x{D}_{q}g\left(x\right)}{g\left(qx\right)g\left(x\right)}}\hfill \\ \hfill & ={\displaystyle \frac{g\left(x\right)k{\mathrm{e}}_q^x-k{\mathrm{e}}_q^x{D}_{q}g\left(x\right)}{g\left(qx\right)g\left(x\right)}}.\hfill \end{array}$$

Accordingly,

$$\begin{array}{cc}\hfill D_{q}y\left(x\right)-{\displaystyle \frac{g\left(x\right)-D_{q}g\left(x\right)}{g\left(qx\right)}}y\left(x\right)& ={\displaystyle \frac{g\left(x\right)k{\mathrm{e}}_q^x-k{\mathrm{e}}_q^x{D}_{q}g\left(x\right)}{g\left(qx\right)g\left(x\right)}}-{\displaystyle \frac{g\left(x\right)-D_{q}g\left(x\right)}{g\left(qx\right)}}{\displaystyle \frac{k{\mathrm{e}}_q^x}{g\left(x\right)}}\hfill \\ \hfill & ={\displaystyle \frac{g\left(x\right)k{\mathrm{e}}_q^x-k{\mathrm{e}}_q^x{D}_{q}g\left(x\right)}{g\left(qx\right)g\left(x\right)}}-{\displaystyle \frac{g\left(x\right)k{\mathrm{e}}_q^x-k{\mathrm{e}}_q^x{D}_{q}g\left(x\right)}{g\left(qx\right)g\left(x\right)}}\hfill \\ \hfill & =0.\hfill \end{array}$$

6.2. A Characterization

The following proposition presenting a crucial equivalence is identified to determine the new characterization of law Logistic q-distribution.

Proposition 5.

Let f be a positive continuous function. Hence,

$$\mathit{for}\mathit{all}x\in \mathbb{R},{\int }_0^{x}f\left(t\right){\mathrm{d}}_{q}t=0,$$

if and only if $f\left(x\right)=0,\forall x\in \mathbb{R}.$

We suppose that $F\left(x\right)$ is a q–primitive of f. Therefore,

$$\begin{array}{cc}\hfill {\int }_0^{x}f\left(t\right){\mathrm{d}}_{q}t& ={\left[F\left(t\right)\right]}_0^x\hfill \\ \hfill & =F\left(x\right)-F\left(0\right)\hfill \\ \hfill & =0.\hfill \end{array}$$

It follows that $F\left(x\right)=F\left(0\right),$ for all $x\in \mathbb{R}.$

This results in the function $F\left(x\right)$ which is constant for all $x\in \mathbb{R}.$

Thus, $f\left(x\right)=D_{q}F\left(x\right)=D_q\left(c\right)=0,\forall c\in \mathbb{R}.$

Theorem 3.

Let X be a random variable that has an absolutely continuous q-density function, denoted by $f_q$, and a q-expectation, denoted by ${\mathbb{E}}_q\left(X\right)$. The random variable X adheres to the standard logistic q-distribution, denoted by $q-L(0,1)$, if and only if:

$${\mathbb{E}}_q\left[\left(-it+h\left(X\right)\right)E_q^{-itqX}{\mathbb{1}}_{]0,{\delta }_q[}\left(X\right)\right]-E_q^{-it{\delta }_q}{f}_q\left({\delta }_q\right)+f_q\left(0\right)=0,{\delta }_q={\displaystyle \frac{1}{1-q}},$$

holds for all $t\in \mathbb{R}$, where

$$h\left(x\right)={\displaystyle \frac{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)-{\mathrm{D}}_q\left[(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)\right]}{(1+{\mathrm{e}}_q^{q^{2}x})(1+{\mathrm{e}}_q^{qx})}},$$

and i denotes the imaginary unit, f q–density.

Suppose X follows the logistic q–distribution q–L$(0,1)$. Thus:

$$f_q\left(x\right)=c\left(q\right){\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathbb{1}}_{]-{\delta }_q,{\delta }_q[}\left(x\right),\mathrm{for}{\delta }_q={\displaystyle \frac{1}{1-q}}.$$

Consequently,

$${\mathbb{E}}_q\left[\left(-it+h\left(X\right)\right)E_q^{-itqX}{\mathbb{1}}_{]0,{\delta }_q[}\left(X\right)\right]$$

is equal to

$$\begin{array}{cc}\hfill & c\left(q\right)\left({\int }_{-{\delta }_q}^{{\delta }_q}-it{E}_q^{-itqx}{\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathbb{1}}_{]0,{\delta }_q[}\left(x\right){\mathrm{d}}_{q}x+{\int }_{-{\delta }_q}^{{\delta }_q}{E}_q^{-itqx}h\left(x\right){\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathbb{1}}_{]0,\delta [}\left(x\right){\mathrm{d}}_{q}x\right)\hfill \\ \hfill & =c\left(q\right)\left({\int }_0^{{\delta }_q}-it{E}_q^{-itqx}{\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathrm{d}}_{q}x+{\int }_0^{{\delta }_q}{E}_q^{-itqx}h\left(x\right){\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathrm{d}}_{q}x\right)\hfill \\ \hfill & =c\left(q\right)\left({\int }_0^{{\delta }_q}{D}_q\left(E_q^{-itx}\right){\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathrm{d}}_{q}x+{\int }_0^{{\delta }_q}{E}_q^{-itqx}{D}_q\left({\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}\right){\mathrm{d}}_{q}x\right)\hfill \\ \hfill & =c\left(q\right){\left[{\displaystyle \frac{E_q^{-itx}{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}\right]}_0^{{\delta }_q}=c\left(q\right){\displaystyle \frac{E_q^{-it{\delta }_q}{\mathrm{e}}_q^{{\delta }_q}}{(1+{\mathrm{e}}_q^{q{\delta }_q})(1+{\mathrm{e}}_q^{{\delta }_q})}}-{\displaystyle \frac{c\left(q\right)}{4}}\hfill \\ \hfill & =E_q^{-it{\delta }_q}{f}_q\left({\delta }_q\right)-f_q\left(0\right).\hfill \end{array}$$

From this perspective,

$$\begin{array}{cc}\hfill & {\mathbb{E}}_q\left[\left(-it+h\left(X\right)\right)E_q^{-itqX}{\mathbb{1}}_{]0,{\delta }_q[}\left(X\right)\right]-E_q^{-it{\delta }_q}{f}_q\left({\delta }_q\right)+f_q\left(0\right)\hfill \\ \hfill & =c\left(q\right){\displaystyle \frac{E_q^{-it{\delta }_q}{\mathrm{e}}_q^{{\delta }_q}}{(1+{\mathrm{e}}_q^{q{\delta }_q})(1+{\mathrm{e}}_q^{{\delta }_q})}}-{\displaystyle \frac{c\left(q\right)}{4}}-c\left(q\right){\displaystyle \frac{E_q^{-it{\delta }_q}{\mathrm{e}}_q^{{\delta }_q}}{(1+{\mathrm{e}}_q^{q{\delta }_q})(1+{\mathrm{e}}_q^{{\delta }_q})}}+{\displaystyle \frac{c\left(q\right)}{4}}=0.\hfill \end{array}$$

It therefore follows that

$${\mathbb{E}}_q\left[\left(-it+h\left(X\right)\right)E_q^{-itqX}{\mathbb{1}}_{]0,{\delta }_q[}\left(X\right)\right]-E_q^{-it{\delta }_q}{f}_q\left({\delta }_q\right)+f_q\left(0\right)=0.$$

Let X be a random variable with an absolutely continuous q–density function $f_q$ such that:

$${\mathbb{E}}_q\left[\left(-it+h\left(X\right)\right)E_q^{-itqX}{\mathbb{1}}_{]0,{\delta }_q[}\left(X\right)\right]-E_q^{-it{\delta }_q}{f}_q\left({\delta }_q\right)+f_q\left(0\right)=0,$$

and

$$h\left(x\right)={\displaystyle \frac{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)-{\mathrm{D}}_q\left[(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)\right]}{(1+{\mathrm{e}}_q^{q^{2}x})(1+{\mathrm{e}}_q^{qx})}}.$$

Using the q–Fourier transform, we infer that:

$$\begin{array}{cc}\hfill -it{\mathbb{E}}_q\left[E_q^{-itqX}{\mathbb{1}}_{]0,{\delta }_q[}\left(X\right)\right]& =-it{\widehat{\left(f_q\left(x\right){\mathbb{1}}_{]0,{\delta }_q[}\left(x\right)\right)}}^q\left(t\right)\hfill \\ \hfill & =-{\widehat{\left(D_{q}f\left(x\right){\mathbb{1}}_{]0,{\delta }_q[}\left(x\right)\right)}}^q\left(t\right)-f_q\left(0\right)+E_q^{-it{\delta }_q}{f}_q\left({\delta }_q\right)\hfill \\ \hfill & ={\int }_0^{{\delta }_q}-D_{q}f\left(t\right)E_q^{-itqx}{\mathrm{d}}_{q}x-f_q\left(0\right)+E_q^{-it{\delta }_q}{f}_q\left({\delta }_q\right).\hfill \end{array}$$

We get,

$$\begin{array}{cc}\hfill 0& ={\mathbb{E}}_q\left[\left(-it+h\left(X\right)\right)E_q^{-itqX}{\mathbb{1}}_{]0,{\delta }_q[}\left(X\right)\right]-E_q^{-it{\delta }_q}{f}_q\left({\delta }_q\right)+f_q\left(0\right)\hfill \\ \hfill & ={\int }_0^{{\delta }_q}\left(-D_q{f}_q\left(x\right)+h\left(x\right)f_q\left(x\right)\right)E_q^{-itqx}{\mathrm{d}}_{q}x\hfill \end{array}$$

Since ${\displaystyle {\int }_0^{{\delta }_q}\left(-D_q{f}_q\left(x\right)+h\left(x\right)f_q\left(x\right)\right)E_q^{-itqx}{\mathrm{d}}_{q}x=0,\forall t\in \mathbb{R}}$, relying upon proposition $6.2$, we get

$$D_q{f}_q\left(x\right)-h\left(x\right)f_q\left(x\right)=D_q{f}_q\left(x\right)-{\displaystyle \frac{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)-{\mathrm{D}}_q\left[(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)\right]}{(1+{\mathrm{e}}_q^{q^{2}x})(1+{\mathrm{e}}_q^{qx})}}{f}_q\left(x\right)=0.$$

Based on properties of the q–Fourier transform, we hence note that $f_q$ must satisfy the q–differential equation $\left(E_q\right)$ which is indicated by:

$$\left(E_q\right):\left\{\begin{array}{c}{D}_{q}y\left(x\right)-{\displaystyle \frac{g\left(x\right)-D_{q}g\left(x\right)}{g\left(qx\right)}}y\left(x\right)=0,\hfill \\ \\ \mathrm{and}y\mathrm{defined}\mathrm{on}]-{\delta }_q,{\delta }_q[.\hfill \end{array}\right.,$$

and

$${\displaystyle \frac{g\left(x\right)-D_{q}g\left(x\right)}{g\left(qx\right)}}={\displaystyle \frac{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)-{\mathrm{D}}_q\left[(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)\right]}{(1+{\mathrm{e}}_q^{q^{2}x})(1+{\mathrm{e}}_q^{qx})}}.$$

With reference to proposition $6.1$, the solutions of the q–differential equation $\left(E_q\right)$ are determined by:

$$y\left(x\right)={\displaystyle \frac{k{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathbb{1}}_{]-{\delta }_q,{\delta }_q[}\left(x\right),\forall k\in \mathbb{R}.$$

Since $c\left(q\right)=1+{\mathrm{e}}_q^{-{\delta }_q}$, then

$$\begin{array}{cc}\hfill {\int }_{\mathbb{R}}y\left(x\right){\mathrm{d}}_{q}x& =k{\int }_{-{\delta }_q}^{{\delta }_q}{\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathrm{d}}_{q}x\hfill \\ \hfill & =k{\displaystyle \frac{1}{1+{\mathrm{e}}_q^{-{\delta }_q}}}.\hfill \end{array}$$

The sole solution of $\left(E_q\right)$ that satisfies

$${\int }_{\mathbb{R}}y\left(x\right){\mathrm{d}}_{q}x=1,$$

is determined to by $k=1+{\mathrm{e}}_q^{-{\delta }_q}=c\left(q\right).$

Thus,

$$y\left(x\right)=f_q\left(x\right)=c\left(q\right){\displaystyle \frac{{\mathrm{e}}_q^x}{(1+{\mathrm{e}}_q^{qx})(1+{\mathrm{e}}_q^x)}}{\mathbb{1}}_{]-{\delta }_q,{\delta }_q[}\left(x\right),\mathrm{for}{\delta }_q={\displaystyle \frac{1}{1-q}},$$

and $f_q$ is the q–density of logistic q–distribution q–L$(0,1)$.

We prove the following theorems, which establish a new characterization between the logistic q-distribution and the exponential q-distribution with parameter 1.

Theorem 4.

Let X be a continuous q–distributed random variable with a probability q–density function $f_q$. Then, the random variable $Y=lo{g}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{E}}_q^{-X}}}-1\right)$ is a q–logistic random variable if and only if X follows an exponential q–distribution with parameter 1 in the interval $[0,{\delta }_q={\displaystyle \frac{1}{1-q}}]$.

The probability q–density function of an exponential random variable X with parameter 1 is identified as follows [9]:

$${\xi }_q\left(x\right)=E_q^{-qx}{\mathbb{1}}_{[0,{\displaystyle \frac{1}{1-q}}]}\left(x\right).$$

Since $Y=lo{g}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{E}}_q^{-X}}}-1\right)$, then $-{\delta }_q\le Y\le {\delta }_q$ and $X=-Lo{g}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{e}}_q^Y+1}}\right).$

Suppose that the random variable Y follows the logistic q–distribution q–L$(0,1)$. Then,

$$f_q\left(y\right)=c\left(q\right){\displaystyle \frac{{\mathrm{e}}_q^y}{(1+{\mathrm{e}}_q^{qy})(1+{\mathrm{e}}_q^y)}}{\mathbb{1}}_{]-{\delta }_q,{\delta }_q[}\left(y\right),\mathrm{for}{\delta }_q={\displaystyle \frac{1}{1-q}},$$

We have

$$\begin{array}{cc}\hfill {\mathbb{P}}_q(X\le x)& ={\mathbb{P}}_q\left(-Lo{g}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{e}}_q^y+1}}\right)\le x\right)\hfill \\ \hfill & ={\mathbb{P}}_q\left(Lo{g}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{e}}_q^y+1}}\right)\ge -x\right)\hfill \\ \hfill & ={\mathbb{P}}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{e}}_q^y+1}}\ge {\mathrm{E}}_q^{-x}\right)\hfill \\ \hfill & ={\mathbb{P}}_q\left({\displaystyle \frac{{\mathrm{e}}_q^y+1}{c\left(q\right)}}\le {\displaystyle \frac{1}{{\mathrm{E}}_q^{-x}}}\right)\hfill \\ \hfill & ={\mathbb{P}}_q\left({\mathrm{e}}_q^y\le {\displaystyle \frac{c\left(q\right)}{{\mathrm{E}}_q^{-x}}}-1\right)\hfill \\ \hfill & ={\mathbb{P}}_q\left(y\le lo{g}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{E}}_q^{-x}}}-1\right)\right)\hfill \\ \hfill & =c\left(q\right){\int }_{-{\delta }_q}^{lo{g}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{E}}_q^{-x}}}-1\right)}{\displaystyle \frac{{\mathrm{e}}_q^y}{(1+{\mathrm{e}}_q^{qy})(1+{\mathrm{e}}_q^y)}}{\mathrm{d}}_{q}y\hfill \\ \hfill & =c\left(q\right){\left[-{\displaystyle \frac{1}{1+{\mathrm{e}}_q^y}}\right]}_{-{\delta }_q}^{lo{g}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{E}}_q^{-x}}}-1\right)}\hfill \\ \hfill & =c\left(q\right)\left[-{\displaystyle \frac{1}{1+\frac{c\left(q\right)}{{\mathrm{E}}_q^{-x}}-1}}+{\displaystyle \frac{1}{1+{\mathrm{e}}_q^{-{\delta }_q}}}\right]\hfill \\ \hfill & =1-{\mathrm{E}}_q^{-x}.\hfill \end{array}$$

The corresponding result represents the q-cumulative q-distribution function of the exponential q-distribution with parameter 1.

Then, X follows the exponential q–distribution.

Conversely, suppose that the random variable X follows the exponential q–distribution with parameter $1.$

We have,

$$\begin{array}{cc}\hfill {\mathbb{P}}_q(Y\le y)& ={\mathbb{P}}_q\left(lo{g}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{E}}_q^{-x}}}-1\right)\le y\right)\hfill \\ \hfill & ={\mathbb{P}}_q\left(\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{E}}_q^{-x}}}-1\right)\le {\mathrm{e}}_q^y\right)\hfill \\ \hfill & ={\mathbb{P}}_q\left({\displaystyle \frac{c\left(q\right)}{{\mathrm{E}}_q^{-x}}}\le {\mathrm{e}}_q^y+1\right)\hfill \\ \hfill & ={\mathbb{P}}_q\left({\mathrm{e}}_q^x\le {\displaystyle \frac{{\mathrm{e}}_q^y+1}{c\left(q\right)}}\right)\hfill \\ \hfill & ={\mathbb{P}}_q\left(lo{g}_q\left({\mathrm{e}}_q^x\right)\le lo{g}_q\left({\displaystyle \frac{{\mathrm{e}}_q^y+1}{c\left(q\right)}}\right)\right)\hfill \\ \hfill & ={\mathbb{P}}_q\left(x\le lo{g}_q\left({\displaystyle \frac{{\mathrm{e}}_q^y+1}{c\left(q\right)}}\right)\right)\hfill \\ \hfill & ={\int }_0^{lo{g}_q\left({\displaystyle \frac{{\mathrm{e}}_q^y+1}{c\left(q\right)}}\right)}{\mathrm{E}}_q^{-qx}{\mathrm{d}}_{q}x={\left[-{\mathrm{E}}_q^{-x}\right]}_0^{lo{g}_q\left({\displaystyle \frac{{\mathrm{e}}_q^y+1}{c\left(q\right)}}\right)}\hfill \\ \hfill & ={\left[-{\displaystyle \frac{1}{{\mathrm{e}}_q^x}}\right]}_0^{lo{g}_q\left({\displaystyle \frac{{\mathrm{e}}_q^y+1}{c\left(q\right)}}\right)}=1-{\displaystyle \frac{c\left(q\right)}{{\mathrm{e}}_q^y+1}}.\hfill \end{array}$$

The obtained result represents the q-cumulative q-distribution function of the logistic q–distribution.

Accordingly, Y follows the logistic q–distribution q–L$(0,1)$.