Optimizing ATM and ATC Procedures for Mitigating CO2 and Non-CO2 Emissions: The Role of Climate Impact Metrics

1. Introduction

Aviation is known to have several adverse impacts on the environment, with aircraft engines considered as one of the major sources of both gaseous and particulate pollutants, at the airport level as well as during the entire flight [1,2,3]. Various campaigns have reported both physical and chemical properties of particulate and gaseous emissions in aviation [4,5,6,7,8]. Pollutants generated in conventional aircraft engines generally include carbon dioxide (CO₂) and monoxide (CO), nitrogen mono- and dioxide (NOx), sulphur oxides (SO_x), particulate matter (PM2.5, PM10), aerosol and concentrations of black carbon (BC), VOC (Volatile Organic Compounds) [9,10,11,12,13], and water vapor. The latter is also emitted in innovative propelling technologies employing hydrogen, along with nitrogen dioxide when a combustion process is exploited.

Each of these emitted species, including water vapor, can have its noxious effect on both the environment and human health through different interaction pathways. CO₂ as well as other pollutants, particularly sulphur oxides, determine a negative impact on planetary radiative forcing. Aviation-induced cloudiness, arising from water vapor emissions, can have the same effect, even if it does not always eventuate. In other cases, the emitted species can bear an adverse impact only in given flight conditions, for instance in proximity of the ground, as the worsening of air quality determined by carbon monoxide. Nitrogen oxides, highly toxic at elevated concentrations, can excerpt their harmful action when emitted at low altitudes (tropospheric NOx), as well as in stratosphere, where they trigger a chain of chemical reactions, ultimately causing the depletion of the ozone layer, possibly determining a positive radiative forcing (stratospheric NOx).

Aviation industry is increasingly focusing on environmental sustainability, with a particular emphasis on reducing emissions, mainly those that contribute to climate change. This paper reviews the approaches applied in ATM and ATC to mitigate aviation environmental impact, with a discussion about the pivotal role of metrics. As it will be discussed, it is important and useful to show if and how a given measure reduces environmental impact, particularly when referring to climate. The focus of both academia and industry in recent years has been and still is on activities aimed to reduce emissions of CO2 and pollutants, in order to achieve both immediate positive consequences on local air quality and long-terms benefits on climate change mitigation. The main strategies to reach the target of CO2 emissions and pollutants reduction rely, in the short-medium term, on propulsion system design updates, usage of alternative fuels, and routes optimization to reduce fuel consumption and related emissions and to allow avoiding already polluted airspace volumes. Over long-term time horizon, then, the introduction has been envisaged and is actively in development of breakthrough aircraft propulsion configurations, such as: 1) intermediate solutions consisting in hybrid powertrains; 2) final target solutions based on full electric propulsion, using new batteries or fuel cells exploiting hydrogen as energy source. Nevertheless, such innovative propulsion technologies, even if able to provide clear and fundamental advantages in terms of strongly reducing (hybrid propulsion) or preventing (full electric) CO2 and pollutants emissions, emphasized the need of focusing also on non-CO2 emissions, which can have relevant negative impacts on climate, because still leading to formation of undesired phenomena such as condensation trails (usually named as “contrails”).

In both the CO2 and pollutants and non-CO2 emissions reduction strategies, a fundamental role is played by the operational aviation management level, i.e. by the Air Traffic Management (ATM) and Air Traffic Control (ATC) operations. This is due to the circumstance that the planned and executed routes, in terms of their geographical, altitude and speed associated requirements, have an impact on the emissions of all kind resulting from the flight execution. One of the aims of this paper is to analyze the existing and proposed optimization methodologies aimed to achieve aircraft route optimization, at pre-tactical and tactical level, in order to reduce CO2 and non-CO2 emissions, in this way reducing in turn the aviation environmental impact. Such methodologies include the most recently introduced (e.g. Continuous Descent Approach) and emerging (e.g. contrails avoidance) ATM and ATC procedures for route optimization, which will be analyzed and summarized in the paper.

The focus of the paper will be on the air-side operations, being the optimization of ground operations (e.g. electric tug operations) out of the scope of this work. The paper will provide a comprehensive framework that integrates various optimization models and algorithms to address the complex problem of routing aircraft in a way that minimizes environmental impact. The framework will include time-dependent vehicle routing considerations, as emissions are not only a function of distance but also of time and operational conditions.

2. Efficient Operation of an Aircraft for Fuel Saving and Emission Reduction

The most efficient operation of an aircraft depends on many factors. For example, flight-plan and routing will be continuously modified and optimized, depending on the traffic situation and weather conditions (see Figure 1). Fuel planning for a commercial aircraft usually follows the same standard scheme as, for example, outlined by Airbus [14]. Below, the different flight phases are considered.

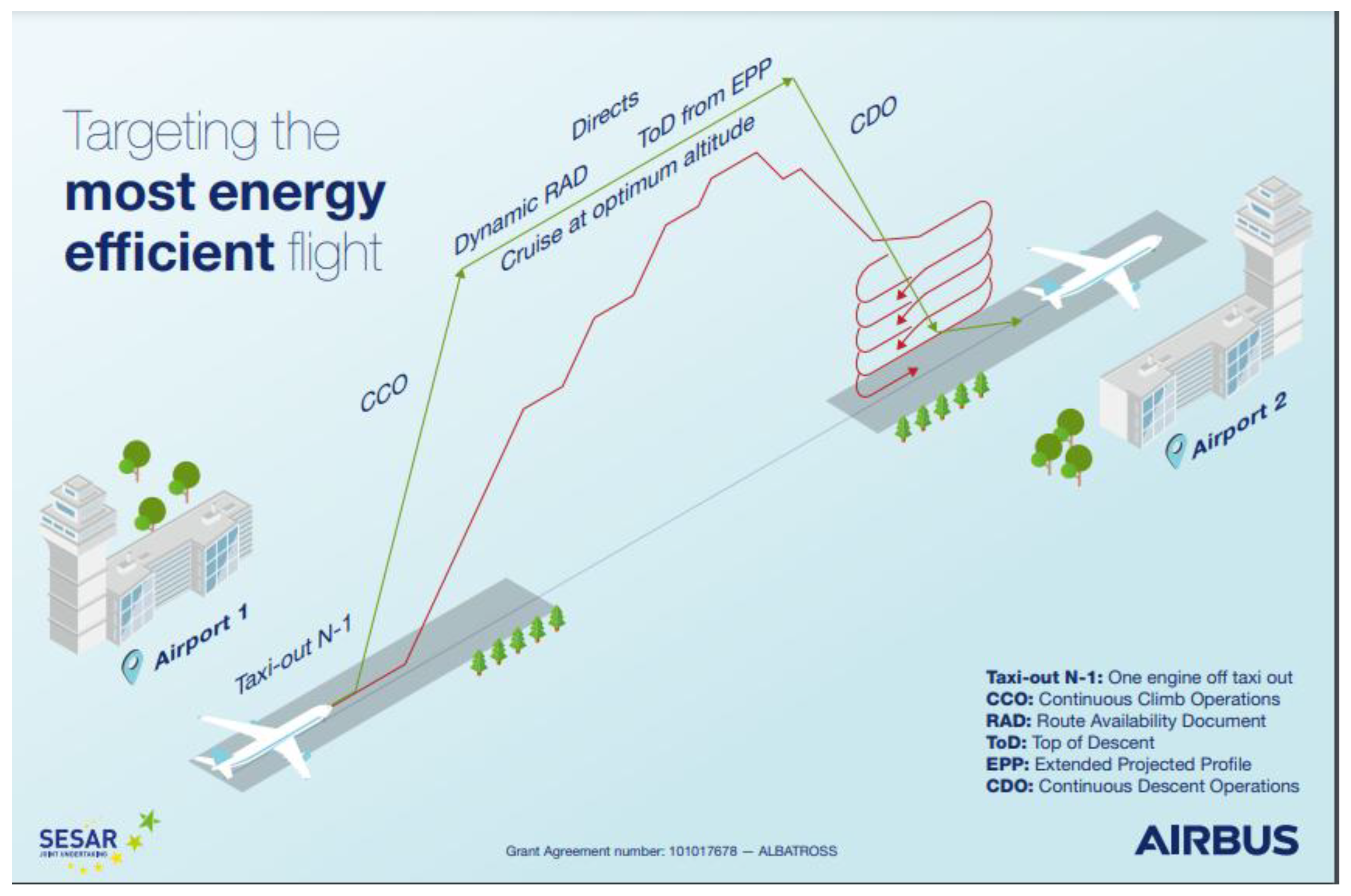
• Taxi on the airport: this is the fuel needed to start the engines and then taxi to the runway. This is a first opportunity to save fuel. Aircraft engines are designed to be efficient in flight, but not during idle on the ground. Airports and air traffic providers are working on projects to optimize the movements and flow of aircraft on the ground to minimize the time from gate to take-off.
• Take-off and climb to an optimum cruise level: each and every flight is different. The climb performance of an aircraft depends on the actual weight, the weather conditions and air traffic situation. The crew is able to calculate with the onboard systems the most efficient climb profile. The cruise altitude or flight level is not primarily the decision of the flight crew. The air traffic controller assigns a certain level, climb rate and speed based on capacity of airspace and trajectory of the aircraft.
• Cruise flight: with regards to efficiency, the cruise altitude needs to change during the flight. This is the result of burning fuel and losing weight. Fuel is 15-40% of the take-off mass of an aircraft. By burning fuel in cruise, the aircraft becomes lighter and able to climb to higher altitudes, where flight is more efficient. This, in turn, offers the opportunity to burn less fuel. Today, an aircraft climbs in steps. By improving the data-transmission between airplanes and air traffic control, the controller is able to assign the aircraft the most efficient flight level. In addition, the routing could be optimized during the flight. Depending on the air traffic situation, the controller could be looking for a direct routing being assigned to a certain flight; this avoids extra fuel burn.
• Descent: the so-called Continuous Descent is the most efficient way for the final phase of the flight. If the crew sets the thrust levers to idle and the aircraft then glides to the airport, fuel is saved and emissions are reduced. But, in many cases, aircraft today have to reduce the altitude through several steps (step-down descent) rather than in a continuous way (Continuous Descent Operations, CDO). This results in inefficient level flying at lower altitudes. The flight management system of the aircraft offers the crew the possibility to calculate the most efficient descent and define a certain point of top of descent for the flight. The air traffic controller then has to check if the traffic situation permits this approach. Consequentially, by jointly optimizing the flightpath, the resulting actual descent profile could be as close as possible to the optimum descent one.
• Holdings: one of the most inefficient flight phases in commercial aviation operations are holdings, i.e. the waiting in near-circular flight until a landing slot is available. For example, an A320-family aircraft burns approximately 100 kg of fuel in a four minutes standard holding.
• Movement to the parking position and ground power: similar to the situation on departure, an efficient surface movement guidance after landing helps saving fuel. The power supply during the turnaround of the aircraft is another opportunity to save fuel. The aircraft could be powered on the ground either by a connector and electricity from the airport or by running the so called APU, Auxiliary Power Unit onboard the aircraft, which is burning kerosene.

3. Terminal Maneuvering Area (TMA) Approaches to Fuel Saving and Emissions Reduction

As well known, the ecological transition of aviation aims to significantly reduce its impact on air quality and noise exposure. Environmental considerations, indeed, have become a priority, in the same way as safety has traditionally always been, to recover a sustainable development of air transport following the unprecedented downturn in activity due to the global health crisis caused by the COVID virus. Thanks to innovative technologies, each stakeholder is totally involved in this transition.

This environmental strategy must be defined by action plans and collaborative partnerships with stakeholders, both locally and at a European level. It must be also consistent with the innovative governance initiated with IATA, the International Air Transport Association, to help better coordinate the implementation of projects.

In this regard, to improve the environmental performance of flights, particular attention must be paid to the climb and descent flight phases. For aircrews, the approach phase is particularly demanding: the pilot has to manage speed, altitude, engine thrust, landing gear, flaps and/or airbrakes as well as to follow ATC instructions. Thanks to an optimised flight profile and an anticipated flight management, the pilot can fly as silently and economically as possible. Controlling the noise impact is thus a challenge that begins with controlling the flight path. This responsibility lies with both pilot and air traffic controller.

By minimising levelling-offs from the top of descent to the runway, the continuous descent approach means reduced engines speed variations, thus reducing noise and fuel consumption in TMA. The airport configuration is considered and the descent profiles must be integrated with the air traffic constraints in terms of safety (management of flight crossings, ensuring separation standards between aircraft) and capacity. Therefore, pilots and controllers are encouraged to use optimised descent profiles whenever the operational conditions are met.

Locally, operational units analyse the departure trajectories, in order to determine, in coordination with the stakeholders, the altitude to reach before leaving the initial trajectory. Continuous climb operations (CCO) at a constant engine thrust prevent traffic dispersion and minimise noise impact. Where possible, a climb to FL100 (about 3.000 metres) on departure route is recommended before reaching the airways in cruising. An independent control authority on airport noise usually closely monitors departure procedures from major airports, as presented to the residents’ association representatives in a local consultative commission for the environment.

Furthermore, strong experience is required over Performance Based Navigation (PBN). GNSS (Global Navigation Satellite System) based navigation enables the possibility of implementing new trajectories for the surrounding areas of an airport, without the need for conventional infrastructure on ground or radar vectoring given by the controller. Consequently, PBN trajectories can constitute relevant enablers to avoid overflights of urbanised areas located under the arrival trajectories and to shorten routes.

Nevertheless, an air traffic impact study must be used to measure and evaluate the environmental impacts which will be caused by the creation or modification of new trajectories. Any modification, indeed, can call complex balances into question. Designing new arrival and departure PBN trajectories offers aircraft trajectories less spread around urbanised areas. Thus, these studies serve to highlight choices between a nuisance concentration (as for a PBN procedure) or nuisance dispersion. These so-called Required Navigation Performance – Authorization Required (RNP AR) satellite-based approaches provide optimal and safe accessibility to an airport surrounded by obstacles, by combining a precise series of lateral and vertical guided turns.

It is possible to demonstrate the benefits of combining the PBN concept with the CDA implementation, by proposing a system for the automatic generation of Curved and Continuous Descent Approach (CCDA) trajectories. These trajectories reduce aircraft fuel consumption and noise impact near to airport. Furthermore, the path curvature property preserves the dispersion of tracks with respect to the conventional ground-based step-down arrival path, in both lateral and vertical profiles. For example, one possible system might implement the procedure described in the following [2].

First, specific paths are elaborated, with calculated Top of Descent (ToD) point, according to predefined angle or with initial fixed altitude up to intercept the descend glide path at constant or variable angle. This elaboration integrates obstacles geo-referenced mapping to avoid potential conflicts with airport/external environmental constraints, by automatically generating corrective manoeuvres. Then, the BADA aircraft performance parameters are properly considered and elaborated in order to compute the fuel consumption associated to each calculated possible descent path. Finally, the CCDA path that minimizes the fuel consumption is selected. The resulting system performances are evaluated in terms of fuel efficiency, noise impact, and lateral and vertical protected areas for tracking tolerance. For this reason, it is evident that, to reduce the effects of aircraft noise, fuel use and related pollutant atmospheric emissions, designed curved and continuous descent approach trajectories would certainly be appropriate. Their adoption would be able to provide suitably optimized vertical profiles, by combining flexible lateral paths and continuous descent operations, such that level flight segments could be completely eliminated [15,16,17].

Furthermore, it is possible to consider airport and external environmental constraints by providing the obstacles mapping from aeronautical charts georeferencing processes and suitable Digital Surface Models (DSMs) and Digital Terrain Models (DTMs). This allows to automatically generate a modified set of trajectories that optimize the track distance within a tolerable range [18]. Here, the identification of all influencing factors in TMA has been provided for a specified airport and related Aerodrome Traffic Zone and Control Zones, reporting the simulations results of the proposed methodology, indicating the benefits deriving from its use.

Indeed, the effects of aircraft noise, fuel consumption and related pollutant atmospheric emissions can impact the quality of life in populated areas near to airports and represent environmental issues resulting in restrictions for air traffic procedures, aircraft manufacturing and airport facilities design. ICAO and EUROCONTROL [19,20,21,22,23] provide guidance and recommendations on environmental measurements in order to overcome these difficulties, contributing to a sustainable balancing between the positive growing demand in the aviation sector and the possible resulting negative consequences on human activities.

In order to mitigate such negative consequences, in [24] it has been studied the development of optimized arrival trajectories automatic generation algorithms. The basic and totally reasonable assumption is that the reduction of the fuel consumption in the arrival phase (i.e. the fuel efficiency improvement) will immediately in turn lead to reduction of the associated chemical emissions deriving from the fuel combustion in the aircraft engine. Based on that, the implementation of the proposed algorithms is aimed to remodelling or adjusting the arrival procedures, for the future efficient flight operations in Terminal Manoeuvring Area (TMA), so increasing environmental efficiency and capacity in proximity of airports. Indeed, the positive effect on capacity is here related to the benefit in terms of emissions deriving from the application of the proposed optimized trajectories, which may lead to an increase of admitted arrivals while still complying with the assigned environmental constraints for the airport. In other words, by reducing the emissions of each flight, an increased number of flights can be accepted without breaching the assigned environmental limits in terms of emissions of any kind. Of course, such possible positive impact on capacity is subject to the acceptability of the capacity increase from the ATC point of view, in terms of separation limits compliance as well as Air Traffic Controllers (ATCOs) acceptable workload limitations. Furthermore, in [24], the main concepts and mathematical models needed to implement an overall system, including the algorithms cited above, able to generate descent profiles suitably optimized in terms of fuel consumption with respect to conventional step-down arrival paths, are reported and discussed.

Finally, it is worth adding that the additional noise over populated areas surrounding most major airports has led to restrictions on traffic, particularly in evening and night operations, and frequently requires aircraft to fly an inefficient, tortuous ground track path to avoid flying over densely populated areas, in this way reducing the noise exposure of people living there. For this reason, as previously stated, one of the primary concepts introduced to reduce the environmental impact is a direct descent, at idle or near-idle thrust, beginning at the entry into the terminal control area, or preferably TOD, from cruise until touchdown. This technique is generally referred to as the Continuous Descent Operation (CDO) concept [25], as also exploited in [24] primarily for fuel efficiency increase purposes, instead of noise emission reduction purposes. On the other hand, this technique is affected by a lack of predictability of the trajectory and by the difficulty of controlling relative spacing, which is of capital importance in a busy traffic environment such as the one of the high density airports, which are indeed the ones where the noise impact issues are more relevant. However, in order to mitigate such drawbacks, it is possible to exploit arrival flow merging techniques [26,27,28] that provide a support to CDO in order to improve and standardize the terminal space after the Initial Approach Fix (IAF) during the approach phase.

4. CO₂ and Non-CO₂ Emission Modelling

In general, the emission of a given species from an aircraft engine is specifically linked to its operative conditions, propulsive technology and consumption rate. The most established technologies for aircraft propulsion are the turbo-fan and turbo-propeller configurations, air-breathing internal combustion engines exploiting fuels containing hydrocarbons. A semiempirical mathematical model of these engines has been developed by Eurocontrol through a collaboration with aircraft engines manufacturers and airlines companies, leading to the steady-state description contained into the well-known and widely adopted Base of Aircraft DAta (BADA) theoretical approach. The output of the model are the thrust T and fuel flow FF, both depending on the control variable altitude (z), true airspeed (v), ambient temperature/pressure and throttle (τ) [29].

In BADA modelling, the amount of emitted pollutant ${\mathit{Q}}_{{\mathit{p}}_{\mathit{i}}}$ can be derived from the calculated fuel flow through the general expression:

$${\mathit{Q}}_{{\mathit{p}}_{\mathit{i}}}={\int }_{{\mathit{t}}_0}^{{\mathit{t}}_{\mathit{f}}}\mathit{E}{\mathit{I}}_{{\mathit{p}}_{\mathit{i}}}\left(\mathit{\tau }\right)\cdot \mathit{F}\mathit{F}\left(\mathit{\tau },\mathit{v},\mathit{z}\right)\mathit{d}\mathit{t},$$

(1)

with its differential counterpart:

$${\displaystyle \frac{\mathit{d}{\mathit{Q}}_{{\mathit{p}}_{\mathit{i}}}}{\mathit{d}\mathit{t}}}=\mathit{E}{\mathit{I}}_{{\mathit{p}}_{\mathit{i}}}\left(\mathit{\tau }\right)\cdot \mathit{F}\mathit{F}\left(\mathit{\tau },\mathit{v},\mathit{z}\right),$$

(2)

where Eurocontrol $\mathit{E}{\mathit{I}}_{{\mathit{p}}_{\mathit{i}}}$ stands for the Emission Index of pollutant ${\mathit{p}}_{\mathit{i}}$. BADA is nowadays considered one of the gold standards for evaluating pollutant emissions in aviation.

An alternative approach to BADA has been introduced by ICAO through an extensive data collection on engine emissions [30]. The ICAO emission indexes, which have the advantage of being fuel-specific, are measured in reference conditions, defined in [31], that for a subsonic engine prescribe 100% of rated engine thrust at take-off, 85% during climb, 30% in approach, and 7% in idle. ICAO has also established an efficient semiempirical model for CO₂ and NO_x emissions computation. It is based on the observation that the main source of CO and BC is the incomplete combustion of the hydrocarbon-based fuel at low throttle settings [32]. Emitted CO₂ can be derived from CO and BC emissions by difference, since all the carbon in the fuel that does not go into CO or BC is transformed in CO₂. Experimentally, the mean emission index for both CO and BC can be derived from the following expression

$$\mathit{E}{\mathit{I}}_{\mathit{C}\mathit{O}-\mathit{H}\mathit{C}}\left(\mathit{\tau }\right)={\mathit{c}}_1+\mathbf{exp}\left(-{\mathit{c}}_2\mathit{\tau }+{\mathit{c}}_3\right),$$

(3)

where the nonlinear regression parameters, estimated using the ICAO database, are $\mathbf{c}=\left\{\mathrm{0.556,10.208,4.068}\right\}$ and $\mathbf{c}=\left\{\mathrm{0.083,13.202,1.967}\right\}$ for, respectively CO and BC [33]. The resulting mean reference value for CO₂ emission index is 3.16 ton CO2/ton fuel, under the ansatz of burning Jet-A1, a widely used hydrocarbon-based fuel for turbofan engines [34].

With similar arguments, it can be estimated the emission of nitrogen oxides, formed at high combustion temperatures, leading to reaction of atmospheric bi-atomic oxygen and nitrogen. Mean NO_x emissions from currently operated aircrafts can be estimated into the ICAO formal framework by using the expression:

$$\mathit{E}{\mathit{I}}_{\mathit{N}{\mathit{O}}_{\mathit{x}}}=7.32{\mathit{\tau }}^2+17.07\mathit{\tau }+3.53.$$

(4)

An empirical correction to ICAO approach, usually dubbed Method 2, has been developed by Boeing since mid-90’s [35,36]. Method 2 increases the accuracy of ICAO estimation, by introducing corrections to EI’s accounting for changes in ambient temperature, pressure, and relative humidity [37,38], leading to differences in the engine chemical reaction efficiency.

Contrails Modelling

The approaches described so far can be employed for evaluating the emissions of CO2 as well as some of the “Non-CO2” compounds, like SOx and NOx. Condensation trails (usually contracted in “contrails”) originating in aviation [39,40,41], given their peculiar nature, deserve a different discussion. Environmental impact of contrails, particularly for their potential radiative forcing, is thought to be comparable to that ascribed to CO2, although its quantitative evaluation is affected by large uncertainties due to the knowledge gaps concerning their formation, persistence, and variability with atmospheric variables.

Contrails form in the expansion of the engine plume, mixing with the atmosphere. The exhaust, warmer than air, bears a larger amount of water vapor. Contrails originated in aviation can be mainly observed in the upper troposphere, when a turbo-fan engine is employed, as it is the case for the currently-operated medium- and long-haul flights. A global thermodynamic criterion for evaluating the probability of a contrail formation is the Schmidt-Appleman Criterion (SAC) [42], named after the scientists who pioneered studies in atmosphere thermodynamics and physical chemistry.

Schmidt-Appleman Criterion assumes an adiabatic and vapor-conserving mixing process between the exhaust and the atmosphere. In fact, the hot and consequently humid engine plume attains local liquid saturation conditions, generating water droplets that can freeze. In order to observe the phenomenon, the slope of the exhaust mixing curve is evaluated, assuming the same diffusion rate for heat and vapor [43]. The point in a Temperature-Partial vapor pressure graph representing the plume-atmosphere mixture evolves along a straight line, whose slope $\mathit{G}$ can be expressed as:

$$G={\displaystyle \frac{P_v-P_{v\mathrm{\infty }}}{T-T_{\mathrm{\infty }}}},$$

(5)

whit $P_v=X_{H_{2}O}P$ representing the water-vapor partial pressure, $X_{H_{2}O}$ the water molar fraction, the underscript $\mathrm{\infty }$ indicates the full mixed system and T indicates the temperature. For a turbo-fan engine, the slope parameter in Equation 5 has an analytical expression as a function of the air pressure and the engine efficiency [44]:

$$G={\displaystyle \frac{c_p{P}_{\infty }}{ϵ}}{\displaystyle \frac{E{I}_{H_{2}O}}{\left(1-\eta \right)Q}},$$

(6)

in which ${\mathit{c}}_{\mathit{p}}$ represents the isobaric specific heat capacity of air, measured at constant pressure, $\mathit{ϵ}=0.622={\mathit{W}}_{{\mathit{H}}_2\mathit{O}}/{\mathit{W}}_{\mathit{a}\mathit{i}\mathit{r}}$ the water/air molar masses ratio, $\mathit{E}{\mathit{I}}_{{\mathit{H}}_2\mathit{O}}$ the water vapor emission index [1,45,46], $\mathit{Q}$ the total heat released per fuel mass, and $\mathit{\eta }$ = (thrust × distance per mass of fuel)/$\mathit{Q}$ the engine efficiency in cruise conditions, with the heat in the engine plume expressed as $\left(1-\mathit{\eta }\right)\mathit{Q}$.

Threshold temperature for contrails is derived from ${\mathit{P}}_{\mathit{s}\mathit{a}{\mathit{t}}_{\mathit{v}}}^{\mathit{l}\mathit{i}\mathit{q}}$, the partial pressure of liquid water-steam phase transition described by the Clausius-Clapeyron equation [47,48]:

$${\displaystyle \frac{d{P}_{sa{t}_v}^{liq}}{dT}}={\displaystyle \frac{1}{T}}{\displaystyle \frac{Q^{lat}\left(T\right)}{{\alpha }_v-{\alpha }_l}},$$

(7)

in which $Q^{lat}\left(T\right)$ is the latent heat of evaporation/condensation, and ${\alpha }_v$, ${\alpha }_l$, the specific volume of the vapour and liquid phases, respectively. Threshold temperature, $T_{th}^{*}$, for condensation is given by the tangent point between the mixing line and the slope curve:

$${\left.{\displaystyle \frac{d{P}_{sa{t}_v}^{liq}}{dT}}\right|}_{T_{th}^{*}}=G.$$

(8)

How long a contrail persists in atmosphere, transforming in a cloud [49] undistinguishable from a natural cirrus [50] at sight, determines its environmental impact. The condition to persist is to lay above the vapour-ice saturation curve. This condition can be relaxed if soot and sulfuric acid aerosols in the plume are available as condensation nuclei for the microscopical water drops. In fact, at microscopical level contrail cirri do are distinguishable from natural clouds for a difference in the water particle dimension spectrum [51,52]. The radiative forcing of a contrail depends on the radiative properties of its ice crystals’ [53], since aggregates of smaller ice particles scatter more shortwave radiation than an equivalent single ice crystal. Unfortunately, measurement campaigns performed so far do not provide a significant statistic, leaving a large range of uncertainty in evaluating contrail formation and evolution [43,54].

The interested reader is referred to [55,56,57,58,59,60,61] for further details on the formation, persistence and radiative forcing modelling of condensation trails in aviation.

5. Emissions Reduction

Fifty years ago, first seminal studies appeared [62], considering the possibility to automatically optimize an aircraft trajectory according with a given objective, generating off-line a static optimal path for the aircraft. These studies have been translated, from the mid 70’s till the end of 90’s, into several algorithmic approaches, mostly optimizing vertical guidance and standard turns, as the well-known direct great circle arcs and constant-bank turns for lateral path planning.

Significant savings were introduced with respect to manual operational paradigms, even if an effective real-time strategy was still missing. In fact, general routes found with static approaches can be largely suboptimal at ATM scale, were weather, traffic congestions and local phenomena (volcanic ash, NOTAM,…) are considered. Four-Dimensional Trajectories (4DT) represent a substantial evolution with respect to the limitations of flight plans submitted offline as static entities, whose optimality is progressively compromised by unforeseen weather and traffic circumstances.

The need for an holistic real-time approach in ATM and ATC has led, in the last two decades, to the development of several innovative approaches to the problem of 4D trajectories optimization. These algorithms aim to replan four-dimensional paths by incorporating updated weather conditions, traffic constraints, and environmental objectives, making them particularly suitable for reducing CO2 and non-CO2 emissions.

5.1. Multi-Objective Optimization

Multi-Objective Trajectory Optimization (MOTO) focuses on optimizing flight paths, accounting for both en-route and Terminal Manoeuvring Area (TMA) operations, thus simultaneously addressing operational efficiency and environmental concerns. In fact, by recalculating and optimizing aircraft trajectories in real-time, MOTO balances multiple objectives, such as fuel efficiency, emissions reduction, and time minimization. This approach has been developed and refined over the last few years, thanks to research in optimal control theory, trajectory planning, and dynamic system optimization [63,64,65,66,67,68].

MOTO algorithms start with an essential modelling of a number of systems and processes involved in the aviation industry, including the environment, operations, and the aircrafts themselves. These models include, among the others, local/global weather, operational costs, pollutant emissions, airspace structure, contrails, and aircraft noise. The optimisation in terms of multiple conflicting objectives $J_k=Q_k\left(p\right)k\in [1,n_J]$ leads to a large set of solutions that can be considered optimal in a broad sense. A point in the design space ${\mathit{p}}^{\mathit{*}}\in P$ is defined Pareto optimal if and only if there does not exist another point $\mathit{p}\in P$ such that $\mathit{Q}\left(\mathit{p}\right)\le \mathit{Q}\left({\mathit{p}}^{\mathit{*}}\right)$ and $Q_i\left(\mathit{p}\right)<Q_i\left({\mathit{p}}^{\mathit{*}}\right)$ for at least one $i$.

The Pareto front, also called the Pareto frontier, is the set of all the Pareto optimal points. Pareto optimal points are non-dominated, meaning that it does not exist another solution that strictly dominates the Pareto optimal solution in terms of any objective. Conceptually, the Pareto front is the multi-objective and multi-dimensional equivalent of the individual optimal solution resulting from single-objective optimisation problems. Due to the fact that, in many applications, a single solution is ultimately sought for, even in large complex problems, multi-objective optimisation techniques shall lead to the selection of a single optimal solution that must be Pareto optimal, eventually at least in the weak sense, and thus must belong to the Pareto front.

Therefore, a trade-off selection strategy must be introduced, in order to identify a single optimal solution from the large set of compromise solutions: this is the subject of multi-objective optimisation theory. Following the growing social concerns on environmental impact, research in MOTO has increasingly addressed CO2 and non-CO2 emissions reduction, including contrails avoidance in both established and innovative propulsive solutions [69,70,71,72,73,74].

5.2. Simulation-Based Evolutionary Optimization

Another effective method for optimizing Air Traffic Management systems leverages computational intelligence techniques, specifically Agent-Based Modelling and Simulation (ABMS) combined with Evolutionary Computing (EC). These methodologies are applied to address the inherent complexities of ATM, a socio-technical system involving numerous physical and human actors working within highly dynamic environments.

As a recognised reference in the field, the study [57] focuses on enhancing ATM performance metrics, such as timeliness, fuel efficiency, safety, and workload distribution, through a simulation-based optimization framework capable of analysing and fine-tuning operational parameters. The core of the approach lies in a distributed simulation architecture designed to perform offline "what-if" analyses during ATM's strategic and pre-tactical phases. This framework incorporates real-world traffic data and simulates ATM scenarios to evaluate ATM related performances under various conditions. The ABMS component models the human behaviour, particularly the one of Air Traffic Controllers (ATCOs), whose decision-making processes are critical to system performances. The simulation framework accounts for human-related variables, such as workload and stress levels, in addition to technical constraints, such as airspace configuration and aircraft separation minima.

In [57], the optimization process is driven by a parallel implementation of the Non-Dominated Sorting Genetic Algorithm (NSGA)-II evolutionary algorithm, a Pareto-based multi-objective optimization method. This algorithm explores a vast search space of possible ATM configurations to identify Pareto-optimal solutions that balance conflicting objectives, such as minimizing delays while ensuring safety. The simulation evaluates each candidate solution against predefined performance metrics, including fuel consumption, sector occupancy, and the timeliness of flight trajectories. The study highlights the utility of evolutionary algorithms in finding trade-offs between competing objectives, enabling ATM improvements that consider both operational and environmental criteria.

Experimental validation is performed in [57] using real-world ATM scenarios, including high-density airspaces managed by Italian control centres. Case studies, such as transitions from direct to emerging free routing paradigm, are used to test the model's ability to replicate complex traffic dynamics and emergent behaviours. Results demonstrate the effectiveness of the framework in optimizing critical parameters like horizontal separation minima and airspace sectorization. These optimizations yield improvements in timeliness and workload distribution while maintaining safety standards.

5.3. Air Traffic Flow Mangaement with Emissions Considerations

Air Traffic Flow Management (ATFM) can also play a crucial role in reducing emissions. By formulating the ATFM problem as a bi-objective Mixed-Integer Linear Programming (MILP) model, it is possible to minimize both CO2 emissions and total delay costs. This approach uses a Pareto-based scalarization technique to balance the trade-offs between emissions and delays. Reference [58] proposes an innovative methodology that incorporates ground delays, air delays, rerouting, and emissions minimization into ATFM decisions. The study addresses a gap in prior research, which has often focused on either operational delays or emissions without integrating the two in a unified optimization framework.

In [58], the model considers various operational constraints, such as airport and airspace capacities, aircraft turnaround times, and predefined flight paths. Objective functions minimize delay costs, factoring ground and air holding penalties and rerouting costs, and CO2 emissions, which are demonstrated based on fuel consumption rates tied to aircraft type and passenger load. A scalarization method, the weighted comprehensive criterion, is employed to solve the bi-objective model, by transforming it into a single-objective optimization problem. The Pareto front generated from varying weights between delay and emission objectives provides insights into the trade-offs involved in achieving a balanced solution.

The authors of the study [58] also performed a numerical study on a 30-airspace sector network with 200 flights, which has demonstrated the practical applications of the model. Results show that the prioritization of the CO2 reduction objective leads to increased ground delays and reduced air holding and rerouting. For example, minimizing CO2 emissions by 0.34% results in a 6.18% increase in delay costs. The study highlights that ground holding is favoured over air holding when focusing on emissions, as airborne delays incur higher CO2 penalties. The model also reveals the impact of operational decisions, such as rerouting limitations, on overall system performances and environmental outcomes.

6. Metrics for Evaluating Impact

The alteration in the atmospheric composition disrupts Earth’s radiative equilibrium. To restore equilibrium, the near-surface temperature increases, prompting the Earth’s surface to emit additional energy back into space. As a result, the Earth eventually establishes a new equilibrium state, albeit at a higher surface temperature. The degree of temperatures increase near the ground, in response to the initial radiative imbalance, is controlled by the climate sensitivity parameter, λ, which varies among different climate forcers.

The duration over which an emission influences near-surface temperatures is determined by two distinct timescales. First, the persistence of the radiative imbalance is governed by the lifetime of the atmospheric perturbation: for instance, while a fraction of emitted CO₂ can remain in the atmosphere for several centuries, contrails typically dissipate within a few hours. The second timescale is related to the physical response of the climate system to the radiative imbalance, a response modulated by the inertia of the coupled atmosphere-ocean system. This means that a one-year pulse emission of a short-lived species will initially produce a substantial near-surface temperature change that, then, gradually diminishes. Instead, a one-year pulse of CO₂ will induce a temperature increase that builds over several decades, before it eventually declines.

Different climate forcers influence the climate in diverse ways, exhibiting variations in sign, lifetime, and spatial distribution. Therefore, it is crucial to employ a metric that takes these differences into account when assessing the climate impact of various technologies or scenarios. A climate metric provides a direct quantitative link between an emission and its climatic effect. The interpretation of climate impact depends on the specific question being posed; as one proceeds further along the chain from emissions to damage, the significance of the impact increases, but so does also the uncertainty associated with its estimation. Furthermore, because economic assumptions (such as depreciation or inflation rates) are integral to monetizing damage, such estimates are no longer regarded as strict physical climate metrics.

An illustrative example [75] underscores the importance of selecting an appropriate climate metric. When considering the radiative forcing of a newly constructed coal-fired power plant over time, initially the cooling effect from both direct and indirect sulphate aerosol processes dominates, leading to an overall cooling influence despite CO₂ emissions. However, owing to the long atmospheric lifetime of CO₂, its warming effect accumulates over time and eventually surpasses the initial cooling, with CO₂’s warming contribution becoming predominant after approximately 20 years. If one were to consider only the radiative forcing at the 20-year mark, the coal-fired power plant might be mistakenly classified as climate-friendly. Thus, the choice of a climate metric must be aligned with the specific research question and is typically composed of three interrelated aspects: the evolution of emissions over time, the selected climate indicator, and the chosen time horizon.

In summary, climate metrics provide a quantitative measure linking emissions (or a pulse of emissions) to their ultimate effect on Earth’s energy balance and near-surface temperature. They are essential for comparing different technologies and emission scenarios, by offering a common scale for impact assessment. Common metrics include:

−

Radiative Forcing (RF), which indicates the instantaneous change in the net (down minus up) radiative flux (W/m²) due to an atmospheric perturbation. The concept of radiative forcing is central to understanding how an emission perturbs the climate system. A common formulation for CO₂ is:

$$\Delta F=\kappa ln\left({\displaystyle \frac{C_0}{C}}\mathrm{}\mathrm{}\right)$$

(9)

where ΔF is the change in radiative forcing (W/m²), κ is a constant (typically about 5.35 W/m² for CO₂), C is the current concentration, and C₀ is the pre-industrial baseline concentration. For non-CO₂ agents, adjustments are made to account for rapid atmospheric adjustments (e.g., stratospheric temperature, cloud effects), leading to definitions of adjusted and Effective Radiative Forcing (ERF).

−

Global Warming Potential (GWP), which is the integrated radiative forcing over a specified time horizon normalized to the forcing of CO₂. GWP is defined over a time horizon τ as:

$${\mathrm{G}\mathrm{W}\mathrm{P}}_x\mathrm{}(\mathrm{\tau })={\displaystyle \frac{{\int }_0^{\tau }{a}_x\left(t\right)dt}{{\int }_0^{\tau }{a}_{C{O}_2}\left(t\right)dt}}$$

(10)

where $a_x\left(t\right)$ is the radiative forcing at time t per unit emission of substance x, and $a_{C{O}_2}\left(t\right)$ is the corresponding radiative forcing for CO₂. Variations on this well-established metric have been developed, including Efficacy-weighted Global Warming Potential (EGWP), that is a modified GWP that incorporates the climate “efficacy” (i.e., the relative effectiveness of a given emission in causing temperature change), and GWP* and Extended GWP*, that aim to better represent the temperature impacts of short-lived climate pollutants.

−

Global Temperature change Potential (GTP), which is the change in near-surface temperature at a given future time due to an emission pulse, relative to CO₂.

−

Average Temperature Response (ATR), referring to the time-averaged temperature change over a defined period following an emission pulse. ATR links the integrated temperature response to a pulse emission. It is often calculated as:

$${\mathrm{A}\mathrm{T}\mathrm{R}}_x\mathrm{}\left(\mathrm{T}\right)={\displaystyle \frac{1}{T}}{\int }_0^T{\mathsf{\Delta }\mathrm{T}}_x\left(t\right)dt$$

(11)

where ${\Delta T}_x\left(t\right)$ is the temperature change at time t following the emission pulse and T is the chosen time horizon (e.g., 100 years).

To facilitate comparisons between different technologies, the Climate Metric (CM) can be converted into equivalent CO₂ emissions (eqCO₂). If $C{M}_{tot}$ is the total climate impact (including all greenhouse and non-greenhouse effects) and $C{M}_{C{O}_2}$is the impact per ton of CO₂, the conversion factor is given by:

$$eqC{O}_2={\displaystyle \frac{C{M}_{tot}}{C{M}_{C{O}_2}}}\times C{O}_2$$

(12)

This factor allows the total impact of a complex emission mix to be expressed in terms of a single and familiar unit: the tons of CO₂.

In the example of the coal-fired plant, the emissions development is a constant over time as the power plant is constantly used, the climate indicator is RF, and the time horizon is 20 years.

Thus, the introduction of a climate metric also allows to concretely measure the impact of solutions designed to reduce or mitigate the effects of the considered emissions.

For instance, current flight planning research [76,77,78,79] predominantly emphasizes micro-scale studies, independently optimizing aircraft trajectories. Nevertheless, the ATM system functions as an intricate network, necessitating the combination of microscale trajectory optimization with macro-scale ATM network oversight for environmentally sustainable operations. Balancing capacity and demand are essential at ATM network level, frequently necessitating measures such as postponing or rerouting aircraft. Conventional capacity-demand alignment is being updated via initiatives aimed at shifting from the usual sector-based to the recently introduced trajectory-based management paradigm. Nevertheless, current methods neglect climate influences and do not incorporate network interactions into strategic deconfliction techniques, missing out on collective behaviour and uncertainties within the ATM network.

Consequently, it is necessary to address the void in existing studies regarding cli-mate-optimized flight planning, which pertains to allowing flight planning to include diverse fuel types and aircraft technologies. Indeed, ongoing studies mainly concentrate on traditional kerosene fuel, and the planning of flights for various fuel types and aircraft categories remains unexamined. To explore how the integration of new technologies and fuel types affects traffic distribution patterns and ATM strategies in particular climate-sensitive regions, evaluating the capacity, efficiency, and environmental consequences of various operational scenarios necessitates flight planning that con-siders diverse fuel types and aircraft propulsion technologies. This also includes the consideration of Sustainable Aviation Fuels (SAF) as well as liquid hydrogen and of new promising powerplants, such as the ones based on the exploitation of fuel cells to power the future aircraft electric propulsion systems.

For example, the climate response to emissions from fuels besides kerosene can differ, leading to alterations in climate-sensitive areas' polygons, and, in some scenarios, it might remove the need for flight rerouting. To tackle this, alongside modifying climate change models, it is necessary to create aircraft dynamic models for these new fuel types and technologies and to adjust flight planning tools to account for these elements. Therefore, the subsequent limitations emerge concerning the ATM network scale:

Flight planning for climate optimization has yet to be conducted for fuels and aircraft types beyond conventional kerosene fuel, which is essential for grasping how emerging technologies affect traffic distribution patterns and ATM strategies.

Climate impacts are not consistently considered to restrict system capacity (as practiced in certain European cities to control road transport) and are typically not integrated into any network-level modelling and solution strategies. Pinpointing environmental hotspots in the airspace and integrating them into comprehensive aerial traffic management strategies constitutes a scientific gap that certainly requires addressing.

The development of self-evolving models based on AI techniques, particularly reinforcement learning, with fast execution times can be useful for addressing the challenges of optimizing trajectories at air transport network level, which involves all daily traffic in Europe, including approximately 30,000 flights. Therefore, the ability to solve large-scale simulations and develop network-wide climate indicators is crucial.

To manage international operations, like aviation, market-driven tools (taxes, charges, marketable permits, etc.) are frequently favoured as they theoretically attain climate objectives in an economical way. Nevertheless, due to the incomplete understanding of the non-CO₂ effects and their association with medium to high uncertainties, no environmental policy measures have been implemented in aviation regarding non-CO₂ effects.

Numerous studies have been proposed to reduce the climate impacts of non-CO2 emissions by changing aircraft manoeuvres to avoid climate-sensitive regions. These studies differ mainly in (1) how the climate-sensitive areas are defined and (2) how climate-friendly trajectories are determined [80]. The first attempts to consider climate hotspots were based on areas sensitive to the formation of persistent contrails [81]. In order to provide information on the spatial and temporal dependency of non-CO2 effects, Climate Change Functions (CCFs) were developed. These CCFs provide the climate impact of aviation emissions per flown kilometre and per emitted mass of the species as five-dimensional datasets (i.e., longitude, latitude, altitude, time, type of emission) [82].

Due to their computational complexity, CCFs were not suited for real-time operations. Therefore, the so-called algorithmic CCFs (aCCFs) were developed. The aCCFs provide a very fast computation of the individual non-CO2 climate impact, as they are based on mathematical formulae, which only need relevant local meteorological input parameters (e.g., [83]). The aCCFs are well-suited for trajectory optimization tools, due to their computational efficiency [84]. An enhanced and consistent set (with respect to emission scenario, metrics, etc.) of aCCFs has recently been developed and introduced within the EU project FlyATM4E [85].

As for climate-optimal trajectory planning methods, various strategies ranging from mathematical programming [86] to meta-heuristic [87], indirect optimal control [88], and direct optimal control methods [89] have been adopted. For instance, the direct optimal control approach has been employed in [90] to minimize flight time (or distance flown) in areas sensitive to persistent contrail formation, in [89] to minimize average temperature response over the next 20 years (ATR20) associated with non-CO2 emissions, and in [91] to minimize the global warming potential (GWP) of NOx, H2O, soot, SO2, and contrails. Using aCCFs to quantify climate impacts, [92] employed a genetic algorithm to determine climate-optimal aircraft trajectories.

Regarding the optimization methodologies, the mathematical programming methods only apply to simplified aircraft trajectory optimization problems (e.g., in the study conducted in [86], the aircraft's dynamic behaviour is represented with a linearized model). The meta-heuristic methods (e.g., genetic algorithm) require very fast aircraft trajectory prediction in order to find an optimal solution with a large number of iterations; thus, the flight planning problem is usually approximated with a simplified but representative enough problem (e.g., in [92], the optimization is defined with 11 decision variables to characterize lateral path and flight altitude, and the speed profile is considered constant).

Finally, with the optimal control methods, the capability to model more accurate aircraft trajectory optimization problems is provided, since the problem is represented as a dynamic optimization problem. Nevertheless, there are some drawbacks associated with addressing the formulated problem. The dynamic programming method (as an optimal control approach) results in the “curse of dimensionality” for complex problems (e.g., a full 4D aircraft trajectory optimization problem). Regarding the indirect optimal control approach, deriving analytical solutions using Pontryagin's maximum principle is daunting, especially for problems with singularities (e.g., only a 2D trajectory optimization problem has been addressed in literature [88]).

The direct optimal control approach, despite being very flexible in modelling aircraft trajectory optimization problems (e.g., considering a full 4D dynamical model with nonlinear path and boundary constraints [89]), has a high sensitivity to initial conditions, and thus local optimality is its main drawback. In addition, considering the airspace structure with indirect and direct optimal control methods is not straightforward. Interested readers are referred to [93] for a recent survey on climate-optimal aircraft trajectory planning, reviewing both the approaches to model climate-sensitive regions and trajectory planning methods.

To quantify the non-CO2 climate effects, specific weather variables are required. In the case of aCCFs, variables such as temperature, potential vorticity, geopotential, relative humidity over ice, and outgoing longwave radiation are needed. These variables are obtained from standard weather forecasts. Several factors, including incomplete understanding of the state of the atmosphere, computational complexity, and nonlinear and sometimes chaotic dynamics, affect the accuracy of weather predictions, implying that the weather forecast is inevitably uncertain [94]. These weather-forecast-related uncertainties in the aCCFs and also in aircraft dynamical behaviour (e.g., uncertainty in wind and temperature), if not accounted for within aircraft trajectory planning, can lead to inefficient trajectories.

Previous research in the field of climate-optimal aircraft trajectory planning has been conducted in a deterministic manner, neglecting the inclusion of any sources of uncertainty [93]. A first step in managing and integrating meteorological uncertainties into aircraft path planning consists of obtaining reliable weather forecasts that can predict probable variations in meteorological conditions. To characterize weather forecast uncertainties, Probabilistic Weather Forecasting (PWF) is typically used [95]. State-of-the-art probabilistic weather forecasting is obtained from the Ensemble Prediction System (EPS), which provides N_EPS possible realizations of meteorological conditions called ensemble members [97].

Thus, from the operational point of view, the mitigation of aviation climate impact is achieved by modifying aircraft manoeuvres to avoid areas where those non-CO₂ effects are significantly enhanced, called Climate-Sensitive Regions (CSR). The manoeuvres can be the change of departure time, cruise altitude, lateral path, speed profile, and combinations of them. Therefore, to select a proper climate-aware trajectory for aircraft, information regarding climate-sensitive regions needs to be available, allowing to evaluate trajectories in the sense of contribution to climate impact. Besides, the approach to determine eco-efficient trajectory based on the considered metric (i.e., representative of CSR) plays an important role in the net mitigation potential [96].

The operational mitigation strategies for aviation’s climate impact can be classified into two categories: Non-Trajectory Optimization (NTO) (or, in some cases, simulation-based) strategies and Trajectory Optimization (TO) techniques. Within NTO methods, after analysing the properties of the climate impact of non-CO₂ emissions, the route, time, or the altitude of flights are slightly changed, and the mitigation potential is explored (through simulating aircraft performance with trajectory predictors). As for TO methods, optimization techniques are employed to determine the aircraft trajectory such that a cost function containing some user-defined objectives (i.e., climate impact in this case) gets minimized.

Depending on the benchmark, there exist various classifications of trajectory optimization techniques. The study reported in [98] aims to review and classify those methods, focusing mainly on mitigating aviation’s climate impacts, in two categories: optimal control and non-optimal control approaches.

The Optimal Control (OC) is known as one of the most reliable dynamic optimization techniques since it works in continuous time, considers the system’s dynamical behaviour, can provide analytic solutions to some types of problems, and adopts numerical methods. Within optimal flight planning, the aim is to determine feasible trajectories for aircraft considering practical constraints and the objectives specified by the flight planner.

One of the main features of optimal control over other mathematical optimization approaches is the consideration of the system’s motion along the time as dynamical constraints in the optimization process, allowing to achieve feasible transition of system. As generally considered within the optimal control framework, the time derivative of the system’s state is modelled as differential algebraic equations [99]. In addition to the dynamical model of the system that is considered as differential constraints, some non-differential restrictions may be imposed over the whole-time horizon, known as path constraints. Generally, these types of constraints are formulated as equality and inequality constraints. The optimal control theory seeks admissible control policies to optimize the performance of the system with respect to some path and boundary constraints. Therefore, the optimization process needs an index to evaluate the performance. In control engineering, precisely, optimal control, such a cost functional is called the performance index. The objectives of the users should be mathematically interpreted and included in the performance index.

There exist various approaches in the literature to solve the optimal control problem. However, to select the suitable one, some factors need to be considered. Depending on the structure of the control policy (i.e., closed-loop and open-loop), online (e.g., receding horizon) and offline, level of optimality (e.g., sub-optimal and optimal or local and global solutions), type of the dynamical system (e.g., linear or nonlinear, number of state and control variables), the form of the cost functional (e.g., linear, quadratic, or nonlinear), constraints, time horizon (i.e., infinite or finite), and computational time, the applicability of these methods changes.

One classification of OC methods can be based on how they solve the optimization problem, i.e., analytically or numerically. Theoretically, Pontryagin’s Minimum Principle (PMP) and the Hamilton–Jacobi–Bellman (HJB) equation are the two main approaches that characterize optimal solutions to the OC problem. The former provides the necessary conditions for optimality, while sufficient conditions are obtained from HJB. As for the numerical approaches, indirect and dynamic programming methods are utilized to solve the problems obtained using PMP and HJB numerically, whereas the direct approach directly attempts to solve the OC problem, by converting the original infinite-dimensional problem to a finite-dimensional one.

Non-optimal control methods try to solve dynamical optimization problems in a more simplified manner. Some of the simplifications commonly assumed within these techniques are disregarding aircraft dynamics and constraints or considering them in a streamlined way, such as linearized ones. These methods aim to provide fast and, to some extent, reliable solutions, even if not resulting in the best trajectories. To tackle such optimization problems, various approaches, such as geometric methods, path-planning algorithms, combinatorial optimization, and meta-heuristics are usually employed [100]. Within these methods, the optimization problem is formulated normally without considering aircraft dynamics or considering it partially to predict the performance of trajectories such as speed, fuel burn, emission indices, and climate impacts. Then, by making use of optimization techniques, the formulated problem is solved.

For instance, if the trajectory of an aircraft is given as a sequence of discrete or/and continuous variables, and its performance can be quickly predicted, a suitable choice is a meta-heuristic approach, applying combinations of randomized heuristic procedures iteratively to enhance the candidate solution. Simulated annealing, genetic algorithms, variable neighbourhood search, and particle swarm optimization are some algorithms that are used as meta-heuristics solvers. Due to exploration and exploitation features, such algorithms are capable of providing approximate global solutions. In addition, they are not restricted to requiring gradient information and are straightforward to be implemented. Moreover, for such a class of problems, classical NLP solvers are beneficial to provide fast solutions. The main drawback of classical (or gradient-based) NLP solvers is the sensitivity to the initial guess, usually leading to local solutions.

The cost function of such optimization problems can be defined similarly in the sense of objectives to those within OC problem formulation. For instance, the Lagrange term of performance index may be approximated with a summation. Such methods are more beneficial when tackling the optimization for a high number of flights and also considering air traffic complexity (e.g., conflicts). Mathematical programming, meta-heuristics, gradient-based NLP solvers such as Successive Quadratic Programming (SQP), and interior-point are non-optimal control methods that have been employed in the literature to solve the climate optimal trajectory planning problem.

7. Conclusions

This paper reported the outcomes of an extensive and articulated multidisciplinary literature analysis about the recent advancements in modelling the aviation emissions, quantifying them in terms of metrics and reduce them thanks to specific operational procedures implementation.

More in details, the paper first provided an assessment of the state of the art, as emerging from an extensive critical analysis of the recent literature, about the main current as well as the more promising perspective operational procedures aimed to increase the efficiency of the aircraft operations while in flight (the ground operations were out of the scope of the study), in particular with reference to the flight segments occurring in the Terminal Manoeuvring Area (TMA). After briefly introducing the main issues and solutions related to all the flight phases, the study addressed the critical analysis of the more relevant approaches aimed to optimize the flight profile in TMA, in order to reduce the fuel consumption and, in turn, the related chemical emissions. Particular attention has been devoted to the consideration of the recent ATM operational paradigms leveraging the exploitation of the GNSS-based capabilities, as enabler for the implementation of the Performance Based Navigation (PBN) and of possible enhancements in the recent Continuous Descent Operations (CDO).

Following this first part of the study, focused on the ATM operational aspects, the paper addressed the assessment of the methodological literature state-of-the-art about the CO2 and non-CO2 emissions modelling. In this framework, the most important approaches have been critically analyzed and their advantages and drawbacks have been outlined. In particular, the study first considered the conventional standard approach based on the exploitation of the BADA database and then addressed the ICAO emission index. Particular attention, finally, has been devoted to the very relevant topic, gaining always increasing attention in the aviation domain, of the condensation trails (contrails) formation modelling, which represents a fundamental base of knowledge as a prerequisite to inform and support the design of future effective solutions for contrails prevention and/or contrails avoidance.

Once assessed in this way the state-of-the-art in terms of both operational and methodological domains, the study reported the analysis of the most recent optimization procedures that are considered when addressing the emissions reduction problem. These methodologies are always evolving, towards the target of enabling a real-time 4D trajectory optimization able to reduce the fuel consumption as well as the chemical emissions, while at the same time adapting the aircraft flight profile to the actual and near-future expected atmospheric conditions that may lead to the formation of contrails. The considered approaches addressed all the flight phases, both enroute and in TMA.

The last part of the paper, finally, outlined the results of an extensive study about the possible metrics that can be used in order to properly design the flight profile and trajectory optimization tools. These metrics can be beneficial in order to integrate in these optimization tools not only the short-term consideration of the aviation operation effects, in terms of immediate pollutant emissions (whose main impact is typically on the local air quality), but also the consideration of the longer-term effects of these emissions (whose impact is at climatic level), in terms of both geographical and time scales.

In summary, the paper aimed to provide an integrated multidisciplinary overview about the problem of CO2 and non-CO2 aviation emissions reduction and about its possible solutions. It addressed both the currently available know-how and operational procedures and the emerging evolutions in the methodological and procedural domains. In addition, the paper provided the reader with a detailed analysis of possible metrics that can be used when addressing the quantification of the impact of such emissions, not only over short-term and at local scale but also over long-term climatic scale and at global level.

Future studies will be devoted to the coverage of also the specific aspects that can be related to: the emerging use of Sustainable Aviation Fuels (SAF) as well as perspective exploitation of the liquid hydrogen; the consideration of future innovative hybrid as well as full electric propulsion powertrains in aviation.