Two-Stage Pricing Strategy for Supply Chain Considering Consumer Fairness Concerns

1. Introduction

The product market lifecycle can be categorized into two primary stages: introduction and maturity. During the introductory stage, there is limited consumer awareness of a new product, leading to low initial market demand. However, as the product matures over time, market demand will increase due to advertising, marketing efforts, and positive word-of-mouth. Companies often consider raising prices to boost profits and exploit this growing demand in the mature stage. However, as consumer fairness becomes increasingly recognized, the price increase during this stage may be perceived as unjust, surpassing the acceptable pricing threshold for consumers. This can lead to negative perceptions of transaction fairness and ultimately decrease market demand in the mature stage.

Numerous studies in behavioral economics have confirmed the significant influence of consumers’ perceptions of fair pricing on their purchasing decisions. Consumers tend to establish subjective benchmarks to determine what they consider a fair price for a product. When corporate pricing strategies exceed these benchmarks, it can lead to a sense of inequity among consumers and trigger negative psychological responses that significantly impact their purchasing behavior (Malc et al. 2016). For instance, in 2014, the famous American streaming platform Netflix announced an abrupt price hike, causing many consumers to view the move as taking advantage of its market dominance and reputation at the expense of loyal users. This perception decreased consumer willingness to maintain subscriptions and prompted them to consider alternative streaming services.

In the face of increasing market demand during the maturity stage, previous studies have noted that companies often choose to raise prices despite the potential for dissatisfaction among price-sensitive consumers and subsequent decreases in demand. This strategic approach aims to enhance per-unit profitability, thereby strengthening overall profitability (Diao et al. 2023). Implementing this strategy requires a deep understanding of market dynamics and consumer behavior, driven by a consistent pursuit of maximizing financial returns.

However, the presence of consumers concerned about fairness does not always lead to reduced demand. When enterprises implement price decrease strategies, it can have a positive psychological impact on fairness-conscious consumers. For instance, renowned retailers like Uniqlo have effectively utilized price decrease strategies to drive market expansion. Regular sales promotions and discounts on popular products have successfully boosted consumer demand (Khan et al. 2023). Similarly, during major shopping events like "Double 11" in China, many companies employ aggressive price reduction tactics to stimulate substantial consumer demand, resulting in year-on-year sales growth (Li and Puyang 2017). The principal driver of increased demand following a price decrease strategy is the consumers’ fairness concerns. They utilize the initially set higher prices as a reference for what they consider a fair price. This establishes a benchmark that, when lowered in the subsequent stage, resonates with their fairness expectations, thereby effectively stimulating demand.

Hence, it is crucial for companies to fully understand and take into consideration the impact of consumer fairness concerns on demand when developing effective two-stage pricing strategies. Examining how factors such as consumer fairness concerns and market growth scale affect the underlying mechanisms of these strategies in supply chain operations is of significant importance. This research addresses profit-driven price increases by monopolistic e-commerce entities and protects consumer rights. In doing so, companies can maintain competitiveness in mature markets, optimize profitability in supply chain management, and minimize adverse effects from pricing inequalities.

This paper differs from existing research in the following two main aspects: (1) Previous studies have primarily focused on the impact of price increase strategies on profits during the maturity stage. However, our research emphasizes that a decrease strategy, influenced by consumer fairness concerns, can stimulate consumer demand and prove advantageous under specific conditions; (2) Consumer fairness concerns establish a correlation between pricing strategies across the two stages, thereby constraining the pricing reaction functions of manufacturers and retailers. This correlation results in notable variations in profitability compared to scenarios that do not account for consumer fairness concerns.

2. Literature Review

The existing body of research relevant to this paper primarily focuses on exploring two main themes: consumer fairness concerns and the implementation of two-stage pricing strategies. These areas have garnered considerable attention due to their profound implications for market dynamics and consumer behavior in various economic contexts.

2.1. Consumer Fairness Concerns

Considerations beyond rational economic self-interest intricately influence consumers’ purchasing decisions. Fairness considerations are pivotal in shaping their perceptions of value, influencing their willingness to pay, and ultimately guiding their purchasing behavior. These non-economic factors are crucial in determining consumer behavior and should be taken into account when analyzing market trends and developing marketing strategies.

Research by Bolton et al. (2003) highlighted that consumer fairness concerns involve subjective evaluation of transaction terms, including price, product quality, and service levels. These evaluations are pivotal as they reflect consumers’ perceptions of whether the transactional process, especially pricing, meets their expectations of fairness and equity. Jiang et al. (2023) emphasized that when consumers perceive prices as aligned with the product’s perceived value, they are more inclined to make purchases. Conversely, as highlighted by Hou et al. (2024), perceived price inequity can significantly deter purchasing behavior, even in the face of solid product appeal. Moreover, the implications of fairness extend beyond individual transactions. Yi et al. (2018) argued that brands perceived as fair benefit from enhanced consumer loyalty and positive word-of-mouth, contributing to sustained market presence and competitive advantage. However, instances of perceived unfairness can trigger assertive consumer responses such as complaints, boycotts, or negative word-of-mouth campaigns, as noted by Allender et al. (2021), posing significant risks to a company’s reputation and market position. Further complicating matters, Diao et al. (2023) suggested that consumers with heightened fairness concerns exhibit greater price sensitivity and hold higher expectations regarding price fairness. This sensitivity underscores the importance of considering fairness in pricing strategies across various industries.

Extensive research has demonstrated the critical importance of considering consumer fairness concerns in developing effective supply chain pricing strategies. This factor directly influences how consumers perceive price changes and subsequently impacts their purchasing decisions, ultimately profoundly affecting corporate profit maximization.

Yang et al. (2022) explored how retailers can strategically leverage fairness perceptions to enhance profitability under specific conditions. Meanwhile, Gönsch et al. (2013) highlighted the profound influence of fairness concerns on supply chain dynamics, affecting profitability and strategic decisions at every stage. Strategically, Zhang et al. (2019) found that addressing consumer fairness concerns can mitigate price competition and help sustain profit margins within supply chains. Moreover, Yoshihara and Matsubayashi (2021) observed that integrating fairness considerations into dynamic pricing decisions can optimize supply chain efficiency, particularly in complex market environments. Ultimately, Liu et al. (2022) argued that collaborative approaches between manufacturers and retailers, grounded in fairness principles, can yield mutually beneficial outcomes. This approach involves setting competitive yet fair prices that resonate with consumer expectations and perceptions, fostering long-term consumer trust and sustained profitability. In sum, integrating fairness considerations into pricing strategies is not just a matter of consumer preference but a strategic imperative for companies aiming to navigate competitive markets effectively while safeguarding their brand reputation and fostering consumer loyalty.

2.2. Two-Stage Pricing

Consumer psychology and behavior play a crucial role in shaping the effectiveness of two-stage pricing strategies within supply chains, particularly concerning how consumers accept and respond to pricing strategies across different sales stages. The impact of these strategies on consumers’ psychological perceptions and behavioral choices significantly influences the dynamics of supply chain management.

Research by Prakash and Spann (2022) highlighted that while dynamic pricing strategies offer flexibility in responding to market changes, frequent price fluctuations can influence consumers’ perceptions of fairness. Retailers can leverage this understanding to mitigate the negative impact of consumer fairness concerns on demand. Similarly, Aviv et al. (2019) argued that adopting a two-stage dynamic pricing strategy can optimize supply chain efficiency and profitability by adjusting prices per market dynamics, thereby effectively addressing consumer fairness concerns. Moreover, Liu et al. (2022) underscored the critical role of consumer fairness concerns in shaping purchasing decisions under two-stage pricing scenarios, emphasizing the need for strategies that enhance perceived fairness and predictability.

Market demand dynamics significantly impact strategic pricing decisions throughout different stages of a product’s life cycle. Enterprises must effectively navigate these fluctuations to ensure that their pricing strategies remain efficient and competitive in the marketplace.

According to Li et al. (2019), adopting tailored pricing strategies throughout a product’s life cycle allows enterprises to effectively accommodate shifts in market demand. Gönsch et al. (2013) advocated for flexible pricing adjustments that align with consumer responses to the dynamic nature of market demand. As products mature, Chen et al. (2020) suggested that enterprises face challenges adjusting pricing strategies to meet evolving market needs, necessitating strategic adaptations to sustain consumer interest and market share. In the maturity stage, strategic choices such as those discussed by Che et al. (2021), balancing brand prestige with promotional pricing strategies, become crucial for market positioning and profitability. Additionally, Taleizadeh et al. (2020) proposed leveraging higher introductory prices to establish a high-end product image, followed by price reductions during maturity to broaden consumer appeal and maintain competitiveness.

Understanding the consumer-centric dynamics is crucial for supply chain enterprises that aim to optimize pricing strategies throughout the product life cycle. By aligning pricing decisions with consumers’ perceptions of fairness and market demand dynamics, businesses can effectively improve profitability, maintain a competitive advantage, and encourage consumer loyalty.

The existing literature extensively discusses consumer fairness concerns and their application in market strategies, highlighting the influence of consumers’ sensitivity to price changes on their purchasing decisions. However, there is a significant research gap concerning how consumers form psychological expectations of pricing based on selling prices and how these expectations shape their responses to price adjustments. Moreover, while existing studies analyze the impact of consumer behavior on supply chain pricing and profits, they often overlook the integration of consumer fairness concerns into two-stage pricing strategies and their impact on strategy effectiveness.

This study aims to bridge these gaps by conducting a comprehensive analysis of consumer fairness concerns and their impact on the pricing strategies adopted by manufacturers and retailers within the supply chain. The research will explore various factors in the dynamic market environment, including market growth scale, consumer fairness concern coefficients, and decision-making strategies within supply chains, all of which collectively influence pricing decisions and affect the profitability of manufacturers and retailers. Specifically, this study will examine the implications of implementing price increase or decrease strategies under different market conditions, providing new insights and strategic recommendations for optimizing supply chain management practices. The goal is to contribute to a deeper understanding of consumer-centric pricing strategies and their role in sustaining supply chain operations and fostering growth to address existing research gaps.

3. Problem Description and Parameter Assumptions

This paper examines the strategy of a manufacturer selling its products through a retailer in two stages. The manufacturer sets the wholesale price within each stage, and then the retailer determines the retail price. The manufacturer operates with a constant marginal cost normalized to zero for simplicity. This paper investigates the impact of implementing price increase or decrease strategies in the second stage on the profits of the manufacturer, retailer, and overall supply chain when facing a growing market with consumer fairness concerns (CFC). The analysis considers both decentralized and centralized decision-making scenarios. The specific decision-making process is depicted in Figure 1.

This paper investigates a scenario where a manufacturer sells its products through a retailer over two stages, $t\in \{1,2\}$. In each stage t, the manufacturer sets the wholesale price $w_t$, and subsequently, the retailer determines the retail price $p_t$. The manufacturer has a constant marginal cost, normalized to zero for generality. The paper explores the impact on the profits of the manufacturer, the retailer, and the overall supply chain when the retailer faces an expanding market that includes consumers concerned with fairness. This analysis is conducted for decentralized and centralized decision-making scenarios, particularly examining the effects of adopting price increase or decrease strategies in the second stage. For clarity, Table 1 presents the parameters and symbols utilized in the model of this paper alongside their respective definitions.

4. Centralized Decision-Making Scenario

4.1. Benchmark Model

In order to better understand and articulate the impact of consumer fairness concerns on supply chain pricing and profits, this paper presents a Stackelberg game model in which the manufacturer acts as the leader and the retailer follows, serving as a benchmark for a scenario without consumer fairness concerns. The decision sequence unfolds as follows: first, the manufacturer determines the wholesale price $w_1$ in the initial stage; next, the retailer establishes the retail price $p_1$; then, for the second stage, the manufacturer sets a new wholesale price $w_2$; finally, the retailer decides on the retail price $p_2$ for sales.

This paper assumes that the market demand for the first stage is $D_1=1-\beta p_1$, where $\beta$ represents the price elasticity of market demand, and this demand function form has also been widely adopted by other scholars (Moorthy 1988, Yan and Bandyopadhyay 2011). As time goes on, considering that consumers will be positively influenced by the effects of advertising and positive word-of-mouth, the market size in the second stage will increase by $\delta$ compared to the first stage, that is $D_2=1+\delta -\beta p_2$. At this point, the total profit of the manufacturer and retailer is $\pi =p_1{D}_1+p_2{D}_2$. The optimal pricing and total profit can be obtained by taking the derivative concerning $p_1,p_2$ simultaneously and solving the system of equations. The equilibrium results are summarized in Proposition 1.

Proposition 1. 

In the centralized decision-making scenario, when there are no consumer fairness concerns in the market, the optimal pricing for the first and second stages is $p_1^{*}={\displaystyle \frac{1}{2\beta }}$ and $p_2^{*}={\displaystyle \frac{1+\delta }{2\beta }}$, respectively, and the optimal total profit for the supply chain is ${\pi }^{*}={\displaystyle \frac{1+{(1+\delta )}^2}{4\beta }}$.

4.2. Pricing Decisions Considering Consumer Fairness Concerns

At this stage, the demand in the first stage remains $D_1=1-\beta p_1$. As time progresses, the initial market size for the second stage will increase. At this juncture, the retailer has two options: a price increase strategy and a decrease strategy.

4.2.1. Price Increase Strategy

If the retailer implements a price increase strategy, it will have a detrimental psychological impact on consumers who prioritize fairness in their purchasing decisions. This, in turn, will affect demand in the second stage of the supply chain. The paper presents the demand of the supply chain in the second stage in the following format:

$$D_2^{PI}=1+\delta -\beta p_2^{PI}-\gamma max\{p_2^{PI}-p_1^{PI},0\}$$

(1)

Here, $\gamma max\{p_2^{PI}-p_1^{PI},0\}$ represents the negative impact of the price increase on the demand of consumers who are concerned with fairness, where $\gamma (0<\gamma <1)$ indicates the degree of consumer fairness concerns. Generally, $\beta >\gamma$, meaning that the demand elasticity for the second stage price is greater than the price elasticity of consumer fairness concerns. This assumption helps simplify subsequent proofs and has also been adopted by many other scholars (Giri et al. 2020, Pan et al. 2022; Taleizadeh et al. 2020).

At this point, the total profit function of the supply chain is:

$${\pi }^{PI}=\left\{\begin{array}{cc}{p}_1^{PI}(1-\beta p_1^{PI})+p_2^{PI}[1+\delta -\beta p_2^{PI}-\gamma (p_2^{PI}-p_1^{PI})],\hfill & \mathrm{if}{p}_1^{PI}<p_2^{PI}\hfill \\ p_1^{PI}(1-\beta p_1^{PI})+p_2^{PI}(1+\delta -\beta p_2^{PI}),\hfill & \mathrm{if}{p}_1^{PI}\ge p_2^{PI}\hfill \end{array}\right.$$

(2)

Using the KKT conditions (Karush-Kuhn-Tucker conditions) to solve this constrained optimization problem, similar to the benchmark model, we take the derivative of $p_1^{PI}$ and $p_2^{PI}$ in the total profit function simultaneously. The equilibrium results obtained are summarized in Proposition 2.

Proposition 2. 

In the centralized decision-making scenario, facing consumers in the market who are concerned with fairness, if the enterprise adopts a price increase strategy, then the optimal two-stage pricing for the supply chain is as follows:

$$p_1^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{\delta +2}{4\beta }},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{2\gamma }{2\beta -\gamma }}\hfill \\ {\displaystyle \frac{2\beta +3\gamma +\delta \gamma }{4\beta (\beta +\gamma )-{\gamma }^2}},\hfill & \mathit{if}\delta \ge {\displaystyle \frac{2\gamma }{2\beta -\gamma }}\hfill \end{array}\right.$$

(3)

$$p_2^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{\delta +2}{4\beta }},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{2\gamma }{2\beta -\gamma }}\hfill \\ {\displaystyle \frac{2\beta +\gamma +2\beta \delta }{4\beta (\beta +\gamma )-{\gamma }^2}},\hfill & \mathit{if}\delta \ge {\displaystyle \frac{2\gamma }{2\beta -\gamma }}\hfill \end{array}\right.$$

(4)

The optimal total profit for the supply chain under centralized decision-making is:

$${\pi }^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{{(2+\delta )}^2}{8\beta }},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{2\gamma }{2\beta -\gamma }}\hfill \\ {\displaystyle \frac{\beta {\delta }^2+(2\beta +\gamma )\delta +2(\beta +\gamma )}{4\beta (\beta +\gamma )-{\gamma }^2}},\hfill & \mathit{if}\delta \ge {\displaystyle \frac{2\gamma }{2\beta -\gamma }}\hfill \end{array}\right.$$

(5)

From Proposition 2, it can be seen that when the market growth scale $\delta$ is small, the optimal prices for the first and second stages of the supply chain are equal, that is, when $0\le \delta \le {\displaystyle \frac{2\gamma }{2\beta -\gamma }}$, $p_1^{P{I}^{*}}=p_2^{P{I}^{*}}={\displaystyle \frac{\delta +2}{4\beta }}$; moreover, the optimal two-stage pricing of the supply chain increases with the increase of the market growth scale $\delta$ and the price elasticity coefficient $\beta$, that is, ${\displaystyle \frac{\partial p_1^{P{I}^{*}}}{\partial \delta }}\ge 0$, ${\displaystyle \frac{\partial p_2^{P{I}^{*}}}{\partial \delta }}\ge 0$, ${\displaystyle \frac{\partial p_1^{P{I}^{*}}}{\partial \beta }}>0$, ${\displaystyle \frac{\partial p_2^{P{I}^{*}}}{\partial \beta }}>0$; $p_1^{P{I}^{*}}$ increases with the increase of the consumer fairness concern coefficient $\gamma$, but $p_2^{P{I}^{*}}$ decreases with the increase of $\gamma$, that is, ${\displaystyle \frac{\partial p_1^{P{I}^{*}}}{\partial \gamma }}>0$, ${\displaystyle \frac{\partial p_2^{P{I}^{*}}}{\partial \gamma }}<0$, which is in line with intuition. When the degree of concern for consumer fairness is high, the supply chain will lower the price in the second stage to reduce the impact.

4.2.2. Price Decrease Strategy

If retailers implement a strategy of decreasing prices, it will have a positive psychological impact on consumers who value fairness when making purchasing decisions, consequently influencing demand in the second stage. In contrast to the price increase strategy discussed in Section 4.2.1, which involves lowering prices in the first stage, a price decrease strategy requires retailers to initially sell at a higher price (thus enabling the implementation of a price decrease strategy in the second stage), resulting in a more negligible market growth compared to that brought about by the price increase strategy. Therefore, this paper introduces parameter $m\in (0,1)$ to distinguish between these two strategies.

Based on the above analysis, the demand function for the second stage under a price decrease strategy is:

$$D_2^{PD}=1+m\delta -\beta p_2^{PD}+\gamma max\{p_1^{PD}-p_2^{PD},0\}$$

(6)

Based on this, the profit function of the supply chain is:

$${\pi }^{PD}=\left\{\begin{array}{cc}{p}_1^{PD}(1-\beta p_1^{PD})+p_2^{PD}[1+m\delta -\beta p_2^{PD}+\gamma (p_1^{PD}-p_2^{PD})],\hfill & \mathrm{if}{p}_2^{PD}<p_1^{PD}\hfill \\ p_1^{PD}(1-\beta p_1^{PD})+p_2^{PD}(1+m\delta -\beta p_2^{PD}),\hfill & \mathrm{if}{p}_2^{PD}\ge p_1^{PD}\hfill \end{array}\right.$$

(7)

Using the KKT conditions (Karush-Kuhn-Tucker conditions) to solve this constrained optimization problem, similar to the benchmark model, we take the derivative of $p_1^{PD}$ and $p_2^{PD}$ in the total profit function simultaneously. The equilibrium results obtained are summarized in Proposition 3.

Proposition 3. 

In the centralized decision-making scenario, facing consumers in the market who are concerned with fairness, if the enterprise adopts a price decrease strategy, then the optimal two-stage pricing for the supply chain is:

$$p_1^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{2\beta +3\gamma +m\delta \gamma }{4\beta (\beta +\gamma )-{\gamma }^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{2\gamma }{m(2\beta -\gamma )}}\hfill \\ {\displaystyle \frac{m\delta +2}{4\beta }},\hfill & \mathit{if}\delta >{\displaystyle \frac{2\gamma }{m(2\beta -\gamma )}}\hfill \end{array}\right.$$

(8)

$$p_2^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{2\beta +\gamma +2m\beta \delta }{4\beta (\beta +\gamma )-{\gamma }^2}},\hfill & \mathrm{if}0\le \delta \le {\displaystyle \frac{2\gamma }{m(2\beta -\gamma )}}\hfill \\ {\displaystyle \frac{m\delta +2}{4\beta }},\hfill & \mathrm{if}\delta >{\displaystyle \frac{2\gamma }{m(2\beta -\gamma )}}\hfill \end{array}\right.$$

(9)

The optimal total profit for the supply chain under centralized decision-making is:

$${\pi }^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{\beta m^2{\delta }^2+(2\beta +\gamma )m\delta +2(\beta +\gamma )}{4\beta (\beta +\gamma )-{\gamma }^2}},\hfill & \mathrm{if}0\le \delta \le {\displaystyle \frac{2\gamma }{m(2\beta -\gamma )}}\hfill \\ {\displaystyle \frac{{(2+m\delta )}^2}{8\beta }},\hfill & \mathrm{if}\delta >{\displaystyle \frac{2\gamma }{m(2\beta -\gamma )}}\hfill \end{array}\right.$$

(10)

Unlike the equilibrium results of Proposition 2 with a price increase strategy, under a price decrease strategy, when the market growth scale $\delta$ is large, the optimal prices for the first and second stages of the supply chain are equal, that is, when $\delta >{\displaystyle \frac{2\gamma }{m(2\beta -\gamma )}}$, $p_1^{P{D}^{*}}=p_2^{P{D}^{*}}={\displaystyle \frac{m\delta +2}{4\beta }}$; the optimal two-stage pricing of the supply chain increases with the increase of the market growth scale $\delta$ and the price elasticity coefficient $\beta$; $p_1^{P{D}^{*}}$ increases with the increase of the consumer fairness concern coefficient $\gamma$, but $p_2^{P{D}^{*}}$ decreases with the increase of $\gamma$.

By comparing the optimal pricing and profits in Proposition 1 with those in Propositions 2 and 3, we can derive Corollary 1.

Theorem 1. 

Under centralized decision-making, the following conclusions exist: $p_1^{*}<p_1^{P{I}^{*}}$, $p_2^{*}>p_2^{P{I}^{*}}$, ${\pi }^{*}>{\pi }^{P{I}^{*}}$; $p_1^{*}<p_1^{P{D}^{*}}$, $p_2^{*}>p_2^{P{D}^{*}}$, ${\pi }^{*}>{\pi }^{P{D}^{*}}$.

From Corollary 1, it is evident that centralized decision-making leads to a higher optimal price in the first stage when considering consumer fairness concerns, as opposed to not considering them. However, the second stage price is lower in this scenario. This conclusion applies to both price increase and decrease strategies. Furthermore, the optimal profit while considering consumer fairness concerns is consistently lower than disregarding such concerns. It can be observed that under centralized decision-making, consumer fairness concerns reduce the retailer’s price increase range and compel the supply chain to make concessions to consumers, ultimately reducing overall profit.

By further comparing the optimal profits in Proposition 2 and Proposition 3, Theorem 2 can be derived.

Theorem 2. 

Under centralized decision-making, when $0<\delta <{\delta }_1$, the supply chain adopts a price decrease strategy; when $\delta \ge {\delta }_1$, the supply chain adopts a price increase strategy. Here, ${\delta }_1=\left(-2B-4\sqrt{\beta (1-m)(\beta -m\beta +\gamma )(4{\beta }^2+4\beta \gamma -{\gamma }^2)}\right)/A$, where $A=8{\beta }^2{m}^2-4{\beta }^2-4\gamma \beta +{\gamma }^2$ and $B=(4{\beta }^2+2\gamma \beta )m-4{\beta }^2-4\gamma \beta +{\gamma }^2$.

5. Decentralized Decision-Making Scenario

5.1. Benchmark Model

Similar to Section 4, in the context of decentralized decision-making, the benchmark model that does not consider consumer fairness concerns is still utilized. This model is then compared and analyzed against the model considering consumer fairness concerns.

When consumer fairness concerns are not considered, the market demand for the first and second stages is $D_1=1-\beta p_1$, $D_2=1+\delta -\beta p_2$. Therefore, the manufacturer’s first and second stage profits, as well as the total profit, are ${\pi }_{M1}={\omega }_1{D}_1$, ${\pi }_{M2}={\omega }_2{D}_2$, ${\pi }_M={\pi }_{M1}+{\pi }_{M2}$; similarly, the retailer’s first and second stage profits, as well as the total profit, are ${\pi }_{R1}=(p_1-{\omega }_1)D_1$, ${\pi }_{R2}=(p_2-{\omega }_2)D_2$, ${\pi }_R={\pi }_{R1}+{\pi }_{R2}$. The equilibrium results are summarized in Proposition 4.

Proposition 4. 

Under the decentralized decision-making scenario, when there are no consumer fairness concerns in the market, the manufacturer’s optimal wholesale prices for the first and second stages are are $w_1^{*}={\displaystyle \frac{1}{2\beta }}$, $w_2^{*}={\displaystyle \frac{1+\delta }{2\beta }}$; the retailer’s optimal retail prices for the first and second stages are $p_1^{*}={\displaystyle \frac{3}{4\beta }}$, $p_2^{*}={\displaystyle \frac{3(1+\delta )}{4\beta }}$; the demands for the two stages are $D_1^{*}={\displaystyle \frac{1}{4}}$, $D_2^{*}={\displaystyle \frac{1+\delta }{4}}$; the manufacturer’s and retailer’s optimal total profits for the two stages are ${\pi }_M^{*}={\displaystyle \frac{1+{(1+\delta )}^2}{8\beta }}$, ${\pi }_R^{*}={\displaystyle \frac{1+{(1+\delta )}^2}{16\beta }}$, respectively.

Proposition 4 elucidates the equilibrium outcomes for manufacturers and retailers in the decentralized decision-making scenario. It is evident that the wholesale and retail prices in the second stage surpass those of the first stage, indicating $w_2^{*}>w_1^{*}$ and $p_2^{*}>p_1^{*}$. Furthermore, both prices escalate with an increase in the market size $\delta$.

5.2. Pricing Decisions Considering Consumer Fairness Concerns

At this stage, the demand for the first stage is represented by $D_1=1-\beta p_1$ as described in Section 4.1. The initial market size for the second stage is expected to increase over time. At this point, retailers have two options: implementing a price increase strategy or a price decrease strategy.

5.2.1. Price Increase Strategy

If retailers choose to implement a price increase strategy, it will have a detrimental psychological impact on consumers who value fairness in their purchasing decisions. This, in turn, will affect the demand for the second stage of the supply chain. Similar to Section 4.2, the demand for the supply chain in the second stage remains:

$$D_2^{PI}=1+\delta -\beta p_2^{PI}-\gamma max\{p_2^{PI}-p_1^{PI},0\}$$

Based on this, the profit functions for manufacturers and retailers are as follows:

$${\pi }_M^{PI}=\left\{\begin{array}{cc}{w}_1^{PI}(1-\beta p_1^{PI})+w_2^{PI}[1+\delta -\beta p_2^{PI}-\gamma (p_2^{PI}-p_1^{PI})],\hfill & \mathrm{if}{p}_1^{PI}<p_2^{PI}\hfill \\ w_1^{PI}(1-\beta p_1^{PI})+w_2^{PI}(1+\delta -\beta p_2^{PI}),\hfill & \mathrm{if}{p}_1^{PI}\ge p_2^{PI}\hfill \end{array}\right.$$

(11)

$${\pi }_R^{PI}=\left\{\begin{array}{cc}(p_1^{PI}-w_1^{PI})(1-\beta p_1^{PI})+(p_2^{PI}-w_2^{PI})[1+\delta -\beta p_2^{PI}-\gamma (p_2^{PI}-p_1^{PI})],\hfill & \mathrm{if}{p}_1^{PI}<p_2^{PI}\hfill \\ (p_1^{PI}-w_1^{PI})(1-\beta p_1^{PI})+(p_2^{PI}-w_2^{PI})(1+\delta -\beta p_2^{PI}),\hfill & \mathrm{if}{p}_1^{PI}\ge p_2^{PI}\hfill \end{array}\right.$$

(12)

Using the KKT conditions (Karush-Kuhn-Tucker conditions) to solve this constrained optimization problem and employing backward induction for solving, the equilibrium results are summarized in Propositions 5.

Proposition 5. 

In the context of decentralized decision-making, and taking into consideration consumer fairness concerns in the market, if retailers choose to implement a price increase strategy, then the manufacturer’s optimal wholesale prices for the first and second stages can be determined as follows:

$${\omega }_1^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{6\beta +\gamma }{12{\beta }^2-\beta \gamma }},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \\ {\displaystyle \frac{10\beta \gamma +8{\beta }^2+{\gamma }^2+2\beta \delta \gamma }{\beta (16{\beta }^2+16\beta \gamma -{\gamma }^2)}},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \end{array}\right.$$

(13)

$${\omega }_2^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{6}{12\beta -\gamma }},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \\ {\displaystyle \frac{8\beta +6\gamma +8\beta \delta }{16{\beta }^2+16\beta \gamma -{\gamma }^2}},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \end{array}\right.$$

(14)

The retailer’s optimal retail prices for the first and second stages are:

$$p_1^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{9}{12\beta -\gamma }},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \\ {\displaystyle \frac{12\beta +13\gamma +\delta \gamma }{16{\beta }^2+16\beta \gamma -{\gamma }^2}},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \end{array}\right.$$

(15)

$$p_2^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{9}{12\beta -\gamma }},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \\ {\displaystyle \frac{12\beta +9\gamma +12\beta \delta }{16{\beta }^2+16\beta \gamma -{\gamma }^2}},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \end{array}\right.$$

(16)

The retailer’s optimal profits for the first and second stages are:

$${\pi }_{R1}^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{{(3\beta -\gamma )}^2}{\beta {(12\beta -\gamma )}^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \\ {\displaystyle \frac{{(3\beta \gamma +4{\beta }^2-{\gamma }^2-\beta \delta \gamma )}^2}{\beta {(16{\beta }^2+16\beta \gamma -{\gamma }^2)}^2}},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \end{array}\right.$$

(17)

$${\pi }_{R2}^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{9(\beta +\gamma )}{{(12\beta -\gamma )}^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \\ {\displaystyle \frac{(\beta +\gamma ){(4\beta +3\gamma +4\beta \delta )}^2}{{(16{\beta }^2+16\beta \gamma -{\gamma }^2)}^2}},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \end{array}\right.$$

(18)

The manufacturer’s optimal profits for the first and second stages are:

$${\pi }_{M1}^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{(6\beta +\gamma )(3\beta -\gamma )}{\beta {(12\beta -\gamma )}^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \\ {\displaystyle \frac{(10\beta \gamma +8{\beta }^2+{\gamma }^2+2\beta \delta \gamma )(3\beta \gamma +4{\beta }^2-{\gamma }^2-\beta \delta \gamma )}{\beta {(16{\beta }^2+16\beta \gamma -{\gamma }^2)}^2}},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \end{array}\right.$$

(19)

$${\pi }_{M2}^{P{I}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{18(\beta +\gamma )}{{(12\beta -\gamma )}^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \\ {\displaystyle \frac{(8\beta +6\gamma +8\beta \delta )(7\beta \gamma +4{\beta }^2\delta -\delta {\gamma }^2+4{\beta }^2-{\gamma }^2+16\beta \delta \gamma )}{{(16{\beta }^2+16\beta \gamma -{\gamma }^2)}^2}},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{12\beta -\gamma }}\hfill \end{array}\right.$$

(20)

Based on Proposition 5, we can derive Corollaries 4-6:

Theorem 3. 

When $\delta >{\displaystyle \frac{4\beta \gamma +4{\gamma }^2}{8{\beta }^2-2\beta \gamma }}$, ${\omega }_2^{P{I}^{*}}>{\omega }_1^{P{I}^{*}}$; and ${\displaystyle \frac{\partial {\omega }_1^{P{I}^{*}}}{\partial \delta }}\ge 0$, ${\displaystyle \frac{\partial {\omega }_2^{P{I}^{*}}}{\partial \delta }}\ge 0$, ${\displaystyle \frac{\partial p_1^{P{I}^{*}}}{\partial \delta }}\ge 0$, ${\displaystyle \frac{\partial p_2^{P{I}^{*}}}{\partial \delta }}\ge 0$.

From Corollary 3, it is apparent that in the case of decentralized decision-making, the manufacturer’s wholesale price in the second stage may not always be higher than that in the first stage. Only when the market growth scale $\delta$ reaches a certain threshold does the manufacturer’s wholesale price in the second stage exceed that of the first stage. Additionally, Theorem 3 indicates that neither the manufacturer’s wholesale prices for both stages nor the retailer’s retail prices for both stages will decrease as the market growth scale $\delta$ increases.

5.2.2. Price Decrease Strategy

If retailers choose to implement a price decrease strategy, it will have a positive psychological impact on consumers who are concerned about fairness when purchasing. This, in turn, will affect the demand for the second stage. Similar to Section 4.2, the demand function for the second stage is as follows:

$$D_2^{PD}=1+m\delta -\beta p_2^{PD}+\gamma max\{p_1^{PD}-p_2^{PD},0\}$$

(21)

Consequently, when the retailer adopts a price decrease strategy, the profit functions for the manufacturer and retailer are as follows:

$${\pi }_M^{PD}=\left\{\begin{array}{cc}{\omega }_1^{PD}(1-\beta p_1^{PD})+{\omega }_2^{PD}[1+m\delta -\beta p_2^{PD}+\gamma (p_1^{PD}-p_2^{PD})],\hfill & \mathrm{if}{p}_2^{PD}<p_1^{PD}\hfill \\ {\omega }_1^{PD}(1-\beta p_1^{PD})+{\omega }_2^{PD}(1+m\delta -\beta p_2^{PD}),\hfill & \mathrm{if}{p}_2^{PD}\ge p_1^{PD}\hfill \end{array}\right.$$

(22)

$${\pi }_R^{PD}=\left\{\begin{array}{cc}(p_1^{PD}-{\omega }_1^{PD})(1-\beta p_1^{PD})+(p_2^{PD}-{\omega }_2^{PD})[1+m\delta -\beta p_2^{PD}+\gamma (p_1^{PD}-p_2^{PD})],\hfill & \mathrm{if}{p}_2^{PD}<p_1^{PD}\hfill \\ (p_1^{PD}-{\omega }_1^{PD})(1-\beta p_1^{PD})+(p_2^{PD}-{\omega }_2^{PD})(1+m\delta -\beta p_2^{PD}),\hfill & \mathrm{if}{p}_2^{PD}\ge p_1^{PD}\hfill \end{array}\right.$$

(23)

Using the KKT conditions (Karush-Kuhn-Tucker conditions) to solve this constrained optimization problem and employing backward induction for solving, the equilibrium results are summarized in Propositions 6.

Proposition 6. 

In the context of decentralized decision-making, considering consumer fairness concerns in the market, if retailers choose to implement a price decrease strategy, the optimal wholesale prices, retail prices, manufacturer’s maximum profit, and retailer’s maximum profit for the second stage with regard to the first stage retail price are as follows:

$${\omega }_1^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{10\beta \gamma +8{\beta }^2+{\gamma }^2+2m\beta \delta \gamma }{\beta (16{\beta }^2+16\beta \gamma -{\gamma }^2)}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \\ {\displaystyle \frac{6\beta +\gamma }{12{\beta }^2-\beta \gamma }},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \end{array}\right.$$

(24)

$${\omega }_2^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{8\beta +6\gamma +8m\beta \delta }{16{\beta }^2+16\beta \gamma -{\gamma }^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \\ {\displaystyle \frac{6\beta +\gamma }{12{\beta }^2-\beta \gamma }},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \end{array}\right.$$

(25)

The retailer’s optimal retail prices for the first and second stages are:

$$p_1^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{12\beta +13\gamma +m\delta \gamma }{16{\beta }^2+16\beta \gamma -{\gamma }^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \\ {\displaystyle \frac{9}{12\beta -\gamma }},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \end{array}\right.$$

(26)

$$p_2^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{12\beta +9\gamma +12m\beta \delta }{16{\beta }^2+16\beta \gamma -{\gamma }^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \\ {\displaystyle \frac{9}{12\beta -\gamma }},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \end{array}\right.$$

(27)

The retailer’s optimal profits for the first and second stages are:

$${\pi }_{R1}^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{{(3\beta \gamma +4{\beta }^2-{\gamma }^2-m\beta \delta \gamma )}^2}{\beta {(16{\beta }^2+16\beta \gamma -{\gamma }^2)}^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \\ {\displaystyle \frac{{(3\beta -\gamma )}^2}{\beta {(12\beta -\gamma )}^2}},\hfill & \mathrm{if}\delta >{\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \end{array}\right.$$

(28)

$${\pi }_{R2}^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{(\beta +\gamma ){(4\beta +3\gamma +4m\beta \delta )}^2}{{(16{\beta }^2+16\beta \gamma -{\gamma }^2)}^2}},\hfill & \mathrm{if}0\le \delta \le {\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \\ {\displaystyle \frac{{(3\beta -\gamma )}^2}{\beta {(12\beta -\gamma )}^2}},\hfill & \mathrm{if}\delta >{\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \end{array}\right.$$

(29)

The manufacturer’s optimal profits for the first and second stages are:

$${\pi }_{M1}^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{(10\beta \gamma +8{\beta }^2+{\gamma }^2+2m\beta \delta \gamma )(3\beta \gamma +4{\beta }^2-{\gamma }^2-m\beta \delta \gamma )}{\beta {(16{\beta }^2+16\beta \gamma -{\gamma }^2)}^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \\ {\displaystyle \frac{(6\beta +\gamma )(3\beta -\gamma )}{\beta {(12\beta -\gamma )}^2}},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \end{array}\right.$$

(30)

$${\pi }_{M2}^{P{D}^{*}}=\left\{\begin{array}{cc}{\displaystyle \frac{(8\beta +6\gamma +8m\beta \delta )(7\beta \gamma +4{\beta }^2\delta -\delta {\gamma }^2+4{\beta }^2-{\gamma }^2+16m\beta \delta \gamma )}{{(16{\beta }^2+16\beta \gamma -{\gamma }^2)}^2}},\hfill & \mathit{if}0\le \delta \le {\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \\ {\displaystyle \frac{18(\beta +\gamma )}{{(12\beta -\gamma )}^2}},\hfill & \mathit{if}\delta >{\displaystyle \frac{4\gamma }{m(12\beta -\gamma )}}\hfill \end{array}\right.$$

(31)

Based on Proposition 6, we can derive Corollaries 4-6:

Theorem 4. 

When $\delta >{\displaystyle \frac{4\beta \gamma +4{\gamma }^2}{m(8{\beta }^2-2\beta \gamma )}}$, ${\omega }_2^{P{D}^{*}}>{\omega }_1^{P{D}^{*}}$; and ${\displaystyle \frac{\partial {\omega }_1^{P{D}^{*}}}{\partial \delta }}\ge 0$, ${\displaystyle \frac{\partial {\omega }_2^{P{D}^{*}}}{\partial \delta }}\ge 0$, ${\displaystyle \frac{\partial p_1^{P{D}^{*}}}{\partial \delta }}\ge 0$, ${\displaystyle \frac{\partial p_2^{P{D}^{*}}}{\partial \delta }}\ge 0$.

From Theorem 4, it is evident that decentralized decision-making results in a divergence from the equilibrium outcomes of the benchmark model. Specifically, when retailers implement a price decrease strategy, the manufacturer’s wholesale price in the second stage may not always exceed that of the first stage. This contrast stems from the fact that the first-order partial derivatives of wholesale and retail prices concerning market growth scale $\delta$ are all positive. Consequently, it can be inferred that an increase in market growth scale will not lead to a decrease in both stages’ manufacturer’s wholesale prices and retailer’s retail prices.

Theorem 5. 

When $0<\beta <1$, ${\pi }_R^{P{I}^{*}}>{\pi }_R$; when $\beta >1$ and $\gamma >{\gamma }_2$, ${\pi }_R^{P{I}^{*}}>{\pi }_R^{*}$; when $\beta >1$ and $0<\gamma <{\gamma }_2$, ${\pi }_R^{P{I}^{*}}<{\pi }_R^{*}$. Here, ${\gamma }_2={\displaystyle \frac{(12{\beta }^2-12\beta +4\beta \sqrt{6(\beta -1)})}{(5-3\beta )}}$.

Theorem 5 demonstrates that when retailers implement a price decrease strategy under decentralized decision-making, the retailer’s profit, considering consumer fairness concerns, is higher than the profit without considering fairness under certain conditions. This finding is counterintuitive, as consumer fairness concerns affect the reaction functions of both the manufacturer and retailer in both stages, differing from the completely independent decentralized decisions made without considering consumer fairness concerns.

Theorem 6. 

Under decentralized decision-making, when considering consumer fairness concerns, the profit from the price increase strategy is always higher than that from the price decrease strategy, i.e., ${\pi }_R^{P{I}^{*}}>{\pi }_R^{P{D}^{*}}$.

Theorem 6 demonstrates that in a decentralized decision-making setting, when retailers encounter consumers with fairness concerns, it is advisable for them to implement a price increase strategy in order to enhance profits, while the consideration of a price decrease strategy is not warranted. Conversely, within a centralized decision-making framework, circumstances may arise wherein the profitability from a price decrease strategy surpasses that associated with a price increase strategy.

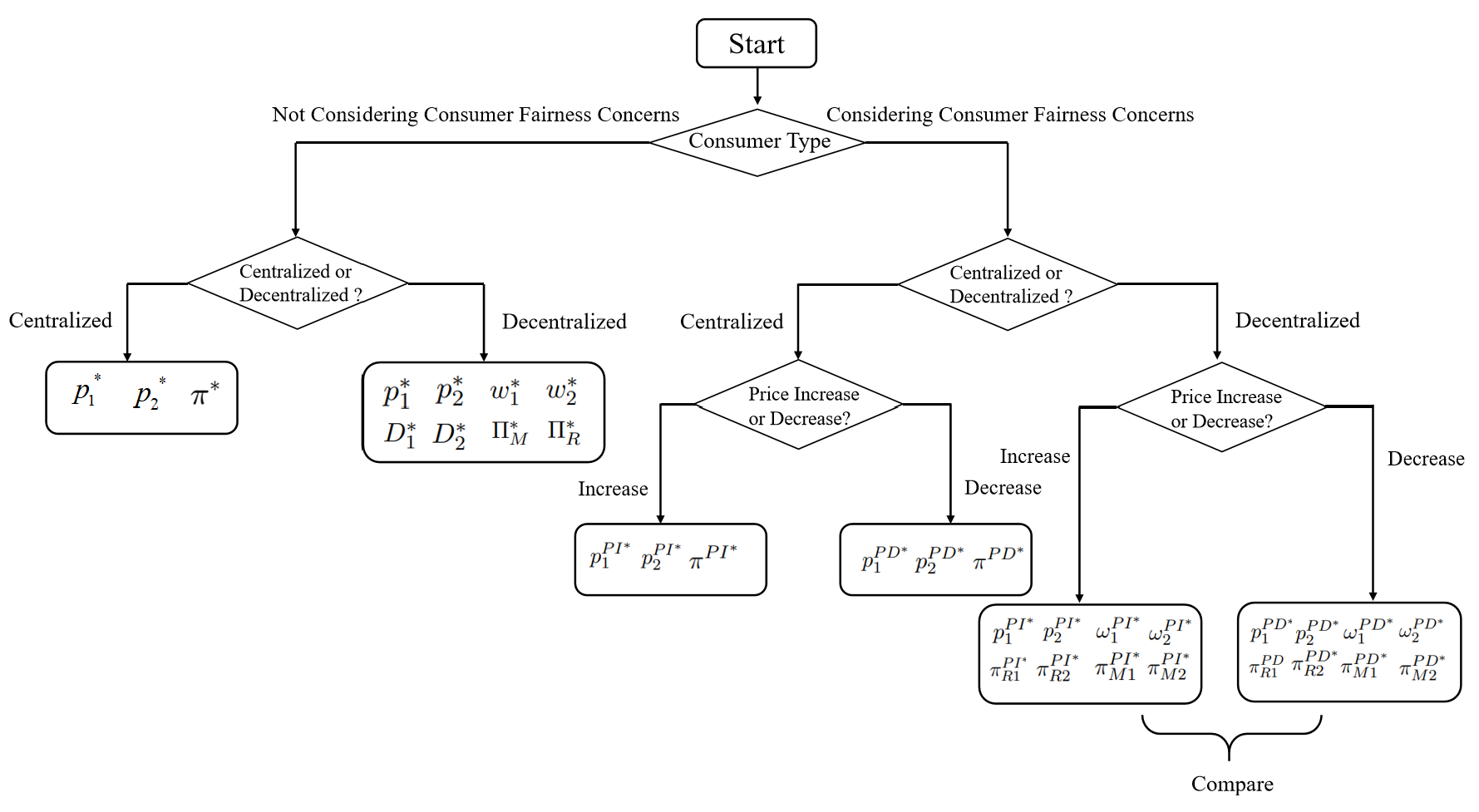
6. Numerical Analysis

This section first examines the impact of parameters such as the price elasticity of demand $\beta$, the coefficient for consumer fairness concern $\gamma$, and the scale of market growth $\delta$ on the optimal two-stage retail prices and profits when the retailer adopts price increase or decrease strategies under centralized decision-making.

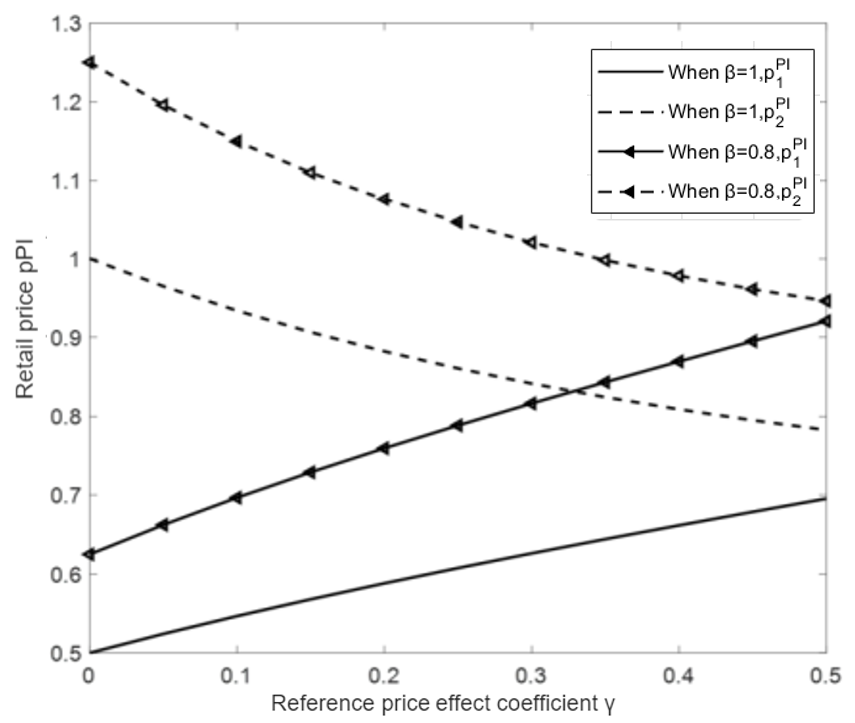
Drawing upon on Proposition 2, we investigate the relationship between the optimal two-stage prices $p_1^{P{I}^{*}}$, $p_2^{P{I}^{*}}$ and the consumer fairness concern coefficient $\gamma$, as illustrated in Figure 2. It presents the variation when $\beta =0.8$ (solid and dashed lines in the figure) and $\beta =1$ (solid and dashed lines with triangle markers) with $\delta =0.5$.

From Figure 2, it is evident that the optimal retail price in the first stage increases regardless of the value of $\beta$, as $\gamma$ increases. Conversely, the optimal retail price in the second stage decreases with an increase in $\gamma$. This phenomenon can be attributed to the fact that as $\gamma$ rises, there is a reduction in the optimal retail price in the second stage, necessitating an increase in the optimal price for the first stage to offset any potential losses. Furthermore, an increase in $\beta$ leads to higher optimal retail prices in both the first and second stages.

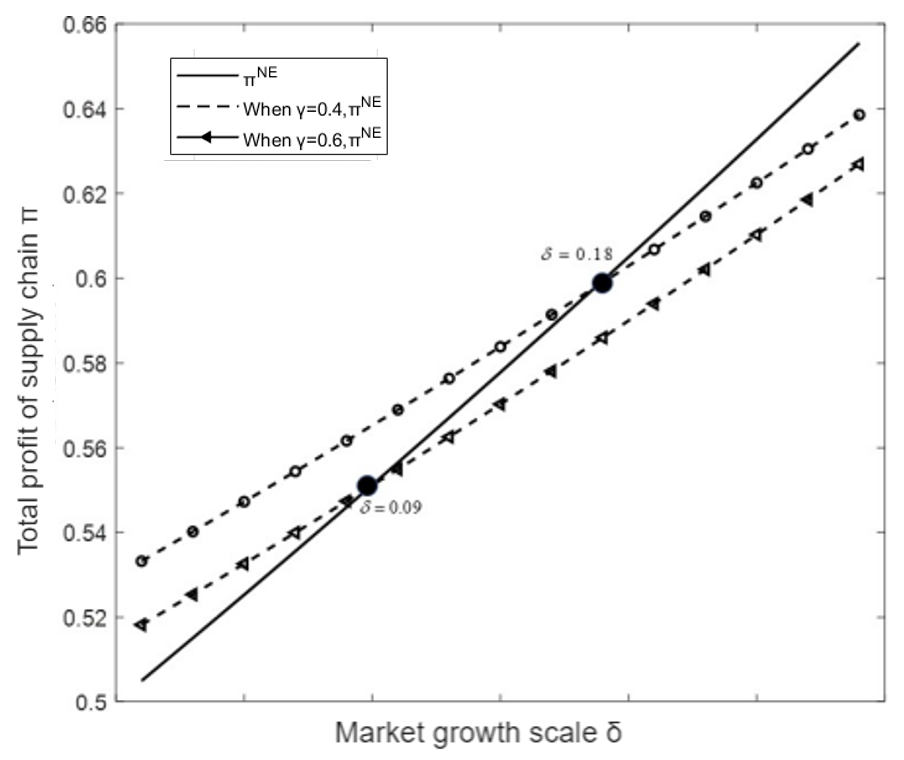
Based on Theorem 2, Figure 3 compares optimal profits when the supply chain adopts price increase or decrease strategies under centralized decision-making. The parameter values are $\beta =1$ and $m=0.8$, demonstrating the results for $\gamma =0.4$ (illustrated by the dashed line with triangle markers) and $\gamma =0.6$ (illustrated by the dashed line with hollow circle markers).

Figure 3 illustrates that when $\gamma =0.4$, profit under the price decrease strategy surpasses that under the price increase strategy if $\delta <0.09$; conversely, if $\delta \ge 0.09$, profit under the price increase strategy exceeds that under the price decrease strategy. When $\gamma =0.6$, the intersection point occurs at a higher value of $\delta$ at 0.18; if $\delta <0.18$, profit under the price decrease strategy is more significant than that under the price increase strategy, while if $\delta \ge 0.18$, the opposite is true. These findings highlight that in centralized decision-making for optimal sequencing in supply chain management, it is preferable to initially implement a price decrease strategy followed by transitioning to a price increase strategy.

Table 2 presents a comprehensive overview of how variations in the consumer fairness concern coefficient $\gamma$ influence the optimal two-stage prices and profits of the supply chain, considering both price increase and decrease strategies. Notably, regardless of the adopted strategy, the optimal pricing in the first stage increases as $\gamma$ rises, indicating consumers’ sensitivity to fairness in initial pricing decisions. Conversely, the optimal pricing in the second stage decreases with increasing $\gamma$, suggesting a strategic adjustment to balance consumer perceptions and profitability across stages.

Furthermore, as $\gamma$ increases, a noticeable trend emerges: profits from the price increase strategy tend to decline, while profits from the price decrease strategy tend to improve. This trend underscores the strategic necessity of integrating consumer fairness concerns into pricing decisions to enhance supply chain profitability. By aligning pricing strategies with consumer expectations of fairness, supply chain stakeholders can optimize their market positioning and effectively navigate dynamic market conditions.

The preceding discussion focused on centralized decision-making scenarios. This section conducts a numerical investigation into the impact of parameters such as the price elasticity of demand $\beta$, consumer fairness concern coefficient $\gamma$, and market growth scale $\delta$ on the optimal two-stage retail prices and profits when retailers adopt price increase or decrease strategies under decentralized decision-making. Unless otherwise specified, the default parameter values in this paper are $\beta =1$, $\delta =0.4$, and $m=0.5$.

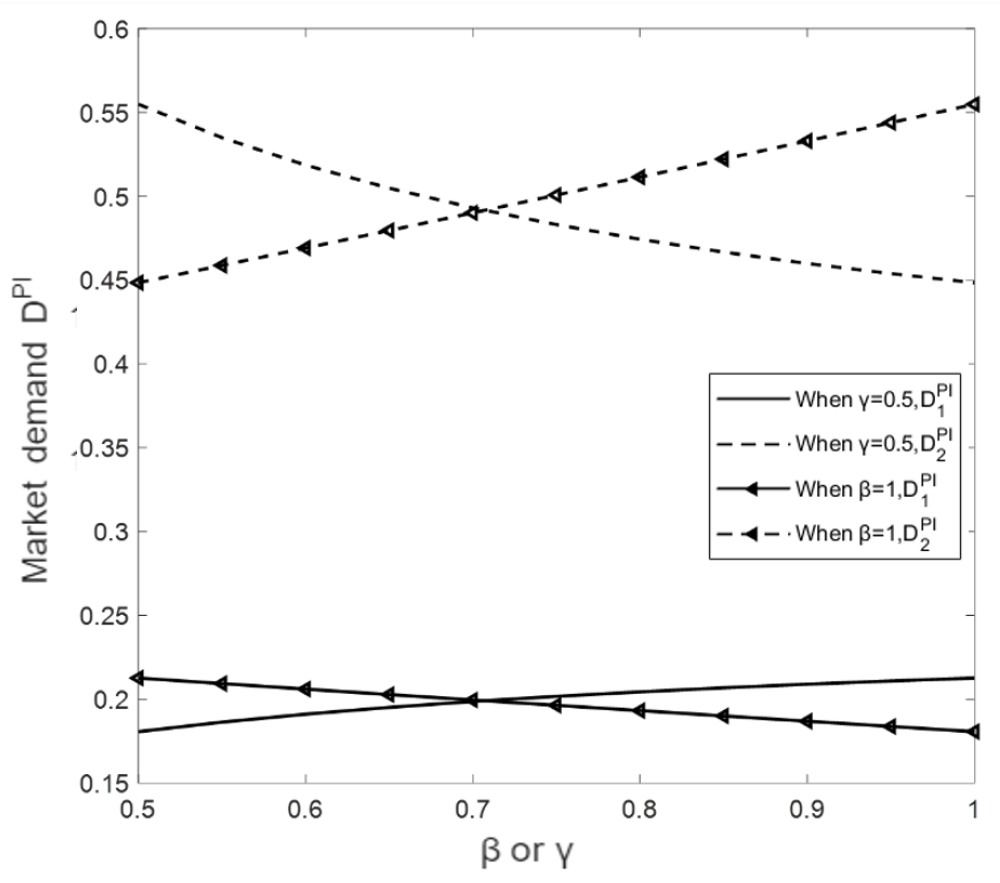
Drawing on Propositions 5, we investigate the correlation between the manufacturers’ and retailers’ second-stage optimal profits under price increase and decrease strategies to the first-stage retail price, as illustrated in Figure 4. To begin, when setting the consumer fairness concern coefficient at $\gamma =0.5$, we analyze variations in $D_1^{P{I}^{*}}$ and $D_2^{P{I}^{*}}$ as $\beta$ increases from 0.5 to 1, represented by solid and dashed lines in the figure. Furthermore, with a fixed price elasticity of demand at $\beta =1$, we examine changes in $D_1^{P{I}^{*}}$ and $D_2^{P{I}^{*}}$ as $\gamma$ increases from 0.5 to 1, shown by solid lines with triangle markers and dashed lines in the figure.

From Figure 4, it is evident that as the parameter $\beta$ increases, the demand in the first stage $D_1^{P{I}^{*}}$ rises monotonically, while the demand in the second stage $D_2^{P{I}^{*}}$ decreases monotonically. On the other hand, as the parameter $\gamma$ increases, there is a counterintuitive trend where the demand in the second stage $D_2^{P{I}^{*}}$ increases with an increasing consumer fairness concern coefficient, while at the same time, the demand in the first stage $D_1^{P{I}^{*}}$ decreases. This can be attributed to a need to raise demand in the second stage to enhance overall profits due to a decrease in first-stage demand caused by an increase in $\gamma$. Simultaneously, this decrease caused by an increase in $\gamma$ is outweighed by a greater increase due to a price reduction.

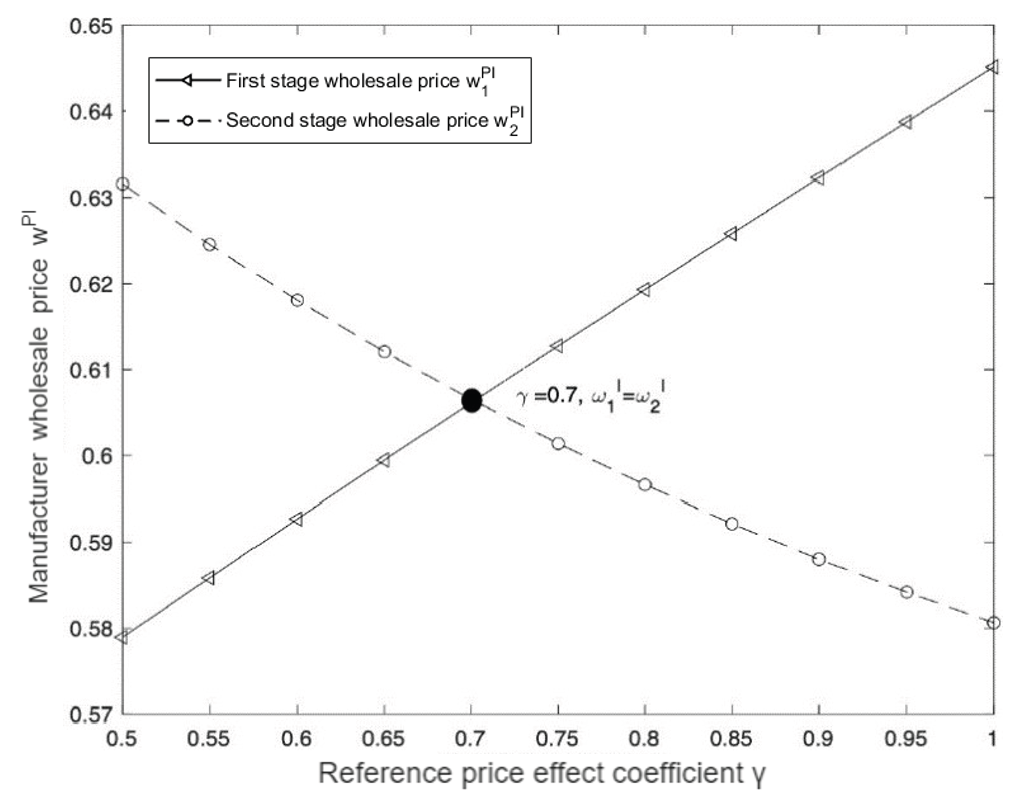
Next, we will investigate the correlation between the manufacturer’s wholesale prices in both stages and the change in $\gamma$, as illustrated in Figure 5. From the figure, it is evident that as $\gamma$ increases, ${\omega }_1^{P{I}^{*}}$ exhibits a monotonically increasing trend with respect to $\gamma$, while ${\omega }_2$ shows a monotonically decreasing pattern. When $\gamma =0.7$, the manufacturer’s wholesale prices in the first and second stages are equal, i.e., ${\omega }_1^{PI}={\omega }_2^{PI}$. On the other hand, when $\gamma$ is relatively large, manufacturers tend to raise the wholesale price in the first stage and lower it in the second stage, thereby boosting demand in the second stage and ultimately securing higher profits.

Table 3 and Table 4 provide a detailed exploration of how consumer fairness concerns, quantified by the coefficient $\gamma$, impact the optimal pricing strategies of manufacturers and retailers when employing price increase and decrease strategies, respectively.

In Table 3, which examines the price increase strategy, the optimal retail prices in the first stage generally rise as $\gamma$ increases. This trend suggests that as consumers become more sensitive to fairness considerations, retailers may perceive the need to set higher initial prices to maintain perceived fairness and safeguard profit margins. However, the optimal prices in the second stage show an initial increase followed by a decrease with increasing $\gamma$. This pattern indicates a strategic response to mitigate potential consumer backlash against perceived price hikes over time, optimizing overall profitability.

In contrast, Table 4 focuses on the strategy of price decrease. As the parameter $\gamma$ increases, manufacturers’ optimal pricing decisions initially rise and then decline. This trend suggests that manufacturers may initially lower prices to meet consumer fairness expectations to stimulate demand and maintain competitive positioning. However, as $\gamma$ continues to increase, manufacturers may adjust prices upward to balance profitability with consumers’ perceived value and fairness expectations.

7. Conclusion

This paper explores the impact of consumer fairness concerns on the two-stage dynamic pricing strategies of a manufacturer and a retailer within a supply chain. When retailers operate in a growing market with consumer fairness considerations, it is crucial to investigate the effects of implementing price increase or decrease strategies in the second stage on the profits of the manufacturer, retailer, and the overall supply chain. This is essential for the long-term operation and development of the supply chain.

This paper initially formulates and solves the Stackelberg game model under decentralized decision-making, with and without considering consumer fairness concerns. When formulating the demand function with consideration for consumer fairness concerns, it also explores the negative impact of such concerns under a price-increase strategy and the positive impact under a price-decrease strategy. Subsequently, a numerical analysis of the model results is performed. A similar research approach is also employed for the modeling, solving, and numerical analysis conducted under a centralized decision-making framework. The main conclusions and insights obtained in this paper are as follows:

(1)

In decentralized decision-making and considering consumer fairness concerns, the retailer’s profit from implementing a price increase strategy always outweighs that of implementing a price decrease strategy. It is evident that under decentralized decision-making, even with consumer fairness concerns in the market, the supply chain will continue to prioritize the implementation of a price increase strategy;

(2)

In decentralized decision-making, the retailer’s profit considering consumer fairness concerns may be higher than the profit without considering consumer fairness concerns under certain conditions. This is a counterintuitive phenomenon, mainly due to consumer fairness concerns, which leads to correlated reaction functions of the manufacturer and retailer in both stages. Consequently, this correlation constrains the pricing reaction functions of manufacturers and retailers, presenting a notable difference from completely independent decentralized decisions that do not take into account consumer fairness concerns;

(3)

In centralized decision-making, the profit of the supply chain, considering consumer fairness concerns, is consistently lower than the profit achieved without such considerations. Specifically, the optimal price in the initial stage is higher when considering consumer fairness concerns but lower in the subsequent stage when not considering these concerns. It is evident that within a centralized decision-making framework, consumer fairness considerations serve to limit retailer’s ability to raise prices and compel concessions from the supply chain toward consumers, ultimately leading to a reduction in overall profit;

(4)

In centralized decision-making and consideration of consumer fairness concerns, retailers will adopt a price decrease strategy when the market growth scale in the second stage is relatively low. Conversely, retailers opt for a price increase strategy when the market growth scale is relatively high. This also indicates that under centralized decision-making, even if retailers face a growing market, they will not always choose to implement a price increase strategy.

Further avenues for future research in this paper could be further explored. Firstly, the paper predominantly delves into examining the impact of consumer fairness concerns on the two-stage dynamic pricing within the supply chain. However, additional investigations can be carried out focusing on the pricing strategy within the supply chain under manufacturers’ and retailers’ fairness concerns; secondly, after comprehending the impact of consumer fairness concerns on supply chain pricing, it is possible to formulate reasonable contract agreements that strike a balance between the profits of manufacturers and retailers. Finally, this paper examines a Stackelberg game model in which the manufacturer holds dominance and is followed by the retailer. If the retailer has a large scale, it may influence supply chain decision-making. Additionally, the Nash game, in which manufacturers and retailers make decisions simultaneously, can also be taken into consideration.