SpaceTime: A Deep Similarity Defense Against Poisoning Attacks in Federated learning

1. Introduction

Federated learning (FL) is an emerging machine learning paradigm designed to address storage constraints and data privacy concerns in IoT sensors with varying resource limitations. FL tackles machine learning scenarios where data is unevenly distributed across numerous nodes [1]. By enabling a centralized model while keeping training data on individual devices, FL prevents data leakage and enhances security.

Federated learning has gained attention as a powerful approach to intrusion detection in IoT networks due to its ability to maintain data privacy and security across distributed devices while enabling effective detection capabilities [2]. In traditional centralized machine learning approaches, data from all IoT devices is typically collected and processed in a central server. However, this method faces several challenges in IoT environments, including privacy concerns, bandwidth limitations, and potential vulnerabilities due to the vast amount of sensitive data transferred across networks. By keeping data local, FL reduces the need for continuous data transmission to a central server, significantly lowering network bandwidth requirements and reducing latency, crucial to IoT systems. IoT environments are dynamic, with devices continuously joining or leaving the network. FL accommodates this by allowing new devices to seamlessly join the learning process. It supports a scalable solution that can adapt to the evolving structure of IoT networks without disrupting the entire intrusion detection framework [3]. Figure 1 presents the architecture of the FL-based intrusion detection system (IDS) for IoT devices. The global model aggregates individual node updates and distributes the refined version across the network.

Although FL shows promise for intrusion detection in the IoT, it also faces challenges. Most IoT networks generate non-IID (non-independent and identically distributed) data sets due to their ubiquitous and heterogeneous nature, which can reduce model precision by up to 55% [4]. Additionally, federated updates might be subject to adversarial attacks, such as poisoning attacks. In these attacks, adversaries compromise the local updates (gradients or model parameters) sent from edge IoT devices to the central server to corrupt the global model. For example, adversaries could inject misleading attack patterns into normal traffic data to trick the IDS into classifying intrusions as legitimate traffic. As these poisoned data samples feed into the model update process, they degrade the accuracy and reliability of the intrusion detection model. For intrusion detection in IoT, even minor modifications to model parameters can cause the IDS to overlook specific types of attacks or generate false positives, compromising its reliability. Additionally, byzantine attacks, a type of poisoning in which attackers manipulate model updates in unpredictable ways exploit weaknesses in the aggregation algorithm to create inconsistent or non-convergent global models. This disrupts the stability of the IDS, making it ineffective over time. Sybil attacks represent another type of poisoning attacks in FL, where Sybil attackers create multiple “dummy” identities or hijack several IoT devices within the network. These identities then submit malicious updates with poisoned data or model parameters, allowing the attacker to disproportionately influence the model aggregation process.

In this research, our goal is to develop defenses against poisoning attacks on anomaly-based intrusion detection system (IDS) for IoT, utilizing federated learning. First, we build a federated anomaly-based IDS tailored for IoT environments, followed by the design of various poisoning attacks aimed at manipulating the weights of the global model by targeting different gradients. We develop a poisoning defense mechanism using a bidirectional long-short-term memory (LSTM) recurrent neural network to evaluate spatial relationships across the different local gradient updates. Our LSTM employs a many-to-one regression architecture that assesses multiple distance-based, pairwise similarities between the vectorized gradients of each local model batch over a temporal dimension.

2. Related Work

There exists a large body of research on poisoning attacks on centralized machine learning models [5,6,7]. Most of these solutions are focused on data poisoning, where adversaries inject malicious data points into the central dataset to disrupt training. Attacks such as label flipping and targeted misclassification were commonly explored with the goal of degrading the accuracy of the model or achieving targeted misclassifications [8,9].

FL introduces new types of attack beyond traditional data poisoning, including model poisoning and Byzantine attacks [10,11]. In FL, byzantine resilience has become critical, as adversaries can control a subset of participants (byzantine clients), sending updates that introduce noise or malicious gradients [10]. Similarly, Sybil attacks, where multiple fake identities submit malicious updates, are an active research focus unique to FL [11].

Gu et. al introduced Fedmvae, a defense strategy for federated learning that counters poisoning attacks by leveraging multiple variational autoencoders and captures patterns in historical model updates to improve robustness against adversarial clients. [12]. However, this approach is limited to static image data and does not account for the operational constraints and dynamic behavior patterns typical in IoT environments. Shen et. al proposed a defense against label-flipping attacks (LFA) that monitors trends in cosine similarity across training rounds [13]. This solution does not consider relationships among clients or address a wider range of adversarial behaviors, such as Byzantine or backdoor attacks.

Kim et. al introduced a filtering mechanism grounded in similarity and distance metrics, conceptually aligned with the idea of examining relationships between client updates [14]. However, their method overlooks update evolution over time and is largely evaluated on static image classification tasks focused on LFAs, limiting its relevance to more dynamic and heterogeneous federated IoT applications.

Several studies have examined similarity metrics such as cosine similarity, triangle area similarity, sector area similarity (TS-SS), and logits in the global model to detect poisoning attacks as shown in Figure 2.

Hammoudeh et. al proposed cosine similarity gradient based defense to defend even against zero-day attacks [15]. Xie et. al demonstrated that this gradient-based poisoning defense can be defeated using distributed backdoor poisoning attacks (DBA) [16]. Heidarian et. al focused on Euclidean distance and magnitude differences to produce better purity in document clustering similarities with the TS-SS algorithm [17]. Fung et. al proposed Foolsgold, a defense mechanism that identifies and limits the influence of malicious clients (Sybils) by comparing gradient similarity across clients [10]. Birchman et. al proposed Area Similarity FoolsGold defense (ASF) that incorporates triangle area and sector area similarity into the FoolsGold algorithm [18]. ASF replaced the gradient defense with Euclidean distance and magnitude difference. The difference resulted in a better functioning of the honest client pardoning. However, the implementation reduced the accuracy of identifying Sybils. ASF still achieved a better convergence measured by loss when poisoned by DBAs, largely due to honest client pardoning.

Zhang et. al identified that the local models of attackers and benign participants had significant differences in the diversity of their output logits [9]. The FoolsGold algorithm also utilized logits; however, they were used to protect low-scoring honest clients with a gradient below 0. When incorporated to identify poisoning attacks, cosine similarity identifies Sybils most accurately. ASF implementation of FoolsGold achieves higher model accuracy in DBAs. Finally, FoolsGold achieves the highest Sybil identification accuracy in label and backdoor attacks.

In this work, we hypothesize that the non-IID nature of IoT networks incorporates space-time relationships, necessitating a deep learning architecture capable of identifying spatial similarity patterns over time. This approach could enhance the model’s ability to predict malicious attackers by utilizing information from both past and future data. We introduce this model as Spacetime (ST-DSD) and evaluate its performance against various attacks in an IoT network.

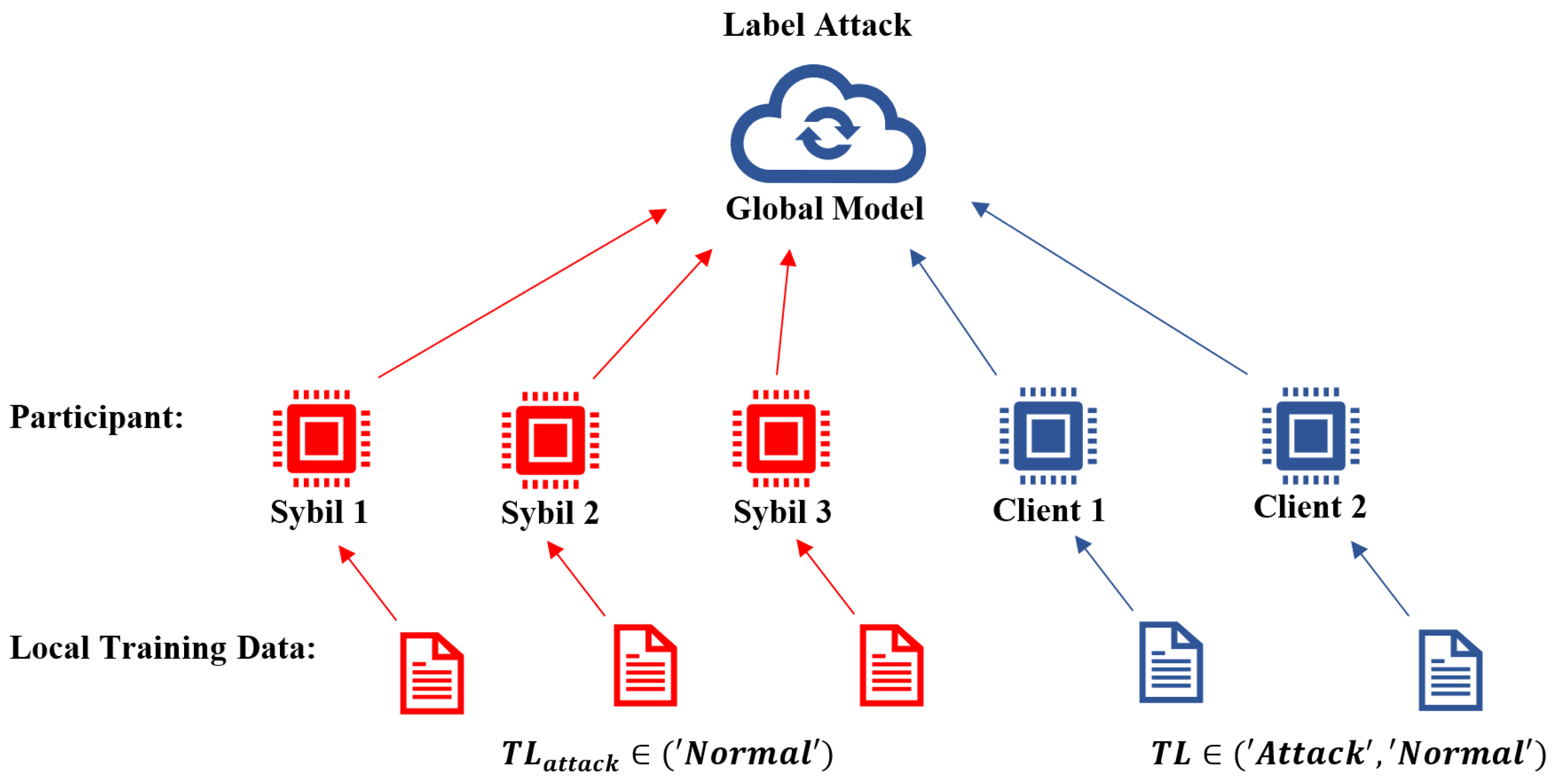
3. Assumptions and Attack Model

The proposed SpaceTime model is based on three assumptions:

3.1. Poison Attacks Shift Towards Multiple or Distributed Attackers

Recent research highlights a shift towards examining the rising success rates of distributed Sybil and Byzantine attacks [10,18,19], as well as the effectiveness of Multi-Krum defense against these threats [20]. This assumption encourages SpaceTime to examine spatial and time relationships between multiple attackers.

3.2. Multiple or Distributed Attackers Create Clustered Signatures

Studies such as [9,10,21] demonstrate clustering using various measures of spatial similarity. In Backdoor attacks, Sybil participants display notable gradient similarities. DBAs create a pronounced magnitude difference for individual gradients because they focus each attacker on a single weight’s convergence. SpaceTime needs to include gradient and distance-based similarities to provide comprehensive protection to the various attacks.

3.3. Poisoning Defenses for Federated IoT IDS Are a Spacetime Problem

Vectorized distances from local batches can be described using the Pythagorean theorem where ${(▵D_{istance})}^2={(▵x)}^2+{(▵y)}^2+{(▵z)}^2$. These are the first three dimensions in spacetime. Those spatial measures could be handled by most machine learning models. However, distributed attackers may be presented in different time continuum’s. Let ’c’ be the constant speed of light, ’t’ be time, and then $▵ct$ = $c▵t$ in ct-coordinate. This creates the three + one dimension of space time where $▵S_{pacetime}$ = spatial time. Then space-time is defined as ${(▵S_{pacetime})}^2={(▵ct)}^2-{(▵x)}^2-{(▵y)}^2-{(▵z)}^2$. Long-Term Short-Term Recurrent Neural Networks can solve spacetime problems due to their architecture allowing the implementation of timesteps. The ability to include long-term memory may help a model contextualize points in the three + dimensions of space and time to identify attackers. This assumption draws this research to implement a novel bidirectional LSTM model to evaluate poisoning defenses in a federated environment through the problem description of spacetime.

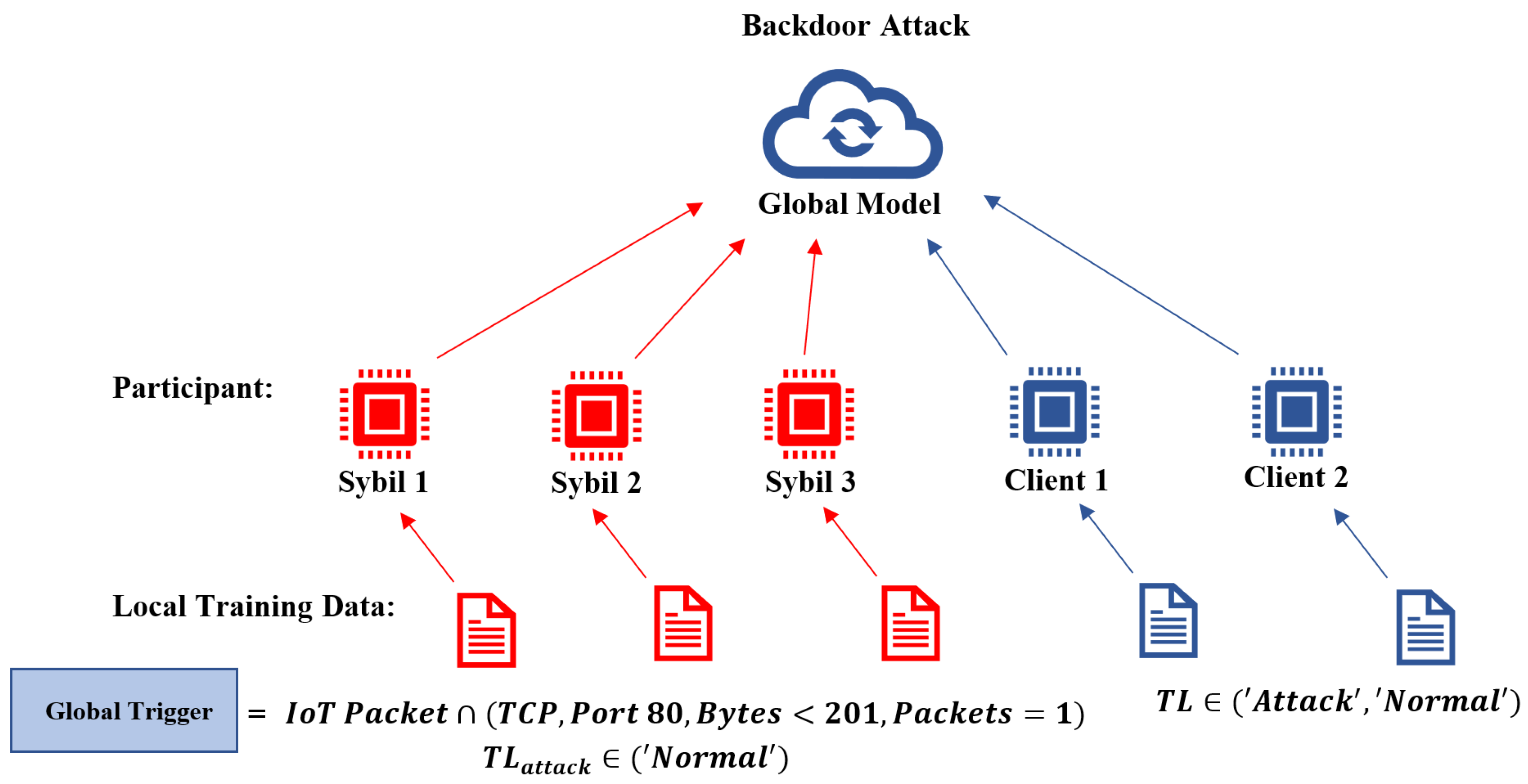
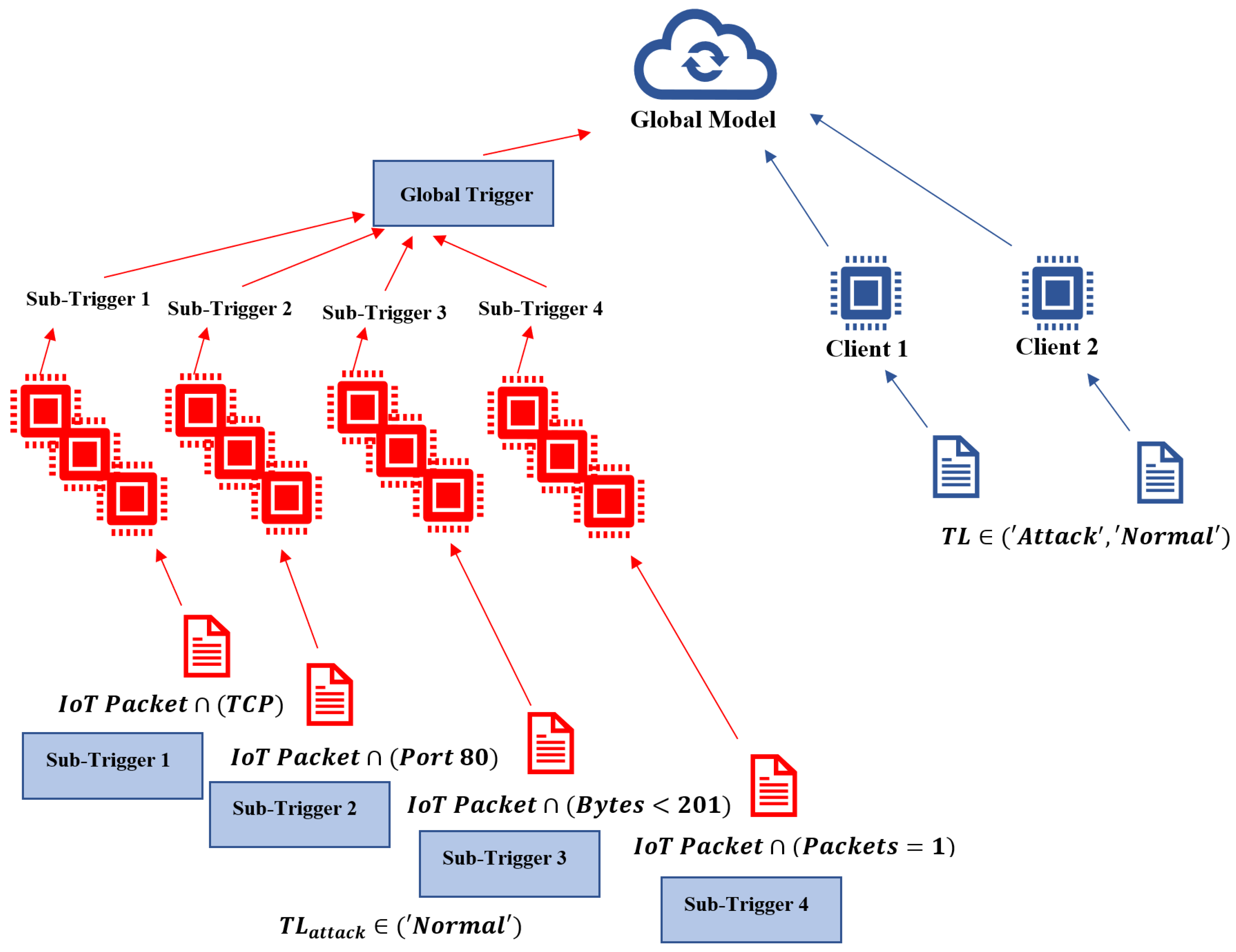
3.4. Attack Model

In this work, we focus on poisoning attacks on the federated learning model. Our attack model includes both Byzantine and Sybil attacks that target the model aggregation process to degrade the global model’s performance or manipulate its behavior. Specifically, we demonstrate label flipping and backdoor as a malicious strategy in both Byzantine and Sybil poisoning attacks within federated learning (FL) systems.

Label flipping attacks involve injecting crafted attack points into the training data by altering the target class labels. Flipping the label will cause the trained model to change its original prediction boundaries, resulting in a misclassification. In our model, Sybil label-flipping attack on an Intrusion Detection System (IDS) for IoT networks with two traffic classes, $ϵ$ (’Attack’ and ’Normal’), the attack might involve mislabeling "Attack" traffic as "Normal." This intentional mislabeling disrupts the model’s ability to accurately identify malicious traffic. Similarly, in the context of Byzantine attacks, labels are randomized instead of intentionally crafted. Such randomization confuses the learning process of the model.

Backdoor attacks differ from label-flipping attacks in their targeting strategy. While label flipping affects class labels broadly, backdoor attacks focus on specific attributes, causing any data with the targeted attribute, referred to as the "trigger," to be misclassified. For example, in an IoT setting, a backdoor attack might involve labeling all traffic as "Normal" if it matches a specific attribute associated with a DoS attack, effectively exploiting the trigger to bypass detection. In this paper, we specifically focus on distributed backdoor attacks (DBA). Unlike traditional backdoor attacks, which are often confined to a single malicious client, distributed backdoor attacks involve multiple malicious participants coordinating their actions to poison the global model while maintaining stealth. For example, in a DoS attack, one Sybil client may poison HTTP protocol packets, while others target packets with fewer than 200 bytes. This level of granularity reduces the distinctiveness and similarity of each Sybil’s contribution, making the attack more difficult to detect. The final outcome is that the DoS attack is able to converge to a "Normal" label, effectively evading current defense mechanisms.

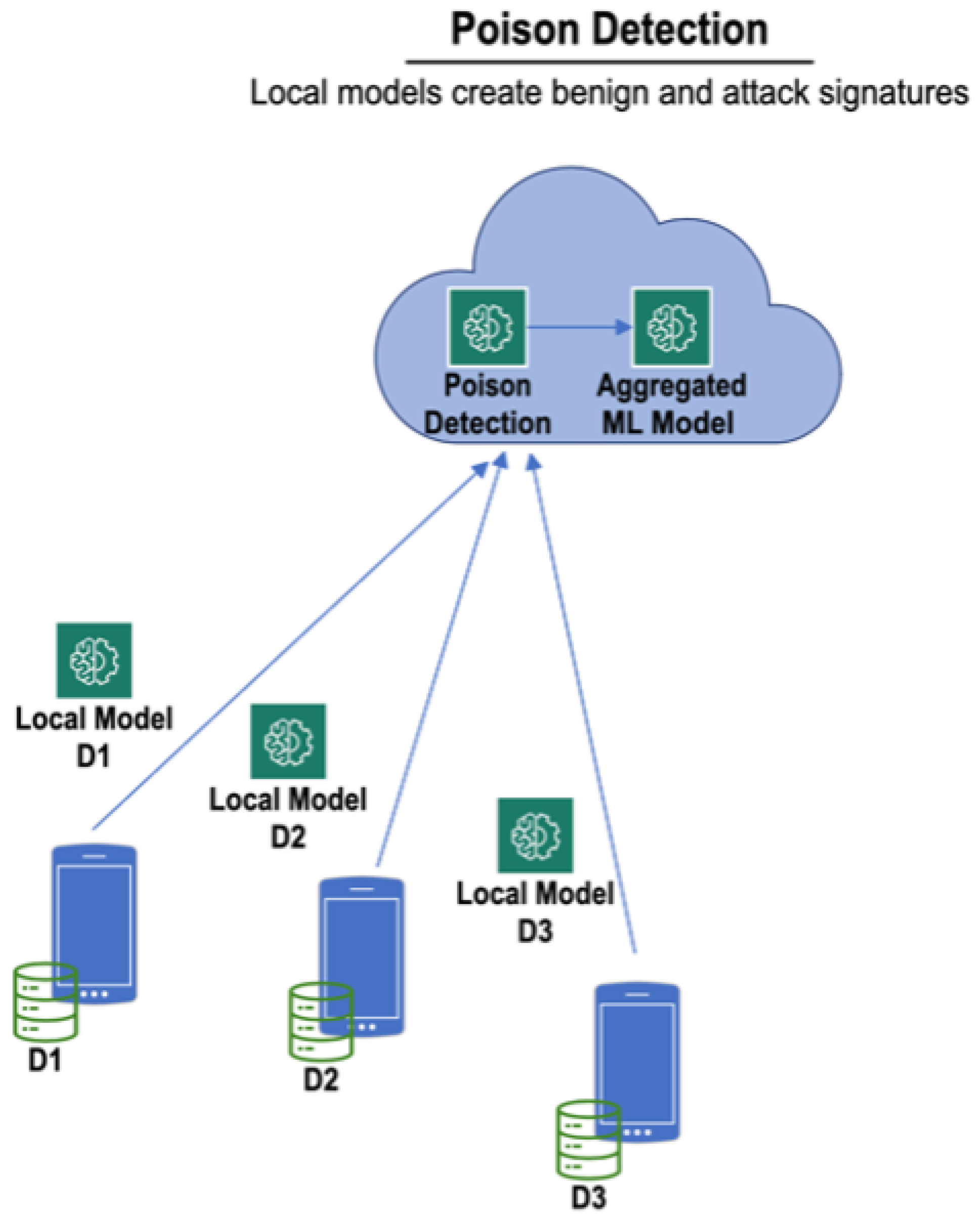
4. Proposed SpaceTime Defense Model

In this section, we describe our proposed SpaceTime defense model that builds an LSTM Recurrent Neural Network using the many-to-one regression architecture for poisoning detection based upon multiple mathematical similarities.

4.1. Defense Architecture

Architecturally, SpaceTime is a microservice that receives the local gradients prior to the global model. Figure 3 shows the architecture of the poison detection defense. SpaceTime integrates as a component to a federated IDS for IoT.

SpaceTime employs a stacked bidirectional LSTM model with timesteps to generate predictions. After predicting the local weights, SpaceTime passes the honest client gradients to the global model for aggregation. The IDS will not aggregate the local models that SpaceTime predict as poison attacks, ensuring the integrity of the global model.

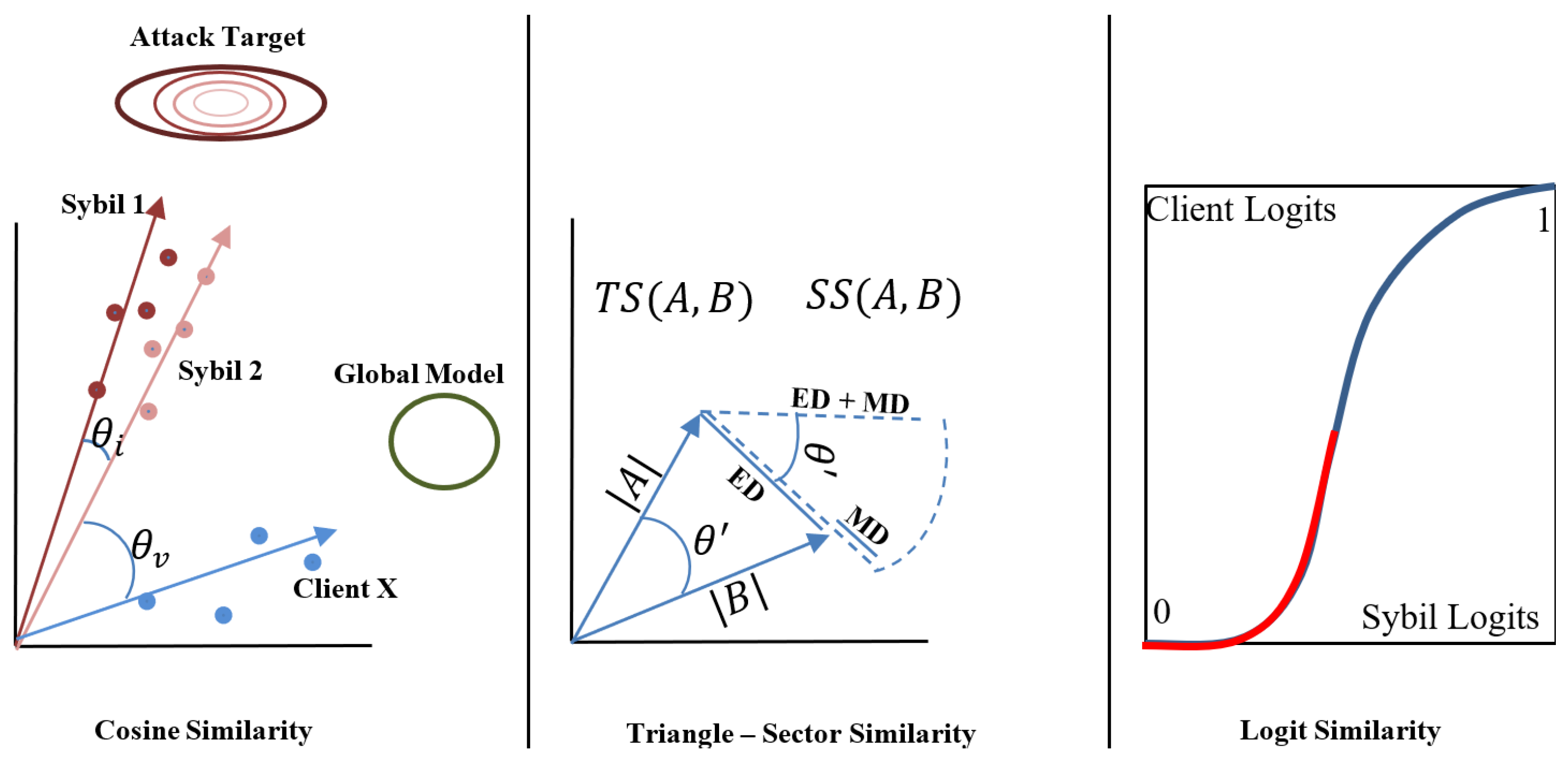
4.2. Similarity Metrics

The proposed solution Computes five similarity metrics, along with a density distribution, probability, and dispersion, for each set of vectorized local gradient updates. Specifically, the system extracts the product of Triangle Area Similarity (TS) and Sector Area Similarity (SS), referred to as Area Similarity FoolsGold (ASF), as well as Cosine Similarity (CS), Manhattan Similarity (MS), Euclidean Distance (ED), and Jaccard Similarity (JS). Additionally, it derives a normalized distribution, inverse logits, and standard deviation from the updates of each local model for every batch.

In the following, we define the similarity metrics used in our proposed SpaceTime Model.

4.2.1. Cosine Similarity

Cosine similarity can be used to describe likeness irrespective of magnitude. This is important in poisoning attack similarity as client-side hyper-parameters can modify magnitude.

Figure 4. Cosine Similarity of Sybils

Figure 4. Cosine Similarity of Sybils

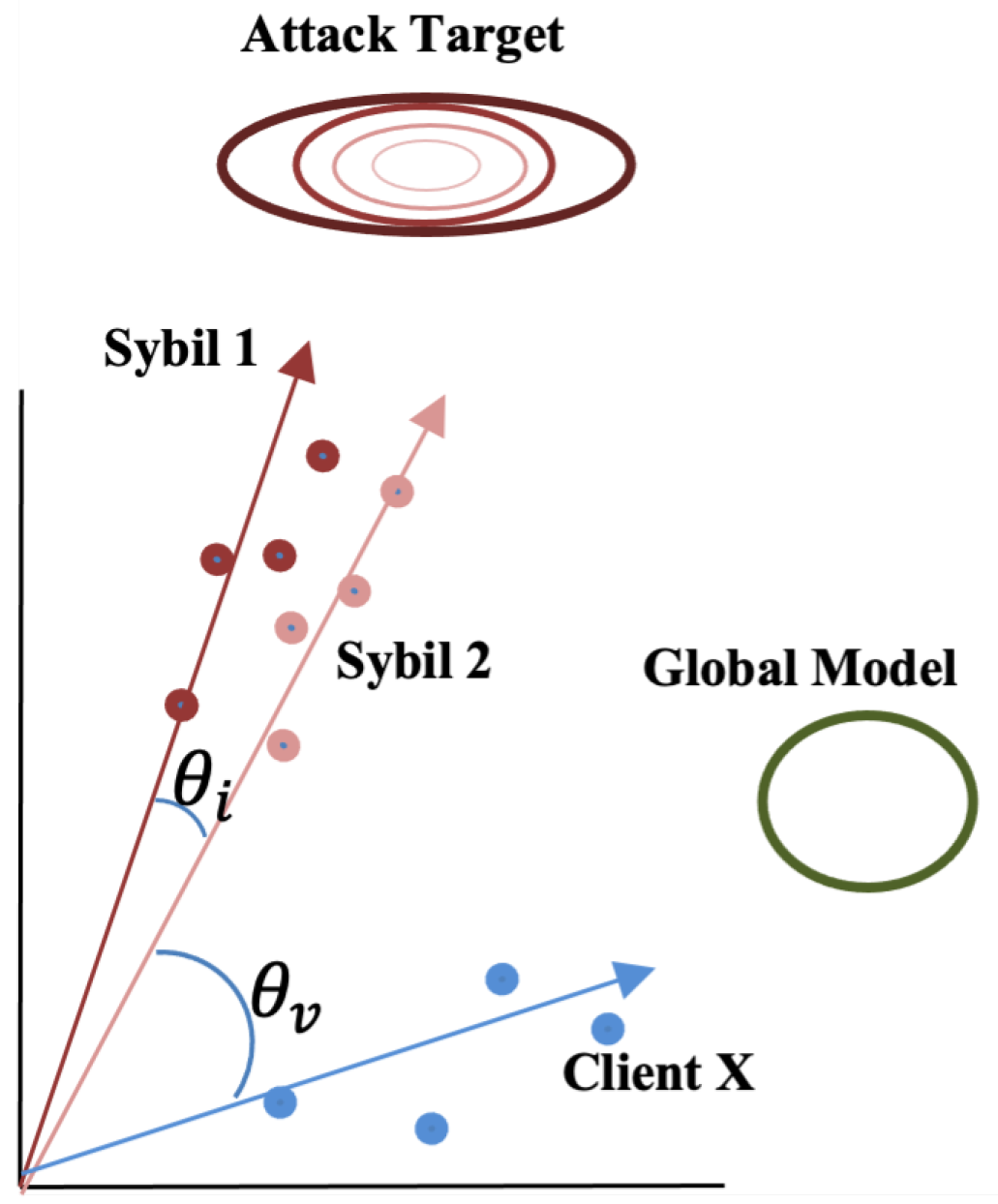
4.2.2. Triangle Area Similarity (TS)

considers the angle, Euclidean distance, and the magnitude of a client’s vectors.

$TS(\overrightarrow{A},\overrightarrow{B})={\displaystyle \frac{|\overrightarrow{A}|·|\overrightarrow{B}|·sin\left({\theta }^{\prime }\right)}{2}}$ where A and B represent vector updates. As the vectors A and B become more similar, the area calculated by this equation decreases proportionally. However, when the vectors fully overlap, the formula fails because the sine of the angle approaches zero. To mitigate this issue, the angle $\theta$ is adjusted to avoid undefined or misleading output. Specifically, $\theta$ is defined as: ${\theta }^{\prime }={cos}^{-1}\left(\overrightarrow{V}\right)+10$

Despite this adjustment, TS may still fail under certain conditions particularly when specific thresholds for angle similarity and Euclidean distance are reached. Consequently, the method may lack the robustness required for consistently accurate similarity assessment, due to some inherent limitations.

4.2.3. Sector Area Similarity (SS)

complements Triangle Area Similarity by incorporating the magnitude differences between client vectors. This approach enables measurement of the area between two vectors from an alternative geometric perspective. The SS metric combines both the squared difference in magnitudes and the squared Euclidean distance, modulated by an angular rotation, to provide a more balanced similarity measure. $SS(A,B)=\pi ·{(ED(A,B)+MD(A,B))}^2·\left({\displaystyle \frac{{\theta }^{\prime }}{360}}\right)$

4.2.4. Area Similarity FoolsGold (ASF)

combines Triangle Similarity (TS) and Sector Similarity (SS) to enhance clustering based on similarity measures [18]. The TS-SS formula multiplies the TS and SS components, and is defined as follows:

$TS-SS(A,B)$ = ${\displaystyle \frac{|\overrightarrow{A}|·|\overrightarrow{B}|·sin\left({\theta }^{\prime }\right)·{\theta }^{\prime }·\pi ·{(ED(A,B)+MD(A,B))}^{\prime }}{720}}$

The output of this function ranges from 0 to ∞, where a value of 0 occurs only when the Euclidean Distance (ED) equals the Magnitude Difference (MD). The magnitude difference is calculated as:

$MD(A,B)=|\sqrt{{\sum }_{n=1}^k{A}_n^2}-\sqrt{{\sum }_{n=1}^k{B}_n^2}|$

This formulation emphasizes the interplay between Euclidean distance and magnitude difference. While local vector magnitude can be an effective defense against data poisoning attacks such as Distributed Backdoor Attacks (DBAs), angle-based similarities remain vulnerable to label flipping and traditional backdoor methods.

4.2.5. Jaccard Distance (JD)

This metric is used to evaluate the similarity between two sets, based on the number of shared elements. The measure is defined as the ratio between the intersection and the union of the sets. For vectors A and B representing local model gradients, $JD={\displaystyle \frac{|\overrightarrow{A}\cap \overrightarrow{B}|}{|\overrightarrow{A}\cup \overrightarrow{B}|}}$ The logit function serves as the quantile function of the logistic distribution. Given a probability p ∈ (0,1), the logit expresses the logarithm of the odds: logit $\left(p\right)=log\left({\displaystyle \frac{p}{1-p}}\right)forpϵ(0,1)$

Its inverse, often referred to as the sigmoid function, maps real-valued inputs back into the (0, 1) interval: inverse logit (p) = ${\displaystyle \frac{exp\left(x\right)}{(1+exp(x\left)\right)}}$

In our framework, we apply the logit transformation to similarity metrics as a "pardoning" mechanism, which emphasizes divergence at the tails. This approach protects clients with low but non zero similarity from being misclassified as Sybil nodes, by compressing outputs into a bounded (0,1) range. Furthermore, we utilize the inverse logit function to distinguish between honest and adversarial participants, based on the techniques described in [22].

In total, eight features were extracted per participant to provide a bi-directional LSTM with a rich representation across spatial dimensions. In the following section, we present our methodology and implementation based on LSTM, which allows temporal exploration of these spatial characteristics.

4.3. Defense Methodology

Our proposed defense mechanism begins by accepting a batch of local gradient updates prior to aggregation within the Federated Learning Intrusion Detection System (FL IDS). For each client i, the ASF similarity is calculated based on the participant vector i = $\overrightarrow{X_i}$ where $\overrightarrow{X_i}$$ϵ$$[\overrightarrow{X_1},\overrightarrow{X_2},\overrightarrow{X_3},...\overrightarrow{X_i}]$ and i denote the total number of clients in the update batch.

Figure 5. Bidirectional LSTM

Figure 5. Bidirectional LSTM

Subsequently, the FoolsGold pardoning algorithm is employed to map the ASF similarity outputs for each $\overrightarrow{X_i}$ to a binary range $[0,1]$. This step addresses the limited discriminative power of ASF in distinguishing between malicious and benign clients. Clients are "pardoned" through a re-weighting mechanism that adjusts the weights of client vectors $\overrightarrow{X_i}$ and $\overrightarrow{X_j}$ based on their similarity. The new client weight ${\alpha }_i$ is derived by inverting the maximum similarity scores, ensuring that the values are within the interval [0,1][0,1]. To further emphasize divergence, a logit function is applied, encouraging separation of Sybil clients and honest clients toward the tails of the distribution.

The outcome of this procedure is a weighted batch vector, $\overrightarrow{B{V}_{asf}}$, which incorporates the ASF-based similarity metrics. This vector is intended to highlight significant differences in magnitude, thus improving the system’s defense against model poisoning by improving the detection of anomalous updates. The same pipeline is applied using alternative metrics, including Cosine Similarity (CS), Mean Norm (MN), Euclidean Distance (ED), Jaccard Distance (JD), inverse logits, Normalized Distance (ND), and Standard Deviation (STD). The corresponding batch vectors are denoted as $\overrightarrow{B{V}_{cs}}$, $\overrightarrow{B{V}_{mn}}$, $\overrightarrow{B{V}_{ed}}$, $\overrightarrow{B{V}_{jd}}$, $\overrightarrow{B{V}_{logits}}$, $\overrightarrow{B{V}_{nd}}$, and $\overrightarrow{B{V}_{std}}$ respectively. Collectively, these weighted batch vectors support robust anomaly detection, aiding in the identification of Sybil attacks, Byzantine failures, and other adversarial behaviors.

We implement a bidirectional Long Short-Term Memory (LSTM) network to model temporal dependencies in client behavior and anomaly patterns. LSTM networks are a class of recurrent neural networks (RNNs) designed to address the vanishing and exploding gradient problems commonly encountered in deep learning [23]. When training on scale, exploding gradients can result in disproportionately large error terms that cause instability in weight updates, ultimately preventing the model from converging. In contrast, vanishing gradients lead to excessively small updates, effectively stopping learning as gradients become negligible.

Various neural architectures can be employed to address the space-time modeling problem in this context. In our case, a many-to-one recurrent architecture is particularly suitable, wherein multiple input features (ASF, CS, ED, MN, JD, logits, ND, and STD) are aggregated to produce a single classification output. Specifically, each input sequence is assigned to a single output $ϵ$$[0,1]$, representing the probability that the client is an honest participant or a poisoning adversary. This formulation is aligned naturally with supervised classification tasks in temporal data analysis.

The strength of LSTM networks lies in their ability to retain information over extended time intervals through their gated cell structure, mimicking aspects of human memory. While standard LSTM architectures effectively capture temporal dependencies by preserving contextual information from past inputs, bidirectional LSTMs (BiLSTMs) extend this capability by processing input sequences in both forward and backward directions. This bidirectional processing enables the model to utilize both past and future contexts, offering enhanced temporal awareness that is not possible with unidirectional LSTMs.

In the context of predicting poisoning participants, the SpaceTime model leverages bidirectional temporal analysis to evaluate client behavior. Each client is characterized by a set of similarity metrics defined in our framework. For example, the model may detect that three of the last five clients exhibit identical Jensen divergence (JD) scores and dispersion patterns. Simultaneously, through the use of a bidirectional LSTM, it also identifies that such patterns are absent in the subsequent 12 clients. This dual temporal perspective, considering both historical and future contexts, enhances the model’s ability to infer that the repeated similarity signatures are indicative of coordinated adversarial behavior. The model integrates this pattern recognition with logit-transformed probability mappings to support robust classification of clients as benign or malicious.

At any given point in the sequence, the model maintains persistent memory that captures both past and future contextual information relative to the current timestep. The time steps allow each set of LSTM cells to utilize the information from $N_{timesteps}$ previous (or future) LSTM cells. Let us assume a training dataset where the target variable Y corresponds to the classification output $ϵ$$[0,1]$, where 0 denotes a poisoning (malicious) client and 1 denotes an honest client.

Let $\overrightarrow{V}$ = $[\overrightarrow{B{V}_{asf}},\overrightarrow{B{V}_{cs}},...,Y]$

Let $N_{timesteps}$ = 3

Then:

$Timestep$ 1 = $[\overrightarrow{B{V}_{asf}},\overrightarrow{B{V}_{cs}},...,0]$

$Timestep$ 2 = $[\overrightarrow{B{V}_{asf}},\overrightarrow{B{V}_{cs}},...,0]$

$Timestep$ 3 = $[\overrightarrow{B{V}_{asf}},\overrightarrow{B{V}_{cs}},...,Y]$

$Timestep$ 4 = $[\overrightarrow{B{V}_{asf}},\overrightarrow{B{V}_{cs}},...,1]$

$Timestep$ 5 = $[\overrightarrow{B{V}_{asf}},\overrightarrow{B{V}_{cs}},...,1]$

The Spacetime Deep Neural Network Architecture in Figure 6 illustrates the implementation for a backdoor attack with 20 Sybil participants. The Bi-LSTM model includes one neuron for each client in the time series. This layer creates the forward and backward propagation sequence of the clients. Next, the Bi-LSTM layer is mapped to 120 time-distributed dense layers that apply transformations across each time step independently. These layers process the output sequences and pass them to a final time-Distributed dense layer. This concluding layer produces the predicted output using a sigmoid activation function, mapping the result to the set $ϵ\subset (0,1)$.

The final output of the SpaceTime defense is a prediction vector whose length corresponds to the number of clients in the current update batch. Let this vector be denoted as $\overrightarrow{St}$ = $[P_1,P_2,P_3,...,P_x]$ where each element $P_x$$ϵ$$[0,1]$ represents the predicted class of client x. A value of 1 indicates an honest participant, while a value of 0 denotes a poisoning attacker. During the aggregation phase of the Intrusion Detection System (IDS), local model updates are selectively included based on predictions produced by the SpaceTime model. Specifically, updates from clients classified as adversarial (i.e.,$P_x$ = 0) are excluded from the aggregation process.

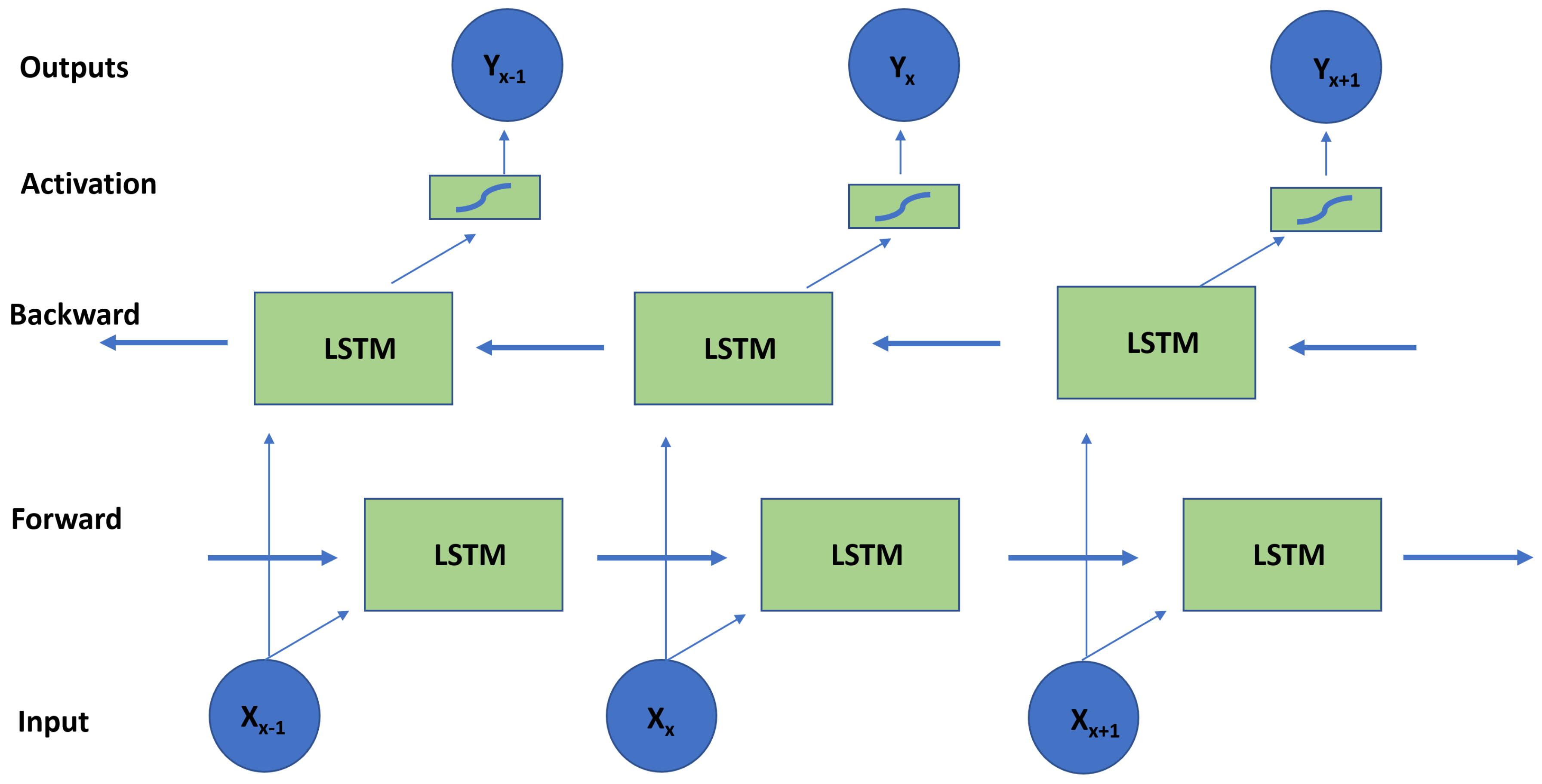
5. Implementation details

5.1. Dataset

We utilized the UNSW Bot-IoT dataset to demonstrate the effectiveness of the proposed Spacetime defense mechanism. For training purposes, a curated subset was extracted from the converted CSV files, comprising 535,051 labeled attack packets and 30,086 normal packets. The attack types represented in the dataset include Distributed Denial-of-Service (DDoS), Denial-of-Service (DoS), Operating System and Service Scans, Keylogging, and Data Exfiltration. We used a test set containing 20,000 records for evaluation.

To simulate backdoor-based adversarial behaviors, a derivative dataset was constructed from the original 565,137 training packets. The goal was to model a backdoor vulnerability that facilitates subsequent DoS attacks. The packets were filtered according to four criteria: (1) the use of the TCP protocol, (2) the destination port 80, (3) consisting of a single packet, and (4) the packet size less than or equal to 201 bytes. All packets satisfying these conditions were re-labeled with the target class $T{C}_i$ as Normal, thus introducing label poisoning into the dataset.

In addition, four additional data sets were created, each isolating one of the aforementioned criteria (1–4) to support systematic design and analysis of Distributed Backdoor Attacks (DBA). These datasets were integrated into the experimental framework and assigned to clients acting as benign participants, backdoor Sybils, or DBA Sybils, depending on the experimental condition.

5.2. Attack Methodology

In this work, we employ a label-flipping strategy to design Byzantine and Sybil attacks within a federated learning framework. For the Sybil attack, sets of Sybil participants $ϵ$$(4,20,40)$ were introduced, each tasked with poisoning the target class label $T{C}_l$, where $T{C}_l$ = ′$Attac{k}^{\prime }$. Each instance of $T{C}_l$ can be described as $T{C}_l$∪$loca{l}_{Io{T}_{packe{t}_x}}$$ϵ$${(}^{\prime }Attac{k}^{\prime })$ representing packets locally labeled as attacks. The Sybil nodes subsequently flipped the label, relabeling $T{C}_l$ = ${(}^{\prime }Norma{l}^{\prime })$. Each Sybil participant then trained a local model using the poisoned data and transmitted its updated weights to the global model during the corresponding communication round. Figure 7 illustrates how this degrades the model’s ability to correctly classify the ${(}^{\prime }Attac{k}^{\prime })$ class while still preserving global convergence.

We design the Byzantine attack in a similar manner. However, each Byzantine set $ϵ$$(4,20,40)$ randomized each $loca{l}_{Io{T}_{packe{t}_x}}$’s output label. Thus, each $T{C}_l$, where $T{C}_l$ = ′$Attac{k}^{\prime }$ or ′$Norma{l}^{\prime }$, was then generated by random permutation. The intent was to construct a gradient vector with substantial divergence that when adopted by the model would cause instability and significantly reduce global accuracy. The global model aggregates updates from participating clients, which may include both honest nodes and adversarial entities—specifically, Sybil or Byzantine attackers, depending on the attack scenario. While all clients perform training on their respective local datasets, Sybil attackers intentionally poison their data by relabeling all IoT packets originally labeled Attack to Normal, thereby introducing targeted label-flipping. In contrast, Byzantine clients disrupt the training process by randomizing the output labels, contributing noise rather than structured poisoning.

To implement the backdoor methodology, Sybil participants $ϵ\in 4,20,40$ were introduced, each targeting a consistent set of features $\cup ,loca{l}_{Io{T}_{packe{t}_x}}$ corresponding to a DoS attack trigger. Let the local dataset be defined as: LD = $\{loca{l}_{Io{T}_{packe{t}_1}},loca{l}_{Io{T}_{packe{t}_2}},\dots ,loca{l}_{Io{T}_{packe{t}_i}}\}$ where each packet is represented as a feature vector:

$|\overrightarrow{loca{l}_{Io{T}_{packe{t}_i}}}|$ = $\{featur{e}_1,featur{e}_2,\dots ,featur{e}_x\}$

Backdoor Sybil nodes aim to poison the training process by relabeling packets with a specific set of features deemed the trigger from Attack to Normal. The IoT IDS global model classifies each $loca{l}_{Io{T}_{packe{t}_x}}$ based on its features $featur{e}_x\in \mathrm{Attack},\mathrm{Normal}$. Let $featur{e}_{target}\in featur{e}_1,featur{e}_2,\dots ,featur{e}_x$ denote the subset of features used to represent the DoS trigger. The objective of the Sybil backdoor attack is to manipulate training so that instances containing $featur{e}_{target}$ converge to the normal class, thus preventing them from being classified as Attack as shown in Figure 8. However, a major limitation of this approach is that influencing the global model at scale requires a large number of Sybil nodes, which increases the uniformity of their gradients and makes them more detectable.

To address this, we introduce Distributed Backdoor Attacks (DBAs), which aim to avoid detectable gradient signatures. In a DBA, each Sybil participant targets only one sub-component of the original trigger, i.e., one feature per attacker group, thus dispersing the attack across independent feature subspaces. Each trigger is assigned a separate Sybil set $ϵ\in 4,20,40$, each flipping the label of relevant local data from Attack to Normal. The global backdoor trigger emerges only when all four sub-triggers collectively converge, as shown in Figure 9.

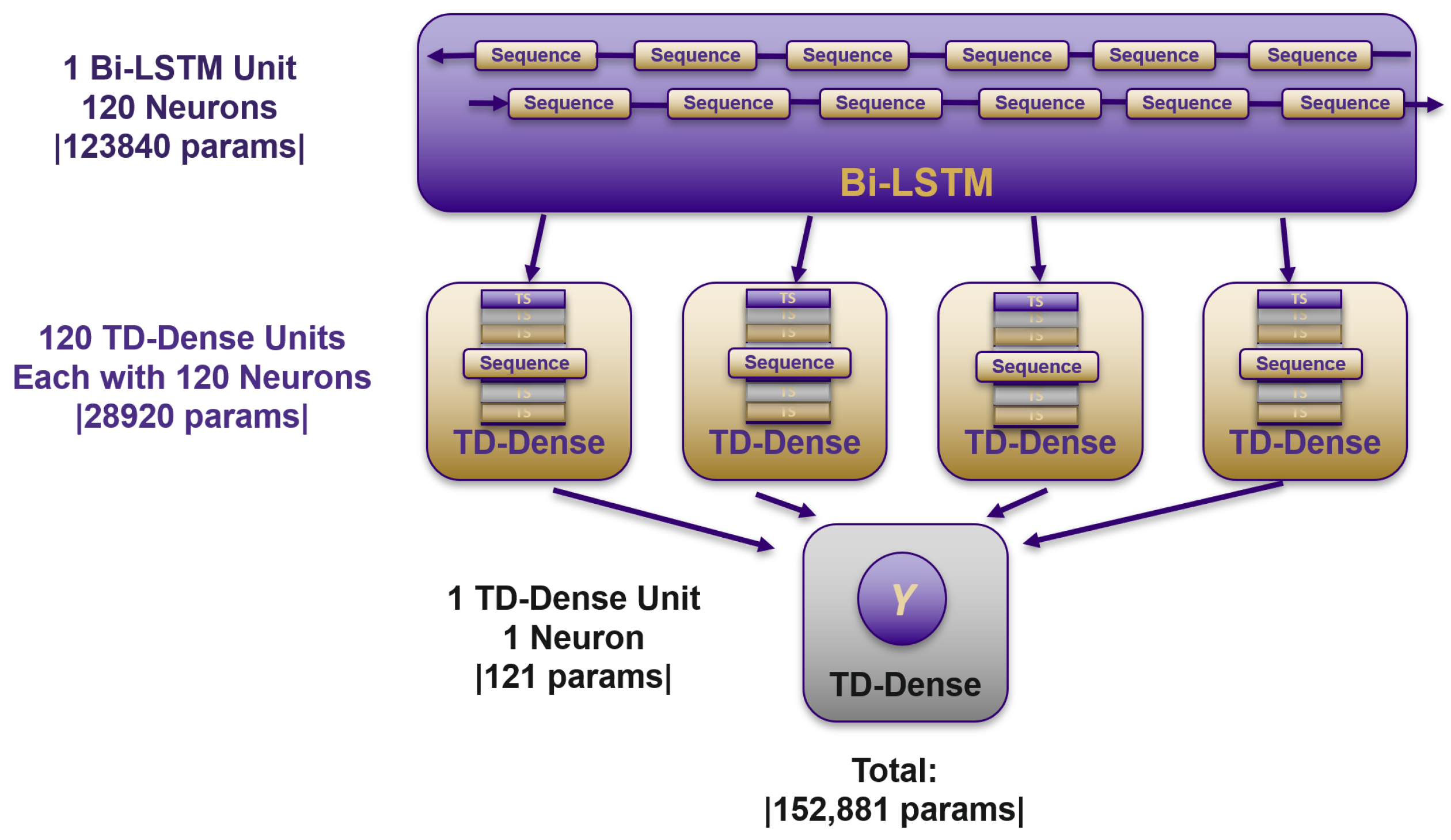
5.3. IDS Architecture and Experiment Setup

An anomaly-based IoT IDS using federated learning was constructed using a sequential LSTM model with 256 timesteps in 6 layers. The LSTM stack resulted in 3,290,113 parameters. Table 1 describes the parameters of the IDS model. To minimize the impact on IoT sensor resources, each local model was trained for a single epoch using this IDS architecture. The model was trained with a batch size of 16 and a validation split of 0.2, resulting in an average client training time of 7 seconds.

The experiment was conducted within a Python environment utilizing the CUDA-accelerated libraries cuDNN, TensorFlow-GPU, PyTorch, and Keras. The experiment comprised four primary stages: (1) IDS Baseline Establishment, (2) Poisoned Data Generation, (3) Poisoned Model Training, and (4) ST-DSD Testing.

The baseline IDS evaluation was executed across three iterations. The first iteration established the baseline detection performance by running the IDS without any defensive mechanisms or adversarial participants. In the second iteration, four distinct attack strategies were applied using various configurations of Byzantine and Sybil participants, with no defense mechanisms employed. This setup enabled assessment of the IDS’s vulnerability and facilitated the collection of similarity metrics required for adversarial training of the ST-DSD model in Stage 3. The third iteration incorporated both the original FoolsGold defense and the modified Area Similarity FoolsGold Defense (ASF) method to demonstrate results against each attack with all attacker permutations.

6. Evaluation Results

In this section, we describe the metrics used for evaluation and present a comparison results of SpaceTime Defense model against FoolsGold and ASF defense mechanisms.

6.1. Evaluation Metrics

We evaluate the performance of our model using three primary metrics: Convergence, Precision, and Poison Rate.

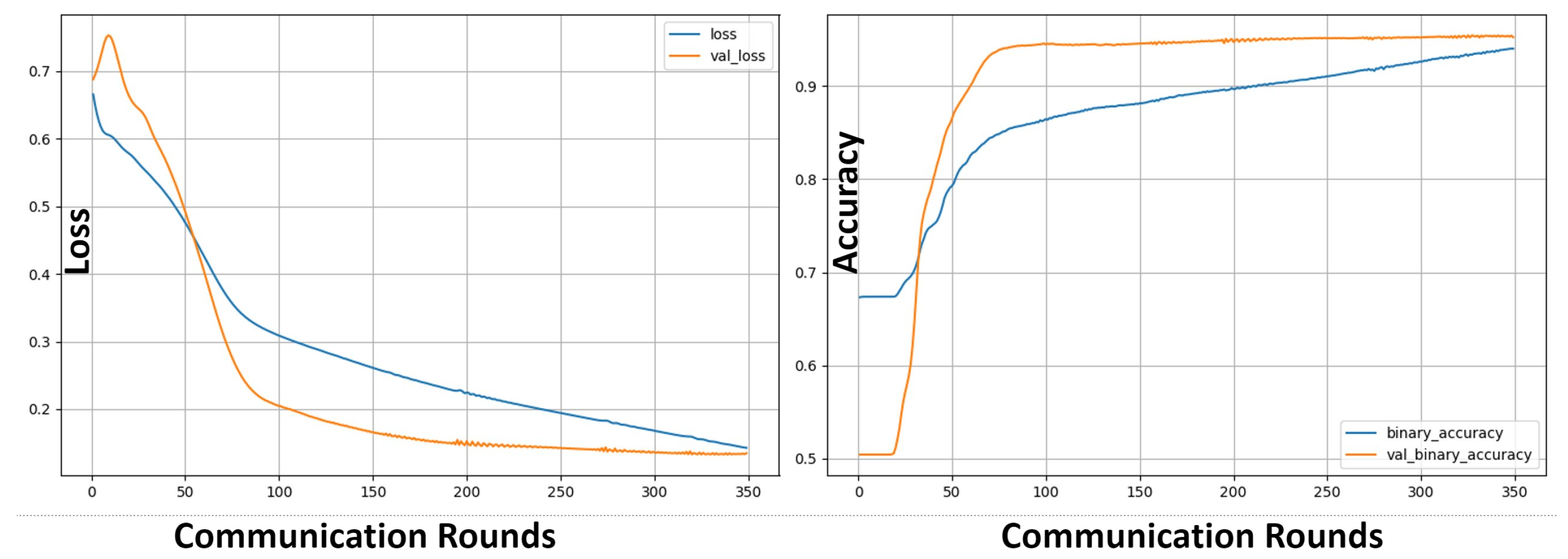
• Convergence : Convergence is defined as the model’s loss per epoch (or training round), convergence reflects the model’s ability to learn under varying attack rates. A consistent downward trend in loss indicates that the model has reached its learning capacity. This metric also helps diagnose overfitting or underfitting when comparing training and validation losses. In the context of adversarial attacks, convergence reflects the resilience of the model. We define poison resilience as successful convergence even with 50% of the participants being attackers.
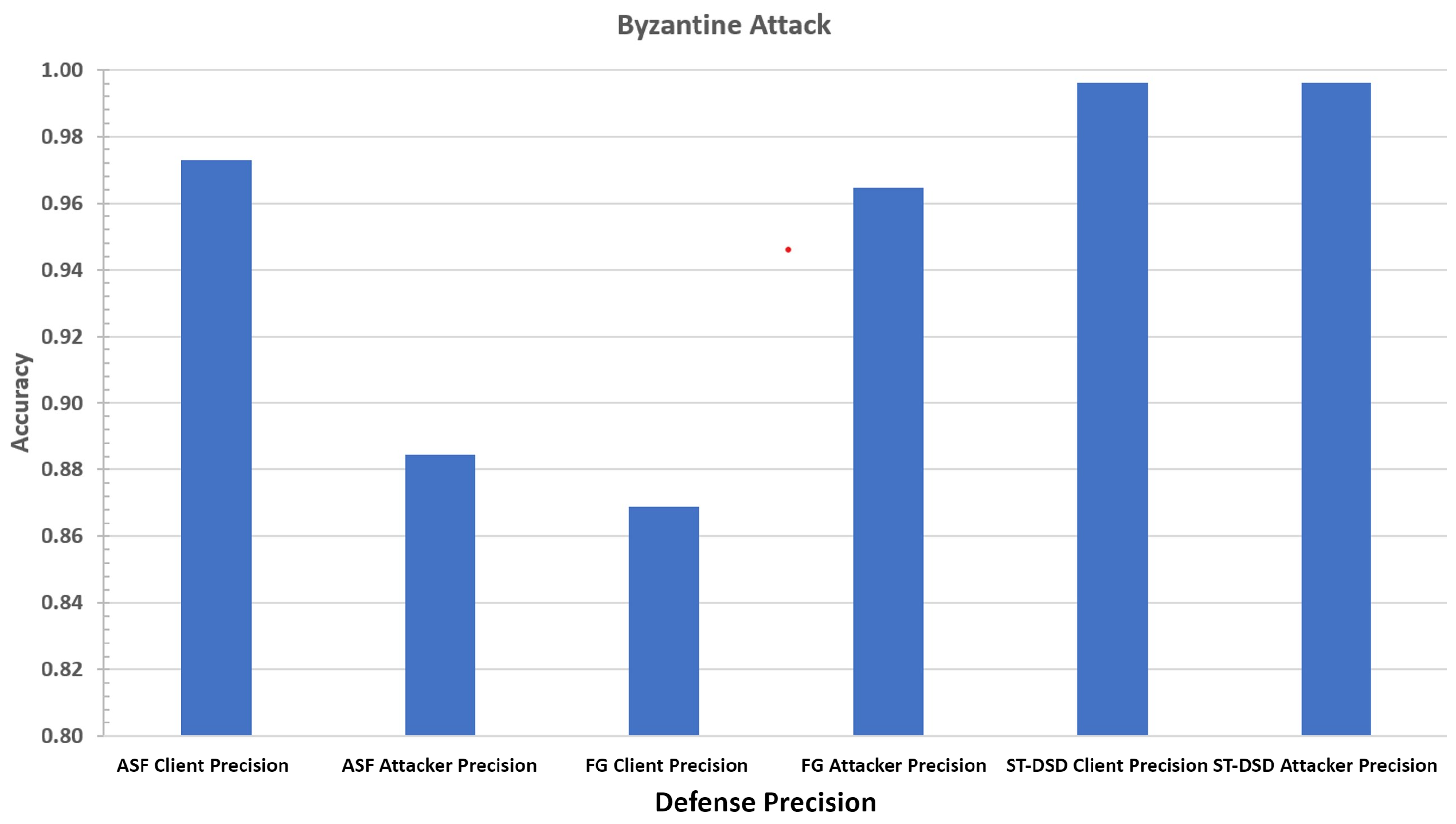
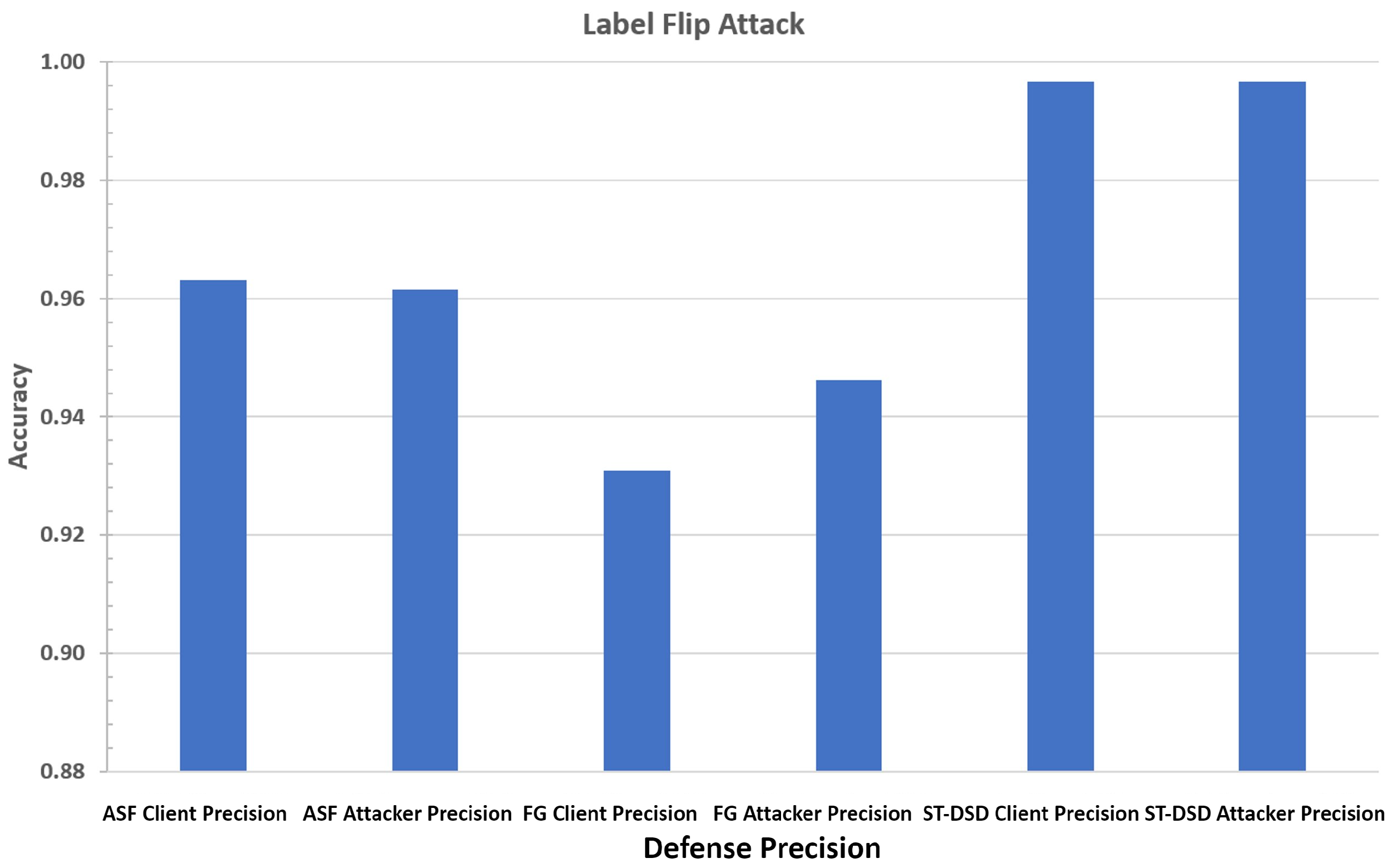
• Precision: We calculate Precision separately for honest clients and poison attackers. Client precision measures the proportion of honest clients correctly identified, while attacker precision measures the proportion of attackers correctly classified. High precision in both categories is critical, as misclassifying honest clients or failing to exclude attackers degrades federated learning performance. This metric helps explain the strengths and weaknesses of each defense mechanism.
• Poison Rate: The poison rate quantifies the percentage of model updates originating from attackers. It differs from the attack rate, which refers to the proportion of attackers in the system. A robust defense may result in a high attack rate but a low poison rate by effectively excluding malicious contributions. Poison rate directly reflects the extent to which an attack influences model performance.

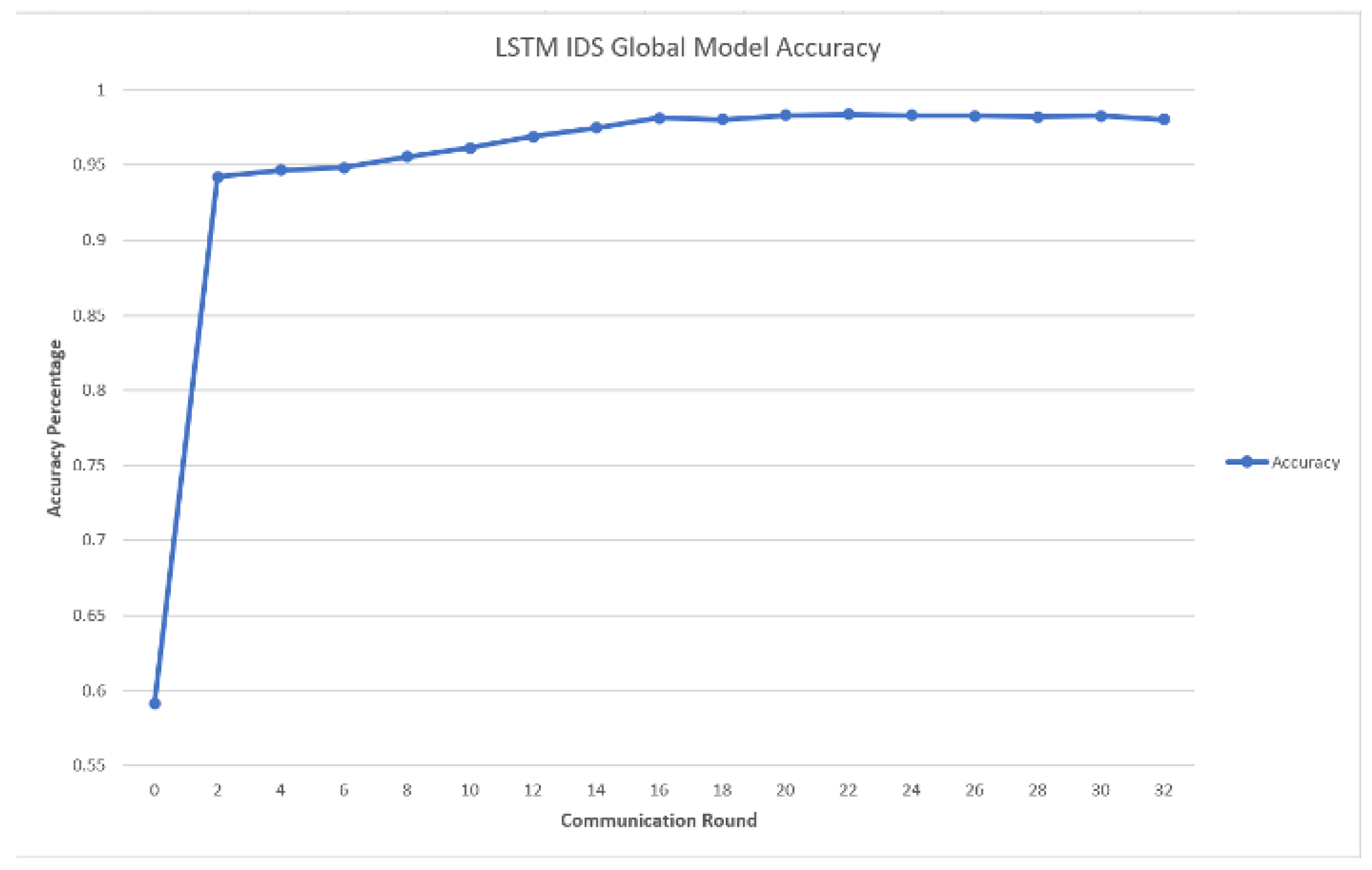
6.2. IDS Baseline Evaluation

The baseline IDS was evaluated without attackers or defensive mechanisms to establish a reference to distinguish between benign and malicious IoT traffic. A total of 23,890 packets were analyzed across 20 clients, comprising 9,490 benign packets and 14,400 attack packets. The dataset included traffic from seven protocols: ARP (467), ICMP (12), IGMP (2), IPv6-ICMP (88), RARP (1), TCP (8,447), and UDP (14,873).

Training was conducted over 33 communication rounds to observe model behavior. Each round aggregated 20 client updates, resulting in 660 total weight updates to the global model.

Figure 10 shows the accuracy of the model in 33 communication rounds, ranging from 0 to 32. The initial round starts with 59% accuracy, which quickly increases to 94. 9% and continues to improve in subsequent rounds. The results show that the anomaly-based IDS powered by federated learning reaches a maximum accuracy of 98. 4%. The model achieves an average accuracy of 94.8% and a median accuracy of 98.0%.

Accuracy convergence is defined as the median accuracy over the final 15 communication rounds, allowing sufficient time for the model to stabilize. Based on this definition, the convergence point—aligned with the inflection in the accuracy curve—yields a final convergence accuracy of 98.2%.acy curve yields a final convergence accuracy of 98.2%.

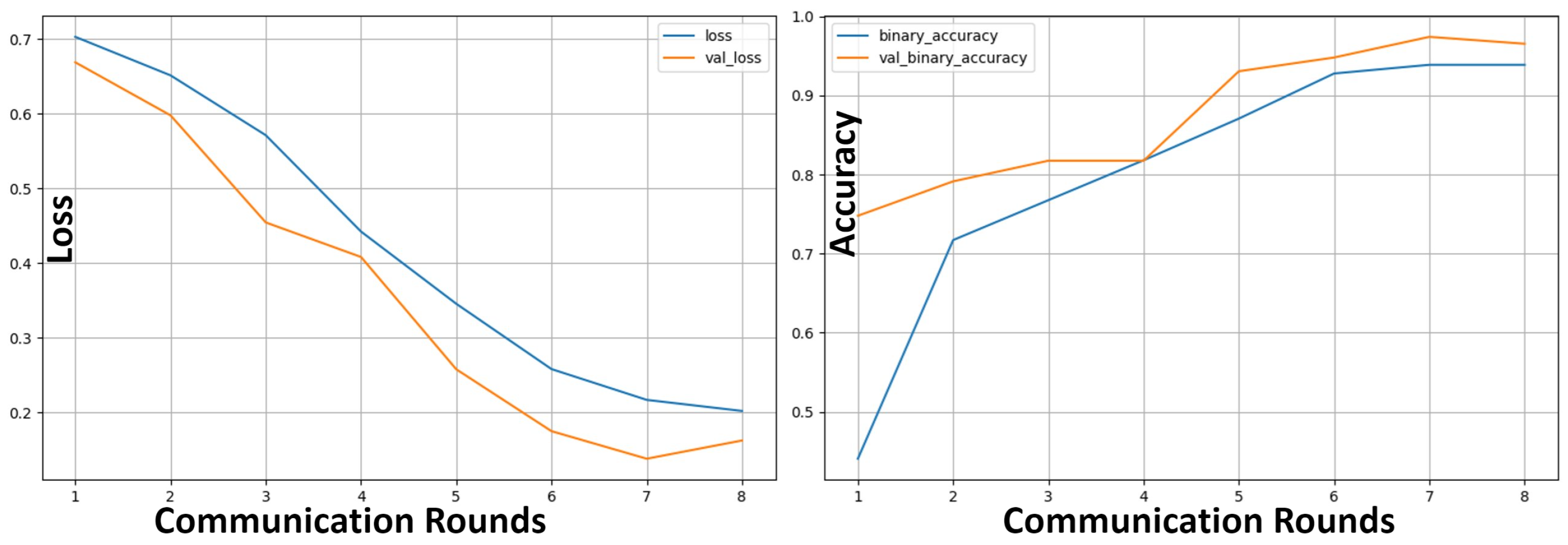
6.3. SpaceTime Model Convergence

Figure 11 presents training and validation metrics across epochs for SpaceTime Model.

The SpaceTime model achieves a loss convergence of 0.1 and an accuracy convergence of 0.99. Although training is allowed up to 10,000 epochs, early stopping is used to prevent overfitting. Specifically, we implement a patience threshold of 1,000 epochs: If no improvement in validation loss is observed within this window, training is halted, and the best-performing model checkpoint is restored. In particular, the use of time Distributed ragged sequencing layers significantly reduced training time, lowering convergence from 15,000 epochs to just 350 epochs.

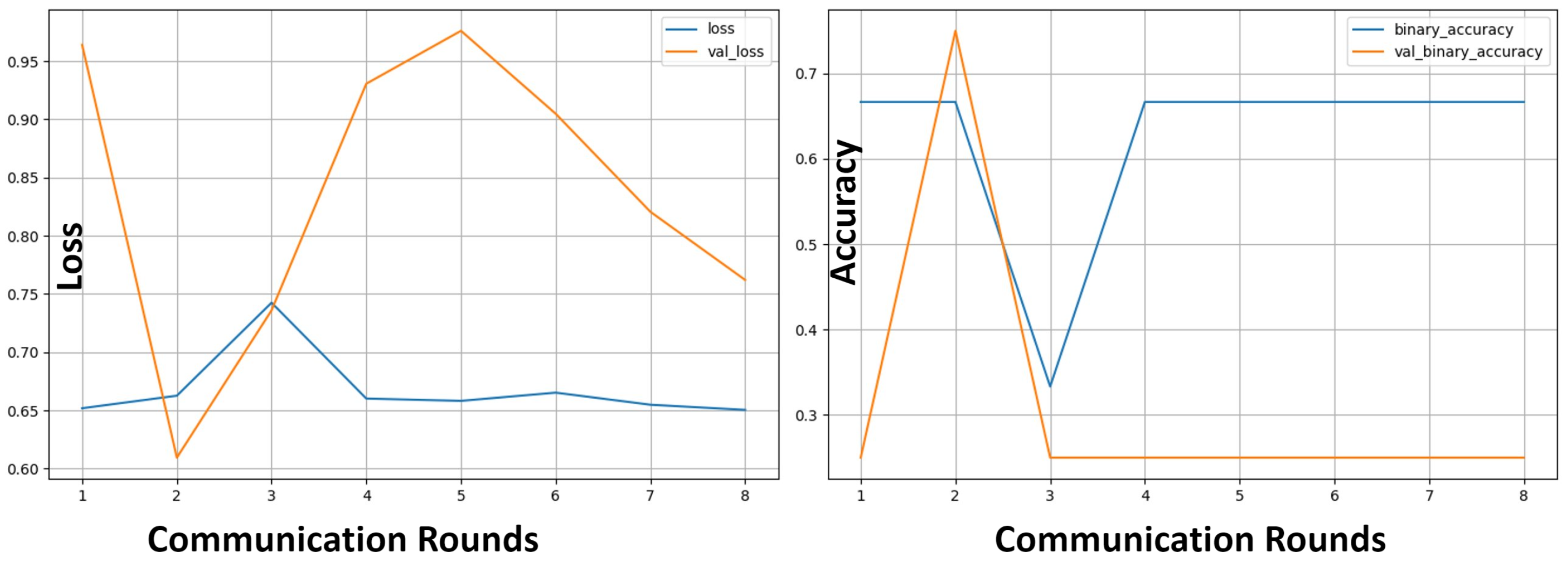
6.4. Poisoning Attacks

To evaluate the effectiveness of each attack methodology, we assess their impact on the IDS baseline accuracy of 98.2% across varying attacker participation levels, denoted by $ϵ\in 1,5,10$ for Byzantine and Sybil attacks. For DBA attacks, due to their structural requirements, attacker participation is scaled to $ϵ\in 4,8,12$. The total number of clients was maintained at 20 per round by adjusting the number of honest participants accordingly: $19,15,10$ for Byzantine and Sybil scenarios, and $16,12,8$ for DBA.

Table 2 presents these results. Each attack is evaluated at increasing levels of attacker presence (1, 5, and 10 participants).

Byzantine attack was specifically designed to disrupt model convergence. It successfully reduced the IDS accuracy from 98.2% to 59.1%, representing a 39.1% decrease. This substantial degradation indicates a successful Byzantine outcome, in which the attack effectively prevented the model from converging to a stable and accurate state.

The backdoor Sybil attacks allowed the global model to converge even in the presence of 1 and 5 malicious participants. The baseline accuracies of the resulting IDS were 98. 3%, 98. 2% and 97. 1% for $ϵ=1,5,10$, respectively. With a 50% attacker participation rate, the attack reduced the overall accuracy of the model by only 1. 1%. This minimal impact suggests that the attack successfully avoids detection while maintaining model performance, which warrants further investigation into its stealth characteristics.

Similarly, the DBA attack exhibited variable effects on the global model. With 4 attackers, the model maintained high accuracy at 99.0%. However, with 8 and 12 attackers, accuracy dropped to 89.1% and 89.2%, reflecting decreases of approximately 9% and 9.1%, respectively. These results may be influenced by the limited scale of the experiment. Smaller client populations reduce the volume of data processed by the model and increase sensitivity to perturbations, even when client update scaling is applied.

6.5. Model Convergence

We evaluate convergence through both loss and accuracy metrics. Figure 12 illustrates the convergence of the IDS model for an honest client over 8 epochs.

Next, we examine a Byzantine-poisoned model that fails to achieve convergence. As shown in Figure 13, the validation loss begins at 0.96 and fluctuates significantly between epochs, reaching a minimum of 0.62. In contrast, the training loss is more stable, converging around 0.65—still far from the 0.1 convergence achieved by the honest client. A similar pattern is observed in the accuracy: the validation accuracy remains low, while the training accuracy peaks at 0.69, falling short of the expected 0.98 convergence.

These convergence results are critical, as they indicate the success of the attack. Our results demonstrate that Byzantine attack results in a 51% degradation in validation loss convergence and a 25% reduction in accuracy convergence. These metrics provide a baseline to quantify the effectiveness of future defenses in mitigating Byzantine threats.

6.6. Poison Rate

Table 3 highlights the correlation between increasing poison rate and decreasing model accuracy, with both attacks conducted at a 50% attacker participation rate.

This comparison evaluates the performance of FoolsGold (FG) defense against proposed SpaceTime model. FG achieved an attacker precision of 0.5, allowing 33% of the model weights to be poisoned by DBA data. This resulted in a 23% reduction in IDS accuracy, dropping to 87%. In contrast, SpaceTime achieved full defense stabilization by epoch 4. It recorded a 0% poison rate and a Sybil attacker precision of 1.0, maintaining IDS accuracy at 96% for that round.

6.7. Poisoning Defense

We highlight our poisoning defense results by focusing on attack rates of 50% or higher to demonstrate the resilience of the defenses. Attacker and client precision metrics are included across different attack types and defenses to facilitate comparison. Our discussion begins with Byzantine attacks and concludes with DBA.

Figure 14 presents the attacker and client precision for each defense - ASF, FG, and proposed SpaceTime (ST-DSD). From the results, we observe a lower precision for ASF mechanism and higher precision for our ST-DSD model.

During Byzantine attacks, ASF showed the lowest attacker precision at 88.4%. FG performed better with 96.4%, while ST-DSD achieved the highest precision at 99.6%. Precision is critical because retaining honest clients directly impacts IDS accuracy. Client precision for the defenses follows the order ASF (97.3%), FG (86.8%), and ST-DSD (99.0%).

Figure 15 shows that all defenses exhibit comparable results against the label flip attack. In particular, ASF demonstrates a significant improvement in client precision compared to its performance against Byzantine attacks, suggesting that it is better suited to defend against Sybil attacks than Byzantine ones. FG shows a slight increase in client precision, though this is offset by a minor drop in attacker precision. Meanwhile, ST-DSD maintains high precision for both attackers and clients at 99%.

The backdoor attack posed significant challenges for both ASF and FG defenses. As shown in Figure 8, ASF proved statistically ineffective, with client precision at 74% and attacker precision at 69%. FG achieved perfect attacker precision at 100%, but its client precision dropped sharply to 17.7%. Although FG was designed to identify attackers in backdoor attacks reflected in its strong attacker precision, the unexpected failure of its pardoning algorithm led to many honest clients being misclassified as attackers. In contrast, ST-DSD remained robust, maintaining a client precision of 99.3% and attacker precision of 100%.

Figure 16. Backdoor Defense precision Comparison at 50% $>=$ Attack Rate

Figure 16. Backdoor Defense precision Comparison at 50% $>=$ Attack Rate

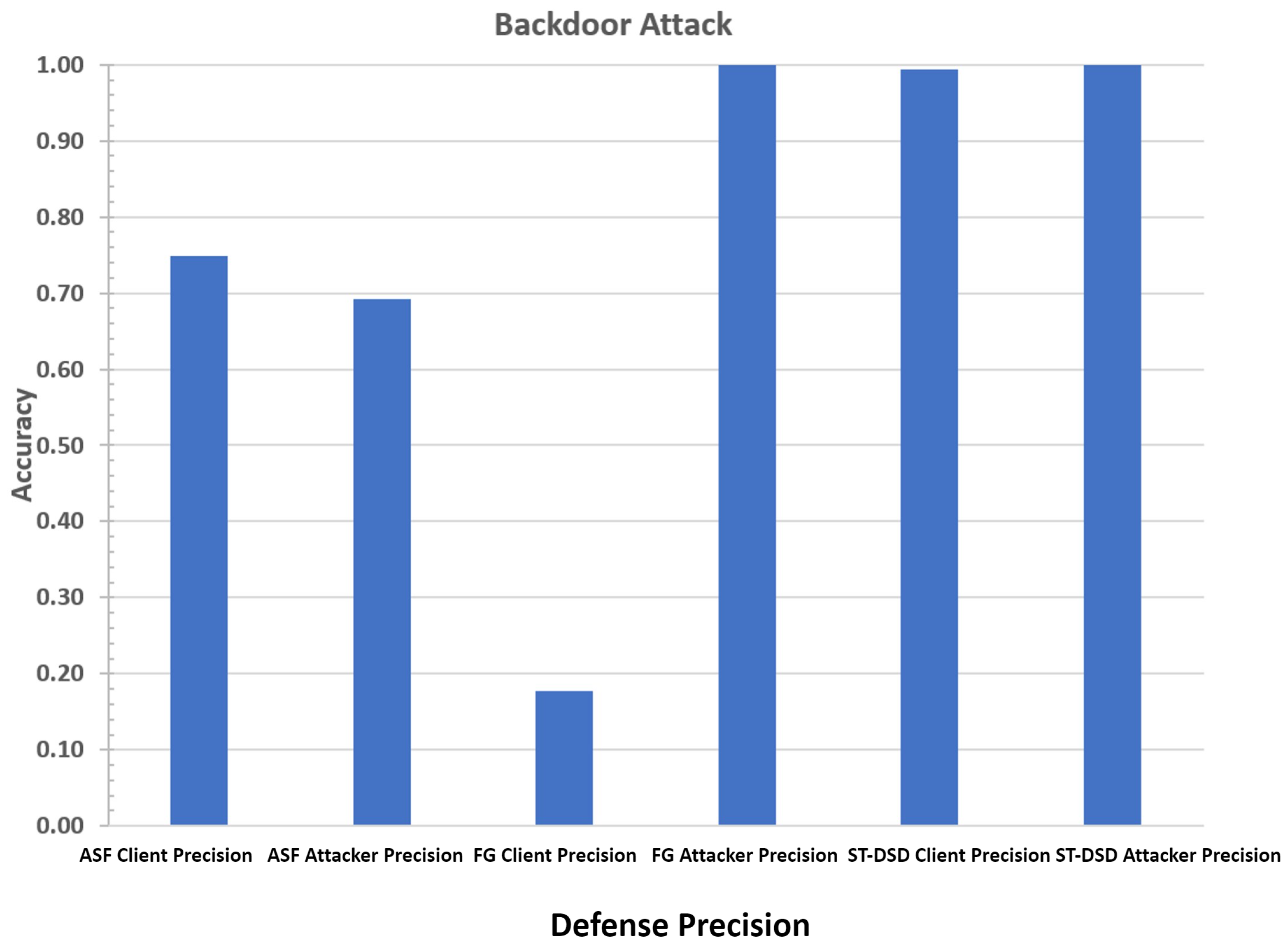
7. Conclusions

In this work, we presented a unique poisoning defense model to provide resistance to poisoning attacks against federated learning based IDS systems in IoT. The proposed SpaceTime deep similarity defense model was constructed using an RNN many-to-one architecture with bidirectional long-short-term memory and time-distributed layers to allow a ragged sequence classification using the space-time manifold. We demonstrated that our state-of-the-art poisoning defense could achieve statistical significance hardening against poisoning attacks by increasing the accuracy, loss convergence, and precision of the IDS model across the spectrum of attacks and attackers with non-IID. Results demonstrate that our defense mechanism achieved 99.9% attacker and honest client identification and laid the groundwork for a new line of poisoning defense.