The Resolution of the Collatz Conjecture: A Unified Arithmetic and Dynamical Framework

1. Introduction

Despite its apparent simplicity, the Collatz Conjecture has resisted proof for more than eight decades. In two prior papers by the author, the arithmetic skeleton of the dynamics was isolated from two complementary directions.

• The local view: a deterministic residue framework of the Reverse Collatz Function that governs admissibility and guarantees unique parentage, describing the step-by-step behavior of individual trajectories [1].
• The global view: an iterative offset–ladder framework that shows how child–parent differences extend to arithmetic progressions whose higher lifts systematically fill all odd residues, achieving complete recursive coverage of the odd integers [2].

Neither perspective alone suffices to prove closure. The local view explains how each odd moves, but not how the whole set of odds fits together. The global view explains how the set of odds closes globally, but not why each trajectory is constrained locally. Only when both perspectives are combined can the Collatz function be recognized as a closed structure. In this work we extend on previous works and present that unified picture and the duality between recursion and iteration, showing that it yields a complete resolution of the conjecture.

To make this framework precise, we first establish the basic definitions that will guide the analysis.

2. Definitions

Definition 2.1

(Classic Collatz function). The classical Collatz map $C:\mathbb{N}\to \mathbb{N}$ is defined by

$$C\left(n\right)=\left\{\begin{array}{cc}n/2,\hfill & \mathit{if}n\mathit{is}\mathit{even},\hfill \\ 3n+1,\hfill & \mathit{if}n\mathit{is}\mathit{odd}.\hfill \end{array}\right.$$

Definition 2.2

(Forward Collatz function). The complete-step (odd-to-odd) Collatz map $T^{*}:{\mathbb{N}}_{\mathit{odd}}\to {\mathbb{N}}_{\mathit{odd}}$ is

$$T\left(n\right)={\displaystyle \frac{3n+1}{2^{k_{max}}}},$$

where $k_{max}\ge 1$ is the maximal exponent such that the denominator $2^{k_{max}}$ divides $3n+1$. Thus $T\left(n\right)$ gives the next odd iterate of n under the Collatz process.

Definition 2.3

(Reverse Collatz function). The complete-step reverse Collatz map $R:{\mathbb{N}}_{\mathit{odd}}\to {\mathbb{N}}_{\mathit{odd}}$ assigns to each odd integer n its admissible parent via

$$R(n;k)={\displaystyle \frac{2^{k}n-1}{3}},k\ge 1,$$

where k is admissible if $2^{k}n\equiv 1(mod3)$. If $k_{min}$ is the minimal admissible doubling count, then $R(n;k_{min})$ is called the first parent of n.

Definition 2.4

(Middle-even values). In the odd-to-odd formulation of the Collatz map, each step factors through an intermediate even value.

• For the forward map, given an odd integer n, the intermediate (middle-even) value is

  $$E_f\left(n\right):=3n+1.$$
• For the reverse map, given an odd integer n and an admissible doubling count $k\ge 1$ (i.e. $2^{k}n\equiv 1(mod3)$), the intermediate (middle-even) value is

  $$E_r(n,k):=2^{k}n.$$

Both $E_f$ and $E_r$ are even and serve as the “middle” stage between odd inputs and odd outputs. Read modulo 18, these values determine the child’s odd class through the fixed gate $10\mapsto C_0$, $4\mapsto C_2$, $16\mapsto C_1$ in the reverse Collatz function.

Definition 2.5

(Parent(reverse Collatz function)).An odd integer n is called a parent. If $n\equiv 3(mod6)$ (that is, n is an odd multiple of 3), then it has no admissible doubling and is called aterminating parent. If $n\equiv 1(mod6)$ or $n\equiv 5(mod6)$, then n is live and admits some $k\ge 1$ that is admissible.

Definition 2.6

(Child(reverse Collatz function)). Given a parent n and an admissible $k\ge 1$, the corresponding child is

$$m={\displaystyle \frac{2^{k}n-1}{3}}\left(\mathit{odd}\right).$$

For a fixed n, admissible k have fixed parity and are exactly

$$k=k_{min}\left(n\right)+2\ell ,\ell \ge 0,$$

where ℓ is the lift index counting successive admissible exponents above the minimal one. As k increases by $+2$, the middle-even residue cycles $10\to 4\to 16\to 10$; under the fixed gate $10\mapsto C_0$, $4\mapsto C_2$, $16\mapsto C_1$, the children of n therefore occur in the deterministic class rotation

$$C_0\to C_2\to C_1\to C_0\to \dots$$

Definition 2.7

(First child). For a live parent n, let $k_{min}$ be the minimal admissible doubling count. The first child of n is

$$m_1={\displaystyle \frac{2^{k_{min}}n-1}{3}}.$$

Definition 2.8

(Admissible doubling and child). Let n be odd. A doubling count $k\ge 1$ is admissible if

$$2^{k}n\equiv 1(mod3).$$

For any admissible k, the reverse child is

$$R(n;k):={\displaystyle \frac{2^{k}n-1}{3}}\in \mathbb{N}.$$

The set of admissible k for a fixed odd n has fixed parity (even if $n\equiv 1(mod3)$, odd if $n\equiv 2(mod3)$), and hence $k\mapsto k+2$ preserves admissibility.

Definition 2.9

(Progression index). For an odd parent n, the progression index t is the integer parameter in the canonical forms

$$n=6t+5\left(C_1\right),n=6t+1\left(C_2\right),$$

with $t\ge 0$. The index t counts the position of n within its mod-6 residue class. In later sections, offsets and ladders are expressed as explicit functions of this progression index.

Definition 2.10

(Admissible parent). For odd $n\ge 1$, define $k_{min}\left(n\right)$ to be the least positive integer k such that $2^{k}n\equiv 1(mod3)$. If such k exists, set

$$P\left(n\right):=R\left(n;k_{min}\left(n\right)\right)={\displaystyle \frac{2^{k_{min}\left(n\right)}n-1}{3}}.$$

If $3\mid n$ we say n is terminating.

Definition 2.11

(Admissible exponents). For an odd integer n, the set of admissible exponents is

$$K\left(n\right):=\{k\ge 1:2^{k}n\equiv 1(mod3)\}.$$

(If $3\mid n$, then $K\left(n\right)=⌀$.)

Definition 2.12

(Middle even and gate residue). For odd m, let $E\left(m\right):=3m+1$ and $k:={\nu }_2\left(E\left(m\right)\right)\ge 1$. The middle even is

$$\tilde{e}\left(m\right):={\displaystyle \frac{E\left(m\right)}{2^{k-1}}}=2T\left(m\right),$$

and its gate residue is $g\left(m\right):=\tilde{e}\left(m\right)\left(\mathrm{mod}18\right)\in \{4,10,16\}$.

Definition 2.13

(Reverse parent and live residues). Let $P\left(m\right)={\displaystyle \frac{2^{k}m-1}{3}}$ be the least-admissible reverse parent on odd m, with k given by Lemma 5.3. Work modulo 18 and call

$${\mathcal{R}}_{\mathrm{live}}=\{1,5,7,11,13,17\},{\mathcal{R}}_{\mathrm{dead}}=\{3,9,15\}$$

the live and dead residue sets. Every odd m can be written uniquely as $m=r+18t$ with $r\in {\mathcal{R}}_{\mathrm{live}}\cup {\mathcal{R}}_{\mathrm{dead}}$ and $t\in {\mathbb{N}}_{\ge 0}$.

Definition 2.14

(Ternary digits and cylinders). For $L\ge 1$, write $t={\sum }_{j=0}^{L-1}{s}_j{3}^j+3^{L}u$ with $s_j\in \{0,1,2\}$ and $u\in {\mathbb{N}}_{\ge 0}$. We call $s_0\dots s_{L-1}$ the length-L ternary word of t, and the congruence class

$${\mathcal{C}}_L(s_0,\dots ,s_{L-1})=\{t\in {\mathbb{N}}_{\ge 0}:t\equiv a(mod{3}^L),a=\sum _{j=0}^{L-1}{s}_j{3}^j\}$$

a length-L cylinder. Each cylinder has natural density $3^{-L}$ in ${\mathbb{N}}_{\ge 0}$.

Definition 2.15

(Canonical decomposition). Let m be odd. Define the layer

$$k:={\nu }_2(3m+1)(\ge 1),\mathrm{and}\mathrm{the}\mathit{odd}\mathrm{part}n:={\displaystyle \frac{3m+1}{2^k}}.$$

Write the odd number n uniquely as

$$n=18q+r,q\in {\mathbb{N}}_0,r\in \{1,5,7,11,13,17\}.$$

We call $(k,r,q)$ the canonical triple of m and write

$$\begin{array}{|c|}\hline m=6·2^{k}q+{\displaystyle \frac{2^{k}r-1}{3}}\\ \hline\end{array}(\mathrm{canonical}\mathrm{form}\mathit{of}m).$$

Here k is the layer, r the rail (the residue mod 18), and q the position on that rail.

Definition 2.16

(Forward odd-to-odd step). For odd m, let $k_{max}\left(m\right):={\nu }_2(3m+1)$ and define

$$T\left(m\right):={\displaystyle \frac{3m+1}{2^{k_{max}\left(m\right)}}}\left(\mathit{odd}\right).$$

Definition 2.17

(Least-admissible reverse parent). For odd m, let $P\left(m\right)={\displaystyle \frac{2^{k}m-1}{3}}$, where $k=2$ if $m\equiv 1(mod3)$ and $k=1$ if $m\equiv 2(mod3)$. Work modulo 18 with live residues ${\mathcal{R}}_{\mathrm{live}}=\{1,5,7,11,13,17\}$ and dead residues $\{3,9,15\}$. Write every odd as $m=r+18t$ with $r\in {\mathcal{R}}_{\mathrm{live}}$ and $t\in {\mathbb{N}}_{\ge 0}$.

Definition 2.18

(Ternary cylinders and words). Fix $L\ge 1$. Decompose t as

$$t=s_0+3s_1+\dots +3^{L-1}{s}_{L-1}+3^{L}u,s_j\in \{0,1,2\},u\in {\mathbb{N}}_{\ge 0}.$$

The residue class ${\mathcal{C}}_L(s_0,\dots ,s_{L-1})=\{t\equiv a(mod{3}^L)\}$ with $a={\sum }_{j=0}^{L-1}{s}_j{3}^j$ is a length-L cylinder; cylinders partition ${\mathbb{N}}_{\ge 0}$ and each has density $3^{-L}$.

3. The Deterministic Residue Framework

This section extends the local residue framework first developed in A Deterministic Residue Framework for the Collatz Operator at $q=3$ [1], together with earlier unpublished notes that identified the mod-9 residue cycle as the source of reverse determinism. The core construction is preserved: admissibility is fixed by residue classes modulo 6, while refinement to mod 9 and its canonical lift to mod 18 determines the child class at each step.

The result is a deterministic lens through which every odd integer is classified and every admissible step is resolved. This local structure now appears explicitly as the microscopic counterpart of the global coverage framework that follows.

Dependency Map (Section 3: Local Residues and Gates)

• Uses (from preliminaries). Basic parity/modular facts (e.g. $2\equiv -1(mod3)$), definitions of the classes $C_0,C_1,C_2$, and the odd-to-odd/least-admissible reverse setup.
• Introduces (proved in §3). Proposition 3.8 (gate determinism mod 18); Lemma 3.9 (forward–reverse gate alignment); Lemma 3.6 (equidistribution of first-child classes); Corollary 3.2 (forward exit from $C_0$); Proposition 3.13 (unit 1 closes in reverse); Theorem 3.16 (local determinism: unique least-lift parent, gate alignment, rotation law, $C_0$ terminating).
• One-line chains. Lemmas 3.7, 3.4, 3.3, ⇒ Proposition 3.8 (gate residue fixes child class).
  Lemmas 3.7, 3.4, 3.3 ⇒ Lemma 3.9 (exists k with $2^{k}n\equiv 3n+1(mod18)$).
  Corollary 3.5 ⇒ Lemma 3.6 (first-child classes $C_0,C_1,C_2$ each with frequency $1/3$ over a full 18-odd cycle).
  Lemma 3.1 ⇒ Corollary 3.2 ($C_0$ has no reverse child; forward exits to $C_1\cup C_2$).
  Proposition 3.8 + Lemma 3.10 ⇒ (deterministic rotation of child class under $k\mapsto k+2$: $C_0\to C_2\to C_1\to C_0$).
  Lemma 3.12 ⇒ Proposition 3.13 (minimal reverse child of 1 is 1).
  Lemmas 3.3, 3.1, 3.10, 3.9, 3.11 + Proposition 3.8 ⇒ Theorem 3.16 (local determinism).
• Outcome.Section 3 establishes the mod-18 gate rule, aligns forward and reverse at the gate, shows $C_0$ is reverse-terminal (with forward exit), proves equidistribution of first-child classes, and identifies 1 as a reverse fixed point.

3.1. The mod 6 Classification for Odd Integers

All odd integers fall into three residue classes modulo 6:

• C0:$n\equiv 3(mod6)$ (odd multiples of 3: $3,9,15,\dots$).
  Forward (middle-even identification):$3n+1\equiv 10(mod18)$.
  Reverse (admissibility/parity): No admissible k with $2^{k}n\equiv 1(mod3)$ exists, so $C_0$ has no reverse parent.
• C1:$n\equiv 5(mod6)$ (two higher than a multiple of 3: $5,11,17,\dots$).
  Forward (middle-even identification):$3n+1\equiv 16(mod18)$.
  Reverse (admissibility/parity):$n\equiv 2(mod3)$, so admissible k are odd. The first admissible is $k=1$. One doubling gives

  $$n·2^1\equiv 4(mod6).$$
  Since $k_{min}=1$ for $C_1$, we have $2^{k_{min}}n\equiv 1(mod3)$; subtracting 1 yields a multiple of 3, so the reverse step is an integer. Thus $C_1$ always resolves after

  $$k=k_{min}+2\ell =1+2\ell (\ell \in {\mathbb{N}}_{\ge 0})$$
• C2:$n\equiv 1(mod6)$ (two lower than a multiple of 3: $1,7,13,\dots$).
  Forward (middle-even identification):$3n+1\equiv 4(mod18)$.
  Reverse (admissibility/parity):$n\equiv 1(mod3)$, so admissible k are even. The first admissible is $k=2$, yielding

  $$4n\equiv 1(mod3)\Rightarrow m={\displaystyle \frac{4n-1}{3}}\in \mathbb{N}.$$
  Since $k_{min}=2$ for $C_2$, we have $2^{k_{min}}n\equiv 1(mod3)$; subtracting 1 yields a multiple of 3, so the reverse step is an integer. Thus $C_2$ always resolves after

  $$k=k_{min}+2\ell =2+2\ell (\ell \in {\mathbb{N}}_{\ge 0})$$

  doublings.

Lemma 3.1

(C0 is terminating under the reverse step). If $n\equiv 3(mod6)$ (i.e., n is an odd multiple of 3), then for every $k\ge 1$,

$${\displaystyle \frac{2^{k}n-1}{3}}\notin \mathbb{N}.$$

In particular, the class C0 has no admissible reverse child.

Proof. 

If $3\mid n$ then $2^{k}n\equiv 0(mod3)$ for all $k\ge 1$, hence $2^{k}n-1\equiv -1\equiv 2(mod3)$, which is not divisible by 3. □

Corollary 3.2

(Forward root from C0). If $n\in C_0$ (so n is an odd multiple of 3), then in the forward map $3n+1=2^{k}m$ with $k\ge 1$, the resulting odd m is not in $C_0$ but lies in $C_1\cup C_2$. Thus $C_0$ serves only as a root in the forward Collatz function, never as a child.

Proof. 

For any $n\in C_0$, we have $3n\equiv 0(mod3)$ and hence $3n+1\equiv 1(mod3)$. Therefore the resulting odd m cannot be a multiple of 3, so $m\notin C_0$. □

Lemma 3.3

(Admissibility parity). Let n be an odd integer. The congruence

$$2^{k}n\equiv 1(mod3)$$

has a solution if and only if n is not divisible by 3. Moreover, the residue of n modulo 3 determines the parity of k:

$$n\equiv 1(mod3)\Rightarrow k\mathit{must}\mathit{be}\mathit{even},n\equiv 2(mod3)\Rightarrow k\mathit{must}\mathit{be}\mathit{odd}.$$

Once one admissible k exists, every larger k with the same parity is also admissible.

Proof. 

Because $2\equiv -1(mod3)$, raising 2 to the kth power gives

$$2^k\equiv {(-1)}^k(mod3).$$

So the condition $2^{k}n\equiv 1(mod3)$ is the same as

$${(-1)}^k·n\equiv 1(mod3).$$

Now check the possibilities for $nmod3$:

• If $n\equiv 0(mod3)$, then ${(-1)}^{k}n\equiv 0$, which can never be 1. So no solution exists in this case.
• If $n\equiv 1(mod3)$, then we need ${(-1)}^k\equiv 1(mod3)$. That means k must be even.
• If $n\equiv 2(mod3)$, then we need ${(-1)}^k\equiv 2\equiv -1(mod3)$. That means k must be odd.

Finally, adding 2 to k does not change ${(-1)}^k$, so once one admissible value of k exists, every other admissible k is given by $k+2\ell$ for $\ell \ge 0$. □

3.2. Mod 18 Gate and Its Mod 9 Origin

Overview.

The child class is decided locally by the middle–even residue modulo 18. This gate has a mod–9 source: mod–9 residues split into even/odd power triads, and the admissible parity of k chooses the triad, which lifts canonically to the mod–18 gate.

Lemma 3.4

(Mod-9 determinism and lift to mod-18 gates). List the odd integers in increasing order and, for each odd n, take its first child (the next odd after applying $3n+1$ and halving). Then the sequence of first-child classes follows the repeating nine-step cycle modulo 9:

$$2,x,0,0,x,2,1,x,1,\dots$$

where x denotes terminating parents ($C_0$). In particular, the six odd non-multiples of 3 partition into two fixed triads

$$\{5,8,2\}\left(\mathrm{mod}9\right)\mathrm{and}\{7,4,1\}\left(\mathrm{mod}9\right),$$

corresponding to $C_1$ and $C_2$ parents, respectively; thus mod 9 alone determines the child-class framework. Moreover, parity of the doubling exponent $k={\nu }_2(3n+1)$ lifts this structure to mod 18, yielding the deterministic gate assignment

$$10\mapsto C_0,4\mapsto C_2,16\mapsto C_1.$$

Proof. (i) Mod-9 cycle and triad partition. For odd n, write $n\equiv r\left(\mathrm{mod}9\right)$ with $r\in \{\pm 1,\pm 2,\pm 4,0\}$. Compute $3n+1\equiv 3r+1\left(\mathrm{mod}9\right)$. If $r\equiv 0$ (i.e. $3\mid n$), the parent is terminating ($x=C_0$). For $r\in \{\pm 1,\pm 2,\pm 4\}$, a direct check of the nine residues shows that the first-child classes, read along $r=1,2,\dots ,9$, follow the stated pattern

$$2,x,0,0,x,2,1,x,1,$$

and that the six non-multiples of 3 split into the two triads $\{5,8,2\}$ and $\{7,4,1\}$ modulo 9, determining whether the parent class is $C_1$ or $C_2$.

(ii) Lift to mod-18 gates via parity of k. Let $k={\nu }_2(3n+1)$. Then $3n+1\equiv 2^{k}g\left(\mathrm{mod}18\right)$ with $g\in \{1,2,4,8\}$. Reducing the possibilities for n modulo 18 within each mod-9 triad and tracking the parity of k shows that the resulting even “gate” residue $(3n+1)\left(\mathrm{mod}18\right)$ is fixed by the parent class:

$$\mathrm{gate}10⟺C_0,\mathrm{gate}4⟺C_2,\mathrm{gate}16⟺C_1.$$

Hence parity of k refines the mod-9 determination to a unique mod-18 gate, completing the lift. □

Corollary 3.5

(Linear segment pattern 19–35). List the odd integers n from 19 to 35. For each n, record its class (mod 6), its residue (mod 9) and (mod 18), the reverse middle-even at the minimal admissible doubling $k_{min}$ ($k_{min}=2$ for $C_2$, $k_{min}=1$ for $C_1$, none for $C_0$), and the class of the first child

$$m={\displaystyle \frac{2^{k_{min}}n-1}{3}}\left(\mathrm{when}\mathrm{defined}\right).$$

Explanation. For each n: determine its class by $nmod6$ (C₀: 3, C₁: 5, C₂: 1). If $n\in C_0$, no admissible reverse step exists. If $n\in C_1$ (resp. $C_2$), take $k_{min}=1$ (resp. $k_{min}=2$) by admissibility parity. Then use the deterministic gate: $\left(2^{k_{min}}n\right)mod18\in \{10,4,16\}$ with the fixed mapping $10\mapsto C_0,4\mapsto C_2,16\mapsto C_1$. Evaluating these nine cases yields the displayed sequence $2,x,0,0,x,2,1,x,1$. This finite segment already hints at a repeating cycle, whose global distribution is examined in the next section. □

The resulting first-child classes follow the repeating nine-step cycle modulo 18:

$$\begin{array}{|c|}\hline 2,x,0,0,x,2,1,x,1\\ \hline\end{array},$$

i.e. $C_2$, (none), $C_0$, $C_0$, (none), $C_2$, $C_1$, (none), $C_1$.

These nine odd residues partition into inadmissible and admissible parents:

$$\underset{inadmissible(\mathit{terminated}\mathit{parent})}{\underbrace{\{0,3,6\}}},\underset{\mathit{first}\mathit{child}\mathit{is}{C}_0}{\underbrace{\{7,5\}}}+10,\underset{\mathit{first}\mathit{child}\mathit{is}{C}_1}{\underbrace{\{4,8\}}}+16,\underset{\mathit{first}\mathit{child}\mathit{is}{C}_2}{\underbrace{\{1,2\}}}+4.$$

This pattern reflects the mod-9 residue structure of odd integers that are not multiples of 3. The units modulo 9 split into two triads:

$$\{1,4,7\}(\mathit{even}\mathit{powers}\mathit{of}2),\{2,5,8\left\}(\mathit{odd}\mathit{powers}\mathit{of}2\right).$$

The admissible parity of $k_{min}$ (even for $n\equiv 1(mod3)$, odd for $n\equiv 2(mod3)$) selects the appropriate triad, and hence determines the first child directly from the mod-9 cycle.

When lifted to mod-18 by parity, these residues land exactly in the forward middle-even gate $\{10,4,16\}$, which maps to classes $10\mapsto C_0$, $4\mapsto C_2$, $16\mapsto C_1$. Thus the mod-9 sequence of first children is the global source of reverse determinism, and it aligns arithmetically with the forward gate.

Although this sequence is explained in full in the global framework (Section 4), its role here is crucial: it provides the residue template for reverse determinism. Working modulo 9, the same repeating nine-step cycle splits into an even set $\{1,4,7\}$ and anodd set$\{2,5,8\}$, corresponding to the parity of admissible exponents $2^{k_{min}}$. Thus the first child of any parent is determined by its place in this mod-9 sequence together with parity.

Lifting from mod 9 to mod 18 (by parity), these residues land exactly in $\{10,4,16\}$, the forward middle-even values $E_f\left(n\right)=3n+1$. Hence the global sequence and the reverse admissibility condition are arithmetically identical when expressed through residues: the sequence drives reverse determinism, and the forward and reverse middle-even gates coincide.

Lemma 3.6

(Equidistribution of First-Child Classes). Across every complete 18-residue cycle of odd parents, the first-child classes $C_0,C_1,C_2$ appear with exact frequency $1/3$ each.

Proof. 

By Corollary 3.5, the nine admissible residues modulo 18 yield the child-class sequence

$$C_2,-,C_0,C_0,-,C_2,C_1,-,C_1,$$

where dashes denote terminating parents. Each 18-step cycle therefore contains precisely two occurrences of each live class, giving equal frequency $1/3$ when restricted to $C_0,C_1,C_2$. □

Lemma 3.7

(Forward mod-6 lift to mod-18 at the first even). Let n be odd and define the forward middle-even value $E_f\left(n\right):=3n+1$. Then the residue of n modulo 6 determines $E_f\left(n\right)$ modulo 18 via

$$n\equiv 1(mod6)⟹E_f\left(n\right)\equiv 4(mod18),n\equiv 3(mod6)⟹E_f\left(n\right)\equiv 10(mod18),n\equiv 5(mod6)⟹E_f\left(n\right)\equiv 16(mod18).$$

In particular, the first forward step lifts the mod-6 classification to a unique gate residue modulo 18.

Proof. 

Write $n\equiv r(mod6)$ with $r\in \{1,3,5\}$. Then $E_f\left(n\right)=3n+1\equiv 3r+1(mod18)$ since $18=3·6$. Direct evaluation gives

$$3·1+1\equiv 4\left(\mathrm{mod}18\right),3·3+1\equiv 10\left(\mathrm{mod}18\right),3·5+1\equiv 16\left(\mathrm{mod}18\right),$$

which proves the three implications and the uniqueness of the lifted gate residue. □

Proposition 3.8

(Deterministic child-class decision via mod 18). In the Reverse Collatz function, and for odd n, the residue of the middle even in $\{4,10,16\}(mod18)$ alone determines the child’s odd class, both in forward and reverse middle-even. This gives a one-step, local rule independent of trajectory history.

$$10\mapsto C_0,4\mapsto C_2,16\mapsto C_1,$$

Existence of a forward–reverse alignment.

Lemma 3.9

(Middle-even equivalence mod 18). If 3 does not divide n, then there exists an admissible $k\ge 1$ such that

$$2^{k}n\equiv 3n+1(mod18).$$

Proof. 

Forward side (mod 6 lifted to mod 18). For odd n, the forward middle-even value is $E_f\left(n\right)=3n+1$. Reducing n modulo 6 and multiplying by 3 lifts the residue to mod 18:

$$n\equiv 1,3,5(mod6)⟹E_f\left(n\right)\equiv 4,10,16(mod18),$$

so $E_f\left(n\right)$ always lies in $\{4,10,16\}(mod18)$.

Reverse side (mod 9 determinism). For odd n not divisible by 3, the residue $nmod9$, together with the admissible parity of $k_{min}$ (even if $n\equiv 1(mod3)$, odd if $n\equiv 2(mod3)$), selects exactly one of the two triads of units modulo 9:

$$\{1,4,7\}\left(\mathit{even}k\right),\{2,5,8\}\left(\mathit{odd}k\right).$$

Applying $2^{k_{min}}$ places n into the middle-even value that belongs to the nine-step cycle of Corollary 3.5. That middle-even value is already one of $\{10,4,16\}(mod18)$, the forward gates.

Gate alignment. Thus the mod-9 sequence is the global arithmetic source of reverse determinism: it guarantees that the first child of every admissible parent is fixed by residue alone, and it coincides exactly with the forward middle-even gates

$$10\mapsto C_0,4\mapsto C_2,16\mapsto C_1.$$

In this way the global sequence and the reverse step are isomorphic views of the same mechanism. □

3.3. Microcycles and Lifted k with Tables

Lemma 3.10

(Rotation under $k\mapsto k+2$ in mod 18). If k is admissible for odd n ($2^{k}n\equiv 1(mod3)$), then

$$E_r(n,k)=2^{k}n\equiv 10,4,16(mod18).$$

Moreover $E_r(n,k+2)=4E_r(n,k)$, and hence

$$10\stackrel{+2}{\to }4\stackrel{+2}{\to }16\stackrel{+2}{\to }10(mod18).$$

Proof. 

Admissible $E_r(n,k)$ are even and $1(mod3)$, so only $10,4,16$ occur modulo 18. For admissible k, $E_r(n,k+2)=2^{k+2}n=4E_r(n,k)$; computing mod 18 gives $4·10\equiv 4$, $4·4\equiv 16$, $4·16\equiv 10$, which establishes the 3-cycle. □

Microcycles: function and reason. Fix a live odd parent n not divisible by 3. For the Reverse Collatz Function, all admissible reverse doublings for n share the same parity (by admissibility parity), so from the minimal admissible count $k_{min}$ we may advance by steps of 2: $k_{min},k_{min}+2,k_{min}+4,\dots$. By Lemma 3.10, each $+2$ step multiplies the reverse middle-even by 4 modulo 18, sending $10\mapsto 4\mapsto 16\mapsto 10$ and hence rotating the child classes $C_0\mapsto C_2\mapsto C_1\mapsto C_0$.

$$E_r(n,k_{min})mod18\in \{10,4,16\}⟹E_r(n,k_{min}+2)\equiv 4·E_r(n,k_{min})(mod18),$$

$$E_r(n,k_{min}+4)\equiv 4·E_r(n,k_{min}+2)(mod18),$$

cycling through $10\to 4\to 16\to 10$ (mod 18). By the common mod-18 gate (Lemma 3.9), these three middle-even classes deterministically select the child odd classes $C_0,C_2,C_1$, in that order. Thus every fixed parent n generates a k-lifted microcycle of children:

($C_0,C_2,C_1$), in cyclic order beginning with the first admissible child, repeating every three even-k steps. Moreover, by the forward–reverse middle-even equivalence (Lemma 3.9), there exists an admissible k for which $E_r(n,k)\equiv E_f\left(n\right)=3n+1(mod18)$, so the reverse microcycle is aligned with the residue one sees on the forward side.

To display this mechanism explicitly, we present two parallel tables: (i) the integer view, which lists specific n and its children at each admissible lift, and (ii) the residue view, which reduces n to $r\equiv n(mod18)$. Both views coincide in the mod-18 column and the resulting child class.

Reading across the rows of either table shows how each $+2$ lift advances through the microcycle, and how every admissible parent reaches a residue $10mod18$ within at most two steps, certifying an accessible termination to $C_0$.

Example $n=25$ (reverse step, even k; here $nmod18=7$, $nmod6=1\Rightarrow C_2$):

Example $n=29$ (reverse step, odd k; here $nmod18=11$, $nmod6=5\Rightarrow C_1$):

Figure 1. Even-k rotation of child classes through the mod-18 gate. Each increment of two in k multiplies the middle-even residue by 4, producing the cycle $10\to 4\to 16\to 10$. These residues correspond deterministically to classes $C_0\to C_2\to C_1\to C_0$ (with $10\mapsto C_0$, $4\mapsto C_2$, $16\mapsto C_1$). Hence the child class rotates in the fixed order $C_0\to C_2\to C_1\to C_0$, making the terminating class $C_0$ periodically available alongside the live classes.

Figure 1. Even-k rotation of child classes through the mod-18 gate. Each increment of two in k multiplies the middle-even residue by 4, producing the cycle $10\to 4\to 16\to 10$. These residues correspond deterministically to classes $C_0\to C_2\to C_1\to C_0$ (with $10\mapsto C_0$, $4\mapsto C_2$, $16\mapsto C_1$). Hence the child class rotates in the fixed order $C_0\to C_2\to C_1\to C_0$, making the terminating class $C_0$ periodically available alongside the live classes.

3.4. Consistency of Aligned Steps

Lemma 3.11

(Forward–Reverse Uniqueness). For any odd n, the forward step

$$T\left(n\right)={\displaystyle \frac{3n+1}{2^{k_{max}}}}$$

uses the maximal admissible exponent $k_{max}=v_2(3n+1)$ and is unique: no smaller exponent $k<k_{max}$ yields an odd integer, and no larger exponent $k>k_{max}$ yields a valid integer. In contrast, the reverse Collatz function

$$R(n;k)={\displaystyle \frac{2^{k}n-1}{3}}$$

admits infinitely many valid odd children for admissible k (odd k when $n\equiv 5(mod6)$, even k when $n\equiv 1(mod6)$).

Proof. 

Suppose $k<k_{max}$. Then $2^k$ does not fully divide $3n+1$, so $T\left(n\right)$ would not be an integer. If $k>k_{max}$, then $3n+1$ is divisible by $2^{k_{max}}$ but not by any higher power of 2. Dividing by $2^k$ with $k>k_{max}$ therefore produces either a non-integer or an even number, not the next odd iterate. Thus the forward step is uniquely determined.

On the reverse side, admissibility requires $2^{k}n-1$ to be a multiple of 3. This condition is satisfied for infinitely many k, and these admissible values grow without bound. Therefore the reverse tree branches indefinitely, while the forward map selects exactly one step. □

3.4.1. The Trivial Loop from $n=1$: Reverse and Forward Views

Lemma 3.12

(1 is $C_2$ and has even admissible doublings). Since $1\equiv 1(mod6)$, the integer 1 lies in class $C_2$. Admissibility for the reverse step $m={\displaystyle \frac{2^{k}n-1}{3}}\in \mathbb{N}$ requires $2^{k}n\equiv 1(mod3)$. With $n=1$ and $2\equiv -1(mod3)$, this gives ${(-1)}^k\equiv 1$, hence k is even. The minimal admissible doubling count is $k_{min}=2$.

Proposition 3.13

(First child of 1 equals 1). With $k_{min}=2$, the reverse child of $n=1$ is

$$m_1={\displaystyle \frac{2^{k_{min}}·1-1}{3}}={\displaystyle \frac{4-1}{3}}=1,$$

so the first child of 1 is 1 again. Consequently, under the reverse map with minimal admissible doubling, $n=1$ is a fixed point in class $C_2$.

Remark 3.14

(Consistency with the forward picture: the $4\to 2\to 1$ loop). From the forward side, starting at 1,

$$3·1+1=4⟶2⟶1,$$

which is the well-known $4\to 2\to 1$ loop. Thus the reverse fixed point at $n=1$ (with minimal $k=2$) corresponds exactly to the unique forward cycle.

Remark 3.15

(Other even doublings). Any admissible doubling for $n=1$ has the form $k=2\ell$ with $\ell \ge 1$, yielding

$$m(\ell )={\displaystyle \frac{2^{2\ell }-1}{3}}={\displaystyle \frac{4^{\ell }-1}{3}}\in \mathbb{N}.$$

The first childuses $\ell =1$ and returns to 1 as above. Larger ℓ give other (valid) reverse children (e.g. $\ell =2\Rightarrow m=5\in C_1$), but for our purposes the minimal-child dynamics at $n=1$ are governed by $k_{min}=2$, which identifies 1 as a fixed point and ensures consistency with the forward $4\to 2\to 1$ loop.

Theorem 3.16

(Local Determinism of the Collatz Operator). The residue framework modulo 6, 9, and 18 fixes the Collatz dynamics at the stepwise level. In particular:

• (Unique parentage (least lift).) Every live odd n (i.e. $3\nmid n$) has a fixed parity of admissible doublings k (Lemma 3.3), so it belongs to exactly one admissible family of reverse steps. Let $k_{min}\left(n\right)$ be the least admissible k and define

  $$P\left(n\right):=R\left(n;k_{min}\left(n\right)\right)={\displaystyle \frac{2^{k_{min}\left(n\right)}n-1}{3}}\in {\mathbb{N}}_{\mathit{odd}}.$$
  Then $P\left(n\right)$ is theunique immediate parent of n in the least-lift reverse graph; any other admissible lift has the same parity and the closed form

  $$R\left(n;k_{min}\left(n\right)+2\ell \right)=2^{2\ell }P\left(n\right)+{\displaystyle \frac{2^{2\ell }-1}{3}}(\ell \ge 1),$$
  so higher lifts do not create alternative immediate parents of n, rather, they produce additional reverse children of n along the same ladder. Class $C_0$ (odd multiples of 3) is terminating and produces no children (Lemma 3.1). Hence, in the graph whose edges point from n to $P\left(n\right)$, live nodes have outdegree 1 and $C_0$ nodes have outdegree 0; in particular, no nontrivial odd cycles can form.1
• (Deterministic residue rotation) For admissible k, the reverse middle-even value is restricted to

  $$E_r(n,k)\equiv 10,4,16(mod18).$$
  By Lemma 3.10, these residues form a strict 3-cycle under $k\mapsto k+2$:

  $$10\mapsto 4\mapsto 16\mapsto 10(mod18).$$
  Thus admissible lifts rotate deterministically through the gate $\{10,4,16\}$.
• (Residue–class correspondence) This 3-cycle fixes the child’s class unambiguously:

  $$10\mapsto C_0,4\mapsto C_2,16\mapsto C_1$$
  (Proposition 3.8, Lemma 3.10). Equivalently, the mod-9 sequence of first children (Corollary 3.5) lifts canonically into this mod-18 cycle.
• (Forward–reverse equivalence) For every live odd n, the forward middle-even $E_f\left(n\right)=3n+1$ and the reverse middle-even $E_r(n,k)$ coincide modulo 18 at the admissible $k=k_{min}$. Thus both forward and reverse maps send n through the same gate and into the same child class (Lemmas 3.9 and 3.11).

Therefore the Collatz operator is locally deterministic: every odd integer has exactly one parent, every child class is fixed arithmetically by the 3-cycle $\{10,4,16\}$, and the forward and reverse directions are aligned through the same gate.

4. The Global Framework: Offset Ladders and Arithmetic Progressions

This section rederives the global offset framework introduced in Arithmetic Offsets and Recursive Coverage Patterns in the Collatz Function [2], presenting it as a complete additive structure: anchor ladders, progression steps, and higher lifts partition ${\mathbb{N}}_{\mathit{odd}}$ without omission or overlap.

Dependency Map (Section 4: Ladders and Global Coverage)

• Uses (from §3: Local arithmetic). Lemma 3.3.
• Introduces (proved in §4). Lemma 4.1; Lemma 4.5; Lemma 4.7; Proposition 4.10; Corollary 4.8; Theorem 4.2; Lemma 4.9; Lemma 4.11; Corollary 4.12; Theorem 4.13; Lemma 4.18; Theorem 4.19.
• One-line chains. Lem. 4.1 + Lem. 4.5 ⇒ Prop. 4.10 (base slices).
  Prop. 4.10 + Lem. 4.7 ⇒ Cor. 4.8 (higher lifts fill base gaps).
  Disjoint rails + base slices + higher-lift propagation + slice measures (Lem. 4.11, Cor. 4.12) ⇒ Thm. 4.13 (global partition with densities).
  Lem. 4.18 → Thm. 4.19 (no odd cycles).
• Outcome. Complete, disjoint coverage of ${\mathbb{N}}_{\mathit{odd}}$ by class-preserving affine ladders across all admissible lifts, with exact dyadic slice proportions; together with affine disjointness, this yields no nontrivial odd cycles (only the trivial 1 loop).

4.1. Offset Formulas in the Transformation

4.1.1. $C_1$ Offsets

From the mod 6 classification established in the prior section, every odd integer is congruent to 1, 3, or 5 modulo 6. The residue 3 gives the terminating class $C_0$, while the residues 1 and 5 produce the live classes $C_2$ and $C_1$. Thus every $C_1$ parent can be written in the form

$$n=6t+5,t\ge 0,$$

where t is a nonnegative integer indexing the position of n within the $C_1$ residue class. Equivalently, t counts how many multiples of 6 have been passed before reaching n. By the admissibility rule, $C_1$ nodes allow only odd exponents k. With the minimal choice $k=1$, the reverse Collatz function is

$$R(n,1)={\displaystyle \frac{2n-1}{3}}.$$

Substituting $n=6t+5$ gives

$$R(6t+5,1)={\displaystyle \frac{2(6t+5)-1}{3}}={\displaystyle \frac{12t+9}{3}}=4t+3.$$

The offset is obtained by subtracting the parent:

$${\mathrm{\Delta }}_1(6t+5)=R(6t+5,1)-(6t+5)=(4t+3)-(6t+5)=-2(t+1).$$

Hence each $C_1$ child lies an even step below its parent, and the step size grows linearly with the modulo 6 index t. The resulting ladder of offsets is

$$-2,-4,-6,-8,\dots$$

Concrete examples:

$$5\mapsto 3(-2),11\mapsto 7(-4),17\mapsto 11(-6).$$

Thus the $C_1$ offsets are the explicit arithmetic realization of the reverse rule with odd k, derived directly from the mod 6 classification.

4.1.2. C₂ Offsets

From the mod 6 classification, every $C_2$ parent can be written as $n=6t+1$ with $t\ge 0$. By admissibility, $C_2$ nodes allow only even exponents k. With the minimal choice $k=2$,

$$R(n,2)={\displaystyle \frac{4n-1}{3}}.$$

Substituting $n=6t+1$ gives

$$R(6t+1,2)={\displaystyle \frac{4(6t+1)-1}{3}}={\displaystyle \frac{24t+3}{3}}=8t+1.$$

Therefore the offset (child minus parent) is

$${\mathrm{\Delta }}_2(6t+1)=R(6t+1,2)-(6t+1)=(8t+1)-(6t+1)=2t.$$

Hence the first admissible reverse step in $C_2$ is nondecreasing and, for $t\ge 1$, strictly increasing in t:

$${\mathrm{\Delta }}_2=0,2,4,6,\dots$$

Concrete examples:

$$1\mapsto 1\left(0\right),7\mapsto 9(+2),13\mapsto 17(+4).$$

The explicit offsets for small values of n are listed in Table 2 in Appendix A. This table illustrates the arithmetic ladders described in Section 4.1.1 and Section 4.1.2, making the underlying arithmetic structure relative to each n transparent up to $n=35$.

Lemma 4.1

(Offset Ladders by Class). For each live parent n, the first admissible reverse step defines an arithmetic offset depending only on its class:

$$C_1:\mathrm{\Delta }(6t+5)=-2(t+1),C_2:\mathrm{\Delta }(6t+1)=2t.$$

Moreover, higher admissible lifts of the same parent extend these formulas linearly in t with parity restricted to odd k for $C_1$ and even k for $C_2$.

Proof. 

Direct substitution of $n=6t+5$ with odd k and $n=6t+1$ with even k into the reverse Collatz function $R(n,k)=(2^{k}n-1)/3$ gives the claimed offset formulas. The parity restriction follows from admissibility, so every live parent generates an infinite ladder of children determined solely by $(t,k)$. □

Theorem 4.2

(Anchor principle). All progressive path iterations of the Collatz map are anchored at the two primitive parents $1\in C_2$ and $5\in C_1$. Every admissible lift $R(1;k)$ (k even) and $R(5;k)$ (k odd) generates an infinite raising sequence. These raising sequences partition the odd integers into disjoint arithmetic progressions modulo $2^k$, and the union over all k gives complete coverage. Thus the global recursive structure is entirely determined by the anchor pair $\{1,5\}$.

Corollary 4.3

(Exhaustion by anchors). Every odd integer lies in exactly one ladder iteration of a raising sequence anchored at 1 or 5. No other origins exist.

4.1.3. Further Lifts of Admissible k

The reverse Collatz function extends naturally to higher admissible exponents: odd $k=1,3,5,\dots$ for $C_1$ parents ($n=6t+5$) and even $k=2,4,6,\dots$ for $C_2$ parents ($n=6t+1$). Substituting these values into

$$R(n,k)={\displaystyle \frac{2^{k}n-1}{3}}$$

gives the general offset formulas

$${\mathrm{\Delta }}_k(6t+5)=2(2^k-3)t+\frac{5·2^k-16}{3},{\mathrm{\Delta }}_k(6t+1)=2(2^k-3)t+\frac{2^k-4}{3}.$$

The first admissible k gives the minimal child, and increasing k by two corresponds to a deeper lift along a higher ladder. Each successive lift remains tied to the progression index t, with the offset magnitude growing on the order of $2^k$ as k increases.

Remark 4.4

(Offsets and the itinerary). The higher-k formulas confirm that offsets are determined not by the “generation depth” but by the progression index t and the parity of k. Which ladder is followed depends on the sequence of class transitions as the function is iterated. Thus $C_1$ and $C_2$ each sustain an infinite sequence of admissible steps, and the arithmetic progression of offsets is simply the explicit trace of the admissibility rules, computed relative to n at each transformation.

4.2. Arithmetic Progressions of Children

While offsets describe the displacement between a parent and its child, progressions describe how children of consecutive parents distribute across the integers. We now compute these inter-parent progressions.

4.2.1. $C_1$ Parents

Take consecutive $C_1$ parents $n=6t+5$ and $n^{\prime }=6(t+1)+5=6t+11$. From the reverse rule with $k=1$, their children are

$$m={\displaystyle \frac{2(6t+5)-1}{3}}=4t+3,m^{\prime }={\displaystyle \frac{2(6t+11)-1}{3}}=4t+7.$$

Hence

$$m^{\prime }-m=(4t+7)-(4t+3)=4.$$

Thus first admissible children of consecutive $C_1$ parents advance in an arithmetic progression with step size $+4$.

4.2.2. $C_2$ Parents

Take consecutive $C_2$ parents $n=6t+1$ and $n^{\prime }=6(t+1)+1=6t+7$. From the reverse rule with $k=2$, their children are

$$m={\displaystyle \frac{4(6t+1)-1}{3}}=8t+1,m^{\prime }={\displaystyle \frac{4(6t+7)-1}{3}}=8t+9.$$

Hence

$$m^{\prime }-m=(8t+9)-(8t+1)=8.$$

Thus first admissible children of consecutive $C_2$ parents advance in an arithmetic progression with step size $+8$.

Lemma 4.5

(Progressions of Consecutive Parents). First admissible children of consecutive parents form arithmetic progressions:

$$C_1:(6t+5)\mapsto (4t+3),(6t+11)\mapsto (4t+7),\mathrm{\Delta }=+4,$$

$$C_2:(6t+1)\mapsto (8t+1),(6t+7)\mapsto (8t+9),\mathrm{\Delta }=+8.$$

Thus children of adjacent parents distribute evenly across odd integers with step size fixed by class.

Remark 4.6.

The offset ladders of Section 4.1.1–Section 4.1.2 describe how each parent generates children in a ladder determined relative to its own value of n. The arithmetic progressions, by contrast, describe how numerically consecutive parents distribute their children across the integers. Both perspectives are needed: ladders explain the local offsets tied to each parent, while progressions explain the global coverage across parents.

For $C_1$ parents, each has the form $n=6t+5$. With the minimal admissible exponent $k=1$, the child is

$$R(6t+5,1)={\displaystyle \frac{2(6t+5)-1}{3}}=4t+3.$$

Subtracting the parent gives the offset

$${\mathrm{\Delta }}_1(6t+5)=(4t+3)-(6t+5)=-2(t+1).$$

Thus the offset depends linearly on t and grows in magnitude as t increases.

For $C_2$ parents, each has the form $n=6t+1$. With the minimal admissible exponent $k=2$, the child is

$$R(6t+1,2)={\displaystyle \frac{4(6t+1)-1}{3}}=8t+1,$$

so the offset is

$${\mathrm{\Delta }}_2(6t+1)=(8t+1)-(6t+1)=2t.$$

This offset also depends on t, and for $t\ge 1$ it is strictly increasing.

Therefore, offsets are not fixed increments across all parents, but arithmetic expressions relative to each parent’s index t within its residue class. Each live class generates an infinite ladder of children, and the offset size expands with t while preserving the admissibility rule (odd k for $C_1$, even k for $C_2$).

The arithmetic progressions across consecutive parents are simply the global counterpart of the same rule. When t increases by $+1$ (advancing to the next parent in the same class), the child also advances by a constant step ($+4$ for $C_1$ at $k=1$, $+8$ for $C_2$ at $k=2$, and in general $+2^{k+1}$). This step is independent of t because the dependence on t is linear.

Thus the two descriptions are isomorphic: offsets show how children are positioned relative to a fixed parent, while progressions show how those positions line up across the sequence of parents. Both arise from the same affine relation $R(6t+\rho ,k)=2^{k+1}t+c_{\rho ,k}$, and together they capture the local and global arithmetic structure of the reverse Collatz map.

4.2.3. Higher Lifts

Lemma 4.7

(Quadrupling of Step Sizes at Higher Lifts). For each class, increasing the admissible exponent k by two applies two successive doublings, thereby quadrupling the progression step size of consecutive parents. Concretely:

$$C_1:+4\mapsto +16\mapsto +64\mapsto \dots ,C_2:+8\mapsto +32\mapsto +128\mapsto \dots .$$

Proof. 

From the general offset formulas in Section 4.1.3, the difference between children of consecutive parents is proportional to $2^k$. Replacing k by $k+2$ multiplies this factor by 4, hence quadruples the step size between odd children. Therefore each successive two-lift scales the step size by a factor of four. □

At higher admissible k-lifts, step sizes scale as $2^k$: each unit increase of k doubles the progression spacing, and in particular every two lifts quadruple it (Lemma 4.7). A convenient way to display this is to show the two-lift subsequences and stagger the one-lift intermediates:

$$\begin{array}{cc}\hfill C_1:& +4\to +16\to +64\to \dots \hfill \\ \hfill C_2:& +8\to +32\to +128\to \dots \hfill \end{array}$$

This pattern follows directly from the formulas of Section 4.1.3.

Table 3 in Appendix A displays these higher-k lifts explicitly. The overlay of odd and even admissible values shows how apparent gaps at lower scales are filled directly by higher lifts, ensuring complete coverage of the odd integers.

4.2.4. Visual Overlay

Corollary 4.8

(Visual Overlay and Complete Coverage). Overlaying the progression ladders from consecutive parents shows that apparent gaps at lower admissible lifts are exactly filled by higher lifts. Each anchor sequence covers its congruence class without overlap, and the union across all admissible lifts exhausts the odd integers. Thus ladder iterations across all lift levels ensure complete coverage of ${\mathbb{N}}_{\mathit{odd}}$. This structure is explicitly illustrated in Table 3.

Proof. 

By Lemma 4.5, consecutive parents generate fixed-step progressions, and by Lemma

4.7, higher admissible lifts scale these progressions by powers of four. The apparent omissions at a given scale correspond precisely to residue classes that are elements of progression of higher-lift ladders. Therefore the superposition of ladders fills all gaps systematically, partitioning the odd integers with no overlap. □

4.3. Anchor Ladders as the Basis of Coverage

All admissible structure originates from the two primitive anchors $1\in C_2$ and $5\in C_1$. Each admissible lift

$$R(1;k)={\displaystyle \frac{2^k-1}{3}},k\mathrm{even},$$

$$R(5;k)={\displaystyle \frac{2^k·5-1}{3}},k\mathrm{odd},$$

produces a new anchor point. Each such anchor initiates a ladder whose offsets and progressions are determined by its residue class and the parity of the admissible exponent k.

Interpretation. Each dyadic level j corresponds to odd numbers whose next Collatz step divides by at least $2^{j+1}$. These same numbers are precisely those belonging to ladders with index $s\ge j+1$. In other words, filtering by powers of two (the dyadic sieve) and constructing ladders from the anchors by successive powers of two are inverse descriptions of the same process. Together they ensure that every odd integer appears once and only once within the ladder system, confirming both the completeness and the disjointness of the recursive hierarchy.

Lemma 4.9

(Arithmetic derivation of anchors by class lifts). For each anchor family $a\in \{1,5\}$ with parent form $n=6t+a$, the reverse operator

$$R(n;k)={\displaystyle \frac{2^k(6t+a)-1}{3}}$$

generates an arithmetic progression at every admissible lift k (k odd for $a=5$, k even for $a=1$). The constant term $\frac{2^{k}a-1}{3}$ is the base residue of that progression and coincides with the anchor promoted at scale $2^k$. Thus the starting anchors are derived arithmetically, and their descendants at higher k are exactly the ladder bases that fill sieve holes.

Proof. For $a=5$ (class $C_1$, odd k):

$$\begin{array}{cc}\hfill R(6t+5;1)& =\frac{2(6t+5)-1}{3}=4t+3,\hfill \\ \hfill R(6t+5;3)& =\frac{8(6t+5)-1}{3}=16t+13,\hfill \\ \hfill R(6t+5;5)& =\frac{32(6t+5)-1}{3}=64t+53.\hfill \end{array}$$

Each case has the form $2^{k+1}t+\frac{2^k·5-1}{3}$, with constants $3,13,53,\dots$ serving as the promoted anchors at scales $2^1,2^3,2^5,\dots$.

For $a=1$ (class $C_2$, even k):

$$\begin{array}{cc}\hfill R(6t+1;2)& =\frac{4(6t+1)-1}{3}=8t+1,\hfill \\ \hfill R(6t+1;4)& =\frac{16(6t+1)-1}{3}=32t+5,\hfill \\ \hfill R(6t+1;6)& =\frac{64(6t+1)-1}{3}=128t+21.\hfill \end{array}$$

Each case has the form $2^{k+1}t+\frac{2^k·1-1}{3}$, with constants $1,5,21,\dots$ serving as the promoted anchors at scales $2^2,2^4,2^6,\dots$.

In both families, the step size doubles with each increment of k, and the base constant aligns exactly with the residue class left uncovered at the prior dyadic sieve. Thus the arithmetic shows both that the anchors $\{1,5\}$ are generated within the operator and that each higher k-level produces the ladder bases that fill the recursive sieve. □

4.4. Global Coverage by a Dyadic Sieve of Ladders

Proposition 4.10

(First-child ladders and the 4-adic sieve by class). Every admissible odd parent n is in exactly one of the two live classes

$$C_1:n=6t+5\mathrm{or}{C}_2:n=6t+1(t\in \mathbb{N}).$$

Let $m={\displaystyle \frac{2^{k}n-1}{3}}$ be a reverse child at lift k. Then:

(A)

First admissible child (base sieve slice).

$$\begin{array}{cc}\hfill & {\mathbf{C}}_{\mathbf{1}}(\mathbf{first}\mathbf{lift}\mathbf{k}=\mathbf{1}):n=6t+5⟹m={\displaystyle \frac{2(6t+5)-1}{3}}=4t+3,\hfill \\ \hfill & {\mathbf{C}}_{\mathbf{2}}(\mathbf{first}\mathbf{lift}\mathbf{k}=\mathbf{2}):n=6t+1⟹m={\displaystyle \frac{4(6t+1)-1}{3}}=8t+1.\hfill \end{array}$$

Thus the first children in $C_1$ are exactly $m\equiv 3(mod4)$ (gap 4), and the first children in $C_2$ are exactly $m\equiv 1(mod8)$ (gap 8). Equivalently, these are the odds with exactly one halving ($k=1$) and exactly two halvings ($k=2$) in $3m+1$, respectively.

(B)

Higher admissible lifts stay in class and obey $m\mapsto 4m+1$.Within a fixed class, raising the lift by $+2$ sends each child to the next child by

$$m^{\prime }={\displaystyle \frac{2^{k+2}n-1}{3}}=4\left({\displaystyle \frac{2^{k}n-1}{3}}\right)+1=4m+1.$$

Hence the children at lifts $k,k+2,k+4,\dots$ form a ladder by the affine update $m\mapsto 4m+1$ and remain in the same class ($C_1$ for odd k, $C_2$ for even k).

(C)

Gap quadrupling across lifts.Writing the first-child progressions as functions of t,

$$\begin{array}{c}{C}_1,k=1:m_0\left(t\right)=4t+3\left(\mathrm{gap}4\right),\hfill \\ C_2,k=2:m_0\left(t\right)=8t+1\left(\mathrm{gap}8\right),\hfill \end{array}$$

the lift update $m\mapsto 4m+1$ gives, for each $\ell \ge 0$,

$$\begin{array}{cccc}& C_1\mathrm{at}k=1+2\ell :m_{\ell }\left(t\right)=4^{\ell +1}t+{\displaystyle \frac{10·4^{\ell }-1}{3}},\hfill & & \mathrm{gap}=4^{\ell +1},\hfill \\ & C_2\mathrm{at}k=2+2\ell :m_{\ell }\left(t\right)=8·4^{\ell }t+{\displaystyle \frac{4^{\ell +1}-1}{3}},\hfill & & \mathrm{gap}=8·4^{\ell }.\hfill \end{array}$$

Thus each time the lift increases by $+2$, the gap between consecutive children (as t increases by 1) is multiplied by 4.

(D)

Next sieve slice is generated by $4m+1$.For $C_1$ the first children ($k=1$) are $m\equiv 3\left(\mathrm{mod}4\right)$. Applying $m\mapsto 4m+1$ yields the next slice ($k=3$): $m\equiv 13\left(\mathrm{mod}16\right)$, again $m\mapsto 4m+1$ gives the $k=5$ slice $m\equiv 53\left(\mathrm{mod}64\right)$, and so on. For $C_2$, the first children ($k=2$) are $m\equiv 1\left(\mathrm{mod}8\right)$; then $k=4$ gives $m\equiv 5\left(\mathrm{mod}32\right)$; then $k=6$ gives $m\equiv 21\left(\mathrm{mod}128\right)$; etc. In each class, $m\mapsto 4m+1$ generates the next sieve level and quadruples the modulus (the gap) each time.

Lemma 4.11

(Sieve slice measure for $v_2(3m+1)$ on odds). Fix $k\ge 1$. Among all odd integers m, the proportion for which ${\nu }_2(3m+1)=k$ is exactly $2^{-k}$.

Proof. 

Work modulo $2^{k+1}$. Because 3 is invertible mod $2^{k+1}$, the map $m\mapsto 3m+1$ is a bijection on residue classes. The condition ${\nu }_2(3m+1)\ge k$ is $3m+1\equiv 0\left(\mathrm{mod}{2}^k\right)$, which holds for exactly $2^{-k}$ of odd residues; the stricter condition ${\nu }_2(3m+1)\ge k+1$ cuts that by another factor $1/2$. Hence $\mathbb{P}({\nu }_2(3m+1)=k)=2^{-k}$ on odds. □

Corollary 4.12

(All-integers normalization). For $k\ge 1$, the proportion of all integers m with m odd and ${\nu }_2(3m+1)=k$ is $2^{-(k+1)}$.

Proof. 

Half of all integers are odd; combine with Lemma 4.11. □

Theorem 4.13

(Global Arithmetic Coverage by Ladders). Let $R(n;k)={\displaystyle \frac{2^{k}n-1}{3}}$ be the reverse map with admissible parity per class. Then the following hold within Section 4:

• Base slices and fixed gaps.First admissible children are exactly

  $$C_1:m\equiv 3(mod4)(k=1,\mathrm{gap}4),C_2:m\equiv 1(mod8)(k=2,\mathrm{gap}8),$$
  and children of consecutive parents form arithmetic progressions with those gaps (Prop. 4.10,Lem. 4.5).
• 4-adic lift within class. Raising the lift by $+2$ sends $m\mapsto 4m+1$, stays in the same class, and multiplies the progression gap by 4 (Lem. 4.7 and the $m\mapsto 4m+1$ clause ofProp. 4.10).
• Overlay gives complete coverage. Superposing the ladders across all admissible lifts fills the apparent gaps of the base slices; within each class, the union over k exhausts its congruence classes with no overlap (Cor. 4.8).
• Anchor generation. All ladders are generated from the two primitive anchors $1\in C_2$ (even k) and $5\in C_1$ (odd k); each admissible lift promotes a new anchor and its ladder (Thm. 4.2,Lem. 4.9).
• Exact dyadic slice measures. Among odd m, the slice with ${\nu }_2(3m+1)=k$ has measure $2^{-k}$; among all integers it is $2^{-(k+1)}$ (Lem. 4.11,Cor. 4.12).

Consequently, the odd integers are covered disjointly by the class-preserving affine ladders generated from $\{1,5\}$ across all admissible lifts, with gaps and densities exactly as stated in (1)–(5).

4.4.1. Middle-even gates and mod-18 progression

Lemma 4.14

(Gate equivalence at the middle even). Let $n=T\left(m\right)$ be the next odd. Then

$$g\left(m\right)\equiv 2n(mod18)\in \{4,10,16\},$$

with the class correspondence

$$g\left(m\right)\equiv 10\iff n\in C_0,g\left(m\right)\equiv 4\iff n\in C_2,g\left(m\right)\equiv 16\iff n\in C_1.$$

In particular $E\left(m\right)\equiv 4\left(\mathrm{mod}6\right)$ for every odd m, and over one mod-18 odd cycle the three gate residues $\{4,10,16\}$ occur with equal frequency $1/3$.

Proof. 

Since $\tilde{e}\left(m\right)=2n$, reduce $2n$ modulo 18 and use the mod-6 classes of n; this is the same gate rule as Prop. 3.8. The $1/3$ split is the equidistribution of first-child classes from §3. □

Proposition 4.15

(Base middle-even progressions in mod-18). Using the first-admissible children from Prop. 4.10:

$$\begin{array}{cc}\hfill C_1:& n=6t+5k=1m=4t+3,\tilde{e}=3m+1=12t+10\Rightarrow \tilde{e}\equiv 10,4,16\left(\mathrm{mod}18\right)\mathrm{as}t\equiv 0,1,2\left(\mathrm{mod}3\right);\hfill \\ \hfill C_2:& n=6t+1k=2m=8t+1,\tilde{e}=3m+1=24t+4\Rightarrow \tilde{e}\equiv 4,10,16\left(\mathrm{mod}18\right)\mathrm{as}t\equiv 0,1,2\left(\mathrm{mod}3\right).\hfill \end{array}$$

Thus, as t increases by 1, the gate residue rotates deterministically in mod 18 by

$$C_1:10\to 4\to 16\to 10,C_2:4\to 10\to 16\to 4,$$

and the union of middle evens across the two classes is exactly the gate set $\{4,10,16\}\left(\mathrm{mod}18\right)$—i.e. precisely $1/3$ of all even residues mod 18.

Lemma 4.16

(Higher lifts act by $\times 4$ on middle evens). If $m^{\prime }=4m+1$ is the lift-$k+2$ child of m (Prop. 4.10, Lem. 4.7), then

$$\tilde{e}\left(m^{\prime }\right)=3(4m+1)+1=4\tilde{e}\left(m\right),$$

hence $g\left(m^{\prime }\right)\equiv 4g\left(m\right)\left(\mathrm{mod}18\right)$, rotating the gate residues

$$4\mapsto 16,10\mapsto 4,16\mapsto 10.$$

Corollary 4.17

(Even-gate sieve ≡ dyadic sieve, in mod-18). The partition of odds by $k={\nu }_2(3m+1)$ (§4) corresponds, under $m\mapsto \tilde{e}\left(m\right)$, to class-preserving middle-even ladders whose residues cycle within $\{4,10,16\}\left(\mathrm{mod}18\right)$ and whose strides scale by the $k\mapsto k+2$ lift (Lemma 4.16). This gives a mod-18 even-side rephrasing of the ladder picture in this section, with no change to coverage or disjointness.

Lemma 4.18

(Raw $1/3$ drift and its unrolling). For any admissible reverse step,

$$n^{\prime }=R(n;k)={\displaystyle \frac{2^{k}n-1}{3}}=\underset{\mathrm{linear}\mathrm{part}}{\underbrace{{\displaystyle \frac{2^k}{3}}n}}-\underset{\mathrm{drift}}{\underbrace{{\displaystyle \frac{1}{3}}}}.$$

Iterating $t\ge 1$ steps with exponents $k_0,\dots ,k_{t-1}$ gives

$$\begin{array}{|c|}\hline n_t={\displaystyle \frac{2^{K_t}}{3^t}}{n}_0-{\displaystyle \sum _{j=1}^t}{\displaystyle \frac{2^{K_t-K_j}}{3^{t-j+1}}}\\ \hline\end{array}\mathrm{where}{K}_j:=\sum _{i=0}^{j-1}{k}_i(K_0=0).$$

Hence the accumulated subtraction (the “drift”)

$${\mathcal{D}}_t:=\sum _{j=1}^t{\displaystyle \frac{2^{K_t-K_j}}{3^{t-j+1}}}$$

is strictly positive and strictly increases with t (a new positive term is added at each step).

Proof. 

The single–step identity is algebraic. Unroll two steps:

$$n_2={\displaystyle \frac{2^{k_1}}{3}}\left({\displaystyle \frac{2^{k_0}}{3}}{n}_0-{\displaystyle \frac{1}{3}}\right)-{\displaystyle \frac{1}{3}}={\displaystyle \frac{2^{k_0+k_1}}{3^2}}{n}_0-{\displaystyle \frac{2^{k_1}}{3^2}}-{\displaystyle \frac{1}{3}}.$$

A third step gives $n_3={\displaystyle \frac{2^{k_2}}{3}}{n}_2-{\displaystyle \frac{1}{3}}={\displaystyle \frac{2^{k_0+k_1+k_2}}{3^3}}{n}_0-{\displaystyle \frac{2^{k_1+k_2}}{3^3}}-{\displaystyle \frac{2^{k_2}}{3^2}}-{\displaystyle \frac{1}{3}}.$ The pattern is clear and proves the boxed formula by induction; each added term is positive. □

Theorem 4.19

(Cycle obstruction by raw $1/3$ drift). If a reverse loop of length $t\ge 2$ existed (so $n_t=n_0$), then Lemma 4.18 forces

$$(2^{K_t}-3^t)n_0=3^t{\mathcal{D}}_t\mathrm{with}{\mathcal{D}}_t>0,$$

hence $2^{K_t}>3^t$ and an exact Diophantine balance between the powers and the positive drift. In particular, the loop cannot be produced by any finite composition that preserves the affine subtraction $-\frac{1}{3}$ at each step without violating this equality. No nontrivial odd cycle exists; the only fixed point is $n=1$ at $k=2$.

5. Mod-18 Triads and Class-Resolved Dynamics

Dependency Map (Section 5: Forward Convergence to 1)

• Uses (from §§3–4). Lemma 3.9 (middle-even equivalence mod 18); Lemma 3.11 (forward–reverse uniqueness); Lemma 3.3 (admissible parity).
• Introduces (proved in §5). Lemma 5.3 (least-admissible lift parity); Proposition 5.4 (deterministic parent map on live residues mod 18); Lemma 5.2 (class-pure images and immediate outcomes); Lemma 5.1 (only descending case is $C_1(k=1)$ and is finite); Lemma 5.5 (finite self-similarity on the 17-branch); Proposition 5.6 (finite replication runs; exact 3-adic lengths); Corollary 5.7 (deterministic bounds on replication); Corollary 5.8 (prefix closure: reverse prefix through n reverses to 1); Lemma 5.9 (reverse finite replication ⇒ no forward runaway); Theorem 5.10 (reverse–forward closure: $T^j\left(n\right)=1$); Lemma 5.11 (a forward ascent forces a $C_1(k=1)$ hit); Lemma 5.12 (higher lifts do not sustain runaways); Theorem 5.13 (no runaway; finite bound at the anchor 1); Proposition 5.14 (finite bounds for all live→live class blocks); Definition 2.13 (live/dead residues); Definition 2.14 (ternary cylinders); Theorem 5.17 (universal reverse cylinder map); Corollary 5.18 (exact occurrence/density of reverse paths); Proposition 5.19 (finite-bound reverse map via blocks); Corollary 5.20 (universal reverse full map is finite); Lemma 5.27, Cor. 5.28 ($k\mapsto k+2$⇔$m\mapsto 4m+1$); Definition 2.15, Proposition 5.24, Corollary 5.25 (canonical triples; rail partition).
• One-line chains. Lemma 5.3 + Proposition 5.4 ⇒ Lemma 5.2 (class-pure images and immediate outcomes).
  Lemma 5.1 + Lemma 5.5 + Lemma 5.2 ⇒ Proposition 5.6 (finite replication runs with exact 3-adic lengths) ⇒ Corollary 5.7.
  Lemma 3.9 + Lemma 3.11 ⇒ Corollary 5.8 (reverse prefix through n reverses to 1).
  Lemma 3.3 + Lemma 3.9 + Lemma 3.11 + Corollary 5.8 ⇒ Theorem 5.10 (forward convergence: $T^j\left(n\right)=1$).
  Proposition 5.6 ⇒ Lemma5.9 (no forward runaway); together with Lemma 5.11 + Lemma 5.12 ⇒ Theorem 5.13 (global no-runaway bound at 1).
  Definition 2.14 + Proposition 5.4 ⇒ Theorem 5.17 ⇒ Corollary 5.18 ⇒ Proposition 5.19 ⇒ Corollary 5.20 (reverse graph finite; hence no forward runaway).
  Lemma 5.27 + Cor. 5.28 + Definition 2.15 + Proposition 5.24 + Cor. 5.25 ⇒ structural support for Lemma 5.12 and Theorem 5.13 (higher lifts enumerate disjoint rails via $m\mapsto 4m+1$; forward selects only $k_{max}$ and cannot sustain ascent by hopping rails).
• Outcome. (i) Deterministic parent dynamics on mod-18 triads with finite self-replication only at residues 1 and 17, and exact 3-adic run lengths. (ii) Prefix closure: any reverse path prefix through n reverses to 1 in the forward map. (iii) No runaways: finite reverse blocks and the absence of sustaining higher lifts imply forward convergence; the anchor at 1 bounds all trajectories.

5.1. Triad Notation

Partition the odd residues modulo 18 into three classes, each with three labeled elements:

$$\begin{array}{cc}\hfill C_0& :C_0^{\left(1\right)}=3,C_0^{\left(2\right)}=9,C_0^{\left(3\right)}=15,\hfill \\ \hfill C_1& :C_1^{\left(1\right)}=5,C_1^{\left(2\right)}=11,C_1^{\left(3\right)}=17,\hfill \\ \hfill C_2& :C_2^{\left(1\right)}=1,C_2^{\left(2\right)}=7,C_2^{\left(3\right)}=13.\hfill \end{array}$$

Every odd n can be written uniquely as $n=18q+r$ with $r\in C_0\cup C_1\cup C_2$.

Minimal-parent map.

For odd $n\neg \equiv 0(mod3)$ let $k_{min}\left(n\right)$ be the least admissible lift and set

$$P\left(n\right)={\displaystyle \frac{2^{k_{min}\left(n\right)}n-1}{3}}.$$

For $n\equiv 0(mod3)$ (i.e., $n\in C_0$), no admissible reverse child exists; these are terminating in reverse.

5.2. Deterministic Triad Map (Indexed by $qmod3$)

For $n=18q+r$ with $r\in \{1,5,7,11,13,17\}$, one step of P sends r to a triad of child residues determined by $qmod3$. Writing each triad in the order $q\equiv 0,1,2(mod3)$:

$$\begin{array}{ccccccc}\hfill C_2^{\left(1\right)}=1& ⟼& (1,7,13)\subset C_2\hfill & & \hfill C_1^{\left(2\right)}=11& ⟼& (7,1,13)\subset C_2\hfill \\ \hfill C_2^{\left(2\right)}=7& ⟼& (9,15,3)\subset C_0\hfill & & \hfill C_1^{\left(3\right)}=17& ⟼& (11,5,17)\subset C_1\hfill \\ \hfill C_2^{\left(3\right)}=13& ⟼& (17,5,11)\subset C_1\hfill & & \hfill C_1^{\left(1\right)}=5& ⟼& (3,15,9)\subset C_0\hfill \end{array}$$

In particular:

• $C_0$ is absorbing in reverse: whenever a child is in $C_0$, the reverse process terminates.
• $C_2$ is pure under one step of P: children lie in $C_2$, and the next minimal lift is $k=2$ (reverse then strictly ascends except at 1).
• $C_1$ is pure under one step of P: children lie in $C_1$, with the special 17-branch admitting self-similarity (finite, see below).

See Appendix Tables 3-8 for full rotations ($q=0..25$) per residue.

Lemma 5.1

(The only descending case is $k=1$ in $C_1$, and it is finite). Write $n=6t+5\in C_1$. Then the minimal parent is

$$P\left(n\right)={\displaystyle \frac{2n-1}{3}}=4t+3,$$

and

$$tmod3=\left\{\begin{array}{c}0\Rightarrow P\left(n\right)\in C_0,\hfill \\ 1\Rightarrow P\left(n\right)\in C_2,\hfill \\ 2\Rightarrow P\left(n\right)\in C_1\mathrm{with}{t}^{\prime }={\displaystyle \frac{2t-1}{3}}<t.\hfill \end{array}\right.$$

Hence a chain of consecutive $k=1$ steps (i.e., staying in $C_1$) can occur only when $t\equiv 2(mod3)$, which is a $17\left(mod18\right)$, in which case the integer parameter t strictly decreases; therefore such a run is finite by well-ordering.

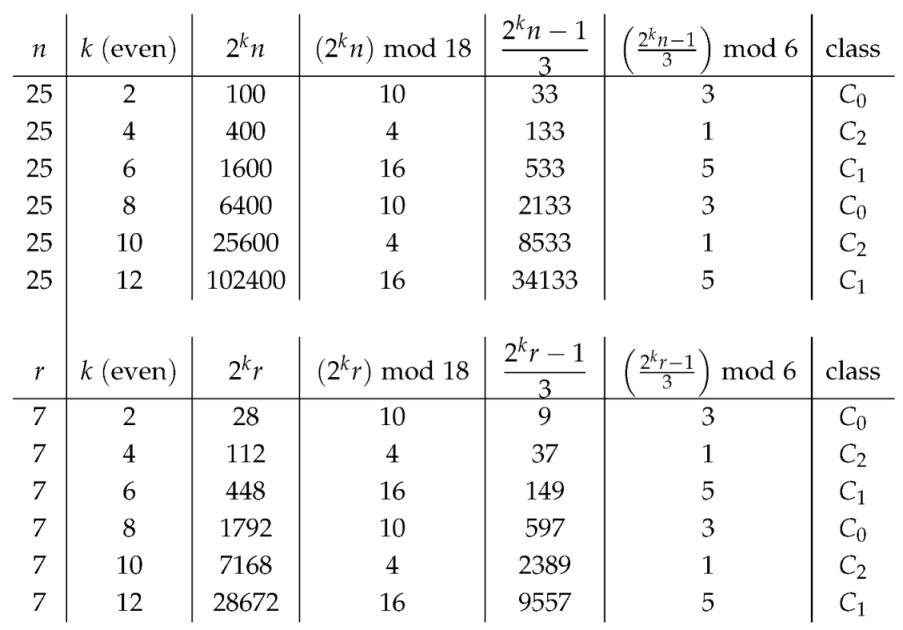
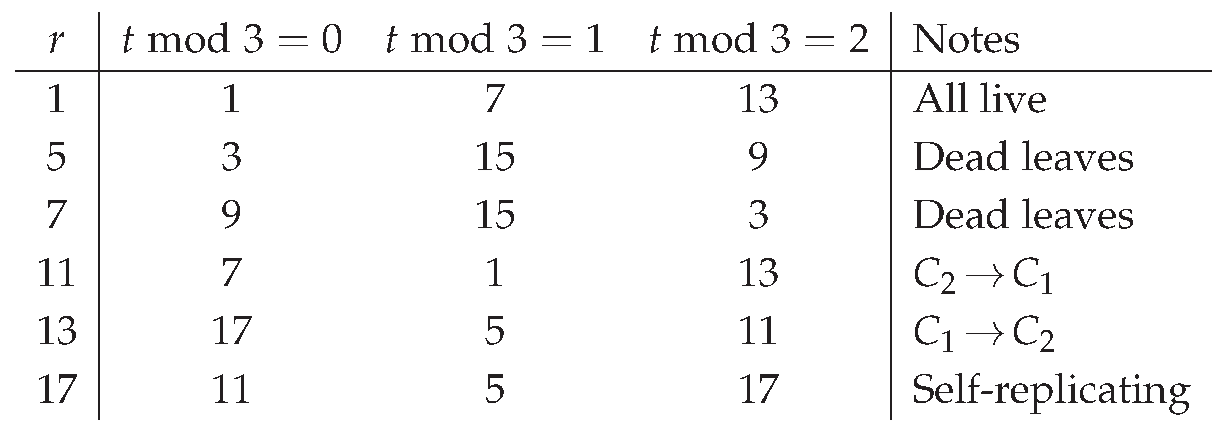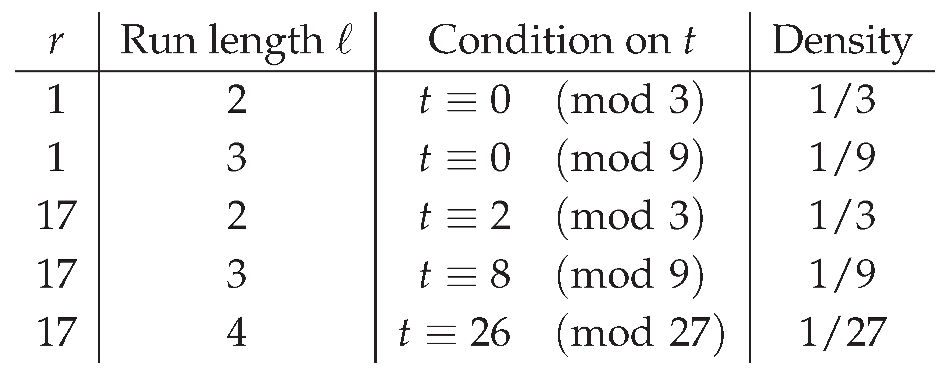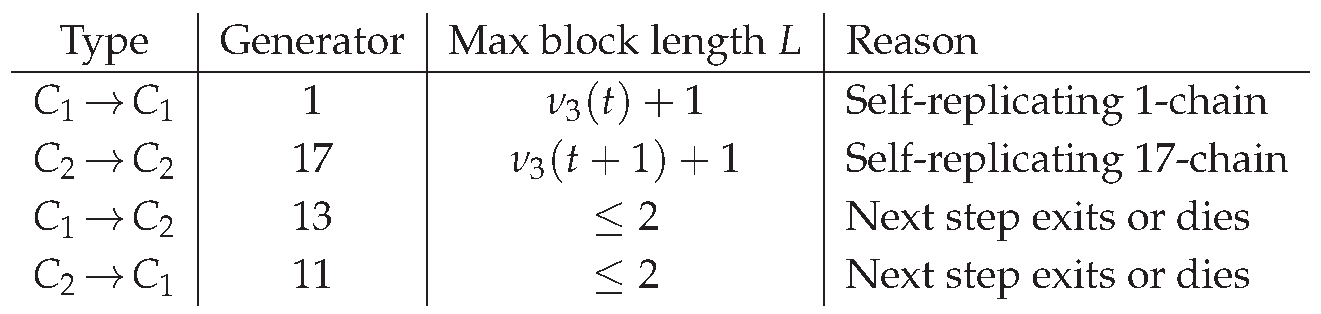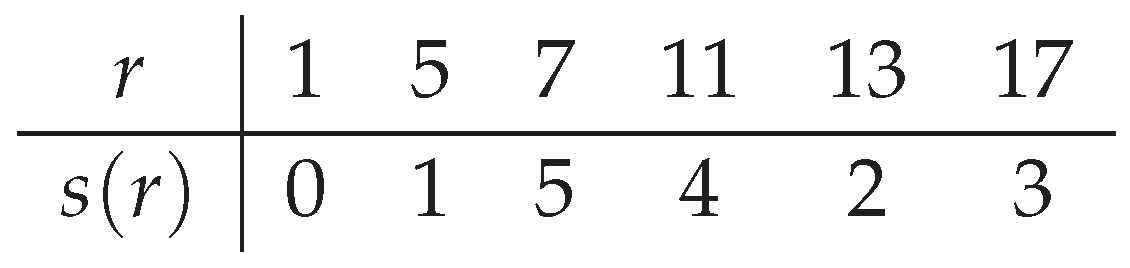5.3. Arithmetic Consequences for Each Class

Lemma 5.2

(Class-pure images and immediate outcomes). For $n=18q+r$ (odd):

• If $r\in C_0$, n has no admissible reverse child (reverse termination).
• If $r\in C_2$, then $k_{min}\left(n\right)=2$ and $P\left(n\right)={\displaystyle \frac{4n-1}{3}}\in C_2$; for $n>1$, $P\left(n\right)>n$ (reverse ascends).
• If $r\in C_1$, then $k_{min}\left(n\right)=1$ and $P\left(n\right)={\displaystyle \frac{2n-1}{3}}\in C_1$. Writing $n=6t+5$, the residue of $tmod3$ decides the next class:

  $$t\equiv 0\Rightarrow P\left(n\right)\in C_0\left(\mathrm{terminate}\right),t\equiv 1\Rightarrow P\left(n\right)\in C_2\left(\mathrm{ascend}\right),t\equiv 2\Rightarrow P\left(n\right)\in C_1\mathrm{with}{t}^{\prime }={\displaystyle \frac{2t-1}{3}}<t.$$

Lemma 5.3

(Least-admissible lift parity). For an odd m, the least $k\ge 1$ making $P_k\left(m\right)={\displaystyle \frac{2^{k}m-1}{3}}$ an odd integer has

$$m\equiv 1(mod3)\Rightarrow k=2,m\equiv 2(mod3)\Rightarrow k=1.$$

Proof.We need $2^{k}m\equiv 1(mod3)$. Since $2\equiv -1(mod3)$, if $m\equiv 1$ then ${(-1)}^k\equiv 1$ forces k even, so take $k=2$. If $m\equiv 2$, then ${(-1)}^k·2\equiv 1$ forces k odd, so take $k=1$. In both cases the numerator $2^{k}m-1$ is odd and divisible by 3, hence $P_k\left(m\right)$ is odd.

Proposition 5.4

(Deterministic parent map on the six live residues mod 18). Write any live odd as $m=r+18t$ with $r\in \{1,5,7,11,13,17\}$ and $t\ge 0$. With k from Lemma 5.3, the parent $P\left(m\right)={\displaystyle \frac{2^{k}m-1}{3}}$ has the following closed forms and residue evolution, where $t=3q+s$ with $s\in \{0,1,2\}$.

(1) $r=1$ (class $C_1$).Here $k=2$ and

$$P\left(m\right)={\displaystyle \frac{4(1+18t)-1}{3}}=1+24t.$$

Decomposing $t=3q+s$,

$$s=0:P\equiv 1\left(18\right),t^{\prime }=4q;s=1:P\equiv 7\left(18\right),t^{\prime }=4q+1;s=2:P\equiv 13\left(18\right),t^{\prime }=4q+2.$$

(2) $r=5$ (class $C_2$).Here $k=1$ and

$$P\left(m\right)={\displaystyle \frac{2(5+18t)-1}{3}}=3+12t.$$

With $t=3q+s$,

$$s=0:P\equiv 3\left(18\right),t^{\prime }=2q;s=1:P\equiv 15\left(18\right),t^{\prime }=2q;s=2:P\equiv 9\left(18\right),t^{\prime }=2q+1.$$

(Note:$3,9,15$ are $3\mid P\left(m\right)$; these are dead leaves.)

(3) $r=7$ (class $C_1$).Here $k=2$ and

$$P\left(m\right)={\displaystyle \frac{4(7+18t)-1}{3}}=9+24t.$$

With $t=3q+s$,

$$s=0:P\equiv 9\left(18\right),t^{\prime }=4q;s=1:P\equiv 15\left(18\right),t^{\prime }=4q+1;s=2:P\equiv 3\left(18\right),t^{\prime }=4q+3.$$

(Dead leavesagain: $3,9,15$.)

(4) $r=11$ (class $C_2$).Here $k=1$ and

$$P\left(m\right)={\displaystyle \frac{2(11+18t)-1}{3}}=7+12t.$$

With $t=3q+s$,

$$s=0:P\equiv 7\left(18\right),t^{\prime }=2q;s=1:P\equiv 1\left(18\right),t^{\prime }=2q+1;s=2:P\equiv 13\left(18\right),t^{\prime }=2q+1.$$

(5) $r=13$ (class $C_1$).Here $k=2$ and

$$P\left(m\right)={\displaystyle \frac{4(13+18t)-1}{3}}=17+24t.$$

With $t=3q+s$,

$$s=0:P\equiv 17\left(18\right),t^{\prime }=4q;s=1:P\equiv 5\left(18\right),t^{\prime }=4q+2;s=2:P\equiv 11\left(18\right),t^{\prime }=4q+3.$$

(6) $r=17$ (class $C_2$).Here $k=1$ and

$$P\left(m\right)={\displaystyle \frac{2(17+18t)-1}{3}}=11+12t.$$

With $t=3q+s$,

$$s=0:P\equiv 11\left(18\right),t^{\prime }=2q;s=1:P\equiv 5\left(18\right),t^{\prime }=2q+1;s=2:P\equiv 17\left(18\right),t^{\prime }=2q+1.$$

In particular:

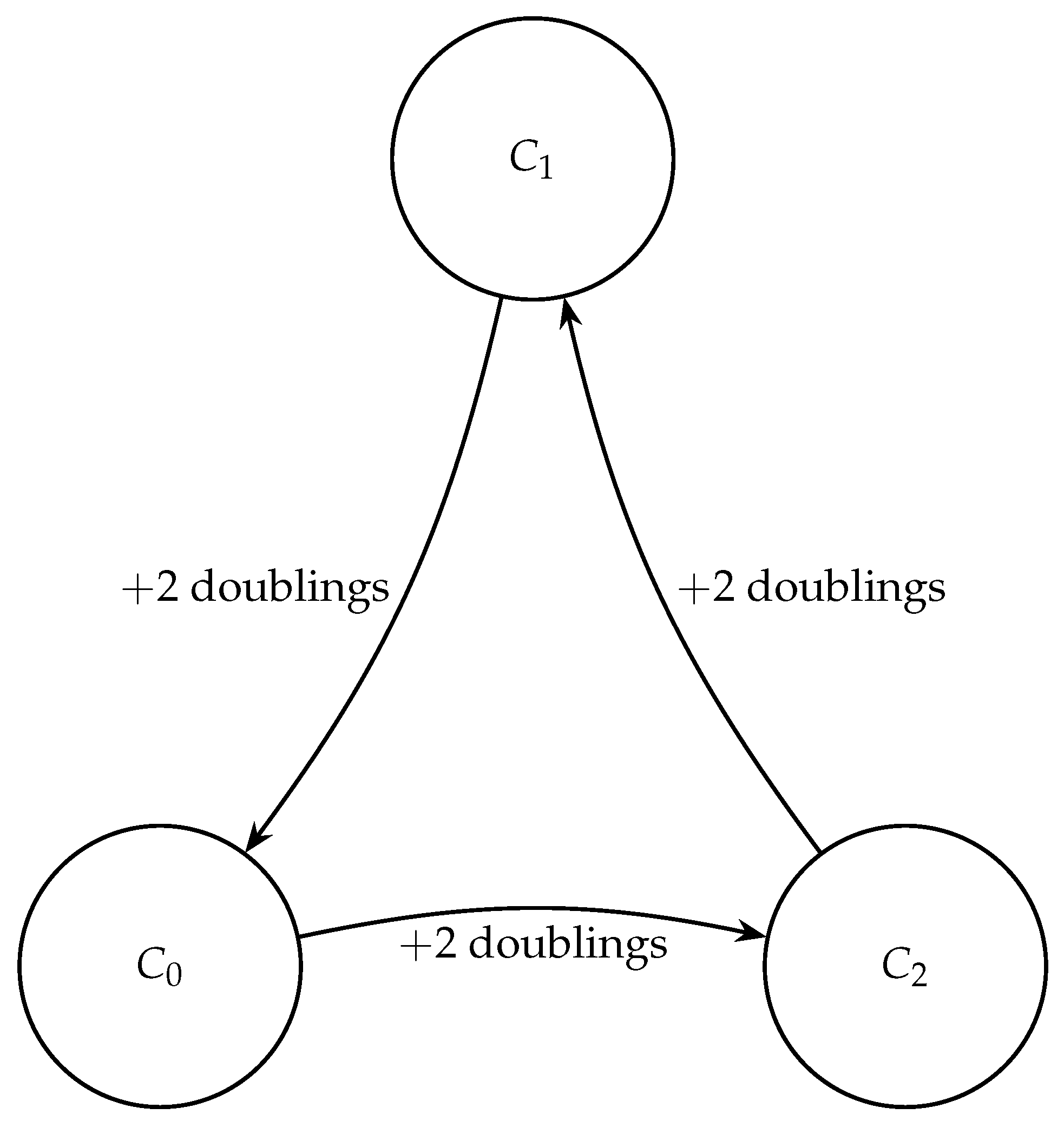
• $r\in \{7,13\}$ (both $C_1$) force either a dead leaf in one step ($r=7$) or a move into the $C_2$ trio ($r=13\to \{17,5,11\}$).
• $r=1$ cycles deterministically within the $C_1$ trio $\{1,7,13\}$ according to $tmod3$.
• $r=11$ injects into the $C_1$ trio; $r=17$ stays within the $C_2$ trio; $r=5$ drops to a dead leaf immediately.

Lemma 5.5

(Finite self-similarity on the 17-branch). If $n\equiv 17(mod18)$, write $n=18q+17$. Then

$$P\left(n\right)=12q+11\equiv 11,5,17(mod18)\mathrm{for}q\equiv 0,1,2(mod3).$$

In the self-preserving case ($17\to 17$), one has $P\left(n\right)=18q^{\prime }+17$ with $q^{\prime }={\displaystyle \frac{2q-1}{3}}<q$. Hence any chain that stays in residue 17 is finite.

Proposition 5.6

(Deterministic replication runs are finite). Let $P\left(m\right)={\displaystyle \frac{2^{k}m-1}{3}}$ be the least-admissible parent map on odd m, with k determined by $mmod3$ (Lemma 5.3), and write every live odd as $m=r+18t$ with $r\in \{1,5,7,11,13,17\}$ and $t\in {\mathbb{N}}_{\ge 0}$. Define thereplication run lengthat residue r by

$$L_r\left(m\right)=max\{\ell \ge 1:\underset{\ell \mathrm{terms}}{\underbrace{r\to r\to \dots \to r}}\mathrm{under}P(\mathrm{i}.\mathrm{e}.\mathrm{consecutive}\mathrm{residue}-r\mathrm{parents})\}.$$

Then:

• Only $r=1$ and $r=17$ can replicate consecutively.For $r\in \{5,7\}$ the next parent is a multiple of 3 (dead), and for $r\in \{11,13\}$ the next parent moves to the other live trio; hence $L_r\left(m\right)=1$ for $r\in \{5,7,11,13\}$.
• Exact run lengths via 3-adic valuations.With ${\nu }_3(·)$ the 3-adic valuation,

  $$\begin{array}{|c|}\hline L_1\left(m\right)={\nu }_3\left(t\right)+1,L_{17}\left(m\right)={\nu }_3(t+1)+1.\\ \hline\end{array}$$
  Equivalently,

  $$\begin{array}{cc}\hfill L_1\left(m\right)\ge \ell & \iff t\equiv 0(mod{3}^{\ell -1}),\hfill \\ \hfill L_{17}\left(m\right)\ge \ell & \iff t\equiv 3^{\ell -1}-1(mod{3}^{\ell -1}),\hfill \end{array}$$
  and

  $$\begin{array}{cc}\hfill L_1\left(m\right)=\ell & \iff t\equiv 0(mod{3}^{\ell -1})\mathrm{but}t\neg \equiv 0(mod{3}^{\ell }),\hfill \\ \hfill L_{17}\left(m\right)=\ell & \iff t\equiv 3^{\ell -1}-1(mod{3}^{\ell -1})\mathrm{but}t\neg \equiv 3^{\ell }-1(mod{3}^{\ell }).\hfill \end{array}$$
• Finite bounds; no infinite replication. For $r=17$ there isnoinfinite replication: $L_{17}\left(m\right)<\infty$ for all $t\ge 0$, since $t\equiv -1(mod{3}^{\ell })$ for all ℓ has no nonnegative solution. For $r=1$, $L_1\left(m\right)=\infty$ occursonlyat $t=0$ (i.e. $m=1$), giving the trivial fixed point $P\left(1\right)=1$. For all $m\ne 1$, $L_1\left(m\right)<\infty$.

Proof. (1) The residue transition law $P\left(m\right)mod18$ from Proposition 5.4 shows $5\mapsto \{3,9,15\}$ and $7\mapsto \{3,9,15\}$ (dead), $11\mapsto \{7,1,13\}$ (moves to the $C_1$ trio), and $13\mapsto \{17,5,11\}$ (moves to the $C_2$ trio). Hence only $r\in \{1,17\}$ can feed r again.

(2) For $r=1$, Proposition 5.4 gives $P(1+18t)=1+24t$ when $t\equiv 0(mod3)$ and otherwise $Pmod18\in \{7,13\}$. Writing $t=3q$, the updated ladder index is $t^{\prime }=4q$; iterating, a run of length ℓ requires t divisible by $3^{\ell -1}$ but not by $3^{\ell }$, so $L_1\left(m\right)={\nu }_3\left(t\right)+1$.

For $r=17$, we have $P(17+18t)\equiv 17(mod18)$ iff $t\equiv 2(mod3)$; write $t=3q+2$, then $t^{\prime }=2q+1$. Requiring another stay forces $q\equiv 2(mod3)$, i.e. $t\equiv 8(mod9)$, etc. Induction yields the cylinder condition $t\equiv 3^{\ell -1}-1(mod{3}^{\ell -1})$ for a run of length at least ℓ, with extension to length $\ell +1$ iff $t\equiv 3^{\ell }-1(mod{3}^{\ell })$. Thus $L_{17}\left(m\right)={\nu }_3(t+1)+1$.

(3) If $L_{17}\left(m\right)=\infty$ then $t\equiv -1(mod{3}^{\ell })$ for all ℓ, forcing $t=-1$ in the 3-adics, contradicting $t\ge 0$. If $L_1\left(m\right)=\infty$ then $3^{\ell -1}\mid t$ for all ℓ, hence $t=0$, i.e. $m=1$; conversely $P\left(1\right)=1$ gives the trivial infinite run. □

Corollary 5.7

(Deterministic bounds on replication). For every odd $m\ne 1$, any consecutive residue replication under the parent map is finite:

$$L_r\left(m\right)\le \left\{\begin{array}{cc}{\nu }_3\left(t\right)+1,\hfill & r=1,\hfill \\ {\nu }_3(t+1)+1,\hfill & r=17,\hfill \\ 1,\hfill & r\in \{5,7,11,13\}.\hfill \end{array}\right.$$

In particular, no nontrivial residue can replicate indefinitely.

Corollary 5.8

(Prefix closure at a chosen start n). Under reverse–forward equivalence at the mod-18 gate (Lemmas 3.9, 3.11), fix an odd n. For every admissible reverse path

$$1=v_0\stackrel{k_0}{\to }{v}_1\stackrel{k_1}{\to }\dots \stackrel{k_{j-1}}{\to }{v}_j=n\stackrel{k_j}{\to }{v}_{j+1}\to \dots ,$$

the forward odd-to-odd trajectory from n is exactly the reversal of the finite prefix to 1:

$$n=v_j\mapsto v_{j-1}\mapsto \dots \mapsto v_1\mapsto v_0=1.$$

In particular, whenever n lies on such a path starting at 1, one has $T^j\left(n\right)=1$. Any live reverse continuation beyond n is irrelevant to the realized forward trajectory.

Proof. 

Let $1=v_0\stackrel{k_0}{\to }\dots \stackrel{k_{j-1}}{\to }{v}_j=n$ be any admissible reverse path. By the gate lemmas (Lemmas 3.9, 3.11), for each $0\le i<j$ we have $T\left(v_{i+1}\right)=v_i$. Composing these identities gives $T^j\left(n\right)=T^j\left(v_j\right)=v_0=1$, so the forward odd-to-odd trajectory from n is exactly the reversal of the finite prefix back to 1. □

Lemma 5.9

(Reverse finite replication ⇒ forward non-runaway). Let T be the forward Collatz operator on odds,

$$T\left(m\right)={\displaystyle \frac{3m+1}{2^{{\nu }_2(3m+1)}}},$$

and let P be the reverse graph map $P\left(m\right)=(2^{k}m-1)/3$ with the least admissible k (Lemma 5.3). If every reverse branch has finite replication length $L_r\left(m\right)$ as in Proposition 5.6, then no forward trajectory can diverge or realize an unbounded runaway.

Proof.Assume some forward trajectory ${\left\{T^{\left(j\right)}\left(m\right)\right\}}_{j\ge 0}$ were unbounded. Reading it backward yields an infinite ancestral chain in the reverse graph, contradicting the hypothesis that every reverse branch has finite replication length. Indeed, by Proposition 5.6 the only self-replicating residues have finite block lengths

$$L_1\left(m\right)={\nu }_3\left(t\right)+1,L_{17}\left(m\right)={\nu }_3(t+1)+1<\infty ,$$

and outside those blocks a reverse branch eitherterminates in $C_0$, moves to a different residue in finitely many steps, or ascends by a higher-lift. Hence no descending reverse chain is infinite. Since each forward step is the inverse of a unique admissible reverse lift (Lemma 6.4, Proposition 6.5), any infinite forward ascent would imply an infinite reverse lineage, which is impossible. Hence no infinite forward trajectory exists.

In particular, whenever a reverse branchclosesby hitting $C_0$, its forward dual segment reaches the odd fixed point 1 (the $4\to 2\to 1$ loop in the full map). □

Theorem 5.10

(Reverse–forward closure). Fix an odd n. We use the following established facts:

• Gate equivalence.Forward and reverse steps coincide at the mod-18 gate (Lemmas 3.9, 3.11).
• Reverse path existence at n.By Lemma 3.3, the admissible-lift set at every odd node is nonempty (with parity fixed by the gate). Consequently, there exists an admissible reverse path

  $$1=v_0\to \dots \to v_j=n\to \dots$$
  (the continuation beyond n may be live; only the finite prefix to n matters).
• Prefix reversal.For any such path through n, the forward odd trajectory from n is exactly the reversal of its finite prefix back to 1 (Corollary 5.8).

Then the forward trajectory from n is finite and terminates at 1.

Proof. 

By (2) choose a finite admissible reverse path through n. Applying (3) (with (1) in force) gives that the forward odd trajectory from n is the reversal of the prefix $n=v_j\mapsto \dots \mapsto v_0=1$, hence $T^j\left(n\right)=1$. □

Lemma 5.11

(Necessity of a $C_1(k=1)$ origin for forward ascent). Let ${\left(t_j\right)}_{j\ge 0}$ be the ladder/progression indices of the odd subsequence of the forward trajectory of n. Assume the forward odd sequence is infinite and $t_{j+1}>t_j$ for infinitely many j. Then along the reverse-compatible path through the mod-18 gate there exists at least one step of type $C_1$ with $k=1$. Equivalently, if no $C_1(k=1)$ step occurs on any reverse-compatible path of n, then $\left(t_j\right)$ is eventually nonincreasing and cannot realize an unbounded forward ascent.

Proof. 

Forward odd steps are determined by $k_{max}={\nu }_2(3n+1)$, while reverse lifts admit multiple k but must respect the same gate. If no $C_1(k=1)$ step ever occurs on any gate-compatible reverse path, then every gate-compatible segment avoids the only mechanism that strictly contracts the index, namely $t\mapsto (2t-1)/3$. In that case, along the forward odd subsequence the index cannot realize infinitely many strict increases without encountering a reverse segment that would force such a contraction; hence $\left(t_j\right)$ is eventually nonincreasing and cannot sustain an unbounded ascent. Contrapositively, if $t_{j+1}>t_j$ occurs infinitely often, some gate-compatible reverse segment must contain $C_1(k=1)$. □

Lemma 5.12

(Forward vs. reverse roles of higher lifts). In the reverse map, $k\ge 2$ yields multiple admissible parent branches but does not contract the ladder index t. In the forward map, only $k_{max}={\nu }_2(3n+1)$ is realized at each odd step, so higher lifts areunselectedand do not contribute to forward ascent. By Lemma 5.11, a forward trajectory cannot “escape” by chaining different $k\ge 2$ lifts while merely interleaving segments between $C_1(k=1)$ occurrences: any unbounded forward ascent would require a $C_1(k=1)$ hit on some gate-compatible reverse segment, and such hits occur only finitely many times. Hence higher lifts do not create or sustain runaways.

Proof. 

By definition of the reverse map, admissible parents with $k\ge 2$ enumerate distinct branches but leave t unchanged up to noncontracting transformations; in particular, no step with $k\ge 2$ produces the strict contraction $t\mapsto (2t-1)/3$ characteristic of $C_1(k=1)$. In the forward map, each odd iterate chooses uniquely $k_{max}={\nu }_2(3n+1)$, so higher lifts ($k\ge 2$) correspond to unselected reverse branches and cannot be chained by the forward dynamics. By Lemma 5.11, any unbounded forward ascent would require at least one $C_1(k=1)$ occurrence on a gate-compatible reverse segment, and such occurrences are finite in number (see, e.g., Theorem 5.13 / Lemma 5.9). Therefore higher lifts cannot create or sustain a runaway in forward trajectories. □

Theorem 5.13

(No runaway; finite bound at the anchor). Every forward trajectory has a finite ladder bound governed by the anchor at 1. In particular, any putative infinite forward ascent must originate from a gate-compatible reverse path containing a $C_1(k=1)$ step; but whenever a $C_1(k=1)$ step occurs (at index t), the next index on that branch strictly contracts to $t^{\prime }=(2t-1)/3<t$. Since repeated $C_1(k=1)$ hits occur only finitely many times, the overall forward index sequence is bounded and the trajectory terminates at the anchor 1.

Proof. 

By Lemmas Lemma 5.9, 5.11, and 5.12, an unbounded forward ascent would require a $C_1(k=1)$ origin on a reverse-compatible path. But each such hit strictly decreases the index $t\mapsto (2t-1)/3$ on the reverse path, and thus can occur only finitely many times. Between these finitely many contractions, the ladder index remains within a finite envelope, so the odd subsequence is bounded above and therefore cannot realize an infinite ascent. The ladder system has the anchor at 1 as its finite lower bound; hence the forward trajectory terminates at 1. □

Proposition 5.14

(Finite bounds for all class-level live→live transformations). Write every live odd as $m=r+18t$ with $r\in \{1,5,7,11,13,17\}$ and $t\in {\mathbb{N}}_{\ge 0}$. Under the least-admissible parent map $P\left(m\right)=(2^{k}m-1)/3$:

(A)

$C_1\to C_1$ (only via $r=1$). A consecutive block of $C_1\to C_1$ steps can occuronlywhile the residue remains $r=1$. Its exact length is

$$L_{C_1\to C_1}\left(m\right)={\nu }_3\left(t\right)+1,$$

with $L_{C_1\to C_1}\left(1\right)=\infty$ (trivial fixed point) and $L_{C_1\to C_1}\left(m\right)<\infty$ for all $m\ne 1$. If the block ever leaves $r=1$ (to 7 or 13), it terminates on the next step (those go to $3\mid n$), so no longer block persists outside $r=1$.

(B)

$C_2\to C_2$ (only via $r=17$). A consecutive block of $C_2\to C_2$ steps can occuronlywhile the residue remains $r=17$. Its exact length is

$$L_{C_2\to C_2}\left(m\right)={\nu }_3(t+1)+1,$$

which is always finite since $t\ge 0$. Any visit to $r=5$ dies immediately ($3\mid n$), and $r=11$ exits to $C_1$ on the next step.

(C)

$C_1\to C_2$ (only via $r=13$).Every $C_1\to C_2$ step arises from $r=13$, with

$$t\equiv 0,1,2(mod3)\Rightarrow P\left(m\right)\equiv 17,5,11(mod18).$$

Hence a consecutive block of $C_1\to C_2$ has length at most 2: the first step (from 13) lands in $C_2$; the next step is either to 5 (dead), to 17 (after which any further $C_2$ step must be of type $C_2\to C_2$ covered by (B)), or to 11 (whichexitsto $C_1$ next). Therefore

$$L_{C_1\to C_2}\left(m\right)\le 2,$$

and in fact any extension beyond length 1 must immediately change type to either $C_2\to C_2$ or $C_2\to C_1$.

(D)

$C_2\to C_1$ (only via $r=11$).Every $C_2\to C_1$ step arises from $r=11$, with

$$t\equiv 0,1,2(mod3)\Rightarrow P\left(m\right)\equiv 7,1,13(mod18).$$

Therefore a consecutive block of $C_2\to C_1$ has length at most 2: the first step (from 11) lands in $C_1$; the next step is either to 7 (dead), to 1 (after which any further $C_1$ step must be of type $C_1\to C_1$ covered by (A)), or to 13 (which immediately yields $C_1\to C_2$ next). Thus

$$L_{C_2\to C_1}\left(m\right)\le 2,$$

and any longer continuation necessarily switches type to (A) or (C).

Corollary 5.15

(Higher lifts define distinct reverse rails). For each odd n and admissible $k\ge 3$, the reverse lift

$$R(n;k)={\displaystyle \frac{2^{k}n-1}{3}}$$

generates a unique and disjoint reverse rail anchored at n. Unlike the $k=1$ case, higher lifts do not produce a contraction of the ladder index t; they simply enumerate separate, non-interacting rails. Since forward dynamics select only $k_{max}$ at each step, a forward trajectory cannot indefinitely ascend by moving among these higher-lift rails.

Corollary 5.16

(Finite-bound map for the reverse function). Every reverse trajectory factors into a concatenation of blocks of the four types $C_1\to C_1$, $C_1\to C_2$, $C_2\to C_1$, $C_2\to C_2$. The lengths of these blocks obey the deterministic bounds

$$\begin{array}{|c|}\hline \begin{array}{cccc}& C_1\to C_1:\hfill & & \le {\nu }_3\left(t\right)+1(\mathrm{equality}\mathrm{while}r=1),\hfill \\ & C_1\to C_2:\hfill & & \le 2,\hfill \\ & C_2\to C_1:\hfill & & \le 2,\hfill \\ & C_2\to C_2:\hfill & & \le {\nu }_3(t+1)+1(\mathrm{equality}\mathrm{while}r=17).\hfill \end{array}\\ \hline\end{array}$$

Consequently, no reverse path can remain forever in the live set: every branch has finite depth before either reaching the anchor 1 (the only infinite self-loop) or hitting a $3\mid n$ dead node.

Theorem 5.17

(Universal reverse cylinder map). Fix a start residue $r_0\in {\mathcal{R}}_{\mathrm{live}}$ and an integer $L\ge 1$. For each ternary word $s_0\dots s_{L-1}\in {\{0,1,2\}}^L$ there exists a unique residue path

$$(r_0,r_1,\dots ,r_L),r_j\in {\mathcal{R}}_{\mathrm{live}}\cup {\mathcal{R}}_{\mathrm{dead}},$$

such that for every $t\in {\mathcal{C}}_L(s_0,\dots ,s_{L-1})$ the L-step reverse trajectory of $m_0=r_0+18t$ under P satisfies $m_j\equiv r_j(mod18)$ for $j=1,\dots ,L$. Moreover, the map

$${\Phi }_{r_0,L}:{\{0,1,2\}}^L⟶{({\mathcal{R}}_{\mathrm{live}}\cup {\mathcal{R}}_{\mathrm{dead}})}^{L+1},(s_0,\dots ,s_{L-1})\mapsto (r_0,\dots ,r_L)$$

is well-defined, and the family of cylinders $\left\{{\mathcal{C}}_L(s_0,\dots ,s_{L-1})\right\}$ forms a partition of ${\mathbb{N}}_{\ge 0}$.

Proof sketch

By Proposition 5.4, for fixed r the image $P(r+18t)mod18$ depends only on $tmod3$, and the next index $t^{\prime }$ is an affine function of $\lfloor t/3\rfloor$ (explicitly computed there). Thus, given $r_0$ and $(s_0,\dots ,s_{L-1})$, we set $t_0\equiv s_0(mod3)$ and obtain $r_1$ uniquely; we then write $t_0=3q_0+s_0$ to get $t_1$ as an explicit affine function of $q_0$, so that $t_{1}mod3$ is determined by $s_1$, hence $r_2$ is determined, and so on. Inductively this defines a unique residue path $(r_0,\dots ,r_L)$ for all t in the cylinder ${\mathcal{C}}_L(s_0,\dots ,s_{L-1})$. Distinct words give disjoint cylinders, and the union of all cylinders is ${\mathbb{N}}_{\ge 0}$. □

Corollary 5.18

(Exact occurrence and density of reverse paths). Fix $r_0$ and L. Every length-L reverse residue path $(r_0,\dots ,r_L)$ arises fromexactly$3^L$ disjoint cylinders ${\mathcal{C}}_L(s_0,\dots ,s_{L-1})$, hence has total occurrence density $3^{-L}$ in $t\in {\mathbb{N}}_{\ge 0}$. In particular, the single-step transition probabilities from any live residue r split evenly among its three admissible images (each $1/3$), and length-L path probabilities are products of these $1/3$ factors.

Proposition 5.19

(Live→live block bounds and finite-bound reverse map). Every reverse trajectory factors into a concatenation of live→live blocks among the four class types

$$C_1=\{1,7,13\},C_2=\{5,11,17\},C_1\to C_1,C_1\to C_2,C_2\to C_1,C_2\to C_2.$$

The maximal lengths of consecutive blocks are deterministically bounded by

$$\begin{array}{cccc}& C_1\to C_1:\hfill & & L_{C_1\to C_1}\left(m\right)={\nu }_3\left(t\right)+1\mathrm{while}r=1;\mathrm{else}\le 1,\hfill \\ & C_1\to C_2:\hfill & & \le 2(\mathrm{forces}\mathrm{via}r=13,\mathrm{then}\mathrm{exits}\mathrm{or}\mathrm{changes}\mathrm{type}),\hfill \\ & C_2\to C_1:\hfill & & \le 2(\mathrm{forces}\mathrm{via}r=11,\mathrm{then}\mathrm{exits}\mathrm{or}\mathrm{changes}\mathrm{type}),\hfill \\ & C_2\to C_2:\hfill & & L_{C_2\to C_2}\left(m\right)={\nu }_3(t+1)+1\mathrm{while}r=17;\mathrm{else}\le 1.\hfill \end{array}$$

Consequently,everyreverse path has finite depth in the live set before either reaching the anchor 1 (the unique fixed point) or hitting a dead residue in $\{3,9,15\}$.

Proof idea.

The bounds for $C_1\to C_1$ and $C_2\to C_2$ are Proposition 5.6 ($L_1={\nu }_3\left(t\right)+1$, $L_{17}={\nu }_3(t+1)+1$). The cross-class bounds $\le 2$ follow from the explicit residue updates in Proposition 5.4: $13\mapsto \{17,5,11\}$ and $11\mapsto \{7,1,13\}$ force either a dead leaf, an immediate change of class type, or entry into one of the two replicated cases already bounded. □

Corollary 5.20

(Universal reverse full map, finite). For each start residue $r_0\in {\mathcal{R}}_{\mathrm{live}}$, the reverse graph decomposes into a radix-3 cylinder tree (Theorem 5.17) whose edges are the deterministic transitions of Proposition 5.4, and whose blocks obey the finite bounds of Proposition 5.19. Hence there is no infinite live branch in the reverse graph, and—by duality with the forward map—no forward runaway trajectory.

Remark 5.21

(Exact locations of long runs). For $r=1$ the path segment $1^{\ell }$ occurs precisely on $t\equiv 0(mod{3}^{\ell -1})$ but $t\neg \equiv 0(mod{3}^{\ell })$ (two APs mod $3^{\ell }$); for $r=17$ the segment ${17}^{\ell }$ occurs precisely on $t\equiv 3^{\ell -1}-1(mod{3}^{\ell -1})$ but $t\neg \equiv 3^{\ell }-1(mod{3}^{\ell })$ (two APs mod $3^{\ell }$). These are the explicit “where they land” formulas used to index long runs without logarithms.

Example 

(Visual summary of the universal reverse map). The following tables illustrate the deterministic structure described in Corollary 5.20.

(A) Single-step residue transitions.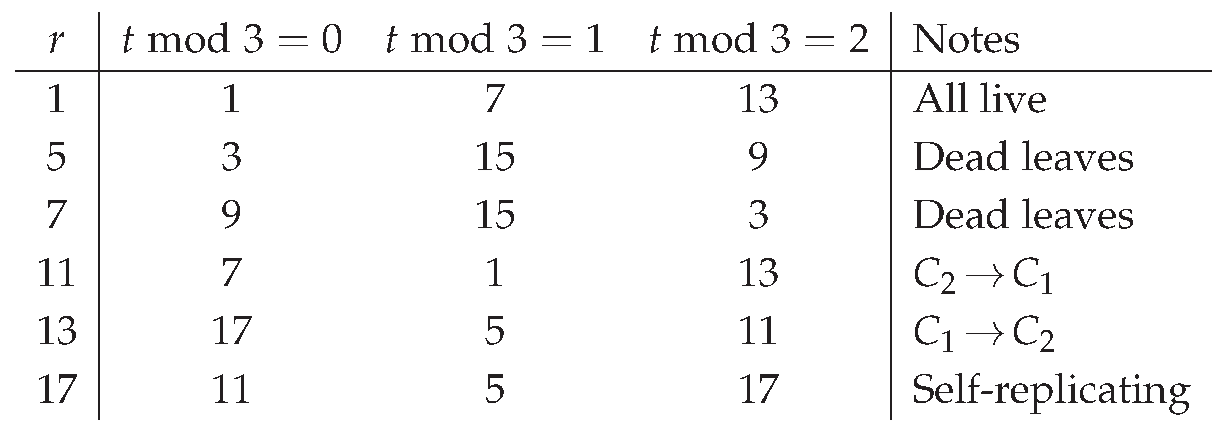

(B) Ternary cylinder trees (depth 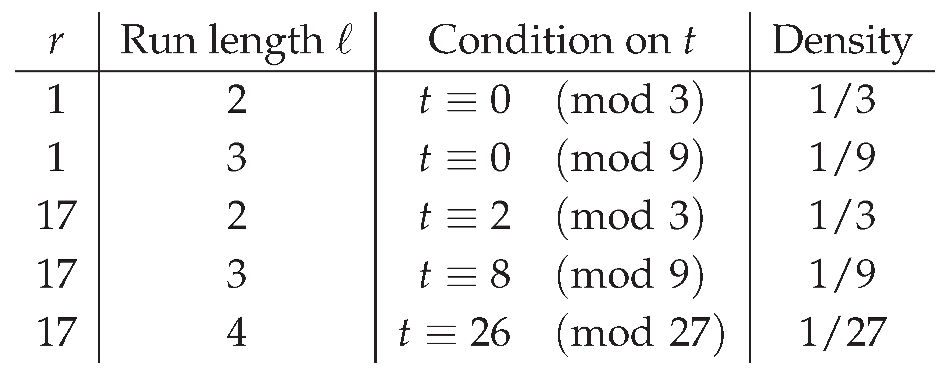$L=3$).

(C) Long-run congruence conditions.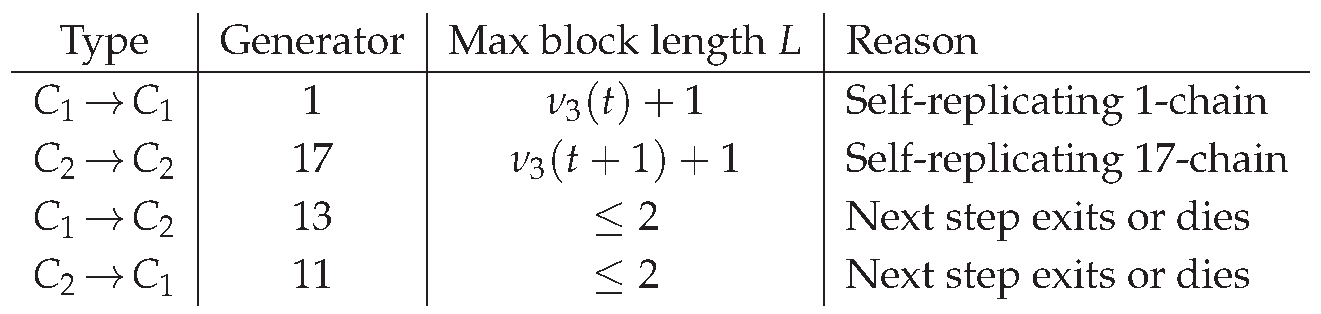

(D) Class-to-class finite bounds.

$$\begin{array}{cccc}\mathrm{Type}& \mathrm{Generator}& \mathrm{Max}\mathrm{block}\mathrm{length}L& \mathrm{Reason}\hfill \\ C_1\to C_1& 1& {\nu }_3\left(t\right)+1& \mathrm{Self}-\mathrm{replicating}1-\mathrm{chain}\hfill \\ C_2\to C_2& 17& {\nu }_3(t+1)+1& \mathrm{Self}-\mathrm{replicating}17-\mathrm{chain}\hfill \\ C_1\to C_2& 13& \le 2& \mathrm{Next}\mathrm{step}\mathrm{exits}\mathrm{or}\mathrm{dies}\hfill \\ C_2\to C_1& 11& \le 2& \mathrm{Next}\mathrm{step}\mathrm{exits}\mathrm{or}\mathrm{dies}\hfill \end{array}$$

(E) Finite-bound map summary.

$$\begin{array}{c}{C}_1:1\to \{1,7,13\},7\to \mathrm{dead},13\to \{17,5,11\};\hfill \\ C_2:17\to \{11,5,17\},5\to \mathrm{dead},11\to \{7,1,13\}.\hfill \end{array}$$

Together these visual fragments show that every reverse branch is a ternary cylinder of finite depth, the only infinite loop being the trivial $1\leftrightarrow 1$.

5.4. Layered Non-Overlap via the Middle-Even

Let $k={\nu }_2(3m+1)$ for odd m. The identity $3m+1=2^{k}n$ (with n odd) implies

$$m=P\left(n\right)={\displaystyle \frac{2^{k}n-1}{3}}.$$

Writing $n=18q+r$ yields the affine form

$$P(18q+r)={\mathrm{\Delta }}_{k}q+c_{r,k},{\mathrm{\Delta }}_k=6·2^{k-1},c_{r,k}={\displaystyle \frac{2^{k}r-1}{3}}\in \mathbb{N},$$

so for fixed k and r the children form a single arithmetic progression $\{{\mathrm{\Delta }}_{k}q+c_{r,k}:q\ge 0\}$. Distinct residues within the same k give distinct cosets modulo ${\mathrm{\Delta }}_k$, hence no overlap; distinct k are disjoint because $k={\nu }_2(3m+1)$ is unique. Thus the union over all k and the six r’s is a partition of the odd integers.

5.5. Middle-Even Scaling and the Next Admissible Child

Fix an odd parent n with an admissible lift k (i.e. $2^{k}n\equiv 1(mod3)$). Define its admissible child at lift k and the corresponding middle-even by

$$c_k:={\displaystyle \frac{2^{k}n-1}{3}}\left(\mathit{odd}\right),M_k:=3c_k+1=2^{k}n.$$

For a fixed n, all admissible lifts have the same parity, so the admissible lifts are $k_0,k_0+2,k_0+4,\dots$ where $k_0=k_{min}\left(n\right)$.

Lemma 5.22

(Middle-even ladder and $k\mapsto k+2$ child). For every admissible lift k,

$$\begin{array}{|c|}\hline M_{k+2}=4M_k\\ \hline\end{array},\begin{array}{|c|}\hline c_{k+2}={\displaystyle \frac{4M_k-1}{3}}=4c_k+1\\ \hline\end{array},\begin{array}{|c|}\hline {\nu }_2(3c_{k+2}+1)={\nu }_2(3c_k+1)+2\\ \hline\end{array}.$$

Proof. 

Since $M_k=2^{k}n$, we have $M_{k+2}=2^{k+2}n=4M_k$. Then

$$c_{k+2}={\displaystyle \frac{2^{k+2}n-1}{3}}={\displaystyle \frac{4M_k-1}{3}}={\displaystyle \frac{4(3c_k+1)-1}{3}}=4c_k+1.$$

Finally $3c_{k+2}+1=4(3c_k+1)$, so ${\nu }_2$ increases by 2. □

Remarks.

(a) The minimal-parent child is $c_{k_0}$; higher children $c_{k_0+2j}$ (with $j\ge 1$) are admissible but non-minimal. (b) The middle-evens form a pure geometric progression: $M_{k_0},4M_{k_0},4^2{M}_{k_0},\dots$. (c) The child ladder is strictly increasing since $c_{k+2}-c_k=3c_k+1>0$.

Examples

(A)

$C_2$ parent: $n=25$ (so $n=6·4+1$, $k_{min}=2$).

$$\begin{array}{cc}& \mathrm{Minimal}\mathrm{child}\mathrm{at}k=2:c_2={\displaystyle \frac{2^2·25-1}{3}}={\displaystyle \frac{100-1}{3}}=33,M_2=3·33+1=100=2^2·25.\hfill \\ & \mathrm{Next}\mathrm{admissible}\mathrm{child}\mathrm{at}k=4:M_4=4M_2=400,c_4={\displaystyle \frac{400-1}{3}}=133=4·33+1.\hfill \\ & \mathrm{Next}\mathrm{at}k=6:M_6=4M_4=1600,c_6={\displaystyle \frac{1600-1}{3}}=533=4·133+1.\hfill \end{array}$$

(Here $c_2\equiv 15(mod18)\in C_0$; higher children need not stay in the same class as the minimal child.)

(B)

$C_1$ parent: $n=17$ (so $n=6·2+5$, $k_{min}=1$).

$$\begin{array}{cc}& \mathrm{Minimal}\mathrm{child}\mathrm{at}k=1:c_1={\displaystyle \frac{2·17-1}{3}}={\displaystyle \frac{34-1}{3}}=11,M_1=3·11+1=34=2^1·17.\hfill \\ & \mathrm{Next}\mathrm{admissible}\mathrm{child}\mathrm{at}k=3:M_3=4M_1=136,c_3={\displaystyle \frac{136-1}{3}}=45=4·11+1.\hfill \end{array}$$

(Here $c_1\equiv 11(mod18)\in C_1$, while the higher child $c_3\equiv 9(mod18)\in C_0$; the $k+2$ step changes class but preserves admissibility.)

Takeaway.

For a fixed parent n, the admissible children form the affine ladder

$$c_{k_0},4c_{k_0}+1,4(4c_{k_0}+1)+1,\dots$$

and the middle-evens scale by factors of 4. The $k\mapsto k+2$ update is the exact arithmetic bridge between a child’s middle-even and the parent’s next admissible child.

Lemma 5.23

(Step size and anchor; integrality). For fixed $k\ge 1$ and $r\in \{1,5,7,11,13,17\}$, set

$${\mathrm{\Delta }}_k:=6·2^k,c_{r,k}:={\displaystyle \frac{2^{k}r-1}{3}}.$$

Then $c_{r,k}\in \mathbb{N}$, and the canonical form is $m={\mathrm{\Delta }}_{k}q+c_{r,k}$.

Proof. 

Since $r\neg \equiv 0(mod3)$ and 2 is invertible mod 3, there is a unique parity of k for which $2^{k}r\equiv 1(mod3)$, hence $c_{r,k}$ is integral. The displayed form follows from

$$m={\displaystyle \frac{2^k(18q+r)-1}{3}}={\displaystyle \frac{2^k·18}{3}}q+{\displaystyle \frac{2^{k}r-1}{3}}={\mathrm{\Delta }}_{k}q+c_{r,k}.$$

□

Proposition 5.24

(Existence and uniqueness). Every odd m admits a canonical triple $(k,r,q)$ as in Definition 2.15, and this triple is unique. Equivalently,

$$3m+1=2^k(18q+r),r\in \{1,5,7,11,13,17\},$$

with $k={\nu }_2(3m+1)$, determines $(k,r,q)$ uniquely.

Proof. 

Existence. Given odd m, set $k={\nu }_2(3m+1)$ and $n=(3m+1)/2^k$ (odd). Write $n=18q+r$ with r one of the six odd residues not divisible by 3. Then by Lemma 5.23, $m={\mathrm{\Delta }}_{k}q+c_{r,k}$.

Uniqueness. If $m={\mathrm{\Delta }}_{k}q+c_{r,k}={\mathrm{\Delta }}_{k^{\prime }}{q}^{\prime }+c_{r^{\prime },k^{\prime }}$, then $k={\nu }_2(3m+1)=k^{\prime }$ (layers match). With k fixed, reduce modulo ${\mathrm{\Delta }}_k$: $m\equiv c_{r,k}\equiv c_{r^{\prime },k}(mod{\mathrm{\Delta }}_k)$. The anchors $c_{r,k}$ are distinct for the six r’s, hence $r=r^{\prime }$; then $q=q^{\prime }$ follows. □

Corollary 5.25

(Partition of odd integers into disjoint rails). For each layer $k\ge 1$, the six sets

$${\mathcal{R}}_{r,k}:=\{{\mathrm{\Delta }}_{k}q+c_{r,k}:q\in {\mathbb{N}}_0\},r\in \{1,5,7,11,13,17\},$$

are pairwise disjoint arithmetic progressions with common difference ${\mathrm{\Delta }}_k$. Different layers are disjoint. Consequently,

$${\mathbb{N}}_{\mathit{odd}}=\underset{k\ge 1}{⨆}\underset{r\in \{1,5,7,11,13,17\}}{⨆}{\mathcal{R}}_{r,k}.$$

5.6. On Exact Odd→Odd Step Counts

Let $T^{*}\left(m\right)={\displaystyle \frac{3m+1}{2^{{\nu }_2(3m+1)}}}$ denote the odd-to-odd Collatz step and let $s\left(m\right)$ be the number of $T^{*}$-steps needed to reach 1 (with $s\left(1\right)=0$).

First-step recursion (address ⇒ next odd).

By the canonical decomposition (Def. 2.15), every odd m has a unique triple $(k,r,q)$ with

$$3m+1=2^k(18q+r),r\in \{1,5,7,11,13,17\}.$$

Consequently

$$\begin{array}{|c|}\hline T^{*}\left(m\right)=18q+r,s\left(m\right)=1+s(18q+r)\\ \hline\end{array}.$$

Proof.$T^{*}\left(m\right)$ is, by definition, $(3m+1)/2^k=18q+r$; counting one step gives $s\left(m\right)=1+s(18q+r)$.

Anchors admit a closed form.

If $q=0$ (an anchor $m={\displaystyle \frac{2^{k}r-1}{3}}$), then the first step lands on r: $T^{*}\left(m\right)=r$. Hence $s\left(m\right)=1+s\left(r\right)$, and the six base values are

(e.g., $7\to 11\to 17\to 13\to 5\to 1$ gives $s\left(7\right)=5$).

Why no closed formula $s=f(k,r,q)$.

After the first step, the next valuation is

$$k_1={\nu }_2\left(3(18q+r)+1\right)={\nu }_2(54q+3r+1).$$

This depends arithmetically on q in a way not determined by the initial address $(k,r,q)$ alone; you must actually evaluate ${\nu }_2(54q+3r+1)$, then repeat. Equivalently, each m has a unique “valuation signature”

$$\sigma \left(m\right)=(k_0,k_1,k_2,\dots ),k_j:={\nu }_2\left(3T^{*j}\left(m\right)+1\right),$$

but that entire sequence is not encoded in the first address. Thus the address gives the next odd exactly, and anchors give closed-form counts, but a general closed form for $s\left(m\right)$ from $(k,r,q)$ alone is not available.

The parenthesis tower (for the curious).

Iterating the first-step recursion yields

$$s\left(m\right)=\left(1+s(18q_0+r_0)\right)=\left(1+\left(1+s(18q_1+r_1)\right)\right)=\dots =\underset{s\left(m\right)\mathrm{pairs}\mathit{of}\mathrm{parentheses}}{\underbrace{\left(1+\left(1+\dots \left(1+s\left(1\right)\right)\dots \right)\right)}}.$$

About a “maximum” number of odd steps.

Define, formally,

$$S_{max}:=\underset{\mathit{odd}m}{sup}s\left(m\right).$$

Our results show $s\left(m\right)<\infty$ for each fixed m (reverse closure ⇒ forward convergence), but they do not supply a uniform finite bound over all m; the initial address does not determine the full signature $\sigma \left(m\right)$. In plain terms: the future ${\nu }_2$ values are part of a number’s unique arithmetic “signature,” and that information gets created step-by-step by evaluating $54q+3r+1$ at each stage—so there is no way to read off a global maximum (or a closed form for $s\left(m\right)$) from the first address alone.

Remark 5.26

(Middle-even interpretation and $k\mapsto k+2$). For $m={\mathrm{\Delta }}_{k}q+c_{r,k}$ one has $3m+1=2^k(18q+r)$ (themiddle-even). Raising the lift by $+2$ multiplies the middle-even by 4 and updates the child by

$$M_{k+2}=4M_k,m^{\prime }={\displaystyle \frac{4M_k-1}{3}}=4m+1,$$

so successive admissible children of a fixed parent form the affine ladder $m,4m+1,4(4m+1)+1,\dots$.

Examples.

• $m=25$.$3m+1=76=2^2·19\Rightarrow k=2$, $n=19=18·1+1$. Thus $r=1$, $q=1$, and

  $$m=6·2^2·1+{\displaystyle \frac{2^2·1-1}{3}}=24+1=25.$$
• $m=17$.$3m+1=52=2^2·13\Rightarrow k=2$, $n=13=18·0+13$. Thus $r=13$, $q=0$, and

  $$m=6·2^2·0+{\displaystyle \frac{2^2·13-1}{3}}={\displaystyle \frac{52-1}{3}}=17.$$

5.7. Dyadic–Affine Scaling Across Lifts

Recall the canonical form for odds in layer $k\ge 1$ and residue $r\in \{1,5,7,11,13,17\}$:

$$m=\underset{=:{\mathrm{\Delta }}_k}{\underbrace{6·2^k}}q+\underset{=:c_{r,k}}{\underbrace{{\displaystyle \frac{2^{k}r-1}{3}}}},q\in {\mathbb{N}}_0.$$

Lemma 5.27

(Dyadic–affine lift $k\mapsto k+2$). For every admissible residue r and lift $k\ge 1$,

$$\begin{array}{|c|}\hline {\mathrm{\Delta }}_{k+2}=4{\mathrm{\Delta }}_k\\ \hline\end{array},\begin{array}{|c|}\hline c_{r,k+2}=4c_{r,k}+1\\ \hline\end{array}.$$

Equivalently, for every $m={\mathrm{\Delta }}_{k}q+c_{r,k}$ one has

$$\begin{array}{|c|}\hline m^{\prime }:=4m+1={\mathrm{\Delta }}_{k+2}q+c_{r,k+2}\\ \hline\end{array},$$

and on middle-evens,

$$\begin{array}{|c|}\hline 3m^{\prime }+1=4(3m+1)\\ \hline\end{array}.$$

Proof. 

From the definitions: ${\mathrm{\Delta }}_{k+2}=6·2^{k+2}=4(6·2^k)=4{\mathrm{\Delta }}_k$, and

$$c_{r,k+2}={\displaystyle \frac{2^{k+2}r-1}{3}}={\displaystyle \frac{4\left(2^{k}r\right)-1}{3}}=4\left({\displaystyle \frac{2^{k}r-1}{3}}\right)+1=4c_{r,k}+1.$$

Then for $m={\mathrm{\Delta }}_{k}q+c_{r,k}$,

$$4m+1=4{\mathrm{\Delta }}_{k}q+(4c_{r,k}+1)={\mathrm{\Delta }}_{k+2}q+c_{r,k+2}.$$

Finally $3m^{\prime }+1=3(4m+1)+1=4(3m+1)$. □

Corollary 5.28

(Layer bijection; invariant rail indices). For each fixed residue r and position q, the map

$${\varphi }_{k\to k+2}:m\mapsto 4m+1$$

is a bijection from the layer-k point ${\mathrm{\Delta }}_{k}q+c_{r,k}$ to the unique layer-$k+2$ point ${\mathrm{\Delta }}_{k+2}q+c_{r,k+2}$. Hence:

• The step size scales dyadically by 4 when the lift increases by 2.
• The anchor advances by the same dyadic factor with a constant additive offset $+1$, independent of r and k.
• Rail labels $(r,q)$ are preserved by ${\varphi }_{k\to k+2}$: same residue r, same position q.

Remark 5.29

(Only the 2-adic layer changes). Since $3m^{\prime }+1=4(3m+1)$, one has ${\nu }_2(3m^{\prime }+1)={\nu }_2(3m+1)+2$. Thus k increases by 2, while the rail index $(r,q)$ is unchanged. This is the arithmetic content of the observation that theadditive dyadic valueamong k-increases matches the k-offsets:

$$(\mathrm{\Delta },c)\mapsto (4\mathrm{\Delta },4c+1)\mathrm{and}m\mapsto 4m+1.$$

Micro-examples.

• $r=1$:$c_{1,2}=1,c_{1,4}=4·1+1=5,c_{1,6}=4·5+1=21$;${\mathrm{\Delta }}_2=24,{\mathrm{\Delta }}_4=96$. Thus $m\equiv 1\left(\mathrm{mod}24\right)$ lifts to $m^{\prime }\equiv 5\left(\mathrm{mod}96\right)$ via $m^{\prime }=4m+1$.
• $r=13$:$c_{13,2}=17,c_{13,4}=4·17+1=69$; again ${\mathrm{\Delta }}_2=24,{\mathrm{\Delta }}_4=96$ and $m^{\prime }=4m+1$.

Theorem 5.30

(Global Iterative Coverage of the Odd Integers). The reverse Collatz operator covers all odd integers via anchor–ladder progressions and a dyadic sieve. In particular:

• Rails from canonical decomposition.By the canonical form (Def. 2.15), every odd m has a unique $s={\nu }_2(3m+1)\ge 1$ and a unique $r\in \{1,5,7,11,13,17\}$ with

  $$3m+1=2^s(18q+r)⟺m=(6·2^s)q+{\displaystyle \frac{2^{s}r-1}{3}}(q\in {\mathbb{N}}_0).$$
  For fixed s, these six arithmetic progressions (“rails”) are pairwise disjoint; layers with different s are disjoint as well (Corollary 5.25).
• First children seed the base slices.For a live parent n, the first admissible lift depends only on its class:

  $$n=6t+5\left(C_1\right)k=1m=4t+3,n=6t+1\left(C_2\right)k=2m=8t+1,$$
  so the base slices are $m\equiv 3\left(\mathrm{mod}4\right)$ for $C_1$ and $m\equiv 1\left(\mathrm{mod}8\right)$ for $C_2$ (Prop. 4.10).
• Lift by $+2$ is $m\mapsto 4m+1$ (gap $\times 4$).Within a fixed class, raising the admissible lift by two sends each child to the next child by

  $$m^{\prime }={\displaystyle \frac{2^{k+2}n-1}{3}}=4\left({\displaystyle \frac{2^{k}n-1}{3}}\right)+1=4m+1,$$
  and multiplies the rail step by 4: ${\mathrm{\Delta }}_{s+2}=4{\mathrm{\Delta }}_s$. Thus each class forms an affine ladder under $\varphi \left(m\right)=4m+1$ (Lemma 5.27).
• Dyadic sieve and exact proportions.Let $A_{=s}=\{m\mathit{odd}:{\nu }_2(3m+1)=s\}$ and $A_{\ge s}=\{m\mathit{odd}:{\nu }_2(3m+1)\ge s\}$. Exactly one odd residue class modulo $2^s$ solves $3m\equiv -1(mod{2}^s)$, so among odd integers

  $${\displaystyle \frac{|A_{\ge s}|}{\left|\mathrm{odds}\right|}}={\displaystyle \frac{1}{2^{s-1}}},{\displaystyle \frac{|A_{=s}|}{\left|\mathrm{odds}\right|}}={\displaystyle \frac{1}{2^s}},$$
  i.e. “exactly k halvings’’ occupies $1/2^k$ of the odds, and the slices $\frac{1}{2},\frac{1}{4},\frac{1}{8},\dots$ sum to 1.
• Completeness and non-overlap.Taking the disjoint union over all layers $s\ge 1$ and residues r yields

  $${\mathbb{N}}_{\mathit{odd}}=\underset{s\ge 1}{⨆}\underset{r\in \{1,5,7,11,13,17\}}{⨆}\left\{(6·2^s)q+\frac{2^{s}r-1}{3}:q\ge 0\right\}.$$
  Hence every odd number lies on exactly one rail and is generated by the anchor–ladder progressions; there are no omissions and no overlaps (Corollary 5.25).

Consequently, the global structure is deterministic and sieve-organized: first-child formulas seed the base slices in $C_1$ and $C_2$, the affine lift $m\mapsto 4m+1$ generates all higher slices within each class (quadrupling the gap each time), and the dyadic proportions ensure that the union across all lifts coversallodd integers exactly once.

6. Why This Is Not a Trajectory Dynamic (but a Branching Number Sequence)

Dependency Map (Section 6: Closure and Convergence)

• Uses (from §§3–5). Lemma 3.4, Lemma 3.7, Proposition 3.8, Lemma 3.9 (gate determinism/equivalence); Lemma 3.3 (admissible parity); Corollary 5.8, Theorem 5.10 (reverse–forward closure); Lemma 5.9, Lemma 5.11, Lemma 5.12, Theorem 5.13 (no-runaway chain).
• Introduces (proved in §6). Lemma 6.1 (unique odd parent at $k_{max}$); Lemma 6.2 (infinitely many admissible children; $c_{j+1}=4c_j+1$); Proposition 6.3 (reverse graph is branching, not a trajectory); Lemma 6.4 (forward step = halving to the unique parent); Proposition 6.5 (forward trajectory is the reverse of a fixed branch); Lemma 6.8 (only descending case is $C_1(k=1)$ and is finite); Theorem 6.11 (universal reverse cylinder map; exact $3^{-L}$ densities); Theorem 6.9 (no infinite residue pattern along a trajectory); Theorem 6.7 (forward trajectory locks to 1); Corollary 6.10 (no nontrivial odd cycles).
• One-line chains. Lemma 6.1 + Lemma 6.2 ⇒ Proposition 6.3 (reverse graph is branching).
  Lemma 6.4 + Lemma 6.1 ⇒ Proposition 6.5 (forward is reverse of a fixed branch).
  Proposition 5.4 (from §5) + Definitions 2.17,2.18 ⇒ Theorem 6.11 (deterministic universal reverse map).
  Lemma 6.8 + Theorem 6.11 ⇒ Theorem 6.9 (no infinite residue word).
  Gate equivalence (Lemmas 3.9, 3.11) + Corollary 5.8 + Proposition 6.5 ⇒ Theorem 6.7 (convergence to 1).
  Theorem 6.7 ⇒ Corollary 6.10 (uniqueness of 1).
• Outcome. Forward trajectories are single-valued and terminate at 1; the reverse graph is a branching number system (not a trajectory map); no nontrivial odd cycles exist.

Admissible reverse relation.

For odd $n\neg \equiv 0(mod3)$, call m an admissible child of n if

$$m={\displaystyle \frac{2^{k}n-1}{3}}\mathrm{for}\mathrm{some}k\equiv k_{min}\left(n\right)(mod2),k\ge k_{min}\left(n\right).$$

Write $\mathcal{A}\left(n\right)$ for the set of all admissible children of n.

Lemma 6.1

(Unique odd parent). For every odd m, write $3m+1=2^{s}n$ with n odd. Then n (if $3\nmid n$) is theuniqueodd parent of m, corresponding to the unique lift $k=s$:

$$T\left(m\right)=n,{\nu }_2(3m+1)=s.$$

If $3\mid n$ (i.e. $m\in C_0$), then m has no admissible odd child.

Lemma 6.2

(Infinitely many children; strict growth along lifts). If $n\neg \equiv 0(mod3)$, set $k_0:=k_{min}\left(n\right)$ and define

$$c_j:={\displaystyle \frac{2^{k_0+2j}n-1}{3}}(j\ge 0).$$

Then $\mathcal{A}\left(n\right)=\{c_j:j\ge 0\}$ and

$$c_{j+1}=4c_j+1\Rightarrow c_{j+1}>c_j\mathrm{for}\mathrm{all}j.$$

Hence every such n has infinitely many distinct children (outdegree $=\infty$).

Proposition 6.3

(Reverse graph is branching, not a trajectory). Consider the directed graph with an edge $n\to m$ iff $m\in \mathcal{A}\left(n\right)$. Then:

• Nodes in $C_0$ have outdegree 0 (reverse termination).
• Nodes in $C_1\cup C_2$ have outdegree ∞ by Lemma 6.2.
• Every node has indegree $\le 1$ and, if $\notin C_0$, indegree $=1$ by Lemma 6.1.

In particular, this graph cannot arise from any single-valued map $F:X\to X$ (a “trajectory dynamic”), which would requireeverynode to have outdegree 1. Thus the Collatz reverse system is intrinsically abranchingstructure.

Residue-level branching (deterministic triads).

Writing $n=18q+r$ with $r\in \{1,5,7,11,13,17\}$, one minimal step produces the deterministic triad indexed by $qmod3$:

$$\begin{array}{ccc}\hfill 1\to (1,7,13)\subset C_2& & 11\to (7,1,13)\subset C_2\hfill \\ \hfill 7\to (9,15,3)\subset C_0& & 17\to (11,5,17)\subset C_1\hfill \\ \hfill 13\to (17,5,11)\subset C_1& & 5\to (3,15,9)\subset C_0\hfill \end{array}$$

so residue choices branch deterministically as q varies. (See Appendix Tables.)

Multidimensional number sequence (global parameterization).

Every odd integer m is uniquely encoded by the triple $(k,r,q)$:

$$k={\nu }_2(3m+1)\ge 1,r\in \{1,5,7,11,13,17\},q\in {\mathbb{N}}_0,$$

via the affine formula

$$m=\underset{{\mathrm{\Delta }}_k}{\underbrace{6·2^k}}q+\underset{c_{r,k}}{\underbrace{{\displaystyle \frac{2^{k}r-1}{3}}}}.$$

Thus the system is a branching number sequence: a disjoint union of affine rails (indexed by $(k,r)$), with residue-level triad branching across $qmod3$ and lift branching along $c_{j+1}=4c_j+1$ from any fixed parent.

6.1. Forward Trajectory is the $k_{max}$–Halving to the Unique Parent

Lemma 6.4

(Closure to the unique reverse parent at $k_{max}$). For every odd m there is a unique odd n such that

$$3m+1=2^{k_{max}\left(m\right)}n⟺m={\displaystyle \frac{2^{k_{max}\left(m\right)}n-1}{3}}.$$

Consequently $T\left(m\right)=n$. Equivalently: among all admissible reverse lifts k for n, the **unique** one that reproduces m is $k=k_{max}\left(m\right)$, i.e. the forward step is exactly the $k_{max}$–halving back to the (unique) parent.

Proof. 

Write $3m+1=2^{s}n$ with n odd; by definition $s={\nu }_2(3m+1)=k_{max}\left(m\right)$, so n is unique and odd, and $T\left(m\right)=n$. Rearranging gives $m=(2^{k_{max}\left(m\right)}n-1)/3$. No other k works since $2^k\mid (3m+1)$ iff $k\le k_{max}\left(m\right)$, and taking fewer halvings would not yield an odd parent. □

Proposition 6.5

(Forward is a single trajectory; it is the reverse of a fixed branch). Let $P\left(n\right):={\displaystyle \frac{2^{k_{min}\left(n\right)}n-1}{3}}$ be the minimal-parent map on odd $n\neg \equiv 0(mod3)$. For any odd m, the forward orbit $m,T\left(m\right),T^2\left(m\right),\dots$ is a **single-valued trajectory** and equals the reverse of some admissible reverse chain

$$m={\displaystyle \frac{2^{k_0}{n}_0-1}{3}},n_0={\displaystyle \frac{2^{k_1}{n}_1-1}{3}},n_1={\displaystyle \frac{2^{k_2}{n}_2-1}{3}},\dots$$

with $k_j=k_{max}\left(T^j\left(m\right)\right)$ and $T^j\left(m\right)=n_{j-1}$ for all $j\ge 1$. In particular, the forward map never branches: each step uses the uniquely determined $k_{max}$.

Remark 6.6

(Closure vs finite step length). A reverse branch is not considered closed merely because it contains finitely many descending $C_1(k=1)$ steps. As long as the branch remains in $C_1\cup C_2$, its odd value remains unbounded and the forward dual is not complete. Only termination in $C_0$ constitutes reverse closure, corresponding to a unique, finite forward trajectory ending at 1.

Theorem 6.7

(Forward trajectory locks to 1). Assume the arithmetic lemmas established earlier:

(A)

(Only descending case) The only reverse decrease is $k=1$ in $C_1$, and any run of such steps is finite (index $t\mapsto (2t-1)/3$ strictly decreases).

(B)

(General ascension) Every reverse step with $k\ge 2$ strictly increases the odd value (and $C_0$ is absorbing in reverse).

(C)

(No odd cycles) The reverse graph has no nontrivial odd cycles.

Then for every odd m there exists $s\ge 0$ such that $T^s\left(m\right)=1$.

Proof. 

By Lemma 6.4 and Proposition 6.5, the forward orbit $(m,T\left(m\right),T^2\left(m\right),\dots )$ is exactly the reverse of an admissible reverse chain read backward. By (A) the only descending reverse steps are $C_1(k=1)$ and they only occur finitely in sequence; by (B) all other admissible reverse steps either terminate in $C_0$ or strictly increase the odd value. Combining these with Theorem 5.13 (and Lemma 5.9) establishes the finiteness of the reverse chain to m with anchor 1. Reading this finite chain forward yields $T^s\left(m\right)=1$ for some $s\ge 0$. □

6.2. No Infinite Combinatorial Pattern Along the Trajectory

Residue triads and realizable words.

Let $\mathcal{R}=\{1,5,7,11,13,17\}$ be the live residues mod 18 and let $\mathsf{S}:\mathcal{R}\to {\mathcal{R}}^3$ be the deterministic triad map (ordered by $qmod3$):

$$\begin{array}{ccc}\hfill 1\mapsto (1,7,13)& & 11\mapsto (7,1,13)\hfill \\ \hfill 7\mapsto (9,15,3)(\subset C_0)& & 17\mapsto (11,5,17)\hfill \\ \hfill 13\mapsto (17,5,11)& & 5\mapsto (3,15,9)(\subset C_0).\hfill \end{array}$$

A (one-sided) residue word $r_0{r}_1{r}_2\dots$ over $\mathcal{R}$ is called realizable if there exist odd integers $n_j=18q_j+r_j$ with $n_{j+1}={\displaystyle \frac{2^{k_j}{n}_j-1}{3}}$ (an admissible reverse step) for all j, and $r_{j+1}$ is the $q_{j}mod3$ child of $r_j$ in $\mathsf{S}\left(r_j\right)$.

Lemma 6.8

(Only one descending case; all others ascend or terminate). With the minimal parent $P\left(n\right)={\displaystyle \frac{2^{k_{min}\left(n\right)}n-1}{3}}$:

• $C_0$ is absorbing in reverse (no parent).
• Every $k\ge 2$ step strictly increases the odd value; in particular any $C_2$ step ($k_{min}=2$) ascends for $n>1$.
• The only descending case is $k=1$ in $C_1$: if $n=6t+5$ and $t\equiv 2(mod3)$, then $P\left(n\right)=6\left({\displaystyle \frac{2t-1}{3}}\right)+5$ with the index $t^{\prime }={\displaystyle \frac{2t-1}{3}}<t$; for $t\equiv 0,1$ the next class is $C_0$ or $C_2$, ending descent.

Theorem 6.9

(No infinite combinatorial pattern along a trajectory). No realizable residue word $r_0{r}_1{r}_2\dots$ can be infinite, except the trivial fixed point $1^{\omega }$ corresponding to $T\left(1\right)=1$. Equivalently: based on the coordinates $(n,t,q,r)$ and the mod-18 triad structure, there isnocombinatorial pattern that can persist indefinitely along the forward trajectory.

Proof. 

Assume a realizable infinite word $r_0{r}_1\dots$ with associated reverse chain $n_{j+1}\mapsto n_j$.

If some $r_j\in \{5,7\}$ occurs, then by the triads $r_j\mapsto C_0$ at the next step, so reverse terminates—contradiction to infinitude. Hence only residues $\{1,11,13,17\}$ can occur infinitely often.

If $r_j\in \{1,11\}$ occurs infinitely often, then those steps are in $C_2$ with $k_{min}=2$, hence strictly increasing by Lemma 6.8. An infinite reverse chain of strictly increasing values cannot be realizable backwards as a forward orbit avoiding 1 (because forward is the $k_{max}$–halving to the unique parent and cannot branch back into a decreasing segment). In any case it does not produce an infinite descent pattern.

It remains to consider $C_1$ residues $\{13,17\}$. From the triads, every 13–step produces a child in $\{17,5,11\}$; if it produces 5 we are back to $C_0$ (next step terminates), and if it produces 11 we move to $C_2$ (ascending thereafter). Thus the only way to remain inside $C_1$ indefinitely is through the self-preserving $17\mapsto 17$ branch. But in that case $n=18q+17$ and the update is $q\mapsto q^{\prime }={\displaystyle \frac{2q-1}{3}}<q$, so the hidden index q is a strictly decreasing nonnegative integer—impossible infinitely. Therefore no infinite $C_1$ run exists.

Combining the cases: any realizable residue word must either hit $C_0$ (stop), enter $C_2$ (eventual ascent), or keep $C_1$ only finitely many times (by the q-descent). Hence no nontrivial infinite combinatorial pattern can persist. The only infinite forward word is the fixed point $1^{\omega }$ (since $T\left(1\right)=1$). □

Corollary 6.10

(No nontrivial odd cycles). There are no odd cycles other than the trivial fixed point $n=1$.

Proof. 

If there were a nontrivial odd cycle $\mathcal{C}$ with some $n\ne 1$, then the forward orbit starting at n would never reach 1, contradicting Theorem 6.7. Moreover, such a cycle would yield a periodic (respectively, ultimately periodic) residue word of positive period, which is ruled out by Theorem 6.9 (the only infinite word allowed is $1^{\omega }$). Hence no nontrivial odd cycle exists. □

Theorem 6.11

(Full Map Formula: deterministic universal reverse map). Fix a start residue $r_0\in \{1,5,7,11,13,17\}$ and a ternary word $(s_0,\dots ,s_{L-1})$. Define sequences ${\left(r_j\right)}_{j=0}^L$, ${\left(t_j\right)}_{j=0}^L$ recursively by

$$\begin{array}{|c|}\hline t_0={\displaystyle \sum _{j=0}^{L-1}}{s}_j{3}^j+3^{L}u,\left\{\begin{array}{c}\mathrm{write}{t}_j=3q_j+s_j,\hfill \\ r_{j+1}=R(r_j,s_j)\mathrm{from}\mathrm{Table},\hfill \\ t_{j+1}=a_{r_j}{q}_j+c_{r_j}\left(s_j\right)\mathrm{from}\mathrm{Table},\hfill \end{array}\right.j=0,\dots ,L-1,\\ \hline\end{array}$$

with $u\in {\mathbb{N}}_{\ge 0}$ arbitrary. Then:

• (Residue path) The L-step reverse trajectory of $m_0=r_0+18t$ satisfies $m_j\equiv r_j(mod18)$ for $j=1,\dots ,L$, and the path $(r_0,\dots ,r_L)$ depends only on the word $(s_0,\dots ,s_{L-1})$.
• (Affine cylinder map) There exist explicit integers

  $$A(r_0;s_0,\dots ,s_{L-1})=\prod _{j=0}^{L-1}{a}_{r_j}\in {\{2,4\}}^L,B(r_0;s_0,\dots ,s_{L-1})\in \mathbb{N},$$
  such that

  $$\begin{array}{|c|}\hline t_L=A(r_0;s_0,\dots ,s_{L-1})·u+B(r_0;s_0,\dots ,s_{L-1}).\\ \hline\end{array}$$
  Consequently

  $$\begin{array}{|c|}\hline m_L=r_L+18t_L=r_L+18Au+18B.\\ \hline\end{array}$$
• (Explicit recursion for $A,B$) Let $A_0=1$, $B_0=0$. For $j=0,\dots ,L-1$ set

  $$A_{j+1}={\displaystyle \frac{a_{r_j}}{3}}{A}_j,B_{j+1}={\displaystyle \frac{a_{r_j}}{3}}(B_j-s_j)+c_{r_j}\left(s_j\right).$$
  Then $A=3^L{A}_L={\prod }_{j=0}^{L-1}{a}_{r_j}$ and $B=B_L$. (All quantities are integers because $a_{r_j}\in \{2,4\}$ and the recurrence is taken over ternary digits.)
• (Occurrence/density) The word $(s_0,\dots ,s_{L-1})$ selects the cylinder $t\equiv \sum s_j{3}^j(mod{3}^L)$, hence has natural density $3^{-L}$. Every length-L residue path $(r_0,\dots ,r_L)$ occurs with total density $3^{-L}$, split among its words.

Table 1. Deterministic reverse step: $(r,t)\mapsto (r^{\prime },t^{\prime })$ from $t=3q+s$, $s\in \{0,1,2\}$.

r	${\mathit{a}}_{\mathit{r}}$	${\mathit{r}}^{\prime }$ as a function of s	${\mathit{t}}^{\prime }$ as ${\mathit{a}}_{\mathit{r}}\mathit{q}+{\mathit{c}}_{\mathit{r}}\left(\mathit{s}\right)$
1	4	$s=0\Rightarrow 1,s=1\Rightarrow 7,s=2\Rightarrow 13$	$c_1\left(0\right)=0,c_1\left(1\right)=1,c_1\left(2\right)=2$
5	2	$s=0\Rightarrow 3,s=1\Rightarrow 15,s=2\Rightarrow 9$	$c_5\left(0\right)=0,c_5\left(1\right)=0,c_5\left(2\right)=1$
7	4	$s=0\Rightarrow 9,s=1\Rightarrow 15,s=2\Rightarrow 3$	$c_7\left(0\right)=0,c_7\left(1\right)=1,c_7\left(2\right)=3$
11	2	$s=0\Rightarrow 7,s=1\Rightarrow 1,s=2\Rightarrow 13$	$c_{11}\left(0\right)=0,c_{11}\left(1\right)=1,c_{11}\left(2\right)=1$
13	4	$s=0\Rightarrow 17,s=1\Rightarrow 5,s=2\Rightarrow 11$	$c_{13}\left(0\right)=0,c_{13}\left(1\right)=2,c_{13}\left(2\right)=3$
17	2	$s=0\Rightarrow 11,s=1\Rightarrow 5,s=2\Rightarrow 17$	$c_{17}\left(0\right)=0,c_{17}\left(1\right)=1,c_{17}\left(2\right)=1$

Table 1. Deterministic reverse step: $(r,t)\mapsto (r^{\prime },t^{\prime })$ from $t=3q+s$, $s\in \{0,1,2\}$.

r	${\mathit{a}}_{\mathit{r}}$	${\mathit{r}}^{\prime }$ as a function of s	${\mathit{t}}^{\prime }$ as ${\mathit{a}}_{\mathit{r}}\mathit{q}+{\mathit{c}}_{\mathit{r}}\left(\mathit{s}\right)$
1	4	$s=0\Rightarrow 1,s=1\Rightarrow 7,s=2\Rightarrow 13$	$c_1\left(0\right)=0,c_1\left(1\right)=1,c_1\left(2\right)=2$
5	2	$s=0\Rightarrow 3,s=1\Rightarrow 15,s=2\Rightarrow 9$	$c_5\left(0\right)=0,c_5\left(1\right)=0,c_5\left(2\right)=1$
7	4	$s=0\Rightarrow 9,s=1\Rightarrow 15,s=2\Rightarrow 3$	$c_7\left(0\right)=0,c_7\left(1\right)=1,c_7\left(2\right)=3$
11	2	$s=0\Rightarrow 7,s=1\Rightarrow 1,s=2\Rightarrow 13$	$c_{11}\left(0\right)=0,c_{11}\left(1\right)=1,c_{11}\left(2\right)=1$
13	4	$s=0\Rightarrow 17,s=1\Rightarrow 5,s=2\Rightarrow 11$	$c_{13}\left(0\right)=0,c_{13}\left(1\right)=2,c_{13}\left(2\right)=3$
17	2	$s=0\Rightarrow 11,s=1\Rightarrow 5,s=2\Rightarrow 17$	$c_{17}\left(0\right)=0,c_{17}\left(1\right)=1,c_{17}\left(2\right)=1$

Remark 6.12

(Two canonical self-run laws (closed form)). The only residues that can replicate are $r=1$ and $r=17$. Writing $m=r+18t$:

$$L_1\left(m\right)={\nu }_3\left(t\right)+1,L_{17}\left(m\right)={\nu }_3(t+1)+1.$$

Equivalently, $1^{\ell }$ occurs iff $t\equiv 0(mod{3}^{\ell -1})$ but $\neg \equiv 0(mod{3}^{\ell })$, and ${17}^{\ell }$ occurs iff $t\equiv 3^{\ell -1}-1(mod{3}^{\ell -1})$ but $\neg \equiv 3^{\ell }-1(mod{3}^{\ell })$.

Corollary 6.13

(Finite-bound reverse map ⇒ no forward runaway). Every reverse branch is a finite concatenation of class-level blocks with deterministic bounds: $C_1\to C_1$ has length ${\nu }_3\left(t\right)+1$ while $r=1$; $C_2\to C_2$ has length ${\nu }_3(t+1)+1$ while $r=17$; the cross-class types $C_1\to C_2$ (via $r=13$) and $C_2\to C_1$ (via $r=11$) have length $\le 2$. Hence the live reverse graph has no infinite branch (the only infinite loop is $m=1$), and by duality the forward Collatz map has no runaway trajectory.

Remark 6.14

(Summary). The reverse Collatz system is intrinsically branching. Each live odd has infinitely many children generated by admissible lifts. The forward map is single-valued, selecting the unique maximal halving back to its parent. From the class-resolved arithmetic, all $k\ge 2$ reverse steps strictly ascend, the only descending case $k=1$ in $C_1$ is finite, and no nontrivial odd cycles exist. Consequently, every forward trajectory reaches 1, and there is no infinite combinatorial residue pattern along any orbit. These facts complete thelocal dynamics ↔ forward trajectorybridge used in Section 7 to unify the residue and ladder frameworks into global closure.

7. Unification of Local and Global Frameworks

Dependency Map (Section 7: Unification of Local and Global Frameworks)

• Uses (from §§3–6).

  –

  Local gates: Lemma 3.3 (admissible parity), Lemma 3.4 (mod-9 source), Lemma 3.7 (lift to mod 18), Proposition 3.8 (gate $\{10,4,16\}$), Lemma 3.9 (forward–reverse gate equivalence), Lemma 3.10 (rotation under $k\mapsto k+2$).

  –

  Global coverage and no odd cycles: Lemma 5.25, Lemma 4.5, Lemma 4.7 (gap $\times 4$), Proposition 4.10 (base slices), Corollary 4.8 (overlay fills gaps), Lemma 4.11, Corollary 4.12 (slice measures), Lemma 4.18, Theorem 4.19 (no odd cycles).

  –

  Rails & dyadic–affine structure: Definition 2.15, Proposition 5.24, Corollary 5.25 (rail partition), Lemma 5.27, Corollary 5.28 ($k\mapsto k+2$⇔$m\mapsto 4m+1$).

  –

  No runaways & closure: Lemma 5.9, Lemma 5.11, Lemma 5.12, Theorem 5.13, Corollary 5.8, Theorem 5.10uid141, Theorem 6.7, Corollary 6.10.

• Introduces (proved in §7).

  –

  Lemma 7.1 (residue vs. ladder are isomorphic projections of R)—uses: Lemma 3.3, Proposition 3.8, Lemma 5.27, Corollary 5.28.

  –

  Lemma 7.2 (coverage by layers and anchors; base gaps $4/8$, gap $\times 4$)—uses: Definition 2.15, Proposition 5.24, Corollary 5.25, Lemma 4.1, Lemma 4.5, Lemma 4.7.

  –

  Corollary 7.3 (unique parentage; no cross-layer/rail overlap)—uses: Definition 2.15, Proposition 5.24, Corollary 5.25.

  –

  Theorem 7.4 (main unification: partition & unique parent & convergence)—uses: Definition 2.15, Proposition 5.24, Corollary 5.25, Proposition 4.10, Lemma 5.27, Corollary 5.28, Lemma 4.11, Corollary 4.12.

• One-line chains.

  –

  Lem. 3.3 + Prop. 3.8 ⇒ (residue projection in) Lem. 7.1.

  –

  Lem. 5.27 + Lem. 4.5 ⇒ (ladder projection in) Lem. 7.1.

  –

  Lem. 4.7 (+ Cor. 5.28) ⇒ (compatibility $k\mapsto k+2$, $m\mapsto 4m+1$) in Lem. 7.1.

  –

  Lem. 5.27 + Cor. 5.25 + Prop. 4.10 + Lem. 4.7 ⇒ Lem. 7.2 (layers/rails; base gaps $4/8$; gap $\times 4$).

  –

  Lem. 7.2 ⇒ Cor. 7.3 (disjoint layers/rails; unique parentage).

  –

  For Thm. 7.4:

  ∗

  (i) Lem. 7.2 + Cor. 5.25.

  ∗

  (ii) Lem. 3.3 + Prop. 3.8 + Prop. 4.10.

  ∗

  (iii) Lem. 5.27 + Cor. 5.28.

  ∗

  (iv) Lem. 4.11 + Cor. 4.12.

  ∗

  (v) Cor. 7.3 + Lem. 6.4.

  ∗

  (vi) Lem. 6.8 + Thm. 5.10 + Thm. 5.13.

  ∗

  (vii) Lem. 4.18 + Thm. 4.19

• Outcome. A unified, isomorphic description of the odd Collatz dynamics: (i) partition of ${\mathbb{N}}_{\mathit{odd}}$ by unique layer k and rail r with stride ${\mathrm{\Delta }}_k$; (ii) unique parentage (no overlap across layers/rails); (iii) compatibility of residue triads with the affine lift $m\mapsto 4m+1$; (iv) global closure: every forward trajectory reaches 1 and no nontrivial odd cycles exist.

The local residue lens (mod 18) and the global progression ladders are two projections of the same arithmetic operator: the reverse map

$$R(n;k)={\displaystyle \frac{2^{k}n-1}{3}}\mathrm{with}k\mathrm{constrained}\mathrm{by}{2}^{k}n\equiv 1(mod3).$$

The local lens records what class a step lands in; the global lens records where inside a disjoint arithmetic progression that step lies. No extra machinery is needed: all identities below are direct consequences of R.

Lemma 7.1

(Two projections of one operator (isomorphic lenses)). Fix an admissible lift $k\ge 1$ and write any live odd as $n=18q+r$ with $r\in \{1,5,7,11,13,17\}$. Then:

• (Residue projection). Admissibility fixes the parity of k (even on $r\in \{1,7,13\}$, odd on $r\in \{5,11,17\}$) and the child’s class is decided by $qmod3$ (Lemma 3.3, Prop. 3.8).
• (Ladder projection). For the same k, the reverse parent is affine in q:

  $$P(18q+r):=R(18q+r;k)={\mathrm{\Delta }}_{k}q+c_{r,k},{\mathrm{\Delta }}_k=6·2^{k-1},c_{r,k}={\displaystyle \frac{2^{k}r-1}{3}}\in \mathbb{N},$$
  and distinct residues r give disjoint cosets modulo ${\mathrm{\Delta }}_k$ (Lemmas 4.5, 4.7).
• (Compatibility / 4-adic lift). Raising the lift by $+2$ scales every $2^k$–quantity by 4:

  $${\mathrm{\Delta }}_{k+2}=4{\mathrm{\Delta }}_k,c_{r,k+2}=4c_{r,k}+1,$$
  i.e. the anchor/rail update is $\varphi \left(m\right)=4m+1$. On the residue side, the middle-even rotates through $\{4,16,10\}(mod18)$, so class membership (and the triad) evolves deterministically with $k\mapsto k+2$ (Lemma 4.7).

Proof. 

The parity constraint is $2^k\equiv \pm 1(mod3)$; the affine form is $R(18q+r;k)={\displaystyle \frac{2^k(18q+r)-1}{3}}=6·2^{k-1}q+{\displaystyle \frac{2^{k}r-1}{3}}.$ For $k\mapsto k+2$, $c_{r,k+2}={\displaystyle \frac{2^{k+2}r-1}{3}}=4c_{r,k}+1$ and ${\mathrm{\Delta }}_{k+2}=4{\mathrm{\Delta }}_k.$ The residue rotation follows from $2^{k+2}\equiv 4·2^k(mod18)$. □

Lemma 7.2

(Coverage by layers and anchors). Every odd integer m lies in exactly one lift layer $k={\nu }_2(3m+1)\ge 1$ and one residue rail $r\in \{1,5,7,11,13,17\}$:

$$m={\mathrm{\Delta }}_{k}q+c_{r,k}(q\in {\mathbb{N}}_0).$$

Within each parity family, the anchors $1\in C_2$ and $5\in C_1$ generate the two parent types $6t+1$ and $6t+5$. Their first admissible lifts give the base steps

$$(6t+1)\mathbf{errorXmapsto}\stackrel{k=2}{\to }8t+1\left(\mathrm{gap}8\right),(6t+5)\mathbf{errorXmapsto}\stackrel{k=1}{\to }4t+3\left(\mathrm{gap}4\right),$$

and $k\mapsto k+2$ multiplies these gaps by 4 (so $8\to 32\to 128\to \dots$ in $C_2$ and $4\to 16\to 64\to \dots$ in $C_1$). In particular, 1 is fixed at $k=2$ and 5 is obtained from 1 at $k=4$.

Proof. 

Layer selection. For odd m, write $3m+1=2^{k}n$ with n odd; then $k={\nu }_2(3m+1)$ is unique and $m=(2^{k}n-1)/3$. Writing $n=18q+r$ with r live gives $m={\mathrm{\Delta }}_{k}q+c_{r,k}$, so m lies on exactly one rail in exactly one layer. Anchors and gaps. For $n=6t+1$ the least lift is $k=2$ and $R(n;2)=8t+1$; for $n=6t+5$ the least lift is $k=1$ and $R(n;1)=4t+3$. The update $k\mapsto k+2$ sends $m\mapsto 4m+1$, which multiplies the rail step by 4. Direct checks give $R(1;2)=1$ and $R(1;4)=5$. □

Corollary 7.3

(Unique parentage; no overlap). Fix a lift k. The six rails ${\{{\mathrm{\Delta }}_{k}q+c_{r,k}\}}_r$ are disjoint; across different k the layers are disjoint since $k={\nu }_2(3m+1)$ is unique. Hence no odd integer can arise from two different admissible parents, and the forward odd map $T\left(m\right)={\displaystyle \frac{3m+1}{2^{{\nu }_2(3m+1)}}}$ is single-valued and non-branching.

Unification.

The reverse operator R admits two faithful projections: the residue projection (class/triad via $qmod3$ and parity of k) and the ladder projection (affine rail via q with stride ${\mathrm{\Delta }}_k$). They commute with the 4-adic lift $k\mapsto k+2$ (anchors/steps scale by 4), so the “mod 18” dynamics and the global ladders are isomorphic descriptions of the same arithmetic action of R on odds.

Theorem 7.4

(Main Unification and Closure of the Odd Collatz Map). Let $T\left(m\right)={\displaystyle \frac{3m+1}{2^{{\nu }_2(3m+1)}}}$ be the odd-to-odd step and let $R(n;k)={\displaystyle \frac{2^{k}n-1}{3}}$ be the reverse lift (admissible when $2^{k}n\equiv 1(mod3)$). Then:

(i)

Partition by valuation layer and rail.For each odd m there are unique

$$k={\nu }_2(3m+1)\ge 1,r\in \{1,5,7,11,13,17\},q\in {\mathbb{N}}_0$$

such that

$$m=(6·2^k)q+{\displaystyle \frac{2^{k}r-1}{3}}.$$

For fixed k the six rails are pairwise disjoint; layers with different k are disjoint. Hence

$${\mathbb{N}}_{\mathit{odd}}=\underset{k\ge 1}{⨆}\underset{r\in \{1,5,7,11,13,17\}}{⨆}\left\{(6·2^k)q+\frac{2^{k}r-1}{3}:q\ge 0\right\}.$$

(Cites: canonical decomposition / rail partition.)

(ii)

Local residue determinism (triads) & first children.Writing a live odd as $n=18q+r$ with $r\in \{1,5,7,11,13,17\}$, admissibility fixes the parity of k (even on $r\in \{1,7,13\}$, odd on $r\in \{5,11,17\}$), and the child’s class is decided by $qmod3$ (the deterministic triads). In particular the first admissible children are

$$n=6t+5\left(C_1\right)k=1m=4t+3,n=6t+1\left(C_2\right)k=2m=8t+1,$$

i.e. base gaps 4 for $C_1$ and 8 for $C_2$.(Cites: admissible-parity; deterministic mod 18; first-child formulas.)

(iii)

4-adic lift $k\mapsto k+2$ (same class, gap $\times 4$).Within a fixed class, raising the lift by two sends each child to the next child by

$$m^{\prime }={\displaystyle \frac{2^{k+2}n-1}{3}}=4\left({\displaystyle \frac{2^{k}n-1}{3}}\right)+1=4m+1,$$

and multiplies the rail step by 4. Thus each class forms an affine ladder under $\varphi \left(m\right)=4m+1$.(Cites: dyadic-affine/lift lemma.)

(iv)

Dyadic sieve: exact proportions. Among odd integers, the slice withexactlyk halvings in $3m+1$ has frequency $1/2^k$ and the slice withat leastk has frequency $1/2^{k-1}$. Consequently the disjoint slices $\frac{1}{2},\frac{1}{4},\frac{1}{8},\dots$ cover all odds.(Cites: dyadic coverage by residue counting.)

(vi)

Unique parentage; forward is the unique $k_{max}$–halving.For live n the least admissible $k_{min}\left(n\right)$ is fixed by $nmod3$, and $P\left(n\right):=R(n;k_{min}\left(n\right))$ is the unique admissible parent. Conversely, for odd m, if $3m+1=2^{k_{max}\left(m\right)}n$ with n odd, then

$$T\left(m\right)=n,m={\displaystyle \frac{2^{k}T\left(m\right)-1}{3}}\in \mathbb{N}\iff k=k_{max}\left(m\right).$$

Hence the forward orbit $m,T\left(m\right),T^2\left(m\right),\dots$ is single-valued and non-branching.(Cites: unique-parentage; closure lemma.)

(vii)

No infinite reverse descent; forward convergence to 1. The only potentially descending reverse case is $k=1$ in $C_1$, and any run of such steps is finite; all lifts with $k\ge 2$ strictly increase (and $C_0$ nodes terminate). Thus every infinite reverse chain is eventually increasing and no odd cycle exists. By right-inverse identity $T\left(R\right(·;k\left)\right)=\mathrm{id}$ on admissible edges, every odd m climbs a finite reverse chain back to 1, so $T^s\left(m\right)=1$ for some $s\ge 0$, and the full Collatz orbit enters $4\to 2\to 1$.(Cites: $k=1$ finiteness; $k\ge 2$ increase; reverse-closure ⇒ forward convergence.)

(vii)

No nontrivial odd cycles (explicit drift obstruction).Along any admissible reverse loop of length $t\ge 2$, the raw $-\frac{1}{3}$ drift unrolling (Lemma 4.18) gives

$$n_t={\displaystyle \frac{2^{K_t}}{3^t}}{n}_0-{\mathcal{D}}_t,{\mathcal{D}}_t>0,$$

so $n_t=n_0$ would force $(2^{K_t}-3^t)n_0=3^t{\mathcal{D}}_t>0$, an impossibility. Hence no nontrivial odd cycles exist; the only fixed point is $n=1$ at $k=2$.

Remark 7.5

(Affine completeness of the $\langle 2,3\rangle$ system). All transformations in the deterministic residue framework arise from the composite action of the multiplicative generators 2 and 3, together with the fixed additive index $+1$. The powers of 2 and factors of 3 determine the scaling structure of every progression and lift, while the additive index shifts each multiplicative layer by one unit, producing the affine residue offsets that generate global coverage. Thus the entire Collatz dynamic is a finite, deterministic affine system on the semigroup $\langle 2,3\rangle$, whose completeness follows from the interaction of these two multiplicative bases with the single additive index of 1. Equivalently, for any odd integer n, the transformation $3n+1$ is always an even number divisible by a fixed power of 2, yielding a unique next odd term after a finite number of divisions. This property constitutes the local arithmetic realization of the global affine structure described above.

8. Consequences

With the local and global frameworks unified, three plain consequences follow.

Corollary 8.1

(Exhaustive inclusion). Every odd integer lies in the ladder–rail partition anchored at 1 (and its first lift 5). No odd integer is left out.

Corollary 8.2

(No divergence). There are no runaway trajectories. Equivalently, every forward odd-to-odd sequence is finite and reaches 1.

Corollary 8.3

(Only the trivial cycle). The sole cycle is $1\to 4\to 2\to 1$. No other odd cycle occurs.