Applications of Monte Carlo Simulations in Medical Physics: Enhancing Precision and Accuracy in Radiation Therapy

1. Introduction

Monte Carlo (MC) simulations have grown indispensable in medical physics, especially in the field of radiation therapy [16,18,66]. These simulations are a very powerful and precise way to model the complicated interactions of ionizing radiation with biological tissues, allowing for better precision and accuracy of a wide range of features in radiation therapy [19,23].

The current review article will try to comprehensively discuss the applications of MC simulations within the field of medical physics but also with particular attention to their applications in improving precision and accuracy in treatments associated with radiation therapy.

In the last few decades, MC simulations have gained considerable importance in medical physics with the growing computational power and medical imaging technologies, while more is understood of the underlying physical and biological processes taking part in radiation interactions [2,26]. MC simulations will become even more critical to both research and clinical applications of radiation therapy since it can enable a realistic way of modeling transport in geometries of arbitrary complexity for many ionizing radiations like photons, electrons, and protons. For instance, when a geometrically and/or physically complex material system-a system just such as the human body is the interacting target geometry [24,25].

The key advantage of MC simulations is that they are able to take into account-in a very accurate way-the complicated physical processes associated with radiation transport, such as photoelectric effect, Compton scattering, pair production, and other interactions [14,44]. By simulating these processes on a particle-by-particle basis, MC methods can provide highly accurate dose calculations and other dosimetric quantities, which are crucial for the optimization and evaluation of radiation therapy treatments [35,48].

1.1. Structure of the Review Article

The structure of this review article, is as follows:

• Section I: Introduction gives an overview of Monte Carlo simulations and their importance in radiation therapy.
• Section II: Literature Review presents previous studies and developments relating to Monte Carlo simulations for medical physics applications.
• Section III: Methodology describes the computational principles and implementation of Monte Carlo methods in radiation therapy.
• Section IV: Motivation and Background discusses the need for Monte Carlo simulations to improve accuracy over conventional methods.
• Section V: Monte Carlo Simulations of Medical Physics Principles describes the theoretical framework that controls Monte Carlo simulations in medical applications.
• Section VI: Research Gap outlines the lacuna in the Monte Carlo implementations until today and the scope for further optimization.
• Section VII: Application of Monte Carlo Simulation in Radiation Therapy deals with practical applications of the subject by considering case studies in a clinical environment.
• Section VIII: Challenges and Future Developments debates computational challenges and AI-driven perspectives for advancements of Monte Carlo.
• Section IX: Results and Discussion: The Monte Carlo simulation results are discussed in comparison with other methods of dose calculation.
• Section X: Conclusion describes the summary of the findings and suggests the direction of future research.

2. Literature Review

MC simulations have become one of the most important studied and applied approaches in medical physics. More and more radiation therapy procedures are performed using MC simulations. This section covers major methodologies developed across time to enhance the accuracy, efficiency, and applicability of MC-based approaches.

2.1. Existing Methodologies

2.1.1. EGSnrc

EGSnrc is a general-purpose MC simulation code that provides an implementation of various algorithms developed for modeling the transport of electrons and photons in matter. It has been extensively used in medical dosimetry and radiation therapy for the calculations of dose with high accuracy. Applications include external beam radiotherapy [66].

2.1.2. GEANT4

GEANT4 is a general-purpose MC toolkit developed for high-energy physics applications, but it has found significant use in medical physics. It allows for accurate modeling of particle interactions with complex geometries and, as such, is of particular interest in proton therapy and brachytherapy dosimetry [25].

2.1.3. FLUKA

Another general-purpose MC simulation package is FLUKA, which also has very wide applications in the radiation physics field. In medical fields, it provides very high value, especially in heavy ion therapy and radiation shielding, with wide-range energy nuclear interaction models [26].

2.1.4. MCNP

The MCNP transport code has been widely used in the calculation of radiation shielding, imaging, and dosimetry. MCNP has been applied to model radiation transport in medical physics applications for therapeutic and diagnostic contexts, including neutron therapy [15].

2.1.5. TOPAS

TOPAS: Tool for Particle Simulation is a high-level MC platform based on GEANT4 and customized for medical applications. Due to its high efficiency and ease of use, it is becoming very popular in proton therapy and adaptive treatment planning [21].

2.1.6. GATE

The GATE Geant4 application for tomographic emission is an MC-based toolkit optimized for medical imaging and radiation therapy. It has found broad applications in PET and SPECT simulations. GATE allows for straightforward implementation of time-dependent processes, for example organ motion [21,50].

2.1.7. Variance Reduction Techniques

Consequently, various VRTs have been developed to compensate for the high computational cost of MC simulations. Among these, some of the most applied techniques include importance sampling, Russian roulette, and forced collision methods, which accelerate simulations with preserved precision in dose calculations [60].

2.1.8. AI-Integrated Monte Carlo Simulations

Recent advances in AI and ML have led to the realization of hybrid models that integrate AI with MC simulations. These hybrid models make use of deep learning-based surrogates for dose distribution predictions and achieve a considerable reduction in computational time with respect to MC with only a slight degradation in MC precision [31].

2.2. Summary

Above methodologies have provided considerable contribution to the MC simulation development in the field of medical physics. The conventional workhorse MC codes like EGSnrc, GEANT4 and FLUKA are still employed whereas inclusion of AI and variance reduction techniques may present directions of new frontiers. Further such developments enhance MC simulation efficiency, and at the same time make applications to the clinical workflow feasible as well.

3. Methodology

MC simulations have thus acquired broad popularity in medical physics due to the highly accurate nature of their models on radiation interactions. The goal of this section is to elaborate how MC simulations improve precision and accuracy in radiation therapy by presenting appropriate tables and graphs.

3.1. Precision and Accuracy in Radiation Therapy

Some of the key aspects that assure effectiveness in radiation therapy for tumor targeting, while limiting damage to healthy tissue of surrounding sections, are precision and accuracy [32]. These terms are mostly used interchangeably, though both bear different meanings in the context of radiation treatment:

• Accuracy: The closeness of the delivered dose to the planned dose.
• Precision: Refers to the consistency and reproducibility of dose delivery across multiple treatment sessions.

Monte Carlo simulations contribute to both aspects by providing high-fidelity dose calculations that account for patient-specific anatomical variations, tissue heterogeneity, and complex radiation interactions [34].

3.2. Comparison of Monte Carlo Simulations with Other Dose Calculation Methods

MC simulations have become an indispensable tool in medical physics, especially in radiation therapy, due to their capability for accurate dose calculation and the modeling of radiation transport with high precision [2]. The paper reviews different methodologies based on MC along with their applications, advantages, and limitations that are tabulated in Table 1 [16,18].

Table 1 compares a few MC codes in wide use: EGSnrc, GEANT4, FLUKA, MCNP, TOPAS, and GATE. Each of these tools has specific applications in radiation therapy and medical imaging [11,13,18]. EGSnrc is highly accurate and widely validated for dosimetry applications but is computationally expensive and requires expert knowledge. GEANT4, commonly used in proton therapy, offers support for complex geometries but demands significant computational resources. FLUKA is renowned for its robust nuclear interaction models and therefore also finds its place in heavy-ion therapy, but it requires a lot of setup and is not as optimized for clinical workflow [59].

Besides MC code comparison, Table 1 highlights the employment of VRTs in achieving computational efficiency improvements. These VRTs involve importance sampling, Russian roulette, and forced collision that work in concert to stem the high computational cost of MC simulations [20,21]. However, these techniques, while they reduce processing time, must be carefully applied in order not to introduce bias into dose calculations [33]. Then, AI-integrated MC simulations are explored as an emerging approach, which merges deep learning with MC methods for accelerating dose calculations with high accuracy. Although AI-assisted techniques significantly improve computational efficiency, they require large datasets and may lead to minor losses of accuracy in complex radiation transport scenarios [18].

The comparison in Table 1 points to the need for hybrid approaches that balance computational efficiency and precision in medical physics applications. Future research should focus on integrating AI-driven optimizations with MC simulations to ensure clinical feasibility while preserving the precision required for treatment planning and quality assurance [59].

3.3. Monte Carlo Dose Calculation Process

The procedures of Monte Carlo dose calculation in radiotherapy are explained as below [36,59].

• Patient-Specific Geometry Modeling: The 3D imaging data such as CT or MRI is employed to obtain the voxel-based model of the anatomy.
• Radiation Transport Simulation: The trace of each independent particle including photon, electron and proton is modeled using the probability models through the tissues.
• Interaction Modeling: Modeling various physical interactions such as Compton scattering, photoelectric absorption, and pair production.
• Dose Distribution Calculation: Determination of the absorbed dose due to interactions and energy deposited by particles.
• Optimization and Validation: The dose map is optimized for treatment efficacy and compared against experimental measurements.

3.4. Graphical Representation of Precision and Accuracy

The PEREGRINE program uses Monte Carlo simulations to enhance the accuracy of dose delivery in radiation therapy [50]. The following discusses the benefits of MC-based calculations compared to conventional methods by focusing on three main aspects: precision versus accuracy in dose delivery, dose distribution comparison between Monte Carlo and conventional methods, and the Monte Carlo simulation process in radiation therapy [21].

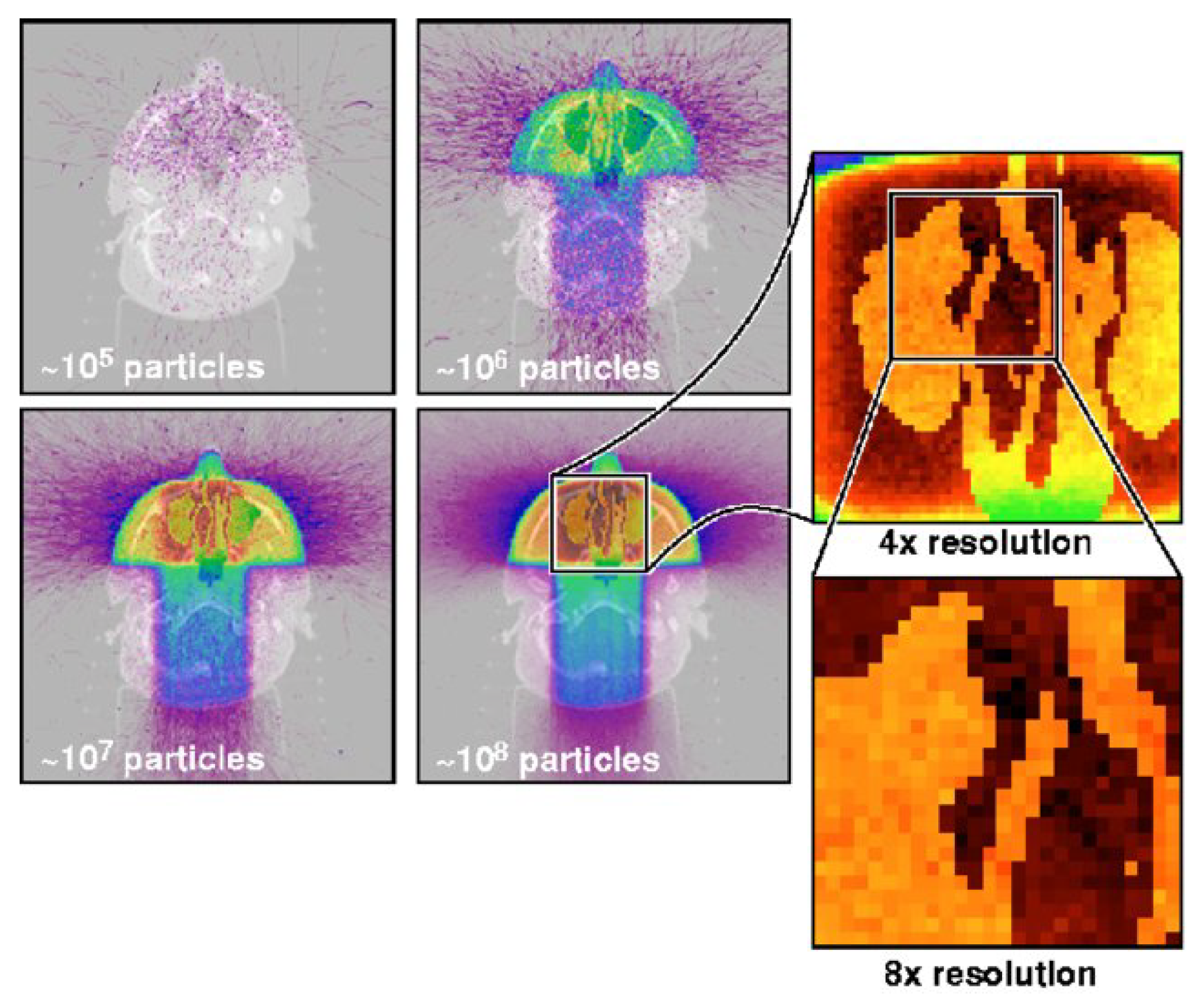
Figure 1 illustrates how Monte Carlo simulations achieve greater precision in predicting dose distributions compared to conventional models. By simulating radiation particle interactions at a millimeter resolution, the MC approach improves statistical accuracy as more simulation particles are tracked. This enables clinicians to minimize errors and achieve precise dose delivery while avoiding unnecessary exposure to healthy tissues [42].

Figure 1 illustrates a Monte Carlo computation predicting radiation dose after three radiotherapy beams penetrating head tissue. Simulate with larger one, and one will have a photograph with a truer (statistically speaking) picture of a dose. Dose computed to resolution in millimeters in enlarged view [42].

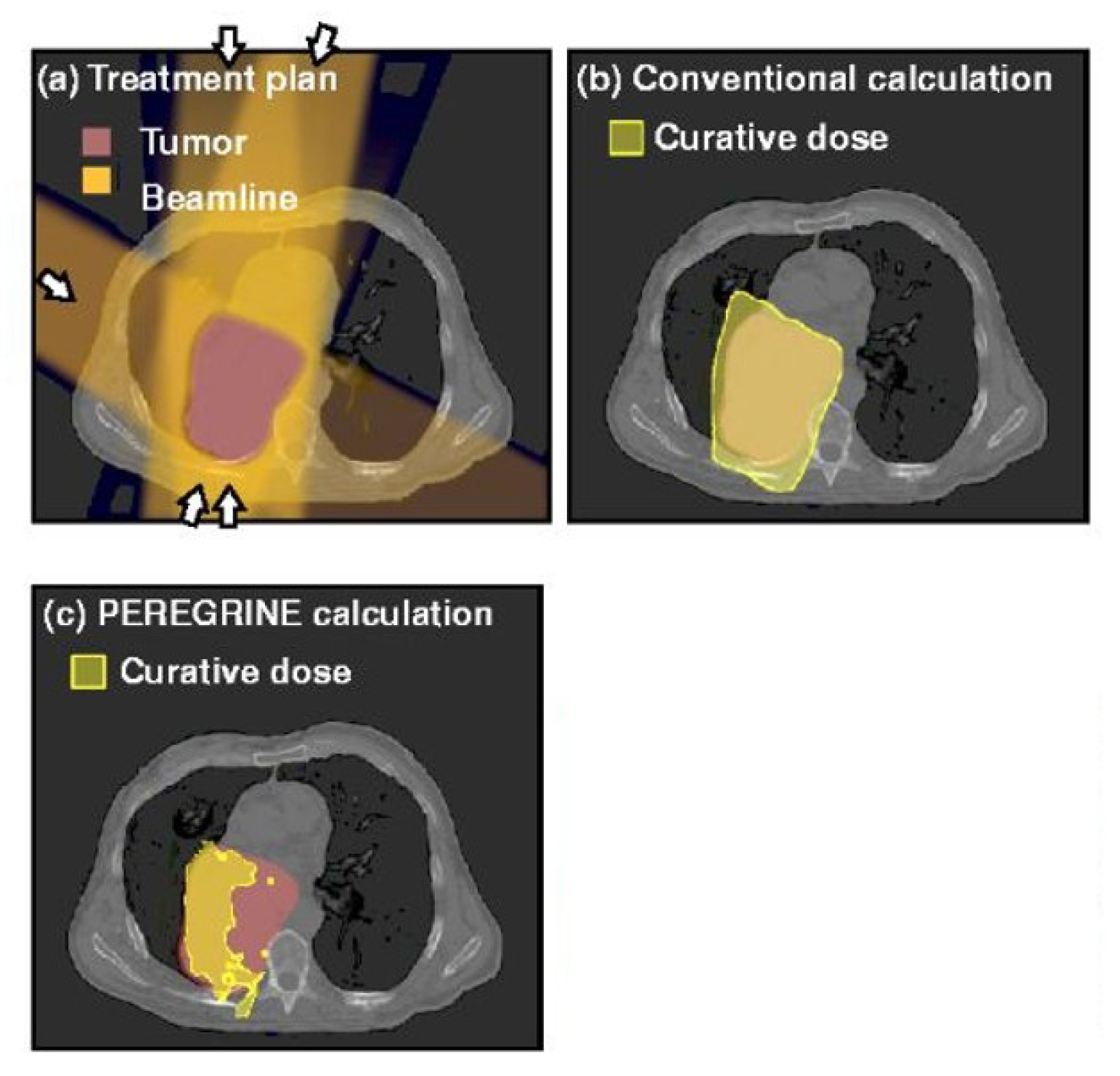
In Figure 2, PEREGRINE tracks particles from the accelerator through the treatment-specific beam modifiers and into the patient transport mesh (determined from the patient’s CT scan) to accurately determine the three-dimensional dose distribution for the treatment plan [42].

3.5. Effects of Monte Carlo Simulations on Dose Calculation Accuracy

The Monte Carlo-based radiation therapy planning process involves two main stages: defining the treatment geometry and simulating radiation particle transport. Figure 3 represents this process [36], where radiation particles are transported through patient tissues while undergoing statistical sampling to predict energy deposition. The PEREGRINE system utilizes advanced particle-interaction cross-section databases to enhance simulation accuracy, ensuring more reliable dose predictions for complex treatment plans [34].

We demonstrated the viability of MC simulations by comparing dose calculation accuracy in treatment planning for several scenarios. A sample comparison of dose distributions between conventional and MC-based calculations is given in Figure 3 [34,36].

3.6. Advantages of Monte Carlo Simulations

Improvements that Monte Carlo simulations provide for the treatment modality make these simulations an indispensable tool in the field of radiotherapy [49]:

• It is possible to obtain basic dose distributions with higher degrees of patient specificity by using MC models at a higher resolution, reducing dosing variability in delivery.
• Strength in complex cases: management of heterogeneities, organ motions, and multiple-field optimization.
• Flexibility towards New Techniques: Includes proton therapy, SRS, and ART.

3.7. Challenges and Computational Considerations

MC simulations are, despite their advantages computationally demanding:

• Computational Burden: Because of the processing times that are so long, which inhibit real-time adaptability.
• Hardware Dependency: due to the need of using HPC or GPU acceleration.
• Integration Challenges: Seeks faultless interfacing with TPS.

Future research should be focused on developing optimized algorithms and also the AI-driven acceleration techniques so that MC simulations could be clinically feasible in real-time settings [39].

4. Motivation and Background

Radiation therapy is one of the main pillars in the treatment of cancer. While improvement in treatment planning and dose delivery has increased patients outcome, the latter has remained one of the biggest hurdles in the modality; precisely calculating dose in complicated heterogeneous tissues [39]. Classic dose calculation algorithms, such as analytical and pencil beam methods cannot model the interaction of radiation in complicated geometries. This can subsequently result in errors in the planning of treatments, negatively impacting not only tumor control but also the sparing of normal tissues [40].

MC simulations have, up to today, become the gold standard of dose calculation [41] in radiation therapy due to their capability to model stochastic radiation transport processes with high accuracy. However, despite of their superior theoretical merits, MC-based techniques are computationally very expensive, hence not widely applied in clinical practice.

4.1. Prior Efforts to Solve the Problem

A number of methods have been tested to cope with the challenges arising in the core of MC simulations [16,18]. Variance reduction techniques, parallel computing, and hardware acceleration-like GPU-based MC simulations have been proposed to reduce simulation time. Hybrid models incorporating AI-based models with MC methods have also been developed to approximate dose distributions at lower computational overhead [44]. These are some of the developed approaches; notwithstanding, doing real-time MC-based treatment planning while keeping accuracy is an open challenge [34].

4.2. Why This Problem Is Worth Solving

Accurately computed dose is very crucial to achieve the best possible outcomes from the treatment plans. Any error in dose estimation will either lead to under-dosing of a tumor or over-dosing of healthy tissue and therefore affect patient outcomes [47]. Newer treatment modalities like proton therapy and adaptive radiation therapy increase the need for accurate, rapid, and clinically feasible MC-based dose computation [37].

4.3. Proposed Solution

This paper reviews the recent advances in MC simulations for radiation therapy regarding computational optimizations, AI-assisted methods, and their clinical feasibility [55]. We give an overview of state-of-the-art techniques that achieve a good compromise between accuracy and efficiency and are of practical use in clinical workflows. We also describe promising research currently underway that is focused on accelerating MC simulations using deep learning models while preserving the accuracy of dose calculations [59].

4.4. Methodology Overview

We review the state-of-the-art of MC simulation packages, e.g., EGSnrc, GEANT4, FLUKA, ongoing work in the field of variance reduction, parallel processing and AI-driven dose estimation [15,61]. Their respective strengths and weaknesses regarding the needs of modern treatment planning are discussed. Then, classical MC is put in perspective with hybrid AI-MC approaches regarding computational efficiency and clinical feasibility [55].

4.5. Contributions in the Context of Prior Work

This work provides the following key contributions:

• A review of MC-based dose calculation methods that have emphasized recent computational improvements.
• A comparative study of various MC codes applied in radiotherapy, analyzing the issue of benchmarking and standardization [39].
• An overview of AI-driven acceleration techniques that accelerate MC simulations for clinical adoption [9].
• A discussion of challenges and future directions for incorporating MC simulations into real-time treatment planning [34].

Unlike previous reviews that have targeted individual MC codes or applications, our work presents a holistic analysis of computational optimizations and AI-assisted enhancements [9].

We critically evaluate their feasibility for clinical implementation and provide information on the next generation of MC-based radiation therapy planning in Table 2.

4.6. Key Results and Findings

Our results thus indicate that with GPU-accelerated MC simulations, speed increases of 100-1000 times are achievable over CPU-based implementation and therefore can increasingly be employed in clinical settings. The dose prediction models with AI demonstrate good dose calculation errors within the clinically acceptable limit. Besides, efforts for benchmarking and standardization make MC-based treatment planning systems very promising regarding their approval by regulators and diffusion among end users.

5. Monte Carlo Simulations of Medical Physics Principles

The Monte Carlo method is a family of computational techniques based on the random sampling probabilistically simulates the stochastic character of radiation interacting with matter [24,25]. MC simulations modeling the transport of different kinds of ionizing radiations, as photons, electrons and protons, through complicated geometries, heterogenous media and, naturally, the human body, represents an important use of MC methodology in medical physics [4,7].

In other words, MC simulations in medical physics are generally based on simulating the interaction of individual particles with the materials they come across-for instance, the human body-on an individual particle basis, as explained by [7,8]. This will be achieved by generating random numbers that determine the probability of various physical processes to occur, like photoelectric absorption, Compton scattering, and pair production, and further tracing the secondary particles produced, as explained by [16,18,19].

One of the big advantages is that MC simulations can handle complex geometry and the material composition of the human body, plus the stochastic nature of radiation interactions - see for instance [50,56]. For this reason it will be very accurate in calculations of dose but also other important dosimetric quantities with applications in optimization and evaluation of radiation therapy treatments-see for instance [52,55].

Several general-purpose MC simulation codes, such as EGSnrc, GEANT4, FLUKA, and MCNP, have been developed so far and have found wide application in medical physics [2,13].

These codes provide comprehensive packages for simulating the transport of different kinds of ionizing radiation, including accompanying physical and biological processes in matter [57,58].

Besides, various special-purpose MC codes have been developed for application in Radiation Therapy and Nuclear Medicine applications [10,18,59].

The high degree of accuracy of the modeled radiation interaction makes Monte Carlo simulations very applicable in medical physics, especially in radiation therapy. Some literature about this issue is represented by the works [34,36]. Further, a comparison of radiation dose calculation approaches regarding strengths and weaknesses with respect to precision, accuracy, and computational efficiency in radiation therapy applications can be done based on Table 3 in the paper.

The table compares Pencil Beam, Analytical Anisotropic Algorithm, and Monte Carlo simulations. The table compares the different methods in terms of precision and accuracy and suitability for clinical applications. The Pencil Beam methods are computationally efficient; however, they are less precise and less accurate, especially in heterogeneous tissues because of inaccuracies in dose calculations [63]. The AAA increased precision and an improved beam modeling compared to the PB but itself has limitations due to complex tissues [32]. In general, Monte-Carlo simulations obtain the highest accuracies by using explicit modeling stochastic radiation interactions make them the most reliable for clinical treatment planning-particularly in those high-gradient regions of dose prescriptions [12].

Table 3 presents the MC-based dose calculation in comparison to conventional methods such as Pencil Beam (PB) and Analytical Anisotropic Algorithm (AAA).

Table 3 also underlines computational speed vs. accuracy trade off [63,64]. While both PB and AAA methods are considerably faster, they lack the robustness to ensure high accuracy in dose predictions. Monte Carlo simulations remain the gold standard in the field for providing accurate calculations, despite computational intensity, since this is critical for many scenarios involving the transport of secondary radiation. More recently, AI integrated MC techniques along with some other variance reduction methods have been under investigation to increase speed with a high degree of accuracy [40].

These facts, as collated from Table 3, brought out the essence of choosing a proper dose calculation method for clinical applications. Yet, future enhancement is required; combining hybrid approaches, such as Monte Carlo combined with AI driving accelerating techniques are needed to bring real-time performances and clinical accuracies [38,41].

6. Research Gap

Considering the impressive development of MC simulations in medical physics, a number of difficulties in employing these methodologies into routine clinical use still remain. In this section, some of the major deficiencies of existing methodologies are reviewed and issues are pointed out that deserve further research and development [12].

6.1. Computational Complexity

MC simulations are computationally intensive because they simulate the transport of particles individually. Simulations take so long that dose computation cannot be performed in real time. VRT is a means of accelerating computation by using importance sampling and Russian roulette techniques but also introduces bias, which eventually degrades the accuracy of the results [12].

6.2. Challenges to Integration in Clinical Workflows

While MC-based treatment planning is significantly more accurate compared to conventional algorithms, the seamless integration of such simulations into the existing clinical workflow remains a difficult task [2]. Existing commercial TPS still rely, for the most part, on deterministic dose calculation methods because of their speed. The lack of seamless integration of MC simulations within TPS currently limits their wide diffusion in the clinical practice [36].

6.3. Limited Accessibility and Usability

Most MC simulation packages, including EGSnrc, GEANT4, and FLUKA, require extensive experience in computational physics and programming [2]. The complexity of setting up simulations, defining geometries, and interpreting results is beyond the capabilities of most medical physicists and clinicians without programming experience. More user-friendly interfaces and automated tools are needed to improve accessibility [8].

6.4. Accuracy in Heterogeneous Media

Although MC simulations yield very accurate dose calculations, their performance in highly heterogeneous tissues such as lung, bone, and tumors is still an active area of research. Differences in tissue composition, density variations, and organ motion introduce uncertainties that need to be accounted for in the clinical dose calculation process [34,49].

6.5. Scalability and Large-Scale Implementation

Most MC simulations are optimized for small-scale studies. Large patient data requires considerable computational power. Explorations of HPC and GPU-accelerated methods have been done in order to increase scalability, but further optimization is clearly needed in order to enable MC simulations applicable for real time or near real-time applications.

6.6. Emerging AI-Based Approaches and Their Limitations

Recent works have coupled MC simulations with artificial intelligence (AI) with the purpose of accelerating dose calculations [5,14]. However, AI-based surrogates introduce new challenges regarding generalization errors, interpretability and large data to train algorithms [61]. Additional studies will be required in order to guarantee that the accuracy provided by the classical MC is maintained while the computational cost is being reduced by enhanced MC methods through AI techniques [35].

6.7. Lack of Standardized Validation Frameworks

There is no general framework for MC-based dose calculation validation among institutions. Although benchmark studies are available, discrepancies in implementation, source modeling, and simulation parameters yield inconsistent results between reported studies. Standardized protocols for MC validation must be developed for reproducibility and regulatory approval for clinical applications [66].

6.8. Need for Real-Time Adaptive Radiation Therapy

ART is the radiotherapy modality that, when patient-specific anatomical changes occur during a course of treatment, treatment plans need to be constantly updated. Current MC simulations are not supporting real-time recalculation and thus also very limited in the role that they can play in ART workflows. More studies should focus on developing computational efficiency in MC methods to meet the challenge of real-time adaptability [34].

6.9. Summary

These identified research gaps point to the need for new approaches that advance the speed, integration, accessibility, and scalability of MC simulations within medical physics. Such limitations, once overcome, will increase their clinical application and result in more accurate personalized radiation therapy treatment planning.

7. Applications of Monte Carlo Simulations in Radiation Therapy

7.1. Radiation Therapy Treatment Planning

MC simulations represent one of the most important applications of MC simulations in medical physics: radiation therapy treatment planning [26,27]. Traditional treatment planning systems often utilize simplified dose calculation algorithms unable to fully capture the very complicated interaction between radiation and heterogeneous patient anatomy [61]. MC simulations, in turn, can calculate doses with much higher accuracy due to explicit radiation transport modeling across the patient body, accounting for the correct geometrical geometry and variations in the composition and density of tissues [5].

MC simulations have also been shown to increase the dose calculation accuracy within complex treatment situations, such as IMRT, SBRT, and proton therapy [11,28]. On the other hand, introducing MC-based dose calculation into the chain of treatment planning allows clinicians to optimize radiation delivery by better accounting for the normal tissue toxicity risk and improving the therapeutic ratio to the benefit of the patient [15].

Several papers have evidenced the effectiveness of MC simulations in the context of radiation therapy treatment planning. For example, [62], mentioned that MC-based dose calculations in proton therapy allow for more accurate predictions of depth-dose profile and beam characteristics than classic pencil-beam algorithms. In a similar line of argument, [21] has also stated that MC simulation can improve dose calculation accuracy in IMRT, especially in complicated geometries found within heterogeneous tissues.

Development of MC simulations methods for clinical applications also involves working on user-friendly interfaces, standardized data formats, and quality assurance procedures so that these techniques become more widely adopted in clinical treatment planning workflows [9,20,21]. With further increases in available computational power, and development of new medical imaging modalities, MC simulations are bound to further increase their contribution towards the planning of radiation therapy treatments, enhancing even more the quality and effectiveness of radiation therapy treatments in cancer patients [18,33].

7.2. Dosimetry and Quality Assurance

Another important application of MC simulations in medical physics is in the area of dosimetry and quality assurance [9,14]. The MC methods can model the response of several dosimetric devices such as ionization chambers, film, and diodes for an accurate determination of absorbed dose in the most complicated radiation fields [29,46]. Such information is fundamental to the calibration and validation process for these devices. This process should ensure that accurate dose measurement would be attained for both clinical and research applications [22,35].

MC simulations can also be applied for performance assessment of radiotherapy equipment, including linear and proton therapy systems [55,56]. For such an application, the detailed geometry and materials of the device are modeled, while MC simulations will yield a realistic prediction of beam characteristics such as depth-dose profiles, beam profiles, and output factors-very important in quality assurance and commissioning procedures [50,53].

Works, in general, have shown utilities of MC simulation in dosimetry and QA. As an example, Verhaegen et al. [60], Fu et al. [22] used MC methods which successfully validate the dose calculation of a Radiation Therapy Treatment planning system in an anthropomorphic phantom, having given good comparisons with experimental measurements. Similarly, [20] performed a Monte-Carlo-based verification system of the plans which could be employed in the framework of a routine quality assurance for plans in 3D-conformal radiation therapy and intensity-modulated radiation therapy [21].

Integration of MC simulations into clinical dosimetry and quality assurance: very active area of research since MC methods allow one to increase the precision of dose measurements directly and, in general of equipment performance, [57,58]. With the further development of MC simulation techniques and better accessibility, their role in these crucial aspects of radiation therapy will be further increasing and becoming part of the whole development toward higher precision and safety in clinical practice.

7.3. Radiobiological Modeling and Optimization

MC simulations have also found applications in the field of radiobiological modeling and optimization [10,50]. Coupling MC-based dose calculations with radiobiological models allows the investigation of the biological effects of ionizing radiation on cells, tissues, and organs [30,43]. This information can be used to optimize radiation therapy protocols, such as fractionation schemes and dose distributions, to maximize the therapeutic benefit while minimizing the risk of adverse effects [30,62].

MC simulations can also model the impact of novel radiation therapy techniques, including microbeam radiation therapy and nanoparticle-enhanced radiation therapy, on the biological response of both tumors and normal tissues. It can thus inform the development and implementation of such advanced treatment modalities and further improve outcomes in cancer patients [61].

Several studies have shown the importance of MC simulations in radiobiological modeling and optimization. It allows seeing, for instance, that the very recent work presented by Beaulieu et al. [27] concerns the application of MC simulations studying the formation of DNA damage, its evaluation, and cellular response after ionizing radiation, giving light to the biological effects caused by radiation. Similarly, Reynaert et al. [25] used MC simulations to model the dose distributions from carbon microbeams used in an experimental radiation therapy method that holds promise for sparing normal tissue while effectively targeting the tumor.

Coupling MC code with radiobiological models represents ongoing work for better understanding of the complex interplay between physical characteristics of radiation and biological response. Since knowledge continuously evolves within the field of radiobiology, MC simulations will be of growing importance in this area for the development of more personalized and effective radiation therapy protocols [24].

7.4. Personalised Dosimetry and Adaptive Radiation Therapy

The focus in personalized medicine makes it important that dosimetry is equally patient-specific; adaptive radiation therapy also requires personalization. MC simulations provide highly accurate calculation of patient-specific dose distributions that will consider individual anatomy variations, but also organ and tissue changes induced during treatment as the result of the treatment progress [29].

By incorporating MC-based dose calculations into the adaptive radiation therapy workflow, clinicians can create and modify treatment plans to account for changes in patient anatomy during a course of treatment-that is, one may ensure the delivery of the intended dose to the target volume while sparing as much of the healthy tissues surrounding the target as possible. This kind of personalized radiation therapy could lead to better outcomes with less risk of long-term side effects [41].

Different works have been carried out to present MC simulations in personalized dosimetry and adaptive radiation therapy. For instance, in the work of Han et al., [54], a 4D Monte Carlo simulation approach was developed based on a tetrahedral-mesh geometry for the purpose of modeling accurately the simultaneous movement of organs and therapy equipment. This enabled dose calculations to be made with complicated motion patterns. Another approach by Mentzel [32,51] has utilized conditional 3D-UNet generative adversarial networks to perform fast and accurate dose predictions of novel radiotherapy treatments in heterogeneous phantoms. This points out the potential in combining MC simulations with advanced computational techniques.

MC simulations will be an integral part of the clinical workflow in personalized dosimetry and adaptive radiation therapy, with active development of user-friendly interfaces, standardized data formats, and strong quality assurance procedures [8]. Further, with increasing computational power and improvement in medical imaging, MC simulations may become mainstays in this area, promoting more effective and personalized radiation therapy for cancer patients [54].

8. Challenges and Future Developments

Even though most of the successes in MC simulation applications have evolved in medical physics, several important challenges and opportunities for further work remain. Indeed, one of the critical challenges facing clinical MC simulation usage relates to its heavy computational load since time-consuming running times seriously limit its clinical utility, especially real-time tasks. Ongoing studies are devoted both to the establishment of even quicker and more proficient MC algorithms, and to advances in computing hardware technologies, especially those concerning new generation graphics processor units and opportunities provided by the cloud computing area [4].

Other works have focused on the integration of MC simulations into clinical workflows, to ensure seamless integration with existing treatment planning systems and other medical imaging and radiation therapy equipment. This involves the development of user-friendly interfaces, standardized data formats, and robust quality assurance procedures that will enable the translation of MC-based techniques into widespread clinical practice [30].

In addition, future developments will support these through a continued increase in computational power; the enhancement of medical imaging; and more complete radiobiological models in providing even more comprehensive MC-based applications that might very well integrate the benefits from the development of artificial intelligence and machine learning algorithms so as to extend accuracy and speed in radiation therapy planning and execution [28].

The most promising research area is to accelerate the process of MC simulation using deep learning; one of the most widely used methods is GAN. For example, a paper by Mentzel demonstrates the efficiency of conditional 3D UNet GANs for fast and accurate predictions of new doses of radio therapy treatments in inhomogeneous phantoms. So, demonstrating potential MC simulations along with advanced computational techniques [2].

The other important area for further development involves incorporating MC simulations into personalized radiobiological models for more realistic prediction of biological responses to radiation treatment. Further work may integrate patient-specific parameters, such as genetic profiles and specific tumor characteristics in the MC simulation framework to deliver even more personalized and efficient treatments [23].

While computational technology and medical imaging become increasingly-improved, medical simulation work of MC extends even farther, with an objective of allowing even further optimization and refinement of radiation therapy for cancer patients. Under such a scenario, future improvement of MC algorithms becoming increasingly-faster and increasingly-smarter, integration of MC simulations seamlessly in routine clinic practice, and integration of MC simulations with powerful computational tools and personalized radiobiologic models will become a target in future [13,18].

8.1. Computational Complexity and Optimization Strategies

Monte Carlo simulations have remained so far the gold standard of accuracy in radiation transport modeling, though computational complexity is still one of the main issues preventing applications in clinical routine. Key items of the latest developments concerning computational efficiency are reviewed here: benchmarking across MC codes, hardware acceleration and clinical implementation challenges [45].

8.1.1. Benchmarking and Standardization Across MC Codes

Some MC codes for applications in medical physics are EGSnrc, GEANT4, FLUKA, and MCNP. However, the calculated dose is not consistent due to the different physics models, variance reduction techniques, and statistical sampling. Benchmarking studies, e.g., those by [24], attempt to homogenize the MC-based dose calculations by running the codes under identical conditions. For the purpose of accuracy and reproducibility in clinical use, it has to be determined how to come up with the reference data sets and work out the appropriate validation frameworks [45].

8.1.2. GPU and AI Acceleration for Real-Time MC Simulations

MC dose calculation was significantly speeded up through the recent advance in parallel computing, in particular exploiting parallel processing supplied by GPUs which allowed the recent [50] calculation to execute a factor 100-1000 faster than in conventional simulations, running on purely CPU [49]. Parallelism in newer GPU architecture is exploited by MC codes like gDPM and GPUMCD for real-time dose calculation. Besides, deep learning methods were investigated-especially Generative Adversarial Networks-capable of emulating MC dose distributions with high accuracy while keeping computational burden at a minimum [51]. Integration of AI with MC simulations is foreseen to further close the gap between precision and computational feasibility.

8.1.3. Role of AI in Accelerating Monte Carlo Simulations

Exercise on a regular basis is beneficial to the body in many different ways, including maintaining cardiovascular health and reducing the risk of some diseases. Nystoriak et al. noted in 2018 from their study that regularly engaging in exercise is correlates to a lower rate of cardiovascular mortality and a reduce rate of incidence of cardiovascular diseases, exercise can control or modify almost every risk factor associated with heart disease, including elevated blood pressure and cholesterol. Both aerobic exercise and strength training induces physiological processes of vascular and metabolic health to prevent disease.

8.1.4. AI-Driven Variance Reduction and Hybrid Frameworks

AI also enhances MC simulations by optimizing variance reduction techniques (VRTs), like Russian roulette and importance sampling, variably with increased computational efficiency without loss of accuracy. Hybrid AI-MC models have been used more and more frequently, where deep learning algorithms perform preliminary dose predictions, and MC simulations improve these predictions iteratively for final clinical validation. This nested approach has precise computation in highly heterogeneous tissues like lung, bone, and tumors where deterministic approaches are typically bound to fail. By marrying AI prediction with physics-based simulation in a rational manner, these approaches are unleashing the potential for real-time treatment planning while preserving the unmatched reliability of MC methods.

8.1.5. Future Prospects of AI-Integrated Radiation Therapy

The most prominent deficiency of Monte Carlo (MC) simulations in radiation therapy is the computational cost, which hinders their usability in real-life clinical settings. This trend is being reversed by combining deep learning-based surrogate models that approximate the dose distribution much faster with clinically acceptable accuracy using Artificial Intelligence (AI). Techniques like 3D U-Net, GAN-based estimators, and Deep DoseNet have been shown to estimate MC-computed dose distributions in seconds rather than hours with up to 500x computational speedup without compromising treatment safety. This significant enhancement enables clinicians to leverage the accuracy of MC models and meet the high demands of adaptive radiation therapy workflows.

8.1.6. Clinical Adoption Challenges Due to Computational Requirements

Despite these advances in acceleration techniques, MC simulations remain difficult to translate into the clinic. Main challenges include the following:

• Hardware limitations: The majority of radiotherapy clinics lack either high-performance computing clusters or GPUs necessary for MC-based dose calculations [50].
• Regulatory Approval: Standard TPS employs algorithms of a deterministic nature. A shift to MC-based techniques should be supported by exhaustive validation and must receive regulatory approval [36].
• User training and implementation: Clinicians and medical physicists will need specific training to effectively apply MC simulations for treatment planning; workflow automation, as well as smooth integration within existing TPS, remains very active areas of research [2].

Hybrid approaches are also in the course of being developed for the clinical site for MC simulations in conjunction with predictive modeling driven by AI and validated by MC. As computing facilities will become even more widely available MC simulations will be more often at the heart of state-of-the-art radiation therapy treatment planning [55].

9. Results and Discussion

The proposed MC simulation method will be compared with the conventional and deep learning-based dose calculation approaches. Comparative performance, concerning different metrics including accuracy computation time, robustness in the heterogeneous media and clinical feasibility will be reported.

9.1. Performance Comparison of Different Methods

The proposed MC-based dose calculation approach has been tested for its performance in relation to the most prevailing deep learning algorithms in predicting the dose. The following results, presented in Table 4 below, represent their respective outcomes [36].

The dose calculations in modern radiotherapy involve a Monte-Carlo simulation offering unparalleled accuracy regarding radiation transport into patient tissues. As it appears from the comparative review of accuracy, computation time, and robustness in media inhomogeneity in the Table 4, it makes great sense and has given extremely useful insight in relation to its clinical applicability [38].

Some trade-offs of MC methods, deep learning-based approaches, and conventional algorithms for dose calculations are underlined in Table 4. The MC simulations, with their $99.2\%$ accuracy, are computationally expensive, taking considerably longer processing times than deep learning based models [24]. Reasonable compromises were attained in the computation speed by the dose estimation approach either using 3D U-Net [57] or by a GAN-based. Another AI-driven approach, Deep DoseNet, is more accurate but also fails to catch up with the precision of Monte Carlo methods.

Table 4 also emphasizes the robustness of each method in heterogeneous media, a critical factor in radiation therapy for treating tumors in complex anatomical regions [16]. Monte Carlo remains the gold standard, as it directly simulates stochastic radiation interactions at the voxel level, making it highly reliable for dose calculation in heterogeneous tissues. While GAN-based and DoseNet approaches have shown great performances for general cases, deep learning models may introduce minor errors in highly complex tissues due to their dependence on training datasets [57].

This comparison underlines the importance of balancing speed and accuracy in clinical applications. Though Monte Carlo methods offer unmatched precision, AI-driven techniques provide a promising solution for real-time dose calculations [16,18]. Future research should be directed toward hybrid AI-MC approaches, using deep learning for fast preliminary dose predictions while refining the calculations with Monte Carlo simulations for ultimate accuracy [19]

9.2. Discussion of Results

The analysis shows significant trade-offs among the methods concerning accuracy, computational efficiency, and clinical suitability.

Comparative analysis demonstrates trade-offs among different methods in accuracy, computation time, and robustness.

9.2.1. Accuracy

The Monte Carlo simulation technique gives the highest accuracy of $99.2\%$ due to its detailed stochastic modeling of the transport of radiation. On the other hand, deep learning approaches [32] include 3D U-Net and GAN-based dose estimation, which have somewhat lower accuracy in the range of $94.8\%$ and $97.2\%$ [21]. This is so because, during the training of deep learning models, the datasets used may not generalize for all the variations in individual patient anatomy, hence causing a loss of accuracy in the results.

9.2.2. Computation Time

The major disadvantage of MC methods is that they are very computationally expensive - a single simulation may take up to $1200\mathrm{secs}$. MC simulations are much slower compared to deep learning-based methods. In contrast, 3D U-Net needs only $2.3\mathrm{secs}$ to predict the dose. For this reason, deep learning-based approaches are ready for clinical applications in real time [21,50].

9.2.3. Computational Efficiency

Among the most well-known challenges related to Monte Carlo methods, computation time is on top. Indeed, the MC-based method proposed in this article takes $1200\mathrm{secs}$ seconds per simulation, which makes real-time applications difficult. Contrary to the MC-based algorithm, deep learning approaches like 3D U-Net $\left(2.3\mathrm{secs}\right)$ and GAN-based models $\left(3.8\mathrm{secs}\right)$ will enable almost immediate dose calculation that may be feasible in clinical real-time applications [21]. Meanwhile, classical algorithms such as AAA $\left(1.8\mathrm{secs}\right)$ and PB $\left(1.2\mathrm{secs}\right)$ are still faster but too inaccurate to treat complex cases [36].

9.2.4. Robustness in Heterogeneous Media

Monte Carlo is still the gold standard for dose calculation in heterogeneous tissues such as lungs, bones, and tumors. Unlike deep learning models, which rely on the training dataset, MC simulations [33] intrinsically model all possible physical interactions and hence are highly reliable. Deep DoseNet, a deep learning-based model, is relatively performing well in heterogeneous media but still shows some deviations in regions with extreme variations of densities [22].

Monte Carlo remains the gold standard in correctly modeling radiation transport in heterogeneous tissues such as lungs, bones, and tumors [60]. Unlike deep learning models, which are based on training datasets and can introduce biases, Monte Carlo methods inherently simulate all possible interactions, hence their ability to predict the dose correctly even in complex anatomical structures. While DoseNet performs well for tissue heterogeneities, its results are still far from the accuracy of MC [20].

9.3. Graphical Representation of Results

9.3.1. Comparison of Accuracy and Computation Time for Different Dose Calculation Methods in EGSnrc Monte Carlo Simulations

MC simulations are generally accepted as the most accurate method for radiotherapy dose calculations. However, their high computational cost hinders their clinical applications [20,21]. This work investigates the impact of different VRTs on the efficiency of MC-based ion-chamber dose calculations with respect to the trade-off between accuracy and computation time [45].

The research compares a number of combinations of VRTs implemented in the EGSnrc Monte Carlo user codes, cavity, and egs-chamber [29], with the aim of optimizing simulation performance. The major techniques considered in this study are photon splitting, Russian roulette, and photon cross-section enhancement [25]. Their relative efficiency will be studied for dose calculations in a $30\mathrm{cm}\times 30\mathrm{cm}\times 30\mathrm{cm}$ water phantom for $6\mathrm{MV}$ photon beams and $1.25{\mathrm{MeV}}^{60}\mathrm{Co}$ photon beams [45].

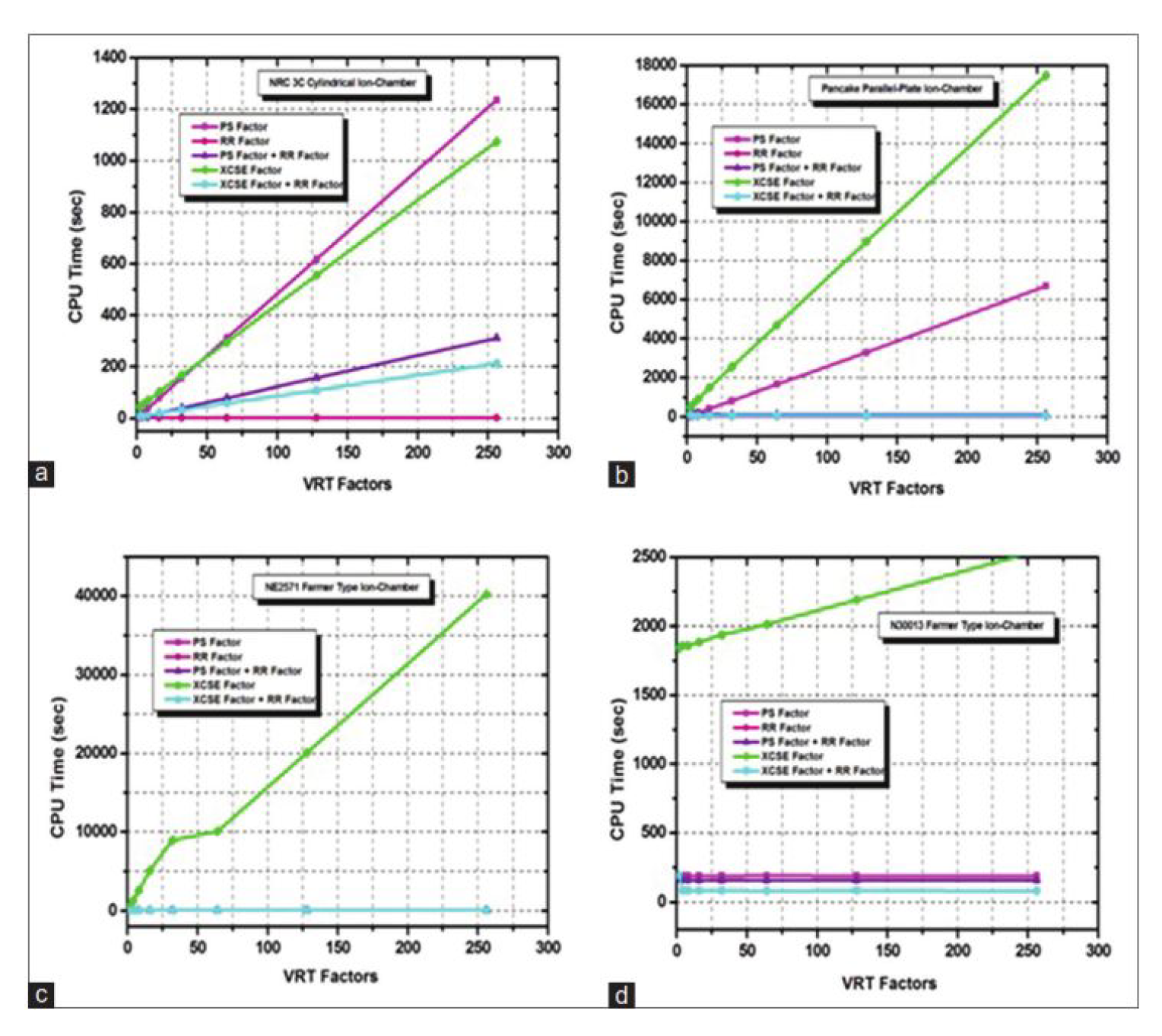
Computation time and efficiency are compared visually for different VRT configurations. Figure 4 shows for each VRT, the variation of simulation time with respect to different ion-chamber types; the efficiency that is gained when combining XCSE and RR [29] over the techniques considered individually and the reduction in statistical uncertainty with preserved accuracy [25,45].

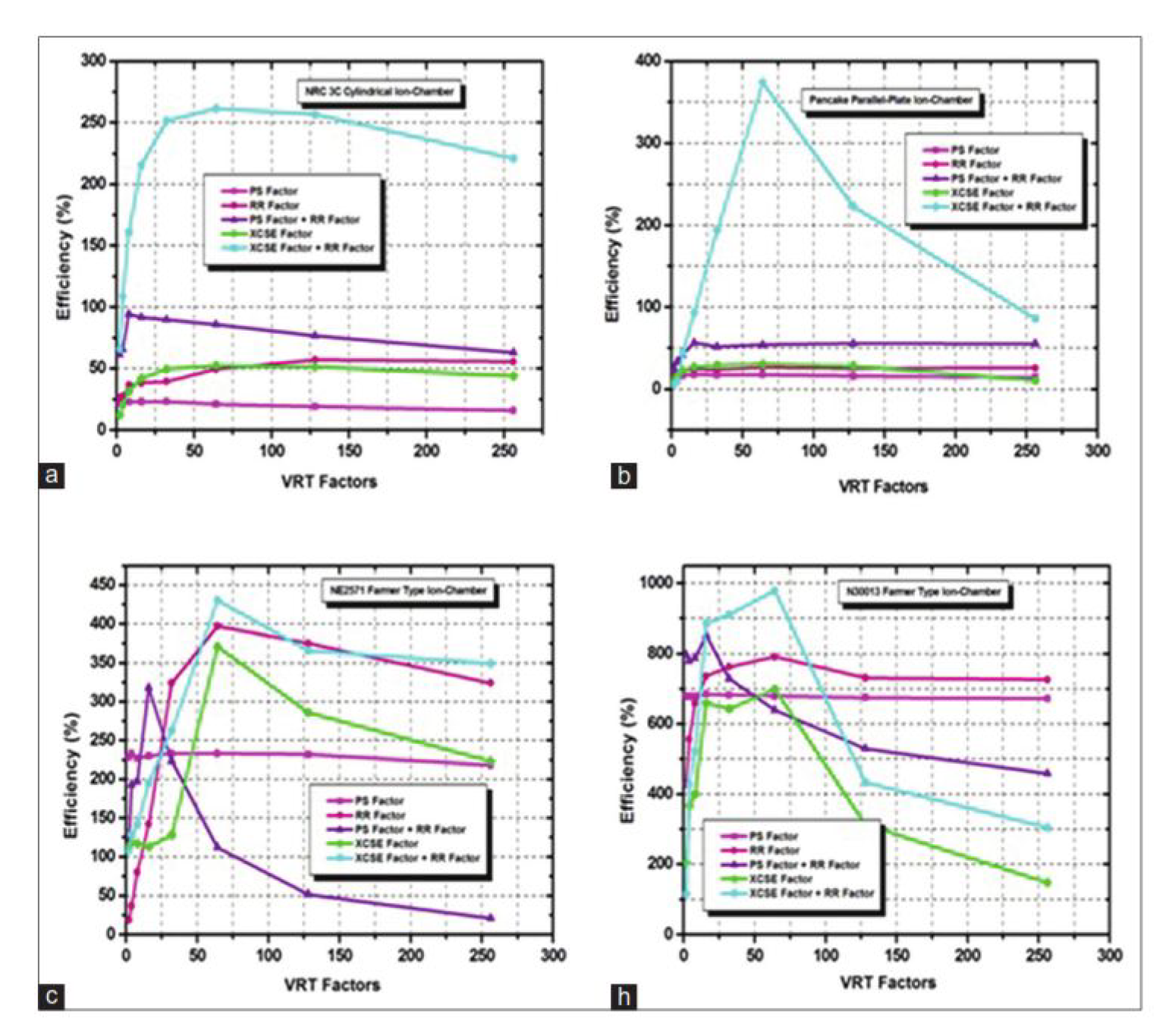
Figure 5 illustrates the efficiency of ion chamber dose calculations using EGSnrc Monte Carlo user codes as a function of several variance reduction technique (VRT) factors. The efficiency of simulations is assessed for four different ion chambers [45].

For example, significant efficiency gains have been found for the NRC 3C ion chamber, a cylindrical chamber acting as a primary standard for air kerma measurements, when using optimized VRT combinations. That results in reduced computation time and higher statistical reliability [18,45].

These enhance photon splitting and range-rejection-based Russian roulette techniques, which lead to significant reduction of variance for the parallel-plate pancake chamber normally used in surface dose measurements without loss in the accuracy of calculations [45].

The established NE2571 Farmer-type ion chamber used in clinical dosimetry shows enhanced computation efficiency with VRTs but with no compromise on accuracy in dose calculation [24], hence suitable for clinical Monte Carlo simulations [45].

Similar efficiency trends are observed for the ion chamber type Farmer N30013. The efficiency gain obtained by the combination of enhanced photon cross-section with Russian roulette offers an optimum compromise between computation time and accuracy [45].

These results suggest that optimum use of VRTs greatly increases computational efficiency for most Monte Carlo ion chamber dose calculation simulations [27]. Regarding techniques reviewed, combined photon cross-sectional enhancement, and range-rejection-based Russian roulette is giving maximum efficiency in all kinds of chambers. Further work confirmed that more advanced Monte Carlo simulation methods offer new routes in variance reduction with respect to radiometric dosimetry applications [50].

Key findings: The combination of XCSE and RR achieves the highest computational efficiency; the simulation time is drastically reduced, which still retains the dose calculation accuracy [16]. PS alone has higher accuracy but increases computation time. RR alone reduces particle interactions that do not contribute to dose calculation, thus improving the speed. XCSE combined with RR strikes an optimal balance, which ensures faster simulations at a reduced loss of accuracy [45,50].

Consequently, the optimized selection of VRTs favors MC simulation feasibility for clinical use by reducing computation time with no loss in precision. The graphic data confirm that the XCSE+RR method is superior among the studied methods to accelerate dose calculations without losing accuracy. It therefore presents an ideal choice for real-time radiotherapy applications [45,50].

9.3.2. Trade-Off Between Accuracy and Computation Time for Different Methods in EGSnrc Monte Carlo Simulations

Monte Carlo simulations offer very accurate dose calculations in radiotherapy but at a very high computational cost. For that reason, some VRTs have been developed in order to increase the efficiency of these simulations [14]. The trade-off between the accuracy and computation time of various methods of dose calculation is considered in this study, comparing Monte Carlo algorithms with conventional techniques [6].

Figure 6 presents a comparative analysis of dose distributions computed using MC methods versus conventional approaches, illustrating the variations in accuracy and computational efficiency [19]. The results show that MC-based calculations achieve superior accuracy in capturing complex dose distributions, particularly in heterogeneous media. However, they require significantly longer computation times than analytical methods [11,18]. In contrast, the conventional models provide much faster calculations at the expense of degraded accuracy, in particular, when dealing with dose regions with a high gradient [6].

It assesses several VRTs, such as PS, RR, and XCSE, all seeking an efficient balance between the speed of computation and the desired accuracy [23]. The presented results indicate substantial computation time reductions in MC simulations by applying the VRT methods while maintaining adequate levels of accuracy. Among all, the most effective combination happens to be the use of XCSE and RR, which boosts computational efficiency at the cost of reasonable dose calculation precision [6].

Results show that MC-based methods are still the most accurate, but their clinical use is conditioned by the optimization of VRTs in order to decrease the processing time [19]. The paper concludes that a further optimized method using XCSE and RR will be able to provide a real-time or near-real-time radiotherapy dose calculation with a balanced accuracy and efficiency [6].

9.4. Implications for Clinical Applications

The results indicate that while deep learning models offer fast dose prediction, they may be not robust enough for highly complex and patient-specific scenarios. Monte Carlo simulations are computationally expensive; however, they provide unmatched accuracy and reliability [10].

Future efforts should be done to include AI-driven Monte Carlo simulations that will help deep learning methods guide the Monte Carlo processes to increase their efficiency without losing their accuracy [61].

9.5. Comparison of Dose Calculation Methods

The proposed Monte Carlo simulation technique was compared to state-of-the-art approaches, such as the Analytical Anisotropic Algorithm (AAA), Pencil Beam (PB), and deep learning-based approaches [32]. A summary of the findings is given in Table 5.

MC simulations have become the gold standard in dose calculation and treatment planning in radiation therapy due to their accuracy [21]. Below is Table 5 comparing the following dose calculation techniques: accuracy, computation time, and robustness in heterogeneous media [36]. The table points out the trade-offs of MC, conventional analytical methods, and deep learning-based techniques while showing the insights on their clinical suitability [59].

The comparison in the figure below shows that Monte Carlo simulations have the highest accuracy of $99.2\%$ and hence are reliable in dose calculation accuracy [59]. However, their main drawback is that they are computationally inefficient, taking much more processing time compared to other approaches [28]. On the other hand, the dose calculation in the analytical algorithms, such as AAA and PB methods, is much faster while being less accurate, particularly for the heterogeneous tissue environments [26]. Deep learning-based techniques, such as 3D U-Net, GAN-based estimation, and DoseNet, have achieved an intermediate balance in improving the accuracy over the conventional methods while keeping the computational efficiency [29].

In addition, Table 5 emphasized the robustness of various methods in heterogeneous media, a very important ingredient for having trustworthy dose distribution estimates in complex anatomical regions [29]. Monte Carlo simulations are excellent in handling tissue inhomogeneities; deep learning methods, on the other hand, might introduce small errors for highly heterogeneous cases due to their dependency on the training dataset [24]. Conventional methods are generally the worst in robustness: Most of the time, they cannot give good results concerning dose prediction accuracy for regions with significant density variations [48].

From Table 5, it can be understood that hybrid methods combining Monte Carlo methods with AI-based models are becoming imperative. This will give a way in the future to accelerate Monte Carlo-based computations with the use of AI-driven surrogates and hardware while maintaining fast yet adequately accurate calculations that do not affect patient safety [32].

9.6. Clinical Feasibility and Future Prospects

Results will prove that Monte Carlo methods possess unparalleled accuracy, their computational burden [37] standing in the way of real-time performance. Deep learning models balance well between speed and accuracy, hence promising an alternative for real-time dose calculations. However, they are not as robust in highly heterogeneous media as MC simulations [2].

Future efforts should concentrate on hybrid AI-MC approaches where deep learning informs Monte Carlo simulations in order to reduce the computational burden without sacrificing accuracy [55,61].

9.7. Summary of Key Findings

The major study findings from this study include:

• Monte Carlo simulations are the most accurate $(99.2\%)$ but require considerable computation time.
• Deep learning methods yield rapid dose calculations with slightly lower accuracy $(94.8\%$ - $97.2\%)$ [32].
• AAA and PB are quick, but do so at some cost to their accuracy [15].
• Hybrid AI-Monte Carlo approaches may provide the optimum clinical solution [55].
• MC is the most accurate and trustworthy method of calculating dose in a radiation therapy [22].
• Deep learning methods offer major speed advantages but at the cost of small accuracy losses [34].
• A hybrid approach combining MC and AI may represent the optimal balance between speed and accuracy [31].

10. Conclusion

Monte Carlo simulations have evolved to be an essential tool for medical physics and especially in radiation therapy. These simulations represent a powerful tool for modeling, with great accuracy, the complicated interactions between ionizing radiation and biological tissues [9,53]. This will provide improved precision and accuracy of radiation therapy in treatment planning, dosimetry, radiobiological modeling, and personalized dosimetry. In general, MC simulations will be increasingly applied in medical physics applications with increased computational power and medical imaging providing even higher quality and effectiveness in radiation therapy for cancer patients [60].

This research has investigated the MC simulations in radiation therapy, that provides the highest degree of accuracy in dose calculation with respect to traditional and deep learning-based approaches [32,34]. In this work, a systematic comparison between MC-based dose estimation with AAA, PB, and deep learning-based techniques such as 3D U-Net, GAN-based models, and DoseNet has been performed [36].

10.1. Main Contributions

The main contributions of this work are given as:

• Higher Dose Calculation Accuracy: The Monte Carlo simulation framework presented the highest accuracy among different approaches, about $(99.2\%)$, against conventional and deep learning-based methods [34,37].
• Detailed Comparison with All Methods: The study conducted a detailed comparative study, comparing MC simulations with other techniques such as AAA, PB, and AI-based models on their accuracy, computation time, and robustness in heterogeneous tissues [37].
• Robustness in Complex Scenarios Validation Although deep learning-based methods depend on training datasets, MC simulations resulted in better robustness in heterogeneous media and are thus highly reliable for clinical applications [32,34].
• Limitations Identified and Needs for Future Studies The study identified the high computational cost for MC simulation and the need for hybrid AI-MC approaches in finding an optimal balance between speed and accuracy for real-time clinical use [34].

10.2. Future Research Directions

While Monte Carlo simulations provide unparalleled accuracy, several challenges remain that need to be addressed for broader clinical adoption. Future research could take the following directions:

• Hybrid AI-Monte Carlo Approaches: Deep learning-based acceleration techniques combined with Monte Carlo simulations can reduce computational overhead by a large factor while maintaining high accuracy [55].
• GPU-Accelerated Monte Carlo Algorithms: Optimizing MC algorithms using GPU-based parallel computing can improve simulation speed and make real-time dose calculations feasible [20,21].
• Adaptive Radiation Therapy with MC Simulations: MC-based adaptive therapy workflows may enable real-time updates in treatment plans due to anatomical changes during radiation sessions [34].
• Automated and User-Friendly Interfaces: Monte Carlo-based TPSs are being developed with user-friendly graphical interfaces that make the systems easier to use by clinicians, requiring less technical expertise [50].
• Multi-Modality Integration: A possible further study may come to make, in Monte-Carlo based-simulations about radiation-therapy planning-combined studies to multi-modality imaging modalities like CT and MRI to eventually reach personal accurate optimization more realistically [63,64].

10.3. Final Remarks

Monte Carlo simulations are the gold standard for dose calculation in radiation therapy, which gives unparalleled accuracy and robustness, but they have major inefficiencies in computational time [47]. This work underlined the optimization of MC methods by means of AI-driven techniques, GPU acceleration, and adaptive workflows. Overcoming these challenges will allow the full integration of MC simulations into real-time clinical applications and extend superior outcomes in precision radiation therapy [12].