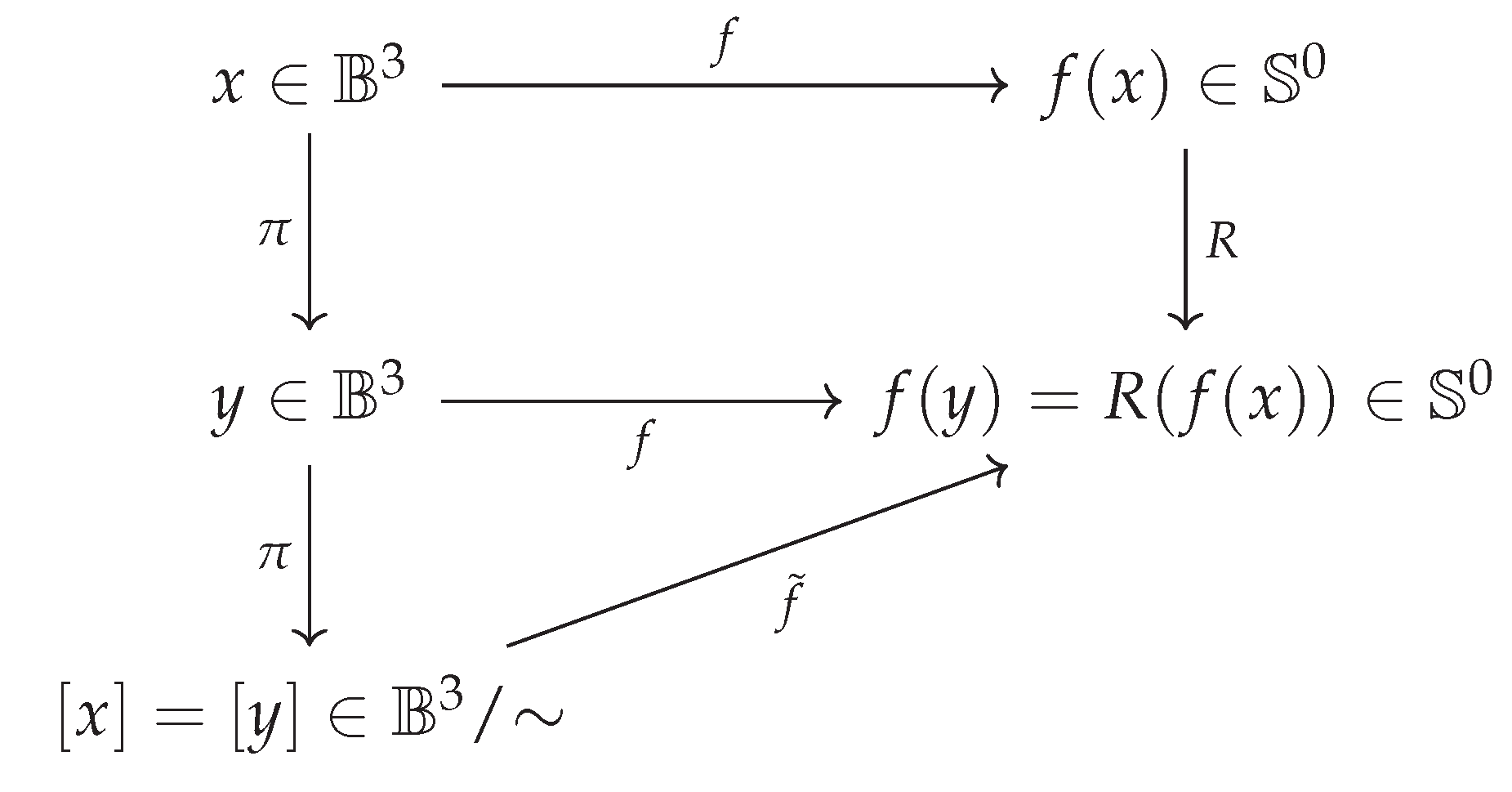Geometric Formalism for Quantum Entanglement via B³ and S⁰ Mappings

1. Introduction

The theory of quantum information has developed into a cornerstone of modern quantum science, with potential applications ranging from quantum algorithms and secure communication [1], to error correction [2,3] and quantum networking [4]. Beyond its technological relevance, quantum information provides a unique perspective on the nature of the Universe and the phenomenon of entanglement [5].

Quantum entanglement, famously described by Einstein as “spooky action at a distance” [6], underlies many protocols in quantum cryptography [7] and serves as a fundamental resource for quantum computation [8]. Despite the progress in quantum information theory, its mathematical language remains under active development [9,10]. New mathematical frameworks are required to fully exploit its potential—both for computational purposes and for deepening our understanding of quantum reality [11].

In this work, we introduce a new geometric formalism for the study of entangled states. We base our approach on two propositions: (1) representing bipartite entangled states as elements of a 3-dimensional ball ${\mathbb{B}}^3$, and (2) modeling the measurement process as a collapse onto the 0-sphere ${\mathbb{S}}^0$, corresponding to the two possible outcomes. This formalism provides a natural mapping between the geometry of entanglement and the measurement process. Previous work on the geometry of quantum states has explored several approaches to characterizing entanglement and measurement outcomes. Brody and Hughston [12] developed a framework for geometric quantum mechanics using the Fubini–Study metric on projective Hilbert space, while Bengtsson and Życzkowski [13] systematically studied the geometry of quantum state spaces, including entanglement polytopes and the Bloch sphere. Our approach builds on this tradition by focusing on a minimal topological representation, modeling the measurement process as a collapse from ${\mathbb{B}}^3$ to ${\mathbb{S}}^0$. This viewpoint offers a simplified but rigorous mapping that may complement metric-based approaches and inspire new geometric methods for quantum information processing.

We further discuss possible extensions of this approach, including its embedding in the Bloch sphere representation [14] and generalizations to higher-dimensional projective spaces $\mathbb{C}{P}^n$ [13]. These developments open the door to a differential-geometric treatment of quantum information, potentially yielding new insights into quantum computation, entanglement classification, and quantum state discrimination [12,13].

Proposition 1. 

(Topological space for quantum entanglement)

Let two particles be maximally entangled, where particle a is associated to a unique coordinate x, and particle b to y, with $x,y\in {\mathbb{B}}^3$. Let the mapping $f:{\mathbb{B}}^3\to {\mathbb{S}}^0$ encode the entangled state, such that $f\left(x\right)$ and $f\left(y\right)$ represent measurement outcomes at positions x and y, respectively.

Let there exist a deterministic relational operation R such that $f\left(y\right)=R\left(f\right(x\left)\right)$, with $R\left(f\right(x\left)\right)=\pm f\left(x\right)$, highlighting the outcome of a measurement on either of the particles. Moreover, we have the induced map $\tilde{f}:{\mathbb{B}}^3/\sim \to {\mathbb{S}}^0$ which is defined by

$$\tilde{f}\left(\left[x\right]\right):=f\left(x\right),$$

where $f=\tilde{f}\circ \pi$ and $\pi :{\mathbb{B}}^3\to {\mathbb{B}}^3/\sim$ is the quotient projection. Then, the space of quantum steering-mediated transformations between the two particles forms a topological manifold homeomorphic to ${\mathbb{S}}^0$, under the following conditions:

• There exists an equivalence relation $x\sim y$ induced by R, such that even though $f\left(x\right)\ne f\left(y\right)$, the entanglement imposes $x\equiv y$ in ${\mathbb{S}}^0$.
• For all scaling maps C, we have $Cx=Cy$ in ${\mathbb{S}}^0$.
• For all operations A, we have $Ax=Ay$ in ${\mathbb{S}}^0$.

The ${\mathbb{S}}^0$ manifold thus represents a state-transformation space in which any metric structure from ${\mathbb{B}}^3$ vanishes. Quantum steering transformations between maximally entangled states are thereby encoded as binary, disconnected, and nonlocal behaviors, yielding only two possible outcomes: $(-1,1)\in {\mathbb{S}}^0$. The topological disconnectivity of ${\mathbb{S}}^0$ reflects the quantum jumps inherent in state collapse, while its binary structure captures the intrinsic duality in the outcomes of entangled quantum systems. The proposition can be formalized into the following diagram.

Figure 1. Entanglement-induced topological mapping from ${\mathbb{B}}^3$ to ${\mathbb{S}}^0$: (1) The state assignments $f\left(x\right)$ and $f\left(y\right)=R\left(f\right(x\left)\right)$ reflect measurement outcomes, (2) The projection $\pi$ collapses entangled positions $x\sim y$ to the equivalence class $\left[x\right]=\left[y\right]$, (3) The induced map $\tilde{f}$ from the quotient space ${\mathbb{B}}^3/\sim$ to ${\mathbb{S}}^0$ confirms that entangled states are topologically identified despite outcome flips (R).

Figure 1. Entanglement-induced topological mapping from ${\mathbb{B}}^3$ to ${\mathbb{S}}^0$: (1) The state assignments $f\left(x\right)$ and $f\left(y\right)=R\left(f\right(x\left)\right)$ reflect measurement outcomes, (2) The projection $\pi$ collapses entangled positions $x\sim y$ to the equivalence class $\left[x\right]=\left[y\right]$, (3) The induced map $\tilde{f}$ from the quotient space ${\mathbb{B}}^3/\sim$ to ${\mathbb{S}}^0$ confirms that entangled states are topologically identified despite outcome flips (R).

Proof. 

Let $\pi :{\mathbb{B}}^3\to {\mathbb{S}}^0$ be the projection from the entangled particles in the base space with coordinates $x,y\in {\mathbb{B}}^3$ to the entangled state space ${\mathbb{S}}^0$. We have the quotient space by ${\mathbb{B}}^3\setminus \sim$ which represents the space of equivalent states in the ${\mathbb{S}}^0$ manifold, mapped by $\pi$. Take for instance $x\in {\mathbb{B}}^3$, and let the map $\pi$ induce a collapse of its spatial state to an identity state $\pm 1\in {\mathbb{S}}^0$. Then, the second particle $y\in {\mathbb{B}}^3$ is forced, by quantum steering to undergo the same collapse into a measure state $\pm 1\in {\mathbb{S}}^0$ by the nature of entanglement. Entanglement invokes hence a state transformation which treats any entangled particle at either positions x or y by the same law, attributing it to a point in $\pm 1\in {\mathbb{S}}^0$ by these particles being considered as equivalent in ${\mathbb{S}}^0$ under $\pi$. This switch in sign given by the function $R\left(f\right(x\left)\right)$ represents one of two outcomes induced by measurement. Since this switch in sign is induced by entanglement, then $R\left(f\right(x),f(y)$ are both states (outcomes) in ${\mathbb{S}}^0$, since the space ${\mathbb{S}}^0$ has only two elements, $\pm 1$. The mapping $\pi$ yields therefore either of two points in ${\mathbb{S}}^0$ for any two entangled states independent of their initial position $\left[x\right]\in {\mathbb{B}}^3\setminus \sim$.

From this, it follows that any operation on particle at position x or position y, given by a scalar C or an operator A yields an equality relation in the same topological space of the assumed quantum state $\pm 1\in {\mathbb{S}}^0$, hence $Cx=Cy,Ax=Ay\in {\mathbb{S}}^0$.

Proving that ${\mathbb{S}}^0$ is disconnected is straight-forward. Having $(U=-1,V=1)\in {\mathbb{S}}^0$, we can readily partition it into two separated open subsets in $\mathbb{R}$, which $U\cap V=\varnothing$ and $U\cup V={\mathbb{S}}^0$. Both U and V are open (and closed) in ${\mathbb{S}}^0$. Hence, ${\mathbb{S}}^0$ is totally disconnected.

□

Remark 1. 

The proposition is equally relevant for two particles on a 2D space, allowed by the map $g:{\mathbb{S}}^2\to {\mathbb{S}}^0$ to assume the same characteristics as implied in the proposition above.

Proposition 2 

(Representation of quantum steering as a fiber). Let x and y from topology of quantum entanglement be two individual points in ${\mathbb{B}}^3$ space. Let each point $x,y\in {\mathbb{B}}^3$ be the endpoints of a line d. Form a mapping $f:[0,d]\to {\mathbb{S}}^1\in \mathbb{C}$ such that $x,y$ become points on the circle ${\mathbb{S}}^1$. Construct a second mapping, $g:{\mathbb{S}}^1\to {\mathbb{S}}^2$ such that $x,y$ are now found on the surface ${\mathbb{S}}^2$. Let a tangent space be formed by assigning two vectors intersecting at each point, for x, $T_1=u\times v$ and for y, $T_2=w\times z$. By the two vector products we can form the tangent bundle $TM={\bigcup }_{p\in M}{T}_{p}M$, for $p=x,y$. Then we have a fiber over x and y which is the tangent space at the respective point

$${\pi }^{-1}\left(p\right)=T_{p}M$$

where $p=x,y$ and $\pi :TM\to M$, where $M={\mathbb{S}}^2$, assigned to x and y in an either stationary state or in a moving state along the tangent vectors or a product thereof. We can then form a second fiber, ${\pi }^{*}:T_{p}M\to {\mathbb{S}}^0$ from each tangent space at $x,y$ respectively, which generates a value $(-1,1)\in {\mathbb{S}}^0$ for each $x,y\in {\mathbb{S}}^2$ in the $0-$manifold ${\mathbb{S}}^0$. Then ${\pi }^{*}$ is a fiber, where ${\mathbb{S}}^2$ forms the base space and ${\mathbb{S}}^0$ is the projection of the fibre space and is a trivially smooth manifold. By considering also topology of quantum entanglement, ${\pi }^{*}$ represents quantum steering upon measurement of the state of either particles at x or y collapsing to either $(-1,1)$ for any two entangled particles stationary at position $x,y\in {\mathbb{S}}^2\subset {\mathbb{B}}^3$ or moving along the tangent vector bundle $TM$.

Proof. 

Let d be the distance between two arbitrary points $x,y\in {\mathbb{B}}^3$ and form a circle ${\mathbb{S}}^1\in \mathbb{C}$ by their diameter using the map $f:[0,d]\to {\mathbb{S}}^1\subset \mathbb{C}$. Assign two tangent vectors $v,u$ intersecting at x and two tangent vectors $w,z$ intersecting at y in ${\mathbb{B}}^3$, then we can form the cotangent spaces $E_1=v\times u$ and $E_2=w\times z$ for each point $x,y\in {\mathbb{B}}^3$ respectively. By this construction, we have formed two base spaces, $E_1$ and $E_2$ at $x,y$ respectively, and $E_1,E_2\subset {\mathbb{B}}^3$. By $\pi$, a generic map described in topology of quantum entanglement, we assign a value $(-1,1)$ for each point $x,y\in E_1,E_2$, resulting by measurement. Thus, we have $\pi :E_1\to S^0$ and $\pi :E_2\to S^0$. Since $E_1,E_2\subset {\mathbb{B}}^3$ then ${\mathbb{S}}^0$ forms the projection of the fibre space while $E_1,E_2\subset {\mathbb{B}}^3$ form the base space, and $\pi$ is the fiber between the base spaces $E_1,E_2\in {\mathbb{B}}^3$ to the projection of the fibre space ${\mathbb{S}}^0$, representing quantum steering. □

2. Conclusions

We have introduced two proposals for a novel perspective of quantum information and quantum entanglement using differential geometry, as an introductory dissemination. Future oulook considers the the complex ball ${\mathbb{B}}_{\mathbb{C}}^3$ because quantum states, such as photon wavefunctions, are naturally complex-valued functions. The complex structure allows us to encode essential phase information, which is crucial for describing interference and polarization phenomena. Working in a complex vector space provides also access to powerful mathematical tools from complex analysis and linear algebra. Furthermore, physical observables in quantum mechanics arise from complex inner products, making the complex space the natural setting for measurements. Finally, using ${\mathbb{B}}_{\mathbb{C}}^3$ aligns with advanced quantum field theories, where photons are modeled in infinite-dimensional complex Hilbert spaces.