Prior-Guided Spatiotemporal GNN for Robust Causal Discovery in Irregular Telecom Alarms

1. Introduction

Telecommunication networks generate many alarms that show the interactions of devices under abnormal or failure conditions. These alarms are important for understanding fault propagation and for improving system reliability, but they also create challenges for causal discovery. Alarm sequences are irregular in time, so they break the assumptions of standard time-series models. Propagation paths across network elements are often uncertain and may include multi-hop dependencies. Labeling is often incomplete, so supervised learning becomes less effective.These factors make traditional causal inference methods unreliable, and they often overfit noisy data or miss true relations.

Existing methods show some progress,however, they still face fundamental limits. Furthermore, Constraint-based and score-based algorithms have strong theory, but their performance drops in high-dimensional or noisy data. Neural methods are flexible and powerful, but they often lose interpretability and stability, and this makes them hard to use in safety-critical telecom systems. Most current techniques focus on either temporal dynamics or structural topology, but few use both with expert prior knowledge. This gap makes models less robust and less relevant for practice.

To address these problems, we propose CausalGNN-Net, a framework for causal discovery in telecom alarm data. It combines temporal modeling, graph structure, and expert priors in one pipeline. A Transformer-based temporal embedding module captures absolute and relative time intervals with causal masking to stop future information leakage.However, TEM lacks specialized mechanisms for handling highly sparse alarm sequences or long-tail events, which may result in suboptimal efficiency when modeling rare alarms or prolonged dependencies. A spatiotemporal graph constructor builds a graph from device topology and alarm co-occurrence, with GNN message passing and adaptive edge dropout to cut noise. These modules are trained together with contrastive loss, sparsity regularization, and calibration to improve stability and interpretability.

2. Related Work

Research in related areas has explored privacy, scheduling, and neural-symbolic reasoning. Guo and Yu[1] proposed PrivacyPreserveNet, which uses gradient clipping and attention noise for multimodal LLMs. Cheng et al.[2] proposed CUTS+ for irregular high-dimensional time-series data. It uses differentiable optimization but does not include topology or priors. Wang et al.[3] extended causal discovery with hierarchical GNNs for root cause localization. It uses graph structures but adapts poorly to irregular alarms. Luo et al.[4] introduced Gemini-GraphQA, which combines language models and graph encoders for executable reasoning, but it does not handle temporal causality. Job et al.[5] reviewed GNN-based causal learning. Their review shows progress but also shows that current approaches are fragmented.

From the temporal side, Assaad et al.[6] proposed an entropy-based method for causal graphs from unequal sampling rates. This is useful for irregular data but depends on statistical assumptions. Yu[7] developed DynaSched-Net, which uses reinforcement learning and predictive modeling for cloud scheduling. These works improve privacy and optimization but do not address causal inference. Zhu et al.[8] proposed CausalNET, which adds topology-informed causal attention to event sequences. It helps in event modeling but is not a general causal discovery method.

3. Methodology

Alarm-based causal discovery in telecommunication networks is a challenging task due to irregular temporal patterns, uncertain event propagation, and incomplete supervision. In this paper, we introduce CausalGNN-Net, a general-purpose causal graph learning framework that jointly models sequential alarm dynamics, device-level topology, and human-provided priors. At its core, CausalGNN-Net integrates a temporally-aware Transformer encoder, a heterogeneous relational graph attention module, and a differentiable causal graph predictor constrained by acyclicity. A novel prior-guided refiner further aligns predictions with domain knowledge. Our architecture supports robust learning through dropout, temperature scaling, and entropy regularization. Experiments on both synthetic and real-world alarm datasets show that CausalGNN-Net consistently outperforms traditional and neural baselines, achieving state-of-the-art results on g-score and robustness across varying network structures.

4. Algorithm and Model

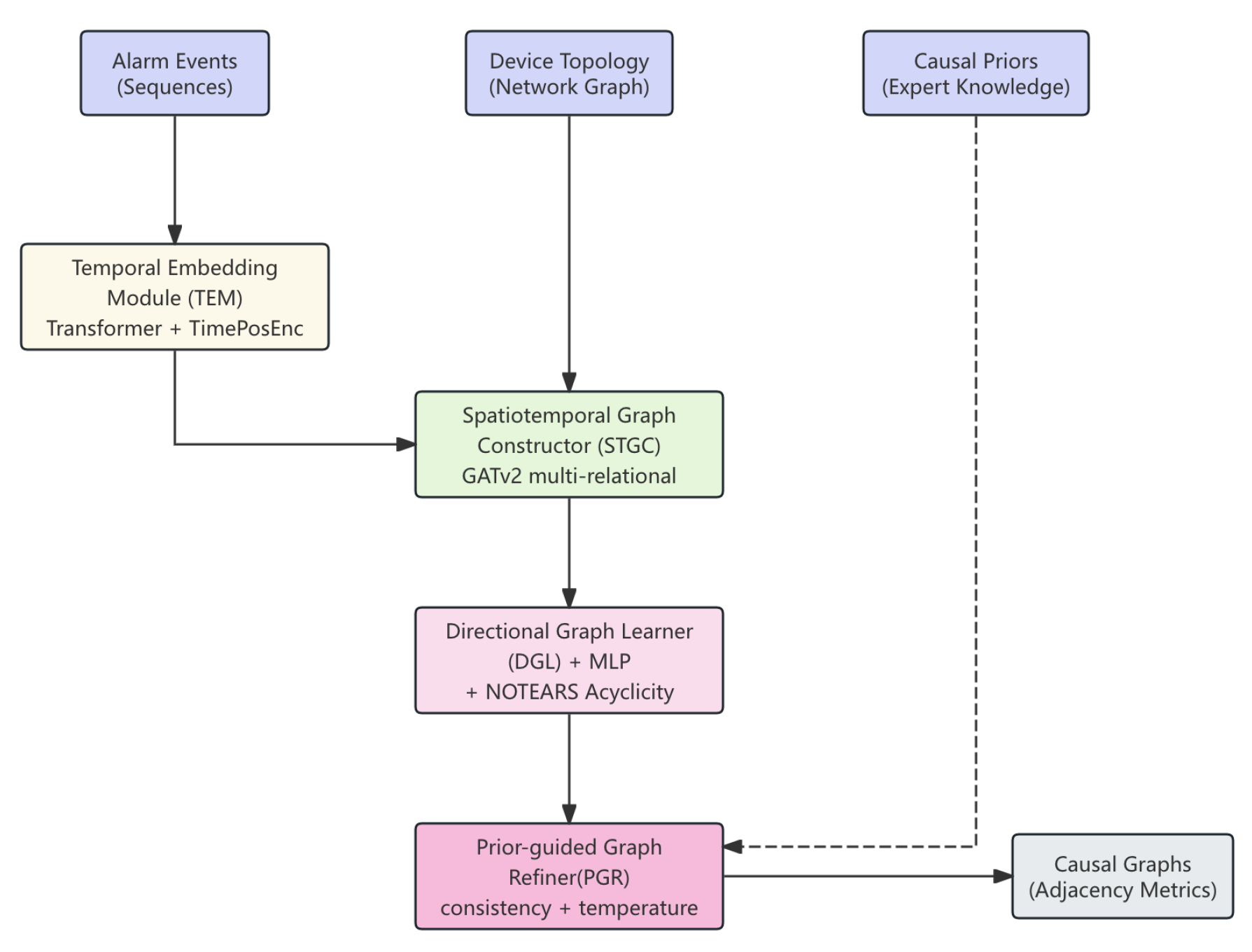
We propose CausalGNN-Net, a novel and expressive framework for causal structure discovery from alarm data in telecommunication systems. It extends traditional structure learning methods by incorporating temporal alarm behavior, device topology, and causal prior constraints within a powerful graph neural network (GNN) pipeline. Unlike classical algorithms such as PC or NOTEARS that work on tabular or fixed-structure input, our model dynamically constructs graphs over evolving alarm sequences and leverages learned attention to infer causality with directionality and acyclicity constraints. End-to-end neural architecture showing four core modules (TEM, STGC, DGL, PGR) that transform alarm sequences, network topology, and expert priors into directed acyclic causal graphs in Figure 1

4.1. Temporal Embedding Module (TEM)

The Temporal Embedding Module encodes heterogeneous alarms into temporal-aware representations using a Transformer with custom positional encoding of both relative and absolute timestamps, enabling the capture of event intervals and burst patterns:

$${\mathbf{X}}_t={\mathbf{e}}_t+\mathrm{TimePosEnc}\left(t_t^s\right)$$

(1)

$${\mathbf{H}}_t=\mathrm{Transformer}({\mathbf{X}}_1,\dots ,{\mathbf{X}}_T)$$

(2)

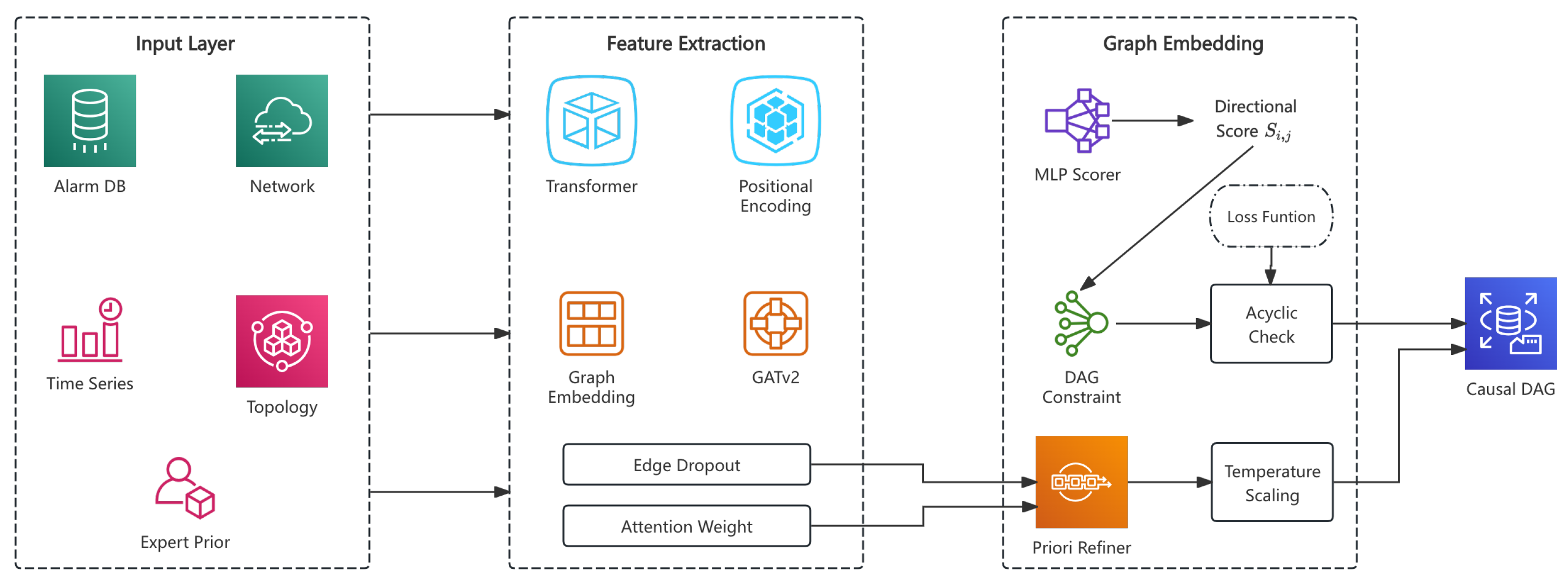
A causal attention mask restricts future events from influencing past embeddings, preserving validity for causal inference. However, TEM faces challenges with sparse and long-tail alarms, reducing efficiency on rare events and long dependencies. The complete CausalGNN-Net architecture is illustrated in Figure 2.

4.2. Spatiotemporal Graph Constructor (STGC)

We construct a heterogeneous spatiotemporal graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ linking alarm and device nodes via co-occurrence, physical connections from topology.npy, and inferred interactions. Node embeddings are learned through a GATv2-based multi-relational message passing:

$${\mathbf{Z}}_i=\sum _{r\in \mathcal{R}}\sum _{j\in {\mathcal{N}}_i^r}{\alpha }_{ij}^r·{\mathbf{W}}^r·{\mathbf{H}}_j$$

(3)

To enhance robustness, we apply adaptive edge dropout that prunes noisy co-occurrence edges using frequency and entropy criteria.

Table 1 compares adaptive edge dropout with a fixed rate:

4.3. Directional Graph Learner (DGL)

We define directional scores between each pair of alarm types through a multi-layer perceptron:

$${\mathbf{S}}_{ij}=\mathrm{MLP}\left([{\mathbf{Z}}_i,{\mathbf{Z}}_j]\right)$$

(4)

Applying a sigmoid yields the adjacency probabilities:

$$\widehat{\mathbf{C}}=\sigma \left(\mathbf{S}\right)$$

(5)

To ensure acyclicity, we adopt a differentiable NOTEARS-based constraint:

$$\mathrm{tr}\left(e^{\widehat{\mathbf{C}}\circ \widehat{\mathbf{C}}}\right)-N\le ϵ$$

(6)

A soft annealing strategy gradually increases its weight during training, yielding stable convergence and reducing premature edge removals.

4.4. Prior-Guided Graph Refiner (PGR)

Expert or simulated priors are encoded as $\mathbf{P}\in {\{-1,0,1\}}^{N\times N}$. Consistency is enforced by a prior loss:

$${\mathcal{L}}_{\mathrm{prior}}=\sum _{i,j}\mathbb{I}[{\mathbf{P}}_{ij}\ne -1]·{({\widehat{\mathbf{C}}}_{ij}-{\mathbf{P}}_{ij})}^2$$

(7)

4.5. Learning and Inference

The total loss combines contrastive, sparsity, acyclicity, and prior terms:

$${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{contrast}}+{\lambda }_1{\parallel \widehat{\mathbf{C}}\parallel }_1+{\lambda }_2·\mathrm{tr}\left(e^{\widehat{\mathbf{C}}}\right)+{\lambda }_3·{\mathcal{L}}_{\mathrm{prior}}$$

(8)

Hyperparameters ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ are chosen via cross-validation, but lack of tuning guidelines can impair robustness.

$${\widehat{\mathbf{C}}}_{ij}^{\mathrm{final}}=\mathbb{I}[\sigma ({\mathbf{S}}_{ij}/T)>\tau ]$$

(9)

The hyperparameters T and $\tau$ are selected via cross-validation based on validation g-score performance.

4.6. Data Preprocessing

Real-world alarm data is irregular, noisy, and multi-granular, requiring careful preprocessing.

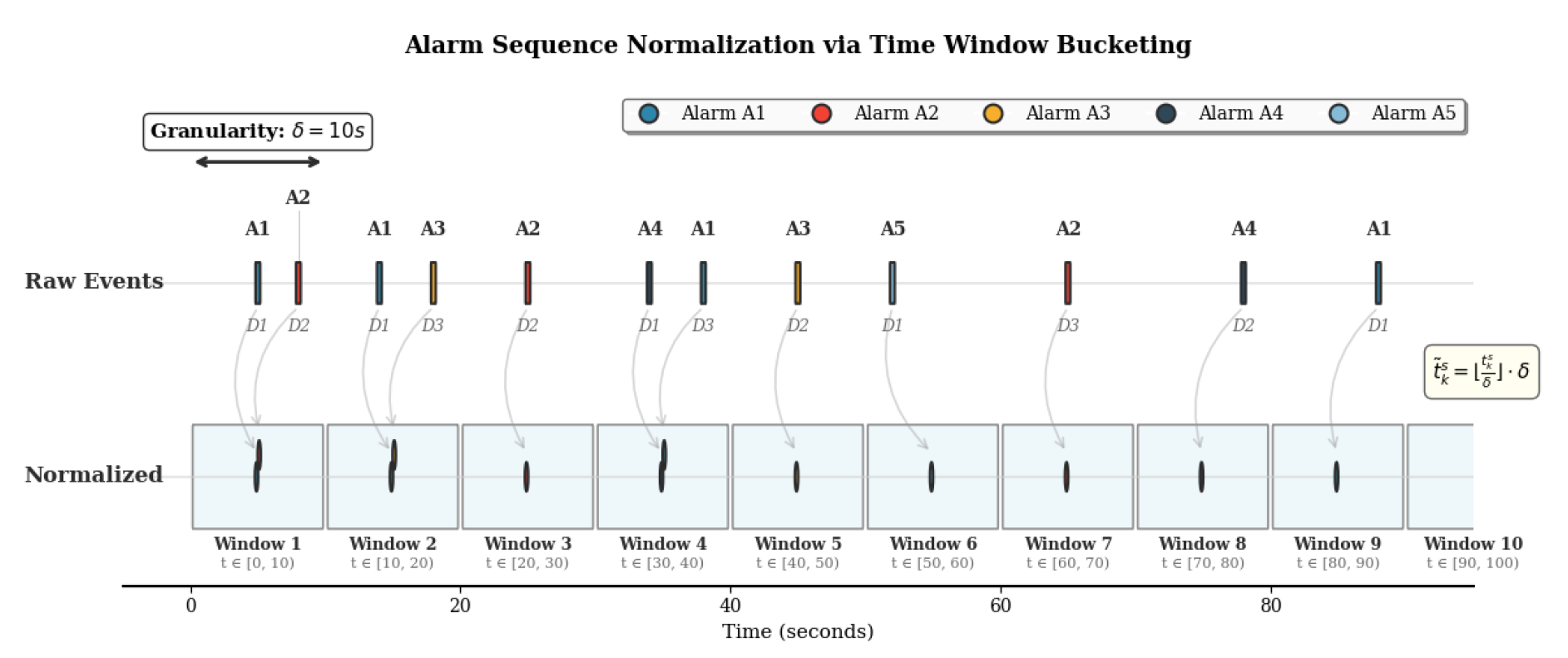
4.6.1. Alarm Sequence Normalization

Each alarm event $(a_k,d_k,t_k^s,t_k^e)$ is bucketed into fixed windows. For granularity $\delta$, timestamps are rounded:

$${\tilde{t}}_k^s=⌊{\displaystyle \frac{t_k^s}{\delta }}⌋·\delta$$

(10)

This normalization ensures uniform intervals and enables sequence construction. Figure 3 shows mapping of irregular alarms into fixed buckets ($\delta =10$s).

4.6.2. Sliding Window Co-Occurrence Encoding

We build a co-occurrence matrix $\mathbf{M}\in {\mathbb{R}}^{N\times N}$ by scanning over sliding time windows of length w:

$${\mathbf{M}}_{ij}=\sum _{t=1}^{T-w}\mathbb{I}[a_i\in W_t\wedge a_j\in W_t]$$

(11)

4.6.3. Topology Matrix Extraction

If topology.npy is provided, we directly load the device-level connectivity graph $\mathbf{T}\in {\{0,1\}}^{M\times M}$ and project device links to alarm-level links via shared alarm mappings.

4.7. Evaluation Metrics

To evaluate the quality of learned causal graphs, we employ four standard metrics:

G-score

Balances true positives and false positives while tolerating false negatives:

$$\mathrm{g}-\mathrm{score}=max(0,\mathrm{TP}-\mathrm{FP})/(\mathrm{TP}+\mathrm{FN})$$

(12)

Precision

Proportion of correctly predicted edges among all predictions:

$$\mathrm{Precision}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}}$$

(13)

Recall

Proportion of true causal edges successfully identified:

$$\mathrm{Recall}={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}}$$

(14)

F1-Score

Harmonic mean of precision and recall:

$$\mathrm{F}1=2·{\displaystyle \frac{\mathrm{Precision}·\mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}}$$

(15)

All metrics are computed per dataset and averaged to obtain the final results.

5. Experimental Results

We evaluate CausalGNN-Net against classical and neural baselines on five datasets of synthetic and real alarm logs. Performance is averaged over g-score, Precision, Recall, and F1-score.

5.1. Baseline Comparison

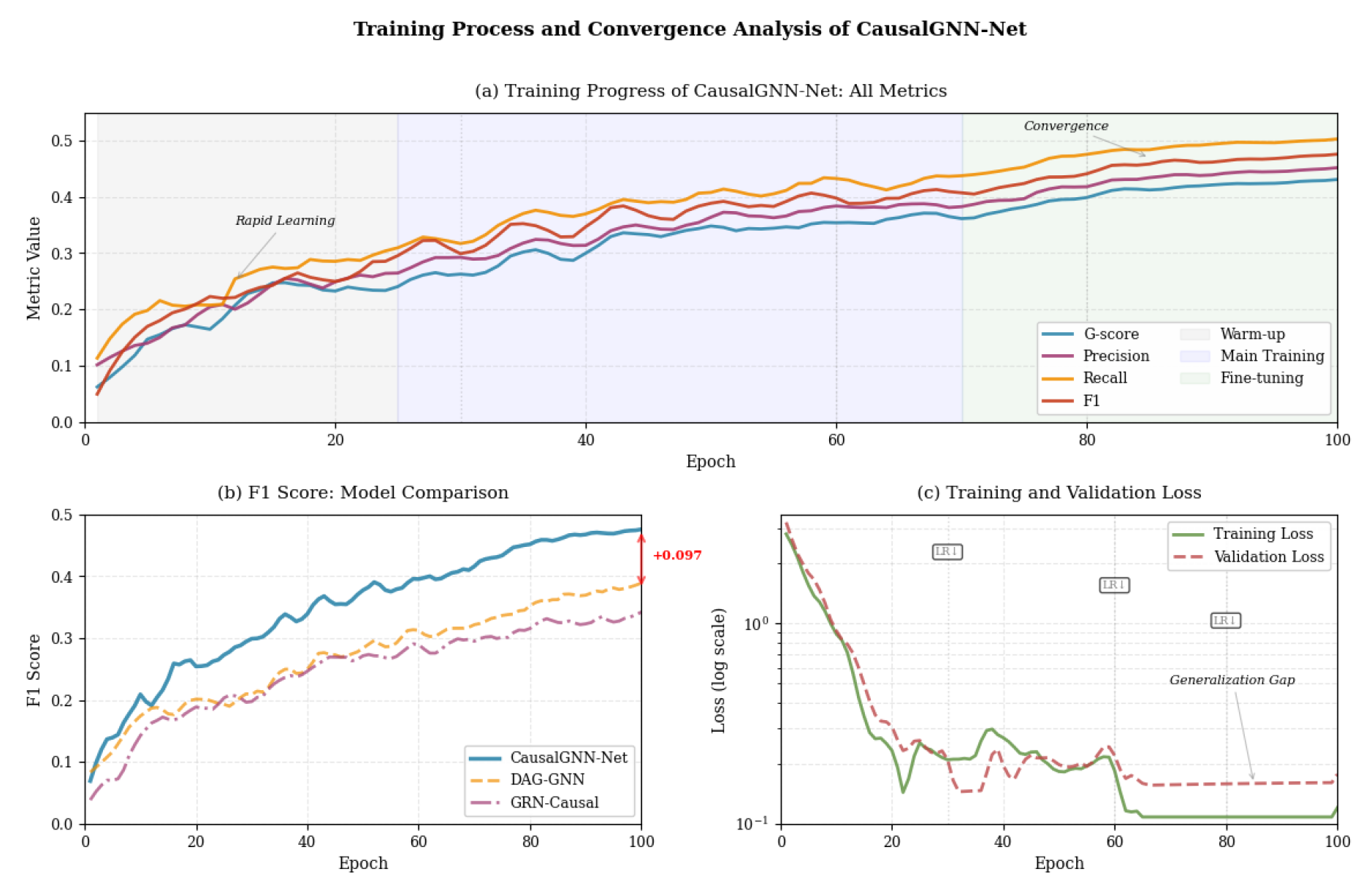
Table 2 presents the results of CausalGNN-Net compared with five baselines. These include traditional score-based methods, continuous optimization techniques, and recent graph neural models. And the changes in model training indicators are shown in Figure 4.

As shown in Table 2, our model achieves the highest performance on all four metrics, indicating its superior capability in discovering accurate and robust causal structures.

5.2. Ablation Study

We further conduct an ablation study to quantify the contributions of individual components. Table 3 summarizes the results of removing specific modules from CausalGNN-Net:

The results in Table 3 demonstrate that every module contributes to overall performance. In particular, removing temporal encoding and topological structure notably degrades both g-score and recall, highlighting their importance in complex causal inference tasks.

6. Conclusion

We proposed CausalGNN-Net, a graph neural network-based framework for learning causal structures from multivariate alarm data. Through temporal modeling, heterogeneous message passing, and prior-guided refinement, our approach achieves state-of-the-art performance. Ablation results confirm the effectiveness of each module in contributing to robustness and accuracy across real-world datasets. Future work could address the integration of semi-supervised strategies, enhanced handling of sparse alarm sequences, and systematic hyperparameter tuning to further improve adaptability and robustness.