Adaptive Critic Control of Frequency and Voltage in Islanded Microgrids Considering Energy Storage Systems

1. Introduction

The growing use of renewable energy sources in isolated microgrids presents significant challenges for controlling frequency and voltage, which are managed at different levels of control: primary, secondary, and tertiary. When there are changes in load or renewable energy production, the primary control system works to stabilize the grid and increase the resilience of the microgrid, as discussed in [32]. The secondary control level, utilizing a UC algorithm, then sets the optimal generation schedule to support the primary control system. The UC problem mainly focuses on cost optimization and improving the efficiency of battery usage while ensuring proper frequency and voltage regulation. The tertiary control level is responsible for managing the long-term operation of the microgrid [2].

Addressing the challenges of frequency and voltage control, the schedule for distributed generation (DG) units in islanded microgrids based on traditional UC remains fixed between dispatch intervals, despite the continuous changes in demand and renewable energy generation. This fixed schedule creates a stair-step pattern, resulting in significant frequency and voltage fluctuations at the ends of each dispatch period. Moreover, the fixed schedule method is not effective in managing operational costs and the lifespan of energy storage systems (ESS), as it does not properly handle variations in renewable energy and demand fluctuations [2,2]. It is assumed that local frequency, voltage, and net demand stabilize within each dispatch interval, creating a separation in timescales between the rapid response of the primary controller and the slower adjustments of the secondary controller. This separation affects power distribution and the dynamic regulation of frequency and voltage, particularly when there are rapid changes in load or renewable energy production, which needs to be managed [2].

1.1. Literature Survey

The conventional UC models typically include operational constraints for distributed generation (DG) units and energy storage systems (ESS), such as ramp-up/down limits, minimum up/down times, and the state of charge (SOC) of ESS. However, these models often fail to effectively address frequency and voltage regulation due to their reliance on fixed and non-optimal generation schedules between dispatch intervals [2]. In real-world scenarios, variability in renewable energy and load fluctuations result in continuous deviations of frequency and voltage from nominal values, while the output of controllable DGs remains fixed between dispatch intervals [2]. To mitigate these issues, modifications to UC models have been proposed, which include reserve-related constraints [2], load-frequency-sensitive indices [9], and averaged energy-block constraints between dispatch intervals [2]. These adjustments aim to reduce the adverse effects of frequency and voltage control on generation output while helping to balance supply and demand. However, incorporating reserve requirements into hourly energy blocks often proves difficult, as energy profiles created using averaging methods lack the precision needed for accurate supply-demand balancing. In optimization problem formulation, traditional UC approaches have mainly relied on offline methods such as mixed-integer linear programming [2], evolutionary algorithms [10], and model predictive control [11]. While these offline methods are relatively easy to implement, they suffer from long decision-making times, which limit their scalability for larger microgrids. Additionally, due to their inherent limitations, these methods struggle to manage optimization with dynamic technical constraints, such as those encountered in frequency and voltage regulation. Furthermore, prediction errors related to load and renewable energy often lead to deviations in DG reference set points from their intended values [12,13].

To overcome these challenges, recent studies have explored various online approaches for UC, such as neural networks [14], reinforcement learning [15], and adaptive critic design [16]. These techniques offer the advantage of faster decision-making, the ability to adapt to changing microgrid conditions, and the potential to optimize objectives based on real-time data [16,17]. In current research, the reference power for dispatchable units is updated during each dispatch interval using UC models. These adjustments to the reference power move the droop curves either up or down, which helps bring the frequency and voltage back to the desired levels. This adjustment process must take place within a defined time window after the primary controller’s action, influenced by factors such as the size and type of distributed generation (DG) units, the characteristics of the electrical network, and the load profiles.

1.2. Contribution and Paper Outline

Unlike existing research, this paper proposes a unified hybrid mid-level controller that interacts with a diffusive distributed primary controller [2] to optimally share the output power of dispatchable DG units. The proposed controller sets the optimal power output of DGs between dispatch intervals for the secondary controller, while maintaining frequency and voltage stability. The main contributions of this paper are summarized as follows:

• We develop a mathematical model for a hybrid mid-level controller, integrated with a diffusive distributed controller at the primary level and a UC framework at the secondary level;
• We propose a two-critic adaptive critic design model to minimize frequency and voltage deviations while ensuring microgrid stability;
• We present a model-free voltage and frequency controller, based on a dynamic programming algorithm, to achieve economic operation and enhance the lifecycle efficiency of the energy storage system (ESS).

The remainder of this paper is organized as follows. Section II describes the system model of the microgrid. Section III introduces the proposed DVFC. Numerical results are presented in Section IV to evaluate the performance of the proposed DVFC, and Section V concludes the paper.

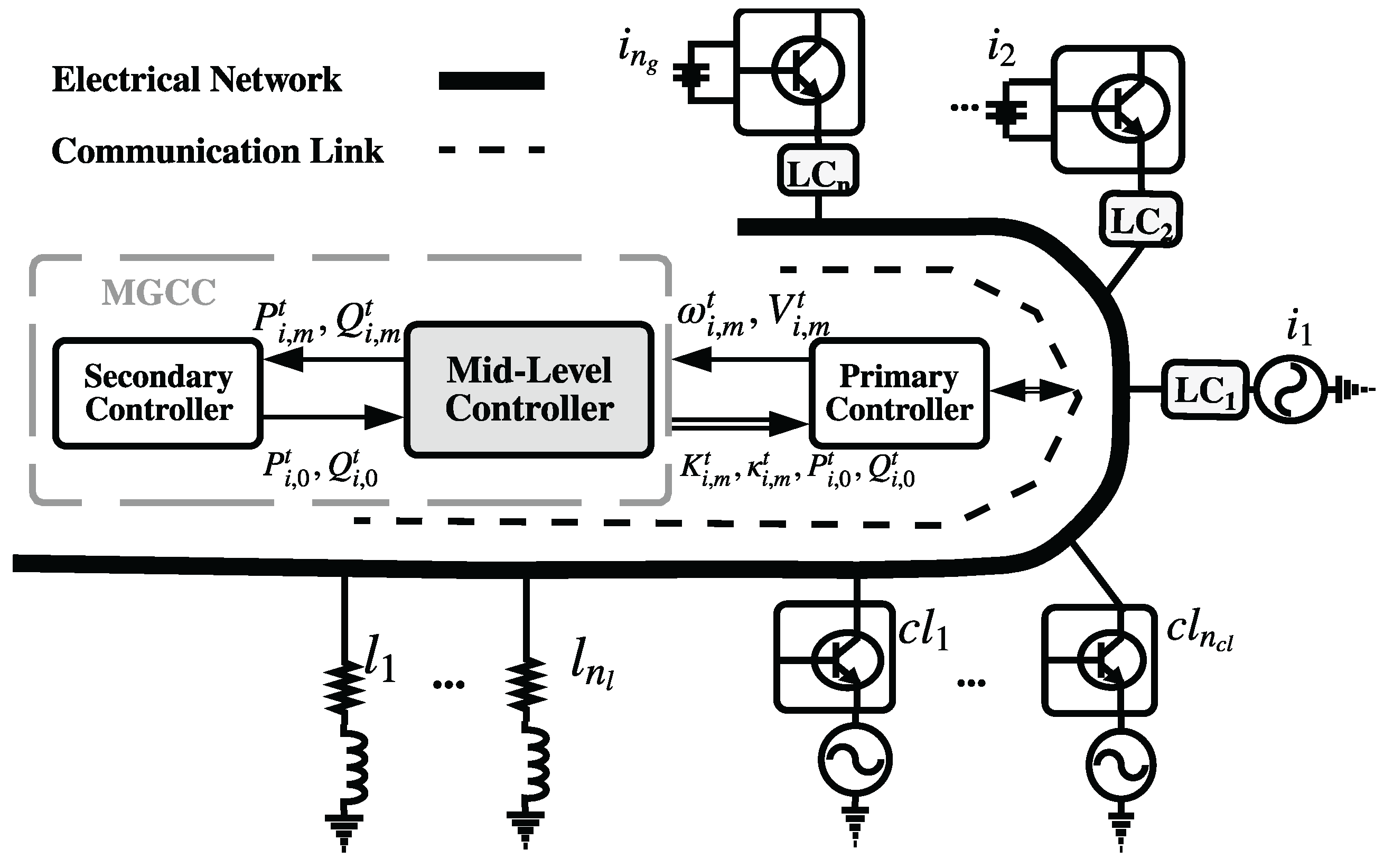
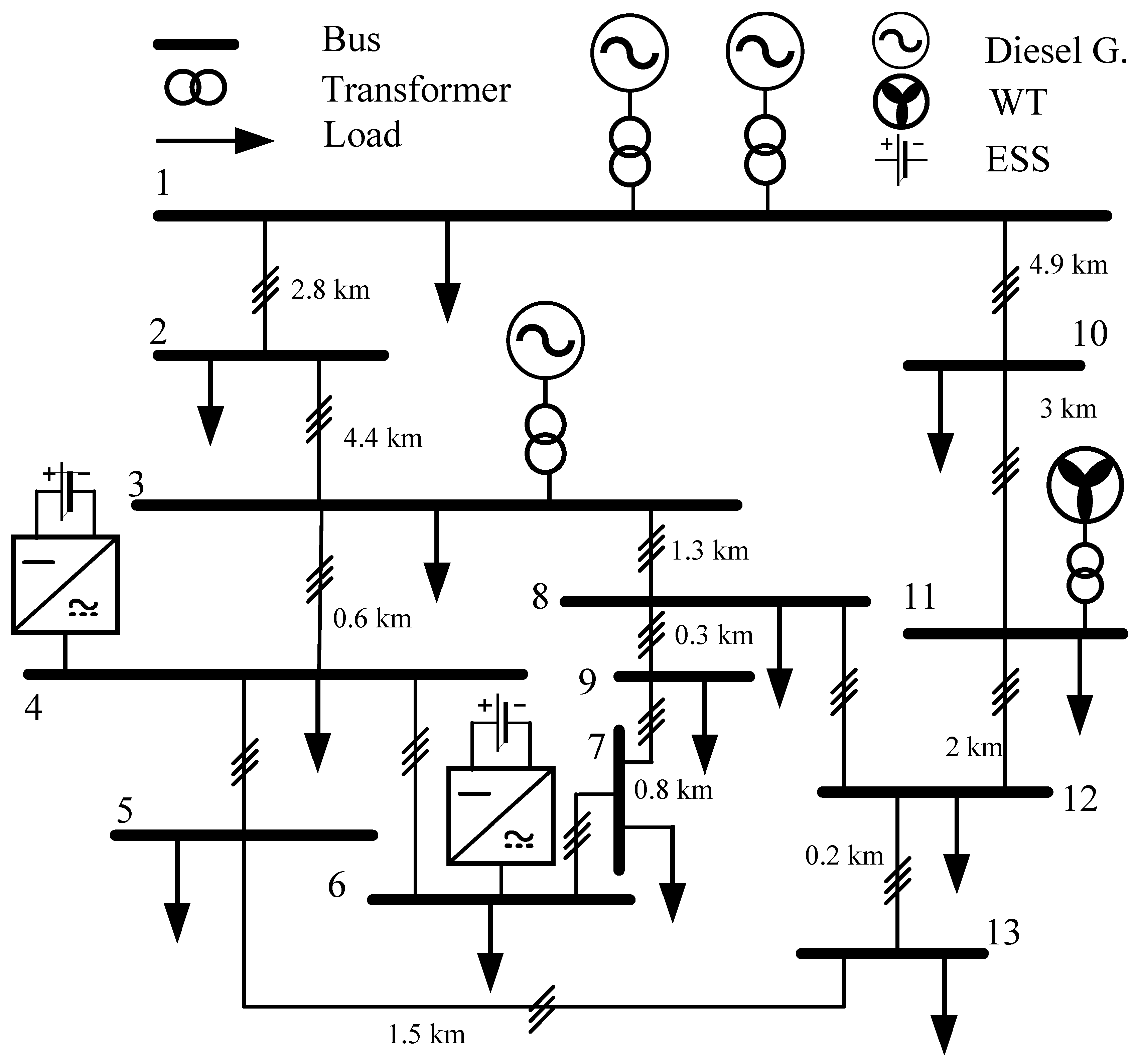
2. System Model and Problem Description

Consider an isolated microgrid within a distribution network, as illustrated in Figure 1, comprising $n_i$ distributed generation (DG) units ($i\in \mathcal{G}$), $n_j$ energy storage systems (batteries) ($j\in \mathcal{E}$), $n_{cl}$ controllable loads ($cl\in \mathcal{CL}$), and $n_l$ critical loads ($l\in \mathcal{L}$), all connected through buses ($b\in \mathcal{B}$) in the electrical grid.

The microgrid consists of n local controllers (LCs) for DG units and dispatchable loads, which manage frequency and voltage at the primary control level. At the secondary control level, the microgrid central controller (MGCC) ensures stable and optimal operation. The mid-level controller addresses the challenges posed by the timescale differences between the fast-acting primary controller, which enforces synchronization, and the slower secondary controller, by optimizing the droop controller parameters to bridge this gap. Figure 2 illustrates the stair-step pattern employed by the mid-level and secondary controllers, with dispatch time intervals M and T indexed by m and t, respectively. The mid-level control significantly reduces the unsupplied actual net demand $P_{L,m}^t$, which is notably higher at the secondary control level, emphasizing the crucial role of mid-level control in ensuring efficient operation.

During each time interval T, the secondary controller adjusts the reference active/reactive power levels $P_{i,0}^t/Q_{i,0}^t$ with the goal of minimizing operational costs and reducing ESS lifecycle degradation. In a traditional UC model, these reference power levels modify the droop control curves at the primary control level, resulting in updated frequency and voltage droop settings. For a larger islanded microgrid with significant renewable energy penetration, frequent adjustments to the active/reactive reference power can lead to system frequency and voltage deviating beyond acceptable operational limits. The mid-level controller reduces these deviations by breaking the dispatch horizon T into $n_m$ sub-intervals, each with duration M, and optimizing droop control parameters to enhance microgrid performance. The primary controller then manages frequency and voltage by coordinating the rated and operating active/reactive power levels $P_{i,m}^t/Q_{i,m}^t$ between neighboring controllable units during each dispatch sub-interval [18].

2.1. Droop Power Sharing Control

An imbalance between the variation in DG power ($\Delta P_{i,m}^t$) and the variation in net electrical power demand ($\Delta P_{L,m}^t$), represented as the total power variation ($\Delta P_{i,m}^t-\Delta P_{L,m}^t$), results in a shift in the nominal frequency (${\omega }_0$). Likewise, variations in the total reactive power cause output voltages to deviate from their desired values. To manage these deviations, DG units and controllable loads adjust their generation and consumption power using droop control, based on the power balance principle of synchronous generators (SGs). To integrate the primary controller with the mid-level control model, a modified diffusive-averaging droop controller (DADC) is introduced [2]. Power sharing is achieved by adjusting the droop slope ($m_{pi}$), the diffusive averaging frequency coefficient ($k_{i,m}^t$), and the control variable (${\Omega }_{i,m}^t$) for each active generator or controllable load within each dispatch interval/sub-interval, indexed by t and m. Local controllers (LCs) communicate to regulate frequency via diffusive averaging terms $a_{ik}({\Omega }_i-{\Omega }_k)\forall i,k\in \mathcal{G}$, where $a_{ik}=1$ if generators/loads i and k are connected, and $a_{ik}=0$ otherwise. The DADC problem is formulated as follows:

$$\begin{array}{cc}\hfill & {\omega }_{i,m}^t={\omega }_0-m_{pi}(P_{i,m}^t-P_{i,0}^t)+k_i{\Omega }_{i,m}^t\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & {\dot{\Omega }}_{i,m}^t=({\omega }_0-{\omega }_{i,m}^t)+\sum _{k\in \mathcal{G}}{a}_{ik}({\Omega }_{i,m}^t-{\Omega }_{k,m}^t),\hfill \end{array}$$

(2)

where ${\omega }_{i,m}^t$ is the frequency of the $i^{th}$ generator/load. A similar approach is used for voltage droop control, where generators share reactive power based on the voltage droop slope ($n_{pi}$), voltage gain (${\beta }_i$), maximum reactive power (${\overline{Q}}_i$), diffusive voltage coefficients (${\kappa }_{i,m}^t$), communication matrix ($b_{ik}$), and control variable ($e_{i,m}^t$). The DADC regulates the bus voltage $V_{d,i,m}^t$ to the nominal value $V_{d0}$ using:

$$\begin{array}{cc}\hfill & V_{d,i,m}^t=V_{d0}-n_{pi}(Q_{i,m}^t-Q_{i,0}^t)+{\kappa }_{i,m}^t{e}_{i,m}^t\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill & {\dot{e}}_{i,m}^t={\beta }_i(V_{d0}-V_{d,i,m}^t)+\sum _{k\in \mathcal{G}}{b}_{ik}\left({\displaystyle \frac{Q_{i,m}^t}{{\overline{Q}}_i}}-{\displaystyle \frac{Q_{k,m}^t}{{\overline{Q}}_k}}\right).\hfill \end{array}$$

(4)

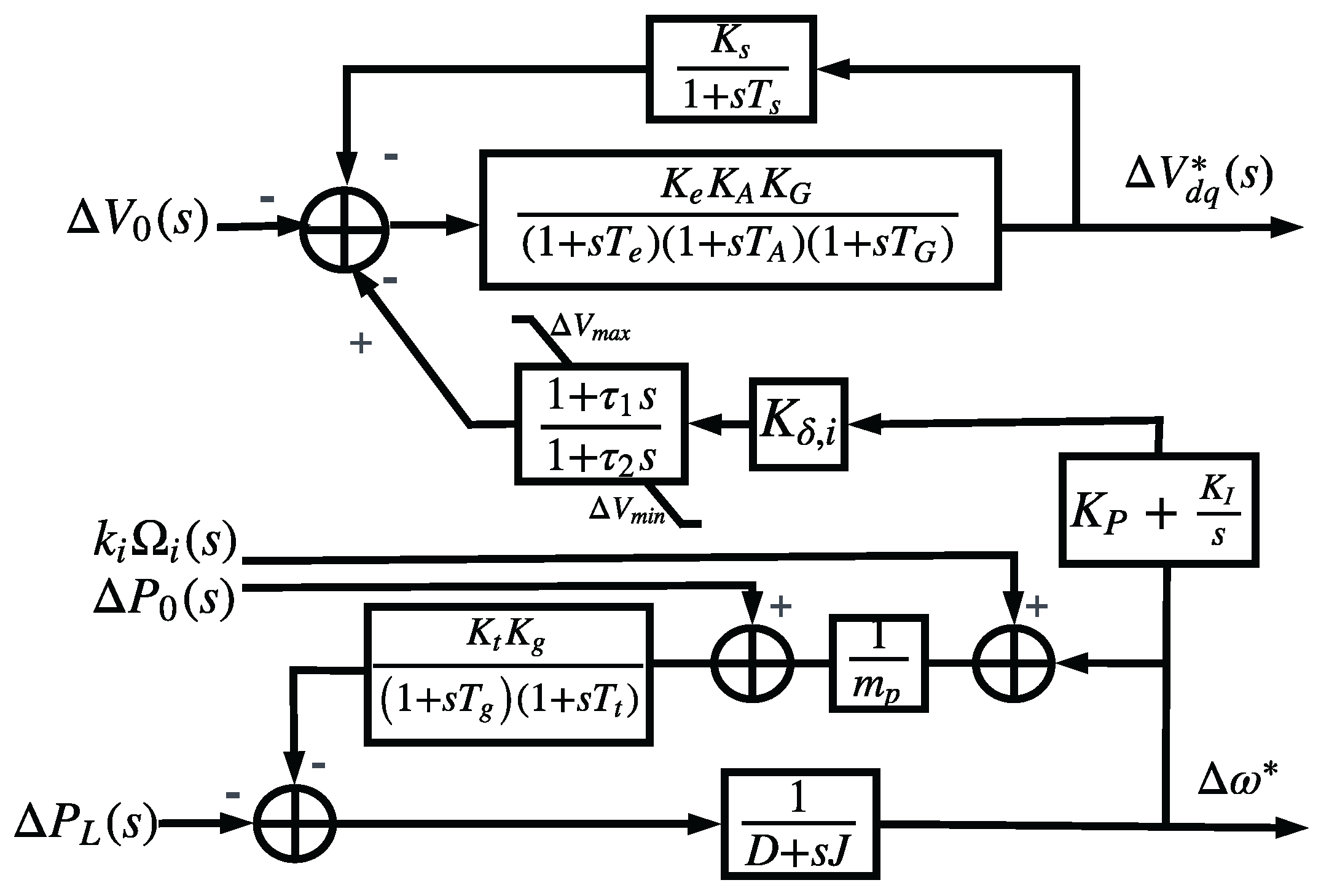
2.2. Components in Frequency and Voltage Control

The components of the islanded microgrid can be categorized into three main groups: inverter-based generators, SGs, and loads.

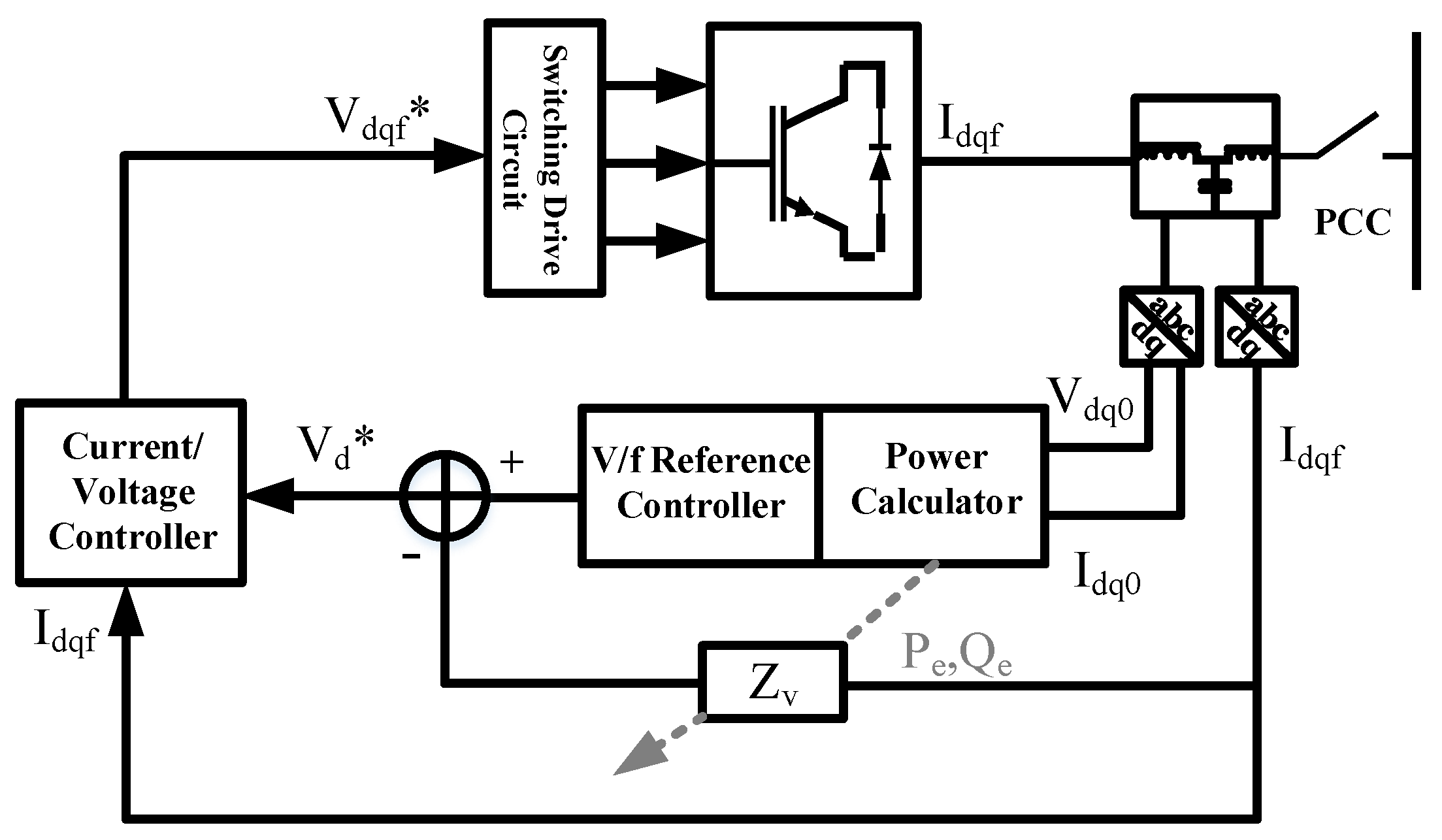
2.2.1. Inverter-Based Generators

Voltage-source inverters, as part of back-to-back converters (e.g., ESS units), consist of three cascaded control loops: power, voltage, and current controllers. These controllers ensure adequate sharing of active and reactive power, as well as stable operating conditions [19]. A virtual impedance is introduced to the voltage control loop to compensate for output voltage deviations and stabilize the voltage control system. Changes in the operating point lead to changes in the virtual impedance value. The proposed adaptive virtual impedance ($Z_v$) is tuned by the mid-level controller, based on a sensitivity analysis of operating active/reactive power ($P_e/Q_e$), as derived in [20]. Figure 3 illustrates the virtual impedance added to the voltage/current controller.

2.2.2. Synchronous Generators

A typical synchronous generator (SG), such as a diesel generator, consists of several key components: the governor, turbine, exciter, and AC machine [21]. The frequency in an SG changes based on the difference between mechanical driving power and the electrical power generated, as described by swing theory. Here, J represents the inertia coefficient in $kW/Hz$, indicating the power change per unit frequency change. The turbine and governor components, with gains ($K_t,K_g$) and time constants ($T_t,T_g$), are used to compensate for power generation changes that occur due to frequency deviations in the microgrid [22]. Voltage is similarly regulated through a sensor ($K_s,T_s$), exciter ($K_e,T_e$), automatic voltage regulator ($K_A,T_A$), and generator ($K_G,T_G$).

2.2.3. Frequency-Voltage Dependent Load

The loads in the microgrid are typically modeled using a voltage-dependent equation and can be represented as equivalent to a ZIP load. The loads operate at their nominal voltage before any voltage change $\Delta V_{b,m}^t$, with the power change $\Delta P_{L,b,m}^t=({(1+\Delta V_{b,m}^t)}^{1.5}-1)P_{L,b,0}^t$, where $P_{L,b,0}^t$ is the active power of the load under nominal operating conditions in the $m^{th}$ sub-interval. In general, the voltage change is highly dependent on the load characteristics. The relationship between changes in voltage and frequency is given by $\Delta V={(-2\Delta \omega \times H/\left({\omega }_0{P}_{L0}\right)+1)}^{0.6}-1$. A detailed study on frequency-voltage dependent loads demonstrates the validity of these equations [23].

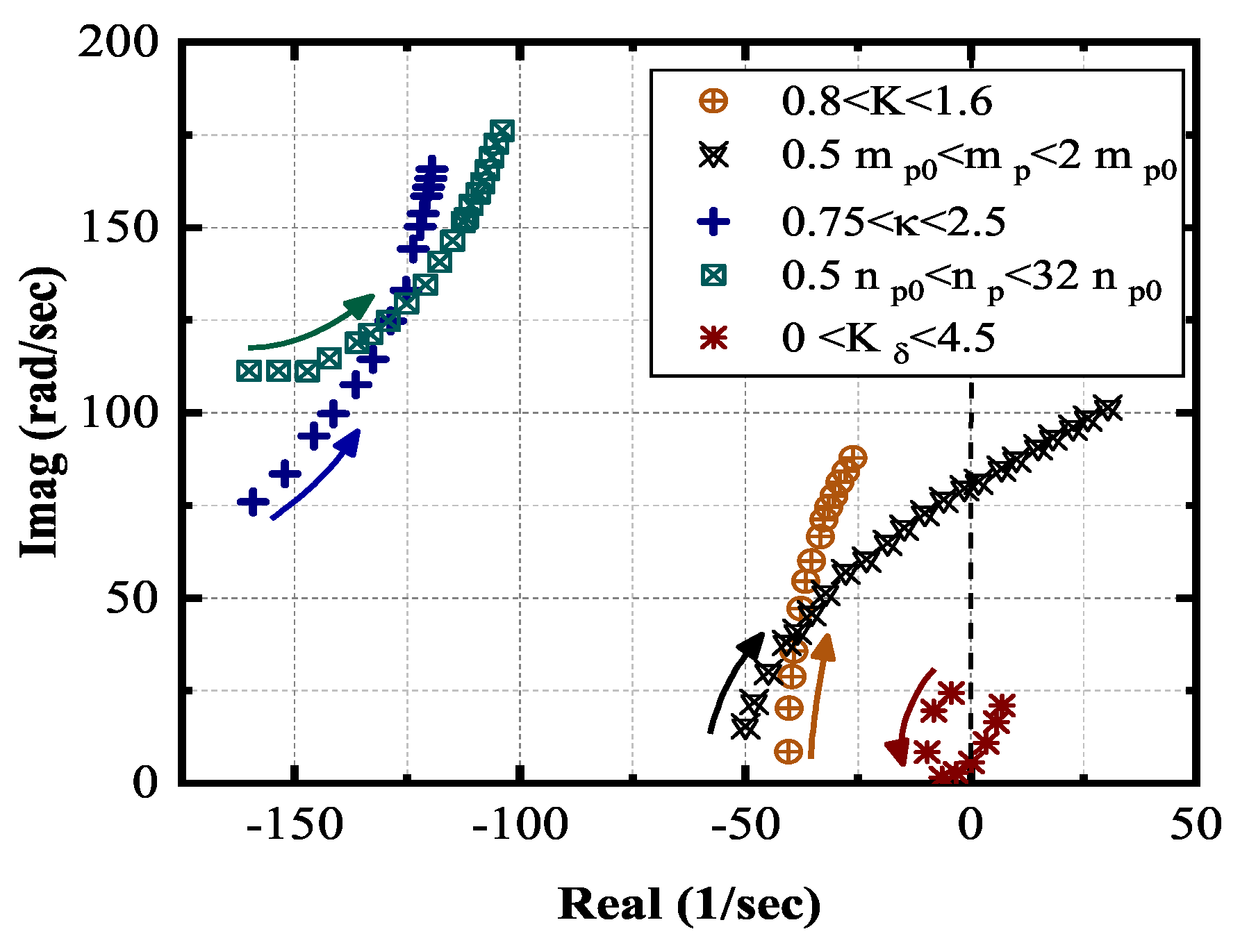
3. Small-Perturbation Stability Analysis

The small-perturbation model is analyzed using eigenvalue analysis by linearizing the islanded microgrid. While this approach is only applicable around the operating point, it provides a necessary condition for the microgrid stability [13]. To perform the eigenvalue analysis, a small-signal state-space model of the entire microgrid is developed at a specific operating point. The microgrid state-space model is divided into three sub-modules: generator, network, and load. Models for all lines and loads are derived from [24,25]. A comprehensive model of the islanded microgrid is constructed by integrating the state-space models of generators, the network, and loads using mapping matrices. These matrices link the output currents from generators or loads to specific nodes within the system.

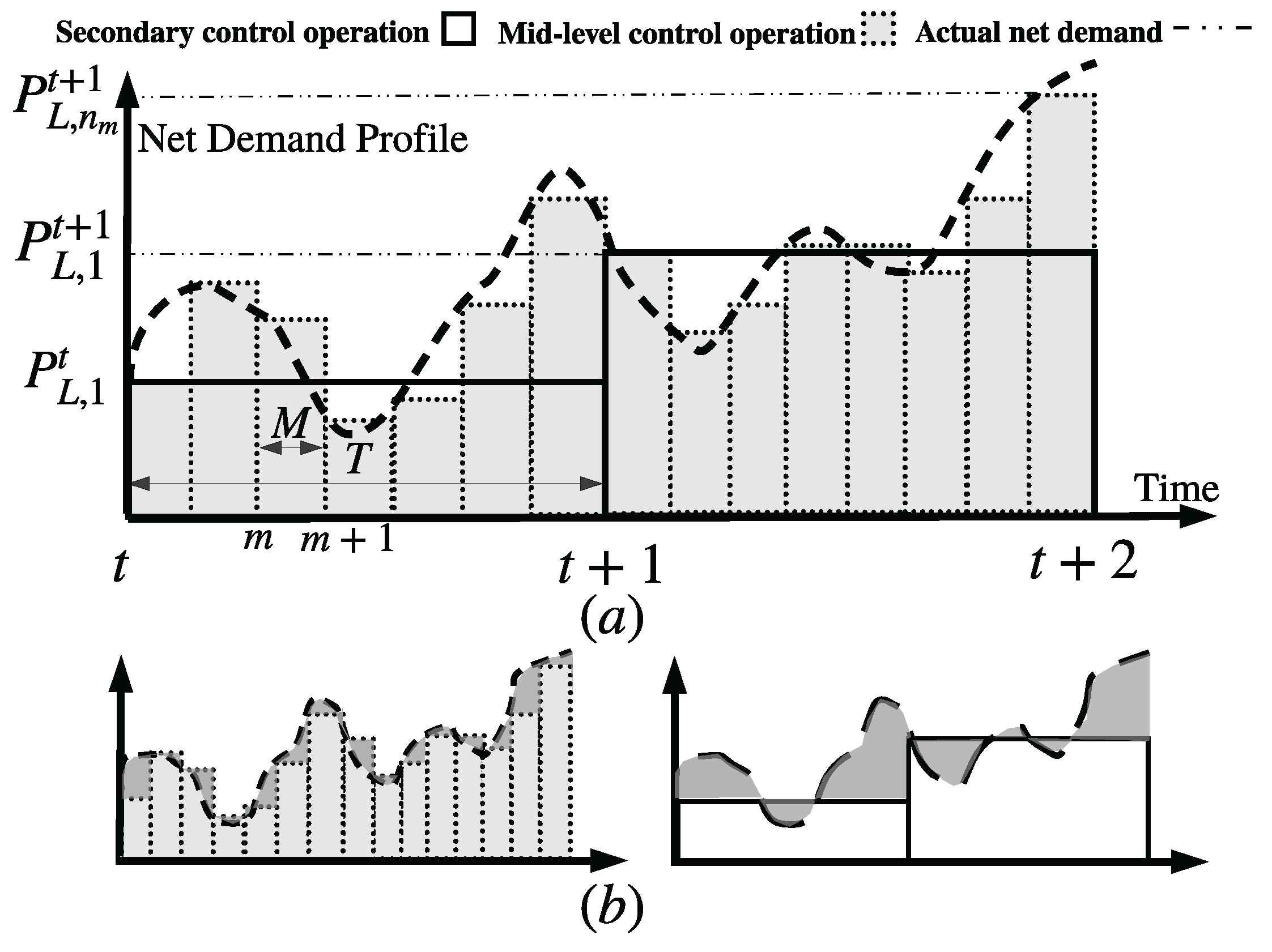
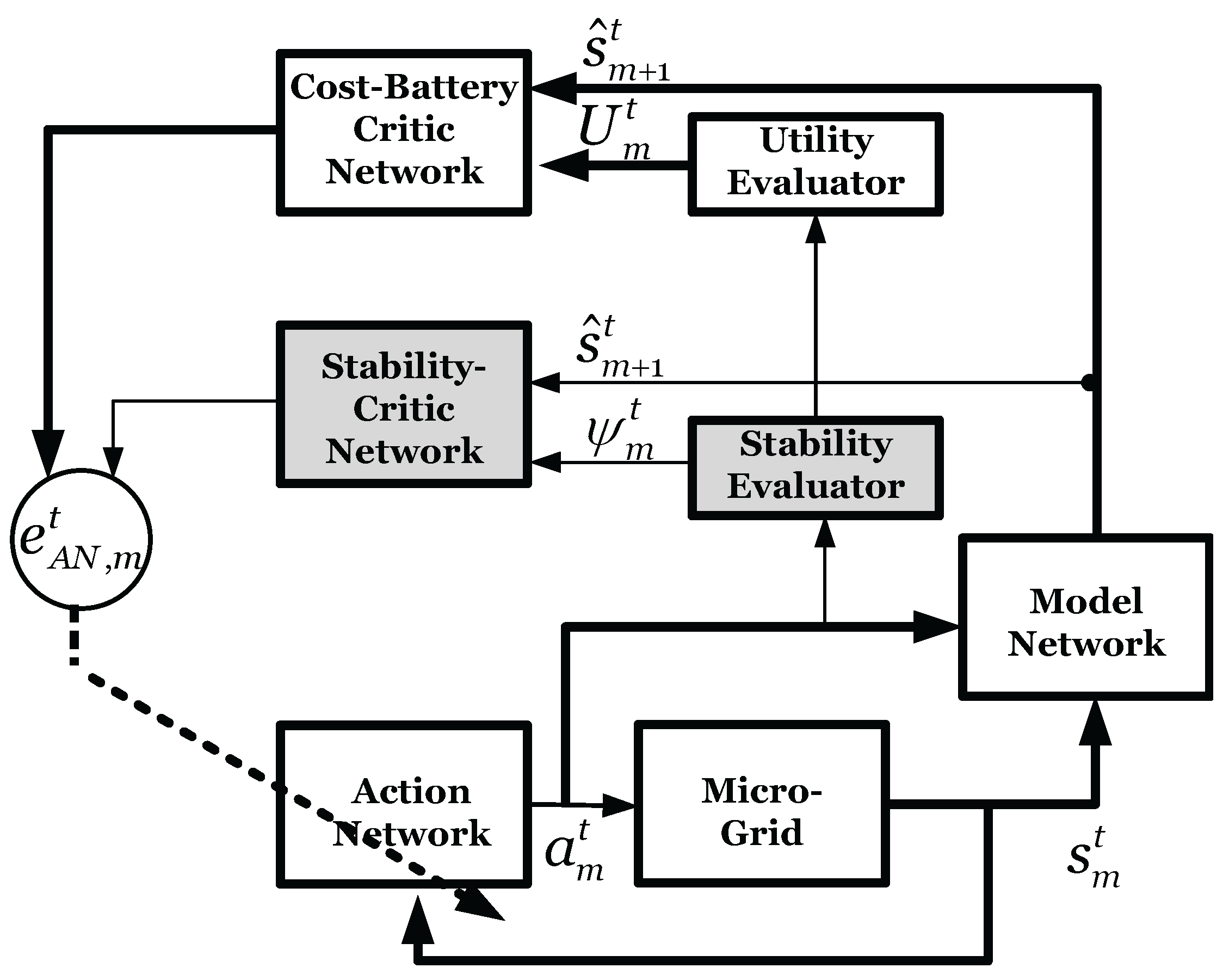
4. Dynamic Voltage and Frequency Controller

As illustrated in Figure 2, the net demand profile does not abruptly transition from $P_{L,m}^t$ to $P_{L,m}^{t+1}$ at the $t^{th}$ dispatch interval but rather changes gradually from $P_{L,m}^t$ to $P_{L,m}^{t+1}$ over the time period T. This gradual change requires real-time adjustments to generation power based on actual measurements taken at time sub-intervals of M.

Dynamic programming is a powerful tool for addressing optimization problems, particularly in complex, non-linear microgrid operations. However, the computational demands of performing feed-forward/backward numerical processes make it challenging to solve such optimization problems, especially in multi-objective microgrid control [16]. To overcome these challenges, adaptive dual heuristic dynamic programming (ADHDP) is developed to approximate the cost-to-go function, involving a model, action, and two critic neural networks (NNs).

As depicted in Figure 4, a two-critic ADHDP architecture is proposed to maintain the microgrid stability margin (${\psi }_m^t$) within an acceptable range while minimizing operating costs and ESS lifecycle degradation ($U_m^t$). This approach relies on measurements of available microgrid states ($s_m^t$), approximated system states (${\widehat{s}}_m^t$), and action control variables ($a_m^t$) at time t over duration T, indexed by m. The action vector comprises four sets of control variables: coefficients ($k_{i,m}^t,{\kappa }_{i,m}^t$) of the diffusive averaging droop controller, virtual impedances ($Z_{v,i,m}^t$), and frequency-voltage controller (FVC) gains ($K_{\delta ,i,m}^t$) for the $i^{th}$ generator [2]. The output states of the microgrid network include seven variables: the active/reactive power of generators and loads ($\Delta P_{i,m}^t,\Delta Q_{i,m}^t,\Delta P_{cl,m}^t,\Delta Q_{cl,m}^t$), frequency/voltage deviations ($\Delta {\omega }_{i,m}^t,\Delta V_{i,m}^t$), and the SOC of storage ($S_{j,m}^t$), represented by:

$$\begin{array}{cc}\hfill & a_m^t:=\{k_{i,m}^t,{\kappa }_{i,m}^t,Z_{v,i,m}^t,K_{\delta ,i,m}^t\}\hfill \\ \hfill & s_m^t:=\{\Delta {\omega }_{i,m}^t,\Delta P_{i,m}^t,\Delta Q_{i,m}^t,\Delta P_{cl,m}^t,\Delta Q_{cl,m}^t,\Delta V_{i,m}^t,S_{j,m}^t\}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & \forall i\in \mathcal{G},j\in \mathcal{E},m\in \{1,2,..,n_m\},t\in \{1,2,..,n_T\}.\hfill \end{array}$$

(6)

The mathematical representation of the ADHDP model, encompassing action variables, microgrid actual and approximated states, and errors in the model ($e_{MN,m}^t$), action ($e_{AN,m}^t$), and critic ($e_{CN,m}^t$) networks, is illustrated in Figure 5. The details of the ADHDP model are discussed as follows.

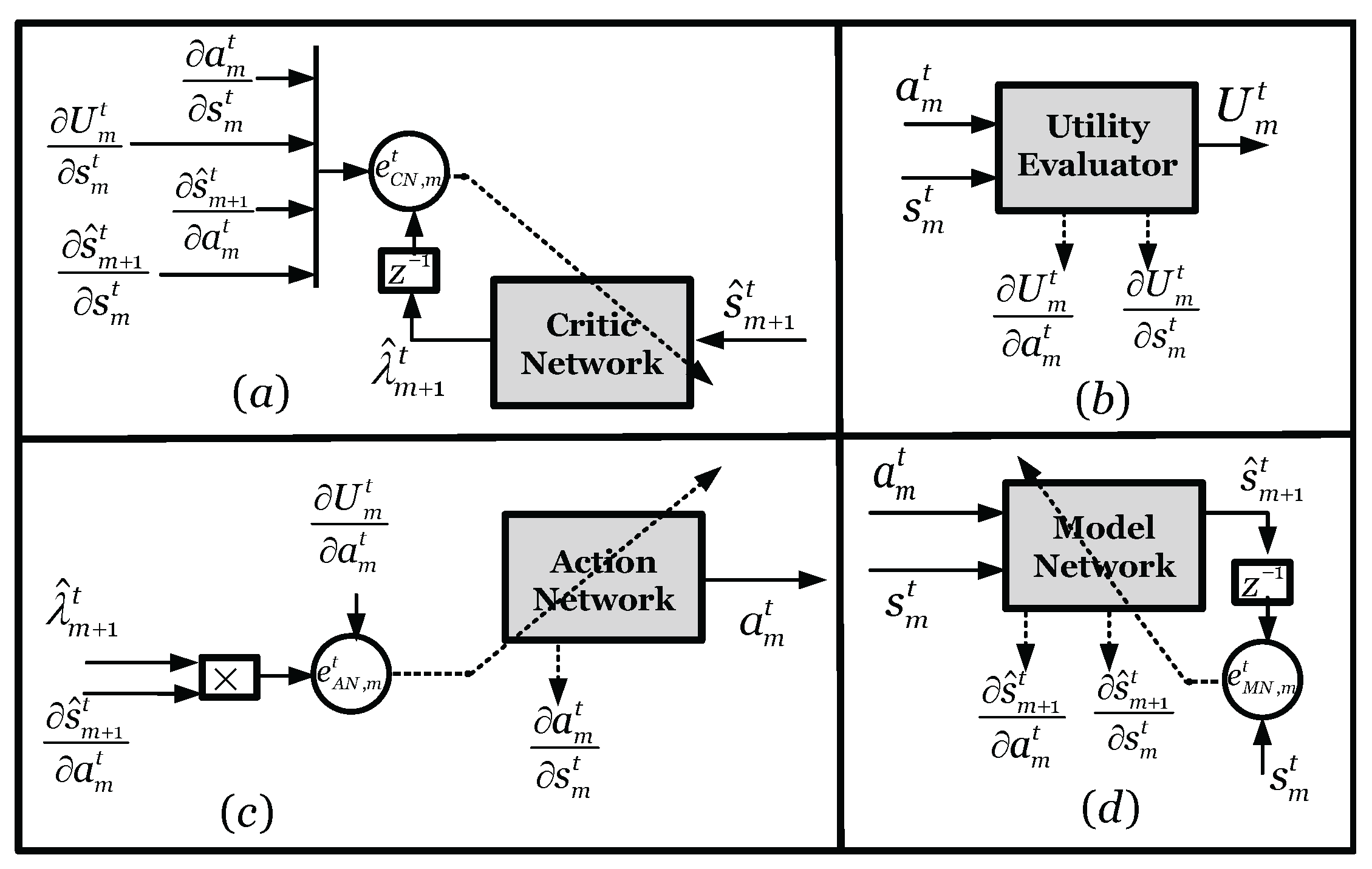
4.1. Model Network Design

The islanded microgrid experiences perturbations such as load variations, resulting in different operating conditions for DG units across current and future dispatch intervals. The model network simulates the behavior of the microgrid in response to the current state and control actions, and predicts future system states to facilitate cost-efficient and energy storage system (ESS)-efficient generation scheduling.

As shown in Figure 6, the error signal generated by the frequency control loop is processed through a PI controller with gains $K_P$ and $K_I$ to minimize the steady-state error. Following this, a lead-lag compensator with time constants ${\tau }_1$ and ${\tau }_2$ is applied to the input and output of the voltage control loops. This FVC introduces a gain, $K_{\delta i}$, to dampen oscillations generated by the frequency control loop and to establish the relationship between the system operating frequency and voltage. Similar to the inverter-based generator controller, the FVC is equipped with a low-pass filter/power calculator (LPF/PC) module to compute the average active and reactive power.

Accurate predictions are only possible if the difference $e_{MN,m}^t$ between the one-step delayed output of the model network (${\widehat{s}}_m^t$) and the actual microgrid output ($s_m^t$) is minimized. The model network prepares estimated states for the next step, ${\widehat{s}}_{m+1}^t$, along with the derivatives of the estimated state at the ${(m+1)}^{th}$ sub-interval with respect to the action and actual state variables at the $m^{th}$ sub-interval, which are used for training the critic networks.

4.2. Feed-Forward Critic Network Process

The distributed generation units react to net demand changes based on the DADC mechanism; however, generation scheduling becomes suboptimal if the frequency and voltage controller parameters remain constant during each dispatch interval. The primary function of the critic model is to approximate objective functions, which depend on the current and estimated states and control actions. The optimal strategy of the critic network is to minimize a multi-objective utility function, which includes the operating costs of DGs, ESS lifecycle degradation, and microgrid frequency and voltage regulation. This is represented by the multi-objective operational cost-to-go function ${\mathcal{J}}_u[a_m^t,s_m^t]$ and the microgrid stability margin ${\mathcal{J}}_s[a_m^t,s_m^t]$, subject to technical constraints.

To ensure the stability of the microgrid within an acceptable margin, the stability critic network operates as an inner control loop of the operational critic network. The stability evaluator checks the stability index (SI) of the DVFC, which reflects stability margin loss or improvement due to changes in effective parameters or loading conditions. Let ${\psi }_0$ and ${\psi }_m^t$ denote the stability margins for the base load (i.e., no change in load) and the loading condition at the $m^{th}$ sub-interval of the $t^{th}$ dispatch time, respectively. Thus, we have:

$$\begin{array}{cc}\hfill & {\psi }_m^t=\underset{\lambda }{argmax}\mathbb{R}\left(\lambda [a_m^t,s_m^t]\right),SI={\displaystyle \frac{{\psi }_m^t}{{\psi }_0}}\times 100\%.\hfill \end{array}$$

(7)

The operational critic network loop, which operates at a slower timescale compared to the stability control loop, aims to mitigate the effects of uncertainties on voltage and frequency control by minimizing ESS lifecycle degradation and operational costs. The output power of DGs influences the voltage $V_{b,m}^t$ at the $b^{th}$ bus and the frequency ${\omega }_m^t$ of the microgrid. The corresponding utility functions for voltage and frequency are expressed as follows:

$$\begin{array}{cc}\hfill U_V& =f\left(V_{b,m}^t\right)(\mathrm{voltage}\mathrm{utility}\mathrm{function})\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill U_{\omega }& =f\left({\omega }_m^t\right)(\mathrm{frequency}\mathrm{utility}\mathrm{function})\hfill \end{array}$$

(9)

These utility functions represent the relationship between the control objectives and the operating conditions, guiding the operational critic network in optimizing microgrid performance while ensuring system stability.

$$\begin{array}{cc}\hfill & \Delta {\mathcal{V}}_m^t=\sum _{b\in \mathcal{B}}\parallel \Delta V_{b,m}^t{\parallel }^2,\Delta {\mathcal{F}}_m^t={\parallel \Delta {\omega }_m^t\parallel }^2.\hfill \end{array}$$

(10)

The operational cost of dispatchable generation unit i changes in response to $\Delta P_{i,m}^t$ at operating generation power $P_{i,m}^t$ by the quadratic cost utility function ($\Delta {\mathcal{C}}_m^t$) as follows:

$$\begin{array}{c}\hfill \Delta {\mathcal{C}}_m^t=\sum _{i\in \mathcal{G}}\left((b_i+2a_i{P}_{i,m}^t)\Delta P_{i,m}^t+a_i\Delta {P_{i,m}^t}^2+C_i^s{y}_{i,m}^t+C_i^d{z}_{i,m}^t\right).\end{array}$$

(11)

where $a_i$ ($\$/kW{s}^2$) and $b_i$ ($\$/kWs$) are economic coefficients for the $i^{th}$ fuel-based generator, and $C_i^s$/$C_i^d$ and $y_{i,m}^t$/$z_{i,m}^t$ denote start-up/shut-down costs and the corresponding binary variables. In conventional UC, fast-response generators (e.g., batteries) must respond to frequency changes in a short time interval, which degrades ESS lifecycle. However, the ESS lifecycle utility function, $\Delta {\mathcal{E}}_m^t$, keeps the discharge depth between minimum and maximum levels for the SOC of the $j^{th}$ ESS ($\underline{S_j},\overline{S_j}$) by controlling $S_{j,m}^t$ as follows:

$$\begin{array}{c}\hfill \Delta {\mathcal{E}}_m^t=\sum _{j\in \mathcal{E}}\left(exp\left({\displaystyle \frac{{\left(S_{j,m}^t\right)}^2}{{\overline{S_j}}^2}}-1\right)+exp\left({\displaystyle \frac{{\underline{S_j}}^2}{{\left(S_{j,m}^t\right)}^2}}-1\right)\right).\end{array}$$

(12)

A weighted-sum method is used to determine a balanced energy dispatch among the solutions obtained from the utility functions. This method adjusts the importance of each utility function using scaling weights ($w_x,\forall x\in \{\mathcal{V},\mathcal{F},\mathcal{C},\mathcal{E}\}$), where a higher scaling weight for a specific utility function indicates a higher priority. The overall utility function is:

$$\begin{array}{cc}\hfill & U_m^t=w_{\mathcal{V}}\Delta {\mathcal{V}}_m^t+w_{\mathcal{F}}\Delta {\mathcal{F}}_m^t+w_{\mathcal{C}}\Delta {\mathcal{C}}_m^t+w_{\mathcal{E}}\Delta {\mathcal{E}}_m^t.\hfill \end{array}$$

(13)

The optimal control problem is to generate the power dispatch of DGs in the $m^{th}$ sub-interval by minimizing the cost-to-go operational function ${\mathcal{J}}_u$ in Bellman’s equation of dynamic programming in a step-by-step way [16]. It also keeps the stability margin of the microgrid within the desired range by maximizing the cost-to-go stability function ${\mathcal{J}}_s$. These functions are given by:

$$\begin{array}{cc}\hfill & {\mathcal{J}}_u[a_m^t,s_m^t]=\sum _{m=1}^{n_m}{\gamma }^m{U}_m^t,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & {\mathcal{J}}_s[a_m^t,s_m^t]=\sum _{m=1}^{n_m}{\gamma }^m{\psi }_m^t,\hfill \end{array}$$

(15)

where $\gamma \in (0,1]$ is the learning factor in dynamic programming. The technical constraints include the following:

1) Power Balance: Unlike conventional UC, the generation power must match demand at each dispatch time, based on equations (1)-(4).

2) Fossil-Fuel Units: Constraints are associated with DG active/reactive power, start-up/shut-down binary variables, and ramp-up/ramp-down power limits for fossil fuel generation units. It is assumed that the ramp-up power equals the ramp-down power ($R_i^u=R_i^d$):

$$\begin{array}{cc}\hfill & u_{i,m}^t\underline{x_i}\le x_{i,m}^t+\Delta x_{i,m}^t\le u_{i,m}^t\overline{x_i},\forall x\in \{P,Q\},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & y_{i,m}^t\ge u_{i,m}^t-u_{i,m-1}^t,z_{i,m}^t\ge u_{i,m-1}^t-u_{i,m}^t,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & |\Delta P_{i,m}^t|\le R_i^{u}M,\forall i\in \mathcal{G},m\in \{1,2,\dots ,n_m\},\hfill \end{array}$$

(18)

where $u_{i,m}^t$ is a binary variable that determines the on/off status of the DG.

3) ESS Charge/Discharge: The $j^{th}$ ESS operates in three different modes, i.e., charging ($u_{c,j,m}^t=1,u_{d,j,m}^t=0$), discharging ($u_{c,j,m}^t=0,u_{d,j,m}^t=1$), and idle status ($u_{c,j,m}^t=u_{d,j,m}^t=0$). The following set of constraints models SOC behaviours:

$$\begin{array}{cc}\hfill & S_{j,m}^t=S_{j,m-1}^t+\Delta P_j^t·{\displaystyle \frac{{\eta }_{c,j}·u_{c,j,m}^t-{\displaystyle \frac{u_{d,j,m}^t}{{\eta }_{d,j}}}}{C_j}}.M\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & {\underline{S}}_j\le S_{j,m}^t\le {\overline{S}}_j\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & u_{c,j,m}^t+u_{d,j,m}^t\le 1,\forall j\in \mathcal{E}\wedge m\in \{1,2,..,n_m\}\hfill \end{array}$$

(21)

where ${\eta }_{c,j}$ and ${\eta }_{d,j}$ represent the efficiency of charging and discharging, and $C_j$ is the ESS capacity.

The DVFC critic network is trained online to approximate the derivatives of estimated cost-to-go ${\widehat{\mathcal{J}}}_u[a_m^t,{\widehat{s}}_m^t]$ with respect to estimated state variable ${\widehat{s}}_{m+1}^t$ of model network called ${\widehat{\lambda }}_{m+1}^t$, and to minimize the critic network error $E_{CN}^t={\parallel e_{CN}^t\parallel }^2$. Here, $e_{CN}^t$ is given by

$$\begin{array}{cc}\hfill & e_{CN}^t={\displaystyle \frac{d\left({\mathcal{J}}_u[a_m^t,s_m^t]-\gamma ·{\widehat{\mathcal{J}}}_u[a_m^t,{\widehat{s}}_{m+1}^t]-U_m^t\right)}{d{s}_m^t}}\hfill \\ \hfill & ={\widehat{\lambda }}_m^t-\{{\displaystyle \frac{U_m^t}{s_m^t}}+{\displaystyle \frac{U_m^t}{a_m^t}}·{\displaystyle \frac{a_m^t}{s_m^t}}\hfill \\ \hfill & +\gamma ·{\widehat{\lambda }}_{m+1}^t[{\displaystyle \frac{{\widehat{s}}_{m+1}^t}{s_m^t}}+{\displaystyle \frac{{\widehat{s}}_{m+1}^t}{a_m^t}}·{\displaystyle \frac{a_m^t}{s_m^t}}]\}.\hfill \end{array}$$

(22)

The same convection is applied for the stability critic network.

4.3. Action Network Design

The action network determines the optimum values for action variables (i.e., $k_{i,m}^t,{\kappa }_{i,m}^t,Z_{v,i,m}^t,K_{\delta ,i,m}^t$) by the the minimization of the cost-to-go function in critic network. This network is trained online to approximate the optimal control law by minimizing the action network error (i.e., $E_{AN,m}^t={\parallel e_{AN,m}^t\parallel }^2$), given by

$$\begin{array}{cc}\hfill & e_{AN,m}^t={\displaystyle \frac{\partial {\widehat{\mathcal{J}}}_u[a_m^t,{\widehat{s}}_m^t]}{\partial a_m^t}}={\displaystyle \frac{\partial U_m^t}{\partial a_m^t}}+\gamma {\widehat{\lambda }}_{m+1}^t{\displaystyle \frac{\partial {\widehat{s}}_{m+1}^t}{\partial a_m^t}}\hfill \end{array}$$

(23)

where the partial derivatives are obtained from the model network, critic network, and utility evaluator as shown in Figure 5 [16]. Note that the computational time of the critic network training is much higher than that for the action and model networks, but has less power to change the action variables from their desired values.

4.4. Design and Initialization of DVFC

The pre-training of the three networks accelerates the convergence of the learning process. The model network, which approximates microgrid dynamics over a wide operating range, is initially trained using the error of state variables. Table 1 provides the typical convergence time for each neural network, evaluated using an Intel(R) Core(TM) i7-8650 1.90GHz (4 processors).

Note that the computational time required for simulation depends significantly on the hardware capability. The pre-training of the critic network is performed using results obtained from a mixed-integer non-linear programming (MINLP) method in GAMS, solved using the CPLEX solver for different load and renewable energy perturbations. This pre-training must be done for each test case based on the configuration of the cost-to-go function.

The online adaptation is carried out sequentially for the model, action, and critic networks. During the training of one network, the other networks remain fixed (no weight updates). The feed-forward and backward training of action and critic networks continues until the errors converge within a range of $[-{10}^{-3},{10}^{-3}]$.

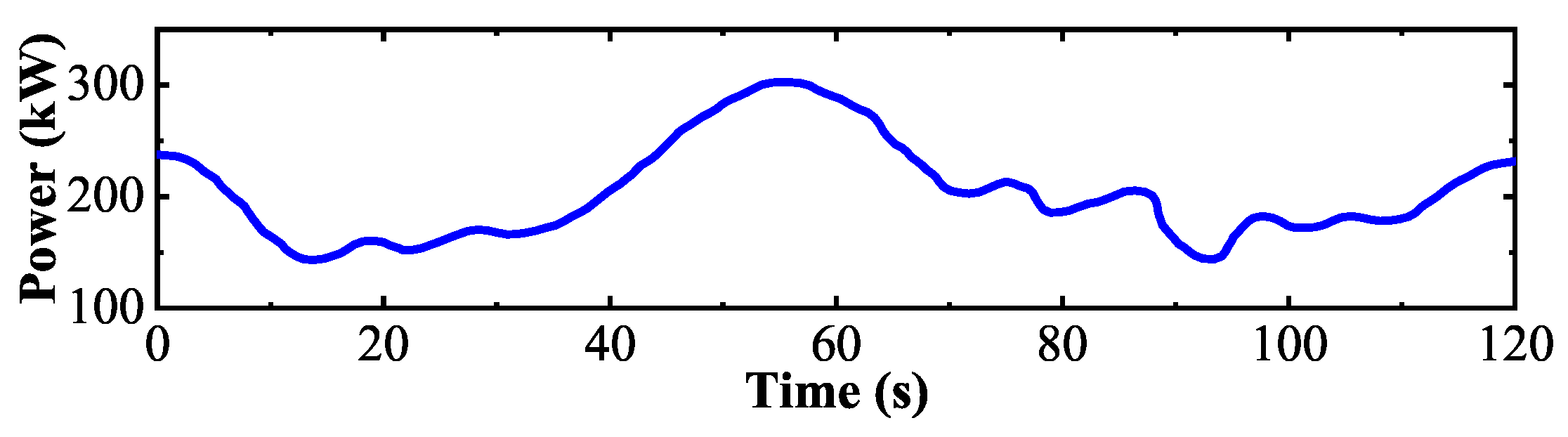
5. Numerical Results

To evaluate the performance of the proposed mid-level controller in an islanded microgrid, a modified CIGRE medium-voltage benchmark network was modeled and simulated exclusively in MATLAB/Simulink. This platform was selected because it provides a comprehensive environment for system-level modeling, control design, and time-domain simulation, offering robust numerical solvers and block libraries well-suited for microgrid dynamics and controller validation. The schematic of the test system is presented in Figure 7 [2]. The benchmark represents a European medium-voltage network with a total installed capacity of 5 MVA, comprising two diesel-based synchronous generators (SGs) connected to buses #1 and #3, a wind turbine (WT) at bus #11, and an energy storage system (ESS) at bus #6. The network includes 13 critical loads, while the feeders are represented by 14 coupled $\pi$-sections. Further details on the system configuration and parameters are provided in [2].

The ESSs at buses #6 and #4 have a maximum power rating of 300 kW and an energy rating of 6000 kWh, and are connected through bidirectional voltage source controllers. The minimum acceptable SOC for the ESSs is 600 kWh. The WT at bus #11 has a nominal rating of 800 kVA. The nominal ratings, operating cost coefficients, start-up/shut-down costs, and ramp rates are provided in [2]. The diesel-based SGs connected to buses #1 and #3 are responsible for voltage regulation using the proposed FVC. These diesel-based SGs act as the master controllers for reactive power sharing, while the batteries and wind turbine (WT) serve as slave units supplying or consuming reactive power. The WT generation over a 120-second period is depicted in Figure 8 [2]. Various initial values for the FVC were tested, with the best performance obtained using time constants of ${\tau }_1=0.015$ s and ${\tau }_2=0.75$ s. The effectiveness of the DVFC during wind fluctuations is evaluated by comparing the microgrid response with and without its presence. The wind power fluctuates between 15% and 35% of the 800 kVA rating, as shown in Figure 8. The initial values for utility weights are set to 0.25 for $w_x$, where $x\in \{\mathcal{F},\mathcal{V},\mathcal{C},\mathcal{E}\}$. Pre-training of the networks is performed on 15,000 scenarios.

5.1. Dominant Eigenvalue Traces Versus System Parameters

We investigate the impact of DVFC inputs on the microgrid’s small-perturbation stability by monitoring the dominant eigenvalues. Controller gains are varied independently around their nominal values within specific intervals, and the resulting eigenvalue trajectories are shown in Figure 9 with respect to changes in K, $\kappa$, $K_{\delta }$, $m_p$, and $n_p$. The eigenvalues for power sharing mode and FVC gains correspond to the low-frequency critical mode of the microgrid, and are particularly sensitive to variations in these parameters. Consequently, eigenvalues along the real axis are closely associated with the frequency dynamics of the ESS and the FVC behavior of the SG, whereas the complex conjugate eigenvalues represent the voltage dynamics of inverter-interfaced ESS. In the DVFC scheme, the stability index (SI) varies from $104\%$ for $0.8K_{i0}$ to $80\%$ for $1.6K_{i0}$, demonstrating improved robustness and stability compared to the changes in the frequency droop controller while maintaining the same power-sharing behavior.

Figure 9 shows that increasing $K_{\delta }$ initially improves the microgrid damping metric until a point where further increments lead to deterioration in overall microgrid damping. It is observed that $K_{\delta }=1.5$ results in the best stability margin and microgrid damping, hence, this value is selected as the FVC gain for time-domain simulation studies. We also assess the time delay margin for each controller to ensure microgrid stability. The time delay margins for the mid-level controller and the secondary controller are 13.2 seconds and 55 seconds, respectively, under stable microgrid operation.

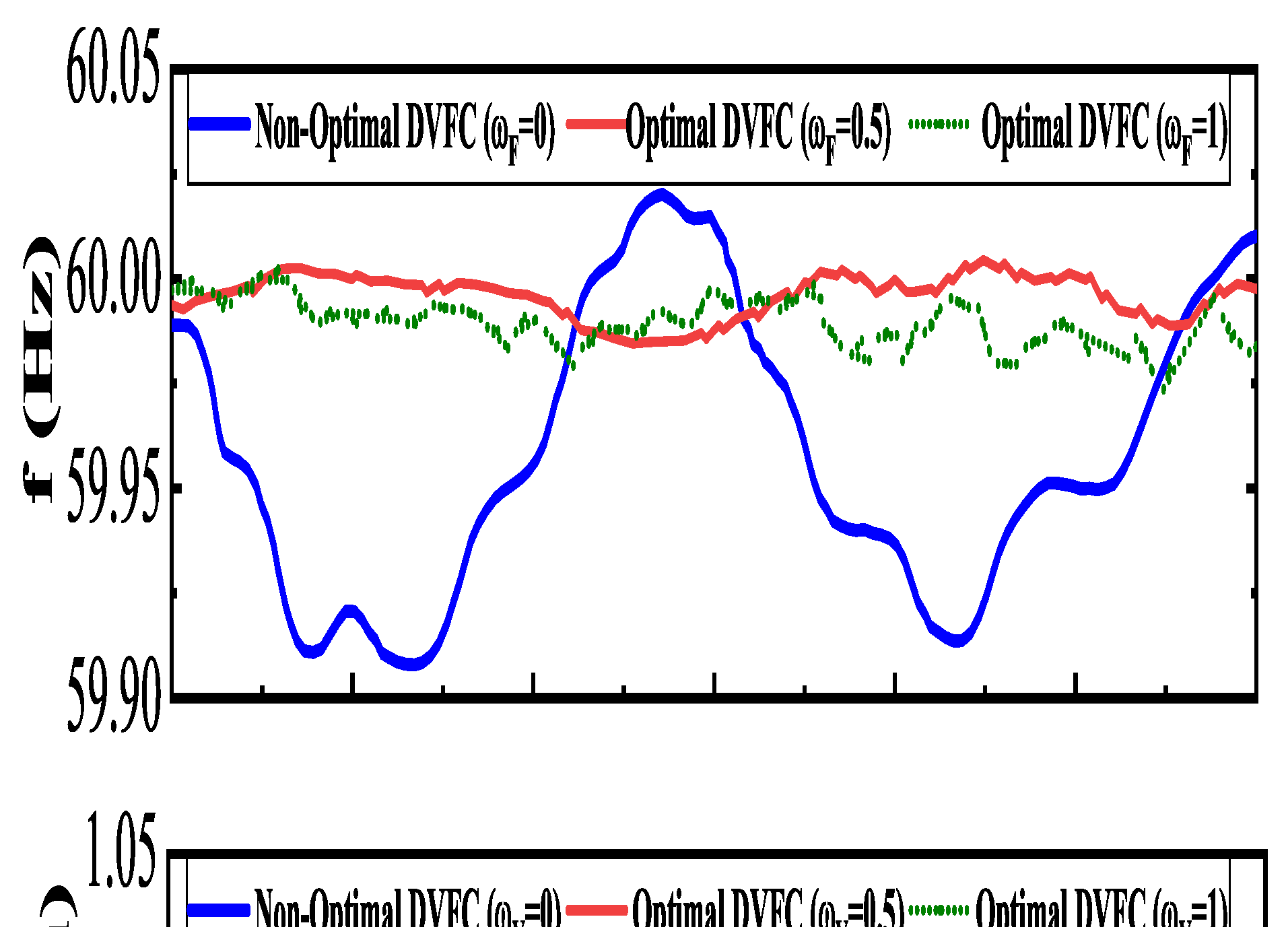
5.2. DVFC for Frequency and Voltage Regulation (Scenarios 1 and 2)

In Scenario 1, the weight $w_{\mathcal{F}}$ associated with frequency regulation is tested over a range from 0 to 1 to evaluate the effectiveness of the cost-to-go function for frequency response. Figure 10 shows the frequency response under different weights, indicating that $w_{\mathcal{F}}=1$ yields a smaller frequency deviation from the nominal value compared to the non-optimal DVFC ($w_{\mathcal{F}}=0$). In Scenario 2, with $0\le w_{\mathcal{V}}\le 1$, the voltage regulation is analyzed to minimize the bus voltage deviation from its nominal value. Figure 10 illustrates that the voltage deviation is maintained within the acceptable operating range of [$0.95,1.05$] pu ($V_{base}=400$ V), compared to a non-optimal solution where the voltage profile drops below $0.95$ pu under wind fluctuations. Overall, the DVFC is capable of providing smooth frequency and voltage regulation as wind power increases up to 35%.

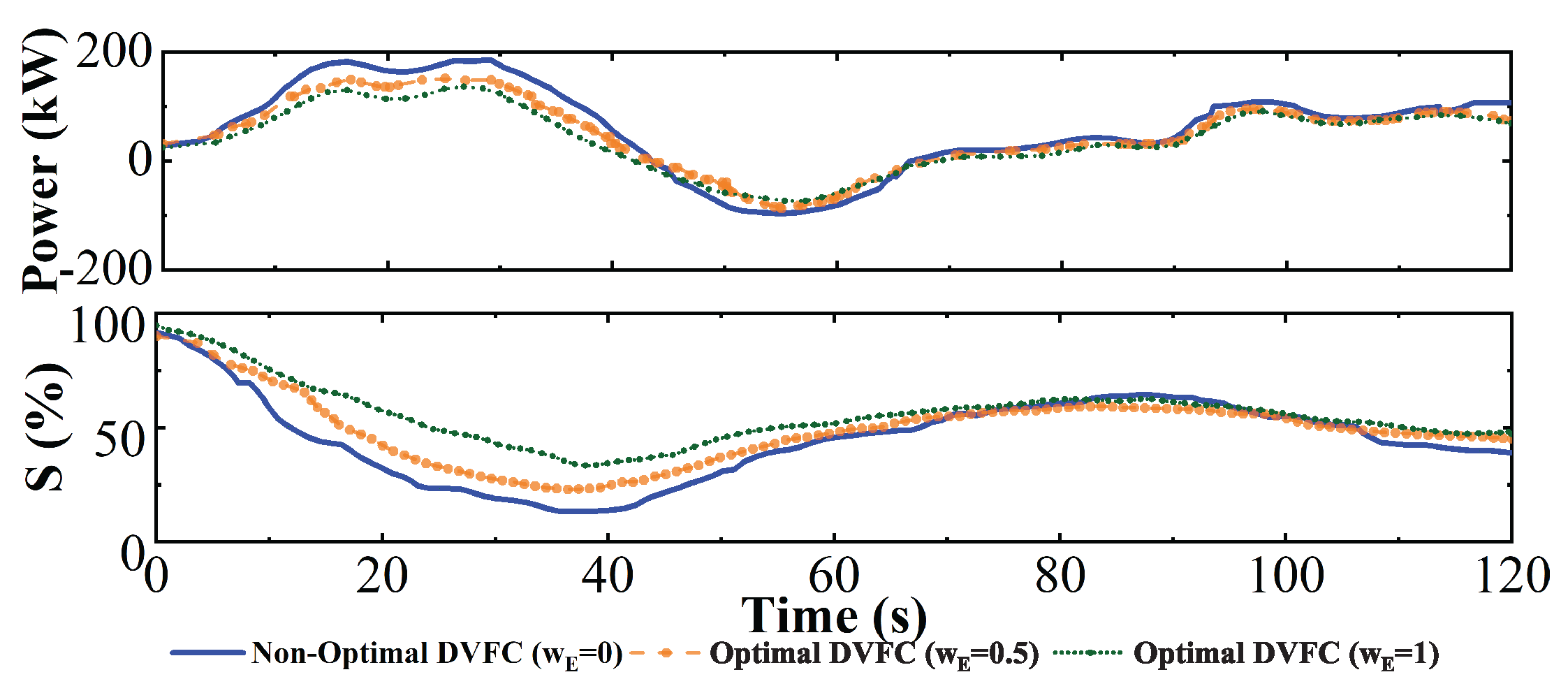
5.3. DVFC Versus ESS Penetration (Scenario 3)

An ESS is connected to bus #6 and is charged or discharged based on the power supply imbalance in the microgrid. The ESS has a regulation capacity of 30 MW/Hz [23], which allows for higher frequency response compared to the diesel-based SGs. To achieve a longer ESS lifetime and improve active/reactive power sharing control, we utilize a droop control model based on Equation (1). Initially, the ESSs are fully charged (approximately 94%), and the minimum state of charge (SOC) is set at 10%. The required ESS capacity over the 120-second interval is assumed to be 20 kWh, with wind power fluctuations as shown in Figure 8, repeating periodically 30 times in an hour. Thus, the ESS should be large enough to store 600 kWh. As shown in Figure 11, the DVFC approach results in a reduction of discharged power compared to the non-optimal one, maintaining the ESS’s SOC within a desired range, which improves the ESS lifecycle over the long term. It is assumed that the charging and discharging modes of the ESS follow the pattern shown in Figure 11 more than 30 times per hour. The lifecycle of Li-ion batteries can be doubled by changing the ESS depth of discharge level. Consequently, the ESS lifecycle is estimated at 2000 cycles for non-optimal DVFC ($w_{\mathcal{E}}=0$), 3500 cycles for optimal DVFC with $w_{\mathcal{E}}=0.5$, and 4200 cycles for optimal DVFC with $w_{\mathcal{E}}=1$.

5.4. Minimum Operating Cost by DVFC (Scenario 4)

Scenario 4 is conducted to evaluate the performance of the DVFC in achieving a more efficient dispatch solution in the CIGRE test case. In this scenario, only diesel-based SGs are considered as dispatchable generators, while the wind turbine (WT) serves as the non-dispatchable generator with wind power penetrations of 30% and 35%. Similar to scenarios 1-3, the DVFC’s performance is compared with that of the non-optimal solution ($w_{\mathcal{C}}=0$) over a 120-second duration. Figure 12 shows the power generation from the diesel unit at bus #3. A higher weight for the cost utility function results in lower power generation from the diesel generators, which act as cost-driven units.

To validate the effects of the operating cost and energy generated by the diesel-based SGs, the system is simulated for 24 hours with dispatch intervals of 55 seconds (i.e., $t=55$ s). Table 2 shows that the operating cost of the DVFC is lower compared to conventional UC, indicating that the conventional UC overestimates the required energy from expensive diesel-based SGs during each sub-interval. The DVFC reduces the operating cost by 3.83%, resulting in savings of $2016 per day compared to conventional UC.

5.5. Optimum Performance of DVFC (Scenario 5)

The best performance of DVFC from all utility functions is obtained to demonstrate how the DVFC results in the optimum dispatch solution. We define performance indices (PIs) for frequency and voltage, given by

$$\begin{array}{cc}\hfill & P{I}_{\mathcal{F}}=\sum _{t=1}^{n_T}\sum _{m=1}^{n_m}{\displaystyle \frac{|{\omega }_m^t-{\omega }_0|}{{\omega }_0}}\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & P{I}_{\mathcal{V}}=\sum _{t=1}^{n_T}\sum _{m=1}^{n_m}{\displaystyle \frac{{\sum }_{b\in \mathcal{B}}|V_{i,m}^t-V_0|}{V_0}}.\hfill \end{array}$$

(25)

To validate the advantage of the proposed DVFC compared to the conventional UC, three deterministic load and wind turbine (WT) profiles are considered. The conventional UC is evaluated using a MINLP approach with the CPLEX solver over a 24-hour operation period. The multi-objective function is solved using a fuzzy weighted sum algorithm. Optimal solutions for each normalized utility function are obtained separately and then ranked based on a fuzzy Pareto front selection. The optimal weights for all normalized utility functions are $w_{\mathcal{F}}=0.12$, $w_{\mathcal{V}}=0.15$, $w_{\mathcal{E}}=0.28$, and $w_{\mathcal{C}}=0.45$ (with ${\sum }_{i\in \{\mathcal{F},\mathcal{V},\mathcal{E},\mathcal{C}\}}{w}_i=1$). Table 3 summarizes the differences between the DVFC and the conventional UC based on four different indices. The conventional UC optimizes different objective functions in each iteration, focusing on two main objectives: a cost-driven function (CDF) and an ESS-driven function (EDF).

To evaluate the DVFC’s performance over a 24-hour period, four different models—cost-driven function (CDF), ESS-driven function (EDF), a combined CDF and EDF without frequency and voltage regulation, and the proposed DVFC—are compared in Table 3. The proposed DVFC shows improvements of 40-50% and 60-65% in frequency and voltage performance indices (PIs) compared to conventional UCs, respectively. The minimum ESS lifecycle degradation, denoted as $\Delta \mathcal{E}=133.1$, is achieved by the individual EDF model, while the minimum operating cost ($\Delta \mathcal{C}=\$50,688$) is achieved by the individual CDF model.

Although the DVFC demonstrates higher operating cost and ESS lifecycle degradation compared to the individual CDF and EDF models, it strikes a balance between optimizing operating cost and minimizing ESS lifecycle degradation while maintaining minimal deviations in frequency and voltage from their desired values. Furthermore, the DVFC exhibits superior performance in covering the net demand profile compared to the conventional UC, as shown in Figure 13. The DVFC reduces the uncovered net demand profile to less than 30% of that observed with the conventional UC, reducing the uncovered energy from 14.85 kWh to 4.7 kWh.

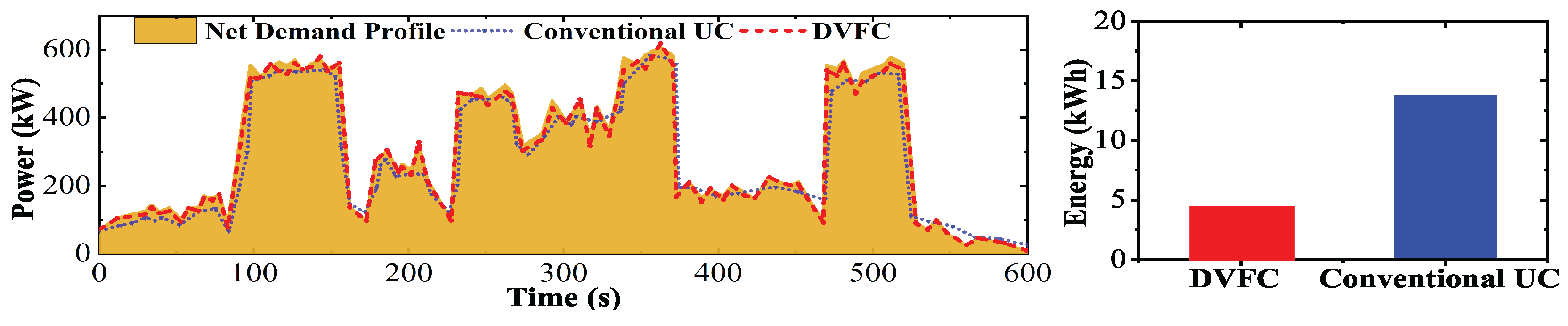
5.6. Plug and Play Functionality of DVFC (Scenario 6)

The plug-and-play functionality is tested by disconnecting diesel-based SG #1 at $t=20$ seconds and reconnecting it at $t=40$ seconds during each minute. This test is repeated for a one-hour simulation (i.e., 60 events) to validate the effectiveness of the DVFC. During the downtime, a synchronization action is performed to synchronize SG #1 with the remaining islanded microgrid before reconnection. Control parameters are the same as in Scenario 1. Two frequency and voltage indices are defined to evaluate the DVFC’s performance during this process. Table 4 presents the average frequency deviation in three cases—UC without ESS, UC with ESS, and DVFC—over the one-hour operation. The DVFC significantly reduces the frequency deviation, ${\sum }_{n=1}^{60}\left({\int }_{20}^{40}\left|\Delta \omega \left(t\right)\right|dt\right)$, during the plug-and-play functionality.

Additionally, the impact of this process on the voltage deviation at bus #1, denoted as ${\sum }_{n=1}^{60}\left({\int }_{20}^{40}\left|\Delta V_1\left(t\right)\right|dt\right)$, is found to be negligible for the DVFC approach compared to the UC model. The ESS utilization is also reported in Table 4, indicating that with the DVFC controller, ESS utilization decreases by 30%, resulting in an active energy saving of approximately 1.32 kWh for each plug-and-play event. Without loss of generality, the DVFC controller ensures accurate power sharing, as well as frequency and voltage regulation, despite the connection and disconnection of SG #1.

6. Conclusion and Future Work

This paper presents a DVFC for an islanded microgrid, aimed at optimizing the operating cost of dispatchable units and extending the ESS lifecycle while maintaining frequency and voltage within a desired range. The DVFC serves as a mid-level controller, bridging the time intervals between the primary and secondary controllers and avoiding the stair-pattern generation scheduling observed in conventional UCs. The DVFC leverages dynamic programming to approximate microgrid operating cost, battery lifecycle, and frequency/voltage regulation requirements for upcoming time steps, thereby determining optimal dispatches for DG units. The DVFC does not require a detailed mathematical model of the microgrid to calculate utility functions such as voltage and frequency regulation. Through several scenarios tested in a modified CIGRE microgrid, it has been demonstrated that the DVFC significantly reduces frequency and voltage deviations from their desired values, and minimizes the operating costs of DGs. The optimal control policy of the DVFC extends the battery lifecycle by up to twofold. With appropriate training and parameter configuration, the DVFC can make islanded microgrids self-adaptive, stable, and efficient in terms of cost and ESS utilization. In future studies, we will focus on extending the DVFC concept to handle the disconnection and reconnection of generation and load units, as well as incorporating dynamic state predictions such as wind power generation.