1. Introduction
The idea of constructing quasi resonant (QR) converters has its origin in papers by K.-H. Liu and F.C. Lee. The concept is explained with the help of the Boost converter and the topologies of a family of converters are depicted in [
1]. The QR Buck converter is explained and a family of QR converters can be found in [
2]. A concept for the syntheses of QR converters based on graph theory is shown in [
3]. QR topologies, including the forward and the flyback converters, are shown in [
4]. A ZVS Zeta for high frequencies and for generating two output voltages is treated in [
5]. A comprehensive reliability assessment of the QR Buck converter is given in [
6]. An adaption of a QR converter between a power interface and an inverter for driving an induction machine is used in [
7]. A theoretical method to study transients in QR converters is explained for a Buck converter in [
8]. One drawback of the QR concept is that it should be used for not too large changing outside parameters. This is treated for the Boost converter in [
9]. A ZVS QR Boost converter is studied by using the simulation tool Matlab/Simulink in [
10]. Starting from the Boost converter, a QR converter for photovoltaic application is studied in [
11]. The effect of reducing the electromagnetic interference (EMI) of a DC/DC converter, when using the QR, is shown in [
12]. An interesting combination of data transmission and power conversion is treated in [
13]. There a Buck converter is used. A ZCS Boost converter is studied with the state-plane in [
14]. A method to get constant switching frequency for a QR converter, demonstrated with a Boost converter, is proposed in [
15]. A QR flyback converter, which switches not at zero but at a low value, which is detected by a special circuit, is explained in [
16]. A comprehensive study concerning Cuk, Zeta and Sepic converters can be found in [
17]. The application of the ZVS QR concept on the modified Boost converter is demonstrated in [
18]. It should be mentioned that all pulse width modulated (pwm) DC/DC converters with one switch can be changed easily into QR converters. The basic converters are discussed in all textbooks on Power Electronics, e.g. [
19,
20,
21].
1.1. The Zeta Converter in the Steady State
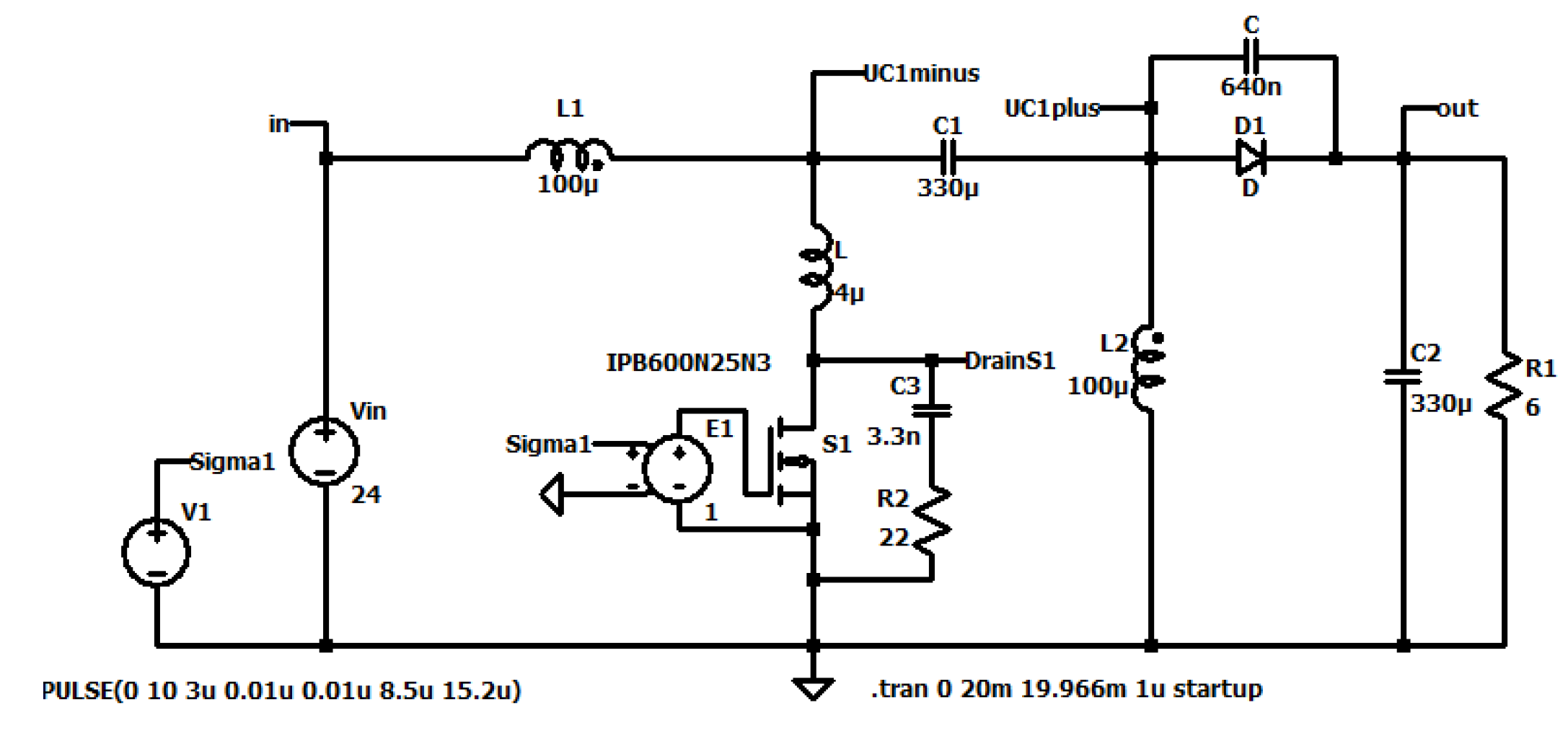
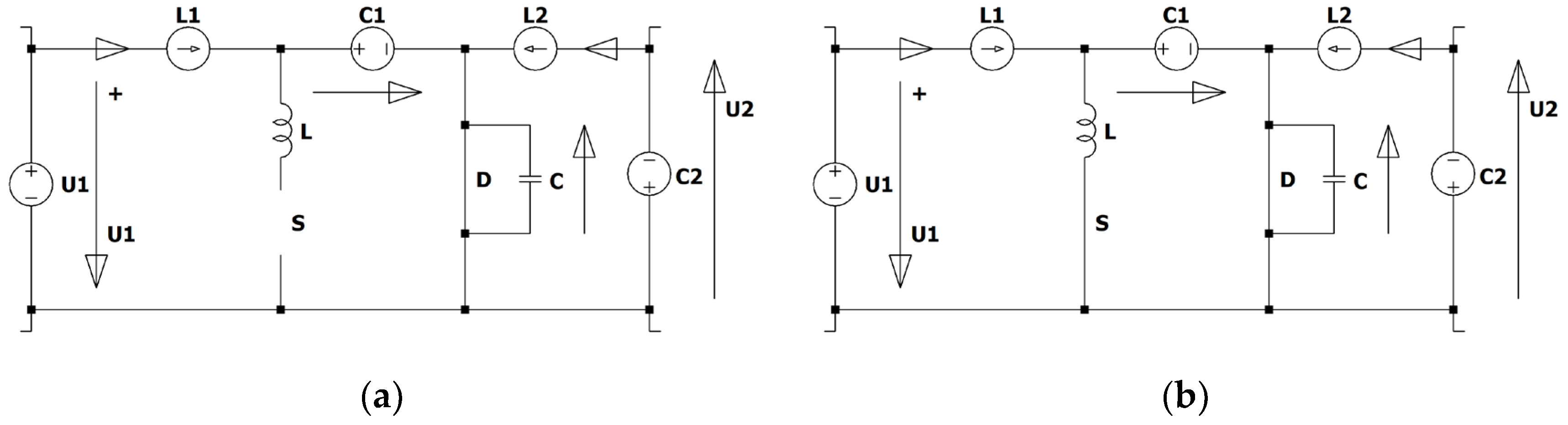
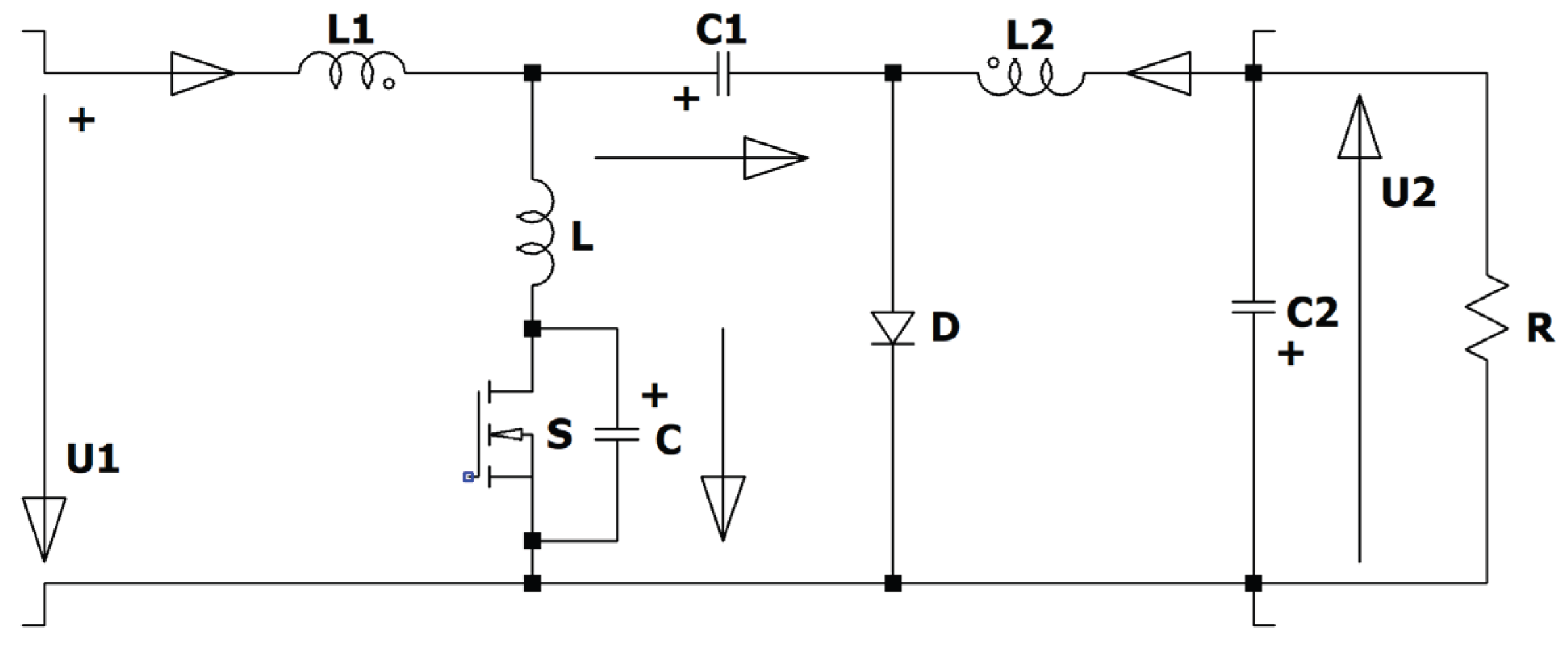
The Zeta converter (
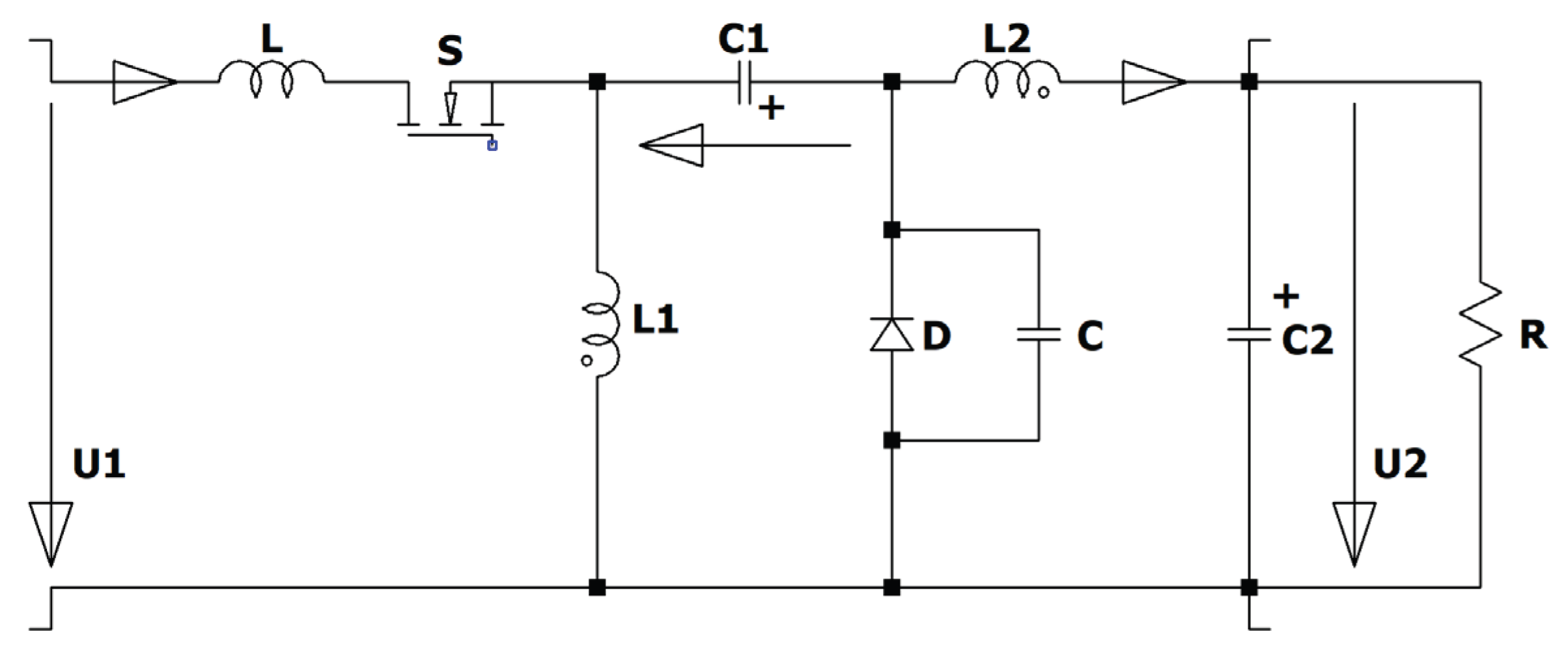
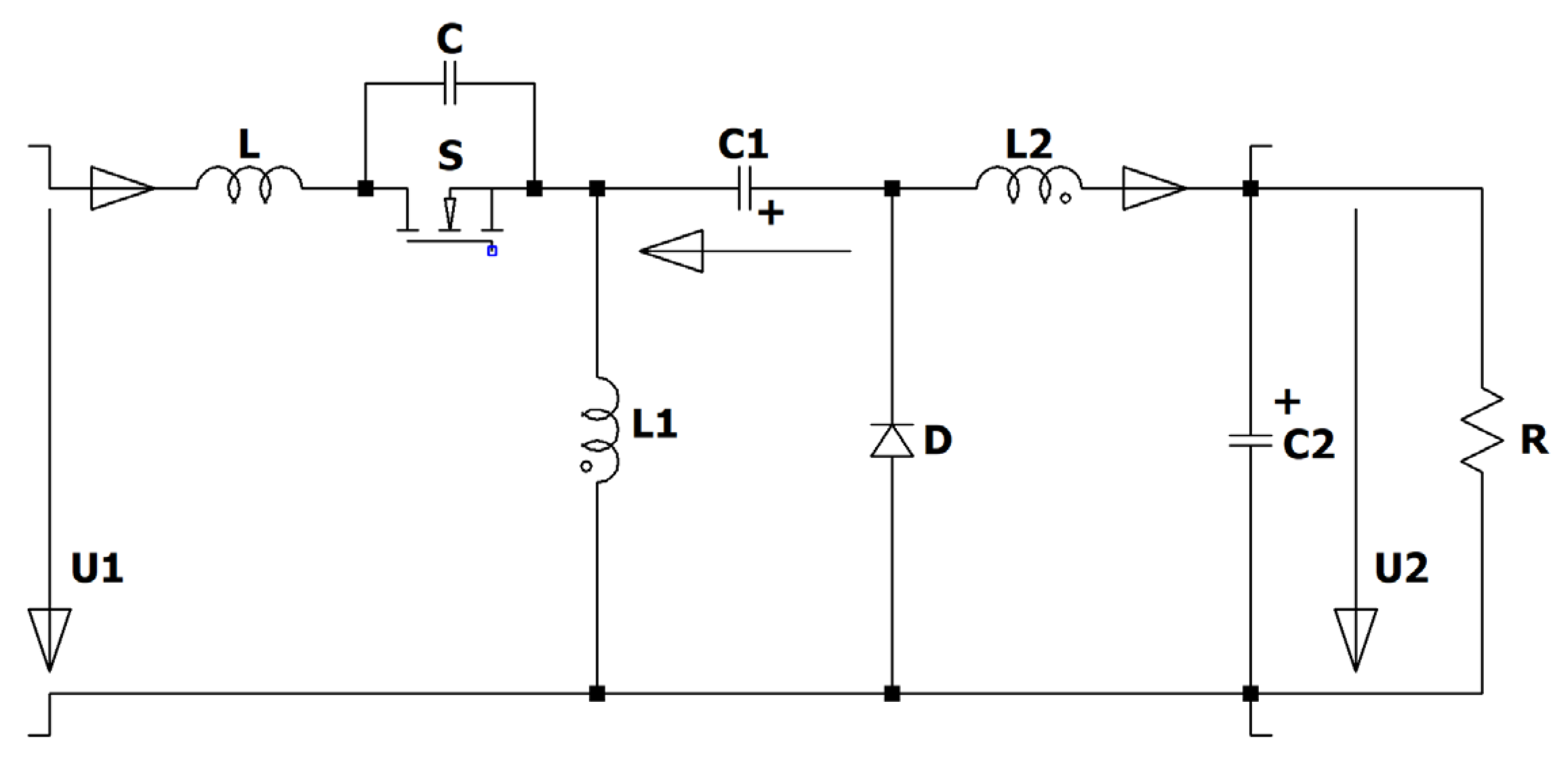
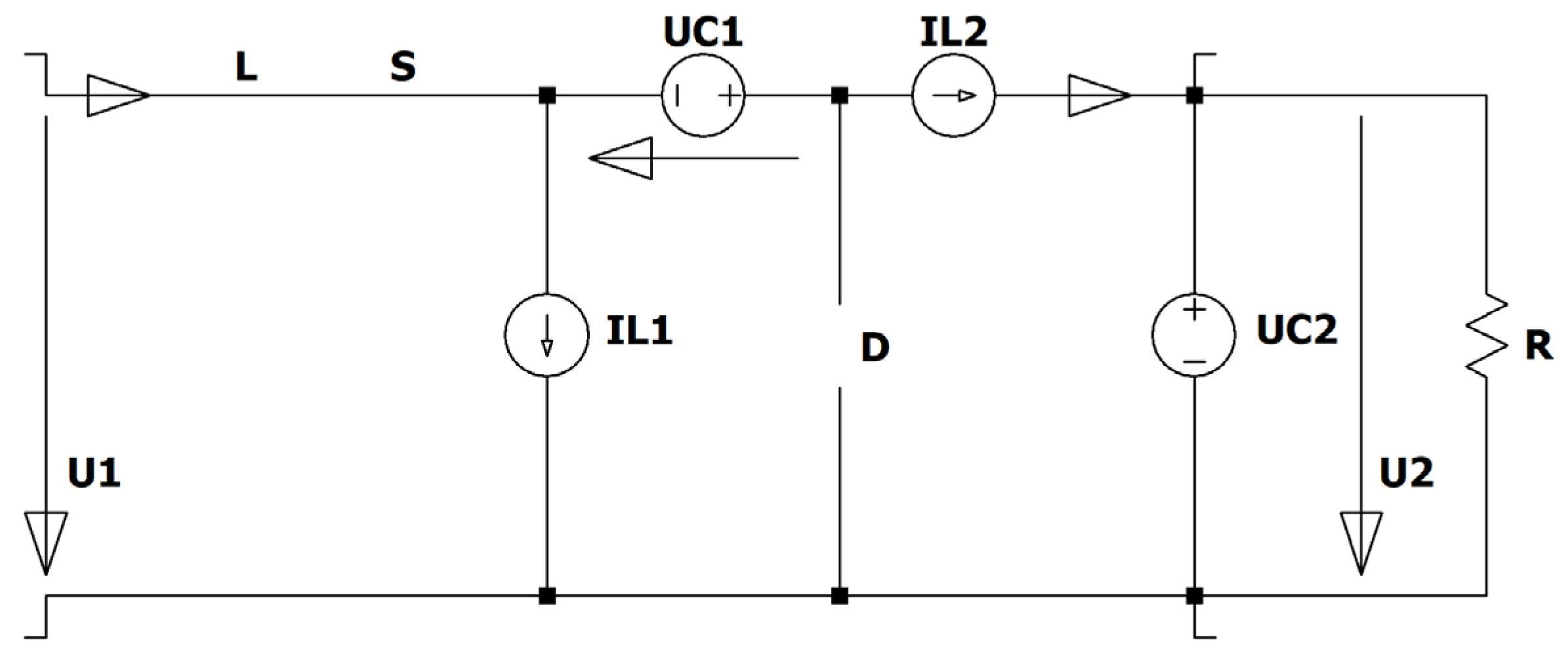
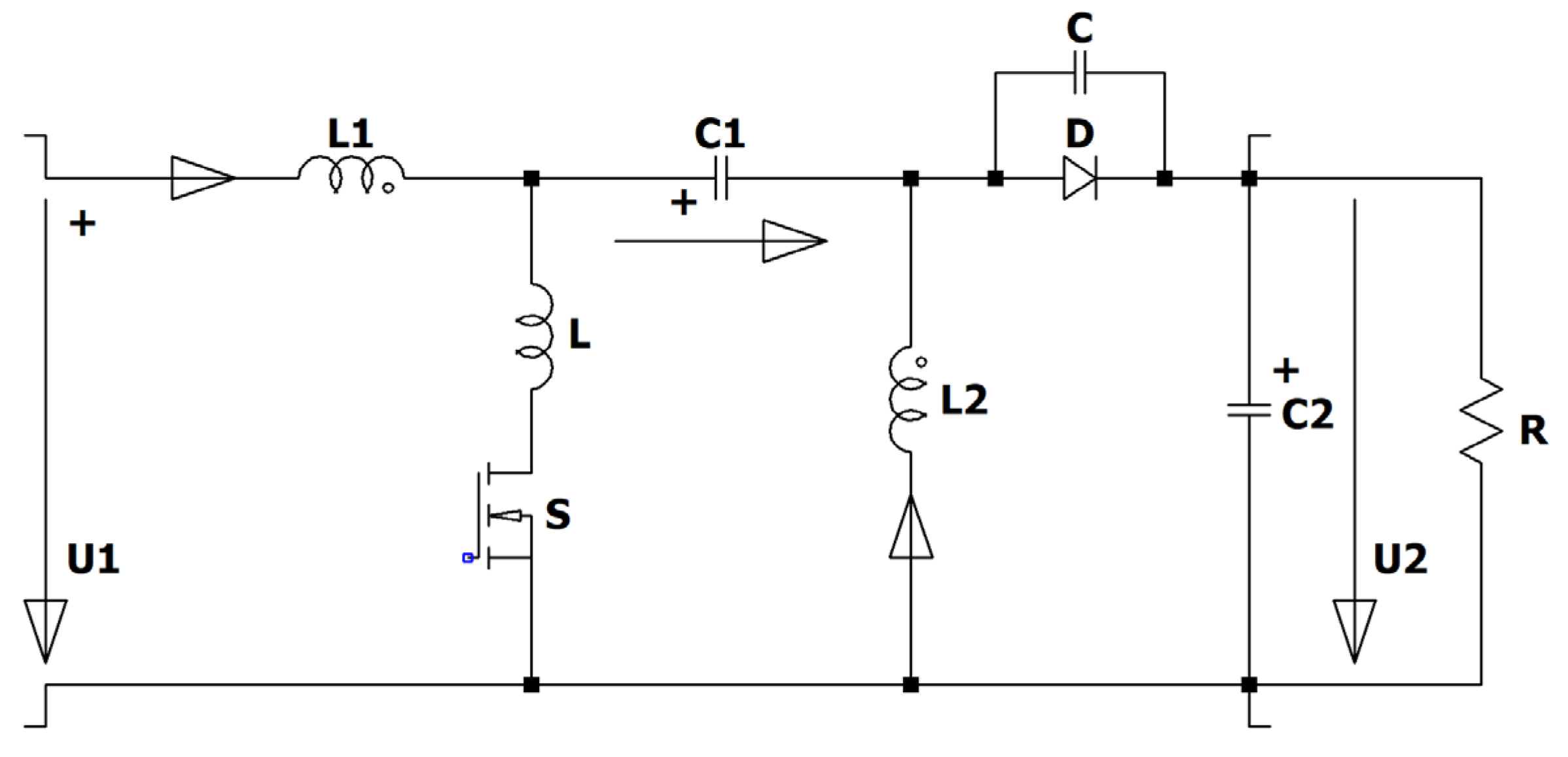
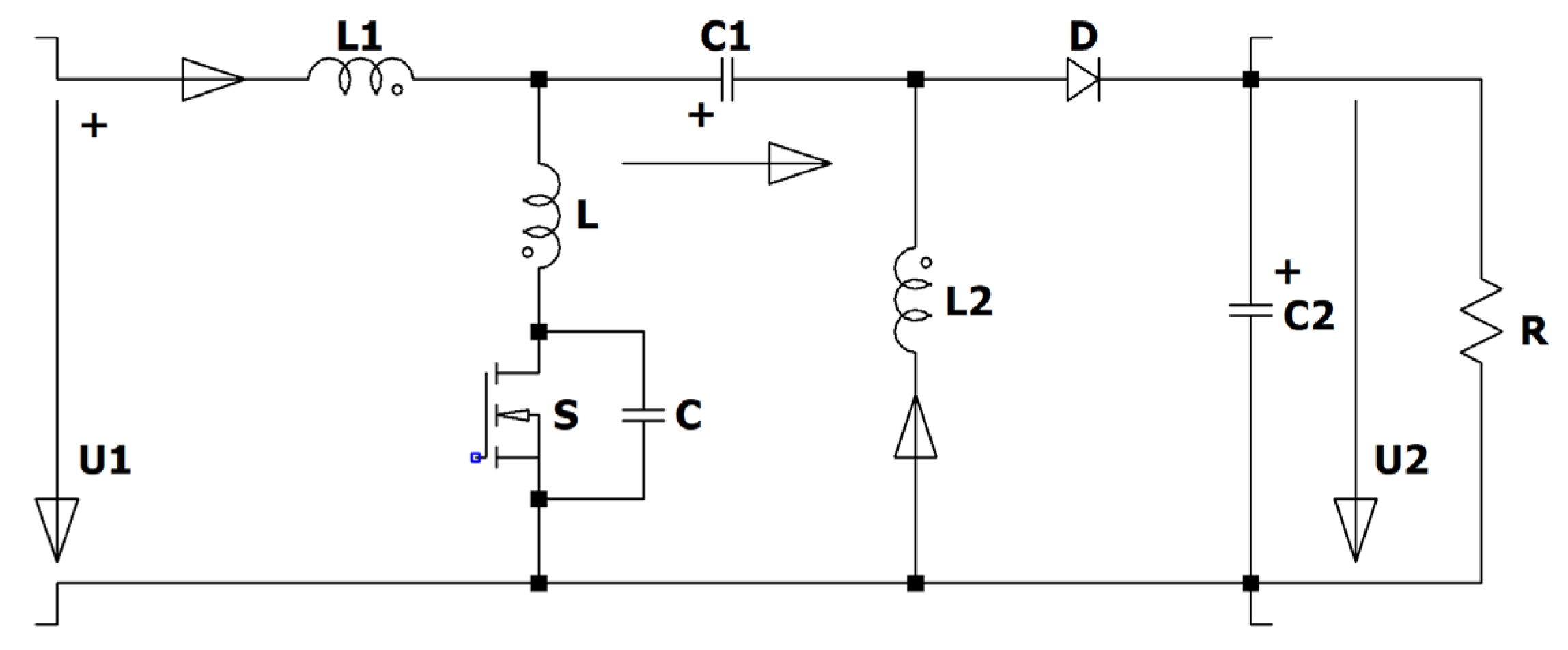
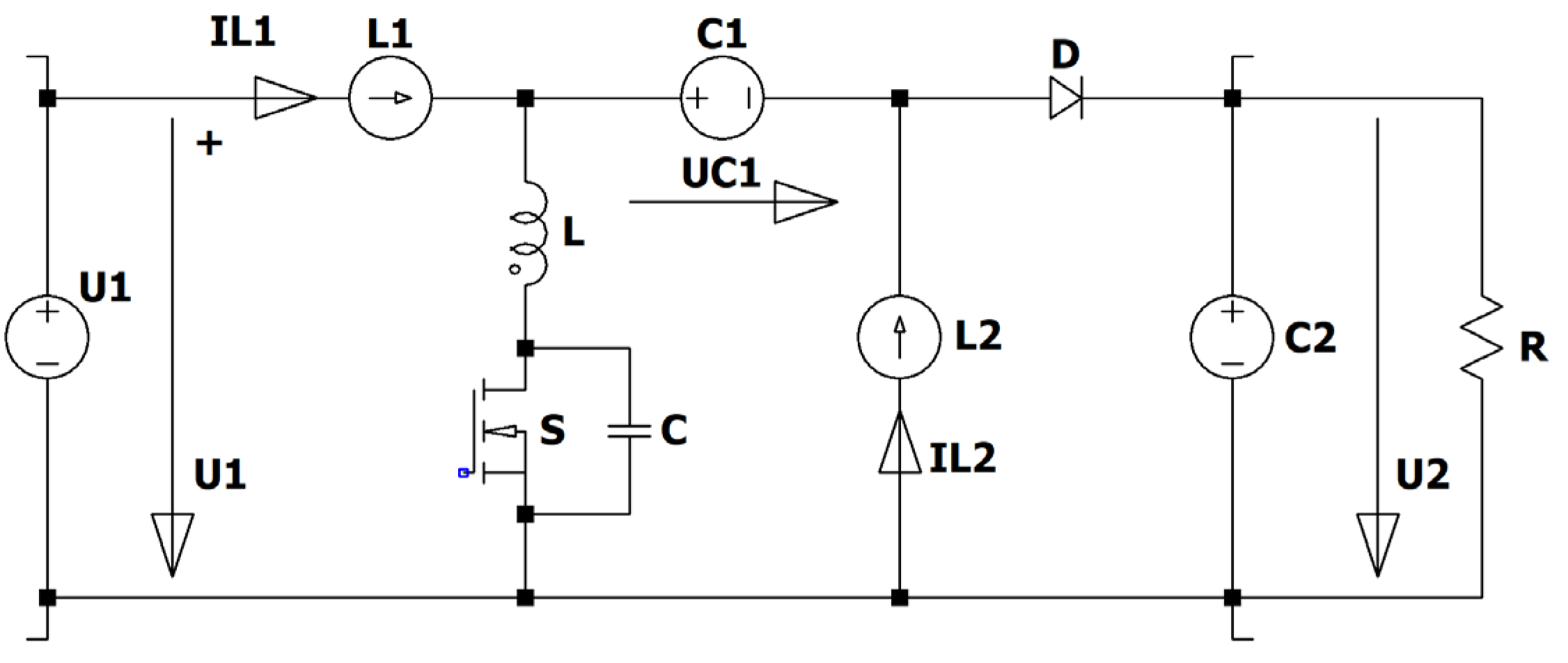
Figure 1) has interesting features. The electronic switch is in series with the input source, therefore no inrush current occurs when the converter is connected to a stable voltage source like car-batteries or a DC micro grid. The start-up is achieved by increasing the duty cycle from zero up to the desired value, so no overshot occurs, and the switch can be used as an electronic fuse in case of a short-circuit of the load or in case of no load. The converter has like the Cuk and the Sepic an intermediate capacitor which is charged. The Zeta converter is a fourth order converter consisting of two coils L1, L2, two capacitors C1, C2, an active S and a passive electronic switch D.
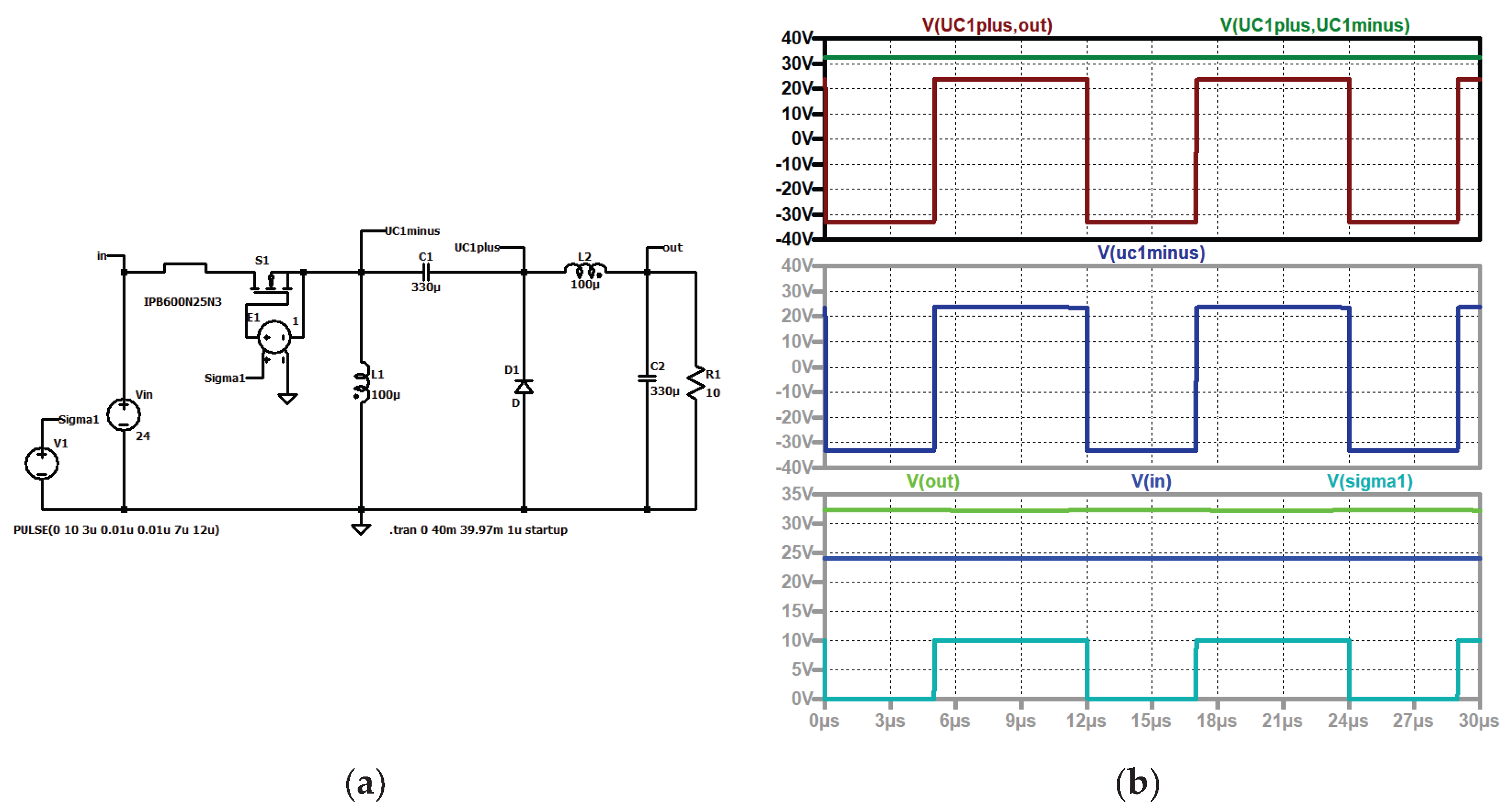
First we explain the Zeta converter in the steady state, in the continuous mode and using ideal components (no parasitic resistors, ideal switching). During the on-time of the electronic switch the input voltage is across L1, and the sum of the voltage across C1, the input voltage and the negative output voltage is across L2. The voltage across C1 must be equal to the output voltage. This is obvious when looking at the loop C1, L1, C2 and L2. In the steady state the voltage across an inductor is zero in the mean, therefore the output voltage and the voltage across the intermediate capacitor C1 must be equal. So the voltage across L2 has the same value as the one across L1. When the switch S is turned off, the current of the coils commutates into the diode D. Now the negative voltage across C1 is across L1 and the negative output voltage is at L2. The voltage across L2 looks equal to the one across L1.
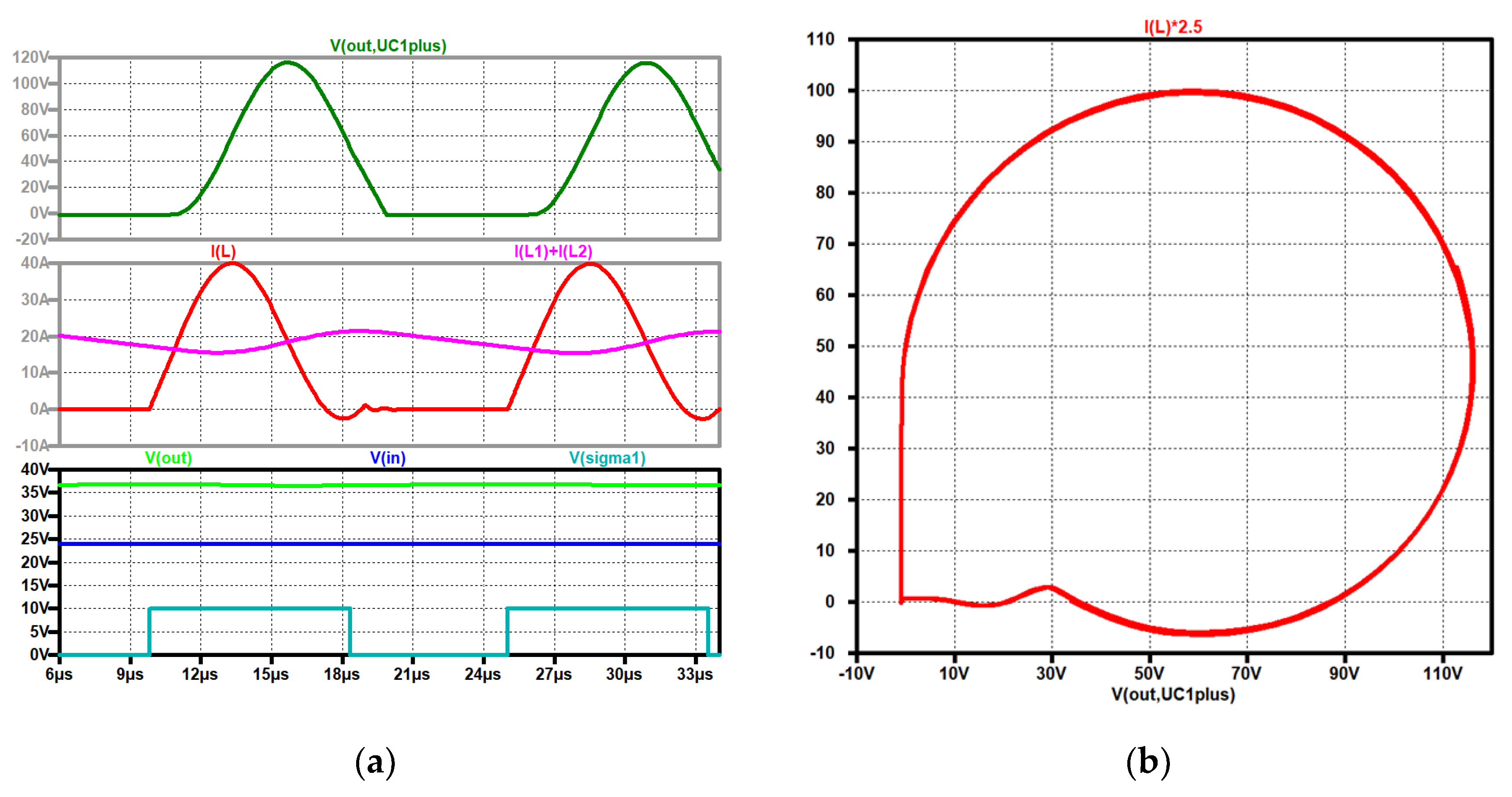
Figure 2 shows the voltage across C1, the voltages across the coils, the output and the input voltages, and the control signal of the electronic switch. The voltage across C1 and the output voltage overlap each other and therefore are drawn in different graphs.
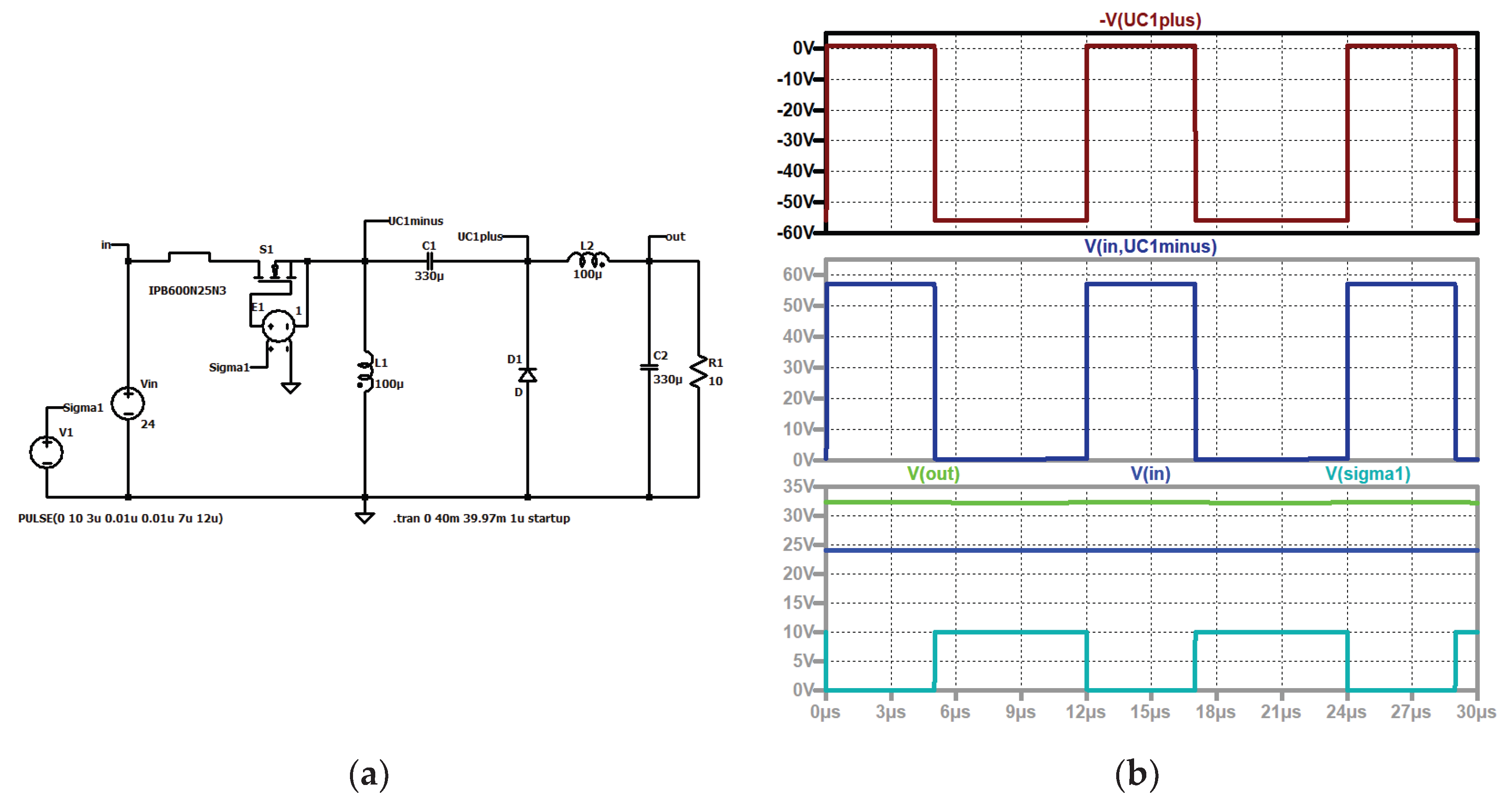
Figure 3 shows the voltage stress across the semiconductors. When the transistor is turned on, the voltage across it is zero in the ideal case, and when it is turned off, the sum of the input voltage and the voltage across C1 is blocked by the electronic switch. One can therefore observe that the sum of the input and the output voltages stresses the transistor. The negative sum of the input voltage and the voltage across C1 is blocked by the diode, when the switch is on and zero (because it turns on when the switch turns off), when the switch is off. Both semiconductors must hold the sum of the input and the output voltages (of course increased by a security factor).
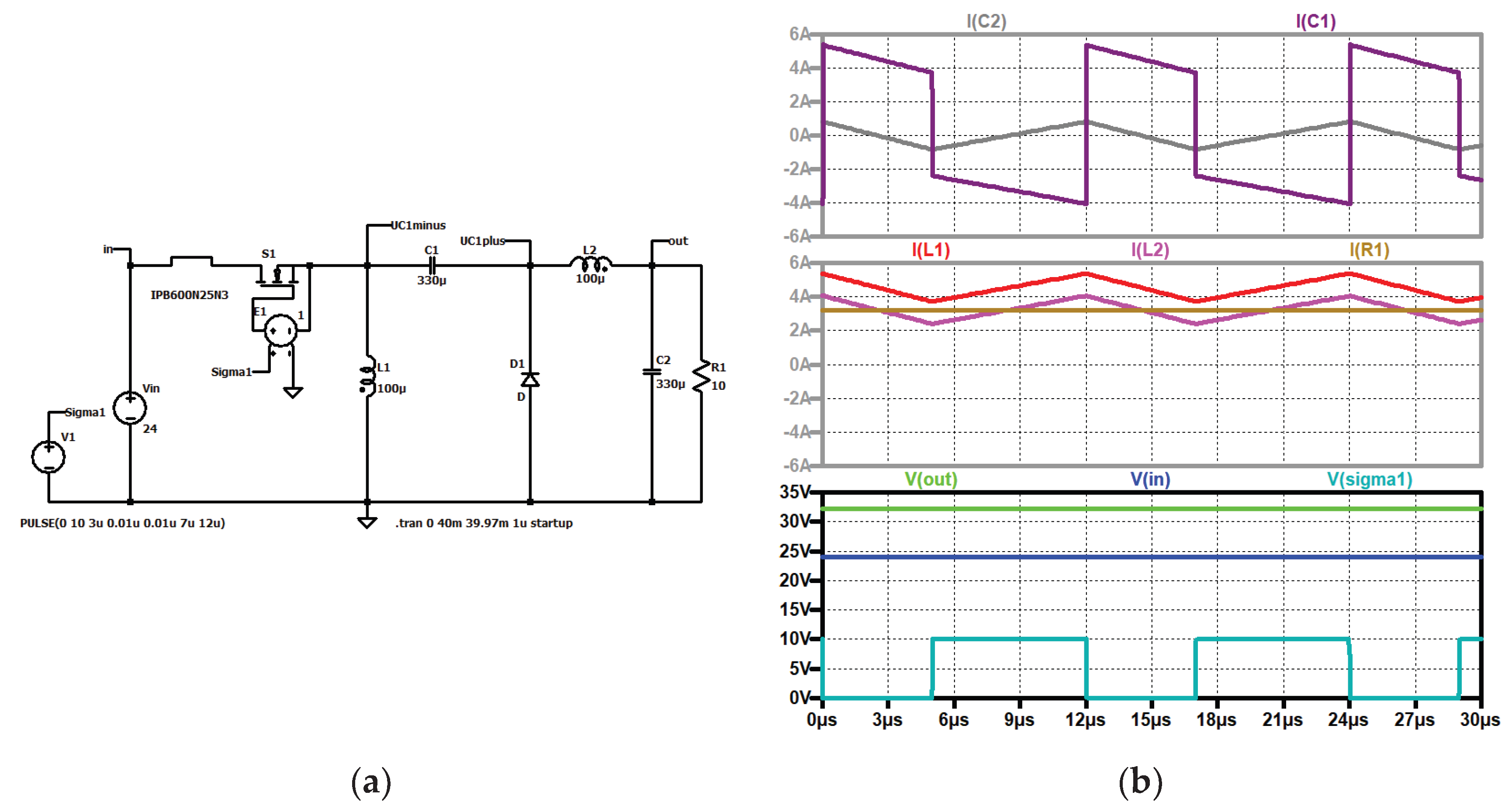
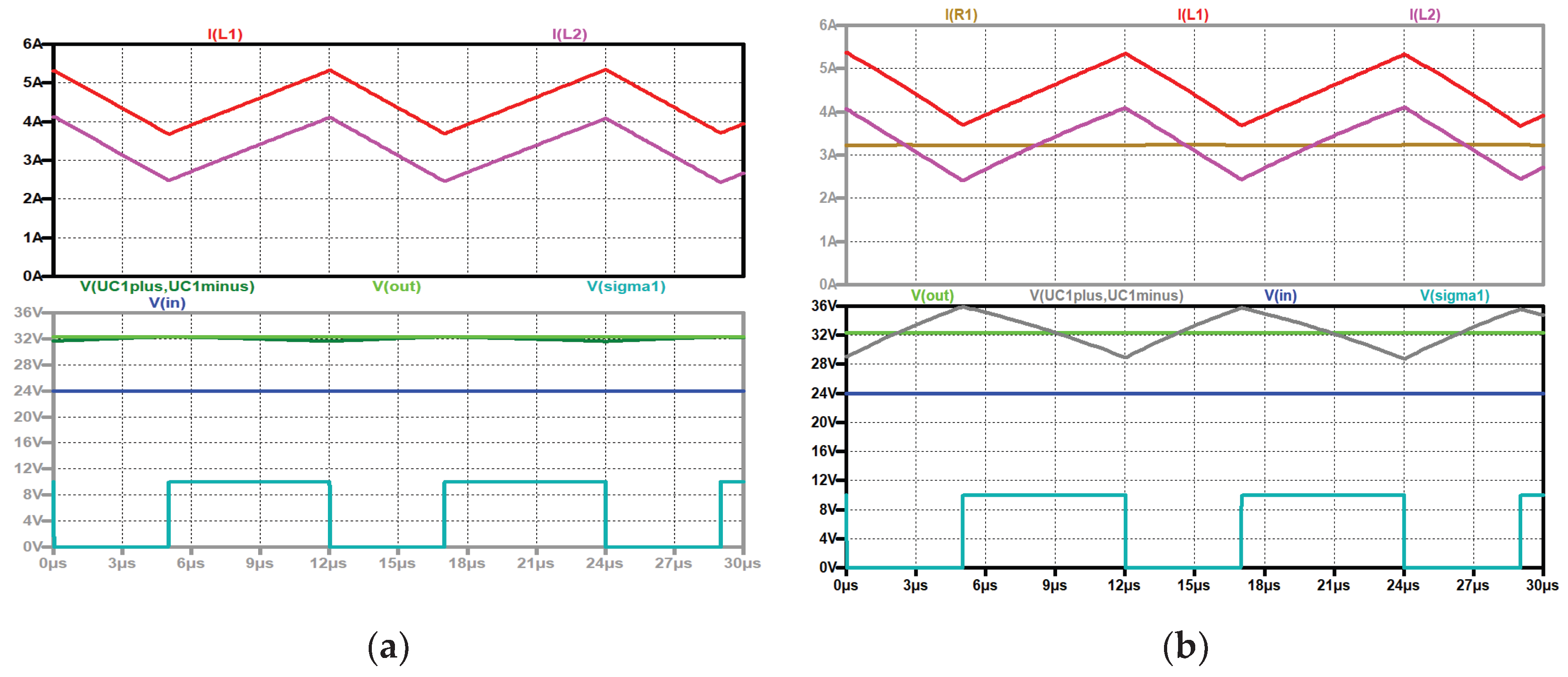
The current through the coils increases during the on-time of the switch and decreases during the off-time. It is obvious that the mean current through the output coil L2 is equal to the load current. The load current is nearly constant. The current through the output capacitor corresponds to the current ripple of the output coil L2. During the on-time the capacitor C1 is discharged by the current through L2 and charged during the off- time by the current through L1.
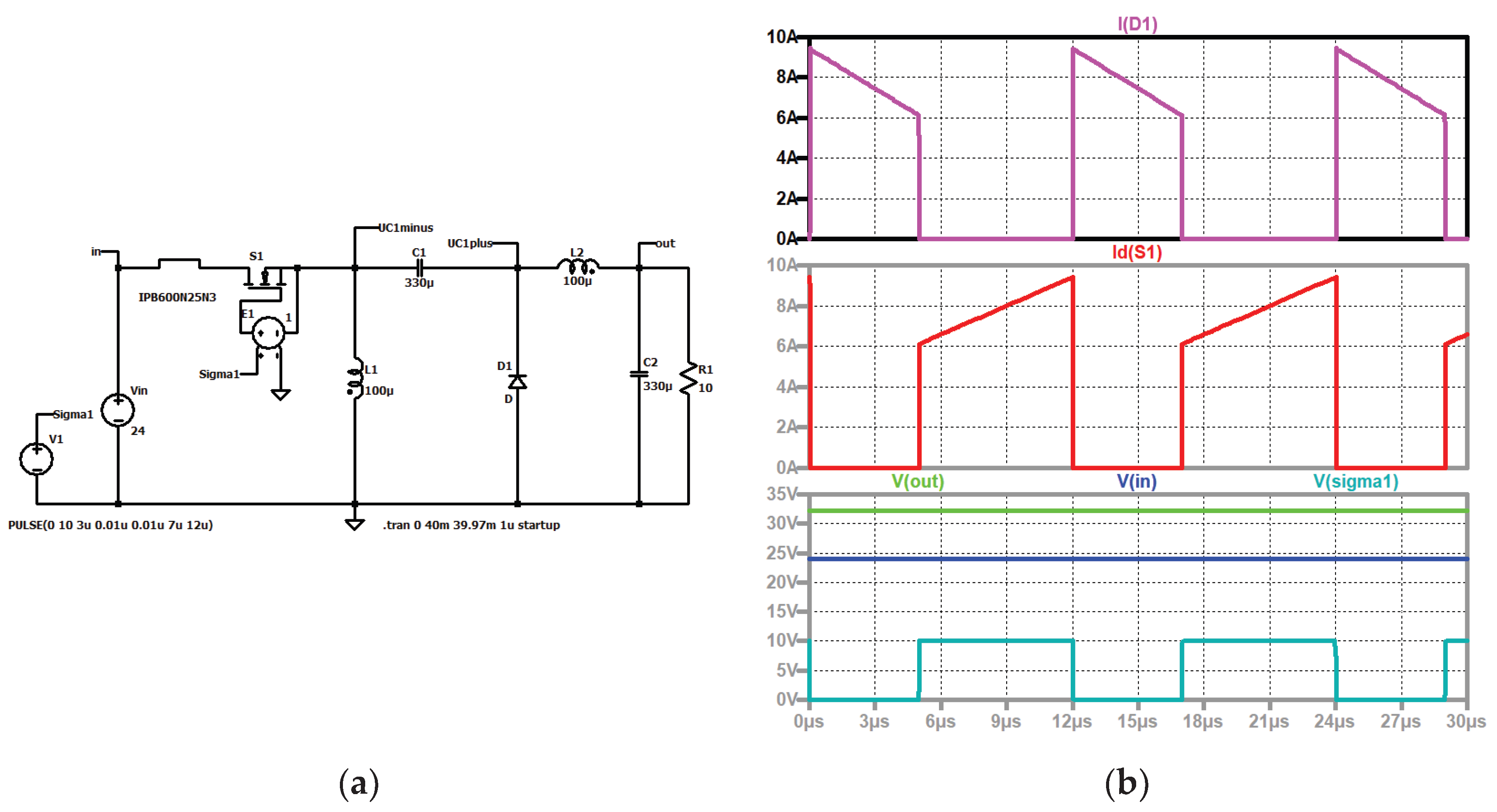
Figure 4 depicts the currents through the capacitors, the coils, and the load current. The input and the output voltages and the control signal of the electronic switch are also shown. The current through the semiconductors is the sum of the currents through the coils as shown in
Figure 5.
1.2. Influence of the Intermediate Capacitor
In the
Figure 2,
Figure 3,
Figure 4 and
Figure 5 the intermediate capacitor is large (330 µF), so the voltage across it is nearly constant. The output voltage is smoothed by the LC filter composed of the coil L2 and the output capacitor C2. A ripple across C1 is therefore permissible. A pulse capacitor can be used instead of an electrolyte capacitor.
Figure 6 shows the influence of the value of the intermediate capacitor. The currents through the coils, the load current, the input voltage, the voltage across C1, the output voltage and the control signal of the electronic switch are shown for two capacitor values.
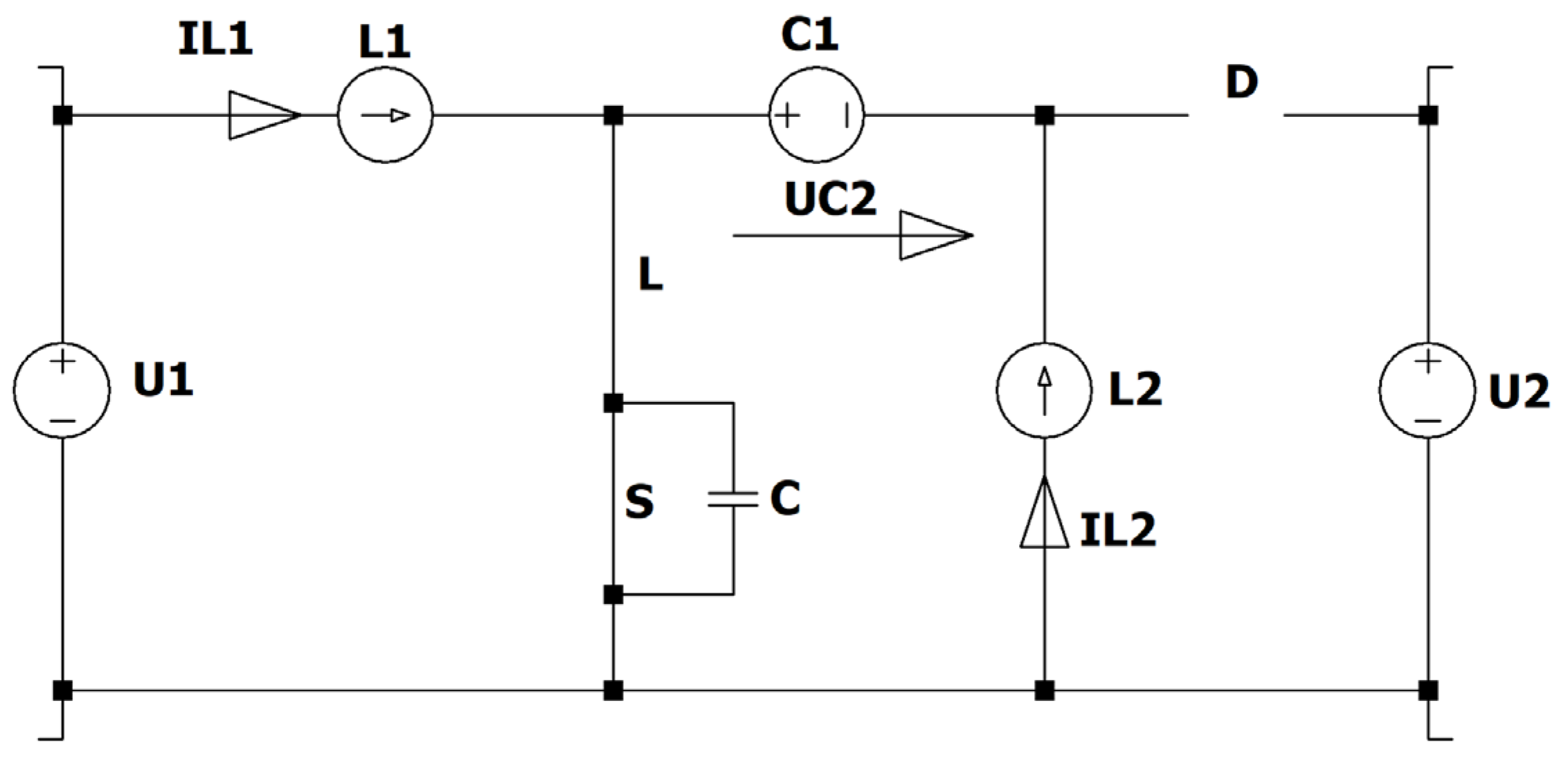
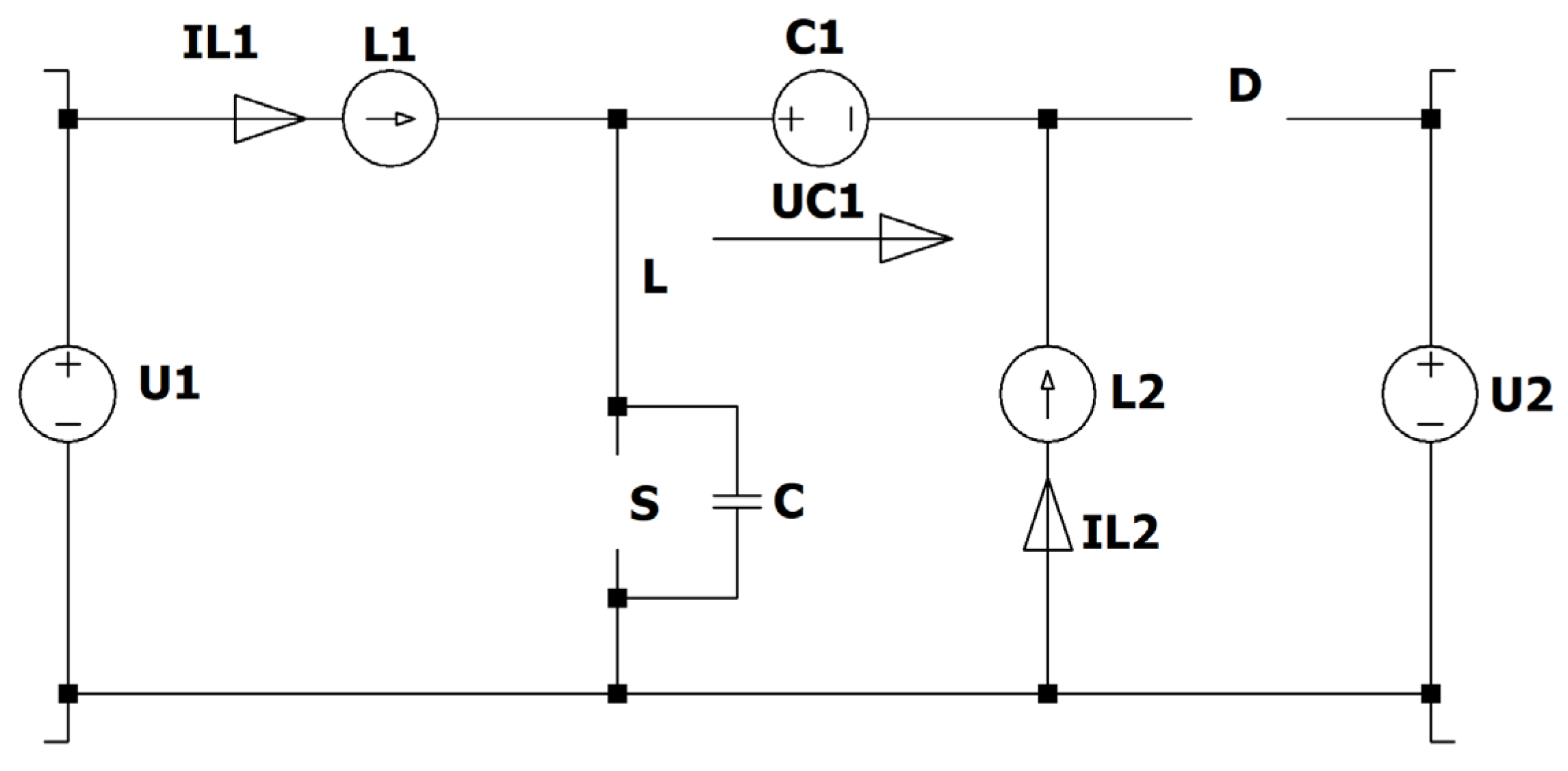
Figure 1.
Circuit diagram of the Zeta converter.
Figure 1.
Circuit diagram of the Zeta converter.
Figure 2.
Zeta converter: (a) simulation circuit; (b) up to down: voltage across the intermediate capacitor C1 (dark green), voltage across L2 (black); voltage across L1 (dark blue); output voltage (green), input voltage (blue), control signal (turquoise)..
Figure 2.
Zeta converter: (a) simulation circuit; (b) up to down: voltage across the intermediate capacitor C1 (dark green), voltage across L2 (black); voltage across L1 (dark blue); output voltage (green), input voltage (blue), control signal (turquoise)..
Figure 3.
Zeta converter: (a) simulation circuit; (b) up to down: voltage across the diode (black); voltage across the electronic switch (dark blue); output voltage (green), input voltage (blue), control signal (turquoise).
Figure 3.
Zeta converter: (a) simulation circuit; (b) up to down: voltage across the diode (black); voltage across the electronic switch (dark blue); output voltage (green), input voltage (blue), control signal (turquoise).
Figure 4.
Zeta converter: (a) simulation circuit; (b) up to down: current through the intermediate capacitor C1 (dark violet), current through the output capacitor C2 (grey); current through L1 (red), current through L2 (violet), load current (brown); output voltage (green), input voltage (blue), control signal (turquoise).
Figure 4.
Zeta converter: (a) simulation circuit; (b) up to down: current through the intermediate capacitor C1 (dark violet), current through the output capacitor C2 (grey); current through L1 (red), current through L2 (violet), load current (brown); output voltage (green), input voltage (blue), control signal (turquoise).
Figure 5.
Zeta converter: (a) simulation circuit; (b) up to down: current through the diode (violet), current through the electronic switch (red); output voltage (green), input voltage (blue), control signal (turquoise).
Figure 5.
Zeta converter: (a) simulation circuit; (b) up to down: current through the diode (violet), current through the electronic switch (red); output voltage (green), input voltage (blue), control signal (turquoise).
Figure 6.
Zeta converter: up to down: current through L1 (red), current through L2 (violet), load current (brown); output voltage (green), voltage across C1 (grey); input voltage (blue), control signal (turquoise), (a) large capacitor 33 µF; (b) small capacitor 3.3 µF.
Figure 6.
Zeta converter: up to down: current through L1 (red), current through L2 (violet), load current (brown); output voltage (green), voltage across C1 (grey); input voltage (blue), control signal (turquoise), (a) large capacitor 33 µF; (b) small capacitor 3.3 µF.
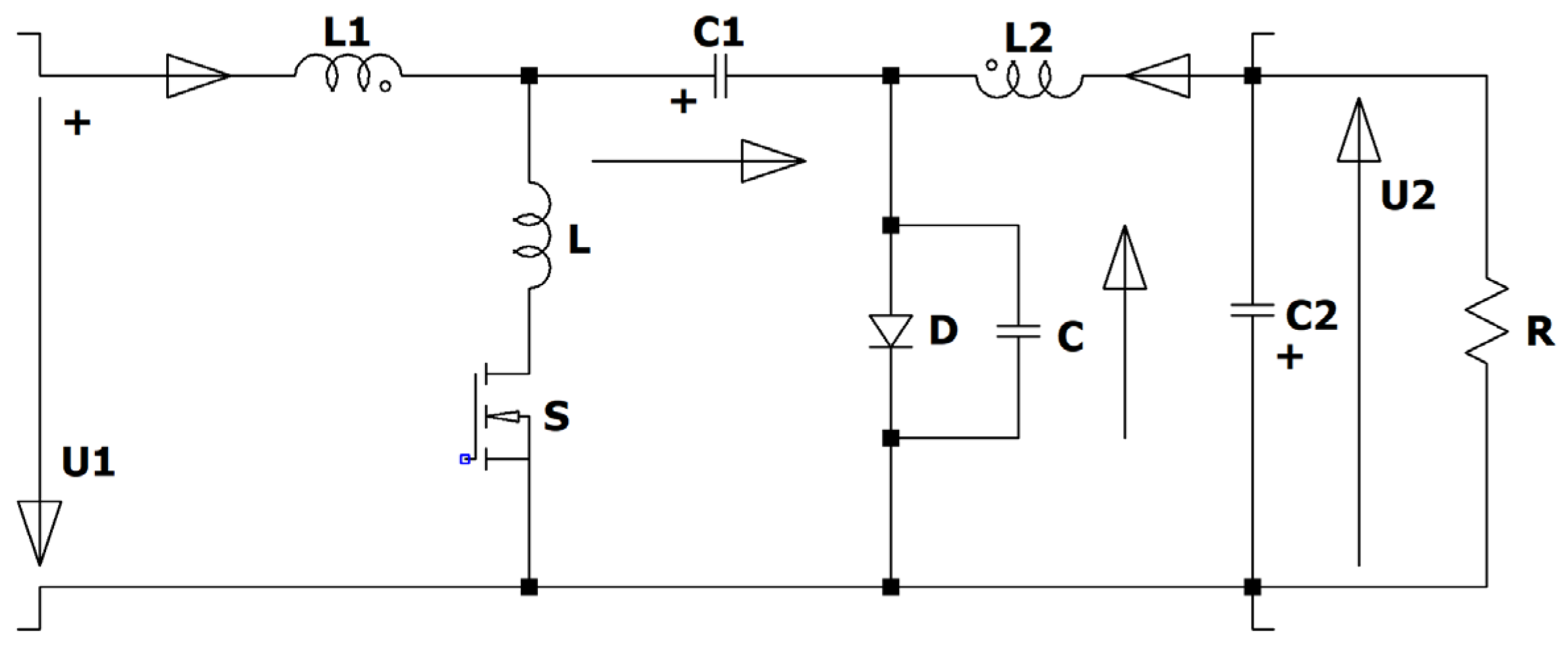
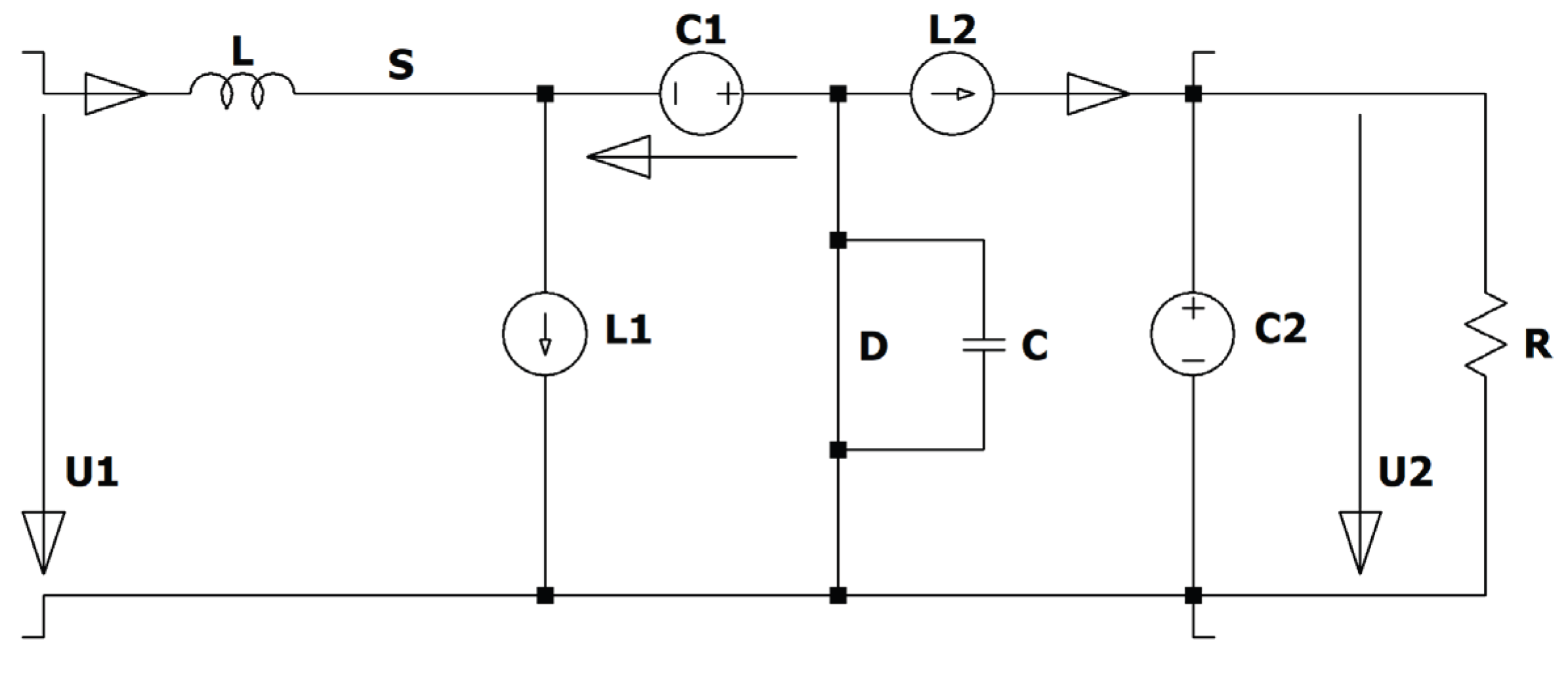
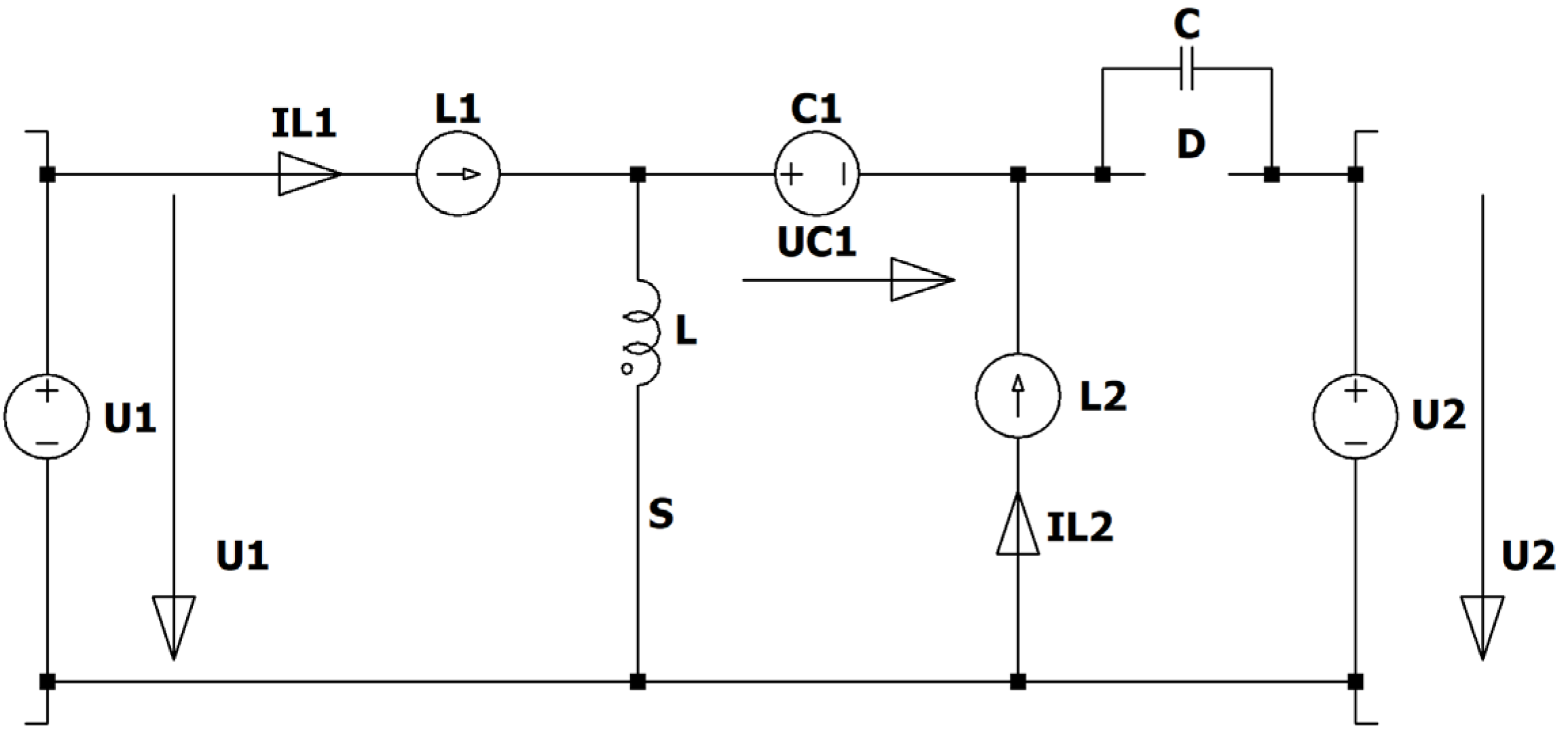
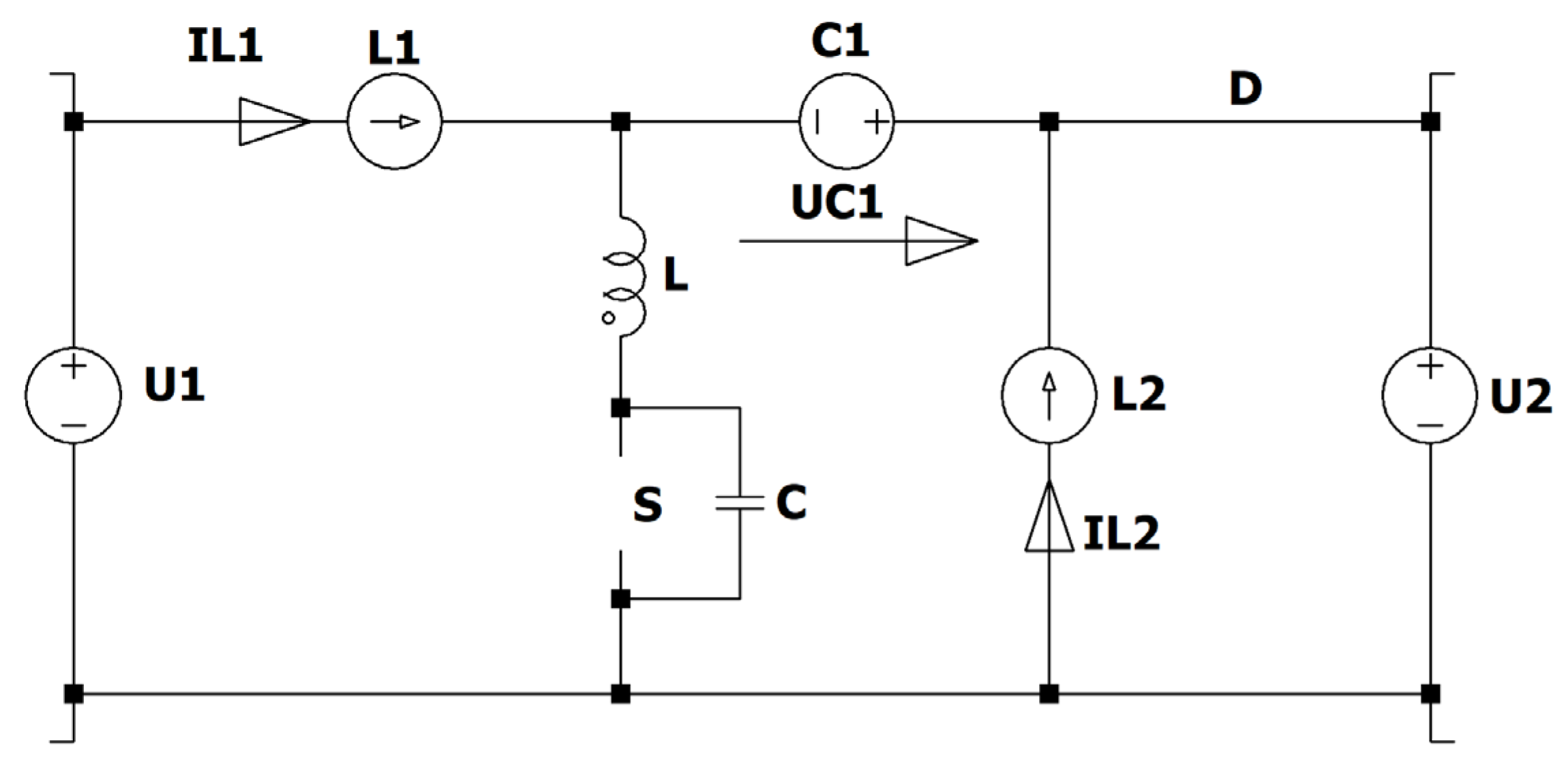
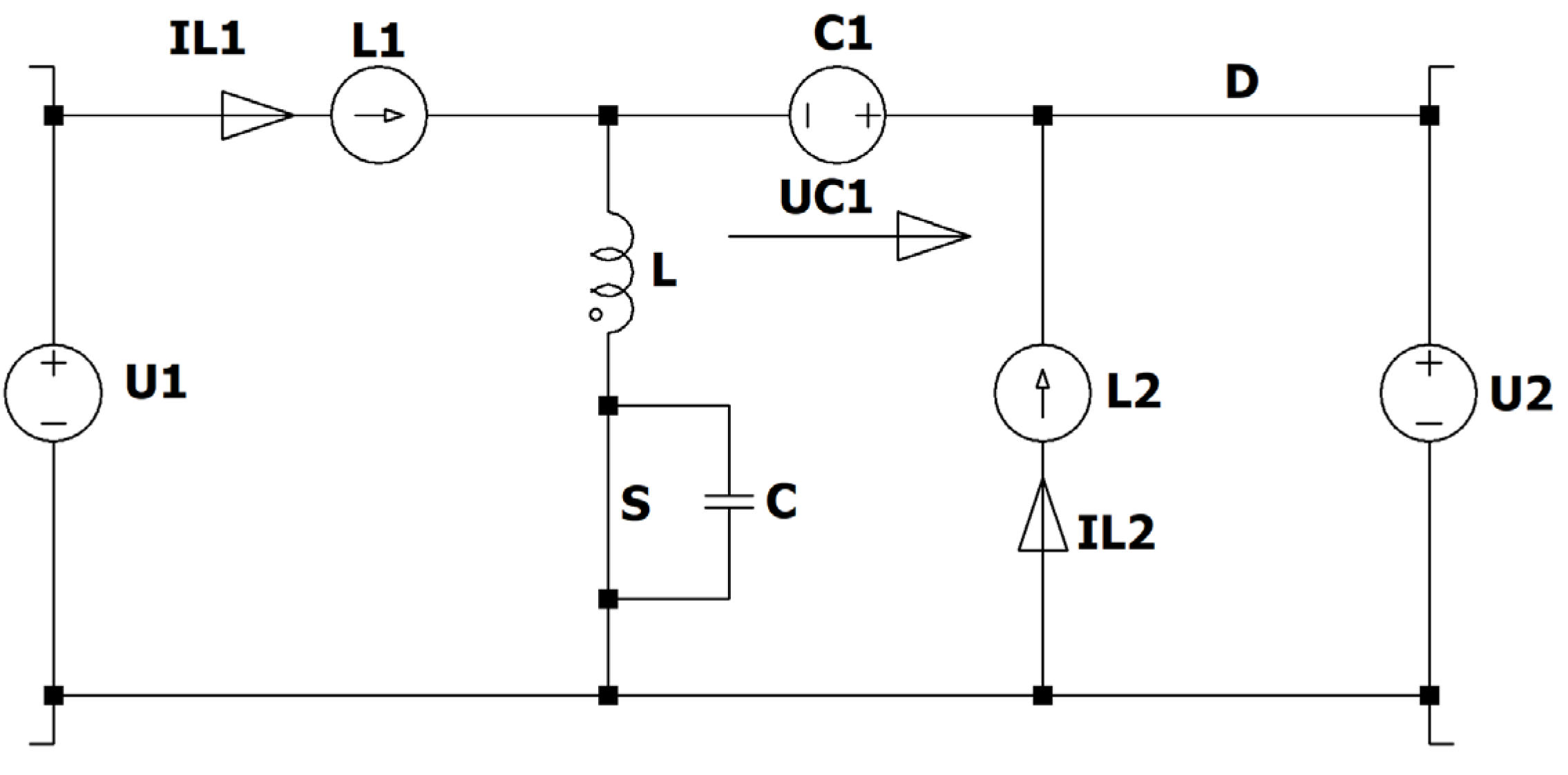
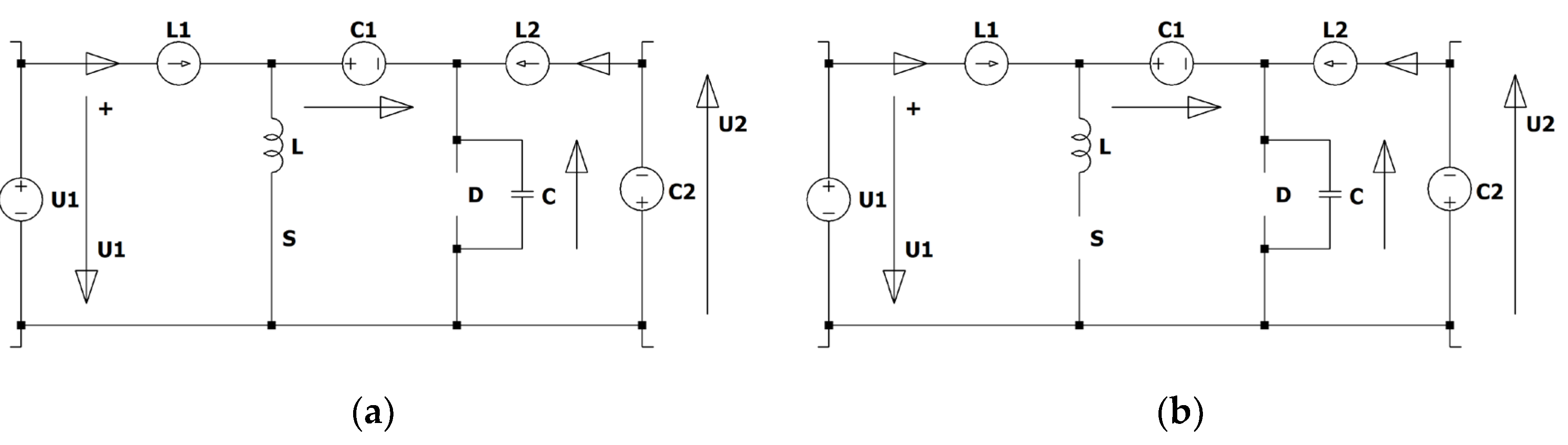
Figure 7.
ZCS QR Zeta converter.
Figure 7.
ZCS QR Zeta converter.
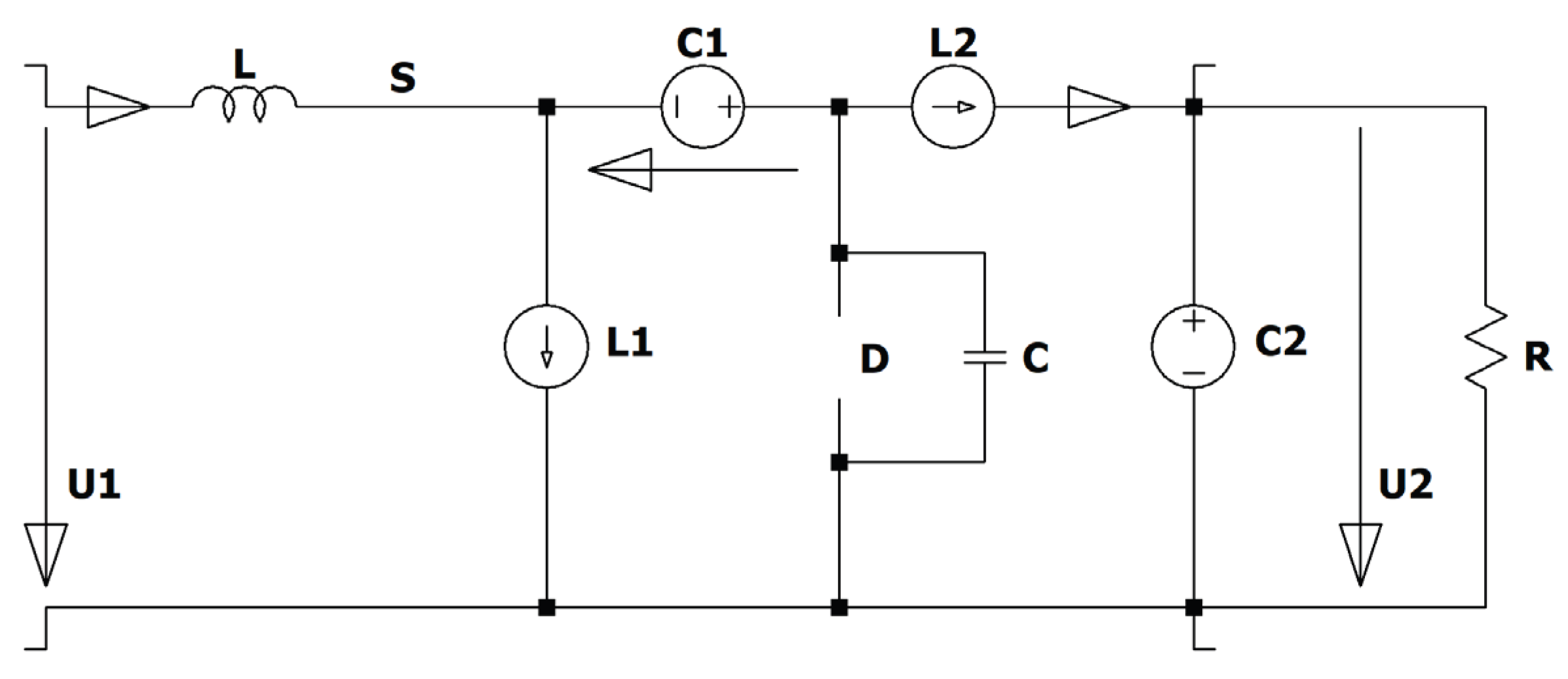
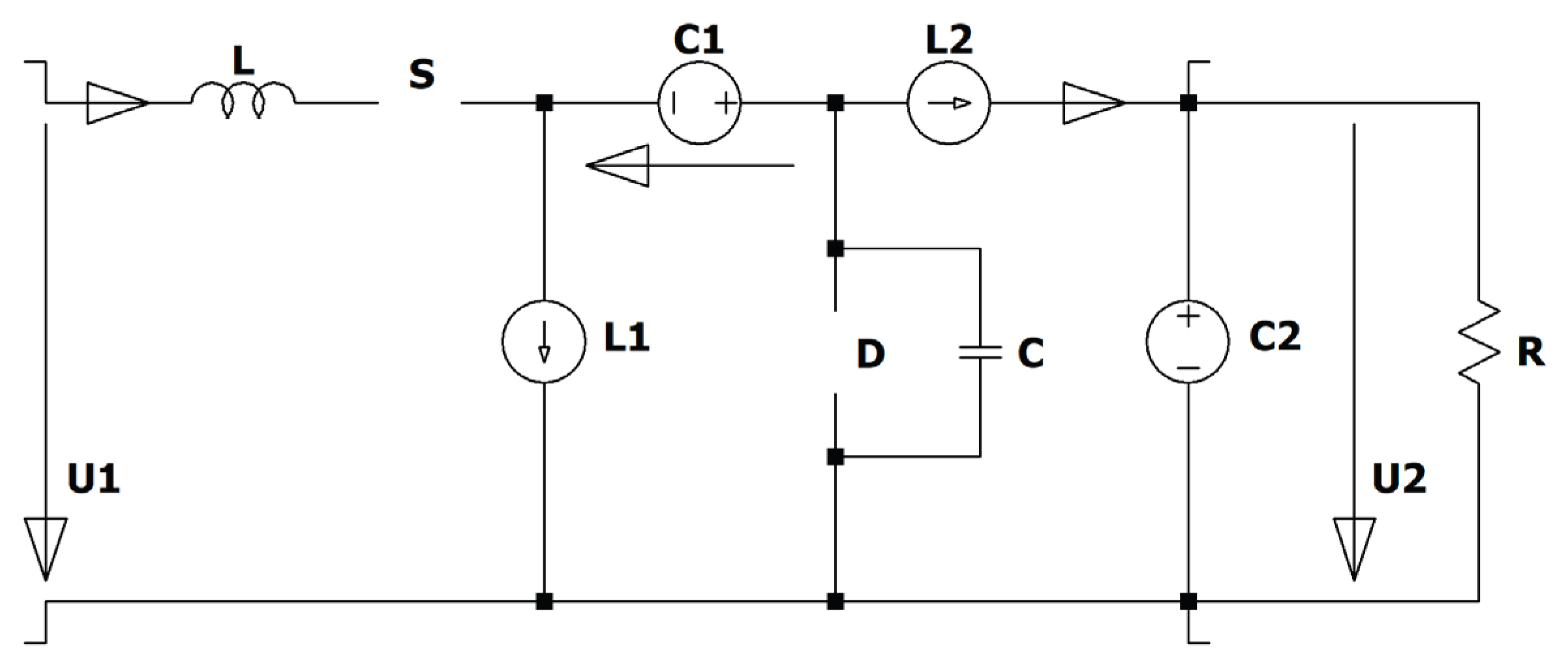
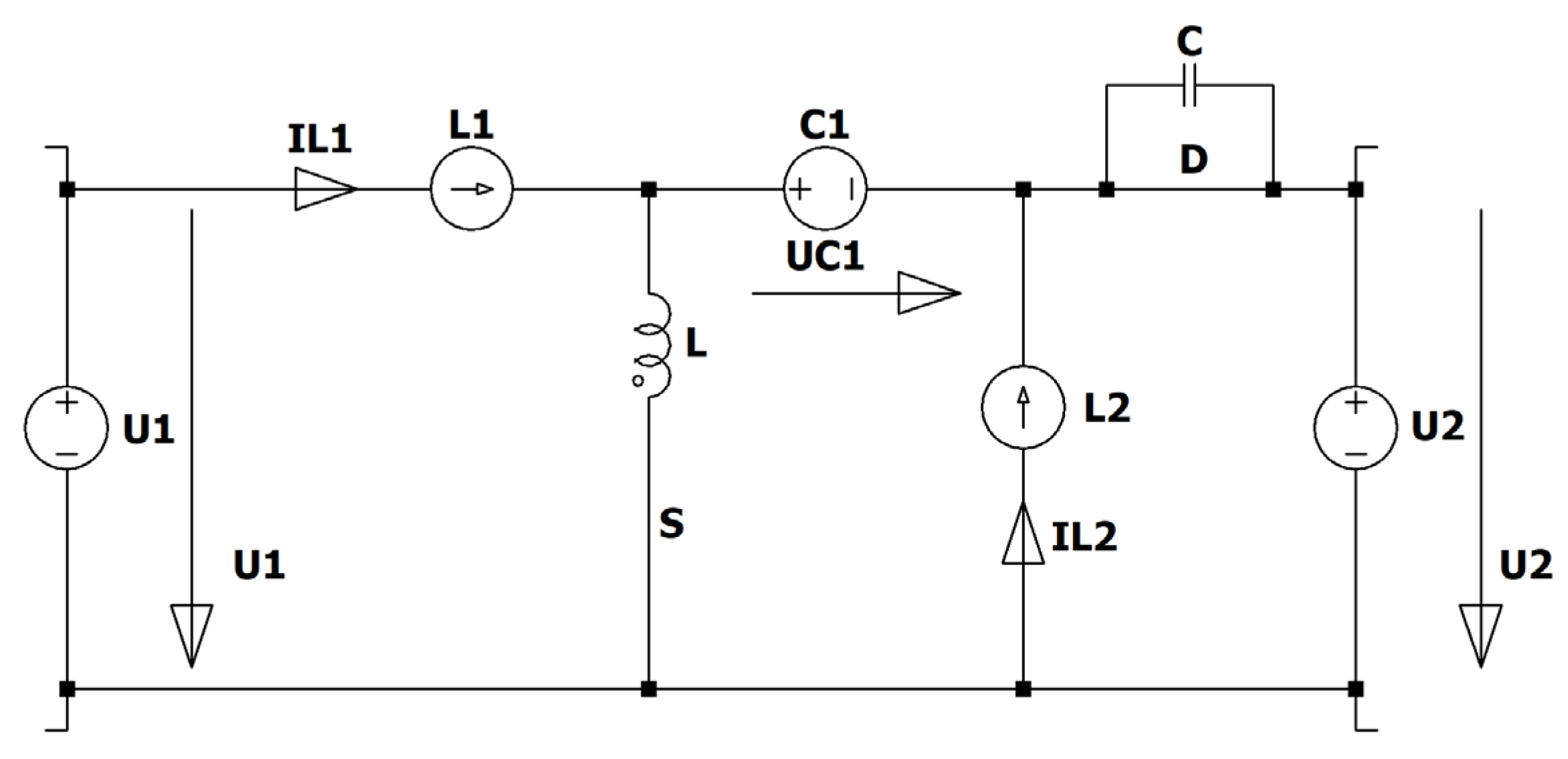
Figure 8.
Reduced (simplified) ZCS QR Zeta converter.
Figure 8.
Reduced (simplified) ZCS QR Zeta converter.
Figure 9.
Equivalent circuit M0 (freewheeling).
Figure 9.
Equivalent circuit M0 (freewheeling).
Figure 10.
Equivalent circuit M1 (switch is turned on).
Figure 10.
Equivalent circuit M1 (switch is turned on).
Figure 11.
Equivalent circuit M2 (resonance).
Figure 11.
Equivalent circuit M2 (resonance).
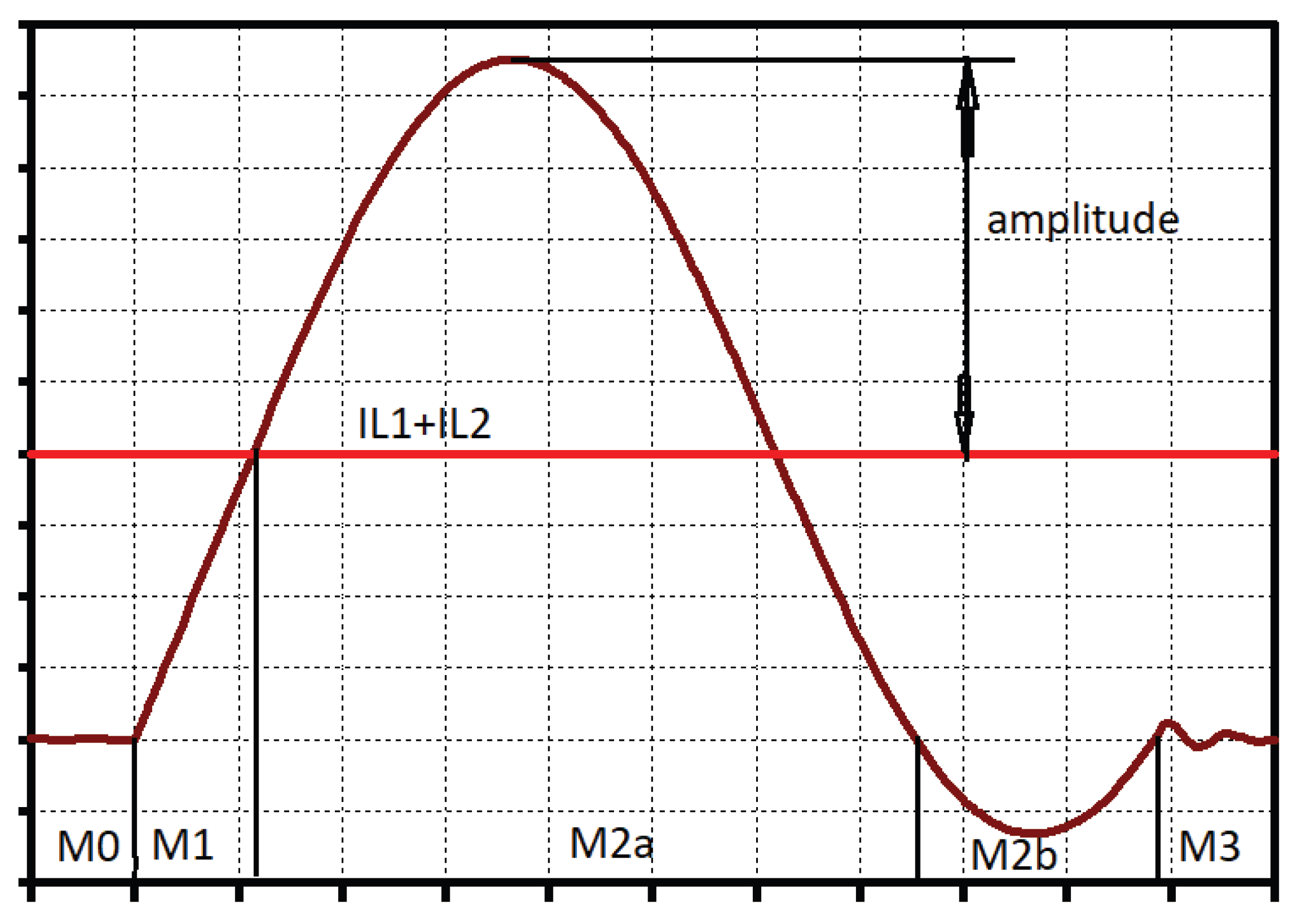
Figure 12.
Current through the resonant coil L.
Figure 12.
Current through the resonant coil L.
Figure 13.
Equivalent circuit M3 (discharge C).
Figure 13.
Equivalent circuit M3 (discharge C).
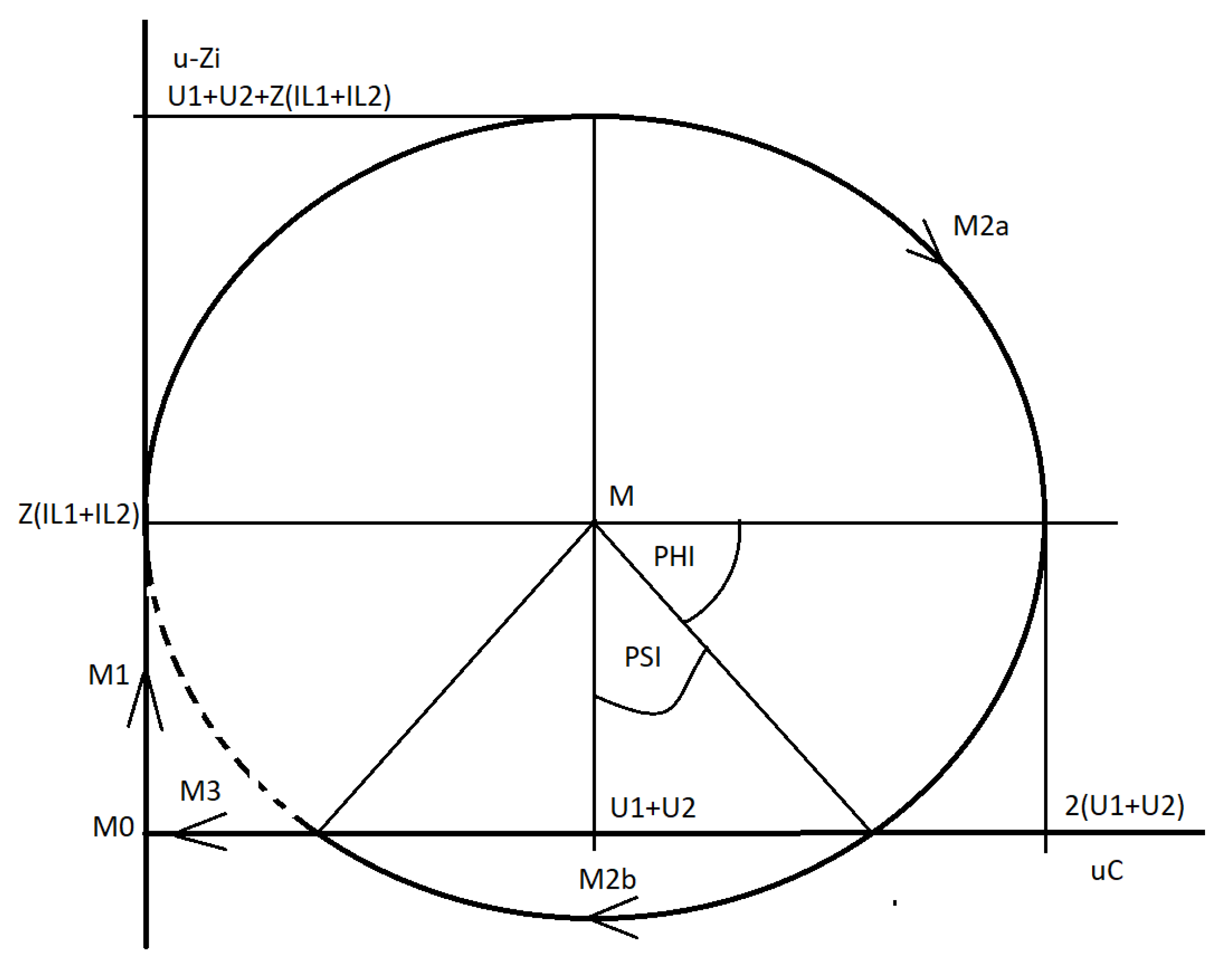
Figure 15.
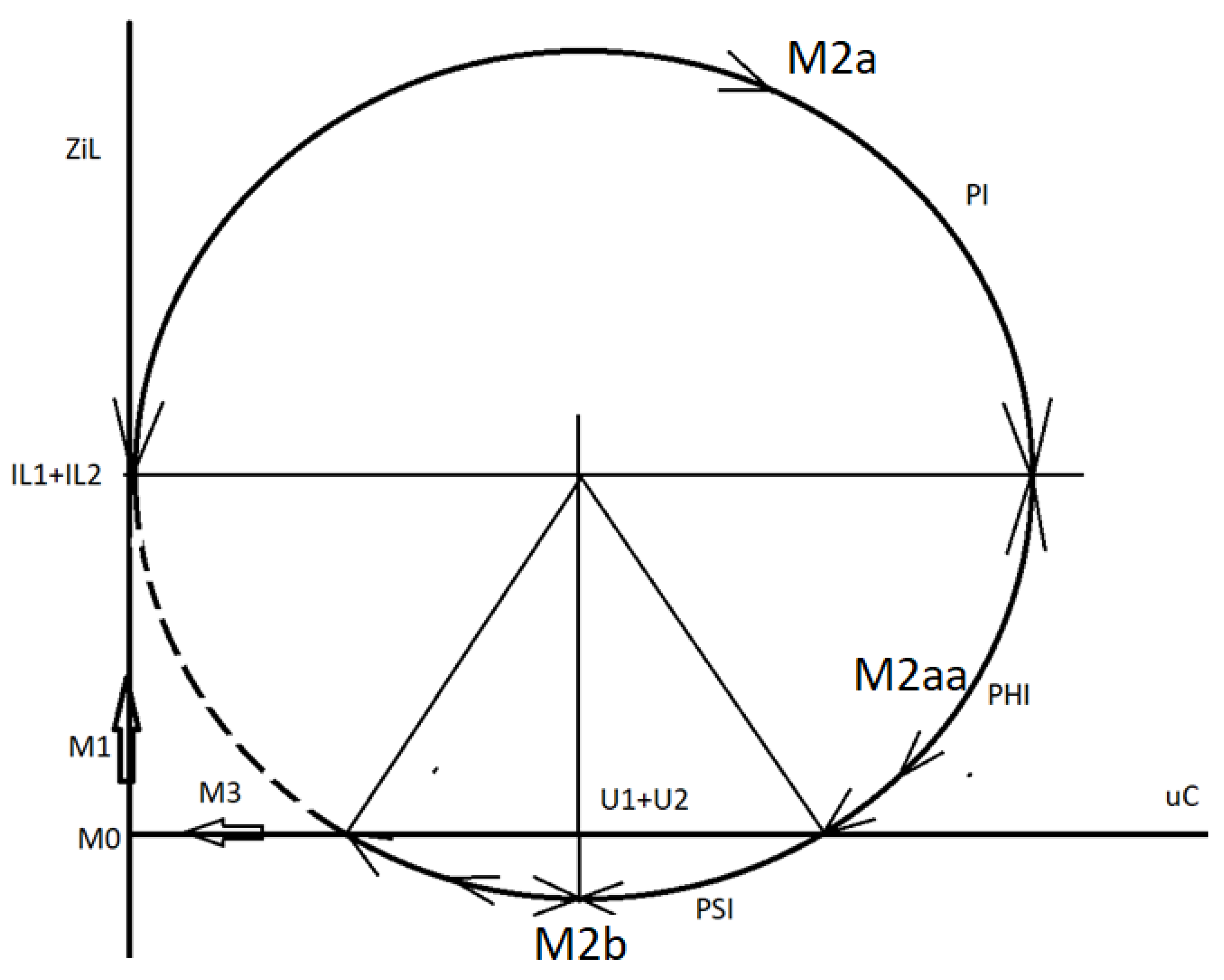
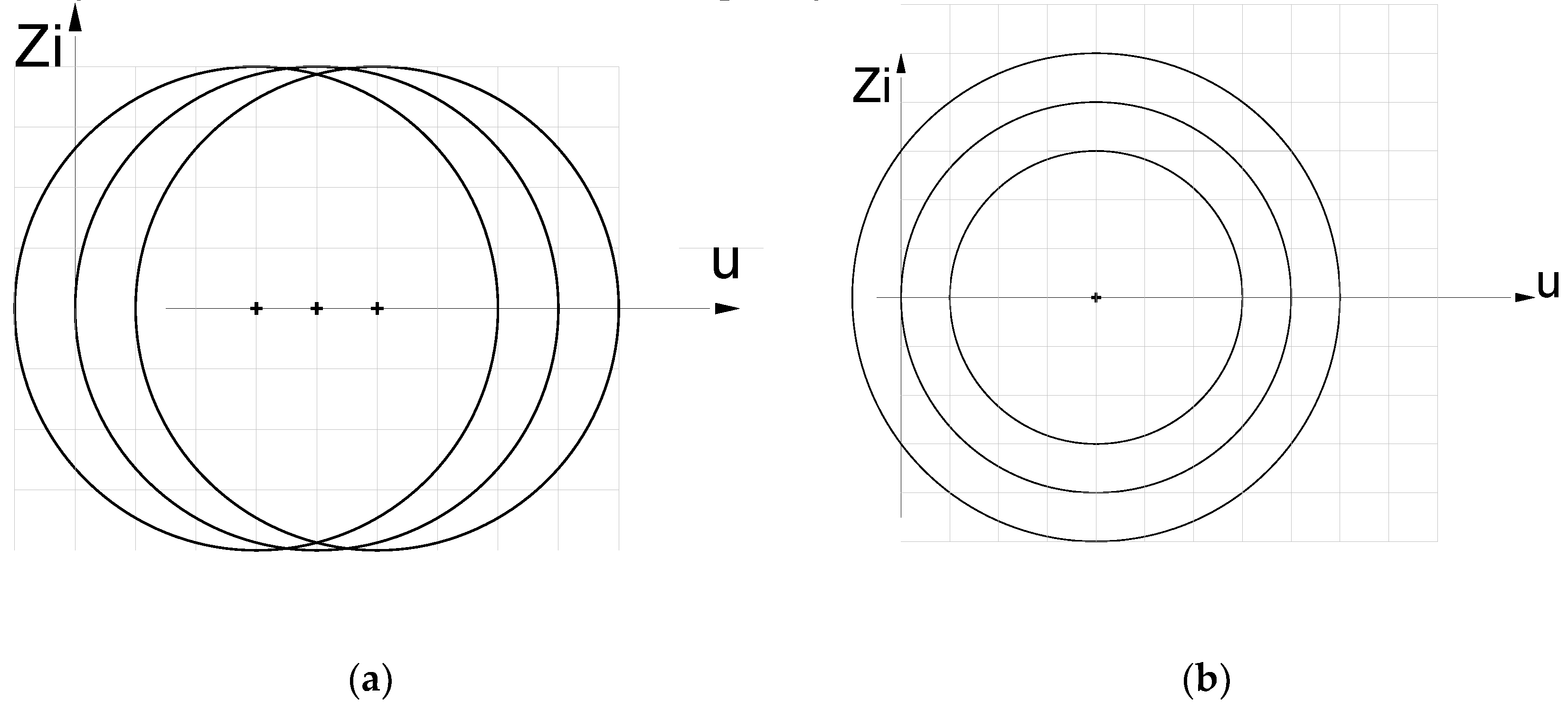
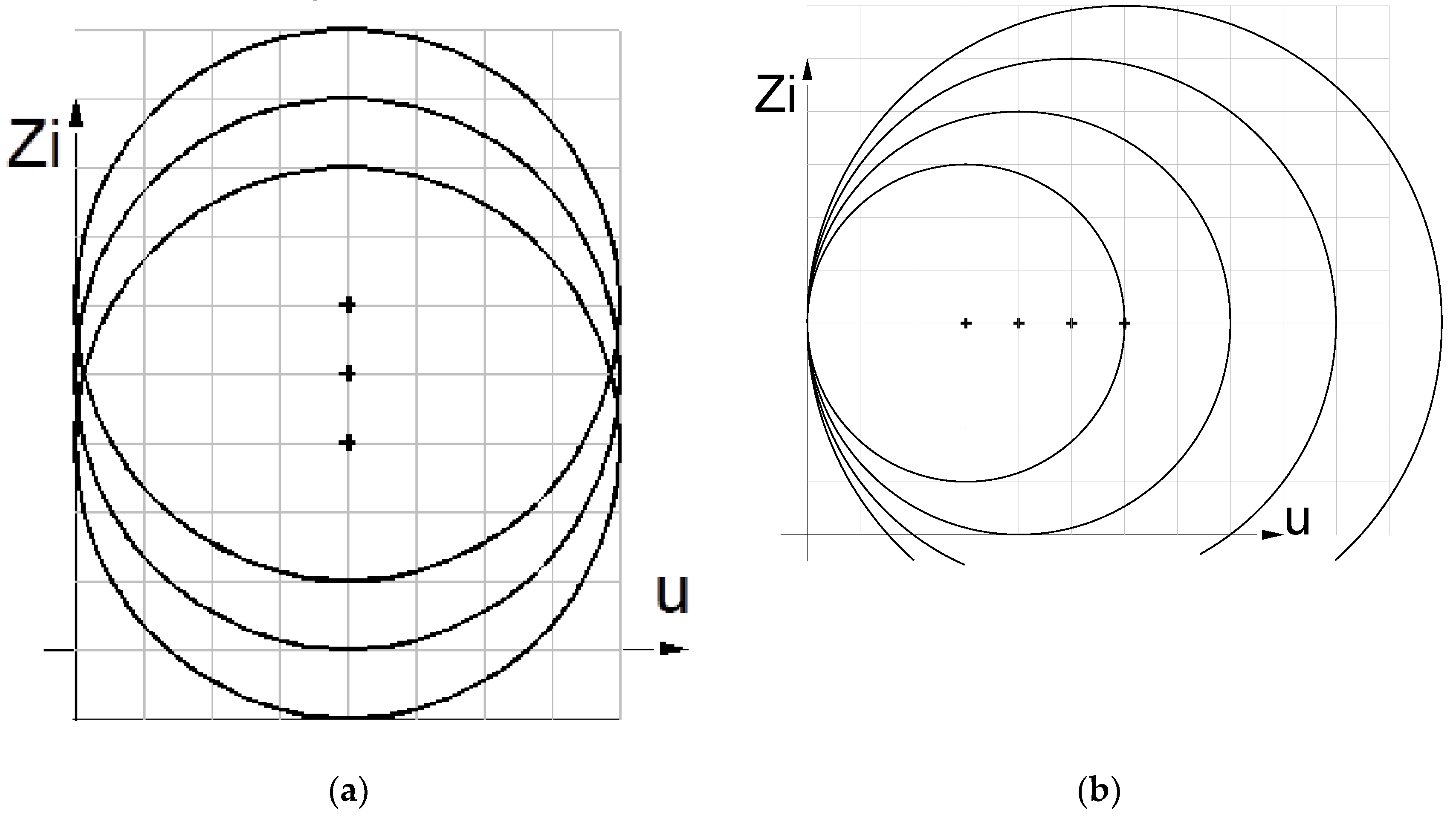
ZCS QR Zeta, circles describing mode M2: (a) constant voltage, variable current; (b) constant current, variable voltage.
Figure 15.
ZCS QR Zeta, circles describing mode M2: (a) constant voltage, variable current; (b) constant current, variable voltage.
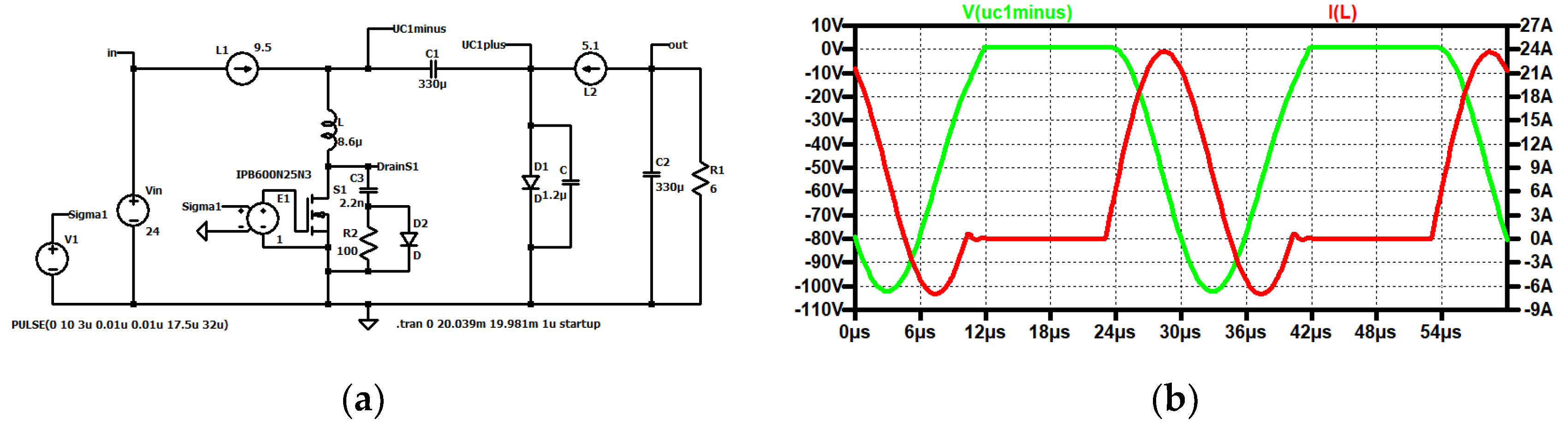
Figure 16.
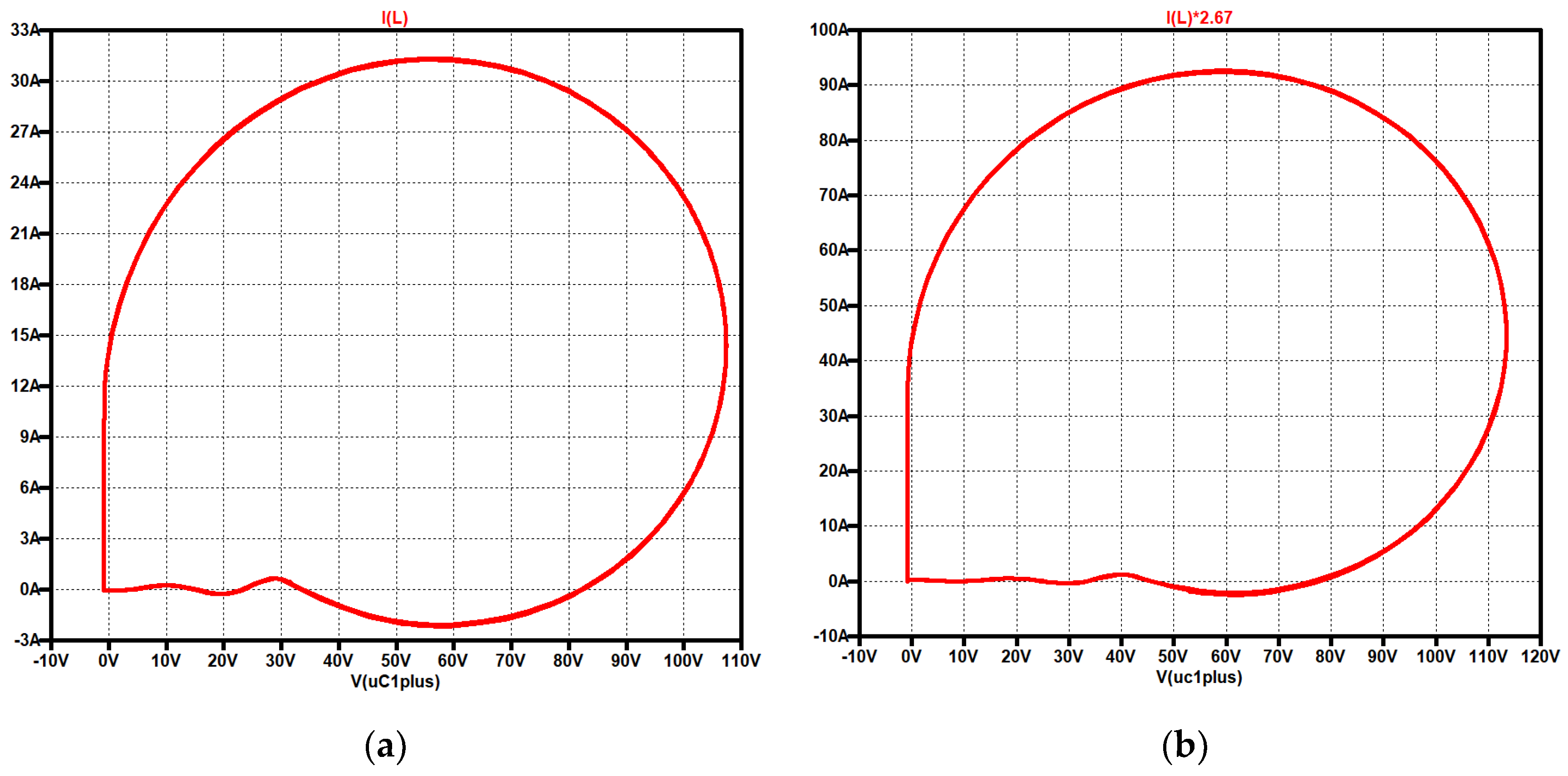
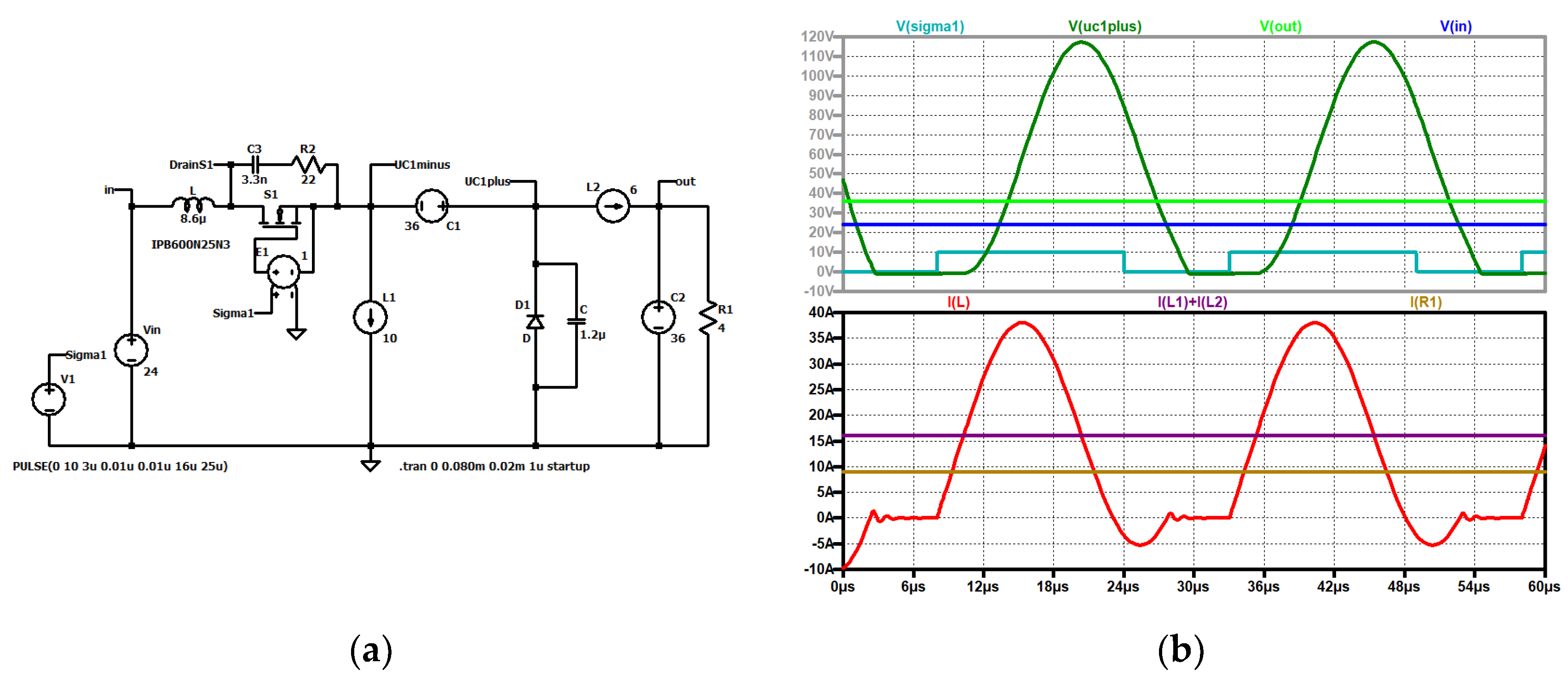
ZCS QR Zeta, simulation with current and voltage sources: (a) simulation circuit; (b) up to down: voltage across the resonant capacitor (dark green), output voltage (green), input voltage (blue), control signal (turquoise); current through the resonant inductor (red), sum of the currents through the converter coils (dark violet), load current (brown).
Figure 16.
ZCS QR Zeta, simulation with current and voltage sources: (a) simulation circuit; (b) up to down: voltage across the resonant capacitor (dark green), output voltage (green), input voltage (blue), control signal (turquoise); current through the resonant inductor (red), sum of the currents through the converter coils (dark violet), load current (brown).
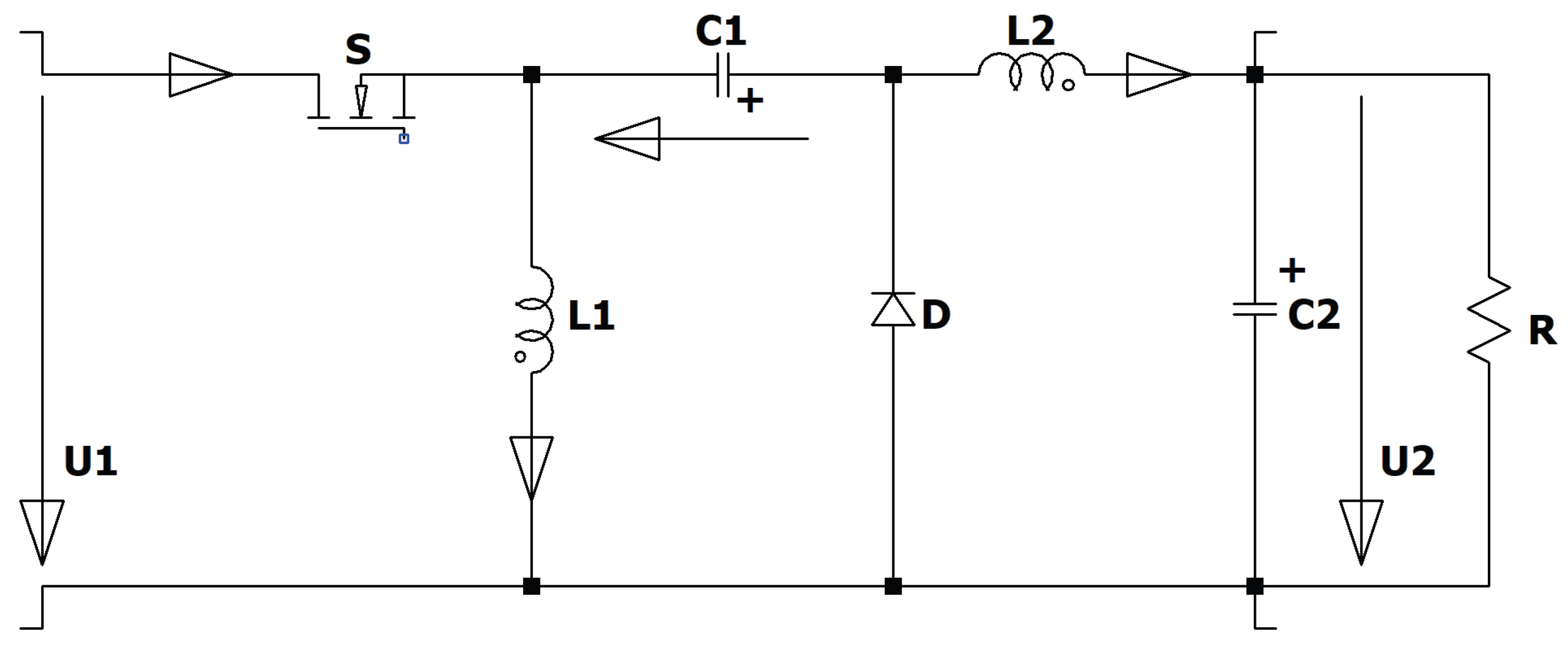
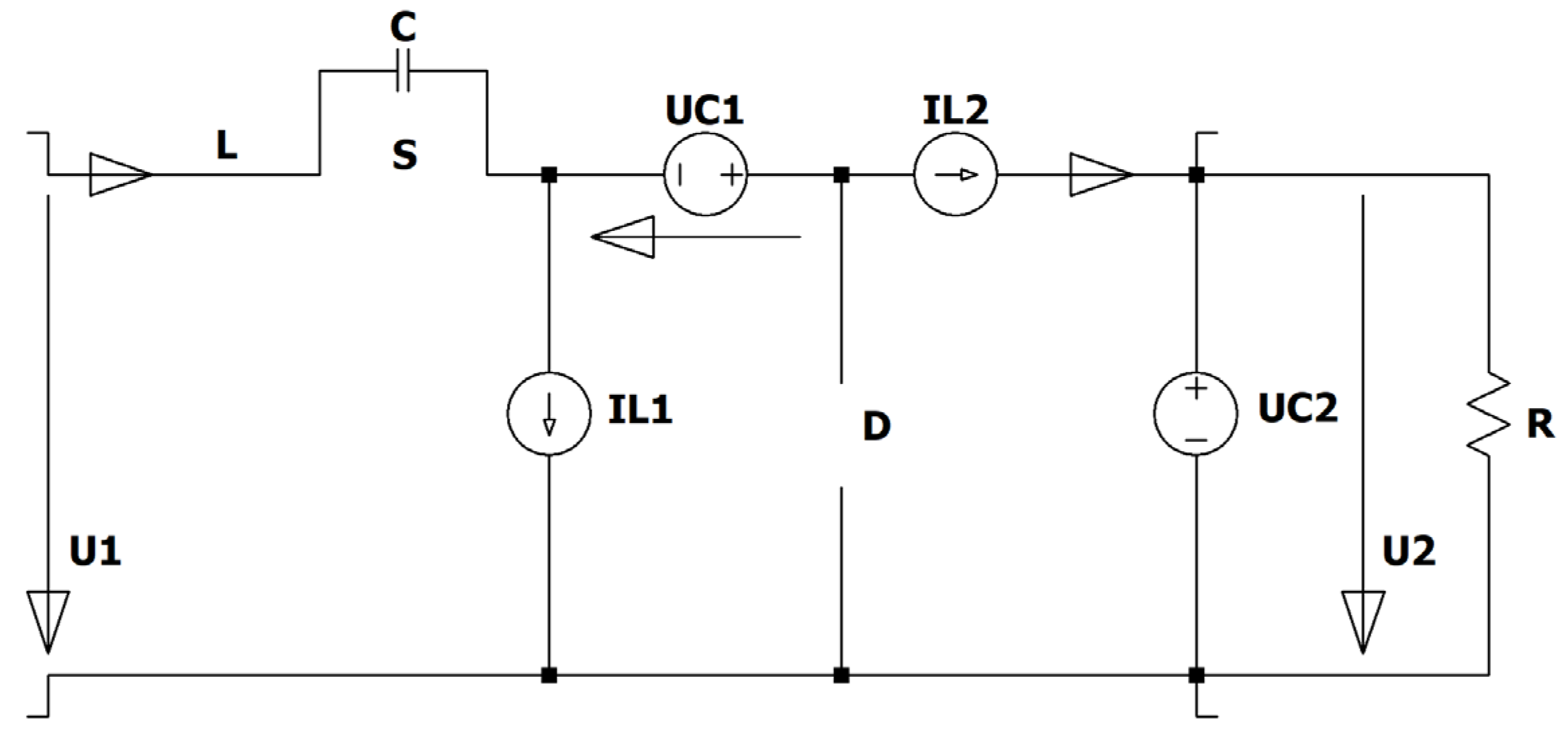
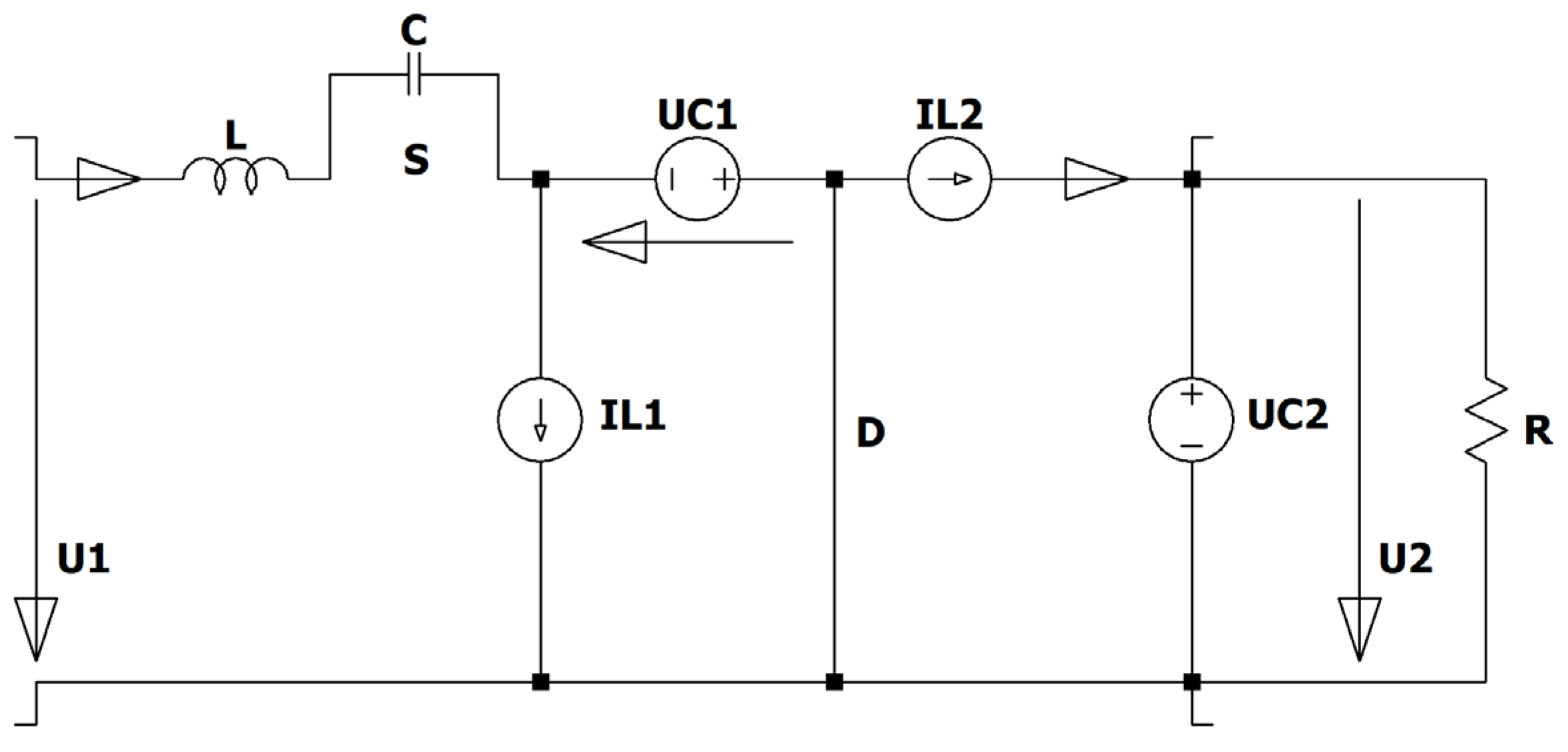
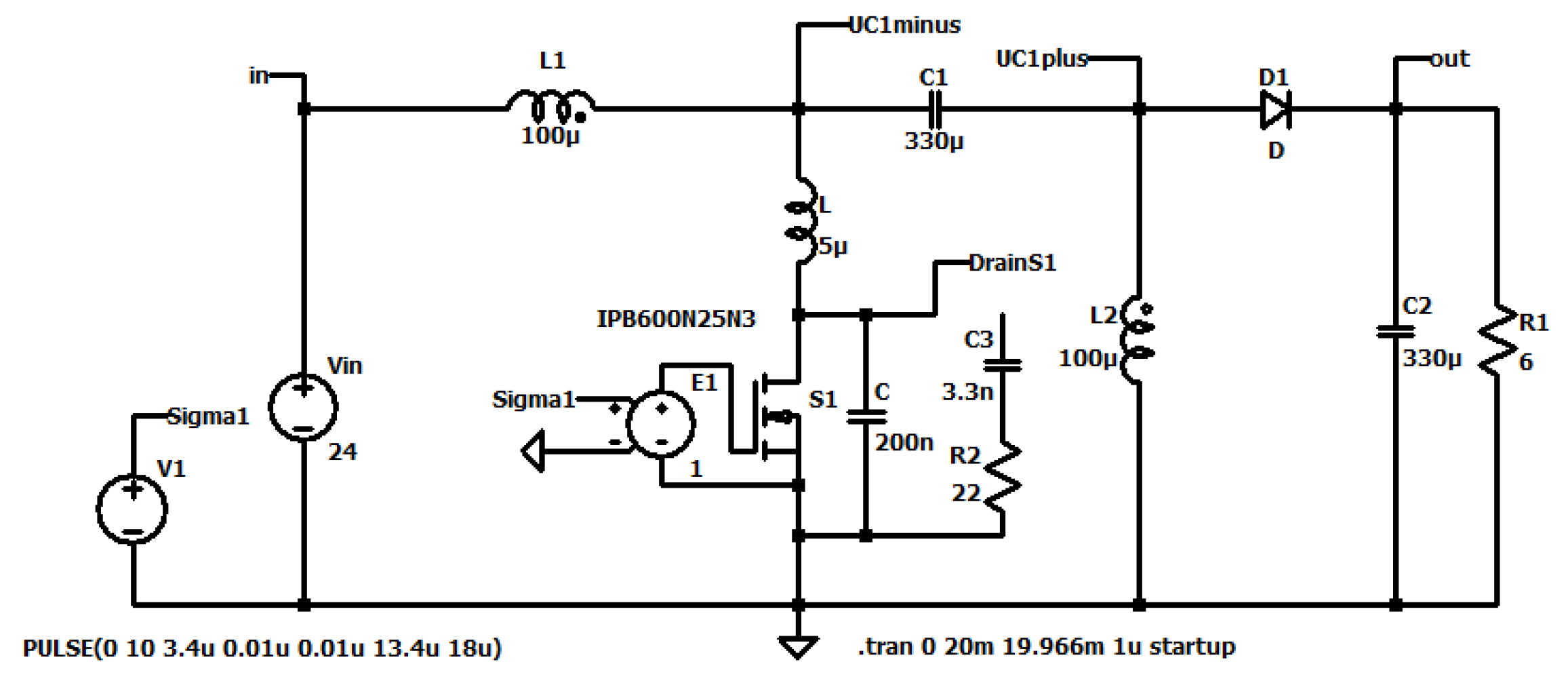
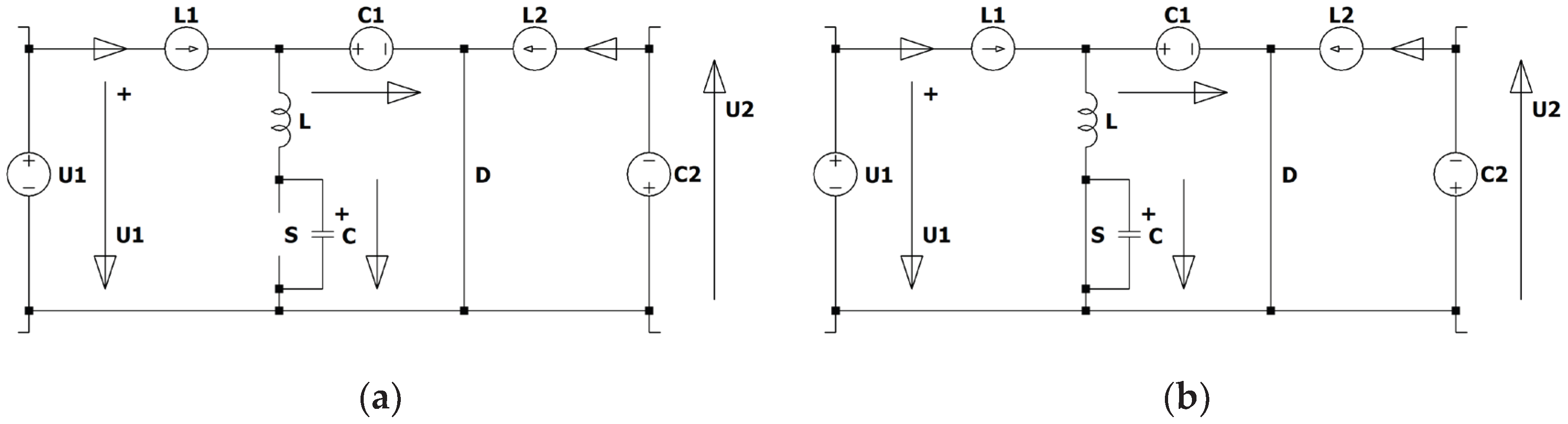
Figure 21.
Circuit diagram of the ZVS QR Zeta converter.
Figure 21.
Circuit diagram of the ZVS QR Zeta converter.
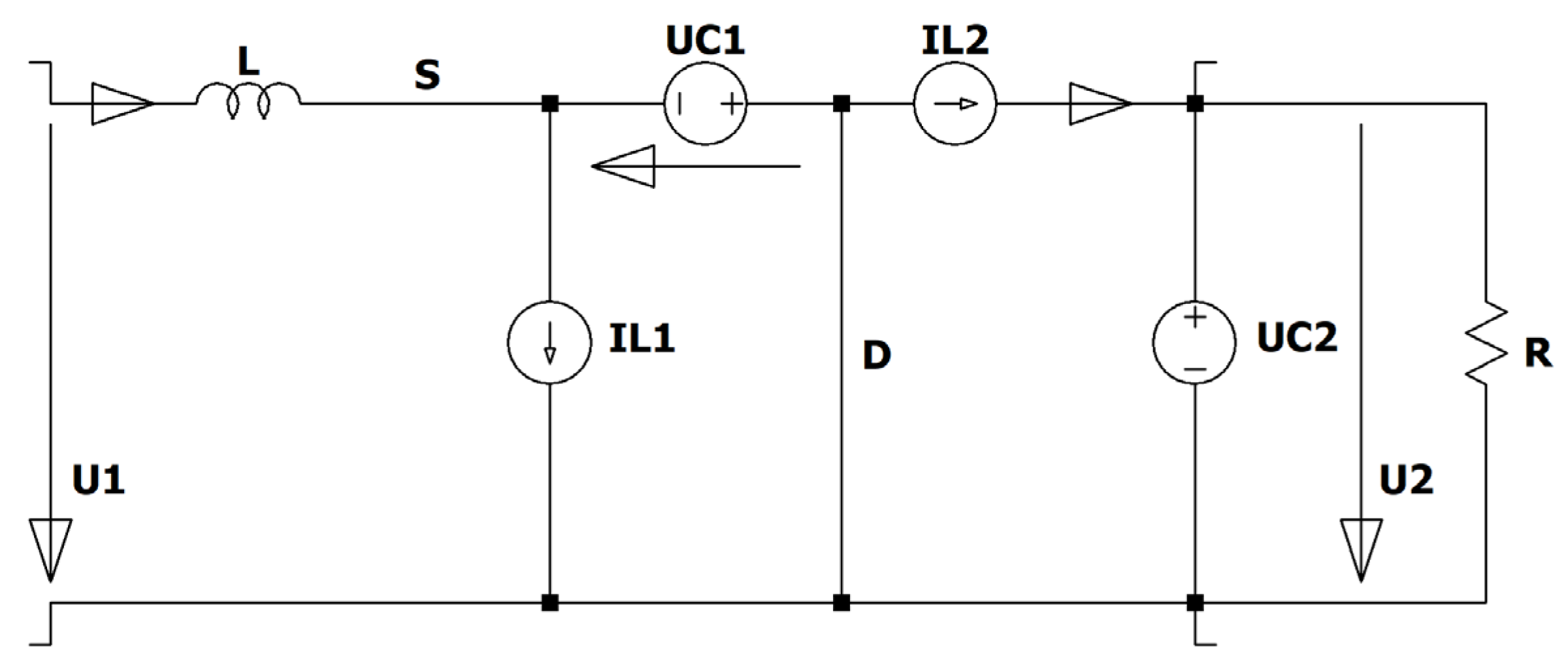
Figure 22.
ZVS QR Zeta converter: mode M0, the switch is on.
Figure 22.
ZVS QR Zeta converter: mode M0, the switch is on.
Figure 23.
ZVS QR Zeta converter: mode M2, the switch is turned off, the resonant capacitor is charged.
Figure 23.
ZVS QR Zeta converter: mode M2, the switch is turned off, the resonant capacitor is charged.
Figure 24.
ZVS QR Zeta converter: mode M2, the resonance.
Figure 24.
ZVS QR Zeta converter: mode M2, the resonance.
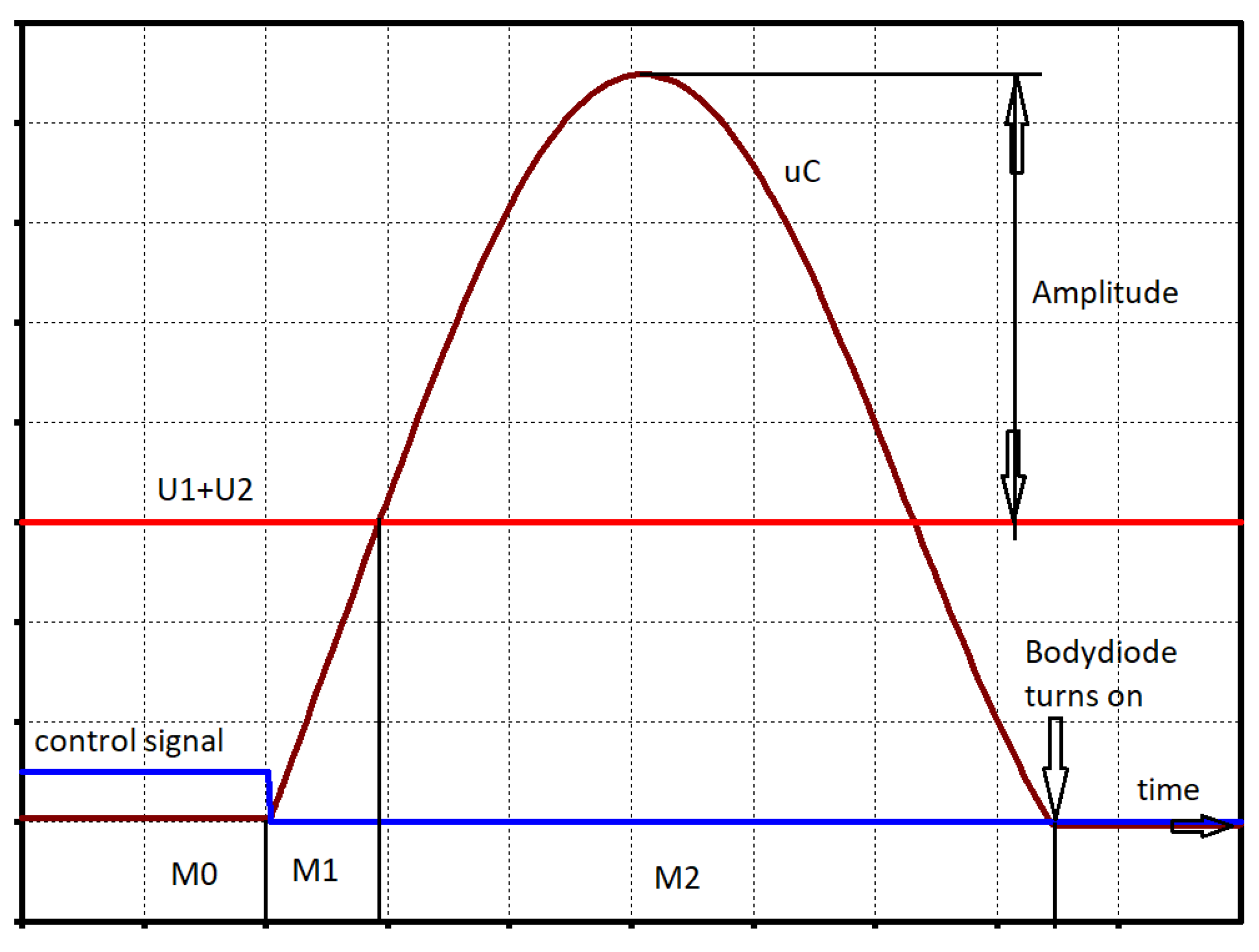
Figure 25.
ZVS QR ZETA converter, voltage across the resonant capacitor.
Figure 25.
ZVS QR ZETA converter, voltage across the resonant capacitor.
Figure 26.
ZVS QR Zeta converter, mode M3, the current commutates from the diode to the switch.
Figure 26.
ZVS QR Zeta converter, mode M3, the current commutates from the diode to the switch.
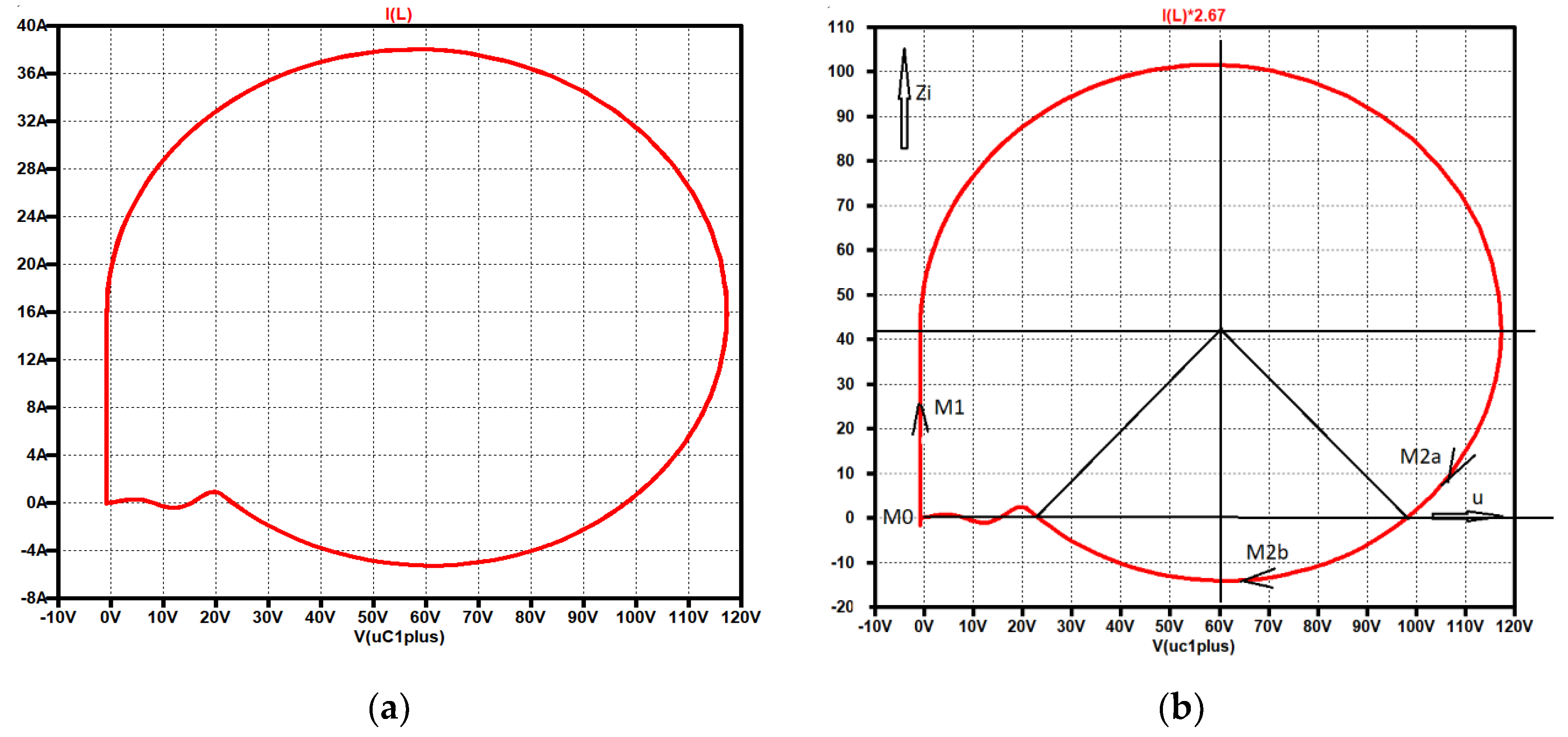
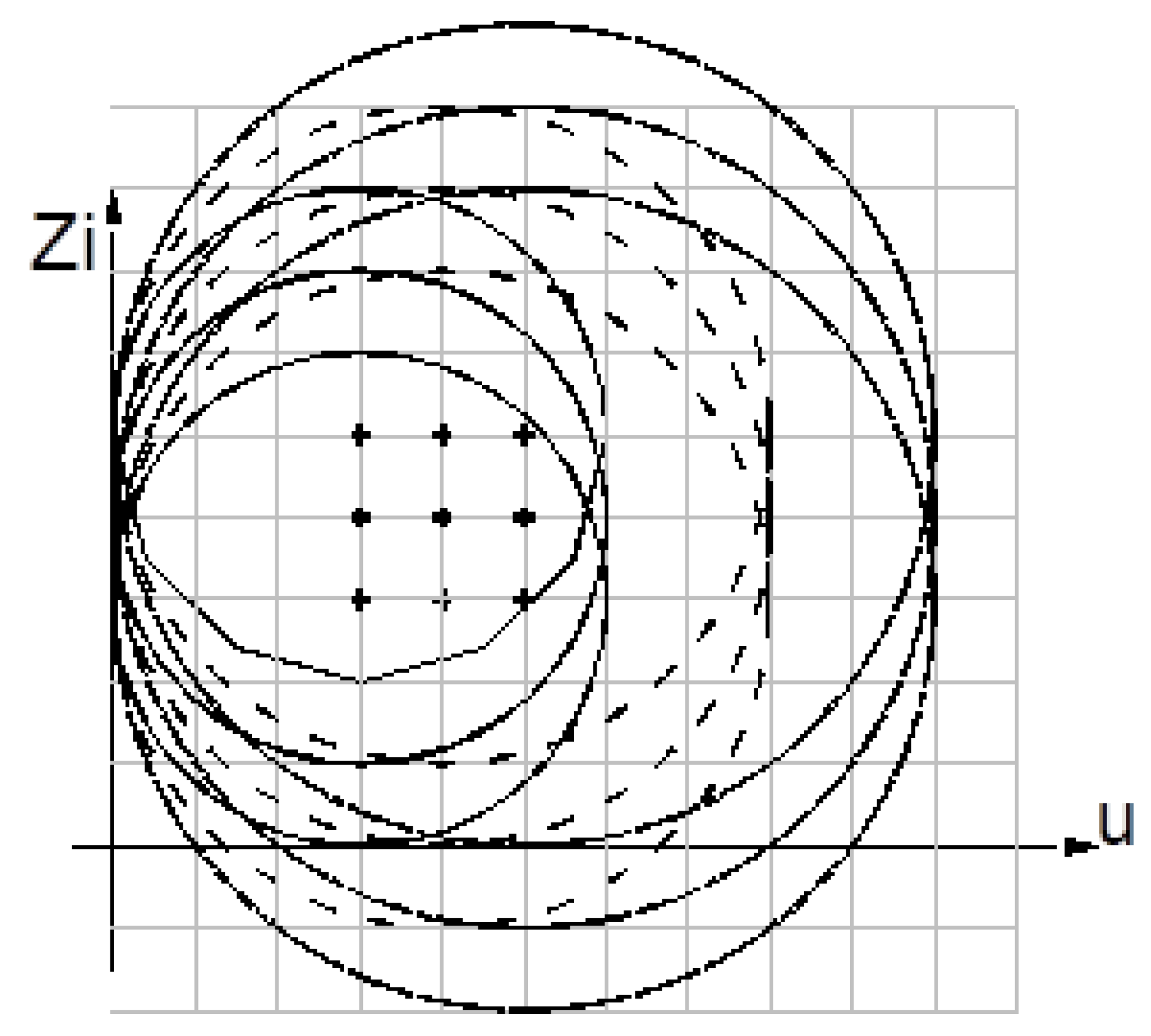
Figure 27.
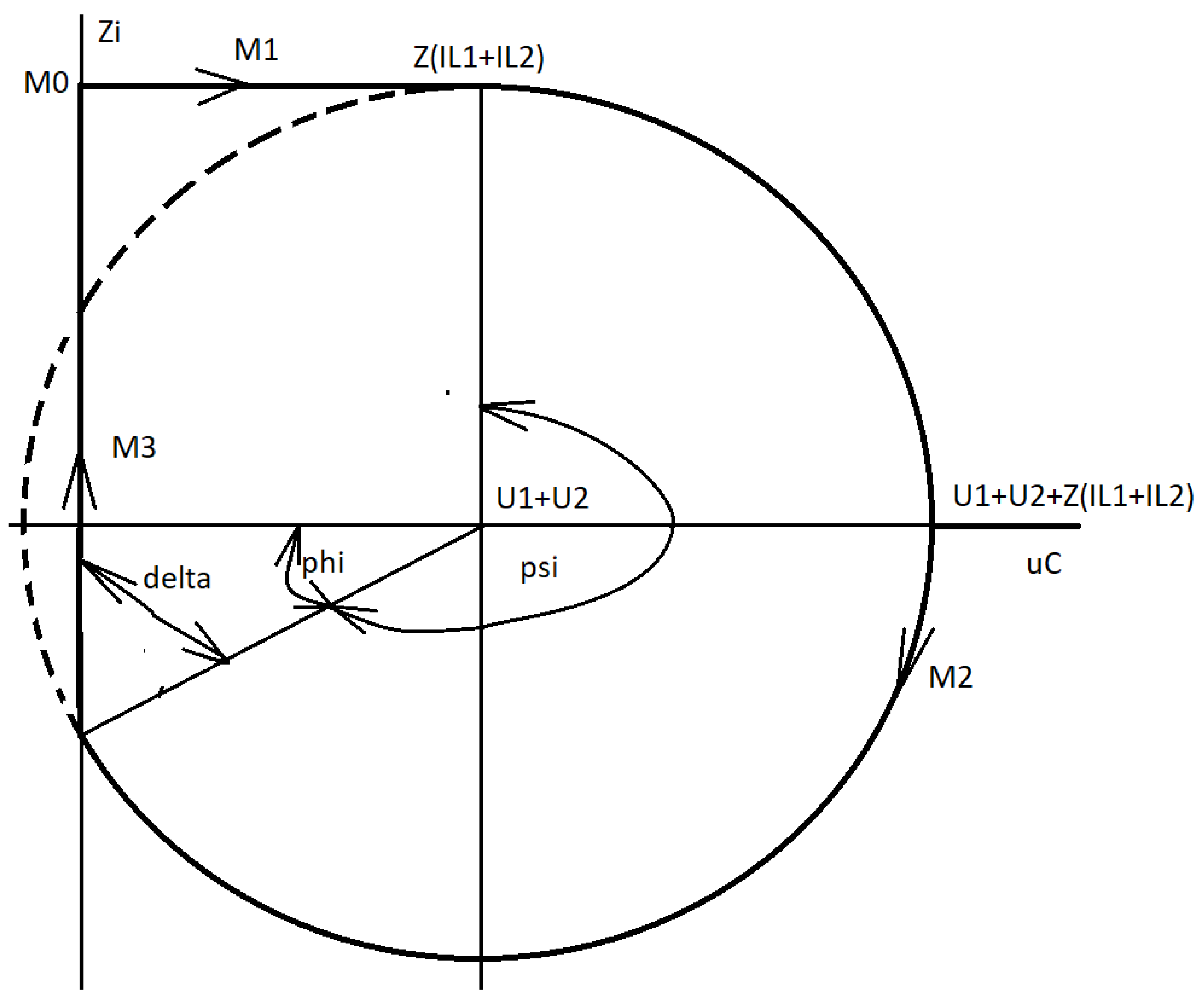
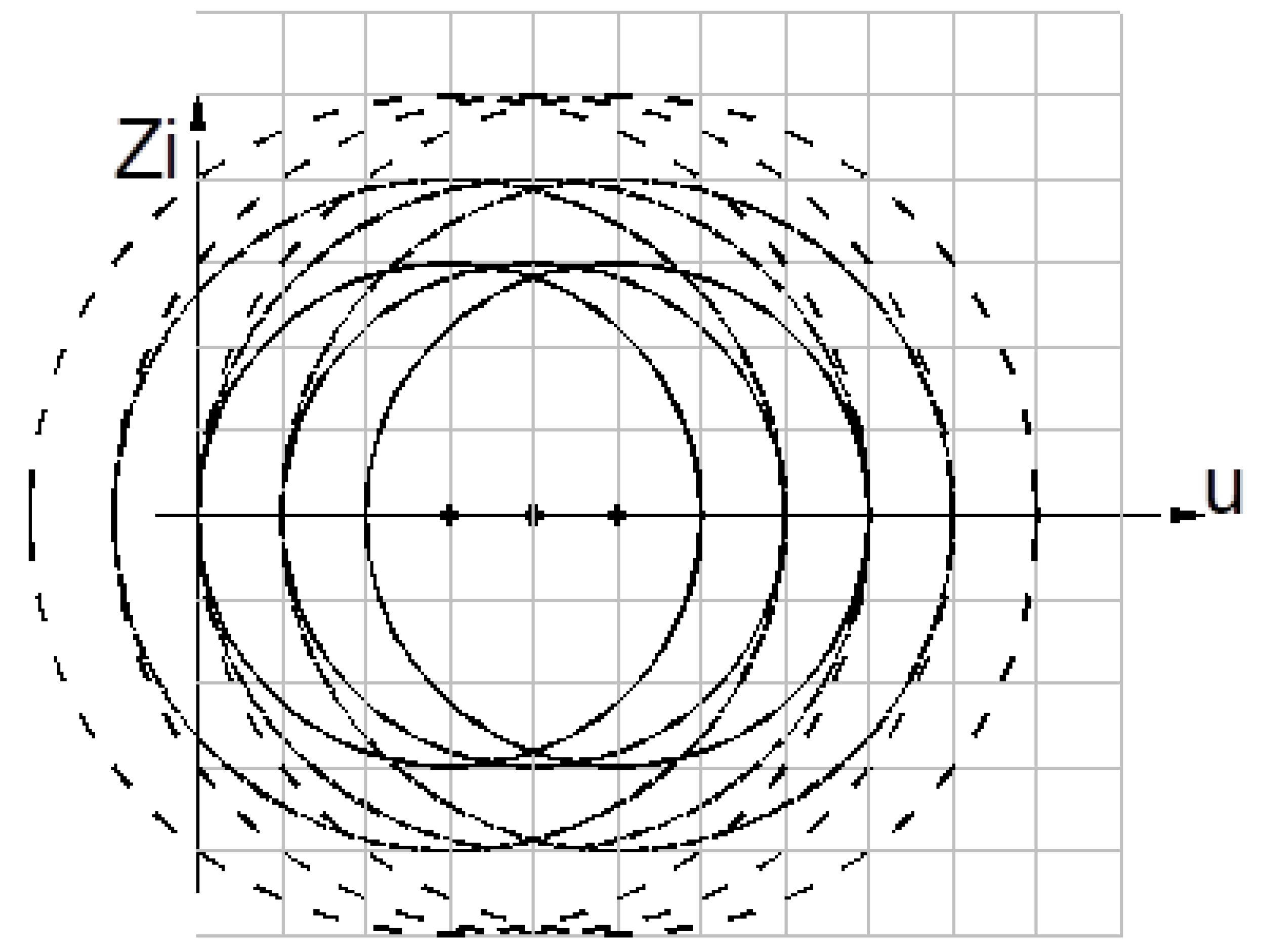
ZVS QR Zeta converter, u-Zi diagram.
Figure 27.
ZVS QR Zeta converter, u-Zi diagram.
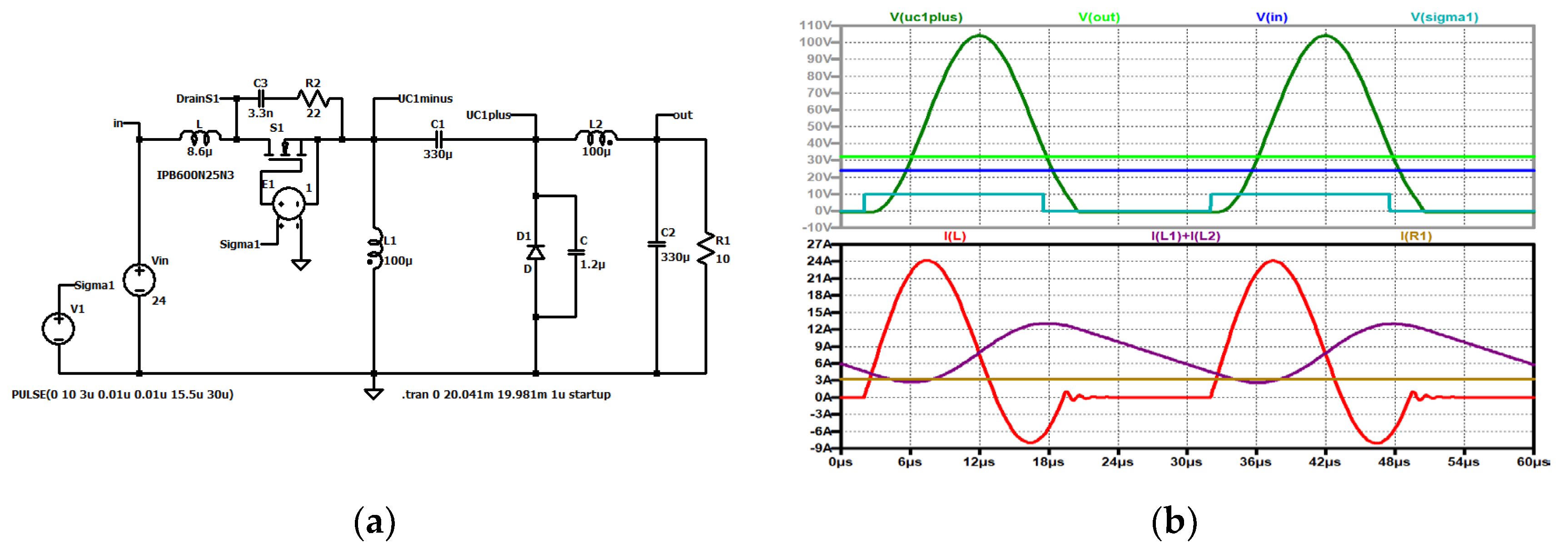
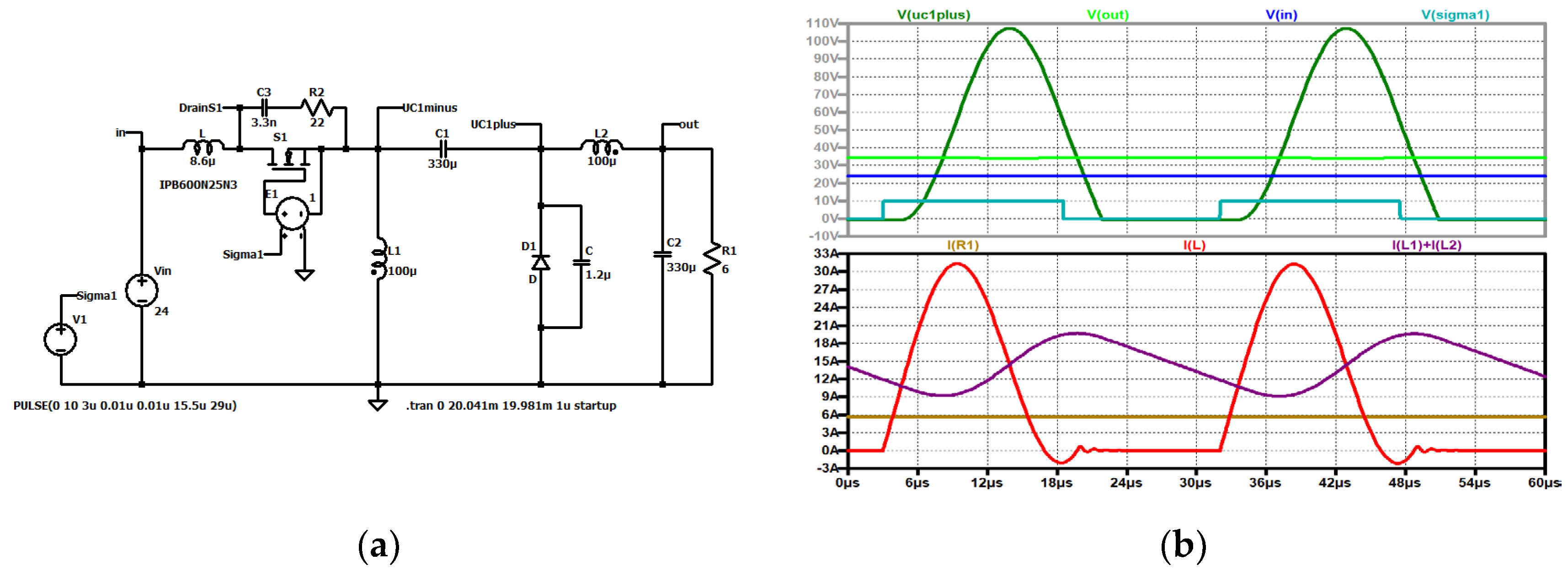
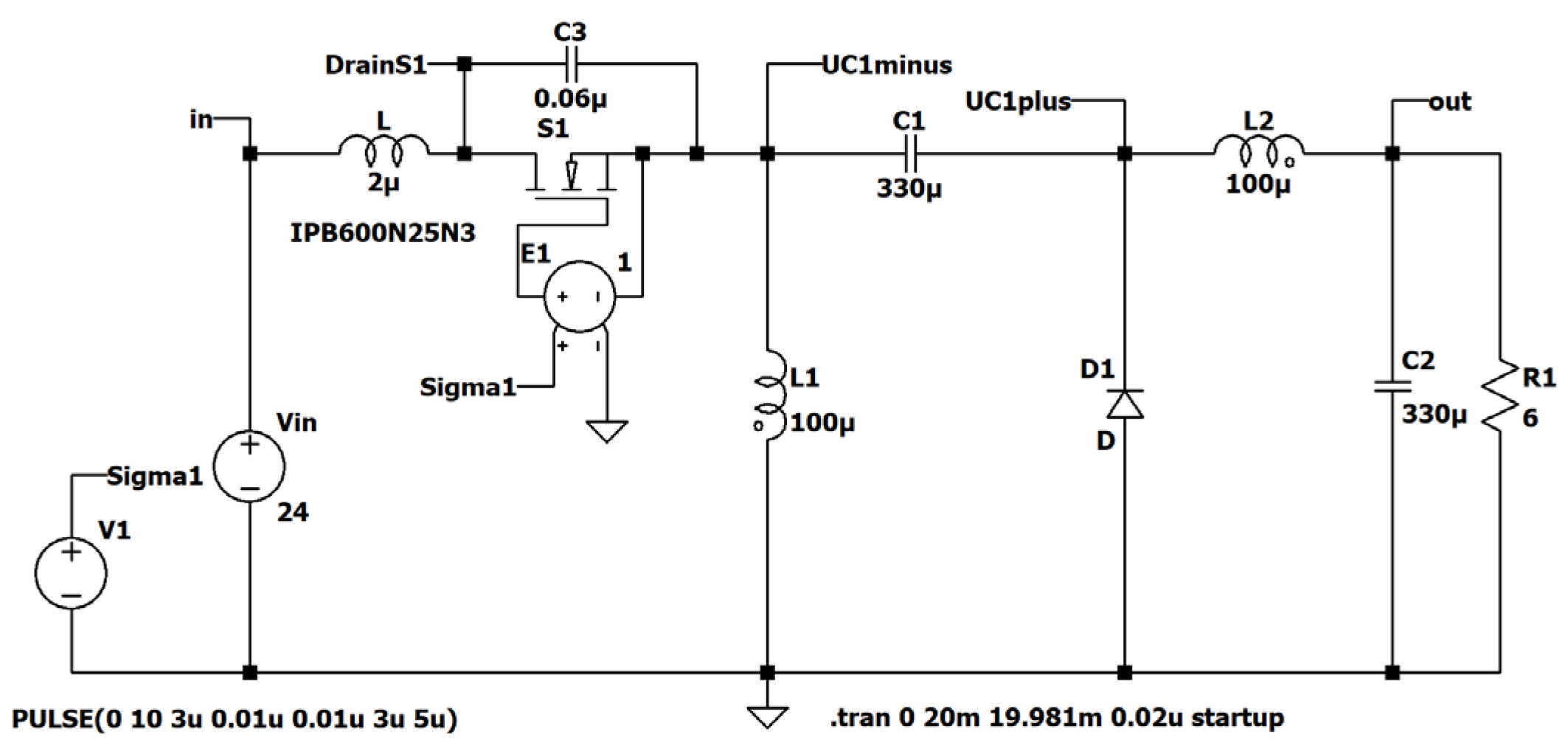
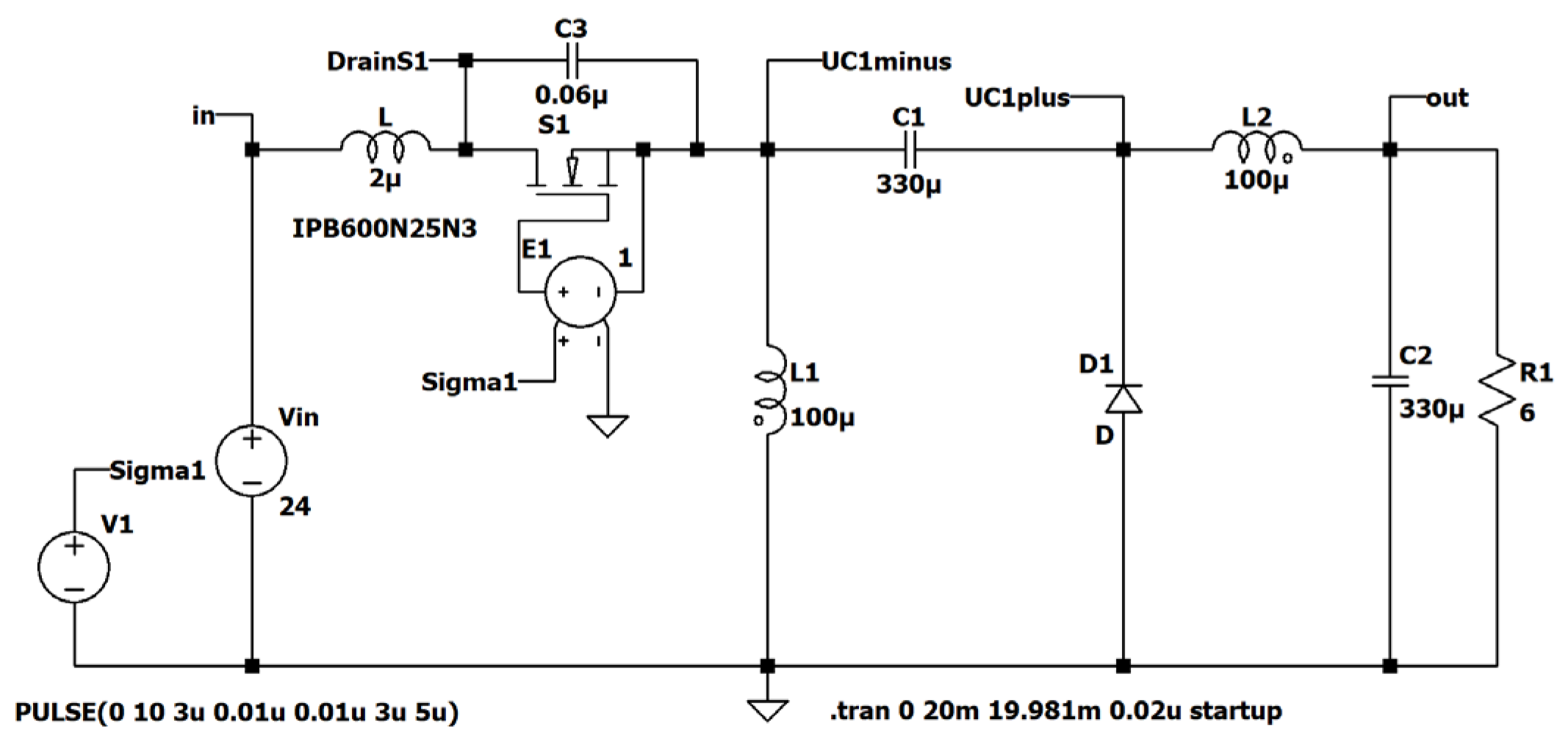
Figure 29.
ZVS QR Zeta: simulation circuit.
Figure 29.
ZVS QR Zeta: simulation circuit.
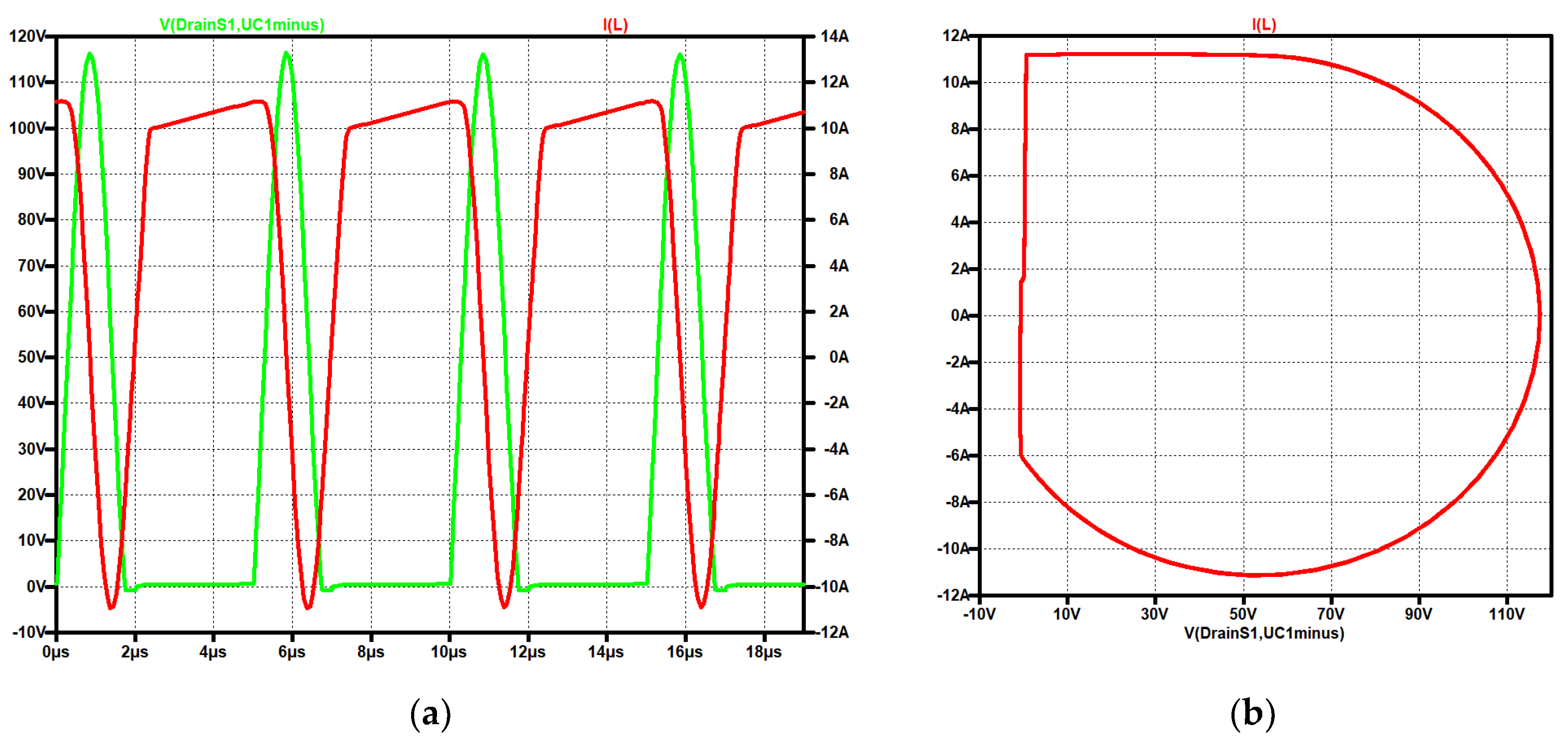
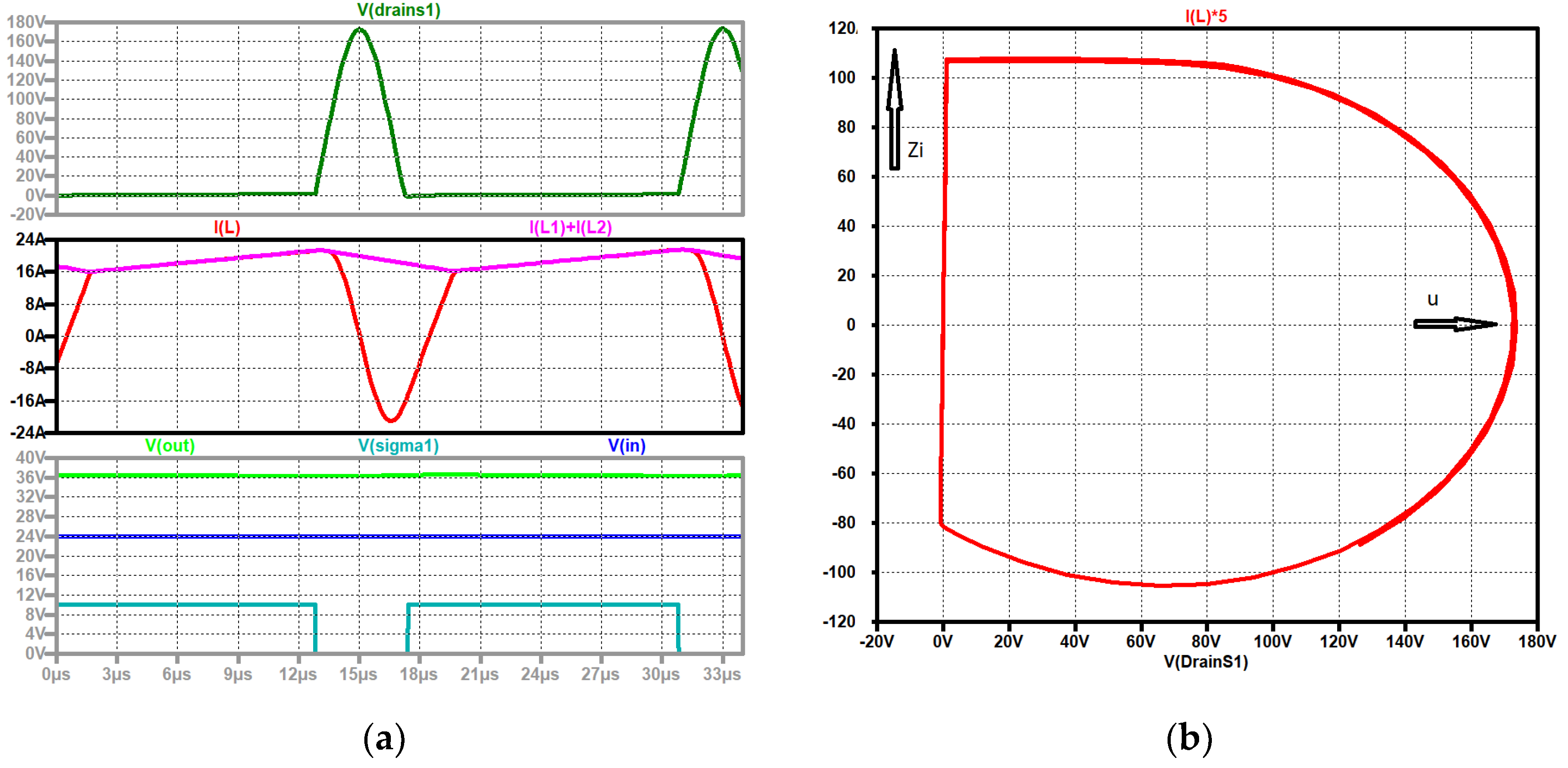
Figure 30.
ZVS QR Zeta: (a) voltage across the resonance capacitor (green), current through the resonance coil (red); (b) trajectory.
Figure 30.
ZVS QR Zeta: (a) voltage across the resonance capacitor (green), current through the resonance coil (red); (b) trajectory.
Figure 31.
Circuit diagram of the SEPIC converter.
Figure 31.
Circuit diagram of the SEPIC converter.
Figure 32.
Circuit diagram of the ZCS QR SEPIC converter.
Figure 32.
Circuit diagram of the ZCS QR SEPIC converter.
Figure 33.
ZCS QR SEPIC: equivalent circuit.
Figure 33.
ZCS QR SEPIC: equivalent circuit.
Figure 34.
ZCS QR SEPIC: mode M0.
Figure 34.
ZCS QR SEPIC: mode M0.
Figure 35.
ZCS QR SEPIC: mode M1.
Figure 35.
ZCS QR SEPIC: mode M1.
Figure 36.
ZCS QR SEPIC: mode M2.
Figure 36.
ZCS QR SEPIC: mode M2.
Figure 37.
ZCS QR SEPIC: mode M3.
Figure 37.
ZCS QR SEPIC: mode M3.
Figure 38.
ZCS QR SEPIC: u-Zi diagram.
Figure 38.
ZCS QR SEPIC: u-Zi diagram.
Figure 39.
ZCS QR SEPIC circles describing mode M2: different currents and voltages are shown.
Figure 39.
ZCS QR SEPIC circles describing mode M2: different currents and voltages are shown.
Figure 40.
ZCS QR Sepic: simulation circuit.
Figure 40.
ZCS QR Sepic: simulation circuit.
Figure 41.
ZCS QR SEPIC: (a) up to down: voltage across the resonant capacitor (dark green); current through the resonant coil (red), sum of the currents through the converter coils (violet); output voltage (green), input voltage (blue), control signal (turquoise); (b) u-Zi diagram.
Figure 41.
ZCS QR SEPIC: (a) up to down: voltage across the resonant capacitor (dark green); current through the resonant coil (red), sum of the currents through the converter coils (violet); output voltage (green), input voltage (blue), control signal (turquoise); (b) u-Zi diagram.
Figure 42.
Circuit diagram of the ZVS QR SEPIC.
Figure 42.
Circuit diagram of the ZVS QR SEPIC.
Figure 43.
ZVS QR SEPIC: equivalent circuit.
Figure 43.
ZVS QR SEPIC: equivalent circuit.
Figure 44.
ZVS QR SEPIC: M0.
Figure 44.
ZVS QR SEPIC: M0.
Figure 45.
ZVS QR SEPIC: M1.
Figure 45.
ZVS QR SEPIC: M1.
Figure 46.
ZVS QR SEPIC: M2.
Figure 46.
ZVS QR SEPIC: M2.
Figure 47.
ZVS QR SEPIC: M3.
Figure 47.
ZVS QR SEPIC: M3.
Figure 48.
ZVS QR SEPIC circles describing mode M2: different currents and voltages are shown.
Figure 48.
ZVS QR SEPIC circles describing mode M2: different currents and voltages are shown.
Figure 49.
ZVS QR SEPIC: simulation circuit.
Figure 49.
ZVS QR SEPIC: simulation circuit.
Figure 50.
ZVS QR SEPIC: (a) up to down: voltage across the resonant capacitor (dark green); current through the resonant coil (red), current through the converter coils (violet); output voltage (green), input voltage (blue), control signal (turquoise); (b) u-Zi diagram.
Figure 50.
ZVS QR SEPIC: (a) up to down: voltage across the resonant capacitor (dark green); current through the resonant coil (red), current through the converter coils (violet); output voltage (green), input voltage (blue), control signal (turquoise); (b) u-Zi diagram.
Figure 52.
ZCS QR CUK: (a) mode M0; (b) mode M1.
Figure 52.
ZCS QR CUK: (a) mode M0; (b) mode M1.
Figure 53.
ZCS QR CUK: (a) mode M2; (b) mode M3.
Figure 53.
ZCS QR CUK: (a) mode M2; (b) mode M3.
Figure 54.
ZCS QR CUK: (a) simulation circuit; (b) up to down: voltage across the resonant capacitor (green), current through the resonant coil (red).
Figure 54.
ZCS QR CUK: (a) simulation circuit; (b) up to down: voltage across the resonant capacitor (green), current through the resonant coil (red).
Figure 55.
ZVS QR converter: circuit diagram.
Figure 55.
ZVS QR converter: circuit diagram.
Figure 56.
ZVS QR CUK: (a) mode M0; (b) mode M1.
Figure 56.
ZVS QR CUK: (a) mode M0; (b) mode M1.
Figure 57.
ZVS QR CUK: (a) mode M2; (b) mode M3.
Figure 57.
ZVS QR CUK: (a) mode M2; (b) mode M3.