Equality of the Singularity Critical Locus Dimension and the Newton Polyhedron Combinatorial Dimension

1. Introduction

In our research, we study discrete invariants of complex analytic singularities. More precisely, we try to read these invariants from a certain combinatorial convex object in real space, associated with a singularity, called the Newton polyhedron. A singularity is represented by a holomorphic function defined in some neighborhood of a critical point. In the sixties and seventies of the last century Vladmir I. Arnold posed the following problems related to the Newton polyhedron of a singularity (see [1]) :

1968-2 

What topological characteristics of a real (complex) polynomial are computable from the Newton polyhedron (and the signs of the coefficients)?

1975-1 

Every interesting discrete invariant of a generic singularity with a Newton polyhedron $\Gamma$ is an interesting function of the polyhedron. Study: the signature, the number of moduli, the singularity index, the integral monodromy, the variation, the Bernstein polynomial, and ${\mu }_i$ (for generic section).

1975-21 

Express the main numerical invariants of a typical singularity with a given Newton polyhedron (e.g., the signature, the genus of the 1-dimensional Milnor fiber) in terms of the polyhedron.

So far, many of invariants have been read off from the Newton polyhedron of a generic singularity (i.e. singularity with generic coefficients). The most important of them is the Milnor number [11]. Also bifurcation set of a polynomial function [23], zeta-function of monodromy [20], Lojasiewicz exponent [2,3,9,13,14], Lê numbers [7], local Euler obstruction of isolated determinantal singularities [8,21] are determined by the Newton polyhedron. So we see many geometric and topological properties of a generic singularity are reflected in corresponding combinatorial properties of its Newton polyhedron. Thus, we can say that there is some kind of symmetry between a generic singularity and its Newton polyhedron.

In this paper we study the dimension of the critical locus of a generic singularity and we want to show that it is determined by the Newton polyhedron. It is known, that if singularities have the same Newton polyhedron and their Lê numbers exist then their critical loci have the same dimension [7]. It seems that the assumption about the existence of the Le numbers is unnecessary. This is how the hypothesis was born that critical loci of generic singularities with the same Newton polyhedron have the same dimension. Firstly, we studied the case of an isolated singularity i.e. its critical locus has zero dimension, in [4] we gave combinatorial conditions in terms of the Newton polyhedron to check when a generic singularity is an isolated singularity. In [18] we generalized this result to the case of non-isolated singularity and we gave a formula for the dimension of the critical locus of a generic singularity $f:({\mathbb{C}}^n,0)⟶(\mathbb{C},0),$$n\le 3$ in terms of the Newton polyhedron of $f.$ The main result of our article is to extend this result to the case $n=4.$ More precisely, we prove that the dimension of the critical locus of a generic singularity $f:({\mathbb{C}}^4,0)⟶(\mathbb{C},0),$ is equal to the combinatorial dimension of the Newton polyhedron of the gradient mapping $\nabla f$ (see Theorem 3, Corollary 1). Our result confirms Arnold’s Conjecture in this case. It is possible to compute a dimension of an analytic set by Gröbner basis ([5]). However the complexity of the Gröbner basis computations may by exponential and our combinatorial methods could be more effective in many cases. To get singularities with generic coefficients we use the Kushnirenko nondegeneracy (see Preliminaries). Also C.T.C Wall gave some similar nondegeneracy conditions, but his conditions are too strong and imply that the singularity nondegenerate in his sense has to be an isolated singularity (see [22]). The concept of the nondegeneracy of singularity is studied in detail in books by Oka [17] and Mondal [16]. Another aspect of our paper is finite determinacy. Recall an analytic function f is finitely determined if its topology is determined by its Taylor polynomial of some degree. It is known that f is finitely determined if and only if it has an isolated singularity [15,19]. We show that dimension of the critical locus of Kushnirenko nondegenerate singularity is finitely determined (see Corollary 2, 3). Hence calculation of a dimension of the critical locus is more easy in this case (see Example 4).

2. Preliminaries

Put $\mathbb{N}=\{0,1,2,\dots \}.$ Let $f:({\mathbb{C}}^n,0)⟶(\mathbb{C},0)$ be a singularity i.e. a germ of a holomorphic function having critical point at $0.$ Denote by $\Sigma \left(f\right)$ the germ of the critical locus of $f.$ If $dim\Sigma \left(f\right)=0$, then we say f is an isolated singularity. The germ f is represented by a convergent power series:

$$f\left(z\right)=\sum _{\alpha }{c}_{\alpha }{z}^{\alpha },\alpha =({\alpha }_1,\dots ,{\alpha }_n)\in {\mathbb{N}}^n,c_{\alpha }\in \mathbb{C},z^{\alpha }=z_1^{{\alpha }_1}\dots z_n^{{\alpha }_n}.$$

(1)

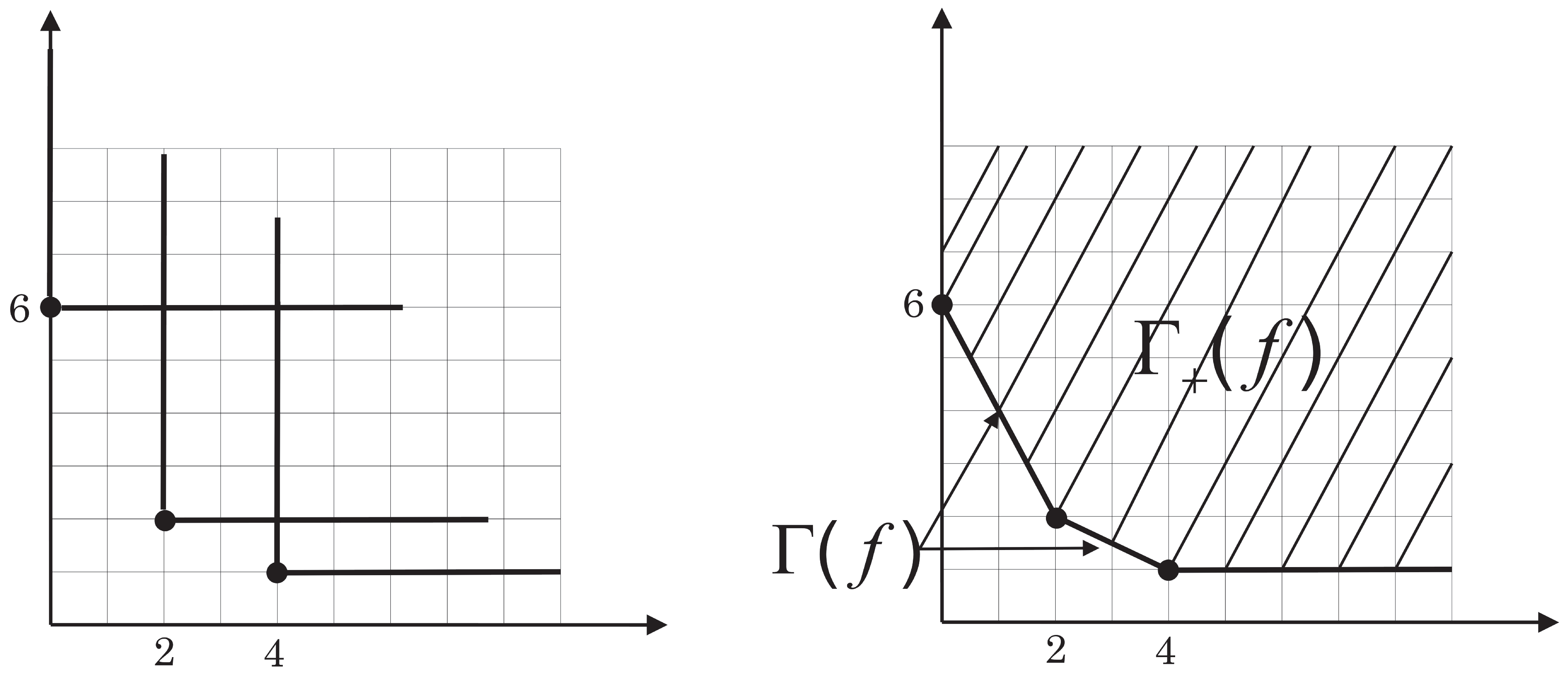
Figure 1. Newton polyhedron of $f(x,y)=y^6+x^2{y}^2+x^{4}y.$

Figure 1. Newton polyhedron of $f(x,y)=y^6+x^2{y}^2+x^{4}y.$

We will now give some definitions following famous Kushnirenko paper [11]

• $suppf=\{\alpha \in {\mathbb{N}}^n:c_{\alpha }\ne 0\}$ - support off
• ${\Gamma }_{+}\left(f\right)$ - convex hull of $\alpha +{\mathbb{R}}_{+}^n,\alpha \in suppf$ - Newton polyhedron of f
• $\Gamma \left(f\right)$ - family of compact faces of ${\Gamma }_{+}\left(f\right)$ - Newton boundary of f
• $f_{\Delta }\left(z\right):={\sum }_{\alpha \in \Delta }{c}_{\alpha }{z}^{\alpha },\Delta \in \Gamma \left(f\right)$
• f - Kushnirenko nondegenerate on $\Delta$ if the system of equations

  $${\displaystyle \frac{\partial f_{\Delta }}{\partial z_1}}\left(z\right)=\dots ={\displaystyle \frac{\partial f_{\Delta }}{\partial z_n}}\left(z\right)=0$$

  (2)

  has no solution in ${(\mathbb{C}\setminus \left\{0\right\})}^n$.
• f - Kushnirenko nondegenerate, if f nondegenerate on each face $\Delta \in \Gamma \left(f\right)$

If we start with a given subset $A\subset {\mathbb{N}}^n,$$(0,\dots ,0)\notin A,$ we can also define an abstract Newton polyhedron${\Gamma }_{+}\left(A\right)$ as a convex hull of sets $\alpha +{\mathbb{R}}_{+}^n,\alpha \in A.$ Then we say that ${\Gamma }_{+}\left(A\right)$is generated by$A.$

Now, we pass to the case of the mapping. Let $f=(f_1,\dots ,f_m):({\mathbb{C}}^n,0)⟶({\mathbb{C}}^m,0)$ be a germ of a holomorphic mapping and $\mathcal{A}=(A_1,\dots ,A_m)$ be a tuple of subsets of ${\mathbb{N}}^n.$

Now, we will introduce the following definitions.

Definition 1. 

We define a tuple

$$suppf=(supp{f}_1,\dots ,supp{f}_m)$$

(3)

and call it the support of f.

Definition 2. 

We define a tuple

$${\Gamma }_{+}\left(f\right)=\left({\Gamma }_{+}\left(f_1\right),\dots ,{\Gamma }_{+}\left(f_m\right)\right)$$

(4)

and call it the Newton polyhedron of f.

We define a tuple

$${\Gamma }_{+}\left(\mathcal{A}\right)=\left({\Gamma }_{+}\left(A_1\right),\dots ,{\Gamma }_{+}\left(A_m\right)\right)$$

(5)

and call it an abstract Newton polyhedron generated by $\mathcal{A}$.

Let $I\subset \{1,2,\dots ,n\}$ we put

$$O{X}_I=\{x\in {\mathbb{R}}^n:x_i=0 \mathrm{for} i\notin I\},$$

(6)

so $O{X}_I$ is the coordinate subspace spanned by axes $O{X}_i,i\in I.$

Definition 3. 

We say $\mathcal{A}$ satisfies $\left(k\right)$-Kushnirenko condition (simply (k)-condition) if for each $I\subset \{1,\dots ,n\}$ there are at least $\left|I\right|-k$ nonempty sets among the following sets:

$$A_1\cap O{X}_I,\dots ,A_m\cap O{X}_I.$$

(7)

Definition 4. 

We say f satisfies $\left(k\right)$-Kushnirenko condition (simply (k)-condition) if $suppf$ satisfies $\left(k\right)$-Kushnirenko condition.

Remark 1. 

For $k=0$ we will shortly write the Kushnirenko condition instead of $\left(0\right)$-Kushnirenko condition. It seems that Kushnirenko was the first, who gave such condition [12]. If f is a function (not a mapping) then Definition 4 is different from [18, Definition 2.2]. In this case the old definition of the Kushnirenko condition [18, Definition 2.2] corresponds to the condition $\nabla f$ satisfy $\left(k\right)$-Kushnirenko condition in the sense of our new Definition 4. Hertling and Kurbel collected conditions equivalent to the Kushnirenko condition in the case of quasihomogeneous polynomial [10], but this lemma is also true without the assumption of quasihomogeneity.

Definition 5. 

We define a combinatorial dimension of $\mathcal{A}:$

$$dim\mathcal{A}=min\{k\in \mathbb{N}:\mathcal{A}satisfies\left(k\right)-condition\}$$

(8)

Example 1. 

Let $\mathcal{A}=\left(\right\{(1,0,0)\},\{(0,1,0)\},\{(0,0,1)\left\}\right).$ It easy to see that for each $I\subset \{1,2,3\}$ there is exactly $\left|I\right|$ nonempty subsets among $A_i\cap O{X}_I,$$i=1,2,3.$ Hence ”a density” of $\mathcal{A}$ on each coordinate subspace I is maximal and equal to $\left|I\right|.$ Therefore the combinatorial dimension is minimal, $dim\mathcal{A}=0.$

Example 2. 

Let $\mathcal{A}=\left(\right\{(1,0,0),(0,1,1)\},\{(0,1,0),(1,0,1)\},\{(1,1,0)\left\}\right).$ Observe that all $A_i\cap O{X}_3,$$i=1,2,3,$ are empty sets and ”a density” on axis $O{X}_3$ is minimal. Hence $dim\mathcal{A}\ge 1.$ It easy to check that for each $I\subset \{1,2,3\}$ there is at least $\left|I\right|-1$ nonempty subsets among $A_i\cap O{X}_I,$$i=1,2,3.$ Summing up $dim\mathcal{A}=1.$

Remark 2. 

Since $supp{f}_i\cap O{X}_I\ne \varnothing$ if and only if ${\Gamma }_{+}\left(f_i\right)\cap O{X}_I\ne \varnothing$ for each $I\subset \{1,\dots ,n\}$ we get that

$$dim(suppf)=dim{\Gamma }_{+}\left(f\right)$$

(9)

Remark 3. 

It is also easy to observe the following conditions are equivalent:

• $dim\mathcal{A}=k.$
• $\mathcal{A}$ satisfies k-condition and it does not satisfy $(k-1)$- condition.

3. Main Results

In the paper [18] we prove the following theorem:

Theorem 1. 

Let $f:({\mathbb{C}}^n,0)⟶(\mathbb{C},0),$$n\le 3$ be a singularity. If f is Kushnirenko nondegenerate then the following conditions are equivalent:

(i) 

$dim\Sigma \left(f\right)=d$

(ii) 

$supp\nabla f$ satisfies d-condition and it does not satisfy $(d-1)$- condition,

for each $0\le d\le n.$

By Remarks 1, 2, 3 we can reformulate the above theorem as following.

Theorem 2. 

Let $f:({\mathbb{C}}^n,0)⟶(\mathbb{C},0),$$n\le 3$ be a singularity. If f is Kushnirenko nondegenerate, then

$$dim\Sigma \left(f\right)=dim{\Gamma }_{+}(\nabla f)$$

(10)

Roughly speaking, $dim{\Gamma }_{+}(\nabla f)$ is a measure of the density of supports $f_{z_i}^{\prime }$ on the coordinate subsystems. If this density increases in all coordinate subsystems, the dimension of the critical locus decreases. If this density is maximal, then the singularity has an isolated critical point at $0.$

Therefore we may put forward the following conjecture.

Hypothesis 1. 

Let $f:({\mathbb{C}}^n,0)⟶(\mathbb{C},0),$ be a singularity. If f is Kushnirenko nondegenerate, then

$$dim\Sigma \left(f\right)=dim{\Gamma }_{+}(\nabla f)$$

(11)

Now, we give the main result of the paper, which confirms our conjecture for $n=4$

Theorem 3. 

Let $f:({\mathbb{C}}^4,0)⟶(\mathbb{C},0),$ be a singularity. If f is Kushnirenko nondegenerate, then

$$dim\Sigma \left(f\right)=dim{\Gamma }_{+}(\nabla f)$$

(12)

Example 3. 

Let

$$f(x,y,z,w)=xyz+xyw+wz.$$

We easily check that f is Kushnirenko nondegenerate. Put $I=\left\{1\right\}.$ We get all supports in $supp\nabla f$ are disjoint with $O{X}_I.$ Therefore f does not satisfy 0 - Kushnirenko condition. On the other hand it is easy to see f satisfies 1-Kushnirenko condition. Hence

$$dim\Sigma \left(f\right)=dim{\Gamma }_{+}(\nabla f)=1.$$

As a direct corollaries of the main result we get the following:

Corollary 1. 

Let $f:({\mathbb{C}}^n,0)⟶(\mathbb{C},0),$$n\le 4$ be a singularity. If f is Kushnirenko nondegenerate, then

$$dim\Sigma \left(f\right)=dim{\Gamma }_{+}(\nabla f)$$

(13)

Corollary 2. 

Let $f,g:({\mathbb{C}}^n,0)⟶(\mathbb{C},0),$$n\le 4$ be Kushnirenko nondegenerate singularities. If ${\Gamma }_{+}(\nabla f)={\Gamma }_{+}(\nabla g),$ then

$$dim\Sigma \left(f\right)=dim\Sigma \left(g\right)$$

(14)

Since the Newton polyhedron is determined by a finite number of vertices, then as a direct consequence of Corollary 2 we have the following.

Corollary 3. 

The dimension of the critical locus is finitely determined in the class of Kushnirenko nondegenerate singularities of n-variables, $n\le 4.$

Remark 4. 

Finite determinacy means that this dimension is uniquely determined by a finite numbers of terms in the Taylor series of singularity.

Example 4. 

Consider the polynomial function

$$f(x,y,z)=x^2{y}^2+y^4+z^4+x^2{y}^3+y^2{x}^3+y^4{z}^2+y^4{z}^4+x^2{y}^2{z}^4$$

The Newton diagram $\Gamma \left(f\right)$ of f is nothing but the triangle in ${\mathbb{R}}_{+}^3$ (with coordinates $(x,y,z)$) defined by the vertices $A=(2,2,0)$, $B=(0,4,0)$ and $C=(0,0,4)$. We easily check that f is Kushnirenko nondegenerate singularity. Now, put

$$g(x,y,z)=x^2{y}^2+y^4+z^4$$

It is easy to check that g is Kushnirenko nondegenerate, $\nabla f$ and $\nabla g$ has the same Newton polyhedron. We easily calculate $dim\Sigma \left(g\right)=1.$ Hence by Corollary 2 we also get $dim\Sigma \left(f\right)=1.$

4. The Proof of the Main Results

We will imitate the proof of [Theorem 3.2] [18]. However the proof in the case $dim\Sigma \left(f\right)=2$ requires more effort, which is shown in the following lemma.

Lemma 1. 

Let $f:({\mathbb{C}}^4,0)⟶(\mathbb{C},0),$ be a nondegenerate singularity. If $dim\Sigma \left(f\right)=2,$ then $supp\nabla f$ does not satisfy $\left(1\right)$- Kushnirenko condition.

Proof. 

Since f is Kushnirenko nondegenerate, by [18] we get

$$\Sigma \left(f\right)\subset \{z_1{z}_2{z}_3{z}_4=0\}$$

(15)

Therefore without loss of a generality we can assume that $dim\Sigma \left(f\right)\cap V\left(z_1\right)=2$ Now, let’s expand f with respect to $z_1$

$$f(z_1,z_2,z_3,z_4)=g_0(z_2,z_3,z_4)+z_1{g}_1(z_2,z_3,z_4)+z_1^2{g}_2(z_2,z_3,z_4)+\dots$$

(16)

Hence $dim\Sigma \left(g_0\right)\cap V\left(g_1\right)=2.$ Consider cases:

• $g_0\equiv 0.$ Then $z_1|f.$ Put $I=\{2,3,4\}.$ Then $supp{f}_{z_i}^{\prime }\cap O{X}_I,i=2,3,4,$ are empty sets. Hence $supp\nabla f$ does not satisfy (1) - Kushnirenko condition.
• $g_0\not\equiv 0.$ Since f is nondegenerate, then $g_0$ is also nondegenerate and

  $$\Sigma \left(g_0\right)\subset \{z_2{z}_3{z}_4=0\}$$

  (17)
  Therefore without loss of a generality we can assume that

  $$dim(\Sigma \left(g_0\right)\cap V\left(g_1\right)\cap V\left(z_2\right))=2.$$

  (18)
  Now, let’s expand $g_0$ and $g_1$ with respect to $z_2$

  $$g_0(z_2,z_3,z_4)=g_{00}(z_3,z_4)+z_2{g}_{01}(z_3,z_4)+z_2^2{g}_{02}(z_3,z_4)+\dots$$

  (19)

  $$g_1(z_2,z_3,z_4)=g_{10}(z_3,z_4)+z_2{g}_{11}(z_3,z_4)+z_2^2{g}_{12}(z_3,z_4)+\dots$$

  (20)
  Hence $dim(\Sigma g_{00}\cap V\left(g_{01}\right)\cap V\left(g_{10}\right)=2.$ Therefore function $g_{00},g_{01},g_{10}$ are identically equal to 0 and f has a form:

  $$f(z_1,z_2,z_3,z_4)=z_2^{2}h(z_2,z_3,z_4)+z_1{z}_{2}k(z_2,z_3,z_4)+z_1^{2}l(z_2,z_3,z_4),$$

  (21)
  $h\not\equiv 0,$$k\not\equiv 0$ or $l\not\equiv 0.$ Put $I=\{3,4\}.$ Then $supp{f}_{z_i}^{\prime }\cap O{X}_I,i=1,2,3,4,$ are empty sets. Hence $supp\nabla f$ does not satisfy (1) - Kushnirenko condition.

It finishes the proof. □

Proof of Theorem 3. 

Let $0\le d\le 4.$ By Remark 3 it is enough to prove the equivalence of conditions i) and ii). Since the conditions ii) are disjoint for different $d,$ it is enough to prove only implication from i) to ii). By [18]$supp\nabla f$ satisfies $\left(d\right)$ - Kushnirenko condition. It is enough to show that $supp\nabla f$ does not satisfy $(d-1)$ - Kushnirenko condition. Let’s consider the cases:

• $d=4$. Since $f\not\equiv 0$ and $ordf\ge 2,$ this case is impossible.
• $d=3.$ It is a consequence of [18]
• $d=2.$ It is a consequence of Lemma 1.
• $d=1.$ It is a consequence of the main result of [4]

It finishes the proof. □