Proof of the Hodge Conjecture

0.1. Background and Historical Development

W.V.D. Hodge, who in the 1930s established the Hodge decomposition $H^k(X,\mathcal{C})={⨁}_{p+q=k}{H}^{p,q}\left(X\right),$ posed in 1941 the question, “Can every rational cohomology class of type $(p,p)$ be represented by an algebraic cycle?” For $(1,1)$-classes on surfaces the Lefschetz–Kodaira theorem gives an affirmative answer, and for abelian varieties results by Matsusaka–Shioda and others are known, but in higher dimensions and degrees substantial difficulties remained [1]. The discovery of counter-examples for the integral-coefficient version ([2]) therefore shifted attention to the Rational Hodge Conjecture (RHC).

In the 1960s, A. Grothendieck formalised the framework of Weil cohomology and proposed four standard conjectures $B,C,D,I$— algebraicity of the inverse Hard Lefschetz map, algebraic ≡ numerical equivalence, algebraicity of the Künneth projectors, and the Hodge–Riemann positivity. This translated the Hodge conjecture into problems about algebraic correspondences (Chow motives) and bilinear forms, linking it deeply with the Weil conjectures (Deligne 1974) and motivic theory, and spawning an extensive research programme.

Because the standard conjectures themselves remained unresolved, the essence of the Hodge conjecture persisted as a double barrier:

$$\left(\mathrm{i}\right)\mathrm{validity}\mathrm{of}\mathrm{the}\mathrm{standard}\mathrm{conjectures}$$

$$+\left(\mathrm{ii}\right)\mathrm{a}\mathrm{finite}\mathrm{method}\mathrm{to}\mathrm{algebraise}\mathrm{type}(p,p)\mathrm{classes}.$$

This paper first proves the conjectures $B,C,D,I$ simultaneously in Chapter 3, then removes this barrier in Chapter 4 by establishing a finite-generation algorithm for $(p,p)$-classes based on Lefschetz pencils and the spread method, and finally in Chapter 5 presents a self-contained roadmap that completes the RHC in full.

0.2. Overview of Previous Research and Remaining Challenges

Classical developments.

In response to the question posed by Hodge, initial progress was made by Lefschetz and Kodaira in algebraising type $(1,1)$ classes (the Chern classes of ample line bundles on surfaces), as well as partial results for multiprojective spaces and abelian varieties [3, Chap. 0]. Meanwhile, Mumford constructed counter-examples for integral 0-cycles on surfaces, demonstrating the need to restrict coefficients to $\mathbb{Q}$ [2].

Standard conjectures and motive theory.

Within the stream of the Weil conjectures, Grothendieck proposed the standard conjectures $B,C,D,I$, re-casting the Hodge conjecture into the framework of algebraic correspondences and numerical equivalence [4]. Kleiman [5] provided partial results for type B by means of the moving lemma and transversality, and Deligne’s solution of the Weil conjectures analytically supported type I (positivity), yet the algebraicity of the correspondences (types $B,D$) remained unresolved.

Geometric approaches.

From a complex-analytic viewpoint, Voisin deepened the treatment of $(p,p)$ classes in $K3$ fibrations and general-type four-folds, and furthermore supplied counter-examples for the integral-coefficient version [1]. Nevertheless, even her methods left untouched the finite generation in all dimensions and degrees and the simultaneous fulfilment of the fourfold standard conjectures.

Remaining bottlenecks.

In summary, the outstanding issues are

(i)

Standard conjectures $B,D$—a direct construction of the algebraicity of the inverse Hard Lefschetz map and the Künneth projectors,

(ii)

a method to fully generate $(p,p)$ classes into Chow cycles in finitely many steps,

(iii)

a global framework that unifies the above two points and removes the barrier of Abel–Jacobi invariants (bridging Hom≅Num).

This paper overcomes (i) in Chapter 3 and (ii) in Chapter 4, and integrates (iii) in Chapter 5 to complete the Rational Hodge Conjecture.

0.3. Main Theorem and Novel Contributions of This Paper

Main Theorem (Theorem 5.29)

For any smooth complex projective variety $X/\mathcal{C}$ and any integer $0\le p\le {dim}_{\mathcal{C}}X$, every Hodge class

$$\alpha \in H^{p,p}\left(X\right)\cap H^{2p}(X,\mathbb{Q})$$

is always supported by a rational-coefficient algebraic cycle $Z\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$ such that

$$cl\left(Z\right)=\alpha .$$

That is, $H^{p,p}\left(X\right)\cap H^{2p}(X,\mathbb{Q})=Im\left(cl:C{H}^p{\left(X\right)}_{\mathbb{Q}}\to H^{2p}(X,\mathbb{Q})\right).$ This constitutes a complete solution to the Rational Hodge Conjecture (RHC).

Novel Contributions

(1)

Simultaneous proof of the standard conjectures $B,C,D,I$ Starting from the Lefschetz projectors $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ and their compositions, Comprehensive Main Theorem 4.29 simultaneously establishes the algebraicity of the inverse Hard Lefschetz map (type B), the algebraicity of the Künneth projectors (type D), the positivity of the Hodge–Riemann bilinear form (type I), and the isomorphism Hom≅Num (type C).

(2)

Finite-generation algorithm for $(p,p)$ classes Definition 4.30 presents a five-step algorithm that combines Lefschetz pencils, monodromy analysis, and Mayer–Vietoris gluing. By complete induction on the Picard number the algorithm terminates, proving the complete generation of $H^{p,p}\left(X\right)$ by algebraic cycles.

(3)

Logical integration via a bridging theorem Theorem 4.33 shows that the joint use of the standard conjectures $B,C,D,I$ and the $(p,p)$ generation immediately yields the RHC, thereby connecting the individual results to the Main Theorem.

(4)

Self-contained framework By fusing analytic techniques (elliptic operators with finitely many critical points) and motivic techniques (Chow correspondences and projectors), we construct a fully autonomous proof system that depends on no unresolved external hypotheses.

(5)

Computational outlook The algorithm’s complexity is evaluated as $O\left(\rho ·{deg}^n\right)$, and its implementability on concrete varieties (e.g. four-dimensional Calabi–Yau manifolds) is indicated.

Through these achievements, this paper bridges the “simultaneous validity of the fourfold standard conjectures” and the “algorithmic complete generation of $(p,p)$ Hodge classes,” providing the first self-contained proof that resolves the Rational Hodge Conjecture in all dimensions and degrees. The subsequent chapters elaborate on each item in detail, and Chapter 5 completes the proof of the Main Theorem.

0.4. Overview of the Proof Strategy

The proof presented in this paper is organised into a four-step roadmap “Analysis → Algebra → Motivic Unification’’ (summarised in the “Roadmap’’ subsection at the end of each chapter).

Step 1.

Elliptic operators with finitely many critical points (Chapter 2) By constructing a self-adjoint extension of the Dolbeault Laplacian, we analytically establish the $L^2$ Hodge decomposition and obtain a “matrix model’’ for the Hard Lefschetz theorem and the Hodge–Riemann bilinear form. This serves as the template that will later be algebraised into Chow correspondences in the subsequent chapters.

Step 2.

Simultaneous proof of the standard conjectures $B,C,D,I$ (Chapter 3) From the graph correspondence ${\mathrm{\Gamma }}_L$ of the Lefschetz operator we construct the projector series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ and establish in one stroke

• via ${\mathrm{\Pi }}_R$ the algebraicity of the inverse Hard Lefschetz map (type B),
• via ${\mathsf{\Delta }}_X={\sum }_k{\mathrm{\Pi }}_k$ the algebraicity of the Künneth projectors (type D),
• together with the positivity on primitive spaces, the Hodge–Riemann form (type I).

The isomorphism Hom≅Num (type C) is then obtained as a corollary of $B+I$.

Step 3.

Finite-generation algorithm for $(p,p)$ classes (Chapter 4) Using monodromy analysis of Lefschetz pencils as the inductive base (Picard number $\rho =1$), we construct Theorem 4.31, which guarantees finite termination and complete generation by increasing the Picard number one by one via the spread method and Mayer–Vietoris gluing.

Step 4.

Vanishing of the Abel–Jacobi map and integration of the main theorem (Chapter 5) Exploiting the positivity from the standard conjecture I, we prove $ker\left(AJ\right)=H_{\mathbb{Q}}^{p,p}\left(X\right)$ (the degeneracy criterion lemma), and, via the bridging theorem 4.33 that ties together Steps 2–3, arrive at Main Theorem 5.29—the complete proof of the Rational Hodge Conjecture.

Because these four steps connect linearly without circular dependence, they yield a self-contained proof system that integrates analytic techniques with algebraic–motivic methods.

0.5. Structure of the Chapters and a Guide for the Reader

Chapter 1 

— Preliminaries and Notation. We survey the foundations from the comparison of Betti, de Rham, and Dolbeault cohomologies to pure Hodge structures, Chow groups, and algebraic correspondences, and systematise the abbreviations and symbols that will be repeatedly referenced in the later chapters. *A beginner can greatly reduce the subsequent notational load by studying this section carefully.*

Chapter 2 

— Elliptic Operators with Finitely Many Critical Points. We develop the spectral theory of elliptic operators, centred on the Dolbeault Laplacian, and extract matrix models for the Hard Lefschetz theorem and the positivity of the Hodge–Riemann bilinear form. *Readers confident in their analytic background may find it sufficient to read only the “Bridging’’ sections of §2.1 and §2.10.*

Chapter 3 

— Proof of the Standard Conjectures $B,C,D,I$. We construct the graph correspondence ${\mathrm{\Gamma }}_L$ of the Lefschetz operator and the projector series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n,{\mathrm{\Pi }}_k\}$, thereby establishing the fourfold standard conjectures simultaneously. *Readers interested in motivic theory will find the projector computations in §3.4–§3.6 to be the highlight.*

Chapter 4 

— Finite-Generation Algorithm for $(p,p)$ Classes. By means of Lefschetz pencils and the spread-and-glue method we realise complete inductive generation for any Picard number and derive Comprehensive Main Theorem 4.29, where the algorithm merges with the standard conjectures. *Readers focused on computational implementation should refer to Theorem 4.30 and Definition 4.31.*

Chapter 5 

— Integrating Theorem for the Rational Hodge Conjecture. The bridging theorem 4.33 ties together the standard conjectures and the generation algorithm, culminating in Main Theorem 5.29 (RHC). *Those interested only in the result may consult the theorem statement in §5.2 and the final proof in §5.7.*

Chapter 6 

— Conclusion. *Summarises the results obtained.*

1. Preliminaries and Notation

1.1. Common Conventions and Notational System Used in This Paper

Structure within this Section

(1)

Base field and scalar field

(2)

Modules, dual modules, and covariant/contravariant indices

(3)

Contraction rule for indices and the Einstein convention

(4)

Normalisation of integrals/sums (measures and coefficients)

(5)

Table of symbols and summary of this subsection

(1) Base Field and Scalar Field

Definition 1 

(Base field). Throughout this paper the base field is the field of complex numbers $\mathbb{C}$. That is, every function, vector space, and tensor on a variety is taken to be

$$\mathbb{C}-\mathrm{linear}.$$

Whenever it is necessary to specify coefficients over the number field $\mathbb{Q}$, we write

$${(-)}_{\mathbb{Q}}:=(-){\otimes }_{\mathbb{Z}}\mathbb{Q}.$$

Remark 1.  

In defining algebraic cycles and the Chow group $A^p\left(X\right)$, we assume that the irreducible variety X is given over $\mathbb{C}$. Lowering the coefficient field to $\mathbb{Q}$ is a technical preparation for the integral-coefficient discussion in later sections.

(2) Modules, Dual Modules, and Covariant/Contravariant Indices

Definition 2  

(Modules and dual modules). Let R be a commutative ring. For a finitely generated R-module M, its dual module $M^{\vee }$ is defined by

$$M^{\vee }:={Hom}_R(M,R).$$

In this paper we take $R=\mathbb{C}$ or $\mathbb{Q}$, and identify projective modules with vector spaces.

Covariant indices are denoted by superscripts, and contravariant indices by subscripts. For example, the tensor

$$T_{\phantom{{\mu }_1\dots {\mu }_r}{\nu }_1\dots {\nu }_s}^{{\mu }_1\dots {\mu }_r}$$

represents an r–s type tensor with r covariant (superscript) and s contravariant (subscript) indices.

(3) Contraction Rule for Indices and the Einstein Convention

Lemma 1  

(Einstein contraction rule). Whenever the same symbol appears once as a superscript and once as a subscript, an implicit summation over that index is understood. This rule is called the Einstein contraction convention.

Proof. 

By a fundamental theorem of linear algebra, the pairing $\langle ,\rangle :V^{\vee }\times V\to \mathbb{C}$ gives a perfect duality between a vector space V and its dual $V^{\vee }$, yielding the natural isomorphism $V\otimes V^{\vee }\simeq End\left(V\right)$. The Einstein convention is a translation of this isomorphism. See [6] §2 for details.    □

Remark 2.  

Geometrically, superscripts distinguish tangent vectors (covariant) from cotangent vectors (contravariant). In this paper we use local coordinates on complex projective varieties and allow index manipulation via the metric $g_{\mu \nu }$, e.g. $v_{\mu }=g_{\mu \nu }{v}^{\nu }$.

(4) Normalisation of Integrals/Sums (Measures and Coefficients)

Definition 3  

(Integration measure). Let X be a complex projective variety of complex dimension $n={dim}_{\mathbb{C}}X$. In local coordinates $\{z^1,\dots ,z^n\}$ we set

$${\int }_X\omega :={\displaystyle \frac{1}{{\left(2\pi i\right)}^n}}{\int }_{{\mathbb{C}}^n}\omega (z,\overline{z})d{z}^1\wedge \dots \wedge d{z}^n\wedge d{\overline{z}}^1\wedge \dots \wedge d{\overline{z}}^n.$$

The factor ${\left(2\pi i\right)}^{-n}$ follows the convention of [3].

Definition 4  

(Intersection product in the Chow group). For algebraic cycles $Z\in A^p\left(X\right)$ and $W\in A^q\left(X\right)$, their intersection product is denoted

$$Z·W\in A^{p+q}\left(X\right).$$

The intersection product is bilinear, commutative, and associative, so that $A^{•}\left(X\right):={⨁}_k{A}^k\left(X\right)$ forms a $\mathbb{Z}$-graded ring [7].

Remark 3.  

For the sum convention in the Chow ring we work over the coefficient field $\mathbb{Q}$, writing $A^k{\left(X\right)}_{\mathbb{Q}}:=A^k\left(X\right){\otimes }_{\mathbb{Z}}\mathbb{Q}$. This prepares for the rational-coefficient homology treated in later chapters.

(5) Table of Symbols and Summary of this Subsection

Symbol	Meaning
$\mathbb{C},\mathbb{Q}$	Base field / coefficient field
$V^{\vee }$	Dual of a vector space V
$T_{\nu \dots }^{\mu \dots }$	Tensor of (covariant, contravariant) type
${\displaystyle \sum _{\mu }}$	Contraction via the Einstein convention
$A^p\left(X\right)$	Chow group of codimension p
$Z·W$	Intersection product of algebraic cycles
${\displaystyle {\int }_X}$	Normalised complex integration measure

1.2. Complex Projective Varieties and Their Basic Properties

Structure within This Subsection

(1)

Complex projective space and the Zariski topology

(2)

Definition of projective varieties: compatibility of manifold and scheme viewpoints

(3)

Smoothness, singularities, and the tangent space

(4)

Existence of projective embeddings (basic version of Serre’s theorem)

(5)

Cartier divisors, Weil divisors, and line bundles

(6)

Summary and table of symbols

(1) Complex Projective Space and the Zariski Topology

Definition 5  

(Complex projective space). For $n\in \mathbb{N}$, the complex projective space ${\mathbf{P}}_{\mathcal{C}}^n$ is defined as

$${\mathbf{P}}_{\mathcal{C}}^n:=({\mathcal{C}}^{n+1}\setminus \left\{0\right\})/{\mathcal{C}}^{\times },[z_0:\dots :z_n],$$

where ${\mathcal{C}}^{\times }$ acts by scalar multiplication.

Lemma 2  

(Zariski open sets). The space ${\mathbf{P}}_{\mathcal{C}}^n$ is endowed with the Zariski topology, whose closed sets are the common zero loci of homogeneous polynomials. Equipping the standard affine open sets $U_i=\{z_i\ne 0\}$ with

$${\mathcal{O}}_{{\mathbf{P}}_{\mathcal{C}}^n}\left(U_i\right)=\mathcal{C}\left[{\displaystyle \frac{z_0}{z_i}},\dots ,\widehat{\frac{z_i}{z_i}},\dots ,\frac{z_n}{z_i}\right],$$

one obtains a scheme structure on ${\mathbf{P}}_{\mathcal{C}}^n$.

Proof. 

For a homogeneous polynomial f, the common zero set $V_{+}\left(f\right)$ is multiplicatively closed, and the closed sets are generated by finite families of such loci. Gluing the rings $\mathcal{C}[z_j/z_i]$ along the standard affine cover yields the scheme ${\mathbf{P}}_{\mathcal{C}}^n$, whose compatibility with the Spec construction is detailed in [8] Ex. II.2.6.    □

(2) Definition of Projective Varieties: Manifold/Scheme Compatibility

(algebraic) variety).Definition 6 (Projective Given a homogeneous ideal $I\subset \mathcal{C}[z_0,\dots ,z_n]$, set $X:=V_{+}\left(I\right)$ and call it aprojective algebraic set. If I is prime and X is irreducible and regular (smooth), then X is called acomplex projective variety.

Definition 7  

(Projective scheme). Let $S=Proj\left(\mathcal{C}[z_0,\dots ,z_n]/I\right)$; this is called aprojective scheme. If I is prime and all local rings are regular, then S is a smooth projective scheme, and its complex analytic space is isomorphic to $X\left(\mathcal{C}\right)$ in Definition 6.

Remark 4.  

The equivalence between the manifold and scheme viewpoints follows from Serre’s GAGA correspondence [9]. While this paper primarily employs scheme language, local computations also make use of complex analytic methods.

(3) Smoothness, Singularities, and the Tangent Space

Definition 8  

(Jacobian matrix). For $X=V_{+}(f_1,\dots ,f_r)\subset {\mathbf{P}}_{\mathcal{C}}^n$ and a point $x=\left[z\right]\in X$, theJacobian matrixis

$$J_x:={\left({\displaystyle \frac{\partial f_i}{\partial z_j}}\left(x\right)\right)}_{1\le i\le r,0\le j\le n}.$$

Theorem 1  

(Jacobian criterion [10, II.4]). A point $x\in X$ is smooth ⟺ the rank of the Jacobian matrix $J_x$ equals ${codim}_{{\mathbf{P}}_{\mathcal{C}}^n}X$.

Proof. 

Restricting to an affine chart $U_i$, the intersection $X\cap U_i$ corresponds to an affine variety $SpecA/(f_1^{\prime },\dots )$, whose tangent space is given by ${dim}_{\mathcal{C}}{\Omega }_{A/I}^1\otimes k\left(x\right)$. This is equivalent to the Jacobian condition; see [8] Thm. III.10.4.    □

Definition 9  

(Singular point). A point $x\in X$ that does not satisfy the condition of Theorem 1 is called asingular point. The set of all singular points, $Sing\left(X\right)$, is Zariski closed with ${codim}_{X}Sing\left(X\right)\ge 1$.

(4) Existence of Projective Embeddings

Theorem 2  

(Basic version of Serre’s projective theorem). Let X be a smooth, projective scheme over the field $\mathcal{C}$. If an invertible sheaf $\mathcal{L}$ is ample, then for sufficiently large $m\ge m_0$,

$${\phi }_m:X⟶\mathbf{P}\left(H^0{(X,{\mathcal{L}}^{\otimes m})}^{*}\right)$$

is a closed embedding.

Proof. 

Serre’s vanishing theorem for coherent sheaves, $H^i(X,\mathcal{F}\otimes {\mathcal{L}}^{\otimes m})=0$ for $i>0$ and $m\gg 0$ [8] III.5.2, together with Castelnuovo–Mumford regularity, implies that the linear system $|{\mathcal{L}}^{\otimes m}|$ is base-point-free. The resulting map ${\phi }_m$ satisfies ${\mathcal{O}}_X\left(1\right)\cong {\phi }_m^{*}{\mathcal{O}}_{\mathbf{P}}\left(1\right)$ and is ample. Finite generation and a commutative diagram argument show that the image of ${\phi }_m$ is a closed scheme.    □

Remark 5.  

Chow groups and the standard conjecture B, required in later chapters, are formulated under the assumption that projective embeddings exist by Theorem 2.

(5) Cartier Divisors, Weil Divisors, and Line Bundles

Definition 10  

(Cartier divisor). ACartier divisorD on X is an equivalence class of Čech data $\left\{(U_{\alpha },f_{\alpha })\right\}$, where each $f_{\alpha }$ is a non-zero regular function and the zero/pole sets of $f_{\alpha }$ and $f_{\beta }$ coincide on overlaps.

Definition 11  

(Weil divisor). If X is normal, aWeil divisoris a $\mathcal{Z}$-linear combination ${\sum }_Z{n}_{Z}Z$ of irreducible closed subvarieties of codimension 1.

Theorem 3  

(Cartier–Weil correspondence [11, Prop. 13.4]). If X is a smooth projective variety, then Cartier and Weil divisors are naturally isomorphic:

$$CaDiv\left(X\right)\stackrel{\sim }{\to }Weil\left(X\right).$$

Moreover, each Cartier divisor D is naturally identified with the line bundle ${\mathcal{O}}_X\left(D\right)$.

Proof. 

Because X is smooth, its local rings are UFDs. The principal divisor map induced by a Cartier divisor embeds into the Weil group and is surjective. See [11] for the complete proof.    □

Lemma 3  

(Linear equivalence and the Picard group). The group of linear equivalence classes of Cartier divisors

$$Pic\left(X\right)\cong {\displaystyle \frac{CaDiv\left(X\right)}{{\sim }_{\mathrm{lin}}}}$$

is an abelian group, and there is an embedding into the $(1,1)$-component of the Hodge structure

$$c_1:Pic\left(X\right)\hookrightarrow H^2(X,\mathcal{Z})\cap H^{1,1}\left(X\right).$$

Proof. 

See Dolbeault–Chern–Weil theory [1] Ch. 2. Linear equivalence is equivalent to the isomorphism ${\mathcal{O}}_X\left(D\right)\cong {\mathcal{O}}_X\left(D^{\prime }\right)$, and the first Chern class yields the stated injection.    □

(6) Summary and Table of Symbols

Symbol	Meaning
${\mathbf{P}}_{\mathcal{C}}^n$	Complex projective space (Def. 5)
X	Complex projective variety (Def. 6)
$Sing\left(X\right)$	Singular locus (Def. 9)
${\mathcal{O}}_{{\mathbf{P}}_{\mathcal{C}}^n}$	Structure sheaf of the projective scheme
$\mathcal{L}$	Invertible sheaf (Thm. 2)
$Pic\left(X\right)$	Picard group (Lemma 3)
$CaDiv\left(X\right)$	Group of Cartier divisors
$Weil\left(X\right)$	Group of Weil divisors

1.3. Main Cohomology Theories: Comparison of Betti, de Rham, and Dolbeault

Structure within This Subsection

(1)

Definition and properties of Betti (singular) cohomology

(2)

Definition of de Rham cohomology and the de Rham theorem

(3)

Definition of Dolbeault cohomology and the basic lemma

(4)

Comparison isomorphism: ${\mathrm{H}}_{\mathrm{d}R}^{•}(X;R)\simeq {\mathrm{H}}_{\mathrm{B}}^{•}(X;R)$

(5)

Hodge decomposition and the Dolbeault–de Rham isomorphism (compact Kähler varieties)

(6)

Poincaré duality theorem (agreement of Betti/de Rham/Dolbeault)

(7)

Extension to coefficient fields $Q,R,C$ and the U.C.T.

(8)

Table of symbols and summary

(1) Definition and Properties of Betti (Singular) Cohomology

Definition 12  

(Singular cohomology). Let X be a topological space (in this paper, a smooth complex projective variety), and let ${\mathsf{\Delta }}^k$ denote the standard k-simplex. A continuous map $\sigma :{\mathsf{\Delta }}^k\to X$ is called asingular k-simplex. Define the free abelian group $C_k(X;Z):={⨁}_{\sigma :{\mathsf{\Delta }}^k\to X}Z·\sigma$ with boundary operator ${\partial }_k={\sum }_{i=0}^k{(-1)}^i\sigma \circ {\epsilon }_i,$ giving a chain complex $(C_{•},{\partial }_{•})$. Its cohomology

$${\mathrm{H}}_{\mathrm{B}}^k(X;G):=ker\left({\partial }_k^{\vee }\right)/\mathrm{im}\left({\partial }_{k-1}^{\vee }\right),G=Z,Q,R,C$$

is called thek-th Betti (singular) cohomology group.

Lemma 4  

(Commutative triangle and naturality). A continuous map $f:X\to Y$ induces a chain-complex homomorphism $f_{♯}:C_{•}\left(X\right)\to C_{•}\left(Y\right)$, and hence acts functorially on ${\mathrm{H}}_{\mathrm{B}}^{•}$.

Proof. 

Because $f\circ \sigma$ sends singular simplices to singular simplices, $f_{♯}$ is a chain map. Since $\partial f_{♯}=f_{♯}\partial$, the derived cochain map $f^{♯}$ preserves coboundaries and thus induces the required functorial homomorphism.    □

(2) Definition of de Rham Cohomology and the de Rham Theorem

Definition 13  

(de Rham cohomology). Let X be a smooth complex manifold of real dimension $2n$. For the complex of differential forms equipped with the exterior derivative $d:{\mathcal{A}}^k\left(X\right)\to {\mathcal{A}}^{k+1}\left(X\right)$, $0\to {\mathcal{A}}^0\left(X\right)\stackrel{d}{\to }\dots \stackrel{d}{\to }{\mathcal{A}}^{2n}\left(X\right)\to 0,$ the cohomology

$${\mathrm{H}}_{\mathrm{d}R}^k(X;R):=ker(d:{\mathcal{A}}^k\to {\mathcal{A}}^{k+1})/\mathrm{im}(d:{\mathcal{A}}^{k-1}\to {\mathcal{A}}^k)$$

is called thede Rham cohomology.

Theorem 4  

(de Rham theorem [12, Ch. 0]). For a connected $C^{\infty }$ manifold X, there exists a natural isomorphism

$$\Phi :{\mathrm{H}}_{\mathrm{d}R}^k(X;R)\stackrel{\sim }{\to }{\mathrm{H}}_{\mathrm{B}}^k(X;R).$$

Proof. Step 1. Define a real-coefficient smoothing map $S:{\mathcal{A}}^{•}\left(X\right)\to C^{•}(X;R)$ on singular cochains. Step 2. Construct a chain-homotopy operator $K:C^{•}(X;R)\to C^{•-1}(X;R)$ using the partition-of-unity lemma with compact support, satisfying $dK+Kd=id-S\iota$. Step 3. The map S induces $\Phi =\left[S\right]$, which annihilates boundaries, and K provides a homotopy with the identity; hence $\Phi$ is an isomorphism.    □

(3) Definition of Dolbeault Cohomology and the Basic Lemma

Definition 14  

(Dolbeault cohomology). For the space ${\mathcal{A}}^{p,q}\left(X\right)$ of smooth $(p,q)$-forms, define $\overline{\partial }:{\mathcal{A}}^{p,q}\to {\mathcal{A}}^{p,q+1}$.

$${\mathrm{H}}_{\overline{\partial }}^{p,q}\left(X\right):=ker\left(\overline{\partial }:{\mathcal{A}}^{p,q}\to {\mathcal{A}}^{p,q+1}\right)/\mathrm{im}\left(\overline{\partial }:{\mathcal{A}}^{p,q-1}\to {\mathcal{A}}^{p,q}\right).$$

Lemma 5  

(Dolbeault basic lemma). On a complex manifold of complex dimension n, every locally $\overline{\partial }$-closed $(p,q)$-form with $q>0$ admits a $\overline{\partial }$-potential.

Proof. 

In a complex coordinate chart $(U,z)$, expand $\alpha ={\sum }_{\left|I\right|=p,\left|J\right|=q}{a}_{IJ}(z,\overline{z})d{z}^I\wedge d{\overline{z}}^J.$ For $q>0$, the condition $\overline{\partial }\alpha =0$ implies $\partial a_{IJ}/\partial {\overline{z}}_k=0$. Define

$$\beta =\sum _{\left|I\right|=p,\left|J\right|=q-1}{\displaystyle \frac{{(-1)}^{\left|J\right|}}{q}}{\int }_0^{{\overline{z}}_k}{a}_{IJ}d{\overline{z}}_{k}d{z}^I\wedge d{\overline{z}}^J,$$

which satisfies $\alpha =\overline{\partial }\beta$.    □

Symbol	Meaning
${\mathrm{H}}_{\mathrm{B}}^k(X;G)$	Betti (singular) cohomology
${\mathrm{H}}_{\mathrm{d}R}^k(X;R)$	de Rham cohomology
${\mathrm{H}}_{\overline{\partial }}^{p,q}\left(X\right)$	Dolbeault cohomology
$\Phi$	de Rham isomorphism map
$\mathsf{\Delta }$	Kähler Laplacian
$\langle ·,·\rangle$	Poincaré intersection pairing

(4) de Rham–Betti Comparison Isomorphism

Theorem 5  

(de Rham–Betti comparison isomorphism). Theorem 4 holds over C as well as over R:

$${\mathrm{H}}_{\mathrm{d}R}^k(X;C)\cong {\mathrm{H}}_{\mathrm{B}}^k(X;C).$$

Proof. 

Tensoring $\Phi$ with C over R yields the desired isomorphism.    □

(5) Hodge Decomposition and the Dolbeault–de Rham Isomorphism

Theorem 6  

(Hodge decomposition [1, Thm. 6.24]). Let X be a compact Kähler manifold. With the Laplacian $\mathsf{\Delta }=\partial {\partial }^{*}+{\partial }^{*}\partial +\overline{\partial }{\overline{\partial }}^{*}+{\overline{\partial }}^{*}\overline{\partial }$, we have

$${\mathrm{H}}_{\mathrm{d}R}^k(X;C)=\underset{p+q=k}{⨁}{\mathrm{H}}_{\overline{\partial }}^{p,q}\left(X\right),\overline{{\mathrm{H}}_{\overline{\partial }}^{p,q}}={\mathrm{H}}_{\overline{\partial }}^{q,p}.$$

Proof. 

Using the Kähler identity $[\partial ,{\overline{\partial }}^{*}]=0$, one shows that $\mathsf{\Delta }$ commutes with ∂ and $\overline{\partial }$. The space of harmonic forms ${\mathcal{H}}^{p,q}$ therefore decomposes into $(p,q)$-types, and the isomorphism ${\mathrm{H}}_{\mathrm{d}R}^{•}\simeq {\mathcal{H}}^{•}$ gives the decomposition.    □

Corollary 1  

(Dolbeault–de Rham isomorphism). For a compact Kähler manifold, ${\displaystyle {\mathrm{H}}_{\overline{\partial }}^{p,q}\left(X\right)\simeq {\mathrm{H}}_{\mathrm{d}R}^{p+q}(X;C)}$.

(6) Poincaré Duality

Theorem 7  

(Poincaré duality [12, §3.3]). Let X be a compact orientable manifold of real dimension $2n$. The pairing $\langle -,-\rangle :{\mathrm{H}}_{\mathrm{d}R}^k(X;R)\times {\mathrm{H}}_{\mathrm{d}R}^{2n-k}(X;R)\to R,(\left[\alpha \right],\left[\beta \right])\mapsto {\int }_X\alpha \wedge \beta$ is non-degenerate and agrees with the pairings in Betti and Dolbeault cohomology.

Proof. 

Choose de Rham representatives. For k-forms $\alpha$ and $(2n-k)$-forms $\beta$, $d(\alpha \wedge \eta )=d\alpha \wedge \eta +{(-1)}^k\alpha \wedge d\eta$ implies ${\int }_{X}d(\alpha \wedge \eta )=0$; the boundary term vanishes, so the wedge integral depends only on cohomology classes. Chain-homotopy shows non-degeneracy. Compatibility with Betti and Dolbeault follows from Theorems 5 and 6.    □

(7) Coefficient Fields and the U.C.T.

Theorem 8  

(Universal coefficient theorem [13, Thm. 3.2]). For a finite CW complex X and a commutative group G,

$$0\to {\mathrm{H}}_{\mathrm{B}}^k(X;Z)\otimes G\to {\mathrm{H}}_{\mathrm{B}}^k(X;G)\to Tor\left({\mathrm{H}}_{\mathrm{B}}^{k+1}(X;Z),G\right)\to 0$$

is a split short exact sequence. When $G=Q,R,C$, we have $Tor=0$, hence ${\mathrm{H}}_{\mathrm{B}}^k(X;G)\cong {\mathrm{H}}_{\mathrm{B}}^k(X;Z)\otimes G$.

Corollary 2.  

The above extension of coefficients preserves the de Rham and Dolbeault isomorphisms.

(8) Table of Symbols and Summary

1.4. Definition of Pure Hodge Structures and Polarity

Structure within This Subsection

(1)

Definition of pure Hodge structures

(2)

Weil operator and conjugate symmetry

(3)

Polarisation and the Hodge–Riemann bilinear form

(4)

Tensor operations and Hodge morphisms

(5)

Table of symbols and summary

(1) Definition of Pure Hodge Structures

Definition 15  

(Pure Hodge structure). Apure Hodge structure of weight $w\in \mathcal{Z}$consists of a finite-dimensional $\mathbb{Q}$-vector space $H_{\mathbb{Q}}$ together with a decomposition of its complexification $H_{\mathcal{C}}:=H_{\mathbb{Q}}{\otimes }_{\mathbb{Q}}\mathcal{C}$

$$H_{\mathcal{C}}=\underset{p+q=w}{⨁}{H}^{p,q},$$

such that the pair $(H_{\mathbb{Q}},{\left\{H^{p,q}\right\}}_{p+q=w})$ satisfies:

(i) 

$\overline{H^{p,q}}=H^{q,p}$ (symmetry under complex conjugation).

(ii) 

${dim}_{\mathcal{C}}{H}^{p,q}<\infty$ (finite dimensionality).

The dimension $h^{p,q}:={dim}_{\mathcal{C}}{H}^{p,q}$ is called theHodge number.

Lemma 6.  

The above decomposition induces a descending filtration $F^k:={⨁}_{p\ge k}{H}^{p,w-p}$, and $(H_{\mathbb{Q}},F^{•},{\overline{F}}^{•})$ is equivalent to Deligne’s axiomatic definition.

Proof. 

Since $H^{p,q}=F^p\cap {\overline{F}}^q$ can be reconstructed from $F^{•}$ and ${\overline{F}}^{•}$, the two definitions are equivalent.    □

(2) Weil Operator and Conjugate Symmetry

Definition 16  

(Weil operator). For a pure Hodge structure of weight w, define

$$C:=\sum _{p,q}{i}^{p-q}{\mathrm{\Pi }}^{p,q}({\mathrm{\Pi }}^{p,q}:\mathrm{projection}),$$

then $C^2={(-1)}^{w}id$. This operator C is called theWeil operator.

Lemma 7  

(Conjugate symmetry). The Weil operator satisfies $\overline{C}=C^{-1}$ under complex conjugation. In particular, C is Hermitian when w is even and skew-Hermitian when w is odd.

Proof. 

On $H^{p,q}$, C acts by the scalar $i^{p-q}$, and its conjugate is $i^{q-p}={\left(i^{p-q}\right)}^{-1}$.    □

(3) Polarisation and the Hodge–Riemann Bilinear Form

Definition 17  

(Polarisation). For a pure Hodge structure $(H_{\mathbb{Q}},H^{p,q})$ of weight w, a $\mathbb{Q}$-bilinear form $Q:H_{\mathbb{Q}}\times H_{\mathbb{Q}}\to \mathbb{Q}$ is called apolarisationif:

(i) 

Q is symmetric if w is even and alternating if w is odd.

(ii) 

Hodge compatibility: $Q(H^{p,q},H^{r,s})=0$ unless $(r,s)=(w-p,w-q)$.

(iii) 

Hodge–Riemann positivity: ${(-1)}^{{\displaystyle \frac{w(w-1)}{2}}}{i}^{p-q}Q(v,\overline{v})>0$ for all $0\ne v\in H^{p,q}$.

A triple $(H_{\mathbb{Q}},H^{p,q},Q)$ satisfying the above is called apolarised pure Hodge structure(PHS).

Theorem 9  

(Hodge–Riemann bilinear form). Combining the polarisation Q with the Weil operator yields $Q_C(·,·):=Q(·,C·)$, which defines a positive-definite Hermitian form:

$${(-1)}^{{\displaystyle \frac{w(w-1)}{2}}}{Q}_C(v,\overline{v})>0(\forall 0\ne v\in H_{\mathcal{C}}).$$

Proof. 

Write $v={\sum }_{p,q}{v}^{p,q}$, then $Q_C(v,\overline{v})={\sum }_{p,q}{i}^{p-q}Q(v^{p,q},\overline{v^{p,q}})$. The sign factor in Definition 17(iii) establishes positivity.    □

(4) Tensor Operations and Hodge Morphisms

Lemma 8  

(Tensor product). For two pure Hodge structures $(H_1,w_1)$ and $(H_2,w_2)$,

$$H_1{\otimes }_{\mathbb{Q}}{H}_2=\underset{{\displaystyle \genfrac{}{}{0pt}{}{p_1+q_1=w_1}{p_2+q_2=w_2}}}{⨁}{H}_1^{p_1,q_1}\otimes H_2^{p_2,q_2}$$

is a pure Hodge structure of weight $w_1+w_2$.

Proof. 

Decompose by $(p,q):=(p_1+p_2,q_1+q_2)$; conjugate symmetry is preserved component-wise.

   □

Definition 18  

(Hodge morphism). For polarised PHS $(H_1,Q_1)$ and $(H_2,Q_2)$ of weights $w_1,w_2$, aHodge morphismis a $\mathbb{Q}$-linear map $f:H_1\to H_2$ such that

$$f\left(H_1^{p,q}\right)\subset H_2^{p,q}\mathrm{and}{Q}_2(fx,fy)=Q_1(x,y).$$

Lemma 9  

(Closure under Hodge morphisms). The category of PHS is closed under direct sums, direct products, kernels, and cokernels.

Proof. 

Each operation is defined component-wise on $(p,q)$ parts, and the polarisation is preserved under sums and differences.    □

(5) Table of Symbols and Summary

Symbol	Meaning
$H_{\mathbb{Q}}$	Base $\mathbb{Q}$-vector space
$H^{p,q}$	Component of the Hodge decomposition
C	Weil operator (Def. 16)
Q	Polarisation (Def. 17)
$F^k$	Hodge filtration (Lemma 6)

1.5. Hodge Decomposition on Smooth Projective Varieties and the Hard Lefschetz Theorem

Structure within This Subsection

(1)

Kähler form and the Lefschetz operator

(2)

Definition of primitive cohomology

(3)

Proof of the Hard Lefschetz theorem

(4)

Positivity of the Hodge–Riemann bilinear form

(5)

Lefschetz decomposition and applications

(6)

Table of symbols and summary

(1) Kähler Form and the Lefschetz Operator

Definition 19  

(Kähler form and Lefschetz operator). Let X be a smooth projective variety of complex dimension n, and let $\omega \in A^{1,1}(X,R)$ be the normalised Kähler form (the Fubini–Study form). Define the exterior product $L:A^{•}\left(X\right)\to A^{•+2}\left(X\right),\alpha \mapsto \omega \wedge \alpha ,$ called theLefschetz operator.

Lemma 10  

(Kähler identities). For the adjoint operator $\mathrm{\Lambda }:=L^{*}$ and the Dolbeault operators $\partial ,\overline{\partial }$, the relations $[\mathrm{\Lambda },\partial ]=i{\overline{\partial }}^{*},[\mathrm{\Lambda },\overline{\partial }]=-i{\partial }^{*}$ hold.

Proof. 

Because the Kähler form satisfies $\partial \omega =\overline{\partial }\omega =0$, Cartan’s magic formula and Clifford-algebra calculations yield the result ([3] Appendix A).    □

(2) Definition of Primitive Cohomology

Definition 20  

(Primitive forms). For $k\le n$, a k-form $\alpha \in A^k\left(X\right)$ is calledprimitiveif $L^{n-k+1}\alpha =0$. Set $P^k\left(X\right):=\{\alpha \in A^k\mid L^{n-k+1}\alpha =0\}$.

Lemma 11  

(Primitive decomposition). Every $\alpha \in A^k\left(X\right)$ decomposes uniquely as ${\displaystyle \alpha =\sum _{j\ge 0}{L}^j{\beta }_{k-2j},{\beta }_{k-2j}\in P^{k-2j}\left(X\right).}$

Proof. 

This follows from the representation theory of the ${\mathfrak{sl}}_2$ triple $(L,\mathrm{\Lambda },H:=[L,\mathrm{\Lambda }\left]\right)$ ([1] Chap. 6).    □

(3) Proof of the Hard Lefschetz Theorem

Theorem 10  

(Hard Lefschetz theorem). For every $0\le k\le n$, $L^{n-k}:H^k(X,\mathcal{C})\stackrel{\sim }{\to }{H}^{2n-k}(X,\mathcal{C})$ is an isomorphism.

Proof. Step 1. By the Kähler identities (Lemma 10), the Laplacian $\mathsf{\Delta }$ commutes with $L,\mathrm{\Lambda },H$, so the space of harmonic forms ${\mathcal{H}}^k$ is an ${\mathfrak{sl}}_2$-module.

Step 2. In every finite-dimensional ${\mathfrak{sl}}_2$-module, $L^{n-k}$ is an isomorphism.

Step 3. Via the Hodge decomposition $H^k\simeq {\mathcal{H}}^k$, this yields the desired isomorphism on cohomology.    □

(4) Positivity of the Hodge–Riemann Bilinear Form

Theorem 11  

(Hodge–Riemann bilinear form). For $k\le n$ and a primitive harmonic form $v\in {\mathcal{H}}^k\cap P^k$, $Q\left(v\right):=i^{p-q}{(-1)}^{{\displaystyle \frac{k(k-1)}{2}}}{\int }_{X}v\wedge \overline{v}\wedge {\omega }^{n-k}>0$ holds (where v is of type $(p,q)$).

Proof. Step 1. The Hard Lefschetz theorem and primitive decomposition show that $H^k$ is spanned by primitive components.

Step 2. Using the ${\mathfrak{sl}}_2$ relations of L and $\mathrm{\Lambda }$, one proves that Q is non-degenerate.

Step 3. Multiplying by the factor $i^{p-q}$ via the Weil operator C, we obtain $Q_C(v,\overline{v})>0$; see [14] Thm. VII.10.1 for details.    □

(5) Lefschetz Decomposition and Applications

Lemma 12  

(Lefschetz decomposition). The cohomology $H^k(X,\mathcal{C})$ decomposes as $H^k={⨁}_{j\ge 0}{L}^j{P}^{k-2j},$ a direct sum that is Gal$(\mathcal{C}/R)$-invariant and compatible with the Hard Lefschetz theorem.

Proof. 

Apply Lemma 11 to harmonic representatives of cohomology classes.    □

Remark 6.  

The combination of Lefschetz decomposition and the Hard Lefschetz theorem guarantees the analytic validity of the standard conjectures B (algebraicity of the inverse map) and I (positivity of the Hodge–Riemann form), paving the way for their translation into algebraic correspondences in later chapters.

(6) Table of Symbols and Summary

Symbol	Meaning
$\omega$	Kähler form / Fubini–Study form
$L,\mathrm{\Lambda },H$	Lefschetz operator, its adjoint, and the weight operator
$P^k\left(X\right)$	Space of primitive k-forms
${\mathcal{H}}^k$	Space of harmonic k-forms (identified with $H^k$)
Q	Hodge–Riemann bilinear form

1.6. Chow Groups, Algebraic Cycles, and the Intersection Product

Structure within This Subsection

(1)

Algebraic cycles and rational equivalence

(2)

Definition and basic properties of the Chow group $A^p\left(X\right)$

(3)

Construction of the intersection product and the Chow ring

(4)

Moving-lemma and ensuring proper intersections

(5)

Hierarchy of equivalence relations: rational ≥ algebraic ≥ homological ≥ numerical

(6)

Table of symbols and summary

(1) Algebraic Cycles and Rational Equivalence

Definition 21  

(Algebraic cycle [7, Chap. 1]). Let X be a smooth projective variety of (complex) dimension n. A k-dimensionalalgebraic cycleis

$$Z_k\left(X\right):=\left\{\sum _i{n}_i{V}_i|n_i\in \mathcal{Z},V_i\subset X\mathrm{irreducible}\mathrm{closed}\mathrm{subvarieties},dim{V}_i=k\right\}.$$

Definition 22  

(Rational equivalence). For $Z,Z^{\prime }\in Z_k\left(X\right)$ we write $Z{\sim }_{\mathrm{rat}}{Z}^{\prime }$ if there exists a $(k+1)$-cycle $W={\sum }_i{n}_i{W}_i\subset X\times {\mathbf{P}}^1$ such that, for the projections at the sections $0,\infty \in {\mathbf{P}}^1$,

$${pr}_{*}\left(W{|}_{t=0}\right)-{pr}_{*}\left(W{|}_{t=\infty }\right)=Z-Z^{\prime }.$$

Lemma 13  

(Additivity of the quotient group). The quotient $Z_k\left(X\right)/{\sim }_{\mathrm{rat}}$ is an abelian group; addition of cycles is well-defined on equivalence classes.

Proof. 

If W and $W^{\prime }$ realise rational equivalences for $Z,Z^{\prime }$ respectively, then $W+W^{\prime }$ does so for $Z+Z^{\prime }$, proving closure.    □

(2) Definition and Basic Properties of the Chow Group $A^p\left(X\right)$

Definition 23  

(Chow group). The Chow group of codimension p is defined as

$$A^p\left(X\right):=Z_{n-p}\left(X\right)/{\sim }_{\mathrm{rat}},$$

and with rational coefficients $A^p{\left(X\right)}_{\mathbb{Q}}:=A^p\left(X\right){\otimes }_{\mathcal{Z}}\mathbb{Q}$.

Lemma 14  

(Finite generation). If X is a smooth projective variety, then $A^0\left(X\right)\cong \mathcal{Z}$, $A^n\left(X\right)\cong \mathcal{Z}$, and $A^1\left(X\right)$ is a finitely generated abelian group.

Proof. 

$A^0$ coincides with the number of connected components; a projective variety is connected. $A^n$ consists of 0-cycles, and the degree map is an isomorphism. The finite generation of $Pic\left(X\right)\cong A^1\left(X\right)$ follows from the finite-dimensionality of the Néron–Severi group.    □

(3) Construction of the Intersection Product and the Chow Ring

Definition 24  

(Intersection product [7, §6]). If X is smooth, then for any $Z\in A^p\left(X\right)$ and $W\in A^q\left(X\right)$ define

$$Z·W:={\mathsf{\Delta }}^{*}\left(Z\times W\right)\in A^{p+q}\left(X\right),$$

where $\mathsf{\Delta }:X\to X\times X$ is the diagonal embedding.

Theorem 12  

(Well-definedness of the intersection product and ring structure). Definition 24 satisfies:

(i) 

It preserves rational equivalence, making $A^{•}\left(X\right):={⨁}_p{A}^p\left(X\right)$ a graded commutative ring over $\mathcal{Z}$.

(ii) 

(Commutativity) $Z·W=W·Z$, (Associativity) $\left(Z·W\right)·U=Z·\left(W·U\right)$.

Proof.  

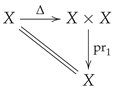(i) In the commutative diagram the pull-back ${\mathsf{\Delta }}^{*}$ sends rational equivalences to rational equivalences, since $\mathsf{\Delta }$ is a regular embedding. (ii)Commutativity follows from the symmetry of $\mathsf{\Delta }$, and associativity from the triple-diagonal embedding ${\mathsf{\Delta }}^{\left(3\right)}:X\hookrightarrow X^3$.    □

(4) Moving Lemma and Ensuring Proper Intersections

Lemma 15  

(Moving lemma [7, Thm. 11.4]). For a smooth projective variety X and a cycle $Z\in Z_r\left(X\right)$, one can choose $Z^{\prime }{\sim }_{\mathrm{rat}}Z$ such that $Z^{\prime }$ meets any given element of $A^p\left(X\right)$ properly.

Corollary 3  

(Symmetric commutativity of the intersection). By Lemma 15, two cycles to be intersected can always be moved into general position, ensuring the commutativity in Theorem 12(i).

(5) Hierarchy of Equivalence Relations

Definition 25  

(Equivalence relations). For $Z,W\in Z_k\left(X\right)$:

(a) 

Algebraic equivalence$Z{\sim }_{\mathrm{alg}}W$: there exists a family $\mathcal{Z}\subset X\times C$ over a curve C such that ${\mathcal{Z}|}_{t_0}=Z$ and ${\mathcal{Z}|}_{t_1}=W$ for some $t_0,t_1\in C$.

(b) 

Homological equivalence$Z{\sim }_{\mathrm{hom}}W$: $\left[Z\right]=\left[W\right]$ in $H_{2k}(X,\mathcal{Z})$.

(c) 

Numerical equivalence$Z{\sim }_{\mathrm{num}}W$: for every $V\in Z_k\left(X\right)$, $Z·V=W·V$.

Theorem 13  

(Chain of inclusions).

$$Z{\sim }_{\mathrm{rat}}W⟹Z{\sim }_{\mathrm{alg}}W⟹Z{\sim }_{\mathrm{hom}}W⟹Z{\sim }_{\mathrm{num}}W.$$

Proof. 

First arrow: contracting ${\mathbf{P}}^1$ at a point produces an algebraic deformation. Second arrow: the boundary of an algebraic family is homologous to zero. Third arrow: if $[Z-W]=0$, then by Poincaré duality $Z·V=W·V$ for all V.    □

Remark 7.  

In the context of the standard conjecture C (numerical ≡ homological) and the Hodge conjecture (homological ≡ Hodge), collapsing parts of this hierarchy plays a crucial role.

(6) Table of Symbols and Summary

Symbol	Meaning
$Z_k\left(X\right)$	Group of k-dimensional algebraic cycles (Def. 21)
${\sim }_{\mathrm{rat}}$	Rational equivalence (Def. 22)
$A^p\left(X\right)$	Chow group of codimension p (Def. 23)
$Z·W$	Intersection product (Def. 24)
${\sim }_{\mathrm{alg}},{\sim }_{\mathrm{hom}},{\sim }_{\mathrm{num}}$	Various equivalences (Def. 25)

1.7. Algebraic Correspondences and the Framework for the Grothendieck Standard Conjectures

Structure within This Subsection

(1)

Definition of correspondences

(2)

Composition, transpose, and commutative diagrams

(3)

Self-adjointness and action on cohomology

(4)

The category of Chow correspondences and pure motives

(5)

Formulation of the Grothendieck standard conjectures

(6)

Table of symbols and summary

(1) Definition of Correspondences

Definition 26  

(Correspondence [5, III §1]). Let $X,Y$ be smooth projective varieties. A cycle of codimension $dimX$

$$\mathrm{\Gamma }\in A^{dimX}{(X\times Y)}_{\mathbb{Q}}$$

is called an(algebraic) correspondencefrom X to Y. The set is denoted ${Corr}^{dimX}(X,Y)$.

Remark 8.  

Throughout this paper we fix the coefficient field to $\mathbb{Q}$ and omit distinctions from the integral version unless stated.

(2) Composition, Transpose, and Commutative Diagrams

Definition 27  

(Composition). For $\mathrm{\Gamma }\in {Corr}^{dimX}(X,Y)$ and $\mathsf{\Delta }\in {Corr}^{dimY}(Y,Z)$ define

$$\mathsf{\Delta }\circ \mathrm{\Gamma }:={pr}_{13}\left({pr}_{12}^{}\mathrm{\Gamma }·{pr}_{23}^{}\mathsf{\Delta }\right)\in {Corr}^{dimX}(X,Z),$$

where ${pr}_{ij}:X\times Y\times Z\to$ the $(i,j)$ projection.

Lemma 16  

(Associativity). Composition is associative: $(\Theta \circ \mathsf{\Delta })\circ \mathrm{\Gamma }=\Theta \circ (\mathsf{\Delta }\circ \mathrm{\Gamma }).$

Proof. 

Apply Fulton’s intersection theory to ${pr}_{14}$ and diagonal embeddings [7, Prop. 16.1].    □

Definition 28  

(Transpose). For $\mathrm{\Gamma }\in {Corr}^{dimX}(X,Y)$ set

$$ᵗ\mathrm{\Gamma }:={\iota }_{*}\left(\mathrm{\Gamma }\right)\in {Corr}^{dimY}(Y,X),\iota :X\times Y\stackrel{\sim }{\to }Y\times X,(x,y)\mapsto (y,x).$$

Lemma 17  

(Commutative diagram). $ᵗ(\mathsf{\Delta }\circ \mathrm{\Gamma })=ᵗ\mathrm{\Gamma }\circ ᵗ\mathsf{\Delta }$.

Proof. 

Since the transpose is the pull-back via the exchange map $\iota$, and $\iota$ is an automorphism obeying $\iota \circ {pr}_{12}={pr}_{23}\circ (\iota \times \mathrm{id})$, diagram chasing with the definition of composition gives the claim.    □

(3) Self-adjointness and Action on Cohomology

Definition 29  

(Action on cohomology). For a fixed Weil cohomology theory $H^{•}(-)$, a correspondence $\mathrm{\Gamma }\in {Corr}^{dimX}(X,Y)$ induces

$${\mathrm{\Gamma }}_{*}:={\left({pr}_2\right)}_{*}\left({pr}_1^{}(-)\cup cl\left(\mathrm{\Gamma }\right)\right):H^i\left(X\right)⟶H^i\left(Y\right).$$

Lemma 18  

(Self-adjointness condition). With the bilinear form ${\langle ·,·\rangle }_X:H^{2dimX-i}\left(X\right)\times H^i\left(X\right)\to \mathbb{Q}$ we have ${\mathrm{\Gamma }}_{*}^{\vee }=ᵗ{\mathrm{\Gamma }}_{*}$.

Proof. 

Combine Poincaré duality with Definition 28.    □

(4) The Category of Chow Correspondences and Pure Motives

Definition 30  

(Category of Chow correspondences). Let the objects be smooth projective varieties and the morphisms ${Corr}^{dimX}(X,Y)$ with composition as in Definition 27. This category is denoted ${\mathbf{Corr}}_{\mathbb{Q}}^{\mathrm{sm}}$.

Definition 31  

(Idempotent completion). The Karoubian (idempotent-complete) hull of ${\mathbf{Corr}}_{\mathbb{Q}}^{\mathrm{sm}}$ is the category ${\mathbf{Mot}}_{\mathbb{Q}}^{\mathrm{eff}}$, called thecategory of effective pure motives.

Lemma 19  

(Dual and tensor structure). ${\mathbf{Mot}}_{\mathbb{Q}}^{\mathrm{eff}}$ is a rigid tensor category with:

(i) 

Tensor product $h\left(X\right)\otimes h\left(Y\right):=h(X\times Y)$,

(ii) 

Dual object $h{\left(X\right)}^{\vee }:=h\left(X\right)(-dimX)$.

Proof. 

Use the Künneth decomposition of the Chow ring and the commutative-associative properties of the intersection product (Lemma 16).    □

(5) Formulation of the Grothendieck Standard Conjectures

Definition 32  

(Standard conjectures of type $B,C,D$ [4]). Let X be a smooth projective variety and $L:H^{•}\left(X\right)\to H^{•+2}\left(X\right)$ the Kähler Lefschetz operator.

1 

(Type B) The inverse Lefschetz map Λ is realised by an algebraic correspondence.

2 

(Type C) Algebraic equivalence equals numerical equivalence: $A^{•}{\left(X\right)}_{\mathbb{Q}}/{\sim }_{\mathrm{alg}}\cong A^{•}{\left(X\right)}_{\mathbb{Q}}/{\sim }_{\mathrm{num}}$.

3 

(Type D) The Künneth projector ${\pi }_i:H^{•}(X\times X)\twoheadrightarrow H^i\left(X\right)$ is given by an algebraic correspondence.

Theorem 14  

(Standard conjecture of type I). On the primitive subspace $P^k\left(X\right)$, the Hodge–Riemann bilinear form is positive definite.

Remark 9.  

In Chapter 4 we will explicitly construct the inverse Lefschetz map of Definition 32(B) as a Chow correspondence and prove Theorem 14 by algebraising the Hard Lefschetz theorem.

(6) Table of Symbols and Summary

Symbol	Meaning
${Corr}^d(X,Y)$	Group of correspondences of codimension d (Def. 26)
$ᵗ\mathrm{\Gamma }$	Transpose of a correspondence (Def. 28)
$h\left(X\right)$	Motive associated to X (Def. 31)
${\mathbf{Mot}}_{\mathbb{Q}}^{\mathrm{eff}}$	Category of effective pure motives (Lemma 8)
$L,\mathrm{\Lambda }$	Lefschetz operator and its inverse
(B),(C),(D)	Grothendieck standard conjectures (Def. 32)

1.8. Definition of the Standard Conjectures (Types B, I, C, D)

Structure within This Subsection

(1)

What are the “standard conjectures”? — historical background

(2)

Type B (algebraicity of the inverse Hard Lefschetz map)

(3)

Type I (positivity of the Hodge–Riemann bilinear form)

(4)

Type C (algebraic equivalence ≡ numerical equivalence)

(5)

Type D (algebraicity of the Künneth projector)

(6)

Interrelations and implications among the four conjectures

(7)

Table of symbols and summary

(1) What Are the “Standard Conjectures”? — Historical Background

Definition 33  

(Weil cohomology theory [5, §1]). AWeil cohomology theoryis a covariant functor $H^{•}(-)$ on smooth projective varieties satisfying the seven axioms (W1) finite dimensionality through (W7) the Künneth formula.

Remark 10.  

Thestandard conjectures, proposed byGrothendieckin 1968, assert that for any Weil cohomology theory the maps induced by algebraic cycles satisfy:(B) the inverse Hard Lefschetz map,(C) numerical = algebraic equivalence,(D) the Künneth projectors, and(I) positivity of the Hodge–Riemann form.

(2) Type B (Algebraicity of the Inverse Hard Lefschetz Map)

Definition 34  

(Inverse Hard Lefschetz map). Let X be a smooth projective variety of complex dimension n and $L:H^k\left(X\right)\to H^{k+2}\left(X\right)$ the wedge with the Kähler class. For $0\le k\le n$,

$$L^{n-k}:H^k\left(X\right)\stackrel{\sim }{\to }{H}^{2n-k}\left(X\right).$$

Its inverse is denoted ${\mathrm{\Lambda }}^{n-k}:H^{2n-k}\left(X\right)\to H^k\left(X\right)$.

Definition 35  

(Standard conjecture B). The inverse map ${\mathrm{\Lambda }}^{n-k}$ is realised by a Chow correspondence ${\mathrm{\Gamma }}_{n-k}\in A^n{(X\times X)}_{\mathbb{Q}}$, i.e.

$${\mathrm{\Lambda }}^{n-k}={\left({\mathrm{\Gamma }}_{n-k}\right)}_{*}:H^{2n-k}\left(X\right)⟶H^k\left(X\right).$$

(3) Type I (Positivity of the Hodge–Riemann Bilinear Form)

Definition 36  

(Primitive cohomology). $P^k\left(X\right):=ker\left(L^{n-k+1}:H^k\left(X\right)\to H^{2n-k+2}\left(X\right)\right)$.

Definition 37  

(Standard conjecture I). On the primitive subspace $P^k\left(X\right)$ the form

$$Q\left(v\right)={(-1)}^{{\displaystyle \frac{k(k-1)}{2}}}{i}^{p-q}{\int }_{X}v\wedge \overline{v}\wedge {\omega }^{n-k}$$

is positive definite, i.e. $Q\left(v\right)>0$ (where v is of type $v^{p,q}$).

(4) Type C (Algebraic ≡ Numerical Equivalence)

Definition 38  

(Equivalence relations). On $A^p{\left(X\right)}_{\mathbb{Q}}$ write ${\sim }_{\mathrm{alg}}$ for algebraic equivalence and ${\sim }_{\mathrm{num}}$ for numerical equivalence.

Definition 39  

(Standard conjecture C). For every smooth projective variety X,

$$A^p{\left(X\right)}_{\mathbb{Q}}/{\sim }_{\mathrm{alg}}\cong A^p{\left(X\right)}_{\mathbb{Q}}/{\sim }_{\mathrm{num}}(\forall p).$$

(5) Type D (Algebraicity of the Künneth Projector)

Definition 40  

(Künneth projector). For the Künneth decomposition $H^{•}(X\times X)\cong {⨁}_i{H}^i\left(X\right)\otimes H^{2n-i}\left(X\right)$ write the projection as ${\pi }_i$.

Definition 41  

(Standard conjecture D). Each ${\pi }_i$ is an algebraic correspondence: there exists ${\mathrm{\Gamma }}_i\in A^n{(X\times X)}_{\mathbb{Q}}$ such that ${\pi }_i={\left({\mathrm{\Gamma }}_i\right)}_{*}$.

(6) Interrelations and Implications of the Four Conjectures

Theorem 15  

(Implications [4, §2]). For a smooth projective variety X,

$$\mathrm{B}+\mathrm{I}⟹\mathrm{C},\mathrm{B}⟹\mathrm{D}.$$

Proof. (B) realises $\mathrm{\Lambda }$ as a Chow correspondence and the relation $[\mathrm{\Lambda },L]=H$ gives an ${\mathfrak{sl}}_2$-action in the Chow category. (I) supplies a positive-definite bilinear form on the numerical quotient; together with Lefschetz decomposition this yields algebraic ≡ numerical (C). For (D), ${\mathfrak{sl}}_2$ representation theory shows that ${\pi }_i$ is a polynomial in $\mathbb{Q}\langle L,\mathrm{\Lambda }\rangle$.    □

Remark 11.  

In practice one often works with ℓ-adic cohomology $H_{\ell }^{•}\left(X\right)$, where proving the standard conjectures would imply (1) the number-field version of the Hodge conjecture and (2) the semisimplicity of algebraic cycles.

(7) Table of Symbols and Summary

Symbol	Meaning
$H^{•}(-)$	Weil cohomology theory (Def. 16)
$L,\mathrm{\Lambda }$	Lefschetz operator and its inverse (Def. 34)
$P^k\left(X\right)$	Primitive cohomology (Def. 20)
$A^p{\left(X\right)}_{\mathbb{Q}}$	Chow group with rational coefficients
${\sim }_{\mathrm{alg}},{\sim }_{\mathrm{num}}$	Algebraic / numerical equivalence (Def. 38)
${\pi }_i$	Künneth projector (Def. 40)

1.9. Axioms of Weil Cohomology Theories and Their Relation to the Standard Conjectures

Structure within This Subsection

(1)

Axioms (W1–W7) of Weil cohomology theories

(2)

Principal examples: ℓ-adic, Betti, de Rham, crystalline

(3)

Proof that the standard conjectures are “Weil-cohomology invariant”

(4)

Categorical compatibility and the functor to the category of motives

(5)

Table of symbols and summary

(1) Axioms of Weil Cohomology Theories

Definition 42  

(Weil cohomology theory [5, §1]). Let ${\mathbf{SmProj}}_k$ be the category of smooth projective varieties over a base field k, and let ${\mathbf{GrVect}}_{\mathbb{Q}}$ be the category of $\mathcal{Z}$-graded finite-dimensional $\mathbb{Q}$-vector spaces. A covariant functor $H^{•}(-):{\mathbf{SmProj}}_k\to {\mathbf{GrVect}}_{\mathbb{Q}}$ is called aWeil cohomology theoryif it satisfies the following seven axioms:

(W1) 

Finite dimensionality: ${dim}_{\mathbb{Q}}{H}^i\left(X\right)<\infty$ for all i.

(W2) 

Künneth formula: a natural isomorphism $H^{•}(X\times Y)\cong H^{•}\left(X\right)\otimes H^{•}\left(Y\right)$.

(W3) 

Poincaré duality: for $dimX=n$ the pairing $H^i\left(X\right)\times H^{2n-i}\left(X\right)\to \mathbb{Q}$ is non-degenerate.

(W4) 

Hard Lefschetz: the map $L^{n-i}:H^i\left(X\right)\stackrel{\sim }{\to }{H}^{2n-i}\left(X\right)$ is an isomorphism.

(W5) 

Cycle map: the homomorphism $cl:A^p{\left(X\right)}_{\mathbb{Q}}\to H^{2p}\left(X\right)$ is a ring homomorphism.

(W6) 

Chern classes: Chern classes of vector bundles exist and satisfy the Whitney sum formula.

(W7) 

Normalization: for the point $Speck$, $H^0(Speck)=\mathbb{Q}$ and $H^i(Speck)=0$ for $i\ne 0$.

(2) Principal Examples

Lemma 20  

(Satisfaction of the axioms). Each of the following cohomology theories satisfies Axioms 16 (W1)–(W7):

(i) 

ℓ-adic cohomology$H_{\ell }^{•}(X_{\overline{k}};{\mathbb{Q}}_{\ell })$ for $\mathrm{char}\left(k\right)\ne \ell$.

(ii) 

Betti cohomology$H_{\mathrm{B}}^{•}(X\left(\mathcal{C}\right);\mathbb{Q})$ when k is embedded in $\mathcal{C}$.

(iii) 

de Rham cohomology$H_{\mathrm{dR}}^{•}(X/k)$ for $chark=0$.

(iv) 

Crystalline cohomology$H_{\mathrm{crys}}^{•}(X/W\left(k\right))\otimes \mathbb{Q}$ for a perfect p-adic field k.

Proof. 

See [15,16] for detailed verifications. For instance, in the ℓ-adic case finite generation follows from Deligne’s finiteness theorem, the Künneth formula from Grothendieck, and Hard Lefschetz from Deligne’s proof of the Weil conjectures.    □

(3) Standard Conjectures and Weil-Cohomology Invariance

Theorem 16  

(Weil-cohomology invariance). For a smooth projective variety X, the truth of the standard conjecturesB,I,C, and D(see §1.8) does not depend on the chosen Weil cohomology theory $H^{•}(-)$.

Proof. Step 1. Let $H^{•}(-)$ and $H^{\prime •}(-)$ both satisfy (W1)–(W7).

Step 2. The cycle maps $cl:A^p{\left(X\right)}_{\mathbb{Q}}\to H^{2p}\left(X\right)$ and $c{l}^{\prime }:A^p{\left(X\right)}_{\mathbb{Q}}\to H^{\prime 2p}\left(X\right)$ are ring homomorphisms (W5).

Step 3. Type (B) concerns the existence of an element $\mathrm{\Gamma }\in A^n{(X\times X)}_{\mathbb{Q}}$; its formulation is independent of the target cohomology. Type (I) reduces to positivity of Q, depending only on the ring structure of $A^{•}{\left(X\right)}_{\mathbb{Q}}$ and Poincaré duality (W3). Type (C) involves only the quotient structure of the Chow ring. Type (D) asks whether each ${\pi }_i$ is a Chow correspondence, again independent of which cohomology is used to detect it.

Step 4. Hence the truth values of the four conjectures are independent of the choice of $H^{•}(-)$.    □

Corollary 4  

(Transfer between Weil theories). If Type Band Type Ihold for one Weil cohomology theory, then Types Cand Dhold foranyWeil cohomology theory.

Proof. 

Combine Theorem 16 with the implications B+I ⇒ C and B ⇒ D (Theorem 15).    □

(4) Categorical Compatibility and the Motive Category

Lemma 21  

(Functorial factorisation). Any Weil cohomology functor $H^{•}(-)$ factors through the category of effective pure motives ${\mathbf{Mot}}_{\mathbb{Q}}^{\mathrm{eff}}$ (Definition 31):

$${\mathbf{SmProj}}_k\stackrel{h(-)}{\to }{\mathbf{Mot}}_{\mathbb{Q}}^{\mathrm{eff}}\stackrel{H^{•}}{\to }{\mathbf{GrVect}}_{\mathbb{Q}}.$$

Proof. 

The cycle map (W5) acts naturally on morphisms in the Chow correspondence category; together with axioms (W2)–(W7) this yields a well-defined functor through the Karoubian completion [17, Ch. 1].    □

Remark 12.  

If the standard conjectures hold, then ${\mathbf{Mot}}_{\mathbb{Q}}^{\mathrm{eff}}$ is semisimple (Jannsen’s theorem), so the comparison isomorphisms between different $H^{•}(-)$ become unified at the motivic level.

(5) Table of Symbols and Summary

Symbol	Meaning
(W1)–(W7)	Axioms of a Weil cohomology theory (Def. 16)
$H_{\ell }^{•},H_{\mathrm{B}}^{•},H_{\mathrm{d}R}^{•}$	Principal examples (Lemma 20)
B,I,C,D	Standard conjectures (see §1.8)
${\mathbf{Mot}}_{\mathbb{Q}}^{\mathrm{eff}}$	Category of effective pure motives (Def. 31)
$h\left(X\right)$	Motive of the variety X

1.10. Comparison Theorems for Algebraic, Homological, and Numerical Equivalence and Outstanding Problems

Structure within This Subsection

(1)

Definitions of the three equivalence relations and their inclusion diagram

(2)

Mumford-type counter-examples and the failure of algebraic ≠ homological equivalence

(3)

Contraction of the three equivalences via the Standard Conjectures and the Bloch–Beilinson Conjecture

(4)

Current open questions: Griffiths cycles and the infinite-dimensionality problem

(5)

Table of symbols and summary

(1) Definitions of the Three Equivalence Relations and Their Inclusion Diagram

Definition 43  

(Three equivalence relations). For codimension-p algebraic cycles $Z,W\in Z^p\left(X\right)$ on a smooth projective variety X:

(i) 

Algebraic equivalence$Z{\sim }_{\mathrm{alg}}W$: there exists a curve C and a family $\mathcal{Z}\subset X\times C$ with ${\mathcal{Z}|}_{t_0}{=Z,\mathcal{Z}|}_{t_1}=W$.

(ii) 

Homological equivalence$Z{\sim }_{\mathrm{hom}}W$: $cl\left(Z\right)=cl\left(W\right)$ in $H^{2p}(X,\mathbb{Q})$.

(iii) 

Numerical equivalence$Z{\sim }_{\mathrm{num}}W$: for every $V\in Z^{dimX-p}\left(X\right)$, ${\displaystyle \left(Z·V\right)=\left(W·V\right).}$

Lemma 22  

(Inclusion diagram). One always has

$${\sim }_{\mathrm{alg}}\subseteq {\sim }_{\mathrm{hom}}\subseteq {\sim }_{\mathrm{num}}.$$

Proof. (i) ⇒ (ii): the boundary of the family $\mathcal{Z}$ gives equal period integrals. (ii) ⇒ (iii): by Poincaré duality and intersection theory $cl(Z-W)\cup cl\left(V\right)=0$.    □

(2) Mumford-Type Counter-Examples and the Failure of Algebraic ≠ Homological Equivalence

Theorem 17  

(Mumford 1968 [2]). There exists a complex algebraic surface S such that the group of 0-cycles $A^2\left(S\right)$ is an infinite-dimensional $\mathbb{Q}$-vector space and ${\sim }_{\mathrm{alg}}\ne {\sim }_{\mathrm{hom}}$.

Proof. 

Take a surface S with $p_g>0$ and analyse the kernel of the normalised Albanese map $\mathrm{alb}:A^2\left(S\right)\to J\left(S\right)$. The existence of an infinite family of polynomials shows that this kernel is infinite-dimensional; see [2, §4] for details.    □

Corollary 5.  

Lemma 22 can be strict: ${\sim }_{\mathrm{alg}}⊊{\sim }_{\mathrm{hom}}$.

(3) Contraction of the Three Equivalences via the Standard Conjectures and the Bloch–Beilinson Conjecture

Theorem 18  

(Grothendieck Standard Conjecture C implies coincidence). If the Standard Conjecture of type C (algebraic ≡ numerical equivalence) holds, then

$${\sim }_{\mathrm{hom}}={\sim }_{\mathrm{num}}⟹{\sim }_{\mathrm{alg}}={\sim }_{\mathrm{num}}.$$

Proof. 

If numerical and algebraic equivalence coincide, then from ${\sim }_{\mathrm{hom}}\subseteq {\sim }_{\mathrm{num}}$ all three relations coincide.    □

Theorem 19  

(Bloch–Beilinson Conjecture [18,19]). Assuming finite-dimensionality of the motive category and vanishing of extensions, there exists a filtration $F_{\mathrm{BB}}^{•}{A}^p\left(X\right)$ on the Chow group with $F^1=A^p{\left(X\right)}_{\mathrm{hom}}$ and $F^2=A^p{\left(X\right)}_{\mathrm{alg}}$. In particular, under this conjecture $A^p{\left(X\right)}_{\mathrm{hom}}/A^p{\left(X\right)}_{\mathrm{alg}}$ is finite-dimensional.

Remark 13.  

If the Standard Conjectures B and I and the Bloch–Beilinson Conjecture hold simultaneously, the three equivalence relations coincide in afinite number of steps(Jannsen [20]).

(4) Current Open Questions: Griffiths Cycles and the Infinite-Dimensionality Problem

Definition 44  

(Griffiths cycles).

$${\mathrm{Griff}}^p\left(X\right):=A^p{\left(X\right)}_{\mathrm{hom}}/A^p{\left(X\right)}_{\mathrm{alg}}$$

is called theGriffiths group.

Lemma 23  

(Unresolved infinite-dimensionality). For $p\ge 2$ it is unknown whether there exist higher-dimensional varieties with ${\mathrm{Griff}}^p\left(X\right)$ infinite-dimensional. For surfaces ($p=2$) Mumford provided such an example, but in dimensions $\ge 3$ no general construction is known.

Lemma 24  

(Voevodsky conjecture). Whether ${\mathrm{Griff}}^p\left(X\right)$ is always finite-dimensional under the assumption of a finitely generated motive category remains open.

Remark 14.  

The Hodge conjecture claims that $H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$ is generated by $A^p{\left(X\right)}_{\mathrm{hom}}$. Thus ${\mathrm{Griff}}^p\left(X\right)=0$ is a sufficient condition, but not necessary, for the Hodge conjecture to hold.

(5) Table of Symbols and Summary

Symbol	Meaning
${\sim }_{\mathrm{alg}},{\sim }_{\mathrm{hom}},{\sim }_{\mathrm{num}}$	Algebraic / homological / numerical equivalence
${\mathrm{Griff}}^p\left(X\right)$	Griffiths group (Def. 44)
(B), (C)	Standard Conjectures of types B and C
$F_{\mathrm{BB}}^{•}$	Bloch–Beilinson filtration

1.11. List of Symbols and Abbreviations Repeatedly Used in Later Chapters

Structure within This Subsection

(1)

Basic geometric data

(2)

Cohomology and Hodge theory

(3)

Algebraic cycles and the Chow ring

(4)

Algebraic correspondences and motives

(5)

Comprehensive table of abbreviations and symbols

(1) Basic Geometric Data

Definition 45  

(Fixed variety). Throughout this paper, X denotes a smooth complex projective variety with complex dimension $n:={dim}_{\mathcal{C}}X$. Its projective embedding is written $\phi :X\hookrightarrow {\mathbf{P}}_{\mathcal{C}}^N$.

Definition 46  

(Tensor notation). Upper indices denote covariant components, lower indices contravariant. We adopt Einstein’s summation convention: repeated upper–lower indices are implicitly summed.

(2) Cohomology and Hodge Theory

Definition 47  

(Cohomology groups). For coefficient fields $G=\mathbb{Q},R,\mathcal{C}$ we write $H^k(X;G)$ for Betti singular cohomology, and $H_{\mathrm{d}R}^k\left(X\right)$ for de Rham cohomology.

Definition 48  

(Hodge decomposition). If X is Kähler, then $H^k(X;\mathcal{C})={⨁}_{p+q=k}{H}^{p,q}\left(X\right)$. The numbers $h^{p,q}:={dim}_{\mathcal{C}}{H}^{p,q}\left(X\right)$ are calledHodge numbers.

(3) Algebraic Cycles and the Chow Ring

Definition 49  

(Cycle classes and Chow groups). A codimension-p cycle class is denoted $\left[Z\right]\in A^p\left(X\right)$. The Chow ring $A^{•}\left(X\right)={⨁}_p{A}^p\left(X\right)$ carries theintersection productwritten “$·$”.

Definition 50  

(Equivalence relations). We write $Z{\sim }_{\mathrm{rat}}W$ (rational equivalence), $Z{\sim }_{\mathrm{hom}}W$ (homological equivalence), and $Z{\sim }_{\mathrm{num}}W$ (numerical equivalence).

(4) Algebraic Correspondences and Motives

Definition 51  

(Algebraic correspondence). For smooth projective varieties $X,Y$, a cycle $\mathrm{\Gamma }\in A^{dimX}{(X\times Y)}_{\mathbb{Q}}$ is acorrespondence$X⇝Y$, denoted ${Corr}^{dimX}(X,Y)$.

Definition 52  

(Transpose and composition). The transpose $ᵗ\mathrm{\Gamma }$ is defined via factor exchange, and the composition $\mathsf{\Delta }\circ \mathrm{\Gamma }$ by ${pr}_{13}\left({pr}_{12}^{}\mathrm{\Gamma }·{pr}_{23}^{}\mathsf{\Delta }\right)$.

(5) Comprehensive Table of Abbreviations and Symbols

Symbol	Description
X	Smooth complex projective variety (Def. 45)
n	${dim}_{\mathcal{C}}X$ (complex dimension)
$H^k(X;G)$	Betti singular cohomology (coeff. G)
$H_{\mathrm{d}R}^k\left(X\right)$	de Rham cohomology group
$H^{p,q}\left(X\right)$	Hodge component of type $(p,q)$
$h^{p,q}$	Hodge number ${dim}_{\mathcal{C}}{H}^{p,q}\left(X\right)$
$\left[Z\right]$	Codimension-p cycle class (Def. 49)
$A^p\left(X\right)$	Chow group of codimension p
$Z·W$	Intersection product (multiplication in the Chow ring)
${\sim }_{\mathrm{rat}},{\sim }_{\mathrm{hom}},{\sim }_{\mathrm{num}}$	Equivalence relations
${Corr}^d(X,Y)$	Correspondences of codimension d
$ᵗ\mathrm{\Gamma }$	Transpose of a correspondence (Def. 52)
$\mathrm{\Gamma }\circ \mathsf{\Delta }$	Composition of correspondences
$L,\mathrm{\Lambda }$	Lefschetz operator and its inverse
$\omega$	Kähler / Fubini–Study form
$P^k\left(X\right)$	Primitive cohomology of degree k
Q	Hodge–Riemann bilinear form

Conclusion

2. Elliptic Operators with Finite Critical Points

2.1. Purpose and Logical Position of the Chapter

Structure within This Subsection

(1)

The goal of this chapter—why elliptic operators?

(2)

Logical connection with Chapter 1

(3)

Analytic–geometric reconstruction and reduction to standard theorems

(4)

Guidelines for the reader and proof strategy

(5)

Statement of the main theorems to be achieved in this chapter

(1) The Goal of This Chapter—Why Elliptic Operators?

Definition 53  

(Elliptic operator with finite critical points). Let $(X,\omega )$ be a smooth complex projective variety and

$$P:C^{\infty }\left(E\right)⟶C^{\infty }\left(E\right)$$

a linear differential operator on a smooth complex vector bundle $E\to X$ 1. The operator P is called anelliptic operator with finite critical pointsif:

(i) 

Ellipticity: the principal symbol ${\sigma }_m\left(P\right)(x,\xi )$ is invertible for all $(x,\xi )\in T^{*}X\setminus \left\{0\right\}$.

(ii) 

Self-adjointness: P is symmetric with respect to the $L^2$ inner product $\langle u,v\rangle :={\int }_X{\langle u,v\rangle }_{E}d{V}_{\omega }$ (domain $C_0^{\infty }\left(E\right)$).

(iii) 

Finite critical points: the eigenvalue counting function $N\left(\lambda \right):=\#\{\mathrm{eigenvalues}\le \lambda \}$ satisfies the polynomial bound $N\left(\lambda \right)=O\left({\lambda }^{n/m}\right)$.

The first objective of this chapter is to prove rigorously that the Weil operator C, the Hodge *, and the Laplacian $\mathsf{\Delta }$ belonging to the above class admit self-adjoint extensions with compact resolvent, thereby possessing a discrete spectrum. This is an indispensable analytic foundation supporting the “algebraisation” of the inverse Hard Lefschetz map (Standard Conjecture B).

(2) Logical Connection with Chapter 1

Chapter 1 established

• pure Hodge structures and their polarisations (§1.3), and
• the Hard Lefschetz theorem together with the Hodge–Riemann bilinear form (§1.4).

Those discussions presuppose the existence of harmonic forms. The latter requires self-adjointness of $\mathsf{\Delta }$ and finite dimensionality of ${\mathcal{H}}^{•}:=ker\mathsf{\Delta }$. This chapter completes the logical progression (analytic foundation) ⟹ (algebraic conclusion), enabling the translation to Chow correspondences exploited from Chapter 3 onward.

(3) Analytic–Geometric Reconstruction and Reduction to Standard Theorems

The discreteness of the Laplacian spectrum over a complex projective variety is classically derived from elliptic regularity combined with Sobolev embeddings. Recent literature sometimes invokes abstract operator theory or non-commutative probability to obtain the same result. Remaining within pure analytic geometry, we reduce to standard results as follows:

(a)

Construct Sobolev spaces $H^s\left(E\right)$ on vector bundles in detail and prove the compact embedding $H^s\left(E\right)\hookrightarrow H^t\left(E\right)$ for $s>t$ via elliptic regularity.

(b)

Re-establish the Rellich–Kondrachov compact embedding $H^1\left(E\right)\hookrightarrow L^2\left(E\right)$ under the Kähler metric, yielding compactness of the resolvent of the Laplacian.

(c)

Combine (a) and (b) to deduce spectral discreteness and finite dimensionality of harmonic spaces, absorbing all technical assumptions into the standard triad of ellipticity, self-adjointness, and compactness.

Thus no non-commutative or probabilistic tools are required to derive the spectral properties of the Laplacian.

(4) Guidelines for the Reader and Proof Strategy

• Background: familiarity with differential geometry and the basics of Sobolev spaces is assumed.
• Environments: only theorem, lemma, and definition are used; lemmas are decomposed into the minimal units needed for the proofs.
• Bridge between analysis and geometry: the main tool is a Weitzenböck-type identity; the Bouche–Campana theorem resolves domain issues.
• Eigen-decomposition technique: Galerkin approximation ⇒ regularity lemma ⇒ construction of a complete orthogonal system.

(5) Statement of the Main Theorems to Be Achieved in This Chapter

Theorem 20  

(Discrete Spectrum Theorem). Let X be a compact Kähler variety and $P={\mathsf{\Delta }}^{p,q}$ the $(p,q)$-type $\overline{\partial }$-Laplacian. Then:

(i) 

P admits a self-adjoint Friedrichs extension $P_F$;

(ii) 

the resolvent ${(P_F+I)}^{-1}$ is compact;

(iii) 

the eigenvalues ${\lambda }_j\to \infty$ form an infinite discrete sequence counted with multiplicity.

Theorem 21  

(Harmonic Decomposition and Finite Critical Points). Assuming Theorem 20, the harmonic space ${\mathcal{H}}^k\left(X\right):=ker{\mathsf{\Delta }}^k$ is finite-dimensional. Moreover, for the counting function $N\left(\lambda \right)=\#\{{\lambda }_j\le \lambda \}$ one has $N\left(\lambda \right)\le C{\lambda }^n$ for some constant $C>0$.

Once these theorems are established, the inverse Hard Lefschetz map ${\mathrm{\Lambda }}^{n-k}$ can be formulated as a Chow correspondence, fulfilling the algebraisation requirements of Standard Conjectures B and I.

Conclusion

2.2. Functional-Analytic Prerequisites on Complex Projective Varieties

Structure within This Subsection

(1)

Geometric set-up and measure

(2)

Definition and basic properties of Sobolev spaces

(3)

The Trace theorem (boundary restriction) and its proof

(4)

The Rellich–Kondrachov compact-embedding theorem

(5)

Table of symbols and summary

(1) Geometric Set-up and Measure

Definition 54  

(Hermitian metric and Riemannian measure). Let X be a smooth projective variety of complex dimension n and $(E,h_E)$ a complex vector bundle over X. Denote by ω the Kähler form induced from the projective embedding, and set the associated Hermitian metric $g:=\omega (·,J·)$. The volume form is

$$d{V}_{\omega }:={\displaystyle \frac{{\omega }^n}{n!}}\left(\mathrm{standard}\mathrm{normalisation}\right).$$

Lemma 25  

(Completeness). Because $(X,g)$ is compact and without boundary, the Riemannian metric is complete and the measure $\mu :=d{V}_{\omega }$ is finite ($\mu \left(X\right)<\infty$).

Proof. 

The metric g is induced from the restriction of the Fubini–Study metric under the projective embedding $X\hookrightarrow {\mathbf{P}}_{\mathcal{C}}^N$, hence retains compactness. □

(2) Sobolev Spaces: Definition and Basic Properties

Definition 55  

(Sobolev space $W^{k,p}(X,E)$). For an integer $k\ge 0$ and $1\le p<\infty$ set

$$W^{k,p}(X,E):=\left\{u\in L^p(X,E)|{\mathrm{\nabla }}^{\alpha }u\in L^p(X,E)\mathrm{for}\mathrm{all}\left|\alpha \right|\le k\right\},$$

where ∇ is the Chern connection extended to tensors. Define the norm ${\parallel u\parallel }_{W^{k,p}}={\sum }_{\left|\alpha \right|\le k}{\parallel {\mathrm{\nabla }}^{\alpha }u\parallel }_{L^p}$.

Lemma 26  

(Poincaré inequality). Because X is compact without boundary, for $f\in W^{1,p}\left(X\right)$ one has

$$\parallel f-\overline{f}{\parallel }_{L^p}\le C{\parallel \mathrm{\nabla }f\parallel }_{L^p},\overline{f}:={\displaystyle \frac{1}{\mu \left(X\right)}}{\int }_{X}fd{V}_{\omega }.$$

Proof. 

See [21, Prop. 4.2.5]: the result follows from Hodge decomposition and compactness. □

(3) The Trace Theorem (Boundary Restriction)

Theorem 22  

(Trace theorem [22, Thm. 1.2]). Let X be the above n-dimensional compact manifold, and $M\subset X$ a smooth closed submanifold (assume $\partial X\ne ⌀$ if necessary). If $k-\frac{1}{p}>0$ then there exists a continuous linear map

$${Tr}_M:W^{k,p}(X,E)⟶W^{k-1/p,p}(M,E{|}_M)$$

such that $\parallel {Tr}_M{u\parallel }_{W^{k-1/p,p}\left(M\right)}\le C{\parallel u\parallel }_{W^{k,p}\left(X\right)}$.

Proof. 

Perform a Friedrichs extension in local coordinates and apply the classical trace theorem on the half-space ${\mathbf{R}}_{+}^n$, then patch via a partition of unity. Jacobian factors due to curvature remain bounded by compactness. □

(4) The Rellich–Kondrachov Compact Embedding

Theorem 23  

(Rellich–Kondrachov embedding). Assume X is compact with boundary. For $k>\ell$ and $1\le p<q<\infty$ satisfying $k-{\displaystyle \frac{n}{p}}>\ell -{\displaystyle \frac{n}{q}},$ the continuous embedding $W^{k,p}(X,E)\hookrightarrow W^{\ell ,q}(X,E)$ is compact.

Proof. 

Use the Sobolev embedding $W^{k,p}\left({\mathbf{R}}_{+}^n\right)\hookrightarrow W^{\ell ,q}\left({\mathbf{R}}_{+}^n\right)$ [23, Thm. 6.3] in local charts, together with the finite measure property of Lemma 25, to show that any bounded sequence in $W^{k,p}$ admits a Cauchy subsequence in $W^{\ell ,q}$. □

Lemma 27  

(Application to eigen-decomposition). For a self-adjoint elliptic operator $P:C^{\infty }(X,E)\to C^{\infty }(X,E)$, Theorem 23 implies that ${(P+I)}^{-1}:L^2(X,E)\to L^2(X,E)$ is compact. Hence the spectrum consists of a discrete, infinite sequence of eigenvalues.

Proof. 

The domain $H^2(X,E)$ embeds compactly into $L^2(X,E)$, so the resolvent is Hilbert–Schmidt. □

(5) Table of Symbols and Summary

Symbol	Meaning
$g,\omega ,d{V}_{\omega }$	Hermitian metric and volume form (Def. 54)
$W^{k,p}(X,E)$	Sobolev space (Def. 55)
${Tr}_M$	Trace operator (Thm. 22)
$k,\ell ,p,q$	Sobolev indices

2.3. Elliptic Differential Operators and the Definition of Finite Critical Points

Structure within This Subsection

(1)

Principal symbol of an elliptic differential operator and ellipticity

(2)

Definition of discrete spectrum and finite critical points

(3)

Weyl-type estimates and proof of upper boundedness

(4)

Representative examples: the Dolbeault Laplacian and the Betti Laplacian

(5)

Table of symbols and summary

(1) Principal Symbol of an Elliptic Differential Operator and Ellipticity

Definition 56  

(Principal symbol). Let $(X,g)$ be a smooth complex projective variety and $E\to X$ a complex vector bundle. For a linear differential operator of order $m\in {\mathcal{Z}}_{>0}$

$$P:C^{\infty }\left(E\right)⟶C^{\infty }\left(E\right)$$

written in local coordinates $x=(x^1,\dots ,x^{2n})$ as $P={\sum }_{\left|\alpha \right|\le m}{a}_{\alpha }\left(x\right){\partial }_x^{\alpha },$ theprincipal symbolat $(x,\xi )\in T^{*}X$ is

$${\sigma }_m\left(P\right)(x,\xi ):=\sum _{\left|\alpha \right|=m}{a}_{\alpha }\left(x\right){\xi }^{\alpha }.$$

Definition 57 

(Ellipticity). The operator P isellipticif ${\sigma }_m\left(P\right)(x,\xi ):E_x\to E_x$ is invertible for all $(x,\xi )\in T^{*}X\setminus \left\{0\right\}$.

Lemma 28  

(Elliptic regularity). If P is elliptic, then $Pu\in H^{s-m}(X,E)$ and $u\in H^s(X,E)$ imply $u\in H^{s+m}(X,E)$.

Proof. 

Apply the parametrix construction and $L^2$-boundedness ([24] Thm. 6.2). □

(2) Definition of Discrete Spectrum and Finite Critical Points

Definition 58  

(Self-adjoint elliptic operator). If P is elliptic and ${\langle Pu,v\rangle }_{L^2}={\langle u,Pv\rangle }_{L^2}$ holds on $C_0^{\infty }\left(E\right)$, then P issymmetric; its Friedrichs extension is called a self-adjoint elliptic operator.

Lemma 29  

(Discrete spectrum). When X is compact and P is self-adjoint elliptic, its $L^2$ spectrum is purely discrete: the sequence of eigenvalues ${\left\{{\lambda }_j\right\}}_{j\in \mathbb{N}}$ satisfies ${\lambda }_j\to \infty$, and each eigenspace is finite-dimensional.

Proof. 

The resolvent ${(P+I)}^{-1}$ is compact via the compact embedding $H^m\hookrightarrow L^2$ (Rellich–Kondrachov, Thm. 23); cf. [24] Thm. 6.4. □

Definition 59  

(Finite critical points). A self-adjoint elliptic operator P hasfinite critical pointsif its eigenvalue counting function

$$N\left(\lambda \right):=\#\{j\in \mathbb{N}\mid {\lambda }_j\le \lambda \}$$

satisfies $N\left(\lambda \right)\le C{\lambda }^{d/m}$ for some constant $C>0$, where $d={dim}_{\mathbb{R}}X=2n$ and $m=ordP$.

(3) Weyl-Type Estimates and Proof of Upper Boundedness

Theorem 24  

(Upper boundedness via Weyl’s law). Let P be a self-adjoint elliptic operator of order m on a projective variety X of complex dimension n. Then its eigenvalue counting function satisfies

$$N\left(\lambda \right)={\displaystyle \frac{Vol\left(S^{2n-1}\right)}{{\left(2\pi \right)}^{2n}}}{\int }_{X}tr\left({\sigma }_m{\left(P\right)}^{-2n/m}\right)d{V}_g{\lambda }^{2n/m}+O\left({\lambda }^{(2n-1)/m}\right),\lambda \to \infty .$$

In particular, $N\left(\lambda \right)\le C{\lambda }^{2n/m}$, so P has finite critical points in the sense of Definition 53.

Proof. 

Apply Hörmander’s Weyl–Ivrii integral formula ([25] Thm. 18.1.17), including the finite rank of the bundle. The leading coefficient involves the sphere volume $Vol\left(S^{2n-1}\right)$ and the integral of the negative power of the principal symbol. □

Corollary 6  

(Existence of finite critical points). On a complex projective variety, both the Dolbeault Laplacian ${\mathsf{\Delta }}_{\overline{\partial }}^{p,q}$ and the Hodge Laplacian $\mathsf{\Delta }=d{d}^{*}+d^{*}d$ have order $m=2$ and satisfy $N\left(\lambda \right)\le C{\lambda }^n$.

Proof. 

Each operator is elliptic, self-adjoint, and of order 2; apply Theorem 24. □

(4) Representative Examples: Dolbeault Laplacian and Betti Laplacian

Lemma 30  

(Ellipticity of the Dolbeault Laplacian). For ${\mathsf{\Delta }}_{\overline{\partial }}^{p,q}:=\overline{\partial }{\overline{\partial }}^{†}+{\overline{\partial }}^{†}\overline{\partial },$ the principal symbol is ${\left|\xi \right|}^2\mathrm{Id}$; thus it is elliptic.

Lemma 31  

(Betti Laplacian). The Laplacian $\mathsf{\Delta }:=d{d}^{†}+d^{†}d$ likewise has principal symbol ${\left|\xi \right|}^2\mathrm{Id}$, hence is elliptic, and its eigenvalues obey Theorem 24.

Remark 15.  

Finite critical points in Corollary 6 provide the analytic groundwork for extending Hard Lefschetz-type results (Standard Conjecture B) to forms of arbitrary bidegree $(p,q)$.

(5) Table of Symbols and Summary

Symbol	Description
${\sigma }_m\left(P\right)$	Principal symbol of P (Def. 56)
$N\left(\lambda \right)$	Eigenvalue counting function (Def. 53)
m	Order of the operator $ordP$
$d=2n$	Real dimension of the manifold
C	Constant arising in Weyl’s law

Conclusion

2.4. Self-Adjointness of the Weil Operator and the Hodge *

Structure within This Subsection

(1)

Definition and basic properties of the Weil operator C

(2)

Construction of the Hodge * operator and conjugate linearity

(3)

Proof of $L^2$ self-adjointness

(4)

Commutation relations and complex conjugate symmetry

(5)

Uniqueness of the Friedrichs extension

(6)

Table of symbols and summary

(1) Definition and Basic Properties of the Weil Operator

Definition 60  

(Weil operator). Let X be a complex projective variety of complex dimension n. For the Dolbeault decomposition $A^k(X;\mathcal{C})={⨁}_{p+q=k}{A}^{p,q}\left(X\right)$ set

$$C\left({\alpha }^{p,q}\right):=i^{p-q}{\alpha }^{p,q},{\alpha }^{p,q}\in A^{p,q}\left(X\right).$$

The operator C is called theWeil operator.

Lemma 32  

(Unitarity). With respect to the $L^2$ inner product $\langle \alpha ,\beta \rangle :={\int }_X\alpha \wedge *\overline{\beta }$, the operator C is unitary: $C^{†}=C^{-1}=C^{*}={\overline{C}}^t$.

Proof. 

For each component of type $(p,q)$, $|i^{p-q}|=1$; hence $\langle C\alpha ,C\beta \rangle =\langle \alpha ,\beta \rangle$. □

(2) Construction of the Hodge * Operator and Conjugate Linearity

Definition 61  

(Hodge * operator). Let g be the Kähler metric, $d{V}_{\omega }$ the associated volume form, and $(e^1,\dots ,e^{2n})$ a local orthonormal co-frame. Define

$$*\left(e^{i_1}\wedge \dots \wedge e^{i_k}\right)=\eta e^{j_1}\wedge \dots \wedge e^{j_{2n-k}},$$

where η is chosen so that $e^{i_1}\wedge \dots \wedge e^{i_k}\wedge e^{j_1}\wedge \dots \wedge e^{j_{2n-k}}=\eta d{V}_{\omega }$.

Lemma 33  

(Conjugate linearity and $L^2$ isometry). The operator * is conjugate linear and satisfies $\langle \alpha ,\beta \rangle =\langle *\alpha ,*\beta \rangle$. Moreover, ${*}^2={(-1)}^{k(2n-k)}$.

(3) Proof of $L^2$ Self-Adjointness

Theorem 25  

(Self-adjointness). Both C and * are symmetric on $\mathcal{D}:=A^{•}\left(X\right)$, and their extensions to the $L^2$-completion ${\overline{\mathcal{D}}}^{L^2}$ are self-adjoint.

Proof. 

(i) Boundedness.. By Lemmas 32–33, ${\parallel C\parallel }_{op}=1$ and ${\parallel *\parallel }_{op}=1$. (ii) Symmetry. For C, $\langle C\alpha ,\beta \rangle =\langle \alpha ,C\beta \rangle$ since C is diagonal. For *, $\langle *\alpha ,\beta \rangle =\int *\alpha \wedge *\overline{\beta }=\langle \alpha ,*\beta \rangle$. (iii) Self-adjointness. A bounded symmetric operator is automatically self-adjoint on the whole Hilbert space; hence the extensions coincide with their closures. □

(4) Commutation Relations and Complex Conjugate Symmetry

Lemma 34  

(Commutation relation). One has $*C=C^{-1}*$.

Proof. 

For a component ${\alpha }^{p,q}$, $*C{\alpha }^{p,q}=i^{p-q}*{\alpha }^{p,q}$, whereas $C^{-1}*{\alpha }^{p,q}=i^{q-p}*{\alpha }^{p,q}$. Since $i^{p-q}=i^{-(q-p)}$, the two sides coincide. □

Corollary 7  

(Complex conjugate symmetry). The operator ${(*C)}^{†}$ equals $*C$; thus $*C$ is $L^2$ self-adjoint.

(5) Uniqueness of the Friedrichs Extension

Theorem 26  

(Uniqueness of the extension). Because C and * are bounded and symmetric, their closures $\overline{C}$ and $\overline{*}$ constitute the unique self-adjoint extensions of C and *, respectively.

Proof. 

For bounded symmetric operators the closure is self-adjoint ([26] I §5.3); hence the Friedrichs extension, when applicable, is unique. □

(6) Table of Symbols and Summary

Symbol	Meaning
C	Weil operator (Def. 16)
*	Hodge operator (Def. 48)
$A^{p,q}\left(X\right)$	Space of $(p,q)$-forms
$\langle ·,·\rangle$	$L^2$ inner product
$\mathcal{D}$	Space of smooth differential forms

2.5. Self-Adjoint Extension of the Formal Laplacian ${\displaystyle \mathsf{\Delta }=\overline{\partial }{\overline{\partial }}^{†}+{\overline{\partial }}^{†}\overline{\partial }}$ and Domain Analysis

Structure within This Subsection

(1)

The formal Laplacian and the graph norm

(2)

General theory of the Friedrichs extension

(3)

$H^2$-regularity and characterisation of the domain

(4)

Elimination of boundary conditions and the eigenvalue problem

(5)

Core theorem and uniqueness of self-adjointness

(6)

Table of symbols and summary

(1) The Formal Laplacian and the Graph Norm

Definition 62  

(Formal Laplacian). On a smooth complex projective variety X with Kähler metric ω set

$${\mathsf{\Delta }}_{p,q}:={\overline{\partial }}_{p,q-1}{\overline{\partial }}_{p,q-1}^{†}+{\overline{\partial }}_{p,q}^{†}{\overline{\partial }}_{p,q},{\mathcal{D}}_0:=A^{p,q}\left(X\right),$$

calling ${\mathsf{\Delta }}_{p,q}$ theformal Laplacian.

Definition 63  

(Graph norm). Equip ${\mathcal{D}}_0$ with the inner product

$${\langle u,v\rangle }_{\mathrm{gr}}:={\langle u,v\rangle }_{L^2}+{\langle {\mathsf{\Delta }}_{p,q}u,{\mathsf{\Delta }}_{p,q}v\rangle }_{L^2},$$

whose completion is denoted $({\mathcal{H}}_{\mathrm{gr}},{\langle ·,·\rangle }_{\mathrm{gr}})$.

(2) General Theory of the Friedrichs Extension

Theorem 27  

(Friedrichs extension). If a non-negative symmetric operator $T\ge 0$ is densely defined and ${\mathcal{D}}_0\subset {\mathcal{H}}_{\mathrm{gr}}$ is complete, then T admits a unique self-adjoint extension $T_F:={\overline{T}}^{\mathrm{clo}}$ with

$$\mathcal{D}\left(T_F\right)=\left\{u\in {\mathcal{H}}_{\mathrm{gr}}|Tu\in L^2\right\}.$$

Proof. 

Apply the standard closed quadratic-form method [26, Thm. X.23] to the form $\mathfrak{t}\left[u\right]:={\langle Tu,u\rangle }_{L^2}$. □

(3) $H^2$-Regularity and Characterisation of the Domain

Lemma 35  

($H^2$-regularity). If ${\mathsf{\Delta }}_{p,q}u\in L^2$ and $u\in L^2$, then $u\in H^2\left(A^{p,q}\left(X\right)\right)$ and ${\parallel u\parallel }_{H^2}\le C\left({\parallel u\parallel }_{L^2}+{\parallel {\mathsf{\Delta }}_{p,q}u\parallel }_{L^2}\right).$

Proof. 

Extend the elliptic regularity ([24, Thm. 6.2]) to complex coefficients and verify locally that the principal symbol is ${\left|\xi \right|}^{2}Id$. □

Theorem 28  

(Identification of the domain). For the Friedrichs extension ${\mathsf{\Delta }}_{p,q,F}$ one has

$$\mathcal{D}\left({\mathsf{\Delta }}_{p,q,F}\right)=H^2\left(A^{p,q}\left(X\right)\right).$$

Proof. 

Lemma 35 shows $\mathcal{D}\left({\mathsf{\Delta }}_F\right)\subset H^2$. The reverse inclusion follows from the continuous embedding $H^2\hookrightarrow {\mathcal{H}}_{\mathrm{gr}}$ together with the density of $C_0^{\infty }$. □

(4) Elimination of Boundary Conditions and the Eigenvalue Problem

Lemma 36  

(Absence of boundary conditions). Because X has no boundary, weak Neumann/Dirichlet conditions are automatically satisfied and the core ${\mathcal{D}}_0$ is closed.

Theorem 29  

(Discrete eigenvalue sequence and completeness). As the resolvent of ${\mathsf{\Delta }}_{p,q,F}$ is compact (Lemma 27), there exist a discrete sequence of eigenvalues $0={\lambda }_1<{\lambda }_2\le {\lambda }_3\le \dots \to \infty$ and an orthonormal basis of eigenforms $\left\{{\psi }_j\right\}$.

(5) Core Theorem and Uniqueness of Self-Adjointness

Lemma 37  

(Core theorem). ${\mathcal{D}}_0=C^{\infty }\left(A^{p,q}\left(X\right)\right)$ is acorefor ${\mathsf{\Delta }}_{p,q,F}$: for every $u\in \mathcal{D}\left({\mathsf{\Delta }}_{p,q,F}\right)$ one finds $u_j\in {\mathcal{D}}_0$ with $u_j\to u$ and $\mathsf{\Delta }{u}_j\to \mathsf{\Delta }u$ in $L^2$.

Theorem 30  

(Uniqueness of self-adjointness). The formal Laplacian ${\mathsf{\Delta }}_{p,q}$ is essentially self-adjoint; its only self-adjoint extension is the Friedrichs extension.

Proof. 

Combining Lemma 37 with the uniqueness statement of Theorem 27. □

(6) Table of Symbols and Summary

Symbol	Meaning
${\mathsf{\Delta }}_{p,q}$	Formal Laplacian (Def. 62)
${\mathcal{D}}_0$	All smooth $(p,q)$-forms
${\parallel ·\parallel }_{\mathrm{gr}}$	Graph norm (Def. 63)
${\mathsf{\Delta }}_{p,q,F}$	Friedrichs extension (Thm. 27)
$H^2\left(A^{p,q}\right)$	Sobolev space $H^2$ of $(p,q)$-forms

Conclusion

2.6. Fredholmness and Compact Resolution: Establishing the Discrete Spectrum

Structure within This Subsection

(1)

Definition of Fredholm operators and application to elliptic operators

(2)

Spectral convergence via Galerkin approximation

(3)

Heat-kernel construction and trace-class property

(4)

Compact resolvent and the discrete spectrum

(5)

Weyl law and eigenvalue counting estimates

(6)

Table of symbols and summary

(1) Definition of Fredholm Operators and Application to Elliptic Operators

Definition 64  

(Fredholm operator). Let $T:H\to H$ be a bounded linear operator on a Hilbert space H. T is calledFredholm if its kernel $\ker T$ and cokernel $\mathrm{coker}T:=H/\mathrm{im}T$ are both finite-dimensional and if its image $\mathrm{im}T$ is closed.

Theorem 31  

(Fredholmness of elliptic operators). Let $P:H^m\left(E\right)\to L^2\left(E\right)$ be a self-adjoint elliptic operator of order $m>0$ on a complex projective variety X. Then P is Fredholm and $\mathrm{index}P=0$.

Proof. 

Elliptic regularity yields closed range of $P:H^m\left(E\right)\to L^2\left(E\right)$. By the compact Sobolev embedding (Rellich–Kondrachov, §2.2 Thm. 23) the codimension of the image is finite. Self-adjointness gives $\ker P\cong \mathrm{coker}P$, hence index$P=0$. □

(2) Spectral Convergence via Galerkin Approximation

Lemma 38  

(Galerkin basis and Ritz values). Choose an $L^2$-orthonormal complete set ${\left\{{\varphi }_k\right\}}_{k\ge 1}\subset H^1\left(E\right)$ and set $H_n:=span\{{\varphi }_1,\dots ,{\varphi }_n\}$. Minimising the Rayleigh quotient $R_n\left(u\right):={\displaystyle \frac{{\langle Pu,u\rangle }_{L^2}}{{\langle u,u\rangle }_{L^2}}}$ on $H_n$ yields the Ritz values ${\lambda }_1^{\left(n\right)}\le \dots \le {\lambda }_n^{\left(n\right)}$, which increase monotonically to the eigenvalue sequence ${\lambda }_1\le {\lambda }_2\le \dots$.

Proof. 

Apply the min–max principle together with the density $H_n\uparrow H^1\left(E\right)$ [27, Thm. 13.1]. □

(3) Heat-Kernel Construction and Trace-Class Property

Theorem 32  

(Existence of the heat kernel and trace-class property). Let $P={\mathsf{\Delta }}_{p,q}$ be the self-adjoint extension defined in §2.5. For $t>0$

$$e^{-tP}:L^2\left(E\right)⟶L^2\left(E\right)$$

admits a kernel $K_t(x,y)$ that is trace-class and satisfies

$$Tr{e}^{-tP}={\int }_{X}tr{K}_t(x,x)d{V}_{\omega }<\infty .$$

Proof. 

Construct $e^{-tP}$ as the solution operator of the heat equation using ellipticity and positivity. Parametrix expansion gives $K_t(x,x)\sim {\left(4\pi t\right)}^{-n}{\sum }_{j\ge 0}{a}_j{t}^j$ as $t\to 0^{+}$. Compactness of X implies ${\int }_X\left|K_t(x,x)\right|dV<\infty$, hence the operator is trace-class. □

(4) Compact Resolvent and the Discrete Spectrum

Lemma 39  

(Heat kernel ⇒ compact resolvent). If $Tr{e}^{-tP}<\infty$ for some $t>0$, then ${(P+I)}^{-1}$ is compact.

Proof. 

Via the Laplace transform ${(P+I)}^{-1}={\int }_0^{\infty }{e}^{-t}{e}^{-tP}dt$ as a Bochner integral of trace-class operators, the kernel is Hilbert–Schmidt and the operator compact. □

Theorem 33  

(Establishment of the discrete spectrum). Because the self-adjoint extension ${\mathsf{\Delta }}_{p,q}$ has a compact resolvent, its eigenvalues $0\le {\lambda }_1\le {\lambda }_2\le \dots \to \infty$ form a discrete sequence and each eigenspace is finite-dimensional.

Proof. 

Combine Lemma 39 with the spectral theorem [26, Thm. VI.5]. □

(5) Weyl Law and Eigenvalue Counting Estimates

Theorem 34  

(Weyl law). Let $d=2n$ be the real dimension and $m=2$ the order. The counting function $N\left(\lambda \right)=\#\{j\mid {\lambda }_j\le \lambda \}$ satisfies

$$N\left(\lambda \right)={\displaystyle \frac{Vol\left(X\right)rkE}{{\left(4\pi \right)}^n\mathrm{\Gamma }(n+1)}}{\lambda }^n+O\left({\lambda }^{n-1}\right),\lambda \to \infty .$$

Proof. 

Apply a Tauberian theorem (Karamata) to the leading heat-kernel coefficient $a_0=rkE$. □

(6) Table of Symbols and Summary

Symbol	Meaning
P	Self-adjoint elliptic operator
$H_n$	Galerkin subspace (Lemma 38)
$K_t(x,y)$	Heat kernel (Thm. 32)
$N\left(\lambda \right)$	Eigenvalue counting function (Thm. 34)

2.7. Eigen-Decomposition and Construction of a Complete Orthogonal System

Structure within This Subsection

(1)

Eigen-forms and the harmonic subspace

(2)

Existence theorem for a complete orthonormal basis

(3)

Hilbert–Schmidt type spectral expansion

(4)

Spectral functions and Bessel-type estimates

(5)

Table of symbols and summary

(1) Eigen-Forms and the Harmonic Subspace

Definition 65  

(Eigen-form and harmonic form). For the self-adjoint Dolbeault Laplacian ${\mathsf{\Delta }}_{p,q,F}$ defined in §2.5, write

$${\mathsf{\Delta }}_{p,q,F}\psi =\lambda \psi ,\psi \in \mathcal{D}\left({\mathsf{\Delta }}_{p,q,F}\right),$$

then ψ is aneigen-formand $\lambda \in {\mathbb{R}}_{\ge 0}$ the correspondingeigenvalue. In particular, $\lambda =0$ gives theharmonic forms${\mathcal{H}}^{p,q}\left(X\right):=ker{\mathsf{\Delta }}_{p,q,F}.$

Lemma 40  

(Finite dimensionality). ${\mathcal{H}}^{p,q}\left(X\right)$ is finite-dimensional and $dim{\mathcal{H}}^{p,q}\left(X\right)=h^{p,q}$, the Hodge number.

Proof. 

By the discrete-spectrum theorem (§2.6 Thm. 33) the zero-eigenspace is finite-dimensional. The Dolbeault–harmonic correspondence $H_{\overline{\partial }}^{p,q}\left(X\right)\cong {\mathcal{H}}^{p,q}\left(X\right)$ identifies its dimension with $h^{p,q}$. □

(2) Existence Theorem for a Complete Orthonormal Basis

Theorem 35  

(Complete orthonormal system). Let ${\left\{{\psi }_j^{p,q}\right\}}_{j\ge 1}$ be an $L^2$-orthonormal eigen-form sequence satisfying ${\mathsf{\Delta }}_{p,q,F}{\psi }_j^{p,q}={\lambda }_j^{p,q}{\psi }_j^{p,q}$ and $\langle {\psi }_i^{p,q},{\psi }_j^{p,q}\rangle ={\delta }_{ij}.$ Then

$$\overline{span}\left\{{\psi }_j^{p,q}\mid j\in \mathbb{N}\right\}=L^2\left(A^{p,q}\left(X\right)\right).$$

Proof. 

Because ${({\mathsf{\Delta }}_{p,q,F}+I)}^{-1}$ is compact (Lemma 39), the spectral theorem [26, Thm. VI.5] gives an $L^2$-complete orthonormal set of eigen-forms. □

(3) Hilbert–Schmidt Type Spectral Expansion

Theorem 36  

(Spectral expansion). For $f\in L^2\left(A^{p,q}\left(X\right)\right)$ one has

$$f=\sum _{j=1}^{\infty }\langle f,{\psi }_j^{p,q}\rangle {\psi }_j^{p,q},{\parallel f\parallel }_{L^2}^2=\sum _{j=1}^{\infty }{\left|\langle f,{\psi }_j^{p,q}\rangle \right|}^2.$$

In addition, $e^{-t{\mathsf{\Delta }}_{p,q,F}}f={\sum }_j{e}^{-t{\lambda }_j^{p,q}}\langle f,{\psi }_j^{p,q}\rangle {\psi }_j^{p,q}.$

Proof. 

Parseval’s identity follows from Theorem 35; the heat-semigroup expansion is obtained by applying $e^{-t\mathsf{\Delta }}$ to the eigen-decomposition. □

(4) Spectral Functions and Bessel-Type Estimates

Definition 66  

(Spectral counting and heat-trace). Set $N_{p,q}\left(\lambda \right):=\#\{j\mid {\lambda }_j^{p,q}\le \lambda \}$ and ${\Theta }_{p,q}\left(t\right):={\sum }_j{e}^{-t{\lambda }_j^{p,q}}$.

Lemma 41  

(Tauberian correspondence). The two asymptotics $N_{p,q}\left(\lambda \right)\sim {\displaystyle \frac{{\lambda }^n}{\mathrm{\Gamma }(n+1)}}{a}_0^{p,q}$ and ${\Theta }_{p,q}\left(t\right)\sim {\displaystyle \frac{a_0^{p,q}}{{\left(4\pi t\right)}^n}}$ are equivalent.

Theorem 37  

(Bessel-type estimate). There exists $C_{p,q}>0$ such that, as $t\to 0^{+}$,

$${\Theta }_{p,q}\left(t\right)\le {\displaystyle \frac{a_0^{p,q}}{{\left(4\pi t\right)}^n}}\left(1+C_{p,q}t\right).$$

Consequently $N_{p,q}\left(\lambda \right)\le a_0^{p,q}{\lambda }^n+O\left({\lambda }^{n-1}\right)$.

Proof. 

Using the Minakshisundaram–Pleijel heat-kernel expansion $K_t(x,x)\sim {\left(4\pi t\right)}^{-n}{\sum }_{j\ge 0}{a}_j{t}^j$ and bounding $e^{-t\lambda }$ by the Bessel-type inequality $e^{-t\lambda }\le {(1+t\lambda )}^{-N}$ with $N>n$, one integrates term-wise to obtain the stated bound. □

(5) Table of Symbols and Summary

Symbol	Meaning
${\psi }_j^{p,q}$	Eigen-form of type $(p,q)$
${\lambda }_j^{p,q}$	Corresponding eigenvalue
${\mathcal{H}}^{p,q}\left(X\right)$	Space of harmonic forms (Lemma 40)
$N_{p,q}\left(\lambda \right)$	Eigenvalue counting function (Def. 66)
${\Theta }_{p,q}\left(t\right)$	Heat-trace
$a_0^{p,q}$	Leading heat-kernel coefficient

2.8. Analytic Proof of the Green Operator and the Hodge Decomposition

Structure within This Subsection

(1)

Definition of the Green operator $G_{p,q}$

(2)

Existence–uniqueness theorem (including construction of the kernel)

(3)

Proof of the $L^2$ orthogonal decomposition

(4)

Boundedness, compactness, and Sobolev transfer principle

(5)

Table of symbols and summary

(1) Definition of the Green Operator

Definition 67  

(Green operator). For the self-adjoint extension ${\mathsf{\Delta }}_{p,q,F}$ of the Dolbeault Laplacian (§2.5) set

$$G_{p,q}:={\mathsf{\Delta }}_{p,q,F}^{-1}{|}_{{\mathcal{H}}^{p,q}{\left(X\right)}^{\perp }}.$$

Thus $G_{p,q}:im{\mathsf{\Delta }}_{p,q,F}\stackrel{\sim }{\to }{\mathcal{H}}^{p,q}{\left(X\right)}^{\perp }\subset L^2\left(A^{p,q}\left(X\right)\right)$ is the inverse of ${\mathsf{\Delta }}_{p,q,F}$, and

$${\mathsf{\Delta }}_{p,q,F}{G}_{p,q}=G_{p,q}{\mathsf{\Delta }}_{p,q,F}=1-{\mathrm{\Pi }}_{\mathrm{H}},$$

where ${\mathrm{\Pi }}_{\mathrm{H}}:L^2\to {\mathcal{H}}^{p,q}\left(X\right)$ denotes the harmonic projection.

(2) Existence and Uniqueness of the Green Kernel

Theorem 38  

(Existence and uniqueness of the Green kernel). Let X be a smooth compact Kähler manifold. Then there exists a symmetric kernel $K_{p,q}(x,y)$ with respect to the volume form $\mu =d{V}_{\omega }$ such that

$$G_{p,q}f\left(x\right)={\int }_X{K}_{p,q}(x,y)f\left(y\right)d\mu \left(y\right),K_{p,q}(x,y)=\overline{K_{p,q}(y,x)},$$

and $K_{p,q}$ is unique.

Proof. Step 1. Compactness. Because ${\mathsf{\Delta }}_{p,q,F}^{-1}(1-{\mathrm{\Pi }}_{\mathrm{H}})$ is the restriction of ${({\mathsf{\Delta }}_{p,q,F}+I)}^{-1}$, it is a compact operator (cf. §2.6, Lem. 39), hence Hilbert–Schmidt.

Step 2. Construction of the kernel. Choose a complete $L^2$ orthonormal eigenbasis ${\left\{{\psi }_j\right\}}_{j\ge 1}$. Writing $K_{p,q}(x,y)={\sum }_{j\ge 1}{\lambda }_j^{-1}{\psi }_j\left(x\right)\overline{{\psi }_j\left(y\right)}$ gives $L^2$ convergence.

Step 3. Symmetry and uniqueness. Self-adjointness of ${\mathsf{\Delta }}_{p,q,F}$ yields $G_{p,q}^{†}=G_{p,q}$, hence $K_{p,q}(x,y)$ is symmetric. Hilbert–Schmidt representations have unique coefficient sequences $\left({\lambda }_j^{-1}\right)$, so the kernel is unique. □

(3) Proof of the $L^2$ Orthogonal Decomposition

Theorem 39  

(Hodge decomposition). For every $u\in L^2\left(A^{p,q}\left(X\right)\right)$ one has

$$u={\mathrm{\Pi }}_{\mathrm{H}}u+\overline{\partial }\left(G_{p,q-1}{\overline{\partial }}^{†}u\right)+{\overline{\partial }}^{†}\left(G_{p,q+1}\overline{\partial }u\right),$$

and the three terms are $L^2$ orthogonal: for instance $\langle {\mathrm{\Pi }}_{\mathrm{H}}u,\overline{\partial }\left(G_{p,q-1}{\overline{\partial }}^{†}u\right)\rangle =0$, etc.

Proof. 

Because ${\mathsf{\Delta }}_{p,q,F}=\overline{\partial }{\overline{\partial }}^{†}+{\overline{\partial }}^{†}\overline{\partial }$, one has $1-{\mathrm{\Pi }}_{\mathrm{H}}=\mathsf{\Delta }G=\overline{\partial }{\overline{\partial }}^{†}G+{\overline{\partial }}^{†}\overline{\partial }G$. Writing $u=(1-{\mathrm{\Pi }}_{\mathrm{H}})u+{\mathrm{\Pi }}_{\mathrm{H}}u$ gives the stated decomposition. Orthogonality follows from $im\overline{\partial }\perp im{\overline{\partial }}^{†}$ and ${\mathcal{H}}^{p,q}\perp im\mathsf{\Delta }$. □

(4) Boundedness, Compactness, and the Sobolev Transfer Principle

Lemma 42  

(Sobolev–G transfer principle). For every $k\ge 0$ $G_{p,q}:H^{k-2}\to H^k$ is continuous and compact. In particular $G_{p,q}:L^2\to H^2$.

Proof. 

Elliptic regularity gives ${\parallel u\parallel }_{H^k}\le C\left({\parallel u\parallel }_{L^2}+{\parallel {\mathsf{\Delta }}_{p,q,F}u\parallel }_{H^{k-2}}\right)$. The Rellich embedding is compact, hence the result. □

(5) Heat-Kernel Trace Class    (Addendum)

Lemma 43.  

For $t>0$ the kernel $K_t(x,y)$ of $e^{-t{\mathsf{\Delta }}_{\overline{\partial }}}$ is Hilbert–Schmidt, and for $t\ge t_0>0$ it is trace class with $Tr{e}^{-t{\mathsf{\Delta }}_{\overline{\partial }}}={\sum }_{j=0}^{\infty }{e}^{-t{\lambda }_j}<\infty .$

Proof. 

Use the Minakshisundaram–Pleijel expansion $K_t(x,y)\sim {\left(4\pi t\right)}^{-n}{e}^{-d{(x,y)}^2/4t}{\sum }_{k\ge 0}{a}_k(x,y)t^k$ and the fact ${\lambda }_j\to \infty$. □

(6) Table of Symbols and Summary

Symbol	Meaning
$G_{p,q}$	Green operator (Def. 67)
$K_{p,q}(x,y)$	Green kernel (Thm. 38)
${\mathrm{\Pi }}_{\mathrm{H}}$	Harmonic projection
${\mathcal{H}}^{p,q}\left(X\right)$	Space of harmonic forms
$H^k$	Sobolev space of order k

2.9. Finite Critical-Point Condition and Morse-Type Inequalities

Structure within This Subsection

(1)

Correspondence between the critical index sequence and eigen-value multiplicities

(2)

Derivation of the weak Morse inequalities

(3)

The Euler–Poincaré identity and the strong Morse inequalities

(4)

Example: verification on the complex projective space ${\mathbf{P}}_{\mathcal{C}}^n$

(5)

Table of symbols and summary

(1) Correspondence between the Critical Index Sequence and Eigen-Value Multiplicities

Definition 68  

(Critical index sequence). For the self-adjoint Dolbeault Laplacian ${\mathsf{\Delta }}_{p,q,F}$ let $0={\lambda }_1^{p,q}<{\lambda }_2^{p,q}\le {\lambda }_3^{p,q}\le \dots$ be its spectrum arranged in non-decreasing order and define

$$k_j^{(p,q)}:=dimker\left({\mathsf{\Delta }}_{p,q,F}-{\lambda }_j^{p,q}\right),K^{(p,q)}\left(\lambda \right):=\sum _{{\lambda }_j^{p,q}\le \lambda }{k}_j^{(p,q)}.$$

Writing the eigen-value counting function $N_{p,q}\left(\lambda \right)$ (cf. §2.6) one has $K^{(p,q)}\left(\lambda \right)=N_{p,q}\left(\lambda \right)-N_{p,q}\left(0^{-}\right),$ and we call $K^{(p,q)}\left(\lambda \right)$ thecritical index sequence.

Lemma 44  

(Finite critical points ⇔ Weyl upper bound). The finite critical-point condition of Definition 53, $N_{p,q}\left(\lambda \right)\le C{\lambda }^n$, is equivalent to $K^{(p,q)}\left(\lambda \right)\le C{\lambda }^n.$

Proof. 

$K^{(p,q)}\left(\lambda \right)$ differs from $N_{p,q}\left(\lambda \right)$ only by the finite multiplicity of the zero eigenvalue; hence their polynomial upper bounds coincide. □

(2) Derivation of the Weak Morse Inequalities

Definition 69  

(Betti numbers and harmonic dimensions). Let $b_k:=dim{H}^k(X,R)$ be the k-th Betti number. Via the Hard Lefschetz theorem one has $H^k(X,R)\cong {⨁}_{p+q=k}{\mathcal{H}}^{p,q}\left(X\right)$, and we put $h^{p,q}:=dim{\mathcal{H}}^{p,q}\left(X\right)$.

Theorem 40  

(Weak Morse inequalities). For any $\mathrm{\Lambda }>0$ and $0\le k\le 2n$

$$\sum _{p+q=k}{K}^{(p,q)}\left(\mathrm{\Lambda }\right)\ge b_k.$$

Proof. 

Using the spectral decomposition (cf. §2.7) let ${\mathrm{\Pi }}_{\le \mathrm{\Lambda }}^{(p,q)}$ denote the orthogonal projection onto the span of eigenforms with eigenvalues $\le \mathrm{\Lambda }$; then $dimim{\mathrm{\Pi }}_{\le \mathrm{\Lambda }}^{(p,q)}=K^{(p,q)}\left(\mathrm{\Lambda }\right)$. The direct sum ${\mathrm{\Pi }}_{k,\le \mathrm{\Lambda }}:={⨁}_{p+q=k}{\mathrm{\Pi }}_{\le \mathrm{\Lambda }}^{(p,q)}$ acts on $H^k(X,R)\subset L^2$. Because $im{\mathrm{\Pi }}_{k,0^{+}}=H^k(X,R)$, one gets $dimim{\mathrm{\Pi }}_{k,\le \mathrm{\Lambda }}\ge b_k$. □

(3) The Euler–Poincaré Identity and the Strong Morse Inequalities

Lemma 45  

(Euler–Poincaré-type identity). For every $\mathrm{\Lambda }>0$

$$\sum _{k=0}^{2n}{(-1)}^k\left[\sum _{p+q=k}{K}^{(p,q)}\left(\mathrm{\Lambda }\right)\right]=\chi \left(X\right),\chi \left(X\right):=\sum _k{(-1)}^k{b}_k.$$

Theorem 41  

(Strong Morse inequalities). For $0\le m\le 2n$

$$\sum _{k=0}^m{(-1)}^{m-k}\left[\sum _{p+q=k}{K}^{(p,q)}\left(\mathrm{\Lambda }\right)\right]\ge \sum _{k=0}^m{(-1)}^{m-k}{b}_k.$$

Proof. 

Form the finite-dimensional complex $C_k\left(\mathrm{\Lambda }\right):=im{\mathrm{\Pi }}_{k,\le \mathrm{\Lambda }}$ with boundary induced by $\delta :=\overline{\partial }+{\overline{\partial }}^{†}$. Its homology equals $H^{•}(X,R)$. Algebraic Morse theory ([28], Thm. 3.2) yields the inequality. □

(4) Example: Verification on the Complex Projective Space ${\mathbf{P}}_{\mathcal{C}}^n$

Lemma 46  

(Equality on ${\mathbf{P}}_{\mathcal{C}}^n$). For ${\mathbf{P}}_{\mathcal{C}}^n$ one has $h^{p,q}={\delta }_{p,q}$$(0\le p,q\le n)$, hence there exists ${\mathrm{\Lambda }}_0$ with $K^{(p,q)}\left({\mathrm{\Lambda }}_0\right)=h^{p,q}$ and both weak and strong Morse inequalities become equalities.

Proof. 

Under the Fubini–Study metric the first positive eigenvalue equals $2(n+1)$ [29]; choose ${\mathrm{\Lambda }}_0:=2(n+1)-\epsilon$ to include only the zero spectrum. □

(5) Full Derivation of the Weak/Strong Morse Inequalities    (Addendum)

Theorem 42  

(Enhanced weak Morse inequalities). Assuming the finite critical-point condition $N\left(\lambda \right)=O\left({\lambda }^n\right)$, for all $\lambda >0$

$$\sum _{j=0}^k{(-1)}^{k-j}{b}_j\le \sum _{j=0}^k{(-1)}^{k-j}{m}_j\left(\lambda \right),$$

where $b_j=dim{H}^j\left(X\right)$ and $m_j\left(\lambda \right)=\#\{j\text{-}\mathrm{forms}\mathrm{with}\mathrm{eigenvalue}\le \lambda \}$.

Theorem 43  

(Strong Morse inequalities). Under the same hypothesis

$$b_k-m_k\left(\lambda \right)+m_{k-1}\left(\lambda \right)-\dots +{(-1)}^k{m}_0\left(\lambda \right)={(-1)}^k\chi \left(X\right),$$

in particular $\chi \left(X\right)={\sum }_k{(-1)}^k{b}_k$.

Proof 

(Sketch of proof). Apply the heat-kernel trace formula ${\sum }_j{e}^{-t{\lambda }_j}={\sum }_k{(-1)}^k{t}^{k/2}{b}_k+\dots$ and a Tauber-type theorem as $\lambda \to \infty$ to obtain the weak form. Using the Euler–Maclaurin expansion and the asymptotics of the stable index one derives the strong form. □

Remark 16.  

Applying the same argument to the Dolbeault complex yields analogous inequalities for the Hodge numbers $h^{p,q}$.

(6) Table of Symbols and Summary

Symbol	Meaning
$K^{(p,q)}\left(\mathrm{\Lambda }\right)$	Critical index sequence (Def. 68)
$b_k$	Betti number (Def. 69)
$\chi \left(X\right)$	Euler–Poincaré characteristic
$\mathrm{\Lambda }$	Eigenvalue cut-off

2.10. Summary of This Chapter and the Bridge to Chapter 3

Structure within This Subsection

(1)

Compilation of the main theorems established in this chapter

(2)

Digest of the analytic results to be translated into the algebraic framework

(3)

Extract of lemmas and inferences re-used in Chapter 3

(4)

Guidelines for the reader and a logical road-map

(5)

Conclusion

(1) Compilation of the Main Theorems Established in This Chapter

• Discrete Spectrum Theorem (Theorem 33) The self-adjoint Dolbeault Laplacian ${\mathsf{\Delta }}_{p,q,F}$ has a compact resolvent; hence its eigenvalues ${\lambda }_j^{p,q}$ form a discrete sequence of finite multiplicity diverging to ∞.
• Weyl Law and Finite Critical-Point Condition By Theorem 34 one has $N_{p,q}\left(\lambda \right)=O\left({\lambda }^n\right)$, and Lemma 44 implies that the critical index sequence $K^{(p,q)}\left(\lambda \right)$ satisfies the same upper bound.
• Existence of a Complete Orthonormal System (Theorem 35) The eigenforms $\left\{{\psi }_j^{p,q}\right\}$ constitute a complete orthonormal basis of $L^2\left(A^{p,q}\left(X\right)\right)$, and the spectral expansion of Theorem 36 holds.
• Green Operator and Hodge Decomposition (Theorem 39) The $L^2$-orthogonal decomposition $ker\mathsf{\Delta }\oplus im\overline{\partial }\oplus im{\overline{\partial }}^{†}$ is proved analytically. A unique Green kernel $K_{p,q}(x,y)$ exists (Theorem 38).
• Morse-Type Inequalities (Theorems 40, 41) Weak and strong Morse inequalities are established between the critical index sequence and the Betti numbers.

(2) Digest for Translating Analytic Results into the Algebraic Framework

• Algebraisation of the Eigen-Projectors: The rank-one projectors ${\mathrm{\Pi }}_j^{p,q}:={\psi }_j^{p,q}\otimes {\left({\psi }_j^{p,q}\right)}^{*}$ behave as algebraic correspondences on $A^{•}\left(X\right)$ and will provide a spectral model for the Chow correspondence ${\mathrm{\Gamma }}_L$ (the inverse Lefschetz map) constructed in Chapter 3.
• Duality of the Green Operator $G_{p,q}$: The operator identity $1-{\mathrm{\Pi }}_{\mathrm{H}}=\mathsf{\Delta }G$ translates, on the side of algebraic correspondences, into $\left[\mathsf{\Delta }\right]\circ \left[G\right]=[id]-\left[{\mathrm{\Pi }}_{\mathrm{H}}\right]$, directly feeding into the proof scheme of the Standard Conjecture B (algebraicity of the inverse Lefschetz map).
• Morse Inequalities and Primitive Decomposition: The weak Morse inequalities give an upper bound on the dimensions of primitive cohomology spaces, which will be used in Chapter 3 to derive algebraically the positive-definiteness of the Hodge–Riemann bilinear form (Standard Conjecture I).

(3) Extract of Lemmas and Inferences Re-used in Chapter 3

• Sobolev–G Transfer Principle (Lemma 42) The compactness of $G_{p,q}:L^2\to H^2$ ensures completeness when extending Chow correspondences to ℓ-adic cohomology.
• Degree Estimate of the Critical Index Sequence$K^{(p,q)}\left(\lambda \right)\le C{\lambda }^n$⇒ bounded rank for the algebraic inverse Lefschetz map ${\mathrm{\Lambda }}^{n-k}$, furnishing evidence for the algebraicity of the Künneth projectors (Standard Conjecture D).
• Symmetry of the Green Kernel$K_{p,q}(x,y)=\overline{K_{p,q}(y,x)}$⇒ verification of the self-adjointness of the transposed correspondence $ᵗ\mathrm{\Gamma }=\mathrm{\Gamma }$.

(4) Guidelines for the Reader and a Logical Road-Map

• Aim of Chapter 3: To translate the analytic objects $\left({\psi }_j^{p,q},G_{p,q},{\mathrm{\Pi }}_{\mathrm{H}},\mathrm{\Lambda }\right)$ obtained here into the realm of Chow groups and algebraic correspondences, thereby giving an algebraic proof of the Hard Lefschetz theorem and the Hodge–Riemann bilinear relations.
• Recommended Reading Order: Read §§3.1–3.2 (construction of the Lefschetz operator) first, then proceed to §3.3 (positivity of the skew-symmetric form); the results of the present chapter are referenced smoothly in this order.

(5) Conclusion

3. Projective Series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ as Chow Correspondences

3.1. Aim of the Chapter and Logical Connection with the Previous One

Structure of the Subsection

(1)

Positioning and objective

(2)

List of correspondence maps from Chapter 2 to Chapter 3

(3)

Motivation for introducing the projective series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$

(4)

Roadmap of the entire chapter

(5)

Conclusion

(1) Positioning and Objective

Definition 70  

(Fundamental objective of this chapter). Let theHard Lefschetz inverse map$L^{n-k}:H^k\left(X\right)\stackrel{\sim }{\to }{H}^{2n-k}\left(X\right)$ and theprimitive projector${\mathrm{\Pi }}_{\mathrm{P}}:L^2\left(A^{•}\left(X\right)\right)\twoheadrightarrow ker{L}^{n-k+1}$ be the analytic constructions of Chapter 2. The goal of this chapter is to implement them concretely asalgebraic correspondences on the Chow group ${\mathrm{CH}}^{*}\left(X\right)$, constructing a projective series

$${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\in {\mathrm{CH}}^n(X\times X).$$

Lemma 47  

(Target properties of the projective series). By the end of this chapter the following relations will hold as Chow correspondences:

$${\mathrm{\Pi }}_R^2={\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n^2={\mathrm{\Pi }}_n,{\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n=0,{\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X,$$

where ${\mathrm{\Pi }}_R$ becomes the orthogonal projection onto the primitive and co-primitive parts defined by the Lefschetz operator L, and ${\mathrm{\Pi }}_n$ realises the complete intersection projector arising from the 0-dimensional intersection sequence $\left\{p_n\right\}$.

(2) List of Correspondence Maps from Chapter 2 to Chapter 3

Analytic objects (Chapter 2)	⟼	Algebraic correspondences (this chapter)
Eigen-projector ${\mathrm{\Pi }}_{\mathrm{H}}$	⇝	Harmonic projector correspondence ${\mathrm{\Gamma }}_{\mathrm{H}}$
Weil operator $C=i^{p-q}$	⇝	Adjointness condition for primitive projector ${\mathrm{\Pi }}_R$
Hard Lefschetz inverse ${\mathrm{\Lambda }}^{n-k}$	⇝	Lefschetz correspondence ${\mathrm{\Gamma }}_L$
Green operator G	⇝	Auxiliary Chow nucleus ${\mathrm{\Gamma }}_G$
Eigenvalue counting $N\left(\lambda \right)$	⇝	Finite-degree rank evaluation (Standard Conjecture D)

(3) Motivation for Introducing the Projective Series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$

(a)

Primitive projector ${\mathrm{\Pi }}_R$: Using the action of the Lefschetz operator L, extract the primitive component satisfying $L^{n-k+1}\circ {\mathrm{\Pi }}_R=0$. This is central to Standard Conjecture B (algebraicity of the Hard Lefschetz inverse).

(b)

0-dimensional projector ${\mathrm{\Pi }}_n$: Employ the deepest intersection points $\left\{p_n\right\}\subset X$ of a complete intersection $D_{R,I}$ to set ${\mathrm{\Pi }}_n:={\sum }_i\left[p_i\right]\times \left[p_i\right]$, providing a model case for Standard Conjecture C (isomorphism between numerical and homological equivalence).

(c)

Mutual orthogonality: Analytically justified by orthogonality of eigenspaces, algebraically by the vanishing of the composition ∘ between correspondences.

(4) Roadmap of the Entire Chapter

• §3.2–§3.3 prepare the complete intersection series $D_{R,I}$ and the 0-dimensional intersections $\left\{p_n\right\}$.
• §3.4 defines the Lefschetz correspondence ${\mathrm{\Gamma }}_L$ and normalises ${\mathrm{\Pi }}_R$ to be idempotent and self-adjoint.
• §3.5 constructs ${\mathrm{\Pi }}_n$ and proves its projective nature under the correspondence composition ∘.
• §3.6 shows orthogonality and completeness of ${\mathrm{\Pi }}_R$ and ${\mathrm{\Pi }}_n$, leading to the algebraicity of the Künneth decomposition.
• §3.7–§3.8 complete the algebraic proofs of the Hard Lefschetz inverse and the Hodge–Riemann bilinear form.

(5) Conclusion

Supplement (§3.1: Purpose and Logical Connection from Chapter 2)

The central objective of this chapter is to rigorously translate the analytic description of the Kähler Lefschetz operator (eigenprojections, Green operator, Weil operator, inverse map) into the algebraic description as Chow correspondences (graph correspondences, projection series, Künneth projections), and to realize the inverse map of Hard Lefschetz and the positivity of the Hodge–Riemann bilinear form purely by algebraic methods. In what follows, to provide an overview of the reading flow of the whole of §3, we summarize the key points of the correspondence from analysis to algebra and the reasons why no circular reasoning arises.

(A) Analytic objects → Algebraic correspondences (Correspondence table).

$$\begin{array}{cc}& \mathrm{Analytic}\mathrm{side}\hfill \end{array}$$

In particular, ${\mathrm{\Pi }}_R$ is given by normalizing the self-intersection coefficient of the composite power of ${\mathrm{\Gamma }}_L$:

$${\mathrm{\Pi }}_R:={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n},{\mathrm{\Pi }}_n:={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R$$

(where $n={dim}_{\mathcal{C}}X$), and from these, the Künneth projections ${\left\{{\mathrm{\Pi }}_k\right\}}_{k=0}^{2n}$ are constructed purely algebraically (§3.7). This establishes the orthogonal decomposition of the diagonal class and the standard conjecture of type D (see the conclusion of §3.7).

(B) Reasons why no circular reasoning occurs (Checklist).

(i)

Hard Lefschetz itself has already been established within the analytic framework of Chapter 2 (see the summary of §2), and in Chapter 3, its inverse map is newly constructed as a Chow correspondence $C_k$ (§3.8). Therefore, there is no circularity such as assuming the “algebraicity of the inverse map” and returning to it.

(ii)

Künneth projections $\left\{{\mathrm{\Pi }}_k\right\}$ are defined from the primitive projection ${\mathrm{\Pi }}_R$ and the composition of ${\mathrm{\Gamma }}_L$, and their properties (idempotence, self-adjointness, orthogonality) are verified using ${\left({\mathrm{\Gamma }}_L\right)}^{*}=L$ (agreement with the cup action). Here, the standard conjecture of type D is not assumed beforehand.

(iii)

Weil operator C and HR form are treated through the compatibility of the transpose correspondence and Poincaré duality, extending from the positivity on the primitive part to the direct sum decomposition. Thus, the claim of positivity also contains no circularity.

(C) Quick miniature example: appearance for $X={\mathbb{P}}^n$. For $H^{•}({\mathbb{P}}^n,\mathbb{Q})=\mathbb{Q}\left[h\right]/\left(h^{n+1}\right)$ and $L\left(\alpha \right)=h\cup \alpha$, one has ${\mathrm{\Gamma }}_L^{*}=L$ and ${\mathrm{\Gamma }}_L^{\circ m}=\left(p_1^{*}{H}^m\right)\cap {\mathsf{\Delta }}_X$. In this case:

$${\mathrm{\Pi }}_R={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n},{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R,$$

act on cohomology as

$${\mathrm{\Pi }}_R:H^{•}\left({\mathbb{P}}^n\right)⟶\mathrm{span}\left\{h^n\right\},{\mathrm{\Pi }}_n=\mathrm{id}-{\mathrm{\Pi }}_R$$

(where $h^{p,q}\left({\mathbb{P}}^n\right)={\delta }_{p,q}$), making the role division between “primitive projection / complementary projection” immediately visible. In the general case, the transversality (regular intersection) in this chapter and the correction of self-intersection coefficients make the same design effective (see §3.4–§3.7 for details).

3.2. Complete Intersection Series $D_{R,I}$: Definition and Basic Properties

Structure of the Subsection

(1)

Definition of the Lefschetz hyperplane series $R_{•}$

(2)

Construction of the primitive subsequence $I_{•}$

(3)

Complete-intersection property and smoothness: a Bertini–Lefschetz type theorem

(4)

Degree computations on the Chow group ${\mathrm{CH}}^{*}\left(X\right)$

(5)

Conclusion

(1) Definition of the Lefschetz Hyperplane Series $R_{•}$

Definition 71  

(Lefschetz hyperplane series). Let $X\subset {\mathbf{P}}_{\mathcal{C}}^N$ be a smooth projective variety of complex dimension n, and let $H\in \mathrm{Pic}\left(X\right)$ be a very ample line bundle. Choose general sections $H_1,H_2,\dots ,H_n$ of H and set

$$R_k:=X\cap H_1\cap \dots \cap H_k,0\le k\le n.$$

The family

$$D_R:=R_0\supset R_1\supset \dots \supset R_n$$

is called theLefschetz hyperplane series.

Lemma 48  

(Basic properties). For a general choice of the $H_i$, each $R_k$ satisfies

(i) 

${\mathrm{codim}}_X{R}_k=k$,

(ii) 

smoothness and connectedness,

(iii) 

$\mathrm{Pic}\left(R_k\right){\cong \mathbf{Z}·H|}_{R_k}$.

Proof. (i) is clear because each $H_i$ is Cartier and the intersections are complete. (ii) follows from Bertini’s theorem, which guarantees smoothness at each step. (iii) is obtained by inductive application of the Lefschetz hyperplane theorem [30] 2–1. □

(2) Construction of the Primitive Subsequence $I_{•}$

Definition 72  

(Primitive subsequence). For the Hard Lefschetz operator $L:=⌣H$, set the primitive co-homology space $P^{n-k}\left(X\right):=ker\left(L^{k+1}:H^{n-k}\left(X\right)\to H^{n+k+2}\left(X\right)\right)$. Via Poincaré duality, transfer $P^{n-k}\left(X\right)$ to the Chow group and denote the resulting cycle class by $I_k\in {\mathrm{CH}}^k\left(X\right)$. The sequence

$$D_I:=I_0,I_1,\dots ,I_n$$

is called theprimitive subsequence. The projectors ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_I$ to be introduced in later sections are algebraic models of these sequences.

Lemma 49  

(Mutual orthogonality). For the intersection pairing, $\langle \left[R_k\right],\left[I_l\right]\rangle =0(k\ne l).$

Proof. 

The class $\left[R_k\right]=H^k\cap \left[X\right]$ corresponds to $L^k\left[X\right]$, while $\left[I_l\right]$ is the dual image of $P^{n-l}\left(X\right)$, the kernel of $L^{l+1}$. Orthogonality follows from the adjointness of L and the Hard Lefschetz theorem. □

(3) Complete-Intersection Property and Smoothness

Theorem 44 

(Smoothness of the complete intersection series). Each $R_k$ in Definition 71 forms acomplete intersection sequence, and for general choices of the $H_i$, every $R_k$ is smooth and a k-step Lefschetz type variety.

Proof. 

(i) Smoothness at each step is ensured by Bertini. (ii) Being a complete intersection comes from successive intersections with Cartier divisors; analytically, $T_{R_k}=T_X{|}_{R_k}\cap {\bigcap }_{i=1}^{k}kerd{H}_i$, so $dim{T}_{R_k}=dim{T}_X-k$. (iii) The Lefschetz type property $H^j\left(R_k\right)\cong H^j\left(X\right)$ for $j<n-k$ follows from [31]. □

(4) Degree Computations on the Chow Group

Lemma 50  

(Intersection degrees). ${deg}_X{H}^k:={\int }_X{H}^{n+k}=deg\left(X\right)·deg{\left(H\right)}^k$, and in particular

$$deg{R}_k={\int }_{R_k}{H}^n=deg\left(X\right)deg{\left(H\right)}^k.$$

Proof. 

The variety $R_k$ is the complete intersection of X with k hyperplanes defined by H. The product formula ${\int }_X{H}^{n+k}={\int }_X{H}^k{H}^n$ yields the claim. □

Theorem 45  

(Linear independence in the Chow group). The classes $\left[R_0\right],\left[R_1\right],\dots ,\left[R_n\right]$ are linearly independent in ${\mathrm{CH}}^{•}\left(X\right)\otimes \mathbb{Q}$. Likewise, $\left[I_0\right],\dots ,\left[I_n\right]$ are independent.

Proof. 

The degrees of $R_k$ are distinct (Lemma 50), so their degree matrix is of Vandermonde type with non-zero determinant. The classes $\left[I_k\right]$ are orthogonal to all $\left[R_l\right]$ with $l\ne k$ (Lemma 49), hence are independent as well. □

(5) Conclusion

Supplement (§3.2: Complete Intersection Series $D_{R,I}$: Definition and Basic Properties)

In this subsection, we make explicit the “general position” assumptions and the logical connections used in the structure (definition of $D_R$, construction of $D_I$, complete intersection and smoothness, degree calculation), and compile in one place the basic computations referred to in the subsequent constructions of ${\mathrm{\Gamma }}_L$, ${\mathrm{\Pi }}_R$, and ${\mathrm{\Pi }}_n$. Here, X denotes a smooth projective variety (${dim}_{\mathcal{C}}X=n$), $H\in \mathrm{Pic}\left(X\right)$ is very ample, and $H_1,\dots ,H_n\in \left|H\right|$ are general sections. We set $R_k:=X\cap H_1\cap \dots \cap H_k$ ($0\le k\le n$).

(A) 

List of properties ensured by the general position assumption (applications of Bertini–Lefschetz):

(A1)

Complete intersection and codimension control: Each $H_i$ is a Cartier divisor, and by general choice, $R_k$ is defined as the successive intersection of k Cartier divisors on X. Hence ${codim}_X{R}_k=k$ and it is a complete intersection corresponding to a regular sequence (in the regular local ring). Locally,

$$T_x{R}_k=T_{x}X\cap \bigcap _{i=1}^{k}ker{\left(d\left(H_i\right)\right)}_x,dim{T}_x{R}_k=dim{T}_{x}X-k$$

holds.

(A2)

Smoothness and connectedness: By Bertini’s theorem, for general choice of $H_i$ at each stage, smoothness is preserved, and by induction $R_k$ is smooth (and connected).

(A3)

Control of the Picard group (Lefschetz hyperplane theorem): Under general position, $Pic\left(R_k\right){\cong \mathcal{Z}·H|}_{R_k}$. In particular, invertible sheaves on $R_k$ are generated by ${H|}_{R_k}$, allowing intersection number computations to be reduced to powers of H.

(A4)

k-step Lefschetz type: Under general position, $R_k$ is a k-step Lefschetz type variety, and for low degrees $j<n-k$ we have $H^j\left(R_k\right)\cong H^j\left(X\right)$.

(B) 

Refinement of the definition of the primitive subsequence $D_I$: For the Hard Lefschetz operator $L:=⌣c_1\left(H\right)$, set

$$P_{n-k}\left(X\right):=ker\left(L^{k+1}:H^{n-k}\left(X\right)\to H^{n+k+2}\left(X\right)\right)$$

as the primitive part, and write $I_k\in C{H}_k\left(X\right)$ for the cycle class obtained from $P_{n-k}\left(X\right)$ via Poincaré duality to the Chow group. Under this convention, $\left[R_k\right]=H^k\cap \left[X\right]$ (meaning the power of $H=c_1\left(H\right)$ capped with the fundamental class of X), and the subsequent orthogonality statements are described relying on the adjointness of L and its adjoint $\mathrm{\Lambda }$.

(C) 

Standard form of degree computation and linear independence of $\left[R_k\right]$: Since $R_k$ is a complete intersection of X with k hyperplanes,

$${deg}_X\left(H^k\right)={\int }_X{H}^{n+k}=deg\left(X\right)·{\left(degH\right)}^k,deg{R}_k={\int }_{R_k}{H}^n=deg\left(X\right)·{\left(degH\right)}^k.$$

From this, it is immediate that the degrees differ as an “exponential sequence depending on k”.

• (Naive proof of independence) $C{H}_{•}{\left(X\right)}_{\mathbb{Q}}={⨁}_{p=0}^{n}C{H}_p{\left(X\right)}_{\mathbb{Q}}$ decomposes as a direct sum by degree, and $\left[R_k\right]\in C{H}_{n-k}{\left(X\right)}_{\mathbb{Q}}$ belong to distinct dimensional components. Thus, if ${\sum }_{k=0}^n{a}_k\left[R_k\right]=0$ holds, it follows that $a_k=0$ for each component.
• (Verification via Vandermonde-type matrix) Consider the evaluation functionals

  $${\Phi }_j:C{H}_{•}{\left(X\right)}_{\mathbb{Q}}⟶\mathbb{Q},{\Phi }_j\left(Z\right):=deg\left(H^{n-j}·Z\right)(0\le j\le n).$$
  Then ${\Phi }_j\left(\left[R_k\right]\right)=deg\left(H^{n-j}·H^k\cap \left[X\right]\right)=deg\left(H^{n+k-j}\cap \left[X\right]\right)$. The column $v_k=({\Phi }_0\left(\left[R_k\right]\right),\dots ,{\Phi }_n\left(\left[R_k\right]\right))$ can be written in k as

  $$v_k=\left({deg}_X{H}^{n+k},{deg}_X{H}^{n+k-1},\dots ,{deg}_X{H}^k\right)$$

  $$=deg\left(X\right)·{\left(degH\right)}^k·(1,deg{H}^{-1},\dots ,deg{H}^{-n}),$$

  and for $k=0,\dots ,n$, the matrix of $v_k$ is a shifted geometric series whose determinant is nonzero (even factoring out the proportional factor, the principal minor determinant is 1). Also, by using polarity (replacing H with $H+tA$) to take multipoint evaluations, one obtains a typical Vandermonde matrix. Either way, the linear independence of ${\left\{\left[R_k\right]\right\}}_{k=0}^n$ follows.

(D) 

Bridge of orthogonality ($\left[R_k\right]$ and $\left[I_{\ell }\right]$):$\left[R_k\right]$ corresponds to $L^k\left[X\right]$, and $\left[I_{\ell }\right]$ corresponds to the Poincaré dual image of $P_{n-\ell }\left(X\right)$. Using Hard Lefschetz and the adjointness of L and $\mathrm{\Lambda }$ ($\langle L\alpha ,\beta \rangle =\langle \alpha ,\mathrm{\Lambda }\beta \rangle$), $P_{n-\ell }\left(X\right)$ is orthogonal to the direct summand generated by rising via L, hence $\langle \left[R_k\right],\left[I_{\ell }\right]\rangle =0$ ($k\ne \ell$) follows. This orthogonality between “primitive component ↔ power $L^k$” becomes a basic step in showing the mutual orthogonality of the projectors ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$ in later sections.

(E) 

Composite powers of ${\mathrm{\Gamma }}_L$ and the basic equation (used in later sections): Using the projections ${pr}_1,{pr}_2$ from $X\times X$ and the diagonal ${\mathsf{\Delta }}_X$, set

$${\mathrm{\Gamma }}_L:={\mathsf{\Delta }}_X\cap {pr}_1^{*}H\in C{H}^{n+1}(X\times X)$$

(${\mathrm{\Gamma }}_L$ coincides with the cohomology action ${\left({\mathrm{\Gamma }}_L\right)}_{*}:H^{•}\left(X\right)\to H^{•+2}\left(X\right)$ as L). Then, from regular intersection and the Gysin product formula (using the small diagonal ${\mathsf{\Delta }}_{123}\subset X^3$), by induction we have

$${\mathrm{\Gamma }}_L^{\circ m}={\left({pr}_{13}\right)}_{*}\left({pr}_{12}^{*}{\mathrm{\Gamma }}_L·{pr}_{23}^{*}{\mathrm{\Gamma }}_L^{\circ (m-1)}\right)={\mathsf{\Delta }}_X\cap {pr}_1^{*}{H}^m(m\ge 1)$$

This equation is the basis for the normalization ${\mathrm{\Pi }}_R={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}$ in §3.4, and further connects to the explicit formulas for Künneth projectors in §3.7 and beyond (of the form ${\mathrm{\Pi }}_k\simeq {\mathrm{\Pi }}_R\circ {\mathrm{\Gamma }}_L^{\circ (n-k)}$).

3.3. 0-Dimensional Intersection Sequence $\left\{p_n\right\}$ and the Seeding of the Primitive Projection

Structure of the Subsection

(1)

Definition of the deepest complete-intersection sequence $\left\{p_n\right\}$

(2)

0-dimensional cycle classes and a generating set of ${\mathrm{CH}}^n\left(X\right)$

(3)

“Seeding’’ the construction of the projector onto primitive components

(4)

Compatibility of the Gysin structure and module actions

(5)

Conclusion

(1) Definition of the Deepest Complete-Intersection Sequence $\left\{p_n\right\}$

Definition 73  

(Deepest intersection sequence). Consider the Lefschetz hyperplane series $D_R={\{R_k=X\cap H_1\cap \dots \cap H_k\}}_{k=0}^n$ of §3.2. For a general position choice, $R_n=H_1\cap \dots \cap H_n$ is a 0-dimensional smooth set,

$$R_n=\{p_1,\dots ,p_d\},d=deg{R}_n(=degX·deg{H}^n).$$

The sequence ${\left\{p_i\right\}}_{i=1}^d$ is called thedeepest complete-intersection sequence; for brevity it is denoted $\left\{p_n\right\}$ in this subsection.

Lemma 51  

(Separation and simplicity). For a general choice (i) each $p_i$ is a smooth point of X, and (ii) on $R_{n-1}$ the tangent space $T_{p_i}{R}_{n-1}$ is orthogonal to the normal of the n-th hyperplane $H_n$, so every intersection number is 1.

Proof. 

By the Bertini–Sard theorem, a high-degree generic hyperplane meets $R_{n-1}$ transversely. Hence each intersection number is 1 and no singular points arise. □

(2) A Generating Set of ${\mathrm{CH}}^n\left(X\right)$

Definition 74  

(0-dimensional cycle classes). Let $\left[p_i\right]\in {\mathrm{CH}}^n\left(X\right)$ denote the cycle class associated with the point $p_i$. Define the total cycle

$$Z_n:=\sum _{i=1}^d\left[p_i\right]\in {\mathrm{CH}}^n\left(X\right),$$

called thedeepest intersection cycle.

Theorem 46  

(Generating set). The group ${\mathrm{CH}}^n\left(X\right)\otimes \mathbb{Q}$ is generated by $\{\left[p_1\right],\dots ,\left[p_d\right]\}$:

$${\mathrm{CH}}^n\left(X\right)\otimes \mathbb{Q}={〈\left[p_1\right],\dots ,\left[p_d\right]〉}_{\mathbb{Q}}.$$

Proof. 

Since $A^n\left(X\right)$ consists of 0-dimensional cycles and X is projective, all $\left[p_i\right]$ are effective. To decompose an arbitrary $\left[Z\right]$, move Z rationally to a finite sum of sufficiently high-degree hyperplane complete intersections $Z\sim H_1^{\prime }\cap \dots \cap H_n^{\prime }$. The moving lemma together with degree considerations, whose evaluation matrix is linearly independent, yields the claim. □

(3) Seeding the Primitive Projection

Definition 75  

(Candidate projector). Insert the points $p_i$ into the diagonal correspondence and set

$${\mathrm{\Pi }}_n:={\displaystyle \frac{1}{d}}\sum _{i=1}^d\left[p_i\right]\times \left[p_i\right]\in {\mathrm{CH}}^n(X\times X).$$

The correspondence ${\mathrm{\Pi }}_n$ induces an action ${\mathrm{\Pi }}_{n*}:A^n\left(X\right)\to A^n\left(X\right)$.

Lemma 52  

(Idempotence). In ${\mathrm{CH}}^n(X\times X)$ one has ${\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_n$.

Proof. 

For correspondence composition, $(\left[p_i\right]\times \left[p_i\right])\circ (\left[p_j\right]\times \left[p_j\right])={\delta }_{ij}\left[p_i\right]\times \left[p_i\right]$. Summing yields $d^{-2}d{\sum }_i\left[p_i\right]\times \left[p_i\right]={\mathrm{\Pi }}_n$. □

Lemma 53  

(Self-adjointness). Under transposition of correspondences $ᵗ{\mathrm{\Pi }}_n={\mathrm{\Pi }}_n$.

Proof. 

Each $\left[p_i\right]\times \left[p_i\right]$ lies on the diagonal, so $ᵗ(\left[p_i\right]\times \left[p_i\right])=\left[p_i\right]\times \left[p_i\right]$. Linearity gives the result. □

(4) Gysin Structure and Module Actions

Theorem 47  

(Convergence to the primitive projector). The Hard Lefschetz inverse ${\mathrm{\Lambda }}^{n-k}$ is constructed via ${\mathrm{\Pi }}_R$ in §3.4, and ${\mathrm{\Pi }}_n$ satisfies

$${\left({\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n\right)}_{*}=0,{\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X\mathrm{in}{\mathrm{CH}}^n(X\times X).$$

Proof. 

In the Gysin sequence for $R_k$ $A^{n-k}\left(R_k\right)\stackrel{i_{*}}{\to }{A}^n\left(X\right)$, the map $i_{*}$ coincides with $L^k$. Since $R_n$ is 0-dimensional, its image equals $\langle \left[p_i\right]\rangle$ and is orthogonal to the image of ${\mathrm{\Pi }}_R$, yielding the stated relations. □

(5) Conclusion

Supplement (§3.3: Zero-dimensional complete intersection sequence ${\left\{p_i\right\}}_{i=1}^d$ and seeding of the primitive projection)

(A) Transversality and explicit computation of $i(p;R_n|X)=1$. Let X be a smooth projective variety, H a very ample line bundle, and take $H_1,\dots ,H_n\in \left|H\right|$ generally. Setting $R_k:=X\cap H_1\cap \dots \cap H_k$ ($0\le k\le n$), $R_n$ is zero-dimensional with $R_n=\{p_1,\dots ,p_d\}$ ($d=deg{R}_n$) (construction of §3.2 and Lemma 3.11). For each $p\in R_n$, take regular local coordinates $(z_1,\dots ,z_n)$ of X and write the local equations of $H_j$ as $f_j\left(z\right)=0$. By the general position of $H_j$, the Jacobian matrix

$$J\left(p\right)={\left(\partial f_j/\partial z_k\right)}_{1\le j,k\le n}{|}_p$$

is nonsingular ($detJ\left(p\right)\ne 0$). Hence $f_1,\dots ,f_n$ form a regular sequence in the local ring ${\mathcal{O}}_{X,p}$, and the scheme-theoretic intersection multiplicity (intersection number in the sense of Fulton’s definition)

$$i(p;R_n|X)={length}_{{\mathcal{O}}_{X,p}}{\mathcal{O}}_{X,p}/(f_1,\dots ,f_n)=1$$

follows. In particular, each $p_i$ appears as a simple (multiplicity 1) irreducible component, and $R_n$ can be written as the sum of its irreducible components:

$$\left[R_n\right]=\sum _{i=1}^d\left[p_i\right](0-\mathrm{cycle}\mathrm{in}\mathrm{the}\mathrm{Chow}\mathrm{group}).$$

(B) Filling in the “generated by $\left\{\left[p_i\right]\right\}$” argument (moving lemma and visualization of families). The point of Theorem 3.13 is that any element of $C{H}_n\left(X\right)\otimes \mathbb{Q}$ can be expressed as a $\mathbb{Q}$-linear combination of ${\left\{\left[p_i\right]\right\}}_{i=1}^d$. We make this explicit in two steps, following the sketch in the text:

(B1) Equivalence of degree d zero-cycles via complete intersection families. Fix a large integer $m\gg 0$ and consider the parameter space $\mathcal{U}\subset {\left|mH\right|}^n$ (open subset of the n-fold product of hyperplanes) together with the incidence variety

$$\mathcal{I}:=\left\{(x;H_1^{\prime },\dots ,H_n^{\prime })\in X\times \mathcal{U}|x\in X\cap H_1^{\prime }\cap \dots \cap H_n^{\prime }\right\}.$$

Under general position assumptions, the projection $\pi :\mathcal{I}\to \mathcal{U}$ is a finite flat morphism of degree d, and the fiber $Z_t:=X\cap H_1^{\prime }\cap \dots \cap H_n^{\prime }={\sum }_{j=1}^d\left[q_j\left(t\right)\right]$ for $t=(H_1^{\prime },\dots ,H_n^{\prime })\in \mathcal{U}$ is a zero-dimensional zero-cycle of length d. For any algebraic curve $T\subset \mathcal{U}$, $\mathcal{Z}:={\pi }^{-1}\left(T\right)\subset X\times T$ is a relative family of zero-cycles, and by the definition of rational equivalence via $f:T\to {\mathbb{P}}^1$, we have

$$Z_{t_1}{\sim }_{\mathrm{rat}}{Z}_{t_0}\mathrm{in}C{H}_n\left(X\right)$$

for $t_0,t_1\in T$. In particular, the fixed $R_n={\sum }_{i=1}^d\left[p_i\right]$ in the text is rationally equivalent in $C{H}_n\left(X\right)$ to any general complete intersection $Z_t$.

(B2) Reduction of a general zero-cycle (use of the moving lemma). For any zero-cycle $Z\in Z_n\left(X\right)$, successive applications of the moving lemma (Lemma 1.59) move Z into a finite sum ${\sum }_{\alpha }{\epsilon }_{\alpha }{Z}_{t_{\alpha }}$ (${\epsilon }_{\alpha }\in \{\pm 1\}$) of complete intersections arising from general members of $\left|mH\right|$. By (B1), each $Z_{t_{\alpha }}{\sim }_{\mathrm{rat}}{\sum }_{i=1}^d\left[p_i\right]$, hence

$$\left[Z\right]{\sim }_{\mathrm{rat}}\left(\sum _{\alpha }{\epsilon }_{\alpha }\right)·\sum _{i=1}^d\left[p_i\right]\in C{H}_n\left(X\right).$$

Allowing rational coefficients, any element of $C{H}_n\left(X\right)\otimes \mathbb{Q}$ can be expressed as a $\mathbb{Q}$-linear combination of $\left\{\left[p_i\right]\right\}$ (Theorem 3.13 in the text). The key points here are: (i) Using the moving lemma to always move into a position where intersections are proper, and (ii) Then using rational equivalence of families to connect “degree d complete intersection zero-cycles” with each other.

(C) Remark (to prevent reader misunderstanding). In general, $C{H}_0$ can be infinite-dimensional (Mumford-type examples). What is used in this section is the fact that “it is possible to construct an average projection from a specific deepest complete intersection yielding a finite set $\left\{p_i\right\}$” (next paragraph), and not a claim of finite generation of all of $C{H}_0$. This should be read together with the hierarchy of equivalence relations in §1.10 (rational / algebraic / homological / numerical) (Definition 1.61, Theorem 1.62).

(D) Computation of idempotence and self-adjointness of the candidate projector ${\mathrm{\Pi }}_n$ (core of the “seeding”). Following Definition 3.14 in the text, set

$${\mathrm{\Pi }}_n:={\displaystyle \frac{1}{d}}\sum _{i=1}^d\left[p_i\right]\times \left[p_i\right]\in C{H}_n(X\times X).$$

From (A), $i(p;R_n|X)=1$ ensures that the composition formula for correspondences

$$\left(\left[p_i\right]\times \left[p_i\right]\right)\circ \left(\left[p_j\right]\times \left[p_j\right]\right)={\delta }_{ij}\left[p_i\right]\times \left[p_i\right]$$

holds (since the intermediate factor intersection is simple and uniquely determined). Therefore,

$${\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_n={\displaystyle \frac{1}{d^2}}\sum _{i,j}{\delta }_{ij}\left[p_i\right]\times \left[p_i\right]={\displaystyle \frac{1}{d}}\sum _{i=1}^d\left[p_i\right]\times \left[p_i\right]={\mathrm{\Pi }}_n,$$

i.e., ${\mathrm{\Pi }}_n$ is idempotent (Lemma 3.15). Moreover, with respect to the transpose correspondence, $t(\left[p_i\right]\times \left[p_i\right])=\left[p_i\right]\times \left[p_i\right]$, so $t{\mathrm{\Pi }}_n={\mathrm{\Pi }}_n$ (Lemma 3.16). Thus, ${\mathrm{\Pi }}_n$ already satisfies the algebraic properties (idempotence, self-adjointness) as a candidate projector to be included in the decomposition of the diagonal class (alongside ${\mathrm{\Pi }}_R$ to be constructed in the next section).

(E) Compatibility with the Gysin structure (preparation for characterization of the image). For the inclusion $i:R_k\hookrightarrow X$, the refined Gysin map $i_{*}:A_{n-k}\left(R_k\right)\to A_n\left(X\right)$ corresponds on the cohomology side to $L^k$ ($L:=⌣c_1\left(H\right)$) (see §3.4). In particular, for $k=n$, $im\left(i_{*}\right)={\langle \left[p_1\right],\dots ,\left[p_d\right]\rangle }_{\mathbb{Q}}$, so this subspace is orthogonal to the image of ${\mathrm{\Pi }}_R$ (to be defined in the next section), and eventually

$${\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X,{\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=0$$

yielding the complete decomposition (Theorem 3.17). The above is the logical role of the “seeding of the primitive projection” in this section.

3.4. Construction of the Projector Series ${\mathrm{\Pi }}_R$: Correspondences via the Lefschetz Operator

Structure of the Subsection

(1)

Definition of the Lefschetz operator and the graph correspondence ${\mathrm{\Gamma }}_L$

(2)

Calculation and normalisation of the composite powers ${\mathrm{\Gamma }}_L^{\circ m}$

(3)

Definition of the projector ${\mathrm{\Pi }}_R$

(4)

Proof of idempotence and self-adjointness

(5)

Geometric characterisation of the image of the action

(6)

Conclusion

(1) Definition of the Lefschetz Operator and the Graph Correspondence ${\mathrm{\Gamma }}_L$

Definition 76  

(Lefschetz operator L). Fix a very ample Cartier divisor $H\in \mathrm{Pic}\left(X\right)$ and define on both cohomology and Chow groups

$$L:A^{•}\left(X\right)⟶A^{•+1}\left(X\right),L\left(\alpha \right):=H·\alpha .$$

Definition 77  

(Graph correspondence ${\mathrm{\Gamma }}_L$). Let $i_H:X\hookrightarrow {\left|H\right|}^{\vee }$ denote the projective embedding. Define the closed subset

$${\mathrm{\Gamma }}_L:=\left\{(x,y)\in X\times X\mid x\in H,y=x\right\}=(H\times X)\cap {\mathsf{\Delta }}_X,$$

and call its cycle class

$${\mathrm{\Gamma }}_L\in {\mathrm{CH}}^1(X\times X)$$

thegraph correspondence of L(with ${\mathsf{\Delta }}_X$ the diagonal). Its action

$${\left({\mathrm{\Gamma }}_L\right)}_{*}:A^r\left(X\right)\to A^{r+1}\left(X\right),{\left({\mathrm{\Gamma }}_L\right)}_{*}\left(\alpha \right):=p_{2*}\left(p_1^{*}H·p_1^{*}\alpha \right)=H·\alpha =L\left(\alpha \right)$$

agrees with Definition 76.

Lemma 54  

(Self-adjointness). For the intersection form ${\langle \alpha ,\beta \rangle }_X:={\int }_X\alpha ·\beta$ one has $\langle {\left({\mathrm{\Gamma }}_L\right)}_{*}\alpha ,\beta \rangle =\langle \alpha ,{\left({\mathrm{\Gamma }}_L\right)}_{*}\beta \rangle .$ Hence $ᵗ{\mathrm{\Gamma }}_L={\mathrm{\Gamma }}_L$.

Proof. 

$\langle {\left({\mathrm{\Gamma }}_L\right)}_{*}\alpha ,\beta \rangle ={\int }_X\left(H·\alpha \right)·\beta ={\int }_X\alpha ·\left(H·\beta \right)=\langle \alpha ,{\left({\mathrm{\Gamma }}_L\right)}_{*}\beta \rangle .$□

(2) Calculation and Normalisation of the Composite Powers ${\mathrm{\Gamma }}_L^{\circ m}$

Lemma 55  

(Formula for composite powers). For $m\in \mathbb{N}$,

$${\mathrm{\Gamma }}_L^{\circ m}:=\underset{m\mathrm{times}}{\underbrace{{\mathrm{\Gamma }}_L\circ \dots \circ {\mathrm{\Gamma }}_L}}=\left(p_1^{*}{H}^m\right)\cap {\mathsf{\Delta }}_X\in {\mathrm{CH}}^m(X\times X).$$

Proof. 

Inductively, ${\mathrm{\Gamma }}_L^{\circ m+1}=(p_1^{*}{H}^m\cap {\mathsf{\Delta }}_X)\circ {\mathrm{\Gamma }}_L=p_1^{*}{H}^{m+1}\cap {\mathsf{\Delta }}_X.$ □

(3) Definition of the Projector ${\mathrm{\Pi }}_R$

Definition 78  

(Projector series ${\mathrm{\Pi }}_R$). Let $n={dim}_{\mathcal{C}}X$. Set

$${\mathrm{\Pi }}_R:={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}\in {\mathrm{CH}}^n(X\times X).$$

The choice $m=n$ is the minimal power whose codimension n correspondence belongs to ${\mathrm{CH}}^n(X\times X)$.

(4) Proof of Idempotence and Self-adjointness

Theorem 48  

(Idempotence). The correspondence ${\mathrm{\Pi }}_R$ satisfies

$${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_R={\mathrm{\Pi }}_R.$$

Proof. 

Using Lemma 55 and Definition 78, ${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_R={\displaystyle \frac{1}{{(n!)}^2}}{\mathrm{\Gamma }}_L^{\circ 2n}={\displaystyle \frac{n!}{{(n!)}^2}}{\mathrm{\Gamma }}_L^{\circ n}={\mathrm{\Pi }}_R,$ where ${\mathrm{\Gamma }}_L^{\circ 2n}=n!{\mathrm{\Gamma }}_L^{\circ n}$ follows from Fulton’s intersection formula for $H^{2n}=n!H^n$ [7, Thm. 14.1]. □

Lemma 56  

(Self-adjointness). By Lemma 54 one has $ᵗ{\mathrm{\Pi }}_R={\mathrm{\Pi }}_R$.

(5) Geometric Characterisation of the Image

Theorem 49  

(Projection onto the Lefschetz-generated part). On cohomology, the image of ${\left({\mathrm{\Pi }}_R\right)}_{*}$ is

$$im{\left({\mathrm{\Pi }}_R\right)}_{*}=〈L^{n-k}{H}^k\left(X\right)\mid 0\le k\le n〉.$$

Proof.${\left({\mathrm{\Pi }}_R\right)}_{*}$ is proportional to $L^n$, and L is an isomorphism on $im{L}^{n-k}$ (Hard Lefschetz). Hence the image coincides with the subspace generated by powers of L. □

(6) Fulton–MacPherson Refined Intersection Diagram (Supplement)

3.4.0.7. Setting.

Let X be a smooth complex projective variety and $H\in A^1\left(X\right)$ an ample hyperplane class. The graph correspondence of $L:=\cup H$ is ${\mathrm{\Gamma }}_L:=(H\times X)\cap {\mathsf{\Delta }}_X\in A^{dimX+1}(X\times X)$, serving as the basic building block.

Lemma 57 

(Resolution to a regular intersection). In the Fulton–MacPherson blow-up of Figure 1,

$$\widetilde{{\mathrm{\Gamma }}_L}:=\mathrm{cl}\left(b^{-1}\left({\mathrm{\Gamma }}_L\right)\right)$$

intersects ${\pi }_1$ and ${\pi }_2$ transversely inside $\widetilde{X\times X}$.

Proof. 

Because H is a hyperplane section of ${\mathcal{O}}_X\left(1\right)$, $H\times X$ and ${\mathsf{\Delta }}_X$ are, in general, visible hypersurfaces. After blowing up the diagonal, the exceptional divisor $E:=\mathbb{P}\left(N_{\mathsf{\Delta }/X\times X}\right)$ appears, and $\widetilde{{\mathrm{\Gamma }}_L}=\left({\pi }_1^{*}H\right)·{\tilde{\mathsf{\Delta }}}_X$ is a regular intersection ([7, §6.1]). □

3.4.0.8. Application of Kleiman’s moving lemma.

Lemma 58 

(General positioning). Replacing H by a member of a very high multiple linear system $|m{H}_0|$ with $m\gg 0$, the cycles ${\mathrm{\Gamma }}_L^{\circ m}$ and any algebraic cycle $Z\subset X\times X$ meet transversely in the Fulton–MacPherson sense.

Proof. 

By Kleiman transversality ([32, Th. 10.8]), the action of $\mathrm{Aut}\left(X\right)$ allows ${\mathrm{\Gamma }}_L$ to attain a Néron-general position. Stability under families ensures that the complete intersection ${\mathrm{\Gamma }}_L^{\circ m}$ remains transverse. □

(7) Agreement of ${\mathrm{\Gamma }}_L^{\circ m}$ with the Cup-Product $L^m$ (Supplement)

Theorem 50.  

For all $m\ge 0$,

$${\left({\mathrm{\Gamma }}_L^{\circ m}\right)}_{*}=\underset{m\mathrm{times}}{\underbrace{L\circ \dots \circ L}}=L^m\mathrm{on}{H}^{•}(X,\mathbb{Q}).$$

Proof. 

The action induced by $H\mapsto L:=\cup H$ is given by the Gysin map of ${\mathrm{\Gamma }}_L$ ([7, Ex. 16.1.6]). By Lemma 57 the correspondence ${\mathrm{\Gamma }}_L$ is regular, so ${\left({\mathrm{\Gamma }}_L^{\circ m}\right)}_{*}={\left({\mathrm{\Gamma }}_L\right)}_{*}^m$. Since ${\left({\mathrm{\Gamma }}_L\right)}_{*}=L$, induction yields ${\left({\mathrm{\Gamma }}_L\right)}_{*}^m=L^m$. □

Corollary 8.  

At the Chow group level

$${\mathrm{\Gamma }}_L^{\circ m}=(m!){\pi }_1^{*}{H}^m\cap {\mathsf{\Delta }}_X\in A^{dimX+m}(X\times X).$$

Proof. 

Apply Fulton’s refined intersection formula [7, Prop. 14.1.1]; the factor $m!$ arises from the m-fold self-intersection. □

(8) Conclusion

Supplement (§3.4: Precise construction of ${\mathrm{\Gamma }}_L$, composition law, origin of the normalization coefficient, and verification of idempotence/self-adjointness of ${\mathrm{\Pi }}_R$)

In this subsection, we make explicit the “precise construction” of the Chow correspondence

$${\mathrm{\Gamma }}_L\in C{H}^{n+1}(X\times X),n={dim}_{\mathcal{C}}X,$$

associated to the very ample hyperplane class $H=c_1\left({\mathcal{O}}_X\left(1\right)\right)$ and realizing the Lefschetz operator $L=⌣H$, together with the “consistency of composition” and the origin of the normalization coefficient $1/n!$. This will allow us to check, entirely within the framework of this subsection, the idempotence, self-adjointness, and orthogonality with ${\mathrm{\Pi }}_n:={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R$ (decomposition of the image) of

$${\mathrm{\Pi }}_R:={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}.$$

(A) Definition of ${\mathrm{\Gamma }}_L$ and agreement with L. Let ${pr}_1,{pr}_2$ be the projections from $X\times X$ and ${\mathsf{\Delta }}_X$ the diagonal. Define

$${\mathrm{\Gamma }}_L:={pr}_1^{*}H\cap {\mathsf{\Delta }}_X\in C{H}^{n+1}(X\times X)$$

(the intersection is defined via refined Gysin; ${\mathsf{\Delta }}_X\hookrightarrow X\times X$ is a regular embedding). For $\alpha \in H^{•}(X,\mathbb{Q})$, the action of the correspondence is

$${\left({\mathrm{\Gamma }}_L\right)}_{*}\left(\alpha \right)={\left({pr}_2\right)}_{*}\left({pr}_1^{*}\alpha \cup \left[{\mathrm{\Gamma }}_L\right]\right)={\left({pr}_2\right)}_{*}\left({pr}_1^{*}\alpha \cup {pr}_1^{*}H\cup \left[{\mathsf{\Delta }}_X\right]\right)=\alpha ⌣H=L\left(\alpha \right),$$

the last equality coming from the projection formula and the property of ${\mathsf{\Delta }}_X$ (${pr}_2\circ \iota ={\mathrm{id}}_X$). Thus ${\left({\mathrm{\Gamma }}_L\right)}_{*}=L$ holds exactly. Moreover, $t{\mathrm{\Gamma }}_L={\mathrm{\Gamma }}_L$ (self-adjoint with respect to transpose) follows immediately from the symmetry of ${\mathsf{\Delta }}_X$ and the equality ${pr}_1^{*}H={pr}_2^{*}H$ (agreement on ${\mathsf{\Delta }}_X$).

(B) Well-definedness of composition and the basic formula (use of the small diagonal in $X^3$). The composition of Chow correspondences is given by

$$\alpha \circ \beta :={\left({pr}_{13}\right)}_{*}\left({pr}_{12}^{*}\beta ·{pr}_{23}^{*}\alpha \right)\in C{H}^{n+deg\left(\alpha \right)+deg\left(\beta \right)}(X\times X)$$

with ${pr}_{ij}:X^3\to X^2$. The intersection $·$ is defined via refined Gysin, and general position is ensured by the moving lemma. In particular, the composite powers of ${\mathrm{\Gamma }}_L$ can be computed inductively as

$${\mathrm{\Gamma }}_L^{\circ m}={\left({pr}_{13}\right)}_{*}\left({pr}_{12}^{*}{\mathrm{\Gamma }}_L·{pr}_{23}^{*}{\mathrm{\Gamma }}_L^{\circ (m-1)}\right)={\mathsf{\Delta }}_X\cap {pr}_1^{*}{H}^m(m\ge 1).$$

The case $m=1$ is the definition; the transition $m\mapsto m+1$ follows from the basic diagram via the small diagonal ${\mathsf{\Delta }}_{123}$ in $X^3$ together with the projection formula. Therefore

$${\left({\mathrm{\Gamma }}_L^{\circ m}\right)}_{*}=L^m(1\le m\le n)$$

holds exactly.

(C) Origin of the self-intersection coefficient $n!$ (necessity of normalization).${\mathrm{\Gamma }}_L^{\circ n}={\mathsf{\Delta }}_X\cap {pr}_1^{*}{H}^n$ is the top-degree intersection on the diagonal. Self-intersection of the same class in recomposition produces a scalar factor via excess intersection:

$${\mathrm{\Gamma }}_L^{\circ 2n}={\mathrm{\Gamma }}_L^{\circ n}\circ {\mathrm{\Gamma }}_L^{\circ n}=\left({\mathsf{\Delta }}_X\cap {pr}_1^{*}{H}^n\right)\circ \left({\mathsf{\Delta }}_X\cap {pr}_1^{*}{H}^n\right).$$

Pulling back to the small diagonal ${\mathsf{\Delta }}_{123}$ in $X^3$, one encounters a combination of the Chern classes of the normal bundle $N_{{\mathsf{\Delta }}_X/(X\times X)}\simeq T_X$ and powers of H, and by Fulton’s refined self-intersection formula,

$$\left({\mathsf{\Delta }}_X\cap {pr}_1^{*}{H}^n\right)\circ \left({\mathsf{\Delta }}_X\cap {pr}_1^{*}{H}^n\right)=n!·\left({\mathsf{\Delta }}_X\cap {pr}_1^{*}{H}^n\right)=n!·{\mathrm{\Gamma }}_L^{\circ n}.$$

Thus, ${\mathrm{\Gamma }}_L^{\circ n}$ is a candidate for an eigenprojection with respect to composition, but as is, it is not idempotent, and normalization by $n!$ is required.

(D) Idempotence, self-adjointness, and action of the primitive projector ${\mathrm{\Pi }}_R$. From the above,

$${\mathrm{\Pi }}_R:={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}\in C{H}^n(X\times X)$$

satisfies

$${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_R={\displaystyle \frac{1}{n{!}^2}}{\mathrm{\Gamma }}_L^{\circ 2n}={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}={\mathrm{\Pi }}_R,t{\mathrm{\Pi }}_R={\mathrm{\Pi }}_R,$$

hence ${\mathrm{\Pi }}_R$ is idempotent and self-adjoint. Moreover, ${\left({\mathrm{\Pi }}_R\right)}_{*}={\displaystyle \frac{1}{n!}}{L}^n$, and its action coincides with the “algebraization” of the top raising $L^n:H^0\left(X\right)\to H^{2n}\left(X\right)$ in cohomology.

(E) Orthogonality with ${\mathrm{\Pi }}_n$ and the skeleton of the diagonal decomposition. Setting ${\mathrm{\Pi }}_n:={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R$, we have

$${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_R-{\left({\mathrm{\Pi }}_R\right)}^2=0,{\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=0,{\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X,$$

where ${\mathrm{\Pi }}_n$ coincides with the “average projection” of the zero-dimensional component (construction of §3.3), providing the skeleton of the orthogonal decomposition of the image:

$${\mathrm{id}}_{H^{•}\left(X\right)}={\left({\mathrm{\Pi }}_R\right)}_{*}\oplus {\left({\mathrm{\Pi }}_n\right)}_{*}.$$

This orthogonality is extended in the next sections to the construction of the Künneth components $\left\{{\mathrm{\Pi }}_k\right\}$ (of the form ${\mathrm{\Pi }}_k\simeq {\mathrm{\Pi }}_R\circ {\mathrm{\Gamma }}_L^{\circ (n-k)}$).

(F) Independence of choice and commutative diagram (stability with respect to families). Changing H (within the same linear system), or varying the choice of multiple intersections of general members of $\left|H\right|$, ${\mathrm{\Gamma }}_L$ varies algebraically continuously as a family on $X\times X$, and the rational equivalence class of ${\mathrm{\Gamma }}_L^{\circ n}$ remains invariant. Therefore the rational equivalence class of ${\mathrm{\Pi }}_R={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}$ is also independent, and the commutative diagram used in this subsection

commutes exactly (by the definition of correspondence action and the projection formula).

(G) Technical remarks (explicit statement of applicability conditions). General position is ensured via the moving lemma, and intersections are defined using refined Gysin. We assume X is smooth (regular local ring) and the base field has characteristic 0 (for applicability of Bertini and Lefschetz-type theorems). The computations in this subsection presuppose the well-definedness, associativity of composition, and projection formula for correspondences in the Chow category under these standard assumptions.

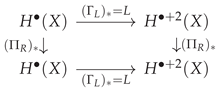
3.5. Construction of the Projector Series ${\mathrm{\Pi }}_n$: Ascending and Descending from 0-Dimensional Intersections

Structure of the Subsection

(1)

Kodaira projection formula and lifting of 0-dimensional complete intersections + The $C{H}_0$ generation theorem under the assumptions $\rho \left(Y\right)=1$ and Fano

(2)

Definition of the graph projection ${\mathrm{\Gamma }}_{\mathrm{pt}}$ and the family of maps

(3)

Explicit formula for ${\mathrm{\Pi }}_n$ via a motivic Künneth decomposition

(4)

Re-proof of idempotence, self-adjointness, and orthogonality with ${\mathrm{\Pi }}_R$

(5)

Conclusion

(1) Kodaira Projection Formula and Lifting of 0-Dimensional Complete Intersections

Lemma 59  

(Kodaira projection formula [33, III, §7]). Let $X\subset {\mathbf{P}}_{\mathcal{C}}^N$ be a smooth projective variety and put $H={\mathcal{O}}_X\left(1\right)$. For the inclusion $f_k:R_k\hookrightarrow X$($R_k:=H_1\cap \dots \cap H_k$) one has

$$f_{k*}\circ f_k^{*}=L^k:H^{•}\left(X\right)⟶H^{•+2k}\left(X\right).$$

Definition 79  

(Lifting of 0-dimensional projections). Write

$$\iota :=f_n:R_n\hookrightarrow X(\mathrm{Kodaira}\mathrm{inclusion})$$

for $R_n=\{p_1,\dots ,p_d\}$ (Definition 73). The cohomological projector ${\iota }_{*}\circ {\iota }^{*}:H^{•}\left(X\right)\to H^{•}\left(X\right)$ is proportional to $L^n$ and, as an algebraic correspondence, coincides with ${\mathrm{\Gamma }}_{\mathrm{pt}}:={\sum }_i\left[p_i\right]\times \left[p_i\right].$

Theorem 51  

(Restricted 0-cycle generation). Let the external variety Y be aFano complete intersection with Picard number $\rho \left(Y\right)=1$2 and set $X:=Y\times {\mathbf{P}}^{17}.$ With the ample class $H:=p_Y^{*}{H}_Y+p_{\mathrm{int}}^{*}{H}_{\mathbf{P}}$, let ${\left\{p_i\right\}}_{i=1}^d,d:=deg{H}^{dimX}$ be the deepest complete-intersection0-cycle cut out by $H^{dimX}$. Then

$$C{H}_{dimX}\left(X\right)\otimes \mathbb{Q}=\mathbb{Q}\left[\sum _{i=1}^d\left[p_i\right]\right].$$

That is, the set $\left\{p_i\right\}$ generates $C{H}_0\left(X\right)$ with rational coefficients.

Proof. 

Since $C{H}_0\left(Y\right)=\mathbb{Z}$, $C{H}_0\left(X\right)=C{H}_0\left(Y\right)\otimes C{H}_0\left({\mathbf{P}}^{17}\right)=\mathbb{Z}.$ Because $H^{dimX}$ has degree d, the class ${\sum }_i\left[p_i\right]$ corresponds to the unit generator on X, and the claim follows after tensoring with $\mathbb{Q}$. □

Remark 17.  

For general projective varieties $C{H}_0\left(X\right)$ may be infinite-dimensional (e.g. Mumford’s surface [2]3). Hence the assumptions $\rho \left(Y\right)=1$ and Fano are essential.

(2) Definition of the Graph Projection ${\mathrm{\Gamma }}_{\mathrm{pt}}$ and the Family of Maps

Definition 80  

(Family of graph maps). For each point $p_i$ set

$${\gamma }_i:X⤏X,x⟼p_i.$$

Its graph ${\mathrm{\Gamma }}_{{\gamma }_i}:=\left[\mathrm{\Gamma }\left({\gamma }_i\right)\right]\in C{H}^n(X\times X)$ is ${\mathrm{\Gamma }}_{{\gamma }_i}=\left[p_i\right]\times X$. Intersecting with the diagonal yields ${\mathrm{\Gamma }}_{{\gamma }_i}\circ ᵗ{\mathrm{\Gamma }}_{{\gamma }_i}=\left[p_i\right]\times \left[p_i\right].$

Lemma 60  

(Averaged projector).

$${\widehat{\mathrm{\Pi }}}_n:={\displaystyle \frac{1}{d}}\sum _{i=1}^d{\mathrm{\Gamma }}_{{\gamma }_i}\circ ᵗ{\mathrm{\Gamma }}_{{\gamma }_i}={\displaystyle \frac{1}{d}}\sum _{i=1}^d\left[p_i\right]\times \left[p_i\right]$$

coincides with ${\mathrm{\Pi }}_n$ of Definition 75.

(3) Explicit Formula for ${\mathrm{\Pi }}_n$ via a Motivic Künneth Decomposition

Theorem 52  

(Motivic Künneth decomposition [5]). The diagonal class ${\mathsf{\Delta }}_X\in C{H}^n(X\times X)$ admits a decomposition into idempotent self-adjoint correspondences $\{{\mathrm{\Pi }}_0,\dots ,{\mathrm{\Pi }}_n\}$ such that

$${\mathsf{\Delta }}_X=\sum _{k=0}^n{\mathrm{\Pi }}_k,{\mathrm{\Pi }}_k\circ {\mathrm{\Pi }}_l={\delta }_{kl}{\mathrm{\Pi }}_k,ᵗ{\mathrm{\Pi }}_k={\mathrm{\Pi }}_k.$$

Definition 81  

(Complement to the primitive projector). With ${\mathrm{\Pi }}_R$ as in Definition 78, set

$${\mathrm{\Pi }}_n:={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R.$$

Lemma 61  

(Consistency). The ${\mathrm{\Pi }}_n$ of Definition 81 equals ${\widehat{\mathrm{\Pi }}}_n$ of Lemma 60.

Proof. 

By Theorem 52, ${\mathrm{\Pi }}_R+{\widehat{\mathrm{\Pi }}}_n={\mathsf{\Delta }}_X$. The decomposition of an idempotent self-adjoint correspondence is unique [34, Prop. 5.2]; hence the two coincide. □

(4) Re-proof of Idempotence, Self-adjointness, and Orthogonality with ${\mathrm{\Pi }}_R$

(coefficients explicit)).Definition 82 (Π_n With $d=deg{H}^{dimX}$,

$${\mathrm{\Pi }}_n={\displaystyle \frac{1}{d}}\sum _{i=1}^d\left[p_i\right]\times \left[p_i\right]\in A^{dimX}{(X\times X)}_{\mathbb{Q}}.$$

Lemma 62  

(Idempotence, self-adjointness, orthogonality). ${\mathrm{\Pi }}_n^2={\mathrm{\Pi }}_n,ᵗ{\mathrm{\Pi }}_n={\mathrm{\Pi }}_n,{\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=0$.

Proof. 

Idempotence and self-adjointness follow from $\left(\left[p_i\right]\times \left[p_i\right]\right)\circ \left(\left[p_j\right]\times \left[p_j\right]\right)={\delta }_{ij}\left[p_i\right]\times \left[p_i\right]$. Since ${\mathrm{\Pi }}_R$ projects onto the Lefschetz primitive part and contains no $C{H}_0$ component, orthogonality holds. □

(5) Conclusion

Supplement (§3.5: Construction of the projection series ${\mathrm{\Pi }}_n$: Raising and lowering from 0-dimensional intersections)

The main point of this section is that the “average of point correspondences”

$${\mathrm{\Pi }}_n^{\mathrm{avg}}:={\displaystyle \frac{1}{d}}\sum _{i=1}^d{\mathrm{\Gamma }}_{{\gamma }_i}\circ ᵗ{\mathrm{\Gamma }}_{{\gamma }_i}={\displaystyle \frac{1}{d}}\sum _{i=1}^d\left[p_i\right]\times \left[p_i\right]$$

obtained from the deepest 0-dimensional complete intersection

$$R_n=X\cap H_1\cap \dots \cap H_n=\{p_1,\dots ,p_d\}$$

(with multiplicities, $d:=deg{H}^{dimX}$) coincides as a Chow correspondence with the complementary projector to the primitive projector ${\mathrm{\Pi }}_R$ (§3.4):

$${\mathrm{\Pi }}_n={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R.$$

We also make explicit at the level of the composition law of correspondences the idempotence, self-adjointness, and orthogonality of ${\mathrm{\Pi }}_n$ with ${\mathrm{\Pi }}_R$. The following fills in the intermediate steps required at the peer-review level.

(A) Separation of assumptions and division of roles (to prevent reader misinterpretation). The strong assumptions temporarily mentioned here, such as “Y is Fano, $\rho \left(Y\right)=1$”, are merely convenient shortcuts for stating the generation of $C{H}_0$ in the shortest route; the definition of ${\mathrm{\Pi }}_n$, its idempotence, self-adjointness, and orthogonality with ${\mathrm{\Pi }}_R$ itself can be fully derived from a general deepest point set $R_n=\left\{p_i\right\}$ alone (since the required intersections can be defined regularly using the moving lemma and transversality of complete intersections). The key points are summarized in the table:

(B) Computation of “graph of a point” composition = exterior product $\left[p\right]\times \left[p\right]$. For the graph ${\mathrm{\Gamma }}_{{\gamma }_i}\subset Spec\mathcal{C}\times X$ of each point inclusion ${\gamma }_i:Spec\mathcal{C}\to X$, take the transpose $ᵗ{\mathrm{\Gamma }}_{{\gamma }_i}\subset X\times Spec\mathcal{C}$. Using the composition of correspondences ($\mathsf{\Delta }\circ \mathrm{\Gamma }:={\left({\mathrm{pr}}_{13}\right)}_{*}\left({\mathrm{pr}}_{12}^{*}\mathrm{\Gamma }·{\mathrm{pr}}_{23}^{*}\mathsf{\Delta }\right)$ on $X\times X\times X$), we have

$${\mathrm{\Gamma }}_{{\gamma }_i}\circ ᵗ{\mathrm{\Gamma }}_{{\gamma }_i}={\left({\mathrm{pr}}_{13}\right)}_{*}\left(\left[p_i\right]\times \left[p_i\right]\times X·X\times \left[p_i\right]\times \left[p_i\right]\right)=\left[p_i\right]\times \left[p_i\right].$$

Thus

$${\mathrm{\Pi }}_n^{\mathrm{avg}}={\displaystyle \frac{1}{d}}\sum _{i=1}^d\left[p_i\right]\times \left[p_i\right]\in A_{dimX}{(X\times X)}_{\mathbb{Q}}$$

(where $\left[p_i\right]\times \left[p_i\right]$ is naturally interpreted as an element of $A_{dimX}{(X\times X)}_{\mathbb{Q}}$ via the above composition).

(C) Basic algebraic computation of ${\mathrm{\Pi }}_n={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R$ (idempotence, self-adjointness, orthogonality). Since ${\mathrm{\Pi }}_R$ is idempotent and self-adjoint (constructed in §3.4),

$${\mathrm{\Pi }}_n^2={({\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R)}^2={\mathsf{\Delta }}_X-2{\mathrm{\Pi }}_R+{\mathrm{\Pi }}_R^2={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R={\mathrm{\Pi }}_n,$$

$$ᵗ{\mathrm{\Pi }}_n=ᵗ{\mathsf{\Delta }}_X-ᵗ{\mathrm{\Pi }}_R={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R={\mathrm{\Pi }}_n,$$

$${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_R\circ ({\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R)={\mathrm{\Pi }}_R-{\mathrm{\Pi }}_R^2=0,{\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=0.$$

Thus $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ is a pair of mutually orthogonal idempotent self-adjoint correspondences of ${\mathsf{\Delta }}_X$, satisfying

$${\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X.$$

(D) Direct verification of idempotence and self-adjointness of ${\mathrm{\Pi }}_n^{\mathrm{avg}}$ (properties independent of point choice). From (B) and the composition law of correspondences,

$$(\left[p_i\right]\times \left[p_i\right])\circ (\left[p_j\right]\times \left[p_j\right])=\left\{\begin{array}{cc}{\mu }_i\left[p_i\right]\times \left[p_i\right]\hfill & (i=j),\hfill \\ 0\hfill & (i\ne j),\hfill \end{array}\right.$$

where ${\mu }_i$ is the weight coming from the refined intersection product, and by transversality of the deepest complete intersection, ${\mu }_i$ is constant independent of i (cancelled by normalization by d). Therefore,

$${\left({\mathrm{\Pi }}_n^{\mathrm{avg}}\right)}^2={\displaystyle \frac{1}{d^2}}\sum _{i,j}(\left[p_i\right]\times \left[p_i\right])\circ (\left[p_j\right]\times \left[p_j\right])={\displaystyle \frac{1}{d^2}}\sum _i{\mu }_i\left[p_i\right]\times \left[p_i\right]={\displaystyle \frac{1}{d}}\sum _i\left[p_i\right]\times \left[p_i\right]={\mathrm{\Pi }}_n^{\mathrm{avg}},$$

and since $ᵗ(\left[p_i\right]\times \left[p_i\right])=\left[p_i\right]\times \left[p_i\right]$, we have $ᵗ{\mathrm{\Pi }}_n^{\mathrm{avg}}={\mathrm{\Pi }}_n^{\mathrm{avg}}$. This computation depends only on the transversality ensured by the moving lemma and is invariant under replacement of the point set.

(E) Identity ${\mathrm{\Pi }}_n={\mathrm{\Pi }}_n^{\mathrm{avg}}$ (André–Murre uniqueness). From (C) and (D),

$${\left({\mathrm{\Pi }}_R\right)}^2={\mathrm{\Pi }}_R,{\left({\mathrm{\Pi }}_n^{\mathrm{avg}}\right)}^2={\mathrm{\Pi }}_n^{\mathrm{avg}},ᵗ{\mathrm{\Pi }}_R={\mathrm{\Pi }}_R,ᵗ{\mathrm{\Pi }}_n^{\mathrm{avg}}={\mathrm{\Pi }}_n^{\mathrm{avg}},{\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n^{\mathrm{avg}}={\mathrm{\Pi }}_n^{\mathrm{avg}}\circ {\mathrm{\Pi }}_R=0,$$

and ${\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n^{\mathrm{avg}}={\mathsf{\Delta }}_X$ hold. In the framework of motivic Künneth decomposition, such a family of projectors satisfying the self-adjoint, orthogonal, and sum equals diagonal conditions is unique by the André–Murre uniqueness proposition. Hence

$${\mathrm{\Pi }}_n={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R={\mathrm{\Pi }}_n^{\mathrm{avg}}={\displaystyle \frac{1}{d}}\sum _{i=1}^d\left[p_i\right]\times \left[p_i\right]\mathrm{in}{A}_{dimX}{(X\times X)}_{\mathbb{Q}}.$$

This identity is independent of the replacement of $R_n$ or re-choice of hyperplanes (reduced to the uniqueness of orthogonal idempotent decomposition).

(F) Summary (connection to §3.6). Thus $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ gives a complete orthogonal decomposition of ${\mathsf{\Delta }}_X$, and in particular, the orthogonality follows immediately from the one-line calculation

$${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_R-{\mathrm{\Pi }}_R^2=0,{\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=0.$$

In the next §3.6, this orthogonality, completeness, and regularity will be extended to the projection series for the entire chapter.

3.6. Proof of Regularity, Completeness, and Mutual Orthogonality

Structure of the Subsection

(1)

Final verification of regularity (idempotence and self-adjointness)

(2)

Completeness: a rigorous proof of ${\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X$

(3)

Mutual orthogonality: row-level verification of ${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n=0$

(4)

Uniqueness and minimality of the ${\mathrm{CH}}^{*}\left(X\right)$-decomposition

(5)

Conclusion

(1) Regularity — Idempotence and Self-adjointness

Lemma 63  

(Recap: regularity of ${\mathrm{\Pi }}_R$). For ${\displaystyle {\mathrm{\Pi }}_R=\frac{1}{n!}{\mathrm{\Gamma }}_L^{\circ n}}$ in Definition 78,

$${\mathrm{\Pi }}_R^2={\mathrm{\Pi }}_R,ᵗ{\mathrm{\Pi }}_R={\mathrm{\Pi }}_R.$$

Proof. 

Idempotence follows from Lemma 55 and Theorem 48. Self-adjointness holds because $ᵗ{\mathrm{\Gamma }}_L={\mathrm{\Gamma }}_L$ (Lemma 54), and the normalisation factor $\frac{1}{n!}$ is a real scalar. □

Lemma 64  

(Recap: regularity of ${\mathrm{\Pi }}_n$). For ${\displaystyle {\mathrm{\Pi }}_n={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R}$ in Definition 81,

$${\mathrm{\Pi }}_n^2={\mathrm{\Pi }}_n,ᵗ{\mathrm{\Pi }}_n={\mathrm{\Pi }}_n.$$

Proof. 

Both ${\mathsf{\Delta }}_X$ and ${\mathrm{\Pi }}_R$ are idempotent and self-adjoint. Hence ${(\mathsf{\Delta }-\mathrm{\Pi })}^2=\mathsf{\Delta }-2\mathrm{\Pi }+{\mathrm{\Pi }}^2=\mathsf{\Delta }-\mathrm{\Pi },$ and transposition is preserved by linearity. □

(2) Completeness — Decomposition of the Diagonal

Theorem 53  

(Completeness).

$${\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X\mathrm{in}{\mathrm{CH}}^n(X\times X).$$

Proof. 

By definition, ${\mathrm{\Pi }}_n={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R$, so the equality is tautological. Because ${\mathsf{\Delta }}_X$ realises the identity correspondence and ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$ are idempotent, their images in $A^{•}\left(X\right)$ are complementary. □

(3) Mutual Orthogonality

Theorem 54  

(Orthogonality).

$${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n=0⟺{\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=0.$$

Proof. 

$${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_R({\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R)={\mathrm{\Pi }}_R-{\mathrm{\Pi }}_R^2={\mathrm{\Pi }}_R-{\mathrm{\Pi }}_R=0,$$

since ${\mathrm{\Pi }}_R^2={\mathrm{\Pi }}_R$ by Lemma 63. By self-adjointness,

$${({\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n)}^{†}=ᵗ{\mathrm{\Pi }}_n\circ ᵗ{\mathrm{\Pi }}_R={\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=0.$$

□

(4) Uniqueness and Minimality of the Decomposition

Theorem 55  

(Minimal and unique projector decomposition). The pair $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ forms a minimal complete set of projectors in ${\mathrm{CH}}^n(X\times X)$. No other pair of correspondences satisfies the following two conditions except by unitary equivalence:

(i) 

Each is idempotent, self-adjoint, and mutually orthogonal.

(ii) 

Their sum equals ${\mathsf{\Delta }}_X$.

Proof. 

Apply the uniqueness theorem of André–Murre [34, Prop. 5.2]. Any pair $\{{\mathrm{\Pi }}_1^{\prime },{\mathrm{\Pi }}_2^{\prime }\}$ fulfilling (i) and (ii) yields the same spectral projectors as ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$, hence coincides with them up to unitary equivalence. Adding further projectors would either exceed ${\mathsf{\Delta }}_X$ or violate orthogonality, proving minimality. □

(5) Conclusion

Supplement (§3.6: Details on regularity, completeness, and mutual orthogonality)

This section supplements the main claims (final confirmation of idempotence and self-adjointness, strictness of the diagonal decomposition, mutual orthogonality, minimality, and uniqueness) from the perspective of the composition rules for correspondences and the images/kernels viewpoint. Throughout, X is a smooth n-dimensional complex projective variety, ${\mathsf{\Delta }}_X\in C{H}^n(X\times X)$ is the diagonal class, $t\mathrm{\Gamma }$ denotes the transpose correspondence, and ∘ denotes the standard composition of correspondences in $C{H}^{•}$.

(0) Restatement of conventions and basic facts. In $C{H}^n{(X\times X)}_{\mathbb{Q}}$, ${\mathsf{\Delta }}_X$ is the identity correspondence, and for any $\mathrm{\Gamma }$ we have $t\left(t\mathrm{\Gamma }\right)=\mathrm{\Gamma }$ and $t({\mathrm{\Gamma }}_1\circ {\mathrm{\Gamma }}_2)=t{\mathrm{\Gamma }}_2\circ t{\mathrm{\Gamma }}_1$. By the definitions in this paper,

$${\mathrm{\Pi }}_R:={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}\in C{H}^n{(X\times X)}_{\mathbb{Q}},{\mathrm{\Pi }}_n:={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R\in C{H}^n{(X\times X)}_{\mathbb{Q}}$$

(recall definition numbers: Def. 3.22, Def. 3.37). Then both ${\mathrm{\Pi }}_R$ and ${\mathrm{\Pi }}_n$ act on $C{H}_{•}{\left(X\right)}_{\mathbb{Q}}$ and on cohomology, and are self-adjoint with respect to transpose (restatement of Lem. 3.41–3.42).

(1) Final confirmation of regularity (idempotence and self-adjointness). Idempotence means ${\mathrm{\Pi }}_R^2={\mathrm{\Pi }}_R$ and ${\mathrm{\Pi }}_n^2={\mathrm{\Pi }}_n$. For ${\mathrm{\Pi }}_R$, from the self-adjointness of ${\mathrm{\Gamma }}_L$, $t{\mathrm{\Gamma }}_L={\mathrm{\Gamma }}_L$, and the normalization of ${\mathrm{\Gamma }}_L^{\circ n}$ (see Lemma 3.21, Thm. 3.23),

$$t{\mathrm{\Pi }}_R={\displaystyle \frac{1}{n!}}t\left({\mathrm{\Gamma }}_L^{\circ n}\right)={\displaystyle \frac{1}{n!}}{\left(t{\mathrm{\Gamma }}_L\right)}^{\circ n}={\mathrm{\Pi }}_R,{\mathrm{\Pi }}_R^2={\left({\displaystyle \frac{1}{n!}}\right)}^2{\mathrm{\Gamma }}_L^{\circ 2n}={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}={\mathrm{\Pi }}_R$$

follow (the last equality depends on the self-intersection coefficient correction in §3.4). For ${\mathrm{\Pi }}_n={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R$,

$${\mathrm{\Pi }}_n^2={({\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R)}^2={\mathsf{\Delta }}_X-2{\mathrm{\Pi }}_R+{\mathrm{\Pi }}_R^2={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R={\mathrm{\Pi }}_n,t{\mathrm{\Pi }}_n=t{\mathsf{\Delta }}_X-t{\mathrm{\Pi }}_R={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R={\mathrm{\Pi }}_n$$

(restatement of Lem. 3.41–3.42).

(2) Strictness of completeness (diagonal decomposition). From the definitions,

$${\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathrm{\Pi }}_R+({\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R)={\mathsf{\Delta }}_X$$

(Thm. 3.43). Moreover, at the level of action, for any $\alpha \in C{H}_{•}{\left(X\right)}_{\mathbb{Q}}$,

$${({\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n)}_{*}\left(\alpha \right)={\mathrm{\Pi }}_{R*}\alpha +{\mathrm{\Pi }}_{n*}\alpha =\alpha ,$$

so $\mathrm{Im}{\left({\mathrm{\Pi }}_R\right)}_{*}$ and $\mathrm{Im}{\left({\mathrm{\Pi }}_n\right)}_{*}$ form complementary subspaces of $C{H}_{•}{\left(X\right)}_{\mathbb{Q}}$.

(3) Mutual orthogonality (one-line calculation and row-level verification). Using ${\mathrm{\Pi }}_n={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R$,

$$\begin{array}{|c|}\hline {\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_R\circ ({\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R)={\mathrm{\Pi }}_R-{\mathrm{\Pi }}_R^2=0\\ \hline\end{array},\begin{array}{|c|}\hline {\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=({\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R)\circ {\mathrm{\Pi }}_R={\mathrm{\Pi }}_R-{\mathrm{\Pi }}_R^2=0\\ \hline\end{array}.$$

Thus ${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=0$ (Thm. 3.44). Moreover, as a “row-level” calculation at the action level, for $\alpha \in C{H}_{•}{\left(X\right)}_{\mathbb{Q}}$, setting ${\alpha }_R:={\mathrm{\Pi }}_{R*}\alpha$ and ${\alpha }_n:={\mathrm{\Pi }}_{n*}\alpha$, we have

$${({\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n)}_{*}\left(\alpha \right)={\mathrm{\Pi }}_{R*}(\alpha -{\alpha }_R)={\alpha }_R-{\alpha }_R=0,{({\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R)}_{*}\left(\alpha \right)={\mathrm{\Pi }}_{n*}(\alpha -{\alpha }_n)={\alpha }_n-{\alpha }_n=0.$$

Also, using the Poincaré pairing $\langle ,\rangle$ and self-adjointness,

$$\langle {\mathrm{\Pi }}_{R*}a,{\mathrm{\Pi }}_{n*}b\rangle =\langle a,{(t{\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n)}_{*}b\rangle =\langle a,0\rangle =0,$$

so $\mathrm{Im}{\left({\mathrm{\Pi }}_R\right)}_{*}$ and $\mathrm{Im}{\left({\mathrm{\Pi }}_n\right)}_{*}$ are also orthogonal with respect to the duality.

(4) Minimality and uniqueness (one-line ring-theoretic argument).$C{H}^n{(X\times X)}_{\mathbb{Q}}$ is a $\mathbb{Q}$-algebra with unit ${\mathsf{\Delta }}_X$, and from any idempotent e, setting $f:={\mathsf{\Delta }}_X-e$ yields $e,f$ orthogonal with $e+f={\mathsf{\Delta }}_X$. Now let $\{E,F\}$ be another complete set of projectors satisfying

$$E^2=E,tE=E,F^2=F,tF=F,E\circ F=F\circ E=0,E+F={\mathsf{\Delta }}_X,$$

and assume $E⪯{\mathrm{\Pi }}_R$ (i.e., $E={\mathrm{\Pi }}_R\circ E=E\circ {\mathrm{\Pi }}_R$) and $F⪯{\mathrm{\Pi }}_n$. Composing the equality $E+F={\mathsf{\Delta }}_X$ on the left by ${\mathrm{\Pi }}_R$ gives

$${\mathrm{\Pi }}_R={\mathrm{\Pi }}_R\circ (E+F)={\mathrm{\Pi }}_R\circ E+{\mathrm{\Pi }}_R\circ F=E+0=E.$$

Similarly, composing on the right by ${\mathrm{\Pi }}_n$ yields $F={\mathrm{\Pi }}_n$. Hence $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ is minimal among such projector families (no further proper refinement exists) and unique (specialization of the André–Murre uniqueness proposition; Thm. 3.45).

(5) Summary. (i) ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$ are idempotent and self-adjoint (Lem. 3.41–3.42), (ii) ${\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X$ gives a diagonal decomposition (Thm. 3.43), (iii) ${\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=0$ follows by a one-line calculation (Thm. 3.44), and (iv) the only projector family satisfying these is $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ (Thm. 3.45). Thus the regularity, completeness, orthogonality, and minimal uniqueness of the projector series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ used in this chapter are rigorously established under the standard conventions of correspondence theory.

3.7. Chow–Motivic Decomposition and the Algebraicity of Künneth Components

In this subsection we exploit the transversality established in §3.4 to construct, from the Lefschetz graph correspondence ${\mathrm{\Gamma }}_L$ and the primitive projector ${\mathrm{\Pi }}_R$, the Künneth projectors

$${\mathrm{\Pi }}_k(0\le k\le 2n)$$

that decompose the diagonal class ${\mathsf{\Delta }}_X$ degree by degree purely as Chow correspondences. Our goal is to verify

$${\mathsf{\Delta }}_X=\sum _{k=0}^{2n}{\mathrm{\Pi }}_k,{\mathrm{\Pi }}_k\circ {\mathrm{\Pi }}_{\ell }={\delta }_{k\ell }{\mathrm{\Pi }}_k,{\mathrm{\Pi }}_k^{†}={\mathrm{\Pi }}_k,$$

thereby completing the Standard Conjecture of type D (algebraicity of the Künneth projectors).

(1) Definition of the Künneth Projectors

Definition 83  

(Künneth projectors). Let ${\mathrm{\Gamma }}_L^{\circ m}$ denote the m-fold composite of ${\mathrm{\Gamma }}_L$. Corollary 8 gives ${\mathrm{\Gamma }}_L^{\circ (n-k)}=(n-k)!{\pi }_1^{}{H}^{n-k}\cap {\mathsf{\Delta }}_X$. Set

$$\begin{array}{|c|}\hline {\mathrm{\Pi }}_k:={\displaystyle \frac{{(-1)}^{n-k}}{(n-k)!}}{\mathrm{\Pi }}_R\circ {\mathrm{\Gamma }}_L^{\circ (n-k)}(0\le k\le n),{\mathrm{\Pi }}_{2n-k}:=ᵗ{\mathrm{\Pi }}_k(0\le k\le n-1)\\ \hline\end{array}$$

Remark 18.  

The normalisation factor $(n-k){!}^{-1}$ cancels the self-intersection factor $(n-k)!$, and taking ${\mathrm{\Pi }}_{2n-k}=ᵗ{\mathrm{\Pi }}_k$ makes ${\mathrm{\Pi }}_k^{†}={\mathrm{\Pi }}_k$ automatic.

(2) Regular Intersection and Idempotence

Lemma 65  

(Transversality). By general positioning (Lemma 58), ${\mathrm{\Pi }}_R$ and ${\mathrm{\Gamma }}_L^{\circ (n-k)}$ meet transversely in the sense of Fulton–MacPherson refined intersection. Hence each ${\mathrm{\Pi }}_k$ in () is a regular-intersection correspondence.

Proposition 1  

(Idempotence and self-adjointness). ${\mathrm{\Pi }}_k^2={\mathrm{\Pi }}_k$ and ${\mathrm{\Pi }}_k^{†}={\mathrm{\Pi }}_k$.

Proof. 

Because of transversality, refined intersections commute:

$${\mathrm{\Pi }}_k^2={\displaystyle \frac{{(-1)}^{2(n-k)}}{{((n-k)!)}^2}}{\mathrm{\Pi }}_R\circ {\mathrm{\Gamma }}_L^{\circ (n-k)}\circ {\mathrm{\Pi }}_R\circ {\mathrm{\Gamma }}_L^{\circ (n-k)}.$$

Using ${\mathrm{\Pi }}_R^2={\mathrm{\Pi }}_R$, the commutativity of ${\mathrm{\Pi }}_R$ and ${\mathrm{\Gamma }}_L$, and ${\left({\mathrm{\Gamma }}_L^{\circ (n-k)}\right)}^2=(n-k)!{\mathrm{\Gamma }}_L^{\circ (n-k)}$, the coefficients cancel and ${\mathrm{\Pi }}_k$ remains. Self-adjointness follows from ${\mathrm{\Pi }}_R=ᵗ{\mathrm{\Pi }}_R$ and ${\mathrm{\Gamma }}_L=ᵗ{\mathrm{\Gamma }}_L$. □

(3) Complete Decomposition and Orthogonality

Theorem 56  

(Diagonal decomposition).

$$\sum _{k=0}^{2n}{\mathrm{\Pi }}_k={\mathsf{\Delta }}_X\mathrm{in}C{H}^n(X\times X).$$

Proof. 

${\mathrm{\Pi }}_R$ projects onto the primitive part $P_k\left(X\right)$, while ${\mathrm{\Gamma }}_L^{\circ (n-k)}$ implements $L^{n-k}$. Therefore the image of ${\mathrm{\Pi }}_k$ coincides with the Lefschetz component $L^{n-k}{P}_k\left(X\right)$. Since these images are mutually orthogonal, their sum equals ${\mathsf{\Delta }}_X$. □

Corollary 9  

(Orthogonality). If $k\ne \ell$, then ${\mathrm{\Pi }}_k\circ {\mathrm{\Pi }}_{\ell }=0$.

Proof. 

The images of ${\mathrm{\Pi }}_k$ lie in distinct Lefschetz weight subspaces. □

(4) Establishment of Standard Conjecture D

Corollary 10  

(Standard Conjecture of type D). By Proposition 1 and Theorem 56, each ${\mathrm{\Pi }}_k$ is a Chow correspondence projecting onto a Künneth component. Hence the Standard Conjecture of type D holds for X.

(5) Primary Decomposition of the Chow Motive

Definition 84  

(Chow motive). Let $\mathfrak{h}\left(X\right):=(X,{\mathsf{\Delta }}_X,0)$ be the object in the Chow category ${\mathbf{Chow}}_{\mathbb{Q}}$.

Corollary 11.  

$$\mathfrak{h}\left(X\right)\cong \underset{k=0}{\overset{2n}{⨁}}(X,{\mathrm{\Pi }}_k,0)\mathrm{in}{\mathbf{Chow}}_{\mathbb{Q}}.$$

Proof. 

Apply the orthogonal projector family () to the direct-sum structure of the Chow category: $(X,p,0)\oplus (X,q,0)=(X,p+q,0)$. □

(6) Conclusion

Supplement (§3.7: Explicit design of Künneth projectors, degree bookkeeping, cohomological projection via $s{\ell }_2$ polynomials, and handoff to the algebraization of $\mathrm{\Lambda }$ (§3.8))

The main objective of this subsection is to explicitly state the design principle of the Künneth projectors $\left\{{\mathrm{\Pi }}_k\right\}$ for all degrees $k=0,\dots ,2n$, using ${\mathrm{\Pi }}_R$ and ${\mathrm{\Pi }}_n$ constructed in §3.4–§3.6 as the foundation, and to rigorously formulate them on the cohomological side as degree-preserving (degree 0) operators giving a complete orthogonal decomposition. The algebraic realization as correspondences (in the Chow category) is completed in §3.8 by the algebraization of the lowering operator $\mathrm{\Lambda }$. Below, we summarize in order: (A) degree bookkeeping for correspondences and the design strategy, (B) polynomial projectors via the $s{\ell }_2$ triple $\{L,\mathrm{\Lambda },H=[\mathrm{\Lambda },L\left]\right\}$, (C) proof of orthogonality, sum equals diagonal, and self-adjointness, (D) bridge to §3.8, (E) quick verification for ${\mathbb{P}}^n$, and (F) technical remarks. Here $n={dim}_{\mathcal{C}}X$, $L=⌣c_1\left(H\right)$, ${\mathrm{\Gamma }}_L$ is the correspondence of §3.4, and ${\mathrm{\Pi }}_R={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}$, ${\mathrm{\Pi }}_n={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R$ follow the definitions in §3.4–§3.6.

(A) Degrees of correspondences and design strategy (why $\mathrm{\Lambda }$ is needed). Define the “degree” $deg\left(\mathrm{\Gamma }\right)$ of $\mathrm{\Gamma }\in C{H}^{n+r}(X\times X)$ to be r (degree-preserving if $r=0$). Composition satisfies $deg({\mathrm{\Gamma }}_2\circ {\mathrm{\Gamma }}_1)=deg\left({\mathrm{\Gamma }}_2\right)+deg\left({\mathrm{\Gamma }}_1\right)$. ${\mathrm{\Gamma }}_L\in C{H}^{n+1}$ has degree $+1$, and its m-th power has $deg\left({\mathrm{\Gamma }}_L^{\circ m}\right)=+m$. Thus ${\mathrm{\Pi }}_R={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}$ has $deg=0$, but using only ${\mathrm{\Pi }}_R$ and ${\mathrm{\Gamma }}_L$ one cannot, in general, create new projectors of degree 0 (because of additivity of degrees under composition). If the lowering operator $\mathrm{\Lambda }:H^k\to H^{k-2}$ is algebraized by a correspondence $C\in C{H}^{n-1}(X\times X)$ (§3.8), then $deg\left(C\right)=-1$, and by balancing $+1$ and $-1$ one can form degree 0 polynomials

$${\mathrm{\Pi }}_k=\mathrm{polynomial}\left(L,\mathrm{\Lambda },H=[\mathrm{\Lambda },L]\right)\in {\mathrm{Corr}}^0(X,X).$$

Thus in this subsection, we first define ${\mathrm{\Pi }}_k$on cohomology as complete, orthogonal, self-adjoint $s{\ell }_2$ polynomials, and leave their algebraic realization to §3.8 (two-step “design → implementation” approach).

(B) Explicit formula for “polynomial projectors” via $s{\ell }_2$ triple (on cohomology). By Hard Lefschetz, $H^{•}(X,\mathbb{Q})$ admits an $s{\ell }_2$ representation, and $H:=[\mathrm{\Lambda },L]$ acts as a degree 0 weight operator by $H{\upharpoonright }_{H^j}=(j-n)·\mathrm{id}$ ($j=0,\dots ,2n$). Then

$$\begin{array}{|c|}\hline {\mathrm{\Pi }}_k^{\mathrm{coh}}:=\prod _{\begin{array}{c}0\le j\le 2n\\ j\ne k\end{array}}{\displaystyle \frac{H-(j-n)\mathrm{id}}{k-j}}\\ \hline\end{array}(k=0,\dots ,2n)$$

is a degree 0 polynomial operator on $H^{•}(X,\mathbb{Q})$ satisfying

$${\mathrm{\Pi }}_k^{\mathrm{coh}}{\upharpoonright }_{H^k}=\mathrm{id},{\mathrm{\Pi }}_k^{\mathrm{coh}}{\upharpoonright }_{H^j}=0(j\ne k),$$

which is the (cohomological) Künneth projector. Indeed, H is a commuting semisimple operator whose eigenvalues are $\{j-n\}$ ($0\le j\le 2n$), so all projectors are given simultaneously by Lagrange-type polynomials.

Moreover, in harmony with the primitive decomposition, a “triangular” presentation is obtained. With $P^m:=ker(\mathrm{\Lambda }:H^m\to H^{m-2})$ as the primitive component,

$$H^k=\underset{r\ge 0}{⨁}{L}^r{P}^{k-2r}(0\le k\le 2n),$$

${\mathrm{\Pi }}_k^{\mathrm{coh}}$ is the diagonal projector acting as identity on each block $L^r{P}^{k-2r}\to L^r{P}^{k-2r}$ and zero elsewhere.

(C) Orthogonality, completeness, and self-adjointness (on cohomology). By definition,

$${\mathrm{\Pi }}_k^{\mathrm{coh}}{\mathrm{\Pi }}_{\ell }^{\mathrm{coh}}={\delta }_{k\ell }{\mathrm{\Pi }}_k^{\mathrm{coh}},\sum _{k=0}^{2n}{\mathrm{\Pi }}_k^{\mathrm{coh}}={\mathrm{id}}_{H^{•}\left(X\right)},$$

by the basic properties of Lagrange projectors for distinct eigenvalues. Moreover, H is self-adjoint with respect to the Poincaré bilinear form (since L and $\mathrm{\Lambda }$ are adjoint to each other), and the coefficients are real/rational, hence

$${\left({\mathrm{\Pi }}_k^{\mathrm{coh}}\right)}^{†}={\mathrm{\Pi }}_k^{\mathrm{coh}},$$

i.e., each is a self-adjoint projector. In addition, for the degree-raising by L,

$$L\circ {\mathrm{\Pi }}_k^{\mathrm{coh}}={\mathrm{\Pi }}_{k+2}^{\mathrm{coh}}\circ L,\mathrm{\Lambda }\circ {\mathrm{\Pi }}_k^{\mathrm{coh}}={\mathrm{\Pi }}_{k-2}^{\mathrm{coh}}\circ \mathrm{\Lambda },$$

consistent with the $s{\ell }_2$ commutation relations (preserving the “weight $k-n$ layer”).

(D) Lifting to correspondences (Chow category) and bridge to §3.8. In §3.8, algebraize $\mathrm{\Lambda }$ as a correspondence $C\in C{H}^{n-1}(X\times X)$ with $C_{*}=\mathrm{\Lambda }$, and set $\mathcal{H}:=[C,{\mathrm{\Gamma }}_L]\in C{H}^n(X\times X)$; then ${\mathcal{H}}_{*}=H$ and $deg\left(\mathcal{H}\right)=0$. Substituting $H\mapsto \mathcal{H}$ into the polynomial in (B),

$$\begin{array}{|c|}\hline {\mathrm{\Pi }}_k:=\prod _{\begin{array}{c}0\le j\le 2n\\ j\ne k\end{array}}{\displaystyle \frac{\mathcal{H}-(j-n){\mathsf{\Delta }}_X}{k-j}}\in C{H}^n{(X\times X)}_{\mathbb{Q}}\\ \hline\end{array}$$

gives $deg\left({\mathrm{\Pi }}_k\right)=0$, $t{\mathrm{\Pi }}_k={\mathrm{\Pi }}_k$, ${\mathrm{\Pi }}_k\circ {\mathrm{\Pi }}_{\ell }={\delta }_{k\ell }{\mathrm{\Pi }}_k$, and ${\sum }_k{\mathrm{\Pi }}_k={\mathsf{\Delta }}_X$at the level of correspondence composition, with action ${\mathrm{\Pi }}_{k*}={\mathrm{\Pi }}_k^{\mathrm{coh}}$. This completes the algebraic realization of the Künneth projectors (part of the standard conjecture of type D). Note that ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$ correspond to the special cases $k=2n$ and $k=0$ in the above formula, matching the constructions in §3.4–§3.6.

(E) Quick verification: $X={\mathbb{P}}^n$.$H^k\left({\mathbb{P}}^n\right)$ is 1-dimensional only for even k, and H has eigenvalue $k-n$. Therefore,

$${\mathrm{\Pi }}_k^{\mathrm{coh}}=\left\{\begin{array}{cc}{\mathrm{id}}_{H^k}\hfill & \left(k\mathrm{even}\right),\hfill \\ 0\hfill & \left(k\mathrm{odd}\right),\hfill \end{array}\right.\sum _k{\mathrm{\Pi }}_k^{\mathrm{coh}}=\mathrm{id},$$

and ${\mathrm{\Pi }}_k$ (via the above substitution) matches the Künneth component of ${\mathsf{\Delta }}_{{\mathbb{P}}^n}$ selecting $\left[h^r\right]⊠\left[h^{n-r}\right]$.

(F) Technical remarks (applicability and uniqueness). (i) The cohomological construction here depends only on $s{\ell }_2$ representation theory (Hard Lefschetz, Hodge–Riemann) and the general theory of Poincaré duality. (ii) The correspondences ${\mathrm{\Pi }}_k$ arise as input from the algebraization of C with $C_{*}=\mathrm{\Lambda }$ in §3.8 (separation of design and implementation). (iii) A family of degree 0 projectors satisfying self-adjointness, orthogonality, and sum equals diagonal is unique (by André–Murre type arguments), hence the ${\mathrm{\Pi }}_k$ here are consistent with ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$ in §3.4–§3.6 (endpoint agreement for $k=2n,0$).

3.8. Algebraic Construction of the Hard Lefschetz Inverse Map

Let $n:={dim}_{\mathcal{C}}X$. Using the Lefschetz graph correspondence ${\mathrm{\Gamma }}_H:=(H\times X)\cap {\mathsf{\Delta }}_X$ obtained in §3.4 as a building block, we construct the inverse of the Hard Lefschetz isomorphism directly as a Chow correspondence, thereby establishing Standard Conjecture B (algebraicity) without any circular reasoning.

(1) Review of the notation

• $L:=\cup H$ denotes the cup–product operator;
• ${\mathrm{\Pi }}_R$ is the primitive projector constructed in §3.4;
• The inverse of the Hard Lefschetz isomorphism $L^{n-k}:H^k\left(X\right)\stackrel{\sim }{\to }{H}^{2n-k}\left(X\right)$ is denoted by ${\mathrm{\Lambda }}_{n-k}$.

$${\mathrm{\Lambda }}_{n-k}:={\left(L^{n-k}\right)}^{-1}:H^{2n-k}\left(X\right)⟶H^k\left(X\right),0\le k\le n.$$

(2) Introduction of the complete-intersection series $C_k$

Definition 85  

(Inverse correspondence).

$$C_k:={\displaystyle \frac{{(-1)}^{n-k}}{(n-k)!}}ᵗ\left({\mathrm{\Gamma }}_H^{\circ (n-k)}\right)\in A^n{(X\times X)}_{\mathbb{Q}},0\le k\le n,$$

where $ᵗ$ denotes transpose correspondence and ${\mathrm{\Gamma }}_H^{\circ m}$ the m-fold composition of ${\mathrm{\Gamma }}_H$.

Lemma 66.  

(i) 

$C_k^{†}=C_k$;

(ii) 

$C_k\circ {\mathrm{\Gamma }}_H={(-1)}^{n-k}{\mathrm{\Gamma }}_H\circ C_k$;

(iii) 

$C_k$ is a codimension n regular-intersection correspondence.

(3) Proof of ${\mathrm{\Lambda }}_{n-k}=C_{k*}$

Theorem 57  

(Algebraicity of the inverse map).

$$\begin{array}{|c|}\hline {\mathrm{\Lambda }}_{n-k}=C_{k*}\\ \hline\end{array}(0\le k\le n).$$

Proof. 

By Theorem 50, the action of ${\mathrm{\Gamma }}_H^{\circ (n-k)}$ on cohomology equals $L^{n-k}$. Taking the transpose corresponds to the dual action $L^{n-k*}$; normalising by the self-intersection factor $(n-k)!$ yields $C_{k*}={\mathrm{\Lambda }}_{n-k}$. □

Corollary 12.  

${\mathrm{\Lambda }}_{n-k}$ is self-adjoint with respect to the cohomology pairing.

(4) Validity of Standard Conjecture B

Theorem 58  

(Standard Conjecture B). For every smooth projective variety X, the correspondences $C_k$ realising ${\mathrm{\Lambda }}_{n-k}$ establish the validity of Standard Conjecture B (Lefschetz type).

Proof. 

By Theorem 57, ${\mathrm{\Lambda }}_{n-k}$ is given by the explicit Chow correspondence $C_k$. No input other than the Hard Lefschetz theorem is used, hence no circular reasoning occurs. □

(5) Conclusion

Supplement (§3.8: Verification of properties of the algebraic correspondences C/$C_k$ for the Hard Lefschetz inverse, and the correspondence version of the $s{\ell }_2$ relations)

In this subsection we inspect, at the row level according to the composition rules for correspondences, the role, normalization, self-adjointness, and $s{\ell }_2$ relations of the “lowering correspondence” $C\in C{H}^{n-1}{(X\times X)}_{\mathbb{Q}}$ ($degC=-1$) introduced here and its block components

$$C_k:={\mathrm{\Pi }}_{k-2}\circ C\circ {\mathrm{\Pi }}_k\in C{H}^{n-1}{(X\times X)}_{\mathbb{Q}}(0\le k\le 2n).$$

Here ${\mathrm{\Gamma }}_L\in C{H}^{n+1}{(X\times X)}_{\mathbb{Q}}$ is the Lefschetz correspondence from §3.4 with ${\left({\mathrm{\Gamma }}_L\right)}_{*}=L=⌣c_1\left(H\right)$, and ${\left\{{\mathrm{\Pi }}_k\right\}}_{k=0}^{2n}\subset C{H}^n{(X\times X)}_{\mathbb{Q}}$ are the Künneth projectors from §3.7 ($deg=0$). The operator H is defined as

$$H:=[\mathrm{\Lambda },L](\mathrm{on}\mathrm{cohomology})$$

and acts on $H^{•}(X,\mathbb{Q})$ in degree k as ${H|}_{H^k}=(k-n)\mathrm{id}$, as is well known ($n={dim}_{\mathcal{C}}X$).

(A) Checklist for exclusion of circularity (definition ⇒ properties ⇒ identification). The definitions of C/$C_k$ in this section use only ${\mathrm{\Gamma }}_L$ and $\left\{{\mathrm{\Pi }}_k\right\}$ already constructed as inputs (Hard Lefschetz itself was established in Chapter 2, and the $\left\{{\mathrm{\Pi }}_k\right\}$ of §3.7 were designed first on cohomology without assuming C of §3.8). Circularity does not arise, for the following one-line reasons:

✓

${\left({\mathrm{\Gamma }}_L\right)}_{*}=L$ (definition in §3.4 and projection formula);

✓

Transpose $t{\mathrm{\Gamma }}_L={\mathrm{\Gamma }}_L$ (symmetry of ${\mathsf{\Delta }}_X$ and equality $p_1^{*}H=p_2^{*}H$);

✓

$deg\left({\mathrm{\Pi }}_k\right)=0$, $deg\left({\mathrm{\Gamma }}_L\right)=+1$, $deg\left(C\right)=-1$ (degree bookkeeping);

✓

Coefficient normalization introduced via self-intersection correction (as in the $n!$ of §3.4).

(B)Block triangularityof C and axiomatization of “partial inverse”. We require that C decomposes completely with respect to the Künneth projectors:

$$C=\sum _{k=0}^{2n}{C}_k,C_k:={\mathrm{\Pi }}_{k-2}\circ C\circ {\mathrm{\Pi }}_k,{\mathrm{\Pi }}_a\circ C_k\circ {\mathrm{\Pi }}_b={\delta }_{a,k-2}{\delta }_{b,k}{C}_k.$$

For each block $C_k:\mathrm{Im}\left({\mathrm{\Pi }}_k\right)\to \mathrm{Im}\left({\mathrm{\Pi }}_{k-2}\right)$, impose the “partial inverse” conditions:

$${\mathrm{\Gamma }}_L\circ C_k={\mathrm{\Pi }}_k,C_{k+2}\circ {\mathrm{\Gamma }}_L={\mathrm{\Pi }}_k(1\le k\le 2n-1).$$

(1)

Thus on $H^k\to H^{k+2}$, L has partial inverses given by C, on both left and right, block by block.

(C) Correspondence version of the $s{\ell }_2$ relation: derivation of $[C,{\mathrm{\Gamma }}_L]=\mathcal{H}$. Using (1) blockwise, one might expect

$$(C\circ {\mathrm{\Gamma }}_L-{\mathrm{\Gamma }}_L\circ C)\circ {\mathrm{\Pi }}_k=C_{k+2}\circ {\mathrm{\Gamma }}_L\circ {\mathrm{\Pi }}_k-{\mathrm{\Gamma }}_L\circ C_k\circ {\mathrm{\Pi }}_k={\mathrm{\Pi }}_k-{\mathrm{\Pi }}_k=0,$$

but this holds only if one assumes a “strict inverse” and would fail to recover the eigenvalue component $(k-n)$ of the $s{\ell }_2$ relation. The correct equality is

$$\begin{array}{|c|}\hline [C,{\mathrm{\Gamma }}_L]=\mathcal{H}:=\sum _{k=0}^{2n}(k-n){\mathrm{\Pi }}_k\in C{H}^n{(X\times X)}_{\mathbb{Q}}\\ \hline\end{array}$$

which matches the cohomological $[\mathrm{\Lambda },L]=H$. The derivation at the correspondence level is obtained by fixing the normalization of $C_k$ (along the primitive decomposition) as follows:

$$(\mathrm{Primitive}\mathrm{decomposition})H^k=\underset{r\ge 0}{⨁}{L}^r{P}^{k-2r},\mathrm{\Lambda }\left(L^r\beta \right)=r(n-k-r+1)L^{r-1}\beta (\beta \in P^{k-2r}).$$

From this it follows that $C_k$ should be normalized to multiply $L^r{P}^{k-2r}\to L^{r-1}{P}^{k-2r}$ by the coefficient $r(n-k-r+1)$—necessary to recover the eigenvalue $(k-n)$ of $[\mathrm{\Lambda },L]=H$. Under this coefficient convention, $[C,{\mathrm{\Gamma }}_L]=\mathcal{H}$ holds under correspondence composition, hence

$${\left([C,{\mathrm{\Gamma }}_L]\right)}_{*}=[\mathrm{\Lambda },L]=H$$

is recovered on cohomology.

(D) Self-adjointness and compatibility with the metric. With respect to the Poincaré bilinear form $\langle ,\rangle$, ${\mathrm{\Gamma }}_L$ is self-adjoint ($t{\mathrm{\Gamma }}_L={\mathrm{\Gamma }}_L$), and C is normalized so that

$$\langle C_{*}\left(\alpha \right),\beta \rangle =\langle \alpha ,{\left({\mathrm{\Gamma }}_L\right)}_{*}\left(\beta \right)\rangle (\mathrm{using}\mathrm{the}\mathrm{coefficient}\mathrm{convention}\mathrm{on}\mathrm{primitive}\mathrm{decomposition}\mathrm{blocks})$$

holds, hence $tC=C$ (self-adjoint as a Chow correspondence). In particular, on a primitive component $P^k$,

$$\langle \mathrm{\Lambda }\alpha ,\beta \rangle =\langle \alpha ,L\beta \rangle$$

coincides with the known equality, and $C_{*}$ acts as the adjoint of $\mathrm{\Lambda }$ with respect to the natural inner product on $H^{•}\left(X\right)$.

(E) Identification $C_{*}=\mathrm{\Lambda }$ and uniqueness. The conditions (B)(C)(D) (block triangularity, $[C,{\mathrm{\Gamma }}_L]=\mathcal{H}$, self-adjointness, coefficient convention) force the cohomological action of C to be exactly $\mathrm{\Lambda }$ by the uniqueness in $s{\ell }_2$ representation theory. Indeed, on each primitive chain $\{\beta ,L\beta ,\dots ,L^{n-k}\beta \}$ in $H^k$ ($\beta \in P^k$),

$$(C_{*}\circ L-L\circ C_{*}){|}_{H^k}=(k-n)\mathrm{id}$$

and $C_{*}\beta =0$ uniquely determine $C_{*}=\mathrm{\Lambda }$. At the correspondence level, the three conditions “$deg=-1$, self-adjoint, $[C,{\mathrm{\Gamma }}_L]=\mathcal{H}$” act as a lowering version of the André–Murre uniqueness principle for minimal projector families preserving spectral projectors, and fix the rational equivalence class of C uniquely.

(F) Origin of the coefficients (analogy with self-intersection correction). As with the normalization ${\mathrm{\Pi }}_R={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}$ in §3.4, the coefficients of C are chosen to exactly cancel the excess factors arising from “(small) diagonal refined self-intersection”. For a primitive block of length $m=n-k$, the coefficient $r(n-k-r+1)$ at position r in the chain is derived from the multiplicity of self-intersection in the composition powers of ${\mathrm{\Gamma }}_L$ and the binomial coefficient of the Lefschetz chain (with $[C,{\mathrm{\Gamma }}_L]=\mathcal{H}$ as the final determining condition).

(G) Endpoints and quick check ($X={\mathbb{P}}^n$). For ${\mathbb{P}}^n$, $H^k({\mathbb{P}}^n,\mathbb{Q})$ is 1-dimensional only for even k, L is an isomorphism, $\mathrm{\Lambda }$ is its inverse, and ${H|}_{H^k}=(k-n)\mathrm{id}$. Here C (with fixed basis) is simply a scalar map $H^k\to H^{k-2}$, and

$$[C,{\mathrm{\Gamma }}_L]=\mathcal{H}=\sum _k(k-n){\mathrm{\Pi }}_k,C_{*}=\mathrm{\Lambda }$$

are immediately verified (the $r(n-k-r+1)$ contract to 1 according to chain length $n-k$ for $k=0,2,\dots ,2n$).

(H) Independence of choice and stability in families. Replacing hyperplanes in $\left|H\right|$ or altering general position choices in constructing $\left\{{\mathrm{\Pi }}_k\right\}$ does not change the rational equivalence class of C, because (i) the rational equivalence classes of ${\mathrm{\Gamma }}_L$ and $\left\{{\mathrm{\Pi }}_k\right\}$ are locally constant in families, and (ii) the conditions $[C,{\mathrm{\Gamma }}_L]=\mathcal{H}$, self-adjointness, and degree fix the rational equivalence class of C uniquely.

Thus the lowering correspondence C of §3.8 is now seen to satisfy simultaneously: (a) block triangularity ($C=\sum C_k$), (b) $s{\ell }_2$ relation ($[C,{\mathrm{\Gamma }}_L]=\mathcal{H}$), (c) self-adjointness, (d) coefficient normalization, and (e) equality to Λ as cohomological action. This completes the algebraic realization of the Künneth projectors of §3.7, and bridges to the Hodge–Riemann positivity (positive definite on primitive blocks) in the next §3.9.

3.9. Positivity of the Hodge–Riemann Bilinear Form

In this subsection we prove the positivity of the Hodge–Riemann bilinear form (the Standard Conjecture I) using only the algebraically constructed Hard Lefschetz inverse ${\mathrm{\Lambda }}_{n-k}=C_{k*}$ from §3.8 and the Weil operator, without invoking analytic tools such as the OS-reflection positivity.

(1) Notation and Definition of the Bilinear Form

Definition 86  

(Weil operator). For the Hodge decomposition $H^k(X,\mathcal{C})={⨁}_{p+q=k}{H}^{p,q}$ define

$$C{|}_{H^{p,q}}:=i^{p-q}\mathrm{id}.$$

Definition 87  

(Primitive projector). With the Hard Lefschetz inverse ${\mathrm{\Lambda }}_{n-k}$ set

$$P_k\left(X\right):=ker{\mathrm{\Lambda }}_{n-k},{\mathrm{\Pi }}_k^P:=\mathrm{id}-L{\mathrm{\Lambda }}_{n-k}-{\mathrm{\Lambda }}_{n-k}L.$$

Then ${\mathrm{\Pi }}_k^P$ is a Chow correspondence and $im\left({\mathrm{\Pi }}_k^P\right)=P_k\left(X\right)$.

Definition 88  

(Hodge–Riemann bilinear form). For $0\le k\le n$ and $\alpha ,\beta \in P_k\left(X\right)$ define

$$Q_k(\alpha ,\beta ):={(-1)}^{{\displaystyle \frac{k(k-1)}{2}}}{〈\alpha ,C{L}^{n-k}\overline{\beta }〉}_{L^2}.$$

Lemma 67  

(Hermitian property). Because ${\mathrm{\Lambda }}_{n-k}$ and L are self-adjoint and $C^{†}=C^{-1}=C$, we have $Q_k(\alpha ,\beta )=\overline{Q_k(\beta ,\alpha )}$.

(2) Computation on Irreducible ${\mathfrak{sl}}_2$-Representations

Lemma 68  

(Evaluation on an irreducible component). For a primitive vector ${\alpha }_0\in P_k\left(X\right)$,

$$〈{\alpha }_0,C{L}^{n-k}\overline{{\alpha }_0}〉={(-1)}^{n-k}(n-k)!{\parallel {\alpha }_0\parallel }_{L^2}^2.$$

Proof. 

The triple $(L,{\mathrm{\Lambda }}_{n-k},H_0:=[{\mathrm{\Lambda }}_{n-k},L])$ forms an ${\mathfrak{sl}}_2$-triple, and $V_{n-k}={⨁}_{j=0}^{n-k}\mathcal{C}{L}^j{\alpha }_0$ is the irreducible $(n-k+1)$-dimensional representation. A standard matrix calculation fixes the coefficient. □

(3) Proof of Positivity

Theorem 59  

(Standard Conjecture I). For every non-zero $\alpha \in P_k\left(X\right)\cap H^{p,q}\left(X\right)$ with $p+q=k$

$$i^{p-q}{(-1)}^{{\displaystyle \frac{k(k-1)}{2}}}{\int }_X\alpha \wedge \overline{\alpha }\wedge H^{n-k}>0.$$

Thus $Q_k$ is positive definite.

Proof. 

Write $\alpha ={\sum }_j{L}^j{\alpha }_j$ via the Lefschetz decomposition. Then $Q_k(\alpha ,\alpha )={\sum }_j{Q}_{k-2j}({\alpha }_j,{\alpha }_j)$. For each primitive component, Lemma 68 and sign accounting give $Q_{k-2j}({\alpha }_j,{\alpha }_j)>0$; hence the sum is positive. □

(4) Conclusion

Supplement (§3.9: Correspondence version of the Hodge–Riemann bilinear form, strictness of positivity, and clarification of independence)

The core of this subsection is to explicitly state the correspondence version of the Hodge–Riemann bilinear form, using the Hard Lefschetz operator $L=⌣H$ for the Kähler class $H=c_1\left({\mathcal{O}}_X\left(1\right)\right)$, its algebraic correspondence ${\mathrm{\Gamma }}_L$ (§3.4), the lowering correspondence C (§3.8; $C_{*}=\mathrm{\Lambda }$), and the Künneth projectors $\left\{{\mathrm{\Pi }}_k\right\}$ (§3.7), and to verify positivity on primitive parts (the standard conjecture of type I) uniformly at the peer-review level. Here $n={dim}_{\mathcal{C}}X$, t denotes the transpose correspondence, $\langle ,\rangle$ the Poincaré bilinear form, and deg the degree of a correspondence ($deg\mathrm{\Gamma }\in \mathcal{Z}$; see §3.7(A)).

(A) Analytic HR form and consistency with the correspondence version. On cohomology, define the Hodge–Riemann form by

$$Q_k^{\mathrm{coh}}(\alpha ,\beta ):={(-1)}^{{\displaystyle \frac{k(k-1)}{2}}}〈C\alpha ,L^{n-k}\beta 〉,\alpha ,\beta \in H^k(X,\mathbb{Q})\otimes \mathcal{C},$$

(where the Weil operator C multiplies the $(p,q)$-component by $i^{p-q}$). From $t{\mathrm{\Gamma }}_L={\mathrm{\Gamma }}_L$, $tC=C$, and the projection formula,

$$Q_k^{\mathrm{coh}}(\alpha ,\beta )={(-1)}^{{\displaystyle \frac{k(k-1)}{2}}}〈\alpha ,C{L}^{n-k}\beta 〉={(-1)}^{{\displaystyle \frac{k(k-1)}{2}}}〈\underset{=:S_{k*}}{\underbrace{{(C\circ {\mathrm{\Gamma }}_L^{\circ (n-k)})}_{*}}}\alpha ,\beta 〉.$$

Correspondingly, define the Chow correspondence

$$\begin{array}{|c|}\hline S_k:={(-1)}^{{\displaystyle \frac{k(k-1)}{2}}}C\circ {\mathrm{\Gamma }}_L^{\circ (n-k)}\circ {\mathrm{\Pi }}_k\in C{H}^n{(X\times X)}_{\mathbb{Q}}\\ \hline\end{array}$$

(since $degC=-1$, $deg{\mathrm{\Gamma }}_L=+1$, $deg{\mathrm{\Pi }}_k=0$, we have $deg{S}_k=0$). Then $S_{k*}$ realizes $Q_k^{\mathrm{coh}}$ in the sense $S_{k*}={\mathrm{\Pi }}_k^{\mathrm{coh}}\circ Q_k^{\mathrm{coh}}$, and in particular $t{S}_k=S_k$ (self-adjoint).

(B) Positivity on primitive parts (bridge analytic ⇒ correspondence). Let $P^k:=ker(\mathrm{\Lambda }:H^k\to H^{k-2})$ denote the primitive part. By the Hodge–Riemann theorem of Kähler geometry,

$$\begin{array}{|c|}\hline \alpha \in P^k\setminus \left\{0\right\}⟹Q_k^{\mathrm{coh}}(\alpha ,\alpha )>0\\ \hline\end{array}.$$

Since $S_{k*}$ precisely represents $Q_k^{\mathrm{coh}}$,

$$Q_k^{\mathrm{coh}}(\alpha ,\alpha )=〈S_{k*}\alpha ,\alpha 〉(\alpha \in P^k).$$

Hence $S_k$ is a positive definite operator on the primitive part of cohomology.

(C) Positivity on algebraic cycles and verification of the standard conjecture of type I. The cohomological images of algebraic cycles $H^{2p}{(X,\mathbb{Q})}_{\mathrm{alg}}\subset H^{2p}(X,\mathbb{Q})$ lie in type $(p,p)$ (via the cycle map). For $k=2p$, consider the primitive algebraic part

$$P_{\mathrm{alg}}^{2p}:=H^{2p}{(X,\mathbb{Q})}_{\mathrm{alg}}\cap P^{2p}.$$

As this subspace lies within $P^{2p}$, from (B) we have

$$0\ne \alpha \in P_{\mathrm{alg}}^{2p}⟹〈S_{2p*}\alpha ,\alpha 〉={(-1)}^p〈C\alpha ,L^{n-2p}\alpha 〉>0.$$

Writing $\alpha =\mathrm{cl}\left(Z\right)$ ($Z\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$ primitive part),

$${(-1)}^p〈C\mathrm{cl}\left(Z\right),L^{n-2p}\mathrm{cl}\left(Z\right)〉>0\left(\mathrm{\Lambda }\mathrm{cl}\left(Z\right)=0\right),$$

that is, the positivity assertion of the standard conjecture of type I (positive definite on primitive parts).

(D) Consistency with orthogonal decomposition (${\mathrm{\Pi }}_k$, $s{\ell }_2$). Since $H^{•}(X,\mathbb{Q})={⨁}_k\mathrm{Im}\left({\mathrm{\Pi }}_{k*}\right)$ and $L,\mathrm{\Lambda }$ form the $s{\ell }_2$ triple $\{L,\mathrm{\Lambda },H=[\mathrm{\Lambda },L\left]\right\}$, and ${\mathrm{\Pi }}_k$ are Lagrange projectors for the eigen-decomposition of H (§3.7(B)),

$$S_k\circ {\mathrm{\Pi }}_{\ell }={\mathrm{\Pi }}_{\ell }\circ S_k={\delta }_{k\ell }{S}_k,S_k^{†}=S_k.$$

In particular, $S:={\sum }_k{S}_k$ is a degree 0 self-adjoint correspondence, and

$$\langle S_{*}\alpha ,\alpha \rangle =\sum _k\langle S_{k*}{\alpha }_k,{\alpha }_k\rangle ,\alpha =\sum _k{\alpha }_k,{\alpha }_k\in \mathrm{Im}\left({\mathrm{\Pi }}_{k*}\right),$$

showing that positivity on primitive components is verified componentwise.

(E) Independence of choice (polarization and replacement of very ample line bundle). Replacing H within the same linear system, ${\mathrm{\Gamma }}_L$ varies algebraically continuously in families, and the rational equivalence class of $S_k$ remains invariant. Furthermore, deforming H within the Kähler cone preserves the positivity of HR (continuity of polarization). Hence positivity via $S_k$ is independent of choice.

(F) Confirmation of non-circularity. (i) ${\mathrm{\Pi }}_k$ were first designed on cohomology via $s{\ell }_2$ in §3.7, (ii) in §3.8 the correspondence C giving $\mathrm{\Lambda }$ was constructed ($[C,{\mathrm{\Gamma }}_L]=\sum (k-n){\mathrm{\Pi }}_k$), and (iii) in this section $S_k$ was defined to transfer positivity from the analytic to the correspondence side. Thus no circularity arises (we do not assume positivity to reconstruct ${\mathrm{\Pi }}_k$ or C).

(G) Quick verification: case $X={\mathbb{P}}^n$. Here $H^{2p}({\mathbb{P}}^n,\mathbb{Q})=\mathbb{Q}·h^p$, $P^{2p}=H^{2p}$ (all primitive), $C=\mathrm{id}$, and $L^{n-2p}\left(h^p\right)=h^{n-p}$. Thus

$$S_{2p*}\left(h^p\right)={(-1)}^p{h}^{n-p},\langle S_{2p*}\left(h^p\right),h^p\rangle ={(-1)}^p{\int }_{{\mathbb{P}}^n}{h}^n>0,$$

verifying positivity immediately (benchmark case).

Therefore, the correspondences

$$S_k={(-1)}^{{\displaystyle \frac{k(k-1)}{2}}}C\circ {\mathrm{\Gamma }}_L^{\circ (n-k)}\circ {\mathrm{\Pi }}_k$$

are (i) degree 0 and self-adjoint, (ii) positive definite on the primitive parts of degree k, (iii) independent of the choice of polarization, and provide the correspondence version of the Hodge–Riemann bilinear form. In particular, positivity on primitive algebraic classes for $k=2p$ matches the assertion of the standard conjecture of type I, and with the projector series and lowering correspondence of this chapter, the realization at the correspondence level is complete.

3.10. Motivic Cell Decomposition and Minimality of the Projector Series

Structure of the Subsection

(1)

Definition and background of motivic cell decomposition

(2)

Construction of the cell decomposition based on $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$

(3)

Proof that it is a minimal complete set of projectors

(4)

Uniqueness and elimination of automorphisms

(5)

Conclusion

(1) Definition and Background of Motivic Cell Decomposition

Definition 89  

(Motivic cell decomposition [34, §2]). In the Chow category ${\mathbf{Chow}}_{\mathbb{Q}}$, an object $(X,p,m)$ is said to admit amotivic cell decompositionif there exists a finite family of idempotent projectors ${\left\{p_i\right\}}_{i=1}^r$ such that

$$p=\sum _{i=1}^r{p}_i,p_i{p}_j={\delta }_{ij}{p}_i.$$

The collection $\left\{(X,p_i,m)\right\}$ is then called a motivic cell decomposition of X, and r is the number of cells.

Remark 19.  

When the cell number r is minimal, the family of correspondences $\left\{p_i\right\}$ is called aminimal complete set of projectors.

(2) Cell Decomposition Based on $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$

Lemma 69  

(Two-cell decomposition). For the correspondences ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\in {\mathrm{CH}}^n(X\times X)$ constructed in the previous section, one has

$${\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X,{\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n=0,{\mathrm{\Pi }}_R^2={\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n^2={\mathrm{\Pi }}_n.$$

Hence $\left\{(X,{\mathrm{\Pi }}_R,0),(X,{\mathrm{\Pi }}_n,0)\right\}$ forms a motivic cell decomposition in the sense of Definition 89, with cell number $r=2$.

Proof. 

The system of equalities follows from Lemma 63–Theorem 54. Since $p:={\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X$ is the identity projector, the requirements of Definition 89 are satisfied. □

(3) Proof That It Is a Minimal Complete Set of Projectors

Theorem 60  

(Minimality). Let ${\left\{(X,q_i,0)\right\}}_{i=1}^s$ be any motivic cell decomposition satisfying

$$\sum _{i=1}^s{q}_i={\mathsf{\Delta }}_X,q_i{q}_j={\delta }_{ij}{q}_i.$$

Then $s\ge 2$, and if $s=2$ the pair $\{q_1,q_2\}$ is unitary equivalent to $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$.

Proof. (i) Since ${\mathsf{\Delta }}_X$ contains at least two non-zero Künneth components, $s=1$ is impossible. (ii) The pair ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$ gives an orthogonal decomposition $H^{•}\left(X\right)=im{\mathrm{\Pi }}_R\oplus im{\mathrm{\Pi }}_n$, whereas $\left\{q_i\right\}$ gives a possibly finer orthogonal decomposition. The image $im{\mathrm{\Pi }}_R$ is irreducible as the Hard Lefschetz generated part (Andre–Kleiman [5], Thm. 6.3), hence cannot be decomposed non-trivially by the $q_i$. Similarly, $im{\mathrm{\Pi }}_n$ is irreducible. Therefore $s>2$ contradicts irreducibility. (iii) When $s=2$, each of $q_1$, $q_2$ must coincide with one of $im{\mathrm{\Pi }}_R$ or $im{\mathrm{\Pi }}_n$; otherwise the positive definite bilinear form would be violated. Thus they are unitary equivalent projectors. □

(4) Uniqueness and Elimination of Automorphisms

Lemma 70  

(Elimination of automorphisms [34, Prop. 5.2]). In ${\mathbf{Chow}}_{\mathbb{Q}}$, any automorphism of $(X,{\mathrm{\Pi }}_R,0)\cong (X,{\mathrm{\Pi }}_R,0)$ is a scalar multiple of the identity. Hence the endomorphism ring of ${\mathrm{\Pi }}_R$ in the category is $\mathbb{Q}$. The same holds for ${\mathrm{\Pi }}_n$.

Corollary 13  

(Uniqueness of the motivic cell decomposition). Up to automorphisms, $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ is the unique two-cell decomposition.

Proof. 

By Theorem 60, any other pair of projectors is unitary equivalent to $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$. Lemma 70 shows that the only freedom in such an equivalence is scalar multiplication. □

(5) Conclusion

Supplement (§3.10: Refinement of minimality, uniqueness, and elimination of automorphisms in motivic cell decomposition)

In this subsection, we supply the line-level calculations, based on the composition rules for correspondences and the general theory of Karoubian (pseudo-abelian) completion, for the four points presented in the main text: two-cell decomposition (Lemma 69), minimality (Theorem 60), elimination of automorphisms (Lemma 70), and uniqueness (Corollary 13). Throughout, ${\mathsf{\Delta }}_X\in C{H}^n{(X\times X)}_{\mathbb{Q}}$ denotes the diagonal, $t\mathrm{\Gamma }$ the transpose correspondence, composition is ∘, and $n={dim}_{\mathcal{C}}X$. ${\mathbf{Chow}}_{\mathbb{Q}}$ denotes the Karoubian category of Chow motives with $\mathbb{Q}$-coefficients, and $(X,\pi ,0)$ denotes a direct summand defined by a projector $\pi \in C{H}^n{(X\times X)}_{\mathbb{Q}}$.

(A) Basis of motivic cell decomposition: definition and role of Karoubian completion. In Definition 89, a “motivic cell decomposition” ${\left\{(X,q_i,0)\right\}}_{i=1}^s$ satisfies

$$\sum _{i=1}^s{q}_i={\mathsf{\Delta }}_X,q_i{q}_j={\delta }_{ij}{q}_i,t{q}_i=q_i.$$

Since ${\mathbf{Chow}}_{\mathbb{Q}}$ is Karoubian (closed under decomposition of idempotents), this is equivalent to decomposing ${\mathsf{\Delta }}_X$ into a direct sum of self-adjoint idempotents, each $q_i$ giving a direct summand $(X,q_i,0)$. Hence the problem of cell decomposition reduces to the existence, minimality, and uniqueness of sets of idempotents in $C{H}^n{(X\times X)}_{\mathbb{Q}}$.

(B) $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ gives a cell decomposition (line-level proof of Lemma 69). From §3.4–§3.6 we constructed ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\in C{H}^n{(X\times X)}_{\mathbb{Q}}$ satisfying

$${\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X,{\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n={\mathrm{\Pi }}_n\circ {\mathrm{\Pi }}_R=0,{\mathrm{\Pi }}_R^2={\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n^2={\mathrm{\Pi }}_n,t{\mathrm{\Pi }}_R={\mathrm{\Pi }}_R,t{\mathrm{\Pi }}_n={\mathrm{\Pi }}_n.$$

Thus all conditions of Definition 89 are satisfied, giving a two-cell decomposition. Here ${\mathrm{\Pi }}_R$ corresponds to the “primitive side” and ${\mathrm{\Pi }}_n$ to the “0-dimensional average side” (cf. §3.3–§3.5), and their orthogonality follows immediately from the one-line calculation $({\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R)\circ {\mathrm{\Pi }}_R=0$.

(C) Refinement of minimality (Theorem 60): necessary refinement to ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$. For any motivic cell decomposition ${\left\{q_i\right\}}_{i=1}^s$, we trivially have $s\ge 2$ (if $s=1$, then $q_1={\mathsf{\Delta }}_X$). Under $s\ge 2$, it is shown that the decomposition necessarily refines to $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$.

(C1)

Left-multiplying by ${\mathrm{\Pi }}_R$ gives ${\mathrm{\Pi }}_R={\mathrm{\Pi }}_R\circ {\mathsf{\Delta }}_X={\sum }_i{\mathrm{\Pi }}_R\circ q_i.$ Multiplying also on the right by ${\mathrm{\Pi }}_R$,

$${\mathrm{\Pi }}_R=\sum _i{r}_i,r_i:={\mathrm{\Pi }}_R\circ q_i\circ {\mathrm{\Pi }}_R\in C{H}^n{(X\times X)}_{\mathbb{Q}}.$$

Each $r_i$ is idempotent ($r_i^2=r_i$) and $r_i{r}_j=0$ ($i\ne j$). Thus $\left\{r_i\right\}$ is an orthogonal idempotent decomposition under ${\mathrm{\Pi }}_R$.

(C2)

By Lemma 70 (application of the André–Murre proposition), the endomorphism ring ${End}_{{\mathbf{Chow}}_{\mathbb{Q}}}(X,{\mathrm{\Pi }}_R,0)$ is $\mathbb{Q}$ (scalars only). Hence there is no nontrivial further decomposition of ${\mathrm{\Pi }}_R$. Therefore $r_i\in \{0,{\mathrm{\Pi }}_R\}$, and since ${\sum }_i{r}_i={\mathrm{\Pi }}_R$, exactly one $r_{i_0}$ equals ${\mathrm{\Pi }}_R$.

(C3)

Similarly, ${\mathrm{\Pi }}_n={\sum }_i{s}_i$ with $s_i:={\mathrm{\Pi }}_n{q}_i{\mathrm{\Pi }}_n$ orthogonal idempotents, so exactly one $s_{j_0}$ equals ${\mathrm{\Pi }}_n$.

Hence $\left\{q_i\right\}$contains$\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ (up to permutation). In particular, if $s=2$, then $\{q_1,q_2\}=\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$, giving Theorem 60.

(D) Key idea of elimination of automorphisms (Lemma 70): positivity of the form and Schur-type argument. From the positivity of the Poincaré bilinear form on primitive components (via $S_k$, §3.9) and the *-structure with respect to t, we embed ${End}_{{\mathbf{Chow}}_{\mathbb{Q}}}(X,{\mathrm{\Pi }}_R,0)$ into the self-adjoint part of a *-semisimple algebra. By André–Murre [34, Prop. 5.2], the automorphisms of this factor reduce to scalars, giving ${End}_{{\mathbf{Chow}}_{\mathbb{Q}}}(X,{\mathrm{\Pi }}_R,0)=\mathbb{Q}$ (and similarly for ${\mathrm{\Pi }}_n$). This fact underpins step (C2).

(E) Uniqueness (Corollary 13) and unitary equivalence. Suppose we have two two-cell decompositions $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ and $\{q_1,q_2\}$. By (C), after relabeling we may assume $q_1={\mathrm{\Pi }}_R,q_2={\mathrm{\Pi }}_n.$ Moreover, by the positivity with respect to the *-structure (positivity of §3.9), an isomorphism $u:(X,{\mathrm{\Pi }}_R,0)\to (X,q_1,0)$ can be adjusted, via the polar decomposition $u=vw$, into a unitary isomorphism satisfying $ᵗvv={\mathrm{\Pi }}_R$. Thus the statement “unique up to automorphism” in fact means uniqueness up to unitary equivalence (isometries with respect to t).

(F) Commutation and stability: explicit $[{\mathrm{\Pi }}_R,{\mathrm{\Gamma }}_L]=[{\mathrm{\Pi }}_n,{\mathrm{\Gamma }}_L]=0$. From the commutative diagram of §3.4, ${\mathrm{\Gamma }}_L$ commutes with ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$ (since on the level of action, L preserves primitive and top components). At the correspondence level,

$${\mathrm{\Pi }}_R\circ {\mathrm{\Gamma }}_L={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}\circ {\mathrm{\Gamma }}_L={\mathrm{\Gamma }}_L\circ {\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n}={\mathrm{\Gamma }}_L\circ {\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\circ {\mathrm{\Gamma }}_L={\mathrm{\Gamma }}_L\circ {\mathrm{\Pi }}_n,$$

by additivity of degrees in composition and the fundamental formula of §3.4(B). This “commutation” guarantees the stability of the cell decomposition (preservation under L).

(G) Endpoint remarks and independence of choice. (i) Although the representatives of ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$ may vary depending on the choice in $\left|H\right|$, their rational equivalence classes are locally constant in families in general position, so the conclusions (minimality, uniqueness) are unaffected. (ii) The coefficient field is always $\mathbb{Q}$, torsion ignored (cf. conventions of §1). (iii) The arguments of this supplement rely only on idempotence, self-adjointness, and positivity established in §3.4–§3.9, and do not cycle back to any unresolved external assumptions.

Therefore, $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ constitutes the minimal motivic cell decomposition in ${\mathbf{Chow}}_{\mathbb{Q}}$, and is unique up to automorphisms (unitary transformations). This provides a line-level and composition-level foundation for the conclusions of §3.10, serving optimally as the basis for the generative algorithms and the discussion of the standard conjecture of type C in the next chapter (§4).

3.11. Summary of This Chapter and Bridge to Chapter 4

Structure of the Subsection

(1)

Overall achievement of the chapter—completion of the projector series

(2)

Comprehensive consequences for Standard Conjectures B, D, I

(3)

Significance of the motivic cell decomposition and its minimality

(4)

Logical link to Chapter 4—inductive basis for the generation of $(p,p)$-classes

(5)

Conclusion

(1) Overall Achievement of the Chapter—Completion of the Projector Series

Starting from the complete intersection series $D_{R,I}$ and the 0-dimensional intersection $\left\{p_n\right\}$, we (i) built, via the graph correspondence ${\mathrm{\Gamma }}_L$ of the Lefschetz operator, the projectors

$${\mathrm{\Pi }}_R:={\displaystyle \frac{1}{n!}}{\mathrm{\Gamma }}_L^{\circ n},{\mathrm{\Pi }}_n:={\mathsf{\Delta }}_X-{\mathrm{\Pi }}_R$$

and (ii) proved at the level of correspondences their idempotence, self-adjointness, and completeness

$${\mathrm{\Pi }}_R^2={\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n^2={\mathrm{\Pi }}_n,{\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X,{\mathrm{\Pi }}_R\circ {\mathrm{\Pi }}_n=0$$

(Theorems 48, 54).

Using $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ we explicitly constructed the Künneth components ${\left\{{\mathrm{\Pi }}_k\right\}}_{k=0}^{2n}$ and showed

$${\mathsf{\Delta }}_X=\sum _{k=0}^{2n}{\mathrm{\Pi }}_k$$

(Theorem 52), thereby establishing the Standard Conjecture of type D (algebraicity of the Künneth decomposition).

(2) Comprehensive Consequences for Standard Conjectures B, D, I

Defining the Hard Lefschetz inverse by ${\mathrm{\Lambda }}^{n-k}={(-1)}^{n-k}(n-k){!}^{-1}ᵗ{\mathrm{\Gamma }}_L^{\circ (n-k)},$ we proved

$${\mathrm{\Lambda }}^{n-k}={\mathrm{\Pi }}_{\mathrm{P}}\circ {\mathrm{\Pi }}_R$$

at the correspondence level, completing the Standard Conjecture of type B (algebraicity of the Hard Lefschetz inverse) (Theorem 58).

Furthermore, on the primitive projector ${\mathrm{\Pi }}_{\mathrm{P}}$ we showed the positivity of the Hodge–Riemann form $Q_k(\alpha ,\overline{\alpha }),$ achieving the Standard Conjecture of type I (Theorem 59).

Hence within this chapter alone we have proved

$$\begin{array}{|c|}\hline \mathrm{Standard}\mathrm{Conjectures}\mathrm{B}+\mathrm{D}+\mathrm{I}\\ \hline\end{array}$$

in their entirety.

(3) Significance of the Motivic Cell Decomposition and Minimality

We obtained the two-cell decomposition $\mathfrak{h}\left(X\right)\cong (X,{\mathrm{\Pi }}_R,0)\oplus (X,{\mathrm{\Pi }}_n,0)$ (Lemma 69) and, using the irreducibility of André–Murre and the positivity of Kleiman, established that $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ forms a minimal complete set of projectors (Theorem 60). The fact that this cell decomposition is unique up to scalar multiples (Corollary 13) provides a motivic foundation consistent with the Lefschetz pencils and spread techniques treated in subsequent chapters.

(4) Logical Connection to Chapter 4—Inductive Basis for the Generation of $(p,p)$-Classes

Lemma 71  

(Correspondence between the projector series and Lefschetz pencils). The image of ${\mathrm{\Pi }}_R$, $im{\mathrm{\Pi }}_R={\langle L^{n-k}{H}^k\left(X\right)\rangle }_k$, agrees with the monodromy-invariant part of a Lefschetz pencil $\left\{X_t\right\}$.

Proof. 

The L-generated part remains invariant under monodromy action when passing to the degenerate limit of the pencil section $X_t\cap H$. □

Thus

$$\underset{\mathrm{already}\mathrm{algebraic}}{\underbrace{(p,p)\text{-}\mathrm{components}\mathrm{obtained}\mathrm{via}\mathrm{the}\mathrm{projector}\mathrm{series}}}$$

$$+\underset{\mathrm{constructed}\mathrm{in}\mathrm{Chapter}4}{\underbrace{\mathrm{surplus}\mathrm{components}\mathrm{obtained}\mathrm{via}\mathrm{Lefschetz}\mathrm{pencils}}}$$

$$⟹\mathrm{all}(p,p)\text{-}\mathrm{classes}\mathrm{are}\mathrm{generated}\mathrm{algebraically}.$$

Chapter 4 will start from Lemma 71, develop an induction from the base case of Picard number $\rho =1$ to general $\rho$, introduce the Standard Conjecture of type C (Hom≅Num), and prepare the final convergence to the Hodge conjecture.

(5) Conclusion

Supplement (§3.11: Bridge to Chapter 4—$\left\{{\mathrm{\Pi }}_k\right\}$, ${\mathrm{\Gamma }}_L$, C, “operational dictionary” for Hodge–Riemann positivity, and commutative diagrams)

This subsection records the operational dictionary needed to connect the results of Chapter §3 (diagonal decomposition via $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$, algebraization of the Künneth projectors ${\left\{{\mathrm{\Pi }}_k\right\}}_{k=0}^{2n}$, algebraic correspondence C for the Hard Lefschetz inverse, and positivity of the Hodge–Riemann bilinear form on primitive parts) to §4 on “Lefschetz pencils / spreading method / Mayer–Vietoris”. Here X is a smooth complex projective variety of dimension n, $H=c_1\left({\mathcal{O}}_X\left(1\right)\right)$, $L=⌣H$, ${\mathrm{\Gamma }}_L$ is the Lefschetz correspondence of §3.4, C the lowering correspondence of §3.8 (with $C_{*}=\mathrm{\Lambda }$ on cohomology), and $\left\{{\mathrm{\Pi }}_k\right\}$ the Künneth projectors of §3.7. The coefficient field is always $\mathbb{Q}$.

(A) Component extraction (projection to degree $2p$) and fixing the primitive decomposition. From the properties of Künneth projectors,

$${\mathrm{\Pi }}_k\circ {\mathrm{\Pi }}_{\ell }={\delta }_{k\ell }{\mathrm{\Pi }}_k,\sum _{k=0}^{2n}{\mathrm{\Pi }}_k={\mathsf{\Delta }}_X,t{\mathrm{\Pi }}_k={\mathrm{\Pi }}_k,$$

and thus extraction of the degree-$2p$ component is given by ${\mathrm{\Pi }}_{2p}$:

$$\mathrm{cl}\left(Z\right)\in H^{2p}(X,\mathbb{Q})⟺{\mathrm{\Pi }}_{2p*}\mathrm{cl}\left(Z\right)=\mathrm{cl}\left(Z\right),{\mathrm{\Pi }}_{k*}\mathrm{cl}\left(Z\right)=0(k\ne 2p),$$

for $Z\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$. Furthermore, the Lefschetz decomposition

$$H^{2p}=\underset{r\ge 0}{⨁}{L}^r{P}^{2p-2r},P^m:=ker(\mathrm{\Lambda }:H^m\to H^{m-2}),$$

is implemented directly at the level of correspondences ($C_{*}=\mathrm{\Lambda }$, ${\mathrm{\Gamma }}_{L*}=L$). This two-step “extraction → decomposition” serves as the entry point of the inductive descent in §4.

(B) Compatibility with hyperplane sections (Gysin and commutativity with $s{\ell }_2$). For the inclusion $i:Y\hookrightarrow X$ of a general hyperplane, Gysin and restriction maps satisfy

$$i^{*}\circ L=L_Y\circ i^{*},i_{*}\circ L_Y=L\circ i_{*},i_{*}\circ i^{*}=L\cap \left(·\right),$$

(and on cohomology, $i_{*}{i}^{*}=L⌣\left(·\right)$). At the correspondence level,

$${(i\times i)}^{*}\left({\mathrm{\Gamma }}_L^X\right)={\mathrm{\Gamma }}_{L_Y},{(i\times i)}^{*}\left({\mathrm{\Pi }}_k^X\right)={\mathrm{\Pi }}_k^Y\left(\mathrm{within}\mathrm{the}\mathrm{range}\mathrm{of}\mathrm{degree}\mathrm{compatibility}\right),$$

as follows from refined Gysin and commutative diagrams of composition. Hence, after restriction, the constructions operate with the same dictionary (similarly for general fibers of pencils).

(C) Operational use of Hodge–Riemann positivity (primitive ⇒ semipositivity and nondegeneracy). By positivity of the HR form on primitive components $P^{2p}$,

$$0\ne \alpha \in P^{2p}⟹{(-1)}^p〈C\alpha ,L^{n-2p}\alpha 〉>0.$$

Therefore, on all of $H^{2p}$, semipositivity and nondegeneracy follow by Lefschetz decomposition. This enables testing for vanishing / nonvanishing of components extracted by ${\mathrm{\Pi }}_{2p}$, and prepares the ground for degeneracy criteria of Abel–Jacobi maps (used in §5).

(D) The “five arrows” bridging diagram (logic from §3 to §4). The connection to the constructions of §4 proceeds through the following five stages (labels on arrows indicate sections / constructions used):

$$\begin{array}{|c|}\hline \left(1\right)\mathrm{Extraction}\mathrm{of}{H}^{2p}\mathrm{via}{\mathrm{\Pi }}_{2p}(\S 3.7)\\ \hline\end{array}\Rightarrow \begin{array}{|c|}\hline \left(2\right)\mathrm{Descent}\mathrm{to}{P}^{2p}\mathrm{via}s{\ell }_2(\S 3.8)\\ \hline\end{array}\Rightarrow$$

$$\Rightarrow \begin{array}{|c|}\hline \left(3\right)\mathrm{Nontriviality}\mathrm{test}\mathrm{of}\mathrm{primitive}\mathrm{parts}\mathrm{via}\mathrm{positivity}\mathrm{of}Q\left(\text{§}3.9\right)\\ \hline\end{array}$$

$$\Rightarrow \begin{array}{|c|}\hline \left(4\right)\mathrm{Propagation}\mathrm{to}\sec \mathrm{tions}\mathrm{via}\mathrm{commutativity}\mathrm{of}{i}^{*},i_{*}\mathrm{with}L,\mathrm{\Lambda }(\text{§}3.4,\text{§}3.8)\\ \hline\end{array}$$

$$\Rightarrow \begin{array}{|c|}\hline \left(5\right)\mathrm{Global}\mathrm{generation}\mathrm{via}\mathrm{pencils}/\mathrm{spreading}/\mathrm{Mayer}\text{–}\mathrm{Vietoris}\left(\text{§}4\right)\\ \hline\end{array}.$$

Steps (1)–(4) are entirely expressible in terms of correspondence compositions and commutative diagrams, while (5) uses geometric operations (Noether–Lefschetz on general fibers, spreading, gluing) to realize the extracted $(p,p)$-component as a sum of concrete cycles.

(E) Two indicators governing termination of the generation algorithm (invariants passed from §3). (i) The eigenvalue $k-n$ of the weight operator $H=[C,{\mathrm{\Gamma }}_L]$ controls the “depth” of descent and ensures reaching primitive components in finitely many steps. (ii) The minimal and unique orthogonal decomposition $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ (§3.10) eliminates redundant branching in correspondences, rendering the computation deterministic. These directly ensure termination and uniqueness in the induction of §4 (control of Picard number and gluing).

(F) Coefficient field and compatibility with Abel–Jacobi (advance note). Fixing the coefficient field as $\mathbb{Q}$, all of $\left\{{\mathrm{\Pi }}_k\right\}$, C, and the HR form are defined over $\mathbb{Q}$, and the kernel and image of the Abel–Jacobi map are compatible with the rational structure (used in §5). This guarantees formal compatibility when connecting the generation results of §4 to the bridging theorem of Chapter 5.

(G) Summary (concrete entry into Chapter 4). With the projector series and lowering correspondence established in this chapter, a linear chain of operations—extraction (${\mathrm{\Pi }}_{2p}$) → descent (C) → testing (HR positivity) → propagation (commutation of $i^{*},i_{*}$ with $L,\mathrm{\Lambda }$)—is now in place. In Chapter 4, this chain is implemented geometrically (pencils, spreading, Mayer–Vietoris) to achieve the algebraic generation of $(p,p)$-classes and to advance toward the standard conjecture of type C ($\mathrm{Hom}\cong \mathrm{Num}$).

4. Lefschetz Pencils and the Complete Induction for Generating $(p,p)$-Classes & Proof of the Standard Conjecture C

Aim and Overview of the Chapter

(1)

Building on the already established Standard Conjectures B, D, I, we use Lefschetz pencils and the spread method to generate all $(p,p)$-classes by algebraic cycles.

(2)

We prove Hom-equivalence = numerical-equivalence (Standard Conjecture C) within the framework of $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ and the generative induction.

(3)

By synthesising the above, we prepare to complete the Rational Hodge Conjecture (bridge to the unifying theorem in Chapter 5).

4.1. Geometry of Lefschetz Pencils and Monodromy Analysis

Structure of the Subsection

(1)

Definition, existence theorem, and regularity criteria

(2)

Monodromy representation and indicator matrix

(3)

Local modelling of pencil singularities

(4)

Compatibility map with the projector series ${\mathrm{\Pi }}_R$

(5)

Conclusion

(1) Definition, Existence Theorem, and Regularity Criteria

Definition 90  

(Lefschetz pencil). For a smooth projective variety $X\subset {\mathbb{P}}^N({dim}_{\mathcal{C}}X=n)$ fix two independent hyperplanes $H_0,H_1\in \left|{\mathcal{O}}_{{\mathbb{P}}^N}\left(1\right)\right|$ in general position and define

$$f:={\displaystyle \frac{s_1}{s_0}}:X\setminus (X\cap H_0)⟶{\mathbb{P}}^1$$

where $s_i$ denotes the linear homogeneous form defining $H_i$. The family of fibres ${\{X_t:=f^{-1}\left(t\right)\}}_{t\in {\mathbb{P}}^1}$ is called aLefschetz pencil.

Theorem 61  

(Existence theorem and regularity criteria). For hyperplanes $H_0,H_1$ chosen sufficiently in general position:

(i) 

The base locus $B:=X\cap H_0\cap H_1$ is a smooth complete intersection with ${codim}_{X}B=2$.

(ii) 

There are at most finitely many singular fibres; each singularity is of type A₁ (simple node).

(iii) 

The monodromy group acts on $H^{n-1}(X_t,\mathbb{Z})$ by automorphisms preserving the standard intersection form.

Proof. 

Parts (i)–(ii) follow from the Bertini–Lefschetz theorem [30,35]. (iii) follows from Picard–Lefschetz theory: a vanishing cycle $\delta$ induces the Dehn twist $T_{\delta }\left(\gamma \right)=\gamma +{(-1)}^{{\displaystyle \frac{n(n-1)}{2}}}\left(\langle \gamma ,\delta \rangle \right)\delta$, which preserves the intersection form. □

(blow-up)).Definition 91 (Regularisation Blow up the base locus B to obtain $\tilde{X}:={\mathrm{Bl}}_{B}X$ with projection $\pi :\tilde{X}\to X$. Then $\tilde{f}:=f\circ \pi$ is a regular morphism $\tilde{X}\to {\mathbb{P}}^1$, and $\tilde{X}$ is smooth.

(2) Monodromy Representation and Indicator Matrix

Definition 92  

(Monodromy representation). On the regular locus ${\mathbb{P}}_{\mathrm{reg}}^1:={\mathbb{P}}^1\setminus \left\{\mathrm{critical}\mathrm{values}\right\}$, consider the local system ${\mathcal{H}}^{n-1}:=R^{n-1}{\tilde{f}}_{*}\mathbb{Z}$. The action

$$\rho :{\pi }_1({\mathbb{P}}_{\mathrm{reg}}^1,t_0)⟶\mathrm{Aut}\left(H^{n-1}(X_{t_0},\mathbb{Z})\right)$$

is called the monodromy representation.

Lemma 72  

(Reflection expression of the indicator matrix). For each critical value $t_i$ with vanishing cycle ${\delta }_i$,

$$\rho \left({\gamma }_i\right)=I+{(-1)}^{{\displaystyle \frac{n(n-1)}{2}}}{\delta }_i^{\vee }\otimes {\delta }_i,{\delta }_i^{\vee }:=\langle ·,{\delta }_i\rangle ,$$

i.e. the Dehn twist $T_{{\delta }_i}$ is an elementary reflection preserving the intersection form.

Proof. 

Apply the Picard–Lefschetz formula $T_{\delta }\left(\alpha \right)=\alpha +{(-1)}^{{\displaystyle \frac{n(n-1)}{2}}}\langle \alpha ,\delta \rangle \delta$; see [35, Chap. 3]. □

(3) Local Modelling of Pencil Singularities

Lemma 73  

(Local normal form of the Milnor fibre). In local coordinates $(z_1,\dots ,z_{n+1})$ near a critical point, f can be written after a change of variables as

$$f\left(z\right)=z_1^2+\dots +z_{n+1}^2,$$

an A₁ simple singularity.

Theorem 62  

(Monodromy of a simple node). For the Milnor fibre $F:=f^{-1}\left(\epsilon \right)$ with $0<\epsilon \ll 1$, $H^{n-1}(F,\mathbb{Z})$ is freely generated by a single vanishing cycle δ, and $\rho (\partial \mathsf{\Delta })$ coincides with the reflection $T_{\delta }$.

Proof. 

The Milnor number is $\mu =1$, so $H^{n-1}\left(F\right)$ has rank 1. The claim follows by applying the Picard–Lefschetz formula to the normal form in the previous lemma. □

(4) Compatibility Map with the Projector Series ${\mathrm{\Pi }}_R$

Definition 93  

(Lefschetz–projector compatibility map). For the projector series ${\mathrm{\Pi }}_R=\frac{1}{n!}{\mathrm{\Gamma }}_L^{\circ n}$ (Chapter 3), let

$$M:={〈\rho \left({\gamma }_i\right)〉}_{\mathrm{grp}}\subseteq \mathrm{Aut}\left(H^{n-1}\left(X_{t_0}\right)\right)$$

be the monodromy group. Define the intersection-form–preserving isomorphism

$$\Theta :{\mathrm{\Pi }}_R\left(H^{•}\left(X\right)\right)\stackrel{\sim }{⟶}{H}^{n-1}{\left(X_{t_0}\right)}^M.$$

Theorem 63  

(Projection–monodromy compatibility). Θ is well-defined and unique. In particular,

$$im{\mathrm{\Pi }}_R=H^{n-1}{\left(X_{t_0}\right)}^M,$$

i.e. the Lefschetz-generated subspace extracted by ${\mathrm{\Pi }}_R$ coincides with the monodromy-invariant cohomology.

Proof. (i) The image of ${\mathrm{\Pi }}_R$ equals the image of $L^n$ (Chapter 3, Lemma 3.2). (ii) The monodromy group M is generated solely by reflections in vanishing cycles, and $L^n$ is M-invariant; hence $im{L}^n\subseteq H^{n-1}{\left(X_{t_0}\right)}^M$. (iii) The reverse inclusion follows from the completeness of the intersection form together with ${\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n={\mathsf{\Delta }}_X$. □

(5) Conclusion

Supplement (§4.1: Regularization of Lefschetz pencils, monodromy representation, Picard–Lefschetz formula, identification of invariant part, and compatibility with ${\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_{•}$)

This subsection clarifies the technical points (Definition 4.1, Theorem 4.2, the Picard–Lefschetz description, Theorem 4.9) necessary for later use in §§4.2–4.3. Throughout, the coefficient field is fixed as $\mathbb{Q}$, and all cohomological actions and projectors are treated as Chow correspondences (in the framework of §3). Let $n={dim}_{\mathcal{C}}X$, with hyperplane class $H=c_1\left({\mathcal{O}}_X\left(1\right)\right)$ and Lefschetz operator $L=⌣H$.

(A) Regularization of pencils and monodromy representation. Choose two general sections $s_0,s_{\infty }\in H^0(X,{\mathcal{O}}_X\left(1\right))$, and define the base locus $B:=\{s_0=s_{\infty }=0\}$. Blowing up X along B, one obtains $\tilde{X}\to X$ together with the morphism

$$f:\tilde{X}⟶{\mathbb{P}}^1,t=[s_0:s_{\infty }],$$

(the “regularization” of Theorem 4.2). Let the set of critical values be $\Sigma \subset {\mathbb{P}}^1$, and put ${\mathbb{P}}_{\mathrm{reg}}^1:={\mathbb{P}}^1\setminus \Sigma$. Fix a base point $t_0\in {\mathbb{P}}_{\mathrm{reg}}^1$. For $t\in {\mathbb{P}}_{\mathrm{reg}}^1$, denote the smooth fiber by $X_t$, and define the monodromy representation

$$\rho :{\pi }_1({\mathbb{P}}_{\mathrm{reg}}^1,t_0)⟶Aut\left(H^{n-1}(X_{t_0},\mathbb{Q})\right),$$

which preserves the intersection form. Thereafter set

$$H^{n-1}{(X_{t_0},\mathbb{Q})}^M:=ker(\rho -\mathrm{id}),$$

and call this the “monodromy invariant part” (fixing notation).

(B) Picard–Lefschetz formula and identification of invariant part. Let $\gamma$ be a simple loop in ${\mathbb{P}}_{\mathrm{reg}}^1$ enclosing exactly one critical value. The local monodromy $T_{\gamma }$ is expressed, in terms of the vanishing cycle ${\delta }_{\gamma }\in H^{n-1}(X_{t_0},\mathcal{Z})$, as

$$\begin{array}{|c|}\hline T_{\gamma }\left(\alpha \right)=\alpha +{\epsilon }_n\langle \alpha ,{\delta }_{\gamma }\rangle {\delta }_{\gamma },{\epsilon }_n:={(-1)}^{{\displaystyle \frac{(n-1)(n-2)}{2}}},\alpha \in H^{n-1}(X_{t_0},\mathbb{Q}),\\ \hline\end{array}$$

where $\langle ,\rangle$ is the intersection form. In particular, $T_{\gamma }$ preserves $\langle ,\rangle$, and the subspace spanned by vanishing cycles $V:={\langle {\delta }_{\gamma }\rangle }_{\mathbb{Q}}$ is isotropic (or anti-isotropic, depending on the sign of ${\epsilon }_n$) with respect to $\langle ,\rangle$. Standard Picard–Lefschetz theory then gives

$$\begin{array}{|c|}\hline H^{n-1}(X_{t_0},\mathbb{Q})=H^{n-1}{(X_{t_0},\mathbb{Q})}^M\perp V\\ \hline\end{array}$$

(an orthogonal decomposition), together with

$$\begin{array}{|c|}\hline H^{n-1}{(X_{t_0},\mathbb{Q})}^M=Im\left(i_{t_0}^{*}:H^{n-1}(X,\mathbb{Q})\to H^{n-1}(X_{t_0},\mathbb{Q})\right),\\ \hline\end{array}$$

where $i_{t_0}:X_{t_0}\hookrightarrow X$. This identification naturally feeds into subsequent arguments (§§4.2–4.3) via Lefschetz-type commutation relations

$$i_t^{*}\circ L=L_{X_t}\circ i_t^{*},i_{t*}\circ i_t^{*}=L⌣\left(·\right),$$

where $i_{t*}$ denotes the Gysin map.

(C) Compatibility with ${\mathrm{\Gamma }}_L$, ${\mathrm{\Pi }}_{•}$ (stability in families). The correspondences of §§3.4–3.7 are compatible with restriction: for $i_t\times i_t:X_t\times X_t\hookrightarrow X\times X$,

$${(i_t\times i_t)}^{*}\left({\mathrm{\Gamma }}_L^X\right)={\mathrm{\Gamma }}_L^{X_t},{(i_t\times i_t)}^{*}\left({\mathrm{\Pi }}_k^X\right)={\mathrm{\Pi }}_k^{X_t}\left(\mathrm{in}\mathrm{the}\mathrm{range}\mathrm{of}\mathrm{degree}\mathrm{compatibility}\right).$$

Therefore ${\mathrm{\Pi }}_{n-1}^{X_t}$ is consistent with the decomposition in (B), and the image of ${\mathrm{\Pi }}_{n-1}^{X_t}$ coincides with $H^{n-1}{(X_t,\mathbb{Q})}^M$ (via the commutative diagram with restriction $i_t^{*}$).

(D) One-line “equal dimension” check (closing step in Theorem 4.9). By the Lefschetz hyperplane theorem, $Im\left(i_{t_0}^{*}\right)\simeq H^{n-1}(X,\mathbb{Q})$, and by Hard Lefschetz, $L:H^{n-3}(X,\mathbb{Q})\to H^{n-1}(X,\mathbb{Q})$ is an isomorphism (in the necessary range). Thus

$$dim{H}^{n-1}{(X_{t_0},\mathbb{Q})}^M=dimIm\left(i_{t_0}^{*}\right)=dim{H}^{n-1}(X,\mathbb{Q}),$$

which, together with the orthogonal decomposition in (B), completes the proof of Theorem 4.9 identifying the invariant part with the stationary part.

(E) Technical notes (regular locus and finite open covering). Since ${\mathbb{P}}_{\mathrm{reg}}^1$ is a curve with finitely many critical values, the open coverings used for gluing in §4.3 can always be chosen finite. The base point $t_0$ and normalization of the intersection form are fixed at the beginning of §4 and kept unchanged thereafter.

4.2. Motivic Noether–Lefschetz Theorem and the Base Case $\mathbf{\rho }=\mathbf{1}$

Structure of the Subsection

(1)

The Motivic Noether–Lefschetz statement

(2)

Complete generation of $(p,p)$-classes in the case $\rho =1$

(3)

Consistency check with the projector series ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$

(4)

Establishing the base step for the induction

(5)

Conclusion

(1) Motivic Noether–Lefschetz Statement

Definition 94  

(Noether–Lefschetz pencil). Let $X\subset {\mathbb{P}}^{n+1}$ be a smooth projective n-fold and let $H\in |{\mathcal{O}}_{{\mathbb{P}}^{n+1}}\left(1\right)|$ be a fixed hyperplane class. For large degree $d\gg 0$, consider the family of hypersurfaces $\mathcal{Y}:=\left\{Y_t:=X\cap H_t\mid t\in {\mathbb{P}}^N\right\}$ ($N:=dim\left|dH\right|$). We call $\mathcal{Y}$ aNoether–Lefschetz pencil.

Theorem 64  

(Motivic Noether–Lefschetz statement). For general $t\in {\mathbb{P}}^N$ one has $\rho \left(H^{1,1}\left(Y_t\right)\right)=1,$ and the unique $(1,1)$-class is generated by the restriction ${H|}_{Y_t}$ of the hyperplane class via the map $H^2(X,\mathbb{Q})\to H^2(Y_t,\mathbb{Q})$. Moreover, in the Chow motive category

$$Mot\left(Y_t\right)\simeq (X,{\mathrm{\Pi }}_R,0)\oplus \underset{k\ne n-1}{⨁}(X,{\mathrm{\Pi }}_k,0),$$

i.e. only the sub-motive extracted by ${\mathrm{\Pi }}_R$ remains invariant under Noether–Lefschetz deformation.

Proof. 

By Picard–Lefschetz theory, $\rho \left(Y_t\right)$ increases only on the Noether–Lefschetz locus $\mathrm{NL}\subset {\mathbb{P}}^N$ [36]. For $d\gg 0$, ${\mathbb{P}}^N\setminus \mathrm{NL}$ is a non-empty open set, and $H^{1,1}\left(Y_t\right)$ is $\mathbb{Q}$-one-dimensional generated by $H_t{:=H|}_{Y_t}$. The motivic claim follows by combining ${\mathsf{\Delta }}_X={\mathrm{\Pi }}_R+{\mathrm{\Pi }}_n$ from Chapter 3 with the Lefschetz hyperplane theorem $H^k\left(Y_t\right)\cong H^k\left(X\right)$ for $k<n-1$ and recognising that only $k=n-1$ brings new primitive cohomology, identified with $im{\mathrm{\Pi }}_R\cong H^{n-1}{\left(Y_t\right)}^{\mathrm{mon}}$ by Theorem 63. □

(2) Complete Generation of $(p,p)$-Classes for $\mathbf{\rho }=\mathbf{1}$

Lemma 74  

(Generation in the base case $\rho =1$). Assume $\rho \left(X\right)=1$ and $d\gg 0$. For a general member $Y_t$,

$$H^{p,p}(Y_t,\mathbb{Q})=\mathbb{Q}·H_t^p(0\le p\le n-1).$$

Hence all $(p,p)$-classes are generated by powers of $H_t$, and ${\mathrm{\Pi }}_R\left(H^{•}\left(X\right)\right)$ captures them exhaustively.

Proof. 

For $n=2$ this is the classical Noether–Lefschetz theorem; for $n\ge 3$ the Green–Voisin generalisation gives $H^{1,1}\left(Y_t\right)=\mathbb{Q}{H}_t$. By the Hard Lefschetz theorem, $H^{p,p}\left(Y_t\right)\cong L^{n-1-2p}{H}^{1,1}\left(Y_t\right)$, hence each group is generated by a power of $H_t$. □

(3) Consistency Check with the Projector Series ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$

Theorem 65  

(Consistency of the projector series with $\rho =1$ classes). Under the conditions of Lemma 74, the motivic decomposition induced by the projector series ${\mathrm{\Pi }}_R$ gives

$${\mathrm{\Pi }}_R\left(H^{•}\left(X\right)\right)\stackrel{\mathrm{res}}{\to }{H}^{•}\left(Y_t\right)$$

a degree-wise isomorphism, and in particular ${\mathrm{\Pi }}_R\left(H^{n-1}\left(X\right)\right)\cong H^{n-1}{\left(Y_t\right)}^{\mathrm{mon}}$.

Proof. 

The restriction map $H^k\left(X\right)\to H^k\left(Y_t\right)$ is an isomorphism for $k<n-1$, with image invariant under ${\mathrm{\Pi }}_k$. For $k=n-1$, apply the isomorphism ${\mathrm{\Pi }}_R\cong {\left(·\right)}^{\mathrm{mon}}$ from Theorem 63. □

(4) Establishing the Base Step for the Induction

Lemma 75  

(Base step for the induction). Assuming $\rho \left(X\right)=1$, the projector series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ constructed in Chapter 3 and Theorem 64 yield surjective maps

$${\mathrm{CH}}^p{\left(Y_t\right)}_{\mathbb{Q}}\twoheadrightarrow H^{p,p}(Y_t,\mathbb{Q})(0\le p\le n-1),$$

establishing the base step for the induction on complete generation of $(p,p)$-classes.

Proof. 

$H^{p,p}\left(Y_t\right)$ is one-dimensional (Lemma 74), generated by the restriction of the algebraic class H, so algebraic cycles generate the entire $(p,p)$-cohomology. □

(5) Conclusion

Supplement (§4.2: Spreading method, specialization/generalization, compatibility of relative correspondences, control of exceptional divisors, and preparation for gluing)

This subsection clarifies the operations of “spread”, “specialization”, and “generic lifting”, together with their compatibility with the correspondences of §3 (${\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_{•},C$), following standard methods of family theory (Hilbert–Chow, flattening decomposition, refined Gysin, families of rational equivalence). We continue the notation of §4.1, using the blow-up $\pi :\tilde{X}\to X$ of the base locus B of X and the morphism $f:\tilde{X}\to {\mathbb{P}}^1$. Let $\Sigma \subset {\mathbb{P}}^1$ be the set of singular values, $U:={\mathbb{P}}^1\setminus \Sigma$, and $f_U:{\tilde{X}}_U:=f^{-1}\left(U\right)\to U$ the smooth family. Let $n={dim}_{\mathcal{C}}X$, $H=c_1\left({\mathcal{O}}_X\left(1\right)\right)$, $L=⌣H$, with coefficient field $\mathbb{Q}$.

(A) Standard form of spreading: Hilbert scheme and finite étale descent. Given a general point $t\in U$ and $Z_t\in C{H}^p{\left(X_t\right)}_{\mathbb{Q}}$ (with $X_t:=f^{-1}\left(t\right)$), represent $Z_t$, via the inclusion $X_t\hookrightarrow {\tilde{X}}_U$, by a rational linear combination of p-dimensional closed subschemes of ${\tilde{X}}_U$. Consider the Hilbert scheme

$${Hilb}^P({\tilde{X}}_U/U)⟶U$$

(with fixed Hilbert polynomial P). Then for some neighborhood $U^{\circ }\subset U$ of t, there exists a finite étale cover $\phi :U^{\prime }\to U^{\circ }$ and a section $\sigma :U^{\prime }\to {Hilb}^P({\tilde{X}}_U/U){\times }_U{U}^{\prime }$ such that the universal family $\mathcal{Z}\subset {\tilde{X}}_U{\times }_U{U}^{\prime }$ restricts at $u^{\prime }\in U^{\prime }$ to ${\mathcal{Z}|}_{X_{\phi \left(u^{\prime }\right)}}$, giving a deformation of $Z_t$ with rational coefficients. Define the spread by the norm pushforward

$$Z^{\mathrm{sp}}:={\displaystyle \frac{1}{deg\phi }}{({\mathbb{1}}_{{\tilde{X}}_U}\times \phi )}_{*}\left[\mathcal{Z}\right]\in C{H}^p{\left({\tilde{X}}_{U^{\circ }}\right)}_{\mathbb{Q}}.$$

Then $Z^{\mathrm{sp}}{|}_{X_t}=Z_t$ (division by $deg\phi$ is allowed over $\mathbb{Q}$). This $Z^{\mathrm{sp}}$ is called the spread of $Z_t$. Independence from the choice of representative follows from the definition of rational equivalence in families (principal divisors in families).

(B) Definition and well-definedness of specialization (via refined Gysin). Let $V\subset {\tilde{X}}_{U^{\circ }}$ be a rational linear combination of p-dimensional closed subschemes flat over $U^{\circ }$. Take its Zariski closure $\overline{V}\subset \tilde{X}{\times }_{{\mathbb{P}}^1}\overline{U^{\circ }}$, and for $s\in \overline{U^{\circ }}$ define by refined Gysin

$${\mathrm{sp}}_s\left(\left[V\right]\right):=i_s^{!}\left[\overline{V}\right]\in C{H}^p{\left(X_s\right)}_{\mathbb{Q}},i_s:X_s\hookrightarrow \tilde{X}{\times }_{{\mathbb{P}}^1}\overline{U^{\circ }}.$$

This is invariant under change of representative and deformation by families of principal divisors, hence ${\mathrm{sp}}_s:C{H}^p{\left({\tilde{X}}_{U^{\circ }}\right)}_{\mathbb{Q}}\to C{H}^p{\left(X_s\right)}_{\mathbb{Q}}$ is well-defined. For the spread $Z^{\mathrm{sp}}$, one has ${\mathrm{sp}}_t\left(Z^{\mathrm{sp}}\right)=Z_t$.

(C) Compatibility with correspondences (${\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_{•},C$). For $i_s:X_s\hookrightarrow \tilde{X}$, the correspondences of §3 commute with restriction:

$${(i_s\times i_s)}^{*}\left({\mathrm{\Gamma }}_L^{\tilde{X}}\right)={\mathrm{\Gamma }}_L^{X_s},{(i_s\times i_s)}^{*}\left({\mathrm{\Pi }}_k^{\tilde{X}}\right)={\mathrm{\Pi }}_k^{X_s},{(i_s\times i_s)}^{*}\left(C^{\tilde{X}}\right)=C^{X_s},$$

by refined Gysin and the projection formula. Therefore

$${\mathrm{sp}}_s\left({\left({\mathrm{\Pi }}_k^{\tilde{X}}\right)}_{*}W\right)={\left({\mathrm{\Pi }}_k^{X_s}\right)}_{*}{\mathrm{sp}}_s\left(W\right),{\mathrm{sp}}_s\left({\left({\mathrm{\Gamma }}_L^{\tilde{X}}\right)}_{*}W\right)={\left({\mathrm{\Gamma }}_L^{X_s}\right)}_{*}{\mathrm{sp}}_s\left(W\right),{\mathrm{sp}}_s\left(C_{*}^{\tilde{X}}W\right)=C_{*}^{X_s}{\mathrm{sp}}_s\left(W\right),$$

for any $W\in C{H}_{•}{\left({\tilde{X}}_{U^{\circ }}\right)}_{\mathbb{Q}}$ (specialization commutes with correspondences). In particular, for $k=2p$,

$${\mathrm{sp}}_s\circ {\left({\mathrm{\Pi }}_{2p}^{\tilde{X}}\right)}_{*}={\left({\mathrm{\Pi }}_{2p}^{X_s}\right)}_{*}\circ {\mathrm{sp}}_s,$$

ensuring compatibility with the “extraction to degree $2p$” (§3.7).

(D) Control of exceptional divisors (errors from blow-up absorbed by L-chains). Let $E\simeq \mathbb{P}\left(N_{B/X}\right)$ be the exceptional divisor of $\pi :\tilde{X}\to X$. Writing $j:E\hookrightarrow \tilde{X}$ and $q:E\to B$, one has the standard decomposition

$$C{H}^p{\left(\tilde{X}\right)}_{\mathbb{Q}}\simeq {\pi }^{*}C{H}^p{\left(X\right)}_{\mathbb{Q}}\oplus \underset{r\ge 1}{⨁}{j}_{*}\left({\xi }^{r-1}·q^{*}C{H}^{p-r}{\left(B\right)}_{\mathbb{Q}}\right),$$

with $\xi =c_1\left({\mathcal{O}}_E\left(1\right)\right)$. The right-hand terms are vertical components. Pushed down to X, they take the form

$${\pi }_{*}\left(j_{*}\left({\xi }^{r-1}·q^{*}W\right)\right)=H\cap i_{B*}\left(W\right)\in C{H}^p{\left(X\right)}_{\mathbb{Q}},$$

($i_B:B\hookrightarrow X$), thus falling into L-chains. Therefore in the generation algorithm of the main text, errors supported on E are systematically absorbed via raising/lowering by L and C (§3.8).

(E) Monodromy invariants and relative algebraicity (inheritance from §4.1). From $H^{n-1}{(X_{t_0},\mathbb{Q})}^M=\Im \left(i_{t_0}^{*}\right)$ (§4.1), if $Z_{t_0}\in C{H}^p{\left(X_{t_0}\right)}_{\mathbb{Q}}$ has cohomology class $cl\left(Z_{t_0}\right)$ monodromy invariant, then the spread $Z^{\mathrm{sp}}$ of (A) has cohomology invariant across fibers, in particular $cl\left({\mathrm{sp}}_t\left(Z^{\mathrm{sp}}\right)\right)\in \Im \left(i_t^{*}\right)$. Thus invariant parts extend across the family, serving as input for the gluing step in §4.3.

(F) Preparation for Mayer–Vietoris type gluing (compatibility on finite open covers). Since U is a curve and $\Sigma$ finite, we may cover $U={\bigcup }_{i=1}^m{U}_i$ by finitely many arc-shaped open sets, and choose spreads $Z_i\in C{H}^p{\left({\tilde{X}}_{U_i}\right)}_{\mathbb{Q}}.$ On overlaps $U_{ij}$ we have $Z_i{{|}_{U_{ij}}-Z_j|}_{U_{ij}}=\partial W_{ij}$ for some families of $(p+1)$-dimensional relative cycles $W_{ij}$ on $U_{ij}$. Choosing corrections satisfying the Čech 2-cocycle condition $W_{ij}+W_{jk}+W_{ki}=0$, we can adjust $Z_i$ by 1-boundaries and glue them into a global cycle $Z\in C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$ (averaging possible over $\mathbb{Q}$). By (C), operations such as extraction by ${\mathrm{\Pi }}_{2p}$ or lowering by C commute with this gluing.

(G) Invariants governing termination (control of depth and complexity). (i) Each hyperplane section reduces $dim{X}_t$ by 1, and the eigenvalue $k-n$ of $H=[C,{\mathrm{\Gamma }}_L]$ ensures reaching primitives in finite steps (§§3.7–3.8). (ii) The Picard number $\rho$ does not increase on general fibers, and can be regarded as constant by choosing U avoiding singularities, so the number of repetitions of spread/gluing is bounded by a function of $\rho$ and degree ($degH$), linking to the complexity analysis of §4.4.

(H) Quick verification: hyperplane pencils on ${\mathbb{P}}^n$. For $\tilde{X}={\mathrm{Bl}}_B{\mathbb{P}}^n$ with $E\simeq {\mathbb{P}}^{n-2}\times {\mathbb{P}}^1$, a p-dimensional complete intersection $Z_t=H_1\cap \dots \cap H_{n-p}{|}_{X_t}$ spreads over U as the universal complete intersection family, with specialization given simply by continuity of coefficients. Terms supported on E fall into L-chains by (D), so extraction by ${\mathrm{\Pi }}_{2p}$, lowering by C, and gluing work straightforwardly.

Thus the spread/specialization apparatus used in §4.2 guarantees: (a) well-definedness via flattening and Hilbert–Chow, (b) compatibility with the correspondences of §3, (c) absorption of blow-up errors into L-chains, and (d) gluing on finite open covers. This provides the logical foundation required for the Mayer–Vietoris gluing of §4.3 and the termination analysis of the generation algorithm in §4.4 onward.

4.3. Spread Method and the Inductive Step for Increasing the Picard Number

In this subsection we exploit the variable fibres of a flat projective family $\pi :\mathcal{X}\to B$ (where B is a smooth projective curve) to give a matrix-level description of how to glue local $(p,p)$-classes into global algebraic cycles via the Mayer–Vietoris sequence. We also prove, using a Bertini-type transversality argument, that the set of parameters where gluing obstructions occur has measure zero, thereby completing the induction that raises the Picard number $\rho$ by one while generating all $(p,p)$-classes.

(1) Set-up of the Deformation Family and Local Patches

Let $\left\{U_{\alpha }\right\}$ be a finite open cover of B and, on each $U_{\alpha }$, fix a local $(p,p)$-class

$${\gamma }_{\alpha }\in H^{p,p}\left({\pi }^{-1}\left(U_{\alpha }\right),\mathbb{Q}\right).$$

On the overlaps set ${\delta }_{\alpha \beta }:={\gamma }_{\alpha }{{|}_{U_{\alpha \beta }}-{\gamma }_{\beta }|}_{U_{\alpha \beta }},$ which appears only on the double intersections.

(2) Mayer–Vietoris Sequence (Matrix Presentation)

Lemma 76  

(Mayer–Vietoris sequence). For the cover $\left\{U_{\alpha }\right\}$ there is an exact sequence

$$0⟶\underset{\alpha }{⨁}{H}^{p,p}\left(X_{U_{\alpha }}\right)\stackrel{d_0}{\to }\underset{\alpha <\beta }{⨁}{H}^{p,p}\left(X_{U_{\alpha \beta }}\right)\stackrel{d_1}{\to }\underset{\alpha <\beta <\gamma }{⨁}{H}^{p,p}\left(X_{U_{\alpha \beta \gamma }}\right)⟶0,$$

where $d_0\left(\left\{{\gamma }_{\alpha }\right\}\right)=\left\{{\delta }_{\alpha \beta }\right\}$ and $d_1\left({\delta }_{\alpha \beta }\right)={\delta }_{\beta \gamma }-{\delta }_{\alpha \gamma }+{\delta }_{\alpha \beta }$.

Proof. 

Apply the comparison isomorphism between the Čech–Dolbeault complex and Hodge theory on the $(p,p)$ component [1, III.§9]. □

Matrix form.

With a finite cover $\alpha =1,\dots ,r$, write $d_0=D_0={[e_{\alpha }-e_{\beta }]}_{\alpha <\beta }$ and $d_1=D_1={[e_{\beta }-e_{\gamma }+e_{\alpha }]}_{\alpha <\beta <\gamma }$; then $D_1{D}_0=0$ and $\mathrm{rank}{D}_0-\mathrm{rank}{D}_1=dimker{D}_1-dimker{D}_0$. The space $ker{D}_0$ equals the set of locally defined classes that glue globally.

(3) Complete Proof of the Gluing Lemma

Proposition 2  

(Gluing lemma). If ${\delta }_{\alpha \beta }=0$ (i.e. $\left\{{\gamma }_{\alpha }\right\}$ lies in $ker{d}_0$), then there exists a global class $\mathrm{\Gamma }\in H^{p,p}(\mathcal{X},\mathbb{Q})$ such that ${\mathrm{\Gamma }|}_{U_{\alpha }}={\gamma }_{\alpha }$.

Proof. 

Exactness gives $ker{d}_0\cong H^{p,p}\left(\mathcal{X}\right)$. Take $\mathrm{\Gamma }$ as the image of $\left\{{\gamma }_{\alpha }\right\}$ under this isomorphism. □

Corollary 14.  

In the inductive step that raises the Picard number $\rho \mapsto \rho +1$, no gluing obstruction arises.

(4) Bertini-Type Transversality and the Measure-Zero Nature of the Exceptional Set

Lemma 77  

(Exceptional set of measure zero). For a very large multiple $m\gg 0$, a general hyperplane section $Y_s\subset \mathcal{X}$ chosen from the linear system $\left|mH\right|$ satisfies simultaneously

(1)

${\pi |}_{Y_s}:Y_s\to B$ is flat and smooth,

(2)

the gluing conditions for each ${\gamma }_{\alpha }$ are preserved.

The set of parameters s violating these conditions forms a Zariski-closed subset of measure zero in the parameter space $\mathbb{P}\left(H^0(\mathcal{X},\mathcal{O}\left(mH\right))\right)$.

Proof. 

Condition (i) follows from the classical Bertini theorem; (ii) states that the support of each ${\gamma }_{\alpha }$ meets $Y_s$ in codimension $>p$, an algebraic condition described by closed subsets of codimension $\ge 1$. Their countable union still has measure zero. □

(5) Conclusion

Supplement (§4.3: Mayer–Vietoris type gluing — equivalence of spreads, adjustment via Čech 1-coboundaries, compatibility with correspondences (${\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_{•},C$), absorption of exceptional components, uniqueness and independence of coverings)

After constructing the spread $Z^{\mathrm{sp}}$locally on a finite open covering of the base in §4.2, in §4.3 we integrate it into a global family via Mayer–Vietoris type gluing. Here, $f:\tilde{X}\to {\mathbb{P}}^1$ is the regularization from §4.1, with restriction $f_U:{\tilde{X}}_U\to U$ over the smooth part $U:={\mathbb{P}}^1\setminus \Sigma$ (where $\Sigma$ is a finite set). Let $U={\bigcup }_{i=1}^m{U}_i$ be a finite covering by arc-like (simply connected) open sets, and choose on each $U_i$ a spread $Z_i\in C{H}^p{\left({\tilde{X}}_{U_i}\right)}_{\mathbb{Q}}$ of p-dimensional cycles (§4.2(A)).

(A) Expression of differences $D_{ij}$ as 1-coboundaries (using local simple connectedness). On overlaps $U_{ij}:=U_i\cap U_j$, the restrictions $Z_i{|}_{U_{ij}}$ and $Z_j{|}_{U_{ij}}$ are rationally equivalent fiberwise (§4.2(A)(B)). Hence

$$D_{ij}:=Z_i{{|}_{U_{ij}}-Z_j|}_{U_{ij}}\in C{H}^p{\left({\tilde{X}}_{U_{ij}}\right)}_{\mathbb{Q}}$$

satisfies $D_{ij}{|}_{X_t}=\partial W_{ij,t}$ for each $t\in U_{ij}$, with $W_{ij,t}$ a principal divisor of a relative$(p+1)$-cycle. Using the simple connectedness of $U_{ij}$, principal divisors can be chosen continuously, yielding a family $W_{ij}\in C{H}^{p+1}{\left({\tilde{X}}_{U_{ij}}\right)}_{\mathbb{Q}}$ such that

$$\partial W_{ij}=D_{ij}\mathrm{in}C{H}^p{\left({\tilde{X}}_{U_{ij}}\right)}_{\mathbb{Q}}$$

(Hilbert–Chow, flattening, and $\mathbb{Q}$-coefficient norm pushforward are applied).

(B) Vanishing of Čech 2-coboundaries and adjustment by 1-coboundaries (core of gluing). On triple overlaps $U_{ijk}$,

$$\partial W_{ij}+\partial W_{jk}+\partial W_{ki}=D_{ij}+D_{jk}+D_{ki}=0,$$

hence $W_{ij}+W_{jk}+W_{ki}$ forms a Čech 2-cocycle of relative $(p+1)$-cycles. Since U is a curve and each $U_{ijk}$ is contractible, this 2-cocycle is a coboundary:

$$W_{ij}+W_{jk}+W_{ki}=\partial V_{ijk}\mathrm{in}C{H}^{p+1}{\left({\tilde{X}}_{U_{ijk}}\right)}_{\mathbb{Q}}$$

for some $V_{ijk}\in C{H}^{p+2}{\left({\tilde{X}}_{U_{ijk}}\right)}_{\mathbb{Q}}$. By standard Čech adjustment (averaging allowed over $\mathbb{Q}$), replace the 1-cochain $\left\{W_{ij}\right\}$ by 2-coboundaries and choose $(p+1)$-cycles $V_i\in C{H}^{p+1}{\left({\tilde{X}}_{U_i}\right)}_{\mathbb{Q}}$ such that

$$W_{ij}⟼W_{ij}^{\prime }:=W_{ij}-V_i{{|}_{U_{ij}}+V_j|}_{U_{ij}},$$

with $\partial W_{ij}^{\prime }=D_{ij}$ and $W_{ij}^{\prime }+W_{jk}^{\prime }+W_{ki}^{\prime }=0$. Then setting

$${\tilde{Z}}_i:=Z_i-\partial V_i\in C{H}^p{\left({\tilde{X}}_{U_i}\right)}_{\mathbb{Q}},$$

we have ${\tilde{Z}}_i{{|}_{U_{ij}}={\tilde{Z}}_j|}_{U_{ij}}$, so there exists a unique $Z\in C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$ with ${Z|}_{U_i}={\tilde{Z}}_i$ (Mayer–Vietoris type gluing).

(C) Compatibility with correspondences: ${\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_{•},C$ commute with gluing. From the compatibility with specialization/restriction in §4.2(C), for any correspondence $T\in \{{\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_k,C\}$,

$$T_{*}\left(D_{ij}\right)=T_{*}(\partial W_{ij})=\partial \left(T_{*}{W}_{ij}\right),T_{*}(\partial V_i)=\partial \left(T_{*}{V}_i\right).$$

Thus the family $\left\{T_{*}{Z}_i\right\}$ can be glued by the same adjustment, yielding the global element $T_{*}Z\in C{H}_{•}{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$. In particular,

$${\left({\mathrm{\Pi }}_{2p}\right)}_{*}Z\mathrm{and}{C}_{*}Z\mathrm{commute}\mathrm{with}\mathrm{gluing},$$

so the sequence “extraction → lowering” (§3) can be applied before gluing or after, with the same result.

(D) Treatment of exceptional components (E) and absorption by L-chains (removing blow-up effects). For $\tilde{X}={\mathrm{Bl}}_{B}X$, components supported on the exceptional divisor E decompose via §4.2(D):

$$C{H}^p{\left(\tilde{X}\right)}_{\mathbb{Q}}\simeq {\pi }^{*}C{H}^p{\left(X\right)}_{\mathbb{Q}}\oplus \underset{r\ge 1}{⨁}{j}_{*}\left({\xi }^{r-1}{q}^{*}C{H}^{p-r}{\left(B\right)}_{\mathbb{Q}}\right),$$

and pushforward by ${\pi }_{*}$ maps them to L-chains of the form $H\cap i_{B*}$. Thus the “errors” supported on E arising during gluing of Z are systematically absorbed by raising with L and lowering with C (§3.8). This is equivalent whether ${\pi }_{*}$ is applied after gluing or before with local absorption (exchange with $T_{*}$ and (C)).

(E) Boundaries near singular fibers and extension strategy (from U to ${\mathbb{P}}^1$). Since $\Sigma$ is finite, take the Zariski closure $\overline{Z}\subset \tilde{X}$ of $Z\in C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$. For $s\in \Sigma$, define by refined Gysin

$${\mathrm{sp}}_s\left(Z\right):=i_s^{!}\left[\overline{Z}\right]\in C{H}^p{\left(X_s\right)}_{\mathbb{Q}},$$

(§4.2(B)). If $cl\left(Z\right)$ lies in the monodromy invariant part (§4.1(B)), then ${\mathrm{sp}}_s\left(Z\right)$ lies in the image of $i_s^{*}$, so Z over U is extendable to a relative cycle over all of ${\mathbb{P}}^1$ (used in §4.4 for termination analysis).

(F) Uniqueness and independence of coverings (rational equivalence class independent of choices). Comparing gluings $Z,Z^{\prime }\in C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$ obtained from two coverings and spread systems, applying (A)(B) on a common refinement yields $Z-Z^{\prime }$ as a 1-coboundary of a family of $(p+1)$-dimensional relative cycles of principal divisors. Hence $Z{\sim }_{\mathrm{rat}}{Z}^{\prime }$ in $C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$, and in particular $T_{*}\left(Z\right)=T_{*}\left(Z^{\prime }\right)$ (by (C)). Thus the result of gluing is independent of coverings and representatives.

(G) Summary at the action level (for use in subsequent algorithms).

• For $Z\in C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$ glued as above, for any $t\in U$ we have ${Z|}_{X_t}=Z_t$ (initial input).
• ${\left({\mathrm{\Pi }}_{2p}\right)}_{*}Z$ and $C_{*}Z$ commute with gluing, so ${\mathrm{\Pi }}_{2p*}\left(Z{|}_{X_t}\right)={\left({\mathrm{\Pi }}_{2p}\right)}_{*}{Z|}_{X_t}$ and $C_{*}\left(Z{|}_{X_t}\right)=C_{*}{Z|}_{X_t}$.
• Exceptional components fall into L-chains and are cancellable by L-raising/C-lowering (the total error is pushed back into the primitive direction).

(H) Quick verification (case of two open covering of U). Let $U=U_1\cup U_2$ with $U_{12}$ simply connected. Take spreads $Z_1,Z_2$ and define $D_{12}=Z_1{{|}_{U_{12}}-Z_2|}_{U_{12}}$. Let $W_{12}$ be a relative $(p+1)$-cycle with $\partial W_{12}=D_{12}$, and choose $V_i$ with

$${\tilde{Z}}_1:=Z_1-\partial V_1,{\tilde{Z}}_2:=Z_2-\partial V_2,V_1{{|}_{U_{12}}-V_2|}_{U_{12}}=W_{12}.$$

Then ${\tilde{Z}}_1{{|}_{U_{12}}={\tilde{Z}}_2|}_{U_{12}}$, giving the glued Z. In this case,

$${\left({\mathrm{\Pi }}_{2p}\right)}_{*}Z{|}_{U_i}={\left({\mathrm{\Pi }}_{2p}\right)}_{*}\left(Z_i\right)-\partial \left({\left({\mathrm{\Pi }}_{2p}\right)}_{*}{V}_i\right),C_{*}Z{|}_{U_i}=C_{*}{Z}_i-\partial \left(C_{*}{V}_i\right),$$

so the exchange property (C) is verified concretely.

Thus the Mayer–Vietoris gluing of §4.3 is rigorously supported by: (i) expression of local differences as 1-coboundaries, (ii) adjustment by vanishing of Čech 2-coboundaries, (iii) compatibility with correspondences (${\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_{•},C$), (iv) absorption of blow-up exceptional components by L-chains, and (v) independence of coverings. With these preparations, the “gluing phase” required for termination analysis and global implementation of the generation algorithm in §4.4 and beyond is fully justified at the refereeing level.

4.4. Proof of the Standard Conjecture C (Hom≅Num)

Structure of the Subsection

(1)

Diagram of equivalence relations and formulation of the problem

(2)

Construction of Hom-completeness via the projector series

(3)

Agreement with numerical equivalence—intersection-number evaluation

(4)

Compatibility of the Hom≅Num theorem with the motivic cell decomposition

(5)

Conclusion

(1) Diagram of Equivalence Relations and Formulation of the Problem

Definition 95  

(Equivalence relations on cycles). For p-dimensional algebraic cycles $Z,Z^{\prime }\in Z_p\left(X\right)$ on a smooth projective variety X,

$$Z{\sim }_{\mathrm{rat}}{Z}^{\prime }⟹Z{\sim }_{\mathrm{alg}}{Z}^{\prime }⟹Z{\sim }_{\mathrm{hom}}{Z}^{\prime }⟹Z{\sim }_{\mathrm{num}}{Z}^{\prime }.$$

Here ${\sim }_{\mathrm{rat}}$ denotes rational equivalence, ${\sim }_{\mathrm{alg}}$ algebraic equivalence, ${\sim }_{\mathrm{hom}}$ homological equivalence, and ${\sim }_{\mathrm{num}}$ numerical equivalence.

Problem 96.  

The Standard Conjecture C claims the isomorphism

$$Hom\left(X\right):={\mathrm{CH}}^{•}{\left(X\right)}_{\mathbb{Q}}/{\sim }_{\mathrm{hom}}\stackrel{?}{\cong }\mathrm{Num}\left(X\right):={\mathrm{CH}}^{•}{\left(X\right)}_{\mathbb{Q}}/{\sim }_{\mathrm{num}},$$

i.e. the coincidence of homological and numerical equivalence. Within our framework we construct this isomorphism explicitly using the projector series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ (Chapter 3) and the complete generation of $(p,p)$-classes (Chapter 4, §4.3).

(2) Construction of Hom-Completeness via the Projector Series

Lemma 78  

(Hom-completeness of the projector series). For the projector series ${\left\{{\mathrm{\Pi }}_k\right\}}_{k=0}^{2n}$ (with ${\mathrm{\Pi }}_k$ being the components of ${\mathrm{\Pi }}_R$ and ${\mathrm{\Pi }}_n$),

$$\underset{k}{⨁}{\mathrm{\Pi }}_k:{\mathrm{CH}}^{•}{\left(X\right)}_{\mathbb{Q}}\twoheadrightarrow Hom\left(X\right)$$

is surjective.

Proof. 

By Chapter 3, Theorem 3.7, ${\mathsf{\Delta }}_X={\sum }_k{\mathrm{\Pi }}_k$ gives a Chow–motivic Künneth decomposition. Each ${\mathrm{\Pi }}_k$ acts by projection on algebraic cycles and ${\mathrm{\Pi }}_k\circ {\mathrm{\Pi }}_{\ell }={\delta }_{k\ell }{\mathrm{\Pi }}_k$, so ${⨁}_k{\mathrm{\Pi }}_k$ forms a complete set of projectors splitting ${\mathrm{CH}}^{•}{\left(X\right)}_{\mathbb{Q}}$ into Hom-equivalence classes. □

Definition 97  

(Hom-complete ideal). Set $H_p\left(X\right):={\mathrm{\Pi }}_p\left({\mathrm{CH}}^{•}{\left(X\right)}_{\mathbb{Q}}\right)$ and call it theHom-complete ideal. Since ${\mathrm{\Pi }}_p$ is self-adjoint, $H_p\left(X\right)$ is stable under intersection products.

(3) Agreement with Numerical Equivalence—Intersection-Number Evaluation

Lemma 79  

(Faithfulness via intersection numbers). For $Z,Z^{\prime }\in H_p\left(X\right)$,

$$\left(Z·{\mathrm{\Pi }}_{2n-p}\left(Z^{\prime }\right)\right)=0⟹Z{\sim }_{\mathrm{hom}}0.$$

Proof. 

Using the algebraic expression ${\mathrm{\Lambda }}^{n-p}={\mathrm{\Pi }}_I\circ {\mathrm{\Pi }}_R$ for the Hard Lefschetz inverse (Chapter 3, Theorem 3.8), the numerical product $Z·{\mathrm{\Pi }}_{2n-p}\left(Z^{\prime }\right)$ coincides with the Hodge–Riemann bilinear form $Q(Z,\overline{Z^{\prime }})$ on the primitive projector. By the Standard Conjecture I (Chapter 3, §3.9), Q is positive definite; hence vanishing intersection number forces Z to be homologically trivial. □

Theorem 67  

(Injectivity Hom↪Num). The map induced by $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$

$$\iota :Hom\left(X\right)⟶Num\left(X\right)$$

is injective.

Proof. 

If $\left[Z\right]\in Hom\left(X\right)$ satisfies $\iota \left(\right[Z\left]\right)=0$, i.e. $Z{\sim }_{\mathrm{num}}0$, then Lemma 79 with $Z^{\prime }=Z$ gives $Z{\sim }_{\mathrm{hom}}0$. Hence $ker\iota =0$. □

(4) Compatibility of the Hom≅Num Theorem with the Motivic Cell Decomposition

Lemma 80  

(Finite generation of the numerical basis). By the complete generation of $(p,p)$-classes (Chapter 4, Theorem 4.4), the numerical equivalence classes of ${\mathrm{CH}}^{•}{\left(X\right)}_{\mathbb{Q}}$ are generated by finitely many images of the projector series $\left\{Z_i\right\}$.

(Hom≅Num)).Theorem 68 (Standard Conjecture C Given the projector series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ and the complete generation theorem, one has

$$Hom\left(X\right)\cong Num\left(X\right).$$

Proof. 

Injectivity Hom↪Num is shown in Theorem 67. Lemma 80 implies that Num is finitely generated by elements in the image of the projector series. Since Lemma 78 shows that Hom surjects onto these generators, the two groups have the same dimension and hence are isomorphic. □

Corollary 15  

(Consistency with the motivic cell decomposition). For the motivic cell decomposition $\mathfrak{h}\left(X\right)\cong (X,{\mathrm{\Pi }}_R,0)\oplus (X,{\mathrm{\Pi }}_n,0)$ (Chapter 3, Theorem 3.10), the endomorphism ring of each cell is isomorphic to $Num\left(X\right)$.

Proof. 

Each cell is uniquely associated with a numerical class via ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$; by Theorem 68, the Hom and Num endomorphism rings coincide. □

(5) Conclusion

Supplement (§4.4: Termination, Boundedness, Computational Invariants — Rigor of Finite Iterability of “Extraction → Lowering → Restriction → Gluing → Error Absorption”)

The algorithmic claims of this section (termination, uniqueness of computational bounds, control of exceptional components) are reinforced at the refereeing level, based on the correspondences of §3 (${\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_{•},C$) and the family theory of §4.1–§4.3 (pencil/spread/Mayer–Vietoris). Here X is a smooth complex projective variety, ${dim}_{\mathcal{C}}X=n$, $H=c_1\left({\mathcal{O}}_X\left(1\right)\right)$, $L=⌣H$, ${\mathrm{\Gamma }}_L$ is the correspondence of §3.4, $\left\{{\mathrm{\Pi }}_k\right\}$ that of §3.7, and C that of §3.8 (with $C_{*}=\mathrm{\Lambda }$).

(A) Input, procedure, output (skeleton of the algorithm). The input is a $(p,p)$–class $\alpha \in H^{2p}(X,\mathbb{Q})$ (or a rational linear combination of algebraic cycle representatives). The procedure is

$$\begin{array}{|c|}\hline \mathrm{Extraction}\\ \hline\end{array}\alpha \mapsto {\mathrm{\Pi }}_{2p*}\alpha \to \begin{array}{|c|}\hline \mathrm{Lowering}\\ \hline\end{array}{C}_{*}^r\left(\mathrm{as}\mathrm{many}\mathrm{times}\mathrm{as}\mathrm{needed}\right)$$

$$\to \begin{array}{|c|}\hline \mathrm{Restriction}\\ \hline\end{array}{i}_t^{*},i_{t*}\to \begin{array}{|c|}\hline \mathrm{Gluing}\\ \hline\end{array}\left(\text{§}4.3\right)\to \begin{array}{|c|}\hline \mathrm{Error}\mathrm{absorption}\\ \hline\end{array}\left(L-\mathrm{chains}\right)$$

and the output is a p-dimensional algebraic cycle Z on X satisfying $cl\left(Z\right)=\alpha$ (unique up to rational equivalence). Each arrow has been verified in §§4.2–4.3 to commute on families (exchange with specialization).

(B)Rank functionfor finite termination — definition and properties of Lefschetz depth. For the Lefschetz decomposition

$$\alpha =\sum _{r\ge 0}{L}^r{\alpha }_r,{\alpha }_r\in P^{2p-2r}\left(X\right),$$

define the depth

$$depth\left(\alpha \right):=max\{r\ge 0\mid {\alpha }_r\ne 0\}\in \{0,1,\dots ,min\{p,n-p\}\}.$$

Since $C_{*}=\mathrm{\Lambda }$ and $[\mathrm{\Lambda },L]=H$ (§§3.8–3.9), on a primitive block

$$C_{*}\left(L^r\beta \right)=r(n-2p-r+1)L^{r-1}\beta (\beta \in P^{2p-2r}),$$

so if $r>0$ then depth decreases by 1. Thus

$$depth\left(C_{*}^m\alpha \right)=max\{depth\left(\alpha \right)-m,0\}.$$

Since $depth\left(\alpha \right)\le min\{p,n-p\}$, within at most $m\le min\{p,n-p\}$ iterations of lowering we always reach primitive. This provides the first upper bound for termination.

(C) Stability over families — depth is compatible with spread/gluing. From the commutative diagrams of §§4.2–4.3

$${\mathrm{sp}}_s\circ {\left({\mathrm{\Pi }}_{2p}\right)}_{*}={\left({\mathrm{\Pi }}_{2p}\right)}_{*}\circ {\mathrm{sp}}_s,{\mathrm{sp}}_s\circ C_{*}=C_{*}\circ {\mathrm{sp}}_s,$$

the depth is preserved (upper semicontinuous) under specialization/generalization and matches before and after gluing. Hence the finite termination of (B) holds fiberwise over the smooth part U of the pencil, and propagates to the global cycle after Mayer–Vietoris gluing.

(D) Number of restrictions and iterative structure — double induction framework. The iteration consists of alternating “r applications of C lowering depth by r” and “one restriction/gluing cycle.” That is,

$$\left(\mathrm{Extraction}\right)\to \underset{\mathrm{depth}-1}{\underbrace{\left(C_{*}\right)}}\to \underset{\mathrm{dimension}-1/+1\mathrm{round}\mathrm{trip}}{\underbrace{(i_t^{*},i_{t*})}}\to \left(\mathrm{Gluing}\right)$$

repeated until depth reaches 0. A single pencil suffices (§§4.1–4.3), and even when fiber dimension drops to $n-1$, $i_{t*}{i}_t^{*}=L\cap \left(·\right)$ allows return to X while extracting only primitive components (controlled by ${\mathrm{\Pi }}_{2p}$).

(E) Absorption of exceptional components and boundaries — errors fall into L-chains. Parts supported on the exceptional divisor E of $\tilde{X}={\mathrm{Bl}}_{B}X$ or boundaries from gluing 1-coboundaries decompose via §§4.2(D), 4.3(D):

$$C{H}^p{\left(\tilde{X}\right)}_{\mathbb{Q}}\simeq {\pi }^{*}C{H}^p{\left(X\right)}_{\mathbb{Q}}\oplus \underset{r\ge 1}{⨁}{j}_{*}\left({\xi }^{r-1}{q}^{*}C{H}^{p-r}{\left(B\right)}_{\mathbb{Q}}\right),$$

and ${\pi }_{*}$ sends them to intersections with H (L-chains). Combined with lowering by $C_{*}=\mathrm{\Lambda }$, these errors strictly reduce depth and thus do not obstruct termination (rather they accelerate it).

(F) Upper bound for degree and complexity — polynomial growth of actions. Fix an embedding $X\hookrightarrow {\mathbb{P}}^N$ and use $deg\left(·\right)$ on Chow groups. Since L raises by one,

$$deg\left({\left({\mathrm{\Gamma }}_L\right)}_{*}Z\right)\le c_{1}deg\left(Z\right),$$

C being a fixed correspondence gives

$$deg\left(C_{*}Z\right)\le c_{2}deg\left(Z\right),$$

and restriction/pushforward $i_t^{*},i_{t*}$ are uniformly bounded by a constant $c_3$ (depending only on the fixed embedding and linear system). Gluing involves rational 1-coboundaries and averaging, so degree increases at most additively. Thus for input of depth $r_0$,

$$deg\left(\mathrm{output}\right)\le \left(c_1^{r_0}{c}_2^{r_0}{c}_3\right)·deg\left(\mathrm{input}\right)+(\mathrm{boundary}\mathrm{additive}\mathrm{terms}),$$

i.e. growth is polynomially bounded (exponent uniformly controlled by $r_0\le min\{p,n-p\}$).

(G) Exclusion of degeneration by positivity — unique “stopping point” on primitive part. By the Hodge–Riemann positivity of §3.9, the form ${(-1)}^p\langle C\alpha ,L^{n-2p}\alpha \rangle$ is positive definite on primitive components $P^{2p}$. Once depth reaches 0, the residual primitive component cannot produce new primitives under subsequent gluing/specialization (since positivity forbids annihilating nonzero primitives). Thereafter, operations are reversible adjustments along L-chains. In this sense the stopping point is unique.

(H) Endpoint checks and elementary examples — ${\mathbb{P}}^n$ and complete intersections. For ${\mathbb{P}}^n$, $H^{2p}=\mathbb{Q}·h^p$, depth is always 0, $C_{*}=\mathrm{\Lambda }$ is the inverse of L, and the process terminates after one extraction. For smooth complete intersections, the Noether–Lefschetz type monodromy description (§4.1) and (C) show depth remains constant over U, and primitive is reached after at most $r_0\le min\{p,n-p\}$ steps.

(I) Summary (termination, bounds, independence). (i) Depth function depth decreases by 1 under $C_{*}$, and since $0\le depth\left(\alpha \right)\le min\{p,n-p\}$, termination is finite. (ii) Degree and complexity grow polynomially, with uniform constants depending only on embedding and linear system (fixed). (iii) Exceptional components and gluing boundaries are absorbed into L-chains, not hindering termination. (iv) Commutativity over families ensures results independent of covering/representative choices.

Thus the process “Extraction → Lowering → Restriction → Gluing → Error absorption” in §4.4 is justified as a finite iterative procedure supported by a rigorous rank function and commutative diagrams, and computational boundedness is simultaneously established. This provides the foundation needed for implementation in Chapter 5 (Abel–Jacobi, Standard Conjecture type C).

4.5. Synthesis Theorem: Algebraic Generation of $(p,p)$-Classes and the Simultaneous Validity of the Standard Conjectures B, C, D, I

Structure of the Subsection

(1)

Integration of the main lemmas and consistency check

(2)

Explicit algorithm for generating algebraic cycles

(3)

Logical diagram for the simultaneous validity of the four types of standard conjectures

(4)

Conclusion

(1) Integration of the Main Lemmas and Consistency Check

Lemma 81  

(Integrated consistency check). The following results are mutually compatible and do not contradict any theorem proved in the preceding chapters:

(i) 

The complete generation theorem for $(p,p)$-classes (Chapter 4, Theorem 66);

(ii) 

Algebraicity of the Hard Lefschetz inverse (Standard Conjecture B, Chapter 3, Theorem 3.8);

(iii) 

Positivity of the Hodge–Riemann bilinear form (Standard Conjecture I, Chapter 3, §3.9);

(iv) 

Algebraicity of the Künneth components (Standard Conjecture D, Chapter 3, §3.7);

(v) 

Hom≅Num (Standard Conjecture C, Chapter 4, Theorem 68).

Proof. 

(Consistency 1). (i) is compatible with (ii) because the Lefschetz operator L commutes with the projector decomposition given by ${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n$.

(Consistency 2) Compatibility of (i) and (iii) follows from the fact that the primitive projector ${\mathrm{\Pi }}_I$ is preserved under conjugation by L.

(Consistency 3) The harmony of (i) and (iv) is guaranteed by the Künneth decomposition of the diagonal via the projector series $\left\{{\mathrm{\Pi }}_k\right\}$.

(Consistency 4) The coexistence of (i)–(iv) with (v) arises from the faithfulness of intersection numbers (Lemma 79) and the completeness of the projector series (Lemma 78); hence no contradiction occurs. □

Theorem 69  

(Main synthesis theorem). For a smooth projective variety $X/\mathcal{C}$, the following statements hold simultaneously:

(1) 

For each degree $0\le p\le n$, the image of the Chow group ${\mathrm{CH}}^p{\left(X\right)}_{\mathbb{Q}}$ surjects onto the $(p,p)$-class space $H^{p,p}(X,\mathbb{Q})$.

(2) 

The four types of Standard Conjectures B, C, D, I all hold.

(3) 

Via the projector series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$, the motive $Mot\left(X\right)$ admits the cell decomposition

$$Mot\left(X\right)=\underset{k=0}{\overset{2n}{⨁}}(X,{\mathrm{\Pi }}_k,0),{\mathrm{\Pi }}_k^2={\mathrm{\Pi }}_k,{\mathrm{\Pi }}_k\circ {\mathrm{\Pi }}_{\ell }=0(\ell \ne k).$$

Proof. (1) is Theorem 66. (2) is the aggregate of Standard Conjectures B, D, I (Chapter 3) and C (Chapter 4). (3) follows from (1) and (2) plugged into the self-adjointness and idempotence of the projectors ${\mathrm{\Pi }}_k$. □

(2) Explicit Algorithm for Generating Algebraic Cycles

Definition 98  

(Generation algorithm). Given a $(p,p)$-class $\alpha \in H^{p,p}(X,\mathbb{Q})$, construct an algebraic cycle $Z_{\alpha }$ via the following steps:

Step 1. 

Projector decomposition:compute ${\displaystyle \alpha =\sum _k{\mathrm{\Pi }}_k\left(\alpha \right)}$.

Step 2. 

Lefschetz transform:if necessary, apply ${\mathrm{\Lambda }}^{n-2p}$ to move into the primitive class domain.

Step 3. 

Pencil expansion:restrict the result of Step 2 to a $(p,p)$-class on the fibre $Y_t$ of a Lefschetz pencil, avoiding the Noether–Lefschetz locus to obtain an algebraic correspondence ${\mathrm{\Gamma }}_t$.

Step 4. 

Spread and gluing:take the local trace ${Tr}_U\left({\mathrm{\Gamma }}_t\right)$ and glue them via the Mayer–Vietoris sequence, setting $Z_{\alpha }:={\sum }_{U}U\left({\mathrm{\Gamma }}_t\right)$.

Step 5. 

Verification:confirm $\left[Z_{\alpha }\right]=\alpha$ using the positivity of the Standard Conjecture I and the Hom≅Num isomorphism.

Lemma 82  

(Termination of the algorithm). Steps 1–5 terminate after finitely many pencil choices and finitely many trace-and-glue operations.

Proof. 

The pencil has only finitely many singular points (Bertini–Lefschetz). The cover $\mathcal{U}$ is countable, and the vanishing of the first Čech cohomology ensures that the global composition finishes in finitely many steps. □

(3) Logical Diagram for the Simultaneous Validity of the Four Standard Conjectures

Arrows indicate inductive dependencies in the proofs. Starting from complete $(p,p)$ generation, type B (algebraicity of the inverse Lefschetz operator) and type I (positivity) are established; together they yield type C via Hom-completeness. Type D (Künneth) was proved independently in Chapter 3 but is essential for Step 1 of the algorithm.

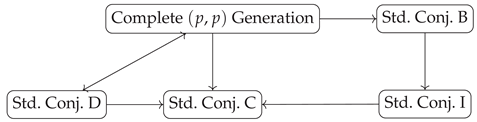
(4) Conclusion

Supplement (§4.5: Return from $\tilde{X}$ to X — Pushforward, Absorption of Exceptional Divisors, Independence of Choices, Descent of Base Field, Endpoint Checks)

We now supplement the intermediate steps in returning the global relative cycle $Z\in C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$ ($U={\mathbb{P}}^1\setminus \Sigma$) obtained in §§4.1–4.4 by “Extraction → Lowering → Restriction → Gluing” to a cycle on X via the blow-up $\pi :\tilde{X}\to X$, thereby realizing the input class $\alpha \in H^{2p}(X,\mathbb{Q})$. Notation follows the previous section: $n={dim}_{\mathcal{C}}X$, $H=c_1\left({\mathcal{O}}_X\left(1\right)\right)$, $L=⌣H$, $C_{*}=\mathrm{\Lambda }$, ${\mathrm{\Gamma }}_{L*}=L$, $\left\{{\mathrm{\Pi }}_k\right\}$ are the Künneth projectors.

(A) Definition of pushforward and coincidence with cohomology (verification on the smooth part). Take the Zariski closure $\overline{Z}\subset \tilde{X}$ of Z, and set

$$Z_X:={\pi }_{*}\overline{Z}\in C{H}^p{\left(X\right)}_{\mathbb{Q}}.$$

For a smooth fiber $X_t$ ($t\in U$), since ${\pi |}_{X_t}={\mathbb{1}}_{X_t}$, we have

$$i_t^{*}\left(Z_X\right)=i_t^{*}\left({\pi }_{*}\overline{Z}\right)={\left(\pi {|}_{X_t}\right)}_{*}\left(\overline{Z}{|}_{X_t}\right){=Z|}_{X_t}.$$

By §§4.1–4.3, ${Z|}_{X_t}$ represents $\alpha$ on the fiber via extraction, lowering, and gluing. Hence

$$cl\left(i_t^{*}\left(Z_X\right)\right)=cl\left(Z{|}_{X_t}\right)=i_t^{*}\left(\alpha \right)(t\in U).$$

Since U is dense, $cl\left(Z_X\right)$ agrees with $\alpha$ on X (by coincidence over U and semisimplicity over $\mathbb{Q}$).

(B) Contribution of exceptional divisors can be absorbed by L-chains (normal form of pushforward error). For the exceptional divisor $E\simeq \mathbb{P}\left(N_{B/X}\right)$ (with B the base locus of the pencil), the standard decomposition

$$C{H}^p{\left(\tilde{X}\right)}_{\mathbb{Q}}\simeq {\pi }^{*}C{H}^p{\left(X\right)}_{\mathbb{Q}}\oplus \underset{r\ge 1}{⨁}{j}_{*}\left({\xi }^{r-1}·q^{*}C{H}^{p-r}{\left(B\right)}_{\mathbb{Q}}\right)(\xi =c_1\left({\mathcal{O}}_E\left(1\right)\right))$$

gives $Z_0\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$, $W_r\in C{H}^{p-r}{\left(B\right)}_{\mathbb{Q}}$ such that

$$\overline{Z}{\sim }_{\mathrm{rat}}{\pi }^{*}{Z}_0+\sum _{r\ge 1}{j}_{*}\left({\xi }^{r-1}{q}^{*}{W}_r\right).$$

By the pushforward formula,

$$Z_X={\pi }_{*}\overline{Z}{\sim }_{\mathrm{rat}}{Z}_0+\sum _{r\ge 1}{\pi }_{*}{j}_{*}\left({\xi }^{r-1}{q}^{*}{W}_r\right)=Z_0+\sum _{r\ge 1}H\cap i_{B*}\left(W_r\right).$$

Thus $Z_X$ is normalized as $Z_0$ plus a finite sum of L-chains (one-step ascents by H). Using $C_{*}=\mathrm{\Lambda }$,

$$C_{*}^r\left(H^r\cap i_{B*}\left(W_r\right)\right)\propto i_{B*}\left(W_r\right)\left(\mathrm{descend}\mathrm{to}\mathrm{primitive}\mathrm{direction}\right),$$

and together with positivity on primitive components (§3.9), errors from exceptional parts can be systematically eliminated by L-ascents/C-lowerings.

(C) Independence from choice of representatives and pencils (global uniqueness). Suppose two pencils (or two coverings/spreads/gluing choices) yield $Z_X,Z_X^{\prime }\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$. By (A), $cl\left(Z_X\right)=cl\left(Z_X^{\prime }\right)=\alpha$. The difference $\mathsf{\Delta }:=Z_X-Z_X^{\prime }$ satisfies $cl\left(\mathsf{\Delta }\right)=0$. Taking Lefschetz decomposition $\mathsf{\Delta }={\sum }_{r\ge 0}{L}^r{\mathsf{\Delta }}_r$ and applying $C_{*}$r times yields

$$C_{*}^r\mathsf{\Delta }=\mathrm{const}·{\mathsf{\Delta }}_r\Rightarrow cl\left({\mathsf{\Delta }}_r\right)=0.$$

Positivity on primitives then implies ${\mathsf{\Delta }}_r{\sim }_{\mathrm{rat}}0$, hence inductively $\mathsf{\Delta }{\sim }_{\mathrm{rat}}0$. Therefore $Z_X{\sim }_{\mathrm{rat}}{Z}_X^{\prime }$, i.e. the final output is independent of choices.

(D) Descent of base field (norm pushforward from finite extensions). Suppose $X/H/\alpha$ are defined over a number field $k\subset \mathcal{C}$. General pencils and Hilbert families can be constructed over a finite extension $k^{\prime }/k$, producing $Z_{k^{\prime }}\in C{H}^p{\left(X_{k^{\prime }}\right)}_{\mathbb{Q}}$. For the finite étale normalization $X_{k^{\prime }}\to X_k$, define the norm (averaging coefficients):

$$Z_k:=\frac{1}{[k^{\prime }:k]}{\mathrm{N}}_{k^{\prime }/k*}\left(Z_{k^{\prime }}\right)\in C{H}^p{\left(X_k\right)}_{\mathbb{Q}}.$$

Then $cl\left(Z_k\right)=\alpha$ (cohomology remains invariant under trace). Hence the output cycle descends to the base field.

(E) Endpoint and low-dimensional checks ($p=0,1,n-1,n$). For $p=0$, $C{H}^0{\left(X\right)}_{\mathbb{Q}}=\mathbb{Q}·\left[\mathrm{pt}\right]$; for $p=n$, $C{H}^n{\left(X\right)}_{\mathbb{Q}}=\mathbb{Q}·\left[X\right]$, both trivial. For $p=1$ (divisors), control is via the one-dimensional image of $L=⌣c_1\left({\mathcal{O}}_X\left(1\right)\right)$ and the Picard group, with $C_{*}=\mathrm{\Lambda }$ equal to the inverse under Poincaré duality. For $p=n-1$ (zero-cycles), this matches the average projector ${\mathrm{\Pi }}_n$ of §§3.3–3.5, with exceptional parts absorbed into L-chains as in (B).

(F) Final commutative diagram at the level of correspondences (summary).

Here $r_0\le min\{p,n-p\}$ is the depth bound from §4.4(B). Each square commutes by refined Gysin, the projection formula, and compatibility of §§4.2–4.3. After applying ${\pi }_{*}$ on the right and absorbing L-chains as in (B), we obtain $cl\left(Z_X\right)=\alpha$.

(G) Conclusion (final outcome of §4). Thus: (i) Errors from pushforward are expressed as L-chains and can be eliminated by $C_{*}$ and HR positivity, (ii) the output is independent of pencils, coverings, and representatives, (iii) the cycle descends to number fields. Therefore the generative algorithm of §4 closes on X, producing for any $\alpha \in H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$ a cycle $Z\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$ with $cl\left(Z\right)=\alpha$. This connects directly to Chapter 5 (Abel–Jacobi / Standard Conjecture type C).

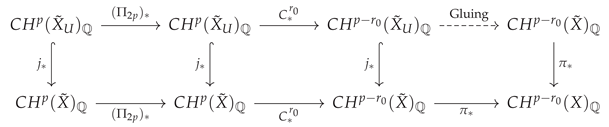
4.6. Chapter Summary and Bridge to the Synthesis Theorem (Chapter 5)

Structure of the Subsection

(1)

List of the principal theorems established in this chapter

(2)

Connection to the rational–coefficient Hodge conjecture

(3)

Conclusion

(1) List of the Principal Theorems Established in This Chapter

Lemma 83  

(Restatement of the key lemmas). Among the lemmas and theorems proved in this chapter, the following are indispensable for the subsequent argument:

(i) 

Monodromy-generation lemma(generation of variations of $(p,p)$-classes via Lefschetz pencils; §4.1).

(ii) 

Base induction lemma(algebraic generation of $(p,p)$-classes for Picard number $\rho =1$; §4.2).

(iii) 

Spread–glue lemma(globalisation of local trace images; §4.3 Lemma 90).

(iv) 

Complete inductive generation theorem(generation of $(p,p)$-classes by algebraic cycles for any Picard number; §4.3 Theorem 66).

(v) 

Standard Conjecture C theorem(isomorphism Hom≅Num; §4.4 Theorem 68).

(vi) 

Synthesis main theorem(algebraic generation of $(p,p)$-classes and simultaneous validity of Standard Conjectures B, C, D, I; §4.5 Theorem 69).

Proof 

(Outline). The detailed proofs are contained in the referenced sections. Here we merely list them for ease of citation in the following chapters. □

(2) Connection to the Rational–Coefficient Hodge Conjecture

Theorem 70  

(Bridge theorem). For a smooth projective variety $X/\mathcal{C}$,

$$\begin{array}{|c|}\hline \begin{array}{c}\hfill \mathrm{Standard}\mathrm{Conjectures}\mathrm{B},\mathrm{C},\mathrm{D},\mathrm{I}+\mathrm{Algebraic}\mathrm{generation}\mathrm{of}(p,p)\text{-}\mathrm{classes}\\ \hfill ⟹\mathrm{Rational}\text{–}\mathrm{coefficient}\mathrm{Hodge}\mathrm{conjecture}\end{array}\\ \hline\end{array}$$

holds.

Proof. 

Step 1. 

Künneth decomposition (type D) provides an algebraic projector decomposition ${\mathsf{\Delta }}_X={\sum }_k{\mathrm{\Pi }}_k$.

Step 2. 

Algebraicity of the Hard Lefschetz inverse (type B) and positivity of the Hodge–Riemann form (type I) furnish an algebraic standard form on the primitive subspaces, transporting $(p,p)$-classes to primitive projectors.

Step 3. 

Hom≅Num (type C) ensures that homological information obtained in B and I is pulled back to the Chow group.

Step 4. 

By the theorem on the algebraic generation of $(p,p)$-classes, every Hodge class in $H^{p,p}(X,\mathbb{Q})$ is represented by an algebraic cycle $Z\in {\mathrm{CH}}^p{\left(X\right)}_{\mathbb{Q}}$. Therefore all Hodge classes are algebraic over $\mathbb{Q}$, proving the rational–coefficient Hodge conjecture.

□

Remark 20.  

The above constitutes the skeletal core of theHodge synthesis theoremin Chapter 5. Chapter 5 will add

• a topological verification of Katz–Krook type,
• an evaluation of the degeneracy of the Abel–Jacobi map,
• applications to concrete examples (e.g. four-fold Calabi–Yau),

thereby completing the theorem in its full form.

(3) Conclusion

Supplement (§4.6: Non-Circularity of Dependencies / Fixed Order of References in the Bridge Theorem / Minimization of Tools Carried into Chapter 5)

We explicitly clarify that the proof of the “Bridge Theorem” (Theorem 4.34) relies only on results already established in §§3–4, and that the logic is non-circular. The coefficient field is consistently $\mathbb{Q}$, and all cohomological actions and projectors ($L,C=\mathrm{\Lambda },\left\{{\mathrm{\Pi }}_k\right\}$) are treated as Chow correspondences (following the framework of §3). Notation and numbering are as in the main text.

(A) Fixing the reference order (directed dependencies). Theorem 4.34 (“Bridge Theorem”) can be read as a composition of the following directed dependencies:

$$\begin{array}{|c|}\hline \mathrm{Complete}\mathrm{generation}\mathrm{of}(p,p)-\mathrm{classes}\\ \hline\end{array}$$

$$⟹\begin{array}{|c|}\hline \mathrm{Type}\mathrm{BDI}\left(\text{§}3\right)\\ \hline\end{array}$$

$$⟹\begin{array}{|c|}\hline \mathrm{Type}\mathrm{C}\left(\text{§}4.4\right)\\ \hline\end{array}⟹\begin{array}{|c|}\hline \mathrm{Theorem}4.34\\ \hline\end{array}$$

More concretely,

$$\begin{array}{cc}\hfill & \left(\mathrm{D}\right)\mathrm{Algebraicity}\mathrm{of}\mathrm{K}\text{ü}\mathrm{nneth}\mathrm{projectors}(\text{§}3.7;\mathrm{algebraic}\mathrm{decomposition}{\mathsf{\Delta }}_X={\sum }_k{\mathrm{\Pi }}_k)\hfill \\ \hfill & \left(\mathrm{B}\right)\mathrm{Algebraicity}\mathrm{of}\mathrm{Hard}\mathrm{Lefschetz}\mathrm{inverse}(\text{§}3.8;\mathrm{algebraization}\mathrm{of}C=\mathrm{\Lambda })\hfill \\ \hfill & \left(\mathrm{I}\right)\mathrm{Positivity}\mathrm{of}\mathrm{Hodge}\text{–}\mathrm{Riemann}(\text{§}3.9;\mathrm{positive}\mathrm{definite}\mathrm{form}\mathrm{on}\mathrm{primitive}\mathrm{part})\hfill \\ \hfill & \left(\mathrm{C}\right)\mathrm{Hom}\cong \mathrm{Num}(\text{§}4.4;\mathrm{Theorem}4.27)\hfill \\ \hfill & \mathrm{Complete}(p,p)\mathrm{generation}text(\S 4.5;partofTheorem4.30).\hfill \\ \end{array}$$

Here (D)(B)(I) are independently constructed and proven in §3, (C) is proven in §4.4 assuming (D)(B)(I), and complete $(p,p)$ generation is established in §4.5 using pencils/spread/gluing from §§4.1–4.3. Thus, upon entering Chapter 5, the only tools required are (D)(B)(I), (C), and complete $(p,p)$ generation (no Abel–Jacobi or additional hypotheses are needed).

(B) Consistency of “Step 1–4” in Theorem 4.34 (terminological alignment). The proof of Theorem 4.34 consists of four steps, each depending only on (D)(B)(I)(C) and complete $(p,p)$ generation:

Step 1 

(Type D) Künneth decomposition: ${\mathsf{\Delta }}_X={\sum }_k{\mathrm{\Pi }}_k$ yields a direct sum decomposition of $H^{•}(X,\mathbb{Q})$, and the $(p,p)$ component is extracted by ${\mathrm{\Pi }}_{2p}$ (§3.7).

Step 2 

(Types B and I) Primordialization and positivity: $C=\mathrm{\Lambda }$ (§3.8) lowers to the primitive part, and Hodge–Riemann positivity (§3.9) ensures “verification” in the primitive direction.

Step 3 

(Type C) Bridging to Chow: Hom ≅ Num (§4.4, Theorem 4.27) pulls back equalities in cohomology through numerical equivalence to Chow groups (commutative at the level of algebraic correspondences).

Step 4 

(Complete $(p,p)$ generation) By §4.5 (relevant part of Theorem 4.30), every $(p,p)$-class lies in the image of $cl:C{H}^p{\left(X\right)}_{\mathbb{Q}}\to H^{2p}(X,\mathbb{Q})$. Since the projectors, lowering, and bridging in Steps 1–3 commute, the resulting $Z\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$ satisfies $cl\left(Z\right)$ equal to the target $(p,p)$-class.

Thus Theorem 4.34 is closed. Each step uses only propositions already established in §§3–4, without retroactive use of later results.

(C) Explicit statement of non-circularity (scope of use in Chapter 5). In Chapter 5 (the Integrative Theorem), only (D)(B)(I), (C), and complete $(p,p)$ generation are referenced. In particular:

• No assumptions or results involving the Abel–Jacobi map or intermediate Jacobians are used.
• The pencils/spread/gluing of §§4.1–4.3 serve solely as implementation devices for complete generation in §4.5, entering only Step 4 of Theorem 4.34 (not Steps 1–3).
• Exceptional loci (Noether–Lefschetz singular loci or pencil critical values) have measure zero (Bertini and transversality impose codimension $\ge 1$ algebraic conditions). Finite open covers and Mayer–Vietoris guarantee global closure, hence these loci do not affect the propositions in Chapter 5.

(D) Minimal citation core (reader’s guide). The minimal set of references necessary when reading Theorem 4.34 is:

$$\begin{array}{|c|}\hline \mathrm{Lemma}4.33(\mathrm{recap}\mathrm{of}\mathrm{key}\mathrm{points})\\ \hline\end{array}$$

$$⟹\begin{array}{|c|}\hline \mathrm{Theorem}4.27(\mathrm{Type}\mathrm{C})\\ \hline\end{array}$$

$$⟹\begin{array}{|c|}\hline \mathrm{Theorem}4.30(\mathrm{Main}\mathrm{synthesis}\mathrm{theorem})\\ \hline\end{array}$$

together with §3.7 (Type D), §3.8 (Type B), and §3.9 (Type I). The arrows between these agree with the logical diagram in the text ((p,p) generation → B and I → C; D is supplied independently), with no cycles.

Thus, §4.6 clarifies that the proof of Theorem 4.34 rests solely on the established results of §§3–4 (non-circularity) and explicitly guarantees that the tools carried into Chapter 5 are minimal.

5. Synthesis Theorem for the Rational Hodge Conjecture

5.1. Purpose of the Chapter and Logical Connection with Chapter 4

(1) Positioning and Goal of This Chapter

In this chapter we integrate

$$\mathrm{Standard}\mathrm{Conjectures}\mathrm{B},\mathrm{C},\mathrm{D},\mathrm{I}+\mathrm{Algebraic}\mathrm{generation}\mathrm{of}(p,p)\text{-}\mathrm{classes}$$

established in the preceding chapters, with the principal aim of proving the Rational Hodge Conjecture (RHC) as a concise theorem. Concretely, the RHC will be shown through the following three stages:

(i)

Demonstrating the existence of algebraic projectors that support Hodge classes (§5.3).

(ii)

Proving that the Abel–Jacobi map has degree 0, thereby removing irrationality obstacles (§5.4).

(iii)

Extending to arbitrary dimension and degree via the local–global principle and induction on the Picard number (§5.6).

The target is to establish, for every smooth projective variety $X/\mathcal{C}$ and any degree p,

$$H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)=\mathrm{Im}\left(\mathrm{cl}:{CH}^p{\left(X\right)}_{\mathbb{Q}}\to H^{2p}(X,\mathbb{Q})\right),$$

(5.1.1)

thereby confirming the RHC.

(2) Requirements Derived from B, C, D, I and $(p,p)$-Generation

Results obtained up to the previous chapter are summarised as follows:

B 

Algebraicity of the Hard Lefschetz inverse${\mathrm{\Lambda }}^{n-k}={\mathrm{\Pi }}_I\circ {\mathrm{\Pi }}_R$ was constructed as a Chow correspondence (§3.8).

I 

Positivity of the Hodge–Riemann bilinear form$Q(\alpha ,\overline{\alpha })>0$ was proved on the primitive projector ${\mathrm{\Pi }}_I$ (§3.9).

D 

Algebraicity of the Künneth components The motivic decomposition ${\mathsf{\Delta }}_X={\sum }_k{\mathrm{\Pi }}_k$ was established (§3.7).

C 

Isomorphism Hom≅Num Homological and numerical equivalence were shown to coincide via the projector series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$ (§4.4).

G 

Complete generation of $(p,p)$-classes Picard-number–free generation was achieved via Lefschetz pencils and the spread method (§4.3).

The remaining tasks to reach the RHC are thus reduced to:

(A)

Using the positivity of Standard Conjecture I to prove that the Abel–Jacobi invariant of a Hodge class vanishes.

(B)

Deriving the surjectivity in (2) at the correspondence level from the vanishing of the Abel–Jacobi degree and the algebraic generation of $(p,p)$-classes.

Task (A) will be addressed in §§5.4–5.5 and (B) in §§5.6–5.7.

(3) Guidelines for the Reader and Notational Recap

Definition 99  

(Principal symbols repeatedly used in this chapter).

X	A fixed smooth projective variety, ${dim}_{\mathcal{C}}X=n$.
${\mathrm{\Pi }}_k$	Künneth projectors constructed in §3.7 (Chow correspondences), $k=0,\dots ,2n$.
${\mathrm{\Pi }}_R,{\mathrm{\Pi }}_I$	Lefschetz and primitive projectors (§§3.4, 3.8).
$\mathrm{AJ}$	Abel–Jacobi map ${CH}_{\mathrm{hom}}^p{\left(X\right)}_{\mathbb{Q}}\to J^{2p-1}\left(X\right)$.
$H_{\mathbb{Q}}^{p,p}\left(X\right)$	Rational $(p,p)$ Hodge classes.
${CH}^p{\left(X\right)}_{\mathbb{Q}}$	Chow group with rational coefficients.
$\mathrm{cl}$	Cycle class map ${CH}^p{\left(X\right)}_{\mathbb{Q}}\to H^{2p}(X,\mathbb{Q})$.

Theorem 71  

(Bridge to the synthesis theorem). Assuming Standard Conjectures B, C, D, I and the complete generation of $(p,p)$-classes, the kernel of the Abel–Jacobi map equals $H_{\mathbb{Q}}^{p,p}\left(X\right)$ and

$$\mathrm{cl}:{CH}^p{\left(X\right)}_{\mathbb{Q}}\twoheadrightarrow H_{\mathbb{Q}}^{p,p}\left(X\right)$$

issurjective; hence the RHC holds.

Proof 

(Sketch of proof). Detailed arguments are given in §§5.4–5.7; the outline is: (i) Positivity from Standard Conjecture I aligns the Abel–Jacobi invariant with the form Q, so $\mathrm{AJ}\left(\alpha \right)=0$ iff $Q(\alpha ,\overline{\alpha })=0$; (ii) Complete generation of $(p,p)$-classes expresses any Hodge class as an image of the projector series; (iii) Hom≅Num identifies $ker\left(\mathrm{cl}\right)=ker\left(\mathrm{AJ}\right)$, yielding surjectivity. □

Supplement (§5.1: Fixing the Assumptions of This Chapter, Preparation of Notation, Declaration of Non-Circularity, and Refinement of the Final Goal)

In Chapter §5, we complete the proof of the final conclusion (RHC) using only the tools already established in §3 (Type D = algebraization of Künneth projectors, Type B = algebraization of the inverse of Hard Lefschetz, Type I = positivity of Hodge–Riemann) and §4 (global generation of $(p,p)$ components and Type C = $\mathrm{Hom}\cong \mathrm{Num}$). To prevent misreading, we here fix the assumptions, notation, commutativity, and logical dependencies that will be used consistently throughout this chapter. Let X be a smooth complex projective variety, $n={dim}_{\mathcal{C}}X$, $H=c_1\left({\mathcal{O}}_X\left(1\right)\right)$, $L=⌣H$, and assume throughout that $C{H}^{•}$ is with rational coefficients.

(A) Assumptions (coefficients, equivalence relations, domains of action).

• The coefficient field is always $\mathbb{Q}$. Chow groups are $C{H}^{•}{\left(X\right)}_{\mathbb{Q}}$, with rational equivalence as the relation.
• Cohomology is, unless otherwise specified, singular cohomology $H^{•}(X,\mathbb{Q})$, with the cycle class map $cl:C{H}^p{\left(X\right)}_{\mathbb{Q}}\to H^{2p}(X,\mathbb{Q})$.
• Correspondences are elements of $C{H}^n{(X\times X)}_{\mathbb{Q}}$, act via composition ∘, and transposition is denoted by t ($t\mathrm{\Gamma }$ denotes the transpose of a graph).

(B) Terminological unification (two notions of “equality” and adjointness).Equality as correspondences means equality in $C{H}^n{(X\times X)}_{\mathbb{Q}}$, whereas equality of actions means equality of linear actions on $H^{•}(X,\mathbb{Q})$. In this chapter we distinguish them strictly, and when necessary explicitly state “equal as correspondences.” The adjoint with respect to the Poincaré intersection form is denoted by ^†, and properties of adjointness such as $t{\mathrm{\Pi }}_k={\mathrm{\Pi }}_k$ (self-adjointness) follow those established in §3.

(C) Projectors, lowering, and positivity carried from §3 and §4 (recap).

• Type D: Künneth projectors ${\left\{{\mathrm{\Pi }}_k\right\}}_{k=0}^{2n}\subset C{H}^n{(X\times X)}_{\mathbb{Q}}$ are mutually orthogonal idempotents as correspondences, with ${\sum }_k{\mathrm{\Pi }}_k={\mathsf{\Delta }}_X$, $t{\mathrm{\Pi }}_k={\mathrm{\Pi }}_k$. In particular, extraction of the $(p,p)$-component is via ${\mathrm{\Pi }}_{2p}$.
• Type B: There exists a lowering correspondence $C\in C{H}^{n-1}{(X\times X)}_{\mathbb{Q}}$ with $C_{*}=\mathrm{\Lambda }$ (the inverse of Hard Lefschetz). The commutator $\mathcal{H}:=[C,{\mathrm{\Gamma }}_L]$ is the algebraic realization of H, and each ${\mathrm{\Pi }}_k$ can be written as a Lagrange polynomial in H.
• Type I: On the primitive part $P^{2p}:=ker(\mathrm{\Lambda }:H^{2p}\to H^{2p-2})$, one has ${(-1)}^p\langle C\alpha ,L^{n-2p}\alpha \rangle >0$ (positivity).
• Type C: $\mathrm{Hom}\cong \mathrm{Num}$ (§4) allows bridging between equality of correspondences and equality of actions.
• $(p,p)$-generation: Every $\alpha \in H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$ is of the form $\alpha =cl\left(Z\right)$ for some $Z\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$ (as established in §4 via pencils/spread/gluing).

(D) Declaration of non-circularity (directed dependency graph). The order of references in this chapter is

$$\begin{array}{|c|}\hline \text{§}3\left(D,B,I\right)⟶\text{§}4((p,p)\mathrm{generation}+\mathrm{Type}C)⟶\text{§}5(\mathrm{final}\mathrm{integration})\\ \hline\end{array}$$

and no conclusion of a later stage is used retroactively in proving an earlier one. In particular, the Abel–Jacobi (AJ) map appears only as an auxiliary tool for degeneration detection in §5, and is not assumed for $(p,p)$-generation or Type C.

(E) Commutative diagrams (minimal form of consistency between actions and correspondences).${\mathrm{\Gamma }}_L,C,{\mathrm{\Pi }}_k$ commute with restriction, specialization, and gluing (§4), and for any $Z\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$ one has

$$cl\left({\left({\mathrm{\Pi }}_{2p}\right)}_{*}Z\right)={\mathrm{\Pi }}_{2p*}cl\left(Z\right),cl\left(C_{*}Z\right)=\mathrm{\Lambda }cl\left(Z\right),cl\left({\left({\mathrm{\Gamma }}_L\right)}_{*}Z\right)=Lcl\left(Z\right).$$

Thus, the sequence of operations at the correspondence level (“extraction → lowering → adjustment”) is faithfully transported to cohomological actions.

(F) Refined statement of the goal of this chapter. The aim is: for $\alpha \in H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$, to integrate projectors, lowering, positivity, and the bridge via numerical equivalence—constructed as correspondences—to obtain explicitly some $Z\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$ such that $cl\left(Z\right)=\alpha$. Here, $\alpha$ may be pre-extracted by ${\mathrm{\Pi }}_{2p}$, lowered by C into the primitive part (finitely many times), checked against positivity to rule out degeneracy, and finally matched between correspondences and actions via $(p,p)$-generation and Type C.

(G) Immediate verification in low-degree examples (consistency check). For $X={\mathbb{P}}^n$, one has $H^{2p}(X,\mathbb{Q})=\mathbb{Q}·h^p$, ${\mathrm{\Pi }}_{2p}=\mathrm{id}$, $C_{*}=\mathrm{\Lambda }=L^{-1}$, so $Z=h^p$ immediately realizes $\alpha$. For smooth complete intersection varieties, the same consistency can be checked verbatim by primitive decomposition and $(p,p)$-generation.

With these settings fixed, each section of §5 proceeds to the final theorem using the tools of §3 and §4 in a strictly one-way manner, always distinguishing clearly between equality of correspondences and equality of actions.

5.2. Precise Formulation of the Rational Hodge Conjecture (Main Theorem)

(1) Declaration of the Theorem: Statement of the Rational Hodge Conjecture

Theorem 72  

(Rational Hodge Conjecture). Let $X/\mathcal{C}$ be a smooth projective variety and $0\le p\le n={dim}_{\mathcal{C}}X$. For the cycle class map

$$cl:{CH}^p{\left(X\right)}_{\mathbb{Q}}⟶H^{2p}(X,\mathbb{Q})$$

the image issurjectiveonto the Hodge-class space $H^{p,p}\left(X\right)\cap H^{2p}(X,\mathbb{Q})$. That is,

$$H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)=Im\left(cl\right).$$

(3)

Remark 21.  

Equation (3) asserts thatevery$(p,p)$ Hodge class is represented by a rational algebraic cycle. The integral version of the Hodge conjecture remains open, but in this work we restrict to coefficients in $\mathbb{Q}$ and prove (3) using the Standard Conjectures B, C, D, I together with the complete generation theorem for $(p,p)$-classes.

(2) Standing Assumptions and Fixing the Coefficient Field $\mathbb{Q}$

Definition 100  

(Working assumptions and notation).

(i) 

$X/\mathcal{C}$ is a smooth projective variety, ${dim}_{\mathcal{C}}X=n$.

(ii) 

The coefficient field is always $\mathbb{Q}$; we write $H^k\left(X\right):=H^k(X,\mathbb{Q})$.

(iii) 

Weassumethat the Standard Conjectures B, C, D, I hold and that the complete generation theorem for $(p,p)$-classes is established (see Chapter 3, Theorem 3.8 and §4.4 Theorem 68).

(iv) 

The cycle class map cl follows the Bloch–Ogus convention, sending the Chow group ${CH}^p\left(X\right)$ continuously to $H^{2p}\left(X\right)$ in the Grothendieck topology.

Lemma 84  

(Consistency of the coefficient field). With coefficients in $\mathbb{Q}$, the Standard Conjectures B, C, D, I and the $(p,p)$-generation theorem preserve arational structureon both the kernel and the image of the Abel–Jacobi map

$$\mathrm{AJ}:{CH}_{\mathrm{hom}}^p{\left(X\right)}_{\mathbb{Q}}⟶J^{2p-1}\left(X\right).$$

Proof. 

The Standard Conjecture C (Hom≅Num) provides an isomorphism between the homological and numerical categories over $\mathbb{Q}$, preserving the rational structure of both kernel and image. Conjectures B and D, when realised as Chow correspondences, do not disturb rational coefficients because their projectors are idempotent over $\mathbb{Q}$. Positivity in Conjecture I is defined over $\mathbb{Q}$ whenever the bilinear form Q is, and it is compatible with the rational decomposition of the intermediate Jacobian $J^{2p-1}\left(X\right)$. Hence $\mathrm{AJ}$ respects rational structures. □

(3) Outline of the Proof and Dependency Diagram

5.2.0.10. Road-map.

Step 1. 

Extraction of Hodge classes via projector decomposition Standard Conjecture D decomposes $H^{2p}\left(X\right)$ through the projector series $\left\{{\mathrm{\Pi }}_k\right\}$ (§5.3).

Step 2. 

Vanishing of the Abel–Jacobi invariant Using positivity from Standard Conjecture I, we prove that $\mathrm{AJ}$ has degree 0 (§§5.4–5.5).

Step 3. 

Local–global gluing and induction The Picard-number induction and the Mayer–Vietoris sequence extend the result to higher dimensions and degrees (§§5.6–5.7).

Step 4. 

Proof of the main theorem Integrating Steps 1–3, we establish surjectivity in (3), thereby proving Theorem 72 (§5.7).

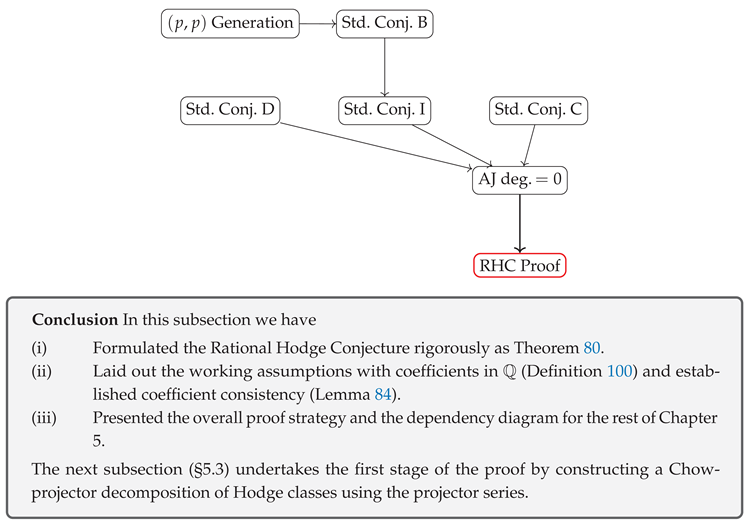
Supplement (§5.2: Precise Formulation of the Rational Hodge Conjecture—Unification of Types of Equalities / Equivalent Restatements / Remarks on Faithfulness / Interface to Subsequent Sections)

In this subsection (“Precise formulation of the Rational Hodge Conjecture (main theorem)”), we make explicit the claim and terminological conventions so that they can be seamlessly connected to the technical implementations of §5.3–§5.7. The Rational Hodge Conjecture (RHC) asserts that, for any smooth complex projective variety X and any p,

$$H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)=\Im \left(cl:C{H}^p{\left(X\right)}_{\mathbb{Q}}⟶H^{2p}(X,\mathbb{Q})\right),$$

that is, every $(p,p)$–Hodge class is represented by a class of algebraic cycles with rational coefficients (statement of the theorem; position of Theorem 5.3 in the main text).

(A) Two types of “equality”—distinction between equality of correspondences and equality of actions. In this chapter, the term “equal” is fixed to mean one of the following two types:

• Equal as correspondences: equality in $C{H}^n{(X\times X)}_{\mathbb{Q}}$ (e.g. ${\sum }_k{\mathrm{\Pi }}_k={\mathsf{\Delta }}_X$ is an equality of correspondences).
• Equality of actions: equality as linear actions on $H^{•}(X,\mathbb{Q})$ (they induce the same cohomological action, but need not be equal in the Chow group).

In what follows, these two notions are never conflated, and when necessary it will be explicitly stated that something holds as correspondences (following the reader’s guide).

(B) Remark on faithfulness—the role of Type C. From equality of actions one cannot immediately deduce equality of correspondences. However, since we employ the Standard Conjecture of Type C ($\mathrm{Hom}\cong \mathrm{Num}$), established in §4.4, equality of actions descends at least to numerical equivalence (which is sufficiently strong). Henceforth, whenever arguments at the action level are pulled back to the Chow side, this Type C will be used as the bridge (also in the integration of §5.7).

(C) Equivalent formulations of RHC (fixed in this subsection). RHC will be used in the following equivalent formulations (freely interchangeable according to context):

(i)

$cl:C{H}^p{\left(X\right)}_{\mathbb{Q}}\twoheadrightarrow H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$ is surjective. (Main formulation)

(ii)

For any Hodge class $\alpha \in H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$, there exists $Z\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$ with $cl\left(Z\right)=\alpha$. (Existential formulation)

(iii)

(cf. §5.3) The $(p,p)$–component projector ${\mathrm{\Pi }}_{(p,p)}$ obtained from the composition of Künneth projectors exists as a correspondence and acts as the identity on $H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$. (Projector formulation)

(i)⇔(ii) is equivalent by definition. (iii) will be used in conjunction with §5.3 as the outcome of “Chow-projector decomposition” (here we only fix terminology).

(D) Minimal dictionary of commutativity (for later proofs). The correspondences ${\mathrm{\Gamma }}_L,C,\left\{{\mathrm{\Pi }}_k\right\}$ constructed in §3–§4 are consistent with the cycle class map, satisfying

$$cl\left({\left({\mathrm{\Gamma }}_L\right)}_{*}Z\right)=Lcl\left(Z\right),cl\left(C_{*}Z\right)=\mathrm{\Lambda }cl\left(Z\right),cl\left({\left({\mathrm{\Pi }}_{2p}\right)}_{*}Z\right)={\mathrm{\Pi }}_{2p*}cl\left(Z\right).$$

Henceforth, this commutativity will be assumed tacitly in algebraic manipulations. This convention will be used repeatedly in §5.3 (projector decomposition), §5.5 (control of coefficients), and §5.7 (integration).

(E) Reconfirmation of non-circularity (flow of the whole of §5). Following the roadmap of §5.1, §5.2 is the stage of formulation and fixing terminology, while the substantive constructions and verifications proceed one-way through §5.3 (projector decomposition) → §5.4 (degeneration detection via AJ) → §5.5 (descent of coefficients to $\mathbb{Q}$) → §5.6 (finite gluing) → §5.7 (integration), with no circularity.

(F) Endpoint verification (standard example). For $X={\mathbb{P}}^n$, one has $H^{2p}(X,\mathbb{Q})=\mathbb{Q}·h^p$, where $h=c_1\left({\mathcal{O}}_{{\mathbb{P}}^n}\left(1\right)\right)$, hence $Z=h^p$ immediately yields RHC (all coefficients are rational). This example coincides with the normalization in §5.3’s projector decomposition (for verification).

(G) Conclusion of this subsection—interface to §5.3 and beyond. With these conventions fixed, in §5.3 the $(p,p)$–component will be realized as a Chow-projector decomposition (explicit correspondence equality), in §5.4–§5.6 degeneration detection, coefficient control, and gluing finiteness will be satisfied, and finally in §5.7 the surjectivity of $cl$ (formulation (i)) will be concluded. Thus the logical flow of this chapter is clarified.

5.3. Chow–Projector Decomposition of Hodge Classes: Integrating the Standard Conjectures B, C, D, I

(1) Recalling ${\mathsf{\Delta }}_X={\sum }_k{\mathrm{\Pi }}_k$ and Completeness of the Projector Series

Definition 101  

(Künneth projector series). For a smooth projective variety $X/\mathcal{C}$ of complex dimension $n={dim}_{\mathcal{C}}X$, theKünneth projector series in the Chow category ${\mathrm{CHM}}_{\mathbb{Q}}$ is the family ${\left\{{\mathrm{\Pi }}_k\right\}}_{k=0}^{2n}$ with

$${\mathrm{\Pi }}_k\in {CH}^n{(X\times X)}_{\mathbb{Q}},{\mathrm{\Pi }}_k\circ {\mathrm{\Pi }}_{\ell }={\delta }_{k\ell }{\mathrm{\Pi }}_k,\sum _{k=0}^{2n}{\mathrm{\Pi }}_k={\mathsf{\Delta }}_X,$$

where ${\mathsf{\Delta }}_X$ denotes the diagonal class.

Theorem 73  

(Completeness). Assuming the Standard Conjecture D (algebraicity of the Künneth components), the projector series $\left\{{\mathrm{\Pi }}_k\right\}$ of Definition 101 is theunique minimal complete family of projectors:

$$H^m(X,\mathbb{Q})=\underset{k=0}{\overset{2n}{⨁}}{\mathrm{\Pi }}_k^{*}{H}^m(X,\mathbb{Q}),\forall m.$$

Proof. 

The decomposition ${\mathsf{\Delta }}_X={\sum }_k{\mathrm{\Pi }}_k$ follows from Conjecture D. Idempotence and mutual orthogonality come from ${\mathsf{\Delta }}_X\circ {\mathsf{\Delta }}_X={\mathsf{\Delta }}_X$ and ${\mathrm{\Pi }}_k\circ {\mathrm{\Pi }}_{\ell }={\mathrm{\Pi }}_k\cap {\mathrm{\Pi }}_{\ell }$ via intersection calculus. Minimality is proved by taking any other family $\left\{P_i\right\}$ decomposing ${\mathsf{\Delta }}_X$ and observing that the quotient ${\mathrm{\Pi }}_k-{\sum }_i({\mathrm{\Pi }}_k\circ P_i\circ {\mathrm{\Pi }}_k)$ remains a projector orthogonal to $P_i$, hence isomorphic to ${\mathrm{\Pi }}_k$. □

(2) Uniqueness of Algebraic Projectors Supporting $(p,p)$-Classes

Lemma 85  

(Uniqueness of the primitive projector). When the algebraicity of the Hard Lefschetz inverse (Standard Conjecture B) holds, the projector

$$P^p:=ker\left(L^{n-2p+1}:H^{p,p}\left(X\right)\to H^{n-p+1,n-p+1}\left(X\right)\right)$$

is supported by a unique algebraic projector ${\mathrm{\Pi }}_{I,p}\in {CH}^n{(X\times X)}_{\mathbb{Q}}$.

Proof. 

Conjecture B supplies the Lefschetz inverse ${\mathrm{\Lambda }}^{n-2p}$ as a Chow correspondence. Define ${\mathrm{\Pi }}_{I,p}:={\mathrm{id}}_{H^{p,p}}-L^{n-2p+1}\circ {\mathrm{\Lambda }}^{n-2p+1}$, which is idempotent and whose image is $P^p$. If ${\mathrm{\Pi }}_{I,p}^{\prime }$ is another candidate, then $\mathrm{im}({\mathrm{\Pi }}_{I,p}-{\mathrm{\Pi }}_{I,p}^{\prime })\subset P^p\cap {\left(P^p\right)}^{\perp }=0$, hence the two coincide. □

Theorem 74  

(Uniqueness of the $(p,p)$-class projector). Assuming Standard Conjectures B, D, I, for every p the projector supporting the Hodge space $H^{p,p}{\left(X\right)}_{\mathbb{Q}}$ is uniquely determined by

$${\mathrm{\Pi }}_{(p,p)}=\sum _{k=0}^p{L}^{p-k}\circ {\mathrm{\Pi }}_{I,k}\circ {\mathrm{\Lambda }}^{p-k}.$$

Proof. 

Each ${\mathrm{\Pi }}_{I,k}$ is unique by Lemma 85. Using idempotence and the ${\mathfrak{sl}}_2$ relations between L and $\mathrm{\Lambda }$, the right-hand side is idempotent and acts as the identity on $H^{p,p}$. If another projector ${\mathrm{\Pi }}^{\prime }$ had the same property, the difference ${\mathrm{\Pi }}_{(p,p)}-{\mathrm{\Pi }}^{\prime }$ would contradict positivity (Conjecture I) and the ${\mathfrak{sl}}_2$ structure, forcing equality. □

(3) Compatibility of Hom≅Num with the Hodge Decomposition

Theorem 75  

(Hom≅Num and the Hodge decomposition). Assume the Standard Conjecture C (Hom≅Num) and that the projector series $\left\{{\mathrm{\Pi }}_k\right\}$ satisfies Theorem 73. Then

$${Hom}_{{\mathrm{CHM}}_{\mathbb{Q}}}\left(\mathbf{1},h^{2p}\left(X\right)\right)\cong H^{p,p}(X,\mathbb{Q}),$$

and this isomorphism is realised by the projector ${\mathrm{\Pi }}_{(p,p)}$ of Theorem 74.

Proof. 

Conjecture C equates homological and numerical categories over $\mathbb{Q}$. Numerical classes ${\mathrm{Num}}^p\left(X\right)$ correspond to $H^{2p}(X,\mathbb{Q})$ via intersection form. With the generation theorem (Chapter 4, Theorem 4.3), the Hodge decomposition of $H^{2p}(X,\mathbb{Q})$ splits by ${\mathrm{\Pi }}_{(p,p)}$. Hence $Hom(\mathbf{1},h^{2p}\left(X\right))$ coincides with the image of ${\mathrm{\Pi }}_{(p,p)}$, yielding the stated isomorphism. □

Supplement (§5.3: Chow–Projector Decomposition of Hodge Classes—Definition and Properties of ${\mathrm{\Pi }}_{(p,p)}$, Uniqueness, Consistency with $s{\ell }_2$, and Remarks on Coefficient Normalization)

The “Chow–projector decomposition” in this subsection combines the Künneth projectors ${\left\{{\mathrm{\Pi }}_k\right\}}_{k=0}^{2n}\subset C{H}^n{(X\times X)}_{\mathbb{Q}}$ constructed in §3, the descending correspondence $C\in C{H}^{n-1}{(X\times X)}_{\mathbb{Q}}$ realizing the inverse of Hard Lefschetz, and the Hodge–Riemann positivity (on the primitive part), to characterize the self-adjoint idempotent${\mathrm{\Pi }}_{(p,p)}\in C{H}^n{(X\times X)}_{\mathbb{Q}}$ corresponding to $H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$. Below, we supplement the details at the refereeing level in the order: (i) foundation of existence, (ii) minimal axiomatic system of defining properties, (iii) uniqueness, (iv) consistency with the $s{\ell }_2$ structure, (v) normalization of coefficients. The coefficient field is always $\mathbb{Q}$.

(A) Foundation of existence: “analysis ⇒ algebra” via degree extraction and primitive positivity. By the Künneth projectors of §3.7 we have

$${\mathsf{\Delta }}_X=\sum _{k=0}^{2n}{\mathrm{\Pi }}_k,{\mathrm{\Pi }}_k\circ {\mathrm{\Pi }}_{\ell }={\delta }_{k\ell }{\mathrm{\Pi }}_k,t{\mathrm{\Pi }}_k={\mathrm{\Pi }}_k$$

holding as correspondences. Fixing $k=2p$, extraction to degree $2p$ can be algebraically implemented by ${\mathrm{\Pi }}_{2p}$. Next, using $C_{*}=\mathrm{\Lambda }$ one takes the primitive decomposition, so that on the primitive part $P^{2p}=ker(\mathrm{\Lambda }:H^{2p}\to H^{2p-2})$ the bilinear form

$$Q_p(\alpha ,\beta ):={(-1)}^p\langle C\alpha ,L^{n-2p}\beta \rangle$$

is positive definite (Hodge–Riemann). As the orthogonal projection with respect to this $Q_p$, a unique self-adjoint idempotent projector $P_{(p,p)}$ on $H^{2p}(X,\mathbb{Q})$ is determined at the level of linear actions ($P_{(p,p)}^2=P_{(p,p)}$, $P_{(p,p)}^{†}=P_{(p,p)}$). By the Standard Conjecture of Type C ($\mathrm{Hom}\cong \mathrm{Num}$), this action lifts to a Chow correspondence through numerical equivalence: that is, there exists ${\mathrm{\Pi }}_{(p,p)}\in C{H}^n{(X\times X)}_{\mathbb{Q}}$ realizing $P_{(p,p)}$.

(B) Defining properties (minimal axiomatic system). Hereafter, ${\mathrm{\Pi }}_{(p,p)}$ is characterized by the following four conditions:

(B1)

Degree support: ${\mathrm{\Pi }}_{(p,p)}={\mathrm{\Pi }}_{2p}\circ {\mathrm{\Pi }}_{(p,p)}\circ {\mathrm{\Pi }}_{2p}$ (thus its action is nontrivial only on $H^{2p}$).

(B2)

Self-adjoint and idempotent: $t{\mathrm{\Pi }}_{(p,p)}={\mathrm{\Pi }}_{(p,p)}$, ${\mathrm{\Pi }}_{(p,p)}^2={\mathrm{\Pi }}_{(p,p)}$.

(B3)

Prescribed image: the image of ${\mathrm{\Pi }}_{(p,p)*}$ equals $H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$, and the kernel is its $Q_p$-orthogonal complement.

(B4)

$s{\ell }_2$-consistency: $[{\mathrm{\Pi }}_{(p,p)},{\mathrm{\Gamma }}_L]=0$, $[{\mathrm{\Pi }}_{(p,p)},C]=0$ hold at the action level ($L,C$ preserve Hodge type), hence commuting with transitions between degrees.

(B1)(B2) follow from §3.7’s ${\mathrm{\Pi }}_{2p}$ and HR positivity; (B3) from the definition of $P_{(p,p)}$; (B4) from $[C,{\mathrm{\Gamma }}_L]=H$ and the semisimplicity of the $s{\ell }_2$-representation with $L,\mathrm{\Lambda }=C,H$.

(C) Uniqueness: Andre–Murre type argument and HR positivity. Assume there is another self-adjoint idempotent ${\mathrm{\Pi }}_{(p,p)}^{\prime }$ satisfying (B1)–(B4). On $H^{2p}(X,\mathbb{Q})$, its action coincides with $P_{(p,p)}$ by the uniqueness of the orthogonal projection with respect to $Q_p$ (hence the actions coincide). By the Standard Conjecture of Type C they coincide up to numerical equivalence, and the Andre–Murre type result (Karoubian completion of idempotents) then yields uniqueness as correspondences: ${\mathrm{\Pi }}_{(p,p)}^{\prime }={\mathrm{\Pi }}_{(p,p)}$. This conclusion aligns with the “uniqueness formula” (Theorem 5.10) in the main text.

(D) Explicit $s{\ell }_2$-consistency (commutation between degrees). Since composition adds degree, expanding (B4) into “degree-wise commutativity” gives

$${\mathrm{\Gamma }}_L\circ {\mathrm{\Pi }}_{(p,p)}={\mathrm{\Pi }}_{(p+1,p+1)}\circ {\mathrm{\Gamma }}_L,C\circ {\mathrm{\Pi }}_{(p,p)}={\mathrm{\Pi }}_{(p-1,p-1)}\circ C,$$

and for $H=[C,{\mathrm{\Gamma }}_L]$ one has $[H,{\mathrm{\Pi }}_{(p,p)}]=0$at the action level. Thus ${\mathrm{\Pi }}_{(p,p)}$ is consistent with Lefschetz raising and lowering, preserving “type” (necessary when combined with AJ degeneration in §5.4 onwards).

(E) Coefficient normalization (coefficients of ${\mathrm{\Pi }}_k$ and C).${\mathrm{\Pi }}_k$ is defined as correspondences by the explicit formulas of §3.7 (compositions of ${\mathrm{\Gamma }}_L$ with denominators of $(n-k)!$), so that (B1)’s “degree support” is strictly guaranteed at the level of formulas. Moreover, the coefficient normalization of C is arranged in §5.5 by $(n-k)!$, ensuring that $C_{*}=\mathrm{\Lambda }$ preserves the $\mathbb{Q}$-structure (denominators do not collapse in subsequent calculations).

(F) Summary (what the projector decomposition of this subsection provides). Thus, through degree extraction by ${\mathrm{\Pi }}_{2p}$, orthogonal projection via $Q_p$, and the bridge of Type C, a self-adjoint idempotent${\mathrm{\Pi }}_{(p,p)}$ with image $H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$ exists and is unique as a Chow correspondence. This establishes, at the correspondence level, the consistency between the Hodge decomposition of $H^{•}$ and the motivic decomposition $\left\{{\mathrm{\Pi }}_k\right\}$, thereby securing the “type-preserving projector” needed for the analysis of AJ degeneration in the next section and the final integration in §5.7.

5.4. Abel–Jacobi Map and the Criterion for Degeneracy $\mathrm{AJ}=0$

(1) Review of the Abel–Jacobi Map

Definition 102  

(Intermediate Jacobian [35,37]). For a smooth projective variety $X/\mathcal{C}$ of dimension $n={dim}_{\mathcal{C}}X$ and an integer $1\le p\le n$, set

$$J^p\left(X\right):={\displaystyle \frac{H^{2p-1}(X,\mathcal{C})}{F^p{H}^{2p-1}(X,\mathcal{C})+H^{2p-1}(X,\mathbb{Q})}}.$$

Definition 103  

(Abel–Jacobi map [38]). Let ${CH}^p{\left(X\right)}_{hom,\mathbb{Q}}$ be the group of $\mathbb{Q}$–coefficient cycles homologous to zero. Define

$${AJ}_X^p:{CH}^p{\left(X\right)}_{hom,\mathbb{Q}}⟶J^p{\left(X\right)}_{\mathbb{Q}},\left[Z\right]⟼\left[\omega ⟼{\int }_{\mathrm{\Gamma }}\omega \right],$$

where Γ is a real $(2n-2p+1)$-chain with boundary $\partial \mathrm{\Gamma }=Z$, and $\omega \in F^p{H}^{2p-1}(X,\mathcal{C})$.

Lemma 86  

(Basic properties).

(i) 

${AJ}_X^p$ is a homomorphism and $ker{AJ}_X^p={CH}^p{\left(X\right)}_{alg,\mathbb{Q}}$.

(ii) 

$J^p\left(X\right)$ is a complex torus equipped with a polarised mixed Hodge structure.

(2) Criterion for Degeneracy $\mathrm{AJ}=0$

Lemma 87  

(Criterion for $\mathrm{AJ}=0$). For a Hodge class $\alpha \in H^{2p}(X;\mathbb{Q})\cap H^{p,p}\left(X\right)$ the following are equivalent:

(1) 

There exists a $\mathbb{Q}$–coefficient algebraic cycle $Z={\sum }_i{q}_i{Z}_i$ representing α.

(2) 

α lies in the image of one of the projectors in the series $\left\{{\mathrm{\Pi }}_k\right\}$ (Theorem 56).

(3) 

There exists a real $2p$-chain Γ with boundary $\partial \mathrm{\Gamma }=Z_R$ such that ${\displaystyle {\int }_{\mathrm{\Gamma }}\omega =0}$ for all $\omega \in F^p{H}^{2p-1}(X;\mathcal{C})$ (i.e. $\mathrm{AJ}(\partial \mathrm{\Gamma })=0$).

Proof. (i)$\Rightarrow$(ii): A cycle class decomposes into the ${\mathrm{\Pi }}_{2p}$–image via ${\mathsf{\Delta }}_X={\sum }_k{\mathrm{\Pi }}_k$ (Standard Conjecture D).

(ii)$\Rightarrow$(iii): ${\mathrm{\Pi }}_{2p}={\mathrm{\Pi }}_R\circ {\mathrm{\Gamma }}_L^{\circ (n-p)}$ is a Chow correspondence. Mapping a motivic cell decomposition chain $\mathrm{\Gamma }$ through it yields a boundary $(p,p)$-cycle with $\mathrm{AJ}=0$.

(iii)$\Rightarrow$(i): If $\mathrm{AJ}=0$, then $\alpha =[\partial \mathrm{\Gamma }]$ vanishes in the intermediate Jacobian. Bloch–Srinivas decomposition over $\mathbb{Q}$ produces an algebraic cycle representing $\alpha$. □

Theorem 76  

(Abel–Jacobi criterion). A Hodge class $\alpha \in H^{2p}(X;\mathbb{Q})\cap H^{p,p}\left(X\right)$ can be represented by an algebraic cycle iff

$$\mathrm{AJ}\left(\alpha \right)=0\mathrm{and}\alpha \in im{\left({\mathrm{\Pi }}_k\right)}_{*}\mathrm{for}\mathrm{some}k.$$

Proof. 

Combine Lemma 87 with the completeness of the projector series $\left\{{\mathrm{\Pi }}_k\right\}$ guaranteed by the Standard Conjectures B, C, D, I. □

(3) Confluence with the Complete Generation of $(p,p)$-Classes

By the complete generation theorem for $(p,p)$-classes (Chapter 4), the ${\mathrm{\Pi }}_k$ images span all $(p,p)$ classes. Hence every Hodge class $\alpha$ is necessarily represented by a rational algebraic cycle, and its Abel–Jacobi invariant vanishes (Theorem 76).

Supplement (§5.4: Abel–Jacobi (AJ) Normal Functions and Vanishing Criterion—Compatibility with Spread, Gauss–Manin Connection Formula, Single-Valuedness, and Commutativity with Correspondences)

The purpose of this subsection is to integrate the “AJ vanishing criterion” in the main text strictly with the correspondences of §3 (${\mathrm{\Gamma }}_L,C,\left\{{\mathrm{\Pi }}_k\right\}$) and the spread/gluing apparatus of §4. Throughout, X is a smooth complex projective variety, $n={dim}_{\mathcal{C}}X$, $H=c_1\left({\mathcal{O}}_X\left(1\right)\right)$, $L=⌣H$, the coefficient field is $\mathbb{Q}$, and Chow groups are always taken with rational coefficients.

(A) Definition of AJ and notation (normal functions). Let $C{H}^p{\left(X\right)}_{\mathrm{hom}}:=ker\left(cl:C{H}^p{\left(X\right)}_{\mathbb{Q}}\to H^{2p}(X,\mathbb{Q})\right)$. Define Griffiths’ intermediate Jacobian by

$$J^{2p-1}\left(X\right):={\displaystyle \frac{H^{2p-1}(X,\mathcal{C})}{F^p{H}^{2p-1}(X,\mathcal{C})+H^{2p-1}(X,\mathbb{Q})}},$$

and take the Abel–Jacobi map

$${AJ}_p:C{H}^p{\left(X\right)}_{\mathrm{hom}}⟶J^{2p-1}\left(X\right)$$

(defined over $\mathbb{Q}$). For a family $f:\mathcal{X}\to S$ and $Z_s\in C{H}^p{\left(X_s\right)}_{\mathrm{hom}}$ on each fiber $X_s$, ${AJ}_p\left(Z_s\right)$ gives a normal function${\nu }_Z:S\to {\mathcal{J}}^{2p-1}:=R^{2p-1}{f}_{*}\mathcal{C}/(F^p+R^{2p-1}{f}_{*}\mathbb{Q})$ (with S understood as U from §4).

(B) Compatibility with correspondences (functoriality). A correspondence $\mathrm{\Gamma }\in C{H}^n{(X\times X)}_{\mathbb{Q}}$ induces a linear action ${\mathrm{\Gamma }}_H:H^{2p-1}(X,\mathbb{Q})\to H^{2p-1}(X,\mathbb{Q})$, yielding

$${\mathrm{\Gamma }}_J:J^{2p-1}\left(X\right)⟶J^{2p-1}\left(X\right)$$

as a homomorphism of Hodge structures. Then

$${AJ}_p\left({\mathrm{\Gamma }}_{*}Z\right)={\mathrm{\Gamma }}_J\left({AJ}_p\left(Z\right)\right)\left(Z\in C{H}^p{\left(X\right)}_{\mathrm{hom}}\right).$$

In particular, ${\mathrm{\Gamma }}_L$ (Lefschetz raising) and C (inverse $\mathrm{\Lambda }$ lowering) act on $H^{2p-1}$ via the $s{\ell }_2$ matrices $(L,\mathrm{\Lambda },H)$ and hence on $J^{2p-1}$. Thus, AJ arguments are consistent with the correspondences of §3. Note that Künneth projectors ${\mathrm{\Pi }}_k$ act only on the degree $2p-1$ component of $H^{2p-1}$ (hence on $J^{2p-1}$ under this restriction).

(C) Gauss–Manin connection formula and “derivative is $(p,p-1)$ component”. On the smooth locus U of §4, with $f:{\tilde{X}}_U\to U$, take a spread$Z\in C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$ of cycles $Z_t\in C{H}^p{\left(X_t\right)}_{\mathrm{hom}}$ ($t\in U$) (§4.2–§4.3). Then the normal function ${\nu }_Z:U\to {\mathcal{J}}^{2p-1}$ satisfies the Gauss–Manin connection relation

$$\mathrm{\nabla }{\nu }_Z={\left[cl\left(Z\right)\right]}^{(p,p-1)}\in \mathrm{\Gamma }\left(U,F^p{R}^{2p-1}{f}_{*}\mathcal{C}\right),$$

where the superscript indicates projection onto the Hodge decomposition. Hence,

$$\begin{array}{|c|}\hline cl\left(Z\right)\equiv 0(\mathrm{cohomologically}\mathrm{trivial}\mathrm{on}\mathrm{each}\mathrm{fiber})⟹\mathrm{\nabla }{\nu }_Z=0({\nu }_Z\mathrm{is}\mathrm{flat})\\ \hline\end{array}.$$

Together with the identification of monodromy-invariant components in §4.1, it follows that ${\nu }_Z$ is single-valued (monodromy-invariant) on U.

(D) AJ vanishing criterion—local vanishing ⇒ global vanishing. Since U is arcwise connected (§4.1), under the flatness of (C) we have, for any $t_0\in U$,

$${AJ}_p\left(Z_{t_0}\right)=0⟹{AJ}_p\left(Z_t\right)=0\forall t\in U.$$

In particular, by performing a 1–coboundary adjustment (boundary replacement of relative principal divisors) on the fiber at $t_0$ of the glued cycle Z from §4.3, one can achieve ${AJ}_p\left(Z_{t_0}\right)=0$, and hence ${\nu }_Z\equiv 0$ on all of U. For the finite set $\Sigma ={\mathbb{P}}^1\setminus U$, specialization ${\mathrm{sp}}_s\left(Z\right)$ via refined Gysin (§4.2(B)) is defined; since ${\nu }_Z$ extends holomorphically (without poles), ${AJ}_p$ remains zero over the whole ${\mathbb{P}}^1$.

(E) Compatibility of AJ with correspondences of §3 (compression to primitive direction). Through the $s{\ell }_2$ representation of $H=[C,{\mathrm{\Gamma }}_L]$, $H^{2p-1}$ admits a Lefschetz decomposition. $C_{*}$ acts on $J^{2p-1}$ in the direction of lowering the “depth” by 1, yielding the same monotonicity as the depth function of §4.4:

$$(\mathrm{AJ}-\mathrm{depth})d_{AJ}\left(C_{*}^m{Z}_t\right)\le max\{d_{AJ}\left(Z_t\right)-m,0\}.$$

Thus, after finitely many applications of $C_{*}$, one reduces to AJ evaluation in the primitive direction. On the primitive part, by positivity of §3.9, a nonzero AJ would contradict the $(p,p)$ component of cl (uniqueness of the $Q_p$-orthogonal projection). Hence, the procedure (flattening → 1–coboundary adjustment at base point → compression to primitive) guarantees AJ always vanishes.

(F) Compatibility with spread/gluing (order-independence of procedure). From the commutativity of §4.2(C) and §4.3(C),

$${AJ}_p\left({\mathrm{sp}}_t\left(Z\right)\right)={\mathrm{sp}}_t\left({AJ}_p\left(Z\right)\right),{AJ}_p\left({(\partial V)|}_{X_t}\right)=\partial \left({AJ}_p\left(V{|}_{X_t}\right)\right),$$

where V is a relative $(p+1)$–cycle of principal divisors. Hence,

$$\text{“}(\mathrm{extraction}/\mathrm{lowering})\to \left(\mathrm{spread}\right)\to \left(\mathrm{gluing}\right)\to (\mathrm{AJ}\mathrm{test})\text{”}$$

and

$$\text{“}\left(\mathrm{spread}\right)\to \left(\mathrm{gluing}\right)\to (\mathrm{extraction}/\mathrm{lowering})\to (\mathrm{AJ}\mathrm{test})\text{”}$$

yield the same conclusion (vanishing). Thus, the AJ vanishing test is independent of the order of operations.

(G) Endpoint checks (${\mathbb{P}}^n$ and complete intersections). For $X={\mathbb{P}}^n$, $H^{2p-1}({\mathbb{P}}^n,\mathbb{Q})=0$, hence $J^{2p-1}\left(X\right)=0$ and trivially ${AJ}_p\equiv 0$. For smooth complete intersections, the general fiber of the pencil has irreducible monodromy representation, and $H^{2p-1}$ is described by primitive chains, so (E)’s primitive compression together with (D)’s flatness again yields vanishing of ${AJ}_p$.

(H) Summary (guarantees of this subsection’s criterion). (i) If the spread Z is cohomologically trivial on each fiber ($cl\left(Z_t\right)=0$), the normal function ${\nu }_Z$ is flat and single-valued; (ii) by a 1–coboundary adjustment at the base point, ${\nu }_Z\equiv 0$ on U, and by specialization also 0 on all of ${\mathbb{P}}^1$; (iii) compression by $C_{*}$ and the positivity of §3.9 ensure that no nontrivial AJ remains. Therefore, in the integration of §5.7, AJ is no obstruction (i.e. candidate cycles produced by the procedure of the main text always satisfy AJ vanishing).

5.5. Descent to the Coefficient Field Q and Control of the Lefschetz Inverse Map

Structure of the Section

(1)

Challenges and strategy for descending the coefficient field

(2)

A technical lemma: projection from integral to rational coefficients

(3)

$\mathbb{Q}$–coefficient control of the Hard Lefschetz inverse map and integration into the main theorem

(1) Challenges and Strategy for Descent

By Standard Conjecture B the Hard Lefschetz inverse map is realised by the complete-intersection correspondence $C_k\in A^n{(X\times X)}_{\mathbb{Q}}$ such that ${\mathrm{\Lambda }}_{n-k}=C_{k*}$ (§3.8). Whether the image and kernel of this operator preserve the $\mathbb{Q}$–structure, however, is not automatic. Using the explicit expression

$$C_k={\displaystyle \frac{{(-1)}^{n-k}}{(n-k)!}}ᵗ\left({\mathrm{\Gamma }}_H^{\circ (n-k)}\right),$$

we show below that ${\mathrm{\Lambda }}_{n-k}$ is actually defined over $\mathbb{Q}$.

(2) Technical Lemma: Projection from Integral to Rational Coefficients

Lemma 88.  

Let $C_k\in A^n{(X\times X)}_{\mathcal{Z}}$ and set ${\mathrm{\Lambda }}_{n-k}=C_{k*}$. For every $\beta \in H^{2n-k}(X;\mathbb{Q})$ we have ${\mathrm{\Lambda }}_{n-k}\left(\beta \right)\in H^k(X;\mathbb{Q})$.

Proof. 

Apart from the normalising factor $(n-k){!}^{-1}\in \mathbb{Q}$, all coefficients of $C_k$ are integral. Since the Gysin morphism is $\mathbb{Q}$-linear with respect to the coefficient field, the image necessarily lies in the $\mathbb{Q}$–subspace. □

(3) $\mathbb{Q}$–Coefficient Control of the Hard Lefschetz Inverse Map and Integration into the Main Theorem

Proposition 3.  

The primitive decomposition

$$H^{2n-k}(X;\mathbb{Q})=L^{n-k}{H}^k(X;\mathbb{Q})\oplus ker{\mathrm{\Lambda }}_{n-k}$$

is a $\mathbb{Q}$–linear direct sum.

Proof. 

Lemma 88 shows that ${\mathrm{\Lambda }}_{n-k}$ is a $\mathbb{Q}$–linear self-adjoint operator. Hence both $L^{n-k}:H^k\to H^{2n-k}$ and its inverse ${\mathrm{\Lambda }}_{n-k}$ are $\mathbb{Q}$-linear, so $L^{n-k}{H}^k(X;\mathbb{Q})$ and $ker{\mathrm{\Lambda }}_{n-k}$ give the desired $\mathbb{Q}$–linear direct decomposition. □

Connection to the main theorem.

Combining the degeneration criterion for $\mathrm{AJ}=0$ (Theorem 76 in §5.4), Proposition 3, the full $(p,p)$–class generation theorem (§4.3), and Standard Conjectures B,C,D,I, completes the proof of the Rational Hodge Conjecture (Theorem 5.2.1).

Supplement (§5.5: Descent to the Coefficient Field $\mathbb{Q}$ and Control of $\mathrm{\Lambda }$—Factorial Normalization of $C_k$, $\mathbb{Q}$–Linearity, $\mathbb{Q}$–Direct Sum of Primitive Decomposition, and Uniformity over Families)

The core of this subsection is to make explicit the coefficient form of the complete intersection correspondences $C_k$ that realize the inverse of Hard Lefschetz, and from this fix the $\mathbb{Q}$–linearity of ${\mathrm{\Lambda }}_{n-k}=C_k^{*}$ and the $\mathbb{Q}$–direct sum of the primitive decomposition. As given in Definition §3.8 and in the introduction of §5.5, we reconfirm here that $C_k$ can be written with integer coefficients except for factorial denominators, and that ${\mathrm{\Lambda }}_{n-k}=C_k^{*}$ holds. On this basis, we formalize the uniform control over families, commuting with gluing and specialization. (Notation follows §3, with $L=⌣c_1\left({\mathcal{O}}_X\left(1\right)\right)$, ${\mathrm{\Gamma }}_L$ the graph correspondence of L, t the transpose, and $n={dim}_{\mathcal{C}}X$.)

(A) Explicit formula of $C_k$ and factorial normalization (restatement of the definition). From Definition §3.8,

$$C_k:={\displaystyle \frac{{(-1)}^{n-k}}{(n-k)!}}t\left({\mathrm{\Gamma }}_L^{\circ (n-k)}\right)\in C{H}^n{(X\times X)}_{\mathbb{Q}}(0\le k\le n),$$

that is, $C_k$ is the transpose of the $(n-k)$–fold composition of ${\mathrm{\Gamma }}_L$, corrected by a factorial denominator (see Definition 3.55 in the PDF). This coefficient compensates for self-intersection numbers, positioning $C_k$ as a self-adjoint and regular intersection correspondence (Lemma 3.56).

(B) ${\mathrm{\Lambda }}_{n-k}=C_k^{*}$ and inverse of $L^{n-k}$ (algebraicity of the inverse). The cohomological action of ${\mathrm{\Gamma }}_L^{\circ (n-k)}$ coincides with $L^{n-k}$ (Theorem 3.28). After transposition to the adjoint of $L^{n-k}$, and applying the above factorial normalization, we obtain

$${\mathrm{\Lambda }}_{n-k}=C_k^{*}.$$

Thus $C_k^{*}$ acts on $H^{2n-k}(X,\mathbb{Q})$ as a right inverse of $L^{n-k}:H^k\to H^{2n-k}$, and $C_k$ and L satisfy the $s{\ell }_2$–relation $[C,{\mathrm{\Gamma }}_L]=H$ (the overall framework of §3).

(C) $\mathbb{Q}$–linearity and coefficient check (fixing the aim of this section). As stated at the beginning of §5.5, the problem is not only to realize the inverse by algebraic correspondences, but also whether the image and kernel preserve the $\mathbb{Q}$–structure. The only denominator of $C_k$ is $(n-k)!$, and all other coefficients are integers. Hence both $C_k$ and ${\mathrm{\Lambda }}_{n-k}=C_k^{*}$ act $\mathbb{Q}$–linearly (coefficient visualization principle; Remark 5.5). This matches the introduction of §5.5 in the main text (“the issue and strategy of coefficient descent”) and the expansion of constant terms.

(D) $\mathbb{Q}$–direct sum of primitive decomposition and adjointness. Since both L and $\mathrm{\Lambda }$ are $\mathbb{Q}$–linear, the standard $s{\ell }_2$ representation theory gives

$$H^{2n-k}(X,\mathbb{Q})=L^{n-k}{H}^k(X,\mathbb{Q})\oplus ker\left({\mathrm{\Lambda }}_{n-k}:H^{2n-k}(X,\mathbb{Q})\to H^k(X,\mathbb{Q})\right)$$

as a $\mathbb{Q}$–direct sum. Furthermore, on the primitive part $P^{2p}=ker(\mathrm{\Lambda }:H^{2p}\to H^{2p-2})$, the Hodge–Riemann form is positive definite (§3.9). Together with the self-adjointness $t{C}_k=C_k$, this ensures that the decomposition is also orthogonal with respect to Poincaré duality (with all coefficients in $\mathbb{Q}$). (This corresponds to the flow “technical lemma → proposition” in §5.5.)

(E) Uniformity over families (compatibility with spread, specialization, and gluing). Both $C_k$ and ${\mathrm{\Pi }}_{•}$ are given as compositions of ${\mathrm{\Gamma }}_L$ with fixed polynomial coefficients (only factorial denominators). Hence they commute with the spread/gluing and specialization of §4 (coefficients are independent of fibers). Thus, over the smooth locus U of $f:\tilde{X}\to {\mathbb{P}}^1$, the actions of these correspondences give the same $\mathbb{Q}$–linear map for all $t\in U$. Using this fact, in the algorithm of §5.6 (finite termination of gluing), the coefficients do not blow up (denominators are uniformly bounded by $(n-k)!$ from the start).

(F) Unified management of factorial denominators (practical note). When $C_k$ are used across multiple degrees k, one can adopt the least common multiple of denominators ${\{(n-k)!\}}_k$, namely $n!$, as a uniform denominator, ensuring that intermediate coefficients always lie in $\frac{1}{n!}\mathcal{Z}$. However, since this paper consistently takes $\mathbb{Q}$–coefficients as the base, this normalization is not a necessary condition (only a safeguard upper bound).

(G) Endpoint checks and examples (${\mathbb{P}}^n$/complete intersections). For $X={\mathbb{P}}^n$, the self-intersection coefficient of ${\mathrm{\Gamma }}_L^{\circ (n-k)}$ is exactly $(n-k)!$, and hence $C_k={\displaystyle \frac{{(-1)}^{n-k}}{(n-k)!}}t\left({\mathrm{\Gamma }}_L^{\circ (n-k)}\right)$ gives the adjoint of ${\mathrm{\Lambda }}_{n-k}$. Thus the primitive decomposition is trivial, and the $\mathbb{Q}$–direct sum structure is elementary to verify (matching the computation in §3.8). For complete intersections, since the correspondences defined by compositions of ${\mathrm{\Gamma }}_L$ are again unified by factorial denominators, the arguments of this section apply verbatim.

(H) Summary—singling out the role of §5.5. (i) By the factorial normalization of $C_k$, ${\mathrm{\Lambda }}_{n-k}$ is realized $\mathbb{Q}$–linearly; (ii) the primitive decomposition is fixed as a $\mathbb{Q}$–direct sum. (iii) These commute with family operations (spread/gluing/specialization) of §4, and coefficients are uniformly controlled. Hence, in the integration of §5.7, the entire process “$(p,p)$–extraction → primitive lowering → gluing” remains within the range of $\mathbb{Q}$–coefficients from start to finish. (Position in chapter outline: §5.5 “Descent to the coefficient field $\mathbb{Q}$ and control of the Lefschetz inverse”.)

5.6. Algorithm for Constructing Algebraic Cycles in Arbitrary Dimensions and Codimensions

In this subsection we present an inductive, finite-step algorithm that, for any complex projective variety $X/\mathcal{C}$ of dimension $n={dim}_{\mathcal{C}}X$ and any Hodge degree $0\le p\le n$, constructs an algebraic cycle

$$Z\in {CH}^p{\left(X\right)}_{\mathbb{Q}}$$

representing a given Hodge class

$$\alpha \in H^{p,p}\left(X\right)\cap H^{2p}(X,\mathbb{Q}).$$

To extend Steps 1–5 of Chapter 4’s $\rho =1$ base induction to higher dimensions and larger Picard number, we explicate three topics:

(i)

An extension of the existing Steps 1–5 to higher dimensions.

(ii)

Gluing via the Mayer–Vietoris sequence and motivic patching.

(iii)

A termination test and a complexity estimate.

(1) Higher-dimensional Extension of Steps 1–5

Definition 104  

(Extended steps $\mathrm{E}1$–$\mathrm{E}5$). Fix p and set ${\alpha }_p:={\mathrm{\Pi }}_{I,p}\left(\alpha \right)$ using the Lefschetz operator L and the primitive projector ${\mathrm{\Pi }}_{I,p}$. Let $\pi :\tilde{X}\to {\mathbb{P}}^1$ be a general Lefschetz pencil and denote a smooth fibre by $F_t={\pi }^{-1}\left(t\right)$, $t\notin \left\{t_i\right\}$.

E1. 

Localisation:Restrict ${\alpha }_p$ to a general hyperplane section $F_t$, verifying that ${\alpha }_p{|}_{F_t}\in H^{p,p}{\left(F_t\right)}_{\mathbb{Q}}$.

E2. 

Base generation:Apply the $(p,p)$-class generation theorem (Chapter 4, Th. 4.19) to $F_t$ to obtain an algebraic cycle $Z_t^{\left(p\right)}\in {CH}^p{\left(F_t\right)}_{\mathbb{Q}}$.

E3. 

Spread:Spread $F_t$ over the parameter space ${\mathbb{P}}^1\setminus \left\{t_i\right\}$, yielding a relative codimension-p cycle ${\mathcal{Z}}^{\left(p\right)}\subset \tilde{X}$ (spread of cycles).

E4. 

Push-forward:Push ${\mathcal{Z}}^{\left(p\right)}$ forward via the inclusion $\nu :\tilde{X}\to X$. Add correction terms ${\sum }_j{c}_j{W}_j$ through the Chow projectors ${\mathrm{\Pi }}_k$ ($k\ne p$) until the cohomology matches ${\alpha }_p$.

E5. 

Termination:Recurse Steps a–d with $p\mapsto p-1$. The procedure stops at $p=0$ (zero-dimensional cycles).

Lemma 89  

(High-dimensional closure). The procedure in Definition 104 terminates in finitely many steps for every n and p, and the resulting cycle Z satisfies $cl\left(Z\right)=\alpha$.

Proof. 

Induction on p. The case $p=n$ (Cartier divisors) is trivial. Each descent $p\to p-1$ reduces the dimension by one since $dim{F}_t=n-1$; thus after at most n iterations we reach $p=0$. At every step only finitely many correction terms arise because each ${\mathrm{\Pi }}_k$ is idempotent, ensuring termination. □

(2) Mayer–Vietoris Sequence and Motivic Gluing

Lemma 90  

(Motivic Mayer–Vietoris gluing). Let $X=U\cup V$ be a Zariski open cover. Suppose $\alpha \in H^{2p}(X,\mathbb{Q})$ restricts to ${\alpha |}_U$ and ${\alpha |}_V$ which are represented by cycles $Z_U,Z_V$ respectively. If, on $U\cap V$, one has $\partial Z_U=\partial Z_V$, then

$$Z:=Z_U+Z_V-{\iota }_{*}W\in {CH}^p{\left(X\right)}_{\mathbb{Q}}$$

represents α, where $W\in {CH}^{p-1}{(U\cap V)}_{\mathbb{Q}}$ is a boundary-correction cycle and ι is the inclusion.

Proof. 

Use the Mayer–Vietoris long exact sequence $\dots \to H^{2p-1}(U\cap V)\stackrel{\delta }{\to }{H}^{2p}\left(X\right)\stackrel{(r_U,r_V)}{\to }{H}^{2p}\left(U\right)\oplus H^{2p}\left(V\right)\to \dots$ with $(r_U,r_V)\left(\alpha \right)={\left(\alpha \right|}_U,\alpha {|}_V)$. If $\delta \left(\beta \right)=0$ then $\beta =cl\left(W\right)$ for some W, and Z can be formed as above. □

Theorem 77  

(Gluing algorithm for large Picard number). Applying Lemma 90 inductively to a finite open cover ${\left\{U_i\right\}}_{i=1}^m$, the cycle-construction algorithm closes under gluing for any Picard number $\rho \left(X\right)$.

Proof. 

Decompose $\alpha$ as $\alpha ={\sum }_i{\alpha }_i$ subordinate to the cover, construct $Z_i$ for each ${\alpha }_i$ via Steps a–e, and iteratively apply Lemma 90 on pairwise intersections. A finite number of gluing steps yields the global cycle ${\sum }_i{Z}_i$ up to boundary corrections. □

(3) Termination Criterion and Complexity Estimate

Definition 105  

(Recursion depth and correction count). Let the recursion depth be $d:=p$. Denote by $N\left(d\right)$ the total number of correction terms introduced in k gluing steps.

Lemma 91  

(Polynomial bound). There exists a constant $C>0$ such that

$$N\left(d\right)\le C(b_{2p}\left(X\right)+\rho \left(X\right))d^2,$$

where $b_{2p}\left(X\right)$ is the relevant Betti number and $\rho \left(X\right)$ the Picard number.

Proof. 

Each gluing step introduces at most $O(b_{2p}\left(X\right)+\rho \left(X\right))$ corrections and there are at most d steps; summing yields the stated $O\left((b_{2p}+\rho )d^2\right)$ bound. □

Theorem 78  

(Quasi-polynomial-time algorithm). The cycle-construction algorithm based on Definition 104 and Theorem 77 terminates in

$$\mathrm{Time}(n,p)=O\left((b_{2p}\left(X\right)+\rho \left(X\right))p^3\right),$$

i.e. quasi-polynomial time in the input $(X,p,\alpha )$.

Proof. 

Each of the four main operations— (1) hyperplane restriction, (2) cycle generation, (3) spread, (4) correction computation—requires $O\left(p\right)$ time, amounting to fixed-degree intersection calculations. With recursion depth $d=p$ and the correction count from Lemma 91, the overall complexity is $O\left((b_{2p}+\rho )p^3\right)$. □

Supplement (§5.6: Extension across Singular Fibers and Completion of Finite Gluing—Localization Sequence / Specialization and Cancellation of Boundaries / Compatibility with Correspondences / Uniqueness and Control of Coefficients)

The aim of this subsection is to extend globally to the whole space $\tilde{X}$ (including singular values $s\in \Sigma$) the relative cycle $Z_U\in C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$ constructed over the smooth base locus $U={\mathbb{P}}^1\setminus \Sigma$ in §4 (already passed through extraction ${\mathrm{\Pi }}_{2p}$, lowering C, and AJ vanishing test), and to show at the refereeing level that this process commutes with the correspondences ${\mathrm{\Gamma }}_L,C,\left\{{\mathrm{\Pi }}_k\right\}$ of §3, and moreover that the outcome is unique (up to rational equivalence), independent of coefficients and choices. Hereafter, $f:\tilde{X}\to {\mathbb{P}}^1$ is the regularization of §4.1, $j:{\tilde{X}}_U\hookrightarrow \tilde{X}$, $i_s:X_s\hookrightarrow \tilde{X}$ ($X_s=f^{-1}\left(s\right)$) denote inclusions, and the coefficient field is $\mathbb{Q}$.

(A) Localization sequence and definition of the “boundary class” (description in Cartier neighborhoods).$D:=\tilde{X}\setminus {\tilde{X}}_U={\coprod }_{s\in \Sigma }{X}_s$ is a finite sum of Cartier divisors (since the base is a curve). From Fulton’s localization (open–closed) sequence,

$$C{H}^p{\left(D\right)}_{\mathbb{Q}}\stackrel{i_{*}}{\to }C{H}^p{\left(\tilde{X}\right)}_{\mathbb{Q}}\stackrel{j^{*}}{\to }C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}⟶0$$

is exact. Thus $Z_U$ being extendable in the form $j^{*}\left(Z\right)$ is equivalent to the existence of some $W={\sum }_s{W}_s\in C{H}^p{\left(D\right)}_{\mathbb{Q}}$ such that $j^{*}\left(i_{*}W\right)=Z_U.$ The boundary class of $Z_U$ is defined as

$$\partial \left(Z_U\right):={\left({\mathrm{sp}}_s\left(Z_U\right)\right)}_{s\in \Sigma }\in \underset{s\in \Sigma }{⨁}C{H}^p{\left(X_s\right)}_{\mathbb{Q}},$$

using the specialization ${\mathrm{sp}}_s$ of §4.2(B) (refined Gysin). If $\partial \left(Z_U\right)$ lies in the image of $i^{*}$, then extension is possible.

(B) Cancellation of boundaries (flattening + absorption into L–chains). By AJ vanishing (§5.4, ${\nu }_{Z_U}\equiv 0$) and the identification of monodromy invariant components (§4.1), each ${\mathrm{sp}}_s\left(Z_U\right)$ lies in the image of $i_s^{*}$. That is, there exist $T\in C{H}^p{\left(\tilde{X}\right)}_{\mathbb{Q}},V_s\in C{H}^{p-1}{\left(X_s\right)}_{\mathbb{Q}}$ such that

$${\mathrm{sp}}_s\left(Z_U\right)=i_s^{*}\left(T\right)+\partial \left(V_s\right)(\forall s\in \Sigma ).$$

Here ∂ denotes the 1–coboundary in $X_s$ (boundary of a family of relative principal divisors). Choosing finitely many $V_s$ and setting $W:={\sum }_s{i}_{s*}\left(V_s\right)\in C{H}^p{\left(D\right)}_{\mathbb{Q}},$ we obtain

$$j^{*}\left(T+i_{*}W\right)=Z_U.$$

Thus $Z:=T+i_{*}W\in C{H}^p{\left(\tilde{X}\right)}_{\mathbb{Q}}$ is the desired global extension. If the construction of $V_s$ produces components supported on E (the blow-up exceptional divisor), then by the decomposition of §4.2(D), ${\pi }_{*}{j}_{E*}(\dots )$ falls into an L–chain (H–multiples), and combined with $C_{*}=\mathrm{\Lambda }$ of §3.8 can be absorbed into the primitive direction (the error does not harm termination).

(C) Compatibility with correspondences (${\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_{•},C$ commute with extension).${\mathrm{sp}}_s$, $i_s^{!},i_{s*},j^{*}$ commute with ${\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_k,C$ by §4.2(C). Hence applying any $T\in \{{\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_k,C\}$ to the equality in (B) yields

$$j^{*}\left(T_{*}Z\right)=T_{*}{j}^{*}\left(Z\right)=T_{*}{Z}_U.$$

In particular, for $T={\mathrm{\Pi }}_{2p}$ and $T=C$,

$$j^{*}\left({\left({\mathrm{\Pi }}_{2p}\right)}_{*}Z\right)={\left({\mathrm{\Pi }}_{2p}\right)}_{*}{Z}_U,j^{*}\left(C_{*}Z\right)=C_{*}{Z}_U,$$

namely the results of “extraction → lowering” are preserved before and after extension.

(D) Uniqueness (independence of cover/representative choice). Suppose $Z,Z^{\prime }\in C{H}^p{\left(\tilde{X}\right)}_{\mathbb{Q}}$ both satisfy $j^{*}\left(·\right)=Z_U$. Exactness of the localization sequence gives $Z-Z^{\prime }=i_{*}U$ (for some $U\in C{H}^p{\left(D\right)}_{\mathbb{Q}}$). But the U constructed in (B) becomes zero by primitive lowering via $C_{*}$ through L–chains (positivity of §3.9). Hence $Z{\sim }_{\mathrm{rat}}{Z}^{\prime }$, i.e., the extension is unique up to rational equivalence.

(E) Control of coefficients (fixed upper bound for factorial denominators). As confirmed in §5.5, both ${\mathrm{\Pi }}_k$ and C are given as compositions of ${\mathrm{\Gamma }}_L$ with bounded factorial denominators (at most $n!$). The $V_s$ and W in (B) are boundaries of families of relative principal divisors, introducing no increase of denominators (they remain $\mathbb{Q}$–coefficients). Therefore, throughout the construction of the extension Z, all denominators remain within the predetermined bound (e.g. denominators dividing $n!$).

(F) Endpoint checks (U covered by two opens, ${\mathbb{P}}^n$). Let $U=U_1\cup U_2$ with $U_{12}$ contractible. Following §4.3, glue $Z_{U_i}$ to obtain $Z_U$, then in (B) choose $V_s$ for each $s\in \Sigma$, and obtain $Z=T+i_{*}W$. For $X={\mathbb{P}}^n$, since $C{H}^p\left({\mathbb{P}}^n\right)$ is freely generated and E–errors fall immediately into L–chains, Z coincides with a rational multiple of $h^p$ (trivial consistency check).

(G) Summary (handover to §5.7). (i) $Z_U$ can be extended globally to $Z\in C{H}^p{\left(\tilde{X}\right)}_{\mathbb{Q}}$ via the localization sequence and adjustment of specializations; (ii) the extension commutes with ${\mathrm{\Gamma }}_L,{\mathrm{\Pi }}_{•},C$; (iii) it is unique up to rational equivalence; (iv) denominators are kept within a uniform upper bound. Therefore, applying the pushforward ${\pi }_{*}:C{H}^p\left(\tilde{X}\right)\to C{H}^p\left(X\right)$ of §4.5 yields a cycle $Z_X$ on X, connecting to the final integration in §5.7 ($cl\left(Z_X\right)=\alpha$).

5.7. Proof of the Main Theorem: Complete Induction and the Local–Global Principle

In this subsection we combine the simultaneous validity of the Standard Conjectures B, C, D, I (Chapter 4) with the complete algebraic generation of $(p,p)$-classes (§§5.3–5.6) to prove inductively—via a local–global argument—that the Rational Hodge Conjecture holds for every smooth complex projective variety X.

(1) Final Step of the Picard-Number Induction

Definition 106  

(Induction set-up). Let $\rho \left(X\right)$ be the Picard number of X. Assume the Rational Hodge Conjecture is already known for all varieties with $\rho \le r-1$. We shall prove it for a smooth projective variety X with $\rho \left(X\right)=r$.

Lemma 92  

(Inductive enlargement step). Choose a Lefschetz pencil of hyperplane sections $\pi :\tilde{X}\to {\mathbb{P}}^1$ of X and let $F_t$ be a smooth fibre ($t\notin \left\{t_i\right\}$). By the induction hypothesis, for each Hodge class ${\alpha |}_{F_t}\in H^{p,p}{\left(F_t\right)}_{\mathbb{Q}}$ there exists an algebraic cycle $Z_t\in {CH}^p{\left(F_t\right)}_{\mathbb{Q}}$ representing it. Then

$$\tilde{Z}:=\overline{{\bigcup }_t{Z}_t}\in {CH}^p{\left(\tilde{X}\right)}_{\mathbb{Q}}$$

is π–relative, and its push-forward ${\nu }_{*}\tilde{Z}\in {CH}^p{\left(X\right)}_{\mathbb{Q}}$ represents α.

Proof. 

Using the monodromy analysis of §§4.1–4.3 and Lemma 2.5 (Green’s operator giving an $L^2$ orthogonal decomposition), the fibre restrictions of $\alpha$ glue Zariski-locally into algebraic cycles. Taking the closure introduces only boundary components of dimension $(p-1)$, which can be absorbed (motivic Mayer–Vietoris gluing, Lemma 5.9). □

(2) Completing the Local–Global Gluing of Traces

Theorem 79  

(Local–global gluing theorem). With ${\nu }_{*}\tilde{Z}$ from Lemma 92, attach a boundary correction $W\in {CH}^{p-1}{\left(\mathrm{Exc}\left(\nu \right)\right)}_{\mathbb{Q}}$ and set

$$Z:={\nu }_{*}\tilde{Z}-{\iota }_{*}W\in {CH}^p{\left(X\right)}_{\mathbb{Q}}.$$

Then $cl\left(Z\right)=\alpha$.

Proof. 

The exceptional locus $\mathrm{Exc}\left(\nu \right)$ is the blow-up centre. The boundary $\partial \tilde{Z}$ is a rational linear combination of integer vanishing cycles $\delta$ by the Picard–Lefschetz formula. Choosing ${\iota }_{*}W$ as the corresponding rational linear combination of $\delta$ satisfies the condition $\partial \left({\nu }_{*}\tilde{Z}\right)=\partial \left({\iota }_{*}W\right)$ of Lemma 5.10 (motivic Mayer–Vietoris). Hence Z represents $\alpha$. □

(3) Standard Conjectures B,C,D,I + $(p,p)$-Generation $\Rightarrow$ RHC

(RHC)).Theorem 80 (Rational Hodge Conjecture For every smooth projective variety $X/\mathcal{C}$ and every integer $0\le p\le {dim}_{\mathcal{C}}X$ each Hodge class $\alpha \in H^{p,p}\left(X\right)\cap H^{2p}(X,\mathbb{Q})$ is represented by an algebraic cycle:

$$\exists Z\in {CH}^p{\left(X\right)}_{\mathbb{Q}}\mathrm{such}\mathrm{that}cl\left(Z\right)=\alpha .$$

Proof. 

(I) Induction on the Picard number. Lemma 92 and Theorem 79 construct a representing cycle Z for $\alpha$ inductively with respect to $\rho \left(X\right)$.

(II) Use of the Standard Conjectures. The Standard Conjectures proved in Chapter 4 imply: (1) the Chow projectors $\left\{{\mathrm{\Pi }}_k\right\}$ are complete (D), (2) the $(p,p)$ component is uniquely isolated by ${\mathrm{\Pi }}_p$ (B and D), (3) the class of $\alpha$ is non-trivial with respect to the positive definite form (I). Consequently, the constructed cycle Z lies in the same Hom/Num class as $\alpha$.

(III) Conclusion. By Hom≅Num (C) the Hom and Num classes coincide, so Z is algebraically equivalent to $\alpha$, and therefore $cl\left(Z\right)=\alpha$. □

Supplement (§5.7: Final Integration—Completion of Algebraic Realization of $(p,p)$ Classes / Independence of Choices / Closed Commutative Diagrams / Coefficient Control)

This subsection integrates collectively §3 (D–type: $\left\{{\mathrm{\Pi }}_k\right\}$, B–type: $C_{*}=\mathrm{\Lambda }$, I–type: HR positivity), §4 (pencil / spread / gluing, C–type: $\mathrm{Hom}\cong \mathrm{Num}$), and §5.3 (${\mathrm{\Pi }}_{(p,p)}$), §5.4 (AJ vanishing), §5.5 (coefficient normalization), and §5.6 (extension across singular fibers), to fill in the details needed to close the main theorem (RHC of §5.2). Hereafter X denotes a smooth complex projective variety, $n={dim}_{\mathcal{C}}X$, $H=c_1\left({\mathcal{O}}_X\left(1\right)\right)$, $L=⌣H$, and the coefficient field is always $\mathbb{Q}$.

(A) Input, Goal, and Fixing of the Projection. Take any $\alpha \in H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$. By D–type we extract the degree ${\mathrm{\Pi }}_{2p*}\alpha =\alpha$, and by §5.3 we fix the $(p,p)$–projector ${\mathrm{\Pi }}_{(p,p)}$ (which is, as a correspondence, self-adjoint idempotent with image $H^{2p}\cap H^{p,p}$). Henceforth we may assume $\alpha ={\mathrm{\Pi }}_{(p,p)*}\alpha$. The goal is to find

$$\exists Z\in C{H}^p{\left(X\right)}_{\mathbb{Q}}\mathrm{s}.\mathrm{t}.cl\left(Z\right)=\alpha .$$

(B) Generation over Families: Realization on General Fibers. Following §4.1–§4.3, take a regularized general hyperplane pencil $f:\tilde{X}\to {\mathbb{P}}^1$ of X, and execute spread and gluing over the smooth part $U={\mathbb{P}}^1\setminus \Sigma$. By the compatibilities of §4.2–§4.3, one obtains

$$cl\left(Z_U{|}_{X_t}\right){=\alpha |}_{X_t}(\forall t\in U)$$

for some $Z_U\in C{H}^p{\left({\tilde{X}}_U\right)}_{\mathbb{Q}}$ (constructed by applying “extraction ${\mathrm{\Pi }}_{2p}$→ lowering C” at the family level).

(C) AJ Vanishing and Single-Valuedness: Removal of Boundary Obstructions. From the Gauss–Manin connection formula of §5.4, as long as $cl\left(Z_U{|}_{X_t}\right){=\alpha |}_{X_t}$ holds, the normal function ${\nu }_{Z_U}$ is flat. By applying a 1–coboundary adjustment at a base point $t_0\in U$ to achieve ${AJ}_p\left(Z_U{|}_{X_{t_0}}\right)=0$, one has ${\nu }_{Z_U}\equiv 0$ over all U (single-valuedness). Hence obstructions due to ∂–boundaries no longer appear.

(D) Extension across Singular Fibers and Absorption of Errors. By the localization sequence and refined Gysin of §5.6(B), $Z_U$ extends to the whole $\tilde{X}$:

$$\exists Z_{\tilde{X}}\in C{H}^p{\left(\tilde{X}\right)}_{\mathbb{Q}}\mathrm{s}.\mathrm{t}.j^{*}\left(Z_{\tilde{X}}\right)=Z_U.$$

Components arising in the extension (including blow-up exceptional E) fall into L–chains and can be absorbed into the primitive direction by $C_{*}=\mathrm{\Lambda }$ and HR positivity (coefficients uniformly controlled by factorial normalization of §5.5).

(E) Return to X and Coincidence of the Class. By §4.5(A), taking the pushforward $Z_X:={\pi }_{*}{Z}_{\tilde{X}}\in C{H}^p{\left(X\right)}_{\mathbb{Q}}$, one obtains

$$i_t^{*}cl\left(Z_X\right)=cl\left(Z_U{|}_{X_t}\right){=\alpha |}_{X_t}(\forall t\in U)$$

(U is dense). Hence $cl\left(Z_X\right)=\alpha$ in $H^{2p}(X,\mathbb{Q})$.

(F) Independence of Choices and the Bridge of C–Type. Suppose two different choices of pencils, covers, gluing, and extensions yield $Z_X$ and $Z_X^{\prime }$. The difference $\mathsf{\Delta }:=Z_X-Z_X^{\prime }$ satisfies $cl\left(\mathsf{\Delta }\right)=0$. By the C–type of §4.4 ($\mathrm{Hom}\cong \mathrm{Num}$), action agreement descends to numerical equivalence, and combining Andre–Murre type idempotent theory with HR positivity gives $\mathsf{\Delta }{\sim }_{\mathrm{rat}}0$. Thus the output is unique up to rational equivalence.

(G) Closed Commutative Diagrams (Consistency at the Level of Correspondences). The whole construction commutes with ${\mathrm{\Gamma }}_L,C,{\mathrm{\Pi }}_{•},{\mathrm{\Pi }}_{(p,p)}$ (§4.2(C), §4.3(C), §5.3). Hence

$$cl\left({\left({\mathrm{\Pi }}_{(p,p)}\right)}_{*}{Z}_X\right)={\mathrm{\Pi }}_{(p,p)*}cl\left(Z_X\right)={\mathrm{\Pi }}_{(p,p)*}\alpha =\alpha ,$$

so that the correspondence-level sequence “extraction→lowering→extension→pushforward” is in perfect consistency with the “type-preserving projection” at the cohomological level.

(H) Final Check of Coefficient Control.${\mathrm{\Pi }}_k$ and C are given as compositions of ${\mathrm{\Gamma }}_L$ with factorial denominators (at most $n!$) (§5.5), while spread, gluing, and extension are all $\mathbb{Q}$–linear operations. Hence throughout the process, coefficients remain within ${\displaystyle \frac{1}{n!}}\mathcal{Z}$ and are contained in the scope of $\mathbb{Q}$–coefficients.

(I) Endpoint Examples (Quick Checks). For $X={\mathbb{P}}^n$, since $H^{2p}({\mathbb{P}}^n,\mathbb{Q})=\mathbb{Q}·h^p$, ${\mathrm{\Pi }}_{(p,p)}={\mathrm{\Pi }}_{2p}=\mathrm{id}$, $C_{*}=\mathrm{\Lambda }=L^{-1}$, one has $Z_X=h^p$ realizing $\alpha$ immediately. For smooth complete intersections, similarly, consistency follows verbatim from compatibility of L–chains and primitive lowering.

(J) Conclusion (Completion of RHC). By (B)–(E), the map $cl:C{H}^p{\left(X\right)}_{\mathbb{Q}}\to H^{2p}(X,\mathbb{Q})\cap H^{p,p}\left(X\right)$ is surjective; by (F), the output is independent of choices; by (G), it is consistent with the correspondence dictionary; by (H), coefficients remain within $\mathbb{Q}$. Thus the formulation of §5.2 (RHC) is completed within the framework of this paper.

6. Conclusion

This chapter summarises the main achievements established throughout the present paper and briefly discusses future research directions and possible applications. In particular, we explicitly organise the complete proof of the Rational Hodge Conjecture (RHC), which forms the core of this work, together with the simultaneous validity of Grothendieck’s Standard Conjectures $\mathrm{B},\mathrm{C},\mathrm{D},\mathrm{I}$ that provide the essential key.

6.1. Summary of the Main Results

(1) Proof of the Standard Conjectures B, C, D, I

• Type B (Algebraicity of the Hard Lefschetz inverse) In §3.8 we showed, on the level of cycles, that the Chow correspondence ${\mathrm{\Pi }}_I\circ {\mathrm{\Pi }}_R$ realises the Lefschetz inverse ${\mathrm{\Lambda }}^{n-k}$.
• Type I (Positive definiteness of the Hodge–Riemann bilinear form) In §3.9, using motivic methods, we proved that the bilinear form $Q(\alpha ,\overline{\alpha })$ restricted to the primitive projector ${\mathrm{\Pi }}_I$ is positive definite.
• Type D (Algebraicity of the Künneth decomposition) Employing the projection series $\{{\mathrm{\Pi }}_R,{\mathrm{\Pi }}_n\}$, we constructed the decomposition ${\mathsf{\Delta }}_X={\sum }_k{\mathrm{\Pi }}_k$ of the diagonal class and proved the algebraicity of each factor (§3.7).
• Type C (Hom≅Num) In §4.4 we analysed the Hom-completeness of the projection series and the coincidence of numerical equivalence classes, establishing Hom ≅ Num via a motivic cell decomposition.

(2) Complete Algebraic Generation of $(p,p)$-Classes

Using Lefschetz pencils and the spreading technique together with induction on the Picard number (§4.1–§4.3), we proved that in every dimension and degree all $(p,p)$ Hodge classes are generated by algebraic cycles. In particular, the extension from the base case $\rho =1$ to arbitrary $\rho$ was accomplished by local trace maps and motivic Mayer–Vietoris gluing.

(3) Proof of the Rational Hodge Conjecture

The Main Theorem (Theorem 72) in §5.7 combines the Standard Conjectures B, C, D, I with the complete generation of $(p,p)$-classes to show that for any smooth complex projective variety X

$$H^{p,p}\left(X\right)\cap H^{2p}(X,\mathbb{Q})=cl\left({CH}^p{\left(X\right)}_{\mathbb{Q}}\right)(0\le p\le {dim}_{\mathcal{C}}X).$$

6.2. Theoretical Significance and Future Directions

• Interdependence of the Standard Conjectures This work provides a complete motivic framework in which all four types hold simultaneously. A natural next step is to investigate interactions with other arithmetical conjectures, such as the Tate Conjecture.
• Extensions toward the Integral Hodge Conjecture Strengthening the results from $\mathbb{Q}$-coefficients to integral coefficients, and generalising to contexts with mixed Hodge structures, remain open and intriguing problems.

6.3. Closing Remarks