1. Introduction
Based on Caputo–Katugampola (C-K) fractional derivative approach due to Katugampola [
1], which expand the theoretical framework of fractional differential via unifying Riemann–Liouville and Hadamard fractional derivatives, Singh et al. [
2] investigated the following prey-predator fractional-order biological population model with carrying capacity and understanding their interactivity:
which contributes significantly to ecological community, where
and
denote the population densities of the prey and predator, respectively,
represents the growth rate of the prey,
the carrying capacity,
and
the competitive interaction rates, and
the growth rate of the predator; all these coefficients are positive constants.
We remark that in recent years, C-K fractional derivative has been widely adopted owing to its capability to capture local differential and integral characteristics and provided a framework for handling systems with fractional exponents. It is especially applicable to modeling and analyzing systems exhibiting fractional dynamic behaviors [
3,
4], which laid an important foundation for the follow-up research. Since then, scholars have carried out systematic research on C-K derivative. In fact, with the in-depth study of complex systems, the traditional integer-order derivative model shows limitations in describing processes with memory, heredity or nonlocal characteristics, which promotes the development of fractional partial differential equations (FPDEs) [
5], which can describe the dynamic evolution of natural phenomena [
6] and model the evolution process of physical quantities with space and time in multivariable systems [
7]. At the same time, the successful application of this mathematical tool in noise suppression [
8], biological engineering [
9], physical science [
10] and other fields further promotes the deep integration of the theoretical development of FPDEs and practical problems.
On the other hand, biodiversity constitutes the most fundamental attribute of an ecosystem. Nevertheless, prior investigations predominantly centered on the survival and proliferation of individual species, thereby overlooking the competitive dynamics engendered by the coexistence of multiple species. Such mutual interrelations are defined as “coupling” [
11] when two or more entities engage in reciprocal interaction and influence. As noted by Ding et al. [
12], coupling mechanisms are capable of effectively characterizing the interaction dynamics between two competing species in ecological systems. A representative instance of such coupled structures is the following elliptic system [
13]:
where
,
and
is a smooth bounded domain, this system possesses significant capability for capturing the intrinsic dynamics of ecosystems. Furthermore, Zhang et al. [
14] applied the fuzzy fractional coupled partial differential equation of Caputo derivative to the initial value problem, and established existence theory of solutions under the gH-type derivative framework. Muatjetjeja et al. [
15] conducted a comprehensive Noether symmetry analysis of a generalized coupled Lane-Emden-Klein-Gordon-Fock system with central symmetry.
It is well known that practical engineering systems often have to face issues such as parameter uncertainties, measurement noise, or model inaccuracies. The deterministic framework of traditional fractional-order models is difficult to fully accommodate these challenges, while the introduction of fuzzy theory provides an effective approach to address such uncertainty problems [
16,
17]. Osman [
18] proposed the fuzzy Adomian decomposition method and the modified Laplace decomposition method, successfully solved the fuzzy fractional Navier-Stokes equations, and developed the fuzzy Elzaki transform to deal with the linear-nonlinear Schrodinger equation. Pandey et al. [
19] realized efficient numerical approximation of variable-order fuzzy partial differential equations (PDEs) by using Bernstein spectral technique. Mazandarani [
20] solved the numerical solution problem of fuzzy fractional initial value problem by improving the fractional Euler method. Furthermore, employing Caputo’s definition of fractional derivatives and gH-difference sets, Singh et al. [
21] described fuzzy differential equations and discussed a numerical solution method for fuzzy fractional differential equations with fuzzy fractional counterparts using power series approximation and Taylor’s theorem. It is worth mentioning that Pythagorean fuzzy fractional calculus provides a new paradigm for complex system analysis by virtue of its strong uncertainty modeling ability. For example, Akram et al. [
22] successfully analyzed the fractional-order fuzzy wave equation by means of multivariate Pythagorean fuzzy Fourier transform. Baleanu et al. [
23] analyzed stability of differential equations under such derivatives by combining Adomian polynomials and fractional Taylor series. Hoa et al. [
24] constructed analytical solutions of C-K fuzzy fractional differential equations by the solution of fuzzy integer order differential equation, and verified existence and uniqueness of the solution under the generalized Lipschitz condition. These results significantly enrich the theory and application boundary of fractional calculus.
Since then, researchers have investgated the symmetry coupled systems from various aspects. In the fuzzy fractional population dynamics model, stability condition reveals the long-term evolution trend of species number under fractal habitat and fuzzy environmental carrying capacity, and guides the protection strategy of endangered species. Wang et al. [
25] constructed a fractional predator-prey model, and characterized the fractal characteristics of habitat by Caputo fractional derivative. We note that the stability analysis shows that the change of fractional order will significantly affect the stability of population equilibrium point. For different equations, the stability of the solution is not the same. By using Banach contraction principle and Krasnoselskii fixed point theorem, Ali et al. [
26] obtained Ulam’s stability of solutions for symmetry coupled systems of fractal fractional differential equations.
where
FD is the Caputo fractional derivative and
,
,
and
are continuous functions. Andr
s et al. [
27] studied Ulam–Hyers stability (U-HS) of a class of elliptic PDEs,
which are defined on a bounded domain with Lipschitz boundary by using the direct technique and the abstract method of Picard operator.
Moreover, in the study of calculus theory, Lipschitz condition has long been the core premise of classical results. However, in practical problems, due to complex nonlinear and non-smooth characteristics of the systems, its applicability is limited [
28]. Long et al. [
29] introduced Schauder-type nonlinear substitution technique to deal with fuzzy-valued continuous functions that do not satisfy Lipschitz condition. By bypassing the traditional dependence on the local smoothness of the function and using the compactness condition of the topological fixed point theory, the second existence result of two kinds of gH-weak solutions for special coupled systems was proved, which expands the scope of application of the theory and provides a more flexible tool for mathematical modeling of complex systems. On this basis, Zhang et al. [
14] proved existence of two kinds of gH-weak solutions of coupled fractional equations by the same method, which promoted the development of multi-scale symmetry coupled system theory. In fact, the strict requirements of Lipschitz conditions on the smoothness of functions make it difficult to cover a large number of non-ideal situations in practice. Thus, we consider the related problems without Lipschitz conditions.
Inspired by the previous work [
2,
14,
27], to enhance the ability of system (
2) to capture the intrinsic dynamic characteristics of ecological systems, particularly slow diffusion behavior and historical uncertainty effects, we make improvements, introducing C-K gH-type differentiable operator to the left-hand side of (
2), more specifically defining the right-hand side, and imposing fuzzy initial conditions. Let
M is a fuzzy number space,
is a space of fuzzy number
, which has the property that the function
is continuous with respect to Hausdorff metric on [0, 1], where
is
-level set of
. Thus, we will consider the following symmetry coupled system of fuzzy fractional partial differential equations (FFPDEs) with C-K gH-type differentiability:
for any
and
,
,
is a C-K gH-type derivative operator with the fractional order
and
and
are continuous,
is a real number. What is noteworthy is that
and
of (
3) suppose the existence of Hukuhara (H-) difference and gH-type difference.
Remark 1. There are the following points to note:
When and in , the form of (3) reduces to the fuzzy fractional coupled PDEs considered by Zhang et al. [
13].
One can easily observe that the right-hand side of the second equation for (3) is a function of or . This feature broadens the scope of solvable problems in comparison with the work in[
13]
and the references therein.
Notably, the C-K gH-type derivative operators in (3) generalize the Caputo gH-type derivative operators in[
13].
Consequently, the system (3) are entirely novel and merit in-depth study.
The rest of this paper is as follows: In
Section 2, some necessary concepts and other necessary conditions are given. By using Schauder fixed point theorem, existence of two kinds of gH-weak solutions of equation (
3) are proved in
Section 3. In
Section 4, a numerical example is presented. U-HS of the solutions of the symmetry coupled system (
3) is proposed in
Section 5. Finally, some conclusions and future work are discussed.
2. Preliminaries
In this section, we will define the fractional integral and C-K gH-derivative for fuzzy-valued multivariate functions, and introduce the theory of relative compactness in fuzzy number space. It should be noted that some of these concepts have been more thoroughly explored in [
2,
12,
30].
Definition 1 ([
14]).
Denote M
as the space of fuzzy number on , which is a mapping satisfying normal, fuzzy convex, upper semi-continuous, and compactly supported properties. The ϱ-level set of fuzzy number ϑ are defined by:
where cl denotes the closure of the sets and is the support of ϑ.
It is evident that the
-level set of the fuzzy number
is a closed and bounded interval
, where
denotes the left-hand endpoint of
, and
denotes the right-hand endpoint. The diameter of the
-level set of
is defined as
. The highest measure
on
M is expressed as
where
. In
, the supremum metric
D is taken into account
Thus,
and
are complete metric spaces. For all
, and any
, by [
31], we know that
where
is H-difference of fuzzy numbers
and
. We suppose that the H-difference always exists. For
, the space
is defined as the collection of fuzzy numbers
that are continuous with respect to the Hausdorff metric (abbreviated as
-continuous). According to [
32,
33], the fuzzy number spaces
M and
are semilinear spaces possessing the cancellation property. Equipped with metric
, both
M and
form complete metric semilinear spaces. Consequently, the set of fuzzy-valued continuous functions
inherits completeness, thereby constituting a Banach semilinear space with the cancellation property. Meanwhile,
is defined as the Lebesgue integrable space for fuzzy-valued continuous functions.
For any positive real number
r, the closed sphere
in the metric space
consists of all fuzzy numbers
satisfying
. Here, the metric
D is defined by (
6), and
is given by
for all
, where
if
, and
otherwise.
Lemma 1 ([
2]).
For all , the following properties hold:
- (i)
.
- (ii)
If and hold, then .
- (iii)
If exist, then hold and .
- (iv)
If and are defined, then is defined and satisfies .
- (v)
If exists, then so does , and we have .
Definition 2 ([
34]).
Let and be a fuzzy-valued mapping. Then f is said to be order gH-type differentiable with respect to x at if the following conditions hold:
- (i)
f is gH-type differentiable of all orders from 1 to at .
- (ii)
There exists an element such that for all sufficiently small with , the gH-difference exists, and the following limit holds
where the gH-type difference , as defined in([
35])
, satisfies
In this case, is called the ι-order gH-type derivative of f with respect to x at .
Remark 2.
By Definition 2
, the higher-order fuzzy gH-type partial derivatives with respect to y are similarly defined. When , the equation (8) simplifies to
representing the first-order partial derivative of f at with respect to x.
Definition 3 ([
36]).
Let , , and . For and , let , then the mixed Riemann–Liouville fractional integral of orders α for fuzzy-valued multivariable function is defined as:
Definition 4 ([
13]).
the mappings f: and g: are said to be jointly continuous at the point if for every , there exists such that whenever , the following inequalities hold:
, .
For all
, define
where
,
,
and
are given functions such that
and
exist. Then define the function spaces:
where
and
are defined by (
12)
For = 0,1,2, denote by the collection of all functions , i=1,2 that possess partial gH-type derivatives up to order m with respect to x and up to n with respect to y in the domain .
Definition 5 ([
36]).
Let , and . Then the C-K gH-type derivative of order α with respect to x and y for the function f is defined by
where the right-hand expression is required to be well-defined, with .
Particularly, we need to distinguish two cases corresponding to
and
in (
9) for any
, as follows:
(i) A function
satisfies the condition of C-K gH-type differentiability of order
concerning
x and
y if
acts as a gH-type derivative of type
(i.e., with
k = 1 in (
3)) at the point
. This property is denoted by
.
(ii)
is
-C-K gH-type differentiable of order
with respect to
x and
y when
serves as a gH-type derivative of type
(i.e., where
k = 2 in (
3)) at
, For this, the notation
is used.
Definition 6 ([
30]).
For a subset , S is equicontinuous at if the following holds: for all , there exists such that for each and , implies . We state that S is equicontinuous if S is equicontinuous at every .
Definition 7 ([
30]).
A subset is said to be compactly supported if for every fuzzy number , there exists a compact set such that the support of w, denoted , is contained in K.
Definition 8 ([
30]).
A subset is defined as level-equicontinuous at when the following holds: for all , there exists , such that implies Hausdorff metric for each . Additionally, S is termed level-equicontinuous on if S is level-equicontinuous at every .
Definition 9 ([
13]).
Let and be -continuous fuzzy number spaces. A continuous mapping is called a compact operator if it maps every bounded subset to a relatively compact set in , i.e., the closure forms a compact subset of .
Lemma 2 ([
30]).
For a subset S in , S is a compact-supported if and only if S is a relatively compact subset of and S is level-equicontinuous on .
Lemma 3.
Let Ψ and Φ be defined as in (12), let and be jointly continuous according toDefinition 4
, and let and be fuzzy-valued functions. Then (3) is equivalent to the following nonlinear fractional Volterra integro-differential symmetry coupled system For all :
or when ,
Proof. The proof process of this equivalence is similar to the proof of (Lemma 3 in [
37]), so it is omitted here. □
3. Main Result
In this section, a novel proof approach is developed, distinct from previous methods. Specifically, the Schauder fixed point theorem is applied in Banach semilinear spaces without requiring Lipschitz conditions on
and
, thereby establishing the existence of both
-weak and
-weak solutions for the general symmetry coupled system (
3).
Lemma 4.
Suppose there exists a constant such that () are compact operators and . Then there exist and such that the operator , here
where , by
is continuous, where , are respectively determined by
Proof. For any two pairs of functions
, we have
The compactness of and implies their boundedness. Let
for
. Then for any
,
, there exist
such that
and
, (since
are positive power polynomials for any
and
). Taking
and
and denoting
, we obtain
We first show that
is a self-mapping on
, i.e.,
. By (20), for any
, we have
From
, we obtain
. Based on
. Substituting into (21) and (23) yields
Similarly,
Combining (24), (25) and (22), gives
, hence
.
We now prove the continuity of
. Let
tends to
in
. By Lemma 1 (i), we have
The compactness and continuity of
imply the continuity of
. Similarly,
hence
is also continuous. Combining (26), (27) and (20), yields
This completes the proof. □
Lemma 5.
Under the assumptions ofLemma 4, if Ψ and Φ are compactly supported, Then is relatively compact in .
Proof. The proof proceeds in two steps.
Step 1: We first show that
is equicontinuous in
. For any
with
,
, and each
, let
,
,
,
then we have
and
Then, by (28)-(30), one obtains
by virtue of Lemma 1 (i), we obtain:
The continuity of
yields
Similarly, for
,
and
which follows from the continuity of
. Combining (
6), (20), (32) and (33) gives
,
. Hence,
is equicontinuous on
.
Step 2: We show that is relatively compact. By Lemma 2, it suffices to verify: is level-equicontinuous; is a compact-supported subset of .
(i) Verify
. For any fixed
,
. If
, then there exists
such that
Let
,
be compact operators with
relatively compact on
and
) relatively compact in
, where
. By Lemma 2,
and
are level-equicontinuous. Thus for any
, there exists
such that for all
and
, when
,
and
Since
and
hold for
, it follows from (34) and (35) that
This implies
is level-equicontinuous on
.
(ii) To verify condition . Given the relative compactness of and , Lemma 2 implies that and possess compact supports and are level-equicontinuous on [0,1]. By Definition 7, there exist compact sets such that , , and for all .
Furthermore, the compact supports of
and
guarantee the existence of compact sets
satisfying:
,
. we obtain the inclusion relation:
Since
is bounded on
, there exists compact
such that
, establishing the compact support of
. Similarly,
for some compact
, proving
has compact supported. From (18), we obtain
confirming
is a compactly supported.
Thus is relatively compact on , and by Ascoli-Arzelá theorem, also on . □
Lemma 6 ([
38]).
Let S be a nonempty, bounded, closed and convex subset of a Banach semilinear space endowed with the cancellation property. If h: is a compact operator, then h admits at least one fixed point in S.
Theorem 1. Assume there exists such that acts as compact operator and are compact-supported. Then there exist and such that the equation (3) admits at least one -weak solution on , where .
Proof. Define the operator
as in (18) and operators
,
as in (19). One readily verifies that
is well-defined. By Lemma 4,
is a continuous. Lemma 5 combined with the Ascoli-Arzel
theorem implies that
is relatively compact. Hence
is a compact operator by Definition 9. Lemma 6 guarantees that
admits at least one fixed point in
, which constitutes a
-weak solution of (
3). □
We now establish the existence of
-weak solution for (
3) under the following hypotheses:
, .
If
, then for all
and each
, the following inclusions hold:
Lemma 7.
Assume hypothesesandhold, and there exists such that
(i)For , is compact operator.
(ii).
Then there exist and such that the operator , constitutes a continuous operator from to itself, where for :
with .
Proof. Since hypotheses
and
hold for all
and every
, we obtain
As the proof follows identical reasoning to Lemma 4, the detailed derivation is omitted here. □
Following an analogous proof to Lemma 5, we obtain the following result.
Lemma 8 ([
14]).
Under all assumptions ofLemma 7
, if Ψ and Φ possess compact supports, then is relatively compact on .
Theorem 2.
If all conditions ofTheorem 1
hold andandare satisfied, then there exist , such that (3) admits at least one -weak solution on , where is as defined inLemma 7.
Proof. The proof follows identical reasoning to Theorem 1 and is therefore omitted. □
Remark 3.
Building upon the methodological framework established in[
29]
, we implementLemmas 6-8
and Ascoli-Arzelá theorem within Banach semilinear spaces without imposing Lipschitz conditions. This approach yields a fundamentally distinct proof methodology for the existence of -weak solutions compared to[
37].
4. Numerical Example with Potential Applications
In the sequel, we present the following numerical example with potential applications to verify our main results: For each
and
,
where
and
are fuzzy-valued functions and
P is a fuzzy number. Corresponding to the system (
3), it is readily verified that the functions
and
are compact operators in (39). Furthermore, from (
12), we immediately obtain
and
.
We note that in [
2], stated that the prey-predator system (
1) is related to ecological models by virtue of their connection with memory and fractal which are distinctive characteristics of these ecological models. Now, we extend model (
1) to FFPDE (i.e., (39)), where the right-hand side of the equations is further generalized to represent a multi-species biological population model under uncertain environments, and consider the symmetry coupled system (39) to verify the existence of solutions to (
3).
Let
be a triangular fuzzy number. From [
15], its
-level set is given by:
Consequently, we obtain:
By Definition 7, one has
Let
and
be compact sets, implying that
and
possess compact supports. Define
, and take
. By metric properties:
,
. Hence, it is established that
,
.
(Case I) For
, applying the Buckley-Feuring (BF) fuzzification strategy along with [
39] and combining Theorem 1 with the compact support and continuity results, the
-weak solution of system (39) is obtained as:
(Case II) For
k = 2, based on Lemma 1 (iii)-(v) and (17), while adopting a strategy analogous to
(Case I), the BF solution of (39) is derived as
By the continuity of the extension principle, the level sets of the fuzzy solutions to (39) are:
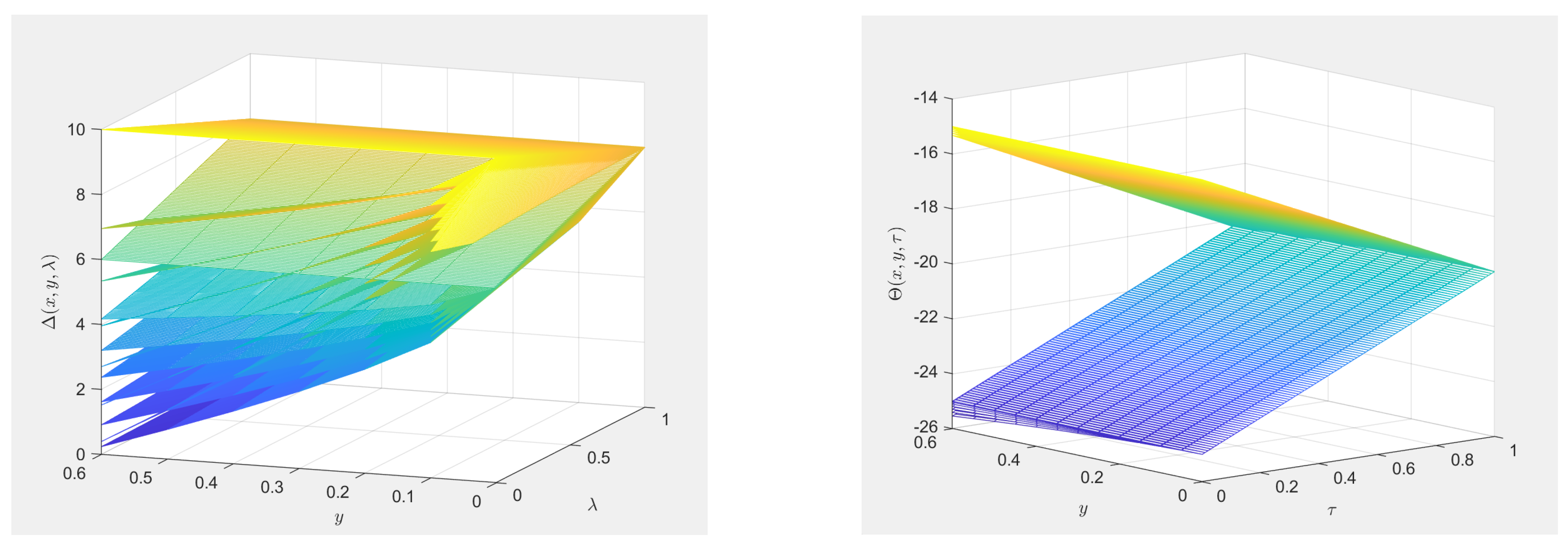
Figure 1. presents simulation results of the level sets for the fuzzy solutions in (40) and (41). The left and right subfigures show seven level sets of
and
at seven fixed
x values, respectively. Each surface group corresponds to a
or
level set, with inter-surface distances characterizing the fuzzy solutions. When six
y values are fixed, the variations of level sets with
x and
are consistent with
Figure 1. The curves in the
planes represent contour lines of
and
, respectively.
To verify
–
, let
,
. Since
we get
and by (
7), one has
Hence,
By Proposition 21 (b) of [
31], the H-difference
exists. Taking
its level set is:
with interval length:
Using an analogous computational approach, we obtain:
Hence, the H-difference
exists.
Similarly, from (42) and (43):
Consequently:
This implies
By Proposition 21(a) of [
31], the H-difference
exists. Using identical methodology:
The aforementioned procedure establishes the existence of the H-difference
. Heretofore, these verify the assumptions
and
in Theorem 2. Given that
and
are compact-supported and
, it follows from Theorem 2 that a
-weak solution to (39) exists on
and