Mitigating the Stability-Plasticity Trade-off in Neural Networks via Shared Extractors in Class-Incremental Learning

1. Introduction

Humans learn new tasks without forgetting what they already know, but neural networks trained on sequential tasks typically suffer catastrophic forgetting [1], especially when access to old data is limited or only a few exemplars are available. Regularization-based methods add penalties that discourage changes to parameters deemed important for previous tasks. Rehearsal-based methods store a small subset of old examples for replay during new-task training. Knowledge distillation is also widely used; for example, iCaRL [2] freezes the model learned up to stage $(t-1)$ and uses it as a teacher to transfer old-task knowledge to the model at stage t. These approaches help, yet continual learning with a single shared backbone remains challenging.

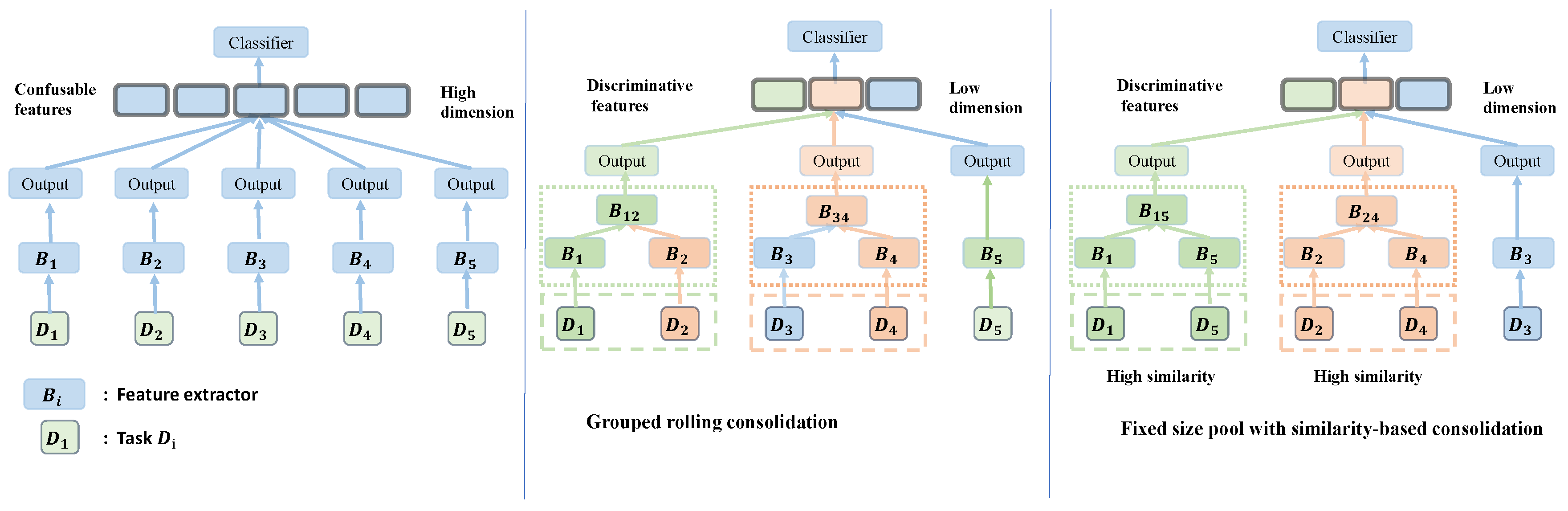
Dynamic-network methods expand the model by assigning a dedicated feature extractor to each task. After training a task, its extractor is frozen, and a new extractor is allocated for the next task (see Figure 1, left). This prevents interference with parameters of previous tasks, but the number of extractors increases linearly with the number of tasks. For example, in methods such as DER, a full CNN backbone is added for every new task, so after M tasks the model contains M extractors. At test time, each input is processed by all extractors, and the resulting features are concatenated and fed into a global classifier. However, since early extractors are trained only on their original task data, their outputs are often irrelevant for later tasks. Consequently, concatenating features from all extractors introduces redundancy and noise, which reduces accuracy. For example, as shown in Table 1, on CIFAR-100, dividing 100 classes into 10 tasks requires 10 extractors and yields $65.26\%$ accuracy with DER. When the dataset is instead split into 20 tasks, the number of extractors doubles to 20, but the accuracy drops to $61.87\%$. This demonstrates that increasing the number of extractors does not guarantee better performance, and excessive extractors can harm generalization by amplifying redundancy.

These observations highlight a key limitation: dedicating one extractor per task is inefficient. We therefore ask whether extractors can be shared across tasks to reduce their total number, mitigate interference from redundant extractors, and still preserve the benefits of dynamic networks. To this end, we propose Task Sharing Distillation(TSD), which reduces the number of extractors by allowing tasks to share them. We study two variants.

Grouped rolling consolidation. Consecutive tasks are grouped and merged to share a single extractor by distillation. For example, tasks 1–2 may share one extractor and tasks 3–4 another (see Figure 1, middle). The group size does not need to be fixed; different extractors may cover different numbers of tasks depending on the experimental setup.

Fixed-Size Pool with Similarity-Based Consolidation. We first set a maximum number of extractors. Early tasks each initialize a new extractor until this limit is reached. For every subsequent task, we train a temporary extractor and then merge it into the most compatible existing extractor through distillation. Compatibility is determined by prototype similarity: the new task’s feature prototypes are compared with those maintained by each existing extractor, and the task is merged into the extractor with the highest similarity. This strategy encourages feature reuse among related tasks while keeping the overall number of extractors bounded (see Figure 1, right).

To further ensure that different extractors maintain independent feature subspaces, we impose a feature distinctness constraint during training. When a new extractor is introduced, we add an explicit constraint that encourages its features to remain distinct from those of existing extractors. This constraint guides the new extractor toward representations that are discriminative with respect to previously learned subspaces, so that each extractor specializes in a subset of task subspaces and different subsets remain independent.

Compared with DER, our approach substantially reduces the number of backbone parameters. In particular, using only three extractors, our methods achieve higher accuracy than DER, which relies on ten extractors.

Although our experiments focus on vision tasks, the underlying idea is more general. Large language models (LLMs) are widely applied in continual and multi-domain settings, where assigning a separate adapter to each task similarly leads to parameter growth and redundancy. Our proposed Task-Sharing Distillation (TSD) offers a promising way to consolidate and share modules in such scenarios, highlighting its potential relevance for scaling LLMs efficiently.

Our main contributions are:

1. We analyze the relationship between the number of extractors and model performance. Increasing the number of extractors not only inflates parameters but also reduces generalization.

2. We propose Task-Sharing Distillation, which reduces the number of extractors by allowing tasks to share them and by consolidating multiple extractors through distillation. We present two practical strategies: grouped rolling consolidation, which groups consecutive tasks into a shared extractor, and Fixed-Size Pool with similarity based consolidation, which allocates a fixed number of extractors and assigns new tasks to the most similar one.

3. Our methods achieve superior accuracy and parameter efficiency compared with state-of-the-art methods such as DER. In particular, our methods outperform DER while using only three extractors, whereas DER requires ten.

2. Related Works

Incremental learning can be categorized into three main types [3,4]: task-incremental, domain-incremental, and class-incremental learning. In task-incremental learning, the model receives the task ID during evaluation and only classifies within the given task. Domain-incremental learning uses the same set of classes across tasks but with different domains [5,6]. Class-incremental learning assigns different classes to each task without providing the task ID at test time, so the model must classify across all classes.

To reduce forgetting, regularization methods such as EWC [1,7] constrain parameter updates based on their importance to previous tasks. Knowledge distillation methods [2,8,9,10,11,12,13] transfer knowledge from old feature extractors and exemplars, using distillation [14] to guide new models. Other works [15,16] address old-class forgetting caused by the imbalance between old and new samples. However, a single shared extractor remains limited. To improve capacity, AANets [17] combine stable and plastic blocks, and DualNet [18] incorporates complementary fast and slow learning systems [19]. GAN-based approaches [20,21] generate old samples to alleviate data scarcity, while auto-encoder based methods [22] learn class-specific subspaces for classification.

Dynamic network methods expand the architecture by adding feature extractors for new tasks. DER [23] assigns a new extractor to each task and freezes old ones. DyTox [24] introduces a transformer encoder-decoder with dynamic task tokens. TagFex [25] captures task-agnostic features and merge them with task-specific ones. FOSTER [26] learns new extractors inspired by gradient boosting and distills both old and new extractors into a unified network. MEMO [27] extend selected blocks instead of full extractors. SEED [28] employs a fixed number of feature extractors and models each class with a Gaussian distribution to select suitable extractors for learning new tasks.

Recently, pre-trained models have been applied to incremental learning [5,29,30,31,32]. These approaches freeze the backbone and insert lightweight modules, such as adapters, LoRa, or prompts, and only fine-tune these modules for efficient adaptation.

3. Methodology

3.1. Problem Setup and Method Overview

In this section, we first define the class incremental learning task, then introduce dynamic-network-based approaches, and finally motivate our two methods that share feature extractors.

Class Incremental Learning Task. The goal of incremental learning is to train on a sequence of tasks and, after completing all tasks, maintain strong performance across all learned classes. Let the total number of tasks be T. For task $t\in \{1,\dots ,T\}$, the dataset is ${\mathcal{S}}_t=\left\{(x,y)\right\}$ with class set ${\mathcal{C}}_t$. The class sets are disjoint, i.e., ${\mathcal{C}}_t\cap {\mathcal{C}}_{t^{\prime }}=⌀$ for $t\ne t^{\prime }$. Let $n_t=\left|{\mathcal{C}}_t\right|$ denote the number of classes in task t. Each sample $(x,y)\in {\mathcal{S}}_t$ belongs to one of these $n_t$ classes.

Dynamic-Network Methods. Traditional incremental learning often uses a single backbone for all tasks, which risks severe forgetting. Dynamic-network methods address this by assigning a dedicated feature extractor to each task. We denote the extractor for task t as ${\varphi }_t$. A representative baseline, DER, trains ${\varphi }_t$ on task t and then freezes its parameters. For the next task, a new extractor ${\varphi }_{t+1}$ is introduced. At inference time, an input x is processed by all extractors, and their features are concatenated before being classified by a global head g:

$$z\left(x\right)=[{\varphi }_1\left(x\right)\parallel {\varphi }_2\left(x\right)\parallel \dots \parallel {\varphi }_T\left(x\right)],\widehat{y}=g\left(z\left(x\right)\right).$$

(1)

Freezing prevents interference with past knowledge and improves performance compared with a single shared backbone. However, this design introduces two major issues. First, the number of parameters grows linearly with the number of tasks. Second, since learning is sequential, an extractor ${\varphi }_i$ ($i<j$) never observes data from a future task ${\mathcal{S}}_j$, making its features irrelevant or even harmful for later tasks.

These limitations raise an important question: can we reduce the number of extractors while still retaining the benefits of dynamic networks? To address this, we introduce Task-Sharing Distillation (TSD), which progressively merges task knowledge into shared extractors through distillation. Building on TSD, our two methods, Grouped Rolling Consolidation and Fixed-Size Pool with Similarity-Based Consolidation, effectively control parameter growth, reduce redundancy, and maintain accuracy on both past and future tasks.

3.2. Grouped Rolling Consolidation (GRC)

Given T tasks, we partition them into groups $\{{\mathcal{G}}_1,\dots ,{\mathcal{G}}_K\}$, where each group ${\mathcal{G}}_k$ contains a contiguous subset of tasks. The group size is not fixed in advance; different groups may cover different numbers of tasks depending on the schedule. After completing the first group ${\mathcal{G}}_1$, we freeze a consolidated extractor ${\Psi }_1\equiv {\psi }_{{\mathcal{G}}_1}$. For later groups, task-specific extractors are temporarily maintained, progressively merged by distillation into a rolling extractor ${\psi }_{t_s:t}$, and finally frozen as ${\Psi }_k$ at the end of the group. Importantly, ${\psi }_{t_s:t}$ denotes a single consolidated extractor obtained from tasks $t_s$ to t, not a concatenation of multiple extractors.

Training inside a group (${\mathcal{G}}_k$, $k\ge 2$).

Let $t_s=min\left({\mathcal{G}}_k\right)$ be the first task in ${\mathcal{G}}_k$. All frozen extractors from previous groups are denoted by $\{{\Psi }_1,\dots ,{\Psi }_{k-1}\}$ and remain fixed.

Case A (first task $t=t_s$). A new extractor ${\varphi }_{t_s}$ and a temporary classifier head $q_{t_s}$ are instantiated. The classifier input concatenates frozen features with the new feature:

$$F_{t_s}^{\mathrm{tea}}\left(x\right)=\left[{\Psi }_1\left(x\right)\parallel \dots \parallel {\Psi }_{k-1}\left(x\right)\parallel {\varphi }_{t_s}\left(x\right)\right],$$

(2)

and the cross-entropy loss is

$${\mathcal{L}}_{\mathrm{CE}}\left(t_s\right)={\mathbb{E}}_{(x,y)\sim {\mathcal{S}}_{t_s}}\mathrm{CE}\left(q_{t_s}\left(F_{t_s}^{\mathrm{tea}}\left(x\right)\right),y\right).$$

(3)

No consolidation is performed since there is only one new extractor in this group.

Case B (subsequent tasks $t>t_s$). For each new task, we instantiate an extractor ${\varphi }_t$ and a temporary head $q_t$. The current-group teacher feature is defined as

$$R_t\left(x\right)=\left\{\begin{array}{cc}\left[{\varphi }_{t_s}\left(x\right)\parallel {\varphi }_t\left(x\right)\right],\hfill & \mathrm{if}\mathrm{no}\mathrm{rolling}\mathrm{extractor}\mathrm{exists},\hfill \\ \left[{\psi }_{t_s:(t-1)}\left(x\right)\parallel {\varphi }_t\left(x\right)\right],\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(4)

The full teacher feature is

$$F_t^{\mathrm{tea}}\left(x\right)=\left[{\Psi }_1\left(x\right)\parallel \dots \parallel {\Psi }_{k-1}\left(x\right)\parallel R_t\left(x\right)\right],$$

(5)

and $q_t$ predicts over ${\mathcal{C}}_{1:t}={\bigcup }_{i=1}^t{\mathcal{C}}_i$.

We first optimize ${\varphi }_t$ and $q_t$ using the cross-entropy loss on $F_t^{\mathrm{tea}}\left(x\right)$:

$${\mathcal{L}}_{\mathrm{CE}}\left(t\right)={\mathbb{E}}_{(x,y)\sim {\mathcal{S}}_t}\mathrm{CE}\left(q_t\left(F_t^{\mathrm{tea}}\left(x\right)\right),y\right).$$

(6)

After this step, ${\varphi }_t$ and $q_t$ are frozen, and consolidation is applied.

Immediate consolidation at step t ($t>t_s$).

We merge the current-group extractors into a rolling extractor ${\psi }_{t_s:t}$ with head $h_{t_s:t}$, while keeping $\{{\Psi }_1,\dots ,{\Psi }_{k-1}\}$ fixed. The student features are

$$F_t^{\mathrm{stu}}\left(x\right)=\left[{\Psi }_1\left(x\right)\parallel \dots \parallel {\Psi }_{k-1}\left(x\right)\parallel {\psi }_{t_s:t}\left(x\right)\right].$$

(7)

Teacher and student logits are

$$z_t^{\mathrm{tea}}\left(x\right)=q_t\left(F_t^{\mathrm{tea}}\left(x\right)\right),z_t^{\mathrm{stu}}\left(x\right)=h_{t_s:t}\left(F_t^{\mathrm{stu}}\left(x\right)\right),$$

(8)

.

Logit distillation with temperature $\tau$ is applied:

$${\mathcal{L}}_{\mathrm{KD}}\left(t\right)=\mathrm{KL}\left(\mathrm{softmax}\left(\frac{z_t^{\mathrm{tea}}\left(x\right)}{\tau }\right)\parallel \mathrm{softmax}\left(\frac{z_t^{\mathrm{stu}}\left(x\right)}{\tau }\right)\right).$$

(9)

After optimization, the temporary teachers forming $R_t$ are discarded, and the rolling extractor ${\psi }_{t_s:t}$ is kept.

End of a group.

When the last task in ${\mathcal{G}}_k$ is completed, the rolling extractor is frozen as the group extractor:

$${\Psi }_k\leftarrow {\psi }_{{\mathcal{G}}_k},H_k\leftarrow h_{{\mathcal{G}}_k}.$$

(10)

Thus, after K groups we obtain $\{{\Psi }_1,\dots ,{\Psi }_K\}$.

Inference.

After completing task $t\in {\mathcal{G}}_k$, prediction uses the concatenation of all frozen group extractors and the current rolling extractor (if the group is not finished):

$$\widehat{y}=h_{t_s:t}\left(\left[{\Psi }_1\left(x\right)\parallel \dots \parallel {\Psi }_{k-1}\left(x\right)\parallel {\psi }_{t_s:t}\left(x\right)\right]\right).$$

(11)

If t is the last task in ${\mathcal{G}}_k$, inference uses the frozen extractors only:

$$\widehat{y}=H_k\left(\left[{\Psi }_1\left(x\right)\parallel \dots \parallel {\Psi }_k\left(x\right)\right]\right).$$

(12)

Worked example.

For instance, if tasks are grouped as ${\mathcal{G}}_1=\{1,2\},{\mathcal{G}}_2=\{3,4,5,6\},{\mathcal{G}}_3=\{7,8,9\},{\mathcal{G}}_4=\left\{10\right\}$, the procedure yields four frozen extractors $\{{\Psi }_1,{\Psi }_2,{\Psi }_3,{\Psi }_4\}$.

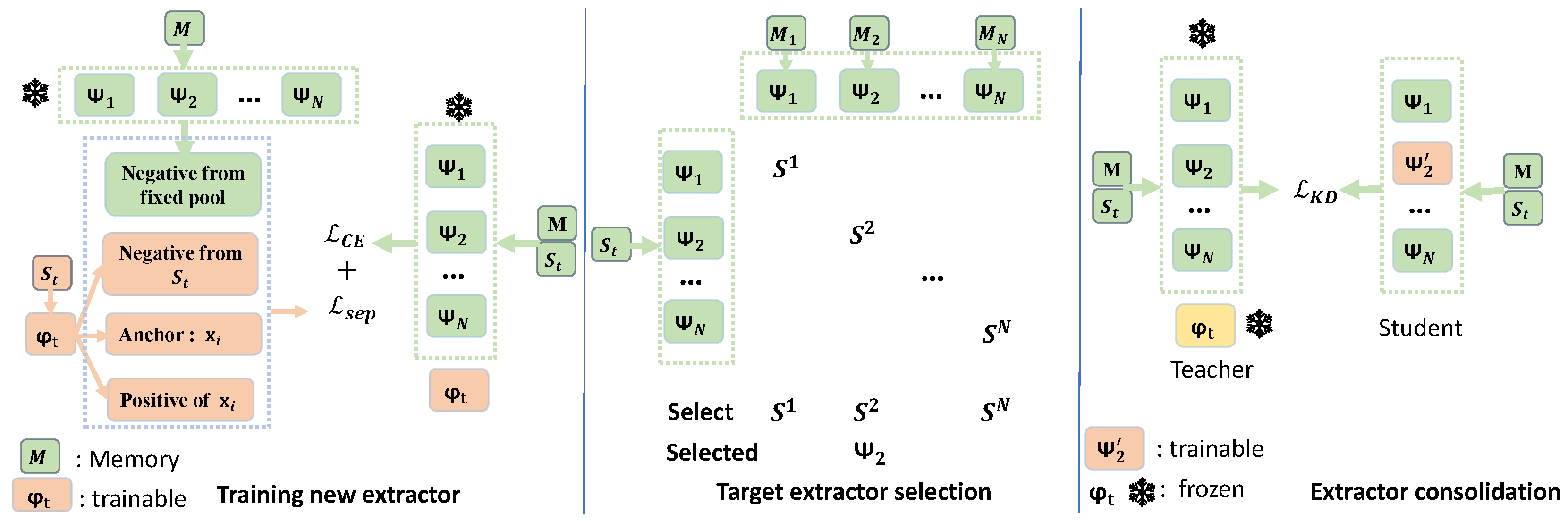
3.3. Method 2: Fixed-Size Pool with Similarity-Based Consolidation

GRC controls parameter growth effectively, but it does not exploit task similarity. This raises a natural question: should similar tasks share extractors to further reduce redundancy? Since task similarity cannot be determined in advance under incremental learning, we adopt a simplified setting: we first allocate extractors to the initial N tasks, forming a fixed-size pool of N extractors. Subsequent tasks are then integrated by sharing with the most related extractor in this pool. The overall framework is illustrated in Figure 2.

Initialization with N extractors.

We predefine the number of available extractors as N. For the first N tasks, each task $t\le N$ is assigned a new extractor ${\varphi }_t$ and a classifier $g_t$. During training, all previous extractors are frozen, and only ${\varphi }_t$ and $g_t$ are updated. The classifier input concatenates features from all frozen extractors and the new one:

$$F_t\left(x\right)=\left[{\varphi }_1\left(x\right)\parallel \dots \parallel {\varphi }_{t-1}\left(x\right)\parallel {\varphi }_t\left(x\right)\right],$$

(13)

$${\mathcal{L}}_{\mathrm{CE}}\left(t\right)={\mathbb{E}}_{(x,y)\sim {\mathcal{S}}_t}\mathrm{CE}\left(g_t\left(F_t\left(x\right)\right),y\right).$$

(14)

After training the N-th task, we retain the extractors $\{{\varphi }_1,\dots ,{\varphi }_N\}$.

Beyond N tasks: triggering consolidation.

When a new task $t>N$ arrives, we instantiate a temporary extractor ${\varphi }_t$ and a classifier $g_t$. The classifier takes as input the concatenation of features from all N frozen extractors $\{{\Psi }_1,\dots ,{\Psi }_N\}$ and the new extractor ${\varphi }_t$:

$$F_t\left(x\right)=\left[{\Psi }_1\left(x\right)\parallel \dots \parallel {\Psi }_N\left(x\right)\parallel {\varphi }_t\left(x\right)\right].$$

(15)

The model is trained with cross-entropy over all classes from tasks 1 through t:

$${\mathcal{L}}_{\mathrm{CE}}\left(t\right)={\mathbb{E}}_{(x,y)\sim {\mathcal{S}}_{1:t}}\mathrm{CE}\left(g_t\left(F_t\left(x\right)\right),y\right).$$

(16)

After training, the temporary extractor ${\varphi }_t$ must be consolidated into one of the existing N extractors $\{{\Psi }_1,\dots ,{\Psi }_N\}$ to keep the pool size fixed.

Similarity-based target selection.

For each class $c_{tj}$ in the new task ${\mathcal{S}}_t$, we compute its prototype on extractor ${\Psi }_k$, with $k\in \{1,\dots ,N\}$:

$$p_{tj}^k={\displaystyle \frac{1}{|{\mathcal{S}}_{tj}|}}\sum _{x\in {\mathcal{S}}_{tj}}{\Psi }_k\left(x\right),$$

(17)

where ${\mathcal{S}}_{tj}$ denotes the set of samples from class $c_{tj}$.

For extractor ${\Psi }_k$ and its own task ${\mathcal{S}}_k$, the prototype of class $c\in {\mathcal{C}}_k$ is

$$M{p}_c^k={\displaystyle \frac{1}{M}}|{\mathcal{M}}_{kc}|\sum _{x\in {\mathcal{M}}_{kc}}{\Psi }_k\left(x\right)M,$$

(18)

where ${\mathcal{M}}_{kc}$ denotes the exemplar set of class c from task ${\mathcal{S}}_k$.

The similarity score for class $c_{tj}$ on ${\Psi }_k$ is

$$s_{tj}^k=\underset{c\in {\mathcal{C}}_k}{max}\mathrm{sim}\left(p_{tj}^k,p_c^k\right).$$

(19)

Summing over all classes in task t, we obtain the task-to-extractor similarity

$$S^k=\sum _{c_{tj}\in {\mathcal{S}}_t}{s}_{tj}^k.$$

(20)

We select the extractor with the maximum similarity score $S^k$ as the consolidation target:

$$i^{*}=arg\underset{k\in \{1,\dots ,N\}}{max}{S}^k.$$

(21)

To avoid overusing a single extractor, we further enforce balanced selection among extractors. If an extractor is chosen for the current task, it is temporarily excluded from the next selection, and the consolidation target is chosen from the remaining extractors.

Consolidation training.

We copy the selected extractor ${\Psi }_{i^{*}}$ and unfreeze it for optimization, while keeping the remaining $N-1$ extractors frozen. The teacher logits are produced by the classifier $g_t$ applied to the concatenation of features from all N frozen extractors and the frozen temporary extractor ${\varphi }_t$:

$$z_t^{\mathrm{tea}}\left(x\right)=g_t\left([{\Psi }_1\left(x\right)\parallel \dots \parallel {\Psi }_N\left(x\right)\parallel {\varphi }_t\left(x\right)]\right).$$

(22)

The student always maintains exactly N extractors. It replaces ${\Psi }_{i^{*}}$ with its trainable copy ${\Psi }_{i^{*}}^{\prime }$ and introduces a trainable head $h_{i^{*}}$:

$$F_t^{\mathrm{stu}}\left(x\right)=[{\Psi }_1\left(x\right)\parallel \dots {\Psi }_{i^{*}}^{\prime }\left(x\right)\parallel \dots \parallel {\Psi }_N\left(x\right)],$$

(23)

$$z_t^{\mathrm{stu}}\left(x\right)=h_{i^{*}}\left(F_t^{\mathrm{stu}}\left(x\right)\right).$$

(24)

We minimize the distillation loss:

$${\mathcal{L}}_{\mathrm{KD}}\left(t\right)=\mathrm{KL}\left(\mathrm{softmax}\left(z_t^{\mathrm{tea}}\left(x\right)/\tau \right)\parallel \mathrm{softmax}\left(z_t^{\mathrm{stu}}\left(x\right)/\tau \right)\right),$$

(25)

where $\tau$ is the temperature.

After optimization, we update ${\Psi }_i\leftarrow {\Psi }_{i^{*}}^{\prime }$ and discard ${\varphi }_t$, ensuring that the extractor pool size remains N.

3.4. Training Objective

For each new task t, the learnable feature extractor ${\varphi }_t$ and its task-specific classifier $g_t$ are optimized with a standard cross-entropy loss as Eq. 3, Eq. 6, Eq. 14 and Eq. 16. To further encourage feature space separation across extractors, we enhance the training of each newly added extractor using contrastive learning [33]. Specifically, memory samples from old tasks, processed by frozen extractors, are incorporated as additional negatives to guide ${\varphi }_t$ toward a distinct representation space.

For a sample $x_i$ from the current task ${\mathcal{S}}_t$ in the minibatch, the positive set ${\mathcal{P}}_i$ consists of embeddings from augmented views of the same class, extracted by the current feature extractor ${\varphi }_t$. The negative set $N_i$ includes two sources: (i) embeddings from different classes in the same minibatch under ${\varphi }_t$, and (ii) embeddings of old classes in the minibatch extracted by the frozen extractors ${\mathcal{E}}_t^{\mathrm{frozen}}$.

Let $z_i=\mathrm{proj}\left({\varphi }_t\left(x_i\right)\right)$, where $\mathrm{proj}(·)$ denotes a projection head [33] applied to the feature extractor output. The contrastive loss for a minibatch of size B from task ${\mathcal{S}}_t$ is

$${\mathcal{L}}_{\mathrm{sep}}\left(t\right)={\displaystyle \frac{1}{2*B}}\sum _{i=1}^{2*B}\left(-{\displaystyle \frac{1}{|{\mathcal{P}}_i|}}\sum _{p\in {\mathcal{P}}_i}log{\displaystyle \frac{exp\left(\mathrm{sim}(z_i,p)/\lambda \right)}{exp\left(\mathrm{sim}(z_i,p)/\lambda \right)+{\sum }_{n\in N_i}exp\left(\mathrm{sim}(z_i,n)/\lambda \right)}}\right).$$

(26)

Overall Objective.

The overall loss for task t is

$${\mathcal{L}}_{\mathrm{new}}\left(t\right)={\mathcal{L}}_{\mathrm{CE}}\left(t\right)+\alpha {\mathcal{L}}_{\mathrm{sep}}\left(t\right),$$

(27)

where $\alpha >0$ balances the two terms.

Here, ${\mathcal{L}}_{\mathrm{CE}}\left(t\right)$ refers to the cross-entropy loss used in Eq. 3 for the first task in a group, Eq. 6 for subsequent tasks before consolidation, and Eq. 14, Eq. 16 for the fixed-pool method.

4. Experiments

4.1. Datasets and Settings

We evaluate our methods on CIFAR-100[34] and ImageNet-100. ImageNet-100 is a subset of ImageNet[35] with 100 classes. The evaluation covers multiple incremental learning settings. Following DER, we adopt two standard protocols on ImageNet-100:

(1) B0S10: 10 classes per task, for a total of 10 tasks;

(2) B50S5: the initial task has 50 classes and each new task adds 5 classes, for a total of 11 tasks.

For CIFAR-100, we consider four variants:

(1) B0S10: 10 classes per task, for a total of 10 tasks;

(2) B0S5: 5 classes per task, for a total of 20 tasks;

(3) B50S5: 50 classes in the initial task, followed by 5 classes per task, for a total of 11 tasks;

(4) B50S2: 50 classes in the initial task, followed by 2 classes per task, for a total of 26 tasks.

Following DER, we use the herding selection strategy [36] to choose and retain old samples. For the B0 setting, we save a total of 2000 samples, while for the B50 setting, we retain 20 samples per class.

Under DER, each task is assigned a separate feature extractor, so the number of extractors grows linearly with the number of tasks. In contrast, our two methods—Fixed-Size Pool and Grouped Rolling Consolidation—use significantly fewer extractors. We first compare our approaches with DER and other baselines under the same settings, and show that using fewer extractors can even surpass the strong baseline DER. For clarity in the experimental tables, we denote our methods as $fi{x}_N$ and $gr{c}_N$, where N indicates the maximum number of extractors used.

For $gr{c}_N$, unless otherwise specified, we assume that all groups (except possibly the last one) share the same number of tasks. For example, with 10 tasks and $gr{c}_4$, tasks 1–3 share one extractor, tasks 4–6 share another, tasks 7–9 share another, and task 10 uses its own extractor.

Following [23,26], we use ResNet18 [37] as the feature extractor on ImageNet100 with a batch size of 256. For CIFAR-100, we employ a modified ResNet32 as the feature extractor with a batch size of 128. The initial learning rate is set to 0.1, and we use a cosine annealing scheduler, running for a total of 170 epochs. We use SGD with a momentum of 0.9. Weight decay is 5e-4 when learning new feature extractors. We set the weight decay to 0 during the distillation phase, and a temperature scalar $\tau$ of 2. Following [33], $\lambda$ is set to 0.07.

Evaluation Metrics.

Following DER, we evaluate models using average accuracy, last-step accuracy, and backward transfer (BWT).

Average accuracy. After completing step i, let $A_i$ denote the average accuracy over tasks 1 to i. With a total of N tasks, the metric is defined as

$$\mathrm{Avg}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{A}_i.$$

(28)

Last-step accuracy. The accuracy after the final task, i.e., $A_N$.

Backward transfer (BWT). Let $A_{S_j}^i$ denote the accuracy on the test set of task $S_j$ after learning task $S_i$. Then BWT is defined as

$$\mathrm{BWT}={\displaystyle \frac{1}{T-1}}\sum _{i=2}^T{\displaystyle \frac{1}{i}}\sum _{j=1}^i\left(A_{S_j}^i-A_{S_j}^j\right),$$

(29)

where T is the total number of tasks. A negative BWT indicates forgetting of previously learned tasks.

4.2. Results on ImageNet100

On the ImageNet100-B0S10 setting, DER uses 10 feature extractors. Our two methods require only 3 extractors yet outperform DER, as shown in Table 2, achieving more than $2\%$ higher average accuracy and over $3\%$ higher last-step accuracy. With 6 extractors, our methods achieve even higher accuracy.

On the ImageNet100-B50-S5 setting, DER uses 11 extractors, while our method uses only 8, yet achieves higher average accuracy than DER, and also consistently outperforms DER in terms of top-5 accuracy, as shown in Table 3

4.3. Results on CIFAR-100

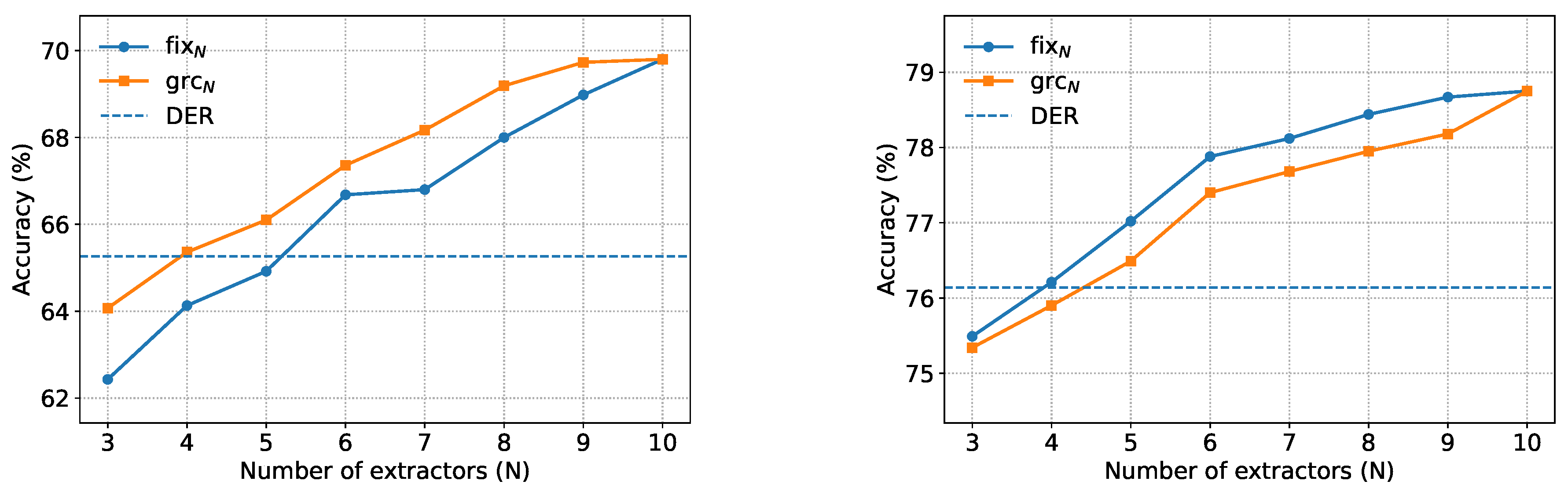
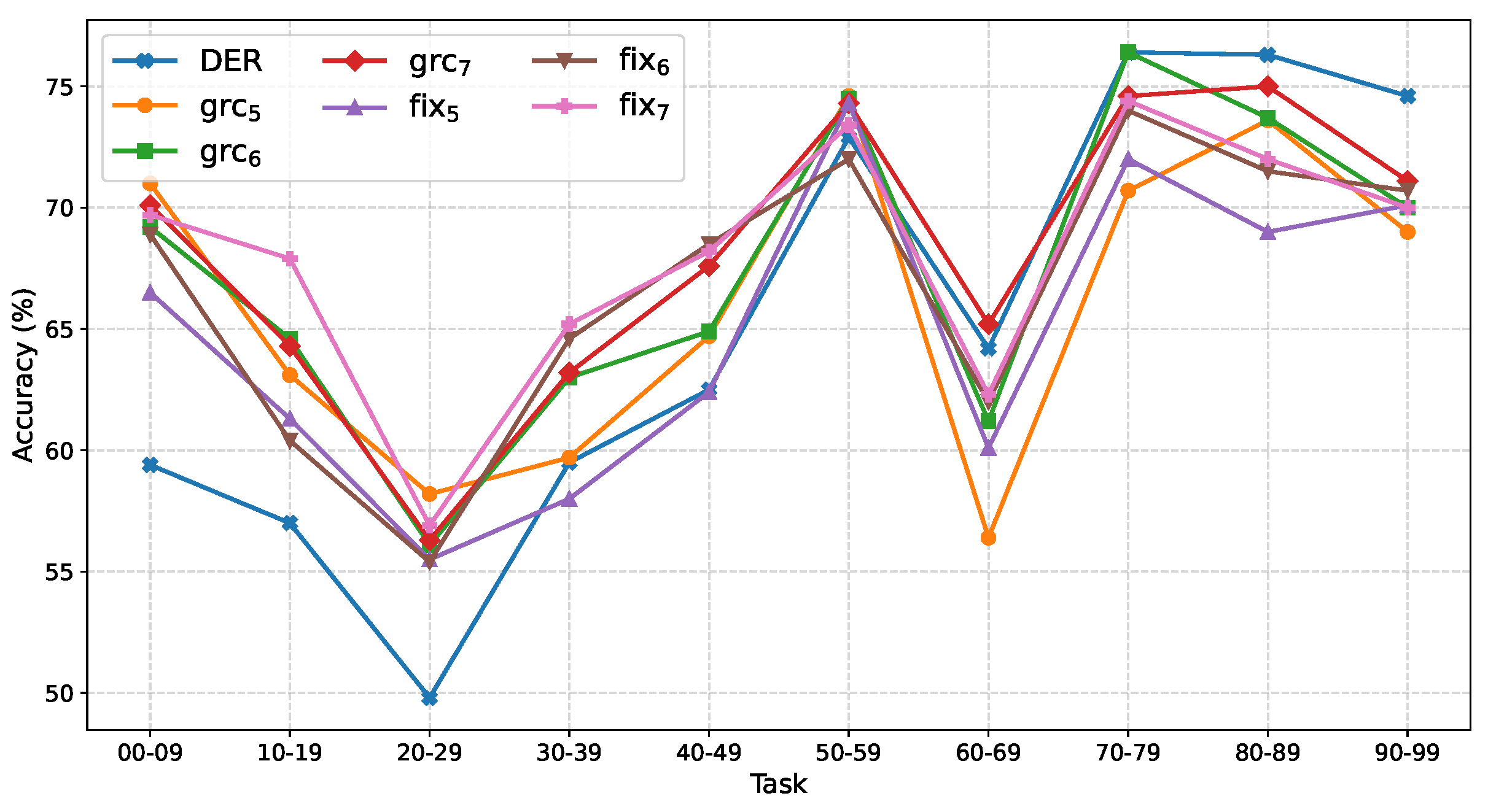
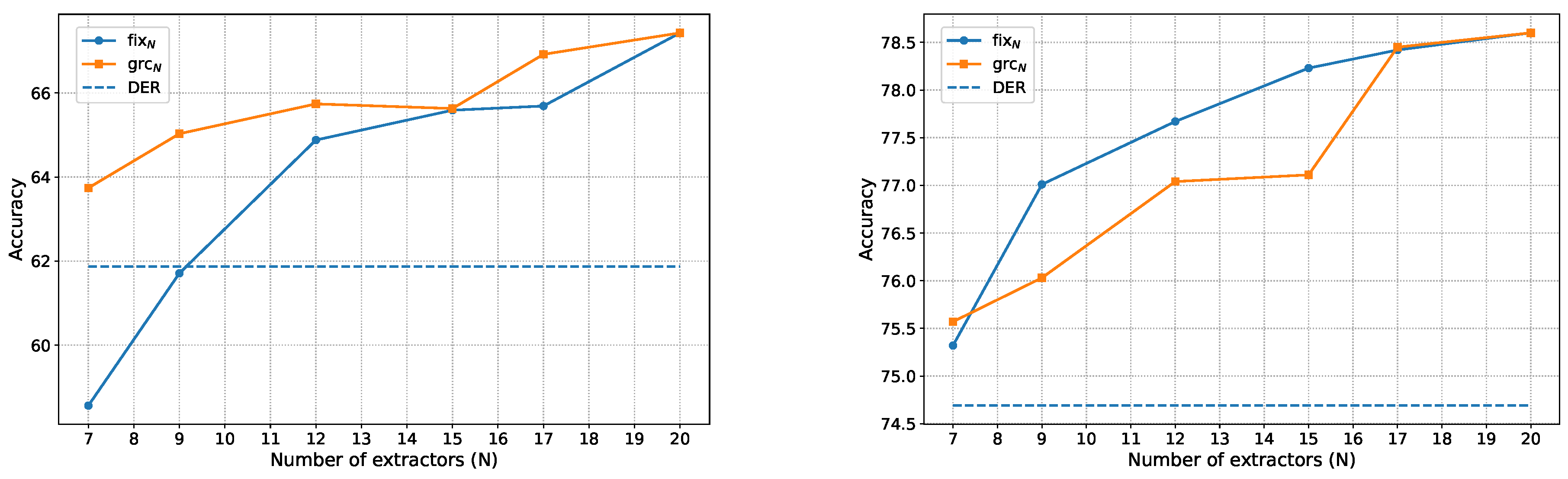
For CIFAR-100 B0S10, our methods achieve higher accuracy with only six extractors than DER with ten extractors, as shown in Table 4. We further examine the effect of increasing the number of extractors. As shown in Figure 3, both average accuracy and last-step accuracy improve consistently as the number of extractors increases. This result suggests that the benefit of adding new extractors outweighs the adverse effect of redundant information, thereby alleviating the stability–plasticity dilemma. 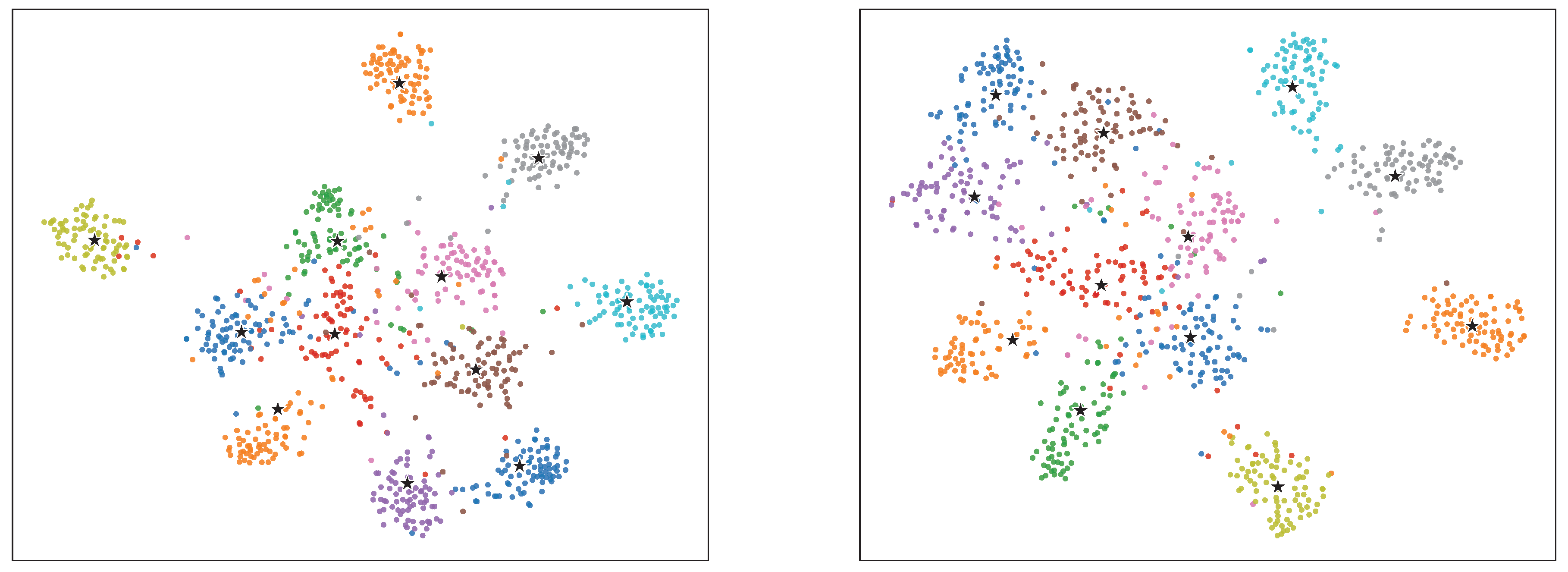We further compare the per-task accuracy after learning 10 tasks, as shown in Figure 4. DER suffers from a significant drop in accuracy on the first three tasks, whereas our methods, even with only five extractors, maintain clear advantages on these early tasks. This demonstrates that reducing the number of extractors and enforcing distinct feature subspaces among them is more effective in alleviating forgetting of early tasks. We further provide a visualization. As shown in Figure 6, DER produces more compact clusters within each class, but several clusters overlap in the central region. In contrast, $fi{x}_5$ achieves clearer separation between classes despite using fewer extractors.

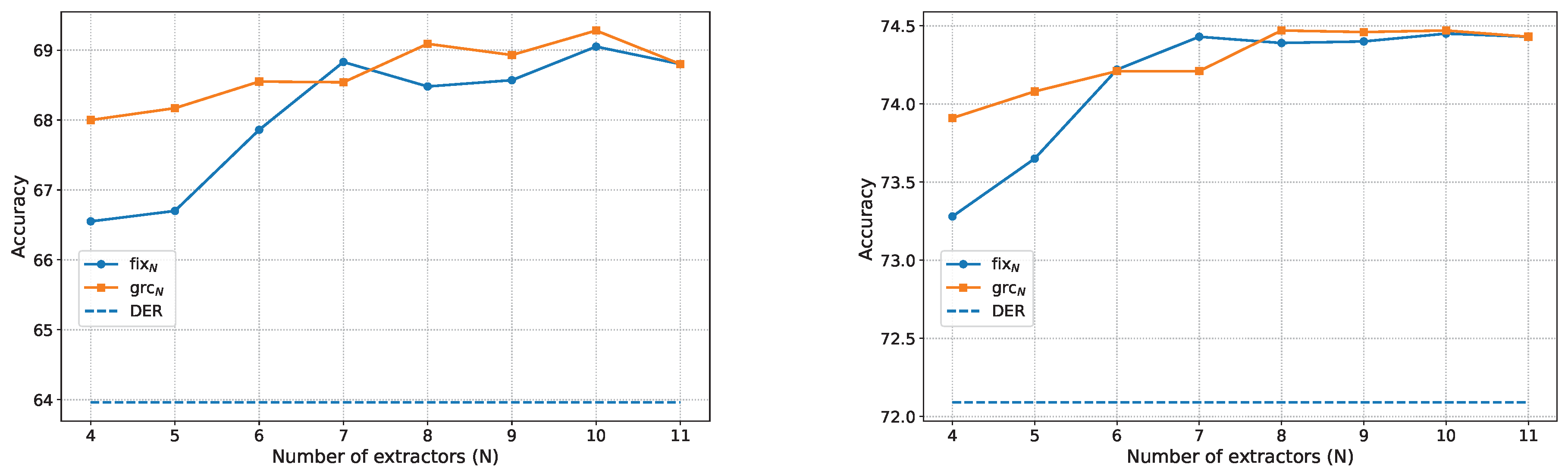
On the CIFAR100-B0S5 setting, both $fi{x}_7$ and $gr{c}_{10}$ achieve clear improvements over DER with 20 extractors, as shown in Table 5. We also analyze the effect of extractor numbers on accuracy. As shown in Figure 5, accuracy increases as the number of extractors grows.

On the CIFAR100-B0S5 setting, both $fi{x}_7$ and $gr{c}_{10}$ achieve clear improvements over DER with 20 extractors, as shown in Table 5. We also analyze the effect of extractor numbers on accuracy. As shown in Figure 5, accuracy grows as the number of extractors increases. For the fix method, increasing the number of extractors from 12 to 15 results in negligible improvement in average accuracy. In contrast, the grc method continues to benefit as more extractors are added.

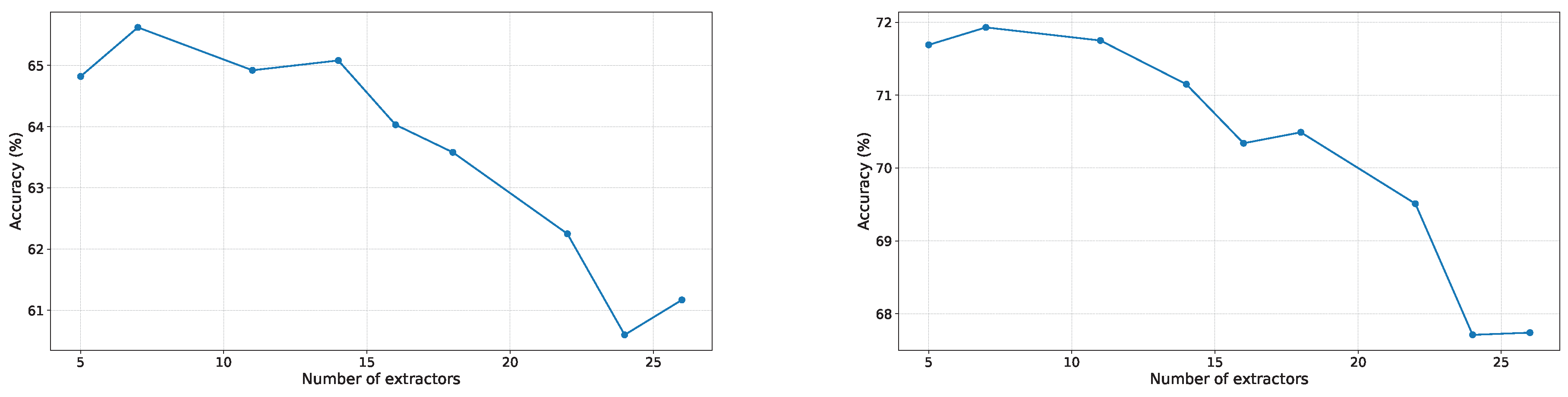
On the CIFAR100-B50S5 setting, DER employs 11 extractors. Our two methods achieve higher accuracy with only 4 extractors, as shown in Table 6. We further analyze the effect of extractor numbers on accuracy. As shown in Figure 7, accuracy improves significantly when the number of extractors increases from 4 to 7. Beyond 7 extractors, the gain becomes marginal, and using 11 extractors does not yield the best accuracy.

On the CIFAR100-B50S2 setting with 26 tasks, DER uses 26 extractors. Our two methods achieve higher accuracy with far fewer extractors, reaching clear advantages with only 7 extractors, as reported in Table 7.

In this setting, more extractors do not always yield better accuracy. As shown in Figure 8, the best results are obtained with about 7 extractors. When the number of extractors increases further, accuracy drops significantly, indicating that too many extractors cause interference across tasks and lead to degradation. This suggests that while preserving task-specific extractors helps retain old knowledge, an excessive number of extractors introduces redundant and noisy information, which can interfere with learning new tasks and degrade overall performance.

4.4. Ablation Study

We conduct an ablation study on ${\mathcal{L}}_{\mathrm{sep}}$. As shown in Table 8, ${\mathcal{L}}_{\mathrm{sep}}$ consistently improves accuracy by enforcing separation across different extractors, making their representations more discriminative. Maintaining distinct feature spaces is particularly important for the fix method, since it selects extractors by assigning similar tasks. With ${\mathcal{L}}_{\mathrm{sep}}$, fix achieves clearer feature separation and larger performance gains.

4.5. BWT

We report the BWT results in Table 9. Compared with DER, our methods exhibit stronger resistance to forgetting. We further analyze the relationship between BWT and the number of extractors without $L_{\mathrm{sep}}$. The results show that using 10 extractors causes more forgetting compared with using 5 extractors. This observation suggests that simply increasing the number of extractors is not beneficial if their boundaries are not well maintained. The $L_{\mathrm{sep}}$ term strengthens the boundaries of individual extractors and reduces the interference introduced by redundant extractors.

4.6. Sensitive Study of Hyperparameters

We evaluate the effect of the hyperparameter $\alpha$ on the $gr{c}_6$ setting, are shown in Table 11. We set $\alpha =0.5$.

Table 10. Backward Transfer (BWT, %) on CIFAR-100 B0-S10 without ${\mathcal{L}}_{\mathrm{sep}}$.

Method	BWT
Fix5 (w/o ${\mathcal{L}}_{\mathrm{sep}}$)	-12.41
Fix10 (w/o ${\mathcal{L}}_{\mathrm{sep}}$)	-13.38

Table 10. Backward Transfer (BWT, %) on CIFAR-100 B0-S10 without ${\mathcal{L}}_{\mathrm{sep}}$.

Method	BWT
Fix5 (w/o ${\mathcal{L}}_{\mathrm{sep}}$)	-12.41
Fix10 (w/o ${\mathcal{L}}_{\mathrm{sep}}$)	-13.38

Table 11. Effect of the hyperparameter $\alpha$ on average accuracy (Avg %).

$\mathit{\alpha }$	Avg (%)
2.0	76.70
1.0	77.03
0.7	77.15
0.5	77.40
0.1	76.92

Table 11. Effect of the hyperparameter $\alpha$ on average accuracy (Avg %).

$\mathit{\alpha }$	Avg (%)
2.0	76.70
1.0	77.03
0.7	77.15
0.5	77.40
0.1	76.92

5. Conclusions

In this work, we analyzed the impact of extractor growth in dynamic-network methods. We showed that old extractors, which never observe new classes, introduce noise and cause interference, while model parameters continue to grow with the number of tasks. To address these issues, we proposed two strategies for sharing extractors: Grouped Rolling Consolidation (GRC), which groups consecutive tasks to share a consolidated extractor, and Fixed-Size Pool with Similarity-Based Consolidation, which first learns N extractors and then allows subsequent tasks to share the most similar one. Furthermore, we encouraged each extractor to preserve discriminative and independent features. Both approaches achieve higher accuracy than the strong baseline DER while requiring significantly fewer extractors. While our study focuses on vision tasks, the idea of Task-Sharing Distillation is also meaningful for large language models. In continual and multi-domain settings, consolidating and sharing adapters could reduce parameter overhead while retaining knowledge transfer, pointing to a promising direction for future work.