1. Introduction
A geometric (
Clifford) algebra is an extension of elementary algebra to work with geometrical objects such as vectors. It is built out of two fundamental operations: addition and geometric product, [
1]. The multiplication of vectors results in objects called multivectors. Compared with any other formalism for manipulating vectors,
Clifford algebra alone supports dividing by vectors. The geometric product was first mentioned by
Grassmann, who founded the so-called external algebra, [
2]. After that,
Clifford himself greatly expanded upon
Grassmann’s work to form geometric algebra, named after him
Clifford algebra [
1], by unifying both
Grassmann’s algebra and
Hamilton’s quaternion algebra (
. In the middle of the 20th century,
Hestenes repopularized the term geometric algebra [
4,
5].
On the other hand, although rarely used explicitly, a geometric representation of complex numbers is implicitly based on its structure of the
Euclidean 2-dimensional vector space. If the binary operation of the product
of two complex numbers
and
z is considered as the sum of the inner product
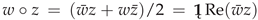
and outer product
, where
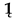
= (1,
i0) and
į, and
i is an imaginary unit, it can be said that
is in the form of a geometric product of two
ivectors (two complex numbers), as two geometric objects belonging to the
ivector field
(to the field of complex numbers
). For any complex number
z, its absolute value
is its
Euclidean norm denoted by
, and the argument
of
z is the polar angle
. Since ordered pairs represent both complex numbers and vectors, the binary operation of the product of two complex numbers (two ordered pairs), in the form of the geometric product
(
), will be the basis for modifying
Grassmann’s geometric product of vectors, which is defined as the sum of the inner (scalar) and outer (vector) products of two vectors. By this modification, the geometric product of two vectors becomes commutative, similar to the product of complex numbers themselves, which still supports vector division.
It is a very old and interesting problem to obtain a natural extension of complex numbers, especially to three-dimensional complex numbers.
Hamilton interpreted complex numbers via couple numbers (ordered pairs of two real numbers), as points in the
Euclidean plane [
3], and he was looking for a way to do the same for points in a three-dimensional space. Points in space are triples of numbers.
Hamilton had known how to add and subtract triples. However, for a long time, he had been stuck on the problem of multiplication and division. In fact,
Frobenius proved, in 1877, that for a division algebra over the real numbers to be finite dimensional and associative, it cannot be three-dimensional. There are only three such division algebras:
,
and
, which have dimension 1, 2 and 4, respectively.
Segre[
15] described bicomplex numbers as points in a 4-dimensional space. Unlike
Hamilton’s quaternions, which are non-commutative and form a division algebra, bicomplex numbers are commutative and do not form a division algebra.
All told, many famous mathematicians have studied how to define multicomplex numbers and the corresponding function theory. Following this, and on the basis of the redefined geometric product of two vectors in the Euclidean plane, this paper presents the algebraic structure of the 3 field of complex vectors, as well as the corresponding integral identities.
The idea, on the basis of which the algebraic structure of the 3 field of complex vectors is defined, is as follows: At the beginning, a 2 field of complex vectors is introduced, which corresponds to the field of complex numbers , defined as a Cartesian product of one 1 real and one 1i-real vector space with a commutative geometric product of elements. Following the same pattern, in the next section a 3 field of complex vectors is introduced, which corresponds to the Cartesian product of one 3 real and one 3i-real vector space with a commutative geometric product of elements, defined as the sum of the geometric products of the elements in three complex planes. Each of these complex planes is the Cartesian products of one 1 real and one 1i-real vector space, which are vector subspaces of 3 real and 3i-real vector space, respectively. Clearly, one can take the Cartesian product of one 2 real and one 2i-real vector space in the same way. In that case, the geometric products of the elements in two complex planes are summed up, in order to obtain the commutative geometric product of the elements in this vector space.
2. The 2 Field of Complex Vectors
The ordered pairs
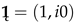
and
į form the basis of a 2-dimensional real
ireal vector (2
i-vector) space
, [
6,
9]. It is obvious that
is the
Cartesian product
of a one-dimensional real vector space and a one-dimensional
ireal vector space, and as such it is an additive
Abelian (commutative) group of
i-vectors
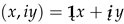
. On the other hand, it is possible to complete the
i-vector space
with a binary operation of the product of two
i-vectors
and
, which corresponds to the matrix product, in such a manner that
The inverse element
of the space
corresponds to the inverse matrix
. Here, both the commutative and associative axioms of multiplication and the distributive axiom are satisfied. Thus, the
i-vector space
becomes the field of complex numbers (
i-vectors)
, to which the field of complex vectors
corresponds. Two ordered pairs of one real and one imaginary vector,
and
, such that the unit vectors
(
) and
(
) are orthonormal basis vectors of the real plane
, form an orthonormal vector basis of the field
, so that
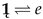
and
į⇌
. The complex vectors
, as elements of
, correspond to the complex numbers
. If
, then
is the norm on the fields
and
. In addition,
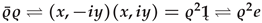
and
. It is quite clear that the inverse element
allows division by a vector in
. On the other hand, on the basis of the above-mentioned geometric product
of two complex numbers (
i-vectors)
and
, the corresponding geometric product of two complex vectors
and
in
can be defined as follows:
where
and
, which is obviously commutative. Here,
So, the dot and cross products of two complex vectors
and
in
are as follows:
where
. Since
, it follows that
3. The 3 Field of Complex Vectors
Let
,
and
be orthonormal basis vectors of the 3
space of real vectors
. Then, the following three pairs of ordered pairs:
and
,
and
, as well as
and
, form orthonormal bases of three 2
fields of complex vectors
, which are component fields of the 3
field of complex vectors with elements
where
are complex vectors in the component fields, and here, as in the following text, the index
(
), repeated as subscript and superscript in the products, represents the summation over the range of the index
, according to the
Einstein summation convention.
The commutative geometric product of two 3
complex vectors
a and
b is defined as the sum of the geometric products of the component vectors
and
, as follows:
Clearly,
and
. In addition, the vector
where
and
, such that
is the inverse vector of the 3
complex vector
a, which allows division by the vector in the 3
field of complex vectors. On the other hand, if
is denoted by the bracket
, it follows that
3.1. Differential Forms in
To represent a complex vector
in polar form, one introduces a vector analogue c
s of the shorthand notation c
is for the algebraic operator
+
, as follows:
Let = cs, where is the exponential form of the operator cs, be a radial unit complex vector in . Therefore, , where and , is a complex vector logarithmic function, and Log, . If and sc, then the ordered pair of unit vectors is the inverse orthonormal basis with respect to the orthonormal basis of the field of complex vectors . For an arbitrary vector , the vector is the rotated vector a, in the positive mathematical direction, by the angle , and the vector by the angle . The geometric products of the vector a with the inverse basis vectors and rotate a by the angles and , respectively, in the positive mathematical direction.
If
is a differential operator, then
. Hence,
and
. Since
and
, the vector operators of partial derivatives are introduced as a vector analogue of the
Virtinger operators [
16],
where
and
. It is important to emphasize that when geometric products and geometric quotients are differentiated, the same rules apply as when ordinary products and quotients are differentiated, so that
. Let’s prove this,
Definition 1. The geometric product is an operator of a differential form.
The symmetric and antisymmetric parts of the geometric product
are as follows:
Therefore,
where
and
are the radial and transverse components of
, respectively. Accordingly, since
, it follows that
which leads to the following vector differential identity,
Consequently,
since
. The vector identity just derived can be obtained explicitly via the
Jacobian determinant of the bijective mapping
, defined by the system of vector equations
and
as follows:
In this case,
, which leads to (
22). The complex vector
, corresponding to the
i-vector
į, is the
Lebesgue vector measure of the infinitesimal surface in the field
.
Definition 2. Let . Then, the geometric product is an operator of a differential form.
3.2. Fundamental Theorem of Integral Calculus in the Field
Let
be a closed smooth
Jordan curve, bounding an arbitrary simply connected region
G in
, and
be a point on
, surrounded by a circle
with center at
and arbitrarily small radius
, which intersects the curve
at the points
and
. Similarly, an arbitrary point
inside
G is surrounded by circle
, which is connected to the circle
by two parallel straight line segments
and
, at a distance
from each other. The region
S, inside which are the points
and
, and which is bounded by the segments
and
as well as the arc segments on the boundaries
and
of the circles
and
, whose endpoints are the intersection points of the boundaries
and
with the segments
and
, is the so-called residue region. If
, the contour integration operators are as follows:
where
is the boundary of
. Based on the additive property of definite integrals, in the limit, as
,
where
and
denote the principal and total integral values [
9]-[
14], respectively, and
(
is the interior of
S).
On the one hand, as a vector analogue of the so-called areolar (weak) derivative in complex analysis, defined by
Pompeiu [
8], the vector differential operator
is the gradient (the plane derivative) of
where
, so that
. Accordingly, on the basis of the result of the
Kelvin-Stokes theorem (
Green’s theorem) [
6],
Here,
so that
Consequently,
where
. The vector integral operator
where
is the vector residue operator in
G. Obviously, the operator
is a synonym for
.
By choosing two points, one on the contour
and the other inside the region
G, the generality of the previously obtained results is not lost, so that the fundamental theorem of integral calculus in
can be formulated in what follows. Previously, let
be a vector differential form
, obtained by applying
to an arbitrary uniform scalar or vector field • in
, [
7].
Theorem 1.
Let γ be a closed smooth Jordan curve, bounding an arbitrary simply connected region G in . For an arbitrary uniform scalar or vector field • in , which is regular almost everywhere on G and whose vector differential form is totally integrable on γ, there holds
where .
So, the integral formula in the previous theorem is a slightly generalized vector analogue of the
Cauchy-Pompeiu integral formula, [
17]. The sum of
, on the compact set of points
, at which the field • is regular (
is identically zero on
), is
. Hence,
, where
is the singular set, with
Lebesgue measure zero, of the field •. The sum on the right-hand side of the last integral equality can be in the indeterminate form of the difference of two infinities, which is equal to the finite integral value on the left-hand side.
3.3. Integral Calculus Formulas in the 3 Field of Complex
Vectors
Let
be simply connected regions bounded by closed smooth
Jordan curves
, such that they are projections of a smooth surface
S onto the component fields of the 3
field of complex vectors. The differential forms in the 3
field of complex vectors are as follows:
where
is an arbitrary uniform vector field in the 3
field of complex vectors,
and
. According to
Theorem 1., if the vector field
F is regular almost everywhere on
S, and the vector differential forms
and
are totally integrable on
, there holds
so that
Hence, to noted
and
.
Furthermore, since
where
,
and
, and in addition
, the vector identities (
41) and (
42) lead to the complex generalized
Stokes integral identity
where
, as well as to the complex vector integral identity
where
. Thus, the complex vector integral identities (
45) and (
46) are explicit consequences of the fundamental theorem of integral calculus in the
field of complex vectors, which follows.
Theorem 2.
Let γ be a closed smooth spatial curve in the field of complex vectors, bounding an arbitrary simply connected spatial surface S. For an arbitrary uniform complex vector field F, which is regular almost everywhere on S and whose differential form is totally integrable on γ, there holds
where .
On the other hand, it is quite possible to formulate the theorem, as follows, using a procedure similar to that used to formulate Theorem 1., based on the result of Green’s theorem, but now on the basis of Gauss-Ostrogradsky’s theorem.
Theorem 3.
Let S be a closed smooth surface in the field of complex vectors, bounding an arbitrary simply connected region V in that field. Then, for an arbitrary uniform complex vector field , which is regular almost everywhere on V and whose differential form is totally integrable on S, there holds
where .
Obviously, the integral formula (
48) is an explicit consequence of the following integral identities
where
,
and
. Therefore, if
and
, then
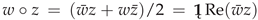 and outer product , where
and outer product , where 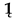 = (1, i0) and į, and i is an imaginary unit, it can be said that is in the form of a geometric product of two ivectors (two complex numbers), as two geometric objects belonging to the ivector field (to the field of complex numbers ). For any complex number z, its absolute value is its Euclidean norm denoted by , and the argument of z is the polar angle . Since ordered pairs represent both complex numbers and vectors, the binary operation of the product of two complex numbers (two ordered pairs), in the form of the geometric product (), will be the basis for modifying Grassmann’s geometric product of vectors, which is defined as the sum of the inner (scalar) and outer (vector) products of two vectors. By this modification, the geometric product of two vectors becomes commutative, similar to the product of complex numbers themselves, which still supports vector division.
= (1, i0) and į, and i is an imaginary unit, it can be said that is in the form of a geometric product of two ivectors (two complex numbers), as two geometric objects belonging to the ivector field (to the field of complex numbers ). For any complex number z, its absolute value is its Euclidean norm denoted by , and the argument of z is the polar angle . Since ordered pairs represent both complex numbers and vectors, the binary operation of the product of two complex numbers (two ordered pairs), in the form of the geometric product (), will be the basis for modifying Grassmann’s geometric product of vectors, which is defined as the sum of the inner (scalar) and outer (vector) products of two vectors. By this modification, the geometric product of two vectors becomes commutative, similar to the product of complex numbers themselves, which still supports vector division.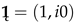 and į form the basis of a 2-dimensional realireal vector (2 i-vector) space , [6,9]. It is obvious that is the Cartesian product of a one-dimensional real vector space and a one-dimensional ireal vector space, and as such it is an additive Abelian (commutative) group of i-vectors
and į form the basis of a 2-dimensional realireal vector (2 i-vector) space , [6,9]. It is obvious that is the Cartesian product of a one-dimensional real vector space and a one-dimensional ireal vector space, and as such it is an additive Abelian (commutative) group of i-vectors 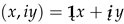 . On the other hand, it is possible to complete the i-vector space with a binary operation of the product of two i-vectors and , which corresponds to the matrix product, in such a manner that
. On the other hand, it is possible to complete the i-vector space with a binary operation of the product of two i-vectors and , which corresponds to the matrix product, in such a manner that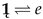 and į⇌. The complex vectors , as elements of , correspond to the complex numbers . If , then is the norm on the fields and . In addition,
and į⇌. The complex vectors , as elements of , correspond to the complex numbers . If , then is the norm on the fields and . In addition, 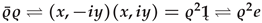 and . It is quite clear that the inverse element allows division by a vector in . On the other hand, on the basis of the above-mentioned geometric product of two complex numbers (i-vectors) and , the corresponding geometric product of two complex vectors and in can be defined as follows:
and . It is quite clear that the inverse element allows division by a vector in . On the other hand, on the basis of the above-mentioned geometric product of two complex numbers (i-vectors) and , the corresponding geometric product of two complex vectors and in can be defined as follows:



