A Two-Phase Genetic Algorithm Approach for Sleep Scheduling, Routing, and Clustering in Heterogeneous Wireless Sensor Networks

1. Introduction

Wireless Sensor Networks (WSNs) have emerged as a cost-effective solution for monitoring diverse environments, particularly in harsh conditions. However, their practical deployment is significantly constrained by the limited energy of sensor nodes, which impacts network lifetime and data delivery. To address this challenge, Heterogeneous Wireless Sensor Networks (HWSNs) have been proposed [1,2,3]. These networks consist of two types of nodes; namely, normal sensors and super nodes [4,5]. Normal nodes, which have less energy are tasked to monitor the environment. Super nodes, on the other hand, collect data from normal nodes, aggregate it, and transmit it to the Base Station (BS). By incorporating more powerful super nodes as Cluster Heads (CHs), HWSNs can enhance energy efficiency, extend network coverage, and improve data gathering capabilities.

As the assigned tasks of super nodes requires, these nodes experience significantly higher energy consumption compared to their counterparts. Consequently, they often exhibit short lifetimes. Therefore, achieving energy-efficient data gathering in HWSNs, aiming energy saving of super nodes, has been a central focus of research. Strategies such as clustering aim to minimize data transmission volumes by consolidating data amount at CHs [6,7]. Conversely, routing protocols prioritize network longevity by balancing workloads across super nodes to prevent individual overload [2]. The other effective way to increase network lifetime is to apply sleep scheduling methods to super nodes [6]. This scheme decides that some nodes are awake and perform their tasks while others go to sleep and save their energy for later uses. By alternating between awake and sleep modes, sleep scheduling can significantly reduce energy consumption, prolonging the overall network lifetime. Additionally, sleep scheduling makes it possible to maintain adequate normal node coverage which ultimately results in enhancing network coverage even with a reduced number of awake nodes.

While prior studies have investigated clustering, routing, and sleep scheduling methods in HWSNs, these approaches have been examined in isolation, without exploring their potential through an integrated framework. These works relied on simplistic or suboptimal strategies to address energy conservation, with fragmented efforts targeting individual aspects: either clustering [8], routing [9,10], clustering and routing [5,11,12], or sleep scheduling [13]. Notably, no existing research has concurrently implemented all three methodologies for HWSNs. Additionally, clustering algorithms frequently prioritize CH selection without adequately balancing normal node distribution among CHs, leading to uneven energy consumption. Tree construction methods, while improving connectivity, often neglect the strong interdependence between sleep scheduling and tree formation, resulting in suboptimal structures that fail to maximize network lifetime. Metaheuristic-based approaches, though effective, frequently rely on standard initialization schemes and generic operators, limiting their adaptability to problem-specific constraints. These shortcoming leaves a critical gap in the pursuit of holistic energy optimization. This gap underscores the novelty of our contribution: a unified framework that combines clustering, routing, and sleep scheduling with advanced optimization techniques, offering a robust and comprehensive solution to enhance energy efficiency in HWSNs.

Based on the aforementioned cases, this paper proposes a data collection method in HWSNs based on sleep scheduling, clustering, and routing. We address the challenges of determining sleep or wake states for super nodes, constructing a tree on the awake super nodes, and clustering the network by assigning awake super nodes as the CHs for normal nodes. To reduce the problem state space and simplify problem-solving, we divide the process into two phases. In the first phase, we simultaneously determine the awake super nodes and create a tree on these super nodes to deliver data to the BS. In the second phase, for each normal node, we select a super node as its CH from the awake super nodes that are adjacent to them. Both phases are modeled and solved using a Genetic Algorithm (GA) to obtain optimal solutions in a short time. By employing GA with customized initialization, problem-specific chromosome representation, and tailored genetic operators, our algorithm achieves superior energy efficiency and network performance. The novel cost functions introduced in both phases further enhance load balancing across super nodes, ensuring prolonged network sustainability.

The innovations of this paper can be summarized as follows:

• The proposed solution for reducing the state space effectively addresses the challenges of sleep scheduling, clustering, and tree construction on awake nodes by dividing the process into two phases, each optimized using a GA.
• Considering the strong interdependence between the sleep scheduling of super nodes and the construction of a tree on these nodes - since the tree must be built on awake super nodes -, these two problems are tackled simultaneously through an innovative modeling approach.
• In the first phase, a novel cost function is employed to enhance environmental monitoring by selecting a set of super nodes as awake ones while minimizing the energy consumption of super nodes.
• Network clustering is modeled and optimized using a GA in the second phase, with a new cost function specifically designed to reduce energy consumption with distributing normal nodes among the awake CHs.
• Considering the pivotal role of initialization in the ultimate solution of GA, we propose a custom initialization in the first phase which helps GA to converge more quickly. The proposed method splits the HWSN into rings, and select equal number of awake super nodes per ring. This scheme, which is inspired from unequal clustering, helps balancing energy exhaustion of super nodes and prolongs network lifetime.
• We modify and customize the GA operators (crossover and mutation) to fit our problem and help achieving better solutions.
• The proposed solution has been rigorously evaluated in simulation environments, consistently demonstrating its superiority over existing methods.

The remainder of this paper is organized as follows: Section 2 reviews the related work, while Section 3 outlines the network model. Section 4 provides a comprehensive description of the proposed method, and Section 5 presents the results obtained using this method. Finally, Section 6 concludes the paper.

2. Related Works

We review related research in three key areas. First, we explore sleep scheduling studies on heterogenous and homogenous WSNs. The second part investigates clustering algorithms within the field. Finally, in the last part, we consider research on tree construction and routing protocols. The mentioned algorithms used different techniques for solving considered problems including greedy, metaheuristic, and learning methods.

The literature on sleep scheduling and resource allocation in WSNs explored various approaches to optimize energy efficiency. Alwasel et al. [13] considered HWSNs and proposed an energy-efficient sleep-and-awake scheme to manage sleep states based on node resources, prioritizing network lifetime. In their work, they proposed iterative local search strategy to construct disjoint dominating sets, activating nodes of one dominating set each time instance. The algorithm prioritized nodes with higher residual energy for being awake while transitioning others to sleep modes. However, their method introduced computational complexity due to exhaustive search processes, limiting scalability in large-scale HWSNs. Additionally, it did not consider clustering and routing problems.

Sleep scheduling in homogenous WSNs was explored in [14,15,16]. Niyato et al. [14] used factors like energy level of nodes, the number of packets in their buffers, and channel condition, to determine sleep scheduling policies for solar-powered networks. The algorithm aimed to awaken nodes with higher energies, less congested buffers, and better channel conditions. References [15,16,17,18,19] employed Reinforcement Learning (RL) to determine the awake and sleep schedule of the nodes. Studies in [15,16,17] developed RL-driven sleep scheduling for star topology networks. Among the mentioned algorithms, references [16,19] focused on wireless body area networks, and considered criteria such as energy level of nodes, emergency of gathered data by sensors, and transmission delay, to decide on awake/sleep statuses of sensors. The algorithm proposed in [18] determined CHs and performed clustering using a greedy approach, followed by applying RL for sleep scheduling.

Clustering is vital in WSNs for efficient data collection and transmission. Reference [20] introduced a RL-based clustering model for IoT and HWSNs, aimed at optimizing resource utilization and reducing energy consumption. In [21], a scheme was presented that categorized sensors into normal and super nodes based on initial energy levels. Clusters were formed with energy-efficient CH selection, which prioritize super nodes by assigning more weights to them. Bhasker et al. [22] introduced a cluster-based data gathering technique for farm irrigation systems, focusing on reducing sensor node energy use and balancing the workload on CHs. They proposed a protocol that selects and rotates CHs near the energy centroid within clusters and designates gateway nodes to assist CHs. In the proposed algorithm in [23], CH selection was guided by a fitness function derived from multi-objective optimization. The objectives included minimizing energy usage and the distance between CHs and their Cluster Members (CMs), and maximizing the coverage of the network. The algorithm applied deep residual network to optimize number of clusters and CH selection. Afterwards, the binary horse herd optimization algorithm was used for route selection and data transmission.

Energy-efficient routing is vital for WSNs. Therefore, the problem of clustering and routing in homogenous WSNs has been studied in various research including [7,24,25,26,27]. Reference [26] proposed a fuzzy logic-based CH selection method, which used the Mamdani inference engine to evaluate factors such as residual energy, node centrality, and distance to the BS, mimicking human decision-making for optimal CH selection. Authors in [24] presented an optimization approach for CH selection in IoT-assisted WSNs. They used factors like energy, delay, and distance as fitness criteria. Additionally, they employed tunicate swarm Gray Wolf Optimization (GWO) algorithm for multipath routing. In [28], the authors introduced a hybrid Particle Swarm Optimization (PSO) and artificial bee colony algorithm to reduce routing costs. Vijayan et al. [29] proposed a machine learning-based routing system for IoT-connected sensor networks that considered energy usage and traffic patterns. Shahid et al. [30] improved packet delivery and energy efficiency by using proper links, where the criteria for link selection was the link quality, energy of nodes, and distance between nodes. The quality of links was estimated using exponential moving average.

Metaheuristic algorithms have also been applied to HWSN optimization, including clustering and routing [4,5,11,12,31,32,33]. In [4], PSO was used to assign super nodes as CHs and build a spanning tree. The criteria in PSO-based clustering were network lifetime and distances between CMs and CHs, while average energy of routes and distances between successive super nodes on routes were considered for tree construction. Reference [11] also employed PSO for clustering and routing, focusing on energy and reliability. Wang et al. [31] performed join clustering and tree construction using bipartite chromosomes. The algorithm aimed to balance energy consumption of CHs while reducing overall energy consumption. Additionally, an improved chaos logistic map was applied to generate initial population to increase population diversity. In [5], a two-phase GA handled clustering and tree construction for multi-channel HWSNs with normal and super nodes. The multi-radio super nodes were designated as CH, while the single-radio normal nodes were assigned to one of its neighboring CHs and connected to it using one of its assigned channels. In the tree construction phase, the algorithm balanced energy of super nodes based on their distances to the BS, which improved network lifetime considerably. Additionally, it offered a novel criterion for even distribution of normal nodes among CHs, further balancing the energy consumption of super nodes. The proposed algorithm in [32] was extended in [12], where authors employed GWO to optimize Transmission Power Control (TPC) in a HWSN with TPC-enabled super nodes. Reference [33] presented a novel algorithm for efficient data gathering in HWSNs. The approach consisted of two key phases: clustering, and spanning tree construction. GA was employed in both phases, utilizing a problem-specific chromosome representation, a tailored population initialization scheme, and customized genetic operators (i.e., mutation and crossover). Specifically, in the tree construction phase, chromosomes were structured as trees, facilitating designing an effective initialization scheme and GA operations.

Despite the advancements in sleep scheduling, clustering, and tree construction for HWSNs, existing methods often suffer from key limitations. Our proposed solution addresses these deficits through an integrated two-phase approach that simultaneously optimizes sleep scheduling, clustering, and tree construction. The proposed GAs for the phases includes customized initialization methods and operators, and novel cost functions, yielding further energy efficiency and network lifetime. Rigorous simulations confirm the robustness of our approach, demonstrating its superiority over existing methods in key performance metrics.

3. Network Model

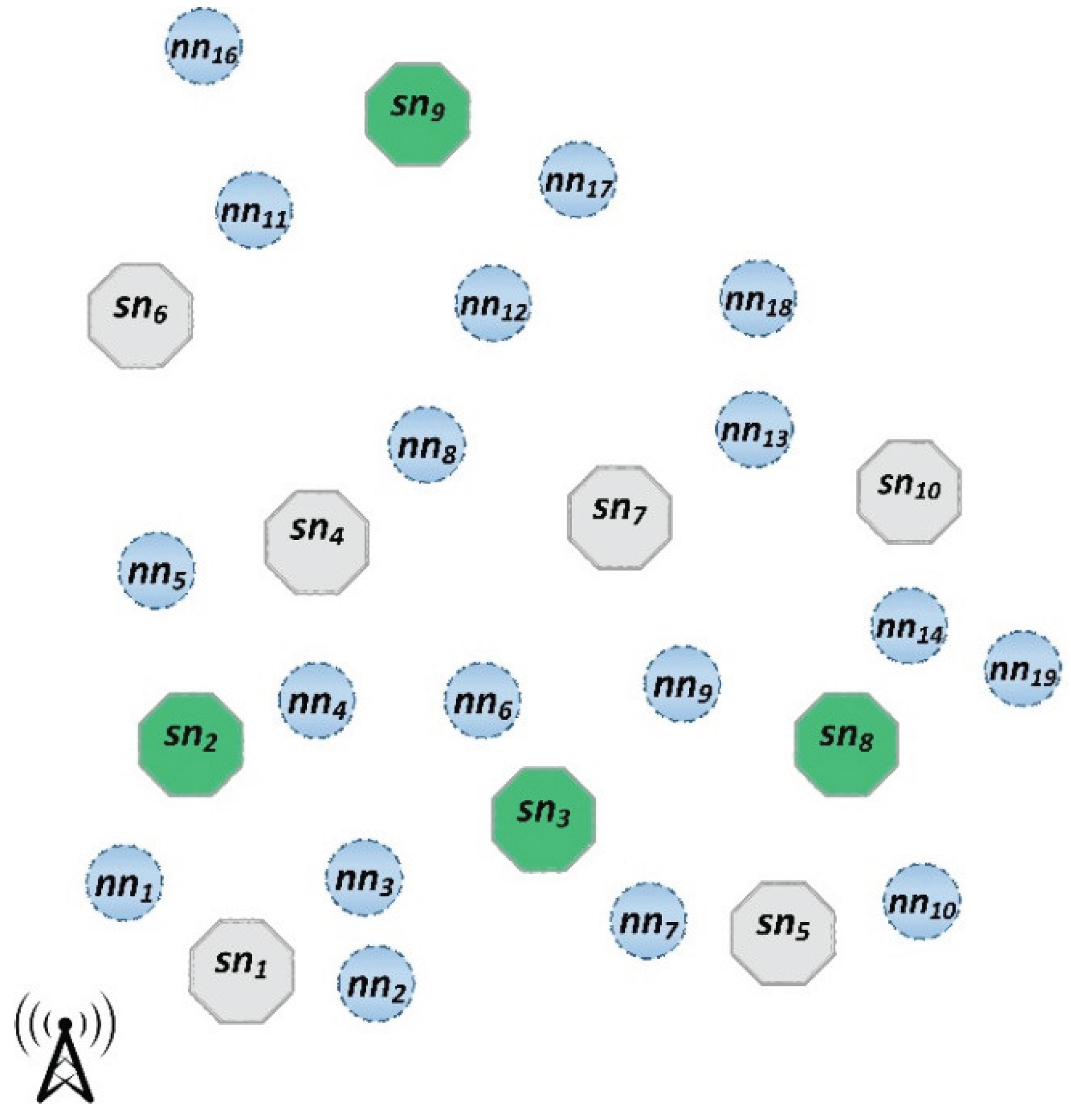
In the assumed network model, there are two types of nodes: super nodes and normal nodes (Figure 1). We use $S$ and $N$ to show the set of super nodes and normal sensors, respectively. Super nodes possess greater initial energy and a larger transmission range compared to normal nodes. The initial energy and transmission range of super nodes are shown by $e_S$ and ${tr}_s$, respectively. These parameters are presented by $e_N$ and ${tr}_N$ for normal sensors. Additionally, there are fewer super nodes compared to normal nodes in the network. Furthermore, we use $e_i$ as the remaining energy of a the $i^{th}$ node, either super node or normal sensor. Finally, $|.|$ shows the cardinality of an assumed set.

Normal nodes are tasked with environmental monitoring. They collect data and send it to a nearby super node, which serves as their CH. The potential CHs for a normal node $n_i$ are super nodes within its transmission range. Each super node aggregates data of its assigned CMs. Since the BS might not be directly reachable by all super nodes, data needs to be relayed. For a super node $s_i$, other super nodes closer to the BS and within its transmission range are considered as its potential parents. One of these super nodes is selected as the parent for forwarding the data.

The network employs Time Division Multiple Access (TDMA) at the MAC layer which divides channel into timeslots. The data exchange process includes intra-cluster communication, where normal nodes transmit their collected data to their designated CHs during allocated timeslots, and inter-cluster communication, where super nodes use multi-hop forwarding to relay the gathered data toward the BS during their assigned timeslots.

All nodes of the network expend energy during communication. This energy consumption is influenced by the size of the data packets transmitted or received. Reference [34] presents (1) and (2) for calculating consumed energy needed for transmission ($e_{trs}$) and reception ($e_{rec}$) based on packet size ($l$), respectively. These formulas incorporate factors like internal circuit energy ($e_{elec}$) and signal amplification energy. The amplification model varies with distance: the free space model for shorter distances, and the multipath fading model for distances beyond the threshold $d_0$. Amplifier energy consumption is denoted by ${\epsilon }_{fs}$ and ${\epsilon }_{mp}$ for these models, respectively.

$$e_{trs}\left(l, d_{tr}\right)=\left\{\begin{array}{c}l e_{elec}+l {\epsilon }_{fs} d_{tr}^2, d_{tr}<d_0\\ l e_{elec}+l {\epsilon }_{mp} d_{tr}^4, d_{tr}\ge d_0\end{array}\right.$$

(1)

$$e_{rec}\left(l\right)=l e_{elec}$$

(2)

4. The Proposed Method

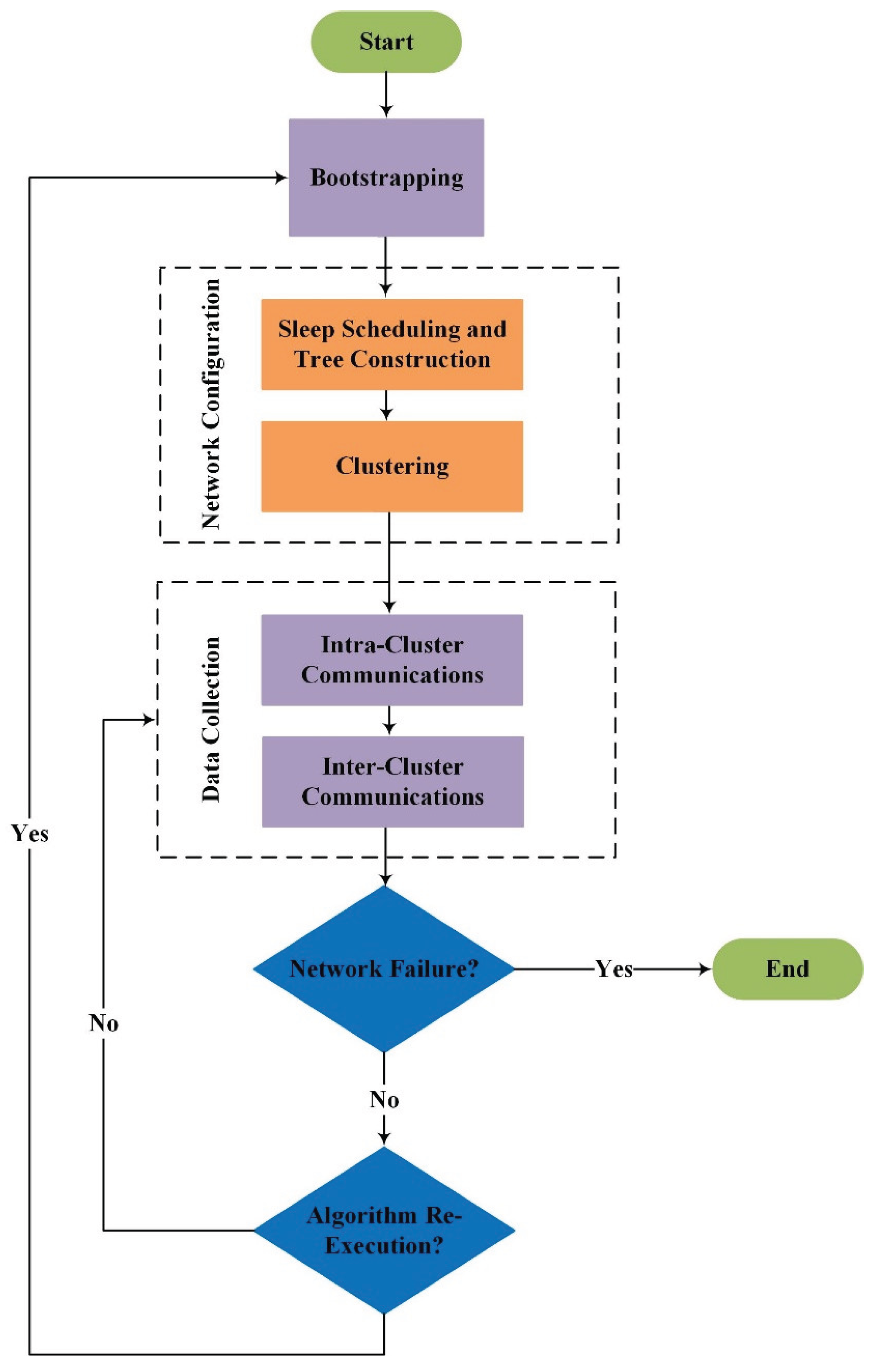
Figure 2 illustrates the workflow cycle during network lifetime. As shown in this figure, the network lifetime is divided into multiple rounds, each consisting of several time slices. During each time slice, data collected by normal nodes is first transmitted to super nodes via intra-cluster communication. Subsequently, super nodes relay this data to the BS through inter-cluster communication. The proposed algorithm is executed at the start of each round, where the BS gathers network information, such as the remaining energy of the nodes, to configure the network for optimal performance. This configuration is then applied throughout the time slices of the round. At the end of each round, the BS re-runs the algorithm to adjust for any changes in node characteristics, ensuring continuous and efficient network operation.

Our algorithm enhances data collection in HWSNs through integrating sleep scheduling, clustering, and routing. Considering the wide solution space of the mentioned problems, we divide the process into two phases to reduce complexity. Additionally, we employ a GA to obtain efficient solutions for each phase within a reasonable time. In the first phase, GA is used to solve the problem of selecting awake nodes and constructing a communication tree. The second phase focuses on network clustering. The specific steps involved in each phase are detailed in Section 4.1 and Section 4.2, respectively.

4.1. Sleep Scheduling and Tree Construction

In WSNs, efficient energy management is crucial for prolonging the network lifetime, particularly in heterogeneous environments where nodes have varying capabilities. Sleep scheduling plays a pivotal role in conserving energy by allowing nodes to enter a low-power sleep mode when not actively transmitting or receiving data. This approach extends the lifetime of nodes, ensuring that critical tasks such as data transmission and routing are handled thoroughly. Simultaneously, during tree construction, it should be ensured that the network avoids overloading certain nodes, preventing premature depletion of their energy resources. The process of tree construction is intrinsically linked to the sleep scheduling, because the awake nodes form the backbone for data gathering within the network. Therefore, the combined approach of optimal sleep scheduling and tree construction is essential for maintaining a balanced load distribution, enhancing the overall efficiency, and extending the longevity of the HWSN. Accordingly, we propose an innovative approach that combines sleep scheduling and tree construction into a single-step process. This unified model, optimized using a GA, is designed to efficiently find the best solution within a reasonable time. The following sections will detail the chromosome representation, initial population construction, cost function, and GA operators proposed in our approach.

4.1.1. Chromosome Representation

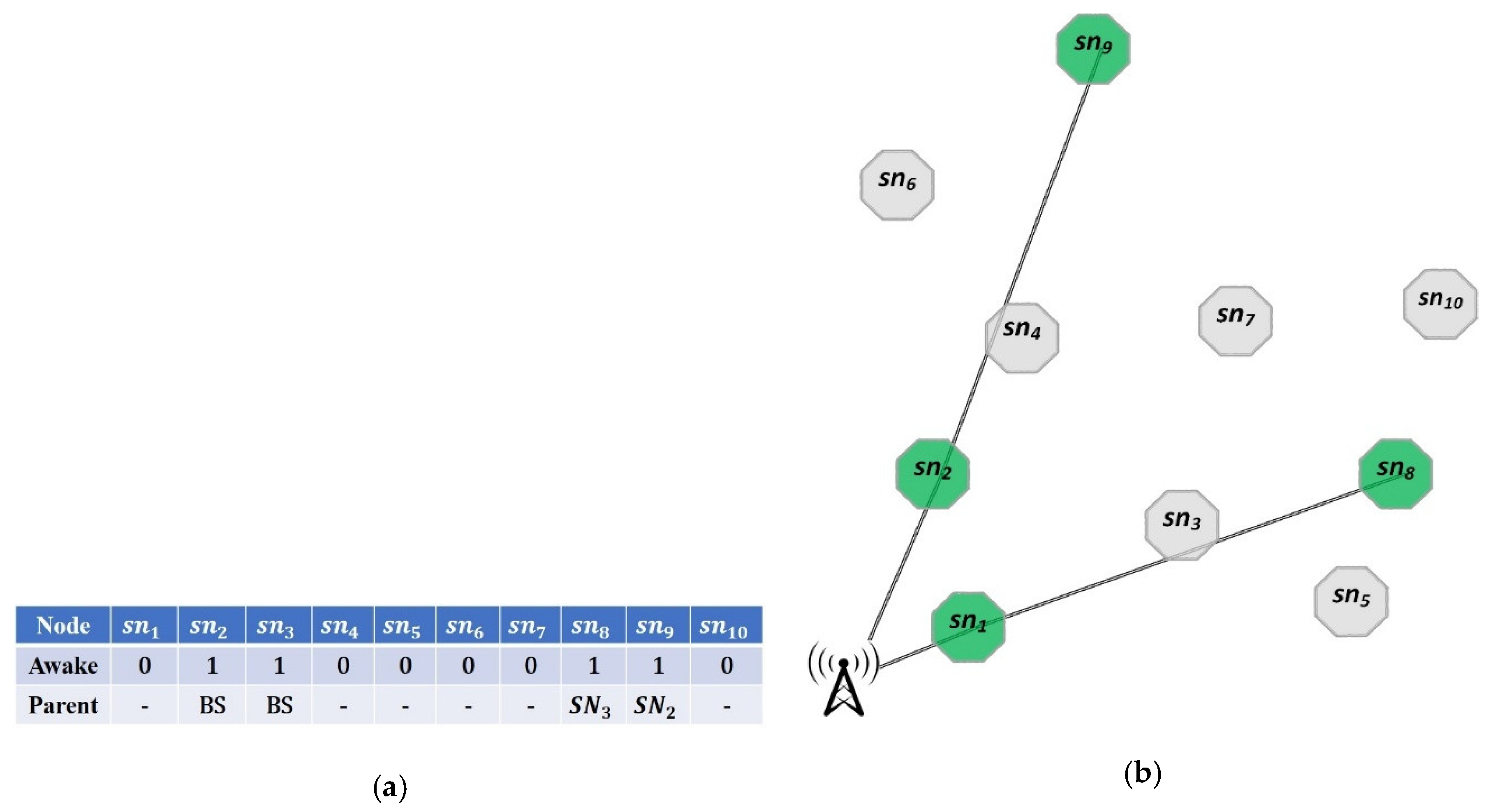
The proposed GA aims to simultaneously address the dual issues of sleep scheduling and tree construction in HWSNs. To achieve this, we design a chromosome structure represented as a matrix with dimensions of $2\times \left|S\right|$. Each column within this matrix corresponds to a specific super node in the network. The first row of the matrix corresponds to sleep state of super nodes, while the second row is dedicated to the tree construction problem. The values in the first row are binary: zero indicates that a super node is in the sleep state, and one indicates that it is awake. Additionally, the second row presents the selected parents for super nodes. In a chromosome, the super nodes are arranged sequentially based on their distance to the BS. Thus, the super node closest to the BS occupies the first column, while the one farthest away is positioned in the last column. 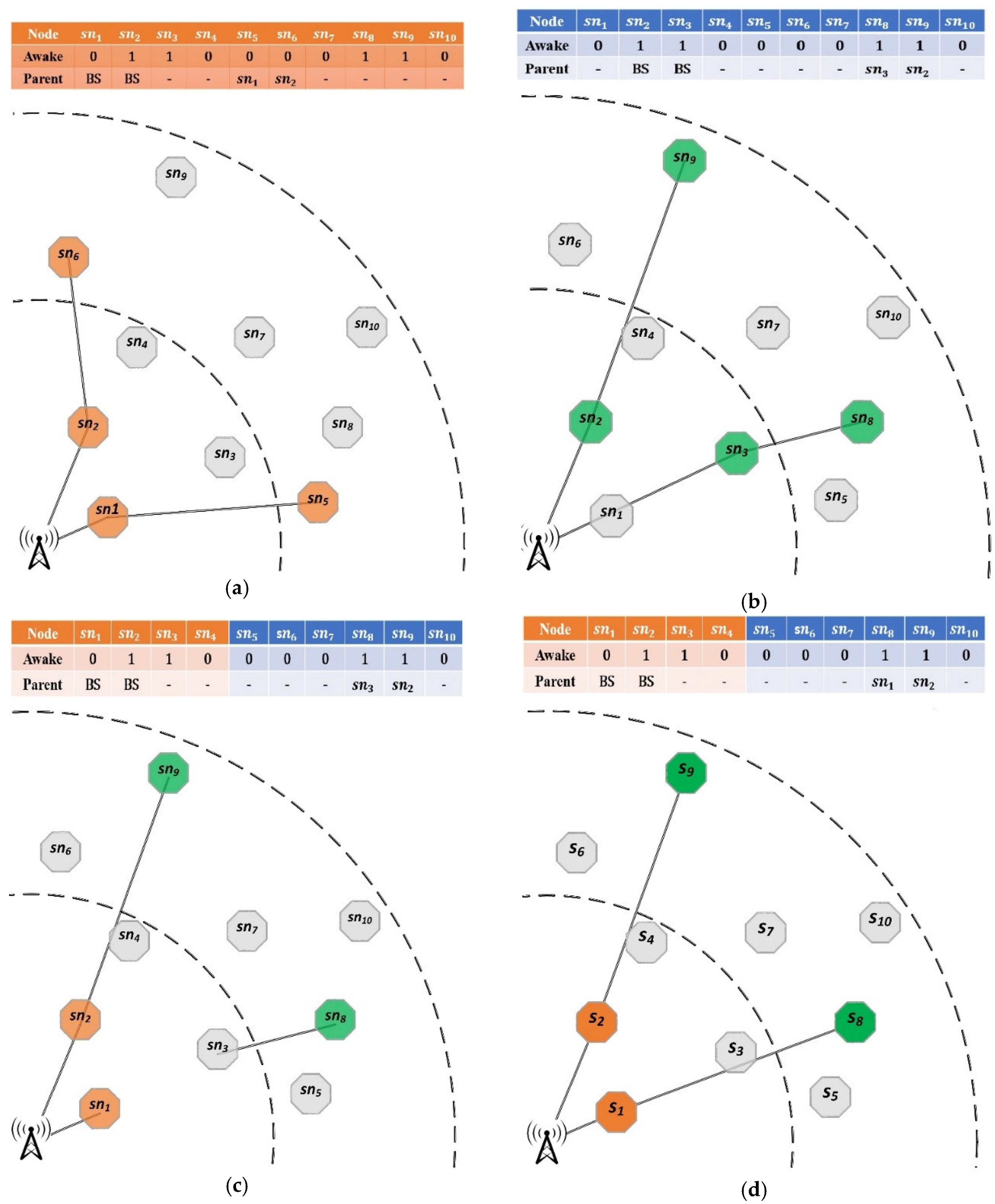Figure 3 shows an example chromosome and its representative tree.

4.1.2. Population Initialization

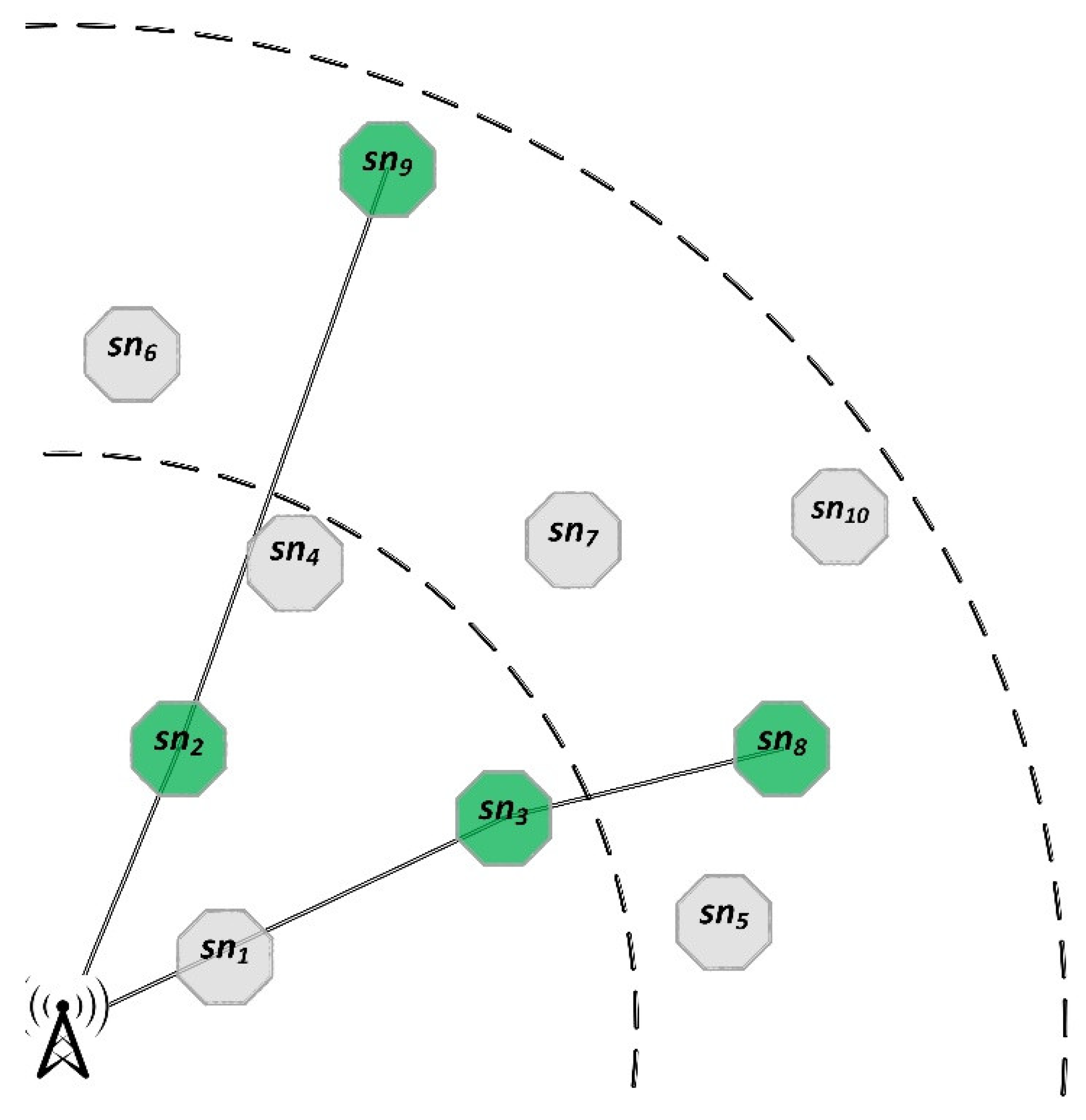
The elements of the proposed chromosome structure are populated according to the following scheme. A critical consideration to construct a chromosome is to select proper awake nodes, ensuring they are evenly distributed across the network. This distribution is essential for having at-least one super node within proximity to each normal node, allowing it to serve as the CH for gathering and forwarding data to the BS.

We divide the network into concentric rings centered around the BS, and awaken $ar$ super nodes per ring (Figure 4). This unequal clustering idea was previously comprehensively discussed in [35] and proved to be a good solution to hot-spot problem. Determining the optimal number of rings is a complex process, refined through trial and error. Rings that are too narrow may limit the selection of suitable nodes, while excessively large rings could lead to suboptimal configurations. Furthermore, the value of $ar$ is determined based on different parameters such as the number of normal nodes and density of super nodes. The selection of awake nodes within each ring is carried out randomly, based on a weighted probability that considers remaining energy of super nodes. Equation (3) calculates $p{r}_{awake}\left(s_i\right)$, the probability of selecting $s_i$ to serve as awake nodes. In this equation, $R\left(s_i\right)$ shows the ring which $s_i$ belongs to.

$$p{r}_{\mathit{awake}}\left(s_i\right)={\displaystyle \frac{e_i}{\sum _{s_k\in R\left(s_i\right)}{e}_k}}$$

(3)

Since the tree construction relies on awake nodes, columns corresponding to super nodes that are in the sleep state do not process. However, for super nodes that are awake (with a value of one), a subsequent step is required to construct the tree. This step involves selecting a random neighbor for each awake super node $s_i$, which must be both awake and positioned closer to the BS than $s_i$, to form the tree structure. If none of the neighbors of $s_i$ is awake, the chromosome is discarded. The selection of the parent among the super nodes which fulfill these constraints is influenced by their remaining energy, as shown in (4). According to this equation, super nodes with higher remaining energy have a greater probability of being selected as the parents, thereby ensuring that the tree construction process favors nodes with sufficient energy reserves. This approach not only helps in balancing the energy consumption across the network but also enhances the overall robustness and longevity of the HWSN.

$$p{r}_{\mathit{parent}}\left(s_j\right)={\displaystyle \frac{e_j}{\sum _{s_k\in N\left(s_i\right)\bigwedge dist\left(s_k,BS\right)<dist\left(s_i,BS\right)\bigwedge s_i is awake}{e}_k}}$$

(4)

where $N\left(s_i\right)$ is the set of neighbor super nodes of $s_i$, and $dist$ is the distance function.

4.1.3. Cost Function

GA uses a cost function to evaluate the acceptability of a particular solution (or chromosome). This function assigns a numerical value to each solution that reflects its quality or fitness. Our objective is to investigate two key factors: 1) the quality of the selection of awake nodes, and 2) the quality of the constructed tree.

To evaluate the first factor, we examine the number of normal nodes that lack an awake super node in their neighborhood, as defined by (5). In this equation, $X_j^T$ stands for the $j^{th}$ chromosome. Additionally, $ON$ shows the set of orphan normal nodes that there is not an awake super node in their vicinity. The smaller value of $facto{r}_1$ indicates choosing better awake nodes, as it designates that the selected awake nodes are distributed evenly in the network, ensuring each normal node has at-least one awake super node nearby. The division by the total number of awake nodes is intended to normalize this metric, making it comparable with other factors.

$$facto{r}_1\left(X_j^T\right)={\displaystyle \frac{\left|ON\right|}{\left|N\right|}}$$

(5)

Another factor for evaluating the chromosomes in this context is the quality of the constructed tree. To assess this, we aim to increase the minimum remaining energy of the nodes, as described in (6). In this equation, $e{r}_{ji}$ demonstrates the remaining energy of super node $s_i$ at the end of the round assuming the proposed network configuration by $X_j^T$. This approach ensures that tree structures which route data through nodes with higher energy levels are considered more suitable.

$$facto{r}_2\left(X_j^T\right)={\displaystyle \frac{{\mathrm{m}\mathrm{i}\mathrm{n}}_{s_k\in S} {er}_{jk}}{e_s}}$$

(6)

Finally, our cost function is defined by (7), and our objective is to minimize it.

$$cos{t}_1\left(X_j^T\right)=w_1\times facto{r}_1\left(X_j^T\right)-w_2\times facto{r}_2\left(X_j^T\right), w_1+w_2=1$$

(7)

4.1.4. GA Operators

The key components of GA, including selection, crossover, and mutation operators, are introduced in this section. We customize each of these operators to suit the specific problem at hand and to align with the proposed chromosome structure model, which we will detail in the following.

Selection: The selection operator in GA is responsible for choosing which individuals from the current population will contribute to the creation of the next generation. The idea is to select the fittest individuals, those that are better suited to the problem according to a predefined fitness function, to pass on their genes (chromosome information) to their offspring. We employ Roulette Wheel Selection (RWS) as our selection operator, detailed in (8). In this equation, the term ${pop}^T$ refers to the population of chromosomes. In the RWS method, the chance of each chromosome to being selected as a parent is proportional to its cost. The lower the cost function value, the higher the probability of selection, and conversely, chromosomes with higher cost values have a reduced chance of selection. This approach increases the likelihood that superior chromosomes, which demonstrate more effective network structures, will produce the next generation. However, we do not completely eliminate the possibility of selecting weaker chromosomes. They are still given a chance to contribute as parents, with the hope that some aspects of their structure might offer a valuable solution to the problem.

$$RWS\left(X_j^T\right)={\displaystyle \frac{1/cos{t}_1\left(X_j^T\right)}{\sum _{X_k^T\in {pop}^T}1/cos{t}_1\left(X_k^T\right)}}$$

(8)

Crossover: The crossover operator in GA is responsible for combining the genetic information of two parent chromosomes to produce offspring. This process mimics biological reproduction and aims to create new solutions (chromosomes) that inherit features from both parents, potentially leading to better solutions. In this phase, we employ the single-point crossover operator. Accordingly, a point is selected on two chromosomes, and the genes on the left side of one chromosome are combined with the genes on the right side of the other chromosome, and vice versa, resulting in two new offspring.

It is crucial to note that this crossover operation may not always yield valid chromosomes. The first issue is that a node may have no awake parent toward the BS. The other concern is that the number of awake nodes may deviate from the desired quantity. To address these issues, a repair procedure is proposed. The method ensures that the number of awake nodes in each ring is equal to $ar$. Accordingly, the number of awake nodes in each ring is examined: if it matches $ar$, no action is required. If there are more awake nodes than desired, we probabilistically reduce their number by switching some of them to the sleep state, based on their remaining energy levels (Equation (9)). Conversely, if there are fewer awake nodes than necessary, additional nodes from the sleep state are selected, again probabilistically based on their remaining energy according to (10), and switched to the awake state. Once the number of awake nodes has been adjusted, we proceed to validate the offspring. For nodes whose have at-least one potential parent in the resultant offspring, no change is required. Otherwise, one of the closer super nodes to the BS is activated probabilistically considering their remaining energy, as shown in (11).

$$p{r}_{\mathit{remove}}\left(s_i\right)={\displaystyle \frac{e_i}{\sum _{s_k\in R\left(s_i\right)\wedge s_k is awake}{e}_k}}$$

(9)

$$p{r}_{\mathit{add}}\left(s_i\right)={\displaystyle \frac{e_i}{\sum _{s_k\in R\left(s_i\right)\wedge s_k is sleep}{e}_k}}$$

(10)

$$p{r}_{\mathit{parent}}\left(s_j\right)={\displaystyle \frac{e_j}{\sum _{s_k\in N\left(s_i\right)\bigwedge dist\left(s_k,BS\right)<dist\left(s_i,BS\right)\bigwedge s_i is sleep}{e}_k}}$$

(11)

Figure 5 demonstrates an example of the proposed crossover operator. In this figure, $s_4$ is selected as crossover point. Accordingly, the left-hand side genes of first chromosome (Figure 5(a)) and the right-hand side genes of the other chromosome (Figure 5(b)) are combined and result two offspring. Here, we demonstrate one of their offspring in Figure 5(c). After production of the offspring, we check for the validity of chromosome and change the structure of the chromosome to produce a valid chromosome (Figure 5(d)).

Mutation: The mutation operator in GA introduces random changes to the genes of a chromosome to maintain genetic diversity within the population. This operator is crucial because, without it, GA might converge too quickly to a suboptimal solution, getting stuck in local optima. According to the chromosome structure, we propose a customized mutation operator. In this approach, the number of genes of adopted chromosomes undergoing mutation is higher in the initial iterations of the algorithm and gradually decreases as the algorithm progresses. The number of genes undergoing mutation at iteration $t$, $m\left(t\right)$, is calculated as:

$$m\left(t\right)=m_{\max }\left(1-{\displaystyle \frac{t}{t_{\max }}}\right)$$

(12)

where $m_{\max }$ and $t_{\max }$ are the initial number of genes undergoing mutation and the total number of iterations, respectively. This strategy enables extensive exploration of the solution space in the early iterations and shifts towards exploitation in the later ones.

The corresponding super nodes to the adopted genes are investigated, and the awake ones are switched from the awake to the sleep state. For each of these asleep super nodes, a node in the same ring must be wakened up. This activation is controlled by the given probabilistic function in (10).

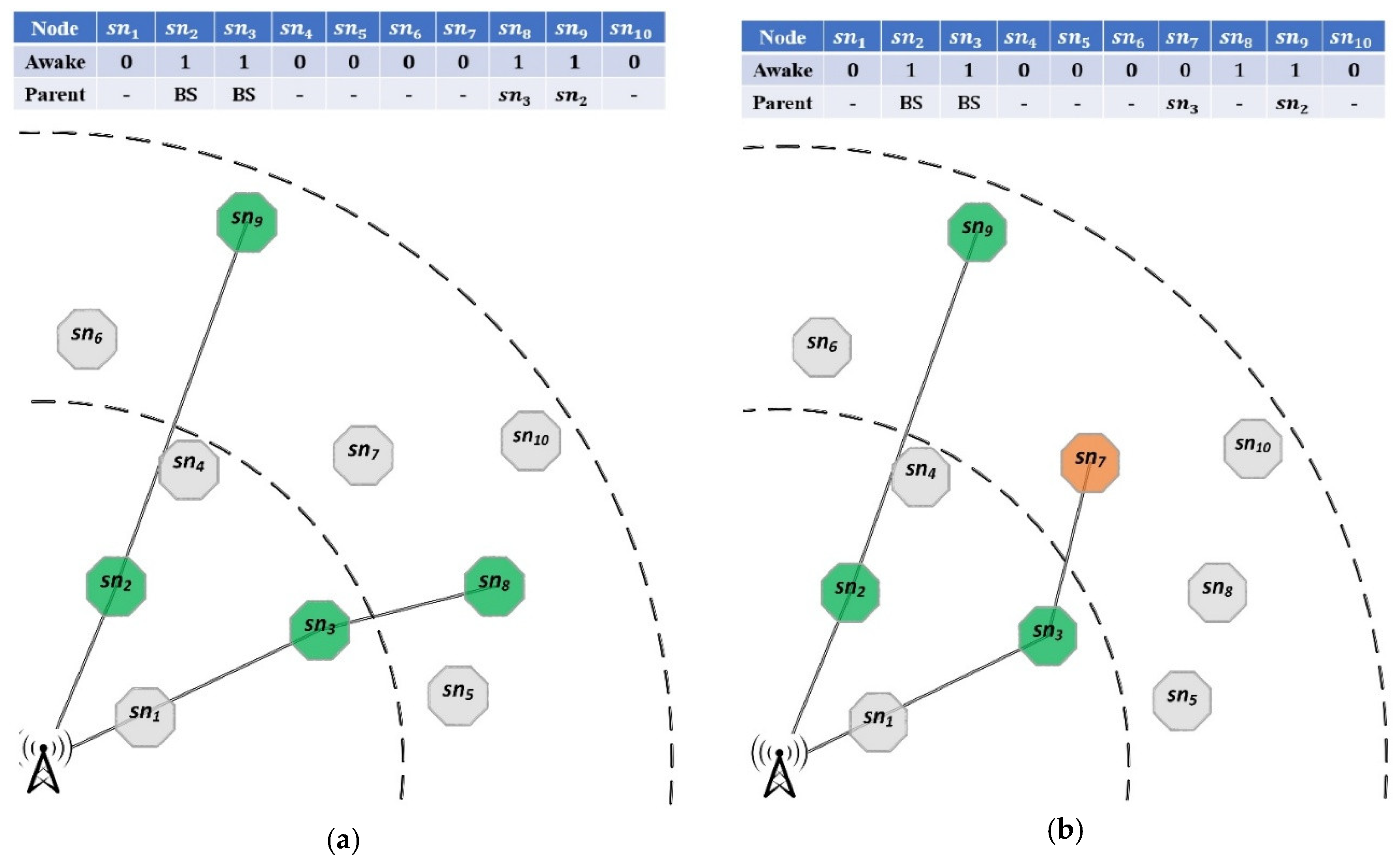
Figure 6 demonstrates of an example of the mutation operator. In this figure, based on the mutation operator, $s_8$ goes to the sleep mode. Accordingly, one other super node, for example $s_7$, is wakened up in the ring and a parent is selected for this node from the awake super nodes.

4.2. Clustering

After completing the first phase, which involves introducing awake nodes in the network and constructing a tree on them, we proceed to the second phase, in which each normal node selects an awake super node in their neighborhood to act as their CH. To achieve this aim, we employ a GA, the details of which are outlined in the following.

4.2.1. Chromosome Representation and Population Initialization

The proposed chromosome structure for network clustering consists of an array of length $\left|N\right|$. Each gene of this chromosome corresponds to a normal node of the HWSN. To ensure a consistent structure across all chromosomes, the normal nodes in each chromosome are sorted based on their distance to the BS. Each gene presents the randomly selected CH for each corresponded normal node, which is selected from the awake super nodes within its transmission range. 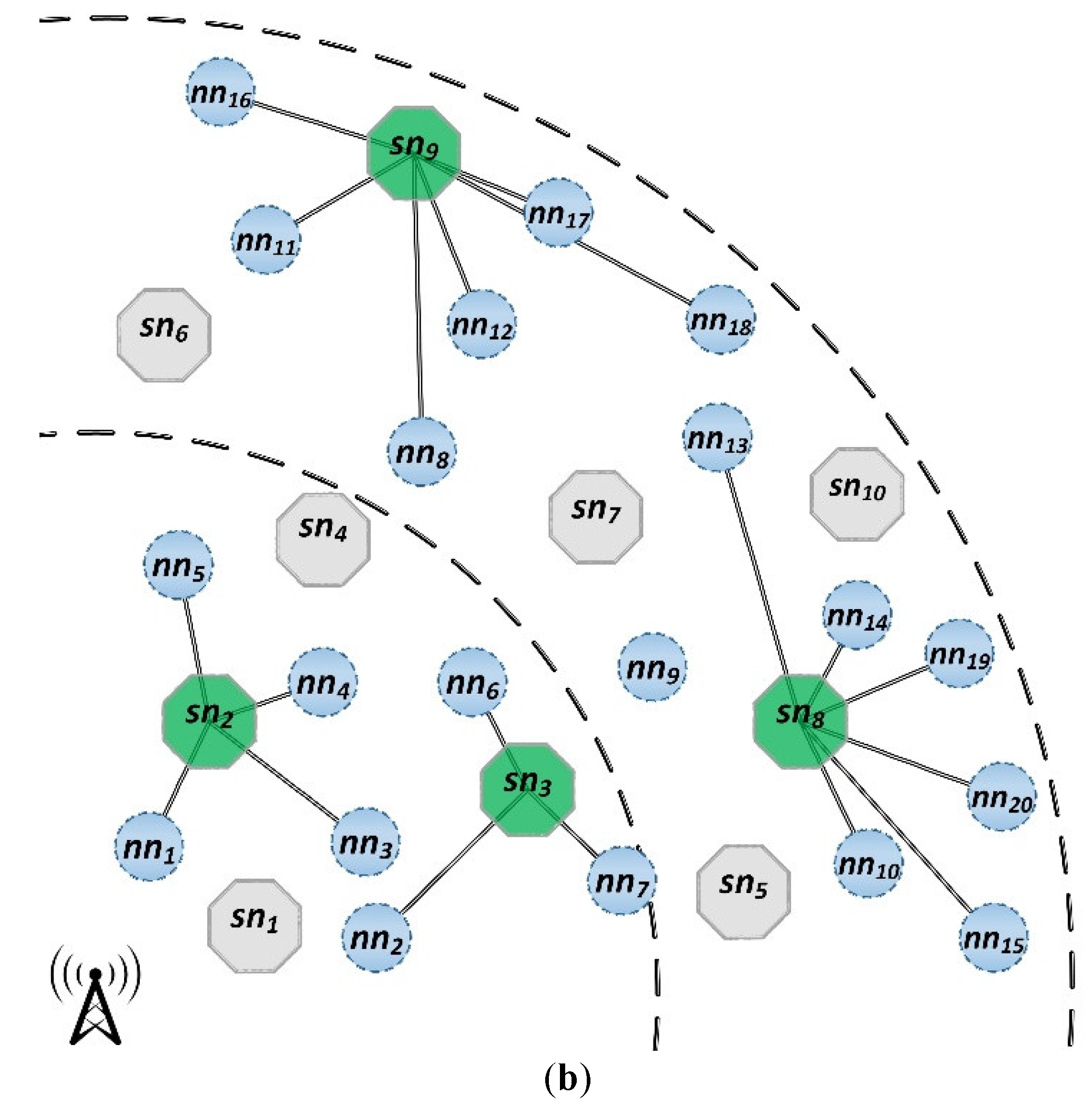Figure 7 illustrates an example clustering chromosome and its corresponding network structure.

4.2.2. Cost Function

A cost function is proposed to assess the quality of clustering chromosomes. In this context, we consider two key criteria: The first metric promotes even clustering by ensuring an equal number of CMs for each CH, and the second one aims to maximize the minimum energy of CHs. The former helps to evenly distribute the load of the network, while the latter accounts for the energy levels of the CHs to prevent any super node from depleting prematurely. Equation (13) describes the first measure, where $AS$ represents the set of awake super nodes selected in the previous phase, and ${nm}_{ji}$indicates the number of cluster members assigned to the super node $s_i$ according to clustering chromosome $X_j^C$. Additionally, $inm$represents the ideal number of cluster members and is calculated by dividing the number of available normal nodes by the number of awake super nodes.

$$facto{r}_3\left(X_j^C\right)=\underset{s_i\in \mathit{AS}}{\mathit{std}}{\displaystyle \frac{{nm}_{ji}}{inm}}$$

(13)

Equation (14) describes $facto{r}_4$, which is similar to $facto{r}_2$ in the tree construction phase. The difference is that $facto{r}_2$ relies solely on the structure of the proposed tree, without knowledge of the number of CMs for each super node. On the other hand, $facto{r}_4$ accounts for the exact number of CMs per super node in the clustering phase, enabling more precise calculation of ${er}_{ji}$.

$$facto{r}_4\left(X_j^C\right)={\displaystyle \frac{{\mathrm{m}\mathrm{i}\mathrm{n}}_{s_k\in S} {er}_{jk}}{e_s}}$$

(14)

Finally, the energy level of normal nodes is balanced as described in (15).

$$facto{r}_5\left(X_j^C\right)={\displaystyle \frac{{\mathrm{m}\mathrm{i}\mathrm{n}}_{n_k\in N} {er}_{jk}}{e_N}}$$

(15)

Our cost function is defined by (16), and our objective is to minimize this function.

$$cos{t}_2\left(X_j^C\right)=w_3\times facto{r}_3\left(X_j^C\right)-w_4\times facto{r}_4\left(X_j^C\right)+w_5\times facto{r}_4\left(X_j^C\right), w_3+w_4+w_5=1$$

(16)

4.2.3. GA Operators

Our GA uses three core operators to iteratively refine the population and guide it towards high-quality solutions including selection, crossover, and mutation. These operators are explored in the following.

Selection: We use RWS as the selection operator, which selects chromosomes based on the value returned by the cost function using a similar probability function to (8). Chromosomes with lower costs (indicating better solutions) have a higher probability of being chosen to produce the next generation.

Crossover: The crossover operator is employed to explore the solution space. In this case, a single-point crossover is used. All offspring produced by this operator are valid solutions for the clustering problem.

Mutation: In the proposed mutation process, for a random chromosome, a number of genes – which are corresponded to CHs of normal nodes – are randomly selected. The CH of each chosen normal node is changed from its current CH to another awake super node within its transmission range.

5. Experimental Results and Discussions

In this section, we evaluate the performance of the proposed method and compare it with HEDHMG [5], EFCRPSO [11], EFEBPSO [4], and CRCGA [31]. The performance metrics used for comparison include area coverage, total energy consumption, First Node Die (FND), Last Node Die (LND), and number of available super nodes. The algorithms are implemented using WSNSimPy, a Python library for discrete event simulation of WSNs. The simulations are performed on networks with dimensions of 200m×200m. Through experimentation, we identify that dividing the networks into four rings provide the best outcomes. Additionally, the experimentation shows that to ensure adequate coverage on normal nodes, keeping half of the super nodes awake provides an optimal balance. We evaluate two different networks, ${WSN}_1$ and ${WSN}_2$, which differ in node density. The network ${WSN}_1$consists of 60 super nodes and 200 normal nodes, with the BS positioned in the lower-left corner of the area. The network ${WSN}_2$ is denser, featuring 80 super nodes and 250 normal nodes, and also has the BS located in the corner, similar to ${WSN}_1$. Table 1 outlines the parameters used in the simulations. Additionally, Table 2 provides the GA parameters for the proposed method, including the weights for the criteria used in the cost functions, the number of iterations, and the population size.

5.1. Normal Node Coverage

This metric quantifies the number of normal nodes that have a super node as their CH. It serves as an indicator of how effectively the first phase of the algorithm selects awake super nodes. In this way, the algorithm can ensure super nodes are evenly spread across the network which increases the likelihood that normal nodes have an accessible awake super node nearby. Effective network coverage is critical for achieving performance and efficiency goals.

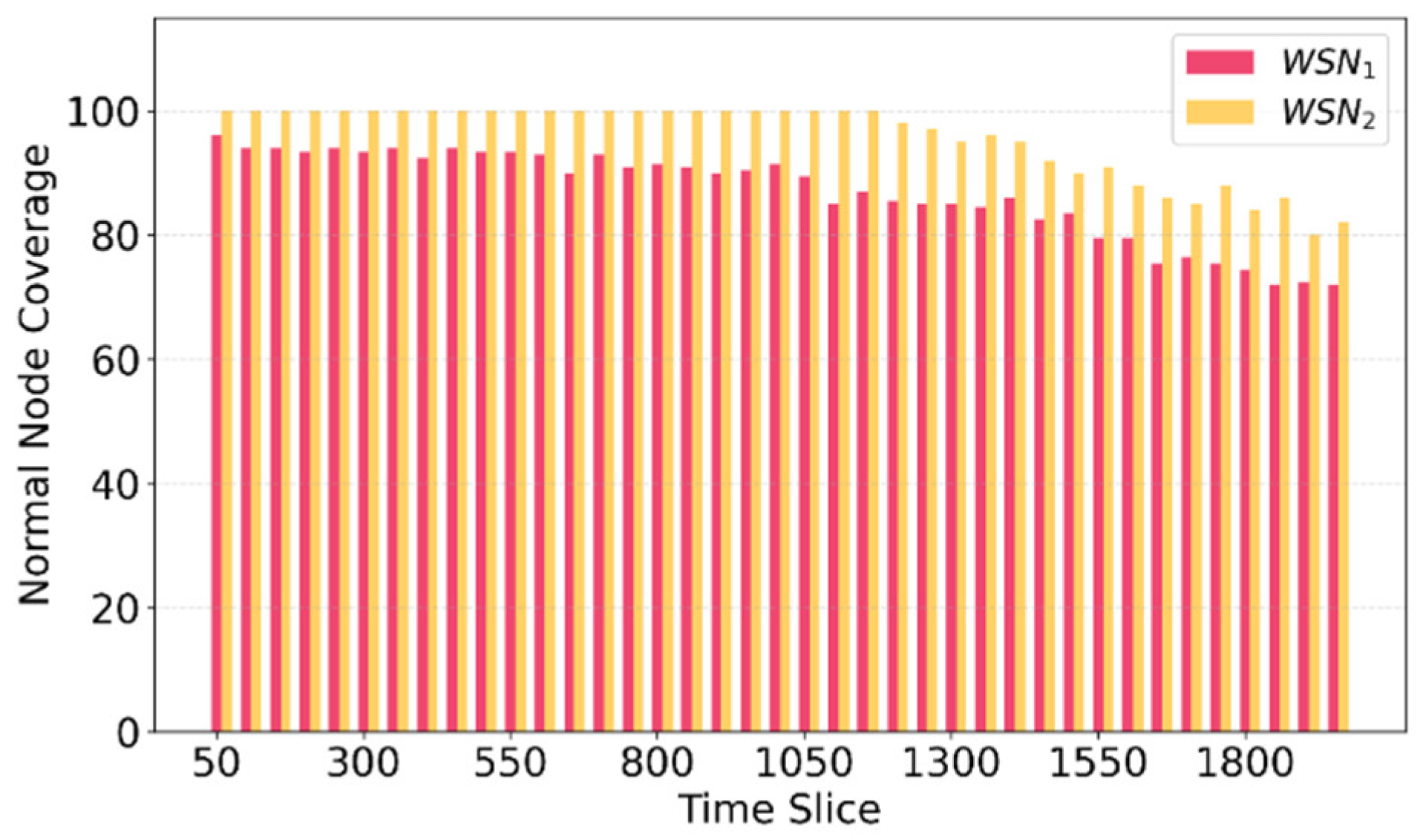
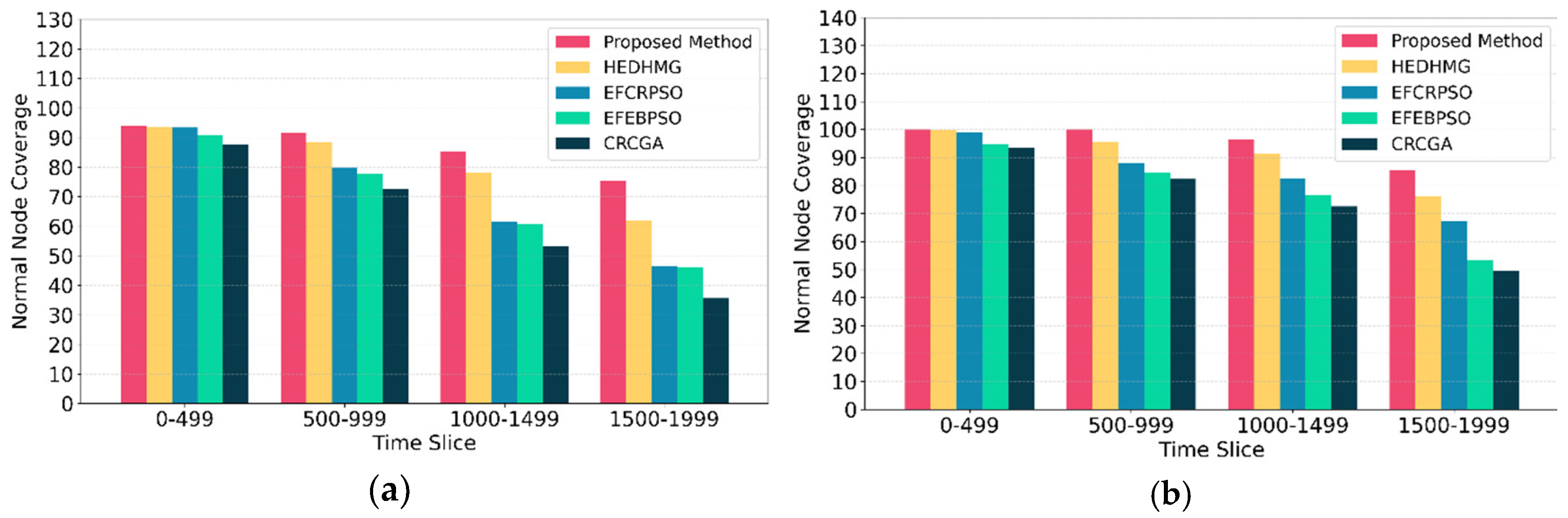
Figure 8 illustrates area coverage for $WS{N}_1$ and $WS{N}_2$ using the proposed method. In the early rounds, ${WSN}_2$ achieves almost full coverage, primarily because it contains a greater number of super nodes compared to $WS{N}_1$. This higher super node density facilitates finding an awake super node in the neighborhood of normal nodes, supporting a strong coverage. Conversely, ${WSN}_1$, which has fewer super nodes, displays slightly lower coverage, as the reduced number of super nodes limits the availability of CHs across the network. As time progresses, coverage decreases in both networks due to the depletion of super nodes. The decrease in the network coverage over time can be attributed to the energy consumption and eventual failure of super nodes, which reduces the ability of the HWSN to maintain consistent communication routes. However, even with this gradual reduction, the area coverage remains within acceptable thresholds in ${WSN}_1$ and ${WSN}_2$.

Figure 9 illustrates a comparison of normal node coverage between the proposed algorithm and other considered approaches. As depicted in the figure, the proposed algorithm significantly outperforms HEDHMG, EFCRPSO, EFEBPSO, and CRCGA in both ${WSN}_1$ and ${WSN}_2$. Specifically, in ${WSN}_1$, the proposed algorithm achieves an average coverage improvement of 8.6%, 29%, 31.1%, and 51.1% over HEDHMG, EFCRPSO, EFEBPSO, and CRCGA, respectively. Similarly, in ${WSN}_2$, the proposed algorithm surpasses these algorithms by 5.6%, 14.5%, 27.4%, and 33.4%, respectively.

This sustained coverage is largely due to the inclusion of $facto{r}_1$ in the algorithm, which optimizes the sleep scheduling of super nodes. Using $facto{r}_1$ ensures that super nodes are cyclically activated, balancing their load to delay energy depletion. By minimizing the extent of orphan nodes through effective sleep scheduling, this factor contributes to prolonged network coverage and functionality. Consequently, despite the inevitable death of super nodes, the proposed method ensures that the network retains satisfactory coverage levels over time, supporting continued data collection and communication within the HWSN. The other factor enhancing our algorithm is proposing customized initialization, and crossover and mutation operators. According to these schemes, the HWSNs are divided into ring of equal width, and it is tried to keep the number of awake super nodes in different rings the same. Therefore, the awake nodes distribute evenly throughout the network.

5.2. Total Consumed Energy

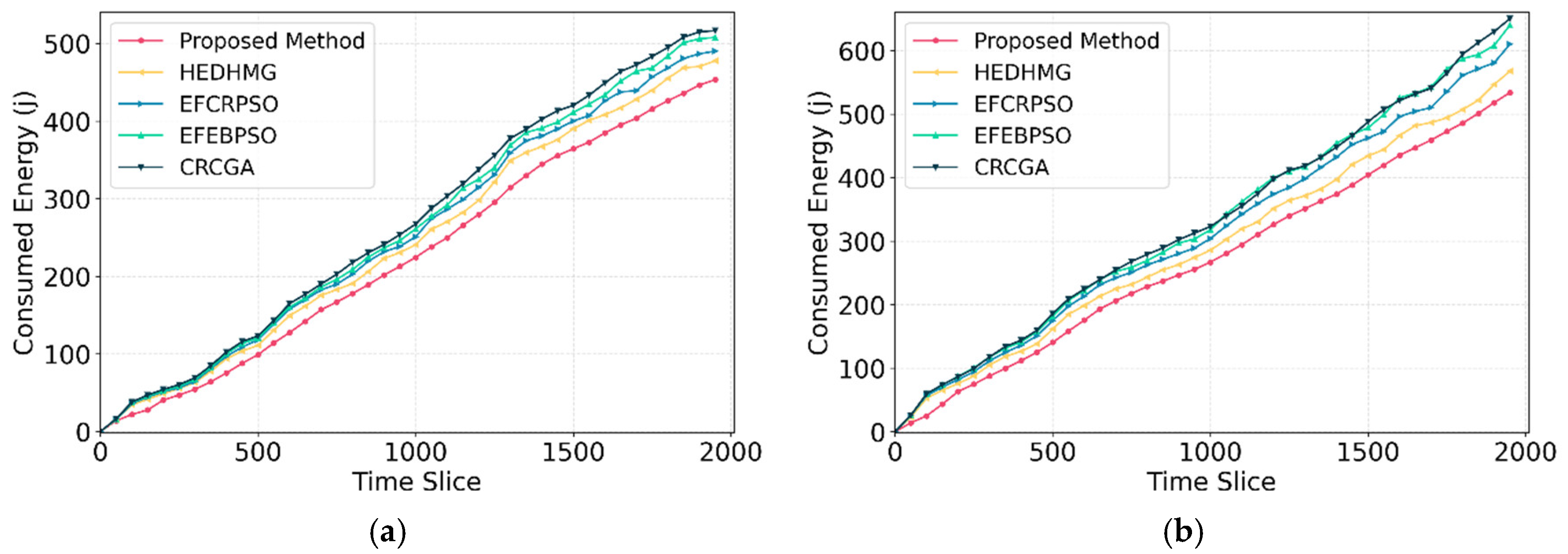
The next metric under consideration is the total consumed energy, which calculates the cumulative energy usage of super nodes that handle the primary task of data transmission and delivery within the network. This metric is essential for evaluating the efficiency of the network, as nodes have limited, non-rechargeable energy sources, and conserving this energy directly influences network longevity. Figure 10 compares total energy consumption of the proposed method with its competitive algorithms in ${WSN}_1$ and ${WSN}_2$. In both networks, the proposed method outperforms competing algorithms in terms of energy exhaustion. Specifically, for ${WSN}_1$, it reduces energy consumption by 10.5%, 14%, 16.4%, and 18.7% when compared to the HEDHMG, EFCRPSO, EFEBPSO, and CRCGA algorithms, respectively. These values are equal to 10.7%, 16.9%, 20.7%, and 21%, for ${WSN}_2$.

The enhanced energy efficiency of our proposed approach in both network types highlights the robustness of the proposed method under varying conditions. This superiority is achieved due to the integration of four critical factors that we apply within the tree construction and clustering phases. The first factor, $facto{r}_1,$ ensures that awake super nodes are distributed uniformly across the network, which is particularly important for the tree construction phase. By spreading awake super nodes evenly, $facto{r}_1$ enables the formation of balanced communication routes. Without such uniform distribution, awake super nodes could become concentrated in some areas, leaving other sections without adequate awake super node coverage. This imbalance would limit the routing options in those uncovered areas, leading to increased energy consumption as nodes are forced to transmit data to distant parents. Furthermore, $facto{r}_2$ prioritizes routes with higher remaining energy in the tree construction phase, helping to balance energy consumption across the WSN. Finally, proposing customized initialization method and GA operators enhances the performance of the proposed algorithm and reduces energy consumption.

In the clustering phase, additional efficiency is achieved through $facto{r}_3$ and $facto{r}_4$. The third factor plays a critical role by distributing normal nodes among super nodes as evenly as possible. This distribution balances the load across all super nodes, reducing the likelihood of any single node being overwhelmed by a large number of connections. Such even distribution not only conserves the energy of individual super nodes but also enhances the overall energy efficiency of the network. By preventing excessive energy consumption in specific nodes, $facto{r}_3$ contributes to a more sustainable energy usage scheme throughout the network. Additionally, $facto{r}_4$ focuses on energy conservation of super nodes. This metric prevents premature exhaustion of any single super node by distributing node responsibilities based on energy levels, similar to the prioritization strategy in the tree construction phase. Finally, $facto{r}_5$ reduces energy consumption of normal nodes and prevent choosing far super nodes as CHs, which required high energy levels for data transmission.

The employed factors In the cost functions create an energy management strategy that optimizes the selection of awake super nodes. This approach not only conserves energy in individual nodes but also maximizes overall network efficiency and ensures that HWSNs maintain robust coverage and functionality over lengthy periods. Using customized initialization, crossover, and mutation in the tree construction phase also improves energy efficiency. Even distribution of awake super nodes avoids long distances between normal nodes and their CHs, reducing exhausted energy for intra-cluster communication.

5.3. Network Lifetime

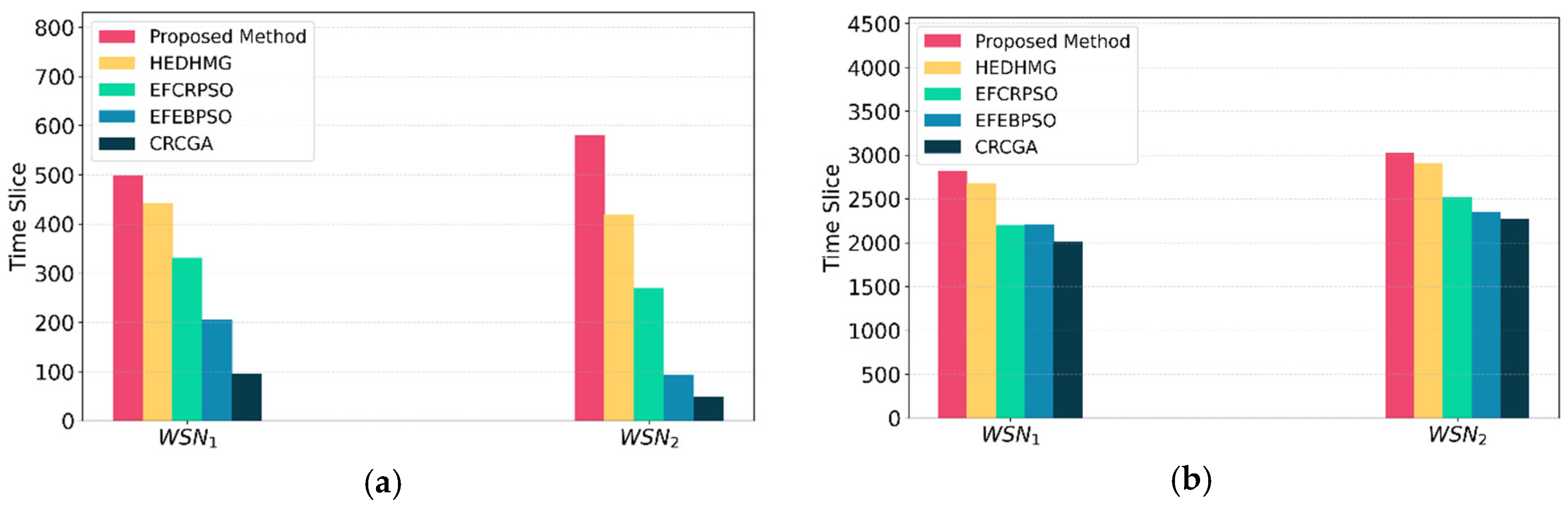
In this section we discuss two important factors: FND and LND, as shown in Figure 11. As the figure illustrates, in our algorithm, both FND and LND occur significantly later compared to competitive algorithms. Specifically, using the proposed method in $WS{N}_1$ results in improvement of 56, 167, 293, and 402 rounds or FND compared to HEDHMG, EFCRPSO, EFEBPSO, and CRCGA, respectively. For LND in ${WSN}_1$, the improvements are 140, 620, 615, and 810 rounds regarding the same algorithms. In ${WSN}_2$, the proposed method yields FND improvements of 161, 311, 487, and 532 rounds, and LND improvements of 128, 508, 681, and 757 rounds compared to HEDHMG, EFCRPSO, EFEBPSO, and CRCGA, respectively.

The enhancements in these results can be attributed to effective sleep scheduling and robust tree construction in the first phase, and efficient clustering in the latter phase. To be more precise, $facto{r}_1$ plays a crucial role in ensuring a uniform distribution of awake super nodes across the network, which yields load-balanced trees and reduces the likelihood of energy depletion in concentrated areas. The second factor, $facto{r}_2$, operating in the tree construction phase, focuses on maximizing the minimum remaining energy of super nodes within the tree. This factor gives priority to choosing super nodes with higher energy reserves, helping to avoid overusing specific nodes and thus balancing energy consumption across the network. By distributing energy usage among super nodes more evenly, $facto{r}_2$ helps extend the lifetime of each node and mitigates the risk of network segmentation due to energy depletion in specific regions. Additionally, the proposed initialization method and GA operators balance the number of awake super nodes in the rings, yielding more even energy exhaustion and longer network lifetime.

In the clustering phase, $facto{r}_3$ and $facto{r}_4$ aid in evenly distributing normal nodes among awake super nodes, further contributing to energy efficiency by preventing any single super node from becoming overloaded. Together, these factors significantly extend the operational lifetime of nodes within the network, leading to delayed FND and LND. Furthermore, $facto{r}_5$ balances energy consumption of normal nodes and prevents their early death.

5.4. Number of Available Super Nodes

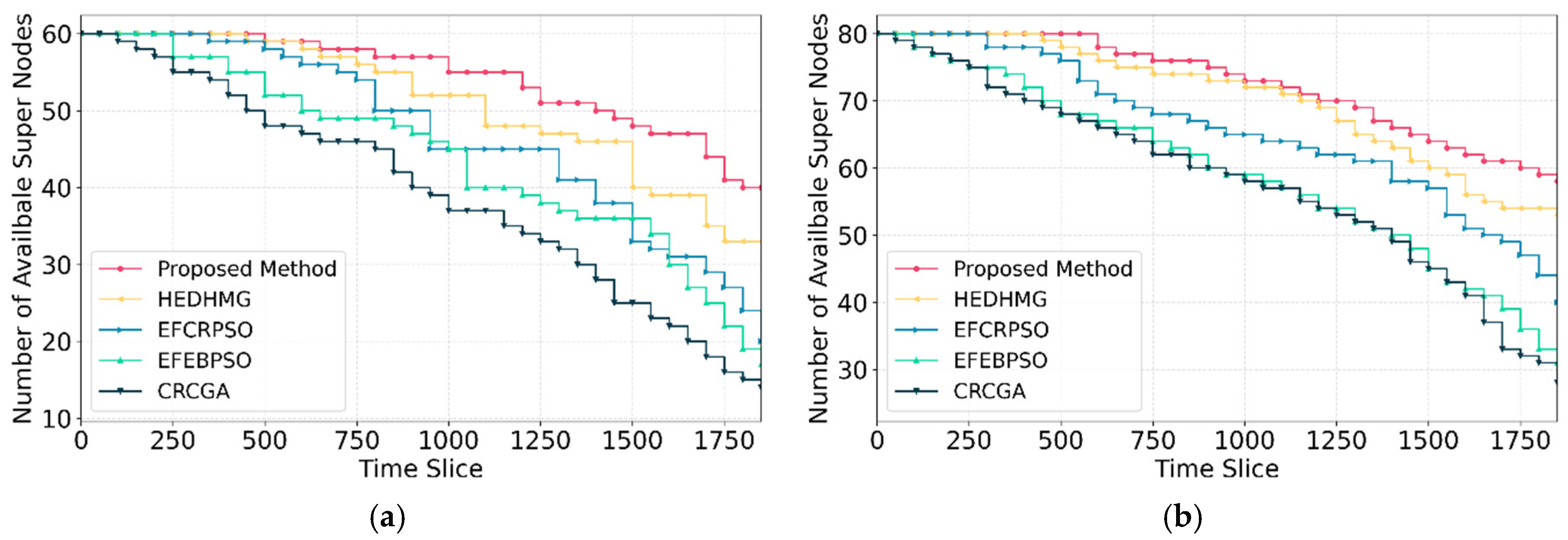
We define available super nodes as those that are alive and have other super nodes in their neighborhood capable of sending data toward the BS. Accordingly, a super node with a good amount of energy is considered unavailable if the BS is out of its transmission range and there is no other nearby super node to catch its data and forward it. The number of available super nodes is an important factor. This is due to a higher number of available super nodes improves area coverage, enabling the network to fulfill its primary goal of data delivery to the BS more efficiently. Figure 12 reports the number of available super nodes in each round. As shown in this figure, the proposed method consistently demonstrates a higher number of available super nodes compared to competitive algorithms in all rounds for both $WS{N}_1$ and ${WSN}_2$. In ${WSN}_1$, the proposed method shows improvements of 5 super nodes over HEDHMG, 16 super nodes over EFCRPSO, 21 super nodes over EFEBPSO, and 35 super nodes over CRCGA, after 1800 time slices. In ${WSN}_2$, the improvements are 5 super nodes over HEDHMG, 15 super nodes over EFCRPSO, 26 super nodes over EFEBPSO, and 28 super nodes over CRCGA, after 1800 time slices.

The main factor to achieve higher number of alive super nodes of our algorithm regarding the competitive schemes is the even distribution of awake nodes. The proposed initialization scheme, customized operators, and $facto{r}_1$ in the first phase, ensures an even distribution of awake super nodes throughout the network. This evenness reduces the chances of energy depletion in localized areas and promotes better coverage, which increases the likelihood of data being successfully forwarded to the BS. The other factors used in $cos{t}_1$ and $cos{t}_2$also play a significant role in achieved results. The $facto{r}_2$ prioritizes super nodes for more energy for tree construction, increasing the chances of sustaining more alive super nodes, contributing to their availability. The third factor, $facto{r}_3$, used in the clustering, focuses on evenly distributing normal nodes among super nodes. This balance prevents individual super nodes from becoming overloaded, allowing them to remain operational and available for data forwarding. The application of customized initialization and GA operators in the first phase for balancing the distribution of super nodes throughout the HWSN increases the number of available super nodes.

6. Conclusion and Future Works

This paper proposed an algorithm for efficient sleep scheduling and data gathering in HWSNs. The algorithm consisted of two main phases, each utilizing a GA to optimize network performance. In the first phase, sleep scheduling and tree construction were handled simultaneously, considering their high dependency. Clustering of normal nodes using the awake super nodes as CHs was performed in the second phase. The objectives of these phases focused on energy efficiency and preserving network coverage. The first objective maximized normal node coverage by selecting proper awake super nodes, ensuring each normal node had an awake super node within its neighborhood. The second objective prioritized energy efficiency by balancing remaining energy of super nodes, encouraging routes that have nodes with higher energy levels, prolonging network lifetime. This energy-centric prioritization was also applied in the clustering phase, where normal nodes were evenly distributed among the awake super nodes to prevent overloading and balance energy use. The other advantage of our algorithm was proposing customized initialization scheme, and crossover and mutation operators in its first phase. These schemes aimed at even distribution of awake super nodes. For this purpose, the HWSN was divided into rings, and the initialization method and GA operators tried to adopt equal number of awake super nodes in these rings.

For the future work, we aim to explore other energy saving techniques, such as dynamic modulation scaling. Furthermore, the proposed sleep scheduling scheme can be integrated into the multi-channel multi-radio HWSNs to improve both energy-efficiency and network capacity. Finally, we will examine other metaheuristic algorithms to attain better network configurations. Swarm intelligence algorithms, such as GWO, have been shown to generate high-quality solutions. Therefore, combining these methods with GA can improve the performance.