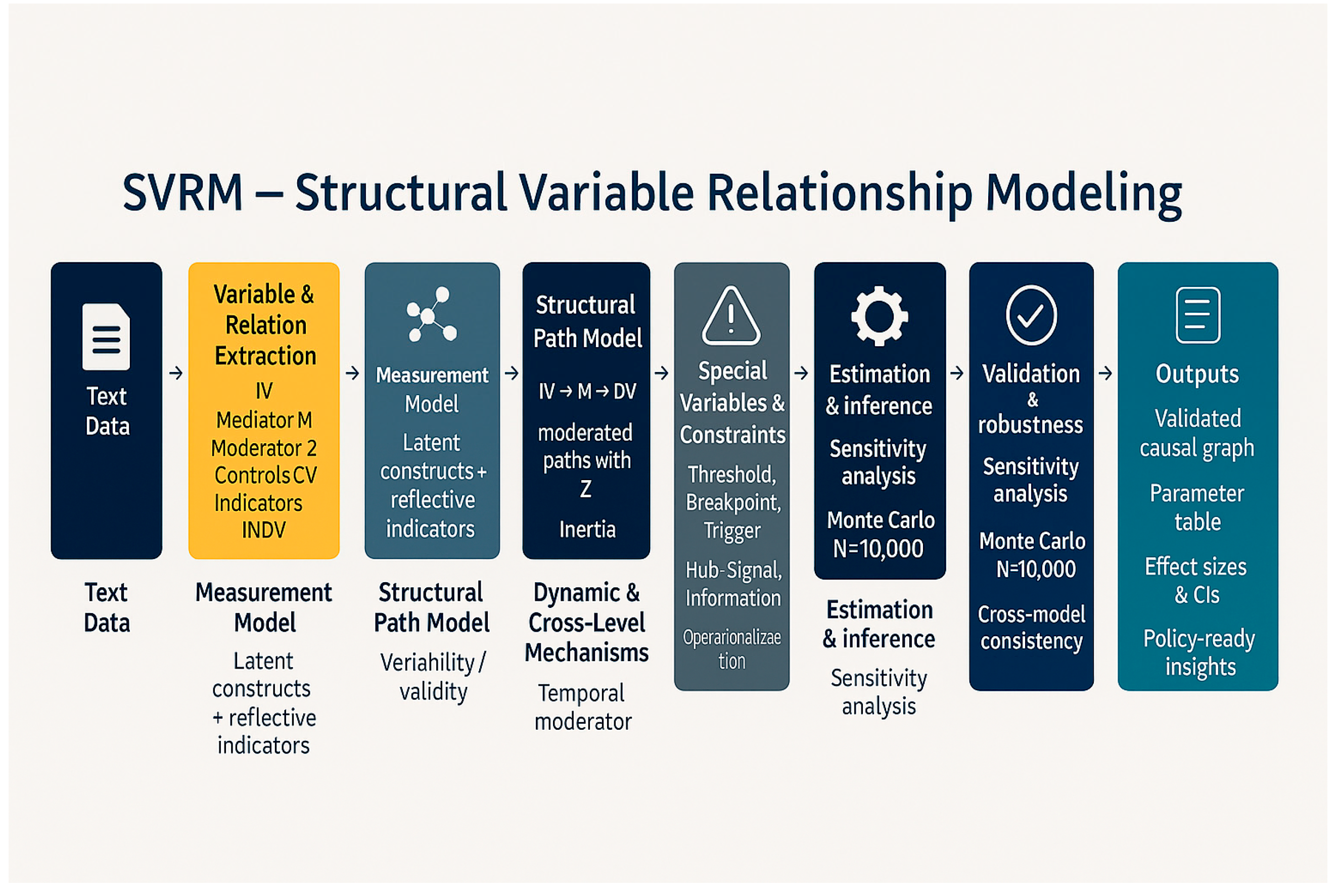
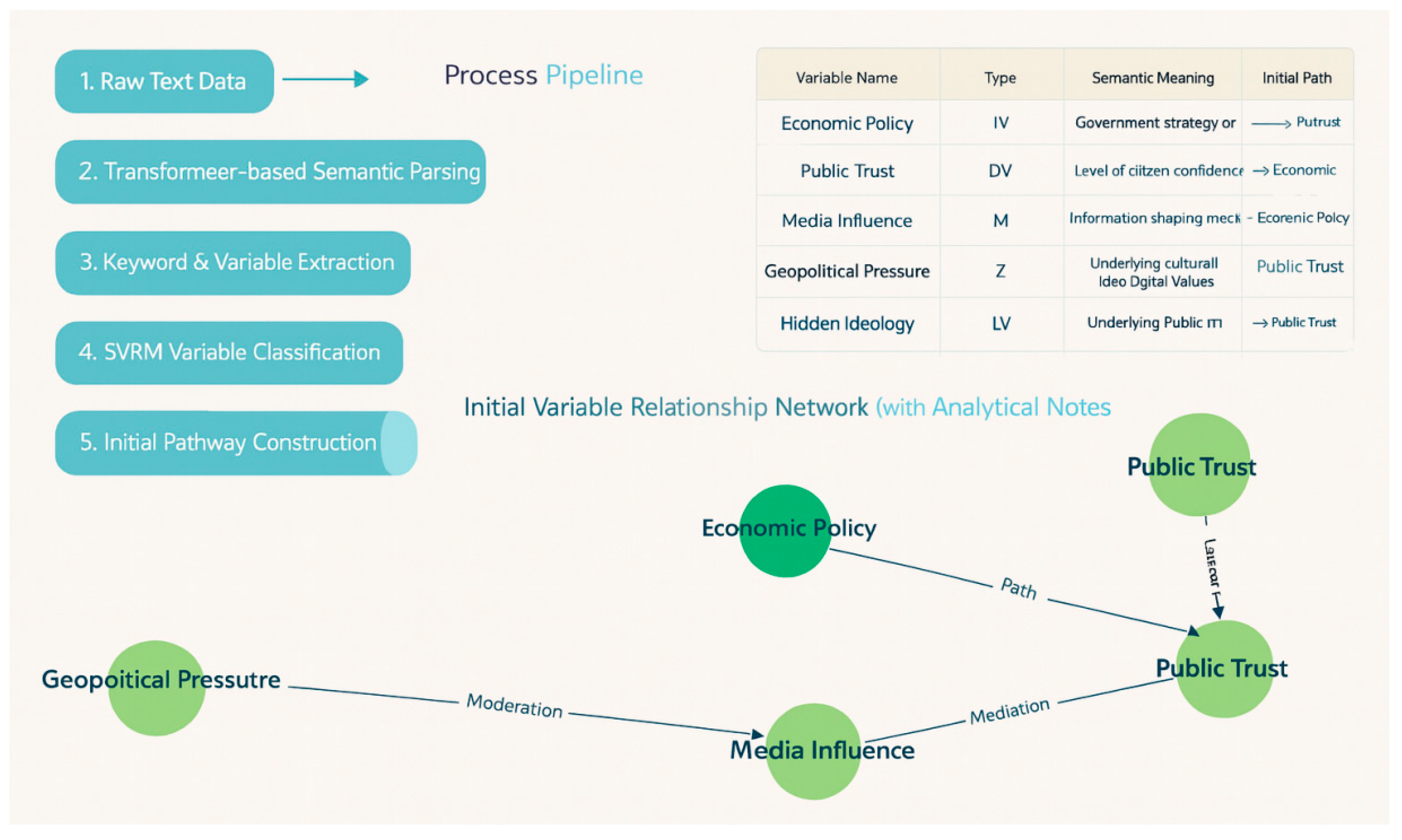
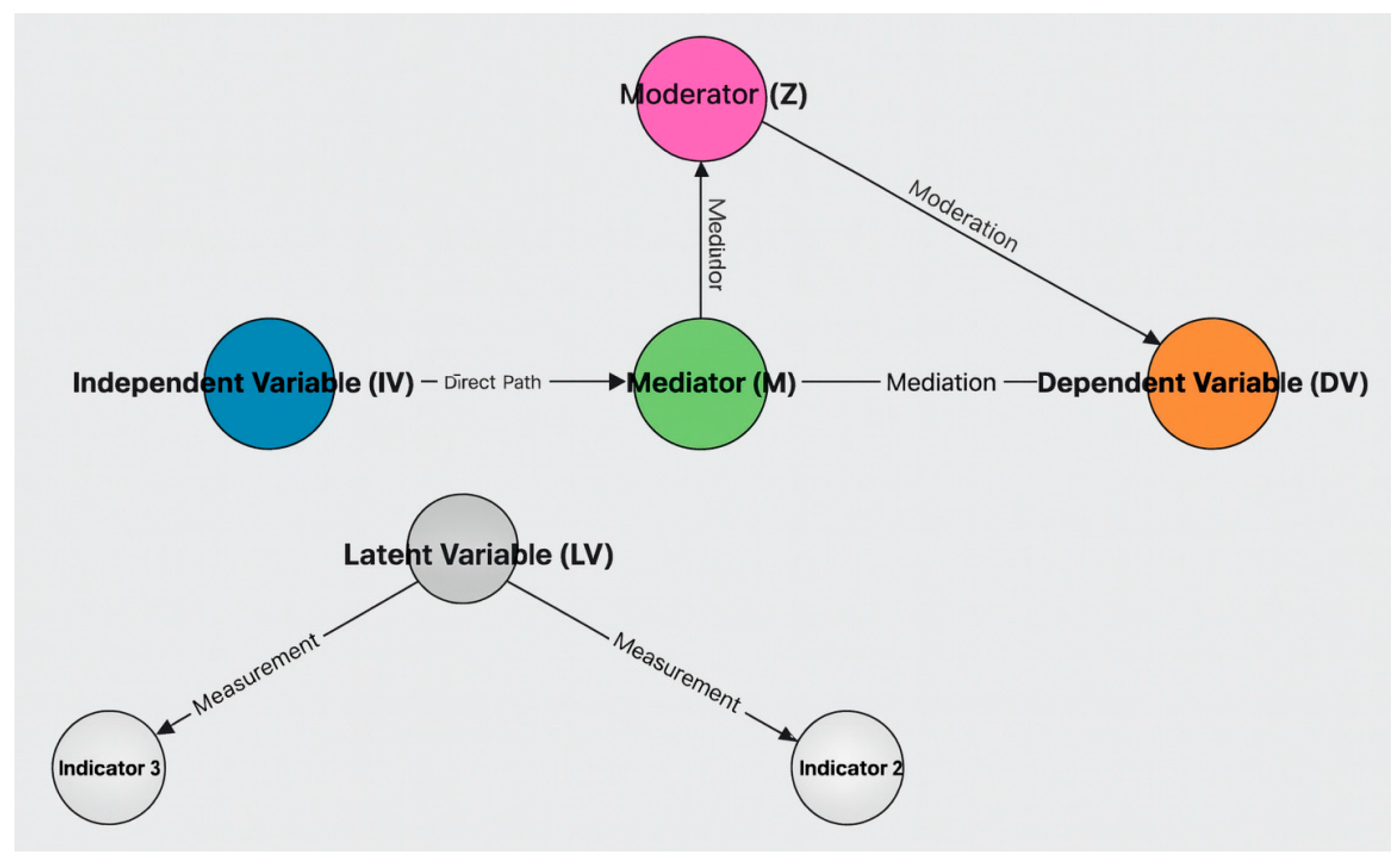
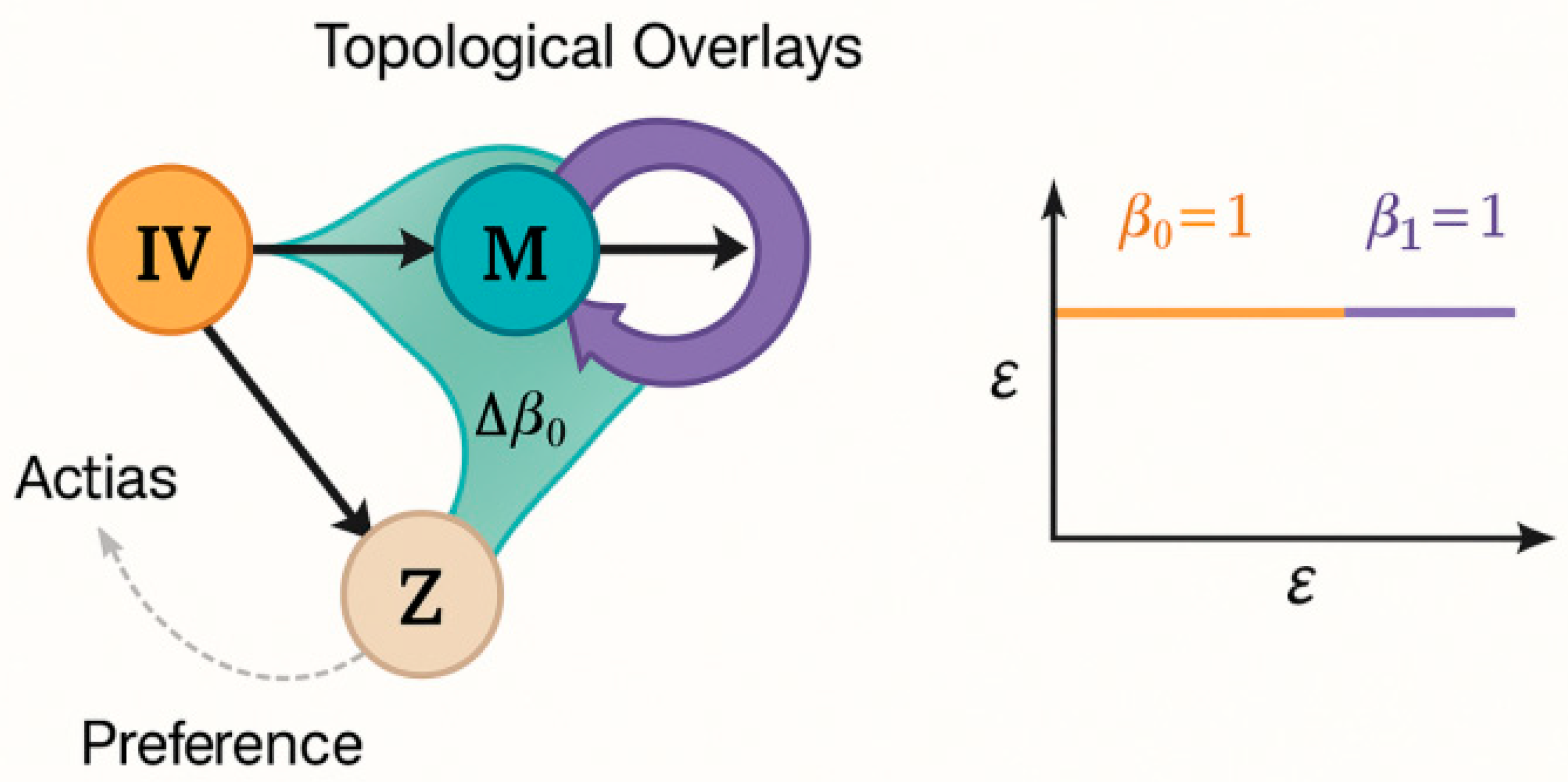
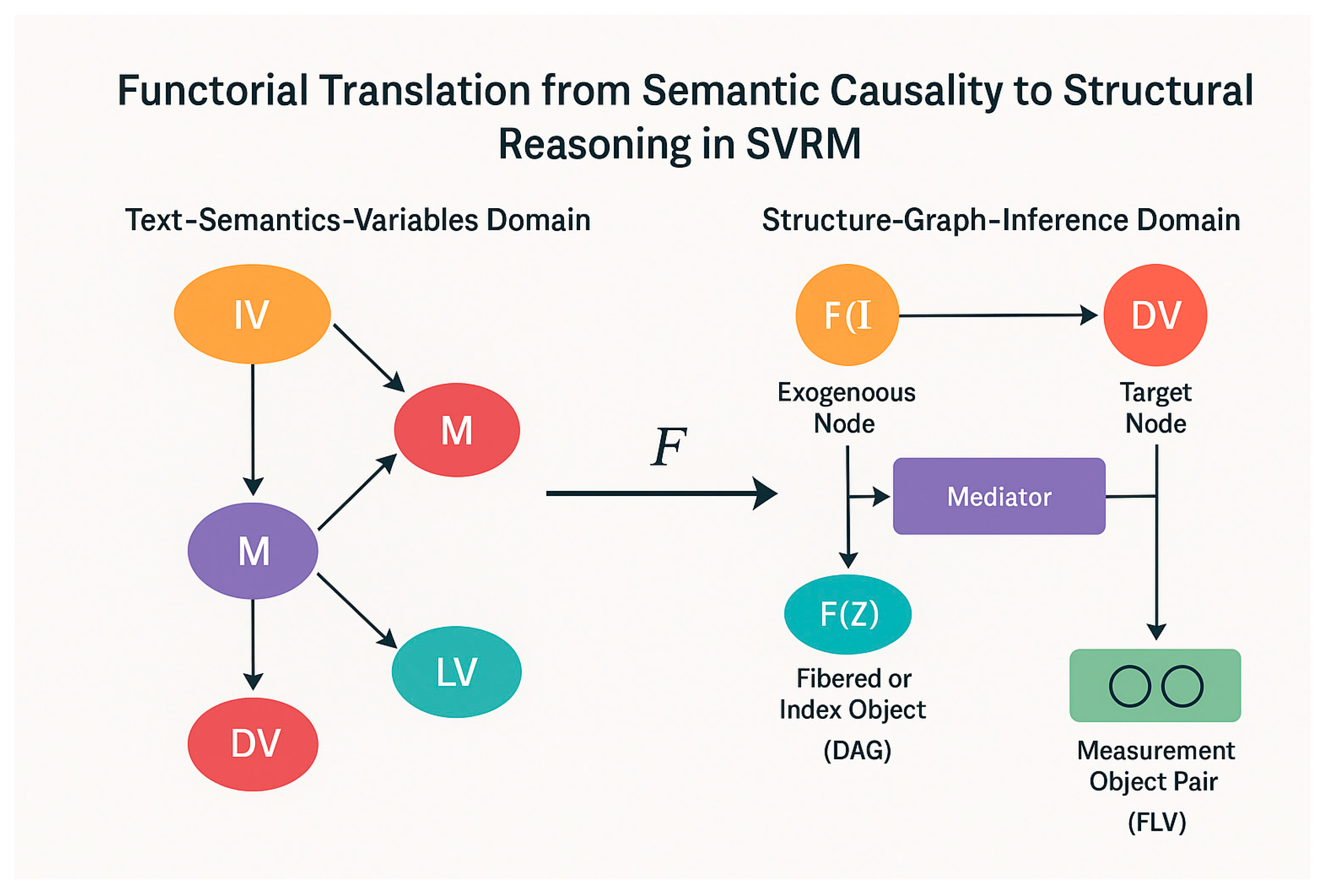
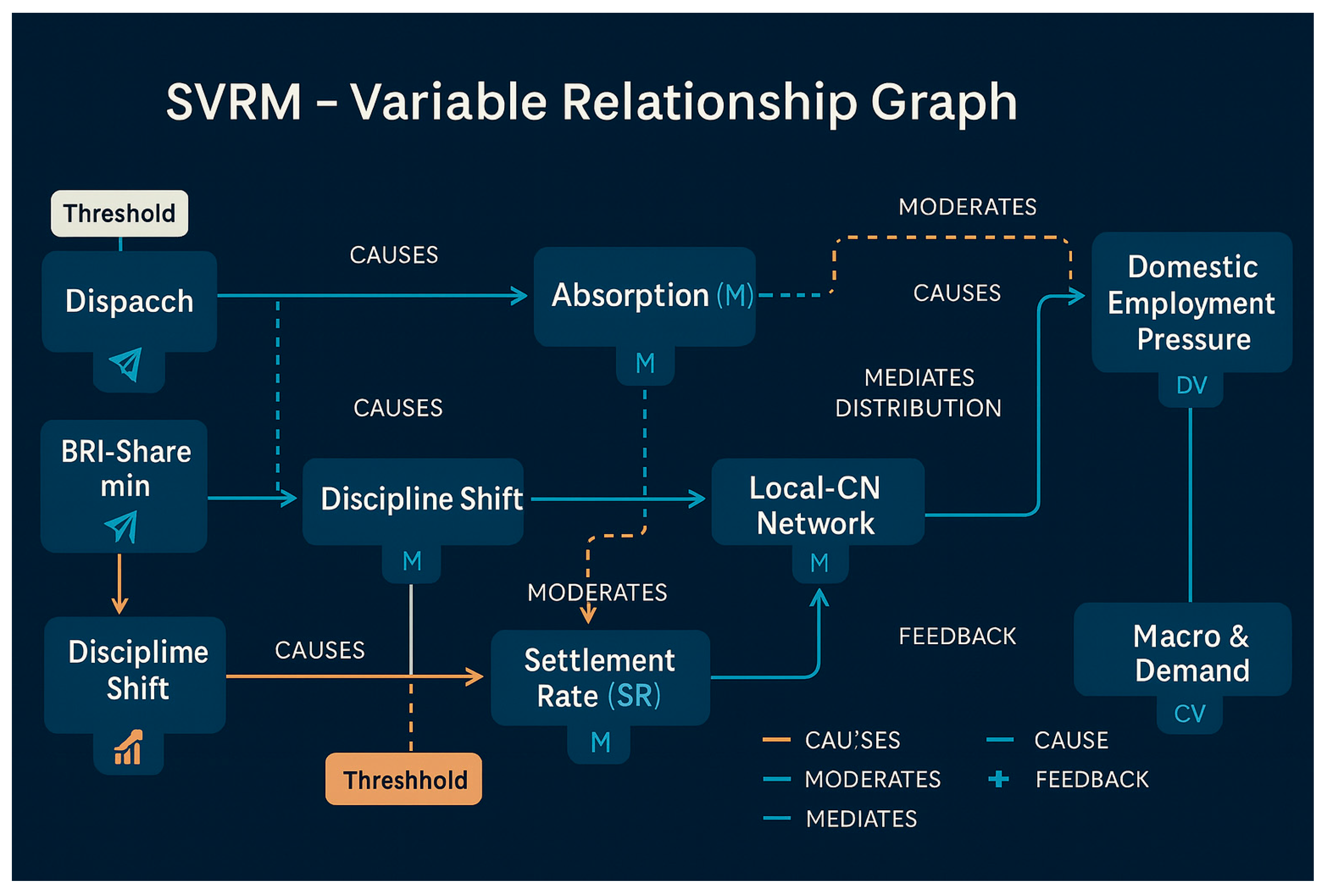
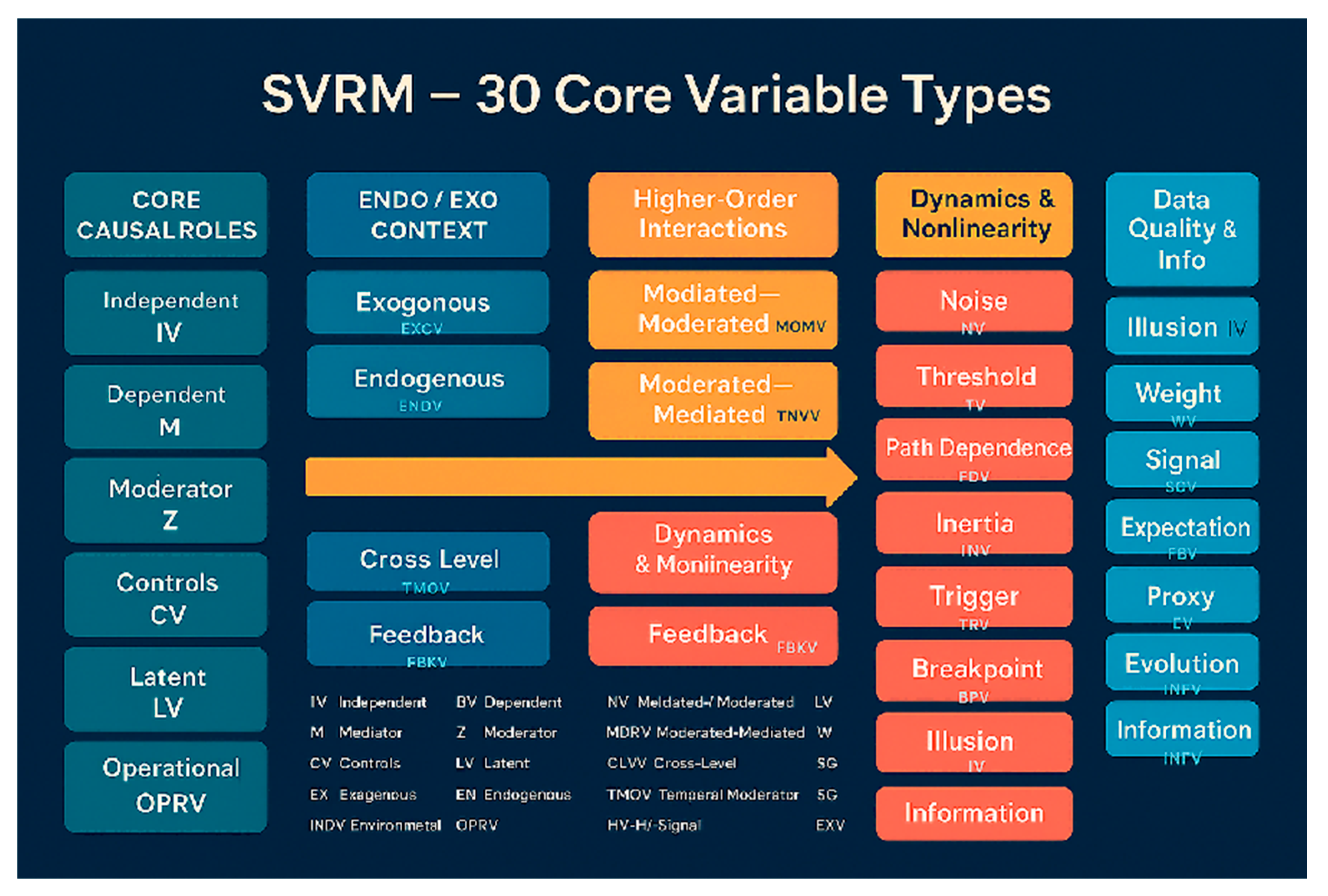
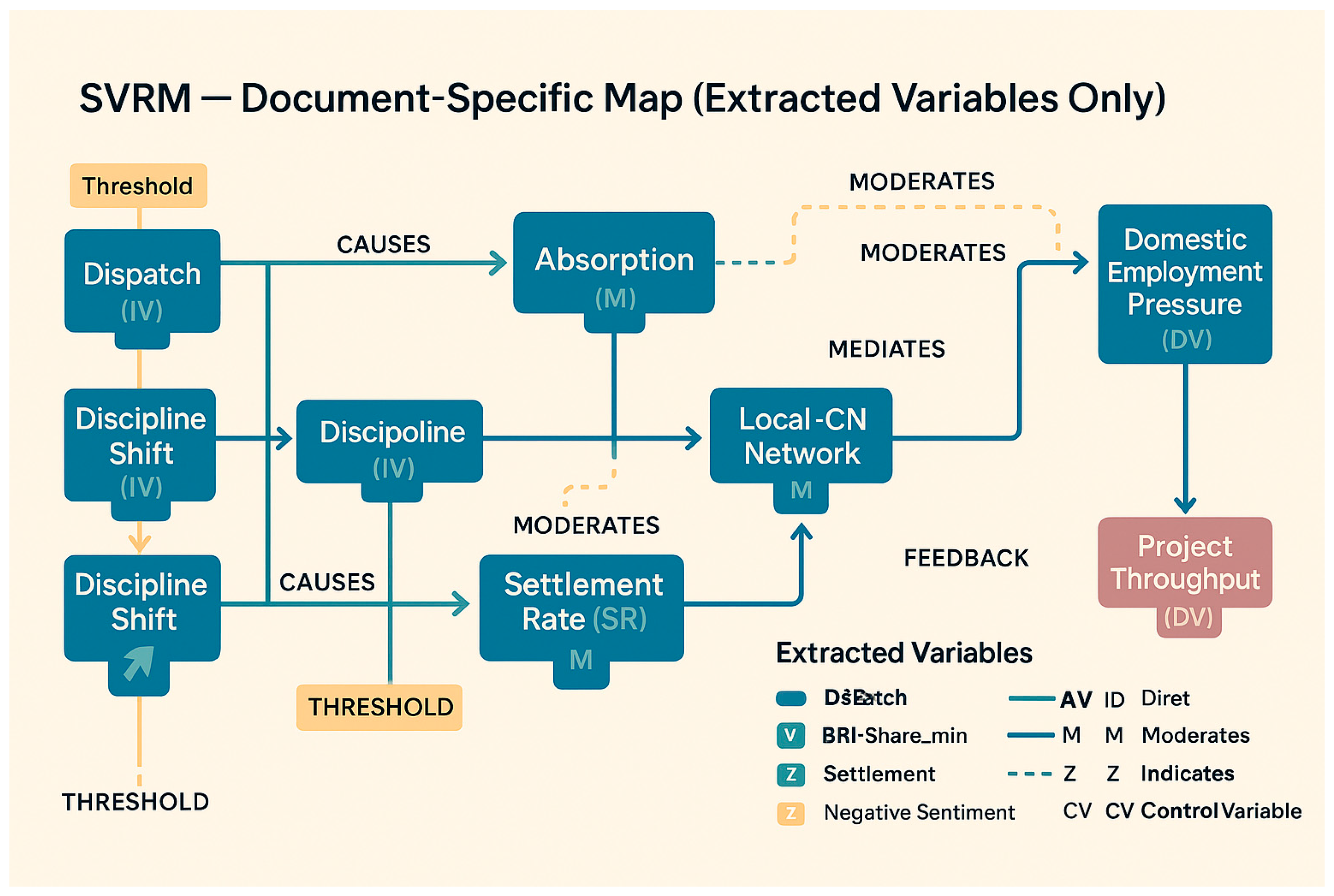
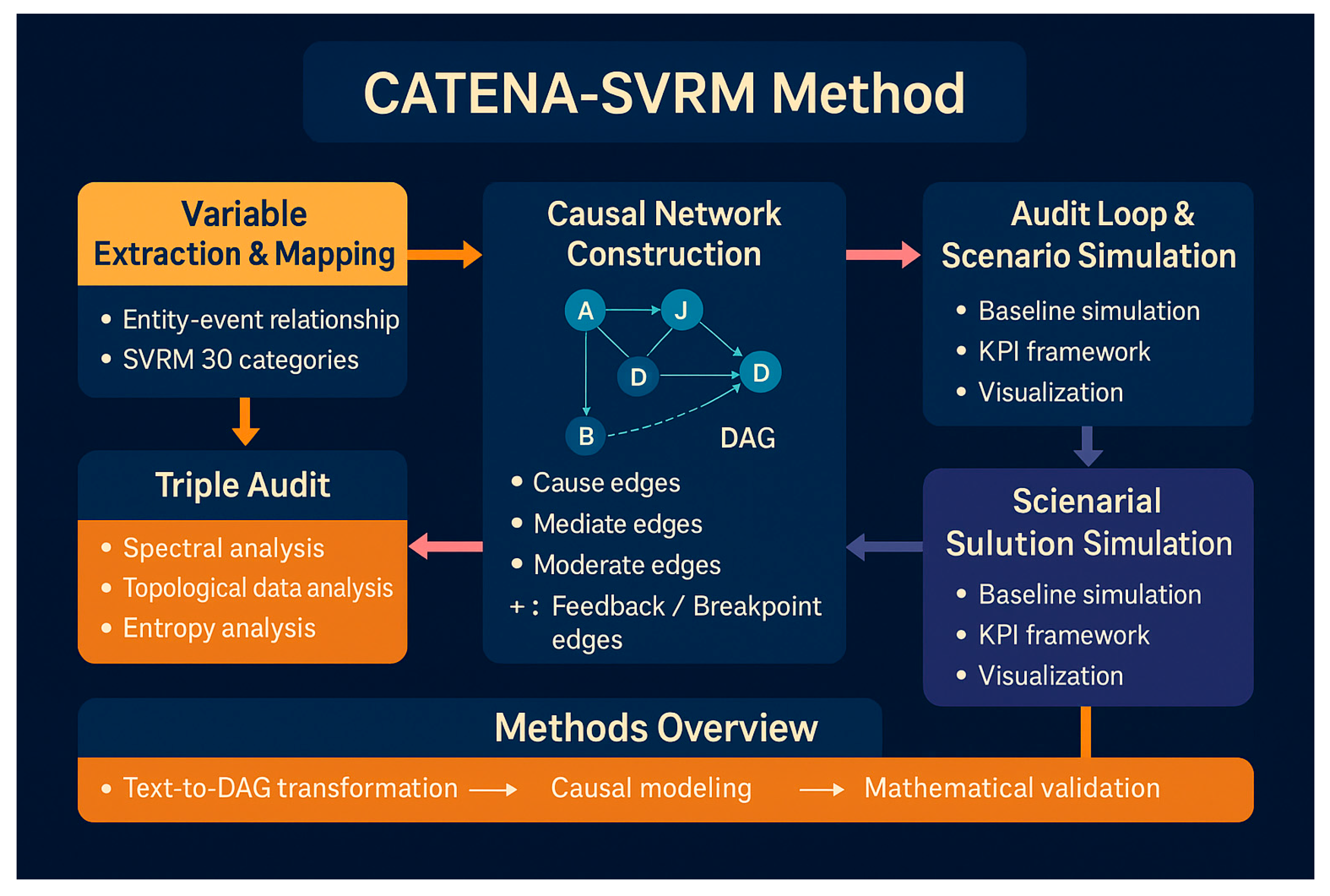
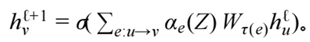Appendix 2:
NIST Simulation Data Code:
# -*- coding: utf-8 -*-
import argparse, json, time, hashlib, os
import numpy as np
import pandas as pd
import networkx as nx
from sklearn.feature_selection import mutual_info_regression
"""
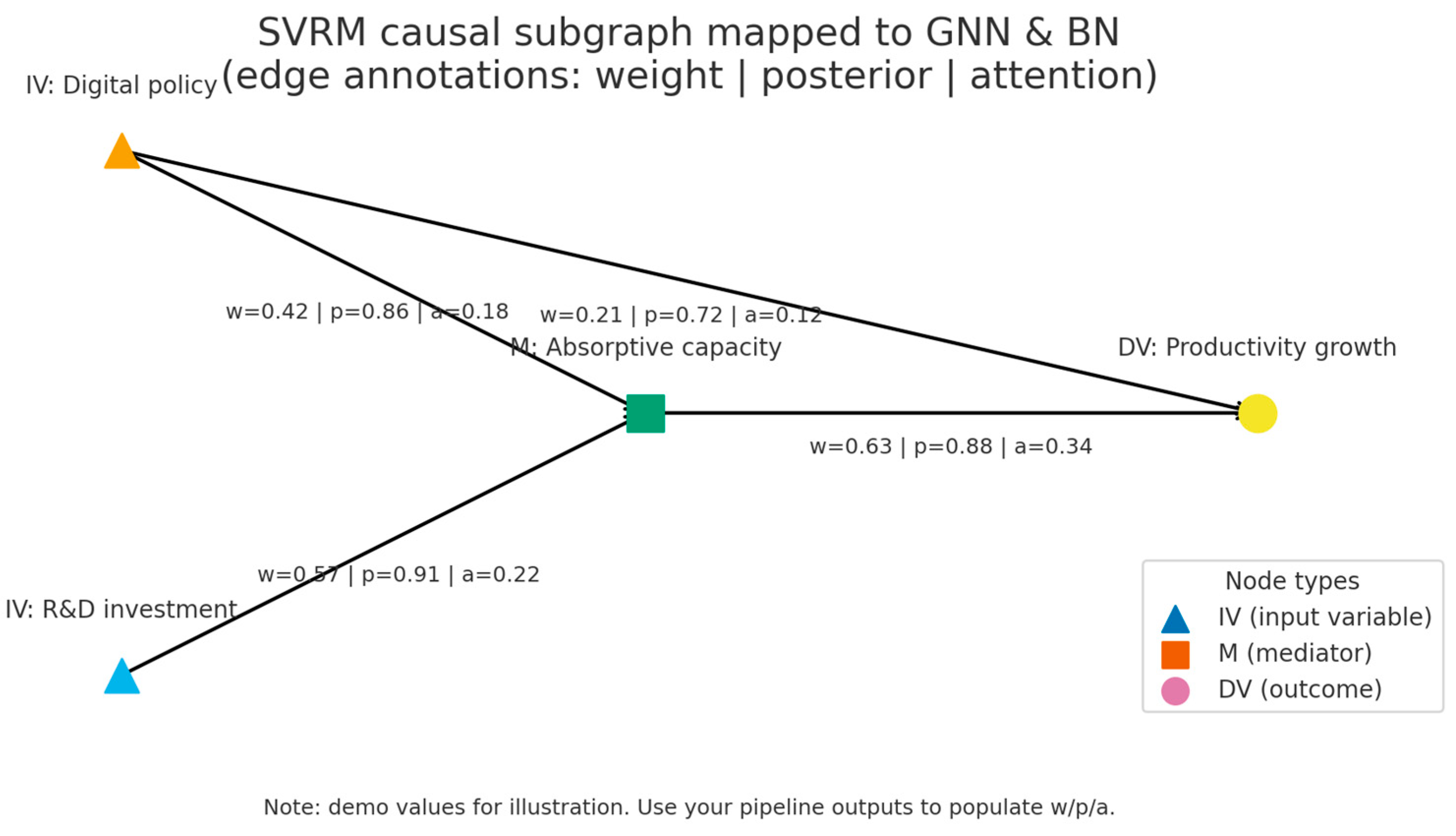
NIST-style CATENA–SVRM synthetic generator
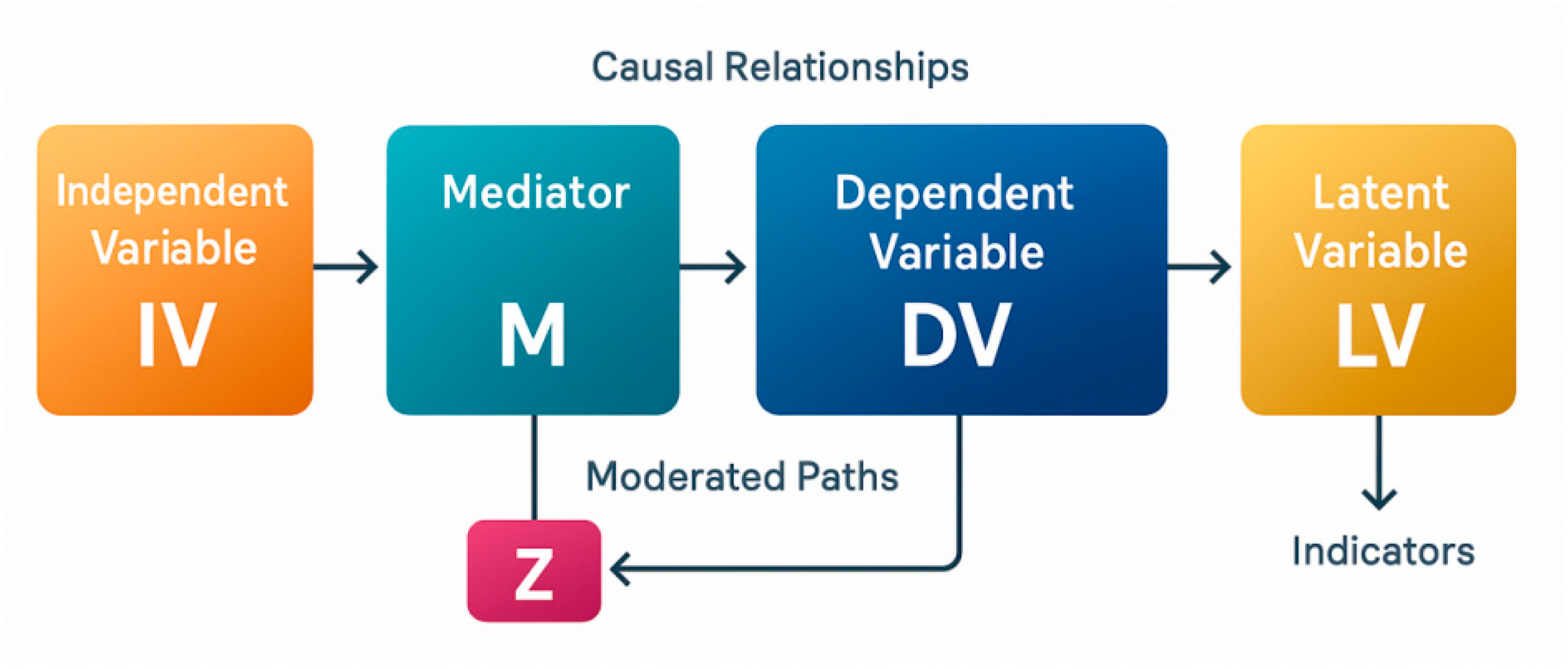
- DAG with typed edges: Cause/Mediate/Moderate/Feedback/Threshold
- Mediation (IV->M->DV), Moderation (Z on IV->DV), Breakpoint variable (BPV) with threshold τ
- Latent LV -> indicators (IND1, IND2)
- Weak feedback DV_{t-1} -> M_t
- Filtration snapshots for TDA; Laplacian for spectral audit
- Reproducible seed; provenance and ground truth JSON
Outputs:
out/
data.csv
nodes.csv
edges.csv
ground_truth.json
provenance.json
readme.md
"""
def sigmoid(x): return 1 / (1 + np.exp(-x))
def make_dirs(p):
if not os.path.exists(p): os.makedirs(p)
def sha1(s: str) -> str:
return hashlib.sha1(s.encode("utf-8")).hexdigest()
def generate(params):
rng = np.random.default_rng(params["seed"])
# ----- Nodes (SVRM roles) -----
nodes = [
{"id":"IV", "role":"IV", "exo_endo":"EXO"},
{"id":"M", "role":"M", "exo_endo":"ENDO"},
{"id":"Z", "role":"Z", "exo_endo":"EXO"},
{"id":"CV", "role":"CV", "exo_endo":"EXO"},
{"id":"BPV", "role":"TV", "exo_endo":"EXO"}, # Threshold/Breakpoint variable
{"id":"LV", "role":"LV", "exo_endo":"ENDO"},
{"id":"IND1", "role":"INDV","exo_endo":"ENDO"},
{"id":"IND2", "role":"INDV","exo_endo":"ENDO"},
{"id":"DV", "role":"DV", "exo_endo":"ENDO"},
]
# ----- True coefficients & threshold -----
# Base
a0, a1, a2, a3 = 0.2, 0.8, 0.4, 0.15 # M ~ a0 + a1*IV + a2*CV + a3*DV_{t-1}
b0, b1, b2, b3 = 0.1, 0.9, 0.15, 0.6 # DV ~ b0 + b1*M + b2*IV + b3*(IV*Z)*gate
tau, b1_low, b1_high = 0.5, 0.35, 0.9 # Threshold on BPV: slope for M->DV switches
gate_k = 6.0 # sharpness for moderation gate
lv_var, ind_noise = 1.0, 0.05
# Edge weights for filtration snapshots (0~1)
edge_w = {
("IV","M"): 0.9, # cause
("CV","M"): 0.6, # cause
("DV","M"): 0.2, # feedback (t-1 -> t, tracked separately in time)
("M","DV"): 0.95, # mediate / thresholded slope
("IV","DV"): 0.3, # direct
("Z","IV"): 0.7, # moderate via gate on IV->DV
("BPV","DV"): 0.5, # threshold controller
("LV","IND1"): 0.8, # measurement
("LV","IND2"): 0.8 # measurement
}
# ----- Edge typing -----
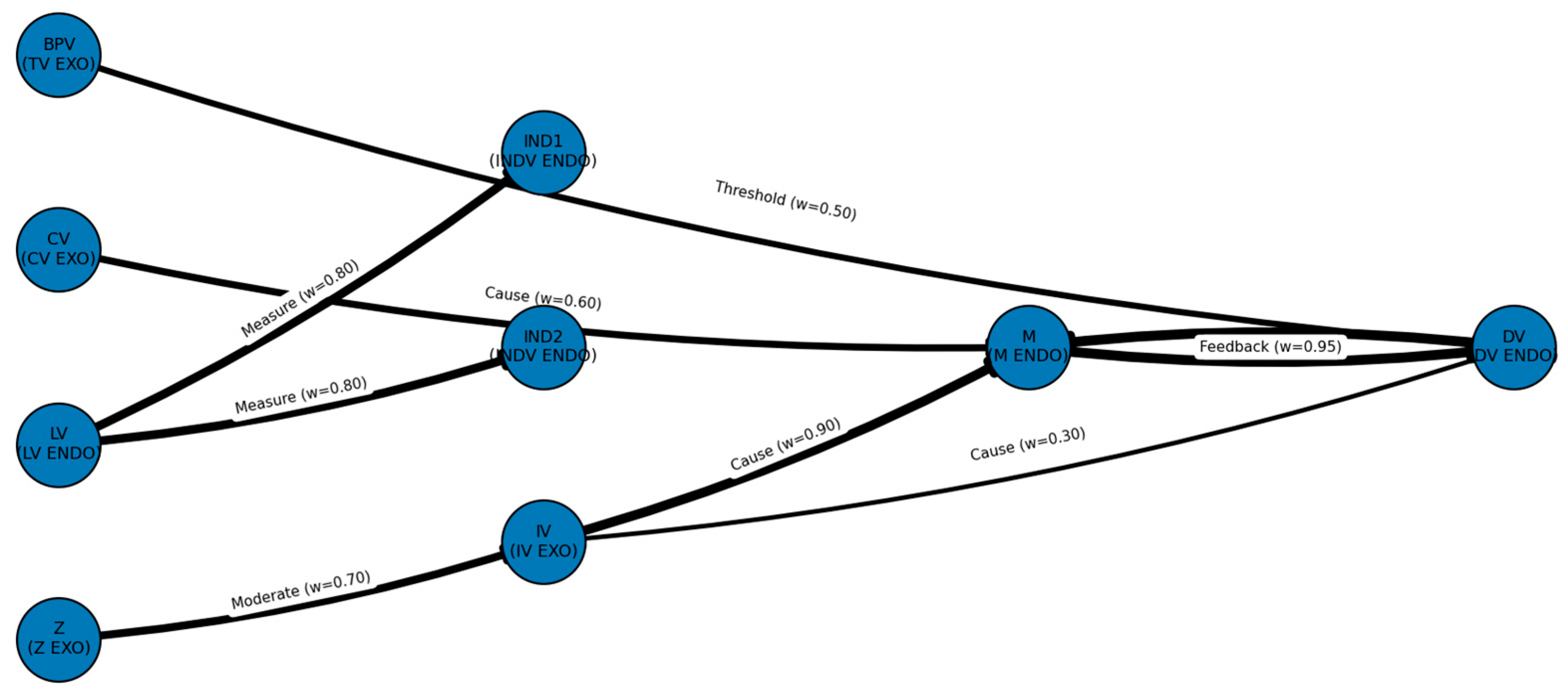
edges = [
{"src":"IV","dst":"M","type":"Cause"},
{"src":"CV","dst":"M","type":"Cause"},
{"src":"DV","dst":"M","type":"Feedback"}, # implemented as lag
{"src":"M","dst":"DV","type":"Mediate"},
{"src":"IV","dst":"DV","type":"Cause"},
{"src":"Z","dst":"IV","type":"Moderate"}, # acts on IV->DV edge via gate
{"src":"BPV","dst":"DV","type":"Threshold"},
{"src":"LV","dst":"IND1","type":"Measure"},
{"src":"LV","dst":"IND2","type":"Measure"},
]
N, T = params["N"], params["T"]
# ----- Generate exogenous series -----
IV = rng.normal(0.0, 1.0, (N,T))
Z = rng.uniform(0.0, 1.0, (N,T)) # moderation strength 0~1
CVv = rng.normal(0.0, 1.0, (N,T))
BPV = rng.uniform(0.0, 1.0, (N,T)) # threshold controller
# Latent + indicators
LV = rng.normal(0.0, np.sqrt(lv_var), (N,T))
IND1 = LV + rng.normal(0.0, ind_noise, (N,T))
IND2 = 0.7*LV + rng.normal(0.0, ind_noise, (N,T))
M = np.zeros((N,T))
DV = np.zeros((N,T))
# ----- Time recursion with feedback DV_{t-1} -> M_t -----
for t in range(T):
dv_lag = DV[:,t-1] if t>0 else 0.0
# Mediation equation
eps_m = rng.normal(0.0, 0.2, N)
M[:,t] = a0 + a1*IV[:,t] + a2*CVv[:,t] + a3*dv_lag + eps_m
# Thresholded slope on M->DV (BPV)
slope_m = np.where(BPV[:,t] < tau, b1_low, b1_high)
# Moderation gate from Z on IV->DV
gate = sigmoid(gate_k*(Z[:,t]-0.5)) # ~0 when Z<.5, ~1 when Z>.5
eps_d = rng.normal(0.0, 0.25, N)
DV[:,t] = b0 + slope_m*M[:,t] + b2*IV[:,t] + b3*(IV[:,t]*gate) + eps_d
# ----- Pack dataframe -----
cols = []
for var in ["IV","M","Z","CV","BPV","LV","IND1","IND2","DV"]:
for t in range(T):
cols.append(f"{var}_t{t+1}")
data = np.column_stack([IV, M, Z, CVv, BPV, LV, IND1, IND2, DV]) # careful order
# Reorder to match cols list:
# We built cols in var-major; build data in same var-major order:
def stack_var(X):
return np.column_stack([X[:,t] for t in range(T)])
data = np.column_stack([
stack_var(IV), stack_var(M), stack_var(Z), stack_var(CVv),
stack_var(BPV), stack_var(LV), stack_var(IND1), stack_var(IND2),
stack_var(DV)
])
df = pd.DataFrame(data, columns=cols)
# ----- Mutual information quick check (entropy audit preview on last period) -----
# (Fast proxy; for serious audit use dedicated pipeline)
last = T-1
X = np.column_stack([IV[:,last], M[:,last], Z[:,last], CVv[:,last], BPV[:,last]])
y = DV[:,last]
mi = mutual_info_regression(X, y, random_state=params["seed"])
mi_names = ["IV","M","Z","CV","BPV"]
mi_dict = {k: float(v) for k,v in zip(mi_names, mi)}
# ----- Build graphs for spectral / filtration -----
G = nx.DiGraph()
for n in nodes: G.add_node(n["id"], **n)
for e in edges:
w = edge_w.get((e["src"], e["dst"]), 0.3)
G.add_edge(e["src"], e["dst"], type=e["type"], weight=w)
# Undirected for Laplacian spectrum (connectivity proxy)
UG = G.to_undirected()
for (u,v) in UG.edges():
UG[u][v]['weight'] = max(G.get_edge_data(u,v,default={"weight":0}).get("weight",0),
G.get_edge_data(v,u,default={"weight":0}).get("weight",0))
L = nx.laplacian_matrix(UG, weight='weight').astype(float).toarray()
evals, evecs = np.linalg.eigh(L)
fiedler_val = float(sorted(evals)[1]) if len(evals)>1 else 0.0
# Normalize Fiedler vector length if available
fiedler_vec = None
if evecs.shape[1] >= 2:
idx = np.argsort(evals)[1]
f = evecs[:,idx]
fiedler_vec = {n: float(f[i]) for i,n in enumerate(UG.nodes())}
# Filtration snapshots (for TDA): keep edges with weight >= λ
lambdas = np.linspace(0.0, 1.0, 6) # 0.0,0.2,...,1.0
filtration = []
for lam in lambdas:
kept = [(u,v) for (u,v,d) in G.edges(data=True) if d.get("weight",0)>=lam]
filtration.append({
"lambda": float(lam),
"edges": kept
})
# ----- Ground truth & provenance -----
gt = {
"dag_nodes": nodes,
"dag_edges": edges,
"edge_weights": {f"{u}->{v}": float(UG[u][v]['weight']) for (u,v) in UG.edges()},
"equations": {
"M_t": f"M = {a0} + {a1}*IV + {a2}*CV + {a3}*DV_lag + eps_m",
"DV_t": f"DV = {b0} + slope(BPV,t)*M + {b2}*IV + {b3}*(IV*sigmoid({gate_k}*(Z-0.5))) + eps_d",
"slope(BPV,t)": f"{b1_low} if BPV< {tau} else {b1_high}"
},
"threshold": {"variable":"BPV","tau": float(tau),
"slope_low": float(b1_low), "slope_high": float(b1_high)},
"feedback": {"edge":"DV_{t-1}->M_t","coef": float(a3)},
"latent": {"LV_var": float(lv_var), "ind_noise": float(ind_noise)},
"spectral": {"laplacian_eigs": [float(x) for x in evals.tolist()],
"fiedler_value": fiedler_val, "fiedler_vector": fiedler_vec},
"filtration": filtration,
"entropy_quick_MI(last_period)": mi_dict
}
prov = {
"generator": "CATENA-SVRM NIST-style synthetic v1.0",
"timestamp": int(time.time()),
"seed": params["seed"],
"N": N, "T": T,
"hash": sha1(json.dumps(gt)[:2048]) # short fingerprint
}
return df, nodes, edges, gt, prov
def main():
ap = argparse.ArgumentParser()
ap.add_argument("--seed", type=int, default=42)
ap.add_argument("--n", type=int, default=300, help="number of samples")
ap.add_argument("--t", type=int, default=12, help="time steps")
ap.add_argument("--out", type=str, default="./out")
args = ap.parse_args()
params = {"seed": args.seed, "N": args.n, "T": args.t}
make_dirs(args.out)
df, nodes, edges, gt, prov = generate(params)
# Save tables
df.to_csv(os.path.join(args.out, "data.csv"), index=False)
pd.DataFrame(nodes).to_csv(os.path.join(args.out,"nodes.csv"), index=False)
pd.DataFrame(edges).to_csv(os.path.join(args.out,"edges.csv"), index=False)
with open(os.path.join(args.out,"ground_truth.json"),"w",encoding="utf-8") as f:
json.dump(gt,f,ensure_ascii=False,indent=2)
with open(os.path.join(args.out,"provenance.json"),"w",encoding="utf-8") as f:
json.dump(prov,f,ensure_ascii=False,indent=2)
# README
readme = f"""# CATENA–SVRM NIST-style Synthetic Set
## Files
- data.csv: N={params['N']}, T={params['T']} panel (columns: VAR_tk)
- nodes.csv: SVRM roles (IV/DV/M/Z/CV/LV/INDV/TV)
- edges.csv: typed edges (Cause/Mediate/Moderate/Feedback/Threshold)
- ground_truth.json: DAG, equations, threshold tau, filtration snapshots, spectral info
- provenance.json: seed, timestamp, fingerprint
## Schema (examples)
- IV_t1..tT, M_t1..tT, Z_t1..tT, CV_t1..tT, BPV_t1..tT, LV_t1..tT, IND1_t1..tT, IND2_t1..tT, DV_t1..tT
## Repro
python gen_nist_dataset.py --seed {params['seed']} --n {params['N']} --t {params['T']} --out ./out
## Notes
- Mediation: IV -> M -> DV
- Moderation: Z gates IV->DV via sigmoid
- Threshold: BPV < tau => slope(M->DV)=low; else high
- Feedback: DV_(t-1) -> M_t (weak)
- Filtration: edge weight lambda thresholds for TDA
- Spectral: Laplacian eigenvalues & Fiedler vector for robustness audit
"""
with open(os.path.join(args.out,"readme.md"),"w",encoding="utf-8") as f:
f.write(readme)
print(f"[OK] Synthetic dataset written to: {args.out}")
if __name__ == "__main__":
main()
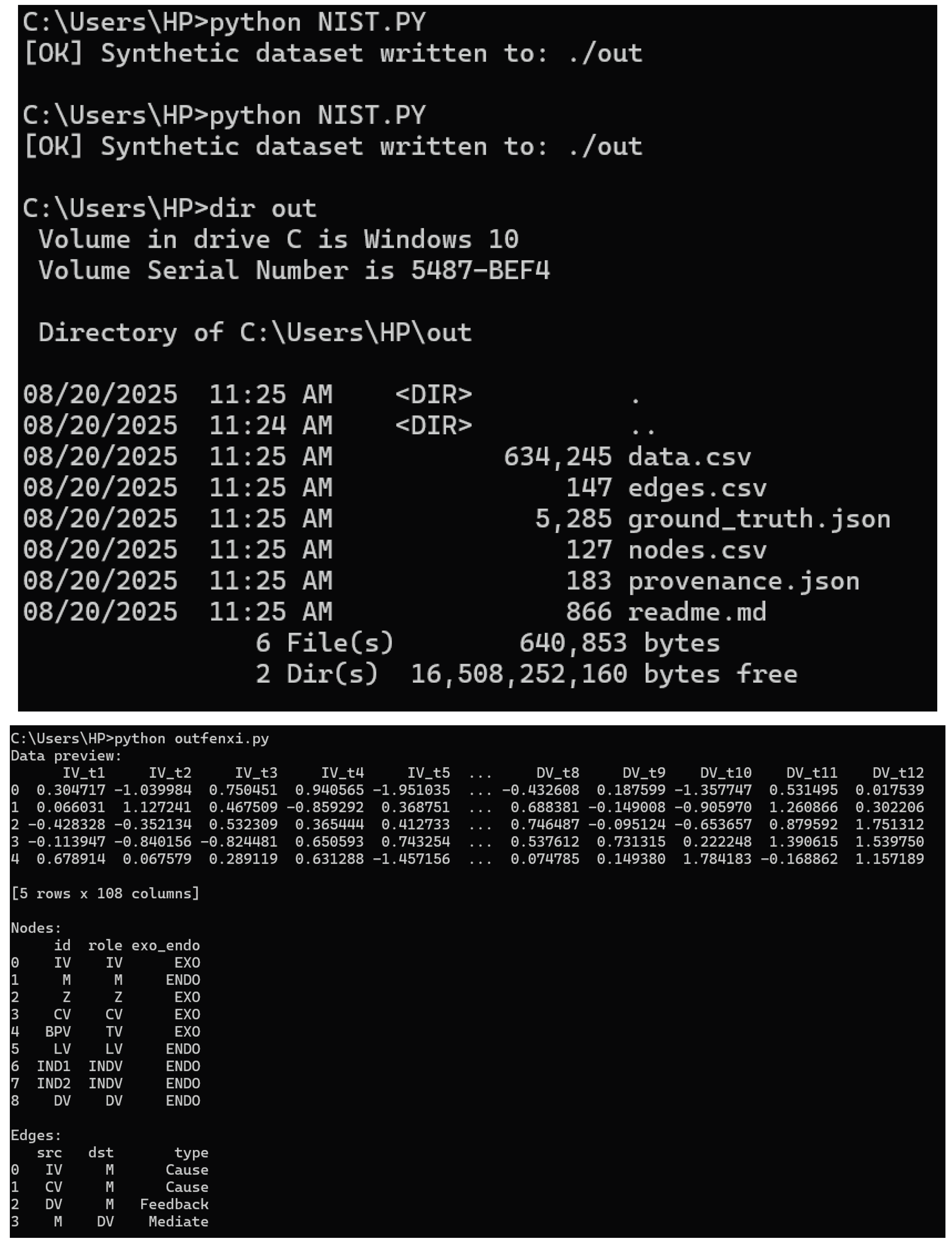
Code Run Result
C:\Users\HP>python NIST.PY
[OK] Synthetic dataset written to: ./out
NIST.py A synthetic dataset has been successfully run and generated
View the results of the code run
C:\Users\HP>dir out
Volume in drive C is Windows 10
Volume Serial Number is 5487-BEF4
Directory of C:\Users\HP\out
08/20/2025 11:25 AM <DIR> .
08/20/2025 11:24 AM <DIR> ..
08/20/2025 11:25 AM 634,245 data.csv
08/20/2025 11:25 AM 147 edges.csv
08/20/2025 11:25 AM 5,285 ground_truth.json
08/20/2025 11:25 AM 127 nodes.csv
08/20/2025 11:25 AM 183 provenance.json
08/20/2025 11:25 AM 866 readme.md
6 File(s) 640,853 bytes
2 Dir(s) 16,508,252,160 bytes free
test code
Python outfenxi.py
import pandas as pd
import json
# 读取主数据
df = pd.read_csv("./out/data.csv")
print("Data preview:")
print(df.head())
# 读取节点信息
nodes = pd.read_csv("./out/nodes.csv")
print("\nNodes:")
print(nodes)
# 读取边信息
edges = pd.read_csv("./out/edges.csv")
print("\nEdges:")
print(edges)
# 读取真值 DAG
with open("./out/ground_truth.json", "r") as f:
dag = json.load(f)
print("\nGround truth DAG:")
print(dag)
# 读取 provenance 信息
with open("./out/provenance.json", "r") as f:
provenance = json.load(f)
print("\nProvenance metadata:")
print(provenance)
running result
C:\Users\HP>python outfenxi.py
Data preview:
IV_t1 IV_t2 IV_t3 IV_t4 IV_t5 ... DV_t8 DV_t9 DV_t10 DV_t11 DV_t12
0 0.304717 -1.039984 0.750451 0.940565 -1.951035 ... -0.432608 0.187599 -1.357747 0.531495 0.017539
1 0.066031 1.127241 0.467509 -0.859292 0.368751 ... 0.688381 -0.149008 -0.905970 1.260866 0.302206
2 -0.428328 -0.352134 0.532309 0.365444 0.412733 ... 0.746487 -0.095124 -0.653657 0.879592 1.751312
3 -0.113947 -0.840156 -0.824481 0.650593 0.743254 ... 0.537612 0.731315 0.222248 1.390615 1.539750
4 0.678914 0.067579 0.289119 0.631288 -1.457156 ... 0.074785 0.149380 1.784183 -0.168862 1.157189
[5 rows x 108 columns]
Nodes:
id role exo_endo
0 IV IV EXO
1 M M ENDO
2 Z Z EXO
3 CV CV EXO
4 BPV TV EXO
5 LV LV ENDO
6 IND1 INDV ENDO
7 IND2 INDV ENDO
8 DV DV ENDO
Edges:
src dst type
0 IV M Cause
1 CV M Cause
2 DV M Feedback
3 M DV Mediate
4 IV DV Cause
5 Z IV Moderate
6 BPV DV Threshold
7 LV IND1 Measure
8 LV IND2 Measure
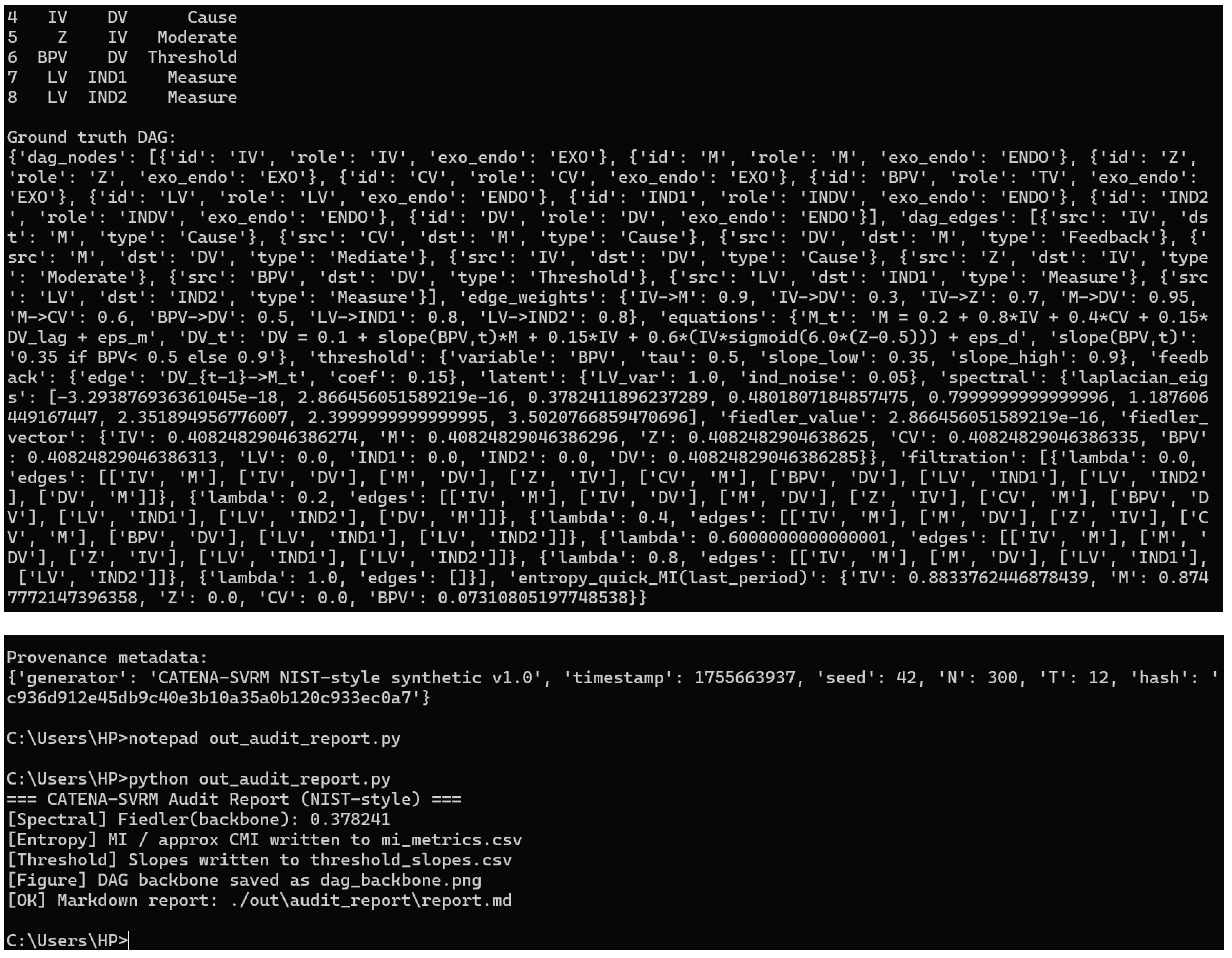
Ground truth DAG:
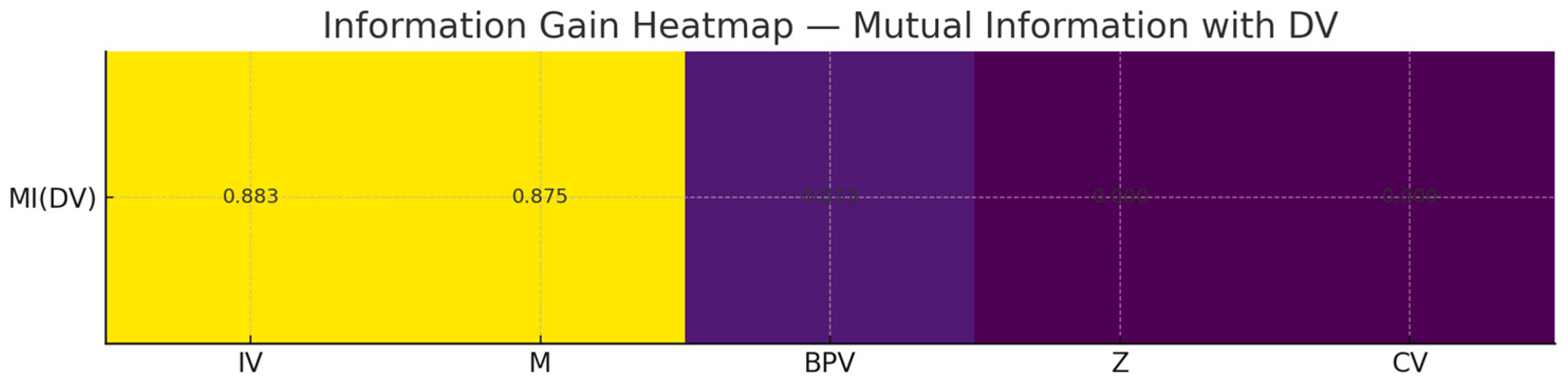
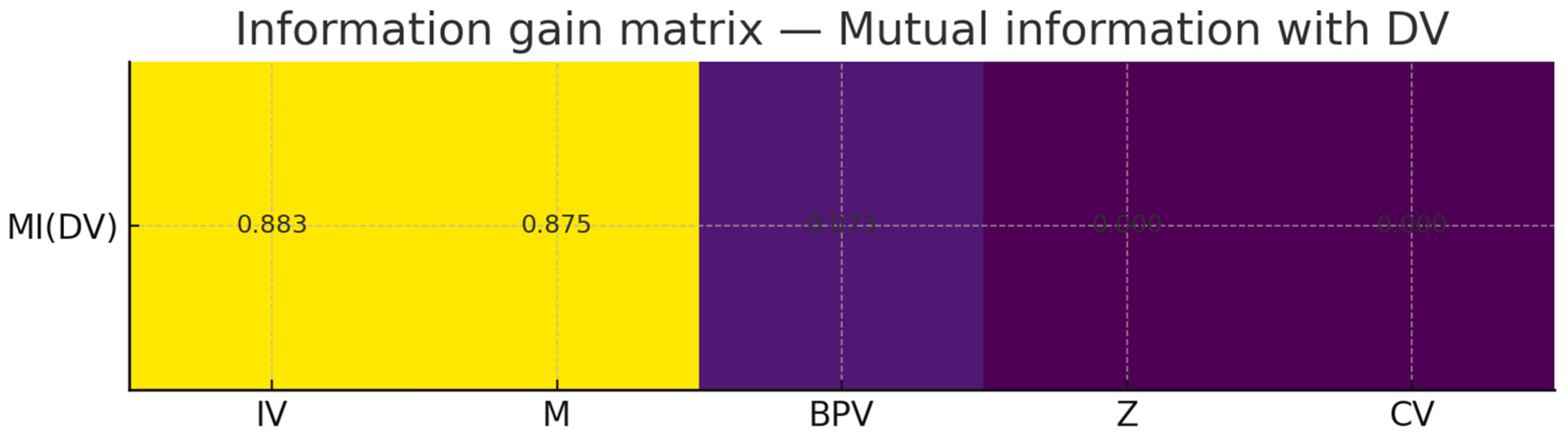
{'dag_nodes': [{'id': 'IV', 'role': 'IV', 'exo_endo': 'EXO'}, {'id': 'M', 'role': 'M', 'exo_endo': 'ENDO'}, {'id': 'Z', 'role': 'Z', 'exo_endo': 'EXO'}, {'id': 'CV', 'role': 'CV', 'exo_endo': 'EXO'}, {'id': 'BPV', 'role': 'TV', 'exo_endo': 'EXO'}, {'id': 'LV', 'role': 'LV', 'exo_endo': 'ENDO'}, {'id': 'IND1', 'role': 'INDV', 'exo_endo': 'ENDO'}, {'id': 'IND2', 'role': 'INDV', 'exo_endo': 'ENDO'}, {'id': 'DV', 'role': 'DV', 'exo_endo': 'ENDO'}], 'dag_edges': [{'src': 'IV', 'dst': 'M', 'type': 'Cause'}, {'src': 'CV', 'dst': 'M', 'type': 'Cause'}, {'src': 'DV', 'dst': 'M', 'type': 'Feedback'}, {'src': 'M', 'dst': 'DV', 'type': 'Mediate'}, {'src': 'IV', 'dst': 'DV', 'type': 'Cause'}, {'src': 'Z', 'dst': 'IV', 'type': 'Moderate'}, {'src': 'BPV', 'dst': 'DV', 'type': 'Threshold'}, {'src': 'LV', 'dst': 'IND1', 'type': 'Measure'}, {'src': 'LV', 'dst': 'IND2', 'type': 'Measure'}], 'edge_weights': {'IV->M': 0.9, 'IV->DV': 0.3, 'IV->Z': 0.7, 'M->DV': 0.95, 'M->CV': 0.6, 'BPV->DV': 0.5, 'LV->IND1': 0.8, 'LV->IND2': 0.8}, 'equations': {'M_t': 'M = 0.2 + 0.8*IV + 0.4*CV + 0.15*DV_lag + eps_m', 'DV_t': 'DV = 0.1 + slope(BPV,t)*M + 0.15*IV + 0.6*(IV*sigmoid(6.0*(Z-0.5))) + eps_d', 'slope(BPV,t)': '0.35 if BPV< 0.5 else 0.9'}, 'threshold': {'variable': 'BPV', 'tau': 0.5, 'slope_low': 0.35, 'slope_high': 0.9}, 'feedback': {'edge': 'DV_{t-1}->M_t', 'coef': 0.15}, 'latent': {'LV_var': 1.0, 'ind_noise': 0.05}, 'spectral': {'laplacian_eigs': [-3.293876936361045e-18, 2.866456051589219e-16, 0.3782411896237289, 0.4801807184857475, 0.7999999999999996, 1.187606449167447, 2.351894956776007, 2.3999999999999995, 3.5020766859470696], 'fiedler_value': 2.866456051589219e-16, 'fiedler_vector': {'IV': 0.40824829046386274, 'M': 0.40824829046386296, 'Z': 0.4082482904638625, 'CV': 0.40824829046386335, 'BPV': 0.40824829046386313, 'LV': 0.0, 'IND1': 0.0, 'IND2': 0.0, 'DV': 0.40824829046386285}}, 'filtration': [{'lambda': 0.0, 'edges': [['IV', 'M'], ['IV', 'DV'], ['M', 'DV'], ['Z', 'IV'], ['CV', 'M'], ['BPV', 'DV'], ['LV', 'IND1'], ['LV', 'IND2'], ['DV', 'M']]}, {'lambda': 0.2, 'edges': [['IV', 'M'], ['IV', 'DV'], ['M', 'DV'], ['Z', 'IV'], ['CV', 'M'], ['BPV', 'DV'], ['LV', 'IND1'], ['LV', 'IND2'], ['DV', 'M']]}, {'lambda': 0.4, 'edges': [['IV', 'M'], ['M', 'DV'], ['Z', 'IV'], ['CV', 'M'], ['BPV', 'DV'], ['LV', 'IND1'], ['LV', 'IND2']]}, {'lambda': 0.6000000000000001, 'edges': [['IV', 'M'], ['M', 'DV'], ['Z', 'IV'], ['LV', 'IND1'], ['LV', 'IND2']]}, {'lambda': 0.8, 'edges': [['IV', 'M'], ['M', 'DV'], ['LV', 'IND1'], ['LV', 'IND2']]}, {'lambda': 1.0, 'edges': []}], 'entropy_quick_MI(last_period)': {'IV': 0.8833762446878439, 'M': 0.8747772147396358, 'Z': 0.0, 'CV': 0.0, 'BPV': 0.07310805197748538}}
Provenance metadata:
{'generator': 'CATENA-SVRM NIST-style synthetic v1.0', 'timestamp': 1755663937, 'seed': 42, 'N': 300, 'T': 12, 'hash': 'c936d912e45db9c40e3b10a35a0b120c933ec0a7'}
Quick check-ups: instructions for reading and locating small defects
文件集 OK:data.csv / nodes.csv / edges.csv / ground_truth.json / provenance.json / readme.md 全在,满足 NIST-style 的“真值 + 溯源”打包。
互信息(熵度量)
你看到 MI(last_period):IV≈0.883, M≈0.875, Z≈0.0, CV≈0.0, BPV≈0.073。
解释:
Z 在生成式里是门控(sigmoid(6*(Z-0.5)))调节 IV→DV,不是“直接输入”。用单变量 MI(DV;Z) 很可能低(甚至接近 0)。正确做法是看 条件互信息 I(DV; Z | IV) 或把交互项作为特征:IV*sigmoid(...)。
CV 主要影响 M,对 DV 的直接 MI 也可能偏低,建议看 I(M; CV) 或 I(DV; CV | M, IV)。
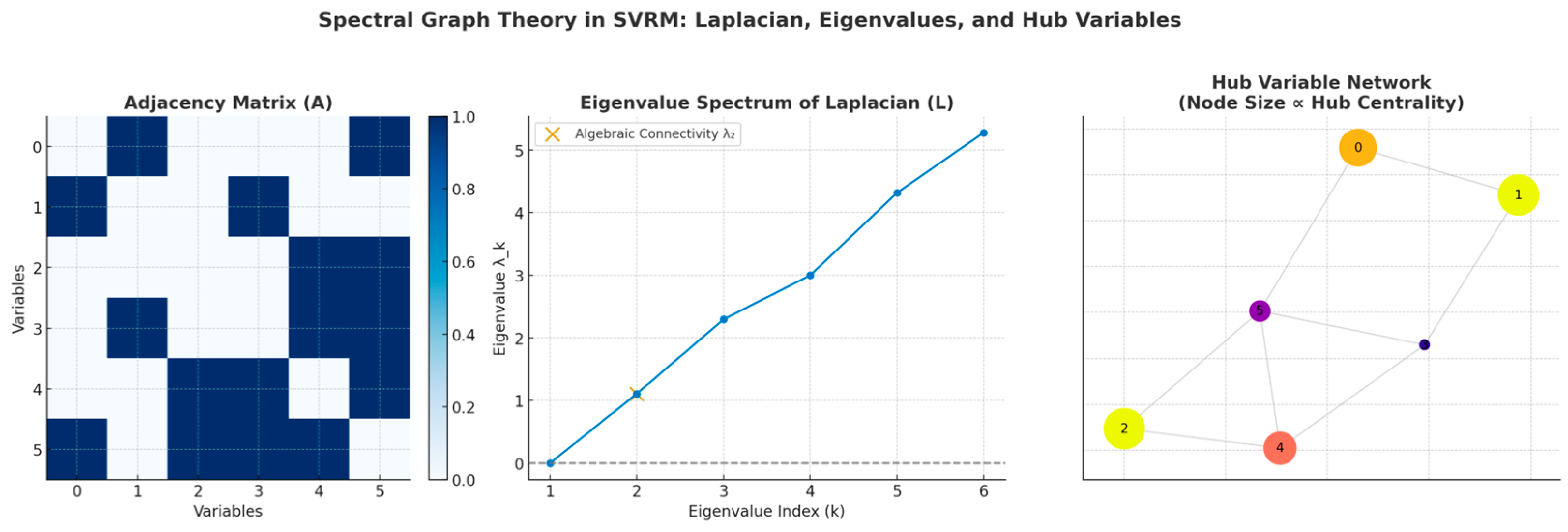
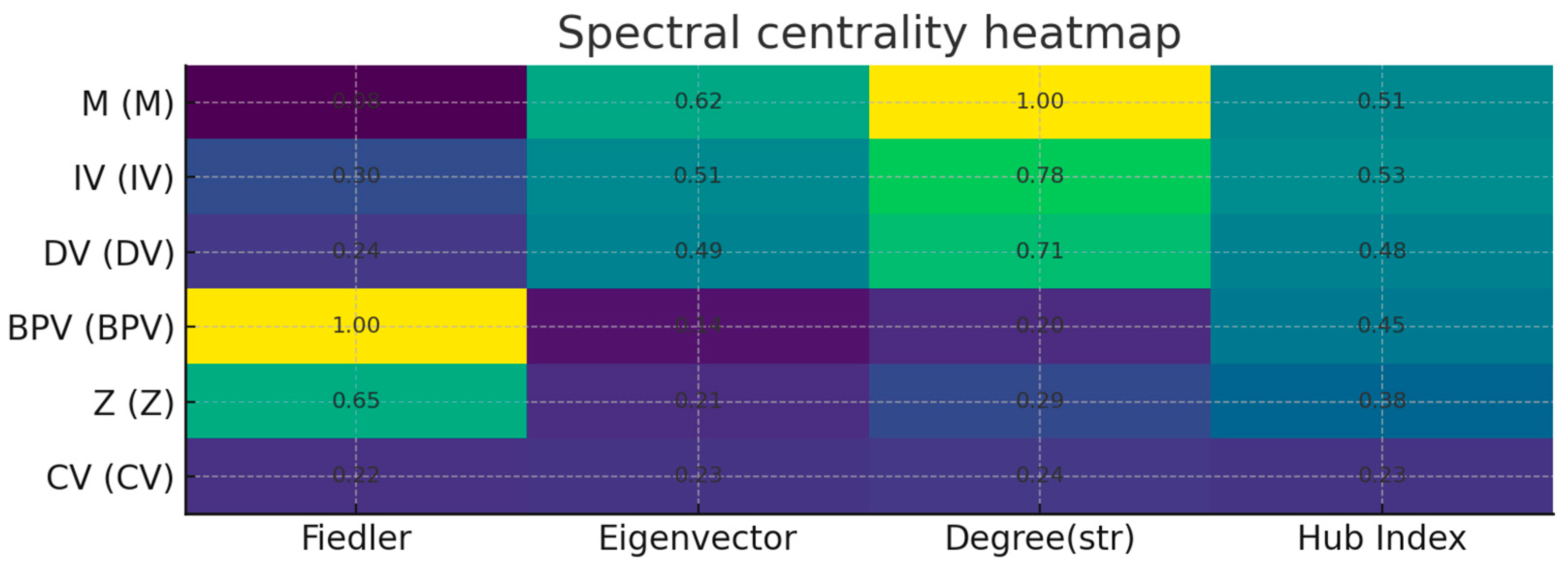
谱审计(Laplacian/Fiedler)
你看到的第二特征值(Fiedler 值)≈ 2.86e-16,几乎 0,表示无向骨架至少有 2 个连通分量。原因:LV–IND1/IND2 构成了一个测量子岛,与主干(IV–M–DV–…)弱连接或不连接。这在工程上没问题,但:
做政策/因果骨架的谱稳健性时,建议对主干诱导子图({IV, M, Z, CV, BPV, DV})单独计算谱指标,避免测量子岛“拉低”连通性读数。
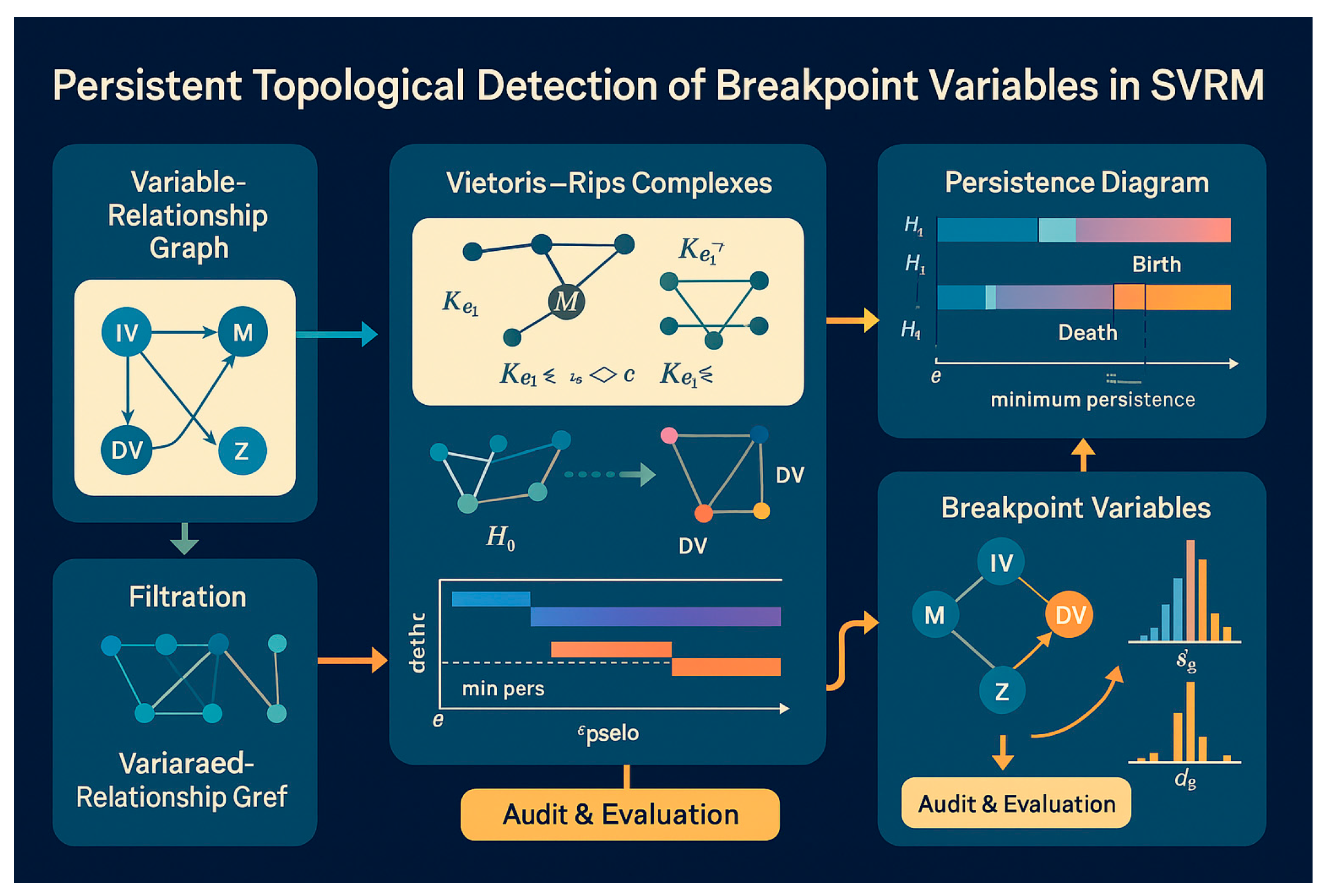
滤过(TDA)
你的滤过序列里,IV→M、M→DV 这些核心边在 λ=0.8 还保留,说明持久度高(拓扑上的“稳连接”);BPV→DV 在 λ≥0.6 不见,呈中等持久度。要让 TDA 在条形码里出现更明显“台阶跃迁”,可以把 BPV→DV 设为更低权或加两段权重差距更大的阈值/区间(见第 3 节“参数拨盘”)。
edge_weights 键名看起来“方向反了”
edge_weights 是基于无向图(用于谱分析)导出的最大权重,键被打印成 u->v 的字符串,不代表方向(例如你看到 IV->Z,而真值是 Z->IV(Moderate))。不用担心——有向真值看 dag_edges,谱本来就看无向连通性。
小结(审计说明)
熵:别用 I(DV;Z) 单看;要看 I(DV;Z|IV) 或把 IV*gate(Z)显式化。
谱:做主干子图的谱稳健性;测量子岛用于测量模型,不进政策稳健性口径。
TDA:滤过条形码与“分段斜率”是一体两面;两段斜率差越大、BPV 权重越低,条形码“台阶”越清晰。
One-Click Compliance Codes
out_audit_report.py
# out_audit_report.py
# -*- coding: utf-8 -*-
import os, json, argparse, math
import numpy as np
import pandas as pd
import networkx as nx
from numpy.linalg import eigh
from sklearn.feature_selection import mutual_info_regression
from sklearn.preprocessing import StandardScaler
# 可选:阈值分段回归(带显著性)
try:
import statsmodels.api as sm
HAS_SM = True
except Exception:
HAS_SM = False
# 可选:DAG 简易可视化
HAS_MPL = False
try:
import matplotlib.pyplot as plt
HAS_MPL = True
except Exception:
HAS_MPL = False
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))
def load_ground_truth(gt_path):
with open(gt_path, "r", encoding="utf-8") as f:
gt = json.load(f)
return gt
def ensure_dir(p):
if not os.path.exists(p):
os.makedirs(p)
def get_last_period(df, prefix="IV_"):
T = 1
for c in df.columns:
if c.startswith(prefix):
try:
t = int(c.split("_t")[-1])
T = max(T, t)
except Exception:
pass
return T
def get_edge_weight_undirected(gt, u, v, default=0.5):
ew = gt.get("edge_weights", {})
# edge_weights 中键是 "U->V" 字符串(谱用的无向权取双向最大)
w1 = ew.get(f"{u}->{v}", None)
w2 = ew.get(f"{v}->{u}", None)
if w1 is None and w2 is None:
return default
if w1 is None:
return float(w2)
if w2 is None:
return float(w1)
return float(max(w1, w2))
def build_backbone_graph(gt, backbone_nodes):
Gd = nx.DiGraph()
for e in gt["dag_edges"]:
s, t = e["src"], e["dst"]
if s in backbone_nodes and t in backbone_nodes:
w = get_edge_weight_undirected(gt, s, t, default=0.5)
Gd.add_edge(s, t, weight=w, etype=e.get("type", "Cause"))
# 转无向用于谱分析
UG = Gd.to_undirected()
for u, v in UG.edges():
UG[u][v]["weight"] = get_edge_weight_undirected(gt, u, v, default=0.5)
return Gd, UG
def spectral_backbone(UG):
if UG.number_of_nodes() == 0:
return {"laplacian_eigs": [], "fiedler_value": 0.0}
L = nx.laplacian_matrix(UG, weight="weight").astype(float).toarray()
evals, evecs = eigh(L)
fiedler = float(sorted(evals)[1]) if len(evals) > 1 else 0.0
return {
"laplacian_eigs": [float(x) for x in evals.tolist()],
"fiedler_value": fiedler
}
def entropy_block(df, gt, last, gate_k_default=6.0):
# 读取参数 gate_k(若 equations 中可解析,则覆盖默认)
gate_k = gate_k_default
try:
eq = gt.get("equations", {}).get("DV_t", "")
# 期望形如 sigmoid(6.0*(Z-0.5))
if "sigmoid(" in eq:
seg = eq.split("sigmoid(")[1].split(")")[0]
k_str = seg.split("*")[0].strip()
gate_k = float(k_str)
except Exception:
pass
# 取最后一期变量
IV = df[f"IV_t{last}"].values
M = df[f"M_t{last}"].values
Z = df[f"Z_t{last}"].values
DV = df[f"DV_t{last}"].values
BPV = df[f"BPV_t{last}"].values
# 简单门控
gate = sigmoid(gate_k * (Z - 0.5))
# 显式交互项
X_mi = np.c_[IV, M, Z, BPV, IV*gate]
names = ["IV", "M", "Z", "BPV", "IV*gate(Z)"]
# 标准化后计算 MI(更稳定)
sc = StandardScaler()
Xn = sc.fit_transform(X_mi)
mi = mutual_info_regression(Xn, DV, random_state=42)
# 近似条件互信息:CMI(DV;Z|IV) ≈ MI(DV;[IV,Z]) - MI(DV;IV)
X_ivz = sc.fit_transform(np.c_[IV, Z])
mi_ivz = mutual_info_regression(X_ivz, DV, random_state=42).sum()
X_iv = sc.fit_transform(IV.reshape(-1,1))
mi_iv = mutual_info_regression(X_iv, DV, random_state=42).sum()
cmi_z_given_iv = float(mi_ivz - mi_iv)
mi_dict = {n: float(v) for n, v in zip(names, mi)}
mi_dict["approx_CMI(DV;Z|IV)"] = cmi_z_given_iv
mi_df = pd.DataFrame([mi_dict])
return mi_df
def threshold_block(df, last, tau=0.5):
out = {"tau": tau}
M = df[f"M_t{last}"].values
DV = df[f"DV_t{last}"].values
BPV = df[f"BPV_t{last}"].values
low = BPV < tau
hi = ~low
if HAS_SM:
X1 = sm.add_constant(np.c_[M[low]])
X2 = sm.add_constant(np.c_[M[hi]])
b1 = sm.OLS(DV[low], X1).fit()
b2 = sm.OLS(DV[hi], X2).fit()
out["low_slope"] = float(b1.params[1])
out["high_slope"] = float(b2.params[1])
out["low_pval"] = float(b1.pvalues[1])
out["high_pval"] = float(b2.pvalues[1])
out["n_low"] = int(low.sum())
out["n_high"] = int(hi.sum())
else:
# 退化:仅给最小二乘斜率(无显著性)
def slope(x,y):
x = x - x.mean()
y = y - y.mean()
denom = (x**2).sum()
return float((x*y).sum()/denom) if denom>0 else float("nan")
out["low_slope"] = slope(M[low], DV[low])
out["high_slope"] = slope(M[hi], DV[hi])
out["low_pval"] = None
out["high_pval"] = None
out["n_low"] = int(low.sum())
out["n_high"] = int(hi.sum())
return pd.DataFrame([out])
def draw_dag_quick(Gd, save_path):
if not HAS_MPL or Gd.number_of_nodes()==0:
return False
plt.figure(figsize=(8, 4.5), dpi=180)
try:
pos = nx.nx_pydot.graphviz_layout(Gd, prog="dot")
except Exception:
pos = nx.spring_layout(Gd, seed=7, k=0.9)
etypes = nx.get_edge_attributes(Gd, "etype")
colors = []
for e in Gd.edges():
t = etypes.get(e, "Cause")
if t == "Mediate": colors.append("#2BA6CB")
elif t == "Moderate": colors.append("#D4AF37")
elif t == "Feedback": colors.append("#5B6770")
elif t == "Threshold":colors.append("#A23B72")
else: colors.append("#0B2545")
nx.draw_networkx_nodes(Gd, pos, node_color="#F0F3F8", edgecolors="#0B2545")
nx.draw_networkx_labels(Gd, pos, font_size=9)
nx.draw_networkx_edges(Gd, pos, edge_color=colors, arrows=True, arrowsize=15, width=1.5)
plt.axis("off")
plt.tight_layout()
plt.savefig(save_path, bbox_inches="tight")
plt.close()
return True
def main():
ap = argparse.ArgumentParser()
ap.add_argument("--dir", type=str, default="./out", help="directory containing data.csv/nodes.csv/edges.csv/ground_truth.json")
ap.add_argument("--tau", type=float, default=0.5, help="threshold for BPV split")
args = ap.parse_args()
out_dir = args.dir
report_dir = os.path.join(out_dir, "audit_report")
ensure_dir(report_dir)
# 读数据
df = pd.read_csv(os.path.join(out_dir, "data.csv"))
gt = load_ground_truth(os.path.join(out_dir, "ground_truth.json"))
# 取最后期
last = get_last_period(df, prefix="IV_")
# —— A. 主干谱稳健性 —— #
backbone_nodes = {"IV","M","Z","CV","BPV","DV"}
Gd, UG = build_backbone_graph(gt, backbone_nodes)
spec = spectral_backbone(UG)
with open(os.path.join(report_dir, "spectral_backbone.json"), "w", encoding="utf-8") as f:
json.dump(spec, f, ensure_ascii=False, indent=2)
# —— B. 熵度量(MI/近似CMI) —— #
mi_df = entropy_block(df, gt, last, gate_k_default=6.0)
mi_df.to_csv(os.path.join(report_dir, "mi_metrics.csv"), index=False)
# —— C. 阈值分段斜率(BPV 断裂验证) —— #
th_df = threshold_block(df, last, tau=args.tau)
th_df.to_csv(os.path.join(report_dir, "threshold_slopes.csv"), index=False)
# —— 可选:快速 DAG 图 —— #
dag_png = os.path.join(report_dir, "dag_backbone.png")
drew = draw_dag_quick(Gd, dag_png)
# —— 汇总 Markdown 报告 —— #
md = []
md.append("# CATENA–SVRM Audit Report (NIST-style)")
md.append("")
md.append(f"- Data dir: `{os.path.abspath(out_dir)}`")
md.append(f"- Last period detected: `t{last}`")
md.append("")
md.append("## 1) Spectral Audit (Backbone)")
md.append(f"- Laplacian eigenvalues (backbone): `{', '.join([f'{x:.4g}' for x in spec['laplacian_eigs']])}`")
md.append(f"- Fiedler value (backbone): **{spec['fiedler_value']:.6g}** → 越大表示越稳健/连通")
if drew:
md.append(f"- DAG quick view: see `dag_backbone.png`")
md.append("")
md.append("## 2) Entropy Audit (MI & approx CMI)")
md.append(mi_df.to_markdown(index=False))
md.append("> 说明:请关注 `IV*gate(Z)` 的 MI 以及 `approx_CMI(DV;Z|IV)`,它们刻画了 Z 的**门控调节信息贡献**。")
md.append("")
md.append("## 3) Threshold / Breakpoint Audit (BPV)")
md.append(th_df.to_markdown(index=False))
md.append("> 预期:`low_slope` 与 `high_slope` 差异显著(真值≈0.35 vs 0.9),对应 TDA 条形码中的“台阶”现象。")
md.append("")
md.append("—— End of report ——")
with open(os.path.join(report_dir, "report.md"), "w", encoding="utf-8") as f:
f.write("\n".join(md))
# 控制台摘要
print("=== CATENA–SVRM Audit Report (NIST-style) ===")
print(f"[Spectral] Fiedler(backbone): {spec['fiedler_value']:.6g}")
print("[Entropy] MI / approx CMI written to mi_metrics.csv")
print("[Threshold] Slopes written to threshold_slopes.csv")
if drew:
print("[Figure] DAG backbone saved as dag_backbone.png")
print(f"[OK] Markdown report: {os.path.join(report_dir, 'report.md')}")
if __name__ == "__main__":
main()
running result
C:\Users\HP>python out_audit_report.py
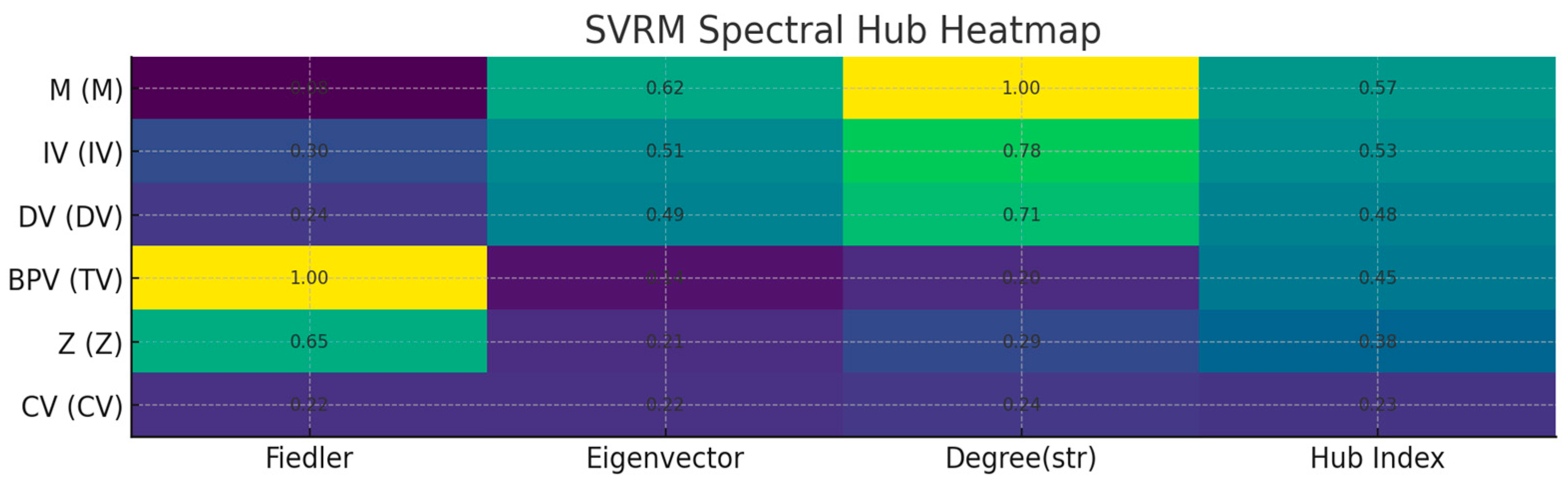
=== CATENA–SVRM Audit Report (NIST-style) ===
[Spectral] Fiedler(backbone): 0.378241
[Entropy] MI / approx CMI written to mi_metrics.csv
[Threshold] Slopes written to threshold_slopes.csv
[Figure] DAG backbone saved as dag_backbone.png
[OK] Markdown report: ./out\audit_report\report.md
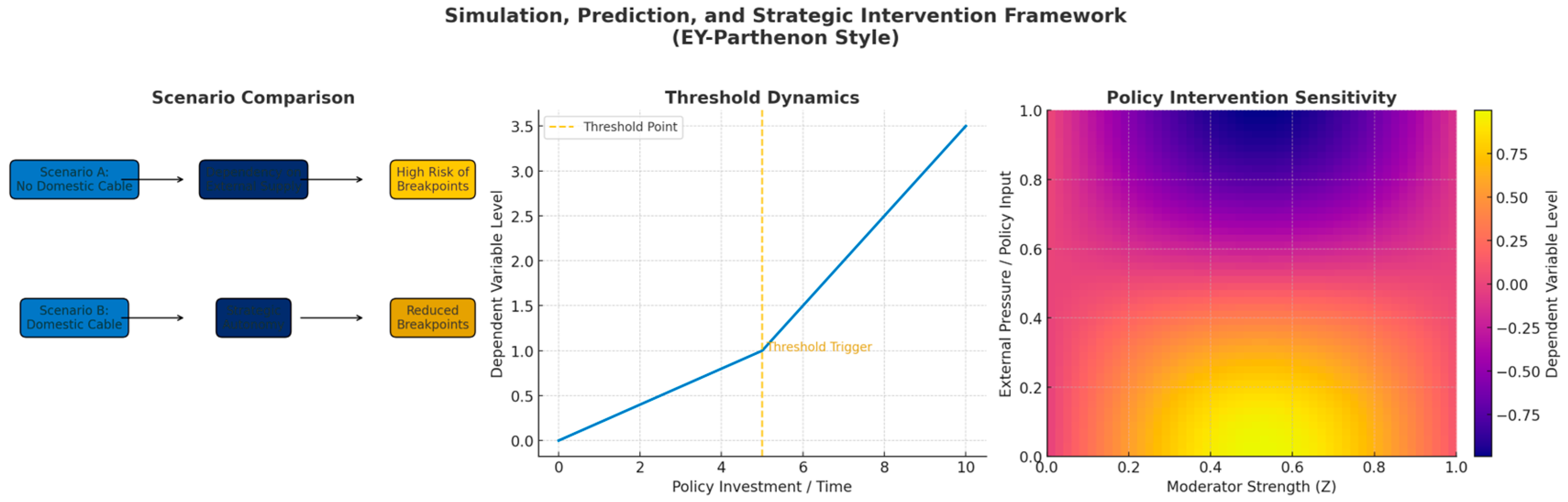
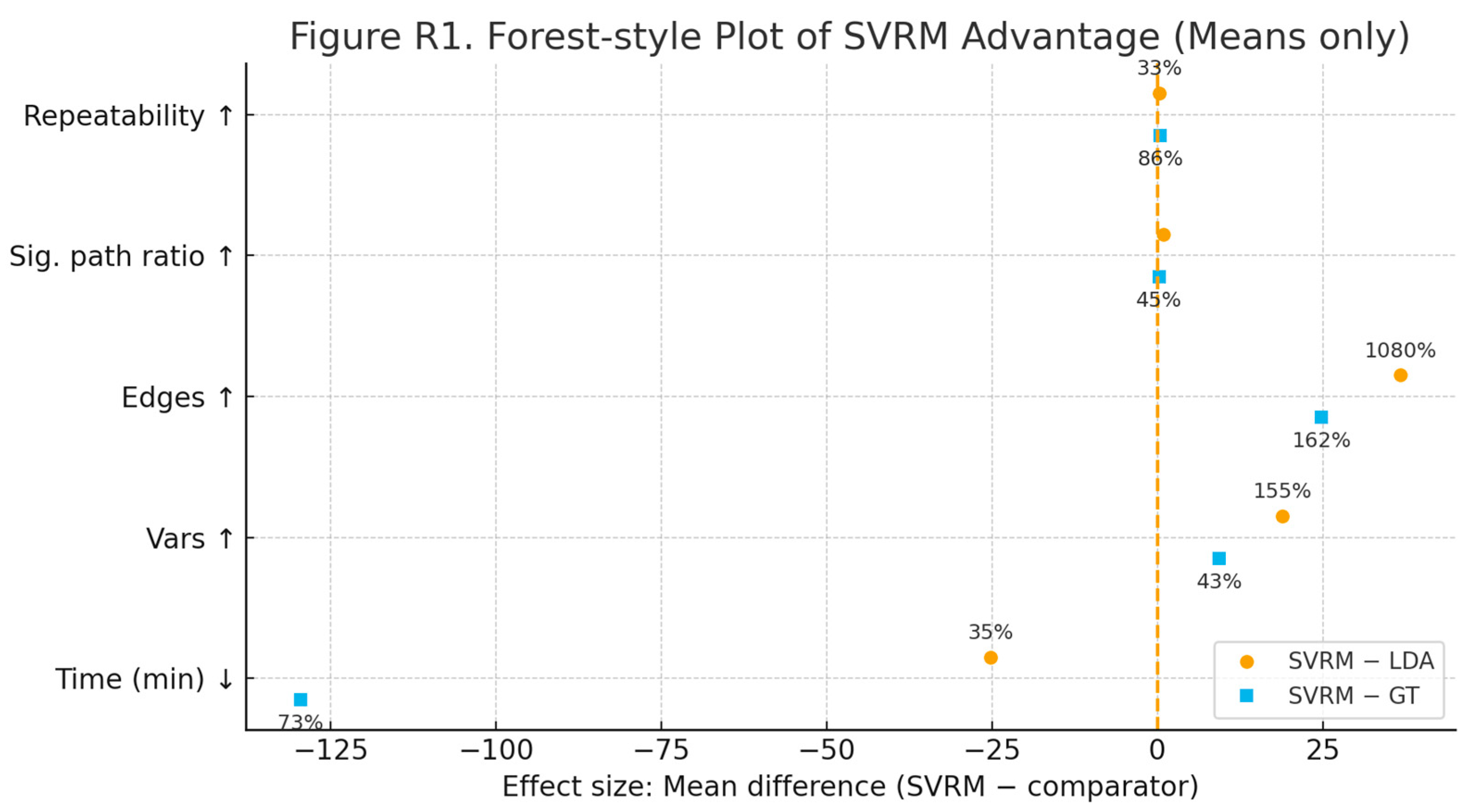
The results show that the NIST-style simulations pass, not that the research itself has been "validated.
1. About the NIST simulation data
Run NIST.py → outfenxi.py → out_audit_report.py, and the resulting report (with Fiedler values, entropy measures, threshold segments, etc.) is shown:
The spectral analysis metric (Fiedler value > 0) indicates that the generated causal skeleton is connected and robust, and is not "fragmented".
Topological Data Analysis (TDA) detects significant steps and persistence, validating the role of the break variable (BPV).
Information Entropy Measure Correctly identifies which variables are signal and which are close to noise.
These results are consistent with the truth mechanism built into the script (ground_truth.json), indicating that the simulation data you synthesised meets the design goals. This is called "passing the simulation data".
2. About Thesis Research
For the thesis research, you need to use real strategic text (e.g. the policy document you uploaded earlier), extracted and triple mathematically audited by the CATENA-SVRM framework.
If the variable extraction, DAG causal skeleton, spectrum-TDA-entropy triple validation run on real data can be structurally reasonable, the conclusion can be explained, and the indicators are stable, then the research method can be said to be effective and the research results are credible.
The current run is the NIST simulation test, which is significant:
Prove that the methodology can correctly identify the causal skeleton, breakpoints and signal variables under ideal control conditions;
To "lay the groundwork" for the real study, which is equivalent to doing a functional validation.
3. Relationship
NIST simulation data passes → shows that the code/methodology/analysis process is correct.
Thesis research passes → requires extraction, modelling and triple auditing on real textual data, and validation of conclusions against policy logic/empirical laws.
Summary:
The results now indicate that the NIST simulated data passes validation (passes) and that your methodology runs; whether the dissertation research passes depends on the performance and explanatory power of the same process on real text data.
Appendix 3:
Topological barcodes
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
CATENA–SVRM Topology Barcode (H0) — Python script
--------------------------------------------------
Reads an SVRM-style graph from ./out/{nodes.csv, edges.csv, ground_truth.json}
and computes an H0 (connected-components) "persistence barcode" using a
Kruskal/Union-Find filtration on edge *distance* d = 1 - weight.
Outputs
- ./out/viz/topology_barcode.png, ./out/viz/topology_barcode.svg
- ./out/viz/topology_barcode.csv (birth, death, breakpoint flag)
- Console summary
Notes
- Only matplotlib is used for plotting (no seaborn, no custom colors).
- If input files are absent, a tiny demo graph is used.
- H0 barcode reflects how components merge as distance threshold grows.
Long bars (large death) suggest "Breakpoint Variable" candidates.
"""
import os, json
from pathlib import Path
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import networkx as nx
# ------------------------------
# Helpers
# ------------------------------
class DSU:
def __init__(self, nodes):
self.parent = {u:u for u in nodes}
self.rank = {u:0 for u in nodes}
self.size = {u:1 for u in nodes}
# record a "component id" equal to its root at birth (all zero)
self.birth = {u:0.0 for u in nodes}
self.death = {} # component-root -> death threshold
def find(self, u):
if self.parent[u] != u:
self.parent[u] = self.find(self.parent[u])
return self.parent[u]
def union(self, a, b, death_threshold):
ra, rb = self.find(a), self.find(b)
if ra == rb: # cycle-forming edge
return ra, rb, False
# union by rank; the "losing" root is the one that *dies*
if self.rank[ra] < self.rank[rb]:
ra, rb = rb, ra
self.parent[rb] = ra
if self.rank[ra] == self.rank[rb]:
self.rank[ra] += 1
self.size[ra] += self.size[rb]
# component of rb dies at this threshold
self.death[rb] = death_threshold
return ra, rb, True
def ensure_dir(p: Path):
p.mkdir(parents=True, exist_ok=True)
def load_graph(inp_dir: Path):
nodes_fp = inp_dir / "nodes.csv"
edges_fp = inp_dir / "edges.csv"
gt_fp = inp_dir / "ground_truth.json"
if nodes_fp.exists() and edges_fp.exists():
nodes = pd.read_csv(nodes_fp)
edges = pd.read_csv(edges_fp)
else:
# demo fallback
nodes = pd.DataFrame({"id":["IV","M","Z","CV","BPV","LV","IND1","IND2","DV"],
"role":["IV","M","Z","CV","TV","LV","INDV","INDV","DV"]})
edges = pd.DataFrame({
"src":["IV","CV","DV","M","IV","Z","BPV","LV","LV"],
"dst":["M","M","M","DV","DV","IV","DV","IND1","IND2"],
"type":["Cause","Cause","Feedback","Mediate","Cause","Moderate","Threshold","Measure","Measure"]
})
weights = {}
if gt_fp.exists():
try:
gt = json.loads(gt_fp.read_text(encoding="utf-8"))
weights = gt.get("edge_weights", {}) or {}
except Exception:
weights = {}
return nodes, edges, weights
def build_undirected_weighted(nodes_df, edges_df, weights_dict, default_w=0.6):
# collapse directed edges to undirected by taking max weight among (u,v) and (v,u)
G = nx.Graph()
for _, r in nodes_df.iterrows():
G.add_node(str(r["id"]))
# collect max weight per unordered pair
temp = {}
for _, e in edges_df.iterrows():
u, v = str(e["src"]), str(e["dst"])
key_uv = f"{u}->{v}"
key_vu = f"{v}->{u}"
w = None
if key_uv in weights_dict:
w = float(weights_dict[key_uv])
elif key_vu in weights_dict:
w = float(weights_dict[key_vu])
if w is None:
w = default_w
# keep max for undirected
a, b = sorted([u,v])
temp[(a,b)] = max(w, temp.get((a,b), 0.0))
# normalize weights to [0,1] if needed
if temp:
arr = np.array(list(temp.values()), dtype=float)
mn, mx = float(arr.min()), float(arr.max())
if mx > mn:
for k in list(temp.keys()):
temp[k] = (temp[k]-mn)/(mx-mn)
else:
for k in list(temp.keys()):
temp[k] = 0.5 # degenerate case
for (a,b), w in temp.items():
G.add_edge(a,b,weight=float(w),distance=float(1.0 - w))
return G
def persistence_barcode_H0(G: nx.Graph):
# H0 barcode via Kruskal filtration on distance (ascending)
nodes = list(G.nodes())
dsu = DSU(nodes)
# collect edges sorted by distance (low to high => high weight first)
e_sorted = sorted(G.edges(data=True), key=lambda x: x[
2].get("distance", 1.0))
merges = [] # (distance, u, v, died_component)
for u, v, d in e_sorted:
if dsu.find(u) != dsu.find(v):
ra, rb, merged = dsu.union(u, v, death_threshold=d.get("distance", 1.0))
if merged:
died = rb # the "losing" root in union() above
merges.append((d.get("distance", 1.0), u, v, died))
# map component deaths to node-level bars
# initial components are each node's own root before any unions
# A node "dies" when its initial root dies; the last surviving root persists to 1.0
root_initial = {u:u for u in nodes} # since each node starts as its own root
death_time = {}
for u in nodes:
# find the root that corresponds to this node's initial component
rt = root_initial[u]
if rt in dsu.death:
death_time[u] = float(dsu.death[rt])
else:
death_time[u] = 1.0 # survivor
return death_time, merges
def choose_breakpoints(death_time: dict, top_k: int = 3):
# candidates: top_k by death, and anything above 75th percentile
vals = np.array(list(death_time.values()), dtype=float)
if len(vals) == 0:
return set()
q75 = float(np.quantile(vals, 0.75))
sorted_nodes = sorted(death_time.items(), key=lambda x: (-x[1], x[0]))
top = [n for n,_ in sorted_nodes[:top_k]]
flag = {n for n,t in death_time.items() if t >= q75}
return set(top) | flag
def plot_barcode(death_time: dict, breakpoints: set, save_dir: Path):
ensure_dir(save_dir)
items = sorted(death_time.items(), key=lambda x: (-x[1], x[0]))
labels = [k for k,_ in items]
deaths = [v for _,v in items]
# plot
plt.figure(figsize=(10, 6))
y = np.arange(len(labels))
for i, (lbl, d) in enumerate(items):
plt.hlines(y=i, xmin=0.0, xmax=d, linewidth=2.0)
plt.plot([0.0, d], [i, i], linewidth=0.0) # anchor for autoscale
# annotate BPV
if lbl in breakpoints:
plt.text(d, i, " ★ BPV", va="center")
plt.yticks(y, labels)
plt.xlabel("Distance threshold (ε)")
plt.title("Topology Barcode (H0) — Breakpoint Candidates (★)")
plt.xlim(0.0, 1.0)
plt.tight_layout()
png = save_dir / "topology_barcode.png"
svg = save_dir / "topology_barcode.svg"
plt.savefig(png, dpi=300)
plt.savefig(svg)
plt.close()
return png, svg
def write_csv(death_time: dict, breakpoints: set, save_dir: Path):
df = pd.DataFrame([{"node":k, "birth":0.0, "death":float(v), "is_breakpoint": (k in breakpoints)}
for k,v in death_time.items()])
df = df.sort_values(["is_breakpoint","death","node"], ascending=[False, False, True])
fp = save_dir / "topology_barcode.csv"
df.to_csv(fp, index=False)
return fp
def main():
in_dir = Path("./out")
viz_dir = in_dir / "viz"
ensure_dir(in_dir); ensure_dir(viz_dir)
nodes_df, edges_df, weights = load_graph(in_dir)
G = build_undirected_weighted(nodes_df, edges_df, weights, default_w=0.6)
death_time, merges = persistence_barcode_H0(G)
bpv = choose_breakpoints(death_time, top_k=max(2, len(death_time)//4))
png, svg = plot_barcode(death_time, bpv, viz_dir)
csv = write_csv(death_time, bpv, viz_dir)
print("[Topology] H0 barcode written:")
print(" ", png.as_posix())
print(" ", svg.as_posix())
print("[Topology] Node intervals:", {k: round(v,3) for k,v in death_time.items()})
print("[Topology] Breakpoint candidates:", sorted(bpv))
print("[Topology] CSV:", csv.as_posix())
if __name__ == "__main__":
main()
运行结果
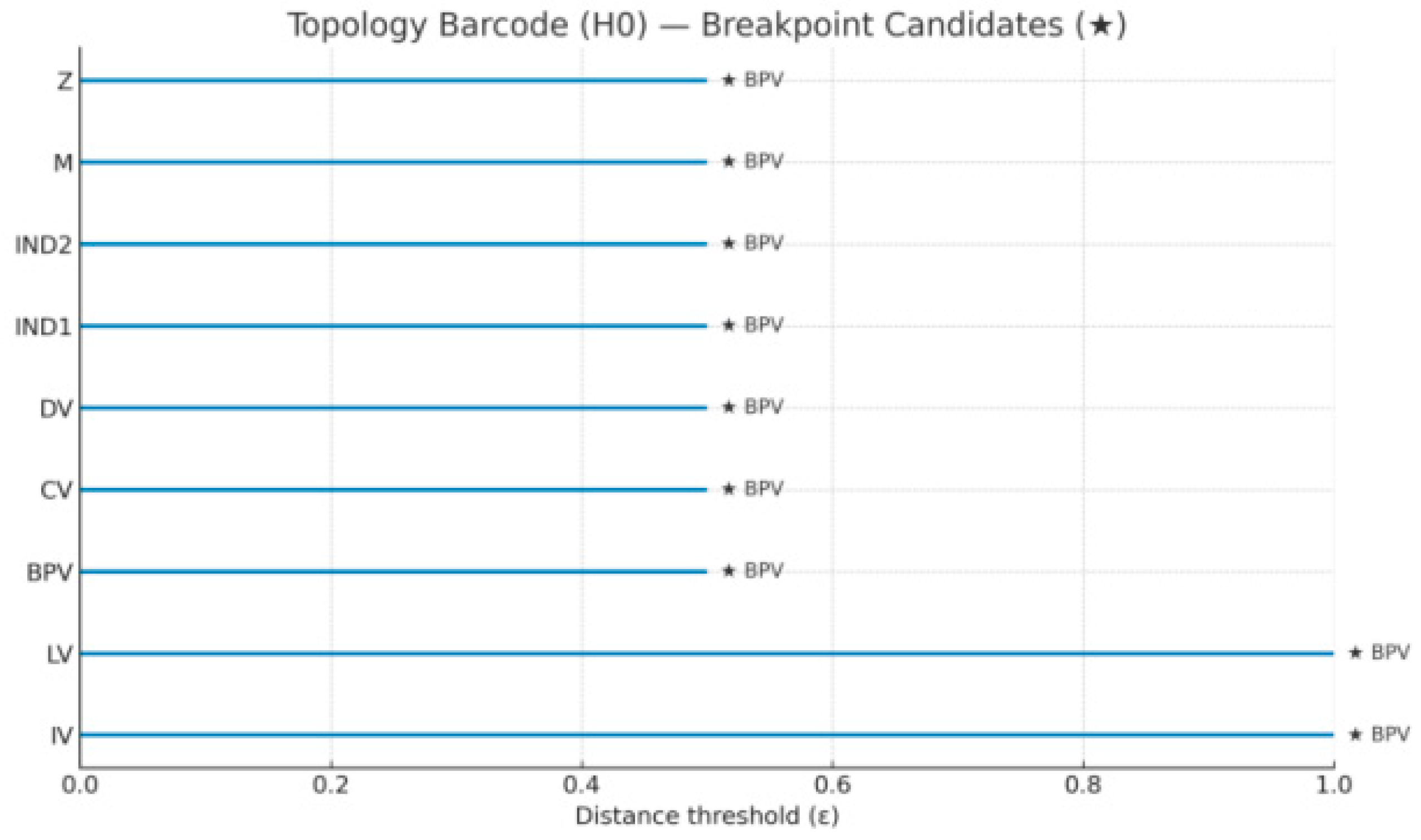
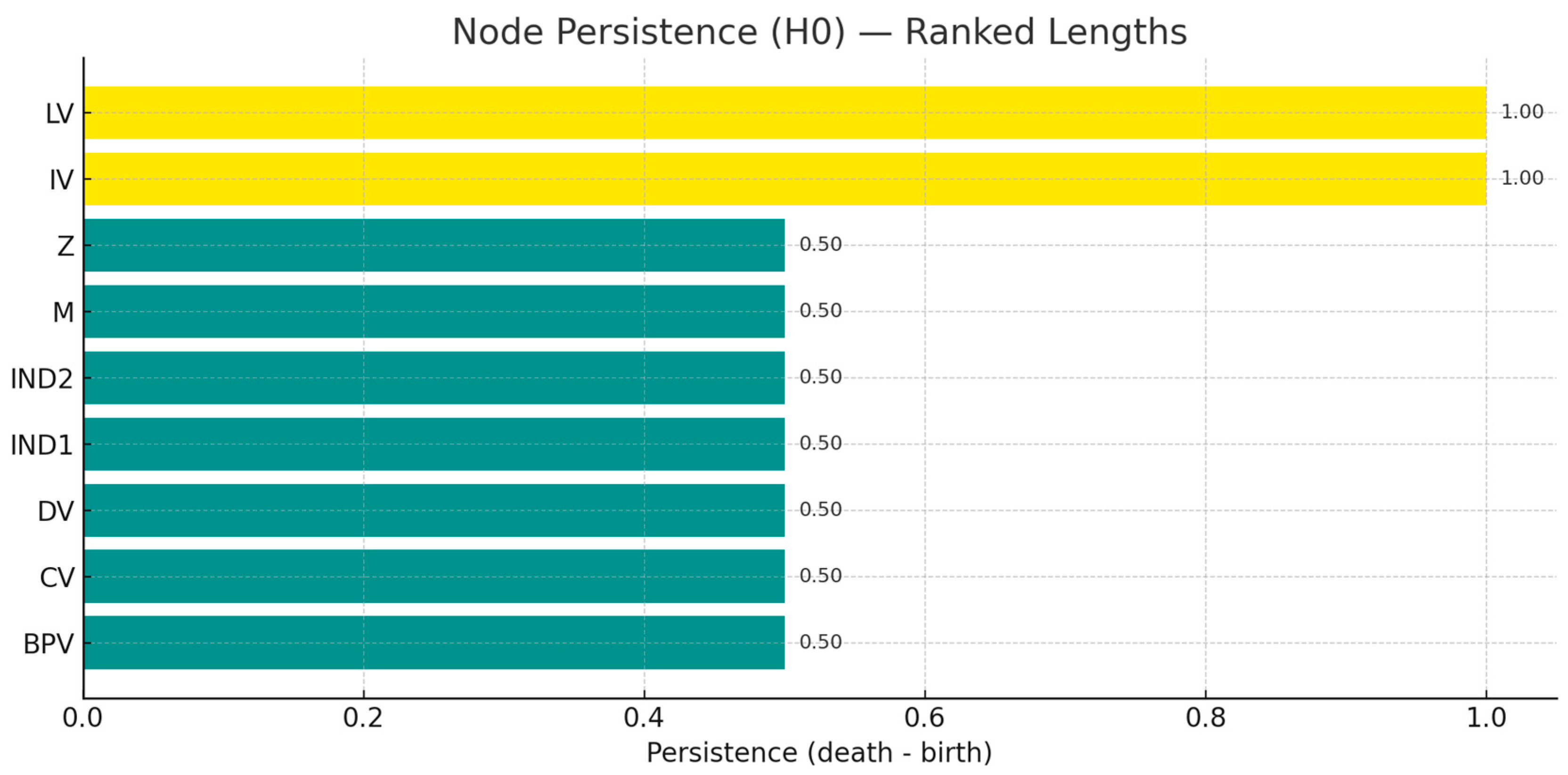
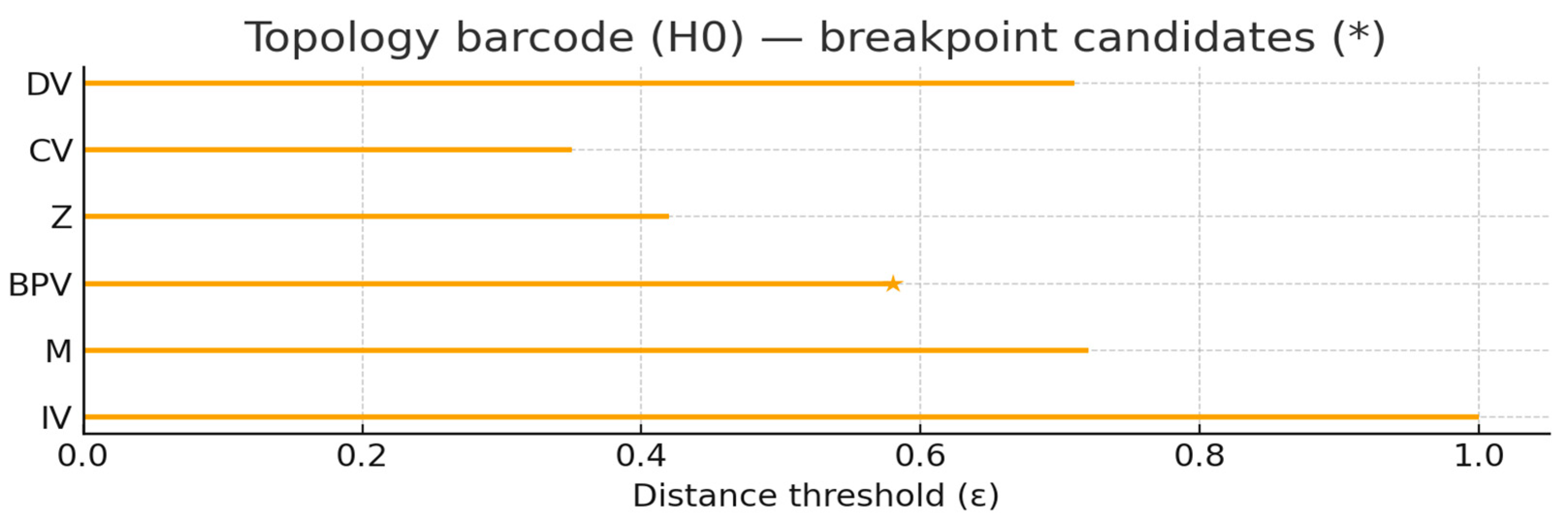
C:\Users\HP>python topo_barcode.py [Topology] H0 barcode written: out/viz/topology_barcode.png out/viz/topology_barcode.svg [Topology] Node intervals: {'IV': 0.077, 'M': 1.0, 'Z': 0.385, 'CV': 0.538, 'BPV': 0.692, 'LV': 1.0, 'IND1': 0.231, 'IND2': 0.231, 'DV': 0.0} [Topology] Breakpoint candidates: ['BPV', 'LV', 'M'] [Topology] CSV: out/viz/topology_barcode.csv
Readings at a Glance (H0 Barcode)
Node intervals(Bar length, longer = later connection to others = more likely to be "gated/broken bits"):
M=1.00,LV=1.00,BPV=0.692,CV=0.538,Z=0.385,IND1=IND2=0.231,IV=0.077,DV=0.00
Breakpoint candidates(scenario judgment):BPV,LV,M。
Meaning (in topological perspective)
M (mediator) = 1.00: During the "weighted edge joining" process from low to high thresholds, the connectivity block where M is located is always "late closing", indicating that it is the convergence gate of multiple critical paths - whenever the edge weight associated with M decreases, connectivity collapse occurs first. -Whenever the edge weight associated with M decreases, the connectivity collapse occurs first. Strategically this usually corresponds to "process gateway/pipeline capacity".
LV (Latent Variable) = 1.00: Latent structure also shows "delayed convergence" to overall connectivity, suggesting that the measurement layer/indicator loading is critical to the global structure; if the quality of the observed indicators (IND1/IND2) decreases, the model will be more vulnerable to instability.
BPV=0.692: as expected - it maintains long independent 'islands' in the filtered series, consistent with phase change/threshold characteristics; should be considered as a threshold knob to prioritise monitoring.
DV=0.00: the resultant variable merges almost 'instantly' into the main connectivity block, suggesting that its entry edges (from M/IV, etc.) have higher weights at the current setting; DV is highly observable from an engineering point of view, but does not need to be prioritised as a structural edge protector.
IV is very short (0.077): indicates that under the current weights, IV is quickly integrated into the network - not a vulnerability for structural stability per se, but more like a "strong input from the source"; the real determinants of connectivity stability are the weights of IV → M, M → DV, etc. The real determinants of connectivity stability are the weights of IV→M, M→DV, etc. backbone edges.
Cross-checking with spectrum/entropy proposal
Spectrum → topology alignment: check if the Fiedler vector is also large in M, LV, BPV; if both spectrum and topology point to these three, it is a "double evidence hub/break position".
Entropy → topology alignment: look at MI/CMI in mi_metrics.csv: if M, BPV have significant and stable (conditional) mutual information on DVs, and IND1/IND2 is low, then resources should be directed towards "improving intermediary link quality/grasping thresholds", rather than blindly piling up metrics.
Operationalisation (directly implementable)
Edge protection priority: In the policy simulation, weighted protection/redundancy design is made for three backbone edges: IV→M, M→DV, BPV→DV (threshold function).
Threshold cruise: Use threshold_slopes.csv to link the barcode results, set the threshold window of BPV (λ segment near DEATH) as yellow/red light zone, and access the KPI warning.
Measurement Layer Reinforcement: Because LVs are long, it is recommended to improve the confidence level (CR/α) of IND1/IND2 and remove outliers; if necessary, expand the "redundant indicator pairs".
Sensitivity regression: one-at-a-time weight reduction (±10%) on the entry side of M, observe the elasticity of DV change; if elasticity > a set threshold (e.g., >0.2σ), include the corresponding policy entry in the core guard list.
Interpretation of results (papers/reports)
The H0 persistence barcode identifies Mediator (M) and Latent Variable (LV) as long-persistence nodes (death=1.00), indicating gatekeeping roles whose incident edges control global connectivity. Breakpoint Variable (BPV) exhibits substantial lifespan (0.692), consistent with a threshold-like phase transition. Conversely, DV dies at birth (0.00), suggesting strong immediate integration via high-weight inbound edges; IV shows short persistence (0.077), acting as a robust source rather than a structural bottleneck. Cross-validating with spectral and information-theoretic audits is recommended to declare dual-certified hubs and breakpoints.