1. Introduction
Quantum key distribution (QKD) provides a novel approach to sharing secret keys between two communicating parties, which can achieve unconditional security when combined with the ‘one-time pad’ [
1,
2]. Although QKD technology has made considerable strides toward practical implementation over the past several decades, it still faces challenges that hinder further development, the most prominent of which are cost and the secure key rate (SKR). On one hand, the integration of QKD with deployed optic fiber network infrastructures has not yet met expectations, resulting in the high cost of current commercial QKD equipment [
3]. On the other hand, the SKR of current commercial QKD devices remains at Kbps level, far below the Tbps capacity of modern communication systems [
4]. Continuous variable (CV) QKD is considered a promising solution for addressing the two issues mentioned above due to its high key rate over metropolitan area and compatibility with commercial off-the-shelf components [
5].
In a typical CVQKD protocol, Alice modulates key information on the quadratures of coherent states and sends it to Bob through a lossy channel. Then Bob recovers the raw keys from the received signal by using coherent detection such as homodyne or heterodyne detection [
6,
7]. This structure of CVQKD shows high similarity to the widely deployed coherent optical transmission systems, indicating the prospect of high-performance and cost-effective QKD system once the state-of-the-art methods of existing coherent optical transmission systems can be effectively adopted for CVQKD [
8,
9]. Actually, the research on CVQKD schemes is just developing in this direction. For example, compared with the early proposed Gaussian-modulated coherent states (GMCS) protocol, the discrete-modulated coherent states (DMCS) protocol uses more efficient modulation formats such as quadrature amplitude modulation (QAM) and thus can be implemented with more efficient forward error correction (FEC) algorithms as well as fewer quantization bits for digital-to-analog converters (DACs) and analog-to-digital converters (ADCs) [
10]. Besides, it has been attractive to use traditional continuous wave (CW) light instead of pulsed light to support a higher SKR and a more accurate track of the phase noise [
11]. Moreover, the emergence of schemes based on a local local oscillator (LLO) also shows advantages over transmitted local oscillator (TLO) schemes, making it feasible to directly use integrated coherent receivers [
12]. It is worth noting that the experimental demonstrations of CVQKD system based on CW light have achieved sub-Gbps SKR within metropolitan area [
13].
Regarding the pursuit of higher-SKR CVQKD, polarization division multiplexing (PDM) can also be introduced to achieve a potential SKR of Gbps-level. The investigation of PDM in CVQKD systems was initially used to transmit reference signals in LLO systems [
14]. More recently, PDM CVQKD systems that transmit QKD signals in both polarization states show promising feasibility mainly because that the hardware structure of classical dual-polarization coherent optical transmission system can be well migrated with only slight adjustment [
8,
15]. Whereas the challenge of these systems is the signal processing. On one hand, auxiliary signal is typically needed to recover raw keys signal from weak and noisy QKD signal, either by adding FDM pilot signal or TDM training symbols to QKD signal [
16,
17]. The performance of such pilot aided schemes in PDM CVQKD system need to be revaluated. On the other hand, the PDM CVQKD induced extra Impairments such as polarization noise [
18,
19], thus corresponding digital signal processing (DSP) algorithms should be designed to compensate these impairments. The influences of these algorithms on the performance of CVQKD need to be analyzed.
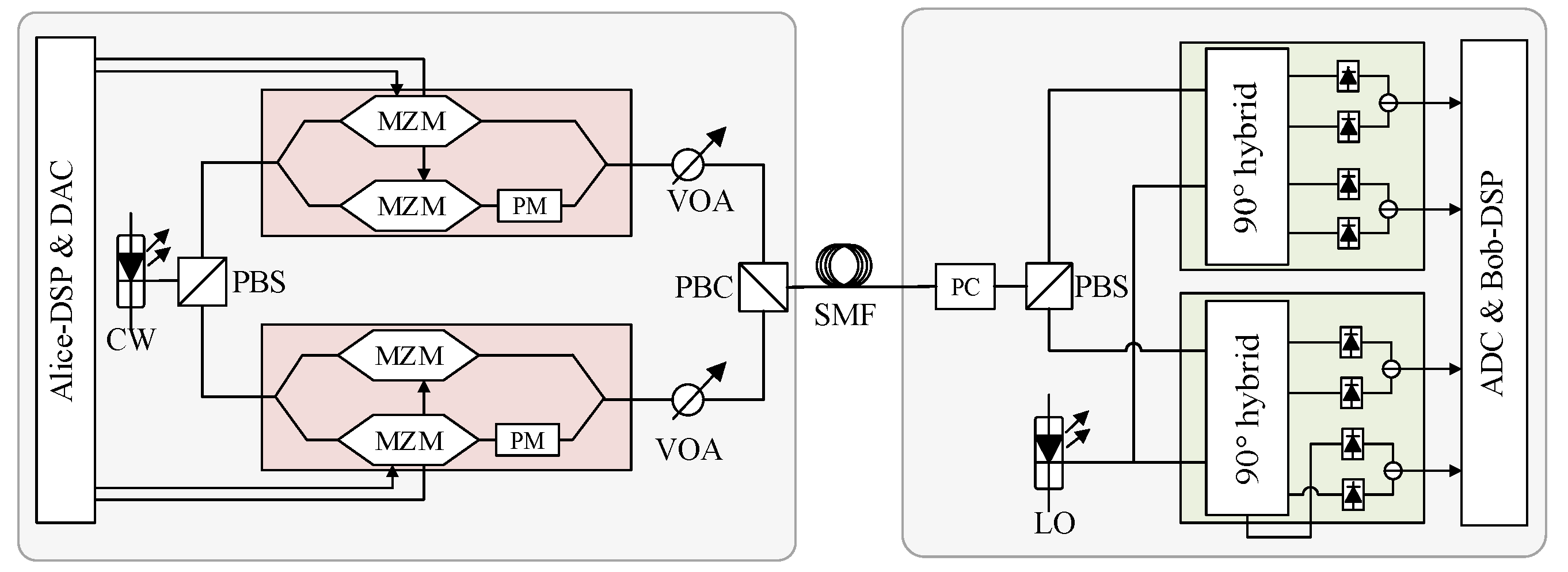
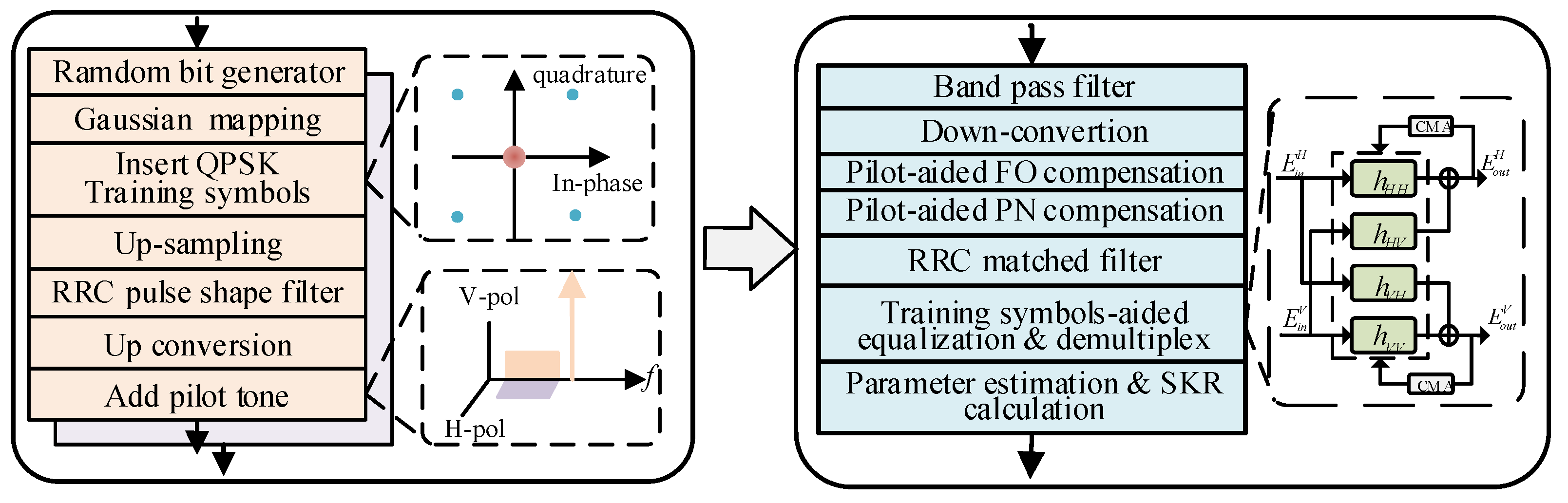
In this paper, we investigate PDM-CVQKD based on the structure of classical coherent optical transmission system, where the CW-GMCS-LLO scheme is applied. Firstly the structure of PDM-CVQKD system is established and the main DSP methods for the system is introduced. Then, a simplified FDM pilot-aided signal processing scheme is proposed for carrier frequency offset (FO) estimation and phase noise (PN) compensation. The excess noise corresponding to the FDM pilot-aided scheme is also modeled in comparison with the traditional TDM pilot-aided scheme. Besides, the two strategies of TS-aided equalization scheme are compared to find the optimal option of the insertion of TS depending on the channel situation. Lastly, the SKR of the PDM-CVQKD system at different transmission distances is evaluated based on the joint optimization of the setup of pilot-aided PN compensation and TS-aided equalization.
3. The Effects of FDM Pilot-Aided Scheme on Security Parameter Estimation
As previously mentioned, a critical prerequisite for secure key generation in QKD system is the accurate estimation of security parameters at the receiver. In practical operation, the security parameters such as
,
,
can be calibrated at receiver and regarded as fixed when the system is stable. However, the estimation of parameters such as
,
T and
may be affected by the imperfections of the transceiver, such as impairments induced by the pilot tone as well as the non-optimize of DSP algorithms. In this section, we focus on the impact of pilot-aided DSP schemes on the estimation of security parameters. First of all, a numerical simulation system based on the scheme in
Figure 1 and
Figure 2 is established. The main parameter setup is shown in
Table 1, where the symbol rate of quantum signal is set to 2 Gbaud, the central frequency of quantum signal is up-converted to 1.5 GHz to avoid low-frequency noise and the frequency of pilot tone is set to be 3.5 GHz to reduce the crosstalks in frequency domain. Note that the shot noise as well as the electronic noise are regarded as Guassian white noise with variance of
. For convenience of analysis we assume that the shot noise variance
of each heterodyne detector are equal, which can be given by:
where
e is the elementary charge,
is the bandwidth of receiver,
is the optical power of LO,
h is the Planck constant,
is the central frequency of lasers.
Firstly, extra impairments will be induced by the pilot tone at transmitter. For example, the calibration of modulation variance
may be effected because the nonlinear effects of MZMs may be amplified when strong pilot is used. Normally, the value of
can be calculated by
, where
is the average photon number of the transmitted optical signal, which can be estimated by measuring the output optical power at transmitter. In our scheme, the output signal of H-pol only consists QKD signal, so
can be estimated directly from the output power. Whereas for V-pol, the output signal consists both the QKD signal and pilot tone, resulting in the inability to directly measure output power of QKD signal. Therefore, once the power ratio of pilot tone to quantum signal
is given, where
and
are the mean voltage of electronic quantum signal and electronic pilot tone assigned to MZM. In this case,
of V-pol can be indirectly estimated by:
can also be estimated at receiver in back to back (B2B) situation, i.e. under a fixed transmittance of
. In this case,
can be estimated as:
where
x is the transmitted symbols that is not normalized to SNU,
y is the received symbols that is normalized to SNU.
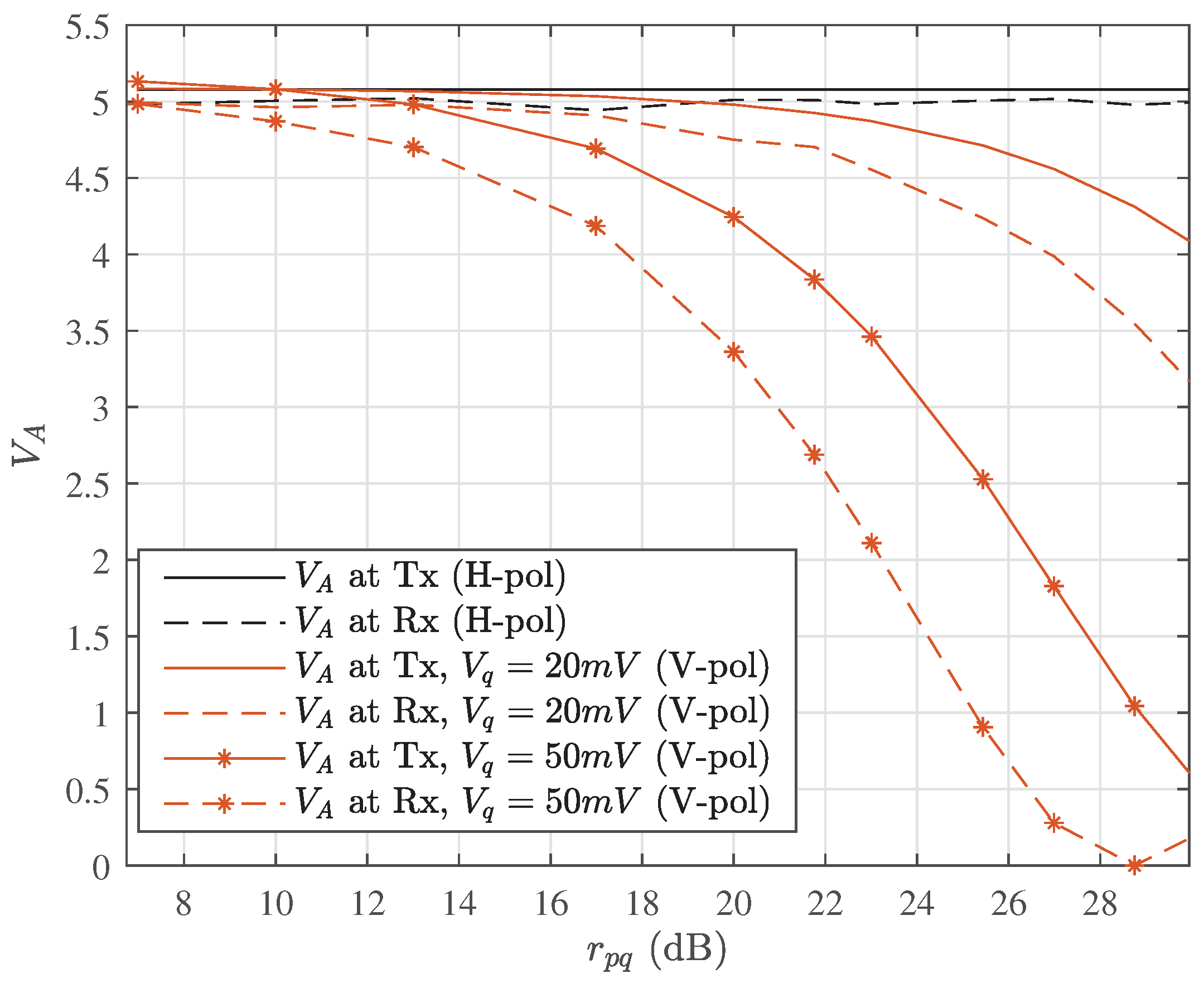
Figure 4 shows the
of V-pol and H-pol estimated at transmitter/receiver with different
(in dB), where the initial
of each polarization are set to 5 in SNU. Note that the QPSK training symbols are not inserted here for simplicity and the results are averaged over 20 acquisitions of received symbols for enough precision. The results indicated that the estimated
of H-pol is matched either estimated at transmitter or receiver. However, for V-pol,
estimated at transmitter is no longer accurate with the increase of
, mainly because the
used in Equation (
8) is the power ratio of baseband electrical pilot tone and quantum signal, which is not the actual
of the output optical signal due to the nonlinear effect of IQ modulators when the power of pilot tone is high. In particular, the nonlinearity grows more pronounced with the increasing of
, as depicted by the star-marked yellow curve in
Figure 4. As a result, it is feasible to calibrate
at transmitter when
is at a relatively low level, whereas more appropriate to perform the calibration of
at the receiver when
is high in practical implementation.
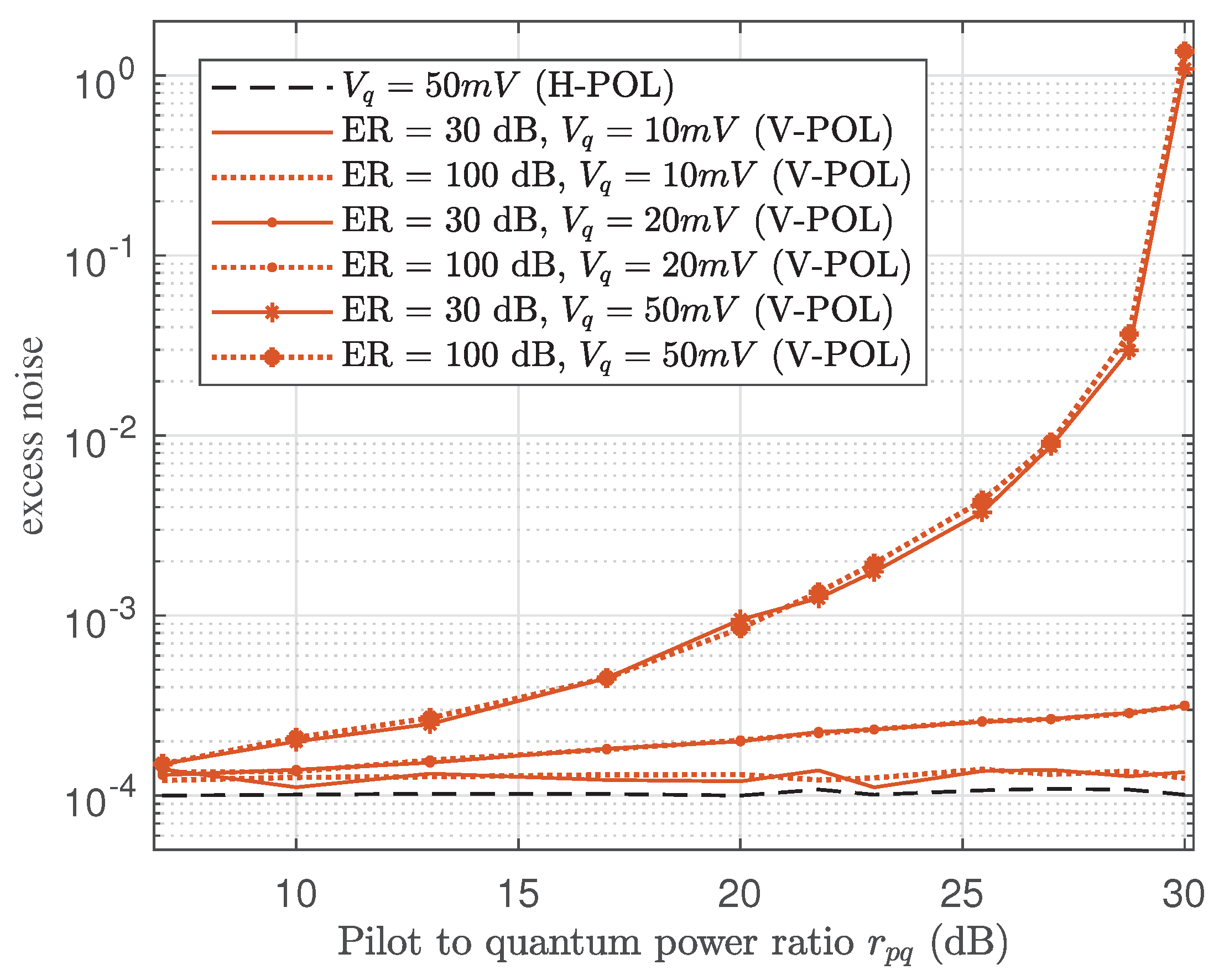
The modulation-related excess noise under the impact of pilot tone is also evaluated as shown in
Figure 5, where the nonlinearity as well as limited dynamic range of MZM is taken into account. Note that the
at each
are all normalized to 5 for the convenience of comparison and the transmission distance is 20 km. The nonlinear effect of MZM can induce the excess noise of
when no pilot is added. Whereas when the pilot is modulated together with QKD signal, the excess noise increases, especially with the increasing of
and
. For example, the excess noise of
is induced at the typical
of 50 mV and
of 20 dB. It means that the FDM pilot tone can cause extra modulation-related excess noise which can not be ignored, which is more dominant compared to the schemes without using FDM pilot. As for the effect of limited dynamic range of MZM, it has been shown that the limited extinction ratio (ER) of amplitude modulator may cause the increasing of excess noise for the pilot-aided schemes based on TDM [
18]. The simulation results in
Figure 5 shows that the limited ER of MZM will not lead to extra excess noise in the FDM pilot-aided scheme.
Another important factor that affect security parameter estimation of pilot-aided scheme lies in the interference of the pilot tone on the quantum signal due to the employing of non-ideal band-pass filter. For the pilot-aided scheme in
Figure 2, the filtered quantum signal of V-pol will contain residual pilot tone components, resulting in parameter estimation errors and an increase of excess noise in the system. In our simulation, the band-pass filter we adopt is a classical FIR filter based on Hamming window.
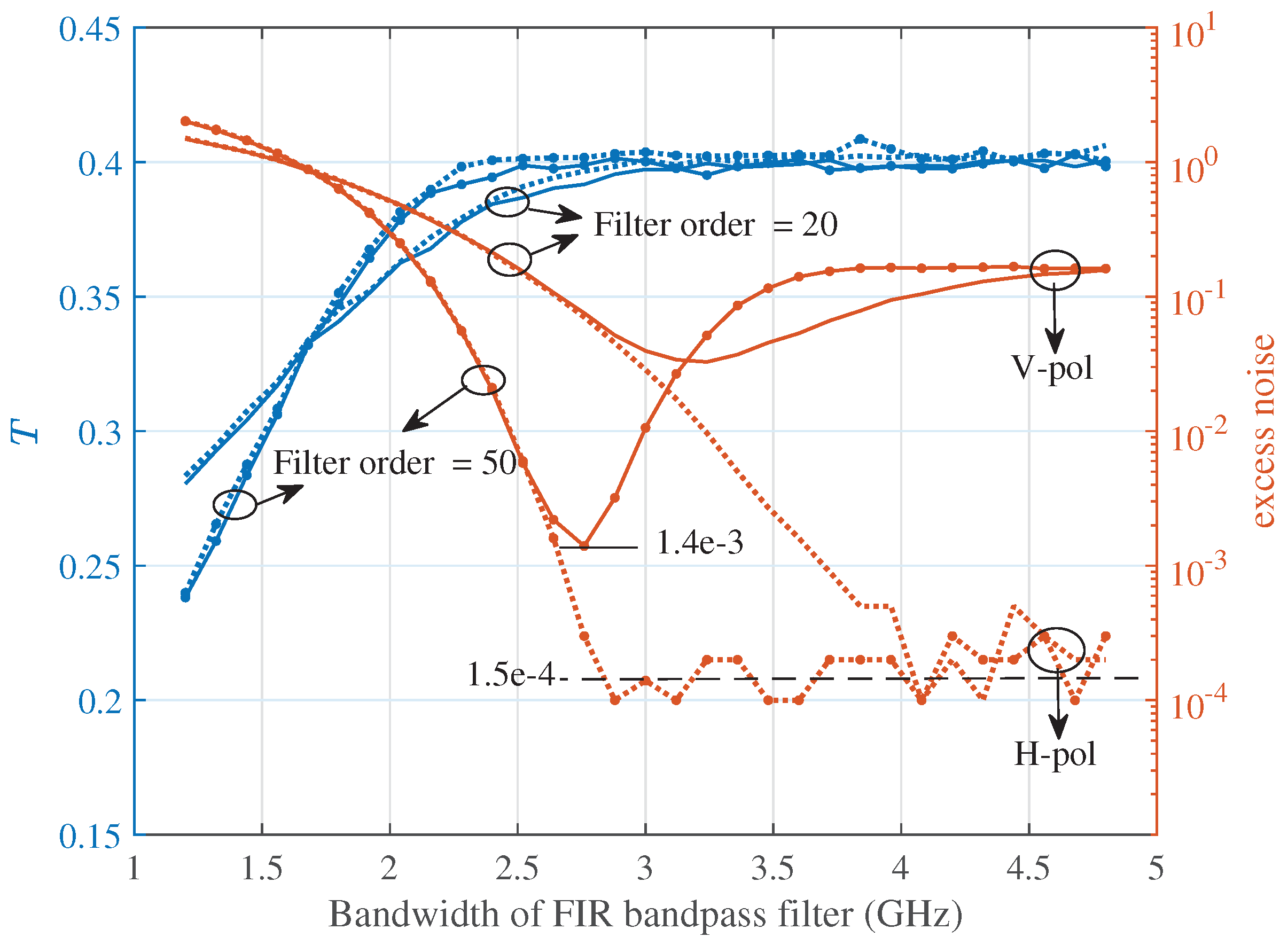
Figure 6 gives the curve of estimated
T and excess noise of each polarization with respect to the bandwidth of band-pass filter after 20 km transmission, where the filter order is set to be 20 for the curves unmarked and 50 for the curves using dot marks. The simulation results indicate that there exist an optimal bandwidth of FIR filter that can achieve the unbiased estimation of
. The excess noise induced by non-ideal filter is about
for V-pol and
for H-pol.
Furthermore, as mentioned before, the implement of pilot-aided PN estimation and compensation can not be perfect in practice because of the estimation error
in Equation (
2). According to the research in [
12], the residual excess noise induce by
in TDM pilot-aided schemes can be estimated by:
where
is the total noise of the pilot tone,
is the amplitude of the pilot tone in SNU. However, for FDM pilot-aided scheme, the total noise of pilot tone is not equal to that of QKD signal because the noise bandwidth of received pilot tone and QKD signal are different. In this case,
is given by:
where
is the total noise of FDM pilot tone,
and
are the bandwidth of filtered QKD signal and filtered pilot tone, respectively. In TDM pilot-aided system,
and
are equal, while
is much less than
in FDM pilot-aided system when narrow-band filter is used to filter the pilot tone. As a result,
is much less than
. The total excess noise induced by pilot tone in each polarization can be eventually calculated as:
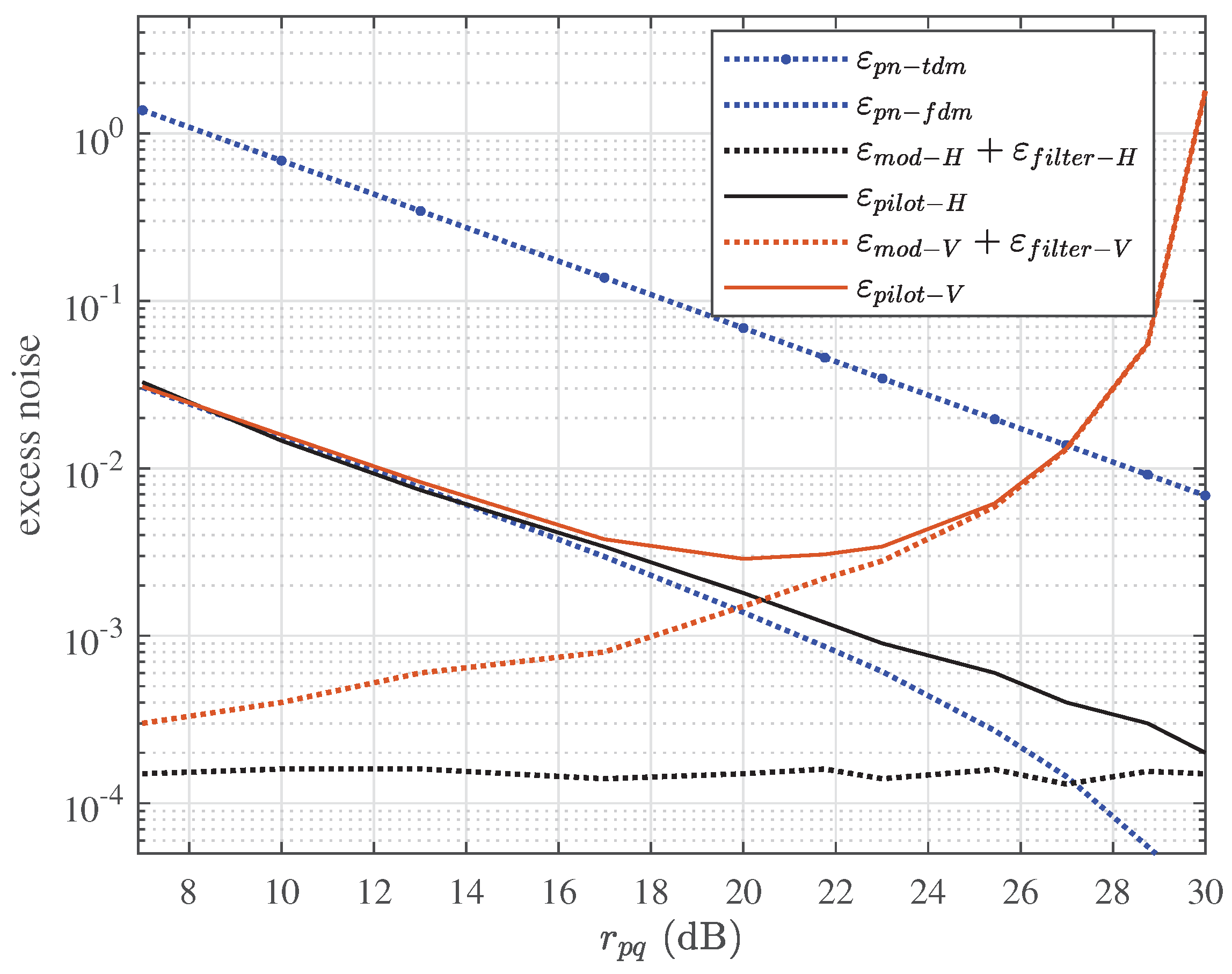
Figure 7 shows the excess noises mentioned in (
12) with respect to
at the transmission distance of 20 km. The total linewidth of CW and LO are set to 1e4 Hz, the bandwidth of bandpass filter is set to be approximately 2.75 GHz for QKD signal and 55 MHz for pilot tone. The result shows that the
is minimized to 2.8e-3 at the
of 20 dB. The corresponding
is 1.5e-3. The estimated
is 1.4e-3 for both polarization states, which is almost 50 times less than
. Note that
and
are neither related to transmission distance, whereas
is increased as the transmission distance increases. It means that the most dominant excess noise induced by pilot tone is
for V-pol and only
for H-pol.
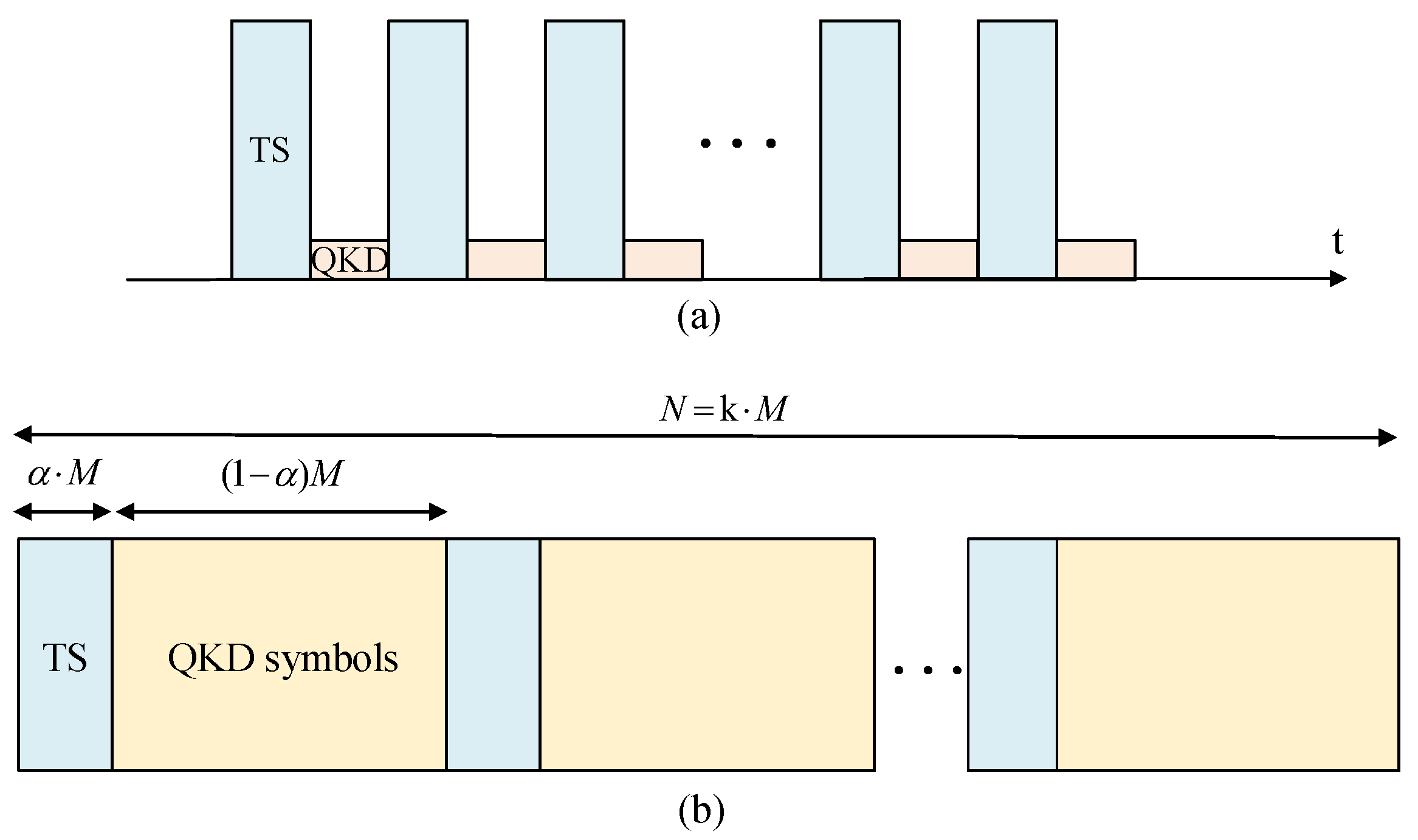
4. Strategy Optimization of TS-Aided Equalization
Compared to the FDM pilot-aided phase noise compensation, the TDM-based TS-aided equalization and demultiplexing scheme achieves RSOP compensation at the expense of reduced QKD spectral efficiency. Therefore, to achieve the optimal SKR, it is necessary to optimize the equalizer parameters while adaptively selecting the optimal TS rate
depending on the channel conditions. In this section, the performance of two TS-aided equalization schemes shown in
Figure 3 are numerically compared to find the optimal strategy of TS insertion, thereby optimize the SKR of QKD system taking into account the impacts of pilot-aided scheme analyzed in section 3. For scheme A, the parameter
is fixed to 0.5, as a result, only the equalizer’s parameters such as the tap number
and step size
u of CMA algorithm are needed to be optimized.
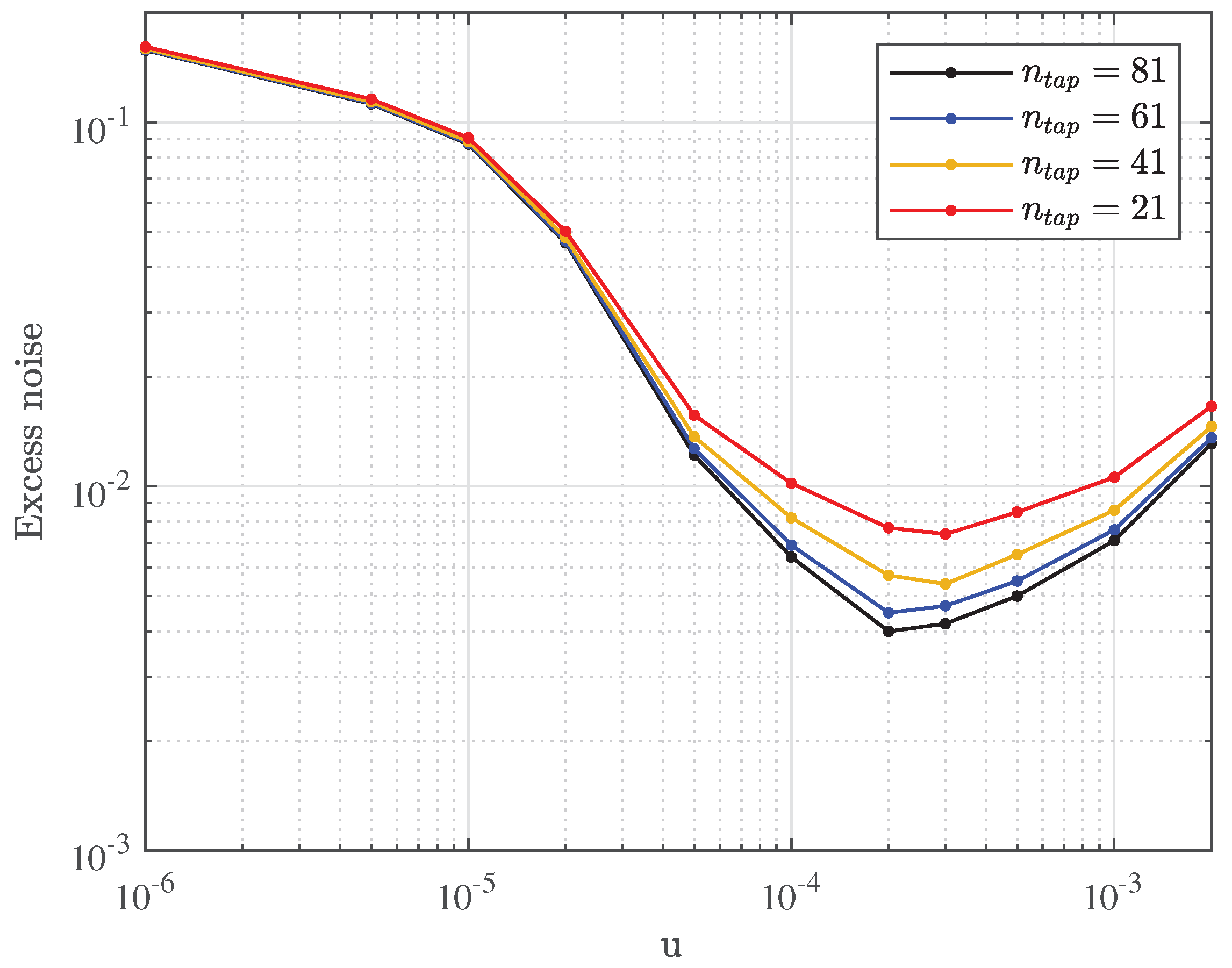
Figure 8 shows the excess noise of scheme A with respect to different
and
u, where the RSOP is set to be 1e4 rad/s and the transmission distance is 20 km. Note that only the excess noise related to equalization is analyzed here, so that the parameters corresponding to the pilot tone are set to be ideal to make
. It can be observed that the lowest excess noise of
can be achieved with
and
. Based on the same parameter setup of equalizer, the lowest excess noise of
can be achieved as well. Apparently, scheme A can effectively compensate RSOP once the parameter of equalizer is optimized.
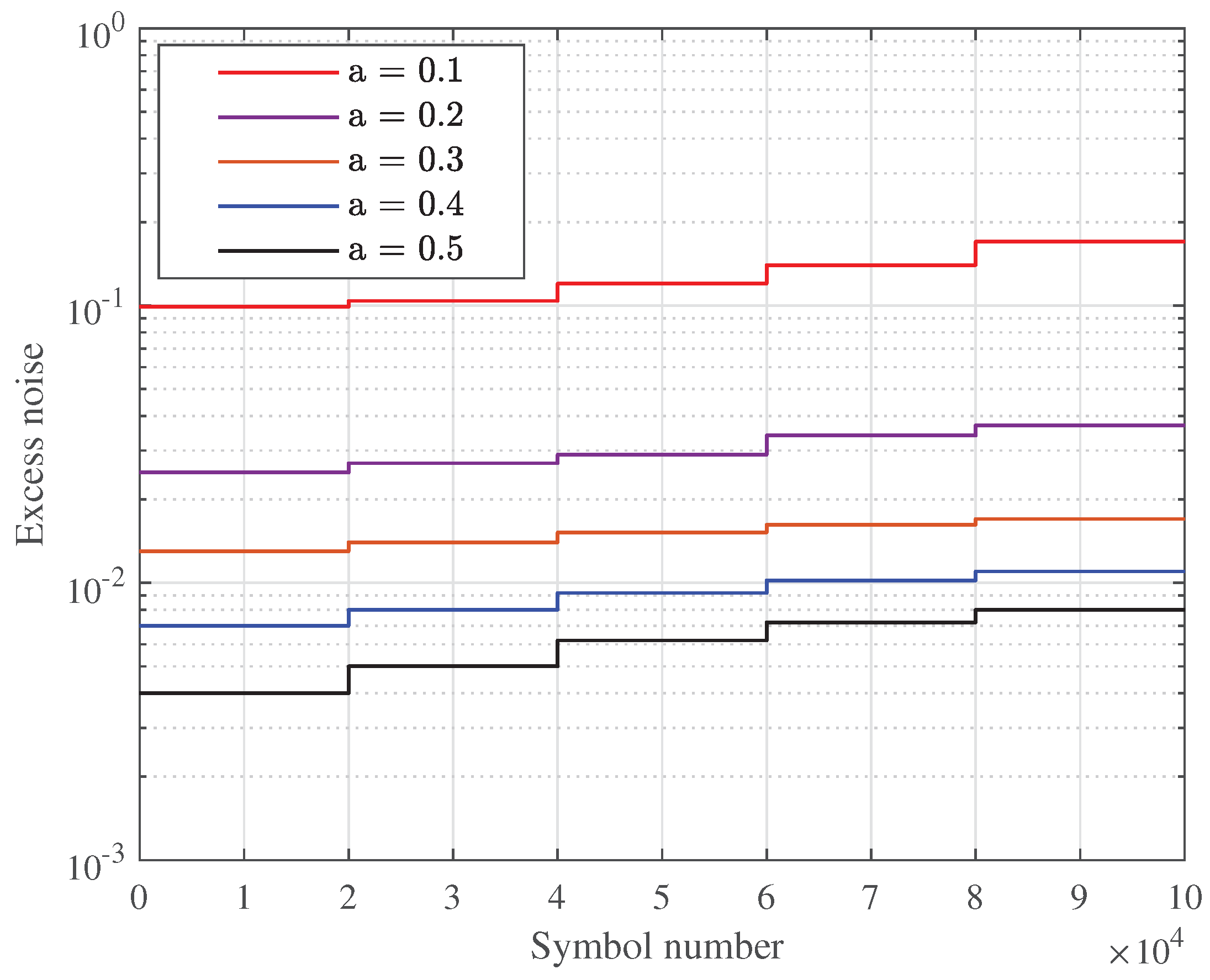
As for scheme B, each
N symbols are divided into
k blocks of length
M and
TS are then used for the convergence of CMA equalizer. For each
symbols, the lowest excess noise can be achieved by jointly optimizing the value of
,
and
u. The total excess noise related to equalizer, denoted by
, can be obtained by averaging the excess noise of
k blocks. Following this strategy, the
of each k blocks with different
are simulated as shown in
Figure 9, where the blocklength
N is set to 1e5 and
k is set to a fixed value of 5 for simplicity. To maintain consistency with scheme B, the parameters of equalizer are set by
and
for both TS and QKD symbols. The results show that for each value of
,
increases with the increasing of symbol number, mainly because of the accumulation RSOP effect over time. It can also be seen that the mean value of
decreases with the increasing of
, specifically, the mean value of
when
is 6e-3 for scheme B, which is higher than the value of 4e-3 for scheme A.
Since the value of
in Scheme A is fixed to 0.5, its
and SKR are constant at a specific distance. However, the value of
in scheme B can be adapted to achieve the highest SKR. As a result, the strategy of scheme B can be optimized by traversing the total excess noise of each polarization with different
to find the highest SKR, where the total excess noise of each polarization is defined by:
where an original system excess noise of
is added to simulate the fixed excess noise contributed by the noise relative intensity noise of lasers, quantisation noise of ADC, nonlinear noise of the MZM, etc. Note that the
is given by the value in
Figure 7.
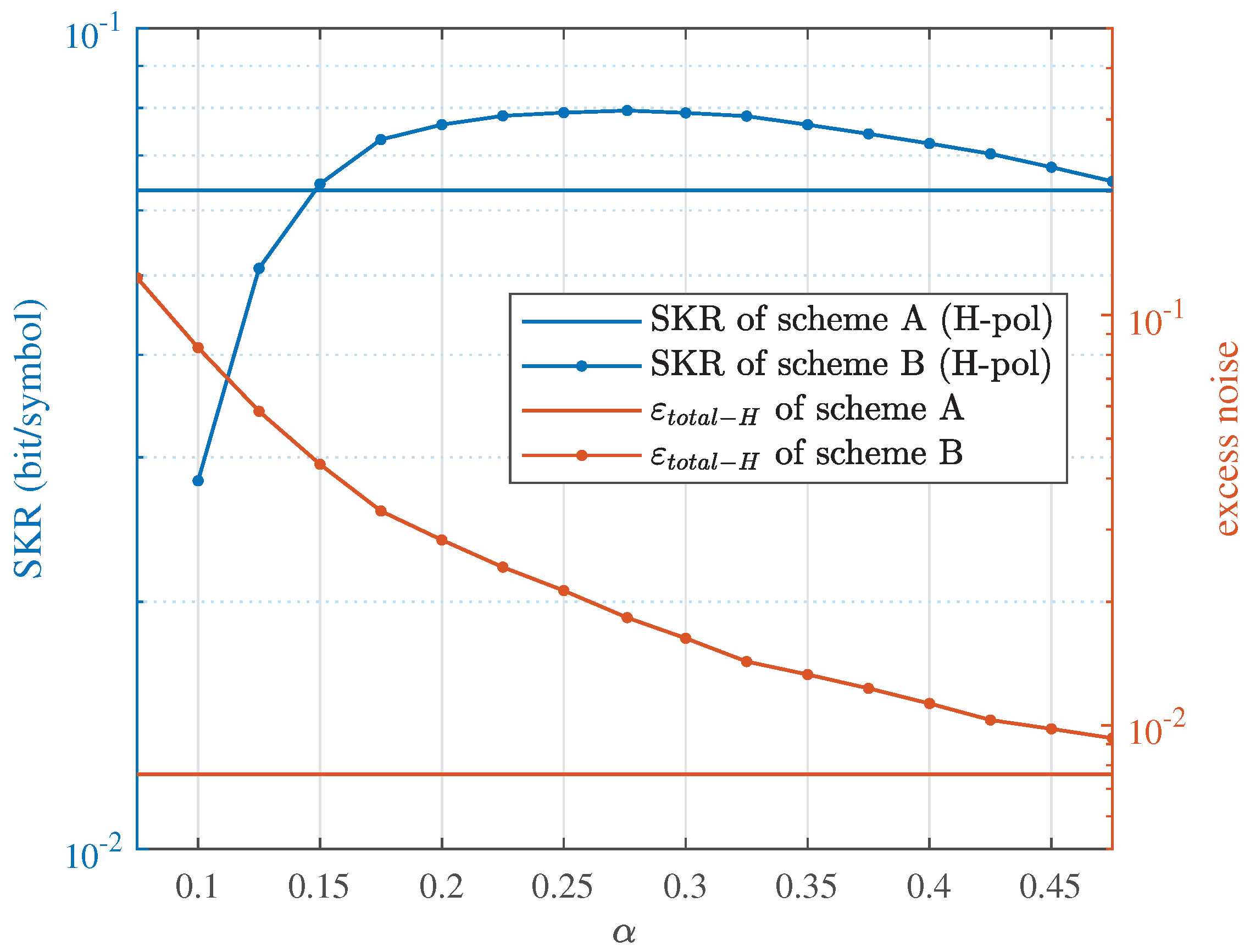
Figure 10 shows the
and SKR of scheme B with respect to different
, with the transmission distance is 20 km. The
and SKR of scheme A are also given to compare the performance of the two schemes. The results in
Figure 10 confirm that at the transmission distance of 20 km, scheme B can achieve higher SKR than scheme A by choosing the optimal
, even though the excess noise is much higher.
Based on the optimized strategy, the total excess noise and the corresponding optimal
that maximize the SKR of scheme B at different transmission distances for both H-pol and V-pol can be obtained, as shown in
Figure 11, where the
of scheme A are also depicted for comparison. For scheme A,
increases with the increase of transmission distance and the proportion of
and
are equivalent because scheme A can achieve the minimum excess noise induced by RSOP. Whereas for scheme B,
exhibits a trend of first decreasing and then increasing with distance, and
dominates the total excess noise because of the non-optimal compensation of RSOP compared to scheme A. The occurrence of the trend for scheme B is primarily because that the increasing of
results in the fast decreasing of
for short transmission distances while the slow decreasing of
for long transmission distances, which can also be seen from the results in
Figure 10. Meanwhile,
is higher than
for both scheme A and scheme B because of the extra excess noise induced by the pilot tone in V-pol. Besides, the optimal
also increases with the increase of transmission distance.
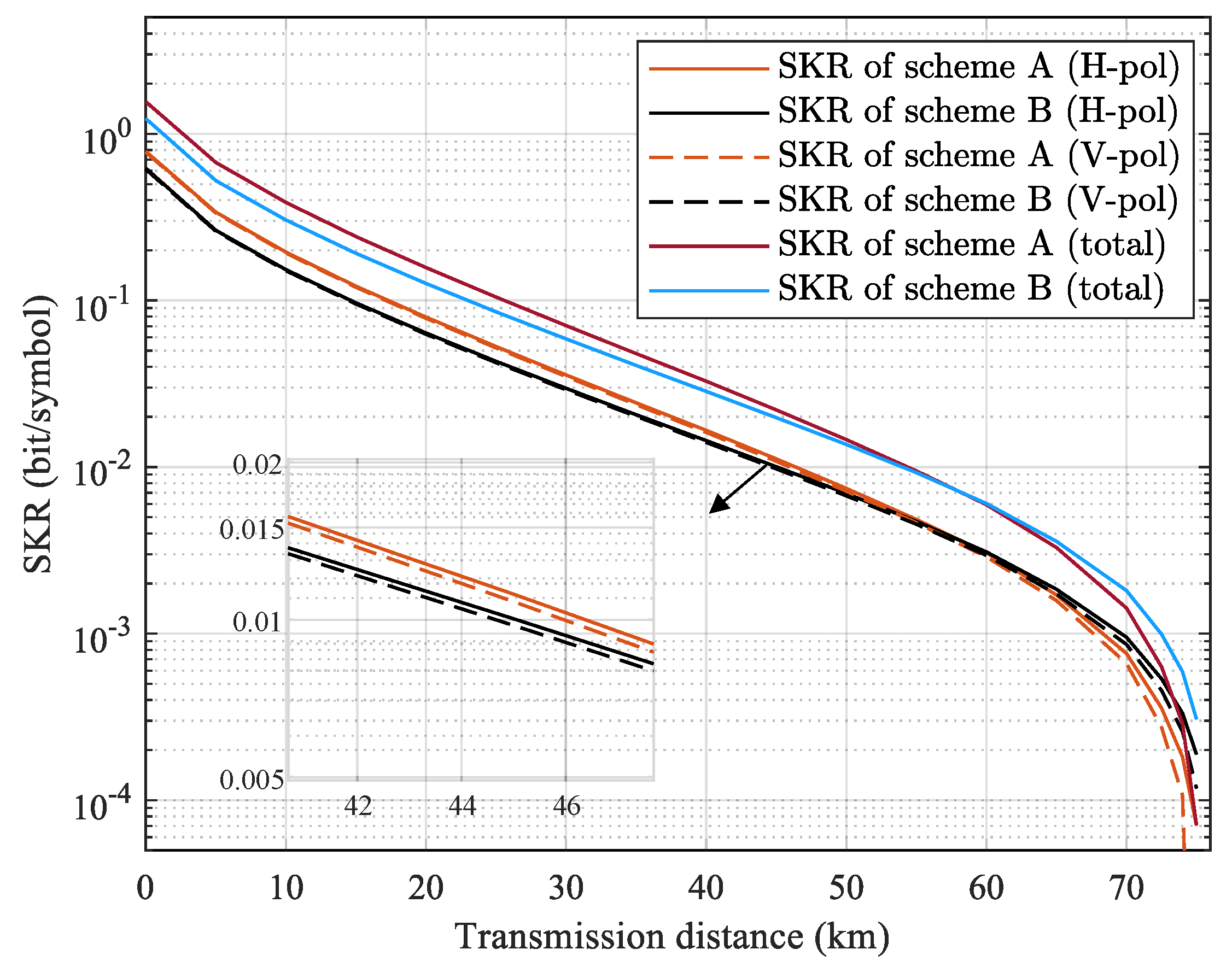
Finally, to evaluate the overall security of the system, the SKR (in bit/symbol) of scheme A and scheme B at different transmission distances are given in
Figure 12, where the SKR of H-pol and V-pol are calculated both individually and summed. The results show that scheme B can obtain higher SKR than scheme A for the transmission distances less than 55 km and lower SKR for the transmission distances more than 55 km. For example, the total SKR of around 0.67 bit/sample, 0.11 bit/sample, 0.015 bit/sample can be achieved for scheme B and 0.52 bit/sample, 0.09 bit/sample, 0.013 bit/sample for scheme A at the transmission distances of 5 km, 25 km and 50 km, respectively. Considering the baud rate of 2 Gbaud, the corresponding SKR in bps are 1340 Mbps, 220 Mbps, 30 Mbps for scheme B and 1040 Mbps, 180 Mbps, 26 Mbps for scheme A at the transmission distances of 5 km, 25 km and 50 km, respectively. It can be figured out that scheme B can realize the SKR gain of around 29 %, 22 %, and 15 % comparing to scheme A at the transmission distance of 5 km, 25 km and 50 km, respectively, which are significant for metropolitan-scale applications. In practical implementation, the noise level and the parameters may vary a lot, but the results shows a strategy of realizing the optimal performance with simplified DSP method. In addition, as shown in the inset of
Figure 12, the extra excess noise induced by the pilot tone in V-pol results in insignificant SKR loss compared with H-pol, which further proof that the FDM-based pilot-aided scheme contributes few impact on the performance of the system.
Author Contributions
Conceptualization, Gao, W. and Han, P.; methodology, Gao, W.; software, Gao, W.; validation, Kong, W., Dou, T. and Tang, J.; investigation, Hao, Y.; writing—original draft preparation, Gao, W.; writing—review and editing, Kong, W., Dou, T. and Tang, J.; supervision, Tang, J.. All authors have read and agreed to the published version of the manuscript.