Submitted:
26 August 2025
Posted:
26 August 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Computational Details
3. Results
- Optimal separation distances that are energetically most favorable for a given solute pair.
- Energy barriers associated with cluster rearrangement and growth.
- The transition from attractive to repulsive interaction regimes with distance.
4. Conclusions
- L12-forming elements — such as Zr, Sc, Ti, and Hf — which exhibit strong, well-defined attraction in the 2nd coordination shell, directly matching the atomic arrangement in coherent L12 trialuminide precipitates. This group also includes several rare-earth elements (e.g., Er, Lu, Tm, Yb) known to form similar coherent L12-type phases under appropriate conditions.
- Elements forming other structured precipitates — for instance, V, Cr, and Cu — which are among the most widely used in practice to produce semi-coherent or incoherent strengthening phases or dispersoids. While these are representative examples, other transition metals, though less frequently employed, can also form non-L12 intermetallics with aluminum.
Data Availability Statement
Acknowledgments
References
- McLeod, C.L.; Shaulis, B.J. Rare Earth Elements in Planetary Crusts: Insights from Chemically Evolved Igneous Suites on Earth and the Moon. Minerals 2018, 8, 455. [Google Scholar] [CrossRef]
- Andersen, S.J.; Marioara, C.D.; Friis, J.; Wenner, S.; Holmestad, R. Precipitates in aluminium alloys. Adv. Phys. X 2018, 3, 1479984. [Google Scholar] [CrossRef]
- Mookherjee, M. Aluminum. In Encyclopedia of Geochemistry; Springer, 2016; pp. 1–3.
- Stojanovic, B.; Bukvic, M.; Epler, I. Application of Aluminum and Aluminum Alloys in Engineering. SCIDAR-Digit. Arch. Univ. Kragujev. 2018. [CrossRef]
- Dyvik, S.; Manum, B.; Mork, J.; Luczkowski, M. Structural aluminum in architecture—The history and future of aluminum as a structural material. Structures and architecture, CRC Press 2019, 1. [Google Scholar]
- De Matteis, G.; Brando, G.; Mazzolani, F.M. Pure aluminium: An innovative material for structural applications in seismic engineering. Constr. Build. Mater. 2012, 26, 677–686. [Google Scholar] [CrossRef]
- Guo, S.; Yu, H.; Wang, Z.; Yu, W.; Cheng, W.; Huang, L.; Liu, C.; Yin, F.; Zhao, W.; Qin, C. Microstructural evolution and mechanical properties of pure aluminum upon multi-pass caliber rolling. Materials 2022, 15, 1206. [Google Scholar] [CrossRef]
- Dong, X.; Chen, F.; Chen, S.; Liu, Y.; Huang, Z.; Chen, H.; Feng, S.; Zhao, L.; Wu, Z.; Zhang, X. Microstructure and microhardness of hot extruded 7075 aluminum alloy micro-gear. J. Mater. Process. Technol. 2015, 219, 199–208. [Google Scholar] [CrossRef]
- Rana, R.; Purohit, R.; Das, S. Reviews on the influences of alloying elements on the microstructure and mechanical properties of aluminum alloys and aluminum alloy composites. Int. J. Sci. Res. Publ. 2012, 2, 1–7. [Google Scholar]
- Bishop, D.; Cahoon, J.; Chaturvedi, M.; Kipouros, G.; Caley, W. On enhancing the mechanical properties of aluminum P/M alloys. Mater. Sci. Eng. A 2000, 290, 16–24. [Google Scholar] [CrossRef]
- Murray, J.L. The Al- Mg (aluminum- magnesium) system. J. Phase Equilibria 1982, 3, 60–74. [Google Scholar] [CrossRef]
- Murray, J.; McAlister, A. The Al-Si (aluminum-silicon) system. Bull. Alloy Phase Diagrams 1984, 5, 74–84. [Google Scholar] [CrossRef]
- Plyushchay, I.; Wei, Z.; Bulut, N.; Gemming, S. First-Principles Modeling of Solid Solution Softening and Hardening Effects in Al–Mg–Zr–Si Aluminum Alloys. Adv. Eng. Mater. 2025, p. 2500321.
- Murray, J.; Peruzzi, A.; Abriata, J. The Al-Zr (aluminum-zirconium) system. J. Phase Equilibria 1992, 13, 277–291. [Google Scholar] [CrossRef]
- Meng, Q.; Frankel, G. Effect of Cu content on corrosion behavior of 7xxx series aluminum alloys. J. Electrochem. Soc. 2004, 151, B271. [Google Scholar] [CrossRef]
- Chuvil’deev, V.; Nokhrin, A.; Kopylov, V.; Gryaznov, M.Y.; Shotin, S.; Likhnitskii, C.; Kozlova, N.; Shadrina, Y.S.; Berendeev, N.; Melekhin, N.; et al. Investigation of mechanical properties and corrosion resistance of fine-grained aluminum alloys Al-Zn with reduced zinc content. J. Alloys Compd. 2022, 891, 162110. [Google Scholar] [CrossRef]
- Nam, S.W.; Lee, D.H. The effect of Mn on the mechanical behavior of Al alloys. Met. Mater. 2000, 6, 13–16. [Google Scholar] [CrossRef]
- Truax, D.; McMahon Jr, C. Plastic behavior of titanium-aluminum alloys. Mater. Sci. Eng. 1974, 13, 125–139. [Google Scholar] [CrossRef]
- Murray, J. The Al-Cr (aluminum-chromium) system. J. Phase Equilibria Diffus. 1998, 19, 368. [Google Scholar] [CrossRef]
- Murray, J. Al-V (aluminum-vanadium). Bull. Alloy Phase Diagrams 1989, 10, 351–357. [Google Scholar] [CrossRef]
- Taylor, A.; Jones, R.M. Constitution and magnetic properties of iron-rich iron-aluminum alloys. J. Phys. Chem. Solids 1958, 6, 16–37. [Google Scholar] [CrossRef]
- Eskin, D.G. Sc applications in aluminum alloys: Overview of Russian research in the 20th century. In Proceedings of the TMS Annual Meeting & Exhibition, Springer; 2018; pp. 1565–1572. [Google Scholar]
- Jia, Z.H.; Huang, H.L.; Wang, X.L.; Xing, Y.; Liu, Q. Hafnium in aluminum alloys: a review. Acta Metall. Sin. (Engl. Lett.) 2016, 29, 105–119. [Google Scholar] [CrossRef]
- Ryen, ∅. ; Holmedal, B.; Nijs, O.; Nes, E.; Sjölander, E.; Ekström, H.E. Strengthening mechanisms in solid solution aluminum alloys. Metall. Mater. Trans. A 2006, 37, 1999–2006. [Google Scholar] [CrossRef]
- Pedersen, K.O.; Westermann, I.; Furu, T.; Børvik, T.; Hopperstad, O.S. Influence of microstructure on work-hardening and ductile fracture of aluminium alloys. Mater. Des. 2015, 70, 31–44. [Google Scholar] [CrossRef]
- Fine, M.E. Precipitation hardening of aluminum alloys. Metall. Trans. A 1975, 6, 625–630. [Google Scholar] [CrossRef]
- Bloch, E. Dispersion-strengthened aluminium alloys. Metall. Rev. 1961, 6, 193–240. [Google Scholar] [CrossRef]
- Nes, E.; Holmedal, B.; Evangelista, E.; Marthinsen, K. Modelling grain boundary strengthening in ultra-fine grained aluminum alloys. Mater. Sci. Eng. A 2005, 410, 178–182. [Google Scholar] [CrossRef]
- Ma, K.; Wen, H.; Hu, T.; Topping, T.D.; Isheim, D.; Seidman, D.N.; Lavernia, E.J.; Schoenung, J.M. Mechanical behavior and strengthening mechanisms in ultrafine grain precipitation-strengthened aluminum alloy. Acta Mater. 2014, 62, 141–155. [Google Scholar] [CrossRef]
- Gupta, R.; Daniel, B. Strengthening mechanisms in Al3Zr-reinforced aluminum composite prepared by ultrasonic assisted casting. J. Mater. Eng. Perform. 2021, 30, 2504–2513. [Google Scholar] [CrossRef]
- Harada, Y.; Dunand, D. Microstructure of Al3Sc with ternary transition-metal additions. Mater. Sci. Eng. A 2002, 329, 686–695. [Google Scholar] [CrossRef]
- Knipling, K.E.; Dunand, D.C.; Seidman, D.N. Precipitation evolution in Al–Zr and Al–Zr–Ti alloys during aging at 450–600 C. Acta Mater. 2008, 56, 1182–1195. [Google Scholar] [CrossRef]
- Zhang, G.; Sun, F.; Liu, H.; Ren, X.; Xu, H.; Wang, M.; Fu, Y. Exploration of D022 type Al3TM (TM = Sc, Ti, V, Zr, Nb, Hf, Ta): elastic anisotropy, electronic structures, work function and experimental design. Materials 2021, 14, 2206. [Google Scholar] [CrossRef] [PubMed]
- Knipling, K.E.; Karnesky, R.A.; Lee, C.P.; Dunand, D.C.; Seidman, D.N. Precipitation evolution in Al–0.1 Sc, Al–0.1 Zr and Al–0.1 Sc–0.1 Zr (at.%) alloys during isochronal aging. Acta Mater. 2010, 58, 5184–5195. [Google Scholar] [CrossRef]
- Knipling, K.E.; Dunand, D.C.; Seidman, D.N. Nucleation and precipitation strengthening in dilute Al-Ti and Al-Zr alloys. Metall. Mater. Trans. A 2007, 38, 2552–2563. [Google Scholar] [CrossRef]
- Liu, S.; Liu, F.; Yan, Z.; Nie, B.; Fan, T.; Chen, D.; Song, Y. Nucleation of L12-Al3M (M = Sc, Er, Y, Zr) nanophases in aluminum alloys: a first-principles thermodynamics study. Crystals 2023, 13, 1228. [Google Scholar] [CrossRef]
- Elasheri, A.; Elgallad, E.M.; Parson, N.; Chen, X.G. Nucleation and transformation of Zr-bearing dispersoids in Al–Mg–Si 6xxx alloys. J. Mater. Res. 2023, 38, 696–707. [Google Scholar] [CrossRef]
- Jassim, A.H.M. Influence of Zirconium Additions and Ageing Time on Some Mechanical Properties of (6063) Aluminum Alloy: The Influence of Zirconium Additions and the Aging Time on Some Mechanical Properties. J. Univ. Kerbala 2016, 14, 3. [Google Scholar]
- Bolibruchová, D.; Sỳkorová, M.; Brüna, M.; Matejka, M.; Širanec, L. Effect of Zr addition on selected properties and microstructure of aluminum alloy AlSi5Cu2Mg. Int. J. Met. 2023, 17, 2598–2611. [Google Scholar] [CrossRef]
- Šmalc, J.; Zaky, A.; Markoli, B.; Šturm, R. Microstructural Stability and High-Temperature Mechanical Behavior of Al–Ni–Zr Alloy Strengthened by L12-Al3Zr Precipitates. Materials 2025, 18, 3068. [Google Scholar] [CrossRef]
- Elasheri, A.; Elgallad, E.; Parson, N.; Chen, X.G. Evolution of Zr-bearing dispersoids during homogenization and their effects on hot deformation and recrystallization resistance in Al-0.8% Mg-1.0% Si alloy. J. Mater. Eng. Perform. 2021, 30, 7851–7862. [Google Scholar] [CrossRef]
- Liu, F.; Chen, S.; Dong, Q.; Qin, J.; Li, Z.; Zhang, B.; Nagaumi, H. Tailoring microstructure and mechanical properties of Al-Mg-Si-Cu alloy with varying Mn and/or Cr additions. Mater. Sci. Eng. A 2024, 892, 146053. [Google Scholar] [CrossRef]
- Knipling, K.E.; Dunand, D.C. Creep resistance of cast and aged Al–0.1 Zr and Al–0.1 Zr–0.1 Ti (at.%) alloys at 300–400 C. Scr. Mater. 2008, 59, 387–390. [Google Scholar] [CrossRef]
- Fuller, C.B.; Murray, J.L.; Seidman, D.N. Temporal evolution of the nanostructure of Al (Sc, Zr) alloys: Part I–Chemical compositions of Al3(Sc1-xZrx) precipitates. Acta Mater. 2005, 53, 5401–5413. [Google Scholar] [CrossRef]
- Miyoshi, H.; Kimizuka, H.; Ishii, A.; Ogata, S. Competing nucleation of single-and double-layer Guinier–Preston zones in Al–Cu alloys. Sci. Rep. 2021, 11, 4503. [Google Scholar] [CrossRef] [PubMed]
- Mehta, B.; Frisk, K.; Nyborg, L. Role of Cr in Mn-rich precipitates for Al–Mn–Cr–Zr-based alloys tailored for additive manufacturing. Calphad 2024, 84, 102667. [Google Scholar] [CrossRef]
- Fan, Y.; Makhlouf, M.M. Precipitation strengthening of aluminum by transition metal aluminides. Master of Science Thesis, Worcester Polytechnic Institute, Worcester, MA 2015, 1609. [Google Scholar]
- Uesugi, T.; Higashi, K. Modeling Solid Solution Strengthening Using First-Principles Results of Misfit Strain with Friedel Model in Al-Based Alloys. In Proceedings of the 12th International Conference on Aluminium Alloys, Yokohama, Japan, September 5-9 2010; pp. 1421–1425. [Google Scholar]
- Gonze, X.; Beuken, J.M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-principles computation of material properties : the ABINIT software project. Comp. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Goedecker, S. Fast radix 2, 3, 4 and 5 kernels for Fast Fourier Transformations on computers with overlapping multiply-add instructions. SIAM J. Sci. Comput. 1997, 18, 1605. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Anglade, P.M.; Beuken, J.M.; et al. The ABINIT code, 2024.
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Hamann, D. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Wendler, E.; Hübner, R.; Anwand, W.; Wang, G.; Chen, X.; Tong, W.; Yang, Z.; Munnik, F.; et al. Defect-induced magnetism in SiC: Interplay between ferromagnetism and paramagnetism. Phys. Rev. B 2015, 92, 174409. [Google Scholar] [CrossRef]
- Berlin, J.; Stegmüller, T.; Haider, F. Observation of in-plane oriented Guinier-Preston zones in Al-Cu. Micron 2023, 173, 103504. [Google Scholar] [CrossRef]
- Suzuki, T.; Yabe, T.; Enoki, M.; Ohtani, H. Thermodynamic investigation of Guinier–Preston zone formation in the Al–Cu binary system. Scr. Mater. 2025, 265, 116746. [Google Scholar] [CrossRef]
- Ahmad, Z.; Aleem, A.A.B.; Abbas, M. Effect of scandium doping on the corrosion resistance and mechanical behavior of Al-3Mg alloy in neutral chloride solutions. Mater. Sci. Appl. 2011, 2, 244–250. [Google Scholar] [CrossRef]
- Wang, F.; Chiu, Y.L.; Eskin, D.; Du, W.; Shearing, P.R. A grain refinement mechanism of cast commercial purity aluminium by vanadium. Mater. Charact. 2021, 181, 111468. [Google Scholar] [CrossRef]
- Wang, S.; Dong, L.; Han, X.; Fan, Y.; Chen, B. Orientations and interfaces between α’-Al13Cr4Si4 and the matrix in Al-Si-Cr-Mg alloy. Mater. Charact. 2020, 160, 110096. [Google Scholar] [CrossRef]
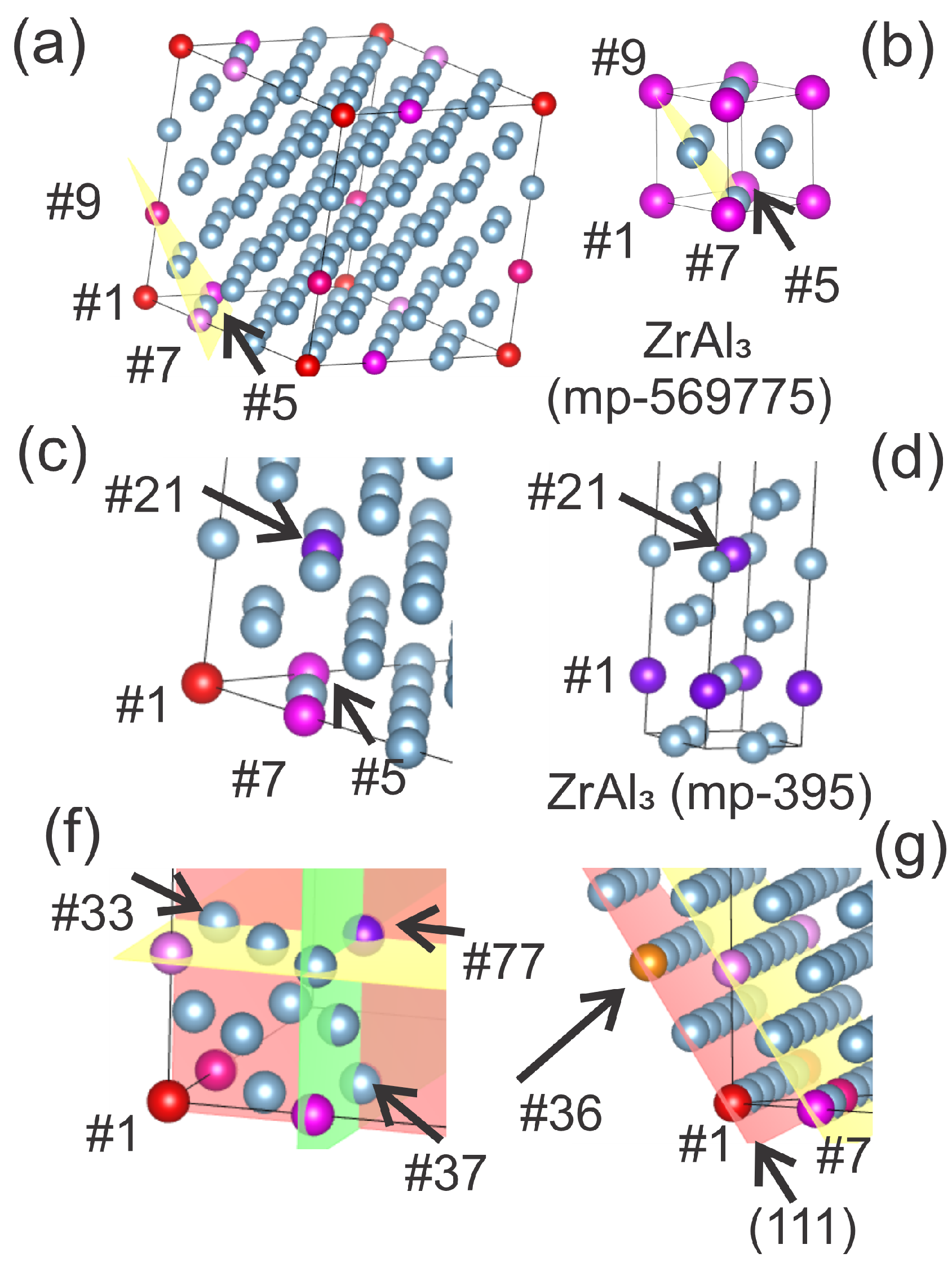
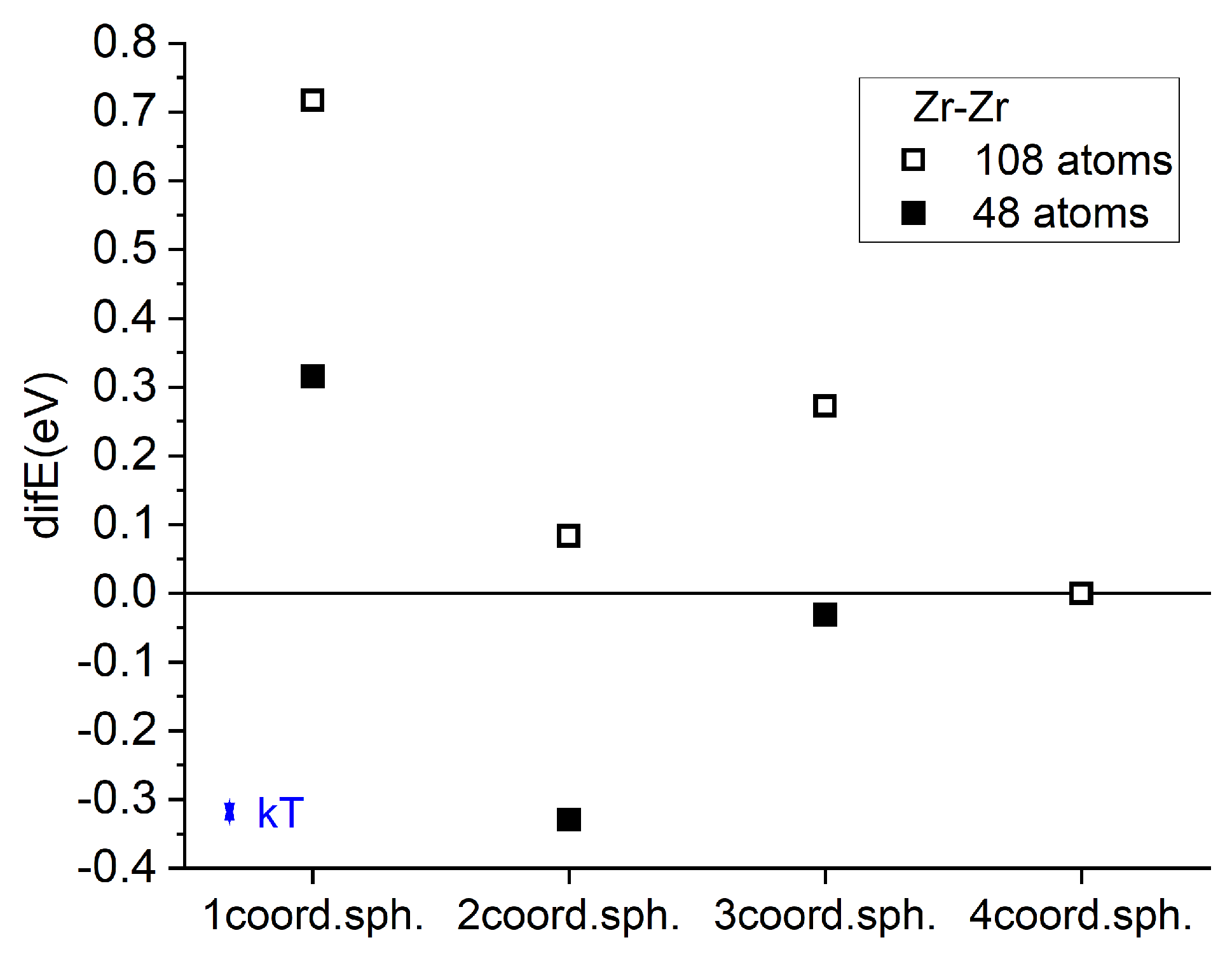
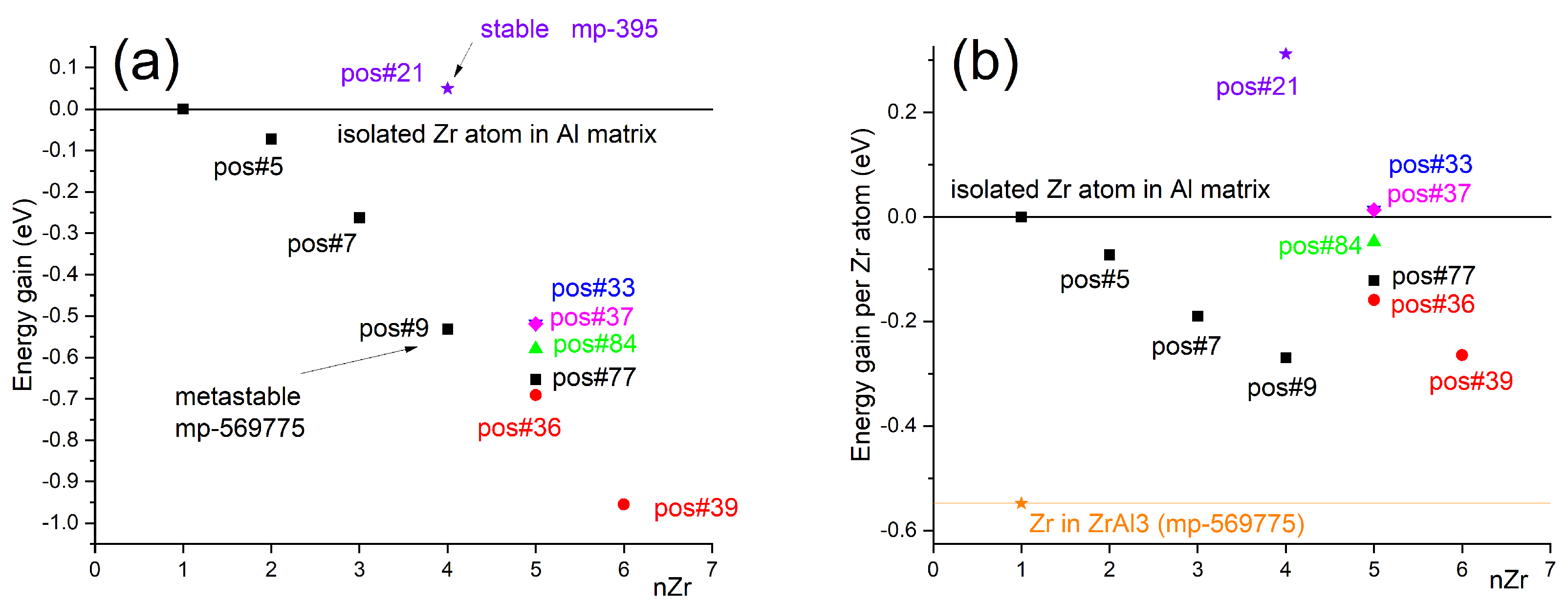

| Precipitate | Phase | Condition | Stability | Lattice constant |
|---|---|---|---|---|
| Al3Zr | L12 | <425 ∘C | metastable | - Å |
| D023 | >450 ∘C | stable | Å, Å, | |
| Al3Sc | L12 | 200-650 ∘C | stable | Å |
| Al3Ti | L12 | rapid cooling | metastable | Å, Å, |
| D022 | 500-650 ∘C | stable | Å, Å, | |
| Al3Hf | L12 | 250-350 ∘C | metastable | - Å |
| D022 | 450-550 ∘C | stable | – | |
| D023 | >550 ∘C | stable | Å, Å |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





