Dynamic and Mixed-Precision Techniques for Scalable Iterative Generative Modeling

1. Introduction

In recent years, the remarkable progress in large-scale generative modeling has been driven by the advent of foundation models, with diffusion models standing out as a particularly powerful class of generative architectures [1]. Diffusion models, which generate data by reversing a gradual noising process, have emerged as the state-of-the-art across a broad spectrum of applications, including high-fidelity image synthesis, text-to-image generation, video creation, molecular design, medical imaging, and multimodal reasoning [2]. Their success is largely attributed to their theoretical grounding in probabilistic modeling, their scalability to massive datasets, and their ability to capture complex, multimodal data distributions with unprecedented precision and realism [3]. However, the adoption and deployment of such models in large-scale real-world settings remain severely constrained by their extreme computational and memory requirements [4]. Unlike earlier generative models such as GANs and VAEs, diffusion-based generative models involve iterative denoising steps, often requiring hundreds or thousands of neural function evaluations during inference, in addition to large parameter footprints that can range from hundreds of millions to tens of billions of parameters [5]. This computational burden has raised critical concerns regarding their training and deployment costs, latency, energy consumption, and accessibility, especially in the context of ubiquitous generative AI services that demand scalability and efficiency [6,7]. To address these challenges, the research community has increasingly focused on model compression techniques, with quantization and low-precision computation emerging as pivotal strategies [8]. Quantization, in its most general sense, refers to the mapping of high-precision numerical representations (e.g., 32-bit floating point) to lower-bit representations (e.g., 16-bit, 8-bit, 4-bit, or even binary), thereby reducing memory consumption and computational complexity while attempting to maintain acceptable levels of performance. Low-precision computation encompasses a broader set of strategies aimed at reducing the numerical resolution of weights, activations, gradients, and intermediate representations, enabling efficient utilization of modern accelerators such as GPUs, TPUs, and emerging custom AI hardware [9]. While quantization has been extensively explored in the context of discriminative deep learning models (e.g., convolutional networks for vision or transformers for language), its application to diffusion models and large-scale foundation models introduces unique technical and theoretical challenges [10]. Unlike discriminative models that primarily optimize for classification or regression accuracy, generative diffusion models must preserve fine-grained probabilistic dynamics over iterative steps, where even small numerical distortions can accumulate and propagate across hundreds of denoising iterations, potentially degrading generative quality in subtle but significant ways [11]. The significance of studying quantization and low-precision techniques for diffusion models in the era of foundation models lies in several converging factors. First, the exponential growth in the size of generative models has led to training costs measured in millions of GPU hours and deployment costs that are infeasible for smaller research groups or industry players outside a handful of technology giants [12]. By enabling reduced precision, it becomes possible to dramatically lower the memory footprint, thereby increasing hardware utilization efficiency, improving inference throughput, and reducing the energy footprint of generative AI systems [13]. Second, the democratization of generative models depends on the ability to make them deployable on resource-constrained environments, such as edge devices, mobile platforms, and personal workstations. Quantization represents a primary enabler of this transition, reducing the gap between high-performance research prototypes and practical, accessible generative AI applications. Third, low-precision optimization offers critical opportunities for scaling future foundation models even further, as memory and bandwidth constraints represent the most significant bottlenecks in training trillion-parameter-scale generative systems. Despite these promises, quantizing diffusion models remains an open and complex research frontier. The iterative structure of diffusion inference pipelines makes them uniquely sensitive to numerical perturbations, as quantization-induced errors can accumulate across timesteps, leading to distributional shifts and degradation in sample quality. Furthermore, the multimodal nature of generative outputs (e.g., images, videos, and audio conditioned on language or other modalities) demands that quantization preserve not only task-level fidelity but also subtle perceptual characteristics such as texture sharpness, color distribution, and semantic consistency. Standard quantization strategies developed for classification models often fail to transfer directly, motivating the need for specialized methods such as timestep-adaptive quantization, error-resilient noise schedulers, quantization-aware training for iterative generative processes, and hybrid approaches that selectively allocate precision across different components of the model (e.g., denoising networks, attention modules, and sampling schedules). Moreover, quantization interacts in non-trivial ways with other efficiency techniques such as pruning, distillation, and accelerator-aware kernel design, raising questions about composability and trade-offs in integrated model compression pipelines. The emergence of foundation models adds further complexity to this landscape. Unlike domain-specific generative models, foundation models are trained on massive, heterogeneous datasets and are designed to generalize across modalities and tasks with minimal fine-tuning [14]. This generality introduces stricter requirements for quantization and low-precision methods, as errors induced by reduced precision can propagate differently depending on the downstream task or modality, making robustness a central challenge. At the same time, foundation models create unique opportunities: their sheer scale may offer redundancy that can be exploited for aggressive quantization without significant loss of performance, while their modular architectures open avenues for heterogeneous precision allocation [15]. The study of quantization in this context is therefore not only about improving efficiency, but also about rethinking the design principles of foundation-scale generative systems, potentially leading to architectures that are explicitly co-designed for low-precision computation from the ground up [16]. This survey undertakes a comprehensive review of the emerging field of quantization and low-precision strategies for diffusion models in the context of large foundation models. Our goal is to provide a detailed account of the theoretical motivations, algorithmic innovations, empirical results, and open challenges that define this research space. We systematically examine existing quantization approaches as applied to diffusion and foundation models, analyze their trade-offs in terms of quality, efficiency, and robustness, and highlight the key challenges that remain unsolved. Furthermore, we situate quantization within the broader landscape of efficiency-oriented methods for large generative models, emphasizing synergies and tensions with related techniques such as distillation, pruning, caching, adaptive sampling, and hardware-aware co-design [17]. By consolidating insights from across the rapidly growing literature, we aim to provide both a roadmap for researchers entering the field and a critical foundation for future innovation at the intersection of generative modeling, numerical optimization, and scalable AI systems. Ultimately, understanding and advancing quantization for diffusion models in foundation-scale contexts is central to unlocking the next generation of generative AI systems that are not only powerful and versatile, but also efficient, sustainable, and accessible to the global community [18].

2. Mathematical Foundations of Quantization for Diffusion Models

The study of quantization in the context of diffusion models requires a rigorous mathematical formalization of both the diffusion generative process and the underlying numerical approximations introduced by reduced-precision computation. In this section, we provide a detailed mathematical treatment of the fundamental principles governing quantization and its interaction with diffusion-based generative modeling. By expressing these ideas explicitly in terms of probability distributions, stochastic differential equations, and quantization operators, we aim to establish a formal foundation for analyzing the accuracy, stability, and robustness of low-precision generative modeling.

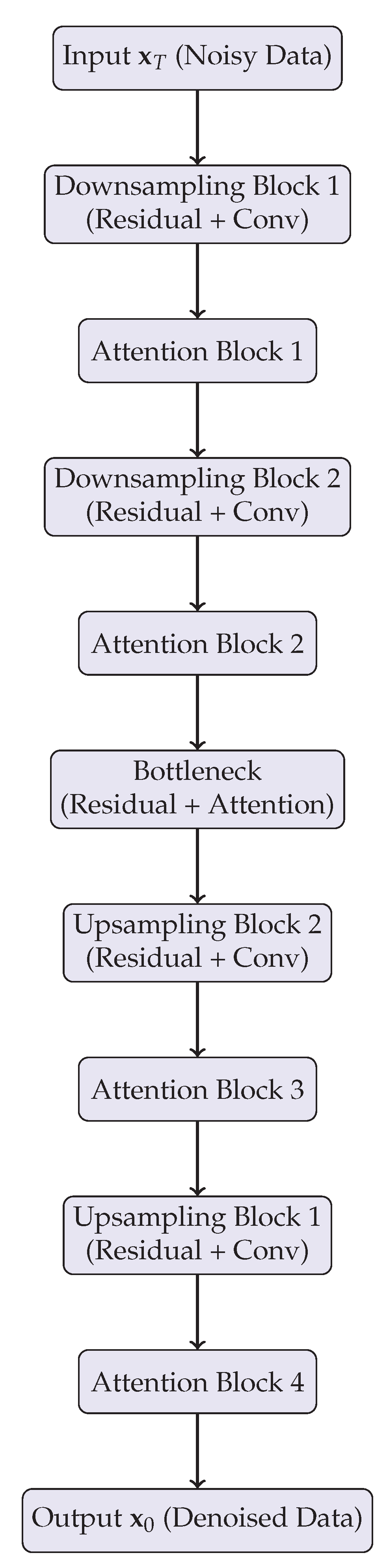
2.1. Diffusion Model Formulation

Let ${\mathbf{x}}_0\in {\mathbb{R}}^d$ denote a data sample drawn from an unknown data distribution $p_{\mathrm{data}}\left({\mathbf{x}}_0\right)$[19]. The forward diffusion process gradually perturbs ${\mathbf{x}}_0$ with additive Gaussian noise according to a predefined variance schedule ${\left\{{\beta }_t\right\}}_{t=1}^T$, where T denotes the number of timesteps [20]. The forward process is defined as a Markov chain:

$$q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I}\right),$$

(1)

for $t=1,\dots ,T$. The marginal distribution of ${\mathbf{x}}_t$ can be expressed in closed form as:

$$q({\mathbf{x}}_t\mid {\mathbf{x}}_0)=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{{\overline{\alpha }}_t}{\mathbf{x}}_0,(1-{\overline{\alpha }}_t)\mathbf{I}\right),$$

(2)

where ${\alpha }_t=1-{\beta }_t$ and ${\overline{\alpha }}_t={\prod }_{s=1}^t{\alpha }_s$[21]. The reverse process is parameterized by a neural network, typically denoted ${ϵ}_{\theta }({\mathbf{x}}_t,t)$, which approximates the noise $ϵ$ added at step t [22]. The reverse transition distribution is modeled as:

$$p_{\theta }({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)=\mathcal{N}\left({\mathbf{x}}_{t-1};{\mu }_{\theta }({\mathbf{x}}_t,t),{\mathrm{\Sigma }}_{\theta }({\mathbf{x}}_t,t)\right),$$

(3)

where the mean ${\mu }_{\theta }$ depends on ${ϵ}_{\theta }$ and the noise variance schedule. Sampling from the model requires iteratively applying these reverse transitions from $t=T$ down to $t=1$, a process that can be computationally intensive due to the repeated evaluations of ${ϵ}_{\theta }$ [23].

2.2. Quantization as a Mapping Operator

Quantization can be mathematically formulated as a mapping function $Q:\mathbb{R}\to \mathcal{C}$, where $\mathcal{C}\subset \mathbb{R}$ is a finite set of representable values determined by the bitwidth b. A generic uniform quantizer for a scalar x with scale factor $s>0$ and integer precision b can be expressed as:

$$Q\left(x\right)=\mathrm{clip}\left(⌊{\displaystyle \frac{x}{s}}⌉,-2^{b-1},2^{b-1}-1\right)·s,$$

(4)

where $\lfloor ·\rceil$ denotes rounding to the nearest integer, and clip ensures values remain within the representable dynamic range [24]. Extending this operator elementwise to vectors, matrices, or tensors yields:

$$Q\left(\mathbf{X}\right)=\left(Q\left(x_{ij}\right)\right)\forall x_{ij}\in \mathbf{X}.$$

(5)

The quantization error for a scalar can be defined as:

$$e\left(x\right)=Q\left(x\right)-x,$$

(6)

and for a tensor $\mathbf{X}$ we define the error distribution as:

$$\mathbf{E}=Q\left(\mathbf{X}\right)-\mathbf{X}.$$

(7)

This error distribution can be modeled as a stochastic perturbation if the rounding scheme is stochastic (e.g., randomized rounding), or as a deterministic bias if rounding is always toward the nearest representable value [25].

2.3. Interaction Between Quantization and Diffusion Processes

In the context of diffusion models, quantization affects multiple components simultaneously, including:

• Model parameters: The neural network parameters $\theta$ are quantized to $\widehat{\theta }=Q\left(\theta \right)$, altering the learned function ${ϵ}_{\widehat{\theta }}(·)$ [26].
• Intermediate activations: During inference, intermediate feature maps ${\mathbf{h}}_t$ are quantized to ${\widehat{\mathbf{h}}}_t=Q\left({\mathbf{h}}_t\right)$ [27].
• Noise predictions: The predicted noise ${ϵ}_{\theta }({\mathbf{x}}_t,t)$ is quantized, introducing additional bias to the reverse denoising process.

Let ${\widehat{p}}_{\theta }$ denote the distribution defined by a quantized diffusion model. The Kullback–Leibler divergence between the quantized generative process ${\widehat{p}}_{\theta }\left({\mathbf{x}}_0\right)$ and the original data distribution $p_{\mathrm{data}}\left({\mathbf{x}}_0\right)$ provides a measure of generative fidelity [28]:

$$D_{\mathrm{KL}}\left(p_{\mathrm{data}}\left({\mathbf{x}}_0\right)\parallel {\widehat{p}}_{\theta }\left({\mathbf{x}}_0\right)\right).$$

(8)

This divergence can be decomposed into contributions from timestep-dependent quantization errors. Specifically, if ${\mathbf{e}}_t$ denotes the quantization error introduced at timestep t, then the cumulative error after T steps can be approximated by:

$${\mathbf{E}}_{\mathrm{cumulative}}=\sum _{t=1}^T{\mathbf{J}}_t{\mathbf{e}}_t,$$

(9)

where ${\mathbf{J}}_t$ is the Jacobian of the denoising function with respect to the quantized components at step t. This formulation reveals that even small quantization errors may accumulate exponentially due to the iterative structure of diffusion sampling [29].

2.4. Precision-Performance Trade-Offs

The central challenge in quantizing diffusion models is to balance the efficiency gains from reduced precision against the degradation in generative quality. Let ${\mathcal{L}}_{\mathrm{full}}$ denote the training objective in full precision, typically a weighted mean-squared error between the true noise $ϵ$ and the predicted noise ${ϵ}_{\theta }$ [30]:

$${\mathcal{L}}_{\mathrm{full}}\left(\theta \right)={\mathbb{E}}_{t,{\mathbf{x}}_0,ϵ}\left[\parallel ϵ-{ϵ}_{\theta }(\sqrt{{\overline{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,t){\parallel }_2^2\right].$$

(10)

Under quantization, this objective becomes:

$${\mathcal{L}}_{\mathrm{quant}}\left(\widehat{\theta }\right)={\mathbb{E}}_{t,{\mathbf{x}}_0,ϵ}\left[\parallel ϵ-Q\left({ϵ}_{\widehat{\theta }}(Q\left({\mathbf{x}}_t\right),t)\right){\parallel }_2^2\right],$$

(11)

which explicitly incorporates quantization into both inputs and outputs. The difference

$$\Delta \mathcal{L}={\mathcal{L}}_{\mathrm{quant}}\left(\widehat{\theta }\right)-{\mathcal{L}}_{\mathrm{full}}\left(\theta \right)$$

(12)

quantifies the penalty introduced by reduced precision. The efficiency gains can be expressed as functions of bitwidth b. For instance, memory footprint $M\left(b\right)$ scales as:

$$M\left(b\right)\propto {\displaystyle \frac{b}{32}},$$

(13)

while computational throughput on modern hardware accelerators often scales superlinearly due to specialized low-precision units (e.g., tensor cores). Thus, the optimization objective in practice becomes a multi-objective trade-off:

$$\underset{b,\widehat{\theta }}{min}\Delta \mathcal{L}(b,\widehat{\theta })\mathrm{subject}\mathrm{to}C\left(b\right)\le C_{\mathrm{budget}},M\left(b\right)\le M_{\mathrm{budget}},$$

(14)

where $C\left(b\right)$ denotes computational cost, $M\left(b\right)$ denotes memory cost, and $C_{\mathrm{budget}},M_{\mathrm{budget}}$ are hardware constraints [31].

2.5. Summary of Mathematical Insights

This mathematical formulation underscores that quantization in diffusion models is not merely an engineering optimization but a deeply probabilistic challenge [32]. The accumulation of quantization errors across iterative stochastic steps, the high sensitivity of generative quality to subtle numerical distortions, and the tight coupling between efficiency and fidelity all demand principled approaches [33]. By leveraging formal error models, divergence measures, and optimization frameworks, researchers can better understand and mitigate the trade-offs inherent in low-precision generative modeling for large foundation models.

3. Quantization Techniques for Diffusion Models

Quantization techniques for diffusion models encompass a diverse set of strategies that aim to reduce precision in a way that balances computational efficiency with the preservation of generative fidelity. Unlike conventional discriminative models, where quantization often affects a single feedforward pass, diffusion models involve iterative denoising across multiple timesteps, which amplifies the influence of even minor quantization errors. Consequently, specialized methods are required to adapt quantization techniques to the unique structure and sensitivity of diffusion-based generative processes. In this section, we provide an extensive discussion of several prominent quantization approaches, ranging from uniform and non-uniform quantization schemes to adaptive precision strategies that explicitly account for timestep dynamics and feature distributions. We also present a taxonomy of methods that distinguishes between post-training quantization, quantization-aware training, mixed-precision quantization, and hybrid approaches that combine quantization with other efficiency-oriented techniques. The discussion is further supplemented by a comprehensive comparative table summarizing the key characteristics, advantages, and challenges of each technique [34]. A fundamental distinction in quantization arises between uniform and non-uniform schemes [35]. Uniform quantization employs evenly spaced quantization levels across the representable range, making it hardware-friendly and efficient for accelerator deployment. In this setting, each real-valued parameter x is mapped to its nearest representable value according to a fixed scale factor. While uniform quantization is widely adopted due to its simplicity and compatibility with integer arithmetic, it is often suboptimal for diffusion models, where parameter and activation distributions can be highly skewed or heavy-tailed [36]. Non-uniform quantization, on the other hand, allocates quantization levels more densely in regions of higher probability density, thereby reducing quantization error for typical values while sacrificing representation capacity for extreme values. This property is particularly relevant for diffusion models, where the noise prediction function frequently operates in regimes dominated by Gaussian-distributed signals, suggesting that logarithmic or learned quantization levels may offer significant advantages [37]. However, non-uniform schemes are more difficult to implement efficiently in hardware, as they require additional lookup operations or nonlinear mapping functions [38]. Another major axis of differentiation is the training strategy employed. Post-training quantization (PTQ) involves quantizing a pre-trained diffusion model without additional fine-tuning. PTQ is attractive because it eliminates the need for costly retraining, making it a practical approach for large foundation-scale diffusion models where retraining can be prohibitively expensive. Nevertheless, PTQ can introduce significant degradation in generative fidelity, particularly under aggressive quantization (e.g., 4-bit or lower). Quantization-aware training (QAT), in contrast, integrates quantization effects into the training loop by simulating quantized computations during forward passes and backpropagation [39]. This allows the model to adapt its parameters to compensate for quantization errors, leading to better robustness at low precision [40]. The cost of QAT, however, is that it requires extensive computational resources, as training large diffusion models from scratch or even fine-tuning them with QAT is nontrivial. Hybrid approaches, such as lightweight QAT applied to specific sensitive modules (e.g., attention layers) while keeping the remainder of the model quantized with PTQ, have recently gained attention as a promising middle ground [41]. Beyond these standard techniques, diffusion models also motivate novel precision-adaptive methods. For instance, timestep-adaptive quantization allocates higher precision to early or late stages of the reverse diffusion process, where error sensitivity is highest, while aggressively quantizing intermediate stages [42]. Similarly, mixed-precision quantization assigns different bitwidths to different network components, such as using higher precision for attention matrices while quantizing feedforward layers more aggressively. This strategy leverages the observation that not all modules contribute equally to generative fidelity, and thus resource allocation can be optimized accordingly. Furthermore, dynamic quantization strategies that adjust precision on the fly depending on input statistics or intermediate feature norms provide another frontier for efficiency optimization. These techniques highlight the increasingly sophisticated interplay between algorithm design, numerical representation, and the stochastic structure of diffusion processes [43]. To summarize the landscape of quantization techniques for diffusion models, we present Table 1, which provides a structured comparison across several key dimensions, including precision allocation strategy, training requirements, hardware compatibility, and impact on generative quality. This table is designed to provide both a quick reference and a foundation for more detailed discussion in subsequent sections

The table emphasizes that no single quantization technique provides a universally optimal solution for diffusion models in the foundation model regime. Instead, the appropriate choice depends heavily on the deployment context, hardware constraints, and fidelity requirements of the target application [44]. For example, uniform PTQ may be sufficient for lightweight deployment on edge devices where computational simplicity is paramount, whereas QAT or mixed-precision schemes may be necessary to preserve fidelity in high-end generative tasks such as photorealistic image synthesis or scientific simulations. Furthermore, as diffusion models evolve toward larger and more modular architectures, the potential for integrating multiple quantization strategies within a single model becomes increasingly attractive, suggesting that the future of quantization lies in compositional and adaptive approaches rather than monolithic schemes [45]. This realization motivates further exploration into precision allocation strategies that are not only hardware-aware but also explicitly tailored to the iterative generative dynamics of diffusion processes [46].

4. Architectural Considerations and Layer-wise Sensitivity in Quantized Diffusion Models

The process of quantizing diffusion models is inextricably linked to the architectural composition of the model itself [47]. Unlike simpler feedforward networks, diffusion models typically consist of multi-scale convolutional blocks, self-attention layers, residual connections, and normalization modules, organized in a manner that reflects the iterative nature of the denoising process [48]. Each architectural component exhibits varying sensitivity to low-precision representation, which necessitates a layer-wise or module-wise analysis to determine optimal quantization strategies [49]. For example, attention mechanisms, which aggregate global information across spatial or temporal dimensions, often dominate the overall error budget due to the accumulation of small quantization errors over high-dimensional operations [50]. Conversely, pointwise feedforward layers may tolerate more aggressive quantization with minimal impact on generative quality [51]. Similarly, normalization layers, which stabilize the distribution of intermediate features, are particularly sensitive to quantization because small shifts in mean or variance can propagate across multiple denoising steps, leading to compounding distortions in the generated output. Understanding these sensitivities is critical for designing mixed-precision or adaptive quantization schemes that exploit the redundancy and error resilience inherent in certain components while preserving high fidelity in critical modules [52]. Layer-wise sensitivity analysis can be formalized using gradient-based or Hessian-based metrics that quantify the impact of perturbations in each parameter block on the model’s output distribution. Let $\mathcal{L}\left(\theta \right)$ denote the training loss of a diffusion model, typically a denoising score matching objective [53]. The sensitivity $S_l$ of layer l to quantization can be defined as the expected squared gradient with respect to the layer parameters ${\theta }_l$ [54]:

$$S_l={\mathbb{E}}_{{\mathbf{x}}_0,t,ϵ}\left[\parallel {\displaystyle \frac{\partial \mathcal{L}\left(\theta \right)}{\partial {\theta }_l}}{\parallel }_2^2\right].$$

(15)

Higher values of $S_l$ indicate that small perturbations, such as quantization errors, have a greater influence on the model’s overall loss [55]. This metric provides a principled way to prioritize precision allocation, suggesting that layers with high $S_l$ should be assigned higher bitwidths, whereas layers with low $S_l$ can be aggressively quantized without significant degradation. From an architectural perspective, modern diffusion models often employ hierarchical U-Net structures with multiple downsampling and upsampling stages, interleaved with residual and attention blocks [56]. Each stage of the hierarchy corresponds to a different spatial scale, and errors introduced at higher-resolution stages tend to have a more pronounced perceptual impact on the final generated image [57]. Therefore, precision allocation strategies that are aware of the hierarchical structure can substantially improve performance. Additionally, the iterative nature of the reverse diffusion process means that early timesteps, which correspond to coarse-grained reconstruction, may tolerate slightly lower precision, while later timesteps, responsible for fine-grained detail refinement, require higher fidelity. This temporal sensitivity interacts with architectural considerations, suggesting that layer-wise, stage-wise, and timestep-wise precision allocation must be considered simultaneously for optimal quantization. To illustrate the hierarchical and layer-wise structure of a typical diffusion model, Figure 1 presents a simplified schematic using TikZ [58]. The figure emphasizes the vertical organization of stages and highlights key modules that are often targeted for precision-aware optimization [59]. The vertical layout aligns with the natural progression of feature resolutions from coarse to fine, facilitating clear visualization of the components most sensitive to quantization [60].

This vertical schematic also conveys the sequential propagation of quantization errors throughout the model. Quantization applied in the early downsampling layers affects subsequent attention computations, which in turn influence the bottleneck and decoder stages. Consequently, naive uniform quantization across all layers can result in error amplification and degraded generative quality. The vertical representation emphasizes the importance of both stage-wise and module-wise precision planning, which, when combined with timestep-adaptive strategies, can achieve an optimized balance between efficiency and fidelity. In practice, this necessitates careful profiling of each module, simulation of quantization effects, and iterative adjustment of bitwidth allocation guided by empirical performance metrics such as FID, IS, or perceptual similarity scores. Collectively, these architectural insights provide a framework for designing quantization schemes that are both theoretically informed and practically effective for large-scale diffusion models.

5. Challenges and Open Problems in Quantizing Large-Scale Diffusion Models

Despite the significant advances in quantization techniques for diffusion models, a number of formidable challenges remain, particularly in the context of large-scale foundation models [62]. The complexity of these challenges arises from the interplay between model scale, iterative generative dynamics, hardware constraints, and the stochastic nature of the data distributions. Large diffusion models often contain billions or even tens of billions of parameters, with intricate hierarchical architectures that include multi-resolution convolutional blocks, attention mechanisms, and normalization layers [63]. Each of these components exhibits different sensitivities to numerical precision, and the iterative nature of the reverse diffusion process amplifies even small quantization errors, making naive approaches ineffective [64]. Consequently, a critical open problem is the development of quantization strategies that can maintain high generative fidelity across all stages of the model while simultaneously reducing memory footprint and computational cost. This challenge is compounded by the diversity of downstream tasks and modalities, ranging from high-resolution image synthesis to text-conditioned video generation, each of which imposes unique fidelity requirements and tolerances for numerical perturbation. One of the most fundamental challenges lies in understanding and mitigating error accumulation across diffusion timesteps [65]. In a standard T-step reverse diffusion process, the output of timestep t becomes the input to timestep $t-1$, such that quantization errors ${\mathbf{e}}_t$ introduced at each step propagate nonlinearly through the subsequent steps. Formally, if ${\mathbf{x}}_{t-1}=f_{\widehat{\theta }}\left({\mathbf{x}}_t\right)+{\mathbf{e}}_t$, the cumulative error after T steps can be represented as a telescoping sum of Jacobian-weighted perturbations:

$${\mathbf{E}}_{\mathrm{cumulative}}=\sum _{t=1}^T{\mathbf{J}}_{t:T}{\mathbf{e}}_t,{\mathbf{J}}_{t:T}=\prod _{k=t}^T{\displaystyle \frac{\partial f_{\widehat{\theta }}\left({\mathbf{x}}_k\right)}{\partial {\mathbf{x}}_k}}.$$

(16)

This formalization highlights the exponential sensitivity of generative quality to early-stage quantization errors, especially in high-dimensional spaces. Theoretical analysis and empirical studies indicate that certain layers and stages disproportionately contribute to this cumulative error, motivating research into adaptive quantization schemes that allocate higher precision to error-sensitive layers or timesteps. However, identifying these sensitivities in models with billions of parameters is computationally expensive and remains a largely unsolved problem [66]. Another significant challenge is the interaction between quantization and multimodal generative tasks. Many modern diffusion models are conditioned on rich auxiliary inputs, such as text, audio, or semantic maps. These conditioning inputs introduce additional pathways for error propagation and can magnify the effects of low-precision representation. For instance, in text-to-image diffusion models, errors in quantized attention mechanisms that integrate text embeddings may lead to semantically inconsistent or visually incoherent outputs. Similarly, in video or 3D generative tasks, quantization errors can accumulate across spatial and temporal dimensions, producing artifacts that are perceptually noticeable even if traditional statistical metrics such as mean squared error remain low. Designing quantization strategies that preserve semantic and perceptual fidelity across multiple modalities is therefore a critical open problem, requiring the development of novel error metrics, perceptually-aware quantization schemes, and task-specific adaptive methods [67]. The hardware constraints associated with low-precision computation also present nontrivial challenges [68]. While modern accelerators, including GPUs and TPUs, support mixed-precision arithmetic and integer operations, the effective utilization of these units depends on careful alignment of model architecture, memory layout, and computational kernels. Large-scale diffusion models exacerbate these challenges due to their enormous parameter count and the high memory bandwidth demands of iterative denoising [69]. For example, implementing aggressive 4-bit quantization across all layers may reduce memory usage but could trigger inefficient kernel execution or increased overhead due to dequantization and re-quantization operations. Additionally, the heterogeneity of hardware platforms means that a quantization scheme optimized for one accelerator may perform poorly on another, necessitating hardware-aware or co-designed approaches [70]. Balancing hardware efficiency, cross-platform portability, and generative fidelity remains an ongoing and highly complex challenge. Finally, the integration of quantization with other model compression techniques, such as pruning, knowledge distillation, and low-rank approximation, introduces additional layers of complexity [71]. While these methods individually contribute to memory and computational savings, their interactions with quantization are nontrivial and can lead to unforeseen degradations in generative quality. For instance, pruning a subset of network weights followed by low-bit quantization can produce instabilities in the reverse diffusion dynamics, as the reduced parameter space may be insufficient to compensate for numerical errors introduced by quantization [72]. Similarly, distillation methods that rely on teacher-student training may propagate quantization artifacts if the student model is trained under low-precision constraints. Developing principled frameworks for combining multiple compression techniques in a way that preserves the delicate probabilistic structure of diffusion models is therefore an open research frontier. In summary, the challenges associated with quantizing large-scale diffusion models are multi-faceted, encompassing error accumulation, layer- and timestep-specific sensitivity, multimodal interactions, hardware constraints, and the integration with other compression strategies [73]. Addressing these challenges requires not only sophisticated algorithmic and mathematical tools but also extensive empirical validation across diverse tasks and datasets. The open problems outlined above underscore the need for continued research into adaptive, hardware-aware, and task-specific quantization strategies that can unlock the full potential of diffusion-based generative models in large-scale, foundation-model contexts.

6. Evaluation Metrics and Benchmarking Strategies for Quantized Diffusion Models

Evaluating the performance of quantized diffusion models is a multidimensional challenge that extends beyond traditional machine learning metrics [74]. The iterative, stochastic nature of diffusion processes, coupled with the sensitivity of generative quality to low-precision computation, necessitates careful selection of evaluation protocols, quantitative metrics, and benchmarking strategies [75]. Unlike standard discriminative tasks, where accuracy or cross-entropy loss provides a straightforward measure of performance, generative models require metrics that capture both statistical fidelity and perceptual quality [76]. Furthermore, the introduction of quantization introduces new sources of variation, such as numerical rounding errors, bitwidth-dependent noise, and precision-induced bias in feature representations, all of which can affect model outputs in subtle ways. Evaluating these effects demands a combination of conventional probabilistic metrics, perceptual measures, hardware-aware performance metrics, and systematic ablation studies that isolate the impact of reduced precision on different components of the model. A key class of metrics for assessing generative fidelity includes distributional similarity measures such as the Fréchet Inception Distance (FID), Kernel Inception Distance (KID), and Maximum Mean Discrepancy (MMD) [77]. The FID, for instance, computes the Wasserstein-2 distance between the statistics of generated samples and real data embeddings in a feature space defined by a pretrained classifier:

$$\mathrm{FID}(X_{\mathrm{gen}},X_{\mathrm{real}})={\parallel {\mu }_{\mathrm{gen}}-{\mu }_{\mathrm{real}}\parallel }_2^2+\mathrm{Tr}\left({\mathrm{\Sigma }}_{\mathrm{gen}}+{\mathrm{\Sigma }}_{\mathrm{real}}-2{\left({\mathrm{\Sigma }}_{\mathrm{gen}}{\mathrm{\Sigma }}_{\mathrm{real}}\right)}^{1/2}\right),$$

(17)

where $\mu$ and $\mathrm{\Sigma }$ are the mean and covariance of the embeddings, respectively. This metric is sensitive to both global structure and fine-grained features, making it particularly relevant for assessing the degradation introduced by quantization [78]. KID and MMD provide complementary perspectives by measuring kernel-based discrepancies between distributions, which can capture different aspects of statistical similarity that may not be fully reflected by FID alone [79]. Importantly, all of these metrics must be interpreted carefully in the context of low-precision models, as quantization can introduce subtle biases that disproportionately affect certain modes or features in the output distribution, leading to metrics that may exaggerate or underestimate perceptual degradation [80]. Perceptual and task-specific metrics provide another critical axis for evaluation. For image synthesis tasks, metrics such as the Learned Perceptual Image Patch Similarity (LPIPS) and Structural Similarity Index Measure (SSIM) capture human-perceptible differences that are not necessarily reflected in pixel-wise errors [81]. LPIPS, for example, computes the distance between features extracted by a pretrained deep network:

$$\mathrm{LPIPS}({\mathbf{x}}_0,{\widehat{\mathbf{x}}}_0)=\sum _l{\displaystyle \frac{1}{H_l{W}_l}}\sum _{h,w}{\parallel w_l\odot ({\varphi }_l{\left({\mathbf{x}}_0\right)}_{h,w}-{\varphi }_l{\left({\widehat{\mathbf{x}}}_0\right)}_{h,w})\parallel }_2^2,$$

(18)

where ${\varphi }_l$ represents the features at layer l, $w_l$ are learned weights, and $H_l,W_l$ are spatial dimensions [82]. These metrics are especially useful for assessing the impact of quantization on fine-grained texture, edge sharpness, and perceptual consistency. In multimodal generation tasks, additional evaluation protocols may include semantic consistency between modalities (e.g., text-image alignment scores in text-conditioned generation) and temporal coherence metrics for video or 3D generation. Quantization can adversely affect these task-specific characteristics, necessitating the development of evaluation pipelines that jointly capture generative fidelity, perceptual quality, and semantic alignment under low-precision computation. Benchmarking strategies for quantized diffusion models also require careful attention to hardware-aware performance metrics. Memory footprint, throughput, latency, and energy efficiency are all critical considerations when assessing the practical benefits of low-precision deployment [83]. Let $M\left(b\right)$ denote the memory usage at bitwidth b, $C\left(b\right)$ denote computational cost, and $T\left(b\right)$ the inference time. Quantization reduces $M\left(b\right)$ approximately linearly with decreasing bitwidth, but the effective throughput improvement is often nonlinear due to hardware-specific constraints such as kernel vectorization, memory alignment, and integer computation pipelines. Therefore, comprehensive benchmarking must include end-to-end evaluation on target hardware platforms, encompassing both the efficiency gains and any degradation in generative quality. Profiling tools and automated pipelines that record per-layer memory usage, operation counts, and latency distributions provide additional granularity, enabling the identification of bottlenecks and opportunities for further optimization [84]. Another key aspect of evaluation is sensitivity analysis and ablation studies, which disentangle the effects of quantization across layers, timesteps, and modules [85]. By selectively varying bitwidths or applying quantization to specific components while keeping the rest of the model at full precision, researchers can systematically quantify the contribution of each component to overall generative performance. Formally, let ${\widehat{\theta }}^{(l,b)}$ denote the parameters of layer l quantized at bitwidth b, and define a per-layer performance metric $P_l\left(b\right)$ as:

$$P_l\left(b\right)=\mathrm{Metric}\left({\mathbf{x}}_0,f_{{\widehat{\theta }}^{(l,b)}}\left({\mathbf{x}}_T\right)\right),$$

(19)

where Metric can be FID, LPIPS, or another relevant score. Analyzing the curve $P_l\left(b\right)$ across layers and bitwidths informs adaptive precision strategies, guiding allocation of higher precision to layers with steep performance degradation [86]. Similarly, timestep-dependent evaluation, where quantization is applied selectively at different stages of the reverse diffusion process, allows researchers to understand temporal sensitivity and design timestep-adaptive schemes [87]. Finally, reproducibility and standardized benchmarks are essential for meaningful comparison across quantization methods [88]. Large-scale diffusion models are often trained on diverse and proprietary datasets, making direct comparison difficult [89]. Efforts to establish publicly available datasets, pre-trained checkpoints, and standardized evaluation protocols facilitate fair and rigorous benchmarking [90]. By combining statistical, perceptual, hardware-aware, and sensitivity-focused metrics, the community can build a comprehensive understanding of the trade-offs involved in quantizing diffusion models [91]. Such a multi-faceted evaluation paradigm is critical for guiding both theoretical development and practical deployment of low-precision foundation-scale generative models [92].

7. Future Directions and Emerging Research Opportunities in Quantized Diffusion Models

The landscape of quantization for large-scale diffusion models is still nascent, and numerous avenues for future research and innovation remain open. As generative AI continues to expand into more complex, multimodal, and foundation-scale applications, the need for highly efficient, low-precision diffusion models will only intensify. Future research directions can be broadly categorized into algorithmic innovations, theoretical analysis, hardware co-design, and applications-oriented studies, each of which offers unique opportunities and challenges for advancing the state of the art. From an algorithmic perspective, one promising direction is the development of adaptive and dynamic quantization schemes that adjust precision not only across layers and timesteps but also based on input content or intermediate feature statistics. Current mixed-precision approaches largely rely on static assignment of bitwidths determined via empirical profiling or gradient-based sensitivity analysis [93]. However, in large-scale foundation models that are deployed in dynamic environments, input distributions can vary significantly, resulting in variable error sensitivity across different samples or modalities [94]. Adaptive quantization mechanisms, potentially informed by reinforcement learning, meta-learning, or attention-based controllers, could dynamically allocate precision in a manner that optimizes both fidelity and efficiency on a per-sample basis. Such methods would require new frameworks for efficient runtime monitoring of quantization-induced error and for real-time adjustment of precision without introducing prohibitive overhead [95]. Another key direction is the integration of quantization with novel diffusion architectures and generative paradigms. The majority of current research focuses on U-Net style hierarchical diffusion models with residual and attention blocks [96]. However, emerging architectures, such as transformer-based diffusion networks, latent diffusion models, and score-based generative models operating in compressed latent spaces, present new opportunities and challenges for low-precision optimization. Transformers, for instance, are dominated by attention and MLP modules, whose scaling properties and numerical sensitivity differ substantially from convolutional structures. Latent diffusion models, by operating in lower-dimensional spaces, reduce memory and computation costs but introduce nontrivial interactions between quantization error and the learned latent space representation [97]. Future work could explore architecture-aware quantization strategies that are co-designed with the generative model itself, optimizing both model structure and numerical representation in tandem. Theoretical analysis of quantization in diffusion models represents another fertile area for research [98]. While empirical studies provide valuable insight into the practical effects of low-precision computation, a rigorous understanding of how quantization errors propagate through iterative denoising processes is still limited. Developing formal error bounds, stability guarantees, and probabilistic models of quantization-induced perturbations would significantly enhance the reliability and predictability of quantized diffusion models [99]. For example, understanding the conditions under which cumulative quantization error remains bounded across T reverse diffusion steps, or deriving the relationship between bitwidth allocation and divergence metrics such as Kullback–Leibler divergence or Wasserstein distance, could guide principled design of quantization schemes [100]. Such theoretical contributions would be particularly impactful in high-stakes applications, such as medical imaging or scientific simulations, where output fidelity and reproducibility are critical. Hardware co-design is another crucial frontier [101]. Efficient deployment of low-precision diffusion models requires not only algorithmic optimization but also alignment with the capabilities and limitations of modern accelerators [102]. Future research may explore custom numerical formats, tensor core optimization, and hardware-aware layer fusion to maximize the efficiency gains of quantization. Emerging AI-specific accelerators that support ultra-low precision operations (e.g., 4-bit or 2-bit integer formats, block floating point) provide both opportunities and constraints that can shape the design of next-generation diffusion models. Co-design approaches that simultaneously optimize model architecture, numerical precision, and hardware utilization could unlock unprecedented levels of efficiency while maintaining high fidelity in foundation-scale generative tasks. Finally, applications-driven research will increasingly shape the evolution of quantized diffusion models. As diffusion models are deployed in real-world systems, questions of robustness, fairness, and reliability under low-precision computation will become increasingly important. For instance, quantization may interact with domain shifts, rare events, or adversarial inputs in unpredictable ways, highlighting the need for evaluation frameworks and mitigation strategies that account for real-world variability [103]. Additionally, integrating quantized diffusion models into interactive or real-time systems, such as mobile AR/VR applications, robotics, or large-scale content generation platforms, will require end-to-end optimization encompassing both algorithmic fidelity and system-level constraints [104]. Addressing these challenges will necessitate interdisciplinary collaboration across machine learning, numerical analysis, hardware engineering, and application domains [7]. In conclusion, the future of quantization in diffusion models is characterized by a rich interplay of algorithmic, theoretical, hardware, and application-oriented considerations [105]. Emerging research opportunities span adaptive and dynamic precision schemes, architecture-aware and latent-space-aware quantization strategies, formal error analysis, hardware co-design, and real-world deployment studies. By addressing these frontiers, the research community can unlock the full potential of low-precision, large-scale generative models, enabling efficient, scalable, and robust diffusion-based foundation models that are accessible to both academia and industry. The confluence of these efforts promises not only to reduce the computational and memory costs of generative AI but also to expand its applicability across a diverse range of domains, ultimately shaping the next generation of efficient, high-fidelity generative systems.

8. Conclusions and Synthesis of Insights on Quantization for Diffusion Models

The exploration of quantization and low-precision strategies for diffusion models in the context of large-scale foundation models represents both a critical challenge and a transformative opportunity within generative artificial intelligence [106]. Over the course of this survey, we have examined the multifaceted nature of this problem, beginning with the mathematical underpinnings of diffusion processes and their sensitivity to numerical perturbations, proceeding through the taxonomy of quantization methods, architectural considerations, evaluation metrics, and finally the open research directions that define the frontier of the field. One of the most salient insights is that diffusion models, due to their iterative denoising pipelines and high-dimensional latent representations, are inherently more sensitive to quantization errors than traditional feedforward networks [107]. Even minor reductions in precision can propagate and amplify across timesteps, affecting both the statistical fidelity of generated outputs and their perceptual quality [108]. This unique characteristic necessitates precision-aware strategies that are adaptive, layer-sensitive, and in many cases, timestep-dependent, moving beyond naive or uniform quantization schemes. A second key observation relates to the interplay between architectural complexity and quantization sensitivity. Modern diffusion models, particularly those at the scale of foundation models, are composed of hierarchical U-Net architectures, attention mechanisms, residual blocks, normalization layers, and latent-space embeddings [109]. Each of these components exhibits distinct numerical properties: attention modules and normalization layers are particularly error-sensitive, while certain feedforward convolutional blocks can tolerate aggressive quantization [110]. The hierarchical and iterative nature of these architectures further complicates the picture, as quantization errors in early stages can cascade and affect downstream modules. This insight underscores the necessity of mixed-precision, adaptive, and hardware-aware quantization strategies that leverage layer-wise and module-wise sensitivity profiling to allocate computational resources optimally [111]. Such an approach not only preserves generative fidelity but also maximizes memory efficiency and throughput, particularly important when deploying models with billions of parameters on constrained hardware. Third, the convergence of algorithmic and hardware considerations emerges as a defining theme in the design of quantized diffusion models. While algorithmic innovations such as quantization-aware training, timestep-adaptive quantization, and mixed-precision allocation can substantially mitigate performance loss, the realization of these benefits in practice requires careful co-design with modern AI accelerators. Hardware constraints, including memory bandwidth, kernel execution patterns, integer operation support, and low-bit precision optimizations, interact non-trivially with quantization schemes. For example, aggressive 4-bit quantization may reduce memory consumption significantly but can introduce runtime overhead due to repeated dequantization and quantization cycles if not supported efficiently by hardware. Conversely, hardware-aware precision allocation that aligns with the native capabilities of tensor cores or specialized AI units can unlock both throughput and energy efficiency gains without sacrificing output quality [112]. The synthesis of algorithmic, architectural, and hardware perspectives thus forms the backbone of effective quantization strategies for large-scale diffusion models. Evaluation and benchmarking constitute a fourth crucial dimension of this field. Quantized generative models cannot be assessed solely through traditional metrics such as loss functions or accuracy, as these measures fail to capture the nuanced impact of low-precision computation on sample quality and fidelity [113]. Metrics like Fréchet Inception Distance (FID), Kernel Inception Distance (KID), Structural Similarity Index Measure (SSIM), and Learned Perceptual Image Patch Similarity (LPIPS) provide quantitative and perceptual evaluations, while task-specific and multimodal metrics assess semantic coherence and cross-modal fidelity [114]. Layer-wise and timestep-dependent ablation studies further elucidate which components are most sensitive to quantization and where precision can be reduced without compromising generative quality. Benchmarking must also incorporate hardware-aware performance metrics, including memory footprint, latency, and energy consumption, to provide a holistic view of trade-offs. Only through such comprehensive evaluation frameworks can researchers and practitioners make informed decisions about quantization strategies in real-world deployment contexts [115]. Finally, the future research trajectory for quantized diffusion models is expansive and interdisciplinary [116]. Emerging opportunities include dynamic, sample-adaptive quantization, integration with novel transformer-based or latent diffusion architectures, formal theoretical analysis of error propagation, and robust, hardware-co-designed systems. Multimodal generative tasks and real-time applications impose additional constraints that necessitate adaptive, task-specific quantization schemes capable of preserving semantic fidelity under low-precision computation. At the intersection of these challenges lies the promise of democratizing large-scale generative AI, making high-quality diffusion models accessible beyond the limited computational resources of a few technology giants. By synthesizing insights from mathematics, architecture, algorithmic design, hardware optimization, and evaluation, the research community is poised to advance the efficiency, scalability, and robustness of diffusion-based foundation models in a principled and systematic manner [117].

In conclusion, quantization for diffusion models is a deeply complex yet profoundly impactful domain, offering the potential to transform the deployment and accessibility of large-scale generative systems. The key principles elucidated in this survey—sensitivity-aware precision allocation, iterative error mitigation, hardware-aligned computation, rigorous evaluation, and integration with novel architectures—constitute a cohesive framework for future research and practical implementation. Achieving this vision requires not only incremental improvements in existing techniques but also bold exploration into adaptive, theory-driven, and co-designed quantization paradigms. As the field progresses, these efforts will be instrumental in realizing efficient, high-fidelity, and widely deployable generative models, shaping the next generation of foundation-scale AI systems that are both sustainable and broadly accessible.