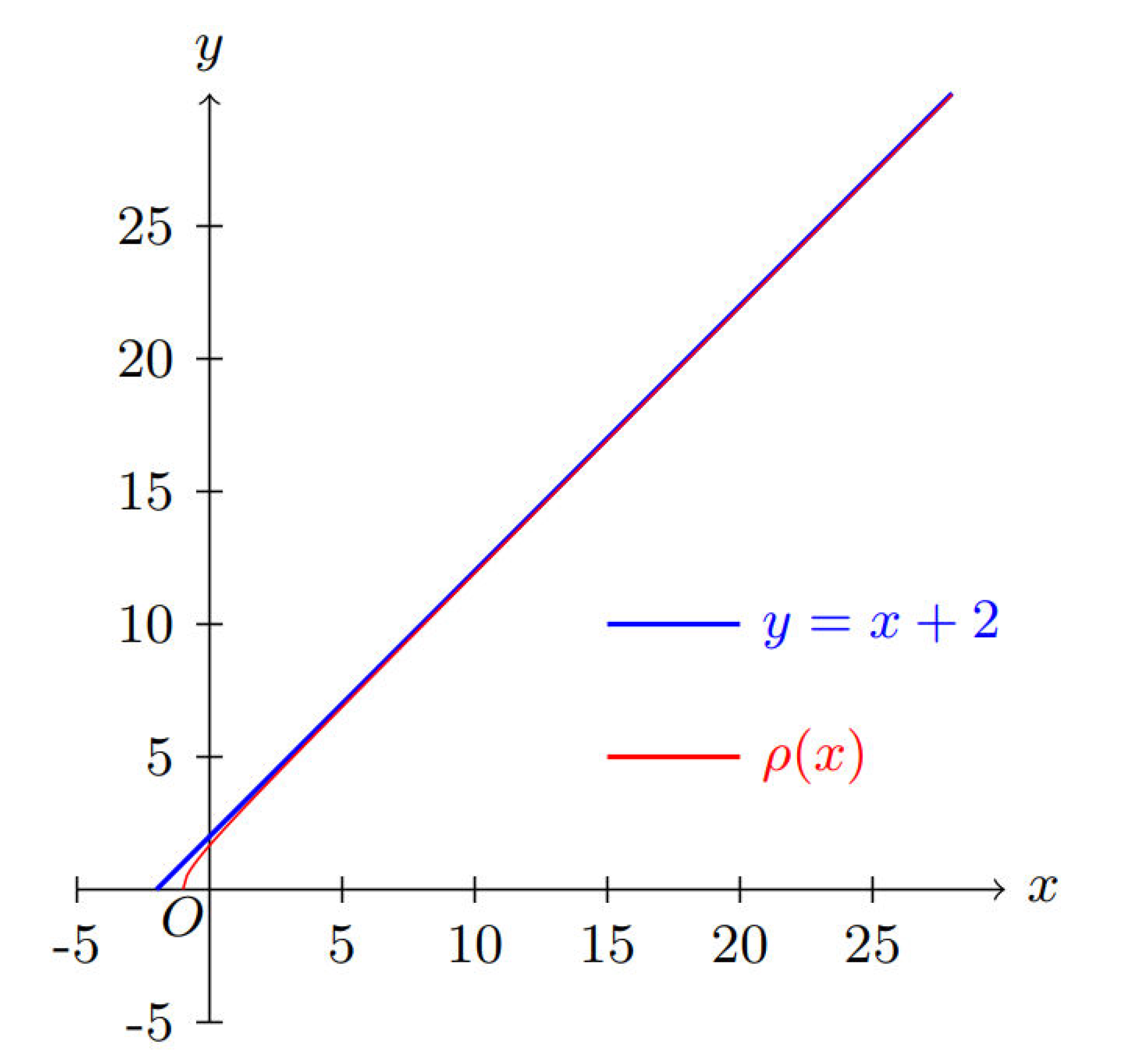
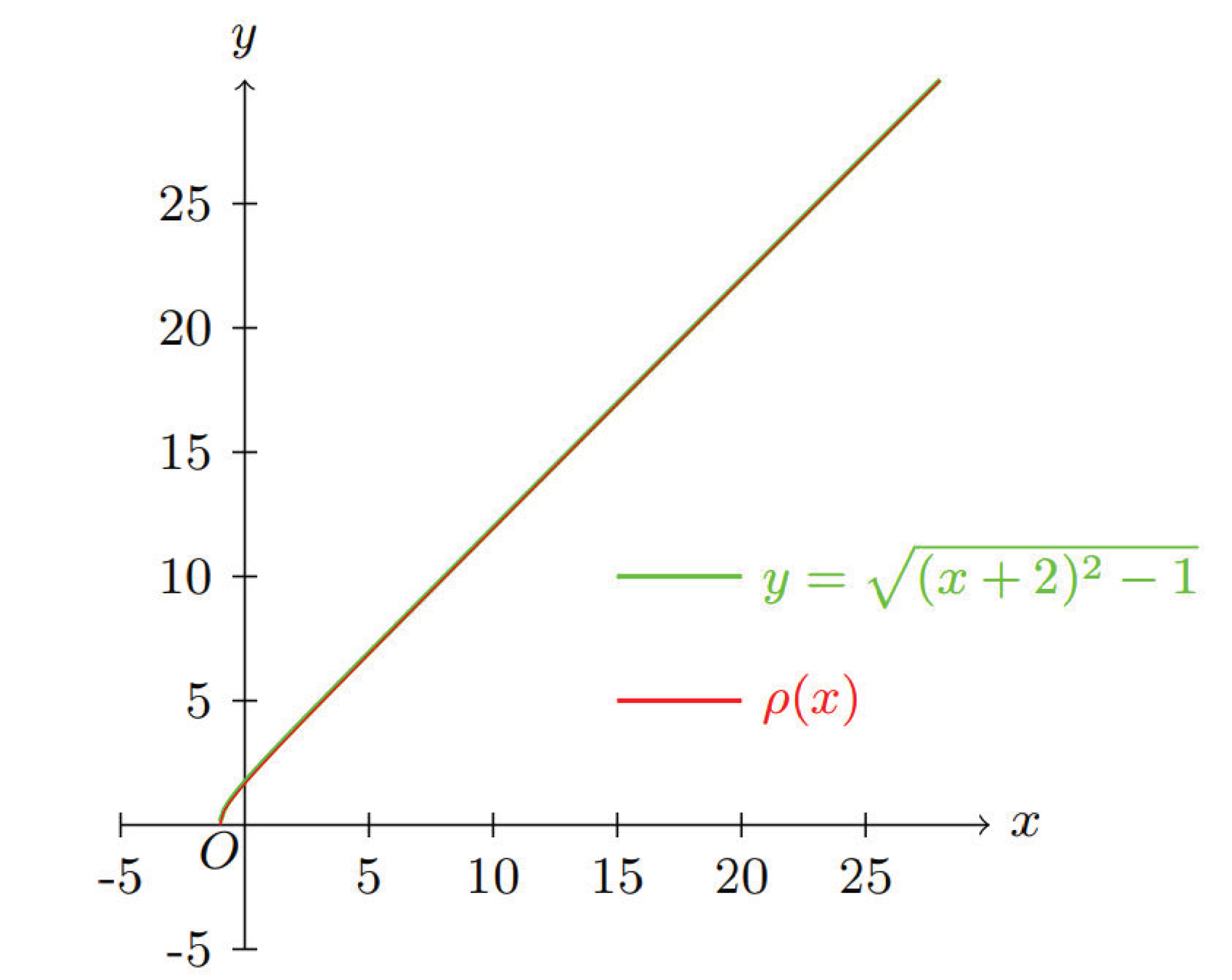
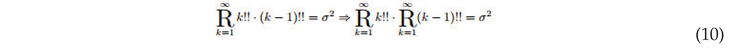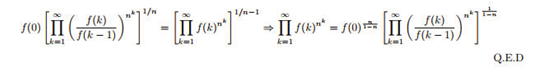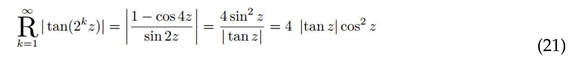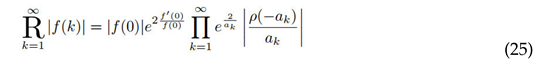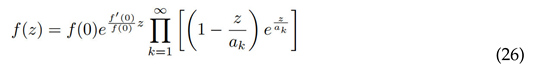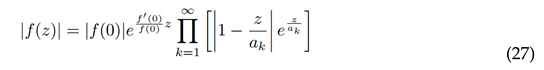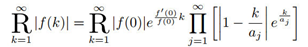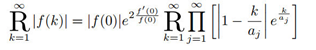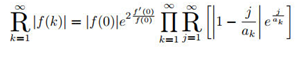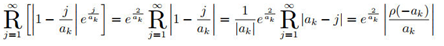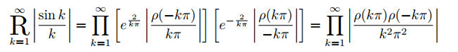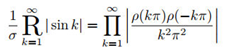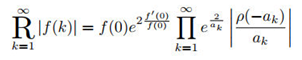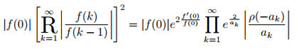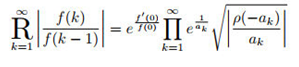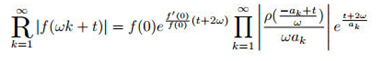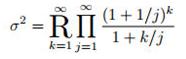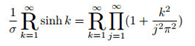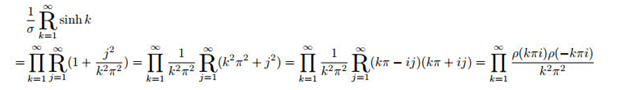1. Introduction
Infinite products, as a core tool in mathematical analysis, have demonstrated profound applications in areas such as the theory of special functions and analytic number theory since the time of Euler and Weierstrass. Classical theory primarily focuses on products of the form
, while systematic research on infinite nested radicals (of the form
) remains largely unexplored. This paper introduces a novel type of operator—the continued radical—denoted by
, rigorously defined as a generalization of the limit
. And we call
partial radicand. Centering on this operator, we establish a tripartite theoretical framework of high innovativeness: 1. Foundational Theory: Convergence criteria are established (
Section 2, related to the series
), and fundamental operational rules for continued radicals are proven Equations (
1), (
2), (
3).
2. Core Tool: The characteristic function
Equation (
4) is introduced. Its relationships with the Lerch transcendent and Somos’s quadratic recurrence constant are revealed, along with its recurrence property
Equation (
6). A crucial formula—the Product Lemma Equation (
9)—is derived:
This lemma enables closed-form representations of combinatorial structures like factorials and double factorials (Examples 1, 2, 3).
3. Function Construction Theory: The operator is extended to the complex domain. A complex continued radical transformation formula
(where
) is established and applied to trigonometric/hyperbolic functions: * Concise expressions are obtained, such as
Equation (
14). * Dobinski’s identity
Equation (
20) is rediscovered, and new identities are derived:
Equation (
22),
Equation (
23).
This paper further constructs a profound connection between continued radicals and Weierstrass infinite products (Theorem 1), providing a continued radical factorization for entire functions :
This framework offers novel analytical perspectives on classical functions such as Example (5) and the Gamma function Proposition (1).
2. Basic Operational Rules and Convergence of the Continued Radical
The continued radical owns the following basic operational rules:
We could interpret it according to the meaning of the radical.
Taking the logarithm of the product into a series
.QED
According to 1 and 2, we can prove it easily.
2.1. The convergence of the continued radical
It’s not difficult to find that the convergence of Equivalent to the convergence of . According to D’Alembert’s test, we can know that if . The continued radical converges.
Unless otherwise specified, all infinite products and continued radicals mentioned hereafter are assumed to be convergent.
3. Function and Somos’s Quadratic Constant
It’s easy to know that
can also be express as:
where
is the Lerch function. We could get the recursive formula by radical meaning:
or can be rigorously proven via the following Product Lemma
9 as well.
Specially, while
,
,where
is Somos’s Quadratic Recurrence Constant [
1], it be defined as
.By Equation (
6) we can get:
Lemma 1.
For the function , the following holds:
Proof. Consider the continued radical ,,where ,According to the definition:
Therefore , so that
shift items and multiplying both sides by yields
Let . Observing that, because , therefore let ,Substitute the two functions into the equation yields
□
In the following text, we refer to this lemma as the Product Lemma.
Example 1. Calculate :
According to Product Lemma, we could know that:
Example 2. Calculate :
By the relationship between factorial with double factorial yields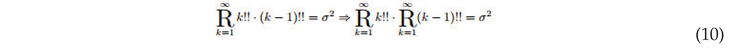
Let , therefore we can get . ,Solve it :
Example 3. Calculate :
Let . According to Equation (9), we know that it equals
Example 4. Calculate , cis a constant:
Let ,According to Equation (9) we could know that it equals to
Corollary 1.
For , let , and the following holds:
Proof.
Consider function : , and let . By iteratively applying the Product Lemma to the continued radical , we obtain:
Thus, we can easily deduce by induction:
Next, we should prove : Observing that, while , the formula holds. Assuming the formula holds for ,Therefore , thus .According to the definition to , we could get:
□
Corollary 2. For function , if is well-defined within the real number domain, the following holds:
Proof.
Consider , therefore:
Thus ,
Shift items and multiplying both sides by yields
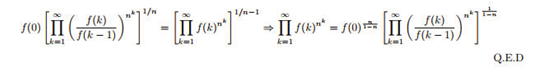
□
4. Trigonometric and Hyperbolic Continued Radical
For a function , If is well-defined within , we call is the constructed continued radical of . And we call the process "construct the function into continued radicals".For example, Somos’s constant could be regarded as the constructed continued radical of .
Lemma 2.
The proof can be found in [2], and we omit further elaboration here.
4.1. Construct the hyperbolic function into continued radicals
According to the properties of hyperbolic function yields
By Equation (
8) we could get:
Substituting
yields:
4.2. Complex continued radical
In this subsection, we only require the partial radicand to be a nonzero real number. This implies that the result of continued radicals is complex. We refer to such expressions as complex continued radicals, which will be thoroughly discussed in this subsection. In contrast, the previously discussed cases with real-valued outcomes are termed real continued radicals.
4.2.1. The relationship between complex and real continued radicals
For real continued radical , where .Consider the sequence . Let. We decompose into two components based on the sign of the partial radicands:
Extracting the factor and converting it into multiplicative form yields:
Observing that
, thus
Let
, and we call
the transformational of
. Therefore:
We could know , while , . Transforming the above expression, we obtain:
According to the auxiliary angle formula, we could get: , where , thus:
Because
, therefore
In it, denotes the fractional part of a.
4.3. Real-complex transformation for continued radicals
In subsection Construct the hyperbolic function into radical, we got the constructed continued radical of . According to the properties of hyperbolic function:, we could get:
Expanding via Euler’s formula, we obtain:
To convert it into a real radical product, we take the absolute value of the inner function:
By the derivation of Equation (
18), we can easily get:
Substituting into the original expression yields:
where
is a periodic function with
as its period. For
,
equivalent to
, therefore
Observing that:
we may introduce a factor of
into the original expression:
Or we do not introduce
. Since the result of the square root is non-negative, we can also derive:
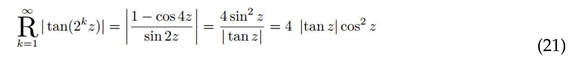
This result coincides precisely with the infinite product identity proposed by Dobinski nearly 150 years ago [
3]. In this paper, we have derived the same result through a novel approach.
4.4. Extending Trigonometric continued radicals via the Product Lemma
Corollary 3. In the preceding subsection, we derived
By applying the Product Lemma to the continued radical, and let , we obtain:
Substituting and simplifying yields :
Applying the half-angle formula, we may further simplify the left-hand side:
Corollary 4. Dividing the result from Example 3, , by Equation (21)
:
Simplifying gives:
We may also employ the generalized Product Lemma 1 to further derive trigonometric nested radicals, with details to be presented later.
4.5. In summary
| |
|
|
| |
|
|
| |
|
|
5. The Relationship Between Continued Radical with Common Infinite Product
Lemma 3.
Proof.
According to the radical meaning, we could get:
Then the continued radical can also be expressed as:
□
This lemma still holds while .
Theorem 1.
Let be an entire function with only non-zero simple zeros at , satisfying . Suppose there exists a sequence of contours on which , where M is a positive constant independent of m. Then, the following holds: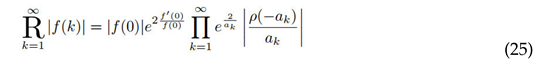
Proof.According to the Weierstrass factorization theorem [4], if a function satisfies the above conditions, it can be expanded as an infinite product: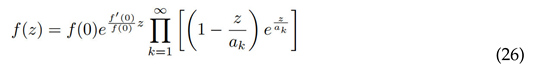
Then must satisfy: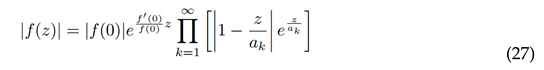
Construct both sides of the equation into continued radicals:
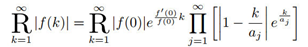
on the left side could be regarded as a constant, so that we could factor it out.
could be regard as the situation of Example 4:
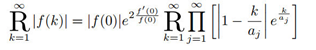
According to Lemma 3, swapping the continued radical product symbol with the product symbol, and interchanging indices k and j, we obtain:
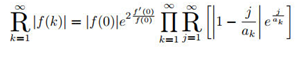
Simplifying the continued radical on the left-hand side of the equation yields:
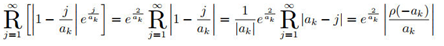
Substituting back into the original equation completes the proof. □
Example 5. Express as an infinite product:
We could note that meets the requirements of Theorem 1. And the zeros of are . Substituting into the theorem yields: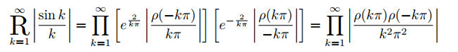
Furthermore, we can factor out to obtain: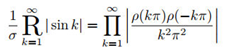
Corollary 5.
According to the Theorem 1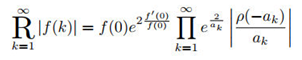
Applying the Product Lemma to the left-hand side of the equation yields: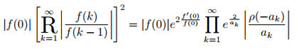
Simplifying and rearranging gives: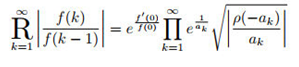
Corollary 6.
If function meets the requirements of Theorem 1, and meets the requirements as well, the following holds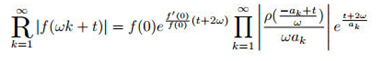
The reader could prove this independently.
5.1. Infinite product forms of continued radicals for other functions:
Proposition 1.
Proof.
Two known infinite product representations of the Gamma function:
Taking the first infinite product and constructing continued radicals on both sides of the equation yields:
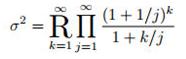
Exchanging the product operator and the continued radical operator while swapping variables yields: Similarly to the proof of Theorem 1, we obtain:
Applying the property of
,
Equation (
6), further simplification completes the proof. Similarly, the second result can be proved following the second equality (details omitted). □
Proposition 2.
Proof.
Writing out the infinite product form of the hyperbolic sine function:
Constructing continued radicals on both sides of the equation yields:
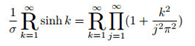
Exchanging the product operator and the continued radical operator, and simplifying it gives:
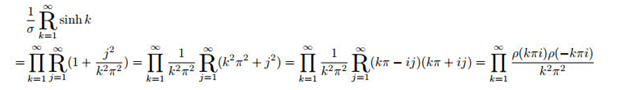
□
References
- Finch, S. Mathematical Constants; Cambridge University Press, 2003.
- Ricksen. How to prove this infinite product? https://www.zhihu.com/question/659016725/answer/1912507630745781602, 2024.
- Dobinski. Product einer unendlichen Factorenreihe. Archiv Math. u. Phys 1876, 59.
- Wang Zhuxi and Guo Dunren. Introduction to Special Functions. Peking University Press, 2000.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).