Three-World Hierarchy for General Neural-Network-in-the-Loop Stochastic Dynamical System

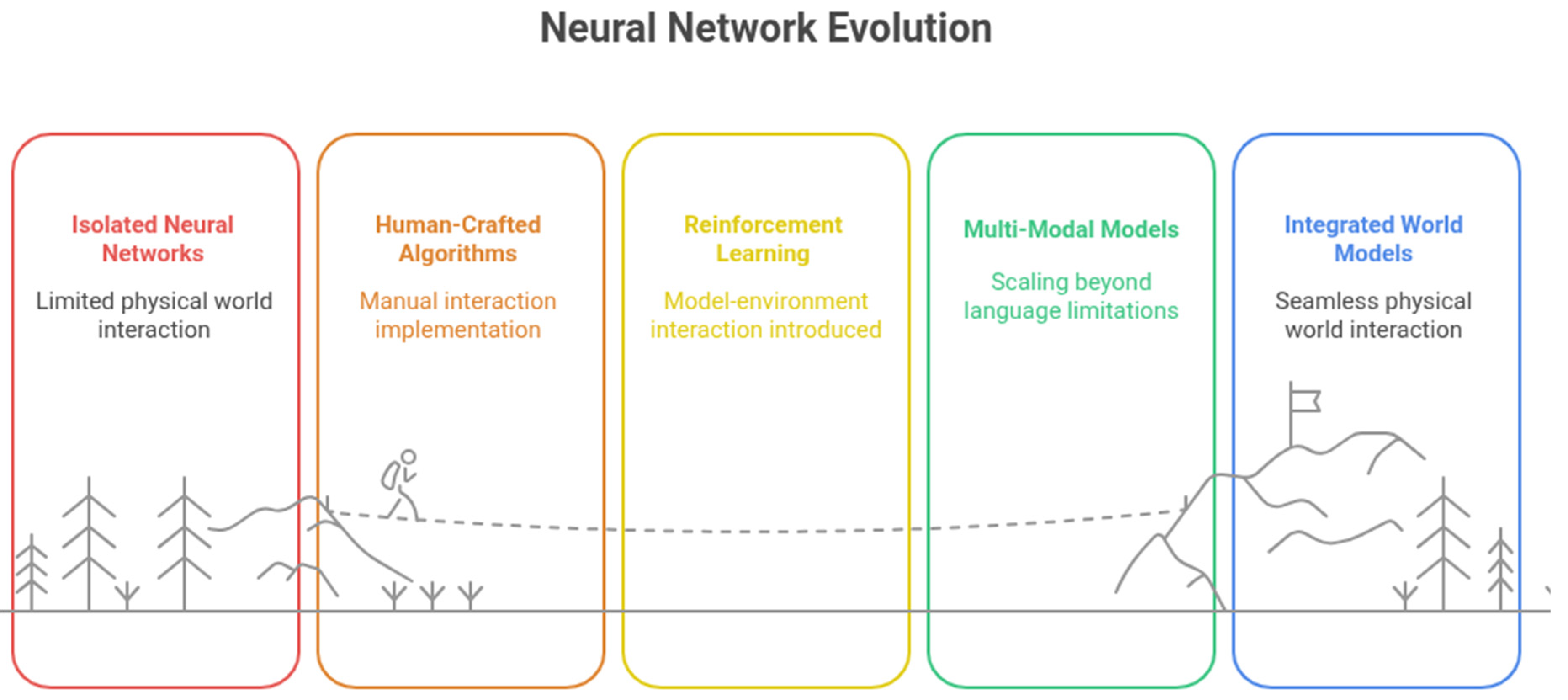
1. Introduction

The remarkable success of large language models (LLMs) like GPT has propelled artificial intelligence (AI) to the forefront of both academia and industry. AI's evolution now extends significantly beyond its initial core task of natural language processing, with advanced neural models impacting diverse fields such as robotics, autonomous driving, and remote sensing.

Increasingly, sophisticated deep learning models are being deployed in the physical world. Historically, interaction between early neural networks and their environments relied on human-crafted algorithms. This evolved with the introduction of the reinforcement learning (RL) paradigm, enabling models to learn interactions directly from their environments. However, as the information processing capabilities of neural models have expanded to encompass multiple modalities (e.g., video, audio, image, LiDAR) beyond just language, RL appears increasingly insufficient for future applications. Since 2025, the concept of "world models" has emerged, playing a pivotal role in the development of the next generation of neural networks (Ha & Schmidhuber, 2018).

The term "world model" is still evolving, and its interpretation remains diverse. Various approaches are being explored to achieve successful interaction between the physical world and neural networks. These include multimodal LLMs (Suzuki & Matsuo, 2022), Joint Embedding Predictive Architectures (JEPA) and their variants (LeCun, 2022; Fei et al., 2023), simulation platforms (Guan et al., 2024), and video world models (Zhen et al., 2024). The very term "world" can sometimes be ambiguous, particularly given the lack of a current consensus on the future evolutionary path of neural networks.

The success of modern neural networks, however, is largely scale-driven. In stark contrast to their widespread deployment, the theoretical understanding and analytical tools for investigating neural network properties remain underdeveloped. This often leads to neural networks being described as "black boxes." The significant gap between practical application and theoretical comprehension poses numerous potential risks for the development of Artificial General Intelligence (AGI) and Artificial Super Intelligence (ASI). These risks include:

●

Hallucination: Models can generate unrealistic or factually inconsistent outputs that diverge from real-world phenomena.

●

Misalignment: Models may not perform as intended, necessitating further training or recalibration to align with desired behaviors.

●

Security Risks: Models might fail to adequately cope with complex or unforeseen environmental conditions. A common example is the need for human intervention (takeover) in autonomous vehicles when the system encounters challenging scenarios.

The aforementioned risks necessitate a deep understanding of the mutual interaction between models (represented as complex neural networks) and the physical world. We use the term "neural network in the loop" to describe this critical combination of models and the physical environment. To clarify this "in-the-loop" concept, this manuscript outlines a three-world hierarchy that distinguishes different levels of the physical environment. We will elaborate on this framework in the next section. Here's a summary of our key definitions:

●

The "model world" is defined as the state space of the trained neural network model. This model world's state space is distinct from that of the real world.

●

The "data world" is spanned by the data used for training and validation, encompassing both real-world and synthetic data.

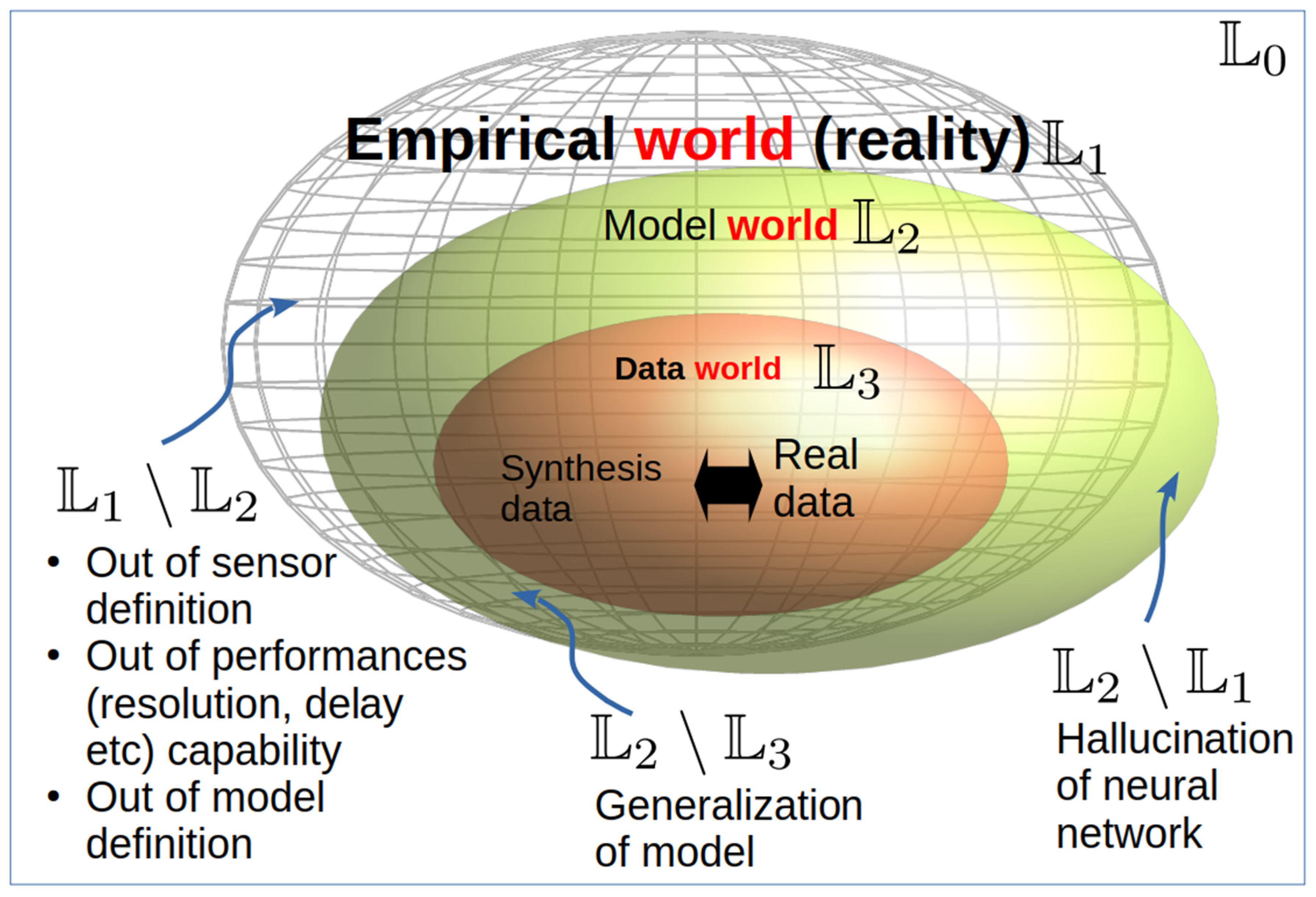
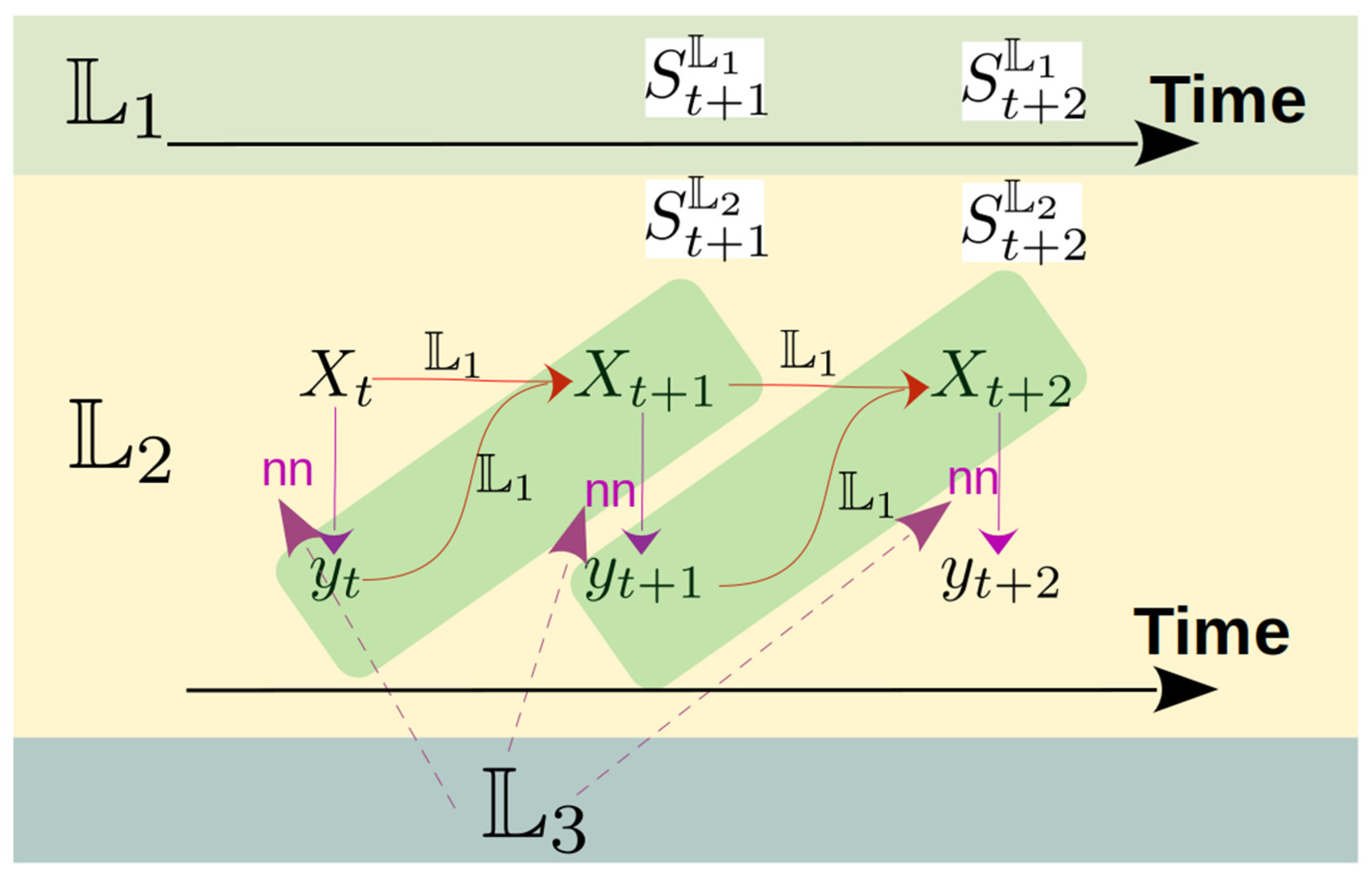
2. Three-World Hierarchy

Figure 1 illustrates our proposed three-level world hierarchy, comprising the Empirical World (${\mathbb{L}}_1$), the Model World (${\mathbb{L}}_2$), and the Data World (${\mathbb{L}}_3$​). Their definitions and interrelationships are detailed below.

●

Empirical World (${\mathbb{L}}_1$)

The Empirical World (${\mathbb{L}}_1$) represents the uppermost layer of this hierarchy, encompassing all phenomena and states that can be perceived, predicted, or interacted with in reality. It is synonymous with objective reality.

●

Model World (${\mathbb{L}}_2$​)

The Model World (${\mathbb{L}}_2$) constitutes the operational space formed by our models, primarily complex neural networks, though it may also integrate theoretically driven models like Newtonian mechanics. Each model is characterized by its specific definition, data structure declarations, and inherent configurations, which collectively determine the scope of its sensory perception and actions.

Compared to the Empirical World (${\mathbb{L}}_1$), the Model World exhibits two key differences:

    ∎

States Not Covered by the Model (${\mathbb{L}}_1$∖${\mathbb{L}}_2$): This set difference represents aspects of the Empirical World that fall outside the model's perceptual or operational capabilities. Several factors contribute to this:

◆

Undefined Sensor Modalities: The model's sensors may not be designed to capture certain states. For example, an autonomous vehicle lacking an infrared detector cannot directly sense pavement temperature, even if it could be indirectly estimated.

◆

Performance Limitations: The model's capabilities may be insufficient to resolve certain details within its defined state space. For instance, an autonomous vehicle's detectors might have limited resolution, preventing the detection of nanoscale pavement details.

◆

Out-of-Definition States: The state space is simply beyond the model's fundamental definition. A standard large language model, for example, cannot inherently perceive audio.

    ∎

Model-Generated States Not Existing in Reality (${\mathbb{L}}_2$\${\mathbb{L}}_1$): This set difference signifies instances where the model generates outputs that have no corresponding existence in the Empirical World. These outputs are often referred to as hallucinations. Examples include a large language model generating a non-existent reference or a text-to-image model producing physically impossible or "weird" images. Numerous underlying reasons contribute to the generation of these non-existent states.

●

Data World (${\mathbb{L}}_3$​)

The Data World (${\mathbb{L}}_3$) is spanned by the datasets used to train deep neural network models. This world comprises both data collected from the real world (Empirical World, ${\mathbb{L}}_1$) and human-crafted or synthetic data.

As observed, these three distinct worlds share overlapping state spaces while also possessing unique characteristics. To comprehensively represent them, we define ${\mathbb{L}}_0={\mathbb{L}}_1\cup {\mathbb{L}}_2\cup {\mathbb{L}}_3$​ . When considering the stochastic dynamics of a neural-network-in-the-loop system, it's beneficial to introduce the concepts of forward and backward dynamics from the perspective of this three-world hierarchy. Discrepancies inevitably exist among these three worlds. Given the system's stochastic nature, any initial state (e.g., state A in Figure 5-b) can evolve into multiple future states. Once an initial state is defined, the potential system evolution trajectories are encapsulated within a "forward dynamics set," visualized as a cone in Figure 5-b. Conversely, a specific final state (e.g., state D in Figure 5-b) can be reached from numerous historical states. Thus, for a given terminal state D, the possible system trajectories form a "backward dynamics set," also represented as a cone in Figure 5-b. A typical observed data trajectory (such as the path from A to D in Figure 5-b) is effectively bounded by an infinite number of these forward and backward dynamics sets. Furthermore, at any given data point along an observed trajectory (e.g., data point B), the system retains the capacity to evolve to alternative states (e.g., state E in Figure 5-b). This illustrates that the dynamics observed within the data world (${\mathbb{L}}_3$) (Figure 5-a) represent only a subset of the broader empirical world (${\mathbb{L}}_1$​) dynamics.

Figure 2. Neural network evolution with physical worlds.

Figure 2. Neural network evolution with physical worlds.

Figure 3. Approaches toward the neural-network-in-the-loop system.

Figure 3. Approaches toward the neural-network-in-the-loop system.

Figure 4. Key points of the three-world hierarchy.

Figure 4. Key points of the three-world hierarchy.

Figure 5. Time evolution of the world.

Figure 5. Time evolution of the world.

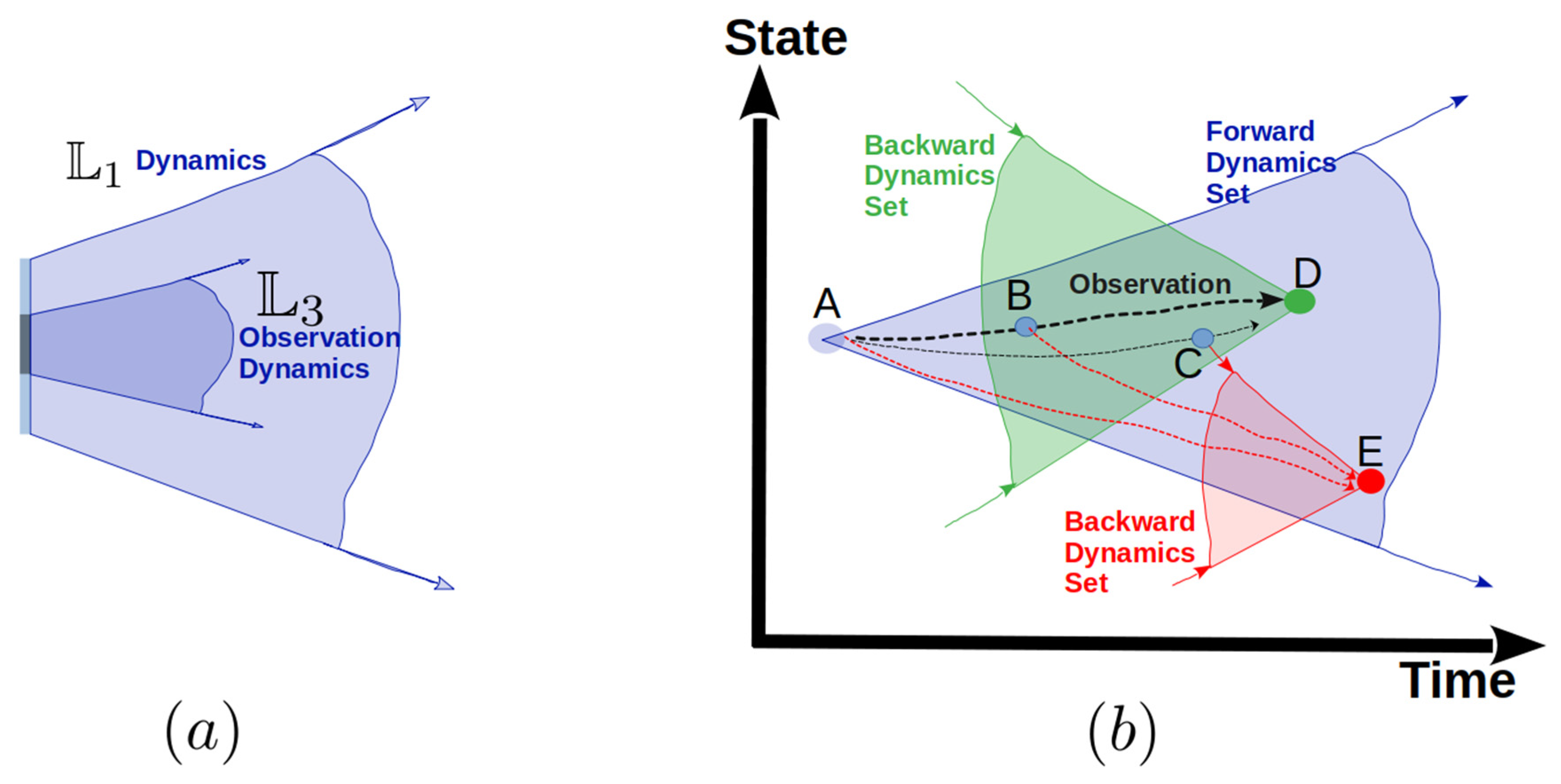
3. Frechet World Distance for Multi-Modal Configurations

Having outlined the three-level world hierarchy, we need tools to quantify the relationships between these distinct levels. We draw inspiration from Fréchet distance (which measures the distance between distributions) and Dynamic Time Warping (which considers temporal dimensions) to introduce a new concept: Fréchet World Distance (FWD). FWD extends these established metrics to address both single-modal scenarios (e.g., only visual data) and multi-modal worlds (e.g., visual, audio, and language data). To further account for the temporal evolution within these worlds, we also propose forward and backward Fréchet World Distance as more detailed measurements for understanding world models.

3.1. Conventional Frechet Distance

We firstly brief the definition of the FD. The FD measure the similarity between two distributions. One popular application of FD is to quantify the quality of a generative model. Suppose the distribution from the outputs of a generative model and reference distribution are ${\mathrm{P}}_{\mathrm{G}}$ and ${\mathrm{P}}_R$. ‘G’ refer to generative and ‘R’ refers to reference. Then the FD is defined as:

$$\mathrm{d}\left({\mathrm{P}}_{\mathrm{G}},{\mathrm{P}}_{\mathrm{R}}\right)=\underset{\mathrm{X}~{\mathrm{P}}_{\mathrm{G}},\mathrm{Y}~{\mathrm{P}}_{\mathrm{R}}}{\min }\left(E{\left|X-Y\right|}^2\right)$$

(1)

The above results are difficult to derive for a general case. However, if both distributions are of Gaussian type, then:

$$\mathrm{d}\left({\mathrm{P}}_{\mathrm{G}},{\mathrm{P}}_{\mathrm{R}}\right)={\left|{\mu }_R-{\mu }_G\right|}^2+Tr\left({\mathsf{\Sigma }}_R+{\mathsf{\Sigma }}_G-2{\left({\mathsf{\Sigma }}_R{\mathsf{\Sigma }}_G\right)}^{1/2}\right)$$

(2)

${\mu }_R$ and ${\mu }_G$ are mean vector of the two distributions, while ${\mathsf{\Sigma }}_R$ and ${\mathsf{\Sigma }}_G$ are co-variance matrices.

3.2. Frechet World Distance for Unimodal C

Firstly we only consider single modal world. The modal is embedded in a context representation $\mathrm{C}$. Given the state at moment t ${\mathrm{X}}_{\mathrm{t}}$ in world ${\mathbb{L}}_2$ (the model world), the neural network (which is trained with dataset from world ${\mathbb{L}}_3$) output the action ${\mathrm{y}}_{\mathrm{t}}$ with some desired objective, as given in Figure 6. The state ${\mathrm{X}}_{\mathrm{t}}$ and ${\mathrm{y}}_{\mathrm{t}}$ leads the evolution of the system state to a new state ${\mathrm{S}}_{t+1}^{{\mathbb{L}}_2}$. At the same time, the nn sense the state ${\mathrm{X}}_{t+1}$. Note that the difference between ${\mathrm{S}}_{t+1}^{{\mathbb{L}}_2}$ and ${\mathrm{S}}_{t+1}^{{\mathbb{L}}_1}$ are characterized by two set-difference operation of ${\mathbb{L}}_1\backslash {\mathbb{L}}_2$ and ${\mathbb{L}}_2\backslash {\mathbb{L}}_1$.

Combining the above description, we have two trajectories from two worlds:

$$\left\{\begin{array}{c}{\mathit{S}}^{{\mathbb{L}}_1}:S_0^{{\mathbb{L}}_1}\to { S}_1^{{\mathbb{L}}_1}\to S_2^{{\mathbb{L}}_1} \dots .. \\ {\mathit{S}}^{{\mathbb{L}}_2}: S_0^{{\mathbb{L}}_2}\to { S}_1^{{\mathbb{L}}_2}\to S_2^{{\mathbb{L}}_2}\dots .. \end{array}\right.$$

(3)

The distribution of the initial state for the two worlds are represented as ${\mathsf{\pi }}_0^{{\mathbb{L}}_1}$ and ${\mathsf{\pi }}_0^{{\mathbb{L}}_2}$. As the system is stochastic, the distribution of the state at moment t is $\mathrm{p}\left(S_t^{{\mathbb{L}}_1}\right)$ for ${\mathbb{L}}_1$ and is $\mathrm{p}\left(S_t^{{\mathbb{L}}_2}\right)$ for ${\mathbb{L}}_2$. Considering the time horizon between $\left[0,T\right]$ and combining the idea from dynamic time wrapping, we define a FWD of the power q for the two worlds ${\mathbb{L}}_1$ and ${\mathbb{L}}_2$:

$${\mathrm{F}\mathrm{W}\mathrm{D}}_{\mathrm{q}}^C\left({\mathbb{L}}_1,{\mathbb{L}}_2\right)=\underset{\mathsf{\lambda }\in \mathcal{A}\left(S^{{\mathbb{L}}_1},S^{{\mathbb{L}}_2}\right)}{\min }{\left(\sum _{\left(i,j\right)\in \mathsf{\lambda }}{\left(FD\left(\mathrm{p}\left(S_i^{{\mathbb{L}}_1}\right),\mathrm{p}\left(S_j^{{\mathbb{L}}_2}\right)\right)\right)}^q\right)}^{1\backslash q}$$

(4)

$\mathsf{\lambda }$ is a alignment path of length K index pairs $\left(\left(i_0,j_0\right),\dots .\left(i_{K-1},j_{K-1}\right) \right)$, and $\mathcal{A}\left(S^{{\mathbb{L}}_1},S^{{\mathbb{L}}_2}\right)$ is all admissible alignment path between two trajectories $S^{{\mathbb{L}}_1}$ and $S^{{\mathbb{L}}_2}$. An alignment path should satisfy the following conditions:

-

Beginning and ending of the sequence are matched together:

∎

${\mathsf{\lambda }}_0=\left(\mathrm{0,0}\right)$

∎

${\mathsf{\lambda }}_{\mathrm{K}-1}=\left(T-1,T-1\right)$

-

The sequence is monotonically increasing in both i and j:

∎

${\mathrm{i}}_{k-1}\le {\mathrm{i}}_{\mathrm{k}}\le i_{k-1}+1$

∎

${\mathrm{j}}_{k-1}\le {\mathrm{j}}_{\mathrm{k}}\le j_{k-1}+1$

3.3. Frechet World Distance for Multi Modal

The above formulation Eq. 4 is developed for single modal trajectory. However, many models are trained via multi-modal information. As an example, autonomous vehicles end2end model are trained with video, LiDAR, Radar etc. Therefore, a world is characterized via the information from many modals. To extend the Frechet world distance to multi-modal setting, we combine the idea from contrastive learning. Suppose there are N modals ${\mathrm{C}}_{\mathrm{i}}$, $\mathrm{i}=\mathrm{1,2},\dots \mathrm{N}$. For each modal ${\mathrm{C}}_{\mathrm{i}}$, we apply an modal-specific encoder ${\mathrm{E}\mathrm{N}\mathrm{C}}_{C_i}\left({\mathrm{S}}_{\mathrm{t}}^{{\mathbb{L}}_{\mathrm{k}}}\right)$ to extract and encode the information at moment t for world ${\mathbb{L}}_{\mathrm{k}}$. The output ${\mathrm{U}}_{\mathrm{t},\mathrm{i}}^{{\mathbb{L}}_{\mathrm{k}}}={\mathrm{E}\mathrm{N}\mathrm{C}}_{C_i}\left({\mathrm{S}}_{\mathrm{t}}^{{\mathbb{L}}_{\mathrm{k}}}\right)$ resides at a shared vector space across all modals. As the multi-modal state space ${\mathrm{S}}_{\mathrm{t}}^{{\mathbb{L}}_{\mathrm{k}}}$ follows the distribution $\mathrm{p}\left(S_t^{{\mathbb{L}}_{\mathrm{k}}}\right)$, and thus the modal specific distribution is $\mathrm{p}\left({\mathrm{U}}_{\mathrm{t},\mathrm{i}}^{{\mathbb{L}}_{\mathrm{k}}}\right)$. We use this distribution to extend the FWD. For a set of modals $\left\{C_k\right\}$, the FWD is defined as follows:

$${\mathrm{F}\mathrm{W}\mathrm{D}}_{\mathrm{q}}^{\left\{C_k\right\}}\left({\mathbb{L}}_1,{\mathbb{L}}_2\right)=\underset{\mathrm{u},\mathrm{v}\in \left\{C_k\right\}}{\min }\underset{\mathsf{\lambda }\in \mathcal{A}\left(S^{{\mathbb{L}}_1},S^{{\mathbb{L}}_2}\right)}{\min }{\left(\sum _{\left(i,j\right)\in \mathsf{\lambda }}{\left(FD\left(\mathrm{p}\left({\mathrm{U}}_{\mathrm{t},\mathrm{u}}^{{\mathbb{L}}_1}\right),\mathrm{p}\left({\mathrm{U}}_{\mathrm{t},\mathrm{v}}^{{\mathbb{L}}_2}\right)\right)\right)}^q\right)}^{1\backslash q}$$

(5)

The above definition iterate over the possible modal u from the first world ${\mathbb{L}}_1$, and the target modal v from the second world ${\mathbb{L}}_2$, and calculate the FWD distance respectively.

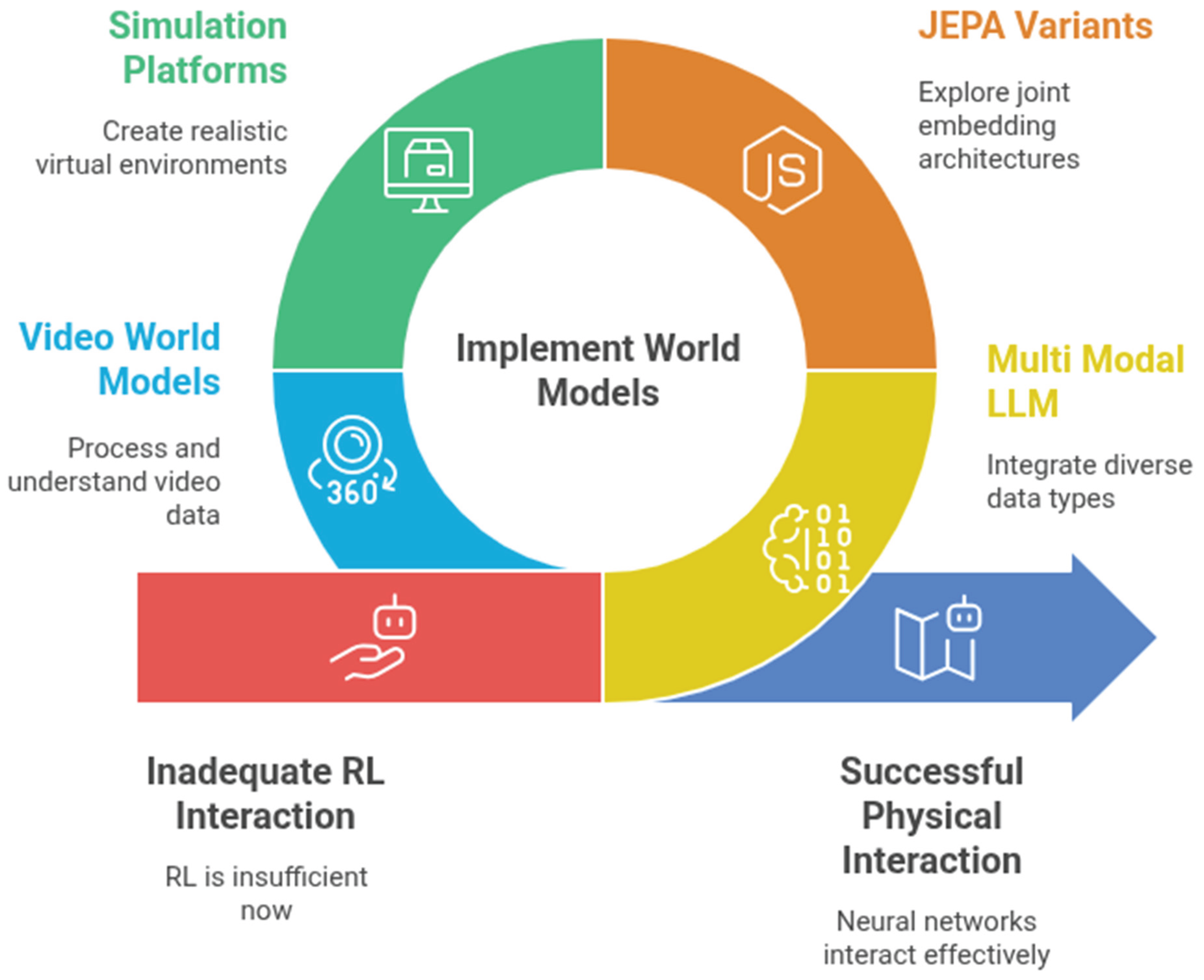
4. Related Work

4.1. World Model

World model is designed to mimic the human brain mechanism “based on what they are able to perceive with their limited senses” (Ha & Schmidhuber, 2018; Assran et al., 2025; Feng et al., 2022; Fu et al., 2023; Ha & Schmidhuber, 2018; Hong et al., 2023; Jiang et al., 2024; Karypidis et al., 2025a, 2025b; Ren et al., 2025; Rimon et al., 2024; Wang et al., 2023; Zhen et al., 2024; Zürn et al., 2024). The agent model includes three components, Vision (V), Memory (M), and Controller. The goals of the world model include understanding and predicting the abstraction of the world and generating/simulate the detail of the world. The world model concept then has been under discussion and become an overloaded word. It is extended beyond the pixel space and language space (i.e., LLM) to video (Ren et al., 2025), LiDAR (Zyrianov et al., 2024), Occupancy (Zheng et al., 2023), etc. Later one, the multi-modal world is conceived (Ashuach et al., 2023; Radford et al., 2021).

Except perception, simulation and prediction of the world, one core function of the world model is to plan the actions embodied environments (Zhen et al., 2024). The interaction between neural network represented model and the world can be achieved via a series of interaction tokens (Zhen et al., 2024), or standalone sub-neural-network modules (Ha & Schmidhuber, 2018). To achieve realistic interaction, the dynamics of the world should be learned, for instance, via the latent dynamics model (Ren et al., 2025; Sobal et al., 2025), or the reinforcement learning (Rimon et al., 2024). World models still is on its early stage. Further investigation is required to study its properties, for instance ergodicity (Bilaloglu et al., 2023), reachability (Fu et al., 2023), etc.

4.2. JEPA and Its Variants

In his seminar paper (LeCun, 2022), LeCun claimed that “best ML systems are still very far from matching human reliability in real-world tasks such as driving”. And he listed three challenges of ML systems: represent the world, learn to predict, and learn to act; reason and plan in ways that are compatible with gradient-based learning; learn to represent percepts and action plans in a hierarchical manner. Corresponding to the above claims, he proposed a framework termed JEPA (Joint-Embedding Predictive Architecture) that encapsulate the world model as its components. Other modules include configurator module, configurator module, cost module, short-term memory module and actor module. Given the architecture, the perception-action loop have two modes: mode 1 and mode 2. Since then, the JEPA are extended to many field (Assran et al., 2023a, 2023b, 2025; Bardes et al., 2023a, 2023b, 2024), encompassing many modals (Bardhan et al., 2025; Chen et al., 2025; Dong et al., 2024; Fei et al., 2023, 2024; Fu et al., 2024; Ghaemi et al., 2025;) including LiDAR (Zhu et al., 2025), audio (Fei et al., 2023), point cloud (Saito et al., 2025), etc (Girgis et al., 2025; Guetschel et al., n.d.; Hu et al., 2024; Kalapos & Gyires-Tóth, 2024; Kenneweg et al., 2025; LeCun, 2022; Li et al., 2024;).

Although JETA in its essence is not a generative model, its combination with generative models and also reinforcement learning (Kenneweg et al., 2025), imitation learning (Vujinović & Kovačević, n.d.), is appealing (Chen et al., 2025).

JEPA with its variants (Mahowald et al., 2023; Mo & Yun, 2024; Riou et al., 2024; Saito et al., 2025; Thimonier et al., 2025; Vujinović & Kovačević, n.d.; Weimann & Conrad, 2024; Zhu et al., 2025) has been successfully applied to different physical world such as collider physics (Bardhan et al., 2025).

4.3. Frechet Distance

The Fréchet distance (FD) is a measure of similarity between curves that takes into account the location and ordering of the points along the curves. The Fréchet distance quantifies the similarity between two curves. Consider two points, each tracing a finite, curvilinear path, such as a person and their dog on a leash. Both entities can adjust their speeds along their respective paths, but movement is restricted to a forward direction. The Fréchet distance is then defined as the minimum leash length required for both to complete their traversals from start to finish without the leash ever becoming taut. This metric is symmetric; the calculated distance remains constant irrespective of which curve is designated as the primary or secondary path.

FD has been successfully extended in the generative modeling (Bringmann et al., 2019; Ciesielski & Lewicki, 2021; Conradi et al., 2024; Dodson, 2011; Driemel & Har-Peled, 2013;). The seminal work is FID (Fréchet inception distance) that measure the quality of generative image neural network models with a reference image set. The Fréchet Inception Distance (FID), or specialized variants thereof, serves as an evaluation metric across diverse domains (Eftekharinasab, 2022; Farahbakhsh Touli, 2020; Gui et al., 2023; Kilgour et al., 2018; Li et al., 2024; Ramos et al., 2018;). For instance, the Fréchet Audio Distance (FAD) assesses music enhancement algorithms, while the Fréchet Video Distance (FVD) evaluates generative models of video. Similarly, the Fréchet ChemNet Distance (FCD) is employed to evaluate AI-generated molecules. However, it should be noted that, only in limited circumstance, the FD can be derived as a analytical form (Reimering et al., 2018; Retkowski et al., 2024; Soloveitchik et al., 2021a, 2021b; Vodolazskiy, 2021).

4.4. Potential Harms of Neural Networks Model in Physical World

Although the neural networks gain great success, its deployment into real world still faces considerable challenges. Given the fact that the practice is way ahead of the theory investigation, the understanding of neural networks still is limited. The magic of neural network are characterized by scale up law: the scale up in data, network size and training. During the test and utilization of the models, researchers find the negative aspects of the models. These negative aspects include reversal curse (Berglund et al., 2023; Zhu et al., 2024), hallucination (Ainslie et al., 2023; Aithal et al., 2024a, 2024b; Bai et al., 2024; Chrysos et al., n.d.; Du et al., 2023; Gao et al., 2024; Jesson et al., 2024; Kim et al., 2024; Lauscher et al., 2025; Oorloff et al., 2025; Rani et al., 2024; Rathkopf, 2025; Sahoo et al., 2024; Shazeer, 2020; Tauman Kalai & Vempala, 2023; H. Wang et al., 2024; Z. Wang et al., 2024; Wei et al., 2024; Xu et al., 2024; Zhang & Sennrich, 2019), interpretability (Conmy et al., 2023; Dunefsky et al., 2024; Gurnee et al., 2023; Kissane et al., 2024; Kramár et al., 2024; Makelov et al., 2024; Marks et al., 2024; Rajamanoharan et al., 2024; Sharkey et al., 2025) etc. Hence it is crucial to build a safe, responsible AI (Batool et al., 2023; Ghamisi et al., 2024; Goellner et al., 2024; Pi, 2023; Wang et al., 2024) stacks that can work as desired in physical world, and still have the capabilities to explore the world in ergodic way.

5. Discussion and Conclusion

In conclusion, the imminent convergence of neural networks with the physical world necessitates a deeper theoretical understanding to mitigate inherent risks. Currently, the practical application of neural networks outpaces our theoretical grasp, leading to potential vulnerabilities in their development and deployment. To address this, we propose a three-tiered world hierarchy: the data world, the model world, and the real world. Furthermore, the introduction of Fréchet World Distance offers a robust metric for quantifying the discrepancies between single and multi-modal representations within these interconnected domains. This framework is crucial for fostering safer and more reliable advancements in neural network technology as it becomes increasingly integrated with our physical reality.

Future works including:

1)

Develop three-worlds hierarchy JEPA models to encapsulate complex dynamics. In the JEPA model, the cost modules can be implemented via the Frechet world distance.

2)

Develop models that detect the hallucination of the neural network models. The hallucination is defined over the difference operation between model world and the real world. Given that the FWD can measure the difference between different levels of world, the FWD can serve as objective that train the models with minimal hallucination.