Design Method of Small Recreational Vehicle’s Interior Space Based on User Behavior Data Analysis

1. Introduction

With the continuous improvement of people’s pursuit of life quality, leisure traveling has become a fashionable and popular way of life. As a kind of travel carrier with promising development, small recreational vehicle has attracted much attention for its characteristics of free, convenient and economic. Statistical data shows that the comfort and convenience of the recreational vehicle’s interior space are the primary factors that drivers and passengers pay attention to [1,2]; meanwhile, in the whole industry chain of recreational vehicle manufacturing, the design cost of the interior space accounts for about 50~60% of the total price [3,4]. Therefore, research on the design method of recreational vehicle’s interior space plays an important guiding role for manufacturing enterprises to reduce costs and improve users’ satisfaction.

At present, researches on the interior space design of recreational vehicle mainly consist of three fields, including the design method based on spatial scale study, modularization idea and performance constraint theory.

1.1. Design Method Based on Spatial Scale Study

Spatial scale research is based on the theories of ergonomics and design psychology, to establish the recreational vehicle’s interior design solutions by studying the furniture scale, human body scale, physiological scale and psychological scale. Its main design methods include: (1) Ergonomics-based design approaches [5,6,7,8,9]. Drawing on the interior design theories, these methods integrate the interior space of the recreational vehicle by analyzing the human-machine dimensions of the recreational vehicle’s functional facilities, to maximize the utilization of the space. (2) Design methods based on design psychology [10,11,12,13,14]. These approaches establish the evaluation methods of the design scheme from physiological scale and psychological scale of the drivers and passengers, to test the comfort of the initial design scheme with the help of computer simulation, to propose improvement measures. The above approaches explored the design techniques of recreational vehicle’s interior space from different perspectives; however, the correlations between different functional facilities are usually neglected. Therefore, starting from the analysis of the correlations between functional facilities and studying the influence effects on the design results is a new direction for the recreational vehicle’s interior space design.

1.2. Design Method Based on Modularization Idea

Modular design is a green design method that combines the product design elements into subsystems with specific functions, i.e., modules, and then to design product by reasonable modules combinations. The applications of these approaches to the recreational vehicle’s interior space design mainly include: (1) Modular design approaches based on functional requirements analysis [15,16,17,18,19]. The basic principle of these methods is to categorize the users’ requirements of recreational vehicle and based on the classification results, establish the standard module library, to establish the design scheme of recreational vehicle’s interior space by combining the modules. (2) Modular design approaches based on manufacturing processes [20,21,22,23,24]. The basic principle of these methods is to establish the design scheme by analyzing the manufacturing process of the recreational vehicle and merging similar processes of different production lines, to simplify the manufacturing process. It can be seen that the comfort needs of drivers and passengers are usually ignored to a certain extent in the modularized design methods. Therefore, taking the users’ experience as the starting point and exploring the influencing effects on the design scheme of recreational vehicle’s interior space design, can further improve the practicality of the modular design methods.

1.3. Design Method Based on Performance Constraint Theory

Performance constraint theory is mainly used for the design of specific functional facilities. Firstly, it puts forward constraints on the usage performance of the specified functional facilities, and then analyzes the parameters, morphology, and structure of the functional facilities from various perspectives, such as the reasonableness of the spatial dimensions, the convenience of the human- machine interaction, the safety and comfort in the usage process, so as to establish an optimized design scheme [25,26,27,28]. Since the precise quantitative descriptions of the constraints are usually required in the mathematical planning algorithms involved in these methods and the solution process is also complex, it is mainly applicable to the design of simple functional facilities.

1.4. Sketch of the Algorithm

Based on the above researches, this paper proposes a method of grouping all functional facilities based on their correlations for designing the interior space of small recreational vehicle. Firstly, drawing on the quantitative representation of the correlation between random variables in statistics, i.e., the nature of the correlation coefficient, the correlation degree between two functional facilities is defined based on the usage time interval, so as to quantitatively represent the correlation between them; secondly, the correlation degrees of all the functional facilities are formed into the correlation degree matrix, and the matrix can be proved to be a real symmetric positive definite one; next, based on the properties of the correlation matrix, the factor analysis method is adopted to group all the functional facilities, so that the correlations of functional facilities within the same group are as large as possible, and the ones between different groups are as small as possible, so as to better satisfy the users’ needs for the convenience of the functional facilities and improve the users’ comfort in traveling; finally, a case analysis is given to prove the effectiveness of the proposed method.

2. Correlation Degree Between Functional Facilities

In travelling, all the needs of the drivers and passengers are realized by operating or using a series of functional facilities inside the recreational vehicle. Considering the convenience of realizing the user’s different needs, the functional facilities for realizing specific needs should be arranged relatively centralized, i.e., the layout scheme of the recreational vehicle’s interior should be designed with reference to the correlations of functional facilities. Therefore, drawing on the quantitative description of correlation between random variables in statistics, this paper begins by defining the correlation degree between two different functional facilities.

In statistics, the correlation between two random variables X and Y can be described by their correlation coefficient ρ_XY, which has the following basic properties: [29,30]

(1) Normality.

For the random variables X and Y, the correlation coefficient ρ_XY satisfies -1 ≤ ρ_XY ≤ 1, where its absolute value |ρ_XY | reflects the correlation degree between X and Y.

(2) Symmetry.

The correlation coefficient between random variables X and Y is equal to the one between Y and X, i.e., ρ_XY = ρ_YX.

It follows that the quantitative definition to characterize the correlation between different functional facilities inside recreational vehicle should satisfy the two properties of the correlation coefficient in statistics.

From the perspective of users’ behavior, drivers and passengers generally need to use multiple functional facilities sequentially in order to satisfy their specific needs during a trip. For different functional facilities, the usage time intervals can indicate the correlations between them. Therefore, the usage time interval could be adopted to quantitatively describe the correlation between two functional facilities.

Let x_i and x_j be two different functional facilities, and the usage time for x_i and x_j are t_i and t_j, then the usage time interval between x_i and x_j is defined as:

$$\Delta T_{ij}=|t_i-t_j|$$

(1)

It is evident that ΔT_ij meets the properties of symmetry, but not normality. Thus, ΔT_ij could be normalized by considering the total duration of the trip. That is, assuming the total duration of the trip is T, then the standardized time interval $\Delta {\overline{T}}_{ij}$ can be defined as follows:

$$\Delta {\overline{T}}_{ij}={\displaystyle \frac{\Delta T_{ij}}{T}}={\displaystyle \frac{|t_i-t_j|}{T}}$$

(2)

It can be seen that the standardized usage interval $\Delta {\overline{T}}_{ij}$satisfies both symmetry and normality. At the same time, $\Delta {\overline{T}}_{ij}$ decreases as the correlation between x_i and x_j increases. In order to be consistent with the statistical connotation of correlation coefficient, $\Delta {\overline{T}}_{ij}$can be further amended as the following definition.

Correlation degree of two functional facilities:Let x_i and x_j be two functional facilities inside recreational vehicle. During the trip, the usage time of x_i and x_j are t_i and t_j, and the duration of the trip is T, then the correlation degree σ_ij between x_i and x_j is defined as:

$${\sigma }_{ij}=1-{\displaystyle \frac{|t_i-t_j|}{T}}$$

(3)

3. Positive Characterization of the Correlation Matrix

The correlation degree σ_ij defined by Equation (3) provides a quantitative description of the relevance between two different functional facilities. Combining all the functional facilities two by two and calculating the corresponding correlation degrees, the correlation degree matrix Σ can be constructed as follow:

$$\Sigma =\left(\begin{array}{cccc}{\sigma }_{11}& {\sigma }_{12}& \dots & {\sigma }_{1n}\\ {\sigma }_{21}& {\sigma }_{22}& \dots & {\sigma }_{21}\\ ⋮& ⋮& ⋮& ⋮\\ {\sigma }_{n1}& {\sigma }_{n2}& \dots & {\sigma }_{nn}\end{array}\right)$$

(4)

For the correlation degree matrix Σ, the following theorem holds:

Symmetry and positive definiteness of the correlation degree matrix: The correlation degree matrix Σ is a real symmetric positive definite matrix.

First prove the symmetry of Σ.

Denote all the functional facilities inside recreational vehicle as the vector X = (x₁, x₂, …, x_n) ^T. From Equations (3) and (4), the correlation degree matrix Σ can be written as:

$$\Sigma =\left(\begin{array}{cccc}1-{\displaystyle \frac{\Delta T_{11}}{T}}& 1--{\displaystyle \frac{\Delta T_{12}}{T}}& \dots & 1-{\displaystyle \frac{\Delta T_{1n}}{T}}\\ 1--{\displaystyle \frac{\Delta T_{21}}{T}}& 1-{\displaystyle \frac{\Delta T_{21}}{T}}& \dots & 1-{\displaystyle \frac{\Delta T_{2n}}{T}}\\ ⋮& ⋮& ⋮& ⋮\\ 1-{\displaystyle \frac{\Delta T_{n1}}{T}}& 1-{\displaystyle \frac{\Delta T_{n2}}{T}}& \dots & 1-{\displaystyle \frac{\Delta T_{nn}}{T}}\end{array}\right)$$

(5)

By the definition of the time interval ΔT_ij in equation (1), we know that Σ is a symmetric matrix.

The following proves the positive definiteness of Σ.

Let a n-dimensional vector c = (c₁, c₂, …, c_n) ^T ≠ 0.

$$c^T\Sigma c=(c_1,c_2,\dots c_n)\Sigma {(c_1,c_2,\dots c_n)}^T$$

(6)

Substituting Equation (5) into Equation (6), after simplifying and combining, we get:

$$c^T\Sigma c=\left({\displaystyle \sum _{i,j=1}^n{c}_i\sqrt{1-\frac{\Delta T_{ij}}{T}}}\right)\left({\displaystyle \sum _{k,j=1}^n\sqrt{1-\frac{\Delta T_{kj}}{T}}{c}_k}\right)$$

(7)

Let the random variable$z={\displaystyle \sum _{i,j=1}^n{c}_i\sqrt{1-\frac{\Delta T_{ij}}{T}}}$, bringing it into Equation (7), we get

$$c^T\Sigma c=E(z^2)\ge 0$$

The definition of the time interval ΔT_ij shows that $1-{\displaystyle \frac{\Delta T_{ij}}{T}}>0$, and hence z ≠ 0, i.e.,

$$c^T\Sigma c=E(z^2)>0$$

The above equation shows that Σ is a positive definite matrix. In summary, the correlation degree matrix Σ is a real symmetric positive definite matrix.

4. Functional Facilities Grouping Model

Based on the definition of correlation degree, all functional facilities can be grouped so that the correlation degrees within the same group are as large as possible, and the ones between different groups are as small as possible, so that the design solution can fully satisfy the users’ needs for convenience.

4.1. Factor Analysis

Factor analysis is a method of grouping components based on the correlations between them with reference to the covariance matrix of a random vector. The basic model of factor analysis method is as follows [31,32].

(1).

X = (x₁, x₂, …, x_n)^T is an observable random vector with covariance matrix Σ.

(2).

The common factor vector F = (F₁, F₂, …, F_m) (m<n) is an unobservable random vector with mean vector E(F) = 0 and covariance matrix D(F) = I, i.e., the components in the common factor vector F are independent of each other.

(3).

The error vector ε = (ε₁, ε₂, …, ε_n) ^Tis independent of the common factor vector F with mean vector E(ε) = 0, and its covariance matrix Σ_ε is diagonal, i.e.:

$${\Sigma }_{\epsilon }=\left(\begin{array}{cccc}{\sigma }_{{\epsilon }_1}^2& & & \\ & {\sigma }_{{\epsilon }_2}^2& & \\ & & \ddots & \\ & & & {\sigma }_{{\epsilon }_n}^2\end{array}\right)$$

(8)

Under the above conditions, the system of Equation (9) is called the factor analysis model.

$$\left\{\begin{array}{l}{x}_1=a_{11}{F}_1+a_{12}{F}_2+\dots +a_{1m}{F}_m+{\epsilon }_1\hfill \\ x_2=a_{21}{F}_1+a_{22}{F}_2+\dots +a_{2m}{F}_m+{\epsilon }_2\hfill \\ \begin{array}{cccc}⋮& & & \end{array}\hfill \\ x_n=a_{n1}{F}_1+a_{n2}{F}_2+\dots +a_{nm}{F}_m+{\epsilon }_n\hfill \end{array}\right.$$

(9)

Express the system of Equation (9) in matrix:

$$X=AF+\epsilon$$

(10)

where the element a_ij in A=(a_ij)_n×m is called the factor loading, and its absolute value indicates the dependence degree between the component x_i and the common factor F_j. The matrix A formed by all the factor loadings is called the factor loading matrix.

Calculating the covariance matrix for each end of equation (10) gives:

$$\Sigma =D(X)=D(AF)+D(\epsilon )=AD(F)A^T+D(\epsilon )=A{A}^T+D(\epsilon )$$

(11)

On the other hand, the proved theorem in section 3 shows that Σ is a real symmetric positive definite matrix, for which the Cholesky decomposition [33,34] is performed:

$$\Sigma =G{G}^T$$

(12)

where $G=(\sqrt{{\lambda }_1}{e}_1,\sqrt{{\lambda }_2}{e}_2,\dots ,\sqrt{{\lambda }_n}{e}_n)$, λ_i (i=1, 2, …, n) are the eigenvalues of the covariance matrix Σ, and λ₁>λ₂>… >λ_p, e_i is the eigenvector corresponding to λ_i.

Comparing Equations (11) and (12) shows that the error vector ε = 0 in Equation (10) when A = G, and the resulting factor analysis model is accurate. However, an exact factor analysis model implies that in the random vector X = (x₁, x₂, …, x_n) ^T, the components will be divided into n groups, i.e., an exact factor analysis model can be obtained only when the correlations between all the components in X are completely ignored. In general, it is necessary to retain most of the correlations between the components, in which case the first m (m<n) columns in G can be used as an approximation of the factor loading matrix A, i.e.,:

$$A\approx (\sqrt{{\lambda }_1}{e}_1,\sqrt{{\lambda }_2}{e}_2,\dots ,\sqrt{{\lambda }_m}{e}_m)$$

(13)

When building the factor analysis model based on the factor loading matrix derived from Equation (13), the error vector ε ≠ 0, which means that there must be a certain amount of information loss when grouping the components in X based on Equation (10).

4.2. Error Analysis

In statistics, the total amount of information contained in a random variable is generally measured by its variance [35,36]. In Equation (10), let A = G, which gives the sum of the variances of the components in X under the exact decomposition condition:

$${\displaystyle \sum _{i=1}^{n}D(x_i})={\displaystyle \sum _{i=1}^n{\lambda }_i}$$

(14)

Equation (14) shows that under the condition of exact decomposition, the sum of the information contained in X is equal to the cumulative sum of all the eigenvalues of X’s covariance matrix Σ.

The factor analysis model is then built from the approximation of matrix A shown in Equation (13), which is obtained from Equation (10):

$${\displaystyle \sum _{i=1}^{n}D(x_i})={\displaystyle \sum _{i=1}^m{\lambda }_i}+{\displaystyle \sum _{i=1}^{n}D({\epsilon }_i)}$$

(15)

Comparing Equations (14) and (15) shows that under imprecise conditions and ignoring the correlations of the components between different groups, the sum of the information loss caused by grouping the components in X with Equation (10) is ${\displaystyle \sum _{i=m+1}^n{\lambda }_i}$. Thus, for a specified error β, the number of groupings m can be determined by the following inequality:

$$\eta ={\displaystyle \frac{{\displaystyle \sum _{i=1}^m{\lambda }_i}}{{\displaystyle \sum _{i=1}^n{\lambda }_i}}}\ge 1-\beta$$

(16)

where η is called the cumulative variance contribution of the first m eigenvalues. In the empirical case, the number of groupings m can be determined from inequality (16) when η > 80%~ 85%. The value of η can be reasonably adjusted in combination with specific applications, but the basic principle of adjustment is that it should be conducive to the reasonable interpretation of the factor analysis model.

4.3. Grouping Model Based on Factor Analysis

To summarize, all the functional facilities inside recreational vehicle are denoted as the vector X = (x₁, x₂, …, x_n) ^T, which can be grouped based on its correlation degree matrix in the following steps.

(1)

Record the usage time t_i (i = 1, 2, …, n) spent by users on functional facility x_i.

(2)

Calculate the correlation degrees between different functional facilities based on equation (3), and then construct the correlation degree matrix Σ.

(3)

Calculate the eigenvalues of Σ and arrange all the eigenvalues in descending order as λ₁>λ₂>…>λ_n.

(4)

Calculate the eigenvector e_i corresponding to the eigenvalue λ_i (i = 1, 2, …, n).

(5)

For the given error β, calculate the number of eigenvectors m for constructing the factor loading matrix according to Equation (16), and then construct the factor loading matrix A from the first m eigenvectors according to Equation (13).

(6)

Grouping of all the functional facilities according to Equation (10).

5. Case Analysis

CCHW-Weiman recreational vehicle is a self-propelled recreational vehicle designed by Lanzhou Lanshi Group on the basis of the special chassis of SAIC Datsun V80, which can be used for 6 people to live and travel. The recreational vehicle contains 14 functional facilities: beds, stoves, sofas, ventilation windows, hanging cabinets, sinks, showers, refrigerator, cupboards, toilet, dressing mirror, storage cabinet, standing cabinets and parlor table, which are denoted as X = (x₁, x₂, …, x₁₄) ^T.

Based on a 300-minute travel, the usage time of the functional facilities inside the recreational vehicle by 20 groups of drivers and passengers are recorded to calculate the usage time interval. The average usage time intervals between different functional facilities are shown in Table 1.

Based on the data in Table 1, the correlation degree matrix Σ for all the functional facilities is calculated according to Equation (3), and then the eigenvalues and eigenvectors of Σ are calculated. All the eigenvalues are sorted in descending order, and the cumulative variance contribution of the first m (m<14) eigenvalues are calculated. The first four eigenvalues, eigenvectors and cumulative variance contributions are listed in Table 2.

$$\Sigma =\left(\begin{array}{llllllllllllll}1\hfill & 0.25\hfill & 0.67\hfill & 0.99\hfill & 0.98\hfill & 0.30\hfill & 0.95\hfill & 0.32\hfill & 0.31\hfill & 0.97\hfill & 0.92\hfill & 0.28\hfill & 0.97\hfill & 0.06\hfill \\ 0.25\hfill & 1\hfill & 0.82\hfill & 0.26\hfill & 0.27\hfill & 0.95\hfill & 0.30\hfill & 0.93\hfill & 0.94\hfill & 0.28\hfill & 0.33\hfill & 0.97\hfill & 0.28\hfill & 0.81\hfill \\ 0.67\hfill & 0.82\hfill & 1\hfill & 0.07\hfill & 0.08\hfill & 0.77\hfill & 0.12\hfill & 0.75\hfill & 0.76\hfill & 0.10\hfill & 0.15\hfill & 0.78\hfill & 0.09\hfill & 0.99\hfill \\ 0.99\hfill & 0.26\hfill & 0.07\hfill & 1\hfill & 0.99\hfill & 0.31\hfill & 0.96\hfill & 0.32\hfill & 0.31\hfill & 0.97\hfill & 0.92\hfill & 0.27\hfill & 0.98\hfill & 0.07\hfill \\ 0.98\hfill & 0.27\hfill & 0.08\hfill & 0.99\hfill & 1\hfill & 0.32\hfill & 0.97\hfill & 0.33\hfill & 0.32\hfill & 0.98\hfill & 0.93\hfill & 0.30\hfill & 0.99\hfill & 0.08\hfill \\ 0.30\hfill & 0.95\hfill & 0.77\hfill & 0.31\hfill & 0.32\hfill & 1\hfill & 0.35\hfill & 0.98\hfill & 0.99\hfill & 0.33\hfill & 0.38\hfill & 0.98\hfill & 0.33\hfill & 0.76\hfill \\ 0.95\hfill & 0.30\hfill & 0.12\hfill & 0.96\hfill & 0.97\hfill & 0.35\hfill & 1\hfill & 0.37\hfill & 0.36\hfill & 0.98\hfill & 0.97\hfill & 0.33\hfill & 0.98\hfill & 0.11\hfill \\ 0.32\hfill & 0.93\hfill & 0.75\hfill & 0.32\hfill & 0.33\hfill & 0.98\hfill & 0.37\hfill & 1\hfill & 0.99\hfill & 0.35\hfill & 0.40\hfill & 0.97\hfill & 0.34\hfill & 0.74\hfill \\ 0.31\hfill & 0.94\hfill & 0.76\hfill & 0.31\hfill & 0.32\hfill & 0.99\hfill & 0.36\hfill & 0.99\hfill & 1\hfill & 0.34\hfill & 0.39\hfill & 0.98\hfill & 0.33\hfill & 0.75\hfill \\ 0.97\hfill & 0.28\hfill & 0.10\hfill & 0.97\hfill & 0.98\hfill & 0.33\hfill & 0.98\hfill & 0.35\hfill & 0.34\hfill & 1\hfill & 0.95\hfill & 0.32\hfill & 0.99\hfill & 0.09\hfill \\ 0.92\hfill & 0.33\hfill & 0.15\hfill & 0.92\hfill & 0.93\hfill & 0.38\hfill & 0.97\hfill & 0.40\hfill & 0.39\hfill & 0.95\hfill & 1\hfill & 0.37\hfill & 0.94\hfill & 0.14\hfill \\ 0.28\hfill & 0.97\hfill & 0.78\hfill & 0.27\hfill & 0.30\hfill & 0.98\hfill & 0.33\hfill & 0.97\hfill & 0.98\hfill & 0.32\hfill & 0.37\hfill & 1\hfill & 0.31\hfill & 0.78\hfill \\ 0.97\hfill & 0.28\hfill & 0.09\hfill & 0.98\hfill & 0.99\hfill & 0.33\hfill & 0.97\hfill & 0.34\hfill & 0.33\hfill & 0.99\hfill & 0.94\hfill & 0.31\hfill & 1\hfill & 0.09\hfill \\ 0.06\hfill & 0.81\hfill & 0.99\hfill & 0.07\hfill & 0.08\hfill & 0.76\hfill & 0.11\hfill & 0.74\hfill & 0.75\hfill & 0.09\hfill & 0.14\hfill & 0.78\hfill & 0.09\hfill & 1\hfill \end{array}\right)$$

From Table 2, it can be seen that the cumulative variance contribution of the first three eigenvalues is 97.99%, so let m=3 and the factor loading matrix is constructed according to equation (13), which in turn creates a system of transformation equations according to equations system (9).

$$\left\{\begin{array}{l}{x}_1=0.81F_1-0.55F_2+0.03F_3\hfill \\ x_2=0.74F_1+0.63F_2-0.08F_3\hfill \\ x_3=0.55F_1+0.71F_2+0.43F_3\hfill \\ x_4=0.82F_1-0.55F_2+0.03F_3\hfill \\ x_5=0.83F_1-0.55F_2+0.03F_3\hfill \\ x_6=0.77F_1+0.59F_2-0.20F_3\hfill \\ x_7=0.84F_1-0.51F_2+0.03F_3\hfill \\ x_8=0.78F_1+0.57F_2-0.21F_3\hfill \\ x_9=0.78F_1+0.58F_2-0.21F_3\hfill \\ x_{10}=0.84F_1-0.53F_2+0.03F_3\hfill \\ x_{11}=0.85F_1-0.46F_2+0.02F_3\hfill \\ x_{12}=0.77F_1+0.60F_2-0.16F_3\hfill \\ x_{13}=0.84F_1-0.54F_2+0.04F_3\hfill \\ x_{14}=0.54F_1+0.71F_2+0.44F_3\hfill \end{array}\right.$$

As can be seen from the transformation equations, x₁，x₄，x₅，x₇，x₁₀，x₁₁，x₁₃ have a greater dependence on the common factor F₁, so they are categorized into a group. Functional facilities in this group are mainly used for user’s living and washing, and constitutes the living and washing area; x₃，x₁₄ are more dependent on the common factor F₂, which are divided into another group to form the recreation area; finally, the remaining facilities x₂，x₆，x₈，x₉，x₁₂ are divided into another group. This group of functional facilities is primarily used for cooking and dining while traveling and constitutes the dining and kitchen area. The final grouping results are shown in Table 3.

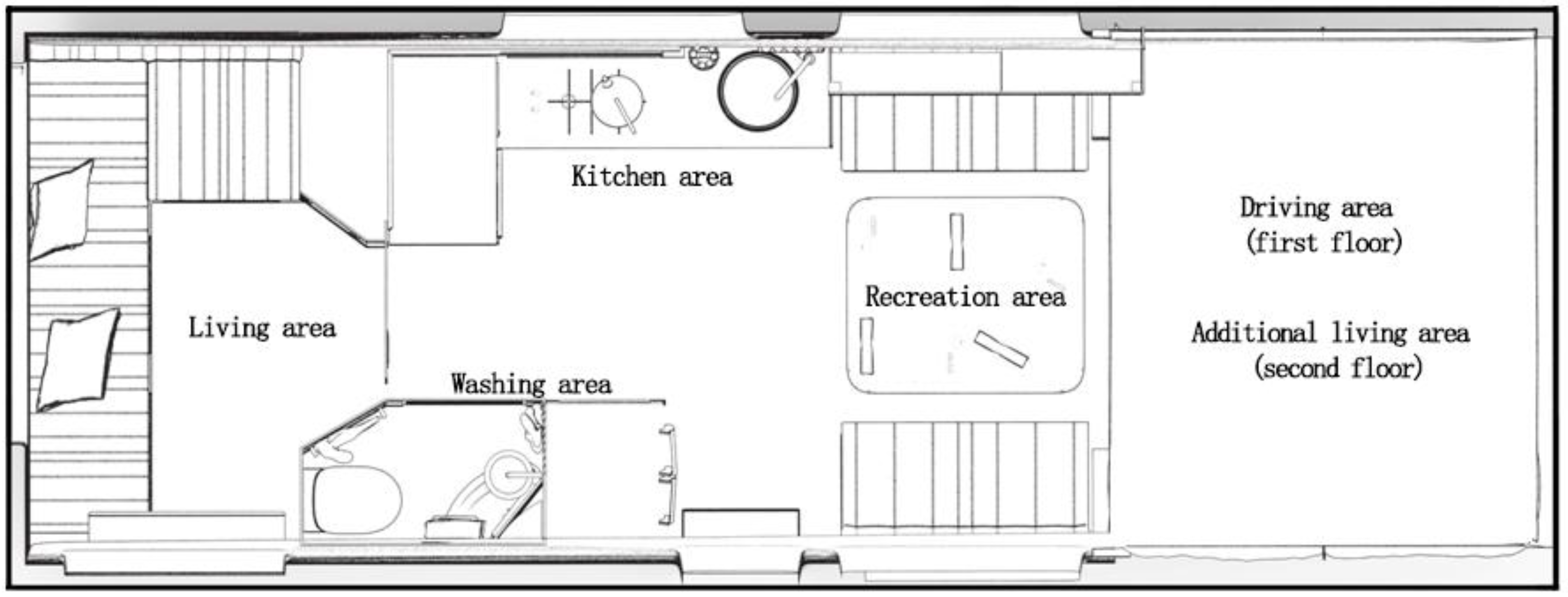
In the grouping results shown in Table 3, the first group has the more functional facilities. Considering that the passengers will usually need washing after sleeping, the functional facilities of the first group are further divided into the living area and the washing area, in which the functional facilities of the living area are beds, hanging cabinets, dressing mirror and standing cabinets, while the washing area consists of ventilator windows, showers, and toilet. The final results of functional facilities grouping are shown in Table 4.

Since the functional facilities in living area and washing area are highly correlated, they are set up as adjacent areas in the space layout. On the other hand, in order to further improve the passenger capacity and space utilization of the small recreational vehicle, the upper part of the driving area is designed as an additional resting area, which can provide a resting space for 1~2 people. The final interior space design scheme is shown in Figure 1.

Light gray is used as the main color and dark gray as the accent color of the interior space, to establish the rendering graph of the interior space of CCHW-Weiman, as shown in Figure 2.

6. Conclusions and Discussion

For the problem of interior space design of small recreational vehicles, this paper proposes a grouping method of functional facilities in recreational vehicles based on the user’s behavior dada analysis. Compared with the present design methods, the method proposed in this paper has the following advantages:

(1) Fully satisfy the user’s need for convenience in terms of functional facilities.

The method proposed in this paper is based on the behavioral data analysis of drivers and passengers, and aims to improve the convenience of the use of functional facilities during travelling, while the design method based on spatial scale study focus on maximize the space utilization, and the design method based on modularization idea mainly to reduce the manufacturing costs. Therefore, the method proposed in this paper can fully satisfy the driver’s need for convenience of functional facilities.

(2) Better generality.

Compared with the design method based on the performance constraint theory, the solution process of the proposed method is simple and avoids the limitation that the design method based on the performance constraint theory is only applicable to the design of simple functional facilities due to the complex calculation. Therefore, the proposed method can be used as a general theoretical model for the interior space design of small recreational vehicles.

The definition of the correlation degree of functional facilities in this paper is based on the usage time interval between different facilities, and therefore the proposed design method aims to improve the convenience of functional facilities. Considering that different functional facilities are also related in terms of material, structure and manufacturing process, if these factors are included in the definition of the correlation degree of the functional facilities, the convenience of using the functional facilities can be improved while optimizing the manufacturing process and manufacturing cost. We will study this issue in depth in our later work.