A Novel Theory Expression for the Impedance of a Ferrite-Loaded CW Illuminator

1. Introduction

Loop antennas and their various modifications are widely used in applications such as UHF RFID [1,2,3], electromagnetic compatibility measurements [4,5], wireless power transfer [6,7], and remote sensing/geophysical exploration [8,9,10]. The fundamental characteristics of loop antennas were established by Storer [11] and Wu [12] in the 1950s and 1960s, respectively, who derived analytical expressions for the impedance and current distribution of unloaded thin-wire loops.

Building upon Storer and Wu’s framework, McKinley [18] introduced a modified formulation that incorporates the surface impedance of metallic wires, enabling accurate impedance characterization even at optical frequencies. Subsequently, the same approach was applied to extend Izuka’s theory to infrared/optical regimes for loops with periodic lumped loads [19], However, the low-frequency characteristics of the loaded loop antenna have not received sufficient attention. Recently, a specialized loop antenna, referred to as the CW illuminator, has been revisited, and a fast numerical simulation method has been proposed for calculating its field distribution [20]. Nevertheless, this work did not account for the theoretical model and the closed-form solution of the impedance.

This paper presents a novel analytical model for characterizing the input impedance of a ferrite-loaded circular loop antenna. A closed-form solution for the input impedance is derived and subsequently validated through full-wave electromagnetic simulations using three-dimensional field analysis software. The proposed model enables systematic investigation of impedance variation patterns under different loading conditions. Furthermore, this work provides an efficient and accurate design methodology for optimizing impedance characteristics in continuous-wave (CW) radiator applications.

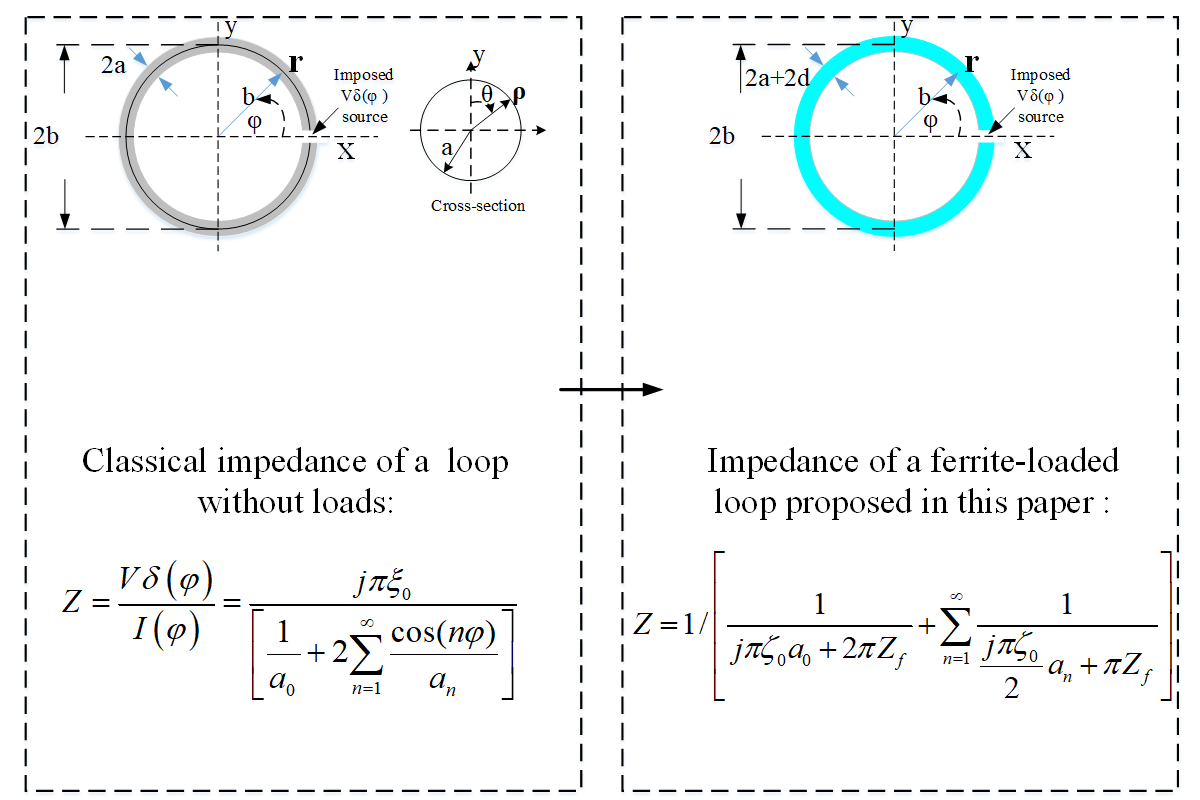
2. Review of the Classical Theory of a Circular Loop

2.1. The Origin of the Problem

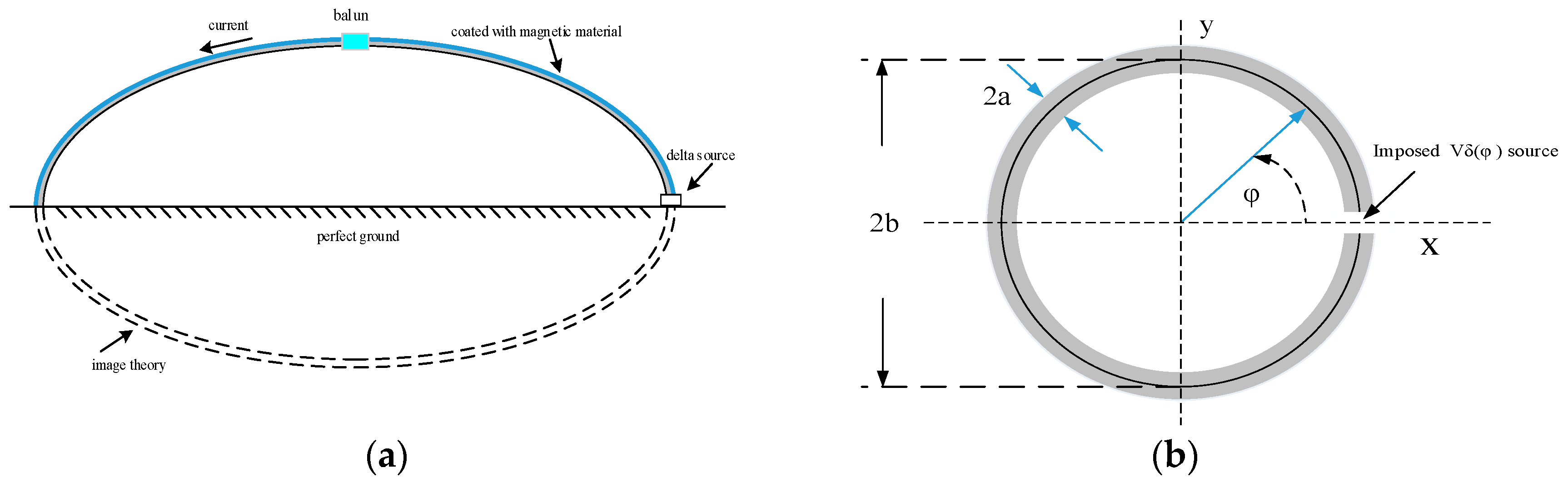
Figure1(a) illustrates the complete equivalent geometry of a continuous wave (CW) illuminator, which consists of a semi-elliptical structure with a delta-function source placed on the ground plane and coated with a ferrite material. In [21], the magnetic medium is initially modeled as a continuous ferrite tube enclosing the wire and subsequently simplified to discrete ferrite beads loaded along the conductor. In this work, the structure is modeled by assuming that the elliptical surface is uniformly coated with a magnetic film. From a theoretical perspective, and based on image theory, the circular loop shown in Figure 1(b) provides a reasonable approximation of the CW illuminator configuration shown in Figure1(a), provided that both loops enclose the same area.

2.2. The Impedance of a Circular Loop Without Loads

The theoretical analysis begins with a thin circular loop, as previously studied by Storer [11] and Wu [12]. Figure1(b) illustrates the geometry and coordinate system for a metallic loop with an infinitesimal gap. The loop has a radius b and a wire radius a, and it is excited by a delta-function voltage source applied across the gap. When the condition a ≪b is satisfied, it is reasonable to assume that the surface current flows only in the azimuthal direction along the loop.

The well-known Pocklington integral equation establishes the relationship between the current distribution and the applied voltage source on an unloaded loop. It is expressed as follows [11]:

$$V\delta \left(\phi \right)={\displaystyle \frac{j{\zeta }_0}{4\pi }}{\displaystyle {\int }_{-\pi }^{\pi }K\left(\phi -{\phi }^{\text{'}}\right)I\left({\phi }^{\text{'}}\right)d{\phi }^{\text{'}}}$$

(1)

The infinite Fourier series is employed to describe the current distribution and it can be written as

$$I\left(\phi \right)={\displaystyle \sum _{n=-\infty }^{\infty }{I}_n\exp (jn\phi )}={\displaystyle \frac{V\delta \left(\phi \right)}{j\pi {\xi }_0}}\left[{\displaystyle \frac{1}{a_0}}+2{\displaystyle \sum _{n=1}^{\infty }\frac{\cos (n\phi )}{a_n}}\right]$$

(2)

where is the wave impedance in free space, $a_0$ …$a_n$ are the coefficients related to the integrand in [11] and $\delta \left(\phi \right)$is the Dirac delta function. The loop input impedance at $\phi =0$ is defined as

$$Z={\displaystyle \frac{V\delta \left(\phi \right)}{I\left(\phi \right)}}={\displaystyle \frac{j\pi {\xi }_0}{\left[\frac{1}{a_0}+2{\displaystyle \sum _{n=1}^{\infty }\frac{\cos (n\phi )}{a_n}}\right]}}$$

(3)

2.3. The Impedance of a Circular Loop Loaded with Ferrite Material

The cylindrical antenna with spatially varying internal impedance was analyzed by Wu [23]. The antenna is composed of a resistive material whose conductivity varies along its length. As current flows along the structure, the resistive material imposes a distributed opposition, effectively forming an internal impedance within the antenna.

In the present study, a circular loop antenna coated with ferrite material is considered. Based on the formulations developed by Wu and Storer [11,23,24], the current distribution on the ferrite-loaded circular loop can be expressed as follows:

$$Z_{f}I\left(\phi \right)=V\delta \left(\phi \right)-{\displaystyle \frac{j{\zeta }_0}{2}}{\displaystyle \sum _{n=-\infty }^{\infty }{a}_n{I}_n\exp (jn\phi )}$$

(4)

where Z_f is the internal impedance caused by the loaded ferrite material in low frequency. Inserting (1) into (4) leads to

$$V\delta \left(\phi \right)={\displaystyle \sum _{n=-\infty }^{\infty }\left(\frac{j{\zeta }_0}{2}{a}_n+Z_f\right)I_n\exp (jn\phi )}$$

(5)

Integrate on both sides of equation (5) and reduce it to

$$\begin{array}{l}{\displaystyle \frac{1}{2\pi }}{\displaystyle {\int }_{-\pi }^{\pi }V\delta \left(\phi \right)}\exp (-jn\phi )d\phi \\ ={\displaystyle \frac{1}{2\pi }}{\displaystyle {\int }_{-\pi }^{\pi }{\displaystyle \sum _{m=-\infty }^{\infty }\left(\frac{j{\zeta }_0}{2}{a}_m+Z_f\right)I_m\exp (jm\phi )}}\exp (-jn\phi )d\phi \\ I_n={\displaystyle \frac{V}{2\pi \left(\frac{j{\zeta }_0}{2}{a}_n+Z_f\right)}}\end{array}$$

(6)

Inserting (6) into (1) and reduce it to

$$\begin{array}{l}I\left(\phi \right)={\displaystyle \sum _{n=-\infty }^{\infty }{I}_n\exp (jn\phi )}\\ ={\displaystyle \sum _{n=-\infty }^{\infty }\frac{V}{2\pi \left(\frac{j{\zeta }_0}{2}{a}_n+Z_f\right)}\exp (jn\phi )}\\ =V\left[{\displaystyle \frac{1}{j\pi {\zeta }_0{a}_0+2\pi Z_f}}+{\displaystyle \sum _{n=1}^{\infty }\frac{\cos (jn\phi )}{\frac{j\pi {\zeta }_0}{2}{a}_n+\pi Z_f}}\right]\end{array}$$

(7)

The impedance at the gap then becomes

$$\begin{array}{l}Z={\displaystyle \frac{V}{I\left(\phi =0\right)}}=1/\left[{\displaystyle \frac{1}{j\pi {\zeta }_0{a}_0+2\pi Z_f}}+{\displaystyle \sum _{n=1}^{\infty }\frac{1}{\frac{j\pi {\zeta }_0}{2}{a}_n+\pi Z_f}}\right]\\ =1/\left[{\displaystyle \frac{1}{Z_0^{\text{'}}}}+{\displaystyle \sum _{n=1}^{\infty }\frac{1}{Z_n^{\text{'}}}}\right]\end{array}$$

(8)

Where

$$Z_0^{\text{'}}=j\pi {\zeta }_0{a}_0+2\pi Z_f$$

(9)

$$Z_n^{\text{'}}=j\pi {\zeta }_0\left(a_n/2\right)+\pi Z_f$$

(10)

3. Analysis of the Internal Impedance

3.1. The Dispersion Characteristic of Ferrites

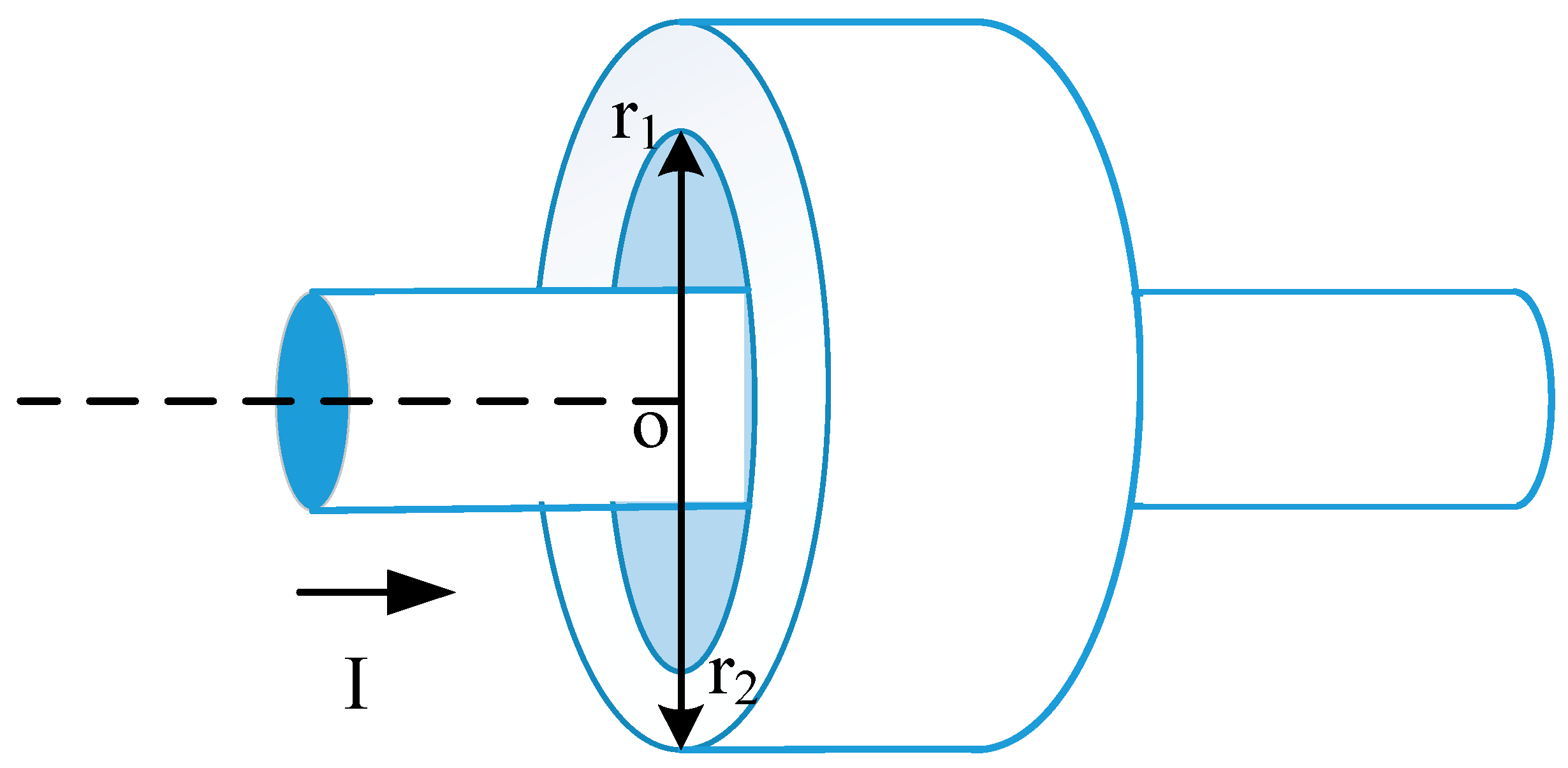
The impedance of the ferrite-loaded loop is expressed in (8), where the internal impedance term Z_f requires further derivation. At low frequencies—where ferrite materials exhibit significant magnetic activity—the interaction between ferrite and the loop wire is illustrated in Figure 2. In this frequency range, the current flowing through the loop is reduced due to two primary mechanisms: energy is consumed in establishing the magnetic flux within the ferrite material, and additional energy is dissipated as losses within the ferrite itself.

The impedance of ferrite beads presented to a loop is expressed as [25]

$$Z_f=j\omega \left[{\displaystyle \frac{{\mu }_0}{2\pi }}\ln \left({\displaystyle \frac{r_2}{r_1}}\right)\right]{\mu }_r·2\pi b$$

(11)

where r₁,r₂ are the inner radius and outer radius of a ferrite bead loading on a loop respectively,μ_r is the relative permeability.

Since the impedance of a ferrite bead is directly influenced by its magnetic permeability characteristics, it is essential to investigate the underlying magnetization mechanisms and the frequency-dependent dispersion behavior of permeability. Extensive research has been conducted on magnetic materials, particularly Ni-Zn and Mn-Zn ferrites [26,27].

As reported by Takanori in [26], two distinct types of magnetic resonance appear in the permeability spectra of Ni-Zn and Mn-Zn ferrites. These resonances are attributed to domain wall motion and spin rotation, respectively. By superimposing the contributions from both mechanisms, the complex relative permeability of these ferrites can be modeled as:

$${\mu }_r=1+{\chi }_d+{\chi }_s=1+{\displaystyle \frac{{\omega }_d^2{\chi }_{d0}}{{\omega }_d^2+\omega +i\omega \beta }}+{\displaystyle \frac{\left({\omega }_s+i\omega \alpha \right){\omega }_s{\chi }_{s0}}{{\left({\omega }_s+i\omega \alpha \right)}^2-{\omega }^2}}$$

(12)

The parameters are listed as follows

• ${\chi }_d$domain-wall motion magnetic susceptibility
• ${\chi }_s$ spin motion magnetic susceptibility
• ${\chi }_{d0}$ static magnetic susceptibility for domain-wall component
• ${\chi }_{s0}$ static magnetic susceptibility for spin component
• ${\omega }_d$ resonance frequency of domain-wall component
• ${\omega }_s$ resonance frequency of spin component;

Inserting equation (12) into (11) leads to

$$Z_f=j\omega \left[{\displaystyle \frac{{\mu }_0}{2\pi }}\ln \left({\displaystyle \frac{r_2}{r_1}}\right)\right]\left(1+{\displaystyle \frac{{\omega }_d^2{\chi }_{d0}}{{\omega }_d^2+\omega +i\omega \beta }}+{\displaystyle \frac{\left({\omega }_s+i\omega \alpha \right){\omega }_s{\chi }_{s0}}{{\left({\omega }_s+i\omega \alpha \right)}^2-{\omega }^2}}\right)·2\pi b$$

(13)

The ferrite model parameters in [25] is illustrated in Table 1 and the Mn-Zn parameters are adopted for theory analysis.

3.2. Comparison of the Surface and Ferrite Impedance

The surface impedance of a cylindrical conductor becomes negligible at low frequencies but becomes significant in the optical frequency range. In contrast, the impedance contribution from ferrite materials is dominant at low frequencies and diminishes as the frequency increases. These distinct impedance behaviors are primarily governed by the permittivity of the conductor [18] and the permeability of the ferrite, respectively.

According to the literature [27,28], both elastic oscillations and interband transitions of the electron gas in metals contribute to the frequency-dependent permittivity. These mechanisms are effectively captured by analytical models. Similarly, in ferrite materials, the motion of magnetic domains exhibits behavior analogous to the electron gas in metals. Domain wall motion corresponds to elastic oscillation, while spin dynamics and resonance bandwidth transitions share a similar mathematical representation [26].

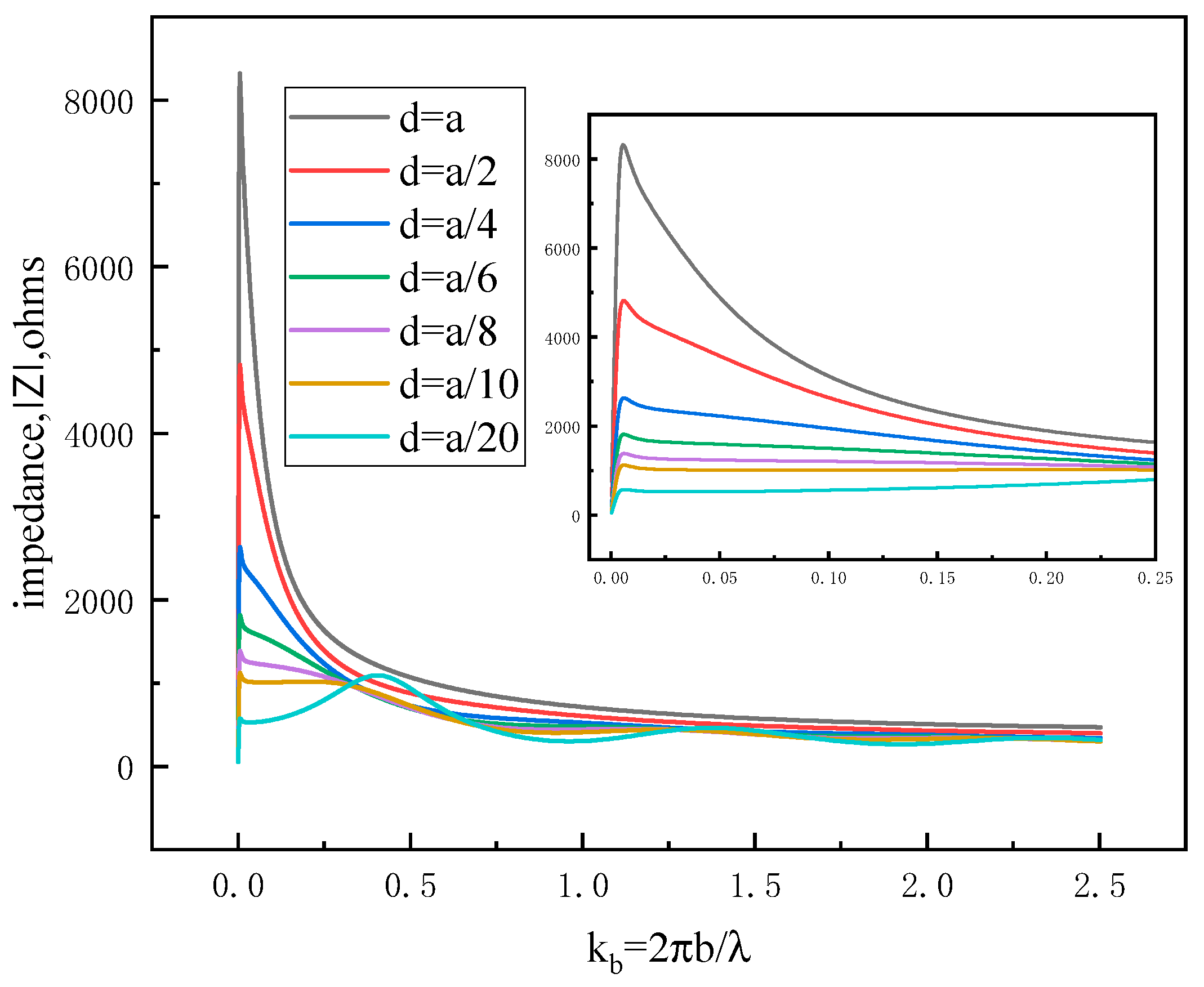
As a result, the impedance characteristics of a ferrite-loaded circular loop become particularly prominent at low frequencies. The introduction of ferrite material leads to a smoother overall impedance profile and reduces the input impedance of the antenna, thereby facilitating improved impedance matching. Figure 3 shows the magnitude of ferrite-loaded loop impedance. For a ferrite-loaded loop antenna with a fixed thickness ratio of b/a=64, the magnitude of the input impedance gradually decreases and becomes smoother as the ferrite material thickness d is reduced.

4. Validations of the Proposed Impedance Formulation

4.1. The evaluation of the Loop Impedance with Ferrite Loads

For loops without ferrite loading, the impedance is given by (2). Storer [11] provided an approximate expression for the parameter $a_n$when the mode number n>5, as follows:

$$a_n\approx {\displaystyle \frac{1}{\pi }}\left(k_b-{\displaystyle \frac{n^2}{k_b}}\right)\left(\ln \left({\displaystyle \frac{2b}{a}}{e}^{-0.5772}\right)-\ln \left(n\right)-j\times {\displaystyle \frac{{\left(k_b\right)}^{2n+1}}{\Gamma \left(2n+2\right)}}\right)n>k_b,n\gg 1$$

(14)

He subsequently replaced the summation over terms for n>5 with an integral representation. Following a series of analytical derivations, the integral was evaluated as:

$$\Psi =2{\displaystyle \sum _{n=5}^{\infty }\frac{\cos (n\phi )}{a_n}}={\displaystyle \frac{2\pi }{\ln \left(\frac{n_0}{4.5}\right)}}{\displaystyle \frac{k_b}{4.5}}\left[J+{\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{k_b}{4.5}}\right)}^2\right]$$

(15)

where $J=\left(0.47,0.9,1.25,1.4,1.4\right)$for $\Omega =\left(8,9,10,11,12\right)$, $n_0=2b/a\exp (-0.5772)$.

The impedance expression in (8) is analytically complex and not easily evaluated through closed-form derivation. To approximate the impedance, a numerical computation approach is employed. Given that the current on the loop is continuous and bounded, the resulting series is convergent. Furthermore, as n increases, the summation over terms with n>5 approaches a constant function that depends solely on the product k_b. Accordingly, the impedance can be reformulated as:

$$Z={\displaystyle \frac{V}{I\left(\phi =0\right)}}=1/\left[{\displaystyle \frac{1}{Z_0^{\text{'}}}}+{\displaystyle \sum _{n=1}^4\frac{1}{Z_n^{\text{'}}}}+\psi \left(k_b\right)\right]$$

(16)

Given that the first five terms in (15) are explicitly known, the remaining task is to estimate the residual sum. According to the Euler–Maclaurin formula, the summation can be approximated by an integral, which yields the following expression:

$$\psi \left(k_b\right)={\displaystyle \sum _{n=5}^{N}f\left(n\right)}={\displaystyle \sum _{n=5}^N\frac{1}{Z_n^{\text{'}}}}\approx {\displaystyle \underset{5}{\overset{N}{\int }}f\left(x\right)dx+}{\displaystyle \frac{\left(f\left(5\right)+f\left(N\right)\right)}{2}}，N\to \infty$$

(17)

Substitute (10), (13) into (16) and reduce it

$$\begin{array}{l}\psi \left(k_b\right)\approx {\displaystyle \underset{5}{\overset{N}{\int }}\frac{1}{j\pi {\zeta }_0\left(\frac{1}{\pi }\left(k_b-\frac{n^2}{k_b}\right)\left(\ln \left(\frac{2b}{an}{e}^{-0.5772}\right)-j\times \frac{{\left(k_b\right)}^{2n+1}}{\Gamma \left(2n+2\right)}\right)/2\right)+\pi Z_f}dx}\\ +{\displaystyle \frac{f\left(N\right)+f\left(5\right)}{2}}\\ \approx {\psi }_0+{\displaystyle \frac{f\left(5\right)}{2}}\end{array}$$

(18)

where a, b are the wire radius and loop radius respectively, and $k_b=2\pi b/\lambda$.

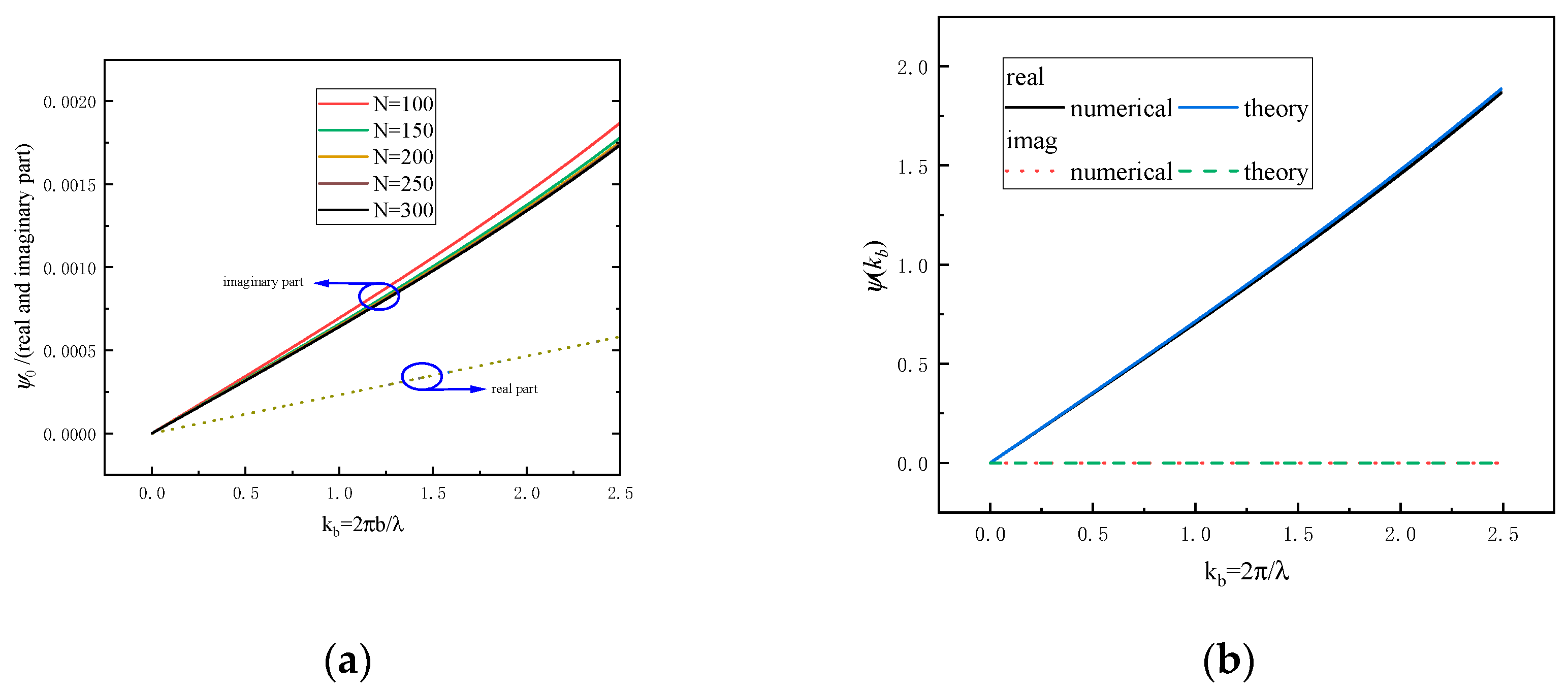
A numerical program was implemented to compute the first term in (17), ${\psi }_0$ ​, for N=100,150,200,250 and 300. Figure 4(a) illustrates the asymptotic behavior of the real and imaginary components of ${\psi }_0$ as N increases. A comparison between the numerical results and the analytical expression given in (14) is presented in Figure 4(b), where the relative error is observed to be less than 0.99%.

As shown in Figure 4(a), both the real and imaginary components of ${\psi }_0$exhibit approximately linear behavior. The imaginary component intersects the points (0, 0) and (2.5, 1.7e-3), while the real component passes through (0, 0) and (2.5, 5.8e-4). Based on these observations, the approximate linear expression for ${\psi }_0$ can be derived as:

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

$$\psi \left(k_b\right)\approx {\displaystyle \frac{\left(0.58+j1.7\right)}{2.5}}\times {10}^{-3}{k}_b+{\displaystyle \frac{\left(f\left(\infty \right)+f\left(5\right)\right)}{2}}$$

(19)

4.2. Comparison Between Theoretical and Simulated Impedance of the Ferrite-Loaded Loop

To validate the closed-form impedance expressions proposed in this study, numerical results are compared with full-wave simulations performed using CST Microwave Studio. The input impedance of the ferrite-loaded loop antenna obtained from the analytical solution is compared with the results from CST simulation in Figure 5, showing excellent agreement between the two. The loop antenna has a radius of 304.8 mm and a wire diameter of 4.8 mm, while the ferrite material features a thickness of 0.625 mm. Due to the limited accuracy of the time-domain solver in CST for low-frequency problems, the frequency-domain solver was employed during the validation process.

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

5. Conclusions

For an unloaded thin loop antenna, its characteristics can be accurately described using classical theory. However, for specific applications, it becomes necessary to load the antenna with ferrite material and derive a theoretical expression for its input impedance. In this work, a new impedance expression is proposed by introducing an additional term to the unloaded case. Comparisons with CST simulation results are conducted to validate the theoretical model. Overall, the proposed expression shows good agreement with simulation in the range 0<kb<2.5. The results presented in this paper can be utilized for the rapid computation of the input impedance of ferrite-loaded loop antennas and for the design of impedance matching networks.

The ferrite loading influences the antenna impedance by affecting the current distribution. The underlying physical mechanisms include spin rotation and magnetic domain wall motion, which contribute to the dispersive behavior of the ferrite material. The permeability data used in the CST simulations is based on a model proposed in [25].