A Local Thresholding Algorithm for Image Segmentation by Using Gradient Aided Histogram

1. Introduction

With the popularization of imaging devices, the demand for image data analyses has significantly increased. As a result, image processing has become an essential component in various applications, with image segmentation serving as a fundamental and crucial step. This step divides an image into multiple regions based on its characteristics such as color, brightness, contour, and semantics. The technique has been extensively applied in numerous fields [1,2,3,4,5] and continues to evolve. Technically, the threshold-based image segmentation has become the most frequently used method due to its simplicity, efficiency, and stability [6].

Threshold-based segmentation can generally be categorized into global and local thresholding methods. The global methods apply a single or multiple thresholds to segment the entire image, offering computational efficiency and algorithmic simplicity. In 1985, Kapur [7] proposed the maximum Shannon entropy threshold method. This method selects an optimal threshold based on the image’s one-dimensional (1-D) gray-level histogram, and then segment it into foreground and background regions. Another typical global thresholding is Otsu’s method [8], which determines the optimal threshold by maximizing the between-class variance of the foreground and background. Both approaches are automatic thresholding algorithms that based on the 1-D gray-level histogram of an image. However, the 1-D histogram only counts the number of pixels that have the same gray-level values without considering the association information between different pixels, such as the spatial distribution information of pixels in the image. If the spatial correlation information between different pixels is nontrivial, the above mentioned global algorithms may not perform optimally [7]. To address the limitations of 1-D histogram, Abutaleb [9] proposed a two-dimensional (2-D) histogram in 1989, which incorporates both the gray values of pixels and their local average gray values. This approach extended Kapur’s method to 2-D histogram, determining the optimal threshold vector by maximizing the sum of the 2-D Shannon entropy of the foreground and background regions, particularly performs well in images with low signal-to-noise ratios (SNR). Since then, many other 2-D histogram-based thresholding methods have been proposed by utilizing different objective function [10,11,12,13,14]. However, the enhanced accuracy comes at the cost of increased computational complexity. The computation time grows exponentially as the number of thresholds increases. Furthermore, traditional 2-D entropy methods tend to recognize the pixels located on the main diagonal of the 2-D histogram, which may result in the loss of edge information [15].

While global thresholding techniques are efficient and straightforward, local techniques offer higher segmentation accuracy [16,17]. The local thresholding methods first divide the image into several independent regions that satisfy a given homogeneity criterion [18,19], and these regions are segmented by using region-specific thresholds subsequently. These methods incorporate pixel-wise correlation information [20,21,22], including backscatters and texture measures [23], statistical measures like mean intensity and standard deviation [24], as well as color and distance [25]. The local thresholding methods employ feature-based preprocessing prior to segmentation, and this hierarchical approach effectively reduces the segmentation error, enhances noise resistance, and achieves superior image quality.

Therefore, incorporating additional image feature information can significantly enhance segmentation accuracy. Among these features, texture information [26], which partially reflects edge characteristics and can be quantified through gradient-based measurements, is widely utilized in image processing applications [27,28,29,30,31,32,33,34,35,36,37,38,39]. Crucially, such edge information of an image captures the outlines, structures, and transitions of objects in the image. It typically corresponds to regions where the gray values changes dramatically in the image, and plays an important role in separating different areas or objects. The extraction of texture information would be helpful to keep the predominant patterns of an image. Specifically, for texture-rich images, proper utilization of such information may play a crucial role in segmentation tasks. Therefore, a unified approach that can effectively act on different texture-rich image categories is important to reveal the relationships between texture patterns and pixel gradient clustering.

In this paper, we propose a local thresholding method that utilizes a gradient orientation histogram to extract local texture features from images. This method clusters pixels with similar gradient directions into distinct subsets using a 2-D gradient orientation histogram, which incorporates both the gray values of pixels and their gradient orientations. Local thresholding is then applied to each subset. The remainder to this paper is organized as follows. Section 2 briefly introduces the pixel-wise gradient orientation and reviews both the 1-D Otsu method and 2-D Otsu method. Section 3 presents the construction of the 2-D gradient orientation histogram and the process of the local threshoding method. Section 4 reports on the experimental results from two datasets and discussions. In Section 5, the conclusions are presented.

2. Related Works

2.1. Pixel-Wise Gradient Orientation

The pixel-wise gradient orientation [40,41,42,43] serves as an effective descriptor for local structural features, particularly in texture characterization. One of the ways to generate it is as follows, for a pixel located at position $(x,y)$, its gradient along the vertical and horizontal axes can be respectively defined as:

$${\displaystyle \frac{\partial f(x,y)}{\partial x}}=f(x+1,y)-f(x-1,y),$$

(1)

$${\displaystyle \frac{\partial f(x,y)}{\partial y}}=f(x,y+1)-f(x,y-1),$$

(2)

where $f(x,y)$ represents the gray-level value of pixel at $(x,y)$,

Then the orientation of this pixel can be calculated by:

$$\theta (x,y)=arctan\left({\displaystyle \frac{\partial f/\partial x}{\partial f/\partial y}}\right),$$

(3)

where the domain of $\theta (x,y)$ is $[-\pi /2,\pi /2]$.

2.2. 1-D Otsu’s Method

Define the range of gray levels in a given image of size $M\times N$ as $i=0,1,2,\dots ,L-1$, where L represents the maximum gray-level of the image, such as 256. Then the gray-level histogram of the image can be computed by the probability distribution:

$$p_i={\displaystyle \frac{n_i}{M\times \mathrm{N}}},p_i\ge 0,\sum _{i=0}^{L-1}{p}_i=1,$$

(4)

where $n_i$ is the number of pixels that gray-level values equal to i.

Assuming that the gray-level histogram of the image is divided into two classes $C_0$ and $C_1$ by a threshold at level t, then the probabilities of class occurrences and the class mean gray-level values are given by:

$$w_0=\sum _{i=0}^t{p}_i,w_1=\sum _{i=t+1}^{L-1}{p}_i,$$

(5)

and

$${\mu }_0=\sum _{i=0}^t{\displaystyle \frac{i{p}_i}{w_0}},{\mu }_1=\sum _{i=t+1}^{L-1}{\displaystyle \frac{i{p}_i}{w_1}}.$$

(6)

Thus, the entire image’s mean gray-level value can be obtained as follows:

$${\mu }_T=\sum _{i=0}^{L-1}i{p}_i.$$

(7)

The between-class variance can be represented by:

$$\begin{array}{cc}\hfill {\sigma }_B^2& =w_0{({\mu }_0-{\mu }_T)}^2+w_1{({\mu }_1-{\mu }_T)}^2\hfill \\ \hfill & =w_0{w}_1{({\mu }_0-{\mu }_1)}^2\hfill \end{array}.$$

(8)

The optimal threshold can be obtained by maximizing Equation (8), i.e.,

$$t^{*}=\underset{0\le t\le L-1}{argmax}\left({\sigma }_B^2\left(t\right)\right).$$

(9)

Based on a set of thresholds $\overrightarrow{t}=(t_1,t_2,\dots ,t_m)$, the image can be divided into $m+1$ classes, denoted as $\overrightarrow{C}=(C_1,C_2,\dots ,C_{m+1})$, and the mean gray-level values are defined as:

$${\mu }_1=\sum _{i=0}^{t_1}{\displaystyle \frac{i{p}_i}{w_1}},{\mu }_2=\sum _{i=t_1+1}^{t_2}{\displaystyle \frac{i{p}_i}{w_2}},...,{\mu }_{m+1}=\sum _{i=t_m+1}^{L-1}{\displaystyle \frac{i{p}_i}{w_{m+1}}},$$

(10)

where

$$w_1=\sum _{i=0}^{t_1}{p}_i,w_2=\sum _{i=t_1+1}^{t_2}{p}_i,...,w_{m+1}=\sum _{i=t_m+1}^{L-1}{p}_i.$$

(11)

Then the between-class variance can be calculated by:

$${\sigma }_B^2=\sum _{j=1}^{m+1}{w}_j{({\mu }_j-{\mu }_T)}^2.$$

(12)

The optimal threshold vector can be obtained by maximizing the multi between-class variance,

$${\left(\overrightarrow{t}\right)}^{*}=\underset{0\le t_1,t_2,\dots ,t_m\le L-1}{argmax}\left({\sigma }_B^2\left(\overrightarrow{t}\right)\right).$$

(13)

2.3. 2-D Otsu’s Method

For 2-D Otsu method [44], for a given image of size $M\times N$, the value of $f(x,y)$ is ranging from 0 to $L-1$. At position $(x,y)$, the average gray value of its local neighborhood can be obtained via:

$$g(x,y)=Round\left[{\displaystyle \frac{1}{n^2}\sum _{i=-\frac{n}{2}}^{\frac{n}{2}}\sum _{j=-\frac{n}{2}}^{\frac{n}{2}}f(x+i,y+j)}\right],$$

(14)

where $Round\left(\mu \right)$ denotes the integer part of $\mu$, n is the size of the local square centered at $(x,y)$. Then the 2-D gray-level histogram of the image is given by:

$$p(i,j)={\displaystyle \frac{1}{M\times N}}\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}{\delta }_{ij},$$

(15)

where ${\delta }_{ij}$ returns 1 when $f(x,y)=i$ and $g(x,y)=j$, else returns 0. Using a threshold vector $(s,t)$ to partition the histogram $p(i,j)$ into two classes $C_0$ and $C_1$ (background and objects), then the probabilities of class occurrence are given by:

$$\begin{array}{c}\hfill \begin{array}{c}{P}_0(s,t)={\displaystyle \sum _{i=0}^s}{\displaystyle \sum _{j=0}^t}p(i,j),\hfill \\ P_1(s,t)={\displaystyle \sum _{i=s+1}^{L-1}}{\displaystyle \sum _{j=t+1}^{L-1}}p(i,j).\hfill \end{array}\end{array}$$

(16)

The corresponding class mean levels are:

$$\begin{array}{c}\hfill \begin{array}{c}{\mu }_0={({\mu }_{00},{\mu }_{01})}^T={({\displaystyle \frac{{\displaystyle \sum _{i=0}^s}{\displaystyle \sum _{j=0}^t}ip(i,j)}{P_0}},{\displaystyle \frac{{\displaystyle \sum _{i=0}^s}{\displaystyle \sum _{j=0}^t}jp(i,j)}{P_0}})}^T,\hfill \\ {\mu }_1={({\mu }_{10},{\mu }_{11})}^T={({\displaystyle \frac{{\displaystyle \sum _{i=s+1}^{L-1}}{\displaystyle \sum _{j=t+1}^{L-1}}ip(i,j)}{P_1}},{\displaystyle \frac{{\displaystyle \sum _{i=s+1}^{L-1}}{\displaystyle \sum _{j=t+1}^{L-1}}jp(i,j)}{P_1}})}^T.\hfill \end{array}\end{array}$$

(17)

The total mean level vector of the 2-D histogram is:

$${\mu }_T={({\mu }_{T0},{\mu }_{T1})}^T={(\sum _{i=0}^{L-1}\sum _{j=0}^{L-1}ip(i,j),\sum _{i=0}^{L-1}\sum _{j=0}^{L-1}jp(i,j))}^T.$$

(18)

The between-class variance matrix is defined as:

$$S_B=\sum _{k=0}^1{P}_k\left[({\mu }_k-{\mu }_T){({\mu }_k-{\mu }_T)}^T\right].$$

(19)

The trace of $S_B$ can be used to measure the between-class variance, it is computed by:

$$\begin{array}{cc}\hfill Trace\left[{\mathcal{S}}_B(s,t)\right]& =P_0\left[{({\mu }_{00}-{\mu }_{T0})}^2+{({\mu }_{01}-{\mu }_{T1})}^2\right]+P_1\left[{({\mu }_{10}-{\mu }_{T0})}^2+{({\mu }_{11}-{\mu }_{T1})}^2\right]\hfill \\ \hfill & ={\displaystyle \frac{{({\mu }_i(s,t)-P_0{\mu }_{T0})}^2+{({\mu }_j(s,t)-P_0{\mu }_{T1})}^2}{P_0(1-P_0)}},\hfill \end{array}$$

(20)

where

$$\begin{array}{c}\hfill \begin{array}{c}\begin{array}{c}{\mu }_i(s,t)={\displaystyle \sum _{i=0}^s}{\displaystyle \sum _{j=0}^t}ip(i,j),\hfill \\ {\mu }_j(s,t)={\displaystyle \sum _{i=0}^s}{\displaystyle \sum _{j=0}^t}jp(i,j).\hfill \end{array}\hfill \end{array}\end{array}$$

(21)

Then the optimal threshold vector ${(S,T)}^{*}$ is determined by:

$${(S,T)}^{*}=\underset{0<s,t<L-1}{argmax}\left\{Trace\left[S_B(s,t)\right]\right\}.$$

(22)

3. Proposed Method

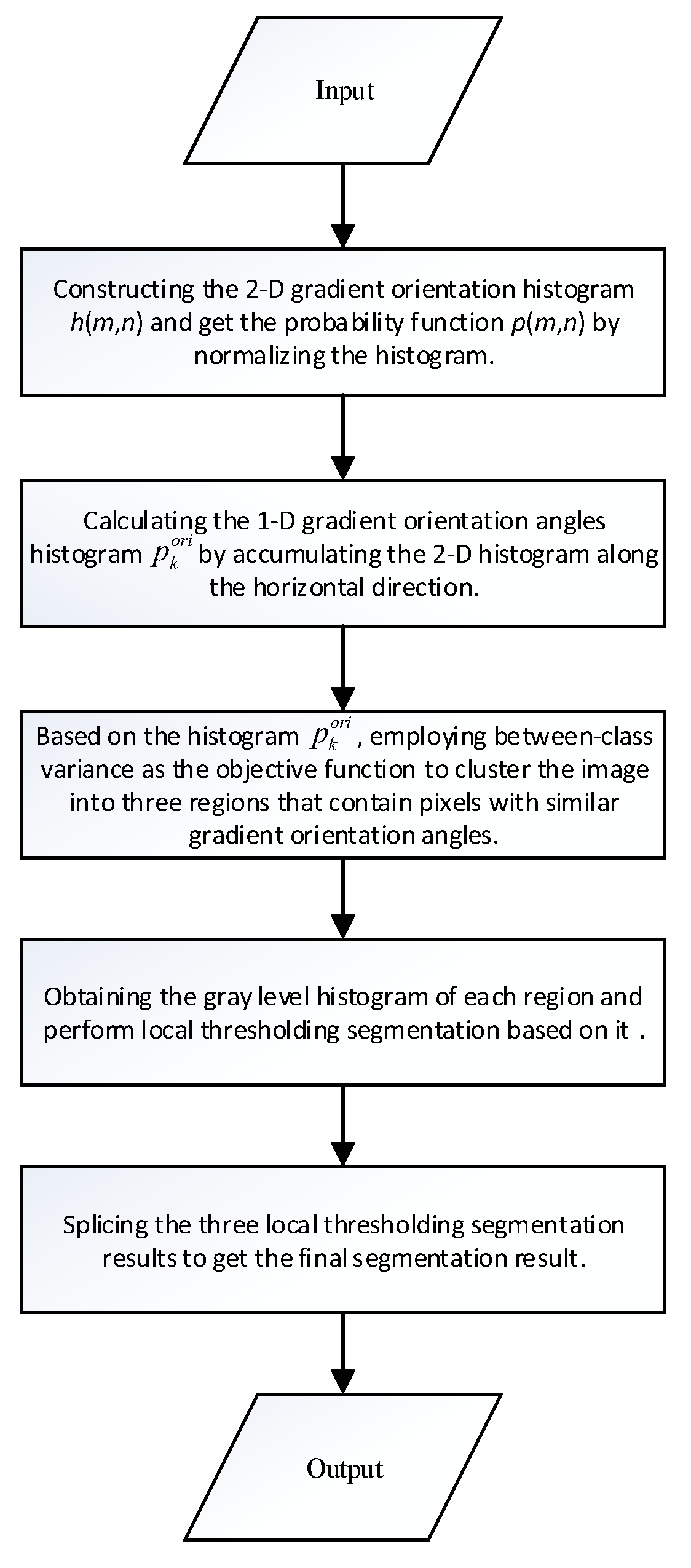
Traditional 2-D entropy threshold methods may cause the loss of a considerable number of pixels, leading to the loss of nontrivial edge information. Consequently, a novel algorithm is proposed to avoid such cases so that the segmentation accuracy can be improved. For a texture-rich image, the edge pattern is deeply related with the gradient of pixels’ gray-level. Therefore, a 2-D gradient orientation histogram is adopted to cluster the image pixels into distinct regions. And the local thresholding to each region demonstrates the advantages.

3.1. Construction of 2-D Gradient Orientation Histogram

For a pixel located at position $(x,y)$ in a given image of size $M\times N$, its gray-level gradient orientation with respect to the horizontal axis is:

$$\theta (x,y)=Round\left[DEG\left(arctan\left({\displaystyle \frac{\frac{\partial f}{\partial y}}{\frac{\partial f}{\partial x}}}\right)\right)\right],$$

(23)

where $DEG\left(\mu \right)$ denotes the transform of the radian angle $\mu$ to degree. ${\displaystyle \frac{\partial f}{\partial x}}$ and ${\displaystyle \frac{\partial f}{\partial y}}$ can be calculated by Equation (1) and Equation (2), and the domain of $\theta (x,y)$ is $[-{90}^{\circ },{90}^{\circ }]$. The pixel’s gray-level value, $f(x,y)$, and the gradient orientation $\theta (x,y)$ can be adopted to construct the 2-D gradient orientation histogram $h(m,n)$ by

$$h(m,n)=C\mathrm{ount}\left(f\right(x,y)=m\&\theta (x,y)=n).$$

(24)

The 2-D probability distribution is determined by normalization of Equation (24),

$$p(m,n)=\widehat{h}(m,n)={\displaystyle \frac{h(m,n)}{M\times N}}.$$

(25)

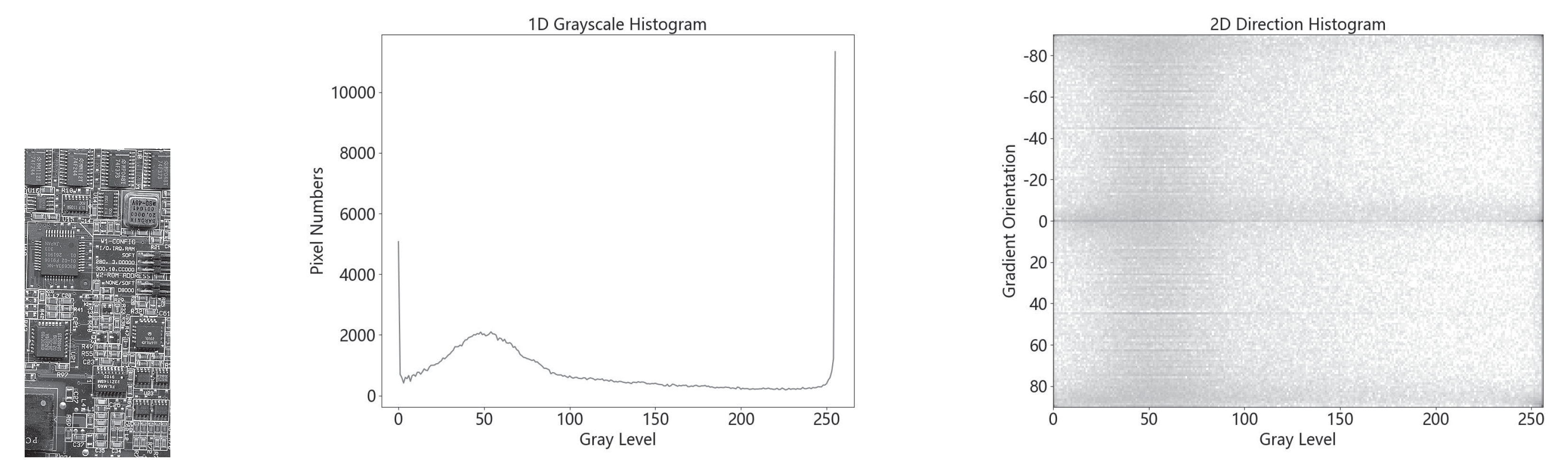
Equation (25) represents the frequency of occurrences at gray level m and gradient orientation n, where $m=\{0,1,2,\dots ,L-1\}$ and $n=\{-{90}^{\circ },-{89}^{\circ },\dots ,{89}^{\circ },{90}^{\circ }\}$. Figure 1 shows the gradient orientation information for the image ‘board’.

3.2. Main Step of Segmentation

For a digital image of size $M\times N$, the normalized 2-D gradient orientation histogram $p(m,n)$ can be obtained via Equation (25). Different from Equation (15), the distribution of $p(m,n)$ is not concentrated at the main diagonal of the 2-D histogram, as it is shown in Figure 1. The probability distribution of each gradient orientation angle in the image can be obtained by:

$$p_k^{ori}=\sum _{i=0}^{L-1}p(i,k),$$

(26)

where k ranging from $[-90,90]$. Using Otsu’s method with a set of thresholds $\overrightarrow{t}=(t_1,t_2)$, the distribution of Equation (26) can be segmented into three distinct parts, denoted as $\overrightarrow{C}=(C_1,C_2,C_3)$, with each part comprising pixels that have similar gradient orientation angles. After normalization, the gray-level probability distribution of three classes are respectively defined as:

$$\begin{array}{cc}\hfill C_1& :{\displaystyle \frac{p_{-90}^{\mathrm{ori}}}{P_1^{\mathrm{ori}}}},{\displaystyle \frac{p_{-89}^{\mathrm{ori}}}{P_1^{\mathrm{ori}}}},\dots ,{\displaystyle \frac{p_{t_1}^{\mathrm{ori}}}{P_1^{\mathrm{ori}}}},\hfill \\ \hfill C_2& :{\displaystyle \frac{p_{t_1+1}^{\mathrm{ori}}}{P_2^{\mathrm{ori}}}},{\displaystyle \frac{p_{t_1+2}^{\mathrm{ori}}}{P_2^{\mathrm{ori}}}},\dots ,{\displaystyle \frac{p_{t_2}^{\mathrm{ori}}}{P_2^{\mathrm{ori}}}},\hfill \\ \hfill C_3& :{\displaystyle \frac{p_{t_2+1}^{\mathrm{ori}}}{P_3^{\mathrm{ori}}}},{\displaystyle \frac{p_{t_2+2}^{\mathrm{ori}}}{P_3^{\mathrm{ori}}}},\dots ,{\displaystyle \frac{p_{90}^{\mathrm{ori}}}{P_3^{\mathrm{ori}}}},\hfill \end{array}$$

(27)

where the cumulative probabilities of three classes are defined as:

$$\begin{array}{cc}\hfill P_1^{\mathrm{ori}}& =\sum _{k=-90}^{t_1}{p}_k^{\mathrm{ori}},\hfill \\ \hfill P_2^{\mathrm{ori}}& =\sum _{k=t_1+1}^{t_2}{p}_k^{\mathrm{ori}},\hfill \\ \hfill P_3^{\mathrm{ori}}& =\sum _{k=t_2+1}^{90}{p}_k^{\mathrm{ori}}.\hfill \end{array}$$

(28)

The mean gradient orientation angles of three classes are as follows:

$$\begin{array}{cc}\hfill {\mu }_1^{\mathrm{ori}}& =\sum _{k=-90}^{t_1}{\displaystyle \frac{k{p}_k^{\mathrm{ori}}}{P_1^{\mathrm{ori}}}},\hfill \\ \hfill {\mu }_2^{\mathrm{ori}}& =\sum _{k=t_1+1}^{t_2}{\displaystyle \frac{k{p}_k^{\mathrm{ori}}}{P_2^{\mathrm{ori}}}},\hfill \\ \hfill {\mu }_3^{\mathrm{ori}}& =\sum _{k=t_2+1}^{90}{\displaystyle \frac{k{p}_k^{\mathrm{ori}}}{P_3^{\mathrm{ori}}}}.\hfill \end{array}$$

(29)

The entire image’s mean gradient orientation angle can be obtained by:

$${\mu }_T^{ori}=\sum _{k=-90}^{90}k{p}_k^{ori}.$$

(30)

The between-class variance of orientation can be represented by:

$$\widehat{{\sigma }_B^2}(t_1,t_2)=P_1^{ori}{({\mu }_1^{ori}-{\mu }_T^{ori})}^2+P_2^{ori}{({\mu }_2^{ori}-{\mu }_T^{ori})}^2+P_3^{ori}{({\mu }_3^{ori}-{\mu }_T^{ori})}^2.$$

(31)

Maximizing the objective function $\widehat{{\sigma }_B^2}(t_1,t_2)$ yields the optimal set of thresholds as follows:

$${\left(\overrightarrow{t}\right)}^{*}=\underset{-90\le t_1,t_2\le 90}{argmax}\left\{\widehat{{\sigma }_B^2}(t_1,t_2)\right\}.$$

(32)

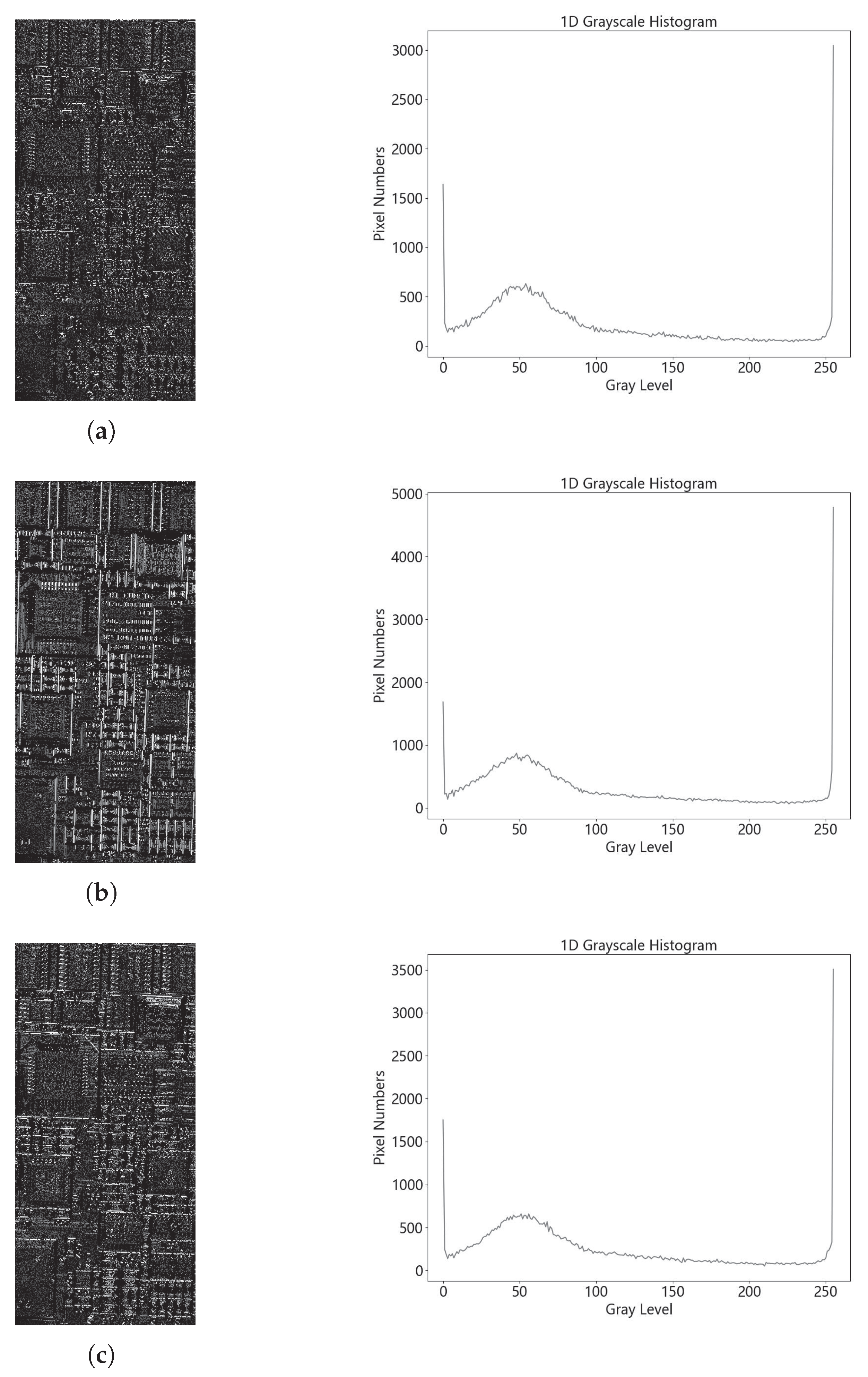
Using the optimal threshold ${\left(\overrightarrow{t}\right)}^{*}$, the 2-D gradient orientation histogram $p(m,n)$ is clustered into three parts with the largest between-class variance. Each part contains pixels with similar gradient orientation information. Figure 2 shows an example, with the optimal vector ${\left(\overrightarrow{t}\right)}^{*}=[-35,34]$, the pixels of each gradient orientation part can be sorted by gray-level value and yields the corresponding histogram.

After clustering the image, the Otsu’s method mentioned in Section 2.2 is used to perform local thresholding segmentation on the three regions. The three segmentation results are then combined to obtain the final segmentation result. Figure 3 illustrates the overall segmentation process.

3.3. Image Test Sets and Quality Evaluation Parameters

Image texture not only characterizes local structural patterns but also effectively captures inter-object boundary information. Due to its important role in object recognition, texture features have been widely employed in image analysis. To further show the relationship between texture information and image segmentation, images with diverse texture characteristics are adopted in the experiments. Figure 4 displays three images with obvious texture features from the MATLAB image library, with resolutions of (a)$306\times 648$,(b)$189\times 250$ and (c)$232\times 205$.

Beside Figure 4, more real-world images from various scenes are essential to test the proposed algorithm. The Describable Textures Dataset (DTD, R1.0.1) [45] is an image dataset consisting of 47 different categories of real-world texture images, with each category named by an adjective. It is designed as a public benchmark and can be used to study the problem of extracting semantic properties of textures and patterns. In this paper, the segmentation experiment employs 81 ’woven’, 119 ’lacelike’, 107 ’pitted’, and 119 ’blotchy’ images. Here are a few examples from this dataset (Figure 5).

To evaluate the effectiveness of the local thresholding method proposed above, we adopt PSNR (Peak Signal-to-Noise Ratio) and FSIM (Feature Similarity Index) as quality indices. PSNR [46] represents the ratio of the peak signal to the noise. As it can precisely measure the difference between the input image and the output image, it is currently the most frequently used objective metric for evaluating image quality. A higher PSNR value indicates less distortion in the output image and better segmentation quality. It is defined as:

$$PSNR=10{log}_{10}\left[{\displaystyle \frac{{(L-1)}^2}{MSE}}\right]$$

(33)

where the $MSE$ is the mean squared error between the input image and the output image, and L is the maximum gray-level value in the image, usually 255. $MSE$ can be written as:

$$MSE={\displaystyle \frac{1}{M\times N}}\sum _{i=1}^M\sum _{j=1}^N{\left[f\right(i,j)-g(i,j\left)\right]}^2$$

(34)

where $M\times N$ is the size of the image, $f(i,j)$ and $g(i,j)$ represent the input image and the output image, respectively.

FSIM [47] is proposed based on the principle that human visual system understands an image mainly according to its low-level features. It is utilized to measure the similarity between two images based on phase congruence (PC) and image gradient magnitude (GM). Here, PC serves as a dimensionless indicator of the importance of local structures and is used as the primary feature in the FSIM. GM acts as the secondary feature in FSIM. Both features playing complementary roles in characterizing the local quality of an image. FSIM is defined as:

$$FSIM={\displaystyle \frac{{\sum }_{x\in \Omega }{S}_L\left(x\right)·P{C}_m\left(x\right)}{{\sum }_{x\in \Omega }P{C}_m\left(x\right)}}$$

(35)

where $\Omega$ means the whole image spatial domain, $S_L\left(x\right)$ is the local similarity at pixel x, ${PC}_m\left(x\right)$ is the maximum PC value at pixel x. Please refer to [47] for more details about $S_L\left(x\right)$ and ${PC}_m\left(x\right)$.

4. Experimental Results and Discussions

To demonstrate the performance of the proposed method, we tested images from MATLAB image library (Figure 4) and the DTD dataset (Figure 5). The Kapur method [48], 1-D Otsu method [49], 2-D Otsu method, and the proposed method were applied to segment these images, with the number of thresholds set to 2, 3, 4, and 5.

4.1. Algorithm Performance and Computational Cost

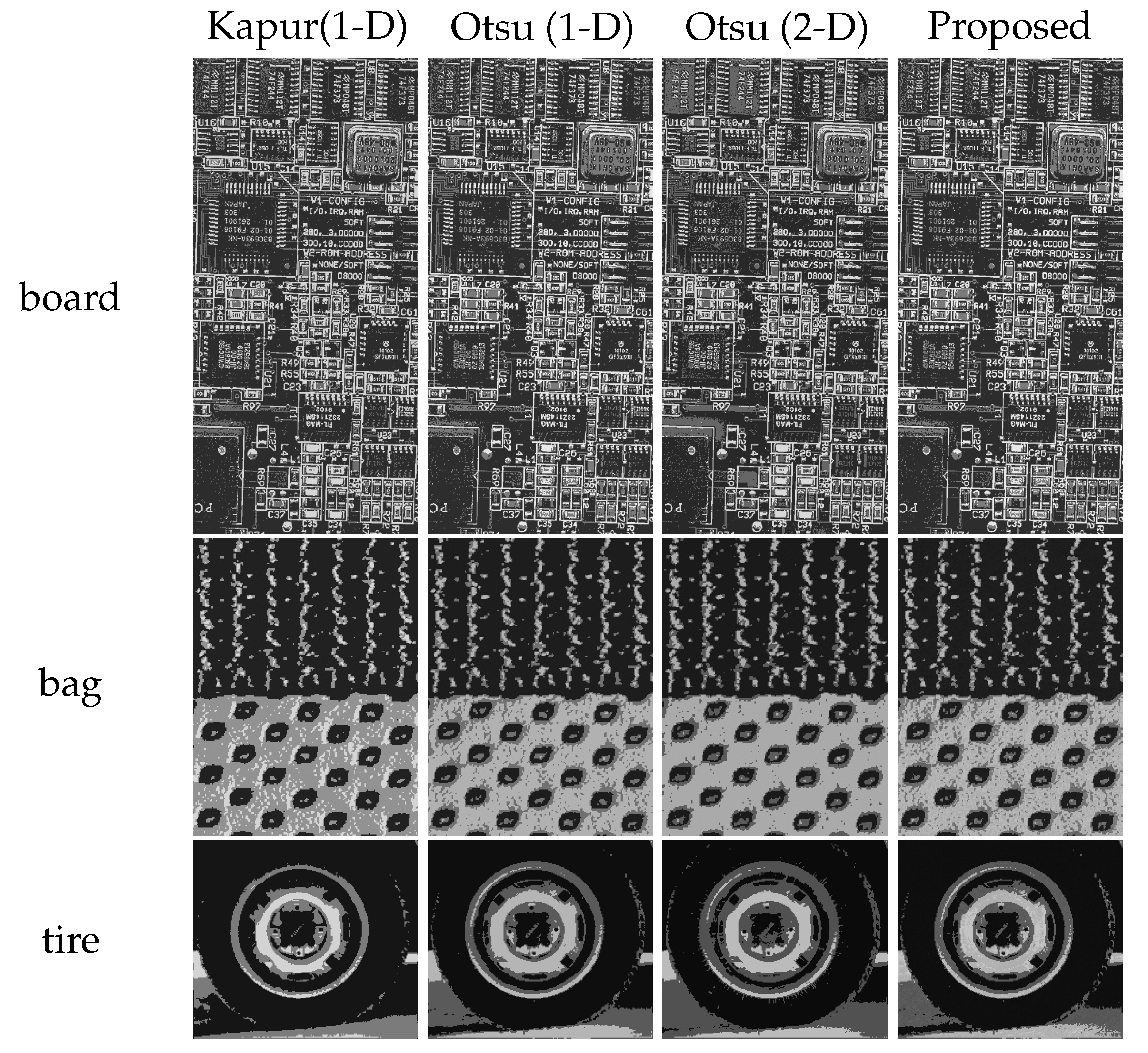
Figure 6 demonstrates the two-level thresholding performances for three images of Figure 4. It is found that the proposed method keeps more details than others, and can avoid lots of mis-segmentations. Notably, this advantage keeps with the increasing number of threshold and can be quantitatively illustrated. Table 1 presents the PSNR and FSIM results at different threshold levels for these three images. In each row, the maximum PSNR and FSIM values (with bold font) indicate that the corresponding method is the most suitable one for the image listed at the beginning of the row. The proposed method achieved the best PSNR and FSIM values for all three texture-rich images across all threshold levels. It performs better than 1-D histogram-based methods because it incorporates more pixel-wise correlation information for segmentation. Meanwhile, traditional 2-D methods neglect off-diagonal pixels’ contributions, leading to image information loss. In contrast, the proposed method utilizes gradient information from all pixels for segmentation, thereby achieving superior performance. This also indicates that, compared to the 2-D average gray values histogram, the gradient aided histogram is more effective in analyzing the texture features of these images.

Table 2 presents the comparative computational time costs across different methods. All algorithms were implemented in Python and executed on a workstation equipped with dual Intel Xeon Gold 6268CL processors (2.80 GHz, 28 cores total) and 256 GB DDR4 RAM (2666 MHz). To ensure fair comparison, all methods were restricted to single-thread execution.

It is shown that, the proposed method obtained more precise segmentation results while requiring less computational time than 2-D Otsu method. It should be noted that the proposed method can adopt multiprocessing computation for segmenting the three clustered regions. So, compared with traditional 1-D methods, it only incurs additional computational cost for constructing 2-D gradient orientation histogram and the corresponding pixels’ clustering. It achieves both stable segmentation accuracy improvement and low computational consumption, showing the potential application in real time scenes.

4.2. Consistency of Algorithm Performance with Increasing Threshold

To further validate the effectiveness of the proposed method, we applied the above four methods to perform 2-level, 3-level, 4-level and 5-level thresholding on images from the DTD dataset mentioned in Section 3.3.

Figure 7 shows parts of the two-level thresholding results of some images. It is evident that for these four images, both 1-D Kapur and 2-D Otsu method yielded unsatisfactory segmentation results. Specifically, the 1-D Kapur method failed to capture the texture details, leading to difficulties in segmenting and preserving complex and diverse texture lines in the original images. The traditional 2-D method only considers pixels along the main diagonal of the histogram, which may result in the loss of important texture information. In comparison, the proposed method effectively preserved the texture lines and features from the original images.

In order to show the performances of these four algorithms objectively, different categories of DTD dataset are adopted to yield the comparisons. For example, the category named “woven” contains 81 images with similar texture structures. At given number of thresholds, each image yields 4 PSNR values by above four algorithms, respectively. The maximum PSNR value leads the count of corresponding algorithm increasing 1. It should be mentioned that two algorithms may occasionally reach the same maximum results. Therefore, the total count of 4 algorithms may slightly exceed the total number of images in the category. By the same way, the distributions of FSIM can be obtained. Table 3 presents the distributions of optimal PSNR and FSIM among four algorithms by using different image categories. For each image category, the bolded values represent the highest frequencies of reaching the optimal segmentation quality, which shows the superiority of corresponding algorithm.

For ‘woven’ category, the proposed method achieved optimal PSNR values over all 81 images at threshold levels 2 and 3, and obtained optimal FSIM values in approximately $75\%$ of cases. This demonstrates that the method maintains both high segmentation accuracy and effective preservation of texture details. With the increasing number of thresholds, such as 4 and 5, the optimal rate of PSNR for proposed algorithm is still dominant, and the corresponding optimal rate of FSIM slightly increases. This suggests that the proposed algorithm is stable in both segmentation accuracy and feature preservation for this image category with increasing threshold numbers.

In order to show the effectiveness of proposed algorithm, more image categories can be involved. For ‘lacelike’ category, the optimal PSNR rate of present algorithm is nearly $100\%$ at threshold levels 2 and 3. For ‘blotchy’ and ‘pitted’ categories, these rates are close to $91\%$ and $92\%$, respectively. When the number of thresholds increases to 4 and 5, the optimal PSNR rates yielded by different image categories keep unchanged within a small interval of fluctuation. From Figure 5, we can see that the texture patterns among 4 image categories are quite different from each other. The proposed method reached an average optimal PSNR rate to $96\%$, showing the powerful ability in texture pattern recognition. Regarding the optimal FSIM rate, the proposed method also keeps far larger than those of the other three typical algorithms. This superiority is unchanged in different image categories, with different threshold levels.

Actually, the superiority of proposed algorithm benefits from the pre-segmentation clustering based on local texture features, which depends closely on the pixels’ gradient orientation distribution. Although the four texture categories exhibit distinct visual characteristics, the proposed method consistently obtains satisfactory PSNR values across all categories. This shows that it effectively identifies texture patterns across diverse image categories, demonstrating strong scalability. FSIM evaluation shows that the proposed method demonstrates superior capability in preserving original image features across all categories. This validates that pixel gradient clustering contributes to analyzing complex texture distributions in different images. Furthermore, the method retains relatively stable performance with small fluctuations across different threshold levels, indicating good robustness and stability.

4.3. Comparative Analysis of Method Performance

The 2-D Otsu method yields unsatisfactory performance across all texture categories, with near-zero counts of images achieving maximum PSNR and FSIM values at all threshold levels. This likely stems from its threshold determination mechanism disregarding certain pixels, leading to significant loss of edge and feature information. Interestingly, while the 1-D Kapur method showed similarly poor PSNR results as 2-D Otsu method, it outperformed 2-D Otsu method in FSIM index. This can be attributed to its global thresholds selection based on all image pixels, which prevents lot feature loss and consequently preserves more texture characteristics in some images. The 1-D Otsu method achieved relatively better results for a small subset of images in both PSNR and FSIM. This may reflect better compatibility between the between-class variance maximization criterion and these texture images.

Clearly, traditional 1-D methods show limited performance for these texture-rich images. They fail to account for spatial correlations between pixels and utilize insufficient image information during threshold selection. However, 2-D Otsu method does not appear to perform significantly better, since the 2-D local average gray values histogram ignored pixels with high contrast to their surroundings. It is more suitable for low SNR scenarios. Consequently, its ability to extract texture information is weak, leading to suboptimal segmentation results.

The superior performance of the proposed method demonstrates the importance of texture information in segmentation tasks. It also confirms that gradient aided histogram serves as an effective descriptor for image texture patterns. This strongly validates the necessity of clustering pixels with similar gradient orientations for multi-level image segmentation.

5. Conclusions

In image segmentation, 2-D thresholding methods extract additional pixel-wise features, thereby overcoming the limitations of 1-D approaches in certain scenarios. This demonstrates that proper utilization of additional image features can effectively improve segmentation accuracy. But traditional 2-D entropy thresholding methods may inadvertently discard a significant proportion of pixels, thereby undermining the preservation of nontrivial edge details.

In this paper, we propose a new local thresholding algorithm to further study the importance of texture features in improving multi-level segmentation quality. To evaluate the performances, we compare our method with Kapur (1-D) and Otsu (1-D and 2-D) methods. Segmentation results are assessed by PSNR index. Experimental results demonstrate that our algorithm can accurately identify common patterns in texture-rich images. Specifically, when segmenting four texture categories of images with distinct characteristics from the DTD dataset, our method achieves significantly higher segmentation quality than other algorithms. This advantage stems from clustering pixels with similar gray-level gradient orientation before segmentation, which facilitates the algorithm’s understanding and analysis of feature distribution patterns in images. And the segmentation quality remains stable as the threshold level increases. Our method also shows superior performance in FSIM index, proving that the gradient aided histogram effectively captures texture information across different images. It can identify diverse texture patterns and periodical structures, preserving complex texture features in segmentation results. The performance sustains stability even as threshold levels increase, highlighting strong scalability. Notably, the improved performance comes with neglectable computational cost, demonstrating potential for real time applications.