Zarvan: An Efficient Gated Architecture for Sequence Modeling with Linear Complexity

1. Introduction

Sequence modeling is a cornerstone of modern artificial intelligence, with applications ranging from natural language processing to time-series analysis. The introduction of the Transformer architecture [5] marked a paradigm shift in this field. Its core component, the self-attention mechanism, allowed for unparalleled performance by capturing complex dependencies between tokens regardless of their distance.

However, this power comes at a significant computational cost. The self-attention mechanism requires pairwise comparisons between all tokens in a sequence, leading to a computational and memory complexity of $O\left(S^2\right)$ with respect to the sequence length S. This quadratic bottleneck makes it prohibitively expensive to apply Transformers to high-resolution images, long documents, or extended time-series data.

This limitation has spurred a wave of research into "Efficient Transformers" that aim to approximate the self-attention mechanism or replace it entirely with a more scalable alternative [4]. These approaches often involve methods like sparse attention, low-rank approximations, or integrations with state-space models.

In this paper, we propose a new path forward with Zarvan, an architecture that eschews attention-based mechanisms in its core block and instead introduces a novel, dual-context gating system. The fundamental hypothesis behind Zarvan is that for a given token, its updated representation can be effectively computed by conditioning it on global summaries of the entire sequence, rather than on every other token individually. This approach reduces the complexity to $O\left(S\right)$ while maintaining a high capacity for information integration.

Our initial exploration revealed a critical nuance: a single, monolithic global context vector, while efficient, struggled on tasks requiring precise, long-range information retrieval, such as the Selective Copy task. A model equipped with only one general context vector often failed to converge as it could not disentangle the sequence's general meaning from the specific tokens it needed to recall. This led to the central innovation in Zarvan: a dual-context system that decouples global understanding from focused memory, a concept elaborated in Section 3.

Our contributions are as follows:

• We introduce Zarvan, a novel architecture with linear complexity that uses a hybrid gating mechanism informed by dual context vectors.
• We detail its core components: the Holistic Context Extractor for capturing the sequence's essence and the Associative Context Extractor for focused, long-range memory.
• We provide a comprehensive empirical evaluation across five distinct benchmarks, demonstrating that Zarvan is accurate, fast, and versatile, making it a viable alternative to the Transformer.

2. Related Work

Our work is situated within the extensive body of research on efficient sequence modeling architectures. We position Zarvan in relation to three major lines of work that aim to overcome the limitations of the standard Transformer.

2.1. The Transformer Architecture

The original Transformer [5] relies on multi-head self-attention. For a sequence of input embeddings X, it projects them into Query (Q), Key (K), and Value (V) matrices. The output is computed as a weighted sum of the values, where the weights are derived from the scaled dot-product of queries and keys. The core computation is $Attention\left(Q,K,V\right)=softmax\left(\left(Q{K}^T\right)/\left(sqrt\left(d_k\right)\right)\right)V$. The $Q{K}^T$ matrix multiplication is the source of the $O\left(S^2\right)$ complexity.

2.2. Efficient Transformer Alternatives

Numerous models have been proposed to mitigate the quadratic bottleneck.

• Linear Attention: This family of models argues that the full self-attention matrix is redundant and can be effectively approximated. For instance, Linformer [6] projects the Key ($K$) and Value ($V$) matrices into a smaller, fixed dimension before the matrix multiplication, reducing complexity to $O\left(S\right)$. Other methods use kernel functions to approximate the softmax attention without explicitly forming the $S\times S$ matrix.
  Comparison with Zarvan: While these methods are effective, they are fundamentally approximations of the original attention mechanism. Zarvan takes a conceptually different path. It does not approximate attention; it replaces it entirely. Zarvan operates on the hypothesis that for many tasks, direct, pairwise token interactions are unnecessary. Instead, it posits that explicit, global summary vectors can provide sufficient context for updating token representations, thereby avoiding potential approximation errors inherent in low-rank or kernel-based methods.
• State Space Models (SSMs): A highly successful line of work, including models like S4 [2] and the more recent Mamba [1], models a sequence as a linear time-invariant system. They achieve linear-time complexity for inference and near-linear time for parallelized training by using a selective state compression mechanism. This allows them to maintain a "memory" of the sequence in a compact state that evolves over time.
  Comparison with Zarvan: Zarvan is architecturally distinct from SSMs. It is not based on state-space formalism or recurrence. Instead of compressing history into an evolving hidden state, Zarvan's core block performs a stateless, parallel computation on the full sequence at each layer to derive its global context vectors. This information is then used in a local, token-wise update. While both achieve linear complexity, Zarvan's approach offers a non-recurrent, conceptually simpler framework for global information aggregation.
• Recurrent Architectures with Linear Complexity: Recent models like RWKV [3] have successfully blended the strengths of RNNs and Transformers. They achieve O(S) complexity by formulating the attention mechanism in a recurrent manner, which allows for both parallelizable training (similar to Transformers) and efficient, constant-memory inference (similar to RNNs).
  Comparison with Zarvan: Although Zarvan's gating mechanism is inspired by RNNs, it is fundamentally a non-recurrent architecture during both training and inference. The computation within a Zarvan block does not depend on the output of the previous token in the same layer. The entire sequence is processed in parallel to compute the global contexts, making its operational paradigm fully parallel, much like the original Transformer.

In summary, Zarvan differentiates itself by proposing a unique architectural choice: instead of approximating attention, modeling state, or re-introducing recurrence, it decouples information aggregation into the explicit computation of specialized global contexts and uses them to parameterize a powerful local gating function. This design provides a novel and effective mechanism for achieving linear scalability in sequence modeling.

3. The Zarvan Architecture

The core of our model is the Zarvan Block, a self-contained unit that can be stacked to create deep networks. This block is designed to efficiently capture both global and sparse information from a sequence and use it to intelligently update each token's representation. This section details its internal mechanisms.

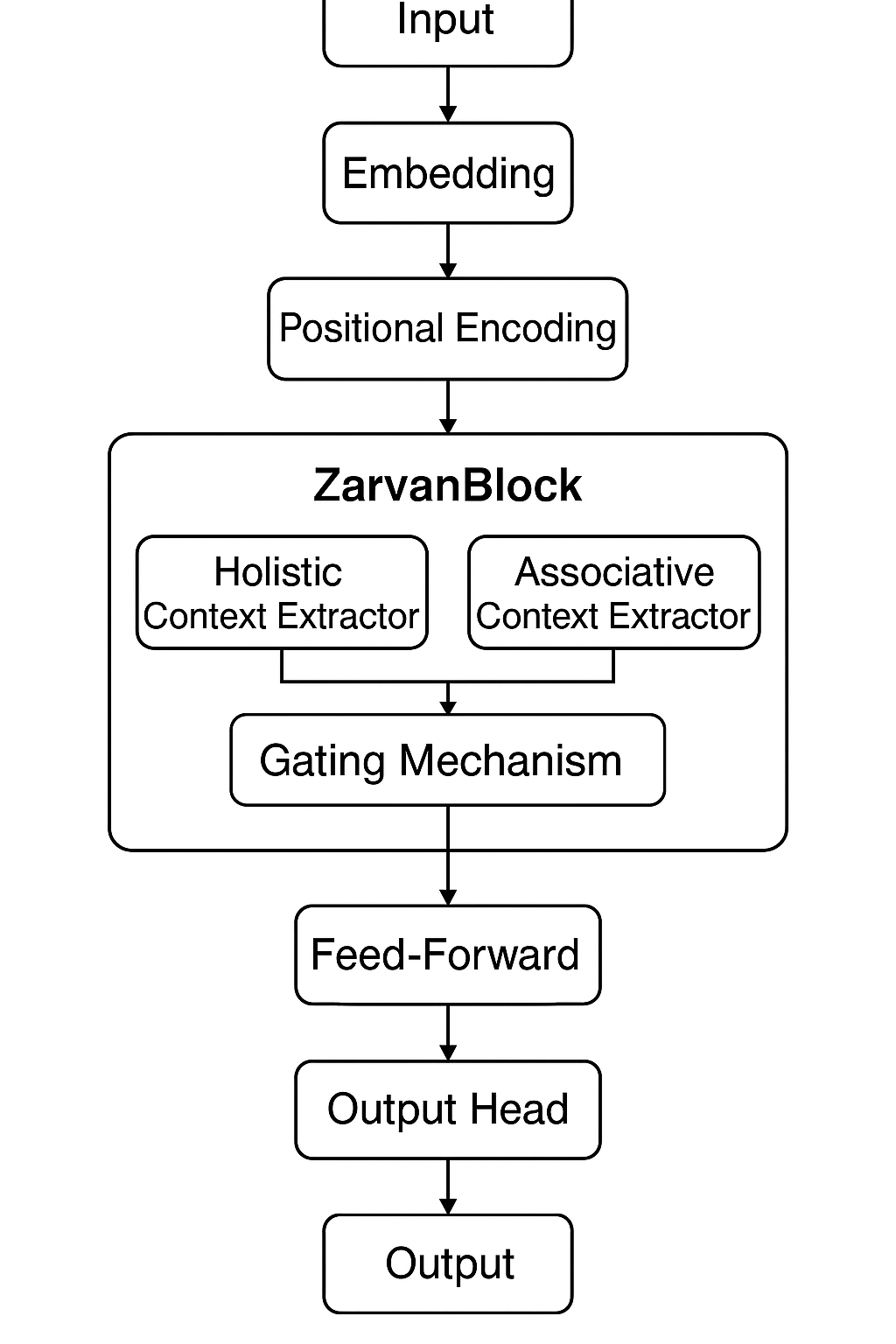
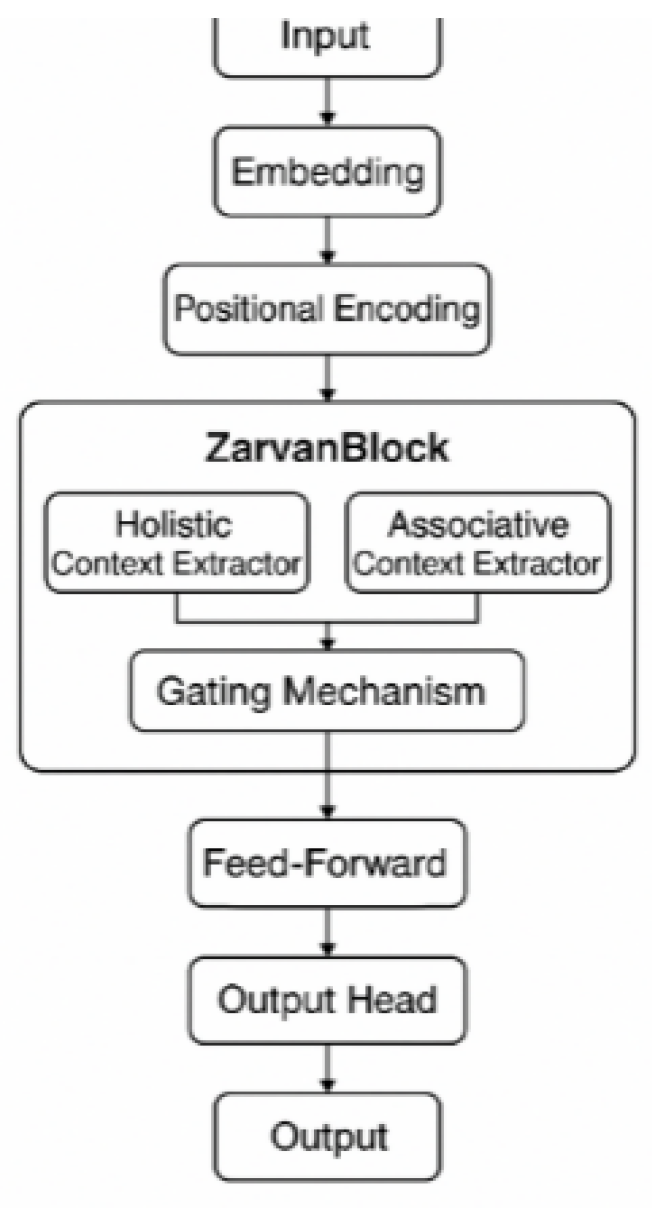
Figure 1. The overall architecture of Zarvan.

Figure 1. The overall architecture of Zarvan.

This diagram illustrates the main components of the Zarvan architecture, including the initial input processing steps (Embedding and Positional Encoding) and the core Zarvan Block with its Holistic and Associative Context Extractors, Gating Mechanism, Feed-Forward network, and Output Head

3.1. Dual Context Extractors

At each layer, for an input sequence of embeddings $X\in R^{S\times E}$ (where $S$ is the sequence length and $\mathit{E}$ is the embedding dimension), Zarvan first computes two parallel global context vectors.

Holistic Context Extractor: This module aims to capture a single, comprehensive summary of the sequence's overall content or "gist". It uses a multi-head weighted-sum mechanism with linear complexity to produce a single context vector $c_{\mathrm{holistic}}\in R^E$. The computation is defined as follows:

• Project the input sequence $X$ into query-like scores ($\mathit{s}$) and values ($v$): $\mathit{s}=\mathit{X}{\mathit{W}}_{\mathit{s}},\hspace{1em}\mathit{v}=\mathit{X}{\mathit{W}}_{\mathit{v}}$ where $W_s,W_v\in R^{E\times E}$ are learnable weight matrices.
• Reshape $s$ and $\mathit{v}$ to accommodate multiple heads ($H$):

  $${\mathit{s}}^{\mathit{\text{'}}}=\mathrm{reshape}\left(\mathit{s},\left[\mathit{B},\mathit{S},\mathit{H},\mathit{E}/\mathit{H}\right]\right),\hspace{1em}{\mathit{v}}^{\mathit{\text{'}}}=\mathrm{reshape}\left(\mathit{v},\left[\mathit{B},\mathit{S},\mathit{H},\mathit{E}/\mathit{H}\right]\right)$$
• Compute weights and aggregate values for each head:

  $$\begin{gathered} \mathsf{\alpha }=\mathrm{softmax}\left(s^{\text{'}},\dim =-1\right) \\ {\mathit{o}}_{\mathrm{head}}={\sum }_{\mathit{i}=1}^{\mathit{S}}{\mathsf{\alpha }}_{\mathit{i}}\cdot {\mathit{v}}_{\mathit{i}}^{\mathit{\text{'}}} \end{gathered}$$
• Combine the head outputs to form the final context vector: $c_{\mathrm{holistic}}=\mathrm{combine}\left(\mathrm{concat}\left(o_{\mathrm{head}1},\dots ,o{\mathrm{head}}_H\right)\right)W_c$

This process, inspired by attention, aggregates information across the entire sequence into a single fixed-size vector with $\mathit{O}\left(\mathit{S}\right)$ complexity, avoiding the quadratic bottleneck of full self-attention.

Associative Context Extractor: This module acts as a "focused memory," designed to identify and aggregate information from the most salient parts of the sequence. It learns a per-token importance score, computes a set of weights via a softmax function, and produces a single weighted average of the input tokens. This produces a context vector $c_{\mathrm{assoc}}$ that is focused on key information. The calculation is formally defined as:

$$\begin{gathered} \mathrm{scores}=X{W}_{score} \\ \mathrm{values}=X{W}_{value} \\ \mathsf{\alpha }=\mathrm{softmax}\left(\mathrm{scores},\dim =1\right) \\ {\mathit{c}}_{\mathrm{assoc}}={\sum }_{\mathit{i}=1}^{\mathit{S}}{\mathsf{\alpha }}_{\mathit{i}}\cdot {\mathit{v}\mathit{a}\mathit{l}\mathit{u}\mathit{e}\mathit{s}}_{\mathit{i}} \end{gathered}$$

Here, $W_{score}\in R^{E\times 1}$ and $W_{value}\in R^{E\times E}$ is a learnable projection matrix that constitutes the $importanc{e}_{scorer}$ network.

Thus, while the Holistic Context creates a diffuse, averaged summary of the entire sequence, the Associative Context actively pinpoints and aggregates information only from tokens deemed most important, enabling focused memory retrieval.

3.2. The Gated Update Mechanism

The power of Zarvan lies in how it uses these global contexts to update each token's representation. For each token $x_i$ in the input sequence $\mathit{X}$, the two global context vectors, ${\mathit{c}}_{\mathrm{holistic}}$ and ${\mathit{c}}_{\mathrm{assoc}}$, are concatenated with it. This combined vector then passes through a dedicated feed-forward network (the GateNet) to compute two modulation gates: an input gate ($i$) and a forget gate ($f$).

The GateNet is implemented as a two-layer Multi-Layer Perceptron (MLP) with a GELU activation function. Its structure is:

$$\mathit{L}\mathit{i}\mathit{n}\mathit{e}\mathit{a}\mathit{r}\left(\mathit{E}\mathit{*}3\to \mathit{H}\right)\to \mathit{G}\mathit{E}\mathit{L}\mathit{U}\to \mathit{L}\mathit{i}\mathit{n}\mathit{e}\mathit{a}\mathit{r}\left(\mathit{H}\to \mathit{E}\mathit{*}2\right)$$

where $E$ is the embedding dimension and $\mathit{H}$ is the hidden dimension.

These gates dynamically control how the original token information is blended with a contextually updated representation of that token. The complete update mechanism within a Zarvan Block is defined as follows:

• Expand Contexts: Expand the global context vectors to match the sequence length $S$.

  $$\begin{gathered} C_{\mathrm{holistic}}=\mathrm{expand}\left(c_{\mathrm{holistic}},S\right) \\ {C}_{\mathrm{assoc}}=\mathrm{expand}\left(c_{\mathrm{assoc}},S\right) \end{gathered}$$
• Form Gate Input: For each token, create the input for the gate network.

  $$G_{\mathrm{input}}=\mathrm{concat}\left(X,C_{\mathrm{holistic}},C_{\mathrm{assoc}}\right)\hspace{1em}\in R^{S\times 3E}$$
• Compute Gates: Generate the input and forget gates using the GateNet.

  $$i,f=\mathrm{split}\left(\mathrm{GateNet}\left(G_{\mathrm{input}}\right)\right)$$
• Apply Gated Update: Modulate the information flow for each token.

  $$X_{\mathrm{gated}}=\mathsf{\sigma }\left(i\right)\odot X+\mathsf{\sigma }\left(f\right)\odot \left(X{W}_{update}\right)$$

  where $\mathsf{\sigma }$ is the sigmoid function, $\odot$ denotes element-wise multiplication, and ${\mathit{W}}_{\mathit{u}\mathit{p}\mathit{d}\mathit{a}\mathit{t}\mathit{e}}$ is a learnable linear projection ($\mathit{u}\mathit{p}\mathit{d}\mathit{a}\mathit{t}{\mathit{e}}_{\mathit{p}\mathit{r}\mathit{o}\mathit{j}}$). This gated update mechanism is inspired by similar concepts in recurrent architectures like LSTMs [7] and GRUs [8]. The 'input gate' ($i$) dynamically controls how much of the original token representation ($X$) is passed through, while the 'forget gate' ($f$) modulates the flow of the contextually transformed information ($X{W}_{update}$​). This allows each token to intelligently decide whether to preserve its local identity or to incorporate a richer, sequence-aware perspective provided by the global contexts.
• Apply FFN and Residual Connection: The final output of the block is computed through a standard feed-forward network (FFN) and a residual connection with layer normalization, a common practice for stabilizing deep networks.

  $$X_{\mathrm{out}}=\mathrm{LayerNorm}\left(X+\mathrm{FFN}\left(X_{\mathrm{gated}}\right)\right)$$

This gating mechanism allows each token to intelligently decide how much of its original representation to keep and how much new, context-informed information to incorporate, providing a flexible and powerful update rule with only linear complexity.

4. Experiments and Results

We conducted five distinct experiments to evaluate Zarvan's performance, scalability, and versatility against a standard Transformer baseline. To ensure a fair comparison, both models were implemented in PyTorch and trained with a similar number of parameters across all tasks.

4.0. Experimental Setup

Our baseline model is a standard Transformer encoder built using PyTorch's nn.TransformerEncoderLayer and nn.TransformerEncoder modules. For all relevant tasks, we provided the Transformer with a source key padding mask to ensure it does not attend to padded tokens, maintaining a fair comparison with Zarvan, which does not require such a mask by design.

All models were trained using the AdamW optimizer. The specific hyperparameters for each task, including learning rates, model dimensions, and batch sizes, were tuned for robust performance and are detailed in Table 1. The parameter counts for Zarvan and the Transformer baseline across the primary benchmarks are presented in Table 2, confirming that the models were configured to have a comparable size.

4.1. Scalability on IMDb Sentiment Classification

This experiment tested the models' performance and training time on a text classification task with varying sequence lengths (128, 256, 512).

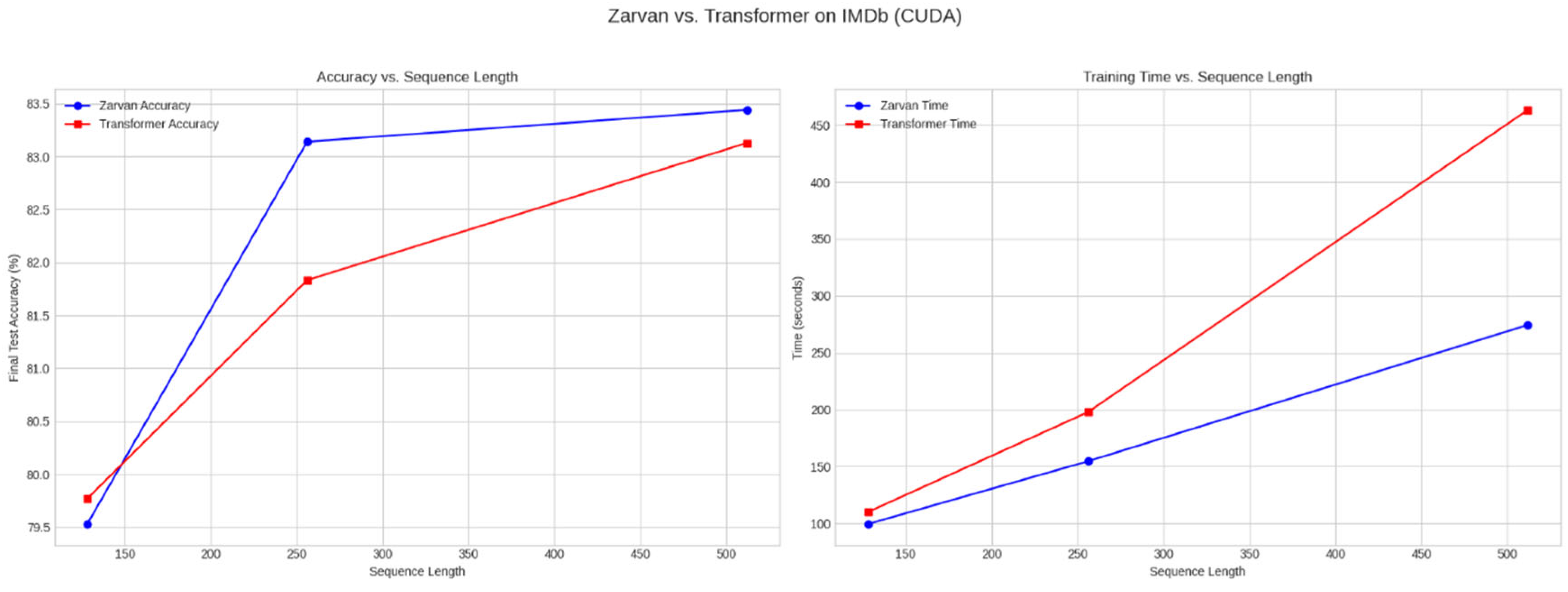
Figure 2. Comparison of Zarvan and Transformer on the IMDb dataset. (Left) Final test accuracy as a function of sequence length. Zarvan's accuracy is competitive and slightly better at longer lengths. (Right) Total training time vs. sequence length. Zarvan exhibits a linear time increase, while the Transformer shows a clear quadratic trend, demonstrating Zarvan's superior scalability.

Figure 2. Comparison of Zarvan and Transformer on the IMDb dataset. (Left) Final test accuracy as a function of sequence length. Zarvan's accuracy is competitive and slightly better at longer lengths. (Right) Total training time vs. sequence length. Zarvan exhibits a linear time increase, while the Transformer shows a clear quadratic trend, demonstrating Zarvan's superior scalability.

The results show that Zarvan's accuracy is comparable and even slightly superior at longer sequence lengths, while its training time scales linearly, confirming its $O\left(S\right)$ complexity. The Transformer's training time grows quadratically, making it much slower at a sequence length of 512.

This suggests that Zarvan's dual-context mechanism is effective for sentiment analysis; the Holistic Context can capture the overall positive or negative tone of a review, while the Associative Context can focus on key sentiment-bearing words like 'excellent' or 'disappointing'.

4.2. Generalization to Vision as a Sequence (MNIST)

To test Zarvan's versatility, we applied it to the MNIST dataset, treating each 28x28 image as a sequence of 784 pixels.

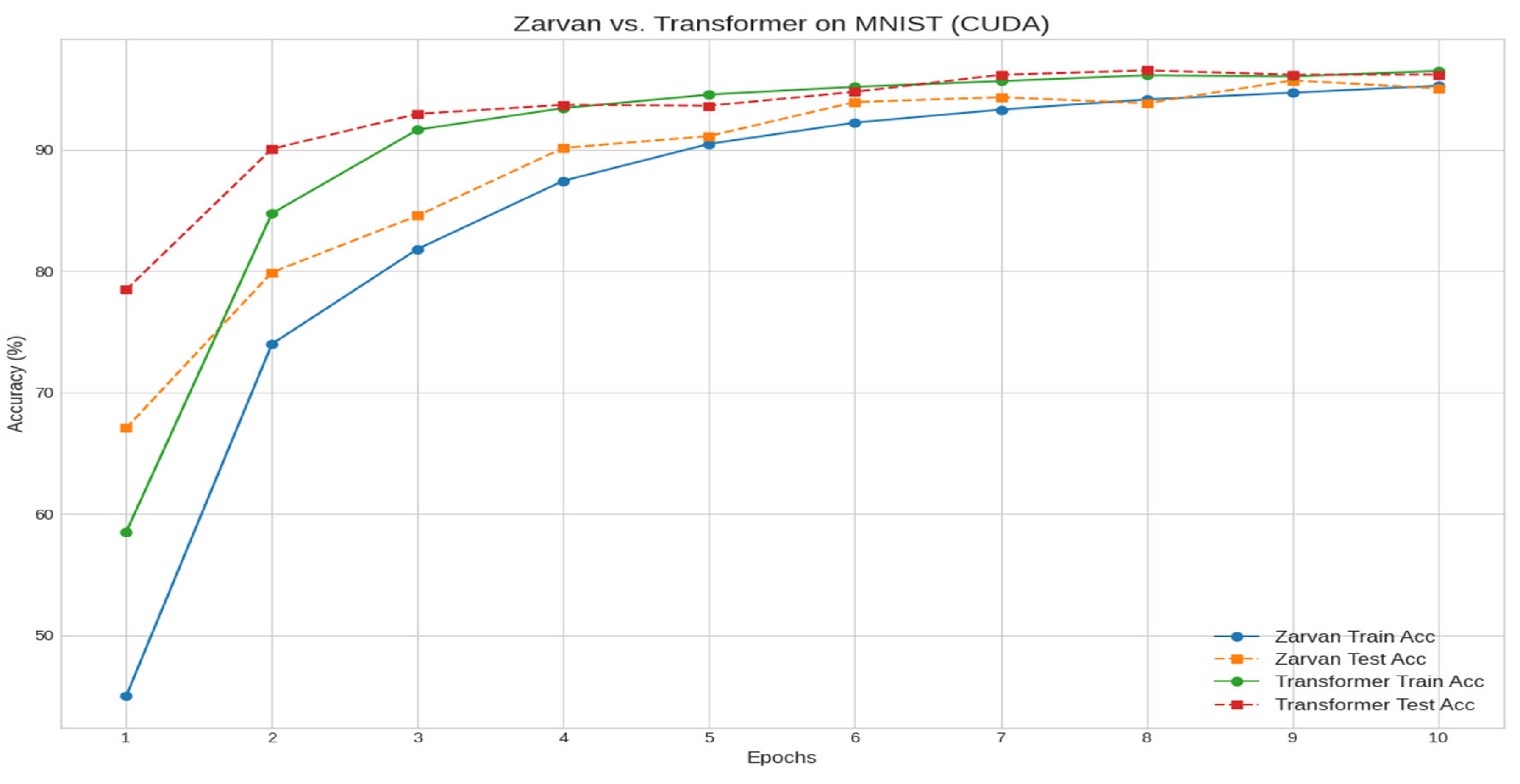
Figure 3. Training and testing accuracy curves on the MNIST dataset. Both models achieve high accuracy, with the Transformer showing slightly faster initial convergence. The final test accuracies are statistically comparable (Zarvan: ~95.7%, Transformer: ~96.5%), demonstrating Zarvan's ability to generalize to non-textual sequence data.

Figure 3. Training and testing accuracy curves on the MNIST dataset. Both models achieve high accuracy, with the Transformer showing slightly faster initial convergence. The final test accuracies are statistically comparable (Zarvan: ~95.7%, Transformer: ~96.5%), demonstrating Zarvan's ability to generalize to non-textual sequence data.

4.3. Information Retrieval on MS MARCO

We evaluated the models as encoders within a two-tower architecture for an information retrieval task. The metric is Ranking Accuracy, measuring if a relevant passage is ranked higher than an irrelevant one.

4.4. Long-Range Dependency Benchmarks

We tested Zarvan on two synthetic tasks from the Long-Range Arena (LRA) benchmark suite [4] to probe its memory and reasoning capabilities.

4.5. Advanced Component Analysis and Sensitivity on Synthetic Tasks

To move beyond standard benchmarks and rigorously test the internal mechanisms of Zarvan, we designed a series of challenging synthetic tasks. These experiments were engineered to isolate the specific functions of Zarvan's core components and to evaluate the model's capacity for complex, multi-step reasoning.

4.5.1. The Role of Associative Context in Information Retrieval: The Selective Copy Task

The Selective Copy task is a direct probe of a model's long-term memory and its ability to retrieve specific information from a long sequence. In this task, the model must identify and recall specific data tokens from a sequence filled with noise, based on cues provided in an instruction portion of the input.

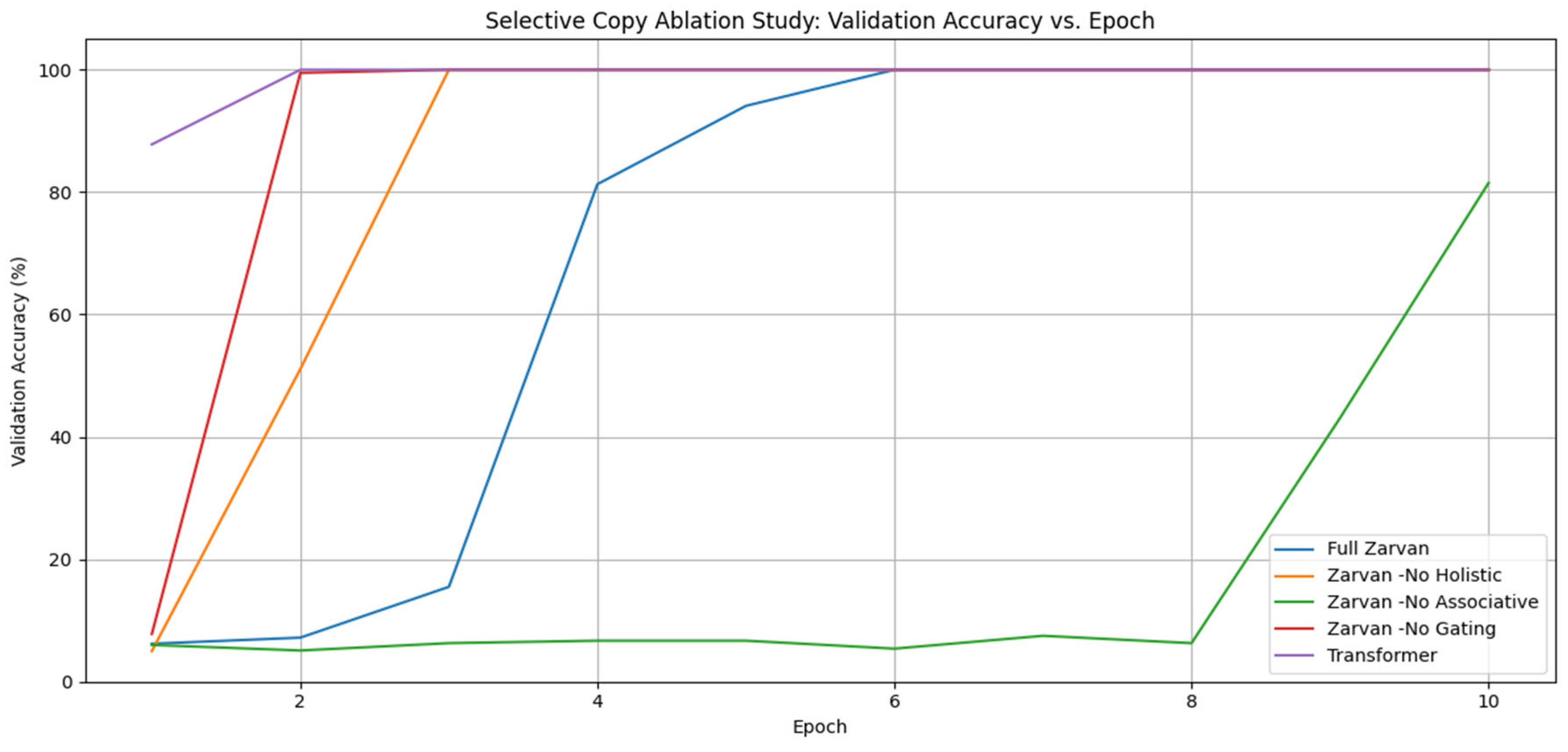
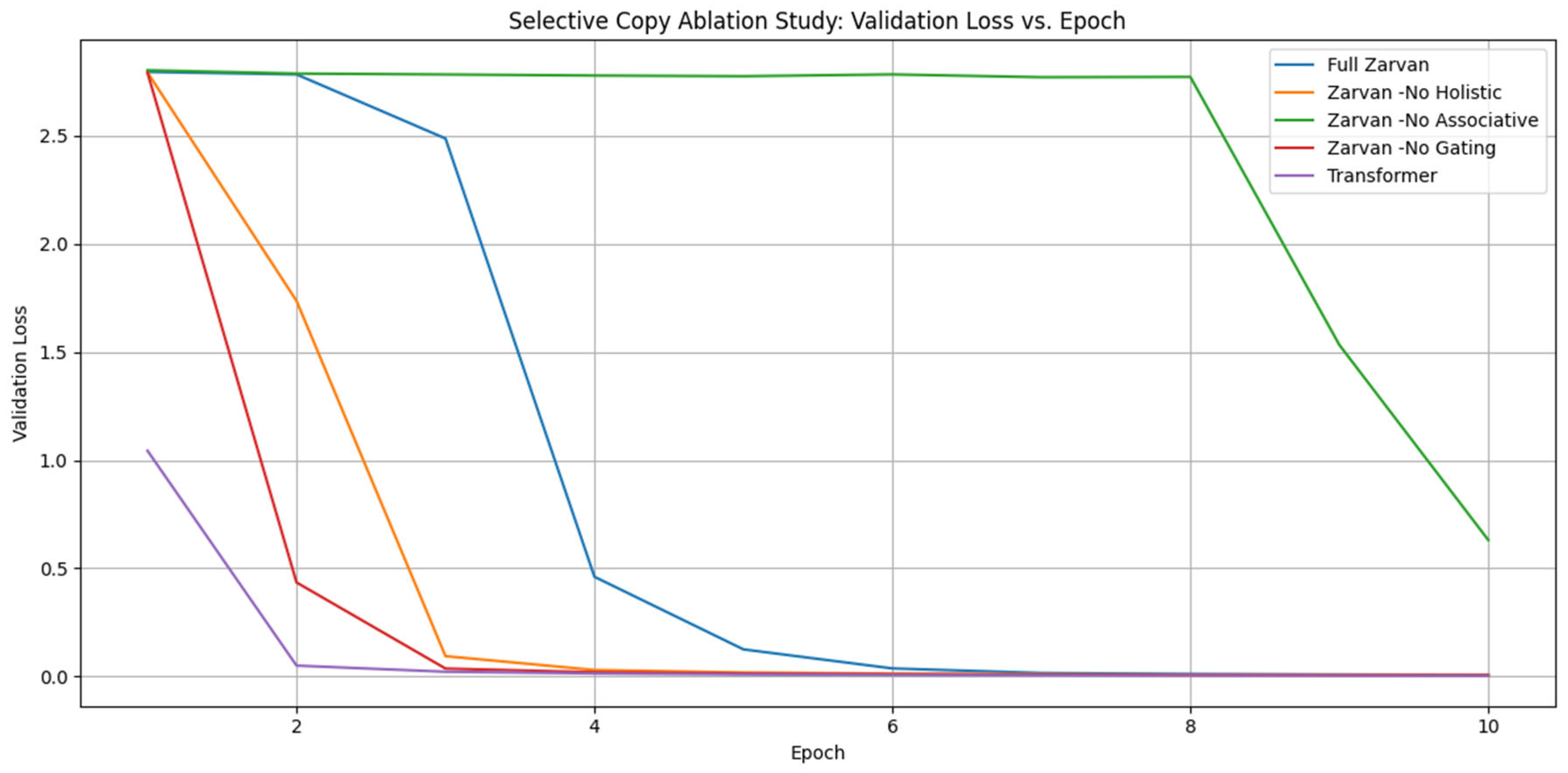
An ablation study was conducted to determine which architectural components are critical for this information retrieval capability. The results, shown in Figure 4, clearly demonstrate the indispensable role of the Associative Context Extractor.

As illustrated in Figure 4, the Full Zarvan model, along with the Transformer and the Zarvan-No Gating variant, successfully learns to solve the task, achieving 100% accuracy. This indicates that for a direct memory retrieval task, the gating mechanism is less critical than the ability to locate the information. The most telling result is the complete failure of the Zarvan-No Associative model. Its inability to learn demonstrates that the Associative Context is the primary mechanism responsible for locating and focusing on sparse, salient information across long distances, which is the core requirement of this task. The Zarvan-No Holistic model also learns, albeit more slowly, suggesting the Holistic context provides a helpful, but not essential, global signal.

4.5.2. Decoupling Memory and Reasoning: The Stateful Parity Check Task

To test if Zarvan could move beyond simple retrieval to stateful reasoning, we designed the "Stateful Parity Check" task. Here, the model must track a binary state (normal/flipped) across a long sequence, where the state is toggled by special [FLIP] tokens. The model's output for any data token depends on the parity (odd or even) of [FLIP] tokens seen in its entire history. This task forces the model to continuously update its understanding of the global state and use that state to make local, conditional decisions.

This task is designed to decouple two core abilities: memory (tracking the parity state across the sequence) and reasoning (using that state to correctly classify a token). Our hypothesis is that global context provides the memory, while the gating mechanism executes the reasoning.

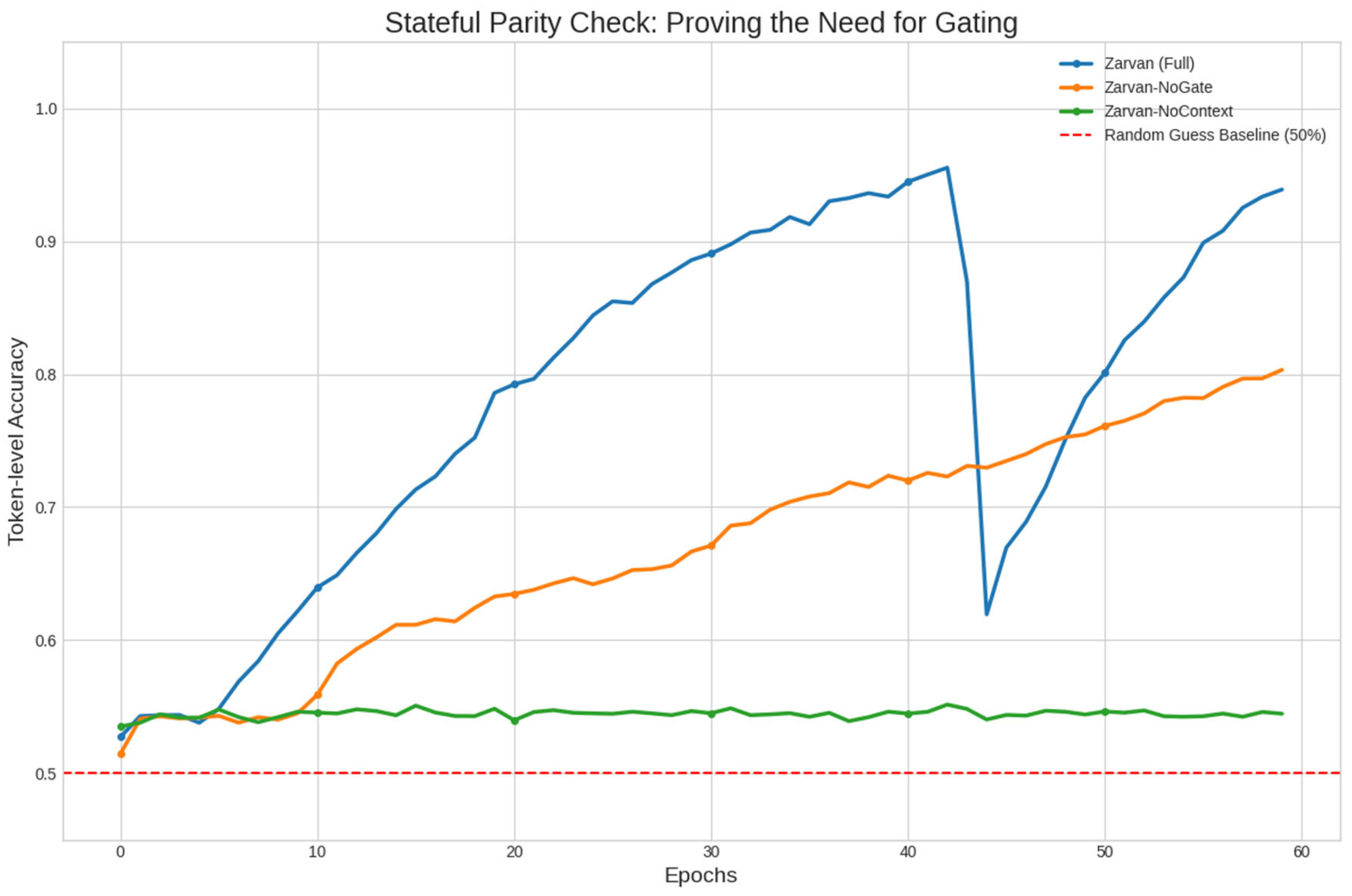
The results in Figure 5 are unequivocal. The Zarvan-NoContext model completely fails, with its accuracy hovering around the 50% random-guess baseline. This proves that access to global context is necessary for maintaining state (memory). In contrast, the Zarvan-NoGate model learns partially, reaching approximately 80% accuracy, but is significantly outperformed by the Full Zarvan model, which achieves near-perfect accuracy (~95%). This performance gap demonstrates that while the context vectors can successfully store the state, the gating mechanism is the critical component for correctly applying that state information to make conditional decisions (reasoning).

4.5.3. Multi-Step Reasoning and Sensitivity Analysis: The Categorical Sum Task

To escalate the complexity further, we created the "Categorical Sum" task. This task requires the model to perform a multi-step algorithmic procedure: (1) locate two specific numbers in a long, noisy sequence, (2) aggregate them by summation, (3) locate a separate "category" token that dictates a rule, and (4) apply the corresponding mathematical rule to the sum to produce a final result.

The ablation study on this task, summarized in Table 3 and Figure 6, reaffirms the findings from the Selective Copy task in a more complex reasoning context.

Table 3. Final results on the MS MARCO information retrieval task. Zarvan achieves a ranking accuracy that is statistically identical to the Transformer while being ~7% faster, even at a short sequence length of 128.

Model	Ranking Accuracy (%)	Total Time (s)
Zarvan	63.85	217.93
Transformer	64.40	235.04

Table 3. Final results on the MS MARCO information retrieval task. Zarvan achieves a ranking accuracy that is statistically identical to the Transformer while being ~7% faster, even at a short sequence length of 128.

Model	Ranking Accuracy (%)	Total Time (s)
Zarvan	63.85	217.93
Transformer	64.40	235.04

Table 4. Performance on long-range dependency tasks. Zarvan perfectly solves the Selective Copy task, demonstrating precise, long-term memory. On the more complex Adding Problem, it achieves near-perfect accuracy, comparable to the Transformer, proving its ability to store and process sparse information over long distances.

Task	Model	Final Accuracy (%)
Selective Copy	Zarvan	100.00
Adding Problem	Zarvan	98.80
Adding Problem	Transformer	99.00

Table 4. Performance on long-range dependency tasks. Zarvan perfectly solves the Selective Copy task, demonstrating precise, long-term memory. On the more complex Adding Problem, it achieves near-perfect accuracy, comparable to the Transformer, proving its ability to store and process sparse information over long distances.

Task	Model	Final Accuracy (%)
Selective Copy	Zarvan	100.00
Adding Problem	Zarvan	98.80
Adding Problem	Transformer	99.00

Table 5. Final validation accuracy on the Categorical Sum task. The results highlight the critical failure of the model variant lacking the Associative Context.

Model	Best Validation Accuracy (%)
Zarvan (Full)	99.88
Transformer	99.92
Zarvan -No Gating	99.12
Zarvan -No Holistic	98.62
Zarvan -No Associative	3.52

Table 5. Final validation accuracy on the Categorical Sum task. The results highlight the critical failure of the model variant lacking the Associative Context.

Model	Best Validation Accuracy (%)
Zarvan (Full)	99.88
Transformer	99.92
Zarvan -No Gating	99.12
Zarvan -No Holistic	98.62
Zarvan -No Associative	3.52

Once again, the Zarvan-No Associative model fails entirely, proving that the ability to locate sparse information is a prerequisite for any subsequent reasoning steps. The other models, including the Transformer baseline, solve the task successfully, demonstrating Zarvan's strong algorithmic reasoning capability when its full architecture is utilized.

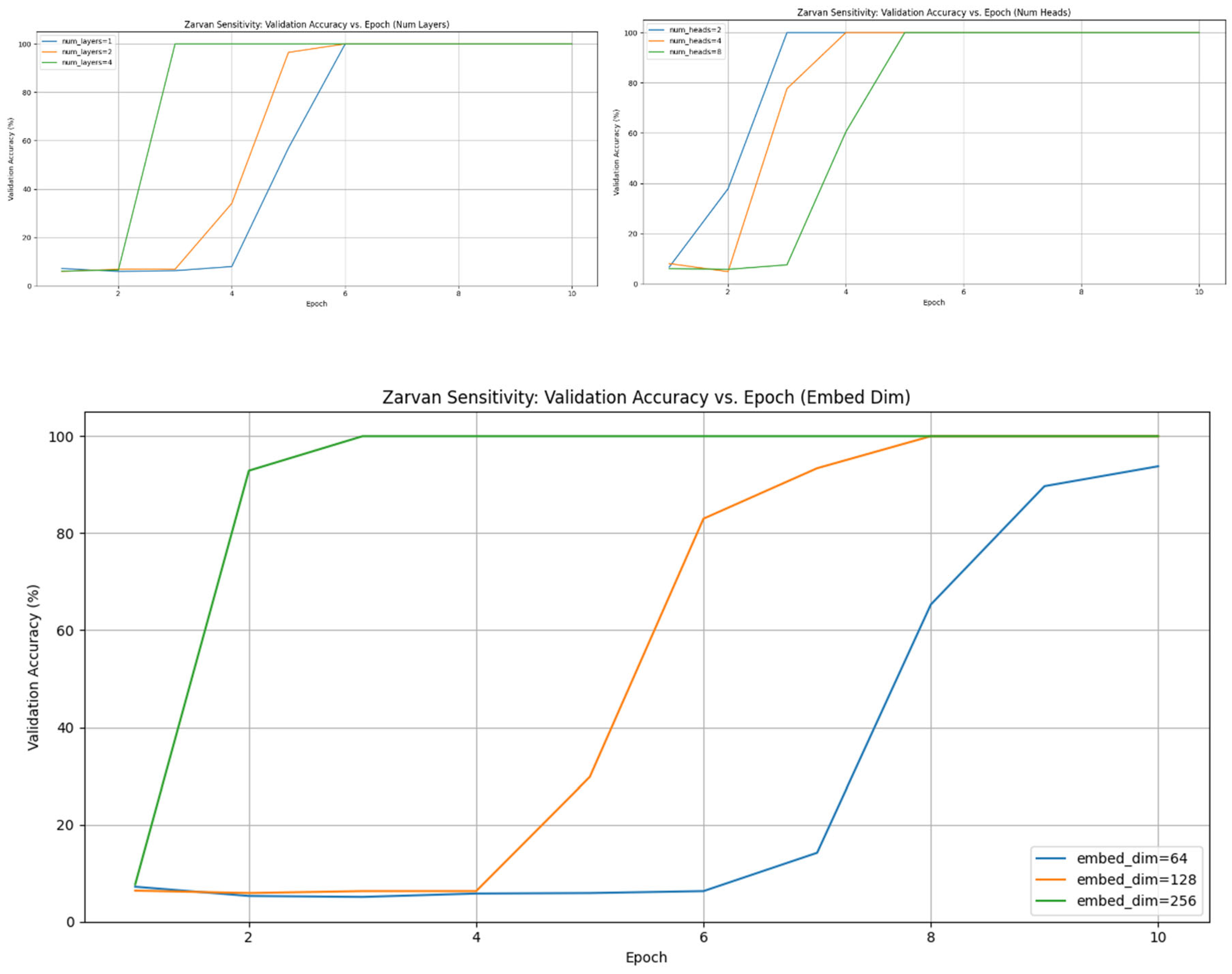
Finally, we conducted a sensitivity analysis on the full Zarvan model to assess its robustness on this difficult task. The results are presented in Figure 7.

The sensitivity analysis shows that: (a) increasing embed_dim from 64 to 256 improves convergence speed and stability; (b) a single layer is insufficient for this task, while 2 or 4 layers enable the model to solve it efficiently, demonstrating the need for architectural depth for multi-step reasoning; and (c) increasing num_heads within the Holistic Context Extractor from 2 to 4 or 8 also accelerates learning. This confirms that Zarvan is a robust architecture whose performance predictably improves with well-chosen hyperparameters.

In summary, the suite of synthetic tasks rigorously validated the design principles of Zarvan. The Selective Copy and Categorical Sum tasks pinpointed the Associative Context as the critical component for sparse information retrieval, while the Stateful Parity Check task decoupled and proved the necessity of both global context for memory and the gating mechanism for conditional reasoning. These findings confirm that Zarvan's architecture provides a robust and effective framework for complex sequence modeling.

5. Discussion

The comprehensive experimental results paint a clear picture. Zarvan consistently delivers performance on par with the Transformer across a wide array of tasks while demonstrating a fundamental advantage in computational efficiency. Its success on challenging synthetic tasks provides strong evidence for the effectiveness of its core design principles. The ablation studies rigorously confirmed that the

Associative Context is the critical component for sparse information retrieval (memory) , while the gating mechanism is essential for applying that stored information to perform conditional reasoning.

5.1. Implications and Strengths

Zarvan's architecture, which separates general understanding (Holistic) from focused memory (Associative), appears particularly well-suited for tasks that involve a mix of signal and noise. This makes it a promising architecture for domains plagued by long sequences where only a fraction of the information is relevant at any given time, such as genomic data analysis, long-form document understanding, and time-series forecasting.

5.2. Limitations

Despite its strong performance, Zarvan's architecture has potential limitations. The compression of the entire sequence into fixed-size context vectors could become a bottleneck on tasks requiring extremely complex, fine-grained, pairwise token interactions for which the full self-attention map is indispensable. Furthermore, the sensitivity analysis shows that while robust, Zarvan's performance is dependent on sufficient model capacity (embedding dimension, number of layers), suggesting that careful hyperparameter tuning is required to achieve optimal results on new tasks.

5.3. Future Work

The success of this architecture opens several promising avenues for future research. One direction is the exploration of more sophisticated context extractors, such as hierarchical methods that compute contexts at multiple resolutions to capture both local and global patterns more effectively. Applying and scaling Zarvan to other long-sequence domains, including speech processing and high-resolution medical imaging, is another critical next step. Finally, pre-training large-scale Zarvan models could further establish their viability as foundational models for a new generation of NLP tasks.

6. Conclusion

In this work, we introduced Zarvan, an efficient, gated architecture with linear-time complexity. By replacing the quadratic self-attention mechanism with a system combining a Holistic Context Extractor, an Associative Context Extractor, and an intelligent gating mechanism, Zarvan effectively overcomes the primary scalability bottleneck of the Transformer. Our extensive evaluations show that Zarvan is not only significantly faster but also maintains highly competitive, and sometimes superior, accuracy on tasks ranging from NLP and vision to synthetic reasoning. Zarvan represents a promising and practical step towards building powerful and scalable models for the next generation of sequence processing challenges.