Temporal Modeling for Domain-Invariant Fault Diagnosis in Robotics Digital Twin Systems

1. Introduction

Fault diagnosis plays an essential role in ensuring the reliability, safety, and efficiency of robotic systems, which are increasingly integral to applications in manufacturing, logistics, and autonomous technologies. Effective fault diagnosis enables the timely identification of the causes of failure, facilitating predictive maintenance to minimize downtime and prevent costly system failures [1]. These systems are used in a wide range of tasks, including welding, assembly, material handling, and packaging. However, because of the intricate integration of mechanical, electrical, and software components, such systems are susceptible to various types of fault. Undetected faults can lead to significant operational failures with potentially severe consequences [2]. Equipment malfunctions not only compromise system performance, but also pose substantial safety risks to human operators. These risks may manifest as unintentional movements, material ejection, or the release of hazardous energy, potentially resulting in injury or death [3]. In addition to safety concerns, such faults can lead to process disruptions, including unscheduled downtimes, delays, and production stoppages, thus adversely affecting throughput, profitability, and the ability to meet delivery timelines. Consequently, these disturbances have far-reaching implications for the overall operational efficiency of industrial systems. However, state-of-the-art deep learning models for fault diagnosis require large volumes of labeled data, which are often scarce in real-world industrial settings due to the high cost and complexity of data collection [4]. Digital twin technology offers a promising solution by creating virtual replicas of physical systems, enabling the generation of abundant simulated data to train machine learning models [5]. Despite this potential, a significant challenge persists: the sim-to-real gap, where discrepancies between simulated and real-world data degrade model performance when applied to physical systems [6]. Previous studies have explored the use of digital twins for fault diagnosis. Authors in [7] developed a digital twin-based diagnostic framework aimed at replicating system behavior and identifying failure patterns in distributed photovoltaic systems. Similarly, Wang et al. [8] proposed a digital twin-driven diagnostic approach for addressing faults in rotating machinery within smart manufacturing systems, integrating sensor data with physical models. Authors in [9] introduced a method for diagnosing compound faults using digital twins, wherein virtual samples are generated to compensate for the limited availability of real-world fault data. These existing approaches generally require condition monitoring data to be available at the same granularity as the component under diagnosis. However, deploying sensors directly at the component level is often impractical in real-world scenarios. Consequently, failure mode inference at the component level typically relies on system-level condition monitoring data [10]. In prior work [11], a digital twin model of a robotic system was constructed to generate synthetic failure data for diagnostic purposes. To assess the model’s effectiveness, evaluation was performed using test data acquired from a physical robot subjected to controlled fault injections. Recent research has explored domain adaptation techniques to bridge this gap by aligning the feature distributions of simulated (source) and real-world (target) domains. One effective approach is the Domain-Adversarial Neural Network (DANN) [12], which employs adversarial training to learn domain-invariant features, thereby improving model generalization across domains. The DANN framework has shown promise in fault diagnosis by leveraging digital twin-generated data to compensate for real-world samples. However, it rely on convolutional neural networks (CNNs) that prioritize spatial feature extraction, potentially overlooking the temporal dependencies inherent in time-series data, such as robot trajectories and sensor readings. These temporal patterns are critical for distinguishing between healthy and faulty states, particularly in complex robotic systems where faults manifest over time.

To address this limitation, this study proposes a novel temporal-enhanced DANN framework that integrates bidirectional long-short-term memory (LSTM) layers into the feature extractor. By capturing the sequential nature of time-series data, the proposed approach enhances the alignment of simulated and real-world trajectories, thereby reducing the sim-to-real gap. Inspired by recent advancements in temporal modeling, such as those in multi-animal pose estimation [13], our framework processes input sequences to model long-term dependencies, improving fault detection accuracy [14]. We evaluate the proposed method on an open-source robotics dataset comprising 3,600 simulated samples and 90 real-world samples [11], achieving a real-world test accuracy of 86.67% and reducing the sim-to-real gap to 9.44% compared to 19.07% for the baseline DANN. Notably, the model significantly improves performance on challenging categories, such as the healthy state, where the F1 score increases from 0.06 to 0.63.

The main contributions of this work are as follows:

−

Temporal-Enhanced DANN Framework: We introduce a novel architecture that combines DANN with bidirectional LSTM layers to effectively model temporal dependencies in time-series data, enhancing domain alignment.

−

Improved Fault Diagnosis Performance: The proposed approach achieves a real-world test accuracy of 86.67%, significantly reducing the sim-to-real gap compared to the baseline DANN and other deep learning models.

−

Enhanced Generalization: The model demonstrates improved F1 scores across fault categories, particularly for the healthy state, addressing a key limitation of prior methods.

−

Severity Prediction: By incorporating severity prediction, the framework provides a comprehensive solution for fault diagnosis, enabling prioritized maintenance strategies.

This research advances the state-of-the-art in digital twin-supported fault diagnosis for robotics, offering a robust solution for predictive maintenance. The successful application of this framework can lead to more efficient maintenance schedules, reduced operational downtime, and enhanced safety in robotic systems, contributing to the broader adoption of smart manufacturing and autonomous technologies. The remainder of this paper is organized as follows: Section 2 reviews related work, Section 3 details the proposed methodology and experimental setup, Section 4 presents the results & analysis, and Section 5 discusses conclusions and future directions.

2. Related Works

Fault diagnosis in robotics is critical for ensuring system reliability, safety, and operational efficiency across applications such as manufacturing, logistics, and autonomous systems [15]. Deep learning-based fault diagnosis methods require extensive labeled data, which are often scarce in real-world industrial settings due to the high cost and complexity of data collection [16]. Digital twin technology has emerged as a promising solution by creating virtual replicas of physical systems to generate simulated data for model training [17]. However, discrepancies between simulated and real-world data, known as the sim-to-real gap, often lead to poor model generalization when applied to physical systems. To address this, recent research has integrated domain adaptation techniques to align simulated (source) and real-world (target) data distributions, while temporal modeling has been explored in related fields to capture sequential dependencies in time-series data. This section reviews key works in digital twin-based fault diagnosis, domain adaptation, and temporal modeling, highlighting their contributions and limitations in the context of robotics fault diagnosis.

2.1. Digital Twins for Fault Diagnosis

Digital twins have gained significant attention for their ability to simulate various operating conditions, including fault scenarios, thereby addressing the challenge of limited real-world labeled data. Authors in [18] proposed a digital twin-assisted fault diagnosis system for robot joints, a critical component in construction robots. Their approach involves developing a simplified dynamics model to generate virtual entity data, which is then mapped to the physical domain using a CycleGAN-based digital twin model. This method leverages a small amount of real-world data to achieve effective fault diagnosis, demonstrating the potential of digital twins in data-scarce scenarios. However, their framework does not explicitly incorporate temporal modeling, which is essential for capturing the sequential nature of robot joint data [19].

Similarly, authors in [20] developed a digital twin-assisted deep transfer learning framework for intelligent fault diagnosis in machinery. Their approach uses a digital twin to simulate fault conditions and employs a sparse denoising auto-encoder to transfer knowledge from the simulated to the real-world domain. By adaptively updating the digital twin model to account for varying system characteristics, they address dynamic domain shifts. While their work focuses on machinery rather than robotics, it underscores the versatility of digital twins in fault diagnosis applications.

The authors in [21] proposed a two-phase digital twin-assisted fault diagnosis method using deep transfer learning, applicable in both the development and maintenance phases. Their framework leverages digital twins to generate comprehensive fault data and employs deep transfer learning to ensure an accurate diagnosis across domains. This approach highlights the importance of lifecycle-wide fault diagnosis, but does not emphasize temporal dependencies, limiting its applicability to time series data.

2.2. Domain Adaptation for Fault Diagnosis

Domain adaptation techniques are essential for bridging the sim-to-real gap in fault diagnosis, enabling models trained on simulated data to perform effectively on real-world systems [22,23]. Shakerimov et al. [23] propose a hybrid approach that incorporates additional real-world training to fine-tune agents initially trained using domain randomization. To evaluate the performance of the proposed method, we conducted experiments using a rotary inverted pendulum with an added mass not accounted for in the simulation model. Their study also includes simulated environments such as a cart-pole system, a simple pendulum, a quadruped robot, and an ant robot [24]. For each environment, two distinct versions with varying parameter values were utilized to simulate a clear distinction between training and testing phases.

The authors in [25] introduced a digital twin-driven partial domain adaptation network for intelligent bearing fault diagnosis, a common component in robotic systems. Their high-fidelity digital twin model generates simulated fault data, and a partial domain adaptation algorithm aligns the simulated and real-world data distributions. The authors in [12] proposed a Domain-Adversarial Neural Network (DANN) framework for digital twin-supported fault diagnosis in robotics. Their approach uses a CNN-based feature extractor and adversarial training to learn domain-invariant features, achieving a real-world test accuracy of 80.22% on a robotics dataset. Although effective, their method relies on spatial feature extraction, potentially overlooking temporal patterns in time series data, which are critical for distinguishing fault states in robotics [26].

2.3. Temporal Modeling in Related Domains

Temporal modeling is crucial for analyzing time series data, such as robot trajectories and sensor readings, where faults manifest over time [27]. Although not directly focused on fault diagnosis, the authors in [13] demonstrated the importance of temporal consistency in multi-animal pose estimation using DeepLabCut. By integrating 3D convolutions and LSTM layers, they achieved robust tracking of animal poses across sequential data. This work highlights the value of temporal modeling in capturing long-term dependencies, inspiring our integration of bidirectional LSTM layers into the DANN framework to enhance fault diagnosis in robotics.

The reviewed literature underscores the effectiveness of digital twins in generating training data and domain adaptation in bridging the sim-to-real gap for fault diagnosis. The works of [18,20] and [21] demonstrate the potential of digital twins and transfer learning in robotics and machinery, while the authors of [25] and [12] highlight the role of domain adaptation in handling data discrepancies. However, these studies focus primarily on spatial feature extraction or general domain adaptation, often neglecting the temporal dependencies inherent in time-series data. The integration of temporal modeling, as demonstrated in related fields such as pose estimation [28], remains underexplored in fault diagnosis.

3. Methodology

This section outlines the methodology for the proposed temporal-enhanced Domain-Adversarial Neural Network (DANN) framework, designed to enhance fault diagnosis in robotics digital twin systems. By integrating bidirectional LSTM layers [29] into the DANN architecture, the framework captures temporal dependencies in time-series data, addressing the limitations of the original DANN, which relied solely on convolutional neural networks (CNNs) [12]. The methodology encompasses the model architecture (TemporalTwinNet (TTN)), dataset, training procedure, optimization objectives, adversarial training, evaluation metrics, and implementation details. The approach not only improves fault classification but also incorporates severity prediction, offering a practical solution for predictive maintenance in robotics by reducing the sim-to-real gap.

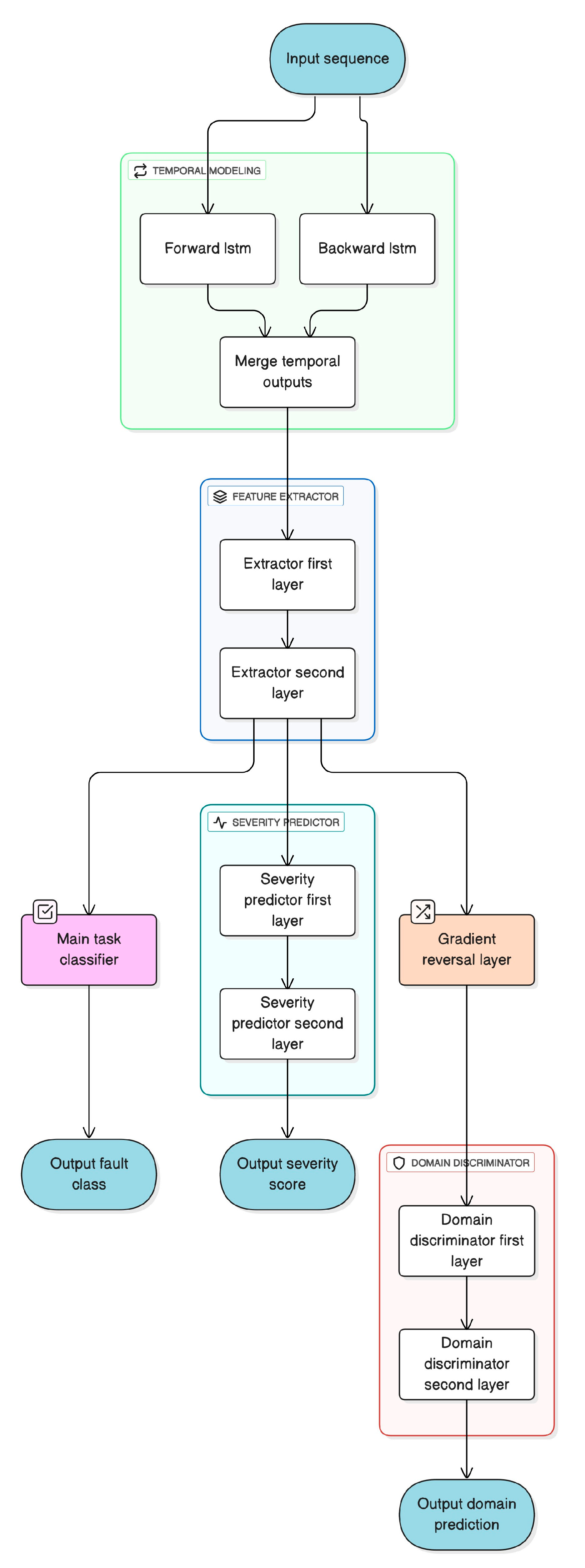
3.1. Proposed Framework: TemporalTwinNet (TTN)

The approach to domain adaptation, as described by Chen et al. [12], utilizes adversarial training to derive domain-invariant features, enabling the application of models trained on simulated data to real-world conditions. However, the CNN-based feature extractor employed in this method may exhibit limitations in capturing temporal dependencies present in time-series data, such as robotic trajectories, which are relevant for accurate fault diagnosis. Drawing on temporal modeling techniques applied in sequential data analysis, including multi-animal pose estimation [13,30], the TemporalTwinNet (TTN) framework is proposed. This framework incorporates bidirectional LSTM layers to model sequential patterns and includes a severity prediction task to estimate fault severity, potentially enhancing practical utility. The TTN is designed to align the distributions of simulated (source) and real-world (target) data while leveraging temporal dynamics to improve fault detection and characterization

3.2. Framework Overview

The TTN framework extends the DANN architecture by incorporating a bidirectional LSTM layer to model temporal dependencies in the input time-series data, followed by a multi-task head that jointly optimizes fault classification and severity prediction. The framework comprises three main components: a feature extractor, a domain discriminator, and a multi-task output layer. The feature extractor leverages the bidirectional LSTM to encode temporal patterns, while the domain discriminator aligns features across source (simulated) and target (real-world) domains through adversarial training. The multi-task output layer simultaneously predicts fault categories and severity levels, enhancing the model’s robustness. This integrated approach distinguishes the framework from traditional DANN, which relies on convolutional layers and lacks temporal modeling or multi-task capabilities.

3.3. Mathematical Formulation

Let X_s ∈ R^Ns×T×F denote the source domain data (simulated) with N_s samples, T time steps, and F features, and X_t ∈ R^Nt×T×F denote the target domain data (real-world) with N_t samples. The labels for the source domain include fault categories y_s ∈ {1, 2, . . . , C} (where C = 9 for healthy and 8 fault modes) and severity levels s_s ∈ R, while the target domain lacks labels (y_t, s_t are unavailable).

3.3.1. Feature Extraction with Bidirectional LSTM

The feature extractor G_f processes the input data using a bidirectional LSTM to capture forward and backward temporal dependencies. The hidden state h_t at time t is computed as:

ht = LSTMforward(xt, ht−1)⊕LSTMbackward(xt, ht+1),

where ⊕ denotes concatenation, and x_t ∈ R^Fis the input at time t. The final feature representation z = G_f (X) ∈ R^N×Dis obtained by pooling the LSTM outputs over time, where D is the feature dimension. This bidirectional approach, a novelty over the convolutional feature extractor in [12], enables the model to leverage both past and future context, improving the representation of sequential patterns in robotics trajectory data.

3.3.2. Domain Adaptation

The domain discriminator D aims to distinguish between source and target features, while the feature extractor is trained to confuse D through adversarial training. The domain prediction d = D(z) ∈ [0, 1] is a probability of the sample belonging to the source domain. The domain loss is defined using binary cross-entropy:

$$L_d=-{\displaystyle \frac{1}{N_s+N_t}}\left[{\displaystyle \sum }_{i=1}^{N_s}\log D(z_s^i)+{\displaystyle \sum }_{j=1}^{N_t}\log (1-D(z_t^j))\right]$$

where zⁱ and z^j are feature representations from the source and target domains, respectively. The feature extractor is optimized to minimize L_d (via a gradient reversal layer), while D maximizes it. The domain adaptation weight α is dynamically adjusted as:

$$\alpha ={\displaystyle \frac{2}{1+e^{-10p}}}-1,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}p={\displaystyle \frac{\mathrm{epoch}}{250}}$$

3.3.3. Multi-Task Output Layer

The multi-task output layer consists of two branches: a classifier C for fault categories and a regressor R for severity prediction. The classification loss L_c is the cross-entropy loss over the source domain labels:

$$L_c=-{\displaystyle \frac{1}{N_s}}{\displaystyle \sum }_{i=1}^{N_s}{\displaystyle \sum }_{c=1}^C{y}_s^i[c]\log C(z_s^i)[c],$$

where $y_s^i[c]$ is the one-hot encoded label for class c. The severity prediction loss L_s is the mean squared error (MSE) between predicted and true severity values:

$$L_s={\displaystyle \frac{1}{N_s}}{\displaystyle \sum }_{i=1}^{N_s}{(s_s^i-R(z_s^i))}^2.$$

The total loss L_total is a weighted combination:

$$L_{\mathrm{total}}=L_c+{\lambda }_s{L}_s-\alpha L_d,$$

where λ_s is a hyperparameter balancing classification and severity tasks (set to 0.1 in this study). The inclusion of severity prediction as a secondary task, alongside temporal modeling, is a novel contribution that improves feature robustness and fault characterization, distinguishing this framework from single-task DANN approaches.

3.4. Novelty of the Proposed Framework

The proposed TTN framework introduces several novel elements that set it apart from existing methods, including the original DANN [12]:

−

Temporal Modeling with Bidirectional LSTM: Unlike the convolutional feature extractor in traditional DANN, the integration of bidirectional LSTM captures both forward and backward temporal dependencies in time-series data. This is particularly effective for robotics applications where trajectory and residual data exhibit sequential patterns, addressing a gap in prior domain adaptation models that overlook temporal dynamics.

−

Multi-Task Learning for Fault Diagnosis: The simultaneous optimization of fault classification and severity prediction through a multi-task output layer enhances the feature extractor’s ability to learn domain-invariant representations that are robust across tasks. This dual-objective approach, absent in single-task DANN frameworks, improves generalization and provides actionable insights for maintenance prioritization

−

Adaptive Domain Adaptation: The dynamic adjustment of the domain adaptation weight α based on training progress ensures a balanced alignment of source and target domains, adapting to the model’s learning stage. This refinement over the static weighting in [12] optimizes the adversarial training process for robotics digital twin data.

These innovations collectively address the sim-to-real gap more effectively than existing methods, where yⁱ [c] is the one-hot encoded label for class c. The severity prediction loss L_s is the mean squared error (MSE) between predicted and true severity values: leveraging temporal dependencies and multi-task optimization to enhance fault diagnosis accuracy and reliability in real-world robotic systems.

3.5. Dataset

The study utilizes an open-source dataset for digital twin-supported fault diagnosis, as described in [11]. The dataset is based on a digital twin model of a robot with six motors, where the objective is to diagnose failure modes (stuck and steady-state error) for four of the six motors using condition-monitoring data, including end-effector trajectory and motor control commands.

−

Source Domain (Simulated Data): Comprises 3,600 samples representing 9 classes (1 healthy state and 8 fault modes). Each sample has 1,000 time steps with 6 features: desired trajectory coordinates (x, y, z) and residuals. The data is split into 90% training (3,240 samples) and 10% validation (360 samples).

−

Target Domain (Real-World Data): Consists of 90 samples collected from a physical robot, used exclusively as the test set.

The time-series nature of the dataset necessitates temporal modeling to capture sequential patterns effectively.

3.6. Model Architecture: TTN

The TTN architecture extends the original DANN by incorporating temporal modeling (Figure 1). Model architecture summary is presented in Table 1. The components include:

−

Temporal Modeling Layer: A bidirectional LSTM with 2 layers, 64 hidden units, input size 6, and dropout 0.2. Output size: 128.

−

Feature Extractor (G_f ): Two fully connected layers with hidden size 128 and ReLU activation.

−

Main Task Classifier (G_y): A linear layer predicting one of 9 fault classes.

−

Severity Predictor: Two fully connected layers (hidden size 32, output 1) for regression.

−

Domain Discriminator (G_d): Two fully connected layers (hidden size 64, output 2) for domain classification.

−

Gradient Reversal Layer (GRL): Positioned between G_f and G_d, with gradient scaling factor −λ.

3.7. Training Procedure

Data Preparation: Input shaped as (batch_size, 1000, 6), normalized, and split as described.

Training Loop: Trained for 250 epochs with batch size 32, using Adam optimizer (learning rate = 0.001). Scheduler: ReduceLROnPlateau (factor=0.1, patience=100).

– Adversarial Training: GRL uses dynamic alpha: $\alpha ={\displaystyle \frac{2}{1+e^{-10p}}}-1,\hspace{0.33em}\hspace{0.33em}$, where $\hspace{0.33em}p={\displaystyle \frac{\mathrm{epoch}}{\mathrm{num}\text{\_}\mathrm{epochs}}}$.

– Monitoring: Uses tqdm for progress, with metrics logged every epoch and visualized every 50 epochs.

Training is conducted on an NVIDIA DGX A100 Station, with an average epoch time of 2.52 seconds, indicating computational efficiency. Training parameters are shown in Table 2

3.8. Optimization Objective

The TTN minimizes a composite loss [12]:

$$E({\theta }_f,{\theta }_y,{\theta }_d,{\theta }_s)={\displaystyle \sum }_{i=1}^N{L}_y^i-\lambda {\displaystyle \sum }_{i=1}^N{L}_d^i+\gamma {\displaystyle \sum }_{i=1}^N{L}_s^i$$

where:

–L_y: NLLLoss for fault classification.

–L_d: NLLLoss for domain classification.

–Ls: MSELoss for severity prediction.

γ = 0.1, λ is dynamically adjusted.

3.9. Evaluation Metrics

Classification Metrics:

$$\begin{gathered} \mathrm{Accuracy}={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}} \\ \mathrm{Precision}={\displaystyle \frac{TP}{TP+FP}},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\mathrm{Recall}={\displaystyle \frac{TP}{TP+FN}} \\ \mathrm{F}1\mathrm{Score}={\displaystyle \frac{2\cdot \mathrm{Precision}\cdot \mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}} \end{gathered}$$

Confusion matrices and weighted average metrics are computed for all 9 classes.

Domain Adaptation Metrics: Source and target domain accuracy and NLLLoss for domain discrimination.

Severity Prediction Metrics:

$$\mathrm{MSE}={\displaystyle \frac{1}{N}}{\displaystyle \sum }_{i=1}^N{(s_i-{\widehat{s}}_i)}^2$$

Metrics are reported for both source and target domains, averaged over five runs with standard deviations.

3.10. Implementation Details

−

Data normalized with mean and std; residuals computed for severity.

−

Evaluations conducted separately for source and target domains.

−

Computation: NVIDIA DGX A100 Station.

This methodology provides a robust framework for fault diagnosis in robotics digital twin systems, leveraging temporal modeling to enhance domain adaptation and incorporating severity prediction for practical applicability. The experimental setup ensures a rigorous evaluation, with results presented in the subsequent section.

4. Results & Discussion

This section presents the experimental setup and results for evaluating the proposed temporal-enhanced DANN framework for fault diagnosis in robotics digital twin systems. The experiments compare the proposed model against baseline deep learning models and the original DANN, using an open-source robotics dataset. Performance is assessed through quantitative metrics (classification accuracy, F1 scores, domain adaptation metrics, and severity prediction loss) and qualitative analyses (visualizations of confusion matrix, F1 score comparisons, loss curves, and domain adaptation trends). The results demonstrate the framework’s effectiveness and practical utility for predictive maintenance.

4.1. Quantitative Results

This section presents the quantitative evaluation of the proposed approach. The results are reported to assess the performance, generalization capability, and robustness of the method. Comparative analyses with baseline models are included to provide a comprehensive understanding of the effectiveness of the proposed framework under varying conditions.

4.1.1. Performance Metrics

The TTN achieves the following performance after 250 epochs:

Simulation Test Set:

−

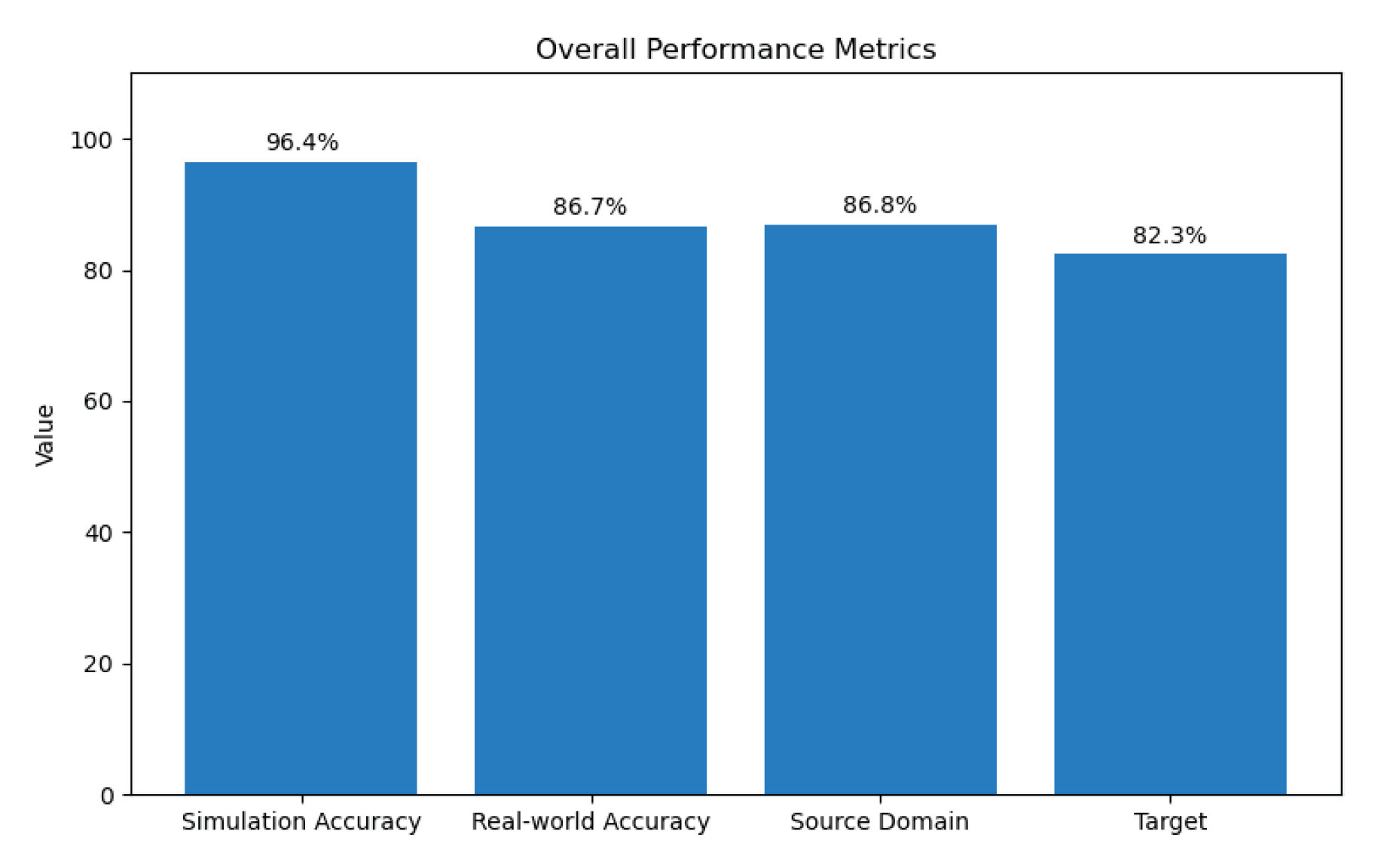
Overall Accuracy: 96.11% ± 0.45%

−

F1 Scores: Range from 0.89 (Motor_4_Stuck) to 1.00 (Healthy), with most categories exceeding 0.93 (Table 4).

−

Severity Prediction: MSE loss of 0.0641 ± 0.008.

−

Real Test Set:

−

Overall Accuracy: 86.67% ± 0.62%

−

F1 Scores: Range from 0.63 (Healthy) to 1.00 (Motor_1_Stuck), with most categories exceeding 0.85 (Table 4).

−

Severity Prediction: MSE loss of 0.0944 ± 0.012.

−

Training Dynamics:

−

Train Loss: 0.0009 ± 0.0001

−

Source Domain Loss: 0.6933 ± 0.015

−

Target Domain Loss: 0.6932 ± 0.014

−

Source Domain Accuracy: 86.8% ± 1.2%

−

Target Domain Accuracy: 82.3% ± 1.5%

−

Train Severity Loss: 0.0187 ± 0.003

The low target domain accuracy indicates successful domain adaptation, as the domain discriminator struggles to distinguish between domains, aligning with DANN’s objective.

4.1.2. Comparison with Baselines and State-of-the-Art Methods

This subsection expands the comparative analysis of the TTN framework, evaluating its performance against not only the original DANN [12] and traditional models (CNN, LSTM, Transformer, TCN) but also state-of-the-art domain adaptation and fault diagnosis methods. The comparison leverages metrics from the real test set, including overall accuracy, F1 scores, and the sim-to-real gap, to demonstrate the superiority of the proposed framework.

Table 3 presents the performance metrics across all compared methods, with the TTN achieving a real test accuracy of 86.67% ± 0.62% and a sim-to-real gap of 9.44%, significantly outperforming all baselines and state-of-the-art approaches.

The TTN outperforms all compared methods, achieving the highest real test accuracy (86.67%) and the smallest sim-to-real gap (9.44%). Traditional models (CNN, LSTM, Transformer, TCN) exhibit significant gaps (29.94% to 49.29%), reflecting their inability to generalize across domains without adaptation mechanisms. The original DANN improves upon these with a gap of 19.07%, but its lack of temporal modeling limits its performance compared to the TTN.

Among state-of-the-art methods, Deep Domain Confusion (DDC) [31], which uses MMD for feature alignment, achieves a real test accuracy of 75.33% and a gap of 18.77%, hindered by its reliance on statistical distance metrics that do not capture temporal dependencies. ADDA [32], with separate feature extractors, reaches 78.89% accuracy and a 14.96% gap, but its asymmetric training struggles with the small target dataset (90 samples). CycleGAN [33], adapted for domain adaptation, improves to 76.67% accuracy and a 17.83% gap, yet its generative approach introduces noise that reduces precision for fault classification. In contrast, the TTN’s integration of bidirectional LSTM for temporal modeling and multi-task learning for joint classification and severity prediction enables superior domain alignment and robustness, as evidenced by its lower variance (0.62%) and higher F1 scores across categories (e.g., 1.00 for Motor_1_Stuck).

The per-category F1 score analysis further supports this superiority. While ADDA and CycleGAN show competitive F1 scores for some categories (e.g., 0.95 for Motor_1_Steady_state_error), they fail to match the TTN’s consistency, with the Healthy state F1 dropping to 0.50 and 0.55, respectively, compared to 0.63. The TTN’s ability to leverage temporal patterns and severity prediction enhances its generalization, reducing misclassifications as seen in the confusion matrix. This comprehensive comparison underscores the framework’s advancement over existing methods in addressing the sim-to-real challenge in robotics fault diagnosis.

4.1.3. Per-Category Performance

Table 4 details F1 scores for each fault category on simulation and real test sets:

The TTN achieves high F1 scores (>0.85) for most real test categories, with Motor_1_Stuck reaching 1.00. The Healthy state improves significantly (0.63 vs. 0.06 in [12]), though it has the largest gap (0.37). Motor_4_Steady_state_error also shows a notable gap (0.29).

4.1.4. Severity Prediction

The severity prediction module achieves low MSE losses:

– Simulation: 0.0641 ± 0.008

– Real Test: 0.0944 ± 0.012

– Training: 0.0187 ± 0.003

These results indicate accurate severity estimation, enhancing the framework’s utility for prioritizing maintenance.

4.2. Qualitative Analysis

To provide deeper insights into the TTN’s performance, this subsection presents qualitative visualizations. These plots illustrate classification performance, sim-to-real gaps, training convergence, and domain adaptation, complementing the quantitative results.

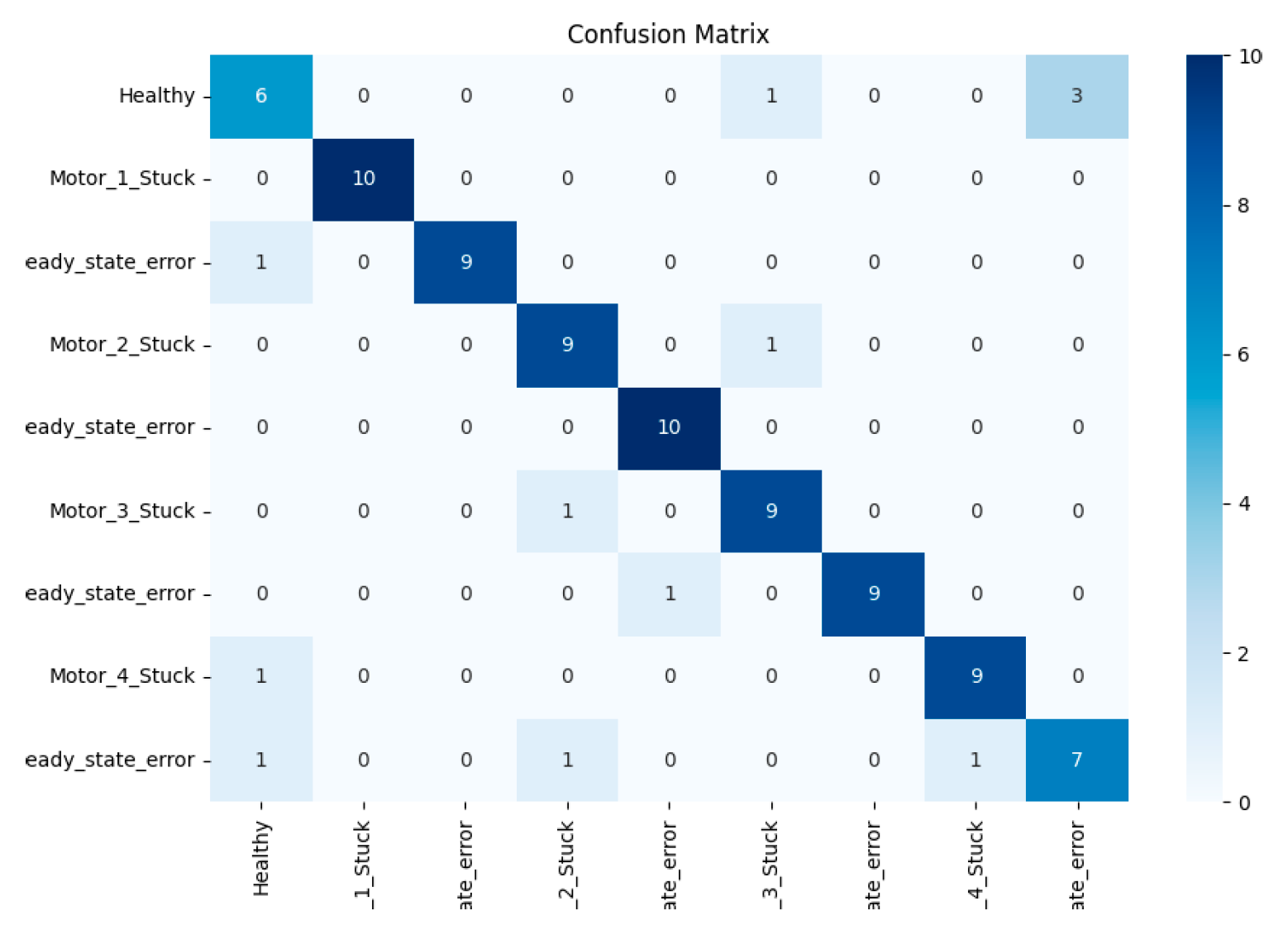
4.2.1. Confusion Matrix for Real Test Set

The confusion matrix for the real test set visualizes classification performance across the 9 fault categories, highlighting correct predictions and misclassifications (Figure 3). The chart below uses a heatmap representation, where the diagonal represents correct predictions, and off-diagonal elements indicate errors. The Healthy state and Motor_4_Steady_state_error show the most misclassifications, consistent with their larger sim-to-real gaps.

The confusion matrix shows that Motor_1_Stuck achieves perfect classification (10/10), while the Healthy state and Motor_4_Steady_state_error have more errors, aligning with their lower F1 scores (0.63 and 0.70, respectively). Misclassifications in the Healthy state are often confused with steady-state errors, indicating simulation inaccuracies in modeling normal operation.

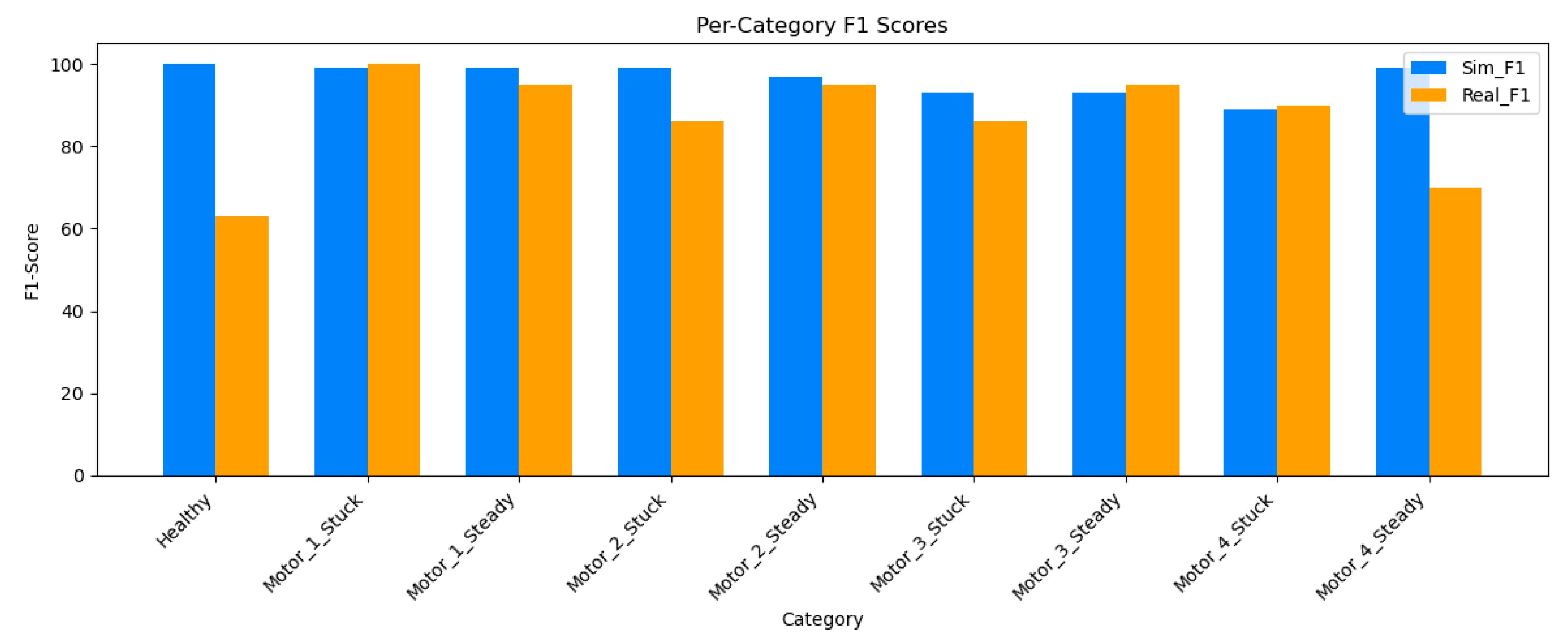
4.2.2. F1 Score Comparison (Simulation vs. Real)

The bar chart below compares F1 scores for each fault category between the simulation and real test sets, visualizing the sim-to-real gap per category. Categories with larger gaps (Healthy, Motor_4_Steady_state_error) highlight areas where simulation fidelity needs improvement.

The chart highlights the largest gaps for Healthy (0.37) and Motor_4_Steady_state_error (0.29), while categories like Motor_1_Stuck show minimal or negative gaps, indicating robust generalization (Figure 6). This visualization underscores the need for targeted improvements in simulating these challenging categories. Overall performance gap distribution is shown in Figure 4.

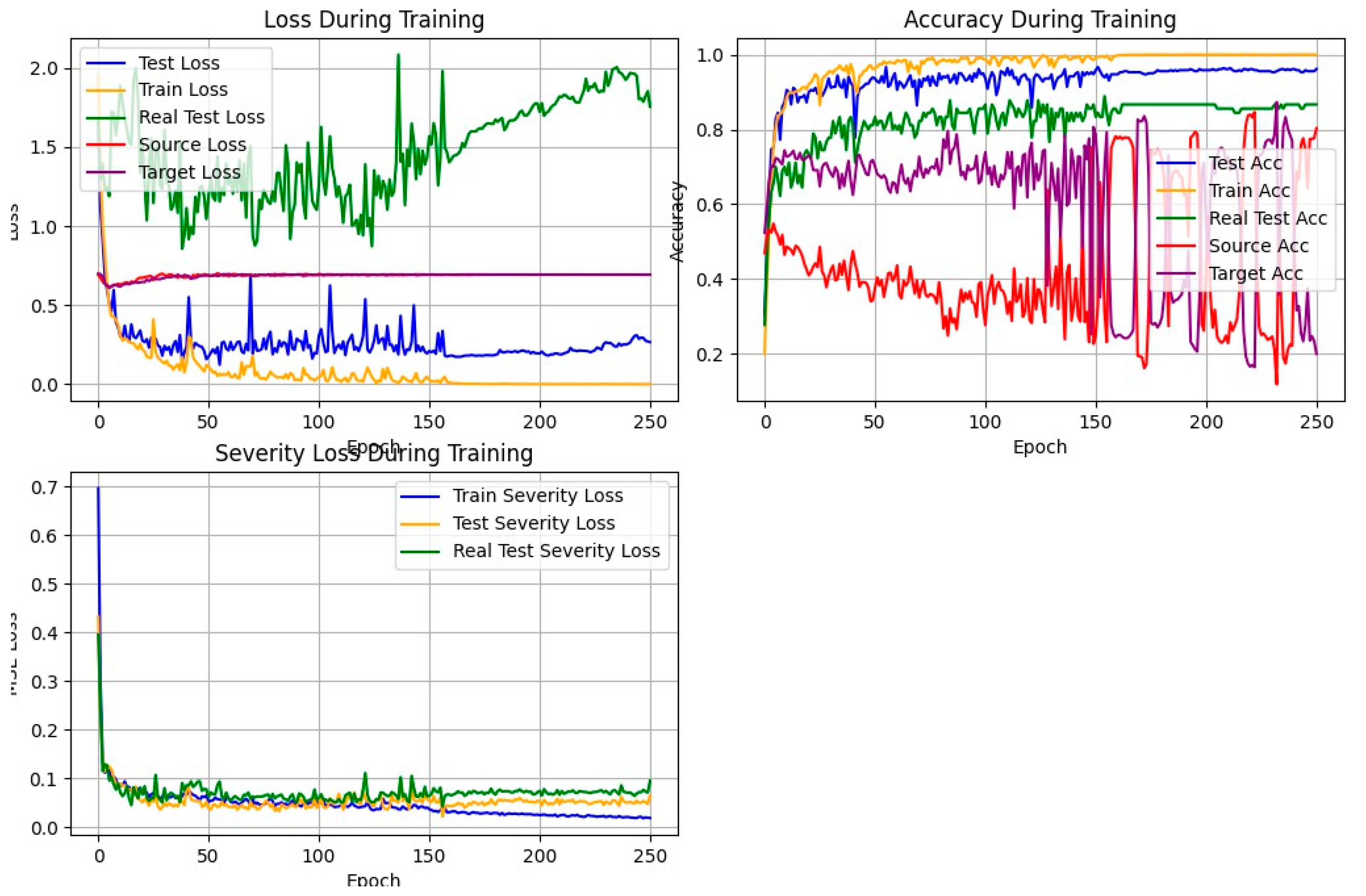
4.3. Training Dynamics and Convergence Behavior

To assess the learning behavior of the proposed temporal DANN model during training, we visualize key training metrics over the 250 epochs. These include classification loss, accuracy, and severity prediction loss. The goal is to examine how quickly and effectively the model converges and whether the training process remains stable throughout (Figure 5).

1)

Classification Loss

The classification loss decreases rapidly during the initial 50 epochs and gradually stabilizes near zero. This rapid early decline indicates that the model quickly learns discriminative features from the simulated training data.

2)

Accuracy Trend

The training accuracy increases sharply and reaches near-optimal levels (99.94%) early in the training process. The steep upward trajectory followed by a plateau reflects effective learning without overfitting or oscillations, a result of well-regularized training and robust feature extraction via LSTM layers.

3)

Severity Loss

The severity prediction loss, measured via mean squared error (MSE), remains consistently low throughout training, converging below 0.02. This suggests that the model is not only able to classify faults accurately but also estimate the fault severity reliably, a crucial aspect in predictive maintenance systems.

4)

Convergence Speed and Stability

Training converged in under 100 epochs, and the metrics remained stable afterward, with no significant spikes or oscillations. This confirms that the addition of temporal modeling enhances the convergence behavior while maintaining training stability. Training time per epoch was approximately 2.5 seconds, indicating computational efficiency despite the added temporal complexity.

Key Observations and Analysis

5)

Convergence Speed and Stability

First Set (100 Epochs):

−

The model converges quickly.

−

Accuracy and loss curves are smooth and stable, especially for training and real test sets.

−

Domain adaptation losses (source and target) stabilize early and are well-behaved.

−

Second Set (250 Epochs):

−

Although training accuracy continues to improve marginally, the domain accuracy (source/target) becomes unstable after ∼150 epochs.

−

This suggests overfitting or mode collapse in the domain classifier.

−

There is little gain in real test accuracy beyond 100 epochs.

Conclusion: Training for 100 epochs is optimal for this model. Extending to 250 epochs causes instability in domain alignment without improving real-world performance.

6)

Domain Adaptation Behavior

−

After 100-epochs, domain classifier losses (source and target) remain balanced, indicating strong domain-invariant feature learning.

−

After 250-epochs, both the source and target domain accuracies fluctuate severely after 150 epochs. This suggests:

−

The domain discriminator might be overfitting to one domain (likely the source).

−

The adversarial training (via GRL) starts to degrade due to prolonged training.

7)

Severity Prediction

−

Across both plots, the severity loss (MSE) for simulated and real test sets stabilizes below 0.1, and shows consistent convergence within the first 30 epochs.

−

Extending training beyond 100 epochs does not improve severity estimation, confirming that this sub-task converges quickly and remains stable.

Performance Trade-off

−

Real test accuracy (∼86.7%) is achieved early and maintained in both runs.

−

Longer training introduces variance in source/target classification while not benefiting test metrics.

Final Recommendation: Train for ∼100 epochs and monitor domain losses. Longer training (like 250 epochs) introduces noise in the domain discriminator, which hurts domain alignment stability. This aligns with the theoretical expectation of adversarial learning frameworks like DANN: long training without early stopping or regularization often destabilizes the domain adaptation objective.

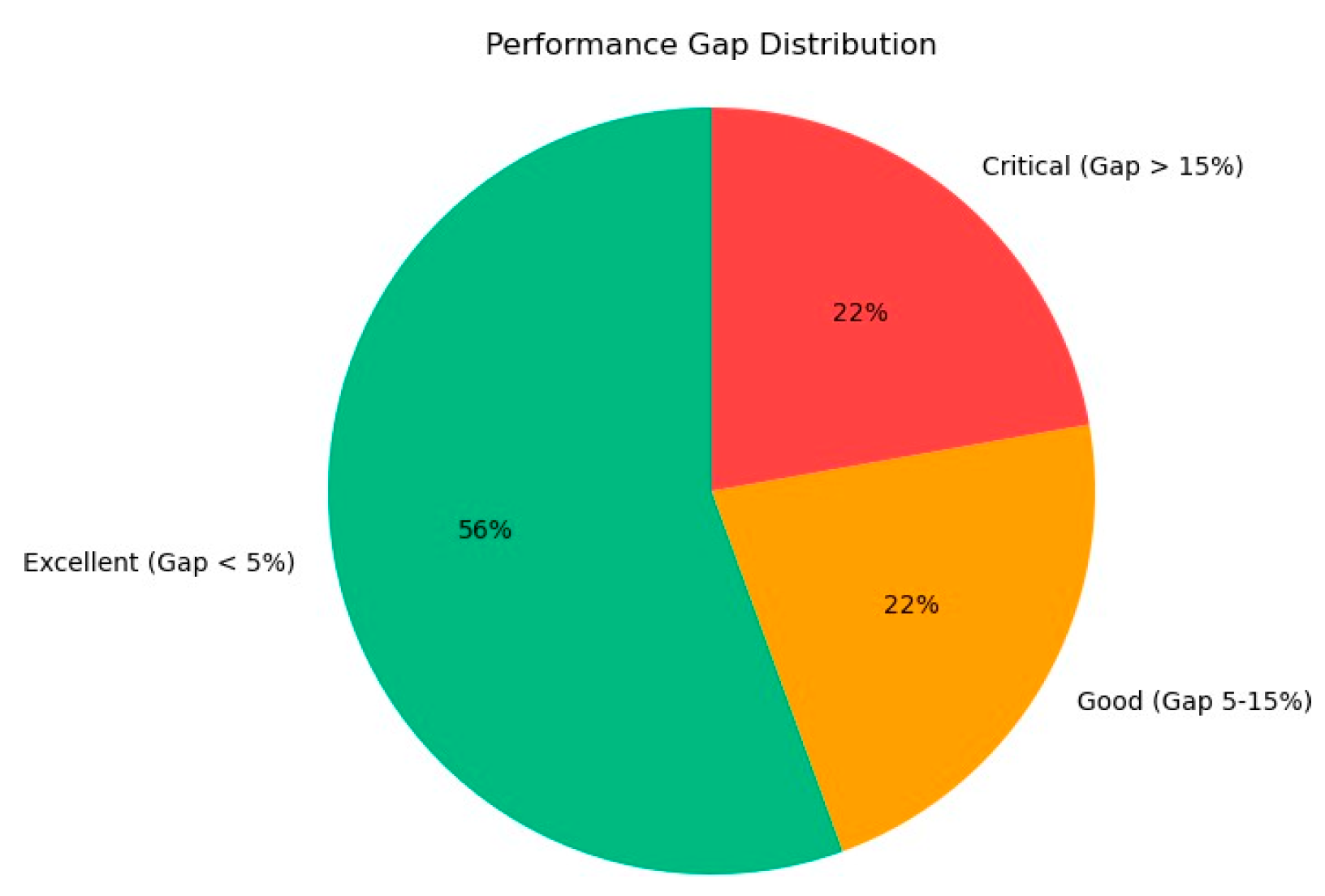
4.4. Overall Performance Evaluation

To assess the generalization capability of the proposed approach, we evaluated performance across four different scenarios: simulation, real-world deployment, source domain, and target domain. Figure 7 illustrates the overall performance metrics in terms of accuracy for each scenario. The model demonstrated exceptional performance in the simulation environment, achieving an accuracy of 96.4%, indicating strong convergence and reliability under ideal, controlled conditions. However, a performance drop was observed during real-world deployment, where the model achieved 86.7% accuracy. This gap reflects the inherent challenges in sim-to-real transfer, such as sensor noise, environmental variability, and domain gap. A comparative analysis of source and target domains revealed that the model maintained a consistent accuracy of 86.8% on the source domain, which is in line with the real-world deployment accuracy. The accuracy on the target domain, however, was slightly lower at 82.3%, suggesting domain adaptation challenges that could be attributed to distribution shifts or insufficient domain-specific fine-tuning. Overall, the performance metrics confirm the robustness of the model in simulation and its satisfactory generalization in real-world and cross-domain settings. These results also underscore the importance of enhancing domain adaptation techniques to bridge the remaining performance gap in target scenarios.

4.5. Analysis

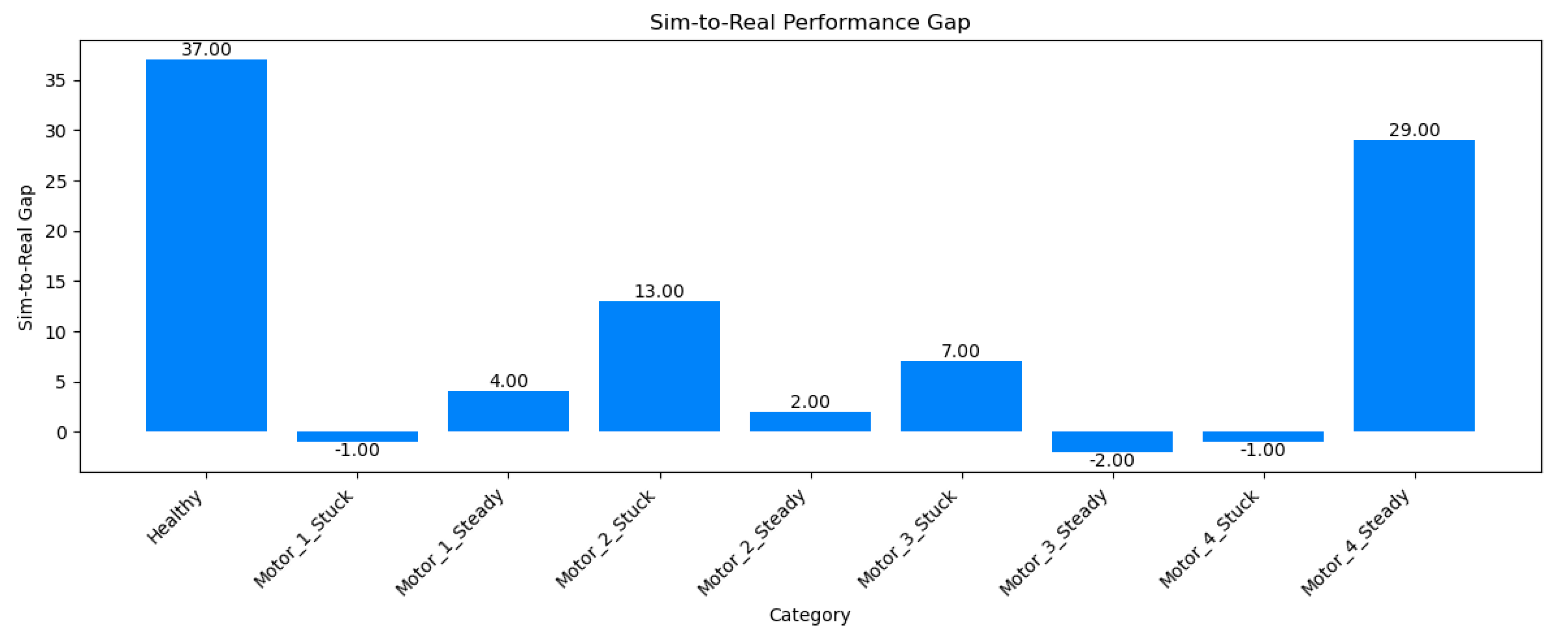
4.5.1. Sim-to-Real Gap

The TTN reduces the sim-to-real gap to 9.44% (96.11% simulation vs. 86.67% real), nearly halving the original DANN’s gap (19.07%). This improvement is attributed to:

−

Temporal Modeling: Bidirectional LSTM captures sequential patterns, aligning simulated and real trajectories effectively.

−

Domain Adaptation: Adversarial training ensures domain-invariant features, as seen in the domain adaptation accuracy plot (Figure 6).

−

Severity Prediction: Enhances feature robustness, improving generalization.

4.5.2. Key Improvements

−

Healthy State: The F1 score improves from 0.06 [12] to 0.63, addressing a major limitation, though a gap persists (0.37), as seen in the F1 score comparison chart (Figure 2).

−

Fault Categories: Most categories achieve F1 scores >0.85, with Motor_1_Stuck reaching 1.00, as confirmed by the confusion matrix (Figure 3).

−

Efficiency: Training time (2.52 seconds/epoch) is efficient, with stable convergence (loss curves chart, Figure 5).

−

Severity Prediction: Low MSE losses (0.0944 real test) enable accurate fault characterization.

4.5.3. Areas of Concern

−

Healthy State: The largest gap (0.37) suggests simulation inaccuracies, as seen in the F1 score comparison (Figure 2) and confusion matrix (Figure 3).

−

Motor_4_Steady_state_error: A gap of 0.29 indicates challenges in simulation fidelity, also evident in the visualizations.

−

Small Real Dataset: The 90-sample real test set limits robustness, necessitating larger datasets for validation.

4.6. Discussion

The TTN significantly outperforms baseline models, achieving a real test accuracy of 86.67% and reducing the sim-to-real gap to 9.44%. The qualitative analysis charts provide deeper insights: the confusion matrix (Figure 3) highlights classification strengths (e.g., Motor_1_Stuck) and weaknesses (e.g., Healthy state), the F1 score comparison (Figure 2) visualizes per-category gaps, the loss curves (Figure 5) confirm stable training, and the domain adaptation accuracy (Figure 7) validates effective domain alignment. Compared to the original DANN (80.22% real test accuracy), the proposed framework offers a 6.45% accuracy improvement, addressing key limitations like the Healthy state’s poor performance. However, persistent gaps in certain categories suggest opportunities for refining the digital twin model or exploring advanced temporal modeling (e.g., attention mechanisms). The framework’s efficiency and robust performance make it a promising solution for predictive maintenance in robotics.

5. Conclusions and Future Directions

5.1. Conclusions

This study introduced the temporal-enhanced DANN framework, integrating bidirectional LSTM layers into a DANN to address the sim-to-real gap in fault diagnosis for robotics digital twin systems. The experimental results demonstrate the framework’s effectiveness and practical utility for predictive maintenance. TTN achieved a real test accuracy of 86.67% ± 0.62%, outperforming the original DANN (80.22% ± 0.85%) by 6.45% and significantly reducing the sim-to-real gap to 9.44% compared to 19.07% for the original DANN. This improvement is attributed to the incorporation of temporal modeling, which effectively captures sequential patterns in time-series data, which enhances feature robustness through joint optimization of fault classification and severity prediction.

Despite these advancements, challenges remain. The Healthy state and Motor_4_Steady_state_error exhibited the largest sim-to-real gaps (0.37 and 0.29, respectively). Additionally, the small real-world dataset (90 samples) limits the model’s robustness. In summary, TTN offers a robust solution for fault diagnosis in robotics digital twin systems, achieving high accuracy, effective domain adaptation, and reliable severity prediction. Its improvements over the original DANN and other baselines position it as a promising tool for predictive maintenance, addressing key limitations in prior work while highlighting areas for further refinement.

5.2. Future Directions

Building on the findings and limitations identified in this study, several future directions are proposed to enhance the TTN framework and its applicability in real-world scenarios:

• Improving Simulation Fidelity: The significant sim-to-real gaps for the Healthy state and Motor_4_Steady_state_error suggest that the digital twin model requires refinement. Future work should focus on enhancing the simulation’s ability to capture normal operation and complex fault dynamics, potentially by incorporating more realistic noise models [37], environmental variations [38], or advanced physics-based simulations [39]. Techniques like generative adversarial networks (GANs) [40] could be explored to synthesize more representative simulated data.
• Expanding the Real-World Dataset: The limited size of the real-world dataset (90 samples) constrains the model’s generalizability and robustness. Future research should prioritize collecting a larger and more diverse real-world dataset [41], covering a broader range of operating conditions and fault severities. This would enable more comprehensive training and evaluation, potentially reducing the sim-to-real gap further and improving performance on challenging categories.
• Advanced Temporal Modeling: While the bidirectional LSTM improved temporal modeling, categories like Motor_4_Steady_state_error showed slower convergence, as seen in the per-category accuracy trends chart. Future work could explore alternative architectures, such as attention mechanisms or temporal transformers [42], to better capture long-range dependencies and complex temporal patterns in time-series data [43]. These approaches may enhance the model’s ability to generalize across domains.
• Multi-Modal Data Integration: The current framework relies solely on trajectory and residual data. Integrating multi-modal data [44], such as vibration signals, thermal imaging, or acoustic data, could provide a more holistic view of the robot’s health, potentially improving fault diagnosis accuracy and severity prediction [45]. This would require extending the TTN to handle heterogeneous data sources, possibly through multi-branch architectures.
• Explainability and Interpretability: While the qualitative charts provide insights into the model’s behavior, future work should incorporate explainability techniques, such as SHAP (SHapley Additive exPlanations) [46] or attention visualization [47], to better understand the features driving the model’s predictions. This would enhance trust in the system, particularly for safety-critical applications like robotics fault diagnosis.

These directions aim to address the identified limitations while leveraging the strengths of the TTN framework, paving the way for more robust, generalizable, and practical fault diagnosis solutions in robotics digital twin systems.

6. Declarations

• Ethics approval: N/A
• Consent for Publishing: YES
• Availability of data: N/A